The Statistical Similarity of Repeating and Non-Repeating Fast Radio Bursts
Abstract
1. Introduction
2. The Statistical Properties of Repeating FRBs
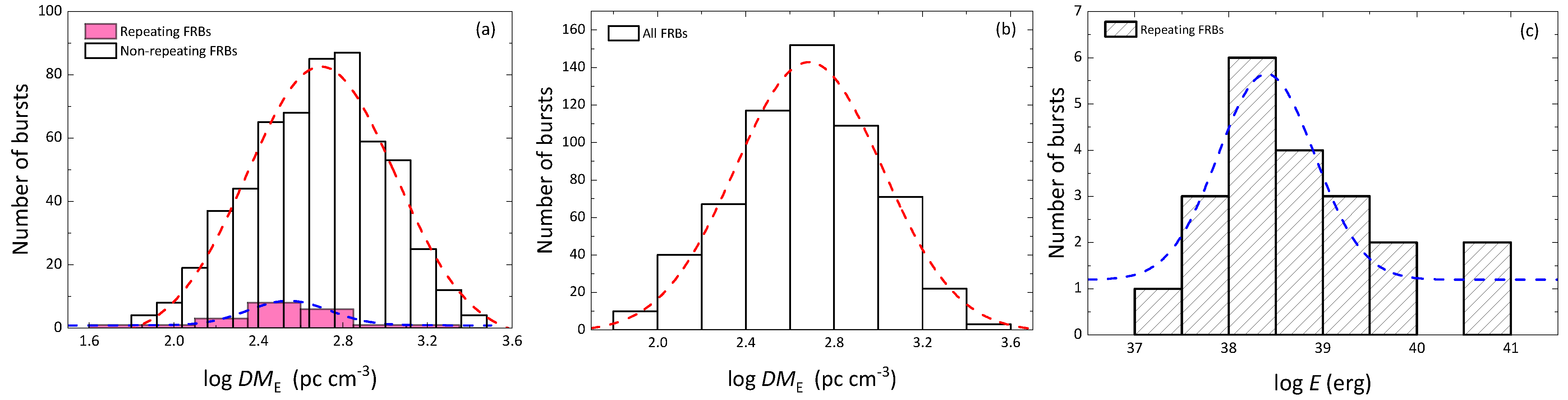
2.1. Distributions of Extra-Galactic Dispersion Measure and Total Energy
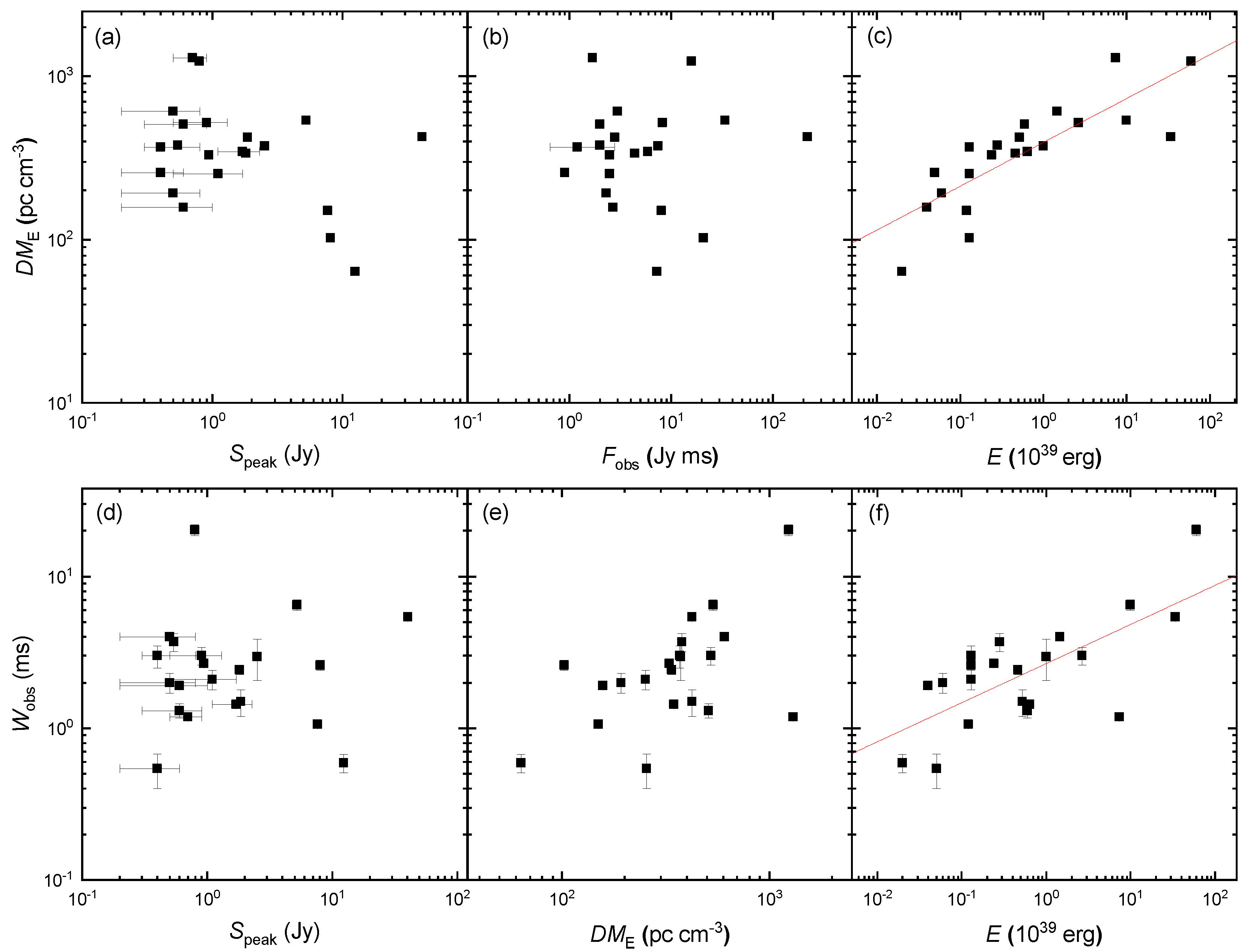
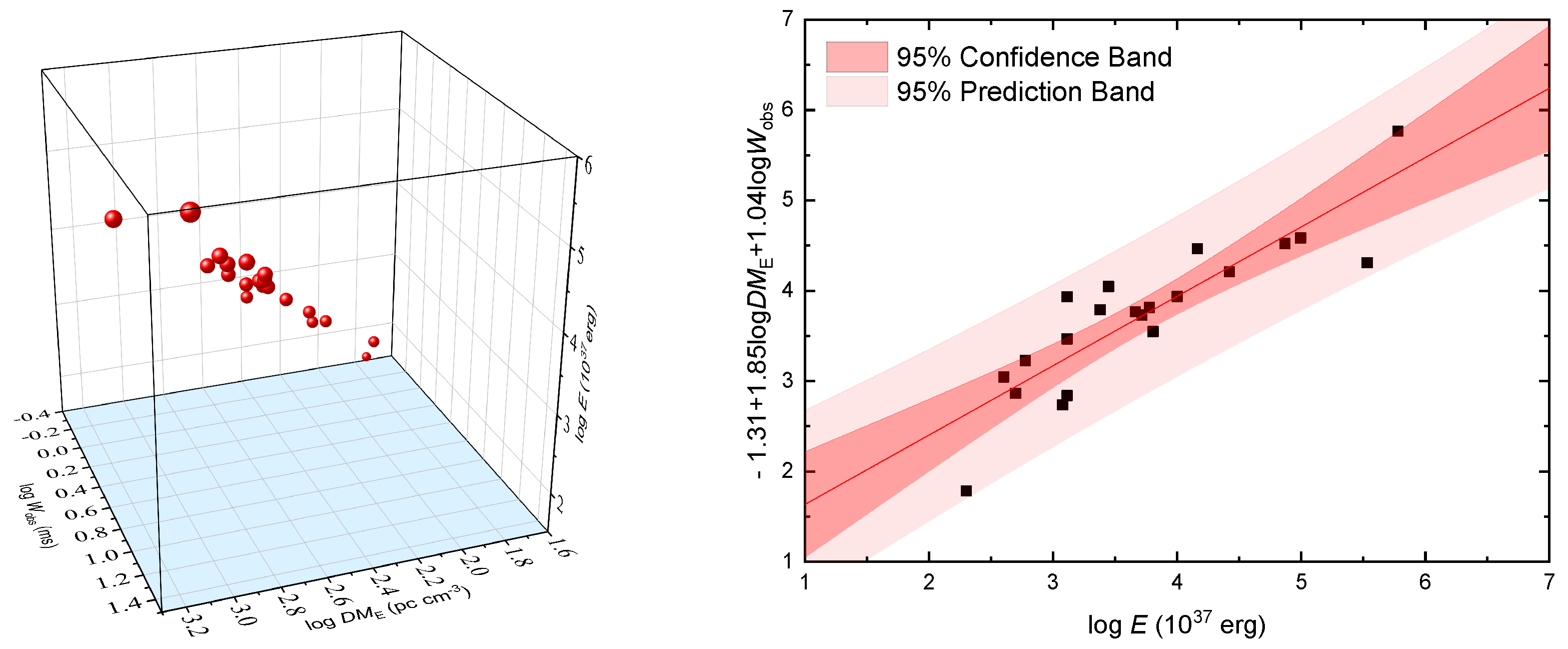
2.2. Correlations between Some Characteristic Parameters
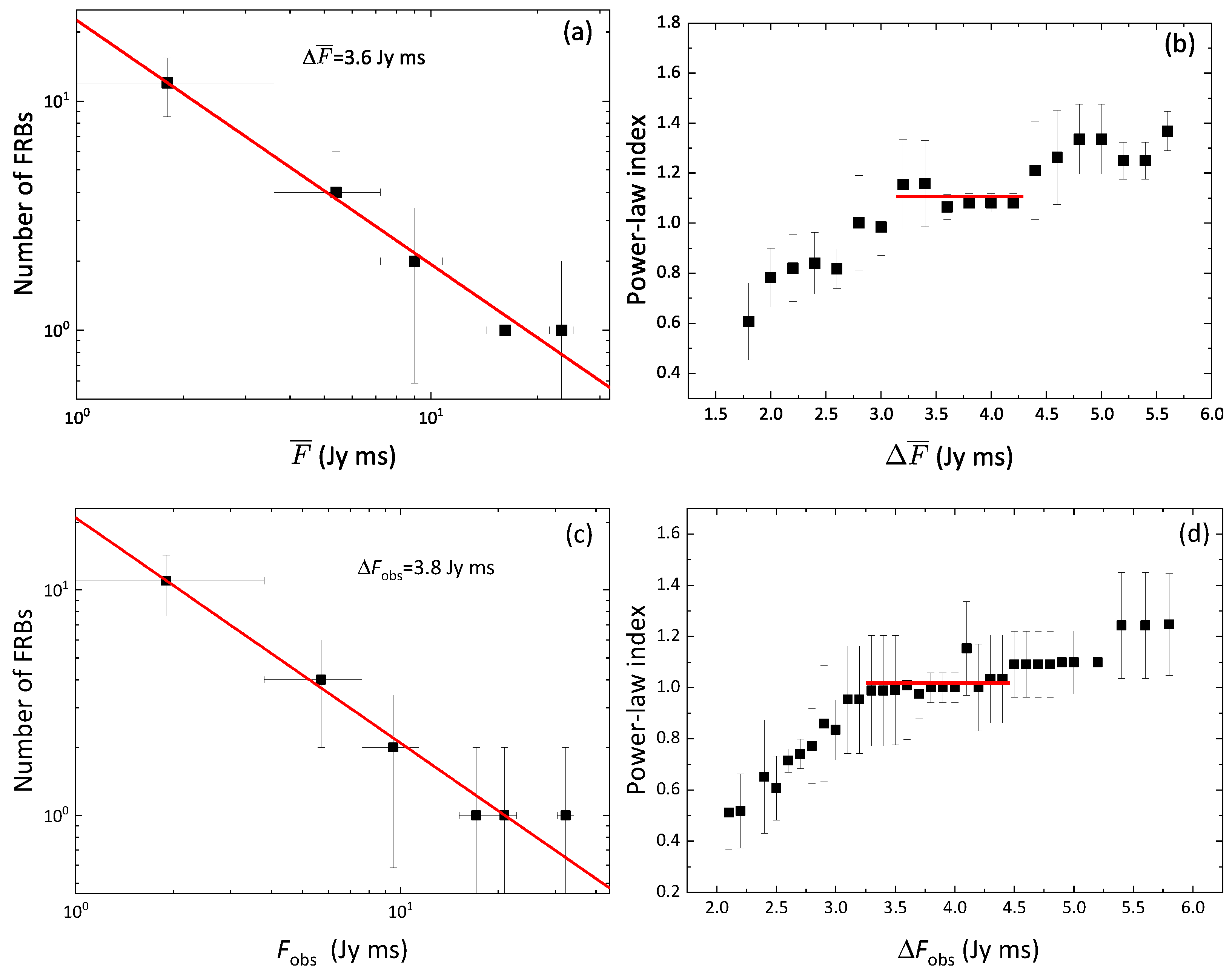
3. Apparent Intensity Distribution Function of Repeating FRBs
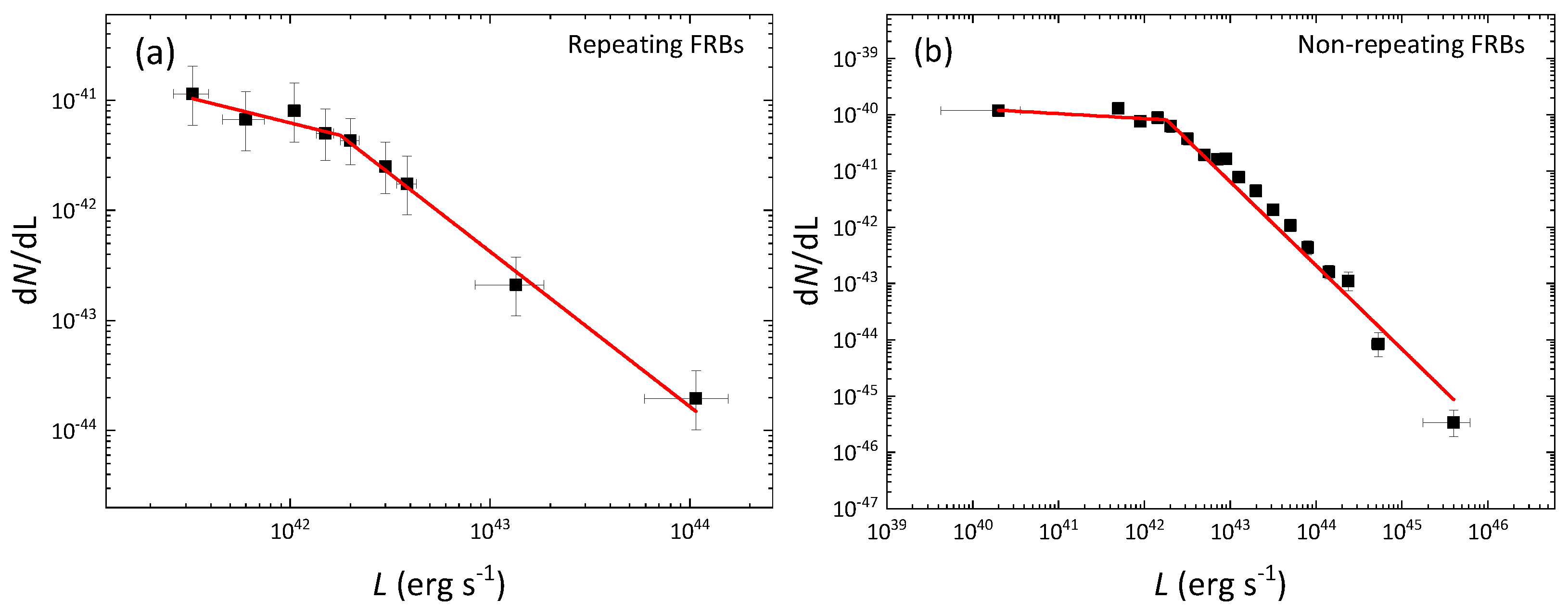
4. Differential Bolometric Luminosity Distributions
5. Conclusions and Discussion
- The extra-Galactic dispersion measures of non-repeating and repeating FRBs were found to be log-normally distributed with mean values of and 349.1 , respectively. The M–W–W test showed that the is drawn from a different distribution.
- It was found that the total radio energies of repeating FRBs are log-normally distributed with a mean value of ergs (1.03 dex), which is smaller than to that of non-repeating FRBs, which is consistent with the conclusion in [5]. Surprisingly, the bimodal energy distribution discovered in FRB 20121102A by Li et al. [18] with FAST was not recovered in our repeating FRB sample any more.
- We statistically analyzed the relationships among , , , E and , and found that most correlations between them are similar to those of non-repeaters given by Li et al. [80], except that the relation of repeaters is tighter. The statistical results hint that the spatial distribution and the local environments of two samples of FRBs may be different, although more samples are needed to verify our argument, as noted by CHIME/FRB Collaboration et al. [55] and Fonseca et al. [74].
- We constructed a three-parameter relation to be , indicating that longer FRBs usually have larger extra-galactic dispersion measures and more energy releases, which supports the early findings by Li et al. [5], no matter whether a FRB is repeating or not.
- We assume that FRBs can be considered as standard candles homogeneously in a flat Euclidean space, with an IDF of (or ), where a should be theoretically 2.5. Using the averaged fluence as a characteristic quantity, we built the IDF of repeating FRBs as . Likewise, using the observed fluence as a statistical indicator, we obtained the IDF as . The power-law index () of IDF deviates from the theoretical value of 2.5 in a flat Euclidean space, and shows that the repeating FRBs may be not uniformly distributed. Assuming the averaged minimum fluence as the threshold, we predicted the detection rate of repeaters to be about sky day or sky day; that is slightly lower in contrast with those non-repeating ones.
- Finally, we constructed and compared the luminosity functions of repeating and non-repeating FRBs. Interestingly, we found that the luminosity functions for both kinds of FRBs can be well characterized by a broken power-law relation; their power-law indices at their luminous ends are equal to , despite the discrepancy at their less-luminous ends.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| TNS Name | (MHz) | DM (pc cm−3) | (pc cm−3) | (pc cm−3) | (Jy ms) | z | (Gpc) | (erg s−1) |
|---|---|---|---|---|---|---|---|---|
| FRBCAT sample | ||||||||
| FRB 20010125A | 1372.5 | 790.30 | 110.00 | 680.30 | 0.54 | 0.57 | 3.42 | 8.91 |
| FRB 20010305A | 1374 | 350.00 | 36.00 | 314.00 | 4.20 | 0.30 | 1.60 | 1.62 |
| FRB 20010312A | 1374 | 1187.00 | 51.00 | 1136.00 | 0.25 | 1.40 | 10.29 | 3.25 |
| FRB 20010621A | 1374 | 745.00 | 523.00 | 225.00 | 0.53 | 0.19 | 0.96 | 7.50 |
| FRB 20010724A | 1374 | 375.00 | 44.58 | 330.42 | 30.00 | 0.28 | 1.48 | 9.94 |
| FRB 20090625A | 1352 | 899.55 | 31.69 | 867.86 | 1.15 | 0.72 | 4.54 | 3.20 |
| FRB 20110214A | 1352 | 168.90 | 31.10 | 137.80 | 27.00 | 0.14 | 0.68 | 1.95 |
| FRB 20110220A | 1352 | 944.38 | 34.77 | 909.61 | 1.30 | 0.76 | 4.85 | 4.09 |
| FRB 20110523A | 800 | 623.30 | 43.52 | 579.78 | 0.60 | 0.48 | 2.78 | 3.89 |
| FRB 20110626A | 1352 | 723.00 | 47.46 | 675.54 | 0.63 | 0.56 | 3.34 | 9.83 |
| FRB 20110703A | 1352 | 1103.60 | 32.33 | 1071.27 | 0.50 | 0.89 | 5.88 | 2.27 |
| FRB 20120127A | 1352 | 553.30 | 31.82 | 521.48 | 0.62 | 0.43 | 2.44 | 5.29 |
| FRB 20121002A | 1352 | 1629.18 | 74.27 | 1554.91 | 0.76 | 1.30 | 9.39 | 8.21 |
| FRB 20121029A | 111 | 732.00 | 71.00 | 661.00 | 0.34 | 0.55 | 3.27 | 4.18 |
| FRB 20130626A | 1352 | 952.40 | 66.87 | 885.53 | 0.74 | 0.74 | 4.69 | 2.19 |
| FRB 20130628A | 1352 | 469.88 | 52.58 | 417.30 | 1.91 | 0.35 | 1.91 | 1.02 |
| FRB 20130729A | 1352 | 861.00 | 31.00 | 830.00 | 0.22 | 0.69 | 4.31 | 5.54 |
| FRB 20131030A | 111 | 203.00 | 64.40 | 138.60 | 0.24 | 0.12 | 0.58 | 1.03 |
| FRB 20131104A | 1352 | 779.00 | 71.10 | 707.90 | 1.16 | 0.59 | 3.56 | 2.04 |
| FRB 20140212A | 111 | 910.00 | 49.80 | 860.20 | 0.26 | 0.72 | 4.54 | 5.93 |
| FRB 20140514A | 1352 | 562.70 | 34.90 | 527.80 | 0.47 | 0.44 | 2.51 | 4.24 |
| FRB 20141113A | 1375 | 400.30 | 188.00 | 212.30 | 0.04 | 0.15 | 0.74 | 3.32 |
| FRB 20141216A | 111 | 545.00 | 69.50 | 475.50 | 0.23 | 0.40 | 2.24 | 1.37 |
| FRB 20150215A | 1352 | 1105.60 | 427.20 | 678.40 | 0.70 | 0.57 | 3.42 | 1.14 |
| FRB 20150418A | 1352 | 776.20 | 188.50 | 587.70 | 2.20 | 0.49 | 2.85 | 2.53 |
| FRB 20150610A | 1352 | 1593.90 | 122.00 | 1471.90 | 0.70 | 1.20 | 8.51 | 6.30 |
| FRB 20150807A | 1352 | 266.50 | 36.90 | 229.60 | 128.00 | 0.19 | 0.96 | 1.78 |
| FRB 20151018A | 111 | 570.00 | 275.00 | 295.00 | 1.40 | 0.24 | 1.24 | 2.67 |
| FRB 20151125A | 2.5 | 273.00 | 50.20 | 222.80 | 0.54 | 0.19 | 0.96 | 1.39 |
| FRB 20151206A | 1352 | 1909.80 | 160.00 | 1749.80 | 0.30 | 1.50 | 11.20 | 4.48 |
| FRB 20151230A | 1352 | 960.40 | 38.00 | 922.40 | 0.42 | 0.80 | 5.16 | 1.49 |
| FRB 20160102A | 1352 | 2596.10 | 13.00 | 2583.10 | 0.50 | 2.10 | 16.91 | 1.59 |
| FRB 20160206A | 111 | 1262.00 | 69.10 | 1192.90 | 0.26 | 0.99 | 6.71 | 1.24 |
| FRB 20160317A | 843 | 1165.00 | 319.60 | 845.40 | 3.00 | 0.70 | 4.38 | 4.87 |
| FRB 20160410A | 843 | 278.00 | 57.70 | 220.30 | 7.00 | 0.18 | 0.90 | 5.41 |
| FRB 20160608A | 843 | 682.00 | 238.30 | 443.70 | 4.30 | 0.37 | 2.04 | 1.63 |
| FRB 20160920A | 111 | 1767.00 | 250.00 | 1517.00 | 0.22 | 1.20 | 8.51 | 1.63 |
| FRB 20161202A | 111 | 291.00 | 69.80 | 221.20 | 0.29 | 0.18 | 0.90 | 2.95 |
| FRB 20170107A | 1320 | 609.50 | 35.00 | 574.50 | 24.10 | 0.48 | 2.78 | 2.58 |
| FRB 20170416A | 1320 | 523.20 | 40.00 | 483.20 | 19.40 | 0.40 | 2.24 | 1.37 |
| FRB 20170428A | 1320 | 991.70 | 40.00 | 951.70 | 7.70 | 0.79 | 5.08 | 2.59 |
| FRB 20170606A | 111 | 247.00 | 250.00 | (3.00) | 0.54 | 0.06 | 0.26 | 4.87 |
| FRB 20170707A | 1297 | 235.20 | 36.00 | 199.20 | 14.80 | 0.17 | 0.84 | 1.56 |
| FRB 20170712A | 1297 | 312.79 | 38.00 | 274.79 | 37.80 | 0.23 | 1.18 | 7.66 |
| FRB 20170827A | 835 | 176.80 | 37.00 | 139.80 | 60.00 | 0.12 | 0.58 | 1.93 |
| FRB 20170906A | 1297 | 390.30 | 39.00 | 351.30 | 29.60 | 0.29 | 1.54 | 1.00 |
| FRB 20170922A | 835 | 1111.00 | 45.00 | 1066.00 | 5.19 | 1.20 | 8.51 | 2.88 |
| FRB 20171003A | 1297 | 463.20 | 40.00 | 423.20 | 40.50 | 0.35 | 1.91 | 2.08 |
| FRB 20171004A | 1297 | 304.00 | 38.00 | 266.00 | 22.00 | 0.22 | 1.13 | 4.05 |
| FRB 20171019A | 1297 | 114.10 | 38.00 | 76.10 | 117.60 | 0.06 | 0.28 | 1.38 |
| FRB 20171020A | 1297 | 618.50 | 36.00 | 582.50 | 19.60 | 0.49 | 2.85 | 2.16 |
| FRB 20171116A | 1352 | 1457.40 | 13.00 | 1444.40 | 1.48 | 1.57 | 11.85 | 2.45 |
| FRB 20171209A | 1297 | 158.60 | 36.00 | 122.60 | 88.60 | 0.10 | 0.48 | 3.01 |
| FRB 20171213A | 1297 | 203.10 | 37.00 | 166.10 | 21.00 | 0.14 | 0.68 | 1.45 |
| FRB 20171216A | 1297 | 715.70 | 38.00 | 677.70 | 128.10 | 0.56 | 3.34 | 1.92 |
| FRB 20180110A | 1297 | 402.70 | 36.00 | 366.70 | 40.70 | 0.31 | 1.66 | 1.60 |
| FRB 20180119A | 1297 | 441.40 | 32.00 | 409.40 | 17.50 | 0.34 | 1.85 | 8.44 |
| FRB 20180128B | 1297 | 495.90 | 40.00 | 455.90 | 28.70 | 0.38 | 2.11 | 1.78 |
| FRB 20180130A | 1297 | 343.50 | 39.00 | 304.50 | 23.10 | 0.25 | 1.30 | 5.62 |
| FRB 20180131A | 1297 | 657.70 | 40.00 | 617.70 | 22.20 | 0.51 | 2.99 | 2.68 |
| FRB 20180212A | 1297 | 167.50 | 33.00 | 134.50 | 53.00 | 0.11 | 0.53 | 2.20 |
| FRB 20180309A | 1352 | 263.42 | 44.69 | 218.73 | 27.60 | 0.19 | 0.96 | 3.84 |
| FRB 20180311A | 1352 | 1570.90 | 45.20 | 1530.40 | 0.20 | 2.00 | 15.94 | 5.70 |
| FRB 20180315A | 1297 | 479.00 | 36.00 | 443.00 | 23.30 | 0.37 | 2.04 | 1.36 |
| FRB 20180321A | 111 | 594.00 | 70.00 | 524.00 | 0.54 | 0.44 | 2.51 | 3.99 |
| FRB 20180324A | 1297 | 431.00 | 70.00 | 361.00 | 16.50 | 0.30 | 1.60 | 6.02 |
| FRB 20180417A | 1272.5 | 474.80 | 26.15 | 448.65 | 21.80 | 0.37 | 2.04 | 1.25 |
| FRB 20180430A | 1297 | 264.10 | 165.44 | 98.66 | 147.50 | 0.08 | 0.38 | 3.14 |
| FRB 20180515A | 1320 | 355.20 | 33.00 | 322.20 | 24.20 | 0.20 | 1.01 | 3.68 |
| FRB 20180525A | 1297 | 388.10 | 31.00 | 357.10 | 78.90 | 0.30 | 1.60 | 2.88 |
| FRB 20180528A | 835 | 899.30 | 69.00 | 830.30 | 15.75 | 0.90 | 5.97 | 4.52 |
| FRB 20180714A | 1352 | 1467.92 | 257.00 | 1212.87 | 5.00 | 1.60 | 12.12 | 8.65 |
| FRB 20180725A | 400 | 715.98 | 71.00 | 644.98 | 38.71 | 0.54 | 3.20 | 1.64 |
| FRB 20180727A | 600 | 642.07 | 21.00 | 621.07 | 17.95 | 0.52 | 3.06 | 1.05 |
| FRB 20180729B | 600 | 317.37 | 95.00 | 222.37 | 112.50 | 0.19 | 0.96 | 6.96 |
| FRB 20180729A | 600 | 109.61 | 31.00 | 78.61 | 283.33 | 0.07 | 0.33 | 2.11 |
| FRB 20180730A | 600 | 849.05 | 57.00 | 792.05 | 119.05 | 0.66 | 4.08 | 1.20 |
| FRB 20180801A | 600 | 656.20 | 90.00 | 566.20 | 54.90 | 0.47 | 2.71 | 2.55 |
| FRB 20180806A | 600 | 739.98 | 41.00 | 698.98 | 34.78 | 0.58 | 3.49 | 2.61 |
| FRB 20180810A | 600 | 414.95 | 104.00 | 310.95 | 40.74 | 0.26 | 1.36 | 5.00 |
| FRB 20180810B | 600 | 169.13 | 47.00 | 122.13 | 60.71 | 0.10 | 0.48 | 9.54 |
| FRB 20180812A | 600 | 802.57 | 83.00 | 719.57 | 14.40 | 0.60 | 3.63 | 1.17 |
| FRB 20180814B | 600 | 238.32 | 41.00 | 197.32 | 138.89 | 0.16 | 0.79 | 5.92 |
| FRB 20180817A | 600 | 1006.84 | 28.00 | 978.84 | 75.68 | 0.82 | 5.32 | 1.26 |
| FRB 20180924B | 1320 | 361.42 | 40.50 | 320.92 | 12.30 | 0.34 | 1.85 | 6.04 |
| FRB 20181016A | 835 | 1982.80 | 90.00 | 1892.80 | 10.19 | 2.20 | 17.90 | 2.21 |
| FRB 20181017C | 835 | 239.97 | 38.00 | 201.97 | 161.00 | 0.20 | 1.01 | 1.55 |
| FRB 20181112A | 1272.5 | 589.27 | 102.00 | 487.27 | 12.38 | 0.41 | 2.31 | 8.93 |
| FRB 20181123B | 1250 | 1812.00 | 149.50 | 1662.50 | 0.07 | 1.39 | 10.20 | 7.56 |
| FRB 20181228D | 835 | 354.20 | 58.00 | 296.20 | 19.23 | 0.30 | 1.60 | 4.51 |
| FRB 20190102C | 1320 | 363.60 | 57.30 | 306.30 | 8.24 | 0.26 | 1.36 | 2.23 |
| FRB 20190523A | 1411 | 760.80 | 37.00 | 723.80 | 666.67 | 0.60 | 3.63 | 1.27 |
| FRB 20190608B | 1320 | 338.70 | 37.20 | 301.50 | 4.33 | 0.25 | 1.30 | 1.07 |
| FRB 20190611B | 1320 | 321.40 | 57.83 | 263.57 | 5.00 | 0.22 | 1.13 | 9.36 |
| FRB 20191108A | 1370 | 588.10 | 52.00 | 536.10 | 27.00 | 0.52 | 3.06 | 3.60 |
| FRB 20190614D | 1400 | 959.20 | 83.50 | 875.70 | 0.12 | 0.73 | 4.61 | 3.68 |
| FRB 20200125A | 350 | 179.47 | 25.00 | 154.47 | 0.37 | 0.17 | 0.84 | 1.04 |
| CHIME sample | ||||||||
| FRB20180725A | 600 | 715.81 | 71.61 | 644.20 | 1.70 | 0.54 | 3.18 | 1.07 |
| FRB20180727A | 600 | 642.13 | 21.23 | 620.90 | 0.58 | 0.52 | 3.04 | 3.35 |
| FRB20180729A | 600 | 109.59 | 30.79 | 78.80 | 11.70 | 0.07 | 0.30 | 7.65 |
| FRB20180729B | 600 | 317.22 | 94.02 | 223.20 | 0.92 | 0.19 | 0.93 | 5.43 |
| FRB20180730A | 600 | 848.90 | 59.20 | 789.70 | 5.20 | 0.66 | 4.07 | 5.22 |
| FRB20180801A | 600 | 655.73 | 90.13 | 565.60 | 1.11 | 0.47 | 2.72 | 5.18 |
| FRB20180806A | 600 | 739.95 | 40.65 | 699.30 | 1.90 | 0.58 | 3.51 | 1.44 |
| FRB20180810A | 600 | 414.88 | 104.68 | 310.20 | 1.10 | 0.26 | 1.35 | 1.33 |
| FRB20180810B | 600 | 169.14 | 45.84 | 123.30 | 5.20 | 0.10 | 0.49 | 8.65 |
| FRB20180812A | 600 | 802.45 | 80.35 | 722.10 | 0.93 | 0.60 | 3.65 | 7.59 |
| FRB20180814B | 600 | 238.35 | 41.15 | 197.20 | 3.40 | 0.16 | 0.81 | 1.54 |
| FRB20180817A | 600 | 1006.77 | 27.67 | 979.10 | 2.40 | 0.82 | 5.29 | 3.95 |
| FRB20180904A | 600 | 361.14 | 55.44 | 305.70 | 3.80 | 0.25 | 1.33 | 4.46 |
| FRB20180906A | 600 | 383.46 | 43.46 | 340.00 | 1.60 | 0.28 | 1.50 | 2.38 |
| FRB20180906B | 600 | 3038.06 | 31.36 | 3006.70 | 0.36 | 2.51 | 20.96 | 7.48 |
| FRB20180907A | 600 | 877.24 | 92.04 | 785.20 | 0.87 | 0.65 | 4.04 | 8.61 |
| FRB20180907B | 600 | 658.19 | 38.09 | 620.10 | 1.08 | 0.52 | 3.04 | 6.22 |
| FRB20180907C | 600 | 638.20 | 91.40 | 546.80 | 1.11 | 0.46 | 2.61 | 4.80 |
| FRB20180907D | 600 | 1447.10 | 56.00 | 1391.10 | 0.89 | 1.16 | 8.15 | 3.28 |
| FRB20180907E | 600 | 383.36 | 30.46 | 352.90 | 0.73 | 0.29 | 1.57 | 1.18 |
| FRB20180909A | 600 | 408.65 | 49.85 | 358.80 | 0.33 | 0.30 | 1.60 | 5.53 |
| FRB20180910A | 600 | 684.41 | 58.11 | 626.30 | 6.50 | 0.52 | 3.07 | 3.83 |
| FRB20180911A | 600 | 221.25 | 56.55 | 164.70 | 1.60 | 0.14 | 0.67 | 4.92 |
| FRB20180915A | 600 | 371.03 | 171.93 | 199.10 | 2.30 | 0.17 | 0.82 | 1.06 |
| FRB20180915B | 600 | 177.13 | 22.43 | 154.70 | 0.99 | 0.13 | 0.62 | 2.66 |
| FRB20180916A | 600 | 296.03 | 78.43 | 217.60 | 2.40 | 0.18 | 0.91 | 1.34 |
| FRB20180916C | 600 | 2252.87 | 73.87 | 2179.00 | 0.39 | 1.82 | 14.16 | 3.98 |
| FRB20180917B | 600 | 857.04 | 43.14 | 813.90 | 1.03 | 0.68 | 4.22 | 1.11 |
| FRB20180918A | 600 | 1453.99 | 79.99 | 1374.00 | 1.45 | 1.15 | 8.03 | 5.20 |
| FRB20180919B | 600 | 560.22 | 32.82 | 527.40 | 2.56 | 0.44 | 2.50 | 1.02 |
| FRB20180920A | 600 | 555.66 | 160.76 | 394.90 | 0.86 | 0.33 | 1.78 | 1.78 |
| FRB20180920B | 600 | 463.40 | 33.20 | 430.20 | 0.35 | 0.36 | 1.97 | 8.80 |
| FRB20180921A | 600 | 394.37 | 35.17 | 359.20 | 0.92 | 0.30 | 1.60 | 1.54 |
| FRB20180922A | 600 | 555.69 | 141.29 | 414.40 | 2.60 | 0.35 | 1.88 | 6.01 |
| FRB20180923A | 600 | 219.44 | 100.04 | 119.40 | 0.76 | 0.10 | 0.47 | 1.18 |
| FRB20180923C | 600 | 173.98 | 29.08 | 144.90 | 0.89 | 0.12 | 0.58 | 2.08 |
| FRB20180923D | 600 | 329.40 | 30.70 | 298.70 | 2.40 | 0.25 | 1.29 | 2.68 |
| FRB20180924A | 600 | 1116.55 | 69.25 | 1047.30 | 1.30 | 0.87 | 5.74 | 2.50 |
| FRB20180925A | 600 | 237.74 | 70.64 | 167.10 | 0.99 | 0.14 | 0.68 | 3.14 |
| FRB20180925B | 600 | 667.87 | 39.67 | 628.20 | 0.76 | 0.52 | 3.08 | 4.51 |
| FRB20180928A | 600 | 252.77 | 158.07 | 94.70 | 1.34 | 0.08 | 0.37 | 1.28 |
| FRB20181012B | 600 | 715.19 | 33.49 | 681.70 | 0.49 | 0.57 | 3.40 | 3.51 |
| FRB20181013A | 600 | 309.31 | 48.11 | 261.20 | 2.81 | 0.22 | 1.11 | 2.34 |
| FRB20181013B | 600 | 277.51 | 85.81 | 191.70 | 0.56 | 0.16 | 0.79 | 2.38 |
| FRB20181013C | 600 | 1005.77 | 38.57 | 967.20 | 0.44 | 0.81 | 5.21 | 7.04 |
| FRB20181013E | 600 | 345.30 | 80.80 | 264.50 | 0.62 | 0.22 | 1.13 | 5.30 |
| FRB20181014A | 600 | 1314.89 | 186.69 | 1128.20 | 0.99 | 0.94 | 6.30 | 2.26 |
| FRB20181014B | 600 | 887.97 | 102.57 | 785.40 | 0.65 | 0.65 | 4.04 | 6.44 |
| FRB20181014C | 600 | 752.17 | 59.87 | 692.30 | 0.57 | 0.58 | 3.47 | 4.22 |
| FRB20181014D | 600 | 377.13 | 30.03 | 347.10 | 8.40 | 0.29 | 1.54 | 1.31 |
| FRB20181015A | 600 | 568.82 | 46.52 | 522.30 | 1.51 | 0.44 | 2.47 | 5.88 |
| FRB20181017B | 600 | 307.37 | 43.67 | 263.70 | 1.06 | 0.22 | 1.12 | 9.00 |
| FRB20181018A | 600 | 1129.45 | 120.95 | 1008.50 | 0.49 | 0.84 | 5.48 | 8.63 |
| FRB20181018B | 600 | 293.87 | 113.17 | 180.70 | 5.10 | 0.15 | 0.74 | 1.91 |
| FRB20181018C | 600 | 411.19 | 146.19 | 265.00 | 2.40 | 0.22 | 1.13 | 2.06 |
| FRB20181019B | 600 | 725.18 | 159.78 | 565.40 | 0.72 | 0.47 | 2.72 | 3.36 |
| FRB20181019C | 600 | 501.64 | 39.24 | 462.40 | 1.16 | 0.39 | 2.14 | 3.43 |
| FRB20181020A | 600 | 1112.47 | 72.17 | 1040.30 | 0.80 | 0.87 | 5.70 | 1.51 |
| FRB20181022C | 600 | 528.47 | 49.87 | 478.60 | 0.91 | 0.40 | 2.23 | 2.91 |
| FRB20181022D | 600 | 514.33 | 20.13 | 494.20 | 2.90 | 0.41 | 2.32 | 9.97 |
| FRB20181022E | 600 | 285.99 | 21.79 | 264.20 | 0.69 | 0.22 | 1.13 | 5.88 |
| FRB20181025A | 600 | 592.56 | 61.66 | 530.90 | 1.52 | 0.44 | 2.52 | 6.14 |
| FRB20181027A | 600 | 727.74 | 64.04 | 663.70 | 4.90 | 0.55 | 3.29 | 3.30 |
| FRB20181030C | 600 | 668.76 | 73.06 | 595.70 | 1.60 | 0.50 | 2.89 | 8.41 |
| FRB20181030D | 600 | 289.44 | 123.54 | 165.90 | 2.74 | 0.14 | 0.67 | 8.55 |
| FRB20181030E | 600 | 159.69 | 49.89 | 109.80 | 2.00 | 0.09 | 0.43 | 2.61 |
| FRB20181101A | 600 | 1472.68 | 144.88 | 1327.80 | 0.50 | 1.11 | 7.70 | 1.66 |
| FRB20181102A | 600 | 414.46 | 155.66 | 258.80 | 1.48 | 0.22 | 1.10 | 1.21 |
| FRB20181104C | 600 | 580.82 | 105.32 | 475.50 | 9.70 | 0.40 | 2.21 | 3.05 |
| FRB20181115A | 600 | 981.61 | 40.01 | 941.60 | 0.44 | 0.78 | 5.04 | 6.62 |
| FRB20181116A | 600 | 355.43 | 37.13 | 318.30 | 4.00 | 0.27 | 1.39 | 5.13 |
| FRB20181116B | 600 | 409.88 | 36.38 | 373.50 | 0.74 | 0.31 | 1.67 | 1.36 |
| FRB20181117A | 600 | 959.28 | 38.08 | 921.20 | 0.61 | 0.77 | 4.91 | 8.72 |
| FRB20181117B | 600 | 538.20 | 65.00 | 473.20 | 3.60 | 0.39 | 2.20 | 1.12 |
| FRB20181117C | 600 | 1773.74 | 66.14 | 1707.60 | 1.57 | 1.42 | 10.50 | 9.24 |
| FRB20181118A | 600 | 557.41 | 31.51 | 525.90 | 4.30 | 0.44 | 2.49 | 1.70 |
| FRB20181118B | 600 | 422.28 | 53.08 | 369.20 | 0.78 | 0.31 | 1.65 | 1.39 |
| FRB20181119B | 600 | 609.10 | 442.30 | 166.80 | 4.50 | 0.14 | 0.68 | 1.42 |
| FRB20181119C | 600 | 284.96 | 44.66 | 240.30 | 2.80 | 0.20 | 1.01 | 1.94 |
| FRB20181119E | 600 | 1169.77 | 220.27 | 949.50 | 0.70 | 0.79 | 5.09 | 1.07 |
| FRB20181122A | 600 | 662.82 | 196.12 | 466.70 | 0.53 | 0.39 | 2.17 | 1.60 |
| FRB20181122B | 600 | 225.76 | 54.36 | 171.40 | 14.70 | 0.14 | 0.70 | 4.92 |
| FRB20181123A | 600 | 798.72 | 103.82 | 694.90 | 0.99 | 0.58 | 3.48 | 7.40 |
| FRB20181124A | 600 | 1108.53 | 34.43 | 1074.10 | 0.66 | 0.90 | 5.93 | 1.34 |
| FRB20181124B | 600 | 801.64 | 104.94 | 696.70 | 2.61 | 0.58 | 3.49 | 1.96 |
| FRB20181125A | 600 | 272.19 | 37.99 | 234.20 | 0.39 | 0.20 | 0.98 | 2.56 |
| FRB20181126A | 600 | 494.22 | 49.62 | 444.60 | 3.50 | 0.37 | 2.05 | 9.47 |
| FRB20181127A | 600 | 930.32 | 32.22 | 898.10 | 0.78 | 0.75 | 4.76 | 1.05 |
| FRB20181128B | 600 | 456.55 | 33.55 | 423.00 | 0.34 | 0.35 | 1.93 | 8.23 |
| FRB20181128C | 600 | 618.35 | 49.15 | 569.20 | 0.39 | 0.47 | 2.74 | 1.85 |
| FRB20181128D | 600 | 146.50 | 32.70 | 113.80 | 2.60 | 0.09 | 0.45 | 3.65 |
| FRB20181129A | 600 | 385.97 | 86.77 | 299.20 | 1.52 | 0.25 | 1.30 | 1.70 |
| FRB20181129B | 600 | 405.91 | 62.11 | 343.80 | 4.00 | 0.29 | 1.52 | 6.09 |
| FRB20181129C | 600 | 502.22 | 26.52 | 475.70 | 0.77 | 0.40 | 2.22 | 2.43 |
| FRB20181130A | 600 | 220.09 | 95.09 | 125.00 | 0.97 | 0.10 | 0.50 | 1.66 |
| FRB20181201A | 600 | 694.36 | 23.96 | 670.40 | 0.40 | 0.56 | 3.33 | 2.75 |
| FRB20181201B | 600 | 876.58 | 51.28 | 825.30 | 0.66 | 0.69 | 4.29 | 7.33 |
| FRB20181202A | 600 | 667.95 | 38.75 | 629.20 | 2.63 | 0.52 | 3.09 | 1.57 |
| FRB20181202B | 600 | 825.88 | 33.68 | 792.20 | 0.99 | 0.66 | 4.08 | 1.00 |
| FRB20181202C | 600 | 557.16 | 126.46 | 430.70 | 0.51 | 0.36 | 1.97 | 1.29 |
| FRB20181203A | 600 | 635.93 | 46.73 | 589.20 | 1.74 | 0.49 | 2.86 | 8.92 |
| FRB20181203B | 600 | 375.39 | 56.69 | 318.70 | 1.45 | 0.27 | 1.39 | 1.87 |
| FRB20181203C | 600 | 2444.57 | 37.47 | 2407.10 | 1.05 | 2.01 | 15.99 | 1.34 |
| FRB20181208A | 600 | 562.78 | 45.18 | 517.60 | 0.95 | 0.43 | 2.45 | 3.63 |
| FRB20181209A | 600 | 328.66 | 65.66 | 263.00 | 2.50 | 0.22 | 1.12 | 2.11 |
| FRB20181213A | 600 | 678.67 | 48.57 | 630.10 | 0.88 | 0.53 | 3.09 | 5.26 |
| FRB20181213B | 600 | 626.59 | 30.59 | 596.00 | 0.75 | 0.50 | 2.90 | 3.95 |
| FRB20181213C | 600 | 380.74 | 30.54 | 350.20 | 0.62 | 0.29 | 1.55 | 9.84 |
| FRB20181214A | 600 | 468.15 | 184.25 | 283.90 | 0.16 | 0.24 | 1.22 | 1.56 |
| FRB20181214B | 600 | 1120.75 | 42.05 | 1078.70 | 0.41 | 0.90 | 5.96 | 8.43 |
| FRB20181214C | 600 | 632.78 | 33.28 | 599.50 | 1.20 | 0.50 | 2.92 | 6.40 |
| FRB20181214D | 600 | 1177.32 | 26.02 | 1151.30 | 0.55 | 0.96 | 6.45 | 1.31 |
| FRB20181214F | 600 | 2105.76 | 40.26 | 2065.50 | 0.31 | 1.72 | 13.26 | 2.80 |
| FRB20181215A | 600 | 412.63 | 128.53 | 284.10 | 0.34 | 0.24 | 1.22 | 3.40 |
| FRB20181215B | 600 | 494.01 | 40.61 | 453.40 | 1.90 | 0.38 | 2.09 | 5.37 |
| FRB20181216A | 600 | 542.74 | 146.74 | 396.00 | 0.94 | 0.33 | 1.79 | 1.96 |
| FRB20181217A | 600 | 1177.17 | 69.77 | 1107.40 | 0.64 | 0.92 | 6.15 | 1.40 |
| FRB20181218A | 600 | 1874.41 | 147.21 | 1727.20 | 0.83 | 1.44 | 10.64 | 5.01 |
| FRB20181218B | 600 | 753.41 | 169.61 | 583.80 | 0.56 | 0.49 | 2.82 | 2.81 |
| FRB20181218C | 600 | 384.15 | 64.35 | 319.80 | 0.25 | 0.27 | 1.40 | 3.24 |
| FRB20181219B | 600 | 1952.17 | 37.27 | 1914.90 | 4.60 | 1.60 | 12.08 | 3.51 |
| FRB20181219C | 600 | 647.89 | 36.19 | 611.70 | 0.21 | 0.51 | 2.99 | 1.16 |
| FRB20181220A | 600 | 209.40 | 125.80 | 83.60 | 1.33 | 0.07 | 0.32 | 9.83 |
| FRB20181220B | 600 | 257.80 | 53.60 | 204.20 | 2.90 | 0.17 | 0.85 | 1.41 |
| FRB20181221A | 600 | 316.24 | 24.44 | 291.80 | 1.25 | 0.24 | 1.26 | 1.32 |
| FRB20181221B | 600 | 1395.02 | 61.92 | 1333.10 | 0.97 | 1.11 | 7.73 | 3.25 |
| FRB20181222B | 600 | 619.25 | 148.25 | 471.00 | 0.46 | 0.39 | 2.19 | 1.42 |
| FRB20181222C | 600 | 1104.89 | 46.39 | 1058.50 | 0.84 | 0.88 | 5.82 | 1.65 |
| FRB20181222D | 600 | 1417.11 | 31.21 | 1385.90 | 0.22 | 1.15 | 8.11 | 8.05 |
| FRB20181222E | 600 | 327.98 | 59.88 | 268.10 | 1.12 | 0.22 | 1.15 | 9.86 |
| FRB20181223B | 600 | 565.66 | 25.45 | 540.20 | 0.68 | 0.45 | 2.57 | 2.86 |
| FRB20181223C | 600 | 112.51 | 19.91 | 92.60 | 1.36 | 0.08 | 0.36 | 1.24 |
| FRB20181224A | 600 | 310.21 | 85.01 | 225.20 | 4.30 | 0.19 | 0.94 | 2.59 |
| FRB20181224B | 600 | 781.01 | 121.31 | 659.70 | 0.77 | 0.55 | 3.27 | 5.11 |
| FRB20181224C | 600 | 596.33 | 55.33 | 541.00 | 0.50 | 0.45 | 2.58 | 2.11 |
| FRB20181224D | 600 | 690.20 | 31.40 | 658.80 | 0.54 | 0.55 | 3.27 | 3.57 |
| FRB20181224E | 600 | 581.85 | 36.55 | 545.30 | 3.60 | 0.45 | 2.60 | 1.55 |
| FRB20181225B | 600 | 299.29 | 58.29 | 241.00 | 1.90 | 0.20 | 1.02 | 1.33 |
| FRB20181226B | 600 | 287.04 | 27.74 | 259.30 | 8.90 | 0.22 | 1.10 | 7.28 |
| FRB20181226C | 600 | 409.02 | 94.02 | 315.00 | 0.88 | 0.26 | 1.37 | 1.10 |
| FRB20181226D | 600 | 385.38 | 64.98 | 320.40 | 1.89 | 0.27 | 1.40 | 2.46 |
| FRB20181226E | 600 | 308.76 | 68.86 | 239.90 | 0.48 | 0.20 | 1.01 | 3.31 |
| FRB20181227A | 600 | 791.21 | 89.01 | 702.20 | 0.93 | 0.59 | 3.53 | 7.12 |
| FRB20181228A | 600 | 748.68 | 34.18 | 714.50 | 1.16 | 0.60 | 3.60 | 9.24 |
| FRB20181228B | 600 | 568.65 | 39.95 | 528.70 | 0.40 | 0.44 | 2.51 | 1.60 |
| FRB20181228C | 600 | 510.70 | 45.60 | 465.10 | 0.45 | 0.39 | 2.16 | 1.35 |
| FRB20181229A | 600 | 955.57 | 42.97 | 912.60 | 1.18 | 0.76 | 4.85 | 1.65 |
| FRB20181229B | 600 | 389.05 | 29.35 | 359.70 | 0.42 | 0.30 | 1.60 | 7.07 |
| FRB20181230A | 600 | 769.61 | 68.41 | 701.20 | 0.94 | 0.58 | 3.52 | 7.17 |
| FRB20181230B | 600 | 1137.36 | 84.96 | 1052.40 | 0.88 | 0.88 | 5.78 | 1.71 |
| FRB20181230C | 600 | 1037.19 | 36.89 | 1000.30 | 0.89 | 0.83 | 5.43 | 1.54 |
| FRB20181230D | 600 | 223.97 | 40.57 | 183.40 | 1.39 | 0.15 | 0.75 | 5.37 |
| FRB20181230E | 600 | 1041.71 | 54.51 | 987.20 | 1.32 | 0.82 | 5.34 | 2.21 |
| FRB20181231A | 600 | 1376.73 | 43.03 | 1333.70 | 1.09 | 1.11 | 7.74 | 3.65 |
| FRB20181231B | 600 | 197.17 | 46.87 | 150.30 | 0.89 | 0.13 | 0.61 | 2.25 |
| FRB20181231C | 600 | 556.09 | 35.49 | 520.60 | 0.68 | 0.43 | 2.46 | 2.63 |
| FRB20190101A | 600 | 854.61 | 24.31 | 830.30 | 0.60 | 0.69 | 4.32 | 6.75 |
| FRB20190101B | 600 | 1323.91 | 234.01 | 1089.90 | 1.02 | 0.91 | 6.03 | 2.15 |
| FRB20190102A | 600 | 699.17 | 43.57 | 655.60 | 1.12 | 0.55 | 3.25 | 7.33 |
| FRB20190102B | 600 | 367.16 | 41.06 | 326.10 | 1.71 | 0.27 | 1.43 | 2.32 |
| FRB20190103B | 600 | 541.13 | 187.13 | 354.00 | 0.68 | 0.30 | 1.57 | 1.10 |
| FRB20190103C | 600 | 1349.13 | 155.53 | 1193.60 | 2.30 | 0.99 | 6.75 | 5.97 |
| FRB20190103D | 600 | 1913.55 | 33.25 | 1880.30 | 0.45 | 1.57 | 11.82 | 3.29 |
| FRB20190103E | 600 | 736.25 | 45.65 | 690.60 | 0.46 | 0.58 | 3.46 | 3.39 |
| FRB20190104A | 600 | 549.43 | 151.53 | 397.90 | 1.45 | 0.33 | 1.80 | 3.06 |
| FRB20190104B | 600 | 530.14 | 49.84 | 480.30 | 2.70 | 0.40 | 2.24 | 8.70 |
| FRB20190105A | 600 | 383.55 | 46.35 | 337.20 | 0.60 | 0.28 | 1.49 | 8.75 |
| FRB20190106A | 600 | 340.06 | 88.86 | 251.20 | 0.27 | 0.21 | 1.06 | 2.06 |
| FRB20190106B | 600 | 316.59 | 141.69 | 174.90 | 1.70 | 0.15 | 0.71 | 5.94 |
| FRB20190107A | 600 | 849.19 | 39.89 | 809.30 | 0.49 | 0.67 | 4.19 | 5.20 |
| FRB20190107B | 600 | 166.09 | 69.99 | 96.10 | 2.80 | 0.08 | 0.38 | 2.76 |
| FRB20190109A | 600 | 324.60 | 147.70 | 176.90 | 1.19 | 0.15 | 0.72 | 4.26 |
| FRB20190109B | 600 | 175.17 | 68.27 | 106.90 | 1.20 | 0.09 | 0.42 | 1.48 |
| FRB20190110A | 600 | 472.75 | 188.55 | 284.20 | 1.54 | 0.24 | 1.22 | 1.54 |
| FRB20190110B | 600 | 486.12 | 45.52 | 440.60 | 0.47 | 0.37 | 2.02 | 1.25 |
| FRB20190110C | 600 | 221.96 | 35.66 | 186.30 | 0.64 | 0.16 | 0.76 | 2.56 |
| FRB20190111A | 600 | 171.97 | 21.47 | 150.50 | 3.60 | 0.13 | 0.61 | 9.13 |
| FRB20190111B | 600 | 1336.93 | 65.13 | 1271.80 | 0.32 | 1.06 | 7.30 | 9.61 |
| FRB20190112A | 600 | 425.85 | 42.05 | 383.80 | 1.40 | 0.32 | 1.72 | 2.72 |
| FRB20190113A | 600 | 428.92 | 178.92 | 250.00 | 1.30 | 0.21 | 1.06 | 9.82 |
| FRB20190114A | 600 | 887.39 | 38.09 | 849.30 | 0.55 | 0.71 | 4.44 | 6.52 |
| FRB20190115A | 600 | 1021.68 | 186.38 | 835.30 | 0.46 | 0.70 | 4.35 | 5.25 |
| FRB20190115B | 600 | 748.29 | 63.79 | 684.50 | 1.45 | 0.57 | 3.42 | 1.05 |
| FRB20190116C | 600 | 629.28 | 41.88 | 587.40 | 28.00 | 0.49 | 2.85 | 1.42 |
| FRB20190116D | 600 | 1164.03 | 78.53 | 1085.50 | 0.51 | 0.90 | 6.00 | 1.06 |
| FRB20190116E | 600 | 1491.00 | 128.40 | 1362.60 | 0.46 | 1.14 | 7.95 | 1.62 |
| FRB20190116F | 600 | 316.92 | 46.82 | 270.10 | 0.49 | 0.23 | 1.15 | 4.38 |
| FRB20190117C | 600 | 865.90 | 53.30 | 812.60 | 0.42 | 0.68 | 4.21 | 4.50 |
| FRB20190117D | 600 | 1178.06 | 22.56 | 1155.50 | 0.78 | 0.96 | 6.48 | 1.88 |
| FRB20190118A | 600 | 225.11 | 53.41 | 171.70 | 9.30 | 0.14 | 0.70 | 3.12 |
| FRB20190118B | 600 | 670.89 | 50.19 | 620.70 | 0.31 | 0.52 | 3.04 | 1.79 |
| FRB20190121A | 600 | 425.35 | 87.35 | 338.00 | 1.70 | 0.28 | 1.49 | 2.49 |
| FRB20190122A | 600 | 1231.21 | 64.61 | 1166.60 | 0.33 | 0.97 | 6.56 | 8.06 |
| FRB20190122B | 600 | 469.57 | 54.47 | 415.10 | 0.41 | 0.35 | 1.89 | 9.51 |
| FRB20190122C | 600 | 689.90 | 24.40 | 665.50 | 4.20 | 0.55 | 3.31 | 2.84 |
| FRB20190124A | 600 | 1275.85 | 176.55 | 1099.30 | 0.61 | 0.92 | 6.10 | 1.31 |
| FRB20190124B | 600 | 441.38 | 21.58 | 419.80 | 0.97 | 0.35 | 1.91 | 2.31 |
| FRB20190124C | 600 | 303.64 | 21.44 | 282.20 | 2.50 | 0.24 | 1.21 | 2.46 |
| FRB20190124D | 600 | 340.12 | 45.62 | 294.50 | 0.50 | 0.25 | 1.27 | 5.41 |
| FRB20190124E | 600 | 617.79 | 391.99 | 225.80 | 0.64 | 0.19 | 0.95 | 3.87 |
| FRB20190124F | 600 | 254.79 | 37.59 | 217.20 | 3.90 | 0.18 | 0.91 | 2.17 |
| FRB20190125A | 600 | 564.70 | 60.40 | 504.30 | 0.37 | 0.42 | 2.37 | 1.33 |
| FRB20190125B | 600 | 178.24 | 33.24 | 145.00 | 0.83 | 0.12 | 0.58 | 1.94 |
| FRB20190127B | 600 | 663.03 | 48.43 | 614.60 | 0.63 | 0.51 | 3.00 | 3.56 |
| FRB20190128A | 600 | 696.12 | 43.62 | 652.50 | 0.58 | 0.54 | 3.23 | 3.75 |
| FRB20190128B | 600 | 248.23 | 57.23 | 191.00 | 0.81 | 0.16 | 0.79 | 3.42 |
| FRB20190128C | 600 | 310.62 | 71.32 | 239.30 | 0.71 | 0.20 | 1.01 | 4.88 |
| FRB20190128D | 600 | 430.23 | 232.83 | 197.40 | 1.20 | 0.16 | 0.81 | 5.43 |
| FRB20190129A | 600 | 484.76 | 52.06 | 432.70 | 0.49 | 0.36 | 1.98 | 1.25 |
| FRB20190130A | 600 | 1367.46 | 37.36 | 1330.10 | 0.47 | 1.11 | 7.71 | 1.56 |
| FRB20190130B | 600 | 989.03 | 29.73 | 959.30 | 0.77 | 0.80 | 5.16 | 1.21 |
| FRB20190131B | 600 | 1805.73 | 35.63 | 1770.10 | 0.99 | 1.48 | 10.97 | 6.32 |
| FRB20190131C | 600 | 507.76 | 32.96 | 474.80 | 0.84 | 0.40 | 2.21 | 2.64 |
| FRB20190131D | 600 | 642.12 | 67.52 | 574.60 | 2.90 | 0.48 | 2.77 | 1.40 |
| FRB20190131E | 600 | 279.80 | 43.30 | 236.50 | 3.00 | 0.20 | 1.00 | 2.01 |
| FRB20190201A | 600 | 242.00 | 62.40 | 179.60 | 2.60 | 0.15 | 0.73 | 9.61 |
| FRB20190201B | 600 | 749.18 | 54.18 | 695.00 | 0.81 | 0.58 | 3.48 | 6.06 |
| FRB20190202A | 600 | 307.36 | 40.76 | 266.60 | 41.00 | 0.22 | 1.14 | 3.56 |
| FRB20190202B | 600 | 464.91 | 70.11 | 394.80 | 1.57 | 0.33 | 1.78 | 3.25 |
| FRB20190203A | 600 | 420.57 | 45.87 | 374.70 | 1.21 | 0.31 | 1.68 | 2.23 |
| FRB20190203B | 600 | 582.22 | 45.82 | 536.40 | 0.49 | 0.45 | 2.55 | 2.03 |
| FRB20190203C | 600 | 370.46 | 29.66 | 340.80 | 1.40 | 0.28 | 1.50 | 2.09 |
| FRB20190204A | 600 | 449.64 | 36.14 | 413.50 | 0.24 | 0.34 | 1.88 | 5.52 |
| FRB20190204B | 600 | 1464.94 | 45.54 | 1419.40 | 1.35 | 1.18 | 8.36 | 5.22 |
| FRB20190205A | 600 | 695.39 | 67.69 | 627.70 | 0.74 | 0.52 | 3.08 | 4.38 |
| FRB20190206A | 600 | 188.34 | 41.44 | 146.90 | 1.40 | 0.12 | 0.59 | 3.37 |
| FRB20190206B | 600 | 352.52 | 78.52 | 274.00 | 0.95 | 0.23 | 1.17 | 8.77 |
| FRB20190206C | 600 | 1043.00 | 38.30 | 1004.70 | 0.56 | 0.84 | 5.46 | 9.78 |
| FRB20190208B | 600 | 714.22 | 60.62 | 653.60 | 10.30 | 0.54 | 3.23 | 6.69 |
| FRB20190208C | 600 | 238.39 | 49.69 | 188.70 | 1.27 | 0.16 | 0.78 | 5.22 |
| FRB20190210B | 600 | 624.19 | 116.49 | 507.70 | 2.60 | 0.42 | 2.39 | 9.50 |
| FRB20190210C | 600 | 643.37 | 55.27 | 588.10 | 2.37 | 0.49 | 2.85 | 1.21 |
| FRB20190210D | 600 | 359.15 | 141.25 | 217.90 | 1.37 | 0.18 | 0.91 | 7.68 |
| FRB20190210E | 600 | 580.58 | 57.88 | 522.70 | 0.69 | 0.44 | 2.48 | 2.69 |
| FRB20190211A | 600 | 1188.26 | 103.86 | 1084.40 | 1.47 | 0.90 | 6.00 | 3.06 |
| FRB20190211B | 600 | 260.70 | 84.50 | 176.20 | 0.30 | 0.15 | 0.72 | 1.06 |
| FRB20190212B | 600 | 600.19 | 41.19 | 559.00 | 1.55 | 0.47 | 2.68 | 7.05 |
| FRB20190212C | 600 | 1016.45 | 22.35 | 994.10 | 0.70 | 0.83 | 5.39 | 1.19 |
| FRB20190212D | 600 | 1139.77 | 35.37 | 1104.40 | 0.42 | 0.92 | 6.13 | 9.12 |
| FRB20190213C | 600 | 357.06 | 175.96 | 181.10 | 0.62 | 0.15 | 0.74 | 2.33 |
| FRB20190213D | 600 | 1346.85 | 234.55 | 1112.30 | 1.00 | 0.93 | 6.19 | 2.21 |
| FRB20190214A | 600 | 497.68 | 69.78 | 427.90 | 0.46 | 0.36 | 1.96 | 1.14 |
| FRB20190214C | 600 | 533.11 | 22.11 | 511.00 | 1.02 | 0.43 | 2.41 | 3.78 |
| FRB20190215B | 600 | 274.63 | 136.23 | 138.40 | 2.20 | 0.12 | 0.55 | 4.67 |
| FRB20190217A | 600 | 798.11 | 110.71 | 687.40 | 0.29 | 0.57 | 3.44 | 2.11 |
| FRB20190217B | 600 | 846.21 | 45.81 | 800.40 | 0.54 | 0.67 | 4.13 | 5.59 |
| FRB20190218A | 600 | 1285.13 | 31.43 | 1253.70 | 0.54 | 1.04 | 7.17 | 1.57 |
| FRB20190218B | 600 | 547.87 | 81.57 | 466.30 | 0.57 | 0.39 | 2.16 | 1.72 |
| FRB20190218C | 600 | 319.32 | 43.72 | 275.60 | 19.00 | 0.23 | 1.18 | 1.78 |
| FRB20190219A | 600 | 657.19 | 78.79 | 578.40 | 0.31 | 0.48 | 2.79 | 1.50 |
| FRB20190219B | 600 | 1681.11 | 37.71 | 1643.40 | 1.10 | 1.37 | 10.01 | 5.94 |
| FRB20190219C | 600 | 806.69 | 124.09 | 682.60 | 0.40 | 0.57 | 3.41 | 2.87 |
| FRB20190220A | 600 | 216.12 | 40.92 | 175.20 | 0.34 | 0.15 | 0.71 | 1.19 |
| FRB20190221A | 600 | 223.81 | 52.91 | 170.90 | 1.23 | 0.14 | 0.70 | 4.09 |
| FRB20190221B | 600 | 393.12 | 165.52 | 227.60 | 0.69 | 0.19 | 0.95 | 4.25 |
| FRB20190221C | 600 | 2042.30 | 220.60 | 1821.70 | 0.59 | 1.52 | 11.37 | 4.02 |
| FRB20190221D | 600 | 473.79 | 189.59 | 284.20 | 0.65 | 0.24 | 1.22 | 6.50 |
| FRB20190222B | 600 | 497.62 | 33.22 | 464.40 | 0.40 | 0.39 | 2.15 | 1.19 |
| FRB20190222C | 600 | 524.01 | 29.51 | 494.50 | 0.44 | 0.41 | 2.32 | 1.51 |
| FRB20190222D | 600 | 895.30 | 115.60 | 779.70 | 0.79 | 0.65 | 4.00 | 7.69 |
| FRB20190223A | 600 | 389.24 | 58.14 | 331.10 | 0.47 | 0.28 | 1.45 | 6.58 |
| FRB20190223B | 600 | 536.51 | 124.71 | 411.80 | 0.55 | 0.34 | 1.87 | 1.25 |
| FRB20190224A | 600 | 818.40 | 65.50 | 752.90 | 0.63 | 0.63 | 3.84 | 5.66 |
| FRB20190224B | 600 | 839.37 | 51.37 | 788.00 | 2.00 | 0.66 | 4.06 | 2.00 |
| FRB20190224C | 600 | 497.40 | 59.90 | 437.50 | 1.37 | 0.36 | 2.01 | 3.58 |
| FRB20190224D | 600 | 752.95 | 56.25 | 696.70 | 2.75 | 0.58 | 3.49 | 2.07 |
| FRB20190224E | 600 | 435.86 | 33.06 | 402.80 | 2.03 | 0.34 | 1.82 | 4.40 |
| FRB20190226A | 600 | 601.57 | 91.27 | 510.30 | 1.45 | 0.43 | 2.41 | 5.36 |
| FRB20190226B | 600 | 631.60 | 50.70 | 580.90 | 0.38 | 0.48 | 2.81 | 1.89 |
| FRB20190226C | 600 | 827.77 | 44.47 | 783.30 | 0.39 | 0.65 | 4.03 | 3.84 |
| FRB20190227A | 600 | 394.04 | 63.44 | 330.60 | 3.58 | 0.28 | 1.45 | 5.00 |
| FRB20190227B | 600 | 331.23 | 23.93 | 307.30 | 0.48 | 0.26 | 1.34 | 5.70 |
| FRB20190228A | 600 | 419.08 | 20.18 | 398.90 | 1.79 | 0.33 | 1.80 | 3.80 |
| FRB20190228B | 600 | 1115.25 | 71.35 | 1043.90 | 4.80 | 0.87 | 5.72 | 9.16 |
| FRB20190301B | 600 | 621.33 | 82.83 | 538.50 | 0.40 | 0.45 | 2.57 | 1.67 |
| FRB20190301C | 600 | 802.91 | 20.51 | 782.40 | 0.34 | 0.65 | 4.02 | 3.34 |
| FRB20190301D | 600 | 1160.69 | 53.09 | 1107.60 | 0.39 | 0.92 | 6.15 | 8.53 |
| FRB20190302A | 600 | 1034.24 | 220.74 | 813.50 | 0.56 | 0.68 | 4.22 | 6.01 |
| FRB20190303B | 600 | 193.51 | 47.11 | 146.40 | 9.40 | 0.12 | 0.59 | 2.25 |
| FRB20190303C | 600 | 1089.66 | 23.06 | 1066.60 | 0.80 | 0.89 | 5.87 | 1.60 |
| FRB20190303D | 600 | 711.15 | 37.05 | 674.10 | 0.59 | 0.56 | 3.36 | 4.11 |
| FRB20190304A | 600 | 483.73 | 49.83 | 433.90 | 0.71 | 0.36 | 1.99 | 1.82 |
| FRB20190304B | 600 | 470.01 | 22.61 | 447.40 | 0.67 | 0.37 | 2.06 | 1.84 |
| FRB20190304C | 600 | 564.99 | 22.09 | 542.90 | 0.53 | 0.45 | 2.59 | 2.25 |
| FRB20190307A | 600 | 355.34 | 58.04 | 297.30 | ... | 0.25 | 1.29 | ... |
| FRB20190307B | 600 | 294.00 | 54.90 | 239.10 | ... | 0.20 | 1.01 | ... |
| FRB20190308B | 600 | 180.18 | 68.68 | 111.50 | 1.11 | 0.09 | 0.44 | 1.49 |
| FRB20190308C | 600 | 500.52 | 23.12 | 477.40 | 0.47 | 0.40 | 2.22 | 1.49 |
| FRB20190309A | 600 | 356.90 | 58.60 | 298.30 | 0.39 | 0.25 | 1.29 | 4.34 |
| FRB20190313B | 600 | 1191.25 | 59.85 | 1131.40 | 0.67 | 0.94 | 6.32 | 1.54 |
| FRB20190316A | 600 | 515.93 | 38.93 | 477.00 | 1.31 | 0.40 | 2.22 | 4.16 |
| FRB20190317A | 600 | 1157.26 | 137.96 | 1019.30 | 0.54 | 0.85 | 5.56 | 9.75 |
| FRB20190317B | 600 | 424.31 | 80.61 | 343.70 | 0.65 | 0.29 | 1.52 | 9.89 |
| FRB20190317C | 600 | 598.26 | 53.56 | 544.70 | 0.43 | 0.45 | 2.60 | 1.84 |
| FRB20190317E | 600 | 800.88 | 134.28 | 666.60 | 2.17 | 0.56 | 3.31 | 1.47 |
| FRB20190317F | 600 | 1118.11 | 33.31 | 1084.80 | 1.65 | 0.90 | 6.00 | 3.44 |
| FRB20190318A | 600 | 419.27 | 85.37 | 333.90 | 1.55 | 0.28 | 1.47 | 2.21 |
| FRB20190319A | 600 | 2039.94 | 107.64 | 1932.30 | 2.78 | 1.61 | 12.22 | 2.16 |
| FRB20190320A | 600 | 614.15 | 143.95 | 470.20 | 0.94 | 0.39 | 2.19 | 2.89 |
| FRB20190320B | 600 | 489.49 | 37.69 | 451.80 | 0.73 | 0.38 | 2.09 | 2.05 |
| FRB20190320C | 600 | 368.79 | 47.09 | 321.70 | 1.24 | 0.27 | 1.41 | 1.63 |
| FRB20190320D | 600 | 1141.35 | 43.85 | 1097.50 | 0.49 | 0.91 | 6.08 | 1.05 |
| FRB20190320E | 600 | 299.14 | 55.84 | 243.30 | 4.40 | 0.20 | 1.03 | 3.13 |
| FRB20190322A | 600 | 1060.12 | 63.62 | 996.50 | 0.64 | 0.83 | 5.40 | 1.10 |
| FRB20190322B | 600 | 576.98 | 46.98 | 530.00 | 0.61 | 0.44 | 2.52 | 2.46 |
| FRB20190322C | 600 | 1192.08 | 65.78 | 1126.30 | 4.10 | 0.94 | 6.28 | 9.32 |
| FRB20190323A | 600 | 857.50 | 72.80 | 784.70 | 0.67 | 0.65 | 4.04 | 6.62 |
| FRB20190323B | 600 | 789.56 | 40.26 | 749.30 | 6.94 | 0.62 | 3.81 | 6.17 |
| FRB20190323C | 600 | 381.12 | 23.62 | 357.50 | 0.56 | 0.30 | 1.59 | 9.30 |
| FRB20190323D | 600 | 763.65 | 162.35 | 601.30 | 0.37 | 0.50 | 2.93 | 1.99 |
| FRB20190325A | 600 | 359.29 | 50.99 | 308.30 | 1.31 | 0.26 | 1.34 | 1.57 |
| FRB20190325B | 600 | 1733.92 | 19.82 | 1714.10 | 0.70 | 1.43 | 10.54 | 4.16 |
| FRB20190325C | 600 | 797.83 | 188.43 | 609.40 | 0.63 | 0.51 | 2.97 | 3.49 |
| FRB20190326A | 600 | 283.31 | 40.71 | 242.60 | 1.02 | 0.20 | 1.02 | 7.22 |
| FRB20190327A | 600 | 346.57 | 88.77 | 257.80 | 2.43 | 0.21 | 1.10 | 1.96 |
| FRB20190328A | 600 | 1303.58 | 51.78 | 1251.80 | 0.43 | 1.04 | 7.16 | 1.25 |
| FRB20190328B | 600 | 565.00 | 50.10 | 514.90 | 0.72 | 0.43 | 2.43 | 2.72 |
| FRB20190328C | 600 | 472.86 | 64.66 | 408.20 | 4.70 | 0.34 | 1.85 | 1.05 |
| FRB20190329A | 600 | 188.61 | 87.81 | 100.80 | 0.52 | 0.08 | 0.40 | 5.67 |
| FRB20190329B | 600 | 406.05 | 65.95 | 340.10 | ... | 0.28 | 1.50 | ... |
| FRB20190329C | 600 | 1256.36 | 60.36 | 1196.00 | ... | 1.00 | 6.76 | ... |
| FRB20190330A | 600 | 508.97 | 24.87 | 484.10 | 0.37 | 0.40 | 2.26 | 1.21 |
| FRB20190330B | 600 | 668.09 | 48.89 | 619.20 | 2.79 | 0.52 | 3.03 | 1.60 |
| FRB20190401A | 600 | 783.22 | 42.42 | 740.80 | 1.05 | 0.62 | 3.76 | 9.09 |
| FRB20190402A | 600 | 1291.69 | 26.39 | 1265.30 | 0.30 | 1.05 | 7.25 | 8.91 |
| FRB20190403A | 600 | 518.83 | 54.23 | 464.60 | 1.12 | 0.39 | 2.15 | 3.35 |
| FRB20190403B | 600 | 292.47 | 54.07 | 238.40 | 2.70 | 0.20 | 1.00 | 1.84 |
| FRB20190403C | 600 | 935.01 | 38.91 | 896.10 | 0.37 | 0.75 | 4.74 | 4.96 |
| FRB20190403D | 600 | 613.46 | 62.96 | 550.50 | 0.65 | 0.46 | 2.63 | 2.85 |
| FRB20190403E | 600 | 226.20 | 49.90 | 176.30 | 3.90 | 0.15 | 0.72 | 1.39 |
| FRB20190403F | 600 | 664.18 | 67.38 | 596.80 | 0.58 | 0.50 | 2.90 | 3.06 |
| FRB20190403G | 600 | 865.31 | 165.31 | 700.00 | 0.75 | 0.58 | 3.51 | 5.70 |
| FRB20190404A | 600 | 1353.90 | 40.30 | 1313.60 | 1.17 | 1.09 | 7.59 | 3.79 |
| FRB20190404B | 600 | 489.42 | 45.02 | 444.40 | 8.60 | 0.37 | 2.05 | 2.33 |
| FRB20190405A | 600 | 424.88 | 47.28 | 377.60 | 0.65 | 0.31 | 1.69 | 1.22 |
| FRB20190405B | 600 | 1113.22 | 53.92 | 1059.30 | 3.40 | 0.88 | 5.83 | 6.71 |
| FRB20190408A | 600 | 863.38 | 45.98 | 817.40 | 0.64 | 0.68 | 4.24 | 6.95 |
| FRB20190409A | 600 | 1791.89 | 84.39 | 1707.50 | 3.00 | 1.42 | 10.49 | 1.77 |
| FRB20190409B | 600 | 285.63 | 47.83 | 237.80 | 0.39 | 0.20 | 1.00 | 2.64 |
| FRB20190409C | 600 | 674.63 | 43.03 | 631.60 | 1.04 | 0.53 | 3.10 | 6.25 |
| FRB20190409D | 600 | 1300.12 | 54.72 | 1245.40 | 0.59 | 1.04 | 7.11 | 1.69 |
| FRB20190410A | 600 | 284.02 | 128.52 | 155.50 | 1.59 | 0.13 | 0.63 | 4.32 |
| FRB20190410B | 600 | 642.17 | 78.37 | 563.80 | 0.22 | 0.47 | 2.71 | 1.02 |
| FRB20190411A | 600 | 460.56 | 60.76 | 399.80 | 1.24 | 0.33 | 1.81 | 2.64 |
| FRB20190411B | 600 | 1229.58 | 35.28 | 1194.30 | 0.89 | 1.00 | 6.75 | 2.31 |
| FRB20190411C | 600 | 233.66 | 38.86 | 194.80 | 3.19 | 0.16 | 0.80 | 1.40 |
| FRB20190412A | 600 | 364.73 | 37.53 | 327.20 | 1.77 | 0.27 | 1.44 | 2.42 |
| FRB20190412B | 600 | 375.75 | 264.85 | 110.90 | 0.68 | 0.09 | 0.44 | 9.06 |
| FRB20190414A | 600 | 811.98 | 20.18 | 791.80 | 0.44 | 0.66 | 4.08 | 4.44 |
| FRB20190414B | 600 | 506.49 | 37.79 | 468.70 | 0.49 | 0.39 | 2.18 | 1.49 |
| FRB20190415A | 600 | 633.68 | 36.98 | 596.70 | 0.57 | 0.50 | 2.90 | 3.01 |
| FRB20190415B | 600 | 722.99 | 155.39 | 567.60 | 0.85 | 0.47 | 2.73 | 4.00 |
| FRB20190415C | 600 | 650.18 | 168.48 | 481.70 | 0.46 | 0.40 | 2.25 | 1.49 |
| FRB20190416A | 600 | 2287.27 | 39.17 | 2248.10 | 0.60 | 1.87 | 14.71 | 6.56 |
| FRB20190416B | 600 | 575.36 | 20.56 | 554.80 | 0.69 | 0.46 | 2.66 | 3.08 |
| FRB20190417B | 600 | 1161.20 | 35.00 | 1126.20 | 0.46 | 0.94 | 6.28 | 1.04 |
| FRB20190417C | 600 | 320.23 | 122.03 | 198.20 | 7.90 | 0.17 | 0.82 | 3.61 |
| FRB20190418A | 600 | 184.51 | 70.11 | 114.40 | 0.99 | 0.10 | 0.45 | 1.41 |
| FRB20190419A | 600 | 439.97 | 62.27 | 377.70 | 0.41 | 0.31 | 1.69 | 7.70 |
| FRB20190419B | 600 | 165.08 | 52.28 | 112.80 | 4.60 | 0.09 | 0.45 | 6.35 |
| FRB20190420A | 600 | 609.10 | 65.70 | 543.40 | 0.88 | 0.45 | 2.59 | 3.75 |
| FRB20190420B | 600 | 846.84 | 67.44 | 779.40 | 2.20 | 0.65 | 4.00 | 2.14 |
| FRB20190420C | 600 | 629.95 | 35.75 | 594.20 | 0.44 | 0.50 | 2.88 | 2.30 |
| FRB20190421B | 600 | 392.25 | 96.45 | 295.80 | 5.10 | 0.25 | 1.28 | 5.57 |
| FRB20190422A | 600 | 452.30 | 79.50 | 372.80 | 0.60 | 0.31 | 1.67 | 1.09 |
| FRB20190422B | 600 | 977.39 | 34.09 | 943.30 | 0.22 | 0.79 | 5.05 | 3.32 |
| FRB20190423A | 600 | 242.65 | 31.65 | 211.00 | 10.80 | 0.18 | 0.88 | 5.65 |
| FRB20190423B | 600 | 584.95 | 482.65 | 102.30 | 0.87 | 0.09 | 0.40 | 9.78 |
| FRB20190423C | 600 | 855.53 | 60.43 | 795.10 | 1.23 | 0.66 | 4.10 | 1.25 |
| FRB20190423D | 600 | 496.46 | 66.16 | 430.30 | 1.71 | 0.36 | 1.97 | 4.30 |
| FRB20190424A | 600 | 758.67 | 35.47 | 723.20 | 1.13 | 0.60 | 3.65 | 9.26 |
| FRB20190425A | 600 | 128.16 | 48.76 | 79.40 | 18.60 | 0.07 | 0.31 | 1.23 |
| FRB20190425B | 600 | 1031.72 | 52.72 | 979.00 | 1.25 | 0.82 | 5.29 | 2.06 |
| FRB20190426A | 600 | 340.66 | 55.86 | 284.80 | 1.59 | 0.24 | 1.23 | 1.60 |
| FRB20190427A | 600 | 455.78 | 84.98 | 370.80 | 3.90 | 0.31 | 1.66 | 7.03 |
| FRB20190428A | 600 | 969.40 | 27.00 | 942.40 | 2.22 | 0.79 | 5.05 | 3.35 |
| FRB20190429A | 600 | 470.88 | 57.58 | 413.30 | 0.80 | 0.34 | 1.88 | 1.84 |
| FRB20190429B | 600 | 295.65 | 42.15 | 253.50 | 0.74 | 0.21 | 1.08 | 5.76 |
| FRB20190430A | 600 | 339.25 | 57.85 | 281.40 | 0.75 | 0.23 | 1.21 | 7.34 |
| FRB20190430B | 600 | 2619.40 | 36.40 | 2583.00 | 0.38 | 2.15 | 17.43 | 5.65 |
| FRB20190430C | 600 | 400.56 | 99.06 | 301.50 | 2.17 | 0.25 | 1.31 | 2.47 |
| FRB20190501B | 600 | 784.07 | 43.57 | 740.50 | 0.88 | 0.62 | 3.76 | 7.61 |
| FRB20190502A | 600 | 625.77 | 34.97 | 590.80 | 3.18 | 0.49 | 2.87 | 1.64 |
| FRB20190502B | 600 | 918.61 | 33.81 | 884.80 | 2.58 | 0.74 | 4.67 | 3.36 |
| FRB20190502C | 600 | 396.84 | 47.44 | 349.40 | 3.60 | 0.29 | 1.55 | 5.68 |
| FRB20190515A | 600 | 450.50 | 157.40 | 293.10 | 0.55 | 0.24 | 1.27 | 5.89 |
| FRB20190515B | 600 | 822.19 | 32.49 | 789.70 | 2.80 | 0.66 | 4.07 | 2.81 |
| FRB20190515D | 600 | 426.06 | 47.76 | 378.30 | 3.00 | 0.32 | 1.70 | 5.65 |
| FRB20190516B | 600 | 1235.42 | 33.32 | 1202.10 | 1.13 | 1.00 | 6.81 | 2.98 |
| FRB20190517C | 600 | 335.57 | 187.97 | 147.60 | 3.10 | 0.12 | 0.59 | 7.54 |
| FRB20190517D | 600 | 1180.15 | 93.35 | 1086.80 | 0.45 | 0.91 | 6.01 | 9.42 |
| FRB20190518B | 600 | 913.77 | 26.07 | 887.70 | 1.53 | 0.74 | 4.69 | 2.01 |
| FRB20190518C | 600 | 444.08 | 41.68 | 402.40 | 6.70 | 0.34 | 1.82 | 1.45 |
| FRB20190518D | 600 | 202.46 | 53.96 | 148.50 | 1.36 | 0.12 | 0.60 | 3.35 |
| FRB20190518G | 600 | 524.95 | 63.05 | 461.90 | 0.99 | 0.38 | 2.14 | 2.92 |
| FRB20190519D | 600 | 539.77 | 30.47 | 509.30 | 0.36 | 0.42 | 2.40 | 1.32 |
| FRB20190519E | 600 | 693.83 | 27.53 | 666.30 | 1.00 | 0.56 | 3.31 | 6.79 |
| FRB20190519F | 600 | 797.77 | 42.07 | 755.70 | 0.75 | 0.63 | 3.85 | 6.80 |
| FRB20190519G | 600 | 430.09 | 73.49 | 356.60 | 1.11 | 0.30 | 1.58 | 1.83 |
| FRB20190519H | 600 | 1170.87 | 59.37 | 1111.50 | 3.20 | 0.93 | 6.18 | 7.05 |
| FRB20190519J | 600 | 642.76 | 56.06 | 586.70 | 0.63 | 0.49 | 2.84 | 3.20 |
| FRB20190520A | 600 | 432.51 | 79.71 | 352.80 | 1.08 | 0.29 | 1.56 | 1.74 |
| FRB20190527A | 600 | 584.58 | 33.68 | 550.90 | 0.47 | 0.46 | 2.64 | 2.07 |
| FRB20190527C | 600 | 535.44 | 73.84 | 461.60 | 3.00 | 0.38 | 2.14 | 8.84 |
| FRB20190529A | 600 | 704.45 | 165.45 | 539.00 | 0.47 | 0.45 | 2.57 | 1.97 |
| FRB20190530A | 600 | 555.45 | 139.25 | 416.20 | 0.58 | 0.35 | 1.89 | 1.35 |
| FRB20190531A | 600 | 324.70 | 44.00 | 280.70 | ... | 0.23 | 1.21 | ... |
| FRB20190531B | 600 | 167.96 | 43.06 | 124.90 | ... | 0.10 | 0.50 | ... |
| FRB20190531C | 600 | 478.20 | 132.40 | 345.80 | 0.37 | 0.29 | 1.53 | 5.71 |
| FRB20190531E | 600 | 328.20 | 32.00 | 296.20 | 2.70 | 0.25 | 1.28 | 2.96 |
| FRB20190601A | 600 | 2227.89 | 32.99 | 2194.90 | 0.73 | 1.83 | 14.29 | 7.56 |
| FRB20190601B | 600 | 787.80 | 41.90 | 745.90 | 1.00 | 0.62 | 3.79 | 8.80 |
| FRB20190601C | 600 | 424.07 | 186.37 | 237.70 | 1.32 | 0.20 | 1.00 | 8.93 |
| FRB20190601D | 600 | 668.47 | 63.87 | 604.60 | 0.63 | 0.50 | 2.95 | 3.42 |
| FRB20190603B | 600 | 504.32 | 100.32 | 404.00 | 1.70 | 0.34 | 1.83 | 3.71 |
| FRB20190604C | 600 | 515.64 | 163.94 | 351.70 | 1.56 | 0.29 | 1.56 | 2.50 |
| FRB20190604D | 600 | 1021.17 | 24.77 | 996.40 | 0.82 | 0.83 | 5.40 | 1.40 |
| FRB20190604E | 600 | 1218.60 | 26.00 | 1192.60 | 1.16 | 0.99 | 6.74 | 3.01 |
| FRB20190604G | 600 | 233.05 | 51.45 | 181.60 | 1.15 | 0.15 | 0.74 | 4.35 |
| FRB20190605C | 600 | 187.64 | 37.84 | 149.80 | 4.60 | 0.12 | 0.60 | 1.15 |
| FRB20190605D | 600 | 1656.53 | 48.83 | 1607.70 | 0.82 | 1.34 | 9.74 | 4.21 |
| FRB20190606B | 600 | 277.49 | 55.09 | 222.40 | 2.62 | 0.19 | 0.93 | 1.53 |
| FRB20190607A | 600 | 562.45 | 43.95 | 518.50 | 4.35 | 0.43 | 2.45 | 1.67 |
| FRB20190607B | 600 | 289.38 | 138.28 | 151.10 | 1.06 | 0.13 | 0.61 | 2.71 |
| FRB20190608A | 600 | 722.18 | 38.38 | 683.80 | 1.29 | 0.57 | 3.42 | 9.29 |
| FRB20190609A | 600 | 316.64 | 58.44 | 258.20 | 3.60 | 0.22 | 1.10 | 2.92 |
| FRB20190609B | 600 | 292.19 | 52.29 | 239.90 | 11.50 | 0.20 | 1.01 | 7.94 |
| FRB20190609C | 600 | 480.28 | 112.68 | 367.60 | 0.64 | 0.31 | 1.64 | 1.13 |
| FRB20190609D | 600 | 511.71 | 57.51 | 454.20 | 0.66 | 0.38 | 2.10 | 1.87 |
| FRB20190612A | 600 | 432.29 | 41.69 | 390.60 | 0.79 | 0.33 | 1.76 | 1.60 |
| FRB20190612B | 600 | 187.60 | 27.70 | 159.90 | 2.41 | 0.13 | 0.65 | 6.95 |
| FRB20190612C | 600 | 1641.57 | 107.77 | 1533.80 | 3.80 | 1.28 | 9.19 | 1.75 |
| FRB20190613A | 600 | 714.98 | 53.48 | 661.50 | 1.07 | 0.55 | 3.28 | 7.14 |
| FRB20190613B | 600 | 285.14 | 168.84 | 116.30 | 1.08 | 0.10 | 0.46 | 1.59 |
| FRB20190614A | 600 | 1064.04 | 52.34 | 1011.70 | 0.83 | 0.84 | 5.51 | 1.47 |
| FRB20190614B | 600 | 581.91 | 54.91 | 527.00 | 4.50 | 0.44 | 2.50 | 1.79 |
| FRB20190614C | 600 | 589.16 | 57.46 | 531.70 | 0.50 | 0.44 | 2.53 | 2.03 |
| FRB20190616A | 600 | 212.59 | 25.49 | 187.10 | 0.73 | 0.16 | 0.77 | 2.95 |
| FRB20190617A | 600 | 195.77 | 46.67 | 149.10 | 5.80 | 0.12 | 0.60 | 1.44 |
| FRB20190617B | 600 | 273.51 | 43.81 | 229.70 | 0.99 | 0.19 | 0.96 | 6.22 |
| FRB20190617C | 600 | 640.16 | 45.36 | 594.80 | 0.54 | 0.50 | 2.89 | 2.83 |
| FRB20190618A | 600 | 228.95 | 77.25 | 151.70 | 2.40 | 0.13 | 0.61 | 6.19 |
| FRB20190619A | 600 | 899.91 | 37.61 | 862.30 | 1.57 | 0.72 | 4.53 | 1.93 |
| FRB20190619B | 600 | 270.59 | 45.89 | 224.70 | 1.96 | 0.19 | 0.94 | 1.17 |
| FRB20190619C | 600 | 488.27 | 69.27 | 419.00 | 0.72 | 0.35 | 1.91 | 1.71 |
| FRB20190619D | 600 | 378.47 | 63.97 | 314.50 | 0.48 | 0.26 | 1.37 | 6.00 |
| FRB20190621B | 600 | 1061.23 | 30.73 | 1030.50 | 0.30 | 0.86 | 5.63 | 5.55 |
| FRB20190621C | 600 | 570.27 | 25.67 | 544.60 | 1.98 | 0.45 | 2.60 | 8.48 |
| FRB20190621D | 600 | 647.51 | 50.71 | 596.80 | 0.89 | 0.50 | 2.90 | 4.70 |
| FRB20190622A | 600 | 1122.82 | 56.82 | 1066.00 | 0.61 | 0.89 | 5.87 | 1.22 |
| FRB20190623A | 600 | 1082.20 | 74.20 | 1008.00 | 0.41 | 0.84 | 5.48 | 7.21 |
| FRB20190623B | 600 | 1556.77 | 143.77 | 1413.00 | 1.58 | 1.18 | 8.31 | 6.04 |
| FRB20190623C | 600 | 1049.83 | 48.83 | 1001.00 | 1.92 | 0.83 | 5.43 | 3.32 |
| FRB20190624A | 600 | 973.85 | 37.85 | 936.00 | 0.58 | 0.78 | 5.00 | 8.60 |
| FRB20190624B | 600 | 213.92 | 69.72 | 144.20 | 16.50 | 0.12 | 0.58 | 3.82 |
| FRB20190625A | 600 | 302.14 | 23.14 | 279.00 | 0.35 | 0.23 | 1.20 | 3.36 |
| FRB20190625C | 600 | 442.24 | 76.14 | 366.10 | 2.22 | 0.31 | 1.63 | 3.89 |
| FRB20190625D | 600 | 717.88 | 101.38 | 616.50 | 5.30 | 0.51 | 3.01 | 3.01 |
| FRB20190627A | 600 | 404.22 | 30.32 | 373.90 | 1.98 | 0.31 | 1.67 | 3.63 |
| FRB20190627B | 600 | 430.32 | 42.02 | 388.30 | 4.06 | 0.32 | 1.75 | 8.11 |
| FRB20190627C | 600 | 968.61 | 48.01 | 920.60 | 4.00 | 0.77 | 4.90 | 5.71 |
| FRB20190627D | 600 | 2002.24 | 132.04 | 1870.20 | 0.24 | 1.56 | 11.74 | 1.71 |
| FRB20190628A | 600 | 745.84 | 29.84 | 716.00 | 0.81 | 0.60 | 3.61 | 6.49 |
| FRB20190628B | 600 | 408.01 | 46.51 | 361.50 | 0.75 | 0.30 | 1.61 | 1.28 |
| FRB20190628C | 600 | 1748.44 | 98.84 | 1649.60 | 0.38 | 1.37 | 10.06 | 2.07 |
| FRB20190629A | 600 | 503.78 | 35.08 | 468.70 | 0.82 | 0.39 | 2.18 | 2.50 |
| FRB20190630B | 600 | 652.15 | 150.55 | 501.60 | 0.92 | 0.42 | 2.36 | 3.27 |
| FRB20190630C | 600 | 1660.35 | 68.05 | 1592.30 | 0.66 | 1.33 | 9.63 | 3.32 |
| FRB20190630D | 600 | 323.52 | 43.72 | 279.80 | 1.73 | 0.23 | 1.20 | 1.67 |
| FRB20190701A | 600 | 637.09 | 54.29 | 582.80 | 1.26 | 0.49 | 2.82 | 6.30 |
| FRB20190701B | 600 | 749.11 | 61.51 | 687.60 | 1.10 | 0.57 | 3.44 | 8.03 |
| FRB20190701C | 600 | 974.20 | 58.40 | 915.80 | 0.88 | 0.76 | 4.87 | 1.24 |
| FRB20190701D | 600 | 933.36 | 55.96 | 877.40 | 1.33 | 0.73 | 4.62 | 1.70 |
| FRB20190701E | 600 | 890.48 | 42.38 | 848.10 | 0.68 | 0.71 | 4.44 | 8.04 |
References
- Lorimer, D.R.; Bailes, M.; McLaughlin, M.A.; Narkevic, D.J.; Crawford, F. A Bright Millisecond Radio Burst of Extragalactic Origin. Science 2007, 318, 777. [Google Scholar] [CrossRef] [PubMed]
- Thornton, D.; Stappers, B.; Bailes, M.; Barsdell, B.; Bates, S.; Bhat, N.D.R.; Burgay, M.; Burke-Spolaor, S.; Champion, D.J.; Coster, P.; et al. A Population of Fast Radio Bursts at Cosmological Distances. Science 2013, 341, 53–56. [Google Scholar] [CrossRef] [PubMed]
- Cordes, J.M.; Chatterjee, S. Fast Radio Bursts: An Extragalactic Enigma. Annu. Rev. Astron. Astrophys. 2019, 57, 417–465. [Google Scholar] [CrossRef]
- Petroff, E.; Barr, E.D.; Jameson, A.; Keane, E.F.; Bailes, M.; Kramer, M.; Morello, V.; Tabbara, D.; van Straten, W. FRBCAT: The Fast Radio Burst Catalogue. Publ. Astron. Soc. Aust. 2016, 33, e045. [Google Scholar] [CrossRef]
- Li, X.J.; Dong, X.F.; Zhang, Z.B.; Li, D. Long and Short Fast Radio Bursts Are Different from Repeating and Nonrepeating Transients. Astrophys. J. 2021, 923, 230. [Google Scholar] [CrossRef]
- CHIME/FRB Collaboration; Amiri, M.; Andersen, B.C.; Bandura, K.; Berger, S.; Bhardwaj, M.; Boyce, M.M.; Boyle, P.J.; Brar, C.; Breitman, D.; et al. The First CHIME/FRB Fast Radio Burst Catalog. Astrophys. J. 2021, 257, 59. [Google Scholar] [CrossRef]
- Keane, E.F.; Petroff, E. Fast radio bursts: Search sensitivities and completeness. Mon. Not. R. Astron. Soc. 2015, 447, 2852–2856. [Google Scholar] [CrossRef][Green Version]
- Law, C.J.; Bower, G.C.; Burke-Spolaor, S.; Butler, B.; Lawrence, E.; Lazio, T.J.W.; Mattmann, C.A.; Rupen, M.; Siemion, A.; VanderWiel, S. A Millisecond Interferometric Search for Fast Radio Bursts with the Very Large Array. Astrophys. J. 2015, 807, 16. [Google Scholar] [CrossRef]
- Champion, D.J.; Petroff, E.; Kramer, M.; Keith, M.J.; Bailes, M.; Barr, E.D.; Bates, S.D.; Bhat, N.D.R.; Burgay, M.; Burke-Spolaor, S.; et al. Five new fast radio bursts from the HTRU high-latitude survey at Parkes: First evidence for two-component bursts. Mon. Not. R. Astron. Soc. Lett. 2016, 460, L30–L34. [Google Scholar] [CrossRef]
- Oppermann, N.; Connor, L.D.; Pen, U.L. The Euclidean distribution of fast radio bursts. Mon. Not. R. Astron. Soc. 2016, 461, 984–987. [Google Scholar] [CrossRef]
- Rane, A.; Lorimer, D.R.; Bates, S.D.; McMann, N.; McLaughlin, M.A.; Rajwade, K. A search for rotating radio transients and fast radio bursts in the Parkes high-latitude pulsar survey. Mon. Not. R. Astron. Soc. 2016, 455, 2207–2215. [Google Scholar] [CrossRef]
- Bhandari, S.; Keane, E.F.; Barr, E.D.; Jameson, A.; Petroff, E.; Johnston, S.; Bailes, M.; Bhat, N.D.R.; Burgay, M.; Burke-Spolaor, S.; et al. The SUrvey for Pulsars and Extragalactic Radio Bursts - II. New FRB discoveries and their follow-up. Mon. Not. R. Astron. Soc. 2018, 475, 1427–1446. [Google Scholar] [CrossRef]
- Connor, L.; Petroff, E. On Detecting Repetition from Fast Radio Bursts. Astrophys. J. 2018, 861, L1. [Google Scholar] [CrossRef]
- Patel, C.; Agarwal, D.; Bhardwaj, M.; Boyce, M.M.; Brazier, A.; Chatterjee, S.; Chawla, P.; Kaspi, V.M.; Lorimer, D.R.; McLaughlin, M.A.; et al. PALFA Single-pulse Pipeline: New Pulsars, Rotating Radio Transients, and a Candidate Fast Radio Burst. Astrophys. J. 2018, 869, 181. [Google Scholar] [CrossRef]
- Shannon, R.M.; Macquart, J.P.; Bannister, K.W.; Ekers, R.D.; James, C.W.; Osłowski, S.; Qiu, H.; Sammons, M.; Hotan, A.W.; Voronkov, M.A.; et al. The dispersion-brightness relation for fast radio bursts from a wide-field survey. Nature 2018, 562, 386–390. [Google Scholar] [CrossRef]
- Farah, W.; Flynn, C.; Bailes, M.; Jameson, A.; Bateman, T.; Campbell-Wilson, D.; Day, C.K.; Deller, A.T.; Green, A.J.; Gupta, V.; et al. Five new real-time detections of fast radio bursts with UTMOST. Mon. Not. R. Astron. Soc. 2019, 488, 2989–3002. [Google Scholar] [CrossRef]
- Parent, E.; Chawla, P.; Kaspi, V.M.; Agazie, G.Y.; Blumer, H.; DeCesar, M.; Fiore, W.; Fonseca, E.; Hessels, J.W.T.; Kaplan, D.L.; et al. First Discovery of a Fast Radio Burst at 350 MHz by the GBNCC Survey. Astrophys. J. 2020, 904, 92. [Google Scholar] [CrossRef]
- Li, D.; Wang, P.; Zhu, W.W.; Zhang, B.; Zhang, X.X.; Duan, R.; Zhang, Y.K.; Feng, Y.; Tang, N.Y.; Chatterjee, S.; et al. A bimodal burst energy distribution of a repeating fast radio burst source. Nature 2021, 598, 267–271. [Google Scholar] [CrossRef]
- Xu, H.; Niu, J.R.; Chen, P.; Lee, K.J.; Zhu, W.W.; Dong, S.; Zhang, B.; Jiang, J.C.; Wang, B.J.; Xu, J.W.; et al. A fast radio burst source at a complex magnetised site in a barred galaxy. arXiv 2021, arXiv:2111.11764. [Google Scholar]
- Li, D.; Wang, P.; Qian, L.; Krco, M.; Jiang, P.; Yue, Y.; Jin, C.; Zhu, Y.; Pan, Z.; Nan, R.; et al. FAST in Space: Considerations for a Multibeam, Multipurpose Survey Using China’s 500-m Aperture Spherical Radio Telescope (FAST). IEEE Microw. Mag. 2018, 19, 112–119. [Google Scholar] [CrossRef]
- CHIME/FRB Collaboration; Andersen, B.C.; Bandura, K.M.; Bhardwaj, M.; Bij, A.; Boyce, M.M.; Boyle, P.J.; Brar, C.; Cassanelli, T.; Chawla, P.; et al. A bright millisecond-duration radio burst from a Galactic magnetar. Nature 2020, 587, 54–58. [Google Scholar] [CrossRef]
- Bochenek, C. A Fast Radio Burst Associated with a Galactic Magnetar. In Proceedings of the American Astronomical Society Meeting Abstracts, New York, NY, USA, 11–15 January 2021; Volume 53, p. 236.05D. [Google Scholar]
- Lin, L.; Zhang, C.F.; Wang, P.; Gao, H.; Guan, X.; Han, J.L.; Jiang, J.C.; Jiang, P.; Lee, K.J.; Li, D.; et al. No pulsed radio emission during a bursting phase of a Galactic magnetar. Nature 2020, 587, 63–65. [Google Scholar] [CrossRef] [PubMed]
- Mereghetti, S.; Savchenko, V.; Ferrigno, C.; Götz, D.; Rigoselli, M.; Tiengo, A.; Bazzano, A.; Bozzo, E.; Coleiro, A.; Courvoisier, T.J.L.; et al. INTEGRAL Discovery of a Burst with Associated Radio Emission from the Magnetar SGR 1935+2154. Astrophys. J. 2020, 898, L29. [Google Scholar] [CrossRef]
- Li, C.K.; Lin, L.; Xiong, S.L.; Ge, M.Y.; Li, X.B.; Li, T.P.; Lu, F.J.; Zhang, S.N.; Tuo, Y.L.; Nang, Y.; et al. HXMT identification of a non-thermal X-ray burst from SGR J1935+2154 and with FRB 200428. Nat. Astron. 2021, 5, 378–384. [Google Scholar] [CrossRef]
- Ridnaia, A.; Svinkin, D.; Frederiks, D.; Bykov, A.; Popov, S.; Aptekar, R.; Golenetskii, S.; Lysenko, A.; Tsvetkova, A.; Ulanov, M.; et al. A peculiar hard X-ray counterpart of a Galactic fast radio burst. Nat. Astron. 2021, 5, 372–377. [Google Scholar] [CrossRef]
- Tavani, M.; Casentini, C.; Ursi, A.; Verrecchia, F.; Addis, A.; Antonelli, L.A.; Argan, A.; Barbiellini, G.; Baroncelli, L.; Bernardi, G.; et al. An X-ray burst from a magnetar enlightening the mechanism of fast radio bursts. Nat. Astron. 2021, 5, 401–407. [Google Scholar] [CrossRef]
- Petroff, E.; Hessels, J.W.T.; Lorimer, D.R. Fast radio bursts. Astron. Astrophys. 2019, 27, 4. [Google Scholar] [CrossRef]
- Zhang, B. Fast Radio Burst Energetics and Detectability from High Redshifts. Astrophys. J. 2018, 867, L21. [Google Scholar] [CrossRef]
- Ravi, V.; Catha, M.; D’Addario, L.; Djorgovski, S.G.; Hallinan, G.; Hobbs, R.; Kocz, J.; Kulkarni, S.R.; Shi, J.; Vedantham, H.K.; et al. A fast radio burst localized to a massive galaxy. Nature 2019, 572, 352–354. [Google Scholar] [CrossRef]
- Platts, E.; Weltman, A.; Walters, A.; Tendulkar, S.P.; Gordin, J.E.B.; Kandhai, S. A living theory catalogue for fast radio bursts. Phys. Rep. 2019, 821, 1–27. [Google Scholar] [CrossRef]
- Yamasaki, S.; Totani, T.; Kiuchi, K. Repeating and non-repeating fast radio bursts from binary neutron star mergers. Publ. Astron. Soc. Jpn. 2018, 70, 39. [Google Scholar] [CrossRef]
- Popov, S.B.; Postnov, K.A. Millisecond extragalactic radio bursts as magnetar flares. arXiv 2013, arXiv:1307.4924. [Google Scholar]
- Metzger, B.D.; Margalit, B.; Sironi, L. Fast radio bursts as synchrotron maser emission from decelerating relativistic blast waves. Mon. Not. R. Astron. Soc. 2019, 485, 4091–4106. [Google Scholar] [CrossRef]
- Geng, J.J.; Huang, Y.F. Fast Radio Bursts: Collisions between Neutron Stars and Asteroids/Comets. Astrophys. J. 2015, 809, 24. [Google Scholar] [CrossRef]
- Dai, Z.G.; Wang, J.S.; Wu, X.F.; Huang, Y.F. Repeating Fast Radio Bursts from Highly Magnetized Pulsars Traveling through Asteroid Belts. Astrophys. J. 2016, 829, 27. [Google Scholar] [CrossRef]
- Xiao, D.; Dai, Z.G. Double-peaked Pulse Profile of FRB 200428: Synchrotron Maser Emission from Magnetized Shocks Encountering a Density Jump. Astrophys. J. 2020, 904, L5. [Google Scholar] [CrossRef]
- Geng, J.J.; Li, B.; Li, L.B.; Xiong, S.L.; Kuiper, R.; Huang, Y.F. FRB 200428: An Impact between an Asteroid and a Magnetar. Astrophys. J. 2020, 898, L55. [Google Scholar] [CrossRef]
- Geng, J.; Li, B.; Huang, Y. Repeating fast radio bursts from collapses of the crust of a strange star. Innovation 2021, 2, 100152. [Google Scholar] [CrossRef]
- Li, L.B.; Huang, Y.F.; Geng, J.J.; Li, B. A model of fast radio bursts: Collisions between episodic magnetic blobs. Res. Astron. Astrophys. 2018, 18, 061. [Google Scholar] [CrossRef]
- Zhang, B. FRB 121102: A Repeatedly Combed Neutron Star by a Nearby Low-luminosity Accreting Supermassive Black Hole. Astrophys. J. 2018, 854, L21. [Google Scholar] [CrossRef]
- Li, Q.C.; Yang, Y.P.; Wang, F.Y.; Xu, K.; Shao, Y.; Liu, Z.N.; Dai, Z.G. Periodic Activities of Repeating Fast Radio Bursts from Be/X-Ray Binary Systems. Astrophys. J. 2021, 918, L5. [Google Scholar] [CrossRef]
- Yang, H.; Zou, Y.C. Orbit-induced Spin Precession as a Possible Origin for Periodicity in Periodically Repeating Fast Radio Bursts. Astrophys. J. 2020, 893, L31. [Google Scholar] [CrossRef]
- Levin, Y.; Beloborodov, A.M.; Bransgrove, A. Precessing Flaring Magnetar as a Source of Repeating FRB 180916.J0158+65. Astrophys. J. Lett. 2020, 895, L30. [Google Scholar] [CrossRef]
- Tong, H.; Wang, W.; Wang, H.G. Periodicity in fast radio bursts due to forced precession by a fallback disk. Res. Astron. Astrophys. 2020, 20, 142. [Google Scholar] [CrossRef]
- Li, D.; Zanazzi, J.J. Emission Properties of Periodic Fast Radio Bursts from the Motion of Magnetars: Testing Dynamical Models. Astrophys. J. Lett. 2021, 909, L25. [Google Scholar] [CrossRef]
- Sridhar, N.; Metzger, B.D.; Beniamini, P.; Margalit, B.; Renzo, M.; Sironi, L.; Kovlakas, K. Periodic Fast Radio Bursts from Luminous X-ray Binaries. Astrophys. J. 2021, 917, 13. [Google Scholar] [CrossRef]
- Zhang, B. Unexpected emission pattern adds to the enigma of fast radio bursts. Nature 2020, 582, 344–346. [Google Scholar] [CrossRef]
- Xu, K.; Li, Q.C.; Yang, Y.P.; Li, X.D.; Dai, Z.G.; Liu, J. Do the Periodic Activities of Repeating Fast Radio Bursts Represent the Spins of Neutron Stars? Astrophys. J. 2021, 917, 2. [Google Scholar] [CrossRef]
- Thompson, A.R.; Clark, B.G.; Wade, C.M.; Napier, P.J. The Very Large Array. Astrophys. J. 1980, 44, 151–167. [Google Scholar] [CrossRef]
- Bannister, K.W.; Shannon, R.M.; Macquart, J.P.; Flynn, C.; Edwards, P.G.; O’Neill, M.; Osłowski, S.; Bailes, M.; Zackay, B.; Clarke, N.; et al. The Detection of an Extremely Bright Fast Radio Burst in a Phased Array Feed Survey. Astrophys. J. Lett. 2017, 841, L12. [Google Scholar] [CrossRef]
- CHIME/FRB Collaboration; Amiri, M.; Bandura, K.; Berger, P.; Bhardwaj, M.; Boyce, M.M.; Boyle, P.J.; Brar, C.; Burhanpurkar, M.; Chawla, P.; et al. The CHIME Fast Radio Burst Project: System Overview. Astrophys. J. 2018, 863, 48. [Google Scholar] [CrossRef]
- Spitler, L.G.; Scholz, P.; Hessels, J.W.T.; Bogdanov, S.; Brazier, A.; Camilo, F.; Chatterjee, S.; Cordes, J.M.; Crawford, F.; Deneva, J.; et al. A repeating fast radio burst. Nature 2016, 531, 202–205. [Google Scholar] [CrossRef] [PubMed]
- CHIME/FRB Collaboration; Amiri, M.; Bandura, K.; Bhardwaj, M.; Boubel, P.; Boyce, M.M.; Boyle, P.J.; . Brar, C.; Burhanpurkar, M.; Cassanelli, T.; et al. A second source of repeating fast radio bursts. Nature 2019, 566, 235–238. [Google Scholar] [CrossRef]
- CHIME/FRB Collaboration; Andersen, B.C.; Bandura, K.; Bhardwaj, M.; Boubel, P.; Boyce, M.M.; Boyle, P.J.; Brar, C.; Cassanelli, T.; Chawla, P.; et al. CHIME/FRB Discovery of Eight New Repeating Fast Radio Burst Sources. Astrophys. J. 2019, 885, L24. [Google Scholar] [CrossRef]
- Kumar, P.; Shannon, R.M.; Osłowski, S.; Qiu, H.; Bhandari, S.; Farah, W.; Flynn, C.; Kerr, M.; Lorimer, D.R.; Macquart, J.P.; et al. Faint Repetitions from a Bright Fast Radio Burst Source. Astrophys. J. 2019, 887, L30. [Google Scholar] [CrossRef]
- Luo, R.; Wang, B.J.; Men, Y.P.; Zhang, C.F.; Jiang, J.C.; Xu, H.; Wang, W.Y.; Lee, K.J.; Han, J.L.; Zhang, B.; et al. Diverse polarization angle swings from a repeating fast radio burst source. Nature 2020, 586, 693–696. [Google Scholar] [CrossRef]
- Zhang, Z.B.; Choi, C.S. An analysis of the durations of Swift gamma-ray bursts. Astron. Astrophys. 2008, 484, 293–297. [Google Scholar] [CrossRef]
- Zhang, Z.B.; Zhang, C.T.; Zhao, Y.X.; Luo, J.J.; Jiang, L.Y.; Wang, X.L.; Han, X.L.; Terheide, R.K. Spectrum-energy Correlations in GRBs: Update, Reliability, and the Long/Short Dichotomy. Publ. Astron. Soc. Pac. 2018, 130, 054202. [Google Scholar] [CrossRef]
- Zhang, Z.B.; Jiang, M.; Zhang, Y.; Zhang, K.; Li, X.J.; Zhang, Q. On the Spectral Peak Energy of Swift Gamma-Ray Bursts. Astrophys. J. 2020, 902, 40. [Google Scholar] [CrossRef]
- Luo, R.; Lee, K.; Lorimer, D.R.; Zhang, B. On the normalized FRB luminosity function. Mon. Not. R. Astron. Soc. 2018, 481, 2320–2337. [Google Scholar] [CrossRef]
- Caleb, M.; Stappers, B.W.; Rajwade, K.; Flynn, C. Are all fast radio bursts repeating sources? Mon. Not. R. Astron. Soc. 2019, 484, 5500–5508. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, B.; Nagamine, K.; Shi, J. The FRB 121102 Host Is Atypical among Nearby Fast Radio Bursts. Astrophys. J. 2019, 884, L26. [Google Scholar] [CrossRef]
- Zhang, B. The physical mechanisms of fast radio bursts. Nature 2020, 587, 45–53. [Google Scholar] [CrossRef] [PubMed]
- Ravi, V. The prevalence of repeating fast radio bursts. Nat. Astron. 2019, 3, 928–931. [Google Scholar] [CrossRef]
- Lu, W.; Piro, A.L.; Waxman, E. Implications of Canadian Hydrogen Intensity Mapping Experiment repeating fast radio bursts. Mon. Not. R. Astron. Soc. 2020, 498, 1973–1982. [Google Scholar] [CrossRef]
- Luo, R.; Men, Y.; Lee, K.; Wang, W.; Lorimer, D.R.; Zhang, B. On the FRB luminosity function—II. Event rate density. Mon. Not. R. Astron. Soc. 2020, 494, 665–679. [Google Scholar] [CrossRef]
- Caleb, M.; Flynn, C.; Bailes, M.; Barr, E.D.; Hunstead, R.W.; Keane, E.F.; Ravi, V.; van Straten, W. Are the distributions of fast radio burst properties consistent with a cosmological population? Mon. Not. R. Astron. Soc. 2016, 458, 708–717. [Google Scholar] [CrossRef]
- Niino, Y. Fast Radio Bursts’ Recipes for the Distributions of Dispersion Measures, Flux Densities, and Fluences. Astrophys. J. 2018, 858, 4. [Google Scholar] [CrossRef]
- Lu, W.; Piro, A.L. Implications from ASKAP Fast Radio Burst Statistics. Astrophys. J. 2019, 883, 40. [Google Scholar] [CrossRef]
- Zhang, G.Q.; Wang, F.Y. Energy function, formation rate, and low-metallicity environment of fast radio bursts. Mon. Not. R. Astron. Soc. 2019, 487, 3672–3678. [Google Scholar] [CrossRef]
- Bhattacharya, M.; Kumar, P. Population Modeling of Fast Radio Bursts from Source Properties. Astrophys. J. 2020, 899, 124. [Google Scholar] [CrossRef]
- Planck Collaboration; Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; et al. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar] [CrossRef]
- Fonseca, E.; Andersen, B.C.; Bhardwaj, M.; Chawla, P.; Good, D.C.; Josephy, A.; Kaspi, V.M.; Masui, K.W.; Mckinven, R.; Michilli, D.; et al. Nine New Repeating Fast Radio Burst Sources from CHIME/FRB. Astrophys. J. 2020, 891, L6. [Google Scholar] [CrossRef]
- Kirsten, F.; Snelders, M.P.; Jenkins, M.; Nimmo, K.; van den Eijnden, J.; Hessels, J.W.T.; Gawroński, M.P.; Yang, J. Detection of two bright radio bursts from magnetar SGR 1935 + 2154. Nat. Astron. 2021, 5, 414–422. [Google Scholar] [CrossRef]
- Bauer, D.F. Constructing confidence sets using rank statistics. J. Am. Stat. Assoc. 1972, 67, 687–690. [Google Scholar] [CrossRef]
- Hollander, M.; Wolfe, D.A.; Chicken, E. Nonparametric Statistical Methods; John Wiley & Sons: Hoboken, NJ, USA, 2013; Volume 751. [Google Scholar]
- Xiao, D.; Wang, F.; Dai, Z. The physics of fast radio bursts. Sci. China Phys. Mech. Astron. 2021, 64, 249501. [Google Scholar] [CrossRef]
- Thode, H.C. Testing for Normality, 1st ed.; CRC Press: Boca Raton, CA, USA, 2002. [Google Scholar]
- Li, L.B.; Huang, Y.F.; Zhang, Z.B.; Li, D.; Li, B. Intensity distribution function and statistical properties of fast radio bursts. Res. Astron. Astrophys. 2017, 17, 6. [Google Scholar] [CrossRef]
- Nan, R.; Li, D. The five-hundred-meter aperture spherical radio telescope (FAST) project. IOP Conf. Ser. Mater. Sci. Eng. 2013, 44, 012022. [Google Scholar] [CrossRef]
- Li, D.; Nan, R.; Pan, Z. The Five-hundred-meter Aperture Spherical radio Telescope project and its early science opportunities. In Proceedings of the Neutron Stars and Pulsars: Challenges and Opportunities after 80 Years, Beijing, China, 20–24 August 2012; van Leeuwen, J., Ed.; Cambridge University Press: Cambridge, UK, 2013; Volume 291, pp. 325–330. [Google Scholar] [CrossRef]
- Zhang, Z.B.; Kong, S.W.; Huang, Y.F.; Li, D.; Li, L.B. Detecting radio afterglows of gamma-ray bursts with FAST. Res. Astron. Astrophys. 2015, 15, 237–251. [Google Scholar] [CrossRef]
- Spitler, L.G.; Cordes, J.M.; Hessels, J.W.T.; Lorimer, D.R.; McLaughlin, M.A.; Chatterjee, S.; Crawford, F.; Deneva, J.S.; Kaspi, V.M.; Wharton, R.S.; et al. Fast Radio Burst Discovered in the Arecibo Pulsar ALFA Survey. Astrophys. J. 2014, 790, 101. [Google Scholar] [CrossRef]
- Crawford, F.; Rane, A.; Tran, L.; Rolph, K.; Lorimer, D.R.; Ridley, J.P. A search for highly dispersed fast radio bursts in three Parkes multibeam surveys. Mon. Not. R. Astron. Soc. 2016, 460, 3370–3375. [Google Scholar] [CrossRef][Green Version]
- Lawrence, E.; Vander Wiel, S.; Law, C.; Burke Spolaor, S.; Bower, G.C. The Nonhomogeneous Poisson Process for Fast Radio Burst Rates. Astron. J. 2017, 154, 117. [Google Scholar] [CrossRef]
- Bera, A.; Bhattacharyya, S.; Bharadwaj, S.; Bhat, N.D.R.; Chengalur, J.N. On modelling the Fast Radio Burst population and event rate predictions. Mon. Not. R. Astron. Soc. 2016, 457, 2530–2539. [Google Scholar] [CrossRef]
- Aggarwal, K. Observational Effects of Banded Repeating FRBs. Astrophys. J. 2021, 920, L18. [Google Scholar] [CrossRef]
- Zhang, Z.B.; Chandra, P.; Huang, Y.F.; Li, D. The Redshift Dependence of the Radio Flux of Gamma-Ray Bursts and Their Host Galaxies. Astrophys. J. 2018, 865, 82. [Google Scholar] [CrossRef]
- Macquart, J.P.; Ekers, R. FRB event rate counts - II. Fluence, redshift, and dispersion measure distributions. Mon. Not. R. Astron. Soc. 2018, 480, 4211–4230. [Google Scholar] [CrossRef]
- Macquart, J.P.; Shannon, R.M.; Bannister, K.W.; James, C.W.; Ekers, R.D.; Bunton, J.D. The Spectral Properties of the Bright Fast Radio Burst Population. Astrophys. J. 2019, 872, L19. [Google Scholar] [CrossRef]
- Salvaterra, R.; Campana, S.; Vergani, S.D.; Covino, S.; D’Avanzo, P.; Fugazza, D.; Ghirlanda, G.; Ghisellini, G.; Melandri, A.; Nava, L.; et al. A Complete Sample of Bright Swift Long Gamma-Ray Bursts. I. Sample Presentation, Luminosity Function and Evolution. Astrophys. J. 2012, 749, 68. [Google Scholar] [CrossRef]
- Pescalli, A.; Ghirlanda, G.; Salvaterra, R.; Ghisellini, G.; Vergani, S.; Nappo, F.; Salafia, O.; Melandri, A.; Götz, D. The rate and luminosity function of long Gamma Ray Bursts. Astron. Astrophys. 2015, 587. [Google Scholar] [CrossRef]
- Deng, C.M.; Wang, X.G.; Guo, B.B.; Lu, R.J.; Wang, Y.Z.; Wei, J.J.; Wu, X.F.; Liang, E.W. Cosmic Evolution of Long Gamma-Ray Burst Luminosity. Astrophys. J. 2016, 820, 66. [Google Scholar] [CrossRef]
- Gehrels, N. Confidence Limits for Small Numbers of Events in Astrophysical Data. Astrophys. J. 1986, 303, 336. [Google Scholar] [CrossRef]
- James, C.W.; Ekers, R.D.; Macquart, J.P.; Bannister, K.W.; Shannon, R.M. The slope of the source-count distribution for fast radio bursts. Mon. Not. R. Astron. Soc. 2019, 483, 1342–1353. [Google Scholar] [CrossRef]
- Heintz, K.E.; Prochaska, J.X.; Simha, S.; Platts, E.; Fong, W.f.; Tejos, N.; Ryder, S.D.; Aggerwal, K.; Bhandari, S.; Day, C.K.; et al. Host Galaxy Properties and Offset Distributions of Fast Radio Bursts: Implications for Their Progenitors. Astrophys. J. 2020, 903, 152. [Google Scholar] [CrossRef]
- Pleunis, Z.; Good, D.C.; Kaspi, V.M.; Mckinven, R.; Ransom, S.M.; Scholz, P.; Bandura, K.; Bhardwaj, M.; Boyle, P.J.; Brar, C.; et al. Fast Radio Burst Morphology in the First CHIME/FRB Catalog. Astrophys. J. 2021, 923, 1. [Google Scholar] [CrossRef]
- Marcote, B.; Nimmo, K.; Hessels, J.W.T.; Tendulkar, S.P.; Bassa, C.G.; Paragi, Z.; Keimpema, A.; Bhardwaj, M.; Karuppusamy, R.; Kaspi, V.M.; et al. A repeating fast radio burst source localized to a nearby spiral galaxy. Nature 2020, 577, 190–194. [Google Scholar] [CrossRef]
- Piro, L.; Bruni, G.; Troja, E.; O’Connor, B.; Panessa, F.; Ricci, R.; Zhang, B.; Burgay, M.; Dichiara, S.; Lee, K.J.; et al. The fast radio burst FRB 20201124A in a star-forming region: Constraints to the progenitor and multiwavelength counterparts. Astron. Astrophys. 2021, 656, L15. [Google Scholar] [CrossRef]
- Bhardwaj, M.; Gaensler, B.M.; Kaspi, V.M.; Landecker, T.L.; Mckinven, R.; Michilli, D.; Pleunis, Z.; Tendulkar, S.P.; Andersen, B.C.; Boyle, P.J.; et al. A Nearby Repeating Fast Radio Burst in the Direction of M81. Astrophys. J. Lett. 2021, 910, L18. [Google Scholar] [CrossRef]
- Ravi, V.; Law, C.J.; Li, D.; Aggarwal, K.; Burke-Spolaor, S.; Connor, L.; Lazio, T.J.W.; Simard, D.; Somalwar, J.; Tendulkar, S.P. The host galaxy and persistent radio counterpart of FRB 20201124A. arXiv 2021, arXiv:2106.09710. [Google Scholar] [CrossRef]
- Bhandari, S.; Heintz, K.E.; Aggarwal, K.; Marnoch, L.; Day, C.K.; Sydnor, J.; Burke-Spolaor, S.; Law, C.J.; Xavier Prochaska, J.; Tejos, N.; et al. Characterizing the Fast Radio Burst Host Galaxy Population and its Connection to Transients in the Local and Extragalactic Universe. Astron. J. 2022, 163, 69. [Google Scholar] [CrossRef]
- Caleb, M.; Spitler, L.G.; Stappers, B.W. One or several populations of fast radio burst sources? Nat. Astron. 2018, 2, 839–841. [Google Scholar] [CrossRef]
- Palaniswamy, D.; Li, Y.; Zhang, B. Are There Multiple Populations of Fast Radio Bursts? Astrophys. J. 2018, 854, L12. [Google Scholar] [CrossRef]
- Hessels, J.W.T.; Spitler, L.G.; Seymour, A.D.; Cordes, J.M.; Michilli, D.; Lynch, R.S.; Gourdji, K.; Archibald, A.M.; Bassa, C.G.; Bower, G.C.; et al. FRB 121102 Bursts Show Complex Time-Frequency Structure. Astrophys. J. Lett. 2019, 876, L23. [Google Scholar] [CrossRef]
- Nimmo, K.; Hessels, J.W.T.; Keimpema, A.; Archibald, A.M.; Cordes, J.M.; Karuppusamy, R.; Kirsten, F.; Li, D.Z.; Marcote, B.; Paragi, Z. Highly polarized microstructure from the repeating FRB 20180916B. Nat. Astron. 2021, 5, 594–603. [Google Scholar] [CrossRef]
- CHIME/FRB Collaboration; Amiri, M.; Andersen, B.C.; Bandura, K.M.; Bhardwaj, M.; Boyle, P.J.; Brar, C.; Chawla, P.; Chen, T.; Cliche, J.F.; et al. Periodic activity from a fast radio burst source. Nature 2020, 582, 351–355. [Google Scholar] [CrossRef]
- Rajwade, K.M.; Mickaliger, M.B.; Stappers, B.W.; Morello, V.; Agarwal, D.; Bassa, C.G.; Breton, R.P.; Caleb, M.; Karastergiou, A.; Keane, E.F.; et al. Possible periodic activity in the repeating FRB 121102. Mon. Not. R. Astron. Soc. 2020, 495, 3551–3558. [Google Scholar] [CrossRef]
- Cruces, M.; Spitler, L.G.; Scholz, P.; Lynch, R.; Seymour, A.; Hessels, J.W.T.; Gouiffés, C.; Hilmarsson, G.H.; Kramer, M.; Munjal, S. Repeating behaviour of FRB 121102: Periodicity, waiting times, and energy distribution. Mon. Not. R. Astron. Soc. 2021, 500, 448–463. [Google Scholar] [CrossRef]
| TNS Name | MHz | (pc cm−3) | (pc cm−3) | (pc cm−3) | (ms) | (Jy) | (Jy ms) | z | E (1039 erg) | (Jy ms) |
|---|---|---|---|---|---|---|---|---|---|---|
| FRB 20121102A | 1375 | 188.00 | 369.00 | 0.31 | 0.13 | 0.36 | ||||
| FRB 20171019A | 1297 | 37.00 | 423.80 | 40.50 | 219.00 | 0.35 | 34.01 | 101.62 | ||
| FRB 20180814A | 600 | 87.00 | 102.38 | 8.08 | 21.00 | 0.09 | 0.13 | 22.57 | ||
| FRB 20180908B | 600 | 38.00 | 157.70 | 2.70 | 0.13 | 0.04 | 2.03 | |||
| FRB 20180916B | 600 | 200.00 | 149.70 | 7.64 | 8.10 | 0.12 | 0.12 | 10.26 | ||
| FRB 20181017A | 600 | 43.00 | 1238.00 | 0.79 | 16.00 | 1.03 | 60.07 | 8.50 | ||
| FRB 20181030A | 600 | 40.00 | 63.50 | 12.37 | 7.30 | 0.05 | 0.02 | 4.75 | ||
| FRB 20181119A | 600 | 34.00 | 330.00 | 0.94 | 2.50 | 0.28 | 0.24 | 1.77 | ||
| FRB 20181128A | 600 | 112.00 | 338.20 | 1.81 | 4.40 | 0.28 | 0.46 | 3.45 | ||
| FRB 20190116B | 600 | 20.00 | 423.60 | 1.87 | 2.80 | 0.35 | 0.52 | 1.80 | ||
| FRB20190117A | 600 | 48.00 | 345.30 | 5.90 | 0.29 | 0.64 | 6.36 | |||
| FRB 20190208A | 600 | 72.00 | 508.20 | 2.00 | 0.42 | 0.60 | 1.70 | |||
| FRB 20190209A | 600 | 46.00 | 378.60 | 0.54 | 2.00 | 0.32 | 0.28 | 1.25 | ||
| FRB 20190213A | 600 | 43.00 | 608.50 | 4.00 | 3.00 | 0.51 | 1.46 | 1.80 | ||
| FRB 20190212A | 600 | 49.00 | 252.40 | 2.50 | 0.21 | 0.13 | 2.67 | |||
| FRB 20190222A | 600 | 87.00 | 373.60 | 2.53 | 7.50 | 0.31 | 1.00 | 5.45 | ||
| FRB 20190303A | 600 | 29.00 | 192.80 | 2.30 | 0.16 | 0.06 | 2.47 | |||
| FRB 20190417A | 600 | 78.00 | 1300.50 | 1.70 | 1.08 | 7.40 | 3.10 | |||
| FRB 20190604A | 600 | 32.00 | 520.60 | 8.30 | 0.43 | 2.64 | 5.00 | |||
| FRB 20190711A | 23.8 | 56.40 | 536.70 | 5.23 | 34.00 | 0.45 | 9.88 | 17.70 | ||
| FRB 20190907A | 600 | 53.00 | 256.50 | 0.90 | 0.21 | 0.05 | 1.10 |
| FRB Sample | Statistic Value | The Critical Value | p-Value | Methods | |
|---|---|---|---|---|---|
| Non-repeating | 0.814 | 1.084 | 0.035 | A–D test | |
| Repeating | 0.427 | 0.963 | 0.285 | A–D test | |
| All | 0.727 | 1.085 | 0.058 | A–D test | |
| Repeating and Non-repeating FRBs | 4328.5 | ... | 0.031 | M–W–W test |
(Jy ms) | (sky −1 day −1) | Reference | Coefficient A (103 sky −1 day −1) | FEB Class |
|---|---|---|---|---|
| 3 | Thornton et al. [2] | non-repeaters | ||
| 0.35 | Spitler et al. [84] | non-repeaters | ||
| 2 | Keane and Petroff [7] | non-repeaters | ||
| 1.8 | Law et al. [8] | non-repeaters | ||
| 4 | Rane et al. [11] | non-repeaters | ||
| 0.13–1.5 | Champion et al. [9] | non-repeaters | ||
| 3.8 | Crawford et al. [85] | non-repeaters | ||
| 0.03 | Li et al. [80] | non-repeaters | ||
| 6 | 587 | Lawrence et al. [86] | non-repeaters | |
| 2 | Bhandari et al. [12] | non-repeaters | ||
| 26 | Shannon et al. [15] | non-repeaters | ||
| 8 | Farah et al. [16] | non-repeaters | ||
| 2 | Parent et al. [17] | non-repeaters | ||
| 5 | CHIME/FRB Collaboration et al. [6] | non-repeaters | ||
| 0.36 | this work | repeaters |
| Sample | A | ||||
|---|---|---|---|---|---|
| Repeating FRBs | 0.17 | ||||
| Non-repeating FRBs | 3.17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Li, L.; Zhang, Z.; Li, Q.; Luo, J.; Jiang, M. The Statistical Similarity of Repeating and Non-Repeating Fast Radio Bursts. Universe 2022, 8, 355. https://doi.org/10.3390/universe8070355
Zhang K, Li L, Zhang Z, Li Q, Luo J, Jiang M. The Statistical Similarity of Repeating and Non-Repeating Fast Radio Bursts. Universe. 2022; 8(7):355. https://doi.org/10.3390/universe8070355
Chicago/Turabian StyleZhang, Kongjun, Longbiao Li, Zhibin Zhang, Qinmei Li, Juanjuan Luo, and Min Jiang. 2022. "The Statistical Similarity of Repeating and Non-Repeating Fast Radio Bursts" Universe 8, no. 7: 355. https://doi.org/10.3390/universe8070355
APA StyleZhang, K., Li, L., Zhang, Z., Li, Q., Luo, J., & Jiang, M. (2022). The Statistical Similarity of Repeating and Non-Repeating Fast Radio Bursts. Universe, 8(7), 355. https://doi.org/10.3390/universe8070355






