Abstract
We consider a QCD cold-plasma-motivated Equation of State (EOS) to examine the impact of an Anomalous Magnetic Moment (AMM) coupling and small shape deformations on the static oblate and prolate core shapes of quark stars. Using the Fogaça QCD-motivated EOS, which shifts from the high-temperature, low-chemical-potential quark–gluon plasma environment to the low-temperature, high-chemical-potential quark stellar core environment, we consider the impact of an AMM coupling with a metric-induced shape deformation parameter in the Tolman–Oppenheimer–Volkov (TOV) equations. The AMM coupling includes a phenomenological scaling that accounts for the weak and strong field characteristics in dense matter. The EOS is developed using a hard gluon and soft gluon decomposition of the gluon field tensor and using a mean-field effective mass for the gluons. The AMM is considered using the Dirac spin tensor coupled to the EM field tensor with quark-flavor-based magnetic moments. The shape parameter is introduced in a metric ansatz that represents oblate and prolate static stellar cores for modified TOV equations. These equations are numerically solved for the final mass and radius states, representing the core collapse of a massive star with a phase transition leading to an unbound quark–gluon plasma. We find that the combined shape parameter and AMM effects can alter the coupled EOS–TOV equations, resulting in an increase in the final mass and a decrease in the final equatorial radius without collapsing the core into a black hole and without violating causality constraints; we find maximum mass values in the range 1.6 Mʘ < M < 2.5 Mʘ. These states are consistent with some astrophysical, high-mass magnetar/pulsar and gravity wave systems and may provide evidence for a core that has undergone a quark–gluon phase transition such as PSR 0943 + 10 and the secondary from the GW 190814 event.
1. Introduction
There has been great interest in finding more realistic, QCD-based Equations of State (EOSs) for compact objects since the discovery of anomalous, compact, astrophysical objects, such as the stellar remnant from the energetic hypernova 2006gy [1]. This event, caused by the sudden collapse of a high-mass star, gave rise to final-state mass and radius values that do not agree very well with standard, compact stellar core models. The ongoing observational datasets also include the anomalous X-ray pulsar [2] RX J1856 [3,4] and pulsars such as PSR 0943 + 10 [5], PSR B1828-11 [6], PSR Jo751 + 1807 [7], PSR B1642-03, PSR J1614-2230 and PSR J0348-0432, along with potential magnetar candidates [8] where masses, radii, dual luminosity peaks and cooling rates do not always give excellent fits to conventional models based upon degenerate neutron matter. In general, as a massive, electric-charge-neutral star collapses with a core mass between 1.4 Mʘ and 2.3 Mʘ, the resulting object is a rapidly spinning neutron star with a strong magnetic field and a radius of about 10 km; details of these objects are being measured with the Neutron Star Interior Composition Explorer (NICER) satellite and will be improved upon by the Large Observatory for X-ray Timing (LOFT) mission, as described in an extensive review by Burgio [9]. For masses beyond this range, a black hole forms where the no-hair theorems indicate that only the mass and spin of a neutral core can be measured [10]. The central core of the neutron star consists of confined quarks under high pressure. At these pressures, it is possible for the confined quarks to undergo a deconfining phase transition while not forming a black hole. Such a phase transition can result in a smaller radius and higher spin core; these smaller objects are often generally characterized as quark stars, and they can have higher-order multipole moments and various I-Love-Q characterizations, as described in the review by Baym [11], and can find effective no-hair theorems for quark stars and neutron stars [12].
As the observational data have become more robust and refined, more detailed models have emerged to help understand the varied mechanisms at play in dense QCD matter. Several models are gaining support from the observations of the quark–gluon plasma, QGP, demonstrating the existence of a high-temperature, low-chemical-potential state of unconfined quarks, as seen at the SPS [13], LHC [14] and RHIC [15,16] laboratories. In recent years, the QGP data have expanded to include the determination of relativistic, QCD-based transport coefficients [17] and measurements of the overall bulk viscosity for free quark matter [18,19]. Observations of X-ray, γ-ray and quasi-periodic objects, such as SAS J1808.4 -3658, which has a 2.49 ms period [20], have been used to understand how the environment [21] and ambient mass density impact fundamental QCD parameters and potentials [22]. The LIGO-VIRGO detectors also observe events that appear to correspond to massive compact secondaries, such as the GW 190814 [23] event, indicating a secondary with a mass near or above 2.5 Mʘ. However, it is difficult to find a unique event without, perhaps, reasonable competing scenarios. For instance, in the GW 190814 event, scenarios could involve the 23 Mʘ primary with a secondary neutron star that is rapidly rotating [24] and could form a black hole by itself or there may be a tertiary object [25] involved which then gives mass values near the conventional neutron star limit of 2.3 Mʘ for the secondary.
Various EOSs have been used to link the strong coupling constant and quark masses to the local density function using the real-time formalism and the Dyson–Schwinger gap equation at finite temperature [26]. In this way, high-density compact cores can be used to give a density-dependent strong coupling that can be expressed as an analytic function that is suitable for EOS and phase transition analysis [27] with high chemical potentials and lower temperatures. For such a case, the overall charge, density and chemical potentials are constrained by overall charge neutrality for particle number density nj, mass density ρf and electric charge qj for particle type j or flavor f where ∑qf nf = qe ne and ρB = ρu + ρd + ρs. An additional constraint from the three light-quark-flavor, weak-interaction equilibrium conditions from quark interactions d↔u + e− + ῡe, s↔u + e− + ῡe, s + u↔d + u constrains the chemical potentials where the neutrinos and antineutrinos exit the core on a short time scale compared to the core formation process, effectively causing their chemical potentials to vanish, resulting in μd = μu + μe, μd = μs. Then, the EOS can be expressed as a pressure function that is related to the chemical potential from P = −∂U/∂V = n2∂(ε/n)/∂n = nμ − ε, where ε is the energy density, and the chemical potential is μ = ∂ε/∂n. For the massless quark case, this gives a direct comparison to the MIT bag model with bag constant , where 3P = (ε − 4) =ε − 4(3μ4/4π), linking [28] the vacuum pressure bag constant to the quark chemical potentials which are energy dependent. Other compact core models focus on modified EOSs for various states of dense matter in the QCD ground state of Color-Flavor-Locked (CFL) dense matter [29,30,31] with 2D and 3D color superconductivity [32,33,34] and in the Nambu–Jona-Lasinio (NJL) model [35]. Many models admit to a comparison to versions of the generalized MIT bag model [36] approach and include QCD mean field approximations [37,38] along with computationally intensive numerical lattice approaches that are being improved to accommodate finite-temperature chemical potentials [39]. Refined models include crustal effects [40], deformations [41], layering [42], cooling rates [43], strange quark cores [44], post-merger analysis [45], finite-temperature boson stars [46], kaon condensation [47,48], superconducting color vector potential effects [30,49], phase transitions and different crystalline cores [50,51,52].
In addition, collapsed stellar cores are, in general, rotating and often possess very strong magnetic fields [53]. For collapsed stellar cores composed of self-bound quark matter, the magnetic field energy density should not exceed the vacuum-bound state energy density for a quark system with an energy of order 1 GeV within a diameter of about 1 fm which results in a maximum magnetic field in the order of:
Detailed mechanisms for achieving magnetic fields of this magnitude are not well understood, and high resolution data from the NASA NICER have given a surface map of PSR J0030 + 0451 showing a complex multipole field structure [54]. A simple and direct method for estimating the magnetic field strength of a collapsed star is to assume that the collapse is magnetic flux conserved from the initial state to the final state, where strong, main-sequence progenitor magnetic fields can be ~1 T with a radius of 1 Gm at 10 Mʘ and collapse to a radius of order 10 km giving:
However, these overly optimistic estimates do not account for the significant mass loss that makes this estimate untenable for most cases. If we consider the size cutoff to be the Schwarzschild radius, R = 2GM/c2, when the magnetic field energy density and the gravitational field energy density are the same, then we find similar maximum field strengths:
Here, we examine the low-temperature interactions that can be expressed as hard, short-wavelength gluons and soft, long-wavelength gluons with an EOS that includes a magnetic field and where the static compact core is distorted into an oblate or prolate shape necessitating the use of the modified TOV equations. One expects the quarks and gluons to contribute differently to the EOS due to their different spin and color degrees of freedom. For a compact core at the Fermi temperature, estimated by assuming a quark separation on the order of a fraction of a neutron with number density n and quark mass m, the Fermi temperature is where is the reduced Planck’s constant, and k is the Boltzmann constant. If we consider the pressure for the noninteracting particles expressed as being due to free-spin ½ fermions and the pressure being due to massless spin-1 bosons for an SU(3)c color symmetry where the number of degrees of freedom depends on spin, color and flavor degrees of freedom, then the pressures are:
indicating that the gluons can play a considerable role in the total pressure of the compact core. The magnetic field resulting from the internal current densities also contributes to the pressure via a Lorentz force density which, by applying Maxwell’s equations, can be expressed as Fj = εjkl jk Bl = −∂iTji where Tji = −(1/2μo) [B2 δji − 2BjBi], resulting in pressure-like forces both parallel and perpendicular to the magnetic field direction, giving rise to anisotropic magnetic field interactions [55]. For the observed field strengths, these magnetic pressure terms can be similar in magnitude to the quark and gluon pressure terms at the Fermi temperature of the stellar core: pmag/pquark ~ 0.5. Fields of this strength alter the EOS and allow for a more massive core where crustal rigidity and rapid rotation [56] can deform [57] the stellar core into a prolate or oblate shape and can alter the long-term stability of the star [58]. For instance, Tatsumi found that when all the quarks stay in the lowest Landau level, there is a critical magnetic field where the EOS can support more mass in a static spherical geometry [59]. However, in general, the magnetic field alters the core shape to be oblate or prolate, which, for neutron stars, results in small changes in the equatorial radius and maximum mass. Such deformations have been observed in rapidly spinning neutron stars, magnetars and tidally deformed binaries [60]. Several shape parameters have been used for neutron star curst deformations and CFL quark stars [61], including oblateness, which is the ratio of the polar radius to the equatorial radius, γ = Rp/Re, and eccentricity defined as e2 = 1 − γ2. For slow-rotating neutron stars, e~10−8, for fast-rotating neutron stars with high magnetic fields, e~0.01, and, with tidal distortions, e > 0.05. To cover slightly more than this range in oblate and prolate cases, we will examine cases where the oblateness ranges from 0.85 to 1.15. For neutron and quark stars, a static shape deformation can be explored with modified TOV equations by introducing a shape parameter into the metric [62]. The structure of the internal magnetic field is difficult to ascertain, in part due to phase change or superconducting boundaries, but some authors parametrize the field by phenomenological models that match a central field strength to the zero pressure surface. For instance, Chatterjee [63] examined several models with improvements on the widely used Sigmoid-like contributions using linear and quadratic exponentials and fixed central core values that match surface values which can be expressed as functions which are not self-consistent solutions to the Einstein–Maxwell equations. Generally, they depend on the ratio of baryon number density to nuclear density, part of which has the form [64,65]: B(nB/no) = Bs + Bc [1 − exp(−β (nB/no)γ)] with two parameters β and γ, which they generalize to a multipole form. As noted by Kayanikhoo [66], these models for neutron stars have surface magnetic fields in a range of about 1012–1014 G with corresponding internal fields from about 1018 to 1020 G. However, for an internal EOS with gravitational and magnetic sources of pressure, there exists an inflection point in the mass vs. radius curve, the Mallick [57] critical point, where the magnetic pressure and the matter pressure are balanced. When the magnetic field is increased beyond this point, there is no longer a maximum to the mass even though the gravitational energy is greater than the magnetic energy, indicating the limit to the application of the EOS. Here, we find the maximum field strength is 3.2 × 1018 G, making this our cutoff maximum value.
The properties of quark matter in a strong magnetic field [67] lead to phenomena such as chiral symmetry breaking [68], magnetic catalysis and critical phenomena. The coupling of the quark AMM to an external magnetic field results in shifts in magnetic susceptibility, changes in confined quark state masses [69], changes in coupling constants [70], shifts in antiscreening [69,71], catalyzing strange matter formation and strange stars [72] and induces inverse magnetic catalysis [73]. While it is known that both the Maxwell electromagnetic AMM and the chromomagnetic QCD AMM can be generated dynamically, here, we are only considering the Maxwell AMM interactions where applications include magnetars, neutron star mergers, heavy ion collisions and early cosmology. In particular, shifts in the two-flavor meson [74] and dilepton [75] spectra of mass values provide insight about the magnitude of the interaction, as observed in particle experiments. Insights have also been gained through lattice simulations used to restrict the form and magnitude of the quark AMM dynamically generated through the spontaneous breaking of chiral symmetry to determine the QCD phase structure in the presence of strong external magnetic fields [76]. Of special interest here are the changes in the QCD phase diagram [77] due to the presence of the quark AMM and magnetic field [78,79] altering the phase boundaries. The magnetic field interaction shifts the critical point and the phase transition boundary, causing a shift in the deconfinement parameters and altering the mass and size of the stellar quark core. For weak fields in a constituent quark model, one can estimate the up- and down-quark AMM couplings using the known magnetic moments of the proton and neutron to find [80] κu = 0.2916 GeV−1 and κd = 0.35986 GeV−1. In this case, the well-known Schwinger term [81] accounts for the interaction; however, as shown by Ferrer [82], this is not the case for the strong field. Using the one-loop fermion self-energy correction for strong magnetic fields in dense matter, they found that the AMM term makes an insignificant contribution to the EOS. In particular, if we ignore the chemical potential and temperature, the critical value where the weak-field Schwinger term is appropriate corresponds to when the magnetic energy, ℏωc, where ω = qB/mc in cgs units, is the cyclotron frequency and is equal to the rest-mass energy mc2. For light quarks where mu~md~5 MeV/c2, the critical field is near Bc(u,d) = 4.4 × 1015 Gauss. There is a small mass shift due to the light quark mass differences; however, it is either significantly below or above this value where the mass difference does not impact the result. To introduce the field transition from weak to strong regimes, we introduce a phenomenological Sigmoid step-down function in the AMM term which removes the AMM interaction above the critical value. Overall, this softens the EOS and lowers the maximum core mass value. To explore the resulting changes in the EOS with a magnetic field, we look at separating the QCD interaction into soft and hard gluon modes, as are often used for the cold quark–gluon QCD condensate [83,84] method developed by Fogaça [85] with magnetic field terms that exhibit an external field and an internal field coupling between the anomalous magnetic moment, AMM, of the quarks and the magnetic field of the form σμν Fμν where σμν is the spin tensor that is proportional to the commutator of the Dirac matrices, and Fμν is the EM field tensor in a fashion similar to Mao [86]. Supporting the more massive and smaller compact core consistent with observations that can be formed by the deconfinement of the quarks requires a modified EOS. Here, we examine such an EOS that results in changes in the maximum mass and radius values for quark stars by including both the magnetic couplings in the EOS and the shape-parameter-generalized TOV equations. In the next section, we summarize the QCD-motivated quark–gluon condensation EOS with a magnetic field and AMM coupling applied in the mean field, followed by the TOV equations. We then numerically solve for the mass–radius dependence and discuss the resulting values with constraints on causality and stability and a comparison of compactness.
2. QCD-Motivated EOS
The EOS of interest here is the cold QGP model of Fogaça modified to include the AMM quark interactions and magnetic field. The method provides a way to extend the high-temperature, low-chemical-potential system to a low-temperature, high-chemical-potential stellar core by decomposing the gluon field into high-momentum hard gluons and low-momentum soft gluons. The hard gluon terms are simplified in the mean field limit, and the soft gluons are replaced by matrix elements of the plasma gluon field. Here, we consider our system to be a remnant quark stellar core that is in weak force equilibrium and in an electric charge neutral state. To find the gluon and quark pressure terms, consider the QCD-core Lagrangian for interacting quarks with flavors denoted by f and the SU(3) generators given by Ta with structure constants fabc, where a is the color index, q is the electric charge, g is the strength of the color coupling and κf = S diag(au, ad) is the AMM coupling with a Sigmoid function, S, to adjust for strong and weak magnetic field regimes, given as:
where the EM tensor, the gluon field tensor and the spin tensors are defined as:
for Dirac matrices in the standard representation with the magnetic field aligned in the positive z-direction using an electromagnetic four-vector potential component in the y-direction Aμ = (A0, A1, A2, A3) = (0, 0, xB, 0). Initially, we consider a system with one flavor and all quarks with the same mass and will later add the contributions for each flavor, allowing us to use Bc = 4.4 × 1015 G, and the result is not sensitive to the slope parameter α = 1 G−1. We decompose the gluon field into low momentum, Aaμ, or soft gluons, and high momentum, αaμ, or hard gluons, using the binomial ansatz:
where the long-wavelength, low-momentum gluons are responsible for the long-range strong force and the short-wavelength, high-momentum gluons give rise to the short-range strong force. Assuming high gluon occupation numbers at the high cold plasma density and taking the hard gluon term to be a function of coordinates then, in the mean field approximation, the gluons in the core can be described by the conditions:
The mean field terms have non-zero matrix elements that arise from the quadratic field terms and the vector potential terms, and the gluons act with an effective mass mG, resulting in a total pressure [58] as a function quark number density n, quark mass mq, strong coupling g, quark degrees of freedom γQ = (2 sf) for spin s and flavor f, quark AMM expressed in terms of the quark charge qf, electron charge, e, αe, and magnetic field B expressed as:
which corresponds to a sum of the hard gluon term, the soft gluon term, the quark term, which includes the AMM term, and the magnetic field term, where the total quark pressure can be found by summing each flavor for u, d and s quarks—quarks heavier than the s quark—giving rise to radial oscillation instabilities that are not included in the sum [28]; for an analysis of charm star stability, see [87,88]. Here, the baryon number density is nB = (nu + nd + ns)/3, and the nuclear number density is n0 = 0.17 fm−3. For numerical studies, we consider the optimized values of Fogaça; for separate quark terms, we take mu = 2.16 MeV, md = 4.67 MeV and ms = 93 MeV from the Particle Data Group [89], the gluon effective mass is set to a value that keeps the core n in the stable zone for the mass vs. radius curve, γQ = 3 for spin ½ and flavor f = 3 degrees of freedom for u, d and s quarks, and the strong coupling in this regime is given by αs = g2/4π = 0.01 where g = 2.7. To characterize the overall stiffness and causality of the EOS, we also calculate the speed of sound in the core and the compressibility k given by:
It is useful to compare these results to the free quark MIT bag model. If we denote the bag constant by , then the pressure p, the baryon density ρB, the speed of sound cs and compressibility κ are given by:
When the gluon terms and quark masses are set to zero, then Equations (9) and (11) agree by identifying the baryon density as one third of the quark density with no bag constant; this is the classic polytrope often used for high-mass white dwarf stars with degenerate relativistic matter with p~ρ4/3. With soft gluons and massless quarks, the gluons produce a term that corresponds to the bag constant given by the effective gluon mass. Instead of using a mean quark mass, Equation (9) can be extended by including a quark term for each flavor using the effective mass of each quark. Using these values in Equation (9) yields an EOS that can be used with the TOV equations to find end-state mass and radius values for the three-flavor cold quark plasma stellar core with an AMM quark term. In Figure 1, we plot EOS pressures and comparison values of dimensionless compressibility factors and sound speeds for a range of typical number densities expected in the core.
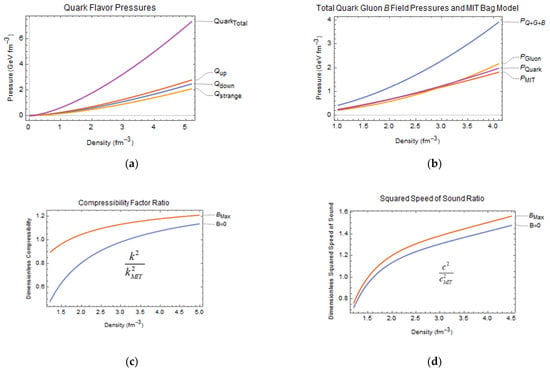
Figure 1.
(a) Each quark flavor pressure and the total core pressure showing a weak dependence on quark mass values. (b) The total quark, gluon and magnetic fields pressures shown with the individual quark, gluon and MIT bag model pressures for a magnetic field at 3.2 × 1018 G and the bag model constant at 0.38 GeV/fm3. (c) Compressibility factors expressed as dimensionless ratios compared to the MIT bag model with a vacuum bag constant of 0.2 GeV/fm3 for no magnetic field and for the maximum field of 3.2 × 1018 G, (d) dimensionless squared speed compared to the MIT bag model for the case of no magnetic field and the same bag constant and for the case of the maximum magnetic field of 3.2 × 1018 G as a function of core density.
The numerical study of the EOS shows the importance of the gluon terms where the soft gluons establish the effective bag constant and the hard gluons display a quadratic dependence on density. Each flavor term contributes to the pressure, with the lighter quarks contributing slightly more pressure, and, as the density increases, the compressibility and the speed of sound increase. Before solving for the core mass, we want the EOS to represent stable compact matter [89]. We select the stability criterion from Franzon [90], imposed for strange matter stability [91,92], where the stability constraint for this EOS can be expressed in terms of the effective gluon mass and coupling in Equation (9) by requiring the bag constant to be in the range: 38 MeV/fm3 < < 75.7 MeV/fm3.
3. TOV Framework
We adopt the method of Zubairi [62] and Yanis [93], which includes deformation and an anisotropic magnetic field, which is similar to the methods developed by Thorne and Hartle [94] for the gravitational field for a static, axisymmetric, oblate/prolate, ellipsoidal mass. In this case, the polar z-direction is scaled by a deformation parameter γ so that z = γr where r is the equatorial radial direction. Then, an oblate shape corresponds to γ < 1, a prolate shape corresponds to γ > 1 and a spherical shape corresponds to γ = 1. This parametrization allows for the field equations to maintain an analytic form as modified TOV equations. The Einstein field equations can be found using the metric ansatz:
with Einstein and stress–energy tensors given by:
the resulting modified TOV equations for the pressure and mass are:
where the EOS, Equation (9), gives the pressure term from the effective quark–gluon Lagrangian, the radius of the object is defined to be where the pressure vanishes and the total mass M is the product of the deformation constant and the mass inside the zero-pressure boundary, M = γ m.
4. Numerical Solutions
We numerically solve the coupled system of equations using the adaptive NDSolve for stiff systems in Mathematica [95,96,97]. Using the EOS given by Equation (9) and the coupled TOV system of Equation (14) and Equation (15), we solve for the mass and pressure functions. The equatorial radius is taken as the radial value in the equatorial plane where the pressure falls to zero. We solve the system for the limiting magnetic field values for the range of oblateness factors describing the expected deformations shown in Figure 2.
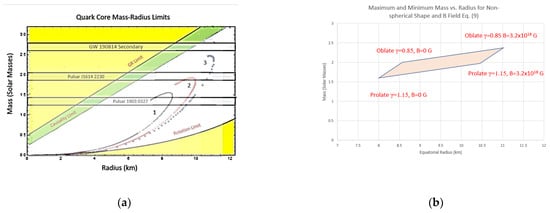
Figure 2.
(a) Quark core mass vs. equatorial radius relation from the TOV equations for an oblate deformation, γ =0.85, and a magnetic field, B = 3.2 × 1018 G, designated as case (1), for no deformation, γ = 1, with a magnetic field, B = 3.2 × 1018 G, designated as case (2), prolate γ = 1.15 with a magnetic field designated as case (3) and, in (b), the change in the mass and equatorial radius of the core is displayed for the range of deformation values from an oblate (γ = 0.85) to prolate (γ = 1.15) shape and the magnetic field range from B = 0 G to B = 3.2 × 1018 G for near the middle of the stability window at
= 57 MeV/fm3.
The numerical solutions to the modified TOV equations show that the magnetic field can produce a stiffer EOS up to the critical value, while the deformation increases the stiffness and mass for oblate shapes and decreases the stiffness and mass for prolate shapes. To compare our results to other models that include deformations or magnetic fields, we examine the compactness values for Mallick [57,98], Zubairi [62], Kayanikhoo [66], Sotani [59] and our results from Equation (9). Compactness is defined as the ratio of total mass to equatorial radius; C = M/Req for the mass expressed in solar masses and the radius in km. The magnetic fields are scaled to the Equation (9) critical central field intensity Bc = 3.2 × 1018 G. These models cover a range of different approaches to EOS formulation, where some focus on magnetic field contributions, and Mallick and Sotani include shape deformations similar in scale to the ones used here. The two pulsars, PSR 1413 and PSR J0740, and the magnetar SGR 1806 hold the near-maximum observed mass and magnetic field values for measured surface fields. The GW 190814 event is near the maximum mass companion observed, but the event is model dependent. Figure 3 also includes the standard values for a white dwarf, neutron star and a Schwarzschild black hole.
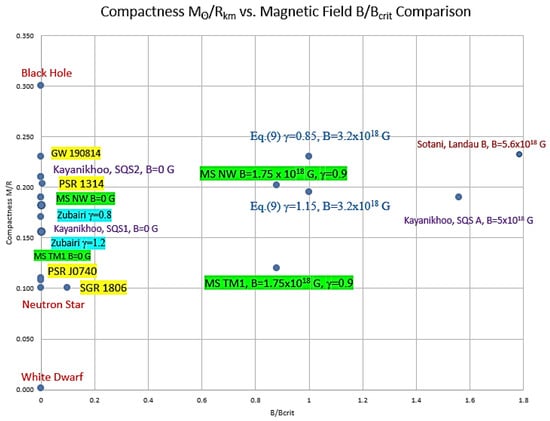
Figure 3.
Comparison of models. The models from Kayanikhoo, Mallick, Sotani and Zubairo are compared with the results for Equation (9) and with observational data from pulsars PSR 1314, PSR J0740, Magnetar SGR 1806 and Gravity Wave event GW 190814 for compactness; magnetic field is compared to the critical field for Equation (9) and oblateness.
5. Conclusions
We examined the combined effects of AMM and shape deformation on a cold compact quark stellar core where the EOS is subject to gluon field decomposition into hard and soft gluons with an additive quark term. The soft gluons produce a QCD vacuum barrier that corresponds to the bag constant, and the hard gluons produce a quadratic density dependent pressure while the quarks yield a polytropic pressure. As the deformation parameter goes from oblate to prolate, the equatorial radius is larger for the same mass. As the AMM linear magnetic effect and the external field quadratic term is increased, the EOS is stiffer and can support more mass for the same equatorial radius. At the highest possible magnetic field with an oblate shape, the final mass and radius states are indicative of the values that were observed in cases similar to PSR 1903 0327. As a result, high magnetic fields, gluon exchange and oblate deformations can stiffen the EOS, allowing for a larger quark star with greater mass than a neutron star with densities close to ten times greater than neutron star densities. While a number of theoretical models and the existence of the quark–gluon plasma indicate the possibility of an intermediate stellar core state between the neutron star and black hole, there is no universally agreed upon conclusive evidence for its existence in the current datasets. Next-generation neutron star observatories, such as LOFT, and the enhanced X-ray Timing and Polarimetry mission, eXTP [99], will enhance resolution and allow for better statistics in the near-term search for the existence of a compact stellar quark core. An interesting extension of this work would be to explicitly examine the effects of quark flavor chemical potentials that are expected to further soften the EOS, resulting in a larger equatorial radius for fixed mass and deformation. We are also exploring the impact of the effective massive gluon term on the cooling rate of the quark core, which can be compared to data from objects such as 3C 58 [100] and Cassiopeia A [101].
Author Contributions
Formal analysis: K.A., E.V.S. and K.A.A.; methodology: K.A., E.V.S. and K.A.A.; investigation: K.A., E.V.S. and K.A.A.; final analysis, numerical solutions and visualization: K.A., E.V.S. and K.A.A.; writing—original Draft: K.A., E.V.S. and K.A.A.; writing—review and editing: K.A., E.V.S. and K.A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
The authors wish to thank Western Kentucky University, Schlarman Academy and the helpful anonymous referees for their kind support throughout the work on this project. All plots and numerical solutions were generated in Mathematica.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Smith, N.; Li, W.; Foley, R.J.; Wheeler, J.C.; Pooley, D.; Chornock, R.; Filippenko, A.V.; Silverman, J.M.; Quimby, R.; Bloom, J.S.; et al. SN 2006gy: Discovery of the most luminous supernova ever recorded, powered by the death of an extremely massive star like η Carinae. Astrophys. J. 2007, 666, 1116. [Google Scholar] [CrossRef]
- Xu, R. Strange quark stars: Observations and speculations. J. Phys. G: Nucl. Part. Phys. 2009, 36, 064010. [Google Scholar] [CrossRef][Green Version]
- Burwitz, V.; Haberl, F.; Neuhäuser, R.; Predehl, P.; Trümper, J.; Zavlin, V.E. The thermal radiation of the isolated neutron star RX J1856. 5–3754 observed with Chandra and XMM-Newton. Astron. Astrophys. 2003, 399, 1109–1114. [Google Scholar] [CrossRef]
- Burwitz, V.; Zavlin, V.E.; Neuhäuser, R.; Predehl, P.; Trümper, J.; Brinkman, A.C. The Chandra LETGS high resolution X-ray spectrum of the isolated neutron star RX J1856. 5-3754. Astron. Astrophys. 2001, 379, L35–L38. [Google Scholar] [CrossRef]
- Xu, R.X.; Qiao, G.J.; Zhang, B. PSR 0943+ 10: A bare strange star? Astrophys. J. Lett. 1999, 522, L109. [Google Scholar] [CrossRef]
- Lyne, A.; Hobbs, G.; Kramer, M.; Stairs, I.; Stappers, B. Switched magnetospheric regulation of pulsar spin-down. Science 2010, 329, 408–412. [Google Scholar] [CrossRef]
- Alford, M.; Braby, M.; Paris, M.; Reddy, S. Hybrid stars that masquerade as neutron stars. Astrophys. J. 2005, 629, 969–978. Available online: https://iopscience.iop.org/article/10.1086/430902/pdf (accessed on 12 September 2017). [CrossRef]
- Olausen, S.A.; Kaspi, V.M. The McGill magnetar catalog. Astrophys. J. Suppl. Ser. 2014, 212, 6. [Google Scholar] [CrossRef]
- Burgio, G.F.; Vidaña, I. The Equation of State of Nuclear Matter: From Finite Nuclei to Neutron Stars. Universe 2020, 6, 119. [Google Scholar] [CrossRef]
- Shapiro, S.L.; Teukolsky, S.A.; Holes, B. White Dwarfs and Neutron Stars: The Physics of Compact Objects; John Wiley and Sons: New York, NY, USA, 1983. [Google Scholar]
- Baym, G.; Hatsuda, T.; Kojo, T.; Powell, P.D.; Song, Y.; Takatsuka, T. From hadrons to quarks in neutron stars: A review. Rep. Prog. Phys. 2018, 81, 056902. [Google Scholar] [CrossRef]
- Yagi, K.; Kyutoku, K.; Pappas, G.; Yunes, N.; Apostolatos, T.A. Effective no-hair relations for neutron stars and quark stars: Relativistic results. Phys. Rev. D 2014, 89, 124013. [Google Scholar] [CrossRef]
- Heinz, U. From SPS to RHIC: Breaking the barrier to the quark-gluon plasma. AIP Conf. Proc. 2001, 602, 281–292. [Google Scholar]
- Emerick, A.; Zhao, X.; Rapp, R. Bottomonia in the quark-gluon plasma and their production at RHIC and LHC. Eur. Phys. J. A 2012, 48, 72. [Google Scholar] [CrossRef]
- Teaney, D.; Lauret, J.; Shuryak, E.V. Flow at the SPS and RHIC as a quark-gluon plasma signature. Phys. Rev. Lett. 2001, 86, 4783–4786. [Google Scholar] [CrossRef]
- Arsene, I.; Bearden, I.; Beavis, D.; Besliu, C.; Budick, B.; Bøggild, H.; Chasman, C.; Christensen, C.; Christiansen, P.; Cibor, J.; et al. Quark–gluon plasma and color glass condensate at RHIC? The perspective from the BRAHMS experiment. Nucl. Phys. A 2005, 757, 1–27. [Google Scholar] [CrossRef]
- Florkowski, W.; Jaiswal, A.; Maksymiuk, E.; Ryblewski, R.; Strickland, M. Relativistic quantum transport coefficients for second-order viscous hydrodynamics. Phys. Rev. C 2015, 91, 054907. [Google Scholar] [CrossRef]
- Heinz, U.; Shen, C.; Song, H. The viscosity of quark-gluon plasma at RHIC and the LHC. AIP Conf. Proc. 2012, 1441, 766–770. [Google Scholar]
- Moore, G.; Saremi, O. Bulk viscosity and spectral functions in QCD. J. High Energy Phys. 2008, 2008, 015. [Google Scholar] [CrossRef]
- Miller, J.M.; Fabian, A.C.; Wijnands, R.; Reynolds, C.S.; Ehle, M.; Freyberg, M.J.; van der Klis, M.; Lewin, W.H.G.; Sanchez-Fernandez, C.; Castro-Tirado, A.J. Evidence of Spin and Energy Extraction in a Galactic Black Hole Candidate: The XMM-Newton/EPIC-pn Spectrum of XTE J1650–500. Astrophys. J. Lett. 2002, 570, L69. [Google Scholar] [CrossRef]
- Olive, K.A.; Pospelov, M. Environmental dependence of masses and coupling constants. Phys. Rev. D 2008, 77, 043524. [Google Scholar] [CrossRef]
- Dey, M.; Bombaci, I.; Dey, J.; Ray, S.; Samanta, B.C. Strange stars with realistic quark vector interaction and phenomenological density-dependent scalar potential. Phys. Lett. B 1998, 438, 123–128. Available online: https://arxiv.org/pdf/astro-ph/9810065.pdf (accessed on 12 May 2021). [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. GW190814: Gravitational waves from the coalescence of a 23 solar mass black hole with a 2.6 solar mass compact object. Astrophys. J. Lett. 2020, 896, L44. [Google Scholar] [CrossRef]
- Most, E.R.; Papenfort, L.J.; Weih, L.R.; Rezzolla, L. A lower bound on the maximum mass if the secondary in GW190814 was once a rapidly spinning neutron star. Mon. Not. R. Astron. Soc. Lett. 2020, 499, L82–L86. [Google Scholar] [CrossRef]
- Lu, W.; Beniamini, P.; Bonnerot, C. On the formation of GW190814. Mon. Not. R. Astron. Soc. 2021, 500, 1817–1832. [Google Scholar] [CrossRef]
- Dolan, L.; Jackiw, R. Symmetry behavior at finite temperature. Phys. Rev. D 1974, 9, 3320–3341. [Google Scholar] [CrossRef]
- Ray, S.; Dey, J.; Dey, M. Density dependent strong coupling constant of QCD derived from compact star data. Mod. Phys. Lett. A 2000, 15, 1301–1306. [Google Scholar] [CrossRef]
- Weber, F. Strange quark matter and compact stars. Prog. Part. Nucl. Phys. 2005, 54, 193–288. [Google Scholar] [CrossRef]
- Alford, M.; Rajagopal, K.; Wilczek, F. Color-flavor locking and chiral symmetry breaking in high density QCD. Nucl. Phys. B 1999, 537, 443–458. [Google Scholar] [CrossRef]
- Andrew, K.; Steinfelds, E.; Andrew, K. QCD Color Vector Potential Effects on Color Flavor Locked Quark Stellar Cores. Bull. Am. Phys. Soc. 2018, 63, BAPS.2018.SES.D05.9. [Google Scholar]
- Rajagopal, K.; Wilczek, F. Enforced electrical neutrality of the color-flavor locked phase. Phys. Rev. Lett. 2001, 86, 3492–3495. [Google Scholar] [CrossRef]
- Alford, M.G.; Schmitt, A.; Rajagopal, K.; Schäfer, T. Color superconductivity in dense quark matter. Rev. Mod. Phys. 2008, 80, 1455. [Google Scholar] [CrossRef]
- Alford, M.; Reddy, S. Compact stars with color superconducting quark matter. Phys. Rev. D 2003, 67, 074024. [Google Scholar] [CrossRef]
- Baldo, M.; Buballa, M.; Burgio, G.F.; Neumann, F.; Oertel, M.; Schulze, H.-J. Neutron stars and the transition to color superconducting quark matter. Phys. Lett. B 2003, 562, 153–160. [Google Scholar] [CrossRef]
- Lawley, S.; Bentz, W.; Thomas, A. Nucleons, nuclear matter and quark matter: A unified NJL approach. J. Phys. G Nucl. Part. Phys. 2006, 32, 667–679. [Google Scholar] [CrossRef]
- Baym, G.; Chin, S.A. Can a neutron star be a giant MIT bag? Phys. Lett. B 1976, 62, 241–244. [Google Scholar] [CrossRef]
- Källman, C.-G. Mean-field QCD model for hot/dense matter. Phys. Lett. B 1984, 134, 363–367. [Google Scholar] [CrossRef]
- Adler, S.L. Generalized bag models as mean-field approximations to QCD. Phys. Lett. B 1982, 110, 302–306. [Google Scholar] [CrossRef]
- Fodor, Z.; Sandor, D.K. A new method to study lattice QCD at finite temperature and chemical potential. Phys. Lett. B 2002, 534, 87–92. [Google Scholar] [CrossRef]
- Glendenning, N.K.; Weber, F. Nuclear solid crust on rotating strange quark stars. Astrophys. J. Lett. 1992, 400, 647–658. [Google Scholar] [CrossRef]
- Owen, B.J. Maximum elastic deformations of compact stars with exotic equations of state. Phys. Rev. Lett. 2005, 95, 211101. [Google Scholar] [CrossRef]
- Sharma, R.; Mukherjee, S. Compact stars: A core-envelope model. Mod. Phys. Lett. A 2002, 17, 2535–2544. [Google Scholar] [CrossRef]
- Ng, C.; Cheng, K.; Chu, M. Cooling properties of Cloudy Bag strange stars. Astropart. Phys. 2003, 19, 171–192. Available online: https://arxiv.org/pdf/astro-ph/0209016.pdf (accessed on 10 March 2018). [CrossRef]
- Bhattacharyya, A.; Ghosh, S.K.; Joarder, P.S.; Mallick, R.; Raha, S. Conversion of a neutron star to a strange star: A two-step process. Phys. Rev. C 2006, 74, 065804. [Google Scholar] [CrossRef]
- Kedia, A.; Kim, H.I.; Suh, I.S.; Mathews, G.J. Binary neutron star mergers as a probe of quark-hadron crossover equations of state. arXiv 2022, arXiv:2203.05461. [Google Scholar]
- Latifah, S.; Sulaksono, A.; Mart, T. Bosons star at Finite temperature. Phys. Rev. D 2014, 90, 127501. [Google Scholar] [CrossRef]
- Andrew, K.; Andrew, K.; Brown, R.; Thornberry, B.; Harper, S.; Steinfelds, E.; Roberts, T. A QCD Model of the Chemical Potential Kaon Boundary Formation for a Compact Quark Star. Bull. Am. Phys. Soc. 2016, 61, BAPS.2016.SES.K1.8. [Google Scholar]
- Thorsson, V.; Prakash, M.; Lattimer, J.M. Composition, structure and evolution of neutron stars with kaon condensates. Nucl. Phys. A 1994, 572, 693–731. [Google Scholar] [CrossRef]
- Alford, M. Color-superconducting quark matter. Annu. Rev. Nucl. Part. Sci. 2001, 51, 131–160. [Google Scholar] [CrossRef]
- Alford, M.; Bowers, J.A.; Rajagopal, K. Crystalline color superconductivity. Phys. Rev. D 2001, 63, 074016. [Google Scholar] [CrossRef]
- Casalbuoni, R.; Gatto, R.; Mannarelli, M.; Nardulli, G. Effective field theory for the crystalline colour superconductive phase of QCD. Phys. Lett. B 2001, 511, 218–228. [Google Scholar] [CrossRef]
- Andrew, K.; Brown, R.; Andrew, K.; Thornberry, B.; Harper, S.; Steinfelds, E.; Roberts, T. Analysis of Mass and Radius Sensitivity of a Crystalline Quark Star to a Strong Repulsive Equation of State. Bull. Am. Phys. Soc. 2016, 61, BAPS.2016.SES.K1.7. [Google Scholar]
- Paerels, F.B.; Mendez, M.; Agüeros, M.A.; Baring, M.; Barret, D.; Bhattacharyya, S.; Cackett, E.; Cottam, J.; Tringo, M.D.; Fox, D.; et al. The Behavior of Matter Under Extreme Conditions. arXiv 2009, arXiv:0904.0435. preprint. Available online: https://arxiv.org/pdf/0904.0435.pdf (accessed on 17 April 2019).
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Harding, A.K.; Ho, W.C.G.; Lattimer, J.M.; et al. PSR J0030+ 0451 mass and radius from NICER data and implications for the properties of neutron star matter. Astrophys. J. Lett. 2019, 887, L24. [Google Scholar] [CrossRef]
- Mak, M.K.; Harko, T. An exact anisotropic quark star model. Chin. J. Astron. Astrophys. 2002, 2, 248. [Google Scholar] [CrossRef]
- Zdunik, J.L.; Bejger, M.; Haensel, P. Crustal rigidity and rotational deformation of neutron stars. arXiv 2008, arXiv:0805.1814. preprint. Available online: https://www.aanda.org/articles/aa/pdf/2008/44/aa10183-08.pdf (accessed on 22 October 2018).
- Mallick, R.; Schramm, S. Deformation of a magnetized neutron star. Phys. Rev. C 2014, 89, 045805. [Google Scholar] [CrossRef]
- Chandrasekhar, S.; Fermi, E. Problems of gravitational stability in the presence of a magnetic field. Astrophys. J. 1953, 118, 116–141. [Google Scholar] [CrossRef]
- Sotani, H.; Tatsumi, T. Hybrid Quark Stars with Strong Magnetic Field. arXiv 2017, arXiv:1702.07843. preprint. Available online: https://arxiv.org/pdf/1702.07843.pdf (accessed on 12 May 2021). [CrossRef]
- Chatziioannou, K. Neutron-star tidal deformability and equation-of-state constraints. Gen. Relativ. Gravit. 2020, 52, 1–49. [Google Scholar] [CrossRef]
- Morsink, S.; Leahy, D.A.; Cadeau, C.; Braga, J. The oblate schwarzschild approximation for light curves of rapidly rotating neutron stars. Astrophys. J. 2007, 663, 1244–1251. [Google Scholar] [CrossRef]
- Zubairi, O.; Spinella, W.; Romero, A.; Mellinger, R.; Weber, F.; Orsaria, M.; Contrera, G. Non-spherical models of neutron stars. arXiv 2015, arXiv:1504.03006. preprint. Available online: https://arxiv.org/pdf/1504.03006.pdf (accessed on 11 July 2020).
- Chatterjee, D.; Novak, J.; Oertel, M. Structure of ultra-magnetised neutron stars. Eur. Phys. J. A 2021, 57, 249. [Google Scholar] [CrossRef]
- Bandyopadhyay, D.; Chakrabarty, S.; Pal, S. Quantizing magnetic field and quark-hadron phase transition in a neutron star. Phys. Rev. Lett. 1997, 79, 2176–2179. [Google Scholar] [CrossRef]
- Chakrabarty, S.; Bandyopadhyay, D.; Pal, S. Dense nuclear matter in a strong magnetic field. Phys. Rev. Lett. 1997, 78, 2898–2901. [Google Scholar] [CrossRef]
- Kayanikhoo, F.; Naficy, K.; Bordbar, G.H. Influence of strong magnetic field on the structure properties of strange quark stars. Eur. Phys. J. A 2020, 56, 2. [Google Scholar] [CrossRef]
- Rabhi, A.; Providência, C. Quark matter under strong magnetic fields in chiral models. Phys. Rev. C 2011, 83, 055801. [Google Scholar] [CrossRef]
- Chaudhuri, N.; Ghosh, S.; Sarkar, S.; Roy, P. Effect of anomalous magnetic moment of quarks on chiral and de-confinement transition in pNJL model. Proc. DAE Symp. Nucl. Phys. 2019, 64, 722. [Google Scholar]
- D’Elia, M.; Mukherjee, S.; Sanfilippo, F. QCD phase transition in a strong magnetic background. Phys. Rev. D 2010, 82, 051501. [Google Scholar] [CrossRef]
- Xu, K.; Chao, J.; Huang, M. Effect of the anomalous magnetic moment of quarks on magnetized QCD matter and meson spectra. Phys. Rev. D 2021, 103, 076015. [Google Scholar] [CrossRef]
- Ferrer, E.J.; De La Incera, V.; Wen, X.J. Quark antiscreening at strong magnetic field and inverse magnetic catalysis. Phys. Rev. D 2015, 91, 054006. [Google Scholar] [CrossRef]
- Martinez, A.; Perez, R.; Felipe, G.; Paret, D.M. Mass–Radius Relation for Magnetized Strange Quarks Stars. Int. J. Mod. Phys. D 2010, 19, 1511–1519. [Google Scholar] [CrossRef]
- Felipe, R.G.; Martínez, A.P.; Rojas, H.P.; Orsaria, M. Magnetized strange quark matter and magnetized strange quark stars. Phys. Rev. C 2008, 77, 015807. [Google Scholar] [CrossRef]
- Mueller, N.; Jan, M.P. Magnetic catalysis and inverse magnetic catalysis in QCD. Phys. Rev. D 2015, 91, 116010. [Google Scholar] [CrossRef]
- Chaudhuri, N.; Ghosh, S.; Sarkar, S.; Roy, P. Dilepton production from magnetized quark matter with an anomalous magnetic moment of the quarks using a three-flavor PNJL model. Phys. Rev. D 2021, 103, 096021. [Google Scholar] [CrossRef]
- Kawaguchi, M.; Huang, M. Restriction on the form of quark anomalous magnetic moment from lattice QCD results. arXiv 2022, arXiv:2205.08169. preprint. [Google Scholar]
- Fukushima, K.; Hatsuda, T. The phase diagram of dense QCD. Rep. Prog. Phys. 2010, 74, 014001. [Google Scholar] [CrossRef]
- Wen, X.-J.; He, R.; Liu, J.-B. Effect of the anomalous magnetic moment on the chiral transition in a strong magnetic field. Phys. Rev. D 2021, 103, 094020. [Google Scholar] [CrossRef]
- Ferrer, E.J.; De La Incera, V.; Portillo, I.; Quiroz, M. New look at the QCD ground state in a magnetic field. Phys. Rev. D 2014, 89, 085034. [Google Scholar] [CrossRef]
- Fayazbakhsh, S.; Sadooghi, N. Anomalous magnetic moment of hot quarks, inverse magnetic catalysis, and reentrance of the chiral symmetry broken phase. Phys. Rev. D 2014, 90, 105030. [Google Scholar] [CrossRef]
- Schwinger, J. On quantum-electrodynamics and the magnetic moment of the electron. Phys. Rev. 1948, 73, 416–417. [Google Scholar] [CrossRef]
- Ferrer, E.J.; De La Incera, V.; Paret, D.M.; Martínez, A.P.; Sanchez, A. Insignificance of the anomalous magnetic moment of charged fermions for the equation of state of a magnetized and dense medium. Phys. Rev. D 2015, 91, 085041. [Google Scholar] [CrossRef]
- Celenza, L.S.; Shakin, C.M. Description of the gluon condensate. Phys. Rev. D 1986, 34, 1591–1600. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Shakin, C.M. Description of gluon propagation in the presence of an A 2 condensate. Phys. Rev. D 2005, 71, 074007. [Google Scholar] [CrossRef]
- Fogaça, D.A.; Navarra, F.S. Gluon condensates in a cold quark–gluon plasma. Phys. Lett. B 2011, 700, 236–242. [Google Scholar] [CrossRef]
- Mao, G.-J.; Iwamoto, A.; Li, Z.-X. A study of neutron star structure in strong magnetic fields that includes anomalous magnetic moments. Chin. J. Astron. Astrophys. 2003, 3, 359–374. [Google Scholar] [CrossRef]
- Kettner, C.; Weber, F.; Weigel, M.K.; Glendenning, N.K. Structure and stability of strange and charm stars at finite temperatures. Phys. Rev. D 1995, 51, 1440–1457. [Google Scholar] [CrossRef]
- Jiménez, J.C.; Eduardo, S.F. Cold quark matter with heavy quarks and the stability of charm stars. Phys. Rev. D 2020, 102, 034015. [Google Scholar] [CrossRef]
- Zyla, P.A. Particle data group. Prog. Theor. Exp. Phys. 2020, 8, 144–146. Available online: https://pdg.lbl.gov/ (accessed on 12 May 2021).
- Dexheimer, V.; Torres, J.R.; Menezes, D.P. Stability windows for proto-quark stars. Eur. Phys. J. C 2013, 73, 2569. [Google Scholar] [CrossRef]
- Franzon, B.; Fogaça, D.; Navarra, F.S.; Horvath, J.E. Self-bound interacting QCD matter in compact stars. Phys. Rev. D 2012, 86, 065031. [Google Scholar] [CrossRef]
- Farhi, E.; Robert, L.J. Strange matter. Phys. Rev. D 1984, 30, 2379. [Google Scholar] [CrossRef]
- Yanis, A.; Sulaksono, A. Deformation and anisotropic magnetic field effects on neutron star. AIP Conf. Proc. 2018, 2023, 020009. [Google Scholar]
- Hartle, J.B.; Kip, S.T. Slowly rotating relativistic stars. II. Models for neutron stars and supermassive stars. Astrophys. J. 1968, 153, 807. [Google Scholar] [CrossRef]
- De Boer, S. Compact Stars as a Laboratory for Nuclear Matter. Bachelor Thesis, Faculty of Physics at University of Bielefeld, Bielefeld, Germany, 2011. [Google Scholar]
- Ganzha, V.G.; Evgenii, V.V. Numerical Solutions for Partial Differential Equations: Problem Solving Using Mathematica; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Koberlein, B.; Meisel, D. Astrophysics through Computation: With Mathematica® Support; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Mallik, R.; Schramm, S.; Dexheimer, V.; Bhattacharyya, A. Magnetic field and neutron stars: A comprehensive study. Proc. Sci. 2017, 242, 066. [Google Scholar]
- Zhang, S.N.; Feroci, M.A.R.C.O.; Santangelo, A.; Dong, Y.W.; Feng, H.; Lu, F.J.; Nandra, K.; Wang, Z.S.; Zhang, S.; Bozzo, E.; et al. eXTP: Enhanced X-ray Timing and Polarization mission. In Space Telescopes and Instrumentation 2016: Ultraviolet to Gamma Ray; International Society for Optics and Photonics: Bellingham, WA, USA, 2017; Volume 9905, p. 99051Q. [Google Scholar]
- Slane, P.O.; David, J.H.; Stephen, S.M. New constraints on neutron star cooling from Chandra observations of 3C 58. Astrophys. J. 2002, 571, L45. [Google Scholar] [CrossRef]
- Ho, W.C.G.; Zhao, Y.; O Heinke, C.; Kaplan, D.L.; Shternin, P.S.; Wijngaarden, M.J.P. X-ray bounds on cooling, composition, and magnetic field of the Cassiopeia A neutron star and young central compact objects. Mon. Not. R. Astron. Soc. 2021, 506, 5015–5029. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).