Testing Lorentz Violation with IceCube Neutrinos

Abstract

Lorentz violation (LV) induced by Quantum Gravity has been tested at much lower energies than the Planck scale with more and more observational evidence. In recent studies, the time of flight difference between the TeV neutrino and MeV photon from Gamma Ray Bursts (GRBs) have been used to constrain the LV energy scale, based on the energy-dependent speed variation. Here, we performed a correlation study between the updated 7.5 year high-energy starting events (HESE), neutrino alert events detected by IceCube, and a full sample of more than 7000 GRBs, and we found six GRB-neutrino candidates, including four alerts and two track events. We obtained the first order energy scale of quantum gravity, namely $E_{\mathrm{QG}}=8_{-5}^{+15}\times {10}^{17}\mathrm{GeV}$, which was consistent with other authors‘ work. We suggest that neutrinos and anti-neutrinos can be identified, respectively, due to the delay or advance of the observed time. For future point source search study of neutrinos, the arrival time difference of different particles may have to be taken into account.

1. Introduction

Lorentz invariance (LV), as one of our most fundamental symmetries, lies at the roots of both the standard model and general relativity and has been tested in various regimes with a tremendous amount of effort over the past decade [1,2,3,4,5]. Theories such as strings [6], spacetime foam [7], and loop quantum gravity [8] could provide the solutions to the violation at extremely high energy of about ${10}^{19}$ GeV, far beyond the capabilities of observation. Even though some models indicate that certain effects can be tested at much lower energies, it is still not accessible with human-made accelerators. The alternative approach to investigate the characteristics of quantum gravity is with cosmic messengers. Even their energies are far below the Plack energy scale, their cosmologcial distances can amplify LV effects. Thanks to the development of instruments and technologies, ground-based and space-based experiments are detecting more and more high-energy gamma rays, neutrinos, and cosmic rays from various extragalactic sources, such as Gamma Ray Bursts (GRBs), Active Galactic Nuclei (AGN), etc. Therefore, the methods using multi-astrophysical messengers have been widely applied and become more favorable than ever before.

Gamma-ray bursts (GRBs), as the most luminous explosions in the universe, are supposed to be the dominant sources of ultra-high-energy cosmic rays (UHECRs). They have particularly interesting features for an LV test, such as a short time structure, high-energy radiation, and long cosmological distance. On the other hand, according to the most popular models, GRBs are believed to be one of the best candidates for multi-messenger study. During the prompt emission, relativistic protons will interact with low energy photons and/or low energy protons to produce TeV neutrinos and MeV gamma rays by internal shocks. However, there has been no significant association found between GRB and neutrinos so far. Most of the early quantum gravity (QG) studies focused on the dispersion relation of electromagnetic radiation from GRBs [3,9,10,11]. As it is believed a particle with higher energy from further distance is more suitable and preferred for the study, the TeV-PeV neutrino as a better probe compared to MeV-GeV gamma ray is expected to play a key role in answering the questions. The relevant studies of the time delays between IceCube neutrinos and GRB photons have been performed by a few groups [4,12,13,14], while the observed time delay includes at least the effects of the intrinsic time delay, the QG time delay, and other terms due to the nonzero rest of mass, as well as the Shapiro effect [15]. The scale of the intrinsic time delay is estimated at the level of thousands of seconds according to the duration of GRBs, which is much smaller than our QG time delay resulting from the propagation of high energy neutrinos. The other effects are also negligible compared to the QG time delay of PeV neutrinos; so, we simply treat the obsevred time delay as the QG time delay. In this work, we perform the analysis for ∼PeV alert events and ∼100 TeV track events from IceCube.

IceCube Neutrino Observatory has been successfully operating for more than 10 years. With tens of events observed every year, no significant association has been found so far [16], which might be proof of the LV effect on astrophysical observations and may provide a hint on the analysis of IceCube neutrinos. There have been more than 7000 GRBs observed by various instruments up to now, and they are still being updated. In this work, to find the time difference of photons and neutrinos we performed the correlation search of high-energy IceCube neutrino and GRBs, calculated the LV parameters, and obtained the typical QG energy scale $E_{\mathrm{QG}}$ at the level of ${10}^{17}$ GeV.

In this paper, we describe the neutrino data sample from IceCube and the GRB catalog adopted in this work in Section 2. In Section 3, we discuss the modified dispersion relation for energetic particles, which leads to the time-of-flight difference. In Section 4, we present our analysis methods for the correlation search and show our results in Section 5. In the end, we provide our conclusion and discussion in Section 6.

2. Data sample

2.1. IceCube Neutrino Events

Since the first announcement of astrophysical neutrinos at the IceCube Neutrino Observatory in 2013, IceCube has detected tens of high-energy starting events (HESE) each year, with the interaction vertices inside the detector fiducial volume. So far there have been 102 events in the 7.5 years from 2010 to 2017 [17,18,19,20,21], including track-like events mainly from charged-current interactions of muon neutrinos, shower-like events from other interactions, and coincident events from cosmic-ray air showers. The recent updated 102 events from the 7.5-year dataset were constructed with a new method, where a minimizer was used to determine the best-fit neutrino direction with more accuracy. However, among these 102 events reported, only 82 of them had arrival time information. Hereafter, we call these 82 events HESE events, including 58 shower-like, 22 track-like, and 2 coincident events. Shower events are likely to be associated with a few GRBs due to the relatively poor angular resolution shown in Figure 1, so they are not included in this analysis. Track events have a much better resolution around $1^{\circ }$, which makes them ideal for the correlation search. The energy uncertainty of all the shower and track events was around 10% to 15%.

In April 2016, the first HESE alert was sent to the network, since then the alert frequency has been about three to four times per year. Another trigger system is extreme high energy (EHE) alerts, which are neutrino events coming from the Northern Hemisphere, passing through the Earth with higher energies. Both of them, instead of providing the reconstructed energy, give the estimated number of photoelectrons in the PMTs, which can not be used easily to estimate the true energy. Therefore, we abandon these two catalogs in the analysis. After 2019, HESE and EHE alerts were replaced by GOLD/BRONZE alerts [22], with the probability of at least 50%/30% astrophysical origin, respectively. We call this the alert catalog in this work. Up to 1 April 2022, there have been 31 GOLD and 45 BRONZE alerts. As can be seen in Figure 1, in general, GOLD alerts have better angular resolution and higher energies than BRONZE.

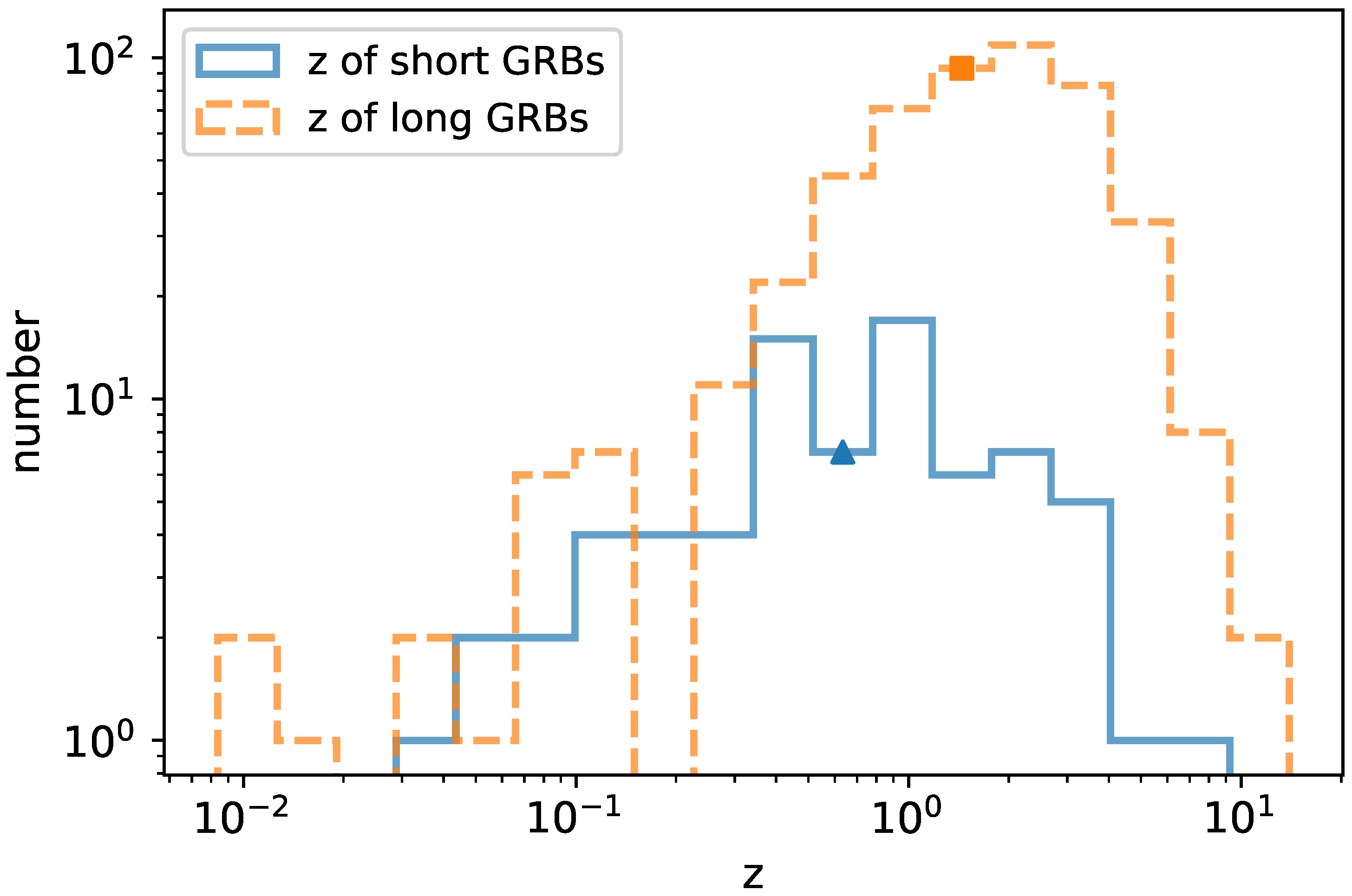
2.2. GRB Catalog

Gamma Ray Bursts (GRBs) are believed to be very promising candidates for producing neutrinos and photons. TeV neutrinos and MeV photons can be generated from the photomeson interaction. The time delay or advance between neutrinos and photons will be key to setting limits on the LV parameters. The theoretical study has shown that for the concerned neutrino and photon energy regime, they are most likely produced simultaneously, or neutrinos are emitted seconds after the prompt emission.

In the correlation study, we used a GRB catalog [23] that merged the observations from a wide range of resources including GCN-circulars [24], Fermi-GBM, Fermi-LAT [25], Swift [26], IPN [27], BeppoSAX [28], and BATSE [29]. This GRB catalog contained 7799 sources from 1991 to 1 April 2022, thanks to the contribution from global observatories. Among them, only 573 GRBs had redshift, which is an essential factor for the analysis. In Figure 2, the histograms show the redshift distribution of short/long GRBs, which were symmetrical about the average value of 0.6/1.4, respectively, and the standard deviation was 0.47/0.42. So we estimated the redshifts of the unknown ones as $0.6$ for the 1118 short GRBs and $1.4$ for the 5159 long GRBs. This assumption is consistent with that in previous studies [4,12].

3. Theoretical Model

The Lorentz violation has been widely studied in many quantum gravity (QG) models in recent years. The typical scale at which the Lorentz invariance would be strongly violated is the so-called Planck energy, ∼${10}^{19}$ GeV. It is beyond the accessibility of the current experiments on Earth and can not be tested with astronomy observation. However, it is very likely that LV violation at the Planck scale could have some relic effects at much lower energies. Many attempts have been made to place constraints on high-energy deviations from the Lorentz invariance, which enters through modified dispersion relations. Here, we considered a simplified model with single symmetry-breaking energy scale of $E_{\mathrm{QG}}$ for both neutrino and anti-neutrino [4]. For a particle propagating in the quantum spacetime with energy $E\ll E_{\mathrm{QG}}$, the LV modified dispersion relation can be written in a general form with only the leading-order correction as in [30],

$$E^2\simeq p^2{c}^2+m^2{c}^4-s_n{E}^2{\left(\frac{E}{E_{\mathrm{QG},n}}\right)}^n,$$

(1)

where n accounts for the order expansion of the leading term, $s_n=+1(-1)$ presents a decrease (increase) in particle speed with energy, $E_{\mathrm{QG},n}$ is the nth-order QG energy scale to be determined by experiments, and m is the rest mass of the particle. Here, the value of $s_n$ depends on the type of particles, such as 1 for neutrino and −1 for anti-neutrino [31,32]. Considering the current status of the experiments, we only focus on the first order; so, we set n as one and dismiss higher orders. Both GRB photons and high energy neutrinos are relativistic particles; hence, it is reasonable to set the rest mass $m=0$. Using the relation $v=\partial E/\partial p$, we obtained the modified propagation velocity [7] as

$$v\left(E\right)=c\left(1-s\frac{E}{E_{\mathrm{QG}}}\right).$$

(2)

Such energy-dependent speed variation can cause a time difference between particles. By taking into account the cosmological expansion, the QG time correction of neutrino and photon with energy $E_{\nu }$ and $E_{\mathrm{p}}$ respectively can be written as [4,30,31]

$$\Delta t_{\mathrm{QG}}=\frac{1}{H_0}\frac{s_{\nu }{E}_{\nu }-s_{\mathrm{p}}{E}_{\mathrm{p}}}{E_{\mathrm{QG}}}{\int }_0^z\frac{(1+z^{\prime })\mathrm{d}{z}^{\prime }}{\sqrt{{\Omega }_{\mathrm{m}}{(1+z^{\prime })}^3+{\Omega }_{\Lambda }}},$$

(3)

where z is the redshift of GRBs, and $s_{\nu }$ and $s_{\mathrm{p}}$ are the sign factors of neutrino and photon. As the studied neutrino energy between 10 TeV and 100 PeV is much higher than that of the GRB photon (below 1 GeV), $s_{\mathrm{p}}{E}_{\mathrm{p}}$ is negligible with respect to $s_{\nu }{E}_{\nu }$. We adopted the cosmological constants as $[{\Omega }_{\mathrm{m}},{\Omega }_{\Lambda }]=[0.3111\pm 0.0056,0.6889\pm 0.0056]$ and the Hubble expansion rate $H_0=67.66\pm 0.42\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$ [33].

The observed arrival time difference $\Delta t_{\mathrm{obs}}$ of two particles includes the QG time correction $\Delta t_{\mathrm{QG}}$ in the propagation and the intrinsic time difference $\Delta t_{\mathrm{in}}$ at the source. Hence, we have

$$\Delta t_{\mathrm{obs}}=t_{\nu }-t_{\mathrm{p}}=\Delta t_{\mathrm{QG}}+(1+z)\Delta t_{\mathrm{in}},$$

(4)

where $t_{\nu }$ and $t_{\mathrm{p}}$ represent the arrival times of neutrino and GRB photon. Taking Equation (3) into this formula, Equation (4) could be rewritten as

$$\frac{\Delta t_{\mathrm{obs}}}{1+z}=s\frac{K}{E_{\mathrm{QG}}}+\Delta t_{\mathrm{in}},$$

(5)

where K can be expressed as

$$K=\frac{E_{\nu }}{H_0}\frac{1}{1+z}{\int }_0^z\frac{(1+z^{\prime })\mathrm{d}{z}^{\prime }}{\sqrt{{\Omega }_{\mathrm{m}}{(1+z^{\prime })}^3+{\Omega }_{\Lambda }}}.$$

(6)

According to Equation (5), there would be a linear relation between $\Delta t_{\mathrm{obs}}/(1+z)$ and $sK$, if the energy dependent speed variation does exist.

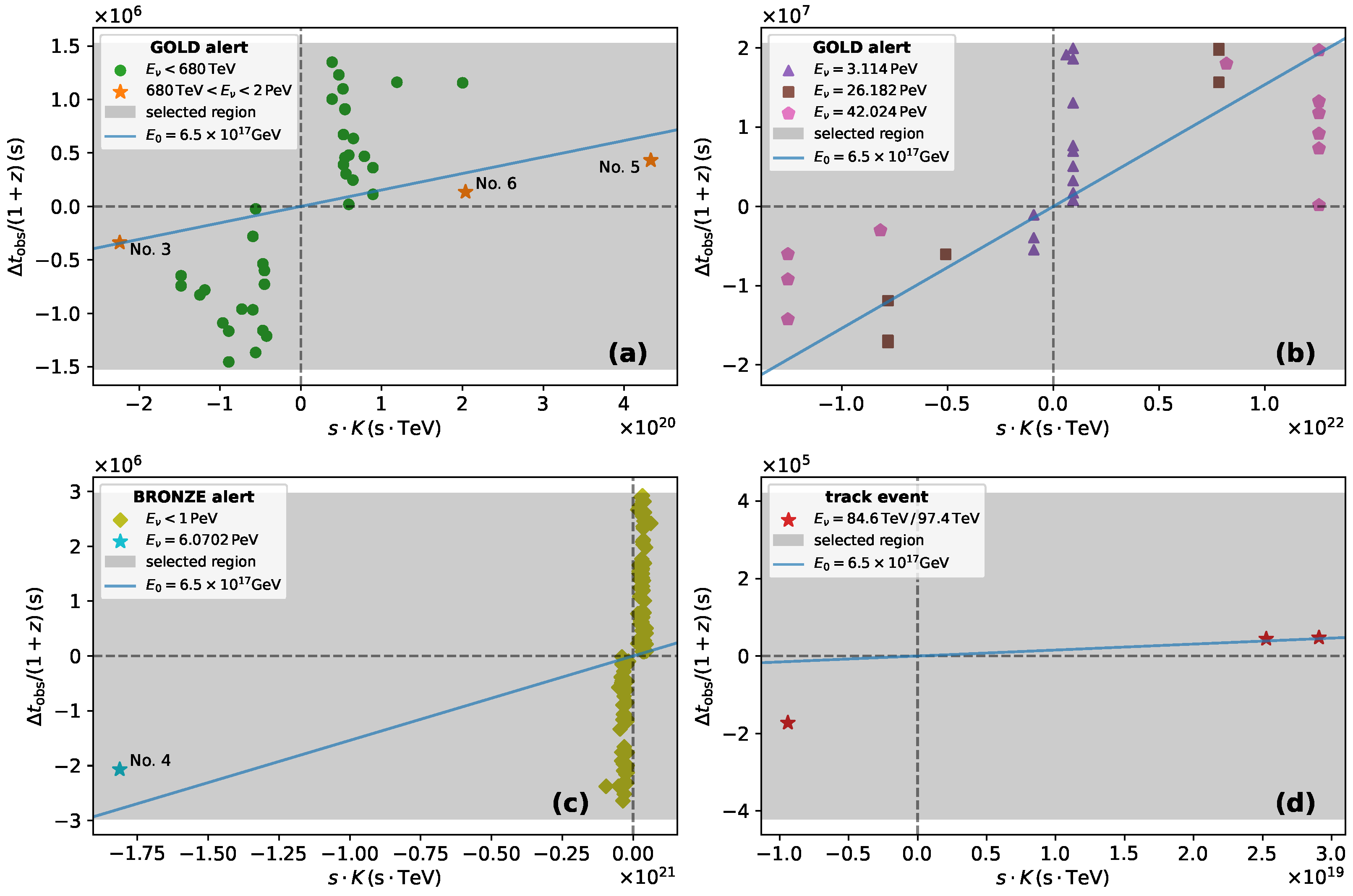
4. Analysis Methods

We searched through the neutrino and GRB datasets with the two conditions below to select the GRBs–neutrino association.

• The angular distance between neutrino and GRB events should not be larger than $3\sqrt{{\sigma }_{\mathrm{p}}^2+{\sigma }_{\nu }^2}$, where ${\sigma }_{\mathrm{p}}$ and ${\sigma }_{\nu }$ are the angular uncertainties of GRB and neutrino events separately.
• $\Delta t_{\mathrm{obs}}/(1+z)$ should be within a specified selection window, which is calculated based on the initial value of $E_0$, as described below.

For the second condition, we calculated the bound $K_{\mathrm{bound}}$ according to the maximum energy of neutrinos, $E_{\nu ,\max }$, and the maximum redshift of GRBs, $z_{\max }$, which is

$$K_{\mathrm{bound}}=\frac{E_{\nu ,\max }}{H_0}\frac{1}{1+z_{\max }}{\int }_0^{z_{\max }}\frac{(1+z^{\prime })\mathrm{d}{z}^{\prime }}{\sqrt{{\Omega }_{\mathrm{m}}{(1+z^{\prime })}^3+{\Omega }_{\Lambda }}}.$$

(7)

We assigned $E_{\mathrm{QG}}$ an initial value obtained from the work of [4], which is

$$E_0=6.5\times {10}^{17}\mathrm{GeV}.$$

(8)

With $E_0$ and limits of K, we set the bound for $\Delta t_{\mathrm{obs}}/(1+z)$ as the gray region in Figure 3, which means $\Delta t_{\mathrm{obs}}/(1+z)$ should be within the range of $[-K_{\mathrm{bound}}/E_{\mathrm{QG}}+\Delta t_{\mathrm{in}},K_{\mathrm{bound}}/E_{\mathrm{QG}}+\Delta t_{\mathrm{in}}]$. For the intrinsic time delay, $\Delta t_{\mathrm{in}}$, which is due to the physical process at the source, our current understanding is not sufficient to provide any robust estimation. We assumed that $\Delta t_{\mathrm{in}}$ was comparable to the duration of GRB up to 1000 s, and $\Delta t_{\mathrm{in}}$ was negligible compared to $\Delta t_{\mathrm{obs}}$ in the analysis. So we assigned $\Delta t_{\mathrm{in}}$ as 0 in the analysis.

As $\Delta t_{\mathrm{in}}=0$, $E_{\mathrm{QG}}$ for each GRB/neutrino association according to Equation (5) can be found from

$$E_{\mathrm{QG}}=s\frac{K(1+z)}{\Delta t_{\mathrm{obs}}}.$$

(9)

With these two conditions, there are 73 remaining neutrinos, including 39 BRONZE alerts, 31 GOLD alerts, and 3 track events. Among these events, most were associated with more than one GRB, which is because the observed time delay of neutrinos can be up to tens of days, and GRBs occur about once per day, even if the angular resolution of our neutrino sample was good enough. There were still some neutrinos associated with only one GRB, which could provide a more intriguing estimation of $E_{\mathrm{QG}}$.

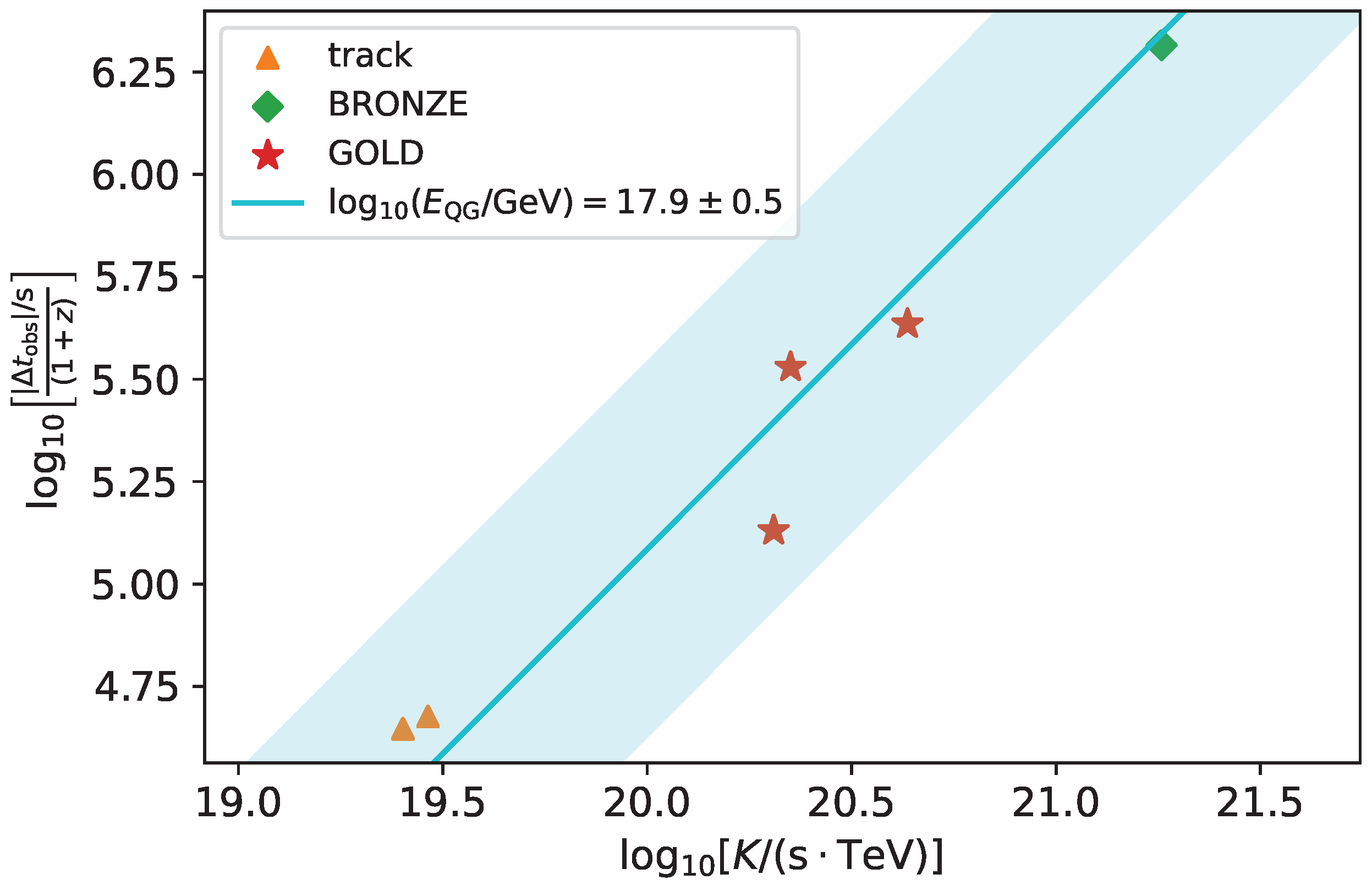
5. Results

In Figure 3, we showed the $\Delta t_{\mathrm{obs}}/(1+z)$ versus K for GRB–neutrino associations satisfying our conditions. (1) In Figure 3a, there were two clusters around the y-axis contributed from neutrinos with energies below 680 TeV. These clusters gave a $E_{\mathrm{QG}}$ much lower than $E_0$, and no strong linear correlation among the clusters was found. So we excluded them from the analysis. There were three GOLD alerts with energies between 680 TeV and 2 PeV shown as orange stars with number 3, 5, and 6 labeled, which only associated with one GRB each. Their calculated $E_{\mathrm{QG}}$ were in agreement with $E_0$. (2) In Figure 3b, we show the three GOLD alerts above 2 PeV, associated with more than one GRB each, meaning the unreliable association between neutrino and GRBs. (3) In Figure 3c, the BRONZE alerts below 1 PeV with associated GRBs are presented as yellow diamonds, with no linear correlation. One BRONZE alert with remarkably high energy 6070.2 TeV was associated with only one GRB shown as a blue star with number 4 labeled. (4) In Figure 3d, three track events were associated with one GRB each, and two of them provided a calculated $E_{\mathrm{QG}}$ in agreement with $E_0$, while the other one was an outlier with a much lower $E_{\mathrm{QG}}$. These two are shown as red stars with number 1 and 2 labeled. Overall, there were six neutrino and GRB associations selected for our analysis, and their labeled numbers were the same as shown in

Table 1. Selected neutrino–GRB associations, sorted by calculated values of $E_{\mathrm{QG}}$. The numbers, type of neutrino events, neutrino IDs, energies, associated GRBs, redshifts, observed time delays, and $E_{\mathrm{QG}}$ are given individually. Redshifts marked with * are estimated as described in Section 2.2.

No.	Type	ID	${\mathit{E}}_{\mathit{\nu }}$	GRB	Redshift	$\Delta {\mathit{t}}_{\mathbf{obs}}$	${\mathit{E}}_{\mathbf{QG}}$
1	track	44	84.6 TeV	140113B	1.4 *	1.25 days	5.8 $\times {10}^{17}$ GeV
2	track	63	97.4 TeV	141207A	1.4 *	1.34 days	6.2 $\times {10}^{17}$ GeV
3	GOLD	135736_30987826	750.76 TeV	211002A	1.4 *	−9.58 days	6.7 $\times {10}^{17}$ GeV
4	BRONZE	133644_43767651	6070.2 TeV	200319A	1.4 *	−58.54 days	8.9 $\times {10}^{17}$ GeV
5	GOLD	134994_1103075	1450.4 TeV	210201A	1.4 *	12.21 days	1.0 $\times {10}^{18}$ GeV
6	GOLD	134577_31638233	682.65 TeV	201004A	1.4 *	3.82 days	1.5 $\times {10}^{18}$ GeV

.

Based on the selected six GRB/neutrino associations in Table 1, we fitted the points and found the best fit value of $E_{\mathrm{QG}}$ as shown in Figure 4, which was ${log}_{10}(E_{\mathrm{QG}}/\mathrm{GeV})=17.9\pm 0.5$. Therefore, the QG energy scale was found to be $E_{\mathrm{QG}}=8_{-5}^{+15}\times {10}^{17}\mathrm{GeV}$. The uncertainty of $E_{\mathrm{QG}}$ was mainly due to the uncertainty of the redshift and neutrino energy.

6. Discussion and Conclusions

With the most recent neutrino events from IceCube and a complete sample of GRBs, we searched for the association candidates. The track and alert neutrino events were adopted in the analysis, thanks to their better angular resolution and higher energies. With our selection conditions, six GRB/neutrino associations listed in Table 1 implied a linear correlation, as plotted in Figure 3.

We found that for TeV to PeV neutrinos, the observed time delays were up to tens of days, which may explain why no significant correlation has been found between astrophysical objects and IceCube neutrinos so far. For later neutrino study and analysis, these QG effects have to be taken into account.

The work by other groups so far has not showm strong evidence of LV effects, and different methods lead to contradictory conclusions about the absence or presence of observable QG effects in time delays. The tightest bound of first order effective QG energy scale obtained with photons from GRB090510 was $E_{\mathrm{QG}}>9.3\times {10}^{19}\mathrm{GeV}$ [9]. Another limit of $E_{\mathrm{QG}}>1.09\times {10}^{17}\mathrm{GeV}$ was obtained assuming a physical association between a PeV neutrino and the blazar PKS B1424-418 [34]. Some other studies adopted statistical approaches combining data from multiple sources, applied to both GRB photons [3,10,11] and GRB-neutrinos [4,12,13], as well as the combination of the two [14]. Their results suggested a correlation between time delay and neutrino energy with $E_{\mathrm{QG}}\sim 5\times {10}^{17}\mathrm{GeV}$. In this work, we analyzed the updated data with an improved statistical method, yielding a QG energy scale $E_{\mathrm{QG}}=8_{-5}^{+15}\times {10}^{17}\mathrm{GeV}$, in agreement with the work in [4]. Our QG energy scale was much lower than the limits from photon analysis, which may indicate different critical energy scales for different particles, as also proposed by Coleman and Glashow [35].

In summary, establishing the association between neutrino and GRB is even more challenging with LV than in a no-LV scenario. To solve this problem, we need more high-energy observations of neutrinos and GRBs with better angular and energy resolution. Early high-energy observations of short GRBs with redshift could also be helpful. Meanwhile, according to the information of delay or advance time, the identification of the neutrino and anti-neutrino could be possible, which is not accessible for now.