Nonsingular Black Holes in 4D Einstein–Gauss–Bonnet Gravity
Abstract
1. Introduction
2. Basic Equations and Black Hole Solution
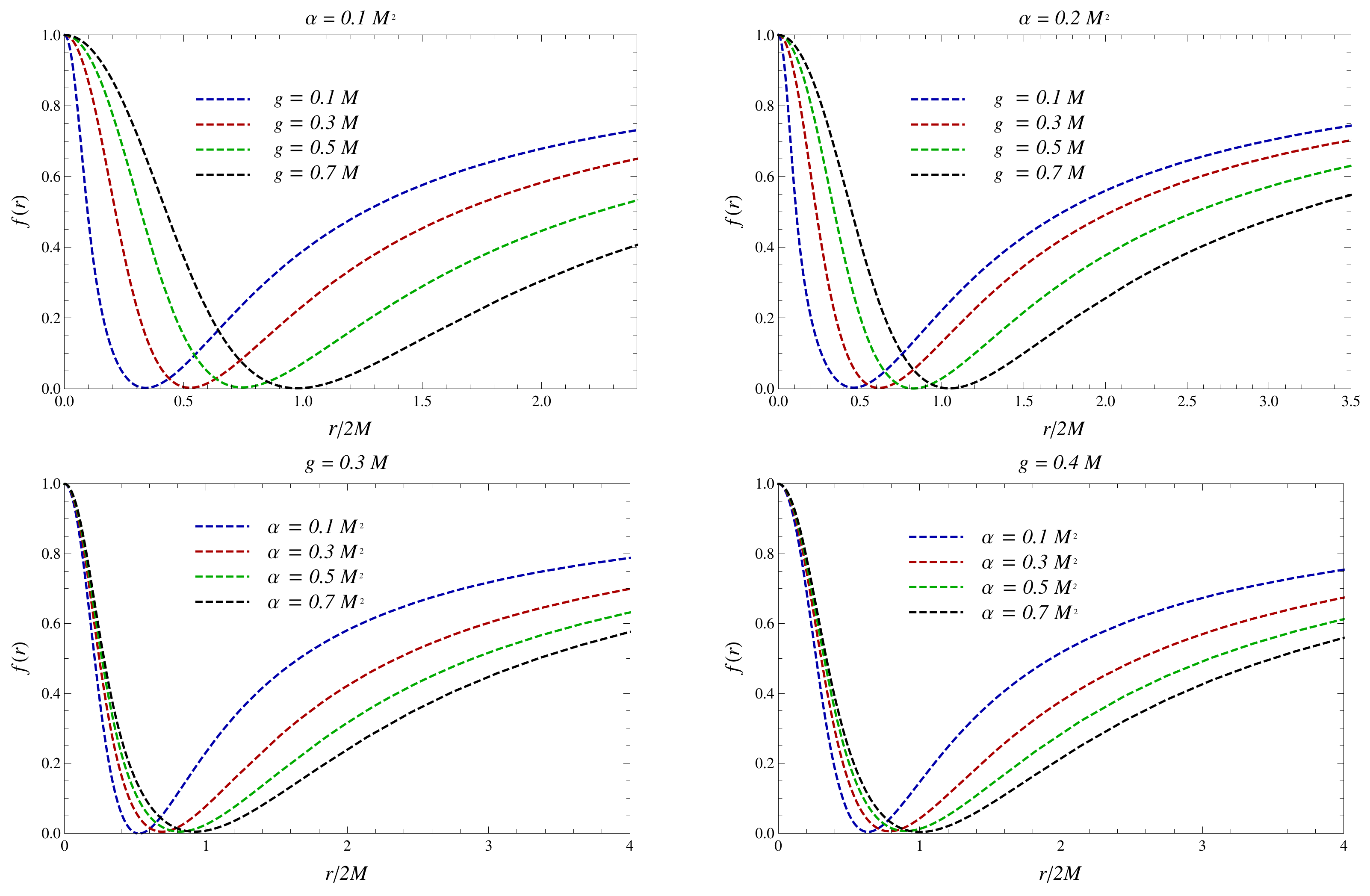
Horizon Structure
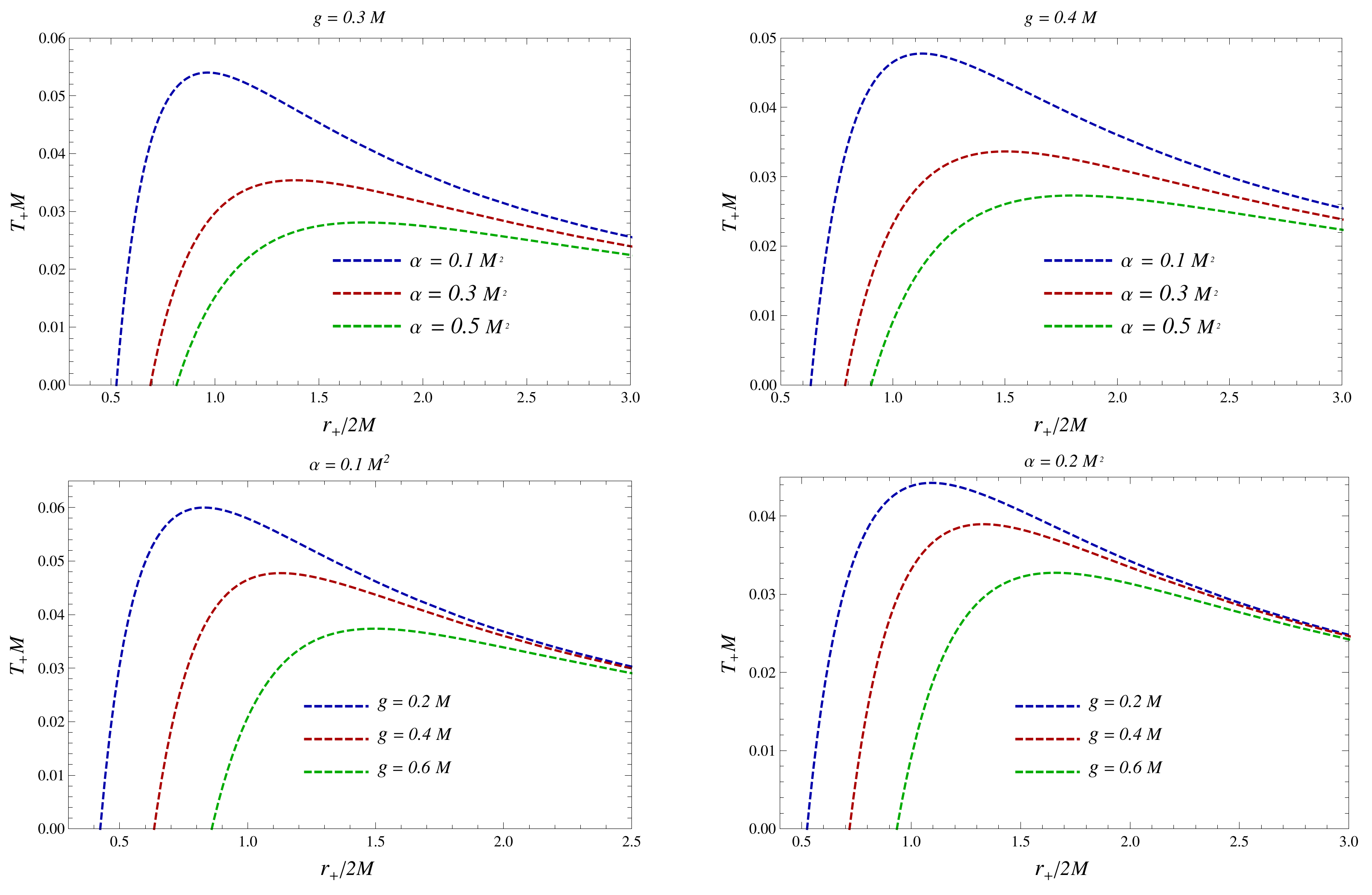
3. Thermodynamics
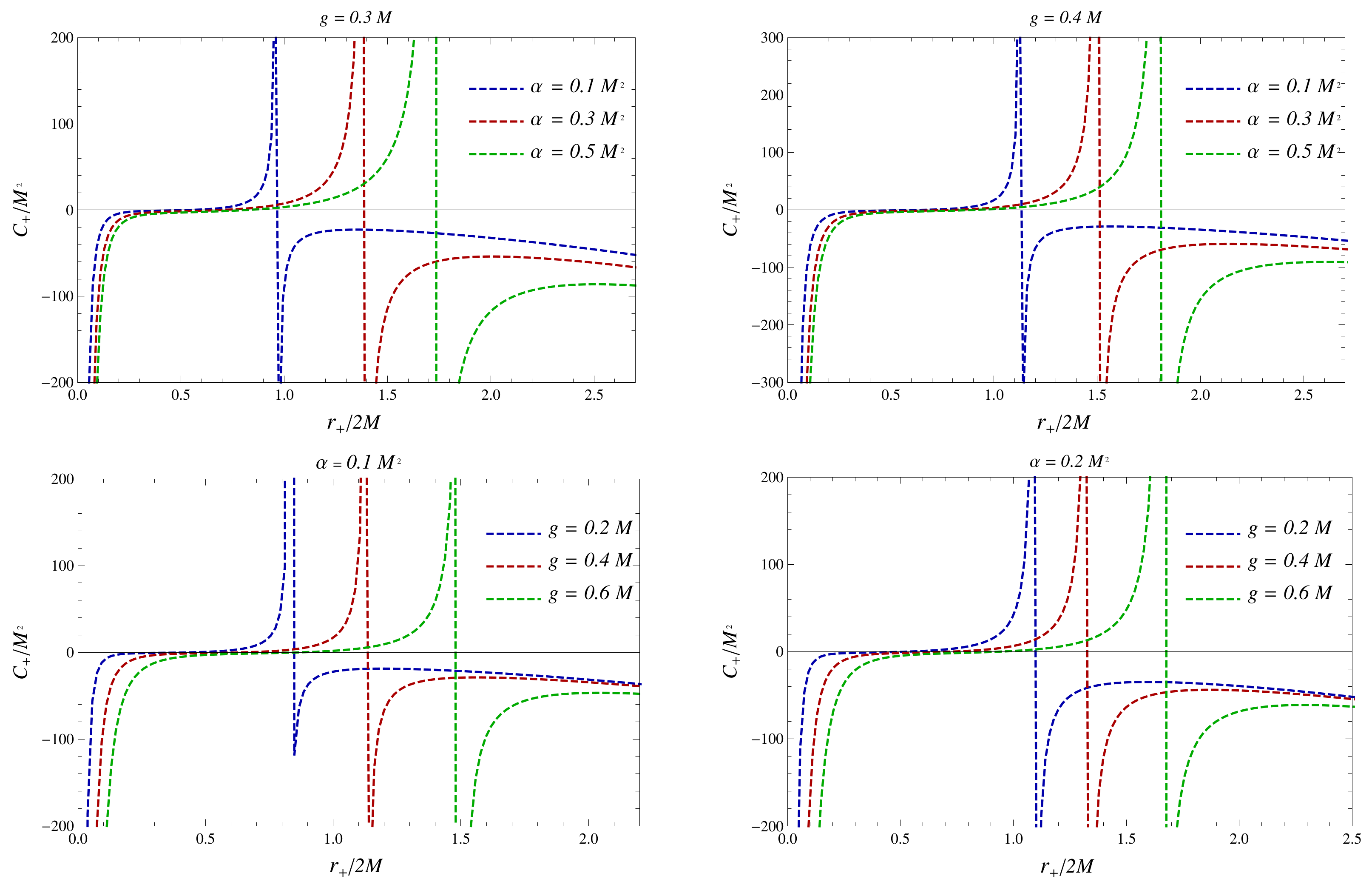
3.1. Stability Analysis
3.2. Black Hole Remnant
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bardeen, J. Non-singular general-relativistic gravitational collapse. In Proceedings of the International Conference GR5, Tbilisi, Russia, 9–13 September 1968; p. 174. [Google Scholar]
- Ansoldi, S. Spherical black holes with regular center: A Review of existing models including a recent realization with Gaussian sources. arXiv 2008, arXiv:0802.0330. [Google Scholar]
- Bronnikov, K.A. Regular magnetic black holes and monopoles from nonlinear electrodynamics. Phys. Rev. D 2001, 63, 044005. [Google Scholar] [CrossRef]
- Hayward, S.A. Formation and evaporation of regular black holes. Phys. Rev. Lett. 2006, 96, 031103. [Google Scholar] [CrossRef] [PubMed]
- Lemos, J.P.S.; Zanchin, V.T. Regular black holes: Electrically charged solutions, Reissner-Nordstróm outside a de Sitter core. Phys. Rev. D 2011, 83, 124005. [Google Scholar] [CrossRef]
- Schee, J.; Stuchlik, Z. Gravitational lensing and ghost images in the regular Bardeen no-horizon spacetimes. J. Cosmol. Astropart. Phys. 2015, 06, 48. [Google Scholar] [CrossRef]
- Frolov, V.P.; Zelnikov, A. Quantum radiation from an evaporating nonsingular black hole. Phys. Rev. D 2017, 95, 124028. [Google Scholar] [CrossRef]
- Frolov, V.P. Notes on nonsingular models of black holes. Phys. Rev. D 2016, 94, 104056. [Google Scholar] [CrossRef]
- Lin, K.; Li, J.; Yang, S. Quasinormal Modes of Hayward Regular Black Hole. Int. J. Theor. Phys. 2013, 52, 3771. [Google Scholar] [CrossRef]
- Chiba, T.; Kimura, M. A note on geodesics in the Hayward metric. Prog. Theor. Exp. Phys. 2017, 2017, 043E01. [Google Scholar] [CrossRef]
- Halilsoy, M.; Ovgun, A.; Mazharimousavi, S.H. Thin-shell wormholes from the regular Hayward black hole. Eur. Phys. J. C 2014, 74, 2796. [Google Scholar] [CrossRef]
- Kuhfittig, P.K.F. Some examples of Hayward wormholes. Aditi J. Math. Phys. 2014, 5, 25. [Google Scholar]
- Sharif, M.; Mumtaz, S. Stability of the Regular Hayward Thin-Shell Wormholes. Adv. High Energy Phys. 2016, 2016, 2868750. [Google Scholar] [CrossRef]
- Maluf, R.V.; Neves, J.C.S. Thermodynamics of a class of regular black holes with a generalized uncertainty principle. Phys. Rev. D 2018, 97, 104015. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, D.V.; Ghosh, S.G. D-dimensional Bardeen-AdS black holes in Einstein-Gauss-Bonnet theory. Eur. Phys. J. C 2019, 79, 275. [Google Scholar] [CrossRef]
- Perez-Roman, I.; Bretón, N. The region interior to the event horizon of the Regular Hayward Black Hole. Gen. Rel. Grav. 2018, 50, 64. [Google Scholar] [CrossRef]
- Mehdipour, S.H.; Ahmadi, M.H. Black Hole Remnants in Hayward Solutions and Noncommutative Effects. Nucl. Phys. B 2018, 926, 49. [Google Scholar] [CrossRef]
- Zhao, S.S.; Xie, Y. Strong deflection gravitational lensing by a modified Hayward black hole. Eur. Phys. J. C 2017, 77, 272. [Google Scholar] [CrossRef]
- Abdujabbarov, A.; Amir, M.; Ahmedov, B.; Ghosh, S.G. Shadow of rotating regular black holes. Phys. Rev. D 2016, 93, 104004. [Google Scholar] [CrossRef]
- Gwak, B. Collision of Two Rotating Hayward Black Holes. Eur. Phys. J. C 2017, 77, 482. [Google Scholar] [CrossRef]
- Amir, M.; Ahmed, F.; Ghosh, S.G. Collision of two general particles around a rotating regular Hayward’s black holes. Eur. Phys. J. C 2016, 76, 532. [Google Scholar] [CrossRef]
- Amir, M.; Ghosh, S.G. Rotating Hayward’s regular black hole as particle accelerator. J. High Energy Phys. 2015, 1507, 15. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, D.V.; Ghosh, S.G. Hayward black holes in Einstein-Gauss-Bonnet gravity. Ann. Phys. 2020, 419, 168214. [Google Scholar] [CrossRef]
- Ghosh, S.G.; Kumar, A.; Singh, D.V. Anti-de Sitter Hayward black holes in Einstein-Gauss-Bonnet gravity. Phys. Dark Univ. 2020, 30, 100660. [Google Scholar] [CrossRef]
- Gross, D.J.; Sloan, J.H. The Quartic Effective Action for the Heterotic String. Nucl. Phys. B 1987, 291, 41–89. [Google Scholar] [CrossRef]
- Bento, M.C.; Bertolami, O. Maximally Symmetric Cosmological Solutions of higher curvature string effective theories with dilatons. Phys. Lett. B 1996, 368, 198–201. [Google Scholar] [CrossRef]
- Guica, M.; Huang, L.; Li, W.; Strominger, A. R2 corrections for 5D black holes and rings. J. High Energy Phys. 2006, 10, 36. [Google Scholar] [CrossRef][Green Version]
- Boulware, D.G.; Deser, S. String Generated Gravity Models. Phys. Rev. Lett. 1985, 55, 2656. [Google Scholar] [CrossRef]
- Lanczos, C. A Remarkable property of the Riemann-Christoffel tensor in four dimensions. Annals Math. 1938, 39, 842. [Google Scholar] [CrossRef]
- Lovelock, D. The Einstein tensor and its generalizations. J. Math. Phys. 1971, 12, 498–501. [Google Scholar] [CrossRef]
- Wiltshire, D.L. Spherically Symmetric Solutions of Einstein-Maxwell Theory With a Gauss-Bonnet Term. Phys. Lett. B 1986, 169, 36. [Google Scholar] [CrossRef]
- Wheeler, J.T. Symmetric Solutions to the Gauss-Bonnet Extended Einstein Equations. Nucl. Phys. B 1986, 268, 737–746. [Google Scholar] [CrossRef]
- Mignemi, S.; Stewart, N.R. Charged black holes in effective string theory. Phys. Rev. D 1993, 47, 5259–5269. [Google Scholar] [CrossRef] [PubMed]
- Alexeev, S.O.; Pomazanov, M.V. Black hole solutions with dilatonic hair in higher curvature gravity. Phys. Rev. D 1997, 55, 2110. [Google Scholar] [CrossRef]
- Kanti, P.; Tamvakis, K. Colored black holes in higher curvature string gravity. Phys. Lett. B 1997, 392, 30–38. [Google Scholar] [CrossRef]
- Kleihaus, B.; Kunz, J.; Radu, E. Rotating Black Holes in Dilatonic Einstein-Gauss-Bonnet Theory. Phys. Rev. Lett. 2011, 106, 151104. [Google Scholar] [CrossRef]
- Ghosh, S.G. 5D Radiating black holes in Einstein-Yang-Mills-Gauss-Bonnet gravity. Phys. Lett. B 2011, 704, 5–9. [Google Scholar] [CrossRef]
- Hansraj, S.; Maharaj, S.D.; Chilambwe, B. Constant potentials in 6D Einstein-Gauss-Bonnet theory. Phys. Rev. D 2019, 100, 124029. [Google Scholar] [CrossRef]
- Antoniou, G.; Bakopoulos, A.; Kanti, P. Black-Hole Solutions with Scalar Hair in Einstein-Scalar-Gauss-Bonnet Theories. Phys. Rev. D 2018, 97, 084037. [Google Scholar] [CrossRef]
- Antoniou, G.; Bakopoulos, A.; Kanti, P. Evasion of No-Hair Theorems and Novel Black-Hole Solutions in Gauss-Bonnet Theories. Phys. Rev. Lett. 2018, 120, 131102. [Google Scholar] [CrossRef]
- Bakopoulos, A.; Antoniou, G.; Kanti, P. Novel Black-Hole Solutions in Einstein-Scalar-Gauss-Bonnet Theories with a Cosmological Constant. Phys. Rev. D 2019, 99, 064003. [Google Scholar] [CrossRef]
- Ghosh, S.G.; Singh, D.V.; Maharaj, S.D. Regular black holes in Einstein-Gauss-Bonnet gravity. Phys. Rev. D 2018, 97, 104050. [Google Scholar] [CrossRef]
- Hyun, S.; Nam, C.H. Charged AdS black holes in Gauss? Bonnet gravity and nonlinear electrodynamics. Eur. Phys. J. C 2019, 79, 737. [Google Scholar] [CrossRef]
- Singh, D.V.; Ghosh, S.G.; Maharaj, S.D. Bardeen-like regular black holes in 5D Einstein-Gauss-Bonnet gravity. Ann. Phys. 2020, 412, 168025. [Google Scholar] [CrossRef]
- Glavan, D.; Lin, C. Einstein-Gauss-Bonnet gravity in 4-dimensional space-time. Phys. Rev. Lett. 2020, 124, 081301. [Google Scholar] [CrossRef]
- Lovelock, D. The four-dimensionality of space and the einstein tensor. J. Math. Phys. 1972, 13, 874–876. [Google Scholar] [CrossRef]
- Cai, R.G.; Cao, L.M.; Ohta, N. Black Holes in Gravity with Conformal Anomaly and Logarithmic Term in Black Hole Entropy. J. High Energy Phys. 2010, 4, 82. [Google Scholar] [CrossRef]
- Cognola, G.; Myrzakulov, R.; Sebastiani, L.; Zerbini, S. Einstein gravity with Gauss-Bonnet entropic corrections. Phys. Rev. D 2013, 88, 024006. [Google Scholar] [CrossRef]
- Casalino, A.; Colleaux, A.; Rinaldi, M.; Vicentini, S. Regularized Lovelock gravity. Phys. Dark Univ. 2021, 31, 100770. [Google Scholar] [CrossRef]
- Fernandes, P.G.S. Charged Black Holes in AdS Spaces in 4D Einstein-Gauss-Bonnet Gravity. Phys. Lett. B 2020, 805, 135468. [Google Scholar] [CrossRef]
- Singh, D.V.; Ghosh, S.G.; Maharaj, S.D. Clouds of string in 4D novel Einstein-Gauss-Bonnet black holes. Phys. Dark Univ. 2020, 30, 100730. [Google Scholar] [CrossRef]
- Ghosh, S.G.; Maharaj, S.D. Radiating black holes in the novel 4D Einstein-Gauss-Bonnet gravity. Phys. Dark Univ. 2020, 30, 100687. [Google Scholar] [CrossRef]
- Ghosh, S.G.; Kumar, R. Generating black holes in the novel 4D Einstein-Gauss-Bonnet gravity. Class. Quant. Grav. 2020, 37, 245008. [Google Scholar] [CrossRef]
- Ghosh, S.G.; Maharaj, S.D. Noncommutative inspired black holes in regularised 4D Einstein-Gauss-Bonnet theory. Phys. Dark Univ. 2021, 31, 100793. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, R.; Ghosh, S.G. Bardeen Black Holes in the Regularized 4D Einstein-Gauss-Bonnet gravity. Universe 2022, 8, 232. [Google Scholar] [CrossRef]
- Kumar, R.; Ghosh, S.G. Rotating black holes in the 4D Einstein-Gauss-Bonnet gravity. J. Cosmol. Astropart. Phys. 2020, 07, 53. [Google Scholar] [CrossRef]
- Wei, S.W.; Liu, Y.X. Testing the nature of Gauss-Bonnet gravity by four-dimensional rotating black hole shadow. Eur. Phys. J. Plus 2021, 136, 436. [Google Scholar] [CrossRef]
- Churilova, M.S. Quasinormal modes of the Dirac field in the novel 4D Einstein-Gauss-Bonnet gravity. Phys. Dark Univ. 2021, 31, 100748. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zhidenko, A. (In)stability of black holes in the 4D Einstein-Gauss-Bonnet and Einstein-Lovelock gravities. Phys. Dark Univ. 2020, 30, 100697. [Google Scholar] [CrossRef]
- Guo, M.; Li, P.C. The innermost stable circular orbit and shadow in the 4D Einstein-Gauss-Bonnet gravity. Eur. Phys. J. C 2020, 80, 588. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zinhailo, A.F. Quasinormal modes, stability and shadows of a black hole in the 4D Einstein-Gauss-Bonnet gravity. Eur. Phys. J. C 2020, 80, 1049. [Google Scholar] [CrossRef]
- Doneva, D.D.; Yazadjiev, S.S. Relativistic stars in 4D Einstein-Gauss-Bonnet gravity. J. Cosmol. Astropart. Phys. 2021, 05, 24. [Google Scholar] [CrossRef]
- Zhang, Y.P.; Wei, S.W.; Liu, Y.X. Spinning test particle in four-dimensional Einstein-Gauss-Bonnet Black Hole. Universe 2020, 6, 103. [Google Scholar] [CrossRef]
- Islam, S.U.; Kumar, R.; Ghosh, S.G. Gravitational lensing by black holes in 4D Einstein-Gauss-Bonnet gravity. J. Cosmol. Astropart. Phys. 2020, 09, 30. [Google Scholar] [CrossRef]
- Heydari-Fard, M.; Heydari-Fard, M.; Sepangi, H.R. Bending of light in novel 4D Gauss-Bonnet-de Sitter black holes by Rindler-Ishak method. Europhys. Lett. 2021, 133, 50006. [Google Scholar] [CrossRef]
- Jin, X.H.; Gao, Y.X.; Liu, D.J. Strong gravitational lensing of a 4-dimensional Einstein-Gauss-Bonnet black hole in homogeneous plasma. Int. J. Mod. Phys. D 2020, 29, 2050065. [Google Scholar] [CrossRef]
- Kumar, R.; Islam, S.U.; Ghosh, S.G. Gravitational lensing by Charged black hole in regularized 4D Einstein-Gauss-Bonnet gravity. Eur. Phys. J. C 2020, 80, 1128. [Google Scholar] [CrossRef]
- Fernandes, P.G.S.; Carrilho, P.; Clifton, T.; Mulryne, D.J. Derivation of Regularized Field Equations for the Einstein-Gauss-Bonnet Theory in Four Dimensions. Phys. Rev. D 2020, 102, 024025. [Google Scholar] [CrossRef]
- Tomozawa, Y. Quantum corrections to gravity. arXiv 2011, arXiv:1107.1424. [Google Scholar]
- Ai, W. A note on the novel 4D Einstein-Gauss-Bonnet gravity. Commun. Theor. Phys. 2020, 72, 095402. [Google Scholar] [CrossRef]
- Hennigar, R.A.; Kubiznak, D.; Mann, R.B.; Pollack, C. On Taking the D → 4 limit of Gauss-Bonnet Gravity: Theory and Solutions. J. High Energy Phys. 2020, 07, 27. [Google Scholar] [CrossRef]
- Shu, F. Vacua in novel 4D Eisntein-Gauss-Bonnet Gravity: Pathology and instability. Phys. Lett. B 2020, 811, 135907. [Google Scholar] [CrossRef]
- Gurses, M.; Sisman, T.C.; Tekin, B. Is there a novel Einstein-Gauss-Bonnet theory in four dimensions? Eur. Phys. J. C 2020, 80, 647. [Google Scholar] [CrossRef]
- Mahapatra, S. A note on the total action of 4D Gauss-Bonnet theory. Eur. Phys. J. C 2020, 80, 992. [Google Scholar] [CrossRef]
- Lu, H.; Pang, Y. Horndeski Gravity as D → 4 Limit of Gauss-Bonnet. Phys. Lett. B 2020, 809, 135717. [Google Scholar] [CrossRef]
- Kobayashi, T. Effective scalar-tensor description of regularized Lovelock gravity in four dimensions. J. Cosmol. Astropart. Phys. 2020, 07, 13. [Google Scholar] [CrossRef]
- Ma, L.; Lu, H. Vacua and Exact Solutions in Lower-D Limits of EGB. Eur. Phys. J. C 2020, 80, 1209. [Google Scholar] [CrossRef]
- Arrechea, J.; Delhom, A.; Jiménez-Cano, A. Yet another comment on four-dimensional Einstein-Gauss-Bonnet gravity. Chin. Phys. C 2021, 45, 013107. [Google Scholar] [CrossRef]
- Aoki, K.; Gorji, M.A.; Mukohyama, S. A consistent theory of D → 4 Einstein-Gauss-Bonnet gravity. Phys. Lett. B 2020, 810, 135843. [Google Scholar] [CrossRef]
- Cai, R.G. Gauss-Bonnet black holes in AdS spaces. Phys. Rev. D 2002, 65, 084014. [Google Scholar] [CrossRef]
- Dehghani, M.H.; Hendi, S.H. Thermodynamics of rotating black branes in Gauss-Bonnet-Born-Infeld gravity. Int. J. Mod. Phys. D 2007, 16, 1829–1843. [Google Scholar] [CrossRef]
- Kastor, D.; Mann, R.B. On black strings and branes in Lovelock gravity. J. High Energy Phys. 2006, 04, 48. [Google Scholar] [CrossRef]
- Myers, R.C.; Perry, M.J. Black Holes in Higher Dimensional Space-Times. Ann. Phys. 1986, 172, 304. [Google Scholar] [CrossRef]
- Xu, D.Y. Exact Solutions of Einstein and Einstein-Maxwell Equations in Higher Dimensional Spacetime. Class. Quant. Grav. 1988, 5, 871–881. [Google Scholar]
- Ghosh, S.G.; Papnoi, U.; Maharaj, S.D. Cloud of strings in third order Lovelock gravity. Phys. Rev. D 2014, 90, 044068. [Google Scholar] [CrossRef]
- Kumar, R.; Ghosh, S.G.; Wang, A. Shadow cast and deflection of light by charged rotating regular black holes. Phys. Rev. D 2019, 100, 124024. [Google Scholar] [CrossRef]
- Kumar, R.; Kumar, A.; Ghosh, S.G. Testing Rotating Regular Metrics as Candidates for Astrophysical Black Holes. Astrophys. J. 2020, 896, 89. [Google Scholar] [CrossRef]
- Abulencia, A. Direct search for Dirac magnetic monopoles in p collisions at = 1.96 TeV. Phys. Rev. Lett. 2006, 96, 201801. [Google Scholar] [CrossRef]
- Hawking, S.W.; Ellis, G.F.R. The Large Scale Structure of Space-Time; Cambridge University Press: Cambridge, UK, 1973; ISBN 978-051-152-464-6. [Google Scholar]
- Cho, Y.M.; Neupane, I.P. Anti-de Sitter black holes, thermal phase transition and holography in higher curvature gravity. Phys. Rev. D 2002, 66, 024044. [Google Scholar] [CrossRef]
- Ruffini, R.; Wheeler, J.A. Introducing the black hole. Phys. Today 1971, 24, 30. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Carter, B.; Hawking, S.W. The Four laws of black hole mechanics. Commun. Math. Phys. 1973, 31, 161–170. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Black holes and entropy. Phys. Rev. D 1973, 7, 2333–2346. [Google Scholar] [CrossRef]
- Ghosh, S.G.; Deshkar, D.W. Horizons of radiating black holes in Einstein-Gauss-Bonnet gravity. Phys. Rev. D 2008, 77, 047504. [Google Scholar] [CrossRef]
- Davies, P.C.W. Thermodynamics of Black Holes. Proc. Roy. Soc. Lond. A 1977, 353, 499–521. [Google Scholar] [CrossRef]
- Herscovich, E.; Richarte, M.G. Black holes in Einstein-Gauss-Bonnet gravity with a string cloud background. Phys. Lett. B 2010, 689, 192–200. [Google Scholar] [CrossRef]
- MacGibbon, J.H. Can Planck-mass relics of evaporating black holes close the universe? Nature 1987, 329, 308–309. [Google Scholar] [CrossRef]
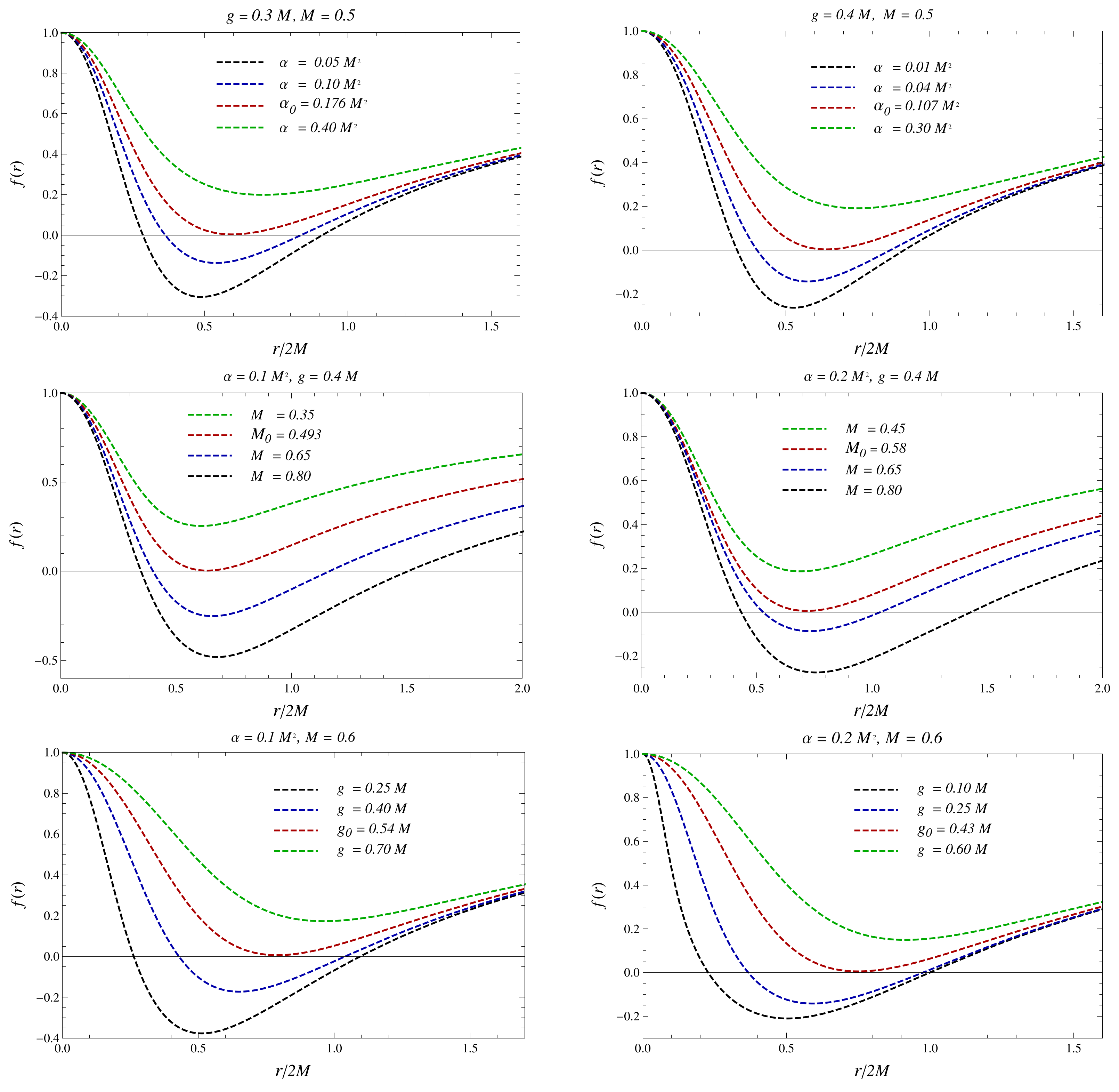

| 0.05 | 0.288 | 0.919 | 0.631 |
| 0.10 | 0.358 | 0.843 | 0.485 |
| = 0.176 | 0.597 | 0.597 | 0 |
| g | |||
| 0.25 | 0.268 | 1.107 | 0.839 |
| 0.40 | 0.432 | 1.044 | 0.612 |
| = 0.54 | 0.797 | 0.797 | 0 |
| M | |||
| 0.80 | 0.352 | 1.513 | 1.161 |
| 0.65 | 0.406 | 1.172 | 0.766 |
| = 0.493 | 0.6515 | 0.6515 | 0 |
| 0.1 | 0.9656 | 0.054 |
| 0.3 | 1.3862 | 0.0353 |
| 0.5 | 1.7165 | 0.0283 |
| g | ||
| 0.2 | 0.8293 | 0.0599 |
| 0.4 | 1.1293 | 0.0477 |
| 0.6 | 1.4964 | 0.0373 |
| 0.1 | 0.423 | 0.538 |
| 0.3 | 0.605 | 0.695 |
| 0.5 | 0.745 | 0.817 |
| 0.7 | 0.864 | 0.918 |
| g | ||
| 0.1 | 0.324 | 0.342 |
| 0.3 | 0.423 | 0.538 |
| 0.5 | 0.571 | 0.757 |
| 0.7 | 0.737 | 0.982 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, A.; Baboolal, D.; Ghosh, S.G. Nonsingular Black Holes in 4D Einstein–Gauss–Bonnet Gravity. Universe 2022, 8, 244. https://doi.org/10.3390/universe8040244
Kumar A, Baboolal D, Ghosh SG. Nonsingular Black Holes in 4D Einstein–Gauss–Bonnet Gravity. Universe. 2022; 8(4):244. https://doi.org/10.3390/universe8040244
Chicago/Turabian StyleKumar, Arun, Dharmanand Baboolal, and Sushant G. Ghosh. 2022. "Nonsingular Black Holes in 4D Einstein–Gauss–Bonnet Gravity" Universe 8, no. 4: 244. https://doi.org/10.3390/universe8040244
APA StyleKumar, A., Baboolal, D., & Ghosh, S. G. (2022). Nonsingular Black Holes in 4D Einstein–Gauss–Bonnet Gravity. Universe, 8(4), 244. https://doi.org/10.3390/universe8040244







