1. Introduction: The Rudiments of the “ER = EPR” Conjecture
The “ER = EPR” is an abridgment pertaining to two fundamental ideas proposed by Einstein back in 1935. The first refers to the notion of non-local linkage between two black holes taking place through
“wormholes” thought of as topological spacetime bridges (ER, for Einstein-Rosen bridges) [
1]. The second refers to the type of linking implied by the ubiquitous phenomenon of
quantum entanglement (EPR entanglement, for Einstein, Podolsky and Rosen) [
2]. The “ER = EPR” conjecture is a ground-breaking proposal by Maldacena and Susskind [
3], which due to the fact that a precise theory of quantum gravity is presently non-existent, aims to clarify the relations between spacetime geometry and quantum field theory in the light of quantum information. If the conjecture “ER = EPR” is valid, then the notions of quantum entanglement and wormholes are not separate, but they constitute two particular manifestations of the same underlying mechanism, which effectively, targets the
connectedness pertaining to the foundation of quantum space-time. In its original formulation, the “ER = EPR” conjecture is conceived in the setting of
dual equivalence pertaining to a theory of gravity in the bulk and the corresponding quantum field theory on the boundary according to the premises of the
AdS/CFT correspondence. The aim of the conjecture is to unravel the correspondence between ER bridges and quantum entanglement. On a cosmological scale the validity of the “ER = EPR” conjecture implies that a complex network of entangled subsystems of the universe as a global entity is equivalent to a complex network of ER bridges. More precisely, since ER bridges pertain to the possible connectivity between black holes, the “ER = EPR” conjecture implies that black holes connected by ER bridges are entangled, and conversely, that entangled black holes are connected by ER bridges.
In the setting of AdS/CFT, the aforementioned correspondence is suggestive, due to the fact that an ER bridge between two asymptotically AdS regions is considered as dually equivalent to two conformal field theories which do not interact but they are entangled thermally [
3,
4], see also [
5,
6]. It has been also pointed out that the area of the minimal surface cut that represents the entanglement entropy and the length of the ER bridge is proportional to the correlations between two dual CFT’s [
7]. This notion has been enriched by the idea that the topological connectivity of spacetime in AdS is in dual correspondence with quantum entanglement taking place on the boundary according to the dual field theory. In this setting, the “ER = EPR” conjecture is a higher order abstraction, since it postulates that the phenomenon of quantum entanglement is
equivalent to the existence of topological handles in spacetime known as wormholes. The conceptual feasibility of this abstraction lies on the qualification of entanglement as an
interchangeable resource. This means that although entanglement may assume various different forms under different physical conditions, these forms may be efficiently inter-transformed to each other under the action of
local unitary transformations. Instances of inter-transformable and, therefore, interchangeable forms of entanglement like; quantum entangled systems, wormholes, entanglement of the vacuum, and Hawking radiation are, in principle, feasible by means of unitary actions. The consequence of this qualification of entanglement is that a typical quantum Bell pair may be cast equivalent to a topological linking bridge in spacetime, and inversely [
3,
8,
9,
10].
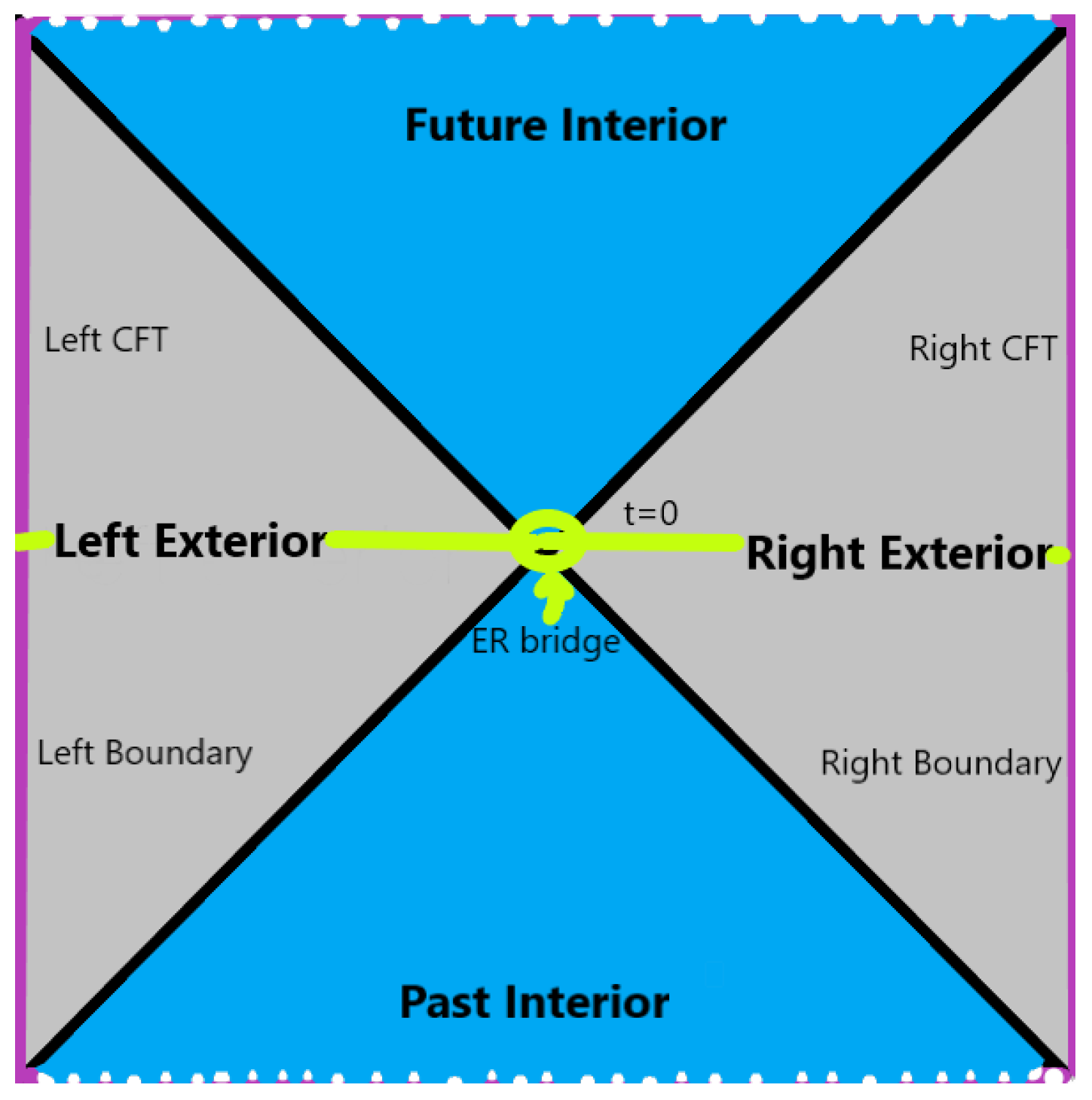
For example, the typical way to view the extended solution of the
Schwarzschild black hole in an asymptotically AdS spacetime involves two black holes located in disconnected spaces with a common time, which are connected by an ER bridge. In this interpretation, we consider two asymptotically flat spatial sheets, where each one bears an identical black hole. But there is an alternative interpretation, according to which, instead of considering the black holes on two disconnected sheets, we view two very distant black holes located in the same space and linked through an ER bridge. Since the minimal radius of this spacetime bridge is dependent on the spacelike slice of the spacetime foliation into leaves, if we take the constant
spacelike slice, there emerge
two AdS exterior regions linked through a wormhole. According to the AdS/CFT correspondence, the AdS space solution of the linked black holes via a spacetime bridge corresponds to a maximally entangled state pertaining to the left and right corresponding conformal field theories on the boundary. In this manner, the entanglement between the left and right CFT’s can be thought of as representing the way that the black holes become linked to each other. In the same context of dual equivalence assumed by the “ER = EPR” conjecture, Maldacena has proposed the interpretation of early
Hawking radiation by means of a black hole that is linked to the interior of the black hole that is emitting via a multiplicity of wormholes that makes them depend on each other [
3].
The starting point of our re-evaluation of the “ER = EPR” conjecture stems from the instance of the maximally entangled Greenberger-Horne-Zeilinger (GHZ) tripartite quantum state, which hints that it is not possible to represent a general maximally entangled quantum state by means of a classical spacetime wormhole. Therefore, there arises the problem of realization of a viable model of a
Planck-scale wormhole that is able to generalize and surpass the standard classical model of a spacetime wormhole [
8]. This instance encapsulates the idea that the relation between entanglement and wormholes may admit a deeper level of explanation, which is suggestive of a
topological linking model that underlies the geometric AdS/CFT correspondence capable to demonstrate the viability of the ER = EPR hypothesis universally. In the same vein, the two perennial problems in the juncture between quantum mechanics and the general theory of relativity, that is; the
quantum state reduction issue in the first, and the issue of
spacetime singularities in the second, can be viewed as concerning the problem of transition into and out of a local spacetime event manifold correspondingly [
11,
12,
13]. Given that the quantum state reduction problem is pertinent due to the quantum entanglement between a system and its measurement means, thus casting reduction as the conceptually inverse pole of entanglement, the validity of “ER = EPR” conjecture may be re-evaluated through an extended categorial framework that moves beyond the premises of the the geometric AdS/CFT correspondence. The objective is the unraveling of a viable linking model which would provide the topological means of expressing the folding into, and inversely, out of the locally smooth event structure of spacetime. This raises the question about the existence and suitability of such a universal topological linking model, which would effectively lead to the manifestation of these two inverse types of transition.
Whereas on the “EPR” side of the conjecture the maximally entangled GHZ tripartite quantum state is suggestive of the possibility of folding out of a locally smooth spacetime structure without causality violation, on the “ER” side of the conjecture the corresponding notion of a Planckian wormhole requires the consideration of a physically plausible distinguishable extension of the standard smooth spacetime manifold model of the gravitational field attaining the validity of Einstein’s equations in a distributional sense.
The above echoes in symphony with the following curious remark of Weyl [
14] that we quote below: “
While topology has succeeded fairly well in mastering continuity, we do not yet understand the inner meaning of the restriction to differential manifolds. Perhaps one day physics will be able to discard it”. It seems that the evaluation of the “ER = EPR” conjecture beyond the confines of the AdS/CFT correspondence requires to examine critically the feasibility of a universal topological linking mechanism that is able to bridge the two sides of the conjecture, allowing in this way the folding into and out of a locally smooth spacetime event structure according to the equivalence between quantum entanglement and Planck-scale wormholes. The physical underpinning of this linking mechanism leads to a criterion that characterizes gravitational generic properties upon entering into the quantum gravity regime.
2. Planck Scale Wormholes, Homology Classes, and Embedded Submanifolds
In the setting of the
AdS/CFT correspondence the extended AdS-Schwarzschild black hole solution is interpreted in terms of two very distant black holes located in the same space and linked through an ER bridge [
3,
4]
Figure 1.
In this context, an ER bridge between two asymptotically AdS regions is considered dually equivalent to two conformal quantum field theories, which although do not interact are thermally entangled to each other. In this manner, if we consider the constant
spacelike slice,
two AdS exterior regions in a thermally entangled state are considered linked through an ER bridge. Equivalently, the solution pertaining to the wormhole linking of these two distant black holes is dually equivalent to the thermofield-double state [
15]. The latter is a highly entangled quantum state referring to the left and right time-reversal symmetric quantum conformal field theories defined on the boundary. According to the above, a wormhole between two distant black holes in the bulk gives rise to the thermofield-double state on the boundary. Thus, the implied proposition “ER ⇒ EPR” seems justified. But, what about the inverse implication “EPR ⇒ ER”?
The critical input comes from the notion of entropy characterizing the highly entangled thermofield-double state, which equals the Bekenstein-Hawking entropy of either black hole, and hence, it is proportional to the black hole horizon area. Furthermore, Ryu and Takayanagi introduced a method of calculating the entanglement entropy that pertains to a region of the conformal field theory, which is based on partitioning the AdS boundary time slice into two regions [
7]. This partition of the AdS boundary is extensible holographically to the time slice referring to the bulk spacetime that is intelligible in the dually equivalent gravitational theory, giving rise to the notion of
holographic entanglement entropy. If the partition on the boundary takes place by means of the regions
Z and
Y, then the boundary
of
Z is extensible holographically to a surface
in the spacetime bulk at the considered time slice, such that
. There are many possible ways that this is plausible, but Ryu and Takayanagi posed the argument that a unique surface having minimal area can be defined, identical with
, such that the holographic entanglement entropy of the region
Z is in proportion to the area of the surface
. This applies to the case of a black hole, where the minimal area surface is the one wrapping around its horizon.
The validity extent of the Ryu-Takayanagi argument—allowing the estimation of the holographic entanglement entropy pertaining to a region of the conformal field theory—comes into question when applied to the thermofield-double state of two highly entangled black holes. In this case, the entanglement entropy pertaining to the region of CFT where the thermofield-double state is pertinent should be amplified by the entanglement entropy characterizing the double state. In case that the black holes are not entangled to each other, the Ryu-Takayanagi argument is directly viable.
In this state of affairs, Susskind [
8] proposed that a bypass of the posed difficulty is possible if the entanglement between the two black holes, which can be described in terms of the quantum thermofield-double state, implicates an ER bridge between them through a global topological alteration of the temporal slice in the bulk spacetime. If we interpret Susskind’s argument in algebraic topological terms, we may assert that what actually pertains to the entanglement between the two black holes, according to the proposed resolution, is the instantiation of a non-trivial
homology class that admits a representation in terms of an
embedded submanifold of the considered temporal slice of spacetime. Therefore, the consideration of the minimal area surface should take into account the pertinent homology class. Then, in view of the role of the latter in estimating the entanglement entropy of a CFT region incorporating the entangled double state, the inverse direction “EPR ⇒ ER” seems to be implied in a reasonable manner.
It is worth pondering on the role of such a homology class in the modification of the global topological characteristics of the considered temporal slice in spacetime that makes the implication “EPR ⇒ ER” intelligible. In the case of classical general relativity [
16], we may
foliate a spacetime manifold
X into 3-dimensional spacelike leaves
by considering an one-parameter family of embeddings
, such that
. In this way, the 3-dimensional Riemann manifold
is thought of as dynamically evolving, where the corresponding metric at time
t,
, is derived by pulling back the spacetime metric
g via
. In this context, all
3-dim leaves are mutually disjoint spacelike leaves, such that the Lorentz manifold
is representative of
X, where the constant time slices are identified with the leaves of the foliation. According to the postulate that the Lorentz manifold
is representative of spacetime
X by means of this foliation, then we may consider the localization of
singular loci by restriction to
. Further, if the topological structure of
is not trivial, then
X is characterized by
geodesic incompleteness, a property equivalent to the fact that
X is singular [
17,
18,
19]. Note that the topological property of
non-simple connectivity amounts always to a non-trivial topology on
[
20]. Henceforth, the existence of singular loci in
constitutes it as a multiple-connected topological space, and thus, topologically different from
.
Let us further utilize the Einstein-Maxwell equations without sources for the electromagnetic field. Then,
bears an orientability, and most importantly, it is cast homotopically equivalent to
as a multiply-connected topological space. We may characterize it as the standard wormhole topology by taking into account the flux lines of the magnetic field that thread through the wormhole, in agreement with the perspective of Misner and Wheeler [
21]. In this setting, the corresponding homology class characterizing all 2-spheres enclosing both of the mouths of the wormhole bears null charge, since the two mouths are of equal and opposite charges. Therefore, a wormhole of the above form may be modelled as representative of an
one-dimensional homology class in spacetime. The association of a wormhole with the notion of a non-trivial homology class is already implicit in the framework of Misner and Wheeler [
21], see also the review by Giulini [
22] in the same context, where the consequences of multiple-connectivity are thoroughly examined. The implications of this association have been also worked out independently in the work of Frolov and Novikov [
23], where they consider the case of a traversable wormhole in spacetime. Furthermore, and in specific relation to the AdS/CFT correspondence, Witten and Yau have pointed out in [
24] that the vanishing of the
nth homology group
, for each applicable
n, implies that there are “no wormholes”.
Additionally, the geometric topology of low-dimensional manifolds informs us that every homology class of a 4-dim spacetime is representable by an
embedded submanifold [
25], which can be localized to
according to the foliation in constant time slices. Because of this correspondence it is possible to conceptualize higher-order ER bridges, for instance, the one corresponding to a two-dimensional homology class, if we manage to unravel the possible physical conditions that force such a type of a wormhole. The geometric interpretation of homology classes in terms of embedded submanifolds stems from the work of Thom [
26,
27]. The general idea is the following: We view a
kth homology
class, which is not zero, as an embedding of an oriented
k-manifold
into
X that cannot be contracted into a point along
X. Note that
represents zero in homology if it is the boundary of a
-manifold in
X. Two different embeddings
and
belong to the same homology class if there is an oriented manifold with boundary
embedded in
X, such that its boundary consists of
and
with one of them bearing the opposite orientation. The respective cohomology classes
are dual to
, and moreover, Poincare duality is in force.
Our main argument is that these wormhole solutions of higher-order should be considered as viable candidates of Planck-scale ER bridges that justify the “ER = EPR” conjecture. The issue arises when we consider a tripartite entangled quantum state, which cannot be represented as a classical ER bridge of the above form. Therefore, a feasible representative model of a
Planckian wormhole, along the previous lines, surpasses and generalizes the standard conception of a spacetime wormhole. This is in agreement with both, the terminology introduced by Susskind in [
8,
10], and the radical position of Maldacena and Susskind expressed in Section 3 of [
3], according to which:
“There are similarities between entanglement (EPR) and Einstein-Rosen Bridges that we want to call attention to. In fact, we are going to take the radical position that in a theory of quantum gravity they are inseparably linked, even for systems consisting of no more than a pair of entangled particles”. Notwithstanding this realization, the association of ER bridges with homology classes under appropriate physical conditions implies the functional role of a topological linking framework underlying the geometric AdS/CFT correspondence in relation to the unraveling of the “ER = EPR” hypothesis in a universal way that we are going to start exploring in what follows.
3. Topological Network of Tripartite Black Hole Entanglement
Let us follow the proposal that a system of
qubits is representative of the degrees of freedom of a black hole from an information-theoretic standpoint [
3,
8,
10,
28,
29]. We recall that the state space of a quantum system that is composed of various subsystems is expressed by the tensor product of the state spaces of these components. Let us consider a qubit, that is, a quantum system whose state space is two-complex dimensional, and let
and
denote the pure states of a basis of this space. Then, for the composite quantum system consisting of two qubits there are states, for instance
, which are not separable, and thus they are entangled. Note that we consider the general abbreviation
.
Let us focus next to the case of
three qubit systems denoted by
A,
B and
C correspondingly. The composite quantum system of these three qubits is characterized by the state space given by the tensor product of the state spaces of the three component subsystems. We consider the so called
GHZ state (Greenberger-Horne-Zeilinger) of the composite system defined by
[
30]. The GHZ state
of the system of three qubits bears the characteristic of maximal entanglement among its components.
For our purposes, we return to the pertinent information-theoretic hypothesis that a system of
N qubits is representative of the degrees of freedom of a black hole, where
N bears the order of the entanglement entropy [
3,
8,
28,
29]. Under this assumption, a pair of entangled black holes dually equivalent with the thermofield-double state, denoted by
, is representable by a state of
qubits that is characteristic of maximal entanglement. In this sense, the initial state of the entangled pair of black holes is expressed by means of the following product:
where each of the
N factors pertains to a Bell pair that is entangled maximally. Hence, we may initially focus on a single such pair, denoted by
:
The measurement of an observable of any of these qubits requires the consideration of an apparatus, which may be identified in this context with a third qubit. The latter is associated in this way with a commutative algebra of observables co-related with the measurement of any of these two qubits. Therefore, the
GHZ state of the system of three qubits emerges:
which expresses the case of maximal tripartite qubit entanglement characterized by threefold permutation symmetry. The unique properties of the maximally entangled tripartite state are the following: (i) If we consider the partial trace with respect to any two of the qubits, the density operator of the third qubit is a maximally mixed state, meaning that any of the qubits bears maximal entanglement with the other two; (ii) If we consider the partial trace with respect to any one of the three qubits, the reduced density operator is separable.
For example, consider a tripartite qubit system of
,
and
, and the measurement basis of projectors
and
related only with the qubit
, where
and
. The state of the tripartite system is reduced to, either the state
, or the state
, after the measurement is completed, such that the latter are separable. The analogous separable reduction result is obtained symmetrically for the case of measurement of any of the other two, since
is symmetric under permutations. Moreover, if we consider the partial trace with respect to
in
, then the reduced density operator;
gives rise to the separable mixed state arising from mixing the separable states
and
.
In this context, Susskind [
8] proposed that the state
may be thought of in terms of a tensor
that is symmetric and representing the three maximally entangled qubits. The underlying idea is that
is transformable by means of local unitary transformations which preserve
. These local unitaries encode the intertransformability of entanglement under alteration of form [
3,
8], for instance from maximally entangled qubits to wormholes, preserving the same entanglement entropy. In this manner, the information-theoretic content of a maximally entangled quantum state of
qubits represents under unitary intertransformability a pair of entangled black holes, whose initial state is equivalent to the tensor power of
N’s, that is:
Similarly, a third black hole bearing again the information content of another system of
N qubits, in its capacity to correlate with a commutative algebra of observables referring to the measurement of any of the other two black holes, leads to maximal tripartite entanglement as pertaining information-theoretically to black holes this time, expressed by the following tensor power:
Therefore, for a fixed entanglement entropy, the information intertransformability induced by local unitary transformations constitute the characteristics of the tripartite black hole entanglement in precise analogy to the corresponding characteristics of tripartite qubit entanglement. Since the former is tantamount to an ER bridge, according to the equivalence “ER = EPR”, the conclusion is that the pertinent wormhole type cannot be a classical one, therefore, bearing the status of a Planckian type. A Planck-scale ER bridge bears an invariant GHZ-core of maximal entanglement, since it is impossible to be erased by the action of local unitaries. According to Susskind, it is this invariant core that admits a representation in terms of appropriate products of the symmetric tensor , giving rise to a tensor network that evolves and grows in information complexity over time.
Despite the profoundness of the ideas involved in the information-theoretic treatment of black hole entanglement along these lines in the context of the AdS/CFT correspondence, no further clue is provided in the justification of the implication “EPR ⇒ ER” beyond the assertion that the entanglement between two black holes in the thermofield-double quantum state implies the existence of an ER bridge between them through a global topological alteration of the temporal slice in the bulk spacetime. As we have pointed out already, based on the notion of the holographic entanglement entropy pertaining to a region of the CFT, what pertains to the entanglement between two black holes, is a homology class that is representable by an embedded submanifold of this slice of the foliation. This perspective is in symphony with the classical case of a wormhole, thought of as the representative of an one-dimensional homology class in spacetime. In the present case, the phenomenon of quantum entanglement between black holes, conceptualized in terms of qubits according to the above, gives rise to these physical conditions for the instantiation of an appropriate two-dimensional homology class, which bears the capacity to act as a Planck-scale wormhole. In this manner, the association of a Planckian ER bridge with a two-dimensional homology class paves the way for unraveling an underlying suitable topological linking framework underlying in relation to our concern about the implication “EPR ⇒ ER” in a universal way.
The most important global topological attribute of a Planckian ER bridge arising from is that tracing over any one of them leaves the remaining two completely unlinked topologically. This is the core idea that needs to be qualified in terms of an appropriate topological link, which subsequently admits a homological interpretation by means of a 2-dim homology class with respect to the pertinent temporal slice in the bulk. Equivalently, this homology class can be represented as a 2-dim embedded submanifold of this slice, thus instantiating the corresponding Planckian wormhole.
This is also relevant to Susskind’s proposal [
8] that
is representable by means of the symmetric tensor
, out of which by iteration the tensor network of the entangled black holes emerges. But, despite the threefold symmetry of
under local unitary transformations, the basic characteristics of tripartite entanglement according to (i) and (ii) above, referring to the GHZ-type of topological linking properties giving rise to an invariant core are absent from the tensorial model. This raises doubts about the status of such a tensor network. Rather, what seems to be more suitable is a topological network conceptualized in terms of the irreducible topological link that encapsulates the type of Planckian wormhole arising from
. The leading idea here is that this particular topological link is expressible in terms of local unitaries leaving the GHZ-core invariant, such that quantum entanglement becomes physically an interchangeable resource for some fixed entanglement entropy.
4. Tripartite Entanglement and Non-Splittable Topological 3-Links
A
topological N-link encapsulates the type of topological entanglement referring to a constellation of
N loops, where
N is a natural number, which are considered as unknotted and tame closed curves [
31]. The type of topological entanglement characterizing a collection of
N loops is expressed through the property of
splittability of the corresponding
N-link. This property designates if the link can be partially disentangled under continuous topological deformation, where cutting is not allowed. Concretely, a link is completely splittable if it can be entirely disentangled, whereas it is non-splittable if the disentanglement of any possible combination of linked loops from the remaining ones in the constellation is impossible under deformation.
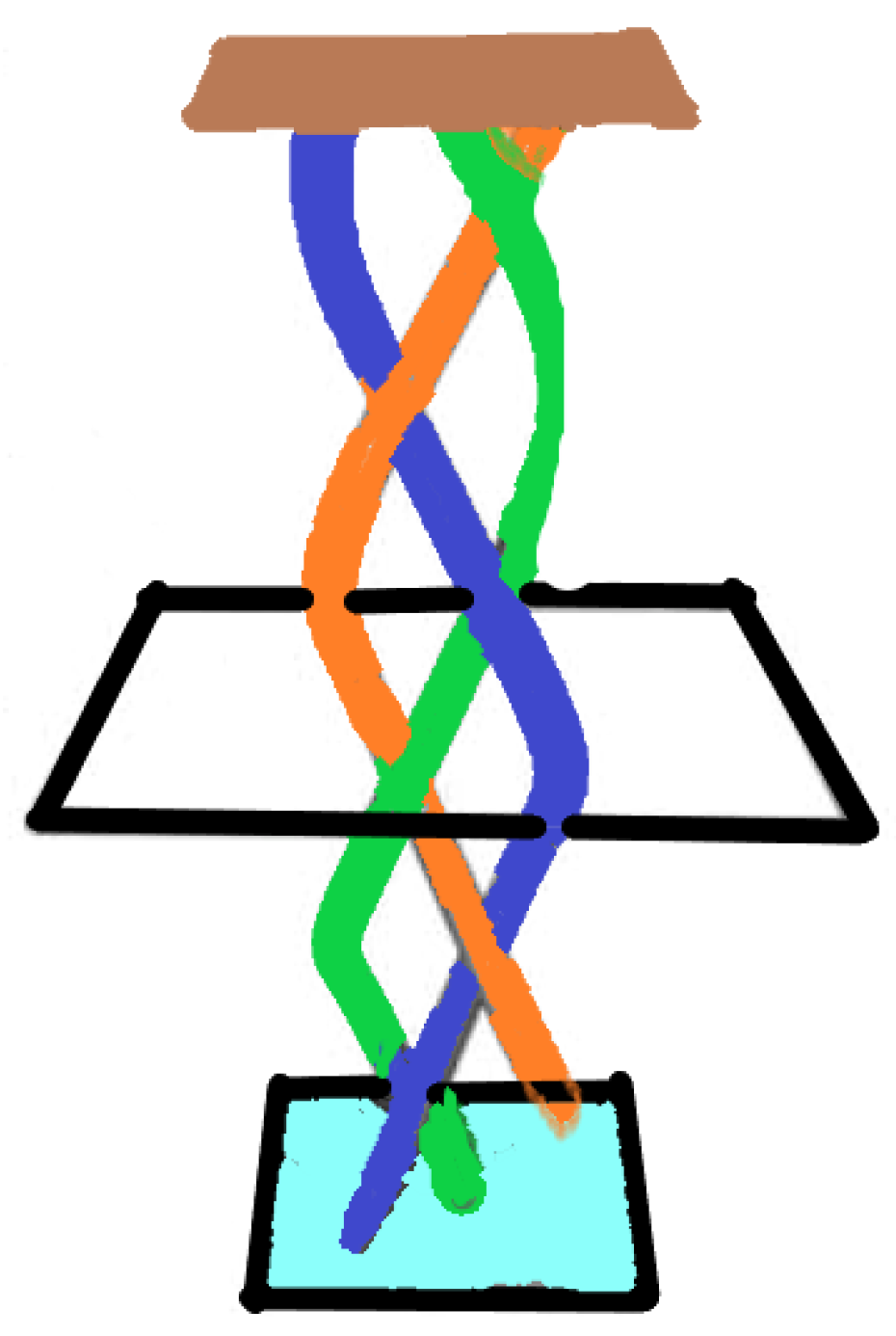
The focus of our work lies on a particular type of a topological 3-link constituted by three loops, which are entangled in such a way that cutting any of the three from the 3-link leaves the other two disentangled. This 3-link is called the
“Borromean rings”. We stress that the rings in the “Borromean link” are considered as loops, or topological circles, and not as perfect geometric circles [
32,
33,
34,
35]. In terms of the splittability property, the Borromean link is a
non-splittable 3-link, such that
every 2-sublink of this 3-link is completely splittable. The “Borromean rings” is a non-splittable 3-link because the type of topological entanglement of the three loops forming the link is such that, disentanglement of any one of them, or any pair, is not feasible under continuous deformation but requires to cut [
12,
36]
Figure 2.
The apparent similarity between the “Borromean link” and the properties of the maximally entangled GHZ state has not remained unnoticed. Aravind attempted to formulate a correspondence between quantum and topological entanglement by thinking of a quantum state in analogy to a loop, such that an entangled state would behave like a topological link [
37]. In this analogy, the process of measurement referring to a component of the composite system leads to the entangled state reduction, which corresponds to cutting the pertinent loop of the link. Of course, the analogy, as it has been formulated, is subordinate to the choice of a basis of measurement making it quite weak. In terms of the topological feature of splittability, the analogy implies that the state of an entangled pair of qubits behaves like a 2-link that is non-splittable, whereas a separable state behaves like a 2-link that is splittable.
Based on the above conceptual compass, the invariant and irreducible core of maximal entanglement characterizing the tripartite qubit case constitutes the state clearly analogous to a 3-link that is non-splittable. Recall that if we think of a tripartite qubit system of , and , together with a measurement basis of projectors and pertaining only to the qubit , the maximally entangled state is reduced to either the state , or the state , upon completion of the measurement, such that the latter are separable. Moreover, the corresponding separable reduction result is obtained symmetrically for the case of measurement of any of the other two, since is symmetric under permutations. In this sense, the topological analogy informs that if the tripartite entangled state is indeed like a non-splittable 3-link, then a measurement reducing this state referring to any of the qubits corresponds to erasing the respective loop from the constellation, such that the emergent reduced state corresponds to a 2-link that is splittable. Henceforth, the maximally entangled tripartite GHZ state behaves in analogy to the Borromean rings.
It is worth pointing out that although the objection referring to the fact that the analogy, in the manner formulated by Aravind, is basis-dependent, a slight modification bypasses this dependence. The modification rests on the idea that it is not measurement per se that corresponds to erasing a respective loop from the non-splittable Borromean link, but it is the reduction itself, as it is expressed in terms of the reduced density operator of the maximally entangled state with respect to the component resembled by this loop. Note that the partial trace operation with respect to in , gives rise to , which is a separable mixed state arising from mixing the separable states and , therefore, indeed behaving like the Borromean rings.
Notwithstanding the value of this analogy, the crucial issue from our perspective stems from the founding hypothesis that a quantum state behaves as a loop. This problem has been already addressed effectively from a group-theoretic viewpoint that encodes the invariance of the Borromean rings through the commutator of the generators in the non-Abelian free group of two generators [
36], which admits a representation on the Hilbert space of state vectors in terms of corresponding
one-parameter unitary transformation groups generated by conjugate observables. The algebraic encoding of the non-splittable 3-link formed by the Borromean rings will be recapitulated briefly in the sequel, since it proves to be instrumental for the modelling of the topological network suited to entangled black holes according to the “ER = EPR” conjecture. In this manner, the Borrromean link is realized by means of one-parameter unitary groups that leave invariant the irreducible GHZ-core under their action, such that quantum entanglement becomes physically an interchangeable resource for some fixed entanglement entropy.
The guiding idea is to think of an one-parameter unitary group infinitesimally generated by an observable as a based loop up to continuous deformation within the algebra of all observables commuting with it, and thus sharing the same spectral resolution [
38]. Since an one-parameter unitary group preserves the degree of distinguishability induced by the spectral resolution of the observable it is generated from, the corresponding based loop may be considered in relation to a topological circle constituting a barrier in its continuous deformation, such that the loop cannot be contracted to its base point upon passing through this topological circle with a prescribed orientation. In this way, the topological circle encodes the resolving capacity of the considered observable in terms of its simultaneous projective resolution, such that the non-contractibility of a respective based loop upon passage through this circle enciphers the preservation of the degree of distinguishability afforded by the corresponding resolution. Although the projections corresponding to conjugate observables are not simultaneously realizable, we have showed that there exists a condition of joint synchronization with respect to an area bounding cycle, which can be derived from the Borromean link through the process of
Abelianization [
39].
The basic result is that the commutator loop expressing algebraically the Borromean link passing through both circles with a prescribed orientation corresponding to the partial ordering of the composite based loops is qualified as a synchronizing loop under the constraint that its winding number is zero, thus, giving rise to an area bounding cycle. The synchronization condition, whose quantum manifestation is the GHZ tripartite entanglement, descends from the Borromean link of based oriented loops in , or , considered as topological spaces, by excluding the contraction barriers B imposed by two non-intersecting topological circles corresponding to conjugate self-adjoint spectral operators. Therefore, the synchronization condition expresses the homological congruence of an entangled area bounding loop. The homological characterization captures the physical fact that entanglement is an interchangeable recourse with respect to the pertinent boundary enclosing the corresponding area. For the sake of completeness, we summarize the algebraic model of the Borromean link in what follows.
5. Non-Commutative Linking in 3-dim Space via the Free Group of Two Based Oriented Loops
Since any tame closed curve in 3-dim space is deformable to a circle, we consider such a circle, denoted by Z. Note that the circle is considered topologically, not geometrically. Next, we consider a loop that is orientable, and based at a fixed reference point p of the 3-dim space, called the base point. The based loop is studied in relation to its passage through the circle Z taking into account its orientation and how many times this passage takes place. If the based loop passes through A once directed away from the base point p it is expressed by the symbol . If the based loop passes through A once directed toward p it is expressed by the symbol . Since a based loop is intelligible up to continuous topological deformation, its symbol pertains to the whole partition class that it represents. Moreover, since a based loop is always considered in relation to a corresponding circle through which it passes, it is natural to examine if two loops related to distinct circles may be composed. This is possible only if these loops share the same base point, but their composition is sensitive to the order that they are composed. This means that although composition of oriented loops based at the same point of 3-dim space is feasible, it is a non-commutative operation. Upon specification of the order of composition, let be the symbol of the composite loop based at the same point, to be interpreted as their non-Abelian product of multiplication. This product is associative and extends to a remarkable group theoretic structure isomorphic with the non-Abelian free group that is generated by two non-commuting elements.
In particular, for each based loop , the inverse is defined by , which has the opposite orientation. In this way, the products , and express the based loop at the same point, which does not pass through any circle at all, expressing the multiplicative neutral element 1. Therefore, these symbols under their associative product give rise to a non-Abelian free group, denoted by . The closure of multiplication in this group allows the formation of any admissible string of symbols which is irreducibly expressed only by means of the group-theoretic relations , , and so on. Syntactic equality of symbols in the group bears the topological semantics of composite oriented based loop equivalence upon deformation. If we consider two based oriented loops—relationally to corresponding circles—as generating the group freely through their associative product without any further constraints, we obtain the structure of the non-Abelian free group in two generators, which we denote . All these groups are isomorphic to each other, thus the above method provides the means of its realization in terms of based loops in 3-dim space.
It has been shown in [
36] that the type of topological entanglement characterizing the Borromean link is encoded algebraically through the non-Abelian multiplicative group-theoretic structure of
in terms of the
group commutator of its generators
Figure 3:
The above irreducible composite string represents a product loop that is based at the same point, obtained after composing , , , in the order that they appear. The fact that the commutator in is syntactically irreducible encapsulates algebraically the non-splittability of the Borromean rings, that is, the type of topological entanglement of the 3-link formed by two based loops and their commutator product. Note that upon cutting both loops and , or and , encoding the topological disentanglement of the circle Z or the circle H from the link, the commutator is reduced to the neutral element 1, expressing the complete splittability of any 2-sublink of the Borromean rings.
We can also view the Borromean link in terms of a Borromean braid after identification of the corresponding initial and final points of the braid. In this manner, the Borromean link appears as the closure of the respective Borromean braid. This follows from the Alexander theorem [
31], according to which every link is isotopic to a closed braid. In practice, we consider the orthogonal axis of symmetry of the Borromean link passing through the center, such that the link encircles this axis according to a specified orientation. Then, moving along this axis the Borromean link can be dissected into three strands whose weaving pattern gives rise to a Borromean braid. Inversely, the link may be re-synthesized by gluing the corresponding initial and final points of the Borromean braid
Figure 4. Note that upon closure, each strand of the braid is expressed as the commutator of the other two, which is the characteristic of the maximal tripartite entanglement. In this sense, all the results obtained in relation to a Borromean topological network may be translated in terms of the corresponding braid network.
At a further stage, due to fact that the free non-commutative group in two generators, realized as above, admits a representation in terms of one-parameter unitaries acting on the Hilbert space of state vectors [
36,
38], which may be generated by any pair of conjugate observables, the Borromean link—expressed through the free group commutator—is transferred to the space of states through the corresponding one-parameter unitary actions, where these actions in Hilbert space has been first studied by Stone [
40]. The semantics of the Borromean link under its free group realization on the quantum state space is interpreted physically as the synchronization condition of the one-parameter unitary groups generated by a pair of conjugate observables.
In this way, although the projection operators corresponding to conjugate observables are not simultaneously realizable, there exists a condition of joint synchronization with respect to an area bounding cycle, which is obtained from the Borromean link through the homological process of Abelianization [
39]. In point of fact, the synchronization condition, which if applied to three qubits gives rise to the GHZ tripartite entanglement, descends from the Borromean link of based oriented loops in
, by excluding the contraction barriers imposed by two non-intersecting topological circles corresponding to conjugate spins, expressing in this manner the homological congruence of the entangled area bounding commutator loop.
6. Topological Origin of Tripartite Entanglement: Unitary Representation of the Borromean Link on the 3-Sphere of Qubits
We recall that the unit 2-sphere
is the space of pure states, or projective rays of a qubit. We may think of the unit 2-sphere in terms of its embedding in
. Since, the Hilbert space of normalized unit state vectors of a qubit is the 3-sphere
, the 2-sphere
is identified with the base space of the Hopf fibration:
If the north pole and south pole of correspond to the orthogonal vectors and of a basis respectively, then antipodes of are orthogonal to each other.
The objective is to realize a representation of the Borromean rings on , which can be lifted to in terms of unitary transformations via the Hopf fibration. For this purpose, we use the realization of the Borromean rings in terms of the commutator of the two generators that give rise to the non-Abelian free group . Since all free groups in two non-commuting generators are isomorphic to each other, the idea is to focus on the non-Abelian group and identify a free subgroup generated by two non-commuting rotations A and B that are independent of each other. The independence refers to the axes of rotation through the center of the sphere. In this case, the commutator of these rotations would give rise to an irreducible string of four rotations in the isomorphic copy of in that bears the same characteristics like the group-theoretic encoding of the Borromean rings.
Let us consider a rotation A that is rotating counterclockwise around the z-axis by an angle , such that for instance, ; and another independent rotation B that is rotating counterclockwise around the x-axis by the same angle . Since the angle is irrational, these two non-commuting rotations generate a free non-Abelian subgroup of . The reason is that any string of symbols involving multiplication of A with B or their respective inverses is not reducible to the neutral element of if the angle of rotation is irrational. Note that each rotation of the non-Abelian subgroup of has two fixed points on , that is, the antipodal points that the centered axis penetrates . The class of all possible points fixed in this manner are countable, therefore the action of the free subgroup on is a free action if we quotient out. Thus, is partitioned into disjoints blocks under this action, identified with the orbits of this subgroup action. Each of these orbits may be identified with the free subgroup under the choice of a base point because the action is free. Not only this, but the class is in principle restorable by means of rotating around an axis that does not overlap with this class, and therefore, can be resolved globally in terms of strings from , generated as above. In the same way that the irreducibility of the commutator of is encoding the non-splittability of the Borromean rings as a topological 3-link, it is here encoding the non-separability of the respective orbits under the choice of a common base point.
The free subgroup of
is lifted as a free subgroup of
via the Hopf fibration. More precisely,
, which is isomorphic with
, is doubly covering
, meaning that for any rotation
A of
there are precisely two unitary rotations
U and
covering it, to be though of as its roots. Let
denote the covering projection:
that is a surjection and has kernel isomorphic with
. Let the rotation
A be characterized in terms of its axis
and angle
. Then the unitary transformation
U corresponding to
A is expressed by:
where
is expressed in terms of the Pauli matrices
,
and
, as
, where
. Then, we obtain:
The implied correspondence is the following: Consider a vector
r of
, such that the action of
A on
r, that is,
, is realized through the conjugation action of
U:
where,
by the covering projection. If the angle
is modified by
, then
A remains invariant, whereas the covering unitary
U alters its sign,
, such that
, as an expression of the fact that rotations are doubly covered by the corresponding unitary transformations, to be thought of as their roots.
Then, for two independent rotations
A and
B of
generating a free subgroup isomorphic with
, the latter is lifted to a free subgroup of
generated by the unitary roots of these rotations. These roots are
unitary matrices over the complex numbers with determinant 1, such that
and
, according to the above. According to the terminology of Von Neumann, both
and
are non-amenable groups [
41], since both of them contain
as a free non-Abelian subgroup. Hence, the group
admits a representation both in terms of rotations as a non-Abelian subgroup of
, and in terms of unitary rotations as a subgroup of
, where the latter is lifted from the former. Therefore, the group
is unitarily represented in the space of unit vectors
of a qubit. Since the irreducibility of the commutator in
is encoding the non-splittability of the Borromean rings, it is also encoding the non-separability of the orbits of one-parameter unitary groups generated by a pair of conjugate spins under the choice of a common unit state vector.
The Borromean type of linking gives rise to a condition of joint synchronization of the corresponding conjugate one-parameter unitary groups with respect to an area bounding cycle, which is obtained from the process of Abelianization [
39] that is concomitant to the choice of a complete set of commuting observables. In this way, if we recall the analogy between GHZ tripartite qubit entanglement and the Borromean rings, the conclusion is that the analogy does not require a direct correspondence between a quantum state and a loop, but it is based on the fact that the free group
encoding the Borromean link through the group commutator of its generators is representable on the space
of unit state vectors by means of one-parameter unitary transformations. Thus, according to the information-theoretic treatment of maximally entangled black holes, where the degrees of freedom of each is represented in terms of a system of
N qubits, we assert that the tripartite black hole entanglement is also descending from the Borromean link. In view of the “ER = EPR” hypothesis, this type of entanglement corresponds to a Planckian ER bridge of the same linking type, giving a way to represent the notion of an invariant and irreducible GHZ-core under the action of local unitaries.
From the above analysis, it is interesting to point out that the correspondence is based on the fact that an one-parameter unitary is homotopically equivalent to a loop. This is the case because it retracts by continuous deformation to a loop through its determinant that takes values in
. The free group commutator generated by two conjugate spins is encoding their non-separability through the non-separability of the corresponding Borromean link. Note that if the group commutator becomes unity, corresponding to the Abelianization of the link, an area-bounding region emerges that is homologically toroidal. More precisely, Abelianization of the Borromean link gives rise to the homology basis of a torus, where the loop generators are linked according to the Hopf link. In this sense, the Abelian degeneration of the Borromean link into a Hopf link, underlying the Hopf fibration pertaining to qubits, allows the qualification of bipartite entanglement in terms of the tripartite entanglement, thus its indirect qualification as a Planckian one when the tripartite is taken into account. This interpretation provides a viable topological way to approach the following claim of Maldacena and Susskind in [
3], and in [
10]:
“In fact we go even further and claim that even for an entangled pair of particles, in a quantum theory of gravity there must be a Planckian bridge between them, albeit a very quantum mechanical bridge which probably cannot be described by classical geometry … According to the ER = EPR connection, such non-trivial topologies simply characterize the entanglement between the black holes and should be allowed as possible quantum states”. “… Even the simple Bell pair has a highly quantum version of an ERB connecting it, and when brought together with a great many other quantum ERB’s, they merge to form a large ERB”. 7. Global Topological Network of ER Bridges via Borromean Modular Blocks
From the standpoint of the Borromean topological link, interpreted as the synchronization condition of the one-parameter unitary groups generated by a pair of conjugate spins, it is worth revisiting Susskind’s proposal [
8] that the tripartite state of maximal entanglement corresponds to a symmetric
pertaining to the three maximally entangled qubits, out of which by iteration the tensor network of the entangled black holes emerges information-theoretically. We already pointed out that despite the threefold symmetry of
under local unitary transformations, the basic characteristics of tripartite entanglement according to the established properties in
Section 3, referring to the descent of GHZ from the topological linking property of the Borromean rings, and giving rise to an invariant core, are absent from the tensorial model. This raises doubts about the status of such a tensor network. Therefore, it seems more appropriate to consider a topological network assembled properly by means of irreducible Borromean linking modular blocks encapsulating the type of Planckian wormhole arising from GHZ through “ER = EPR”. The leading idea again is that the Borromean link is expressible in terms of local unitaries leaving the GHZ-core invariant, such that quantum entanglement becomes physically an interchangeable resource for some fixed entanglement entropy.
As a first step in this direction, we point out that if we consider any of the loops in the Borromean link and substitute it with a Borromean link, then we obtain a Borromean link of Borromean links. This might be considered as the first step of an iteration procedure that preserves the invariant core of this type of topological entanglement. If we associate each iteration with an increase in the order of complexity, then a network emerges, which is growing in complexity from the invariant core. Given this observation, the pertinent question for the conceptualization of such a topological network that may accommodate other types of entanglement as well, is the following: Can it be shown that every possible type of topological linking can be assembled appropriately from the 3-link of the Borromean rings, playing in this case the role of an invariant building block that preserves the invariance of the core? The demonstration that this is indeed the case for a topological network, as a more suitable model of a tensor network, would qualify the “ER = EPR” hypothesis beyond the framework of its initial formulation. Note that the Hopf link of two rings is a degenerate case of the Borromean link obtained via the process of Abelianization that transforms the commutator to a neutral element, which may be thought of topologically as a homological boundary [
39].
For this purpose, the main idea again is that the irreducible commutator in expresses group-theoretically the fact that the Borromean rings form an entangled 3-link, which bears the non-splittability proparty, but all 2-sublinks of this 3-link bear the complete splittability property. We denote this type of entanglement by the symbol . Hence, the designation of the Borromean rings as a modular block of entanglement for any type of linking behavior in a topological network would necessarily involve the free group commutator iteratively in its function as a sufficient means to encode these types of linking.
It is natural to start from the case of a
link as a direct generalization of the Borromean
link. This case refers to the type of entanglement of three spectral topological circles
A,
B and
C by means of the first order iteration of the Borrommean rings. First, we consider the Borromean entanglement of
A and
B by their commutator product, and then, the entanglement of the latter with
C. The standard one is expressed by the commutator
,
. The first order iteration of the joint commutator formation is expressed by the commutator of
with
. Thus, the first higher Borromean product loop is expressible according to following syntactic string in
Figure 5:
The above is analytically expanded as follows:
Therefore, the Borromean rings indeed plays the role of a modular building block for expressing syntactically other links of higher order that they are non-splittable, but all of their lower sublinks split entirely, as a generalization of the Borromeanicity property. The modularity is expressed through commutators of the general type . Clearly, in the above case of , the erasure of all instances of any symbol and its inverse reduces the formula to the neutral element 1.
In general, if we consider three symbols e, f, g under the intended interpretation, the Borromean entanglement of e with f takes place through , which is subsequently linked with g to obtain the first order iteration of the Borromean linking, expressed through the commutator stacking . The latter provides the required fourth symbol in the group , which is decoded topologically as a link. Analogously, if we iterate twice the commutator formation starting with four symbols e, f, g, h, we obtain the model of a link. The same procedure can be generalized inductively, showing that any link in the network can be modelled by means of Borromean modular blocks, where . The inductive generalization pertains to stacked commutators nested within each other, expressing in this manner any link in the network in terms of Borromean entanglement modular blocks. We conclude that any link is modelled in terms of a stacked commutator of order expressed in terms of symbols in , where . The order of refers to how many of the symbols become disentangled upon deleting anyone of the symbols from . To be consice, we call a stack of order .
The final step needed for the consistent emergence of a topological network, consisting of Borromean blocks that capture all the features of GHZ entanglement, refers to the instantiation of a link , where . stands for a non-splittable N-link, whose all K-sublinks split entirely, although each and , …, -sublink, including the N-link itself, does not split. Can we assemble a link in the network by means of Borromean modular blocks? We already know that refers to a stacking of order .
It is clear that requires to consider strings involving suitable products of modular commutator blocks, which they could be synthesized with stacks of some relevant order. Topologically, this product may be interpreted as the means of emergence of a Borromean chain of some length consisting of Borromean modular blocks. The chain product operation can be synthesized with the stacking operation, such that, chains of stacks become feasible. We will show that the synthesis of these two operations is sufficient for assembling an arbitrary out of commutator blocks. Concomitantly, it is these two operations that encode how a complex topological network may grow out of the invariant core on the modular basis of Borromean blocks.
The key notion is that, if we consider
e,
f,
g under the intended interpretation as previously, they give rise not only to the stack
, but the commutators
,
and
arise in their function as modular blocks as well. Each one furnishes a new symbol, and the same holds for their product. We interpret this product arising out of the composition of blocks, a chain of length 3, equal to the number of its factors. We can easily verify that such a chain encodes a
link from the fact that the erasure of any pair of the involved symbols reduces this chain to the neutral element, whereas erasure of any one of them results in the entangled Borromean block that remains intact
Figure 6. Hence, the above chain gives rise to the fourth required symbol, in consistency with the topological description of a
link, such that the latter is constructed in modular terms. The length of the Borromean chain modelling a
-link is expressed by the number of combinations of 2 symbols out of 3, where a combination is simply the formation of the commutator of 2 symbols in this case.
It is clear that the process of composing Borromean links in Borromean chains can be generalized to the case of composition of Borromean stacks, such that these operations in
are synthesized. From a physical viewpoint, we think of stacking as the iterative ordered concatenation of modular blocks within each other growing the network depth-wise. Analogously, we think of chain formation as a process of complexity growth in length through blocks of the same type. Let us consider the case of a
link, which exemplifies both of these two types of growth. From the defining feature of a
link in terms of topological splittability, if we cut any of its constituent loops what remains is a
link, which is encoded in the stack
in terms of the symbols
e,
f, and
g. Thus, the expression of a
link involving four symbols
a,
b,
c, and
d, is feasible in terms of a composition product having the property that erasure of any of these symbols reduces the link to the stack
. This product pertains to a Borromean chain of length 4, according to the following formula in
:
Finally, let us consider the general case of an arbitrarily complex link in the network , where . For any M, the link is encoded syntactically as a stack of M-order. At the following stage, the objective is to construct a link out of symbols in . If we cut any of the constituent loops from a link, what remains is a link. Thus, this case is treated analogously to the case of a link. In detail, we compose a chain out of M-order stacks whose length is determined by . The chain gives rise to the name of a new symbol, identified with the one. Next, the objective is to express a link in terms of Borromean modular blocks out of symbols. We simply compose a chain out of M-order stacks whose length is determined by . The chain gives rise to the name of a new symbol, identified with the one. The composition of new extended length chains is iterated inductively in the same way until N is reached. This leads to the conclusion that a link , irrespectively of its complexity, is constructible through the synthesis of Borromean entanglement modular blocks out of depth-growing ordered stacks and their composition length-extending chains.
Therefore, we have showed that a global topological network is solely constructible by means of Borromean modular blocks encapsulating the type of Planckian ER bridges corresponding to the maximally entangled type of black holes. This is conducted through the unitary representation of these Borromean linking blocks that preserve the GHZ-core, such that quantum entanglement constitutes an interchangeable resource for some fixed entanglement entropy.
8. Relative Homology Classes on Dense Complements of Borromean Blocks on the 3-Sphere
Due to the prime role of a Borromean modular block in a global topological network, the “ER = EPR” conjecture requires to scrutinize the quantum gravity consequences arising from the ER side. In this manner, let the foliation
represent the spacetime
X, which is characterized by geodesic incompleteness due to the localization of singularities within the three-dimensinal manifold
. The assumption is that this qualification emerges topologically from multiple-connectivity because of the singularities in
. The basic notion in this context, according to [
42], is that a constellation of singular topological disk boundaries qualified in terms of
nowhere dense and closed subsets of an open set of
, or better, its compactification
, gives rise to a topological link in
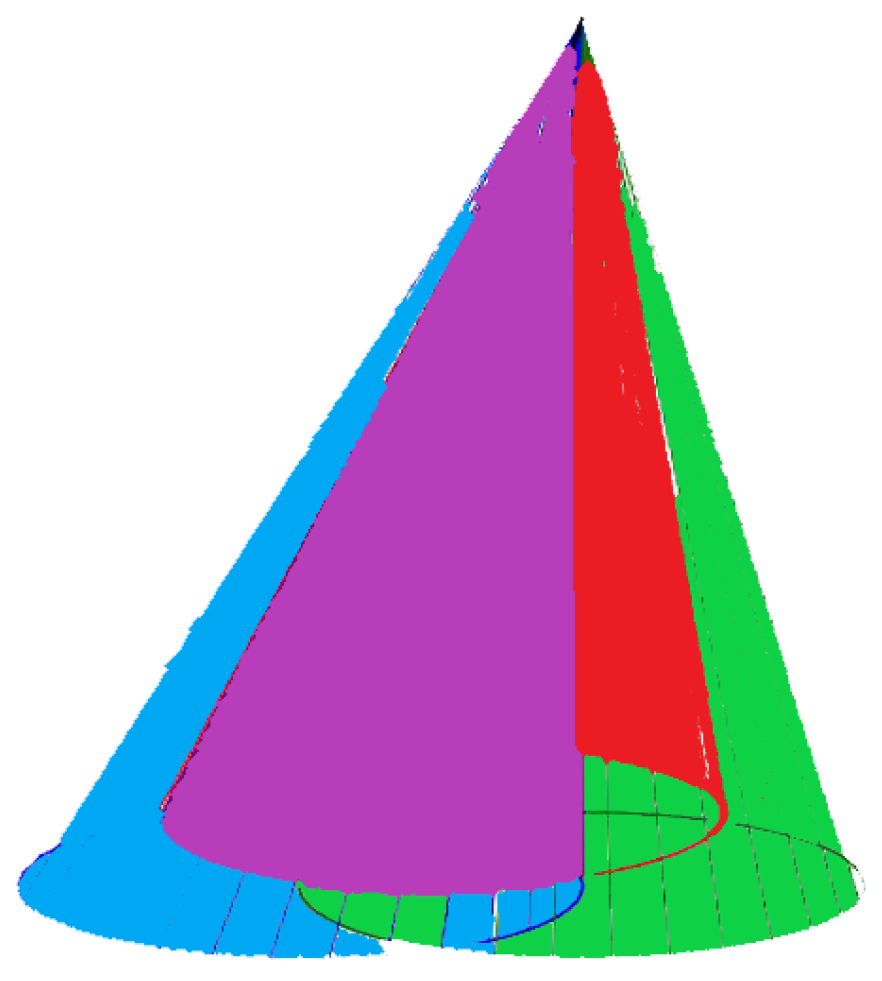
. According to this, a singular locus is thought of as a singular disk that is cut off from
. We may view such a singular locus by means of a cone having a base identified with the singular disk boundary while its apex extends to infinity
Figure 7.
The interesting aspect of the above in relation to the modelling of Planckian ER bridges is that a singular disk excised from gives rise to a two-dimensional relative homology class of , which is equivalently interpreted as a two-dimensional embedded compact submanifold. We emphasize that the boundary of such a singular disk is a closed and nowhere dense subset with respect to an open set of . In particular, we consider the excision of more than one singular disks from , such that their circular boundaries, instantiating collectively a closed and nowhere dense subset of an open set of , give rise to a topological link of . The loops constituting such a topological link can be replaced by open non-intersecting tubular neighborhoods, such that the complement of the link in can be given the structure of a 3-dimensional compact and oriented manifold with boundary. Most importantly, the operation of retraction under deformation casts the homology of the derived space equivalent to the original one.
At the following stage, let us define a
partial ordering of the loops
constituting the link, or equivalently, a partial ordering of their tubular neighborhoods
. Then, if we consider
,
, together with their ordering, we are able to instantiate the relative homology class
. This is representable by an embedded submanifold that is oriented and compact. In particular, it is characterized by two boundary components
and
lying on the total boundary, such that, it is oriented negatively on
and positively on
. This gives rise to a path from
to
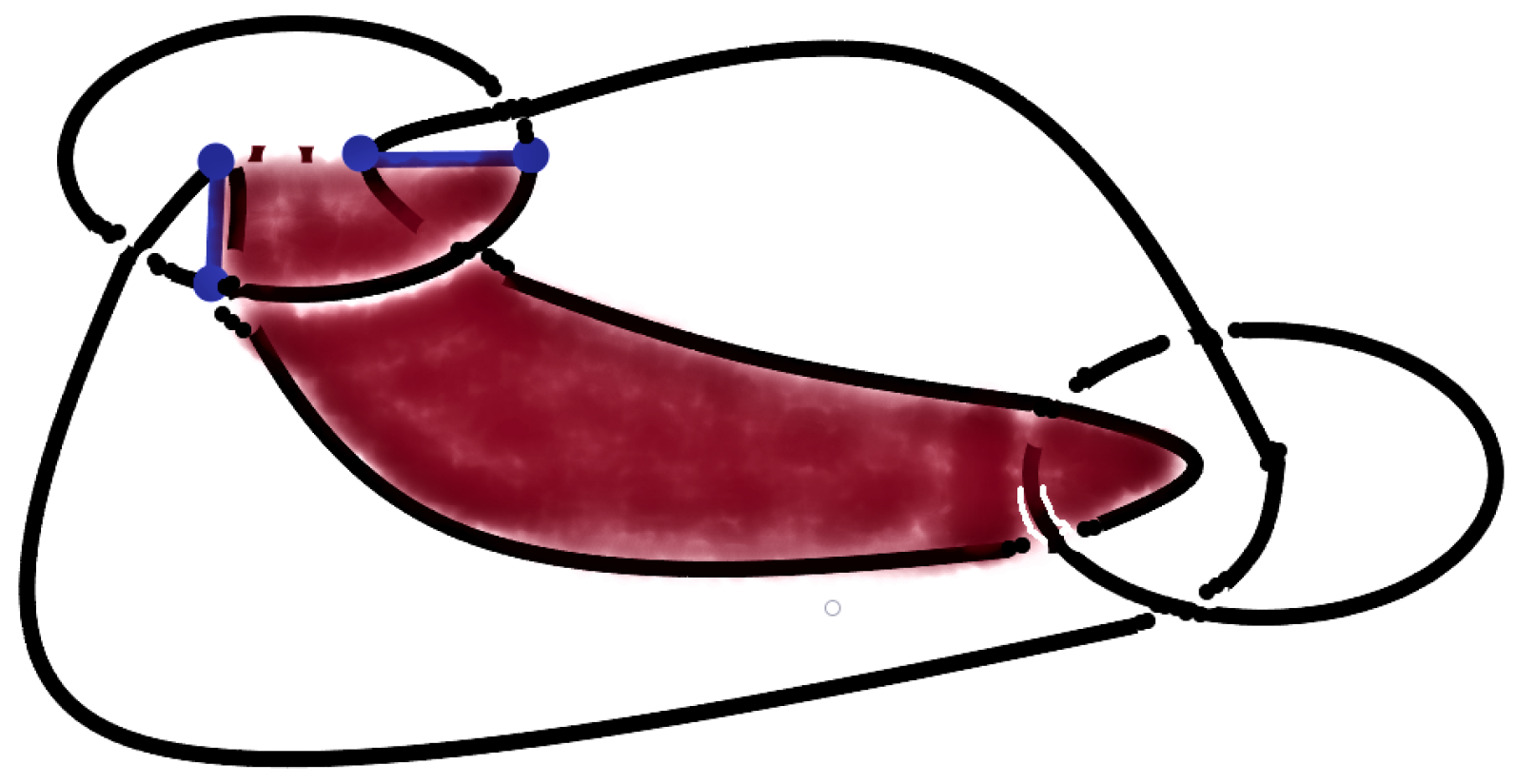
. In the case of the Borromean link, the homological characterization takes place by means of a non-vanishing
triple Massey product [
43], where all pairwise intersection products of one-dimensional homology classes vanish, reflecting the fact that the components of the Borromean link are not pairwise linked. Note that the intersection product is geometrically expressed by transverse intersection of cycles. If we order the components of the Borromean link
by
, the triple Massey product is expressed by means of a two-dimensional cohomology class in the dense complement of
in
, or equivalently, it instantiates a non-trivial class in
, which may be visualized as follows
Figure 8:
The pertinent issue arising in the above context is the following: How can we
inversely express the 3-dimensional manifold
without boundary in terms of such a topological link, which is formed by circular singular disk boundaries delineating a nowhere dense subset of an open set of
? Among all possible topological links, the Borromean rings constitute a universal link. This is because
, as a 3-dim manifold, can be realized universally through the Borromean rings in
under the hypothesis that they express the type of linking of the singular disk boundaries. The universal realization of
rests on the theorem that any 3-dimensional manifold without boundary, like
, which is compact and oriented, is representable in the form of a
branched covering space of the 3-sphere
whose
branched locus is the Borromean rings [
42,
44].
This is a generalization of the notion of a surjective locally homeomorphic covering projection, through which we may lift uniquely paths and homotopies from the base to the fibers, where the underlying notion of a singular point is substituted by a branched locus [
34]. A branched covering space of
is a locally homeomorphic map from
to
, such that this map is a covering space upon the exclusion the branched locus. The universal characterization of
rests on its instantiation as a branched covering space of
whose branched locus is the Borromean linked singular boundaries, identified through a closed and nowhere dense set with respect to an open set in
, in our setting. In other words, there is no need to impose any particular topology on
ab initio, since it is derived universally as the branched covering space of
over the branch nowhere dense subset of singular boundaries linked as Borromean rings. The nowhere dense and closed subset may be extended to four dimensions through the timelike axis orthogonally to the Borromean rings, preserving their symmetry under rotation. In this manner, a Borromean modular block leaving invariant the GHZ-core of entanglement, and represented in terms of the corresponding topological link of circular singular disk boundaries delineating a nowhere dense subset of an open set of
, gives rise to a Planck scale ER bridge in spacetime, and conversely.
The representation of a Borromean modular linking block takes place in terms of local unitary transformations, which are generated by local actions of quantum observables on the boundary. In this manner, they are realized by means of 1-parameter unitary groups preserving the GHZ-core. In the regime of quantum gravity, where these weaving actions are intelligible in relation to leaving invariant the maximal tripartite entanglement, the emerging non-trivial class in , where B is the Borromean link, interpreted in terms of the dual embedded submanifold, bears the status of a Planckian wormhole. From a classical perspective, such a wormhole is intrinsically unstable without the inclusion of some type of exotic matter, and arguably non-traversable due to topological censorship conditions.
As a matter of fact, the original formulation of the ER = EPR hypothesis does not allow traversable wormholes even if they are of Planck scale. The reason is that the conjecture has been inspired by considering a Bell pair (bipartite entanglement) in terms of an ER bridge and conversely. From the viewpoint of the present work, the conjecture admits a topological justification only in terms of maximal tripartite entanglement that gives rise to Borromean modular linking blocks. In other words, the bipartite entanglement is viewed as the Abelian degeneration of the tripartite one, which corresponds to a Hopf link. Because of the Hopf linking property the possibility of traversing is excluded without external considerations involving other types of interacting matter. In this sense, the founding of the ER = EPR conjecture on bipartite entanglement owing to the structure of the thermofield double state does not capture the full strength of the conjecture. At least, the proposed topological framework of interpreting the conjecture suggests that the maximal tripartite entanglement serves as a model of a Planck scale ER bridge.
From this perspective, the idea of a traversable wormhole without direct external couplings seems to be a possibility that is not excluded. Nevertheless, the possible interior traversability through a Planckian wormhole does not mean that superluminal information can be directly transmitted. This is so for the same reason that entanglement cannot be used for superluminal information transmission. Rather what is required is the exterior intervention of a classical maximal commutative algebra of co-measurable observables between any two of the parties. This is how bipartite entanglement emerges indirectly from the tripartite one through Abelianization. It is the latter that allows the re-synthesis of information by Abelian homological means, that is, by means of the Massey product class in the complement of the tripartite entanglement Borromean link.
From a group-theoretic viewpoint, Abelianization amounts to the reduction of the free group commutator in two generators to unity, such that the generators commute. Homologically, this means that the non-trivial homology class in the complement of the link in the 3-sphere, expressed as an embedded submanifold, becomes a boundary. Such a boundary can be always realized on a torus in the 3-sphere, since the two commuting generators can be identified with the homology basis of a torus. Thus, Abelianization gives rise to the Hopf linking symptom between the generators in the 3-sphere -underlying the Hopf fibration- that physically synchronizes them along their joint area-bounding homological boundary. In turn, this is what allows the indirect inference of a measurement result obtained by one party to the other through their joint classical homological boundary characteristic of bipartite entanglement. In brief, bipartite entanglement is the Abelian shadow of tripartite Borromean entanglement through which a topological justification of the ER = EPR conjecture emerges. This is rather sketchy at the moment, regarding the transversability of a Planck scale wormhole in view of the ER = EPR conjecture, and further work is required in this direction to join appropriately this discussion with the ongoing debates on the information aspects of black holes.
In the same context, it is interesting to point out that an arbitrarily complex entanglement link in a Borromean topological network, where , according to the analysis of the previous section is expressed as an element of the free group in two non-commuting generators. The reason is that it can be composed solely in terms of stacks and chains of tripartite entanglement blocks. As such can be always represented topologically in the interior of the 3-sphere . In this vein, and in relation to our discussion above, we note that the only constellations of qubits admitting a Hopf fibration in their state spaces are the cases of one, two, and three qubits. This takes place by climbing the Hopf ladder of sphere state spaces from (with fiber over ), to (with fiber over ), and finally (with fiber over ), according to the pattern that the total space on a stair becomes the fiber in the next consecutive stair, and terminating on the third stair. However, the maximal entanglement structure or GHZ core at the third and final Hopf-fibered state space stair is already incorporated in in its double role, as the total state space of a qubit, and as the fiber in the fibration of the two qubit-state space. These are also facts that require further study in view of the ubiquitous role of in accommodating the representation of all links emanating modularly from the tripartite entanglement link in a Borromean network out of stacks and chains. From a dual perspective, all corresponding types of Planckian wormholes are representable in terms of homology classes—as embedded submanifolds—in the complement of these links in .
9. “ER = EPR” Correspondence and Gravitational Generic Properties in the Quantum Gravity Regime
Due to the universality in the characterization of all possible Planckian ER bridges by means of Borromean modular blocks in the topological network, and in consonance with the “ER = EPR” conjecture, the following interesting novel possibility arises in the quantum gravitational context: Active gravitational mass/energy may emerge from these purely topological considerations taking into account the constraints imposed by Einstein’s field equations in the vacuum [
45]. From a physical perspective, this may be interpreted in accordance to Wheeler’s insight referring to
“mass without mass” [
21] as follows: Constellations of singular loci localized within open sets of
X, which upon restriction to a temporal slice
are nowhere dense and closed subsets of linked singular boundaries, give rise to active gravitational mass/energy in the open and dense subsets complementary to them. The “positive mass theorem” in the considered vacuum informs us that the gravitational mass/energy is positive and not null. At a further stage, this realization could potentially throw some new light to the understanding of dark matter, a problem that will be tackled in a separate work.
The emergence of active gravitational mass/energy, according to the above interpretation of the “ER = EPR” conjecture in terms of Borromean modular blocks, leads to a criterion that characterizes properties which are gravitationally generic upon transition to the regime of quantum gravity: In particular,
gravitationally generic properties are the ones which pertain only to a
dense open set. Inversely, a property characterized as non-generic gravitationally holds only on a nowhere dense and closed subset. We may broadly think of the latter as the analogues of sets whose measure is zero. This is not strictly true, since these subsets can bear Lebesgue measure, but it is suitable to guide our intuition. The concept of genericity has its roots in the ground-breaking work of Cohen in model theory. More concretely, generic properties make possible the construction of certain legitimate extensions of the standard model of set theory by means of a well-defined partial order of
forcing conditions [
46]. Our proposal is to adapt Cohen’s method as the means to express the transition to the quantum gravity regime. This transition amounts to the viability of
distinguishable extensions of the classical general relativistic differentiable spacetime manifold in view of the articulation of the “ER = EPR” hypothesis by means of Borromean modular blocks. In this setting, the notion of topological density may be transcribed physically in terms of the corresponding gravitational energy density induced by singular sources, according to the preceding. Hence, the concept of generic property can be expressed by means of certain conditions, called forcing ones, as follows: A property, which is forced by a certain condition, is qualified as a gravitational property if the property pertains to an open set that is dense.
The proposed topological interpretation of the “ER = EPR” conjecture in terms of modular blocks exemplifying the Borromean type of entanglement leads to the assertion that forcing conditions in the bulk are induced by means of local unitary transformations, or equivalently, local actions of quantum observables on the boundary identified in terms of 1-parameter unitary groups. In more detail, for a Bell pair, the local action of an observable of any of the qubits corresponding to a commutative algebra, which is induced through measurement by a third qubit gives rise to maximal tripartite entanglement, encapsulated by the Borromean rings. According to our articulation of the “ER = EPR” correspondence, this is equivalent to the instantiation of a Planckian ER bridge, which pertains to the Borromean link of three circular singular boundaries giving rise to a closed and nowhere dense subset of an open set of , which is lifted to the bulk. Note that, due to non-commutativity, local actions of observables on the singular boundaries give rise to a partial order, which in turn, may be identified with the partial order of the respective topological link constituents, or equivalently, of their tubular neighborhoods. This implies that, upon transition to the regime of quantum gravity, distinguishable extensions of the general relativistic differentiable spacetime manifold of the bulk take place, which are induced by such partially ordered sets of link components in a topological network interpreted in terms of forcing conditions.
In this state of affairs, if we adopt an algebraic viewpoint, it is well known that the general relativistic field equations are formulated by means of local spacetime coefficients belonging to the sheaf of germs of differentiable functions. Every extension of the differentiable manifold model in the bulk, which can be distinguished, should be formulated by means of a novel sheaf of coefficients, which is modified from the standard one according to a forcing condition. The objective is that Einstein’s equations in vacuum retain their covariant form under the re-formulation of all tensorial coefficients in terms of this new sheaf. Equivalently, this implies that the transition to the regime of quantum gravity respecting the norms of the “ER = EPR” correspondence as well as the form of Einstein’s equations in the bulk should take place in symphony with the encapsulation of the forcing conditions into a novel distributional sheaf of coefficients extending the classical smooth one.
According to our previous work pertaining to the possible extensions of the domain of validity of the field equations, an admissible algebra sheaf of coefficients supporting an extension of the everywhere differentiable model over singularities is necessarily of a distribution-like form [
42], under the proviso that is not of the standard Schwarz linear one. A typical example refers to a singular matter distribution restricted to a submanifold whose density can be integrated. Since gravity is non-linear, Schwarz’s linear space of distribution
cannot encapsulate adequately a locus behaving singularly. Essentially the non-suitability of
is due to the non-existence of a mapping that is bilinear and symmetric of the form:
such that
is the usual pointwise product of continuous functions, when
. This means that the extension of the multiplication of continuous functions, restricted to
V open of
X, does not fulfill the requirement of closure in
. Since this is of a local nature with respect to the sought after new sheaf of coefficients—capable to extend the differentiable one over singular loci—we may simply consider
V as an open subset of
.
This issue has been addressed by defining the map
, which embeds the linear space of distributions
as a linear subspace in a generalized quotient algebra
, which bears the following form [
42,
47]:
where,
is a subalgebra of
, for some indexing set
, whereas
is an ideal of
. For our present objective, the idea is that the indexing set should play the role of a
partial order of forcing conditions according to which distinguishable extensions can be constructed that
retain the form of Einstein’s equations in the bulk. In particular, generalized quotient algebras
are locally generated according to the following:
We consider an open subset , and the partially ordered set , where is the index set of the forcing conditions, induced by these local actions giving rise to the GHZ-type of entanglement, which is modelled in terms of the Borromean topological link. In this sense, the partially ordered set of these conditions pertains to the ordering of the loops constituting the link, or equivalently, the order of their tubular neighborhoods . The partially ordered set of the loops together with the 2-dim partition class of cohomology in the complement of the singular boundaries, which is dense, instantiates a Planckian ER bridge. This bridge corresponds to the Borromean block of three circular singular boundaries identified collectively by means of a closed and nowhere dense subset of an open set of , which is lifted to the bulk in . The same method may be extended to the partial order of forcing conditions emerging from a topological network that is constituted via Borromean modular blocks of the above form.
Let that for
,
∈
, there exists
∈
such that
,
≤
. The algebra
is clearly a commutative algebra over the real numbers. The ideal
in
corresponding to the partial order
is defined as follows [
42]:
According to the above, denotes collectively the locus of singular boundaries in , corresponding to a closed and nowhere dense subset relative to the open set , such that its complement in V is dense. The commutative algebra consists of sequences of smooth functions indexed by the partially ordered set . The ideal in consists of all these sequences of smooth functions whose support covers the singular locus , whereas they vanish asymptotically outside together with all their partial derivatives. In this way, the locus of singular boundaries is encoded algebraically in the ideal in . Therefore, the quotient commutative algebra is an algebra of residues of sequences of smooth functions modulo the ideal encoding the singular boundaries.
Of course, the complement
of the singular locus
in
V should be dense. The reason is that only in this case there exists an embedding
of the classical algebra of smooth functions
into the quotient algebra
:
such that:
where
is the diagonal morphism with respect to
, defined for an open set
V as follows:
Therefore, for every smooth function
in
, the diagonal image
of
in
is a sequence of smooth functions, which are indexed by
and are all identical to
. The embedding
takes place if and only if the ideal
satisfies the following off-diagonality condition [
42]:
The important point is that the
embedding of the algebra of smooth functions
into the quotient algebra
:
extends to an embedding of
differential algebras making the following diagram commutative:
This is due to the fact that the standard partial derivative operators on
extend to
:
We conclude that the above embedding preserves not only the algebraic structure of
, but also its differential structure, whence the off diagonality condition guarantees that
contains the space of linear distributions as a vector subspace. Furthermore, if we take into account that the qualification of a subset as nowhere dense and closed is of a local nature, the quotient algebras
are qualified as legitimate sheaves of coefficients of the sought after form, characterized as soft and flabby [
48,
49,
50,
51]. The softness property of the sheaves of coefficients
implies that any section over any closed subset can be extended to a global section, whence the flabbiness property means that the restriction map of sections over open subsets of an open set is an epimorphism. Thus, the extension of any locally defined section by zero gives rise to a global section of the distribution-like sheaf
.
The physical significance of
is that it accomplishes the objective of generating legitimate extensions of the standard differentiable spacetime manifold, which are distinguishable and pertain to the transition into the quantum regime, by means of forcing conditions, such that the covariance of the field equations is retained upon transference of the smooth tensorial coefficients into the distributional ones of
. As it has been demonstrated in [
42], see also [
52,
53,
54] for the general framework, this is due to the fact that the sheaf-theoretic de Rham complex—underlying all the operations of differential calculus on a smooth spacetime manifold—retains its validity when the coefficients are generalized from the smooth to distributional ones in an algebra sheaf of the form
, realized in the present case via forcing conditions.
In view of the unifying topological interpretation of the “ER = EPR” conjecture in terms of Borromean modular blocks, a distribution-like sheaf of the form where the classical smooth one is differentially embedded, specifies extensions of the differentiable bulk spacetime in terms of partially ordered sets of forcing conditions qualifying the quantum gravitational transition, such that the covariance of the field equations is retained. The most interesting facet of these distributional algebras is that they physically encode the notion of a gravitational generic property. Recall that the emergence of active gravitational mass/energy from an argument of topological nature pertaining to closed and nowhere dense singular boundaries, according to the link-theoretic light on the “ER = EPR” conjecture, implies that a property is qualified as a generic one upon the quantum gravitational transition, if the property pertains to an open set that is dense. Therefore, a non-generic gravitational property should hold solely on a nowhere dense and closed subset, expressed algebraically by means of an ideal of the form .
If we interpret the notion of topological density in this context in terms of the corresponding gravitational energy density induced by singular sources, then the property of gravitational genericity is expressed by means of forcing conditions as follows: A forcing condition induces a gravitational property if it pertains to an open set that is dense. In this manner, a forcing condition is generic, since it forces the articulation of an induced property as a gravitational one, or not, solely in relation to the density characterization. The notion of a generic gravitational property transcribes Cohen’s method of forcing [
46]—for the instantiation of distinguishable models extending the standard one—in the present quantum gravitational context in the light of the proposed topological articulation of the “ER = EPR” conjecture. Conclusively, a soft and flabby sheaf of the form
induces a distinguishable extension of the smooth spacetime model by encoding generic gravitational properties.