Black Hole and Wormhole Solutions in Einstein–Maxwell Scalar Theory
Abstract
:1. Introduction
2. Field Equations and General Solutions
3. Classifying the Static, Spherically Symmetric Solutions
3.1. Independent Solutions in the Canonical Sector
- : In this case, the metric takes the form,and the constants are related by:Therefore, we can see that for , we have . Thus, there may be a horizon at this surface. However, analyzing the angular term of the metric, for large values of u, it can be approximated to:and since , we have,Hence, we have another singular surface. This case can only describe a naked singularity with an asymptotic flat spacetime;
- : Using the appropriate functions for this case, the metric is written as,where:Because the sine function has a finite range and it is a periodic function, there is no surface where ; thus, it has no horizon, but it has many singular points. The singular points of the first term of the metric are at,Other interesting surfaces are at , where we have:which describes another singular surface. This case has only naked singularities;
- : The metric in this case takes the form,The constants of integration are related by,This case is exactly the same as the previous one, where there is no horizon, and we also have the same singular points and local minimums;
- : Writing the metric for this case, we find,with the relation,Again, the first term of the metric is the same as the last cases, but the angular term now has another sine function. Therefore, we still have the singular points , but now, we have different local minimums. Another interesting surface in this case is,where,indicating an asymptotic surface. Since, , we have that the interval between the singular points is smaller than the interval between the asymptotic regions . Hence,and there is always a singular surface between the asymptotic surfaces. Thus, this can only be a naked singularity.
- : Here, the metric is written as,with the relation,Here, we can identify that in the surface , but one can verify that at this surface, the third criterion for BH selection is not satisfied. Moreover, for those points. Thus, this is not a horizon. This solution describes also a naked singularity.
3.2. Independent Solutions in the Phantom Sector
- : In this case, we have the metric as,with the relation:We can see that for , we have , which is one condition for having a horizon. Analyzing the angular term for large values of u, we can approximate it as:Since we have that , the surface implies . Therefore, it is a singular surface rather than a horizon. On the other hand, for , we have , which characterizes a horizon with an infinite surface area. Then, working in the range , this solution indeed represents a BH. This solution can be mapped to one of the charged Brans–Dicke BH (Case [1-] of [14]) through a conformal transformation. This is expected since the conformal transformation that maps the Einstein frame in the Jordan frame is given by an exponential of the scalar field , being regular. However, the overall structure and features of the solution are affected by this conformal transformation.In fact, the conformal transformation connects the metric in the Einstein frame (used here) and the metric in the Jordan frame, used in [14], according to the relation,where the subscripts E and J indicate the Einstein and Jordan frames, respectively, and is the original Brans–Dicke field, which is related to the gravitational coupling. The scalar field used here and the original Brans–Dicke field obey the following relation:In this way, the metric in the original frame that corresponds to the metric (53) in the Einstein frame takes the form,The overall conformal factor introduces, with respect to the metric in the Einstein frame, the constant C, implying new conditions to have a black hole, that is to obtain with . Moreover, the conditions to have an analytical extension of the metric beyond the horizon are affected by the presence of the parameter C, leading to a large spectrum of possibilities, with different structures. This remark applies to other black hole and wormhole solutions discussed above;
- :The metric in this case is written as,where we have the relation:In the limit , this case has and . Therefore, for the appropriate coordinate range, this solution represents a BH and is connected, by a conformal transformation, to the other charged Brans–Dicke BH in the Jordan frame (Case [2-] of [14]). Again, the conformal transformation maps the solution in one frame into the solution in the other frame;
- : For this case, the metric takes the form,with:The radial function, , connects two spatial infinities, which is a characteristic of WHs. Thus, for an appropriate range, excluding the singularity at , this can be a wormhole;
- :For this case we have,with,The radial term of the metric function diverges at , with n any integer, while the first term, , is singular at . Since , oscillates faster than , thus we can always choose a coordinate range where we have two spatial infinities and avoid the singularity at , therefore a WH solution;
- : The last independent solution is,with,As in the previous cases where we have a sine function in , there are Minkowski asymptotics at and horizons only at . Thus, in the appropriate coordinate range, excluding the singularity at , this is a WH solution.
4. Black Hole and Wormhole Solutions
4.1. Criteria for Black Hole and Wormhole Selection
- The timelike Killing vector becomes null, which means ;
- The surface area of the horizon is always positive non-null, so ;
- For an observer at rest, the horizon is invisible; thus, the integral
- The Hawking temperature is finite. One may use the following expression for the Hawking temperature of a surface , in natural units,
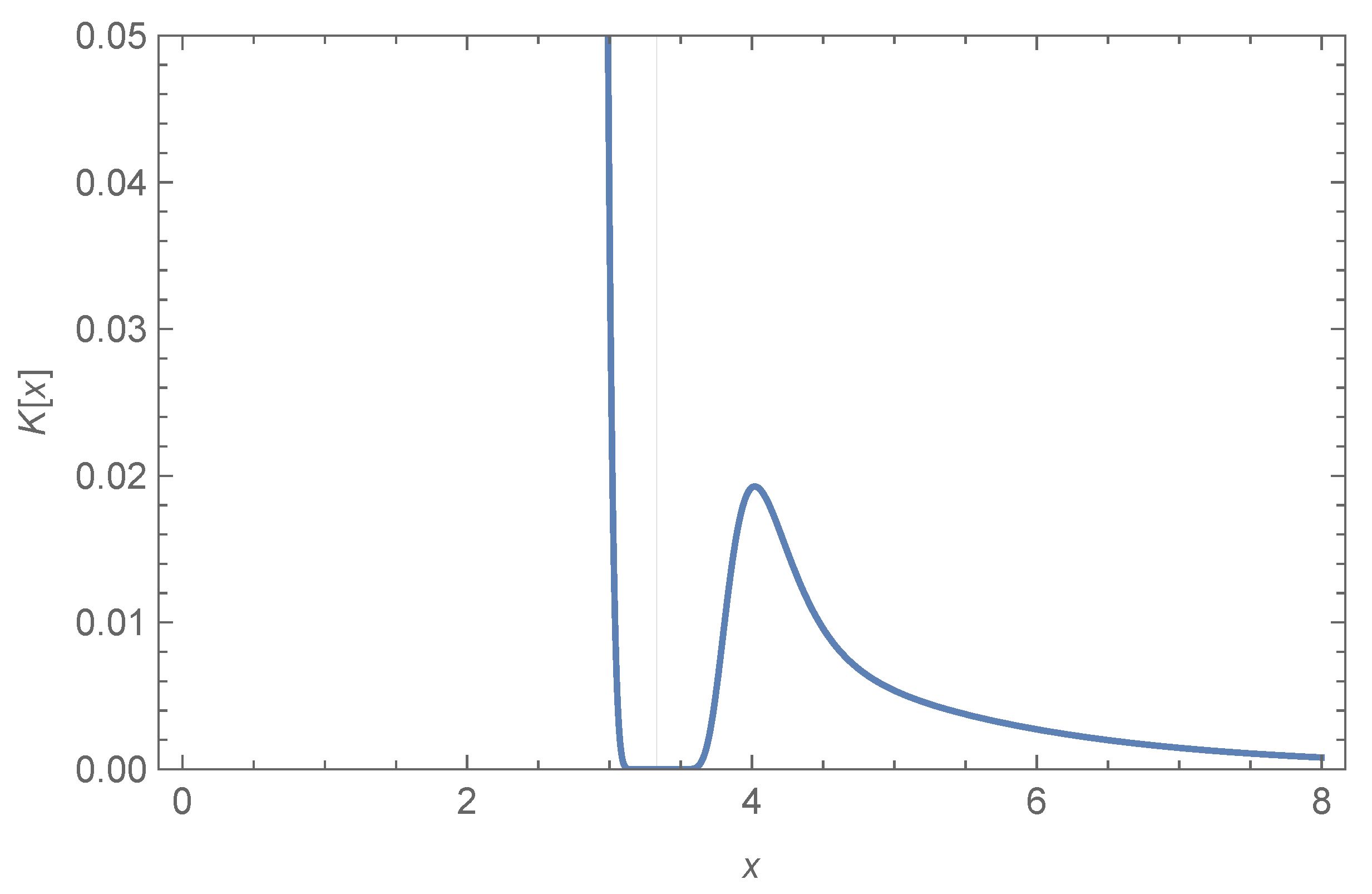
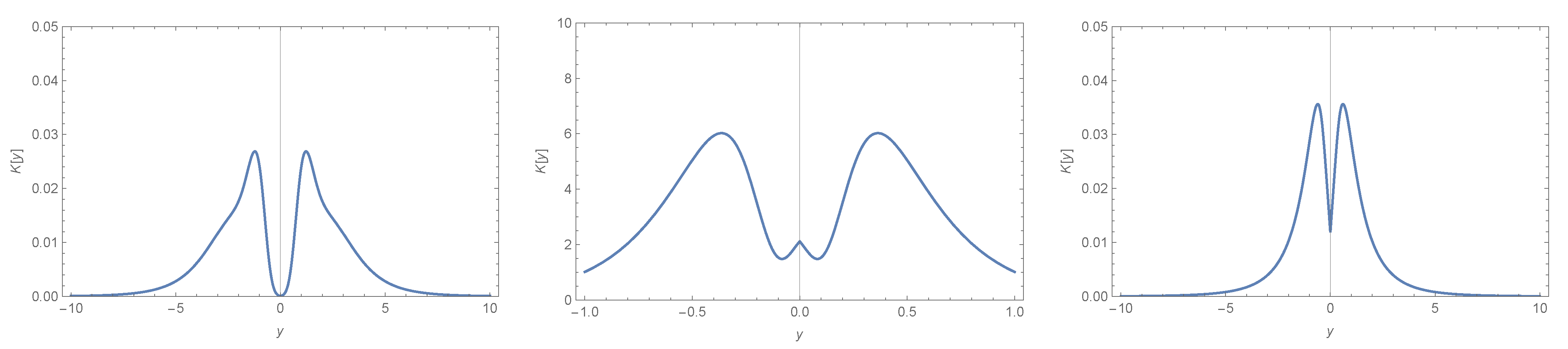
- The Kretschmann scalar is finite. We discuss more about this scalar in Appendix A;
- The metric must admit an analytical extension beyond the horizon.
4.2. First Black Hole Solution
4.2.1. Case of a Odd
4.2.2. Case of a Even
4.3. Second Black Hole Solution
4.4. Wormhole Solutions
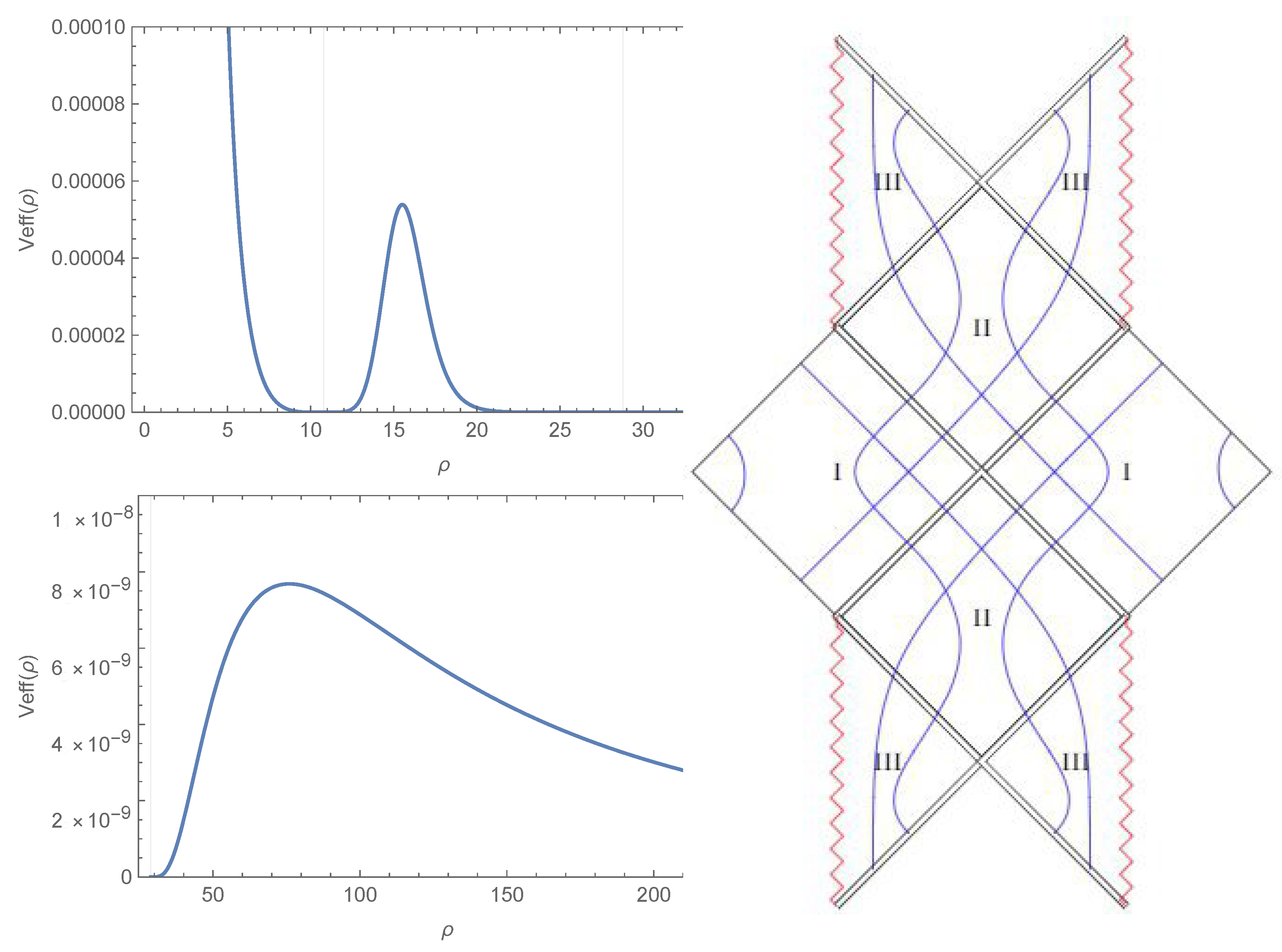
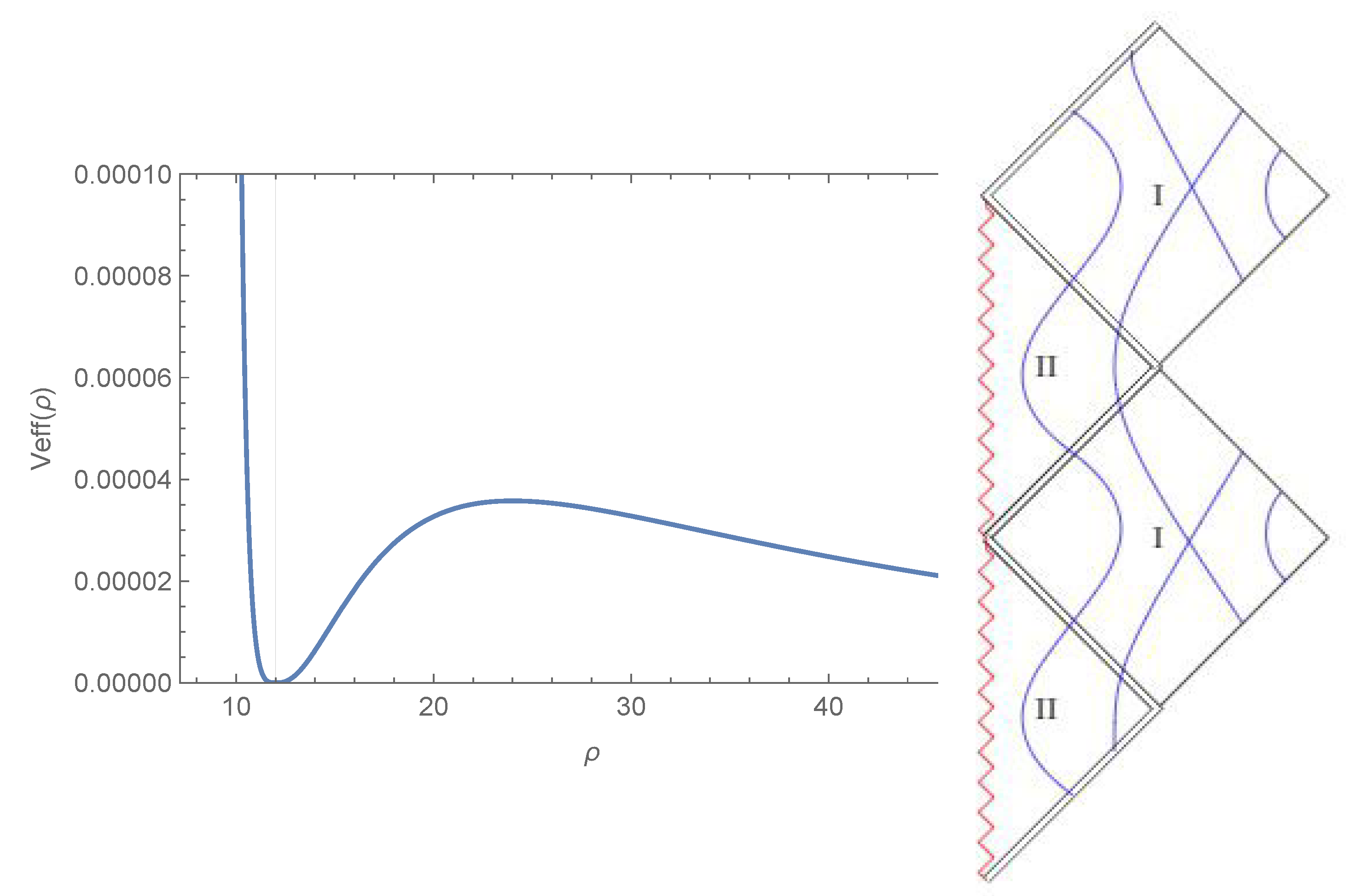
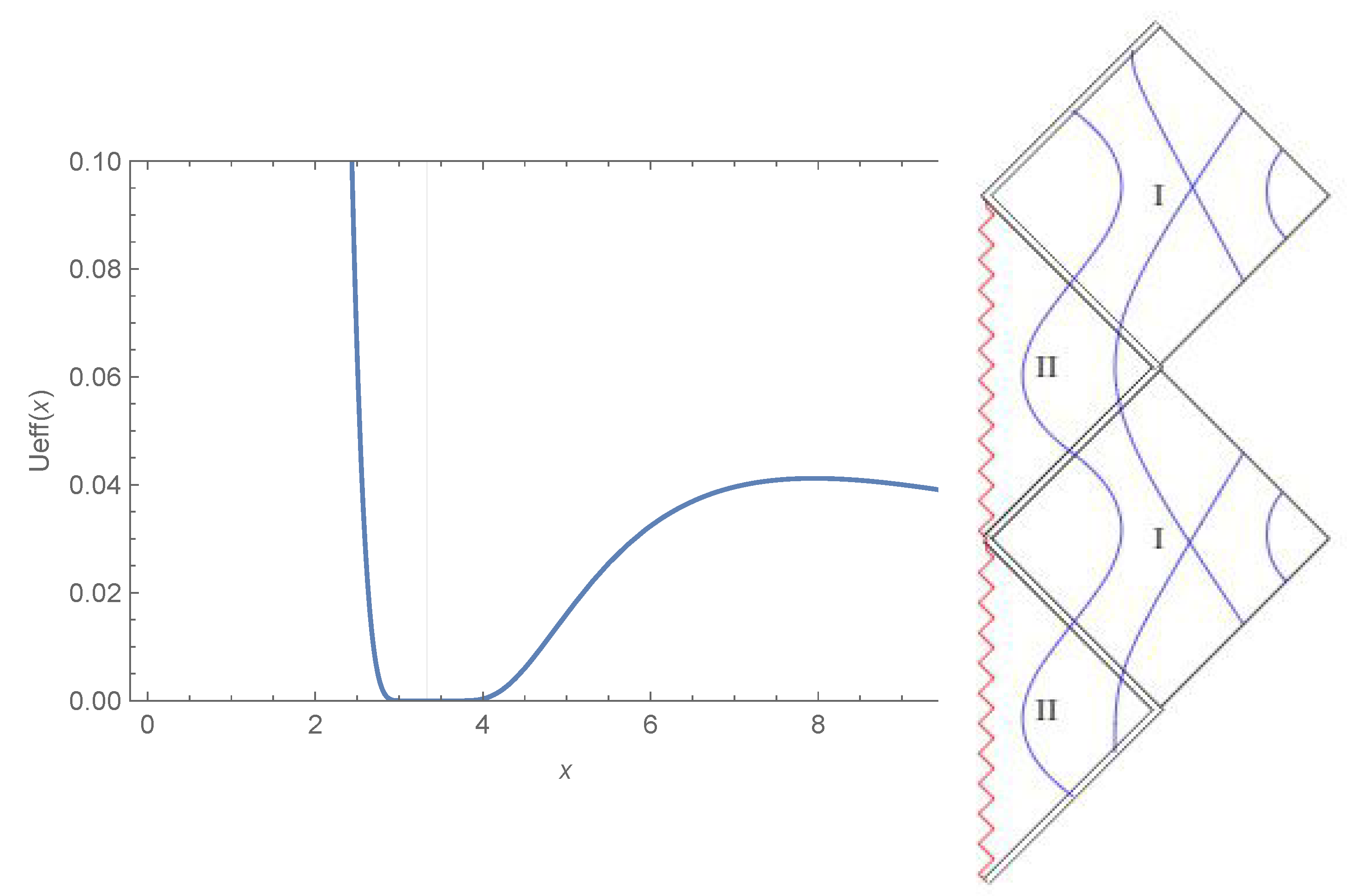
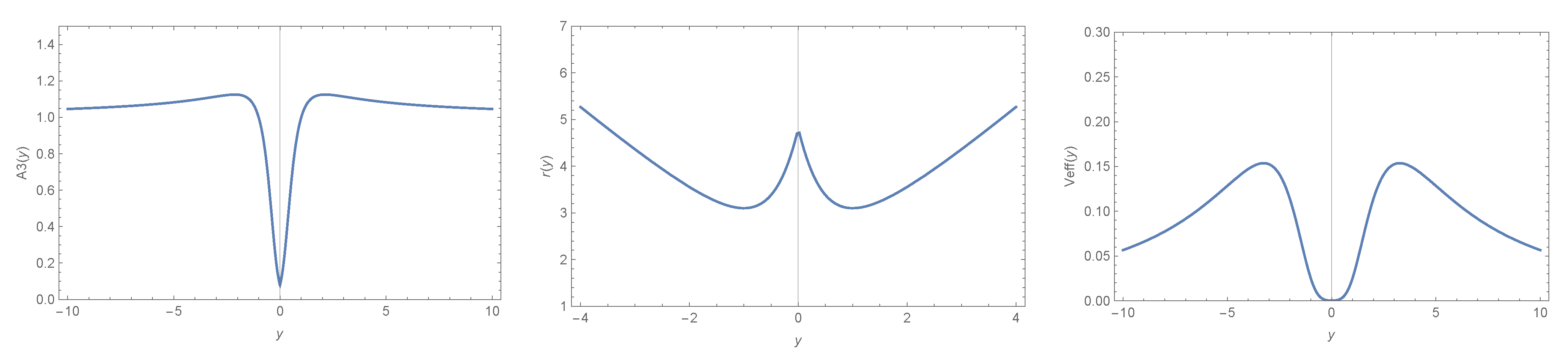
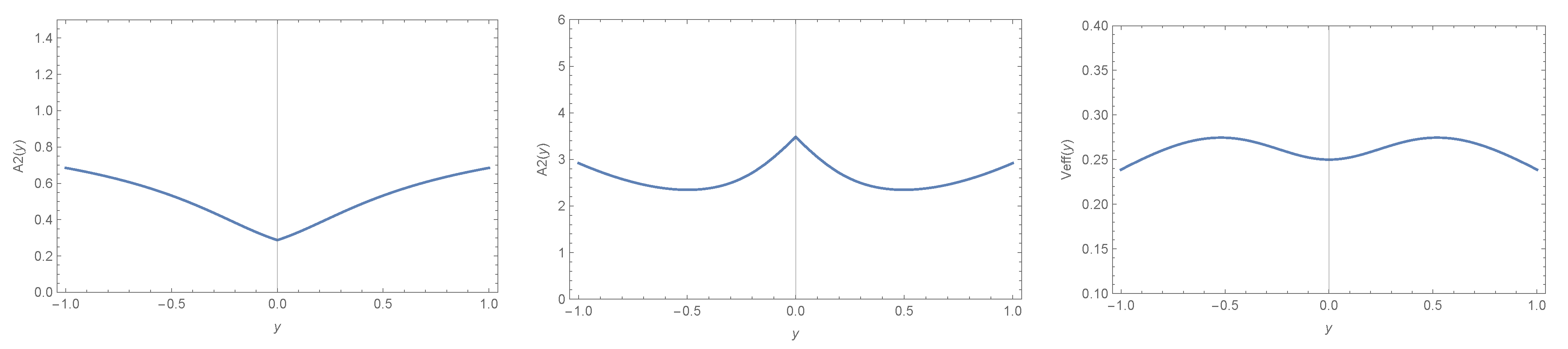
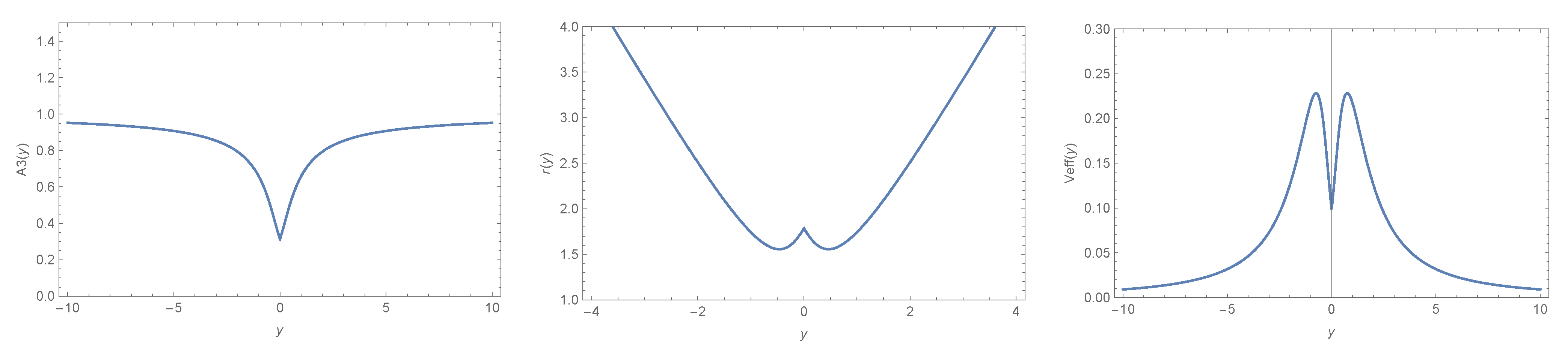
- Since is a real constant, the above relation gives us , for a non-null electric charge. The radius of the throat in this case is:The effective potential of the geodesic motion for massless particles, has a local minimum at the throat and a maximum around it, where it is possible to have a photon sphere. In Figure 4, there is a plot of , the radius , and the effective potential. In the limit , which corresponds to , the metric (85) takes the form of:
- Here, we have the condition that , which gives us that . The radius of the throat is:The plot of the effective potential for geodesic motion for massless particles (Figure 5) shows that there is the possibility for photons to orbit the throat;
- At the throat, , the radius is:
5. Final Comments and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Kretschmann Scalar
Appendix A.1. Kretschmann for the First Black Hole Solution
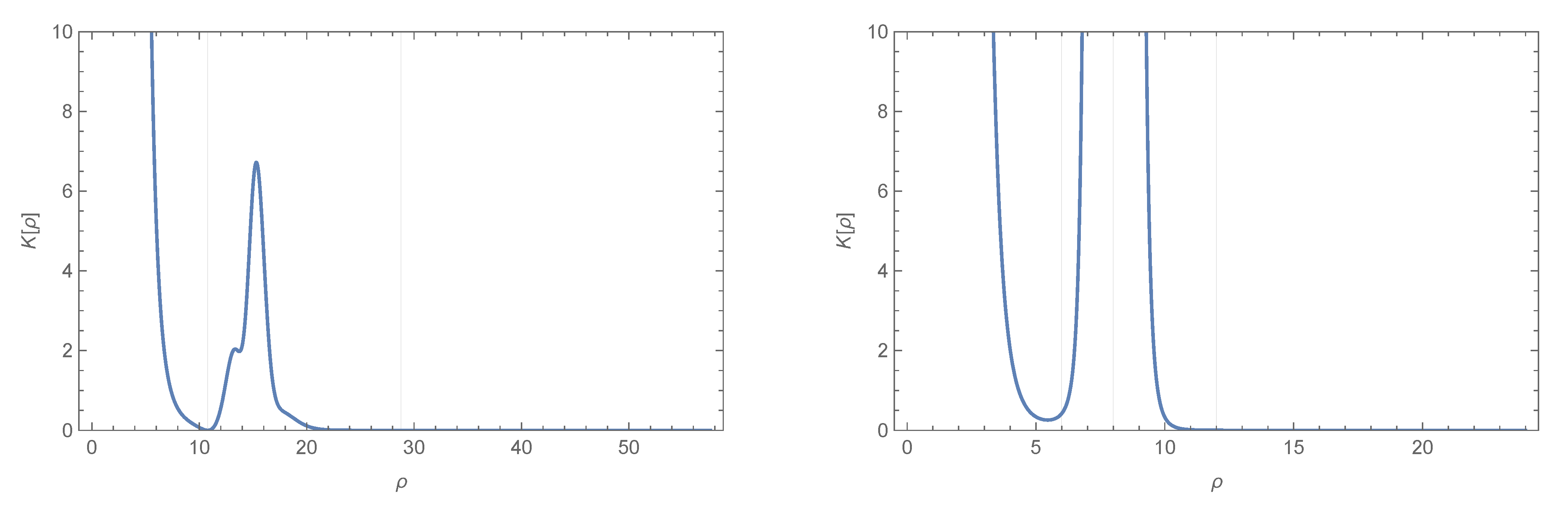
Appendix A.2. Kretschmann for the Second Black Hole Solution
Appendix A.3. Kretschmann for Wormhole Solutions
Appendix B. General Form of Geodesic Equations
Geodesic Equation for the General Solution
References
- Herdeiro, C.A.R.; Radu, E. Kerr black holes with scalar hair. Phys. Phys. Rev. Lett. 2014, 112, 221101. [Google Scholar] [CrossRef] [Green Version]
- Hong, J.P.; Suzuki, M.; Yamada, M. Spherically symmetric scalar hair for charged black holes. Phys. Rev. Lett. 2020, 125, 111104. [Google Scholar] [CrossRef] [PubMed]
- Chandrasekhar, S. The Mathematical Theory of Black Holes; Oxford University Press: Oxford, UK, 1992. [Google Scholar]
- Visser, M. Lorentzian Wormholes: From Einstein to Hawking; AIP: Woodbury, NY, USA, 1996. [Google Scholar]
- Frolov, V.; Zelnikov, A. Introduction to Black Hole Physics; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Abbott, B.P.; Jawahar, S.; Lockerbie, N.A.; Tokmakov, K.V. LIGO Scientific Collaboration and Virgo Collaboration. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L1. [Google Scholar] [CrossRef]
- Herdeiro, C.A.R.; Paturyan, V.; Radu, E.; Tchrakian, D.H. Reissner–Nordström black holes with non-Abelian hair. Phys. Lett. 2017, 772, 63–69. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Rubin, S.G. Black Holes, Cosmology and Extra Dimensions; World Scientific: Singapore, 2013. [Google Scholar]
- Gibbons, G.W.; Maeda, K. Black holes and membranes in higher-dimensional theories with dilaton fields. Nucl. Phys. 1988, 298, 741–775. [Google Scholar] [CrossRef]
- Garfinkle, D.; Horowitz, G.T.; Strominger, A. Charged black holes in string theory. Phys. Rev. 1991, 43, 3140–3143. [Google Scholar] [CrossRef]
- Clément, G.; Leygnac, C. Linear dilaton black holes. Phys. Rev. 2004, 70, 084018. [Google Scholar] [CrossRef] [Green Version]
- Clément, G.; Fabris, J.C.; Rodrigues, M.E. Phantom black holes in Einstein–Maxwell-dilaton theory. Phys. Rev. 2009, 79, 064021. [Google Scholar] [CrossRef] [Green Version]
- Bronnikov, K.A.; Constantinidis, C.P.; Evangelista, R.L.; Fabris, J.C. Electrically charged cold black holes in scalar–tensor theories. Int. J. Mod. Phys. 1999, 8, 481–505. [Google Scholar] [CrossRef] [Green Version]
- Bronnikov, K.A.; Fabris, J.C.; Zhidenko, A. On the stability of scalar-vacuum spacetimes. Eur. Phys J. 2011, 71, 1791. [Google Scholar] [CrossRef] [Green Version]
- Bronnikov, K.A.; Clément, G.; Constantinidis, C.P.; Fabris, J.C. Structure and stability of cold scalar–tensor black holes. Phys. Lett. A 1998, 243, 121–127. [Google Scholar] [CrossRef] [Green Version]
- Bronnikov, K.A.; Clément, G.; Constantinidis, C.P.; Fabris, J.C. Cold Scalar-Tensor Black Holes: Causal Structure, Geodesics, Stability. Grav. Cosmol. 1998, 4, 128–138. [Google Scholar]
- Bronnikov, K.A.; Fabris, J.C.; Pinto-Neto, N.; Rodrigues, M.E. Cold black holes and conformal continuations. Int. J. Mod. Phys. 2008, 17, 25. [Google Scholar] [CrossRef] [Green Version]
- De Felice, A.; Tsujikawa, S. f(R) theories. Living Rev. Rel. 2010, 13, 3. [Google Scholar] [CrossRef] [Green Version]
- Bronnikov, K.A. Scalar-tensor theory and scalar charge. Acta Phys. Pol. 1973, 4, 251–266. [Google Scholar]
- Wald, R.M. General Relativity; Chicago University Press: Chicago, IL, USA, 1984. [Google Scholar]
- Ellis, H.G. Ether flow through a drainhole: A particle model in general relativity. J. Math. Phys. 1973, 14, 104–118. [Google Scholar] [CrossRef]
- Gonzalez, J.A.; Guzman, F.S.; Sarbach, O. Instability of wormholes supported by a ghost scalar field: I. Linear stability analysis. Class. Quantum Grav. 2009, 26, 015010. [Google Scholar] [CrossRef] [Green Version]
- Bronnikov, K.A.; Barcellos, V.A.G.; de Carvalho, L.P.; Fabris, J.C. The simplest wormhole in Rastall and k-essence theories. Eur. Phys. J. 2021, 81, 395. [Google Scholar] [CrossRef]
- Dotti, G.; Gleiser, R.J. Gravitational instability of the inner static region of a Reissner-Nordström black hole. Class. Quantum Grav. 2010, 27, 185007. [Google Scholar] [CrossRef] [Green Version]
- Dotti, G. Linear Stability of Black Holes and Naked Singularitie. Universe 2022, 8, 38. [Google Scholar] [CrossRef]
- Alvarenga, F.G.; Batista, A.B.; Fabris, J.C.; Marques, G.T. Quantum modes around a scalar-tensor black hole: Breakdown of the normalization conditions. Grav. Cosm. 2004, 10, 184–186. [Google Scholar]
- Hawking, S.W.; Horowitz, G.T.; Ross, S.F. Entropy, area, and black hole pairs. Phys. Rev. 1995, 51, 4302–4314. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zaslavskii, O.B. Thermodynamics of black holes with an infinite effective area of a horizon. Class. Quantum Grav. 2002, 19, 3783–3806. [Google Scholar] [CrossRef]
| * | |||
| * | * | ||
| * | |||
| * | * |
| and |
| and |
| and |
| and |
| and |
| and |
| and |
| and |
| and |
| and |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fabris, J.C.; Gomes, T.A.O.; Rodrigues, D.C. Black Hole and Wormhole Solutions in Einstein–Maxwell Scalar Theory. Universe 2022, 8, 151. https://doi.org/10.3390/universe8030151
Fabris JC, Gomes TAO, Rodrigues DC. Black Hole and Wormhole Solutions in Einstein–Maxwell Scalar Theory. Universe. 2022; 8(3):151. https://doi.org/10.3390/universe8030151
Chicago/Turabian StyleFabris, Júlio C., Tales Augusto Oliveira Gomes, and Denis Campos Rodrigues. 2022. "Black Hole and Wormhole Solutions in Einstein–Maxwell Scalar Theory" Universe 8, no. 3: 151. https://doi.org/10.3390/universe8030151
APA StyleFabris, J. C., Gomes, T. A. O., & Rodrigues, D. C. (2022). Black Hole and Wormhole Solutions in Einstein–Maxwell Scalar Theory. Universe, 8(3), 151. https://doi.org/10.3390/universe8030151