The Speed of Light Predicts the Number of Lepton Families

Abstract

Vacuum fluctuations of charged particles appear in the vacuum as particle-antiparticle pairs so that quantum numbers such as charge, baryon number, and lepton number are conserved. To minimize the violation of conservation of energy and conserve angular momentum, the pair appears in the most tightly bound state that has zero angular momentum. The permittivity ${ϵ}_0$ of the vacuum results primarily from bound, charged lepton-charged antilepton vacuum fluctuations that are polarized by photons traveling in the vacuum. The formula for ${ϵ}_0$ depends on the number ${\mathcal{N}}_L$ of lepton families but is independent of the charged lepton masses. The formula for the speed c of light in the vacuum is obtained from $c=1/\sqrt{{\mu }_0{ϵ}_0}$, where ${\mu }_0$ is the permeability of the vacuum. The formula for c is shown to depend on the number ${\mathcal{N}}_L$ of lepton families. The calculated value of c agrees with the defined value when ${\mathcal{N}}_L=2.92$.

1. Introduction

The idea that the properties of vacuum fluctuations affect the permittivity of the vacuum has existed at least since 1934: Furry and Oppenheimer [1] wrote that vacuum fluctuations of charged particle-antiparticle pairs would affect the value of the dielectric constant of the vacuum: “Because of the polarizability of the nascent pairs, the dielectric constant of space into which no matter has been introduced differs from that of truly empty space.” Additionally, in that same year, Pauli and Weisskopf [2] discussed the idea that the vacuum could be treated as a medium with electric and magnetic polarizability.

Maxwell’s equations are valid for any value of the speed of light c in the vacuum; therefore, something in addition to Maxwell’s equations must determine c. A basic postulate of physics is that the structure of a system determines the properties of the system. Since c is a property of the vacuum, it should be possible to calculate c using Maxwell’s equations to describe the interaction of photons with the quantum vacuum.

In 2010 Leuchs, Villar, and Sanchesz-Soto [3,4] began a program to derive formulas for the permittivity ${ϵ}_0$ and permeability ${\mu }_0$ of the vacuum. Their program was an important beginning. The formulas they derived for the permittivity and permeability of the vacuum had “an astonishing property ”…“ they are independent of the mass” of the particle-antiparticle pairs that constitute vacuum fluctuations. The formula for ${ϵ}_0$ derived by the authors [5,6,7,8] of the present paper is independent of the masses of the contributing vacuum fluctuations as originally suggested by Leuchs, et al. In a similar vein, in 2013 Urban, Couchot, Sarazin, and Djannati-Atai [9] wrote “We show that the vacuum permeability ${\mu }_0$ and permittivity ${ϵ}_0$ may originate from the magnetization and the polarization of continuously appearing and disappearing fermion pairs.”

There are three lepton families consisting, respectively, of (1) the electron and the electron neutrino, (2) the muon and the muon neutrino, and (3) the tau and the tau neutrino. The formula for ${ϵ}_0$ depends on the sum $\Sigma {(q_j/e)}^2$, where $\mp q_j$ are the respective charges on each type of charged particle-antiparticle pair that contributes to ${ϵ}_0$ and e is the magnitude of the electron’s charge. Once it is understood that vacuum fluctuations of the charged leptons are the primary contributors to ${ϵ}_0$, the sum is simply a sum over the three types of charged lepton-charged antilepton vacuum fluctuations or, equivalently, a sum over the lepton families [5]. From Maxwell’s equations for a light wave in the vacuum, its speed $c=1/\sqrt{{\mu }_0{ϵ}_0}$ can be written in the form [6,7]:

$$c=\frac{1}{\sqrt{{\mathcal{N}}_L}}\sqrt{\frac{\pi }{2}}\frac{ћ}{8e^2{\mu }_0},$$

(1)

where ${\mathcal{N}}_L$ is the number of lepton families and ћ is Planck’s constant divided by $2\pi$. Using the numerical value of the defined speed of light in the vacuum, the number of lepton families calculated from (1) is ${\mathcal{N}}_L=2.92$. The value of ${\mathcal{N}}_L$ must, of course, be an integer, but here it is not calculated to be exactly an integer because the value of ${ϵ}_0$, and as a consequence, the value of c, is calculated only to lowest order in what turns out to be a power series expansion in the fine-structure constant $\alpha$. Corrections proportional to higher orders of $\alpha$ arise from more than one source as will be discussed later in this article. The calculated value 2.92 for ${\mathcal{N}}_L$ is consistent with, but more restrictive than the limit on the number of lepton families discussed in the much earlier article [10] that showed “that observational limits to the primordial abundance of ⁴He lead to the constraint that the total number of types of heavy leptons must be less than or equal to 5”. A more recent article [11] “discusses the possibility of additional fermion generations” and concludes that “a fourth family remains disfavored”.

This article is organized as follows: In Section 2 properties of the quantum vacuum are discussed with an emphasis on the structure of type 1 vacuum fluctuations. In Section 3 the calculation of the permittivity ${ϵ}_0$ of the vacuum is carried out. In the first subsection, the expectation value is calculated for the induced electric dipole moment of a charged lepton-charged antilepton vacuum fluctuation when interacting with a photon. The calculation is performed using a one-dimensional harmonic oscillator model of the charged lepton-charged antilepton vacuum fluctuation; a one-dimensional Schrödinger equation describing a harmonic oscillator interacting electromagnetically with a photon is solved exactly. In the second subsection, the number density of charged lepton-charged antilepton vacuum fluctuations that are available to interact with a photon is calculated. The value of ${ϵ}_0$ immediately follows from the calculations in these two subsections. The section concludes with a discussion of why the contribution of quark-antiquark vacuum fluctuations to ${ϵ}_0$ is small. Finally, a theoretical formula for the speed c of light in the vacuum is calculated using $c=1/\sqrt{{\mu }_0{ϵ}_0}$ and is shown to be a function of the number of lepton families. Section 4 contains a summary and discussion of the results. The formula for the speed of light satisfies a self-consistency condition and two additional conditions that any such formula must satisfy. The energy levels of the harmonic oscillator model of parapositronium and a constraint on the validity of the harmonic oscillator model are discussed in Appendix A.

2. The Quantum Vacuum

Dyson [12] defines the vacuum as follows: “The vacuum state is by definition the state of lowest energy, so that all absorption operators operating on it give zero.” As a result, the vacuum contains no ordinary energy (including ordinary matter). Furthermore, the vacuum is at rest with respect to all inertial frames of reference. Were this not the case, it would not have the lowest possible energy in all inertial frames as required by Dyson’s definition. Since the vacuum is the same in every direction in any inertial frame, it is invariant under space and time translations. That is, the vacuum is Poincaré invariant. If vacuum energy could be permanently converted into ordinary energy, Poincaré invariance of the vacuum would be destroyed; consequently, vacuum energy is conserved independently of ordinary energy.

Planck’s discovery of the photon and its associated vacuum is important in understanding the quantum vacuum. In his 1911 article “A New Radiation Hypothesis”, using classical physics Planck [13] derived the black-body distribution of the energy of electromagnetic radiation as a stochastic process associated with the vibration of a large number of identical, independent oscillators. The average energy $\overline{E}$ of a single photon with an angular frequency $\omega$ in a black-body distribution is:

$$\overline{E}=\frac{1}{2}ћ\omega +\frac{ћ\omega }{e^{ћ\omega /\left(k_{B}T\right)}-1}.$$

(2)

In (2) $k_B$ is Boltzmann’s constant, and the Kelvin temperature T appears as a result of the statistical nature of the distribution.

As pointed out by Leighton [14], a simpler derivation of Planck’s 1911 formula is possible using the energy spectrum of a single quantum harmonic oscillator, a spectrum unknown in 1911: the energy $E_{\mathrm{osc}}$ of a single quantum harmonic oscillator is $E_{\mathrm{osc}}=ћ\omega (n+1/2)$ [15], where the integer $n=0,1,2\dots$ characterizes the state and $\omega$ is the resonant angular frequency of the harmonic oscillator. The presence of the ground-state energy $ћ\omega /2$ in the formula for $E_{\mathrm{osc}}$ is required to avoid violating the Heisenberg uncertainty principle $\Delta p\Delta x\ge ћ/2$ [16] and is responsible for presence of the term $ћ\omega /2$ in (2). Note that, consistent with Dyson’s definition of the vacuum, the second term in (2) vanishes when all thermal energy is removed.

This article discusses the interaction of ordinary photons with vacuum fluctuations of massive particles. A particle with mass m, energy E, and momentum p that satisfies the “mass shell condition” [17] $E^2-{\left(\mathbf{p}c\right)}^2=m^2{c}^4$ is said to be “on mass shell” [18] or just “on shell”. Similarly, since a photon is massless, it is said to be “on shell” if it satisfies $E^2-{\left(\mathbf{p}c\right)}^2=0$. Ordinary particles are always on shell.

Physicists are usually precise when using language; however, the term “vacuum fluctuation” refers to two rather different entities: a type 1 vacuum fluctuation [19,20] consists of a particle and antiparticle pair that are on shell. For particles that are either charged, massive, or both, a type 1 vacuum fluctuation appears in the vacuum as the bound state with the maximum binding energy that has zero angular momentum, thus minimizing the violation of energy conservation and conserving angular momentum. Henceforth, the term “VF” will refer exclusively to type 1 vacuum fluctuations. An electron-positron VF appears as parapositronium, a singlet state with zero angular momentum in the ground state of positronium. A VF exists only for a time allowed by the uncertainty principle and appears as a pair of external particles in Feynman diagrams. Vacuum energy is the source of the energy that creates VFs.

While a VF exists, it can interact with ordinary matter, but only in ways in which both ordinary energy and vacuum energy are independently conserved. In this article, the permittivity of the vacuum is shown to be determined by ordinary photons interacting with charged lepton-charged antilepton VFs. When such an interaction occurs, charged lepton-charged antilepton VFs are polarized and become quasi-stationary states that have lifetimes much longer than that of the VF itself [21]. When the particle-antiparticle VF annihilates, a photon identical to the original photon is emitted. The interaction is allowed for VFs because the energy required for the creation of the VF is returned to the vacuum. Calculation of the induced electric dipole moments of charged lepton-charged antilepton VFs is a crucial piece in the calculation of the permittivity of the vacuum. The other critical piece is the calculation of the number density of charged lepton-charged antilepton VFs that are available to interact with an ordinary photon.

There is a second, important way in which ordinary matter commonly interacts with VFs. As an example, an ordinary electron can annihilate with the positron in a parapositronium VF. The vacuum energy required to create the VF returns to the vacuum, and the electron that was originally part of the parapositronium VF becomes an ordinary electron with precisely the energy of the original, ordinary electron. However, the electron is now in a different location: the apparent motion of the electron is zitterbewegung [20]. If a VF does not interact during its lifetime, the constituent particle and antiparticle annihilate, returning to the vacuum the energy originally used to create the VF.

Type 2 vacuum fluctuations are sometimes called vacuum bubbles [19] or vacuum diagrams [22]. Feynman diagrams of type 2 vacuum fluctuations consist of virtual particles that appear out of the vacuum and then disappear back into the vacuum. Type 2 vacuum fluctuations do not contribute to physical processes [18,19,22] such as cross-sections and decay rates, but do contribute to vacuum energy. Virtual particles are off shell, are represented by internal lines in Feynman diagrams, occur in perturbation calculations, but are not detected as particles.

3. Calculation of the Permittivity ${ϵ}_0$ of the Vacuum from the Properties of Charged-Lepton Vacuum Fluctuations

The VFs that contribute the most to the permittivity of the vacuum are those of the charged leptons. Since VFs of charged leptons appear in the most tightly bound state that has zero angular momentum, an electron-positron VF appears as a parapositronium VF.

In the case of a physical dielectric, in the presence of an electric field $\mathbf{E}\left(t\right)$, the electric displacement $\mathbf{D}\left(t\right)$ in the dielectric [23] satisfies:

$$\mathrm{physical}\mathrm{dielectric}:\mathbf{D}\left(t\right)={ϵ}_0\mathbf{E}\left(t\right)+\mathbf{P}\left(t\right).$$

(3)

The polarization density $\mathbf{P}\left(t\right)$ in the above equation is given by:

$$\mathbf{P}\left(t\right)=\sum _j{N}_j⟨{\mathbf{p}}_j\left(t\right)⟩.$$

(4)

$N_j$ is the number of atoms or molecules per unit volume of the jth variety that are available to interact with a photon; $⟨{\mathbf{p}}_j\left(t\right)⟩$ is the expectation value of the electric dipole moment of the jth atom or molecule. $⟨{\mathbf{p}}_j\left(t\right)⟩$ is proportional to the electric field $\mathbf{E}\left(t\right)$, so for this situation it follows from (3) that $\mathbf{D}\left(t\right)$ is proportional to $\mathbf{E}\left(t\right)$ and can be rewritten in the form

$$\mathrm{physical}\mathrm{dielectric}:\mathbf{D}\left(t\right)=ϵ\mathbf{E}\left(t\right)={ϵ}_0\mathbf{E}\left(t\right)+\mathbf{P}\left(t\right),$$

(5)

where $ϵ$ is the permittivity of the physical dielectric. In (5) the polarization density $\mathbf{P}\left(t\right)$ of the dielectric increases the value of the electric displacement $\mathbf{D}\left(t\right)$ from the vacuum value ${ϵ}_0\mathbf{E}\left(t\right)$ to the value $ϵ\mathbf{E}\left(t\right)$. The increase in $ϵ\mathbf{E}\left(t\right)$ from its vacuum value occurs because photons interact with and polarize atoms and molecules in the dielectric.

The following changes must be made to (5) if it is to describe the vacuum instead of an ordinary dielectric: (1) The permittivity $ϵ$ of the dielectric must be replaced by the permittivity ${ϵ}_0$ of the vacuum. In (5),

$$ϵ\mathbf{E}\left(t\right)\to {ϵ}_0\mathbf{E}\left(t\right).$$

(6a)

(2) In contrast to a physical dielectric where the electric displacement and permittivity $ϵ$ of the dielectric are determined by both the permittivity of the vacuum and the polarization density of the dielectric, in the vacuum the electric displacement $\mathbf{D}\left(t\right)$ and the permittivity ${ϵ}_0$ of the vacuum are determined solely by the polarization density ${\mathbf{P}}^{VF}\left(t\right)$ of VFs. Thus to apply (5) to the vacuum, the combination:

$${ϵ}_0\mathbf{E}\left(t\right)+\mathbf{P}\left(t\right)\to {\mathbf{P}}^{VF}\left(t\right).$$

(6b)

As a consequence, when modified to describe the vacuum, (5) becomes

$$\mathrm{vacuum}:\mathbf{D}\left(t\right)={ϵ}_0\mathbf{E}\left(t\right)={\mathbf{P}}^{VF}\left(t\right).$$

(7)

Using the second equality in (7) and then (4),

$${ϵ}_0=\frac{P^{VF}\left(t_i\right)}{{\mathbb{E}}_0}=\sum _j\frac{N_j^{VF}⟨p_j^{VF}\left(t_i\right)⟩}{{\mathbb{E}}_0}.$$

(8)

In the above equation the electric field at the instant $t_i$ when the photon interacts with the VF is denoted ${\mathbb{E}}_0\equiv E\left(t_i\right)$. From (8) it follows that it is the induced electric dipole moments of the vacuum fluctuations that are responsible for the observed value of ${ϵ}_0$. The contributions to ${ϵ}_0$ from muon-antimuon VFs, and tau-antitau VFs follow immediately from the calculated contribution from electron-positron VFs (parapositronium VFs); consequently, attention is initially restricted to parapositronium VFs.

3.1. Calculation of the Expectation Value of the Electric Dipole Moment Induced in a Parapositronium VF by a Photon’s Electric Field

Because a parapositronium VF has spin-0, it can be described relativistically by the Klein-Gordon equation. Solutions are obtained by exploiting the fact that a parapositronium VF is non-relativistic: in this limit the Klein-Gordon equation reduces to two Schrödinger equations [24,25], one describing a particle and the other an antiparticle. The properties of parapositronium, including the electric dipole moment induced by an electric field, are calculated using the two Schrödinger equations.

As shown in (8), the expectation value of the electric dipole moment $⟨p_j^{VF}\left(t_i\right)⟩$ induced in a parapositronium VF by a photon’s electric field is one of the two quantities that must be calculated to obtain a formula for ${ϵ}_0$. $⟨p_j^{VF}\left(t_i\right)⟩$ was originally calculated using classical physics [5]. The classical calculation relies crucially on the fact that a parapositronium VF never experiences a drag force and only radiates energy at the moment the constituent electron and positron annihilate and emit a photon identical to the incident, polarizing photon. If this were not the case, vacuum energy and ordinary energy would not be independently conserved. Dissipation is forbidden by the independent conservation of ordinary and vacuum energy. Thus the fluctuation-dissipation theorem [26,27] does not apply to vacuum fluctuations. $⟨p_j^{VF}\left(t_i\right)⟩$ has also been calculated using first-order time-dependent perturbation theory [6], first-order stationary perturbation theory [7], and, finally, exactly [8]. All four calculations yield the same formula for $⟨p_j^{VF}\left(t_i\right)⟩$ because the only nonzero harmonic oscillator matrix element $⟨\mathrm{excited}\mathrm{state}\left|x\right|\mathrm{ground}\mathrm{state}⟩$ between the ground state and excited states occurs for the first excited state.

Even in an intense laser beam, the number density of parapositronium VFs is much greater than the number density of photons (the number density of muon-antimuon VFs and tau-antitau VFs is greater still) [7]; consequently, if a charged lepton-charged antilepton VF interacts with a photon, it essentially always interacts with just one photon. Therefore a test photon traveling through the vacuum (or the Grid [28]) encounters charged lepton-charged antilepton VFs sequentially. Since the interaction of a photon with a VF does not depend on previous interactions of the photon with a VF, each interaction is part of a Markov chain [29]. The average interaction in the chain is the average over many interactions, justifying the use of expectation values to calculate the interaction.

Each photon in a beam of light will have a specific direction for its electric field that is chosen here to be in the x-direction when describing the interaction of that particular photon. The interaction can be described as a VF interacting with the electric field $E\left(t_i\right)={\mathbb{E}}_0$ of a single photon at the instant $t_i$ when the photon interacts with the VF. That single interaction can be described in a one-dimensional space $U\left(1\right)$, significantly simplifying the calculation of ${ϵ}_0$ (and c).

The Hamiltonian describing a parapositronium VF interacting with a photon at the instant when the photon’s electric field is ${\mathbb{E}}_0$ is constructed as follows: Let the coordinates ${\mathbf{x}}_{+}$ and ${\mathbf{x}}_{-}$ label the respective positions of the positron and electron. Choosing the x-axis to point in the direction of the electric field, the induced electric dipole moment $\mathbf{p}$, which points from the negative charge to the positive charge, is $\mathbf{p}=e(x_{+}-x_{-})\widehat{x}$. The Hamiltonian associated with the induced electric dipole moment is $H_{\mathrm{dipole}}=-\mathbf{p}·{\mathbb{E}}_0\widehat{x}=-e{\mathbb{E}}_0(x_{+}-x_{-})$. Thus the Hamiltonian H describing a parapositronium VF interacting with a photon is:

$$H=\frac{{\mathbf{p}}_{+}^2}{2m_e}+\frac{{\mathbf{p}}_{-}^2}{2m_e}-\frac{e^2}{4\pi {ϵ}_0}\frac{1}{|{\mathbf{x}}_{+}-{\mathbf{x}}_{-}|}-e{\mathbb{E}}_0(x_{+}-x_{-}).$$

(9)

The mass $m_e$ is the mass of an electron, ${\mathbf{p}}_{+}$ and ${\mathbf{p}}_{-}$ are, respectively, the momenta of the positron and electron, and the third term on the right-hand side of the above equation is the Coulomb potential energy. The above Hamiltonian provides a six-dimensional description of the system because both three-dimensional coordinates ${\mathbf{x}}_{+}$ and ${\mathbf{x}}_{-}$ are required.

When written in terms of center-of-mass variables ${\mathbf{X}}_{\mathrm{cm}}$ and momenta ${\mathbf{P}}_{\mathrm{cm}}$ and relative variables $\mathbf{x}$ and momenta $\mathbf{p}$ [15],

$$\begin{array}{cc}\hfill & {\mathbf{X}}_{\mathrm{cm}}\equiv \frac{m_e{\mathbf{x}}_{+}+m_e{\mathbf{x}}_{-}}{2m_e},\hfill \end{array}$$

(10a)

$$\begin{array}{cc}\hfill & {\mathbf{P}}_{\mathrm{cm}}={\mathbf{p}}_{+}+{\mathbf{p}}_{-},\hfill \end{array}$$

(10b)

$$\begin{array}{cc}\hfill & \mathbf{x}\equiv {\mathbf{x}}_{+}-{\mathbf{x}}_{-},\hfill \end{array}$$

(10c)

$$\begin{array}{cc}\hfill & \mathbf{p}\equiv \frac{m_e{\mathbf{p}}_{+}-m_e{\mathbf{p}}_{-}}{2m_e},\hfill \end{array}$$

(10d)

the Hamiltonian (9) separates into a Hamiltonian $H_{\mathrm{cm}}$ that depends only on the three center-of-mass variables and a second Hamiltonian $H_{\mathrm{relative}}$ that depends only on the three relative variables:

$$H=H_{\mathrm{cm}}+H_{\mathrm{relative}},$$

(11)

where

$$\begin{array}{cc}\hfill & H_{\mathrm{cm}}=\frac{{\mathbf{P}}_{\mathrm{cm}}^2}{2M},M=2m_e,\hfill \end{array}$$

(12a)

$$\begin{array}{cc}\hfill & H_{\mathrm{relative}}=\frac{{\mathbf{p}}^2}{2\mu }-\frac{e^2}{4\pi {ϵ}_0}\frac{1}{\left|\mathbf{x}\right|}-e{\mathbb{E}}_{0}x,\mu =\frac{m_e}{2}.\hfill \end{array}$$

(12b)

The Hamiltonian $H_{\mathrm{cm}}$ is the kinetic energy associated with the motion of the center of mass and can be ignored since vacuum fluctuations of massive particles appear at rest in any inertial frame.

The Schrödinger equation corresponding to $H_{\mathrm{relative}}$ is

$$\left(-\frac{{ћ}^2}{2\mu }{\nabla }^2-\frac{e^2}{4\pi {ϵ}_0}\frac{1}{\left|\mathbf{x}\right|}-e{\mathbb{E}}_{0}x\right)\psi \left(\mathbf{x}\right)=E\psi \left(\mathbf{x}\right).$$

(13)

As originally discussed by Kramers [30], when calculating the permittivity of atoms and molecules, the most important characteristic is that when interacting with an external electric field they oscillate along a single, linear direction denoted here by $\widehat{x}$. As will be demonstrated, using the harmonic oscillator model of parapositronium, the expectation value of the induced electric dipole can be calculated exactly.

The angular frequency of the harmonic oscillator corresponding to parapositronium is determined by requiring the expectation value of the harmonic oscillator potential energy, $(1/2)k{(x-x_0)}^2$ ($k=$ spring constant) be the same when calculated either for parapositronium or for the ground state of the harmonic oscillator. Using the notation ${⟨x^n⟩}_{\mathrm{p}-\mathrm{Ps}}$ and ${⟨x^n⟩}_{\mathrm{osc}}$, respectively, for the expectation value of $x^n$ for parapositronium and for a harmonic oscillator in the ground state,

$$x_0={⟨x⟩}_{\mathrm{p}-\mathrm{Ps}}={⟨x⟩}_{\mathrm{osc}}$$

(14)

where $x_0$ is the zero-point of the oscillation. The normalized parapositronium wave function [15] and normalized, ground-state, harmonic oscillator wave function [31] are, respectively,

$$\begin{array}{cc}\hfill & \psi {\left(r\right)}_{\mathrm{p}-\mathrm{Ps}}=\frac{1}{\sqrt{\pi a_0^3}}{e}^{-r/a_0},a_0=\frac{ћ}{\alpha \mu c},\hfill \end{array}$$

(15a)

$$\begin{array}{cc}\hfill & {\psi }^0{\left(x\right)}_{\mathrm{osc}}={\left(\frac{\mu {\omega }^0}{\pi ћ}\right)}^{\frac{1}{4}}{e}^{-\mu {\omega }^0{x}^2/2ћ}.\hfill \end{array}$$

(15b)

In (15) the fine structure constant $\alpha =e^2/\left(4\pi {ϵ}_0ћc\right)$, and the angular frequency of the harmonic oscillator is ${\omega }^0$. Since both wave functions are invariant under the transformation $x\to -x,x_0=0.$

Setting $x_0=0$, the requirement that the expectation value of the harmonic oscillator potential be the same for a parapositronium atom and a harmonic oscillator in the ground state becomes:

$$\frac{1}{2}k{⟨x^2⟩}_{\mathrm{p}-\mathrm{Ps}}=\frac{1}{2}k{⟨x^2⟩}_{\mathrm{osc}}.$$

(16)

The expectation values in (16) can be calculated using (15), yielding:

$$\begin{array}{cc}\hfill & {⟨x^2⟩}_{\mathrm{p}-\mathrm{Ps}}=a_0^2,\hfill \end{array}$$

(17a)

$$\begin{array}{cc}\hfill & {⟨x^2⟩}_{\mathrm{osc}}=\frac{ћ}{2\mu {\omega }^0}.\hfill \end{array}$$

(17b)

Substituting (17a) and (17b) into (16) and using the formula for $a_0$ in (15a) determines the resonant angular frequency ${\omega }^0$ of a parapositronium atom:

$$ћ{\omega }^0=\frac{\mu {\alpha }^2{c}^2}{2}.$$

(18)

The quantity on the right-hand side of the above equation equals the magnitude of the bound-state energy of parapositronium, which is also the ionization energy of parapositronium. Feynman [32] determines the angular frequency ${\omega }^0$ of a harmonic oscillator that corresponds to an atom by equating $ћ{\omega }^0$ to the ionization energy of the atom, which is identical to the formula for $ћ{\omega }^0$ in (18).

Using the harmonic oscillator model of parapositronium converts the three-dimensional description of the interaction of parapositronium with an electric field ${\mathbb{E}}_0$ into a one-dimensional description of a charged harmonic oscillator in an electric field ${\mathbb{E}}_0$. The Hamiltonian describing the interacting harmonic oscillator is obtained from (12b) by replacing the three-dimensional momentum $\mathbf{p}$ by the one-dimensional momentum p and replacing the coulomb potential energy $-e^2/(4\pi {ϵ}_0\left|\mathbf{x}\right|)$ with the harmonic oscillator potential energy $k{x}^2/2=\mu {\left({\omega }^0\right)}^2{x}^2/2$.

$$H_{\mathrm{interacting}\mathrm{harmonic}\mathrm{oscillator}}=\frac{p^2}{2\mu }+\frac{1}{2}\mu {\left({\omega }^0\right)}^2{x}^2-e{\mathbb{E}}_{0}x,\mu =\frac{m_e}{2}.$$

(19)

The one-dimensional Schrödinger equation corresponding to (19) is:

$$\left[-\frac{{ћ}^2}{2\mu }\frac{{\mathrm{d}}^2}{\mathrm{d}{x}^2}+\frac{1}{2}\mu {\left({\omega }^0\right)}^2{x}^2-e{\mathbb{E}}_{0}x\right]\psi \left(x\right)=E\psi \left(x\right).$$

(20)

Equation (20) can be solved exactly by introducing a new coordinate $u=x+b$, where b is a constant, chosen so that the potential energy is the sum of a term proportional to $u^2$ and a constant term. The new coordinate is easily identified by factoring $\frac{1}{2}\mu {\left({\omega }^0\right)}^2$ from the two potential energy terms:

$$\left\{-\frac{{ћ}^2}{2\mu }\frac{{\mathrm{d}}^2}{\mathrm{d}{x}^2}+\frac{1}{2}\mu {\left({\omega }^0\right)}^2\left[x^2-\frac{2e{\mathbb{E}}_0}{\mu {\left({\omega }^0\right)}^2}x\right]\right\}\psi \left(x\right)=E\psi \left(x\right)$$

(21)

In the above equation the harmonic potential energy term is of the form $(\mu /2){\left({\omega }^0\right)}^2{u}^2=(\mu /2){\left({\omega }^0\right)}^2{(x+b)}^2$, so the second term in square brackets must equal $2bx$. Therefore,

$$u\equiv x-\frac{e{\mathbb{E}}_0}{\mu {\left({\omega }^0\right)}^2}.$$

(22)

When written in terms of the coordinate u, (21) becomes:

$$\left[-\frac{{ћ}^2}{2\mu }\frac{{\mathrm{d}}^2}{\mathrm{d}{u}^2}+\frac{1}{2}\mu {\left({\omega }^0\right)}^2{u}^2-\frac{{\left(e{\mathbb{E}}_0\right)}^2}{2\mu {\left({\omega }^0\right)}^2}\right]\psi \left(u\right)=E\psi \left(u\right).$$

(23)

A parapositronium VF can interact with a photon that has any energy, thereby creating a quasi-stationary state. The photon temporarily polarizes the parapositronium VF, but does not cause it to dissociate: the constituent electron and positron must eventually annihilate and return to the vacuum the vacuum energy originally responsible for their creation. Otherwise, neither vacuum energy nor ordinary energy would be conserved.

From (15b) the normalized, ground-state solution to (23) is:

$${\psi }^0\left(u\right)={\left(\frac{\mu {\omega }^0}{\pi ћ}\right)}^{\frac{1}{4}}{e}^{-\mu {\omega }^0{u}^2/2ћ}.$$

(24)

The expectation value $⟨p_{\mathrm{p}-\mathrm{Ps}}^{\mathrm{VF}}⟩$ of the electric dipole moment of a polarized parapositronium VF in the state characterized by ${\psi }^0\left(u\right)$ is:

$$⟨p_{\mathrm{p}-\mathrm{Ps}}^{\mathrm{VF}}⟩={\int }_{-\infty }^{\infty }\mathrm{d}u{\psi }^{0*}\left(u\right)ex{\psi }^0\left(u\right)=\frac{e^2}{\mu {\left({\omega }^0\right)}^2}{\mathbb{E}}_0=\frac{32{ћ}^2{e}^2}{{\alpha }^4{c}^4{m}_e^3}{\mathbb{E}}_0.$$

(25)

The final equality is obtained using $\mu =m_e/2$ and the formula for ${\omega }^0$ implied by (18). The energy levels of the harmonic oscillator model are discussed in the Appendix; however, in the above formula for $⟨p_{\mathrm{p}-\mathrm{Ps}}^{\mathrm{VF}}⟩$, the absolute energy level would appear only as a phase difference ${\psi }^0\left(u\right)\to {\psi }^0\left(u\right)e^{-iEt/ћ}$ and thus for any E would not contribute to $⟨p_{\mathrm{p}-\mathrm{Ps}}^{\mathrm{VF}}⟩$, which depends on the product of the wave function and its complex conjugate.

3.2. Calculation of the Density of Parapositronium VFs Available to Interact with a Photon

As discussed in Section 2, vacuum energy is conserved independently of ordinary energy. Because type 1 vacuum fluctuations are the manifestation of vacuum energy, the energy associated with a vacuum fluctuation obeys the uncertainty principle,

$$\Delta E\Delta t\ge \frac{ћ}{2}.$$

(26)

Neglecting the binding energy of parapositronium, which is small in comparison with $2m_e{c}^2$, $\Delta E_{\mathrm{p}-\mathrm{Ps}}=2m_e{c}^2$ for a parapositronium VF. The average lifetime $\Delta t_{\mathrm{p}-\mathrm{Ps}}$ for the existence of parapositronium VF is the minimum time $\Delta t$ in (26),

$$\Delta t_{\mathrm{p}-\mathrm{Ps}}=\frac{ћ}{4m_e{c}^2}.$$

(27)

During a time $\Delta t_{\mathrm{p}-\mathrm{Ps}}$ light travels a distance:

$$L_{\mathrm{p}-\mathrm{Ps}}=c\Delta t_{\mathrm{p}-\mathrm{Ps}}=\frac{ћ}{4m_{e}c}.$$

(28)

A parapositronium VF appears in the vacuum with its center of mass at rest. Because the constituent electron and positron appear at almost the same location and because nothing travels faster than the speed of light, the maximum distance between the electron and positron is $L_{\mathrm{p}-\mathrm{Ps}}$. Since $2m_e{c}^2$ of the vacuum energy has already been borrowed from the volume $L_{\mathrm{p}-\mathrm{Ps}}^3$ of the vacuum, it is unlikely that another parapositronium VF will form in the same volume, suggesting the ansatz that there are $1/L_{\mathrm{p}-\mathrm{Ps}}^3$ parapositronium atoms per unit volume. If applied to VFs, the Pauli principle also restricts the presence of a second, identical VF at exactly the same point in space.

An isolated, charged particle-antiparticle VF can absorb a photon and then emit an identical photon when the VF annihilates. The electromagnetic decay rate ${\Gamma }_{\mathrm{p}-\mathrm{Ps}}$ for a photon-excited, parapositronium VF atom is [7]:

$${\Gamma }_{\mathrm{p}-\mathrm{Ps}}=\frac{{\alpha }^5{m}_e{c}^2}{ћ}.$$

(29)

The above calculation is compatible with quantum electrodynamics, as is also the calculation by Leuchs et al. [33].

Now $N\left(t\right)=N_0{e}^{-{\Gamma }_{\mathrm{p}-\mathrm{Ps}}t}$, where $N_0$ and $N\left(t\right)$ are, respectively, the number of photon-excited parapositronium VFs at the initial time $t=0$ and the later time t. It then follows that $N\left(t\right)/N_0=e^{-{\Gamma }_{\mathrm{p}-\mathrm{Ps}}t}$ is the probability that a photon-excited parapositronium VF has not decayed electromagnetically during a time t. The probability that photon-excited parapositronium VF has decayed during the time t is $1-N\left(t\right)/N_0=1-e^{-{\Gamma }_{\mathrm{p}-\mathrm{Ps}}t}$.

When a uniform, time-independent beam of light travels through the vacuum, the rate for a parapositronium VF to annihilate and emit a photon must equal the rate for a parapositronium VF to absorb a photon. If this condition were not satisfied, over time as the beam of light passed through the vacuum, the vacuum through which the beam traveled would change sufficiently that the speed of light would be changed. Thus the quantity $1-e^{-{\Gamma }_{\mathrm{p}-\mathrm{Ps}}t}$ is both the probability that photon-excited parapositronium VF has decayed during a time t and the probability that a parapositronium VF absorbs a photon during a time t.

The number density of parapositronium VFs with which a photon actually interacts is $N_{p-Ps}^{VF}$, which for a parapositronium VF equals the product of the number density of parapositronium VFs and the probability that a parapositronium VF will absorb an incoming photon during its lifetime $\Delta t_{\mathrm{p}-\mathrm{Ps}}$:

$$\begin{array}{cc}\hfill N_{\mathrm{p}-\mathrm{Ps}}^{VF}& =\frac{1}{L_{\mathrm{p}-\mathrm{Ps}}^3}\times (1-e^{-{\Gamma }_{\mathrm{p}-\mathrm{Ps}}\Delta t_{\mathrm{p}-\mathrm{Ps}}}).\hfill \end{array}$$

(30)

The term ${\Gamma }_{\mathrm{p}-\mathrm{Ps}}\Delta t_{\mathrm{p}-\mathrm{Ps}}\ll 1$, implying that $1-e^{-{\Gamma }_{\mathrm{p}-\mathrm{Ps}}\Delta t_{\mathrm{p}-\mathrm{Ps}}}\simeq {\Gamma }_{\mathrm{p}-\mathrm{Ps}}\Delta t_{\mathrm{p}-\mathrm{Ps}}$ so (30) becomes:

$$\begin{array}{c}\hfill N_{\mathrm{p}-\mathrm{Ps}}^{VF}\simeq \frac{1}{L_{\mathrm{p}-\mathrm{Ps}}^3}\times {\Gamma }_{\mathrm{p}-\mathrm{Ps}}\Delta t_{\mathrm{p}-\mathrm{Ps}}=\frac{{\alpha }^5}{4}{\left(\frac{4m_{e}c}{ћ}\right)}^3.\end{array}$$

(31)

The final equality in the above equation follows from (27)–(29).

Substituting (31) and (25) into (8),

$${ϵ}_0\simeq \sum _j\frac{8^3\alpha e^2}{ћc}.$$

(32)

Note that the mass of the electron has canceled out of the formula for ${ϵ}_0$; thus, each lepton family contributes equally to ${ϵ}_0$. Including the contributions from ${\mathcal{N}}_L$ lepton families results in the sum on the right-hand side of (32) being replaced by the number of lepton families ${\mathcal{N}}_L$:

$${ϵ}_0\simeq {\mathcal{N}}_L\frac{8^3\alpha e^2}{ћc}+\begin{array}{c}\mathrm{possible}\mathrm{quark}-\mathrm{antiquark}\\ \\ \mathrm{VF}\mathrm{contributions}.\end{array}$$

(33)

The contribution to ${ϵ}_0$ from oscillations of quark-antiquark VFs is small in comparison with oscillations of charged lepton-charged antilepton VFs. As is the case with charged lepton-charged antilepton VFs, quark-antiquark VFs must appear as the least massive state that has zero angular momentum. Additionally, the state must have positive charge conjugation parity so that a photon-excited quark-antiquark VF can decay into a single photon.

The binding of the heavy quarks $Q=c,b,\mathrm{or}t$ into $Q\overline{Q}$ states is described by static quark potentials so an estimate of the contribution that a quark-antiquark VF would make to ${ϵ}_0$ is somewhat similar a calculation of a parapositronium VF’s contribution to ${ϵ}_0$. From (8), (25), and (31), the contribution to ${ϵ}_0$ from parapositronium VFs can be written in the following form that can readily be generalized to estimate the contribution to ${ϵ}_0$ from $Q\overline{Q}$ VFs,

$${ϵ}_{0\mathrm{p}-\mathrm{Ps}}=\frac{{\Gamma }_{\mathrm{p}-\mathrm{Ps}}\Delta t_{\mathrm{p}-\mathrm{Ps}}}{L_{\mathrm{p}-\mathrm{Ps}}^3}\frac{e^2}{\frac{m_e}{2}{\left({\omega }_{\mathrm{p}-\mathrm{Ps}}^0\right)}^2}.$$

(34)

The decay rates of photon-excited $Q\overline{Q}$ VFs is not known. For some $Q\overline{Q}$ states, however, the decay rate into two photons is known. For parapositronium the decay rate of a photon-excited parapositronium VF into a photon and the decay rate of ordinary parapositronium into two photons are related by

$${\Gamma }_{\gamma +p-P{s}^{\mathrm{VF}}\to \gamma }=2{\Gamma }_{p-Ps\to \gamma +\gamma }.$$

(35)

The above equation suggests the approximation:

$${\Gamma }_{\gamma +Q{\overline{Q}}^{\mathrm{VF}}\to \gamma }\sim 2{\Gamma }_{Q\overline{Q}\to \gamma +\gamma }.$$

(36)

Denoting the energy of a $Q{\overline{Q}}^{\mathrm{VF}}$ by $E_{Q{\overline{Q}}^{\mathrm{VF}}}$, from the uncertainty principle it immediately follows that $\Delta t_{Q{\overline{Q}}^{\mathrm{VF}}}=ћ/\left(2E_{Q{\overline{Q}}^{\mathrm{VF}}}\right)$. Then $L_{Q{\overline{Q}}^{\mathrm{VF}}}=c\Delta t_{Q{\overline{Q}}^{\mathrm{VF}}}$. In (34) the charge e of a lepton is replaced by the quark charge, and the electron mass $m_e$ is replaced by the mass of an “almost-free” quark Q. How to calculate the angular frequency ${\omega }_{Q{\overline{Q}}^{\mathrm{VF}}}^0$ is less clear. To obtain the maximum possible contribution to ${ϵ}_0$, the angular frequency ${\omega }_{Q{\overline{Q}}^{\mathrm{VF}}}^0$ is calculated using the minimum possible energy. Here that is the energy of the $Q{\overline{Q}}^{\mathrm{VF}}$ minus the energy associated with the two constituent quarks when they are almost free.

$c\overline{c}$ VFs and $b\overline{b}$ VFs appear, respectively, as ${\eta }_c\left(1S\right)$ and ${\eta }_b\left(1S\right)$ [34]. Their respective contributions to ${ϵ}_0$ are estimated to be ${10}^{-4}$ times and ${10}^{-6}$ times the total contribution from charged lepton-charged antilepton VFs [6]. There is insufficient information, either experimental or theoretical, to directly estimate the contribution that $t\overline{t}$ VFs would contribute to ${ϵ}_0$. However, as the mass of the constituent quarks increases from $m_c$ to $m_b$, the decay rate of the photon-excited $Q\overline{Q}$ VF decreases, and the angular oscillator frequency ${\omega }^0$ increases. Both changes cause $b\overline{b}$ VFs to contribute less to ${ϵ}_0$ than $c\overline{c}$ VFs. This suggests that $t\overline{t}$ VFs would contribute even less to ${ϵ}_0$ although the contribution from quark charges would be four times greater for the $t\overline{t}$ VFs as compared with $b\overline{b}$ VFs.

For the light quarks $q=u,d,\mathrm{or}s$, the least massive $J=0$ combinations of $q\overline{q}$ VFs that have positive charge conjugation parity are ${\pi }^0,\eta$, and ${\eta }^{\prime }$ [34]. A relativistic treatment is necessary to describe these bound states [35], and it does not seem possible that they can be described as oscillators. Additionally, the light quarks are predominantly bound by strong interactions while charged lepton-charged antilepton VFs are bound by electromagnetism; therefore, the binding energy (and ${\omega }^0$) would be much larger for $q\overline{q}$ VFs than for charged lepton-charged antilepton VFs. From (34) it then follows that $q\overline{q}$ VFs contribute much less to ${ϵ}_0$ than charged lepton-charged antilepton VFs.

Neglecting the small contribution to ${ϵ}_0$ from quark-antiquark VFs, (33) becomes:

$${ϵ}_0\simeq {\mathcal{N}}_L\frac{8^3\alpha e^2}{ћc}={\mathcal{N}}_L\frac{2{\mu }_0}{\pi }{\left(\frac{8e^2}{ћ}\right)}^2.$$

(37)

The second equality is obtained using the defining formula for $\alpha$. A formula for c follows immediately from the second equality in the above equation:

$$c=\frac{1}{\sqrt{{\mu }_0{ϵ}_0}}=\frac{1}{\sqrt{{\mathcal{N}}_L}}\sqrt{\frac{\pi }{2}}\frac{ћ}{8e^2{\mu }_0}.$$

(38)

Solving for ${\mathcal{N}}_L$ in (38) and using the defined value for c,

$${\mathcal{N}}_L=2.92.$$

(39)

The calculated value of ${\mathcal{N}}_L$ is not exactly an integer because ${ϵ}_0$ (and c) are only calculated to lowest order in a power series in $\alpha$. Using (38) the bar graph in Figure 1 plots the calculated value of c as a function of the number of lepton families. Not surprisingly, the best fit occurs when there are three lepton families.

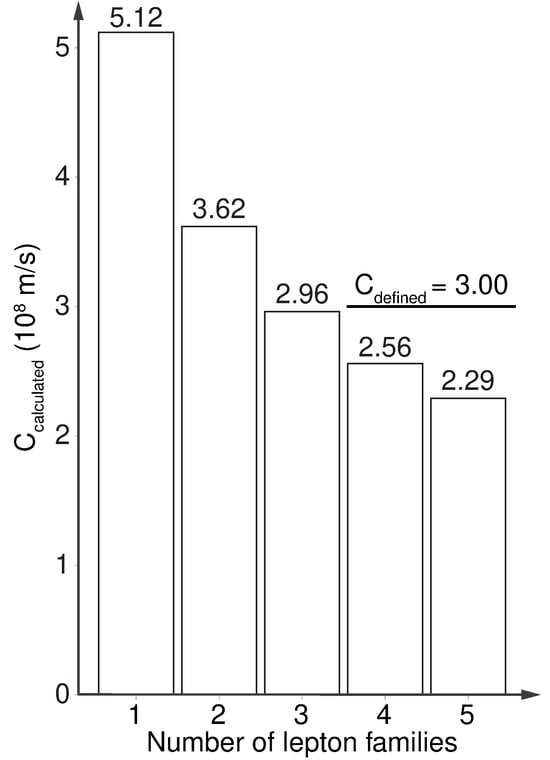
Figure 1. The calculated speed of light in the vacuum as a function of the number ${\mathcal{N}}_L$ of lepton families.

4. Summary and Discussion

The permittivity ${ϵ}_0$ of the vacuum is calculated somewhat similarly to the way that the permittivity of a dielectric is calculated. A formula for the permittivity of a dielectric that typically consists of stable atoms and molecules is obtained by calculating the polarization density of the dielectric, which equals the product of the number density of each type of atom or molecule and the corresponding induced electric dipole moment. Generally, the polarization density is proportional to the electric field that induces the polarization. Substituting the formula for the polarization density into (5), the electric field cancels, yielding a formula for the permittivity $ϵ$ of the dielectric.

In the vacuum the polarization density results primarily from the polarization of type 1, charged lepton-charged antilepton vacuum fluctuations that appear in the vacuum in the most tightly bound state that has zero angular momentum; consequently, the violation of conservation of energy is minimized and angular momentum is conserved. The calculation of the electric dipole moment induced by a photon interacting with a type 1, charged lepton-charged antilepton vacuum fluctuations is similar to the calculation of the induced electric dipole moment of a stable atom or molecule and can be calculated using a harmonic oscillator model of a bound, type 1, charged lepton-charged antilepton vacuum fluctuation. The method for determining the harmonic oscillator corresponding to a charged lepton-charged antilepton vacuum fluctuation is discussed in detail. The Schrödinger equation describing a harmonic oscillator interacting with a photon with an electric field ${\mathbb{E}}_0$ at the moment of interaction is solved exactly.

The number density used when the dielectric consists of stable atoms or molecules, however, must be replaced by the number density of type 1 charged lepton-charged antilepton vacuum fluctuations that are available to interact with a photon, denoted $N_j^{\mathrm{VF}}$, where j labels the type of type 1 charged lepton-charged antilepton vacuum fluctuation (electron-positron, muon-antimuon, tau-antitau). For the jth type of vacuum fluctuation, $N_j^{\mathrm{VF}}$ depends not only on the number density of the type of type 1 vacuum fluctuation but also on the lifetime of the vacuum fluctuation and the decay rate of the photon-excited, type 1 vacuum fluctuation.

Although the permittivity of the vacuum and the speed of light in the vacuum depend only on the number of lepton families and not on the individual masses of the charged leptons, the masses of the three charged leptons, which result from the Higgs mechanism [36,37,38,39] play a significant role in other physical processes. Weinberg’s three-volume treatise The Quantum Theory of Fields [40] contains the chapter “Spontaneously Broken Gauge Symmetries”. At the end of that chapter, one of the questions he asks is, “What would be the effect of the discovery of a fourth generation of quarks and leptons on the predictions of the unified theories of strong and electroweak interactions…?” The Higgs boson plays a role not only in broken symmetries, but also in fixing the number of lepton families, thus playing a major role in determining the speed of light c in the vacuum and the strength of the electromagnetic interaction. (The value of the fine structure constant $\alpha$ follows immediately from the formula for ${ϵ}_0$.) In fact, the calculations discussed here do not answer Weinberg’s question. Rather, they show that such fundamental quantities as the speed of light in the vacuum and the strength of the electromagnetic interaction are related directly to the number of lepton families and indirectly to the Higgs boson and spontaneous symmetry breaking.

There are two issues that are crucial to the ultimate success or failure of this program:

(1)

Do the calculated results satisfy all theoretical constraints?

The formula for the speed of light in the vacuum satisfies the following self-consistency condition: The calculated value of the speed c of light in the vacuum automatically satisfies the second postulate of special relativity: “ The speed of light in the vacuum has the same value c in every direction in all inertial reference frames.” The speed of light in the vacuum is calculated using Maxwell’s equations and the properties of the vacuum. According to the relativity postulate, Maxwell’s equations are the same in every inertial reference frame. Additionally, since the vacuum is the same in any inertial reference frame and is Poincaré invariant, the calculated value of c satisfies the condition that it is the same in every direction in all inertial reference frames. Consequently, the calculation of c automatically satisfies the second postulate of relativity, eliminating the need for the postulate.

(2)

Do the predictions agree with experimental results?

(a)

The calculated values of ${ϵ}_0$ and c are independent of photon frequencies.

(b)

The calculated values of ${ϵ}_0$ and c are correct only to within a few percent because they are calculated only to the lowest order in what turns out to be an expansion in powers of the fine-structure constant $\alpha$. Only the leading term in the formula for the ground-state energy of parapositronium, which is proportional to ${\alpha }^2$, is used to calculate ${ϵ}_0$. Additionally, the induced electric dipole moment of a parapositronium VF and the decay rate of photon-excited parapositronium have only been calculated to the lowest order in $\alpha$. Because $\alpha \simeq 1/137$, in the formulas for ${ϵ}_0$ and c, higher-order terms in $\alpha$ would be expected to be on the order of a percent or so. A major step in determining the predictive power of the theory would be to calculate ${ϵ}_0$ to higher order in $\alpha$, which would yield more precisely predicted values for c and $\alpha$.