Abstract
The causal set program and the Wolfram physics project leave open the problem of how a graph that is a (3+1)-dimensional Minkowski spacetime according to its simple geodesic distances could be generated solely from simple deterministic rules. This paper provides a solution by describing simple rules that characterize discrete Lorentz boosts between 4D lattice graphs, which combine further to form Wigner rotations that produce isotropy and lead to the emergence of the continuous Lorentz group and the (3+1)-dimensional Minkowski spacetime. On such graphs, the speed of light, the proper time interval, as well as the proper length are all shown to be highly accurate.
1. Introduction
The Causal Set Program [1,2,3,4] and the recent Wolfram Physics Project [5,6] both seek to uncover the network of causal relations at the Planck scale, which is the fundamental structure of spacetime. When zooming out to the macroscopic scale, this structure should at least manifest the following properties of Minkowski spacetime:
- -
- (3+1)-dimensionality: one temporal and three spatial dimensions.
- -
- Apparent continuity of space and time.
- -
- Lorentz symmetry, which includes the following:
- -
- Isotropy, i.e., rotational invariance.
- -
- Constancy of the maximal speed, i.e., the speed of light.
- -
- Geodesics with accurate time dilations for all possible velocities.
- -
- Euclidean distance (Pythagorean Theorem can be derived).
In this paper, we present novel discrete structures generated solely by local deterministic rules of remarkable simplicity that fulfill all of the above requirements.
This is different from previous approaches to Lorentz symmetry, such as randomly sprinkled causal sets, which date back to Bombelli [1,3,7]. While randomly sprinkled causal sets were quite useful for study purposes, their construction process employed a pre-existing continuous (3+1)-dimensional space, which becomes unnecessary with our approach.
Previously, Bolognesi [8,9] achieved Lorentz symmetry deterministically, without presupposing a continuous space. However, his emerging spacetimes were restricted to 1+1 dimensions only. Paradoxically, our approach can generate 2+1 or 3+1 dimensions while in some ways being even simpler than Bolognesi’s approach. This is because these additional spatial dimensions facilitate the emergence of isotropy.
Zuse, the inventor of the first functioning programmable computer, originally thought of spacetime as a cellular automaton [10]. While our graphs contain lattices, they cannot be emulated by a cellular automaton. This is in concordance with Zuse’s suspicion that his own cellular automata would ultimately be insufficient due to them lacking isotropy [10].
A distinct approach was previously taken by Cortês and Smolin [11,12]. They solved the emergence of Minkowski spacetime by adding intrinsic quantities to the events, i.e., energies and momenta. In contrast, our approach does not mention energy nor momentum. We do not need to add any such quantities to the events, since we show that simple rule sets concerning only causal relations already suffice.
Another previous approach to Lorentz symmetry by Gorard [13] and Wolfram [6] was used before in order to derive aspects of general relativity from Wolfram models [13]. They employed a more loose concept of Lorentz covariance, such that Wolfram models would be called Lorentz symmetric even when lacking isotropy. They also avoided the simplest distance measures and instead employed a more sophisticated distance measure based on random walks and the Wasserstein transportation metric. We instead provide concrete, fully described graphs that adhere to an accurate version of Lorentz symmetry that includes isotropy, even when measured using simple graph geodesic distances.
Similar to various other approaches, our approach is also background independent [14]. We hope to inspire further refinements of such theories through these graphs. In Section 3, we describe our main ideas and theorems in terms of directed graphs. Due to their high regularity, such structures could then in principle be reformulated and generated within the frameworks of causal sets, pure lambda calculus [15], graph rewriting systems [16], Wolfram models [6], and others. We show algebraically that the properties of Minkowski spacetime emerge at the large scale. Then, we determine the resulting accuracy of the speed of light as well as the resulting accuracy of the proper time interval.
However, before moving to Section 3, it is helpful to firstly understand an analogous graph, from which only the two-dimensional Euclidean plane emerges. We provide this entry point in the following section.
2. The Emergent Euclidean Plane
This section concerns the emergence of the two-dimensional Euclidean plane from an undirected graph. We describe its construction and show its geometric properties algebraically. Note that this graph is not even a subgraph of our relativistic graph of Section 3. However, their construction procedures as well as their mathematical treatments are analogous, which is why we recommend understanding Section 2 here before moving to Section 3.
2.1. One Pair of Interlaced Lattice Graphs
The shortest path metric, also known as the geodesic distance or simply, the between two vertices U and V of a graph, is the least number of steps across its edges to travel from U to V. It is obvious that while an infinite square lattice graph, also known as grid graph or mesh graph, at the large scale, can approximate , its geodesic distance will approximate the Manhattan distance instead of the desired Euclidean distance [17]. Thus, it is often assumed that such regular structures must be avoided and some irregular structure must be used instead. However, our construction involves multiple interlacing square lattices, each of which represents a different angle of orientation1, which leads to a geodesic distance that converges to the Euclidean distance, as we will show in Section 2.2.
Here, we describe how to interlace just two infinite square lattice graphs with each other in order to form a graph that we call . Let the two infinite SLGs (square lattice graphs) be called and . They are both subgraphs of . and share vertices with each other; i.e., there are some vertices that are both part of as well as part of ; let these be called ‘shared vertices’. We postulate two simple rules. To formulate our first rule, it is helpful to assign the four cardinal directions to the steps taken on the lattices. One may imagine instructing a taxicab through the rectilinear Manhattan. Note however that the cardinal directions assigned on will not be aligned with the cardinal directions assigned on .
Rule 1: For each shared vertex A and for each cardinal direction D, there is a shared vertex B, such that both of the following two paths are correct:
- -
- Path on : Starting at A, take two steps in direction D, then take a right turn and one step to arrive at B.
- -
- Path on : Starting at A, take two steps in direction D, then take a left turn and one step to arrive at B.
Rule 2: For and , their shared vertices never neighbor each other.
If these two rules are followed, then the graph is obtained, which is illustrated in Figure 1.

Figure 1.
Graph that was formed from two interlacing square lattice graphs by simple local rules. Shared vertices can be seen to have eight edges.
It can easily be seen that each vertex of either neighbors a shared vertex or is itself a shared vertex, which will be of importance in the next section. Note that we now constructed this graph solely from simple local rules without assigning coordinates to vertices and without performing arithmetic. We now will, however, start to assign coordinates to all vertices for study purposes and only later return to a coordinate-free formulation, that is in Corollary 4. Firstly, we assign integer coordinates to all vertices of such that two vertices P and Q are connected by an edge exactly if . We can then use a second integer coordinate system for the vertices of that works identically. Note that shared vertices A will have coordinates on but will simultaneously also have different coordinates on except for the central vertex O, which we define as having zero coordinates on both lattices, i.e., . We can now reformulate the interlacing by using linear algebra. By applying Rule 1 successively, we obtain the following equation for all shared vertices A:
Then, this linear equation can be rewritten equivalently as follows:
where . Alternative formulation:
Note that these are rotation matrices with rotation angle . Thus far, we have only dealt with the integer-valued coordinates of the shared vertices, but we could in principle use the same rotation matrices to map all of the vertices of onto the real-valued Euclidean plane , such that each edge corresponds to a Euclidean distance of one. Since such a mapping is possible, is itself also a unit distance graph. Note however, that one pair of SLGs is insufficient to further approximate Euclidean distance. In the following subsection, this is solved by extending to an arbitrary number of interlaced lattice graphs.
2.2. Multitudinous Interlaced Lattice Graphs
The previously used pair of lattice graphs is now replaced by an ordered list of lattice graphs . Let n be the length of this list. To construct a new graph , we re-use the same two rules that we introduced in the previous subsection. We apply these rules to each of the ordered pairs of neighboring elements of the list. Thus, for example, the rules must hold if we set , but they must also hold if we set , and they must also hold if we set , and so forth. To remove ambiguity, we further require that vertices are not shared between the lattice graphs unless required by the previous rules.
As shown in the previous section, applying these rules corresponds to a rotation by the angle . In our example, this would result in being rotated by relative to L. For a list of length , we illustrate such a construction in Figure 2.

Figure 2.
Graph that was formed from a sequence of interlacing square lattice graphs by simple local rules, for .
Note that the resulting graph remains a unit distance graph, regardless of the length of the list of SLGs. As is true for any unit distance graph, if we assign the corresponding real-valued coordinates to the vertices , it follows that the geodesic distance between two vertices, that is the minimal number of steps between them, is greater than or equal to the Euclidean distance according to their coordinates. While this provides us with a lower bound for the geodesic distance on , more interestingly, we will now derive a probabilistic upper bound, or rather, the relative deviation of the geodesic distance from the Euclidean distance.
Theorem 1.
Accuracy of Euclidean Geodesic Distances on :
For any sufficiently large and for randomly selected vertices of :
Proof.
Obviously, to each of ’s SLGs, an angle of orientation can be assigned that is an integer multiple of . We may now ask whether it is possible that after multiple successive rotations by , the initial orientation is restored, i.e., Is there any such that in radians? Or equivalently, is there any such that ? Note that the product of a natural number and an irrational number is always an irrational number. The answer to our question therefore depends on whether is rational or not. The number in question is called Plouffe’s constant [20], and it was proven to be a transcendental number by Margolius [21]. It is therefore also an irrational number, i.e., . From this theorem it thus follows that successive rotations by angle will never return the orientation to its original state, and thus all orientations of the SLGs are different from one another. If we let the length n of the list go toward infinity, we can furthermore use the equidistribution theorem [22], which implies that the angles of orientation of the lattice graphs are uniformly distributed on the interval . This means that for sufficiently large n, the angles of orientation of the lattice graphs are approximately uniformly distributed on .
We can use these approximately uniformly distributed directions to construct a path between two vertices U and V that will provide us with an upper bound for the geodesic distance . We are concerned with the case where the distance is much larger than n. Our heuristic approach to constructing a short path from U to V involves two SLGs, and , that have orientations that are approximately aligned with the straight line from U to V. Note that and are usually not neighbors in the list. To take the most direct path, the largest portion of the distance of the path is covered within these three approximately aligned SLGs. The path from U to V can be split into the following sequence of five paths:
- (1)
- Shortest path from U to
- (2)
- Straight path within on line
- (3)
- Shortest path from in to in
- (4)
- Straight path within on line
- (5)
- Shortest path from to V
While the straight paths (2) and (4) are located within single SLGs, the other paths (1), (3), and (5) are not straight and lead through multiple different SLGs in as few steps as possible. Recall from the previous subsection that each vertex of either neighbors a shared vertex or is itself a shared vertex, which means that each vertex of is at a distance from L or that is less than two. Similarly, it can easily be seen for with that each vertex of is at a distance from L, , or that is less than three. And more generally, for all : For each SLG and each vertex of , the distance between the SLG and the vertex is less than n. Therefore, both paths (1) and (5) are of a length of less than n. Furthermore, the straight lines and cross such that the path (3) between them will also be of a length of less than n, analogously to (1) and (5). From these three equal upper bounds, we now get a first upper bound for the total length: is less than or equal to plus the length of (2) plus the length of (4). To further specify this bound, we now move on to estimate the lengths of the two straight paths (2) and (4). Let be the coordinate vectors assigned to the vertices U and V in the Euclidean plane and let be the straight line connecting them. The lengths of the two paths depend on how well the straight lines and are aligned with . In other words, it depends on how small the angles and are. Let be a value that is larger than both of these angles, i.e., . Consider a triangle that has two internal angles that are equal to . Due to this symmetry, it will have two sides that are equally long and whose summed length will be equal to , where d is the length of the remaining side. It is then easy to see that a triangle that has two internal angles that are less than or equal to , will have two sides whose summed length will be less than or equal to , where d is again the length of the remaining side. Analogously, the sum of the lengths of the two paths (2) and (4) is less than , where have been added to account for the possible increase in the length of the paths (2) and (4) due to the changes in location when moving through each of the three paths (1), (3), and (5), that are each limited to a radius of n. This is not to be confused with the previously obtained bound on the sum of lengths of (1), (3), and (5) themselves. By combining both together, we obtain the following bound:
We may now reshape this inequality to show the relative error of , i.e., the deviation of the geodesic distance from the Euclidean distance relative to the Euclidean distance itself:
Recall that in our heuristic approach, and are selected from the list of SLGs, such that their orientations allow for the angles , to be minimal. The larger n is, the more SLGs with different orientations there are to choose from, which allows for a smaller to exist, which implies a smaller relative error. It now remains to be estimated how small this could be depending on n. By observing the case of , we can see that a minimized must be less than or equal to , which then obviously also holds for all larger n. We therefore define the range of as follows: . Within this range the following inequality holds: .
By combining this inequality with the previous relative error’s inequality we get a new formula: relative error . We can use this simpler formula in combination with the variance identity to calculate the expected relative error:
In order to complete this estimate we now only need to calculate the expectation value and the variance of a minimal .
Let be an angle between the orientation of an SLG and the line . As previously discussed, the angles of orientation of SLGs are approximately uniformly distributed for sufficiently large n. can therefore be sampled from a uniform distribution over . The probability p that will lie within an interval of size will thus be equal to .
Since is a line that points in one of the four orthogonal directions of an SLG, the probability that a minimized will be smaller than or equal to will be four times larger and furthermore doubled because we are taking the absolute value, thus resulting in a probability of .
For the situation is analogous, except that the angle should have the correct sign for to intersect with such that will be minimal, i.e., We are interested in the following probability that is halved due the prescribed sign:
We can now use and to determine the probability F that the path from U to V can be constructed by choosing out of the list of n SLGs, and then choosing out of the remaining SLGs, given the constraint :
The smaller function G was introduced in order to simplify the terms. For the minimized , the derivatives then give us the pdfs (probability density functions) f and g:
Since all of these functions are monotone within our range of interest, and we know that G is smaller than F (because G increases slower than F), it follows that the pdf g is more spread out than the pdf f, and therefore, its expectation value is larger and its variance is larger, i.e.,
We now derive an upper bound for the expectation value:
Next, we calculate the variance:
( by analogous steps to earlier )
So, to summarize:
We can now insert these two values into our earlier relative error formula:
□
From Theorem 1, the following few corollaries are easily obtained. These corollaries are kept more general than the theorem, such that they also apply to similar graphs that are mentioned in the following Section 2.3. Firstly, it is worth pointing out that the approximation of the Euclidean distance is perfect in the limit when stated as follows:
Corollary 1.
We can use the Bachmann–Landau notation to characterize the limiting behavior of the deviation:
Corollary 2.
A common related critical question is whether a square’s diagonal’s length will equal relative to the square’s side’s length k, to which the answer is yes, in the limit:
Corollary 3.
, where and .
Finally, we may also formulate a corollary that is void of any coordinates:
Corollary 4.
For : For any set S of vertices of , where all the geodesic distances between these vertices are larger than a constant d: There exists a set of points in the Euclidean plane, such that the set of ratios between the Euclidean distances between these points is identical to the set of ratios between the geodesic distances between the vertices in S.
2.3. Variations, Generalizations, and Alternatives
Some alternatives to the aforedescribed graph that are variations of the same concept are briefly discussed here in order to provide a more generalized picture.
2.3.1. Alternative Angles
The angle was determined by the pair of numbers of steps taken in different directions within Rule 1. This pair of integers was chosen for its simplicity but could otherwise have been chosen arbitrarily as long as the two integers were not equal to each other nor equal to zero; our corollaries would still be holding then. This is because our proof of Theorem 1 is based on the irrationality of Plouffe’s constant , where the ratio appears, which can be generalized to other ratios q, i.e., , where and , as proven by Smith [23]. Hence, any angle of the form would be admissible with SLGs.
2.3.2. Alternative Lattice Graphs
While we only employed square lattice graphs, other obvious choices are the hexagonal as well as the triangular lattice graphs. Our corollaries also apply when triangular lattice graphs are used instead of the SLG, since both allow for straight line paths, whereas for the hexagonal lattice, the geodesic distance would have to be multiplied with a correction factor of in order to account for the absence of straight line paths. A further possibility is to use square lattice graphs but where the rules are altered such that the SLGs are interlaced so that each square represents a rhombus rather than a square while still maintaining the unit distance graph property as well as our corollaries.
2.3.3. Non-Unit Distance Graphs
All graphs that we discussed so far were unit distance graphs. However, this unit distance property is unnecessary for a scaled version of Theorem 1 to hold. Examples of such non-unit distance graphs can be obtained as variations of by cancelling Rule 2 and replacing it with a simple rule that lets the two SLGs share more vertices with each other. Each of these additional shared vertices has to correspond to a pair of close-by vertices in . Geodesic distances then become shorter than the Euclidean distance, while a lower bound, proportional to the Euclidean distance, remains, and thus, an accordingly scaled version of Theorem 1 persists.
3. The Emergent Minkowski Spacetime
In the following subsections, we construct an example of a GRIDS, which is our acronym for a directed Graph that is Relativistic, Isotropic, Deterministic, and Simple (GRIDS), a general concept that we shall briefly present here. Firstly, we require GRIDS to be inherently relativistic; i.e., Lorentz symmetry must be a property of the graph itself, rather than just a property of a distance measure. This means that for all subluminal velocities in any direction, the resulting time dilations must accurately match relativistic formulae [24,25,26,27], despite having been measured by simply counting steps along time-like edges while uninformed by relativistic formulae. Furthermore, GRIDS must exhibit Lorentz symmetry in a strong sense, i.e., involving 3+1 dimensions while including accurate isotropy. In general, the plausibility of theories decreases exponentially with their description complexity [28]. Therefore, we require GRIDS to be sufficiently repetitive to be described or generated by simple deterministic local rules; i.e., the rules should only concern the structures of all small neighborhoods of vertices. Furthermore, any non-integer and large numbers, such as coordinates, momenta, energies, areas, and lengths of edges, are forbidden from being required in the construction process of a GRIDS.
To understand how a graph could possibly fulfill all of these requirements, let us firstly introduce the concept of a frame-grid, which is a repeatedly occurring subgraph of a GRIDS. A frame-grid is a 4D lattice graph that corresponds to a single inertial frame of reference of the emergent Minkowski spacetime of a GRIDS. As will be shown in Section 3.2, it is nearly trivial to interlace two frame-grids by simple rules, such that they are Lorentz-boosted relative to each other. Then, one can simply keep on adding and interlacing many more frame-grids boosted in different directions such that the relations between the frame-grids will form a tree structure of Lorentz boosts. What is less trivial to understand is that this process can already suffice to generate the whole Lorentz group. This can be enabled by the Wigner rotations, which automatically position all of the frame-grids at different velocities and orientations, such that there is no preferred inertial frame nor a preferred orientation, as we show in Section 3.3, using our concrete example, , which serves as a proof of concept for GRIDS. features both light-like edges and time-like edges and is constructed with an emphasis on the ease of coordinatization and the ease of understanding. We demonstrate the accurate relativistic properties of in the Theorems 2–4. Finally, we briefly discuss these theorems in Section 3.3.5.
3.1. Single Frame-Grid
We now proceed to describe a specific example of a frame-grid, , that we will use to construct our GRIDS example, , in the following subsections. is an infinite directed graph and is also a four-dimensional lattice graph. Note that is not the vertex-edge graph of a hypercubic honeycomb. can easily be understood when integer coordinates are assigned to each of its vertices. The set of vertices of corresponds to the subset of where the sum is an even number, i.e., the set .
Let us now define the light-like edges of . Each vertex is the origin of six light-like edges directed away from it, leading in six different directions to six other vertices. Following such a directed edge always leads to another vertex with its t greater by one and exactly one of its the three other coordinates changed by , while the remaining two coordinates are the same as in the previous vertex. is two possible values, and hence the six directions. Therefore, each vertex also has six light-like edges directed at it, originating from six other vertices.
Let these six directions be labeled , , , , , and .
We now also define the time-like edges of . Each vertex is the origin of one time-like edge directed away from it, leading to another vertex with its t greater by two, while the other coordinates, and , remain the same. Therefore, each vertex also has one time-like edge directed at it, which originates from another vertex.
Due to the many regularities, we may assume that such lattice graphs can be constructed without coordinates solely through simple graph rewriting rules that are beyond the scope of this paper. These rules can easily be made to tag all light-like edges with their corresponding direction labels. In the following subsection, we will be using these direction labels to denote steps from one vertex to another along single light-like edges. See the following four examples of our notation of steps along single light-like edges and their associated movements in coordinates :
3.2. Interlaced Pair of Frame-Grids
In this subsection, we describe how two frame-grids, and , are interlaced with each other in order to form , which is a graph that is a helpful intermediate step before understanding the GRIDS . Both frame-grids, and , are subgraphs of , which represents an ‘elementary’ Lorentz transformation between their two inertial frames of reference. is also a repeatedly occurring subgraph of .
3.2.1. Primitive Local Rules
and share vertices with each other; i.e., there are some vertices that are both part of as well as part of . Let these be called ‘shared vertices’. These shared vertices are arranged in a regular fashion as characterized by the following rules. We denote a step along a light-like edge of as described in the previous subsection, and we denote a step along a light-like edge of identically but with a stroke.
Rule 1: and share a vertex O. Their other vertices are not shared unless required by the following rules.
Rule 2: For all shared vertices A:
Explanation: From the strokes, it can be seen that the left sides of the equations denote paths through , while the right sides denote paths through . Therefore, for instance, if A is a shared vertex, then is also a shared vertex. By successive application of Rule 2, the graph depicted in Figure 3 is obtained:
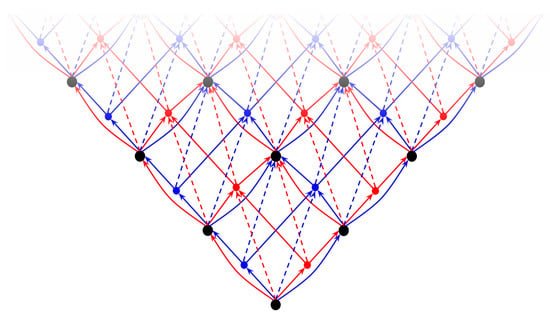
Figure 3.
Part of the graph formed by the repeated application of Rule 2. is shown in red, is shown in blue, and their shared vertices are shown in black. The solid arrows represent light-like edges while the dashed arrows represent time-like edges.
So far, we have interlaced two two-dimensional subgraphs of and to form the graph, as depicted in Figure 3. Combined with the following rule, Rule 3, the interlacing is extended to four dimensions.
Explanation: From the strokes, it can again be seen that the left sides of the equations denote paths through , while the right sides denote paths through . Note that the paths in Rule 3 move once forwards and once backwards in time, thus not changing the position in time overall. This rule simply copies the interlacing of the subgraph seen in Figure 3 onto the many parallel subgraphs that have different y and z positions.
The repeated application of Rule 2 propagates only forwards in time. Analogously, Rule 3 does not propagate in all directions. Therefore, we add the following final rule in order to propagate the interlacing into all times and all directions for the sake of completeness:
Rule 4: The previous rules also apply with all of their paths reversed.
(Note that all edges remain pointed forwards in time).
3.2.2. Reformulation through Coordinates
While our set of rules was based on individual steps along edges, we now reformulate this set of rules using integer coordinates that can be assigned to the vertices of , as we described in Section 3.1.
Let be the integer coordinates assigned on . These eight coordinates belong to the same vertex if and only if the following four equations hold:
Note that these equations are sufficient to fully replace our four primitive rules; i.e., these equations already fully describe . We further translate these equations into linear algebra. Let and be the coordinates on and , respectively, in the form of column vectors. Then, the following linear equation is equivalent to the previous four equations:
This linear equation can be rewritten equivalently as follows:
We can immediately see that this matrix represents a Lorentz transformation without rotation, thus called a Lorentz boost, with the following values:
In special relativity, the relation between these three physical quantities is given by:
3.3. Multitudinous Interlaced Frame-Grids
We now describe the construction of the GRIDS example and then go on to calculate the accuracy of both the speed of light and the proper time interval. The construction is most easily shown visually by using the conformal disk model of the hyperbolic plane, also known as Poincaré disk model, although originally discovered by Beltrami [29]. We use it to represent the relative rapidities and the angles between Lorentz boosts. This hyperbolic space later emerges naturally from many successive Lorentz boosts due to repeated interlacing. In the previous subsection, we described how a frame-grid can be interlaced with another frame-grid, resulting in a Lorentz boost in the direction of dimension x, which is now depicted in the first disk of Figure 4. The second disk shows a frame-grid in the center that is interlaced analogously with other frame-grids but in different perpendicular directions. These boosts in different perpendicular directions can easily be achieved by permuting the directions within rule 2 and rule 3 of the previous subsection accordingly. Note that these disks are only 2D cross-sections of the 3D Poincaré ball model, where there are six such perpendicular directions. Let be the graph consisting of a central frame-grid that is interlaced with frame-grids in all six of these perpendicular directions, totaling a number of seven frame-grids. When there is a sequence of interlaced frame-grids, we can assign a different Lorentz transformation to each frame-grid through the corresponding successive applications of the aforedescribed coordinate transformation. Note that this graph has a special property that resembles the unit-distance graph property; that is, the graph can be embedded in a Minkowski spacetime such that all the time-like edges correspond to time-like paths of the same unit time, while all the light-like edges will correspond to light-like paths. This property is automatically retained by for all . Then, let be the graph consisting of , where all frame-grids are interlaced with further frame-grids in all unoccupied perpendicular directions, resulting in the 2D cross-section depicted in the third disk and totaling a number of 37 frame-grids. Note that since this is a hyperbolic space, no square was formed, even though the angles are perpendicular and all lines are of the same length as well as straight. In the third disk, we can furthermore start to observe the Wigner rotations [30,31] caused by successive Lorentz boosts in different directions. The Wigner rotation is a consequence of special relativity that is similarly astonishing to the twin paradox. While the twin paradox concerns the time difference caused by successive Lorentz boosts, the Wigner rotation concerns the change in orientation caused by successive Lorentz boosts. We obtain by repeating the same procedure and so forth; this is also how we define recursively for all . The remaining disks visualize a few more of these steps.
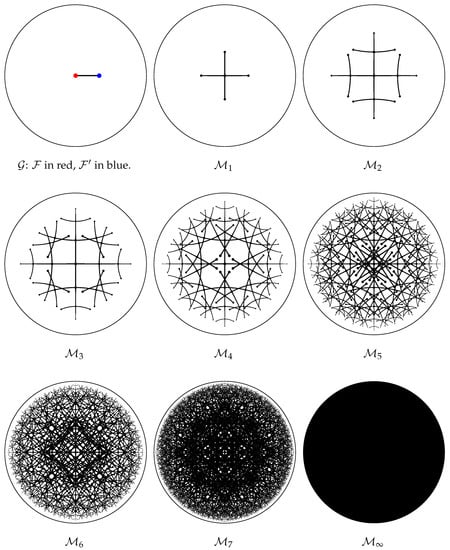
Figure 4.
Depicted are nine Poincaré disk representations of the hyperbolic space of the Lorentz group. Each dot represents one frame-grid. If two dots are connected by one line, they are interlaced, as previously described, corresponding to a Lorentz boost with a rapidity . The first disk corresponds to Figure 3 of the previous section. The other eight disks are 2D cross sections of 3D Poincaré ball models corresponding to graphs that can be seen to be constructed through recursive interlacing of further frame-grids. As n goes toward infinity, the hyperbolic space is filled completely, as depicted in the last disk according to Theorem 2. A further disk, , is shown in greater detail in Figure A1 of the appendix. We provide the program to generate these images at [32].
3.3.1. Emergent Isotropy
Previously, also Dribus [3] intuited that the Wigner rotation might play a role in the emergence of the Lorentz group from causal sets due to the ‘information–theoretic preeminence’ of boosts over rotations, meaning that the former can generate the latter. However, by what kind of process this emergence could occur remained shrouded in mystery. Now, our aforedescribed GRIDS, such as , resolve this mystery since the infinitely repeated occurrence of Wigner rotations yields all possible orientations combined with all possible rapidities and thus yields isotropy without requiring any additional rules; i.e., the rules of Section 2 become obsolete here. We show this claim to be true in the proof of Theorem 2. In preparation for it, we firstly prove the following lemma.
Lemma 1.
In the hyperbolic plane, let us perform a sequence of steps, each covering the same distance w; between the steps, we change our direction by the angle ϕ. Then, the resulting set of visited points will be uniformly distributed on a circle if w and ϕ meet the following condition:
Proof.
Starting at a point , perform one of the described steps to visit another point . Let the center of a circle, on which all visited points are located, be called A. Then the center A must lie on the perpendicular bisector line of the line segment . Let the midpoint of the line segment be called C. Continuing from , perform the next step to visit another point . The center A then must also lie on the angle bisector line of the angle . Note that the hyperbolic triangle is a right triangle, since . Let , , and , as is usual in trigonometry.
Due to the bisections, we get as well as .
The following equation applies to right hyperbolic triangles such as : , from which it follows that: .
By taking further steps, we visit the set of points . Due to the required regularities, each step moves us around the center A by the same angle that is equal to , due to the bisections, i.e., , .
Therefore, if is an irrational number, we will never revisit the exact starting point, no matter how many laps we completed on the circle. Furthermore, according to the equidistribution theorem [22], if is an irrational number, then the points will be uniformly distributed on the circle.
Therefore, in order to prove our lemma, we only need to show that the condition implies the irrationality of , i.e., .
Recall that and . We can use these two equations to rewrite the condition as follows: .
We then substitute with a variable r: .
The theorem about the arccosine function of Varona [33] then implies that the number cannot be rational, i.e., .
Then, we unpack r and get: .
Recall that ; and thus it follows that . q.e.d. □
Corollary 5.
If the sequence of steps is infinite, then the set of visited points will form a continuous circle.
Theorem 2.
fills the Lorentz group:
Let be for . The set of Lorentz transformations corresponding to all frame-grids of is equal to the continuous set of all Lorentz transformations, i.e., the entire Lorentz group.
Proof.
We firstly need to show that for each point in the 3D hyperbolic space, it is possible to reach the point through some sequence of steps corresponding to the Lorentz transformations corresponding to some sequence of interlaced frame-grids within when starting from the central frame-grid that is the center point in the the disk models of Figure 4. Recall that the rapidity w of the individual Lorentz boosts between frame-grids in is equal to . In , the angle by which the direction changes after each boost is either zero or . Let us therefore apply Lemma 1 with and . We need to verify whether the condition of Lemma 1 holds for these values of w and :
Now, since is true, the condition is fulfilled. Due to the infinities, we can furthermore apply Corollary 5. It implies that the set of Lorentz transformations corresponding to all frame-grids of forms a shape that contains many continuous circles in the 3D hyperbolic space of the Lorentz group. As a side note, it therefore forms continuous helices in the Lorentz group itself, which is six-dimensional, due to the three additional degrees of freedom for rotations. Thus, in the 3D hyperbolic space, we can choose a sequence of perpendicular steps of length w to move arbitrarily close to any point on a continuous circle, thus also allowing us to move by arbitrarily small distances from the origin. At any point of this circle, we can then choose to keep moving on a different circle that is perpendicular to the previous circle. Then, we may change to further circles an arbitrary number of times, resulting in a path that can be thought of as a composition or concatenation of perpendicular circular arcs. Such a path has enough degrees of freedom to reach any point of the 3D hyperbolic space. Furthermore, such a path can reach any point at an arbitrary orientation; thus, the entire Lorentz group, which is six-dimensional, is continuously filled by the Lorentz transformations of the frame-grids of . q.e.d. □
3.3.2. Speed of Light
Recall Theorem 1, where the geodesic distance on a graph approximated the Euclidean distance. The following theorem, Theorem 3, is analogous to this, in that the speed of the quickest path along light-like edges of approximates a constant speed equal to one through the 3D Euclidean space. Let these speeds of the quickest paths be called the speed of light for simplicity, in accordance with Fermat’s principle of least time. The following theorem then says that the longer the path traveled by the light is, the more accurately its speed will approximate a constant in any direction, i.e., isotropically. Some concrete examples of calculations are provided in Section 3.3.3.
Theorem 3.
Accuracy of the Speed of Light on
For all frame-grids of :
Given two randomly selected spatial locations on :
Let . Consider the following path: Starting at a vertex of , located at , at a randomly selected departure time, move along light-like edges of to arrive as quickly as possible at another vertex of , located at , at the resulting arrival time. Let the integer then be the difference between the departure and the arrival time in the frame of reference of . The following inequality then expresses how little the velocity will deviate from one:
Proof.
To prove this formula, we show the existence of a sufficiently quick path. Our path starts on frame-grid at location ; then, it usually leads through multiple other frame-grids of before returning back to the same frame-grid but at a different location that is . This path is an alternation of several long straight paths on single frame-grids with several shorter non-straight paths that lead through multiple frame-grids. It is therefore analogous to the path that we described back in Theorem 1 but consists of seven instead of five parts due to the increased number of dimensions.
In what follows, for simplicity, we shall restrict the set of frame-grids that the path is allowed to lead through. Recall from the proof of Theorem 2 that the condition of Lemma 1 is fulfilled for and . Hence, there are sequences of interlaced frame-grids of , such that their corresponding sequences of points within the 3D hyperbolic space are uniformly distributed on circles. Also note that each such point is part of twelve such circles that are located on three perpendicular planes; obviously, these twelve circles are the pairwise intersections of eight spheres. We are concerned with only one of these spheres. Analogously to how the sequence resulted in a uniform distribution over a circle, a binary tree can result in a uniform distribution over an aforementioned sphere. For simplicity, we restrict the set of frame-grids that our path is allowed to lead through, to such a spherical binary tree, where each node is a frame-grid. One of these frame-grids must be . Each edge in the binary tree indicates that the two frame-grids are interlaced with each other. In the 3D hyperbolic space, the points corresponding to these frame-grids are uniformly distributed across a sphere. Let this binary tree be an unrooted binary tree containing nodes, such that the number of steps required to move between any two nodes is at most n. We will set the parameter n later in this proof. Note that not only are these points uniformly distributed across that sphere, but also the orientations of these frame-grids are uniformly distributed.
Recall that the relative rapidity between interlaced frame-grids was and in the binary tree, each non-leaf node has three neighboring nodes. This translates to a point on the sphere, let it be called A, being at a distance of from three other points on the sphere in three perpendicular directions. We now use this fact in order to calculate the radius of this sphere within the hyperbolic space. We use a right hyperbolic triangle, where the hypotenuse is the line segment from the sphere’s center to the point A, which is of length r, i.e., the radius of the sphere. One of the catheti, b, is a half of the line segment from A to one of the three aforementioned points. This cathetus b is thus of length . Due to the symmetry between the three aforementioned points located in perpendicular directions, the angle at A must be equal to the angle between the diagonal of a cube and one of its edges. We therefore obtain , which we can use to calculate the length r of the hypotenuse as follows: . We use this radius later for the calculation of time delays.
Let , , and be frame-grids that should be thought of having orientations that are approximately aligned with the straight line from to , i.e., some of the most well aligned out of the set of frame-grids. To take the most direct path, the largest portion of the distance of the path is covered within these three approximately aligned frame-grids. There are three of them because three vectors can be linearly composed to reach any point within a 3D volume. The entire path can be split into the following sequence of seven paths:
- (1)
- Quickest path from at location to .
- (2)
- Straight light-like path within on line .
- (3)
- Quickest path from in to in .
- (4)
- Straight light-like path within on line .
- (5)
- Quickest path from in to in .
- (6)
- Straight light-like path within on line .
- (7)
- Quickest path from to at location .
While the straight paths (2), (4), and (6) are located within single frame-grids, the other paths (1), (3), (5), and (7) are not straight and lead through multiple different frame-grids in as little time as possible, thus only covering little distance when compared to the straight paths.
We now calculate the worst-case time delays caused by the four non-straight paths (1), (3), (5), and (7). The relative rapidity between frame-grids in the binary tree must be smaller or equal to the largest distance between their positions in the hyperbolic space, which is equal to the diameter of the sphere. The distance traveled along a single light-like edge of any frame-grid of the tree would then have to be at most and at least in the frame of reference of . Also the elapsed time would then accordingly have to be between and . In the absolute worst-case, the path would lead across a light-like edge that leads in the opposite direction of the path’s final destination, thus causing a time delay of . For any two interlaced frame-grids, the maximal number of steps along light-like edges required to move from any vertex of the first frame-grid to a vertex shared with the second frame-grid is just two, as can be derived from the rules in Section 3.2.1. This yields a worst-case time delay of less than per move from one frame-grid to the next one. Recall that the number of steps required to move between any two frame-grids that are nodes of the binary tree is at most n. This results in a time-delay of less than per non-straight path, of which there are four, hence resulting in less than . By inserting the previously calculated value for the radius r, we then obtain:
We now proceed to the other time delays that are caused by the small deviations of the orientations of the three straight paths (2), (4), and (6) from the direction of the ’direct line’ from to . These deviations of directions are three small angles. Let be a small value that is larger than each of these three angles. The paths would thus at most be elongated by the factor . Recall that is the total time taken and . By adding all time-delays, we obtain the bound shown in the following inequality:
( since for )
( since for )
On the left side of this last formula is the error of the fastest average speed, i.e., the speed of light. We let the unknown values and n disappear from the right side in what follows. We firstly rewrite the previous formula in terms of expectation values:
We now need to calculate bounds for the expectation value and the variance of a minimal depending on n. The larger the parameter n is, the more frame-grids with different orientations there are available to choose from, which allows for a smaller to exist, which implies a smaller time-delay on the straight paths. Each frame-grid provides six possible directions for straight light-like paths. Note that two interlaced frame-grids share directions with each other, such that together they provide only ten rather than twelve such directions. To count the total number of directions provided by the binary tree, we can therefore count six per node minus two per connection between nodes, i.e., , where m is the total number of possible directions of straight light-like paths within frame-grids that are the nodes of the binary tree. Let be an angle that is the great-circle distance between two points that are sampled from a uniform distribution on a unit sphere. The probability p that will be less than or equal to will then obviously be equal to , i.e., .
Then is the probability that, within a great-circle distance of of a given point, there will be at least three points out of a set of m points sampled from the uniform distribution over the whole unit sphere.
The three directions in 3D space of the paths (2), (4), and (6), when mapped to points on the unit sphere, are the corners of a small spherical triangle that needs to encase the point that is the direction from to , otherwise the path would miss its target. For three randomly sampled corners there is obviously a probability of that this triangle will encase that point. To obtain the probability that the whole path exists we therefore multiply the last exponent in the aforementioned probability by :
( since )
( since for )
The smaller function G was introduced in order to simplify the terms. For the minimized , the derivatives then give us the probability density functions (pdf) h and g:
As previously shown G is smaller than H for . Larger values for are not considered since the minimal will be much smaller than 1 for large m. Since increases slower than , it follows that the pdf g is more spread out than the pdf h and therefore its expectation value is larger as well as its variance is larger, i.e.,
We now derive an upper bound for the expectation value:
( For any : )
( Let : )
Next, we derive an upper bound for the variance:
( By analogous steps to earlier. )
( with )
So, to summarize: and .
We can now insert these two values into our earlier formula and afterwards set the parameter n depending on s:
□
3.3.3. Examples for Theorem 3
Here, we provide examples where we use Theorem 3 to calculate upper bounds on the deviation of the speed of light traveling one meter, one parsec, and one ångström in any direction. As the Planck length is often speculated to be the fundamental length, here, we set the light-like edges to cover a distance equal to one within their respective frame of reference.
To convert to SI units, we multiply with the speed of light constant . For light traveling one meter, we get the dimensionless distance . By inserting this s into the formula of the theorem, we obtain:
This indicates that the speed of light deviates only by an extremely small speed, which means high accuracy for one meter. For light traveling the astronomical distance of one parsec, we get another , which we insert again:
We can see that for this astronomical distance, the speed of light becomes 15 orders of magnitude more accurate, theoretically. But more interestingly; is it still accurate at microscopic distances, such as one ångström?
For light traveling one ångström, we get and subsequently:
In conclusion, even at a distance as short as one ångström, the speed of light is still so accurate that the speed by which it can deviate is still around a hundred times slower than the speed of fingernail growth or the speed of continental drift. It should also be noted that with more work, our bound could be optimized even further.
Theorem 3 also provided the general error term that applies to not only the speed of light on , but to the speed of light on other GRIDS as well. A similar term will reappear concerning the proper time interval in the following section.
3.3.4. Proper Time Interval
In special relativity, the proper time interval of a geodesic between two events is given by the formula , where s is the spatial distance between the two events and is the time difference. While and s differ depending on the inertial frame of reference, does not, i.e., is Lorentz invariant. The difference between and is called time dilation. can also be written in terms of a Lorentz factor as follows: , where v is the velocity of an inertial observer following the geodesic between the two events and would then be the time that elapsed on their clock. Light-like paths have a proper time interval equal to zero. While a geodesic between two points in a Euclidean space is the shortest possible path, in a Minkowski space, conversely, a geodesic is the longest possible path, i.e., The path between two given events forwards in time with the longest possible proper time interval. is a directed acyclic graph (DAG). Recall the geodesic distance on graphs that was a shortest path metric between vertices introduced in Section 2.1. Analogously, we now use a geodesic distance on DAGs that is a longest path metric between vertices. The length of such paths is determined by counting the number of steps; there are, however, multiple different possible methods for counting the number of steps for different types of GRIDS. For GRIDS that consist of only time-like edges, one simply counts the number of steps along the time-like edges. For GRIDS that consist of only light-like edges, one should count the number of direction changes of a path along light-like edges. For GRIDS that consist of both light-like as well as time-like edges, such as our , we count the number of time-like edges while not counting the light-like edges along a path that consists of both time-like as well as light-like edges. In the following theorem, we show how accurately this geodesic distance approximates the formula of the proper time interval for any v that is slower than the speed of light by some arbitrarily small constant .
Theorem 4.
Accuracy of the Proper Time Interval on
For any arbitrarily small positive constant δ:
For all frame-grids of :
Given two randomly selected vertices Q and U of :
Let s and be the spatial distance and the temporal distance between the integer coordinates of Q and U on and let .
Let be the geodesic distance between Q and U that is a longest path metric on .
If holds, then the following limiting behavior holds:
Proof.
Recall that the proofs of Theorems 1 and 3 both involved the construction of a sufficiently short or quick path. Analogously, the proof of Theorem 4 here would involve the construction of a sufficiently long path, i.e., a path from the vertex Q to the vertex U forwards in time along sufficiently many time-like edges. The quick path in the proof of Theorem 3 contained three approximately aligned straight light-like paths that alternated with four paths that quickly transition between frame-grids. Analogously, the optimal long path here would contain four approximately aligned straight time-like paths that alternate with five paths that quickly transition between frame-grids. This increase in numbers stems from the additional degree of freedom provided by the random selection of the time coordinates of Q and U, which was not present in back in Theorem 3.
Our path starts at Q on . Recall that , as all other frame-grids, corresponds to a point in the hyperbolic space. The initial part of our path leads from along interlacings across other frame-grids through hyperbolic space toward the vicinity of the point corresponding to the velocity vector from Q to U. This initial part of the path can be thought of as a quick acceleration nearing the desired velocity. For the extreme cases where Q and U are selected such that the velocity is very close to the speed of light while the time is too minuscule to allow for the required acceleration, we introduced the constant that limits the velocities. can be selected to be arbitrarily small, so long as it is positive and constant in order to allow for the error’s limiting behavior (formulated in the theorem) when tends toward infinity.
The path continues through a tree that is analogous to the binary tree that we employed in the proof of Theorem 3, with the difference being that the nodes of the tree populate a 3D region instead of populating the spherical surface. The tree is used in order to move to a frame-grid that is close to a desired velocity rather than being close to a desired orientation. The rest of the proof is analogous to the proof of Theorem 3 and is thus not described further here (q.e.d.). The proof technique described here also works to show the accuracy of the proper time interval on GRIDS consisting solely of time-like edges as well as GRIDS consisting solely of light-like edges. □
It should also be noted that the patterns in Figure 2 happen to bear resemblance to quasicrystals [34], which are related to Penrose tilings [35]. Thus, we can infer that GRIDS will likely also contain patterns that bear resemblance to 4D-quasicrystals, which might lead to further insights in the future.
3.3.5. Discussion of the Theorems
For , our previous two theorems have shown the accuracy of the speed of light as well as the accuracy of the proper time interval for any inertial frame of reference. Obviously, it would be possible to demonstrate such accuracies for many other similarly constructed GRIDS. This is analogous to Section 2.3. A further obvious consequence of our theorems is that the Poincaré group is also covered by GRIDS.
The proper length of an object can be calculated from the time taken for a flash of light to travel back and forth along the object when measured by a clock in the rest frame of the object. Therefore, the proper length measured on inherits the same accuracy as the speed of light and the proper time interval, i.e., the error of the proper length relative to itself is . Analogously to the geodesic distance in Corollary 4, measuring the proper lengths between multiple spatial locations of the same inertial frame in then yields exactly the values that one would expect from distances between points in a 3D Euclidean space, up to minuscule errors. We conjecture that the familiar 3D Euclidean space of our everyday reality is actually exactly this feature of a GRIDS.
Recall that Theorems 3 and 4 are concerned with paths that lead through multiple frame-grids but ultimately return to the same frame-grid that they started on, since these paths connect two vertices that belong to the same frame-grid. In some form, these theorems would also be valid for paths between two vertices that belong to the same finite subset of interlaced frame-grids rather than just the same single frame-grid. However, the larger these subsets of frame-grids are, the lower the resulting accuracies. Note that two frame-grids that were not interlaced directly can have an arbitrarily low density of shared vertices while being located arbitrarily close in the hyperbolic space. Hence, one could interpret these frame-grids as residing in different worlds of Everett [36]. Therefore, the decreased accuracies of measurements between the vertices of two completely arbitrary frame-grids would not hinder the emergence of Minkowski spacetime, since the measurements need only be accurate within each world rather than between worlds. GRIDS can be regarded as superpositions of many spacetimes, which is also related to Lloyd’s theory of quantum gravity [37]. If particles are localized self-sustaining disturbances of the regularities of a GRIDS, then within a subset of frame-grids that can be interpreted as constituting one single such world, quantum superposition would occur, since many different versions of the same particle could occupy the same space with almost no interference between them due to the low density of shared nodes between some of these frame-grids. This means that GRIDS, such as , possess the causal structure of quantum superpositions. Further investigation of these features of GRIDS is outside the scope of our paper. Note that such quantum properties were a natural side effect of merely having searched for the simplest graphs that follow (3+1)-dimensional special relativity.
4. Conclusions
The lengths of the shortest paths, or geodesic paths, on simple square lattices are non-Euclidean. It was thus often assumed that the same lack of isotropy would apply to all structures of similar simplicity and regularity. However, in this paper, we showed that similar structures can exhibit isotropy and even yield the full (3+1)-dimensional Minkowski spacetime when measured using simple geodesic paths. We called such structures GRIDS, which stands for Graphs that are Relativistic, Isotropic, Deterministic, and Simple. Due to Occam’s Razor, our key insight further increased the plausibility of the pre-existing theories that assumed spacetime to be a discrete structure. We demonstrated the high accuracy of the speed of light, the high accuracy of the proper time interval, as well as the high accuracy of the proper length. Causal structures reminiscent of quantum superposition emerged as a side effect.
Future Research
Immediate future research could firstly attempt to merge the GRIDS concept with existing theories of quantum gravity, such as Lloyd’s theory [37], Gorard’s theory [13], Quantum Graphity [38,39], and others [11,12,40]. This will allow one to determine how curvature is induced through small irregularities in the graph. While we provided simple rule sets that fully characterized two examples of GRIDS, we did not provide the actual rewriting rules, since they were unnecessary to obtain our theorems. The rewriting rules can be determined by researchers later on, depending on their graph rewriting framework [6,15,16] of choice as well as depending on their selected theory of quantum gravity. Rather than merging complete frame-grids, the rewriting rules should repeatedly rewrite a space-like graph in partial order, such that its causal history will form a GRIDS, i.e., The interlaced frame-grids are to be generated incrementally, confluently, and together in parallel. An interesting future research task could be to determine the shortest possible rule set that yields some GRIDS. Our previous proof techniques can also help to confirm whether some future novel network structure is indeed a GRIDS or not. In Section 3.3.5, we invoked a many-worlds interpretation to preserve the accuracies. Therefore, another future research question is whether such an interpretation is generally necessary or not. As can partially be seen from our illustrations, GRIDS could be rich in various patterns, such as quasicrystalline appearances, horocycles, and others, which one may explore in the future, in search of aspects of the standard model. Ultimately, a deeper understanding of the structure that underlies spacetime could allow for further steps toward the ultimate theory of fundamental physics.
Funding
This research received no external funding. The APC was funded by the University of Groningen and the Multidisciplinary Digital Publishing Institute.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A. Illustration with Greater Detail

Figure A1.
, the disk that would directly succeed shown in Figure 4.
Appendix B. Bonus GRIDS
In this appendix, we briefly describe , which is a slightly modified version of . It is composed of the same frame-grids. These are interlaced by the same set of rules introduced in Section 3.2.1 with a modification to Rule 2 and a simplification of Rule 3. On the one hand, such simplification is an improvement. On the other hand, this simplification shears each frame-grid such that its internal angles will not be perpendicular anymore, thereby making it harder to imagine. Therefore, we recommend to obtain a good understanding of before proceeding to the following modified rules.
Modified Version of Rule 2: For all shared vertices A:
Modified Version of Rule 3: For all shared vertices A:
Recall that the strokes indicate that the left sides of the equations denote paths through a frame-grid , while the right sides denote paths through another frame-grid . Aside from being simpler, this modified version of Rule 3 also holds the advantage of only using steps forwards in time, i.e., There is no present anymore. This property is especially useful if is to be generated incrementally by a rewriting system that progresses forwards in time. Note that Rule 2 was modified such that the x coordinates are reversed for one of the frame-grids, i.e., There now is a mirror symmetry between the x coordinates of the two frame-grids. Figure 3 is also still valid for . Let us now derive the resulting non-perpendicular angles. From the mirror symmetries of these two rules, we can immediately deduce that the directions and would be exactly vertical when mapped onto Figure 3. Note that the same does not hold for and . It is easy to see that such vertical movement within this figure corresponds to one time-like plus one light-like step within the same frame-grid. Note that such a movement corresponds to increasing the time t by three while changing x by one. This is a velocity of . Rather than projecting to the plane, let us now project onto the plane. Here, the directions x and y cannot be orthogonal to each other, since a velocity of 1 along y mapped orthogonally onto x is equal to rather than zero. It follows that the angle between the directions x and y must be equal to . If further frame-grids are added as usual, the same angle must reoccur between x and z as well as between y and z. is depicted on Poincaré disks in Figure A2. All of our theorems concerning shown in Section 3 also hold for in an analogous fashion. We gave our Conclusions in Section 4.
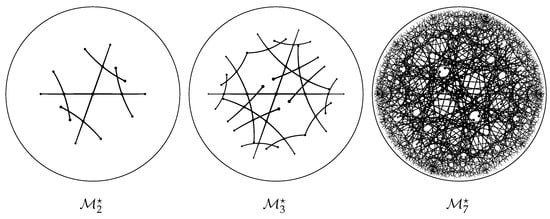
Figure A2.
Depicted are three 2D cross sections of 3D Poincaré ball models of the hyperbolic space of the Lorentz group. Each dot represents one frame-grid. If two dots are connected by one line, they are interlaced, as previously described, corresponding to a Lorentz boost with a rapidity . In the first disk, the angle of and its mirroring are shown. In the second disk, two hyperbolic hexagons have formed incidentally. In the third disk, various horocycles and hypercycles emerged. We show one further disk, , in greater detail in Figure A3.

Figure A3.
, a Poincaré disk succeeding the disks shown in Figure A2.
Note
| 1 | A vaguely distantly related concept was developed for fluid dynamics simulations [18,19]. |
References
- Bombelli, L.; Lee, J.; Meyer, D.; Sorkin, R.D. Space-time as a causal set. Phys. Rev. Lett. 1987, 59, 521. [Google Scholar] [CrossRef] [PubMed]
- Reid, D.D. Introduction to causal sets: An alternate view of spacetime structure. arXiv 1999, arXiv:gr-qc/9909075. [Google Scholar]
- Dribus, B.F. Discrete Causal Theory; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Dribus, B.F. On the axioms of causal set theory. arXiv 2013, arXiv:1311.2148. [Google Scholar]
- Wolfram, S. A New Kind of Science; Wolfram Media: Champaign, IL, USA, 2002; Volume 5. [Google Scholar]
- Wolfram, S. A Class of Models with the Potential to Represent Fundamental Physics. arXiv 2020, arXiv:2004.08210. [Google Scholar]
- Bombelli, L.; Henson, J.; Sorkin, R.D. Discreteness without symmetry breaking: A theorem. Mod. Phys. Lett. A 2009, 24, 2579–2587. [Google Scholar] [CrossRef] [Green Version]
- Bolognesi, T. Algorithmic Causal Sets for a Computational Spacetime; World Scientific: Singapore, 2013. [Google Scholar]
- Bolognesi, T. Spacetime computing: Towards algorithmic causal sets with special-relativistic properties. In Advances in Unconventional Computing; Springer: Berlin/Heidelberg, Germany, 2017; pp. 267–304. [Google Scholar]
- Zuse, K. Rechnender Raum (calculating space). Schriften Dataverarbeitung 1969, 1, VIII. [Google Scholar]
- Cortês, M.; Smolin, L. Quantum energetic causal sets. Phys. Rev. D 2014, 90, 044035. [Google Scholar] [CrossRef] [Green Version]
- Cortês, M.; Smolin, L. The universe as a process of unique events. Phys. Rev. D 2014, 90, 084007. [Google Scholar] [CrossRef] [Green Version]
- Gorard, J. Some Relativistic and Gravitational Properties of the Wolfram Model. arXiv 2020, arXiv:2004.14810. [Google Scholar] [CrossRef]
- Smolin, L. The case for background independence. In The Structural Foundations of Quantum Gravity; Oxford University Press: Oxford, UK, 2006; pp. 196–239. [Google Scholar]
- Church, A. The Calculi of Lambda-Conversion; Princeton University Press: Princeton, NJ, USA, 1941. [Google Scholar]
- Rozenberg, G. Handbook of Graph Grammars and Computing by Graph Transformation; World Scientific: Singapore, 1997; Volume 1. [Google Scholar]
- Deza, M.M.; Deza, E. Encyclopedia of Distances; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Wolfram, S. Cellular automaton fluids 1: Basic theory. J. Stat. Phys. 1986, 45, 471–526. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Zhang, R.; Staroselsky, I.; Jhon, M. Recovery of full rotational invariance in lattice Boltzmann formulations for high Knudsen number flows. Phys. A Stat. Mech. Appl. 2006, 362, 125–131. [Google Scholar] [CrossRef]
- Plouffe, S. The computation of certain numbers using a ruler and compass. J. Integer Seq. 1998, 1, 3. [Google Scholar]
- Margolius, B.H. Plouffe’s Constant is Transcendental; Citeseer: Princeton, NJ, USA, 2003. [Google Scholar]
- Weyl, H. Über die Gleichverteilung von Zahlen mod. eins. Math. Ann. 1916, 77, 313–352. [Google Scholar] [CrossRef] [Green Version]
- Smith, W.D. Pythagorean triples, rational angles, and space-filling simplices. Preprint 2003. [Google Scholar]
- Einstein, A. Zur Elektrodynamik bewegter Körper. Annalen Phys. 1905, 4, 1–28. [Google Scholar] [CrossRef]
- Minkowski, H. Raum und Zeit. Jahresber. Dtsch. Math.-Ver. 1909, 18, 75–88. [Google Scholar]
- Poincaré, H. On the dynamics of the electron, Rend. Circolo Mat. Palermo 1906, 21, 129–176. [Google Scholar] [CrossRef]
- Lorentz, H.A. Electromagnetic phenomena in a system moving with any velocity less than that of light p. 809 in. Proc. Acad. Sci. Amst. 1904, 6, 172–197. [Google Scholar]
- Li, M.; Vitányi, P. An Introduction to Kolmogorov Complexity and Its Applications; Springer: Berlin/Heidelberg, Germany, 2008; Volume 3. [Google Scholar]
- Beltrami, E. Teoria fondamentale degli spazii di curvatura costante. Ann. Mat. Pura Appl. 1868, 2, 232–255. [Google Scholar] [CrossRef] [Green Version]
- Thomas, L.H. The motion of the spinning electron. Nature 1926, 117, 514. [Google Scholar] [CrossRef]
- Wigner, E. On unitary representations of the inhomogeneous Lorentz group. Ann. Math. 1939, 40, 149–204. [Google Scholar] [CrossRef]
- Leuenberger, G. Tree of Lorentz Boosts in Poincare Disk Model. 2021. GitHub Repository. Available online: https://github.com/Leuenberger/Tree-of-Lorentz-Boosts-in-Poincare-Disk-Model (accessed on 20 December 2021).
- Varona, J.L. Rational values of the arccosine function. Cent. Eur. J. Math. 2006, 4, 319–322. [Google Scholar] [CrossRef]
- Levine, D.; Steinhardt, P.J. Quasicrystals: A new class of ordered structures. Phys. Rev. Lett. 1984, 53, 2477. [Google Scholar] [CrossRef] [Green Version]
- Penrose, R. Pentaplexity a class of non-periodic tilings of the plane. Math. Intell. 1979, 2, 32–37. [Google Scholar] [CrossRef]
- Dewitt, B.S.; Everett, H.; Graham, N. The many-worlds interpretation of quantum mechanics. In The Many-Worlds Interpretation of Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 1973. [Google Scholar]
- Lloyd, S. A theory of quantum gravity based on quantum computation. arXiv 2005, arXiv:quant-ph/0501135. [Google Scholar]
- Konopka, T.; Markopoulou, F.; Smolin, L. Quantum graphity. arXiv 2006, arXiv:hep-th/0611197. [Google Scholar]
- Konopka, T.; Markopoulou, F.; Severini, S. Quantum graphity: A model of emergent locality. Phys. Rev. D 2008, 77, 104029. [Google Scholar] [CrossRef] [Green Version]
- Rovelli, C. Black hole entropy from loop quantum gravity. Phys. Rev. Lett. 1996, 77, 3288. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).