A Novel Approach to β-Decay: PANDORA, a New Experimental Setup for Future In-Plasma Measurements
Abstract
1. Introduction
2. Impact in Astrophysical Scenarios
3. Experimental Method
- A buffer plasma is created using He, O, or Ar gas at densities of 1012–1013 atoms/cm3.
- The isotope is then directly injected (if gaseous) or vaporized by appropriate ovens in the chamber to be turned into a plasma state.
- Relative abundances of buffer vs. isotope densities range from 100:1 (for isotopes in metallic state) to 3:1 (for gaseous elements).
- The plasma is maintained in a dynamic equilibrium by equalizing input fluxes of the particles to the losses from the magnetic confinement. This can be achieved when the plasma operates in magneto-hydrodynamic equilibrium under proper tuning conditions of the magnetic field profile, background pressure, and radiofrequency (RF) power; an accuracy of about 7% (estimated using the fastest response diagnostics, i.e., soft-X ray spectroscopy, see Table 2) can be achieved in terms of the maximal fluctuation of the main plasma parameters, which are deemed to be sufficient to get a good overall sensitivity in the measurement of the radioactive isotope decay.
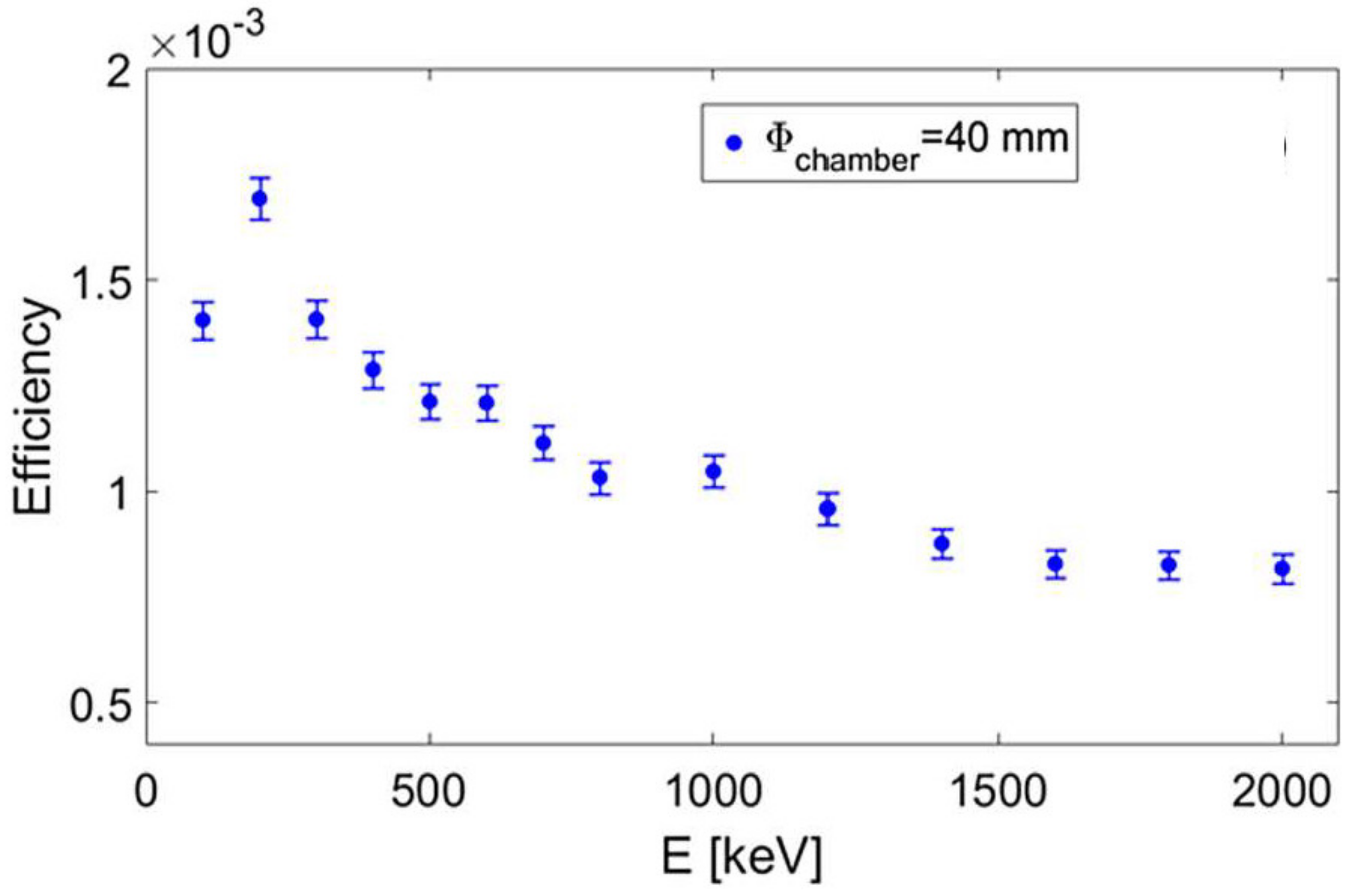
- After the β-decay, the daughter nuclei, still confined in the plasma, emit γ-rays, which are detected through an array of HPGe detectors placed around the magnetic trap.
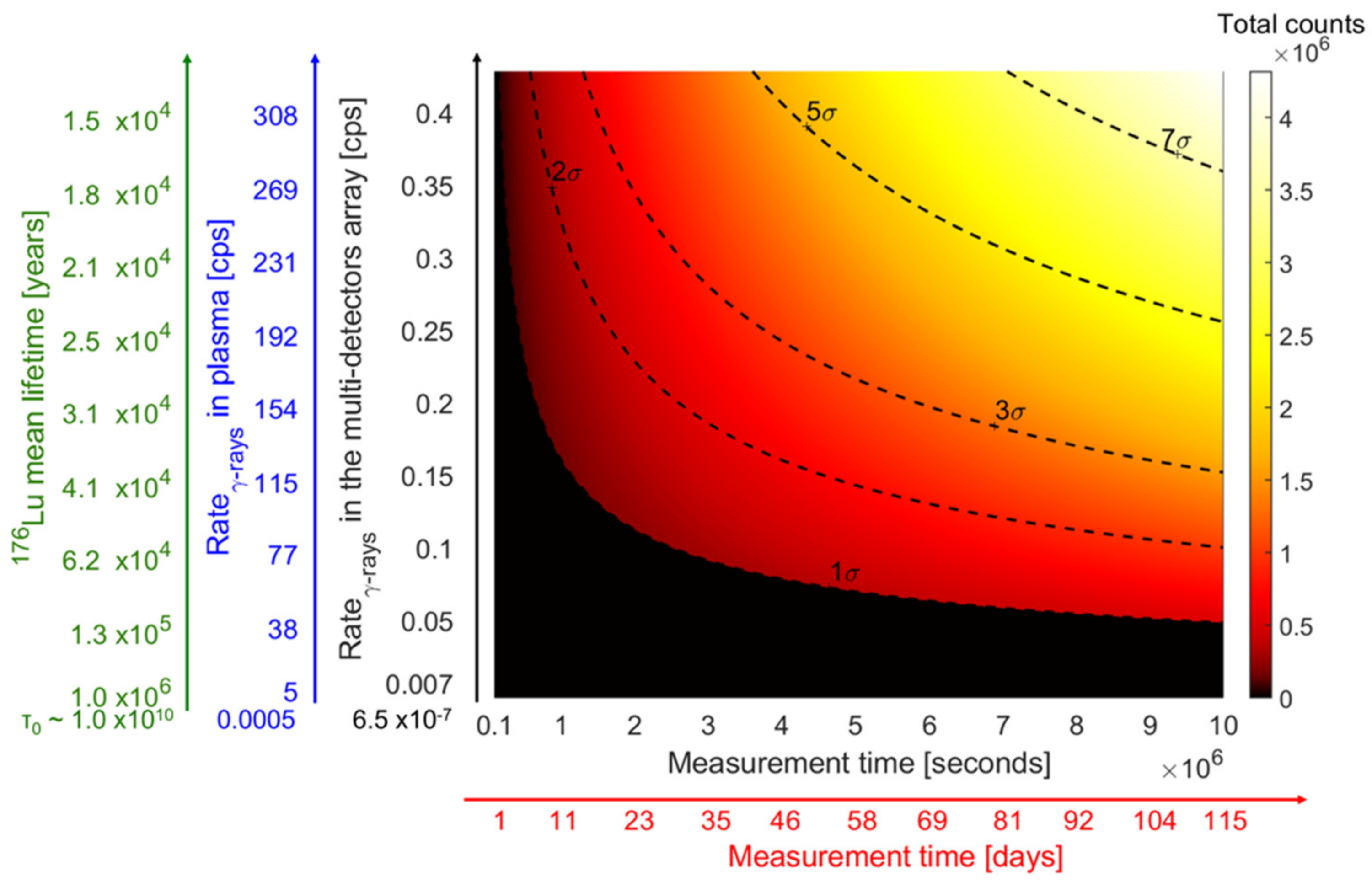
- The in-plasma measured radioactivity is directly correlated to the plasma density and temperature, which will be monitored by a multi-diagnostics setup.
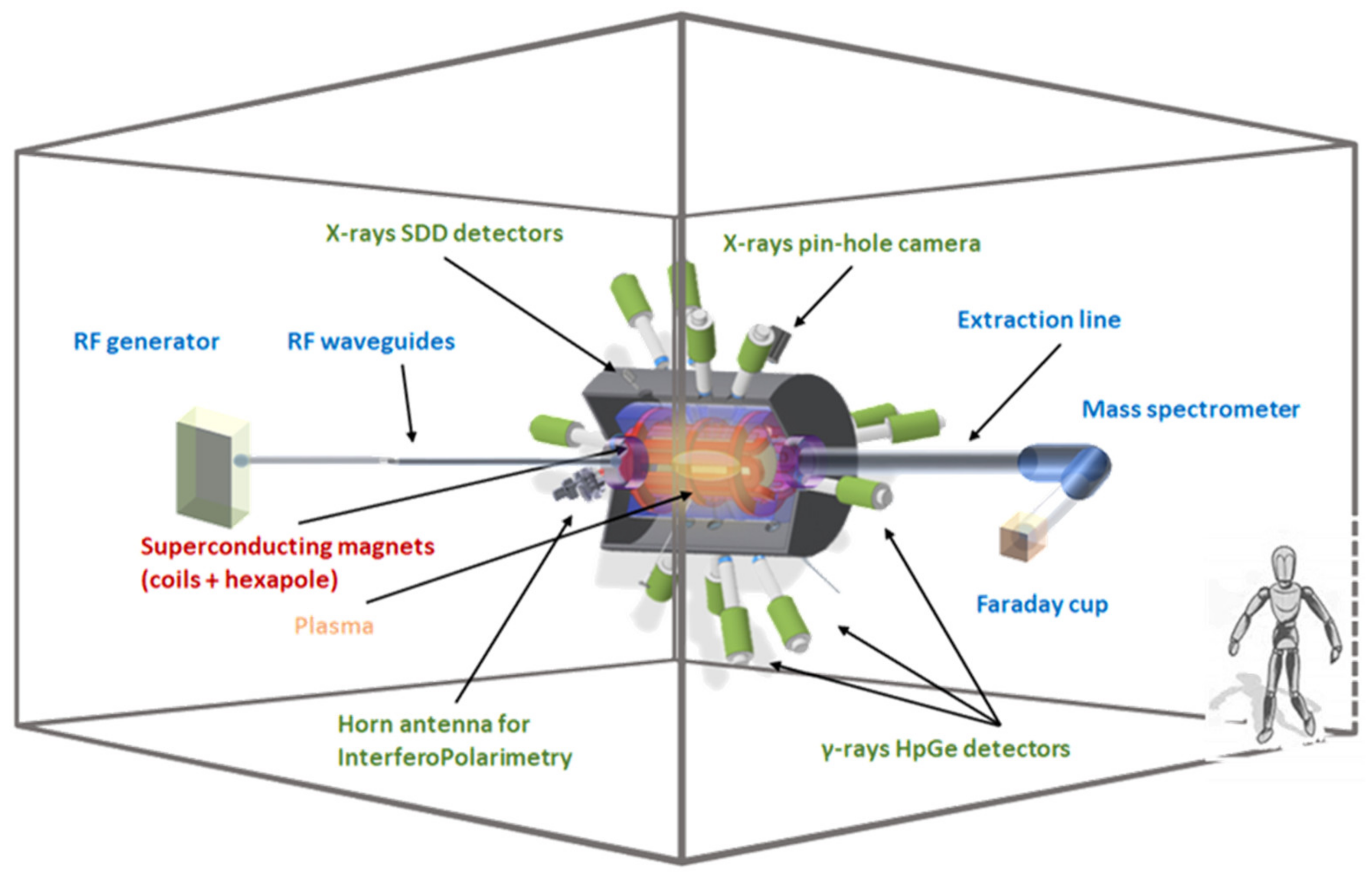
3.1. Experimental Setup
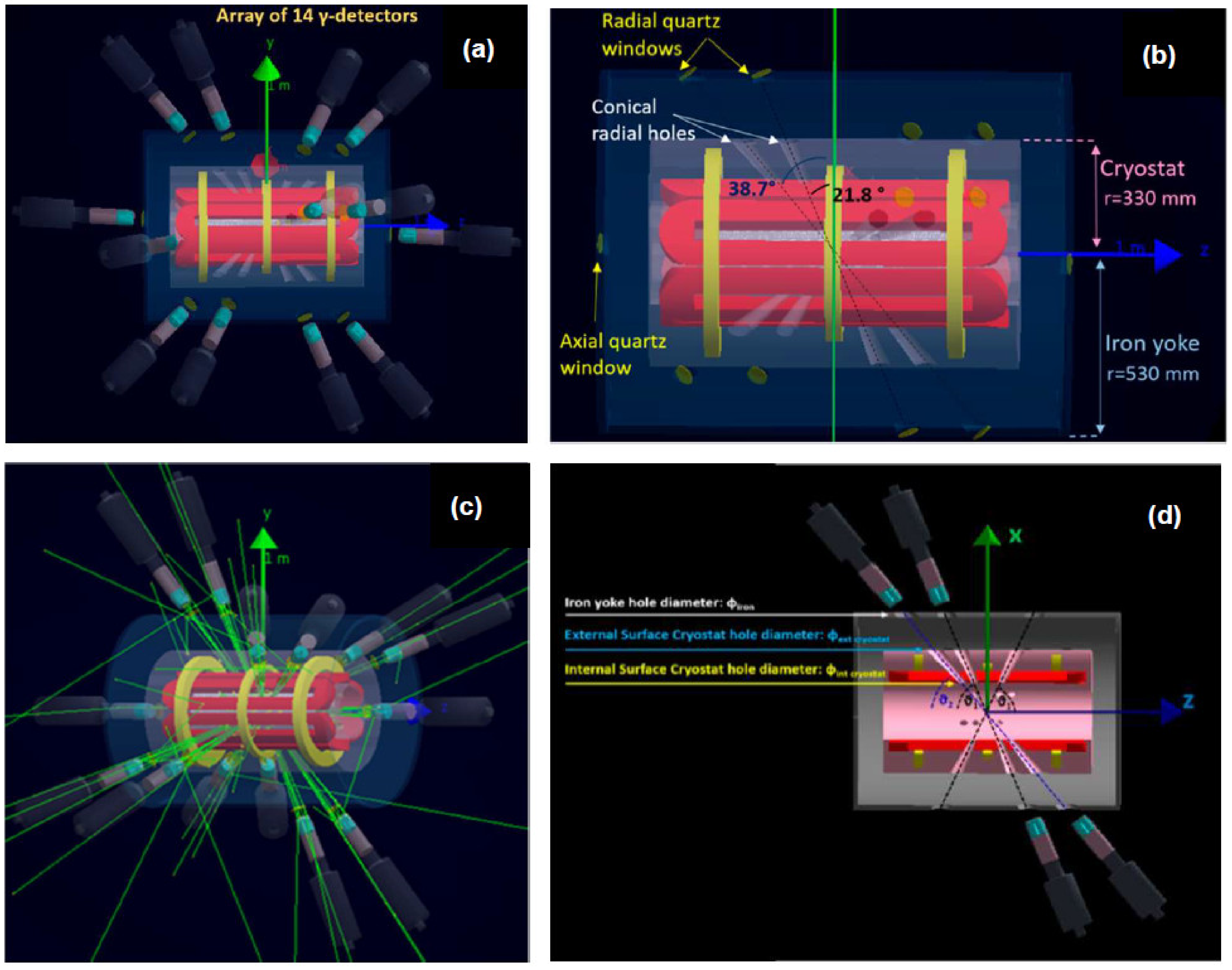
3.1.1. Magnetic Trap
- # 3 solenoids for axial confinement; and
- # 6 hexapole coils for radial confinement, the hexapole being coaxial with the solenoids.
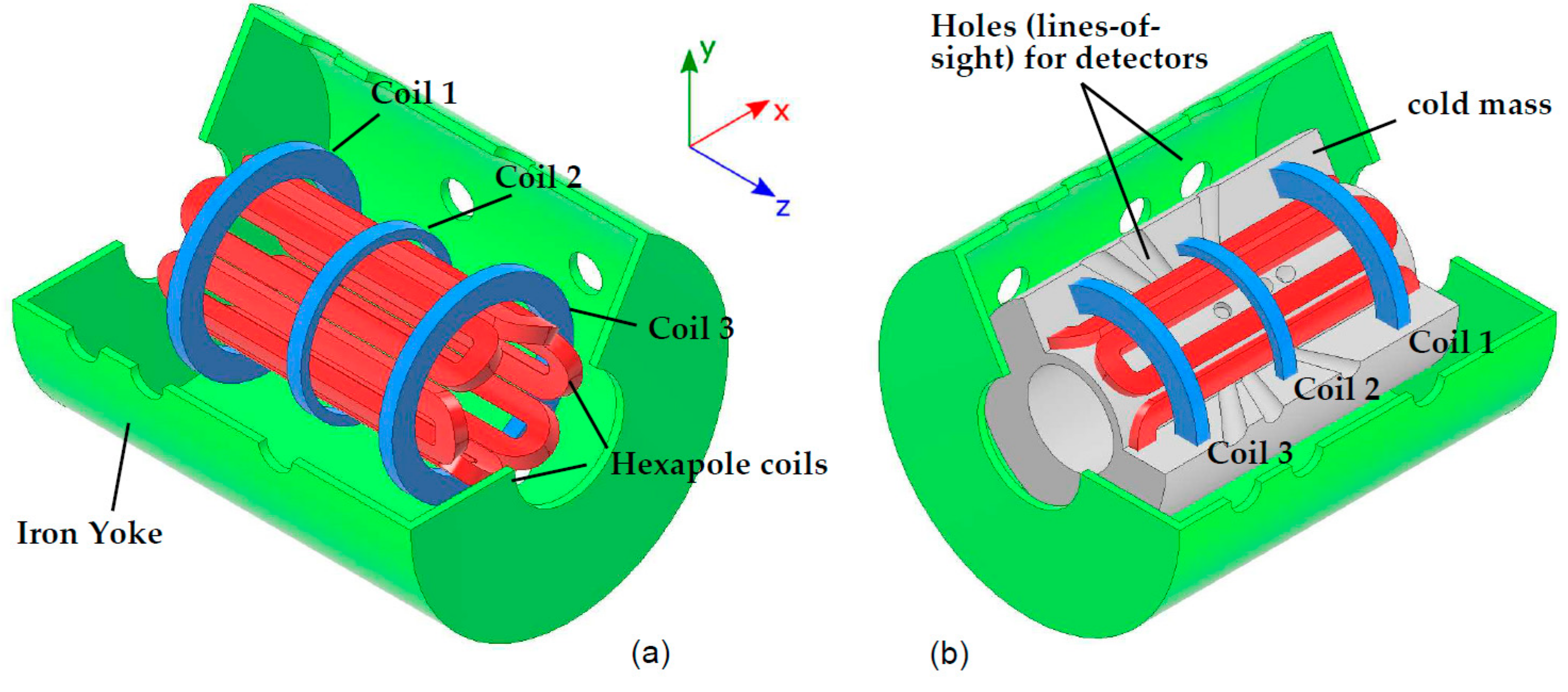
3.1.2. Isotope Injection System
3.1.3. HPGe Gamma Ray Detectors’ Array
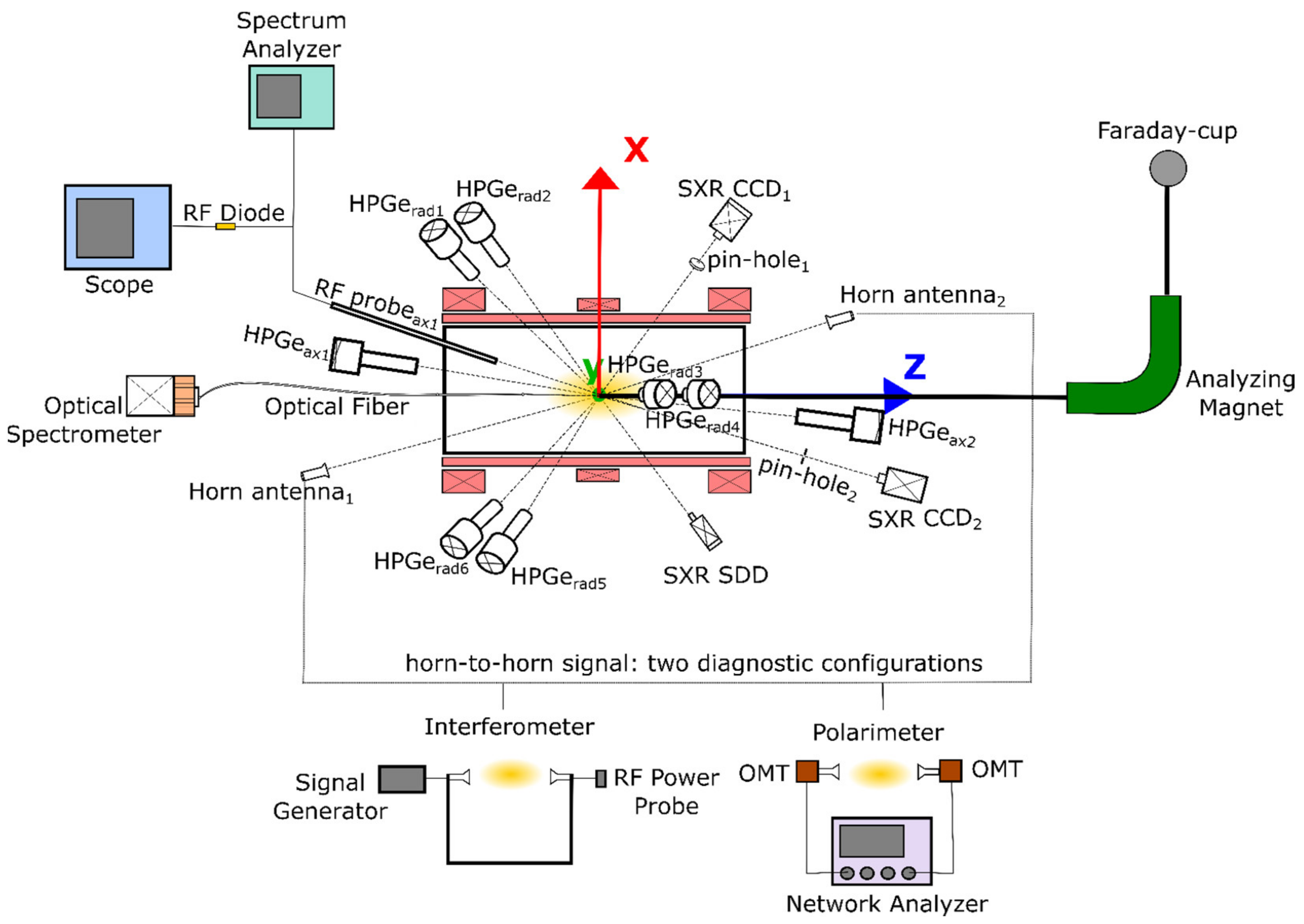
3.1.4. Multi-Diagnostic System
- A High-purity Germanium (HPGe) detector for spectral temperature measurement of hard X-rays, including time-resolved spectroscopy.
- A Silicon Drift Detector (SDD) for plasma density and temperature measurements in the warm electron domain.
- Two X-rays pin-hole cameras for 2D space-resolved spectroscopy. Recent developments have also allowed investigating the intensity of the electron losses [20].
- A camera and spectrometer for the plasma-emitted visible light characterization with a resolution of R = 13,900 (Δλ = 0.035 nm) at λ = 486 nm.
- A two-pins’ RF probe installed inside the plasma chamber in the injection plate, connected to a Spectrum Analyzer (SA) in order to detect the plasma-emitted EM wave in GHz ranges [21].
- A RF probe connected with a diode and an oscilloscope in order to obtain the time-resolved (but totally integrated) power emitted from the plasma; this value will be used as a trigger signal for instability signature and to perform time-resolved X-ray analysis, via an 80-Gs/s-20-GHz bandwidth oscilloscope.
- A microwave Interferometer and a Microwave Polarimeter for line-integrated total density measurement.
- The spectrograph SARG (Spettrografo Alta Risoluzione Galileo) [22] will be able to reach a very high resolution: R = λ/Δλ = 160.000, in the range: 370–900 nm, suitable to discriminate plasma-emitted spectra coming from different charge state distributions.
- SARG will operate in addition to the spectrometer by HORIBA© of nominal resolution around 35 picometers (R = 13,900 at λ = 486 nm) that has been already commissioned as a “bridging-the-gap” instrument supporting SARG.
- Concerning X-ray measurements, the INFN-LNS in collaboration with ATOMKI-laboratories (Institute of Nuclear Research, Hungary) recently completed the development of a new Single Photon Counting (SPhC) images’ analysis algorithm, in order to perform pixel-by-pixel energy-resolved investigations [23].
- Microwave Imaging Profilometry (MIP), devoted to an online measurement of local values of the electron density, was successfully experimented on the ECRIS-like trap ([24,25]). MIP requires the use of probing frequencies much higher than the cyclotron resonance and well above the plasma frequency. Taking into account expected peak values of 1012–1013 cm−3 electron density at an ECR frequency of 18 GHz, the so-called V frequency band (50–75 GHz) and W-band (75–110 GHz) can be exploited to reconstruct on-line the plasma shape. This system can be synergic with the polarimeter already planned in the PANDORA multi-diagnostic system.
- An alternative technique for investigating the absolute plasma density, the electron energy distribution functions, and even the electron global drift velocity, is Incoherent Thomson Scattering (ITS). This non-invasive and direct technique, which relies on the scattering of an electromagnetic field on free charges, has a long history of application in the study of diverse high- and low-temperature plasmas. It is now possible to achieve unprecedented sensitivity (measurements in plasma environments with electron densities as low as 1010 cm−3). The implementation of a recently developed sensitive diagnostic of this type, known as THETIS [26], will be performed. This technique will be well-suited to the measurement of electron temperatures in the hundreds of eV range, with a potential measurement sensitivity < 1 eV and volumetric resolution on the order of 1 mm3. The planned implementation will validate the method as a future diagnostic for PANDORA and also provide key electron property measurements in density and temperature ranges, which will complement the capabilities of other non-invasive diagnostic tools used for electron characterization.
4. First Physics’ Cases
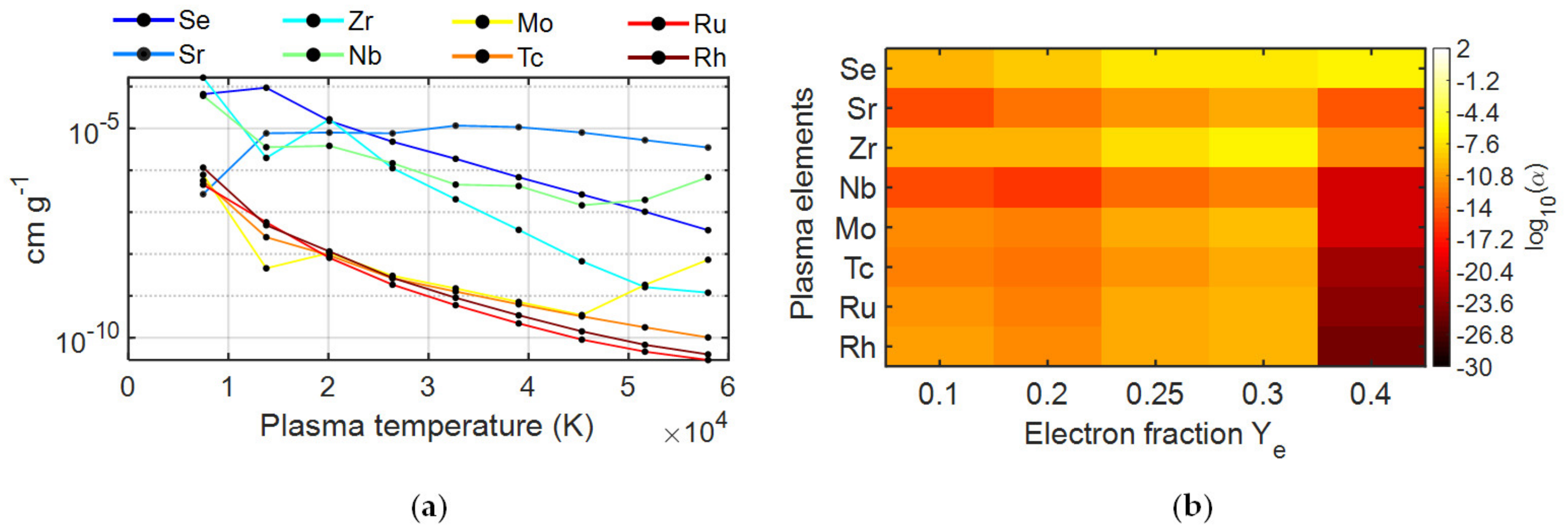
Study of Plasma Opacity for Compact Binary Objects
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Emery, G.T. Perturbation of nuclear decay rates. Ann. Rev. Nucl. Sci. 1972, 22, 165–202. [Google Scholar] [CrossRef]
- Simonucci, S.; Taioli, S.; Palmerini, S.; Busso, M. Theoretical estimates of Stellar e–Captures. I. The half-life of 7Be in evolved stars. Astrophys. J. 2013, 764, 118. [Google Scholar] [CrossRef]
- Bahcall, J.N. Theory of Bound-State Beta Decay. Phys. Rev. 1961, 124, 495. [Google Scholar] [CrossRef]
- Bosch, F.; Faestermann, T.; Friese, J.; Heine, F.; Kienle, P.; Wefers, E.; Zeitelhack, K.; Beckert, K.; Franzke, B.; Klepper, O.; et al. Observation of bound state β decay of fully ionized 187Re: 187Re–187Os cosmochronometry. Phys. Rev. Lett. 1996, 77, 5190. [Google Scholar] [CrossRef] [PubMed]
- Jung, M.; Bosch, F.; Beckert, K.; Eickhoff, H.; Folger, H.; Franzke, B.; Gruber, A.; Kienle, P.; Klepper, O.; Koenig, W.; et al. First observation of bound state β decay. Phys. Rev. Lett. 1992, 69, 2164. [Google Scholar] [CrossRef]
- Mascali, D.; Busso, M.; Mengoni, A.; Amaducci, S.; Guiseppe, C.; Celona, L.; Cosentino, G.; Cristallo, S.; Finocchiaro, P.; Galata, A.; et al. The PANDORA project: An experimental setup for measuring in-plasma β-decays of astrophysical interest. EPJ Web Conf. 2020, 227, 01013. [Google Scholar] [CrossRef]
- Mascali, D.; Musumarra, A.; Leone, F.; Romano, F.P.; Galata, A.; Gammino, S.; Massimi, C. PANDORA, a new facility for interdisciplinary in-plasma physics. Eur. Phys. J. A 2017, 53, 145. [Google Scholar] [CrossRef]
- Metzger, B. FRIB Summer School Lecture on “Kilonovae”. 2018. Available online: https://indico.fnal.gov/event/15789/attachments/20936/26096/Metzger_FRIB_kilonovae.pdf (accessed on 14 May 2018).
- Burbidge, M.E.; Burbidge, G.R.; Fowler, W.A.; Hoyle, F. Synthesis of the elements in stars. Rev. Mod. Phys. 1957, 29, 547. [Google Scholar] [CrossRef]
- Litvinov, Y.; Bosch, F. Beta decay of highly charged ions. Rep. Progr. Phys. 2011, 74, 016301. [Google Scholar] [CrossRef]
- Tanaka, M.; Kato, D.; Gaigalas, G.; Kawaguchi, K. Systematic opacity calculations for Kilonovae. Mon. Not. R. Astron. Soc. 2020, 496, 1369. [Google Scholar] [CrossRef]
- Galatà, A.; Roncolato, C.; Bisoffi, G.; Francescon, P.; Bellan, L.; Bermudez, J.; Bortolato, D.; Comunian, M.; Conte, A.; De Lazzari, M.; et al. Towards the first beams from the ADIGE injector for the SPES Project. J. Phys. Conf. Ser. 2019, 1350, 01209. [Google Scholar] [CrossRef]
- Tinschert, K.; Lang, R.; Mäder, J.; Maimone, F.; Roßbach, J. Metal ion beam production with improved evaporation ovens. In Proceedings of the 20th International Workshop on Electron Cyclotron Resonance Ion Sources (ECRIS-2012), JaCoW-WEPP15, Sydney, Australia, 25–28 September 2012. [Google Scholar]
- Agostinelli, S.; Allison, J.; Amako, K.A.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.J.N.I.; et al. GEANT4—A Simulation Toolkit. Nucl. Inst. Meth. A 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Naselli, E.; Mascali, D.; Caliri, C.; Castro, G.; Celona, L.; Galata, A.; Gammino, S.; Mazzaglia, M.; Romano, F.P.; Guiseppe, T.; et al. Nuclear β-decays in plasmas: How to correlate plasma density and temperature to the activity. EPJ Web Conf. 2020, 227, 02006. [Google Scholar] [CrossRef][Green Version]
- Goasduff, A.; Mengoni, D.; Recchia, F.; Valiente-Dobon, J.J.; Menegazzo, R.; Benzoni, G.; Barrientos, D.; Bellato, M.; Bez, N.; Biasotto, M.; et al. The GALILEO g-ray array at the Legnaro National Laboratories. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2021, 1015, 165753. [Google Scholar] [CrossRef]
- Geller, R. Electron Cyclotron Resonance Ion Sources and ECR Plasmas; PA Institute of Physics: Philadelphia, PA, USA, 1996. [Google Scholar]
- Naselli, E.; Mascali, D.; Biri, S.; Caliri, C.; Castro, G.; Celona, L.; Consetino, L.G.; Galata, A.; Gammino, S.; Giarrusso, M.; et al. Multidiagnostics setups for magnetoplasmas devoted to astrophysics and nuclear astrophysics research in compact traps. J. Instrum. 2019, 14, C10008. [Google Scholar] [CrossRef]
- Biri, S.; Palinkas, J.; Perduk, Z.; Racz, R.; Caliri, C.; Castro, G.; Celona, L.; Gammino, S.; Mazzaglia, M.; Naselli, E.; et al. Multi diagnostic setup at the Atomki-ECRIS to investigate the two-close-frequency heating phenomena. J. Instrum. 2018, 13, C11016. [Google Scholar] [CrossRef]
- Naselli, E.; Racz, R.; Biri, S.; Mazzaglia, M.; Galata, A.; Celona, L.; Gammino, S.; Torrisi, G.; Mascali, D. Quantitative analysis of an ECR Ar plasma structure by X-ray spectroscopy at high spatial resolution. J. Instrum. 2022, 17, C01009. [Google Scholar]
- Torrisi, G.; Mascali, D.; Sorbello, G.; Castro, G.; Celona, L.; Gammino, S. Numerical and experimental characterization of RF waves propagation in ion sources magnetoplasmas. IEEE Trans. Antennas Propagat. 2019, 67, 2142. [Google Scholar] [CrossRef]
- Giarrusso, M.; Avila, G.; Del Zanna, G.; Landi, E.; Leone, F.; Munari, M.; Castro, G.; Celona, L.; Gammino, S.; Mascali, D.; et al. High resolution spectropolarimetry: From Astrophysics to ECR plasmas. J. Instrum. 2018, 13, C11020. [Google Scholar] [CrossRef]
- Naselli, E.; Racz, R.; Biri, S.; Mazzaglia, M.; Celona, L.; Gammino, S.; Torrisi, G.; Perduk, Z.; Galata, A.; Mascali, D. Innovative Analytical Method for X-Ray Imaging and Space-Resolved Spectroscopy of ECR Plasmas. Condens. Matter 2022, 7, 5. [Google Scholar] [CrossRef]
- Di Donato, L.; Morabito, A.F.; Torrisi, G.; Isernia, T.; Sorbello, G. Electromagnetic Inverse Profiling for Plasma Diagnostics via Sparse Recovery Approaches. IEEE Trans. Plasma Sci. 2019, 47, 1781–1787. [Google Scholar] [CrossRef]
- Di Donato, L.; Mascali, D.; Morabito, A.F.; Sorbello, G. A Finite-Difference Approach for Plasma Microwave Imaging Profilometry. J. Imaging 2019, 5, 70. [Google Scholar] [CrossRef] [PubMed]
- Vincent, B.; Tsikata, S.; Mazouffre, S.; Minea, T.; Fils, J. A compact new incoherent Thomson scattering diagnostic for low-temperature plasma studies. Plasma Sources Sci. Technol. 2018, 27, 055002. [Google Scholar] [CrossRef]
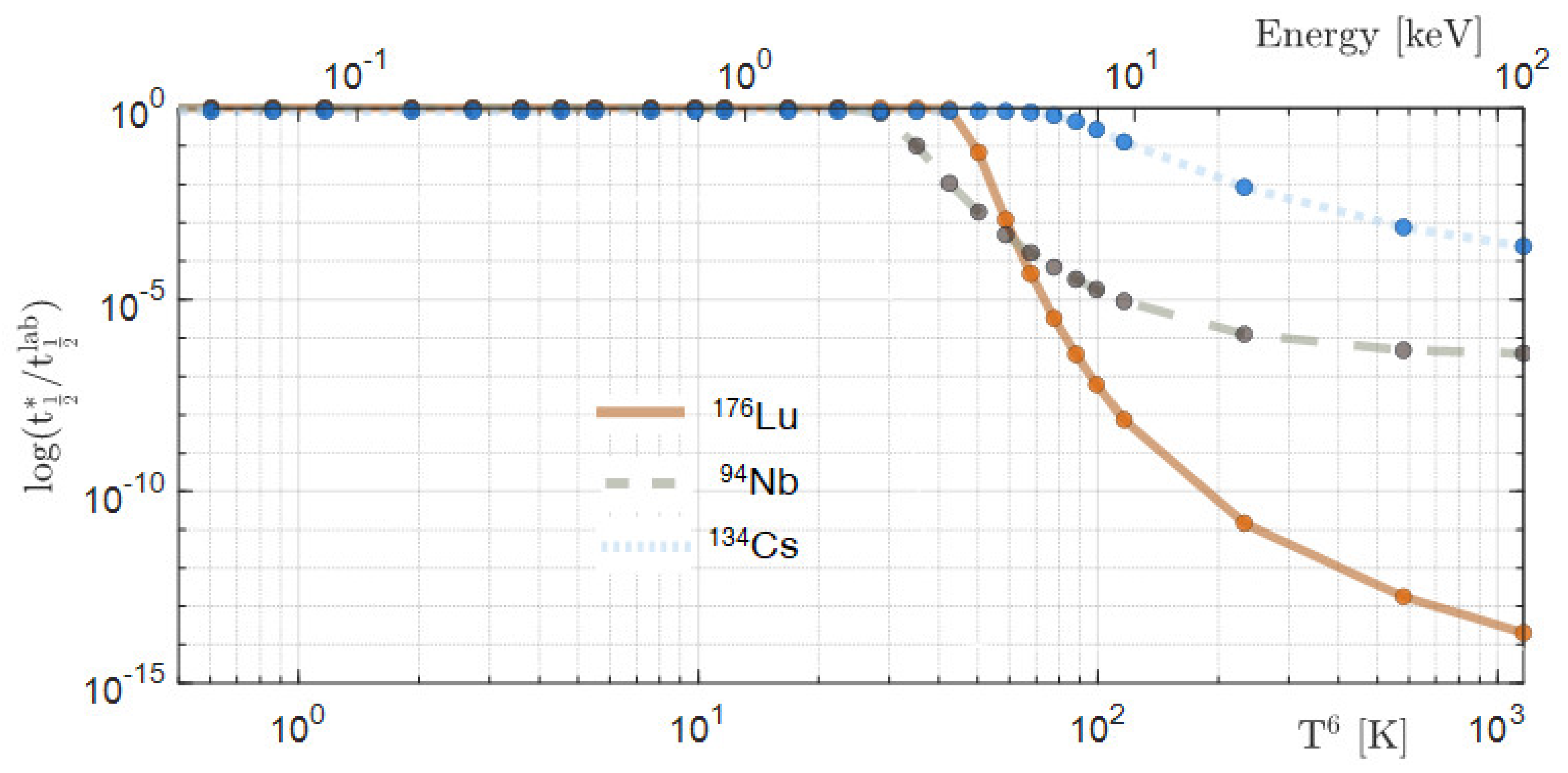
- Takahashi, K.; Yokoi, K. Beta-Decay Rates of Highly Ionized Heavy Atoms in Stellar Interiors. At. Data Nucl. Data Tables 1983, 36, 375. [Google Scholar] [CrossRef]
- Klay, N.; Käppeler, F.; Beer, H.; Schatz, G.; Börner, H.; Hoyler, F.; Robinson, S.J.; Schreckenbach, K.; Krusche, B.; Mayerhofer, U.; et al. Nuclear structure of 176Lu and its astrophysical consequences. I. Level scheme of 176Lu. Phys. Rev. C 1991, 44, 2801. [Google Scholar] [CrossRef] [PubMed]
- Klay, N.; Käppeler, F.; Beer, H.; Schatz, G. Nuclear structure of 176Lu and its astrophysical consequences II. 176Lu, a thermometer for stellar helium burning. Phys. Rev. C 1991, 44, 2839. [Google Scholar] [CrossRef]
- Palmerini, S.; Busso, M.; Vescovi, D.; Naselli, E.; Pidatella, A.; Mucciola, R.; Cristallo, S.; Mascali, D.; Mengoni, A.; Simonucci, S.; et al. Presolar Grain Isotopic Ratios as Constraints to Nuclear and Stellar Parameters of Asymptotic Giant Branch Star Nucleosynthesis. Astrophys. J. 2021, 921, 7. [Google Scholar] [CrossRef]
- Taioli, S.; Vescovi, D.; Busso, M.; Palmerini, S.; Cristallo, S.; Mengoni, A.; Simonucci, S. Theoretical estimate of the half-life for the radioactive 134Cs and 135Cs in astrophysical scenarios. arXiv 2021, arXiv:2109.14230. [Google Scholar]
- Cristallo, S.; Straniero, O.; Gallino, R.; Piersanti, L.; Dominguez, I.; Lederer, M.T. Evolution, Nucleosynthesis, and Yields of Low-mass Asymptotic Giant Branch Stars at Different Metallicities. II. The FRUITY Database. Astrophys. J. Suppl. 2011, 197, 17. [Google Scholar] [CrossRef]
- Busso, M.; Gallino, R.; Wasserburg, G.J. Nucleosynthesis in Asymptotic Giant Branch Stars: Relevance for Galactic Enrichment and Solar System Formation. Ann. Rev. Astron. Astrophys. 1999, 37, 239. [Google Scholar] [CrossRef]
- Burns, E. Neutron star mergers and how to study them. Living Rev. Relativ. 2020, 23, 1–177. [Google Scholar] [CrossRef]
- Pidatella, A.; Cristallo, S.; Galata, A.; La Cognata, M.; Mazzaglia, M.; Perego, A.; Tumino, A.; Vescovi, D.; Mascali, D. In Plasma study of opacity relevant for compact binary ejecta. Nuovo Cim. C 2021, 44, 65. [Google Scholar]
- Lippuner, J.; Roberts, L.F. SkyNet: A Modular Nuclear Reaction Network Library. Astrophys. J. Suppl. 2017, 233, 18. [Google Scholar] [CrossRef]
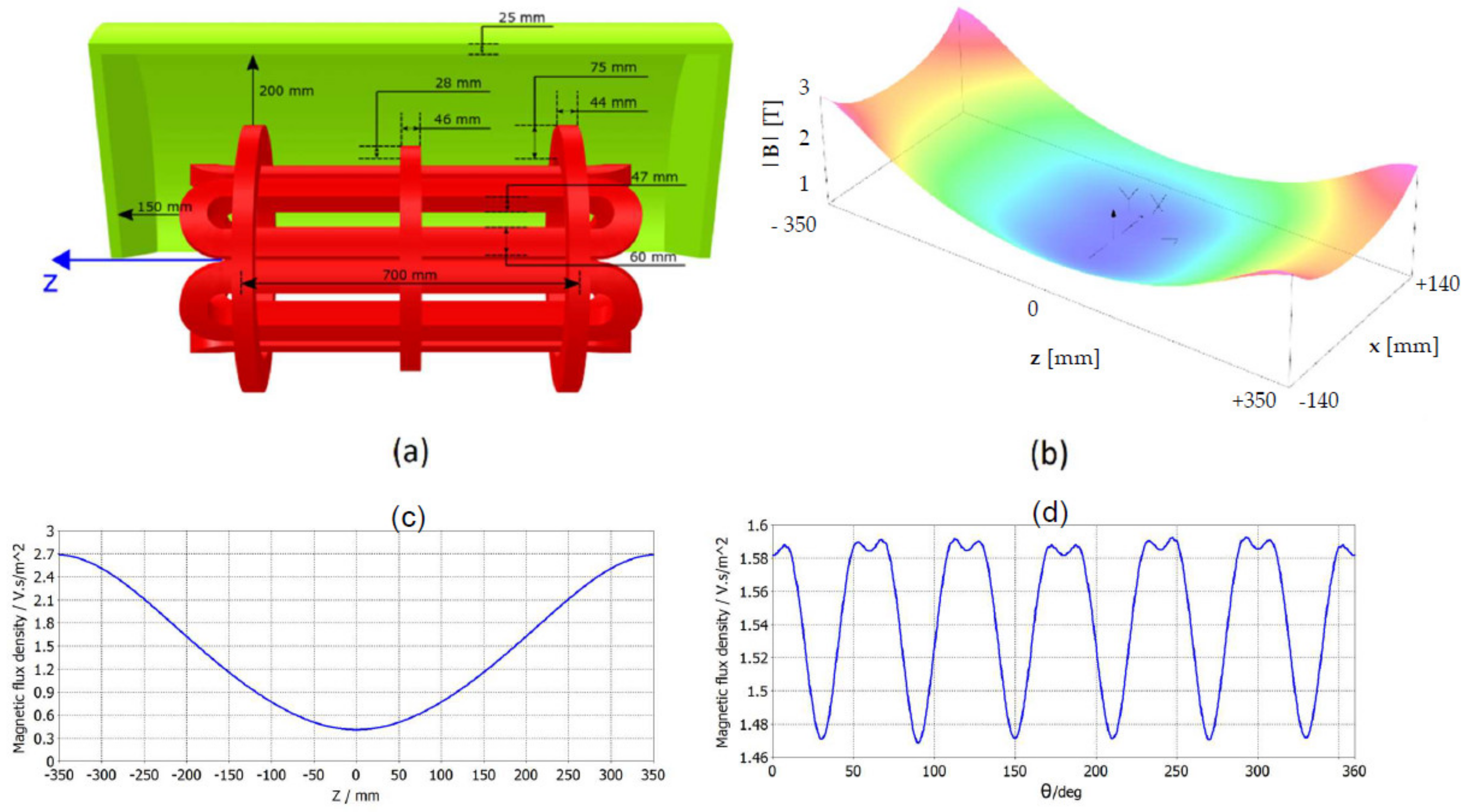
| Magnetic System Field Specifications | |
|---|---|
| Binj max @ z = −350 mm Binj operative range | 3 T 1.7 T–3 T |
| Bext max @ z = 350 mm Bext operative range | 3 T 1.7 T–3 T |
| Bmin @ z = 0 mm | 0.4 T |
| Bhex @ RCH_IN = 140 mm Liquid He | 1.6 T Free |
| Diagnostic Tool | Sensitive Range | Measurement | Resolution-Measure Error |
|---|---|---|---|
| SDD | 1 ÷ 30 keV | Volumetric soft X-ray Spectroscopy: warm electrons’ temperature and density | Resolution~120 eV εne~7%, εTe~5% |
| HPGe detector | 30 ÷ 2000 keV | Volumetric hard X-ray Spectroscopy: | FWHM @ 1332.5 keV < 2.4 keV |
| hot electrons’ temperature and density | εne ~7%, εTe~5% | ||
| Visible Light Camera | 1 ÷ 12 eV | Optical Emission Spectroscopy: cold electrons’ temperature and density | Δλ = 0.035 nm R = 13900 |
| X-ray pin-hole camera | 2 ÷ 15 keV | 2D Space-resolved spectroscopy: soft X-ray Imaging and plasma structure | Energy Resolution~0.3 keV Spatial Resolution~0.5 mm |
| W-band super-heterodyne polarimeter | W-band 90 ÷ 100 GHz | Plasma-induced Faraday rotation: line-integrated electron density | εne~25% |
| Microwave Imaging Profilometry (MIP) | 60 ÷ 100 GHz | Electron density profile | εne ~1% ÷ 13% |
| Multi-pins RF probe Multi-pins RF probe + Spectrum Analyzer (SA) Multi-pins RF probe + Scope + HPGe detector | 10 ÷ 26.5 GHz 10 ÷ 26.5 GHz (probe range) 10 ÷ 26.5 GHz (probe range) | Local EM field intensity Frequency-domain RF wave Time-resolved radiofrequency burst and X-ray time-resolved Spectroscopy | ε~0.073 ÷ 0.138 dB SA Resolution bandwidth: RBW = 3 MHz 80 Gs/s (scope) time scales below ns |
| Thomson Scattering | 0.5 ÷ 500 eV | EEDF, absolute electron density global electron drift velocity | Condition-dependent (a function of spectral width, dependent on temperature, and area, dependent on density) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mascali, D.; Santonocito, D.; Amaducci, S.; Andò, L.; Antonuccio, V.; Biri, S.; Bonanno, A.; Bonanno, V.P.; Briefi, S.; Busso, M.; et al. A Novel Approach to β-Decay: PANDORA, a New Experimental Setup for Future In-Plasma Measurements. Universe 2022, 8, 80. https://doi.org/10.3390/universe8020080
Mascali D, Santonocito D, Amaducci S, Andò L, Antonuccio V, Biri S, Bonanno A, Bonanno VP, Briefi S, Busso M, et al. A Novel Approach to β-Decay: PANDORA, a New Experimental Setup for Future In-Plasma Measurements. Universe. 2022; 8(2):80. https://doi.org/10.3390/universe8020080
Chicago/Turabian StyleMascali, David, Domenico Santonocito, Simone Amaducci, Lucio Andò, Vincenzo Antonuccio, Sándor Biri, Alfio Bonanno, Vincenza Piera Bonanno, Stefan Briefi, Maurizio Busso, and et al. 2022. "A Novel Approach to β-Decay: PANDORA, a New Experimental Setup for Future In-Plasma Measurements" Universe 8, no. 2: 80. https://doi.org/10.3390/universe8020080
APA StyleMascali, D., Santonocito, D., Amaducci, S., Andò, L., Antonuccio, V., Biri, S., Bonanno, A., Bonanno, V. P., Briefi, S., Busso, M., Celona, L., Cosentino, L., Cristallo, S., Cuffiani, M., De Angelis, C., De Angelis, G., De Salvador, D., Di Donato, L., Ducret, J.-E., ... Vincetti, L. (2022). A Novel Approach to β-Decay: PANDORA, a New Experimental Setup for Future In-Plasma Measurements. Universe, 8(2), 80. https://doi.org/10.3390/universe8020080


















