1. Introduction
General relativity (GR) is a very remarkable and astonishing theory that has resolved many issues since its birth. It is considered a pillar of modern physics and has revolutionized the understanding of the universe. The gravitational red shift, precession of the perihelion of Mercury, and light bending by the Sun are predicted by GR. Although it is no exaggeration to say that GR is the most successful theory, many issues are still unresolved. Some of the most important unresolved issues are the localization of energy and the singularity problem, etc. In addition, the most fundamental and fascinating theoretical problem of the 21st century is considered to be the current accelerating expansion of the universe or dark energy problem. Initially, Einstein believed that the universe is neither expanding nor contracting but static. In order to show this behavior of the universe, Einstein modified the field equations by adding a cosmological constant, . Later on (1929), Hubble performed an experiment on more than twenty galaxies and observed that light coming from these galaxies is red-shifted, which shows that the universe is expanding. After this, Einstein admitted that his idea of the static universe was the largest blunder of his life. Consequently, he removed from the field equations.
Recent observations of astrophysics and modern cosmology, such as cosmic microwave background radiations, supernovae surveys, and large-scale structures of our universe [
1,
2,
3,
4], indicate that, at present, the universe is expanding with acceleration. The energy composition of the universe was found to be 4.9% of ordinary baryonic matter, 26.8% of dark matter (DM), and 68.3% of dark energy (DE). The description provided by GR may need to be modified to understand these observational data. There are several approaches to describe the cosmic acceleration, among which the inclusion of the cosmological constant in Einstein’s field equations is one of the primary models used for this purpose. The term DM means a form of matter that is unknown and cannot be deducted by its radiation but the gravitational force is exerted by it. Dark energy refers to unknown energy and an exotic substance having large negative pressure. The cosmological constant is the primary and most relevant candidate of DE, which provides the most reasonable explanation of the universe. The notion of
could be used to explain the inflationary era in the early universe.
Bowers and Liang [
5] established a framework to study the effect of anisotropy on self-gravitating stars by the observer. Herrera and Santos [
6] considered the radial perturbation approach to analyze a few properties of anisotropic self-gravitating spheres. Di Prisco et al. [
7] found little but continuous variation in pressure anisotropy during the phenomenon of cracking of the relativistic celestial spherical bodies. Abreu et al. [
8] checked the impact of local anisotropy on the existence of matter distributions in GR after its departure from the state of equilibrium. They also analyzed the stability of stars with the help of tangential and radial sound speeds. Bhar et al. [
9] performed theoretical analysis on static diagonally symmetric relativistic spheres in GR and found few stable stellar models due to anisotropic pressure. Maurya and Govender [
10] performed a physical analysis of their calculated exact solutions in the formation of strange anisotropic stars. They found anisotropic pressure as an additional force in sustaining the star’s stability against cracking.
Morales and Tello-Ortiz [
11] calculated a few anisotropic solutions for the relativistic spherical structures. After performing stability tests, they inferred that their anisotropic solutions are well-behaved and well-posed. Chanda et al. [
12] found that static irrotational stellar models can be described well if such systems have a high level of anisotropic stresses around the central region. Yousaf et al. [
13,
14,
15,
16] performed mathematical modeling of radiating and non-radiating matter configurations in an environment of unequal principal stresses and found stable fluid configurations under specific parametric choices. Raposo et al. [
17] described the modeling of anisotropic self-gravitating objects and found relatively more massive and compact objects due to the presence of anisotropicity in pressure. Godani and Samanta [
18,
19] found stable anisotropic wormhole solutions in modified gravity through graphical representations. Gómez-Leyton et al. [
20] explored a stable exact model of locally anisotropic matter configurations. After computing a relation among anisotropic pressure and matter variables, they found stable regimes for spherical stars.
Hyperbolically symmetrical spacetimes (HSS) are thought to be capable of explaining many unresolved cosmological puzzles. Harrison [
21] considered HSS and obtained the corresponding analytical models through the separation of variable method. Malik et al. [
22] described the distribution of hyperbolically symmetric matter over the cylindrical geometry and presented a few numerical solutions after solving the corresponding differential equations. Gaudin et al. [
23] calculated exact analytical models of the GR equation of motion with massless scalar space and described a few characteristics of the hyperbolic metric in a vacuum. Maciel et al. [
24] explored locally isotropic solutions of interior spacetime and claimed that such an incompressible spherical solution could be treated as a unique one with a HSS background. Herrera et al. [
25] presented a HSS version of LTB geometry and explored its less complex exact solutions. Miguel [
26] studied a few characteristics of HSS and found the non-convex Cauchy temporal function for the conformal families of solutions. Cao and Wu [
27] considered the metric version of
gravity and discussed the occurrence of strong hyperbolicity under some specific gauge constraints. Recently, Herrera et al. [
25] carried out a brief study on HSS after calculating conformally flat and zero complexity solutions. They also described the physical applications by adopting a general approach in solving analytical solutions. Bhatti et al. [
28] described conformally flat solutions of HSS in static charged medium. Yousaf et al. [
29] calculated the Tolman mass of HSS and then explored the occurrence of core formation by taking the constant energy density of the matter distribution.
Structure scalars are the scalars that are obtained from the orthogonal splitting of the Riemann tensor introduced by Bel [
30]. They are related to the fundamental properties of the fluid directly. Timelike vectors are useful in order to perform orthogonal splitting of a tensor, which gives rise to three tensors, namely
, and
. The scalars corresponding to these, i.e.,
, and
, are called structure scalars [
31]. Here,
appears to be proportional to the Tolman mass density for systems in equilibrium [
32,
33]. It also controls the evolution of the expansion scalar;
gives the energy density of the fluid and
Z deals with dissipation fluxes for non-spherical systems. Because of these scalars, it is easy to deal with complex systems (as compared to vectors and tensors). This single tool deals with different aspects of the system, providing a lot of information about the evolution of the system, e.g., shear and expansion evolution, inhomogeneity, complexity, etc., can be dealt with through these structure scalars [
34,
35,
36]. Yousaf and his collaborators [
16,
37,
38,
39,
40,
41] computed the modified version of these scalars by invoking extra curvature terms and described their influences in understanding the evolutionary mechanisms of adiabatic and non-adiabatic relativistic structures. Herrera [
42] introduced a new concept of complexity factor in terms of one of these scalars for the static anisotropic spherical objects. He concluded that
plays a role in the fixing of the complexity of relativistic systems. Applications of these results were then provided for various cosmic and stellar backgrounds, first by Herrera et al. [
43,
44,
45] and then by their followers [
46,
47,
48].
This paper aims to study the effects of the cosmological constant on HSS analysis by following the procedure initially presented by Herrera et al. [
25]. After describing the metric as well as its gravitating source, I shall describe the total matter quantity of the HSS through two well-known formalisms at the
-dominated epoch in
Section 3. A few important relations among these with the matter variables will also be specified in the same section.
Section 4 is devoted to the calculation of structure scalars from the decomposition of the curvature tensor. Three different families of exact analytical models will be established for Einstein-
gravity in
Section 5. The last section will summarize our results and discussions.
2. Spatially Hyperbolic Geometry and Matter Content
I assume two different types of boundary surfaces, i.e., external and internal ones. I shall represent these with and , respectively. The hypersurface demarcates the static anisotropic fluid with the external de Sitter vacuum spacetime, while keeps the matter configuration from the central vacuole. This type of mathematical model gives rise to the formation of the central Minkowskian cavity. Such types of cosmic configurations could be effective to discuss cosmological voids and other aspects of mathematical cosmology.
I take the following form of line element as
where
, and metric variables are dependent on
r only. I assume the Eckart frame; this would keep the system’s fluid in a rest state. The above system is assumed to be coupled with the locally anisotropic fluid, which can be written mathematically as
where
is the eigenvalue of the energy momentum tensor with respect to the eigenvector
,
P is the pressure, and
is the anisotropic tensor. These can be defined through the projection tensor
as
I take the following vacuum solution of the field equation outside
with de Sitter–Schwarzschild hyperbolic spacetime as
where
, and
M are the cosmological constant, radial distance, and constant mass, respectively. I am interested in performing our analysis in the region
. It is worth noting that the space inside the black hole horizon can be well discussed through the above metric. However, the outer manifold to the black hole horizon can be described with the usual de Sitter–Schwarzschild metric. The matching of the above metric with the interior fluid requires the fulfilment of the Darmois junction conditions [
49]. These conditions facilitate the smooth joining of both the exterior and interior manifolds at
. These constraints after calculations are found as below:
Next, I adopt the Bondi approach [
50] to obtain HSS from the generic formulation of the axial static symmetric manifold. I define the locally Minkowskian frame (LMF) associated with the tetrad field as
Here, I use the breve notation to indicate that the terms are estimated by an observer residing in LMF. Then, the associated stress–energy tensor is described through principal stresses
, and
as follows:
Such a type of configuration is found to produce axially symmetric gravitational geometry. It is noticed that the HSS experienced
along with the null contribution of
. In the environment of the Minkowskian frame, the four vector are defined as below:
With the help of these vectors, one can elaborate the fluid distribution mathematically as
Thus, the back-transformation to
in LMF provides the following form of matter content for HSS as
where
in the comoving reference frame and
. The smooth joining of locally anisotropic HSS matter content with the Minkowski metric at the internal boundary can be dealt with using Darmois conditions [
49]. These are found after a few calculations as below:
Here, the matter content is compelled not to follow inward motion near the axis of symmetry. This gives rise to a Minkowskian core.
Now, the equations of motion for Einstein-
gravity are described as
where
are the Ricci scalar, gravitational potential, and the Ricci tensors, respectively. These equations for the set of system (
1) and (
5) are found to be
I shall use
and
in the coming equations. The law of conservation at the
-dominated regime for the static, locally anisotropic, relativistic spherical interiors are found as below:
The Misner-Sharp formalism [
51] provides the following configurations of the mass function:
which can be rendered after using the field equation as
It is interesting to note from Equation (
12) that the mass of the spatially hyperbolic object is positive. In order to maintain this logic, one can deduce from the above equation that the energy density should be negative. This leads to the breaching of weak energy conditions by the HSS. To avoid negativity of energy density, I shall use
instead of
in our calculations. It follows from Equation (
13) that
Equations (
9) and (
12) give
Upon making use of the above value, I obtain from Equation (
11)
This equation describes the state of hydrostatic equilibrium of the HSS within Einstein- gravity.
3. Active Gravitating Mass with Cosmological Constant
The well-known Weyl tensor can be written through its electric part, fluid four velocity, and the Levi–Civita tensor (
) as
where
. The scalar associated with the electric part of the above equation is calculated for the static spheres as
Thus, after making use of the equations of motion, Equations (
12) and (
16) give the following form of the Misner-Sharp mass function:
Equation (
13), after using above expression, provides
Feeding back
from the above equation in Equation (
17) gives
In this way, I have been able to relate the Misner-Sharp function with the system energy density and cosmological constant. One can realize the effects of dark energy through in the static fluids from the above expression.
Now, I adopt another approach to calculate the quantity of matter ingredients of the static relativistic compact bodies. In HSS, two types of boundary surfaces are likely to appear. Therefore, at the outer surface, I can provide the generic formula for finding the active gravitating matter quantity for HSS in the environment of the cosmological constant as
which, after using the equations of motion at the
-dominated epoch, gives
Its solution is found as below:
After substituting the value of the metric coefficient from Equation (
14), it follows that
thereby providing the repulsive nature (if
) induced by the gravitational force within the locally anisotropic static metric. This also describes the importance of
terms in the estimation of active gravitating static matter. Now, I wish to relate this mass function in terms of the scalar corresponding to four acceleration (
). One can easily check
with
. This can be re-expressed as
The simultaneous use of Equations (
20) and (
22) provides
This is the first-order differential equation in
. Its solution is found as below:
This provides the expression of Tolman mass in terms of the cosmological constant, tidal forces, and locally anisotropic pressure. The above equation after substituting
yields
This relation has related Tolman spherical mass with the inhomogeneous energy density with repulsive energy effects due to terms and local anisotropic pressure. This result reduces to GR upon substituting .
Herrera et al. [
31,
32] described the orthogonal decomposition of the curvature tensor into two different tensorial objects. These can be found for our system in the context of the cosmological constant as below:
where
stand for the right and left dual of the curvature object. The trace (
T) and trace-less (
TF) values of the above equations after using field equations become
The second of Equations (
26) and (27) after using
from Equation (
18) turn out to be
One can notice that
is trying to control the effects of the energy density inhomogeneity of the self-gravitating system in Einstein-
gravity, while the
not only takes the effects of energy density but also the influences of pressure anisotropicity on the subsequent changes within the static spherical bodies. The effects of pressure can be dealt with through the trace-less parts of Equations (
24) and (25) as
Equations (
20) and (
23) transform the trace and trace-less components as follows:
The first of the above equations provides us with the means to study the non-complex state of the system through Tolman mass. This equation has linked
with
. Thus, the combined analysis of Equations (29) and (
31) states that
could be treated as a complexity factor. The second of the above equations describes the direct connection of
with the gravitating passive static fluid mass of the relativistic system even in the presence of
. This result is equivalent to the one obtained by Herrera et al. [
25] in the absence of
.
4. Static HSS Fluids
In this section, I present an analytical solution of Einstein-
equations of motion for the anisotropic HSS by following a general method presented by Lake [
52] and Herrera et al. [
53]. The subtraction of Equation (10) from Equation (9) provides
To proceed forward for the sake of solutions, I define
and
. After this, the above equation becomes
This is a first-order partial differential equation in
. Its solution after substituting back the definition of
gives
On can notice that the above model is presented in the form of two generating functions (GF), i.e.,
and
. The corresponding matter variables for the locally anisotropic HSS become
In the following subsection, I shall describe families of GR- models for HSS under some realistic backgrounds.
4.1. Conformal Flatness in HSS
When a Riemannian space is conformally related to a flat Riemannian space, it is called a
conformally flat spacetime. Thus, for a conformally flat spacetime, the Weyl tensor vanishes equivalently, and every point has a neighborhood conformal to an open subset of the Minkowski spacetime. As a result, a conformally flat spacetime possesses the local conformal symmetry of the Minkowski spacetime, i.e., it has 15 independent conformal killing vector fields. However, the global topology may not be the same as that of the Minkowski spacetime. In order to present the solution of HSS in this context, I take
. Thus, Equation (
16) becomes
which, after substituting
and
, transforms Equation (
38) into
This is again a first-order differential equation, which gives
After back-substitution, I obtain
In Equation (
39),
and
k are defined as
while
is an integration constant, and
appearing in Equation (
40) is also an integration function. Its value after matching the interior region with de Sitter spacetime provides
Equation (
40) gives
where
To proceed with our solutions, I take another constraint, i.e.,
, thereby considering the only non-zero component of pressure in the gravitating source of HSS. Against this background, Equation (9) eventually provides
Upon using Equation (
41) in Equation (
16), the conformal flat model of our system (after considering
) can be recast as
This is again a first-order differential equation. Its solution can easily be calculated as below:
where
is an integration function. By simultaneously making use of Equations (
40) and (
41), one can find
In this way, I have been able to find the unknown metric variable. Substituting this into the corresponding Einstein-
equations of motion, I obtain structural variables as
The associated GF are calculated as below:
One can notice that the constraint on the metric coefficient will cause it to lie in the positive region. This also distributes the system to occupy the minimum value to the radial coordinate. Thus, the vacuum core can be expected to present within this HSS at the hypersurface even in the presence of the cosmological constant. It is worth mentioning that this model describes the static solutions of conformally flat HSS, which is assumed to be coupled with matter having only one non-zero component of pressure. This model could be considered as a toy model for irrotational HSS cosmic bodies experiencing zero tidal forces due to .
4.2. Non-Complex HSS Model
Not only for static but also in the non-static case, the structure scalar
has been identified as the complexity factor in GR [
42,
43]. This result has also been found applicable in various modified theories of gravity [
46,
47]. One can study the non-complex Bondi as well as axially symmetric solutions by keeping
[
44,
45]. It is easy to understand that such solutions are many in number, even in the presence of the cosmological constant. In order to specify them in a particular area field, I take a constraint, i.e.,
. Thus, Equation (9) yields
where
g is the same as in the previous subsection. The zero complexity condition, i.e.,
, gives
Equations (
21), (
44), and (
45) provide
For the non-complex HSS isotropic matter configurations, I obtain
which further gives
thereby providing the value of
g by means of an integration function
. The structural quantities for relativistic HSS are found as below:
In this environment, the GF are computed as
4.3. Stiff Fluid Configurations
In this subsection, I shall provide the solution of HSS obeying a stiff state equation. This equation states that the difference between pressure and energy density should be equal to zero, thus indicating it as
. With this setup, Equation (
15) reads
This conservation equation could be applicable to the ultradense matter content that is distributed over the region by maintaining the constraints of the stiff state equation. I proceed with our analysis with these two assumptions. In the first case, I take
, and the second one keeps the non-complex state of HSS. Thus, the first condition reduces Equation (
47) to
where
is an integration constant. In this context, the mass function and metric variables of HSS are found as below:
Then, the associated GF are calculated as
Now, I consider
. With this environment, the non-complex phase of HSS coupled with the matter obeying the stiff sate equation can be observed. Equations (29) and (
47) give
This is a first-order differential equation whose solution is an easy task. It provides
where
are constants of integration. The corresponding matter quantity for HSS is
With the help of this equation, one can obtain the values of the metric coefficient from Equation (
14). In HSS, the formation of a Minkowskian core appears to emerge. This gives rise to the formation of two boundaries. At the outer hypersurface, i.e.,
, the associated values of the radial component of pressure and mass function become
The difference between these expressions provides
Eventually,
for the less complex HSS becomes
These solutions are presented in the presence of the cosmological constant.
5. Energy Conditions
The general form of the energy conditions can be obtained from the Raychaudhuri equation for expansion [
54]. One can analyze the nature of gravity (attractive/non-attractive) from these conditions. The null energy conditions (NEC), weak energy conditions (WEC), strong energy conditions (SEC), and dominant energy condition (DEC) can be defined as follows:
NEC: ,
WEC: , ,
SEC: , ,
DEC: ,
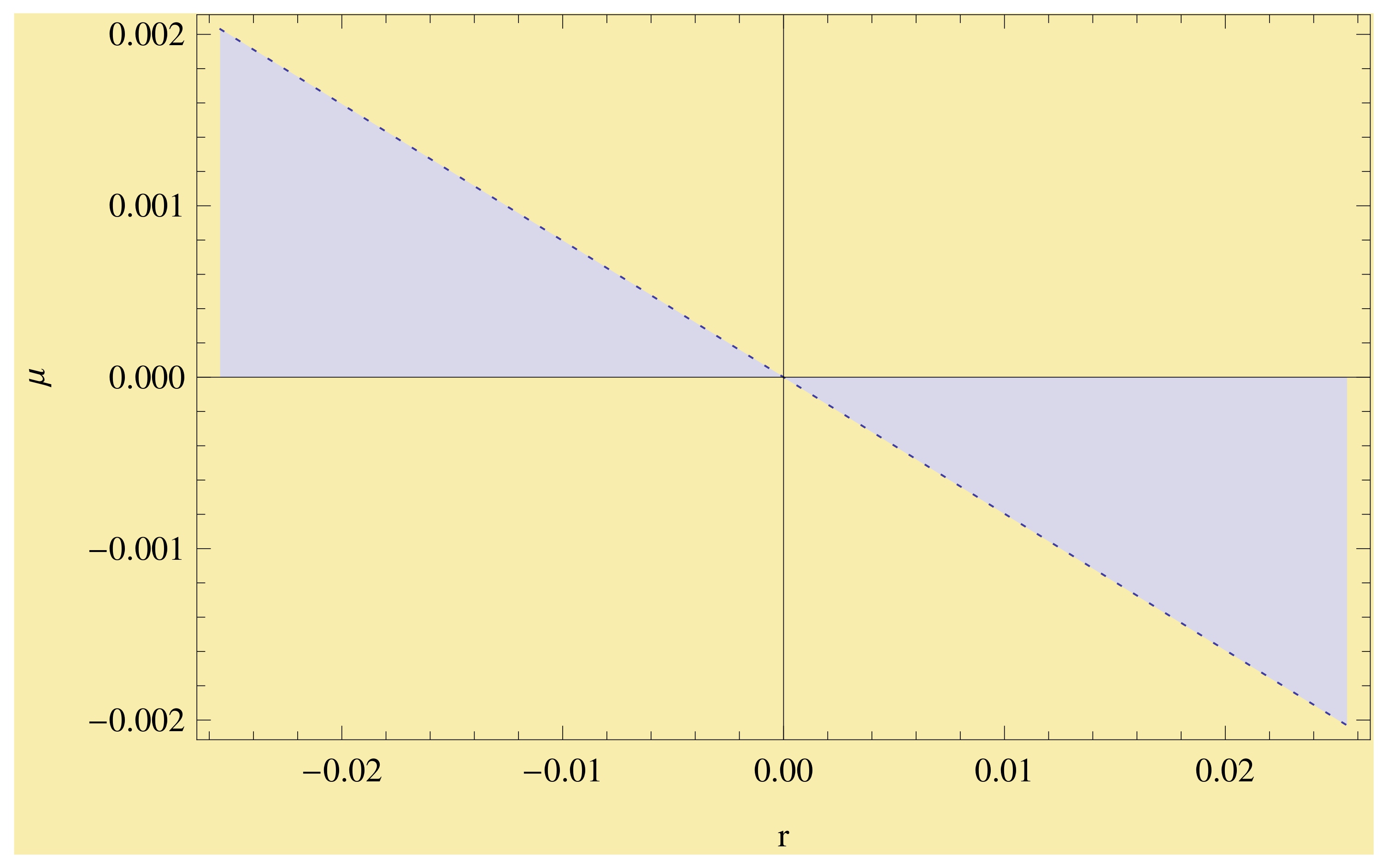
Figure 1 indicates that the energy density of the hyperbolically symmetric static solutions is negative, if I take
to be a positive quantity. This suggests the close connection of our results with quantum field theory. Such analysis could be helpful in the examination of virtual particles, squeezed vacuum particle states, and the Casimir effect. Next, I consider three different strange star candidates, i.e., Her X-1, SAX J 1808.4-3658, 4U1820-30. I would label these strange stars with SS1, SS2, and SS3, respectively. It is observationally seen that SS1, SS2, and SS3 have 0.88
, 1.435
, and 2.25
stellar masses, respectively [
55,
56]. I shall graphically observe the behavior of energy conditions for the toy model mentioned in Equations (
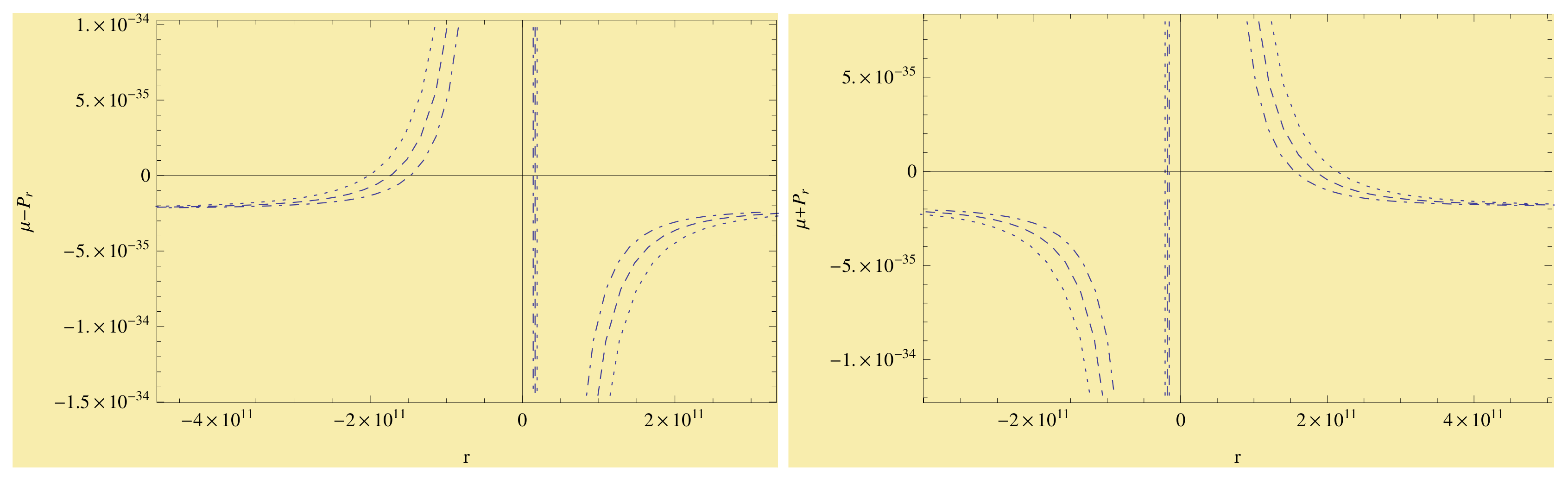
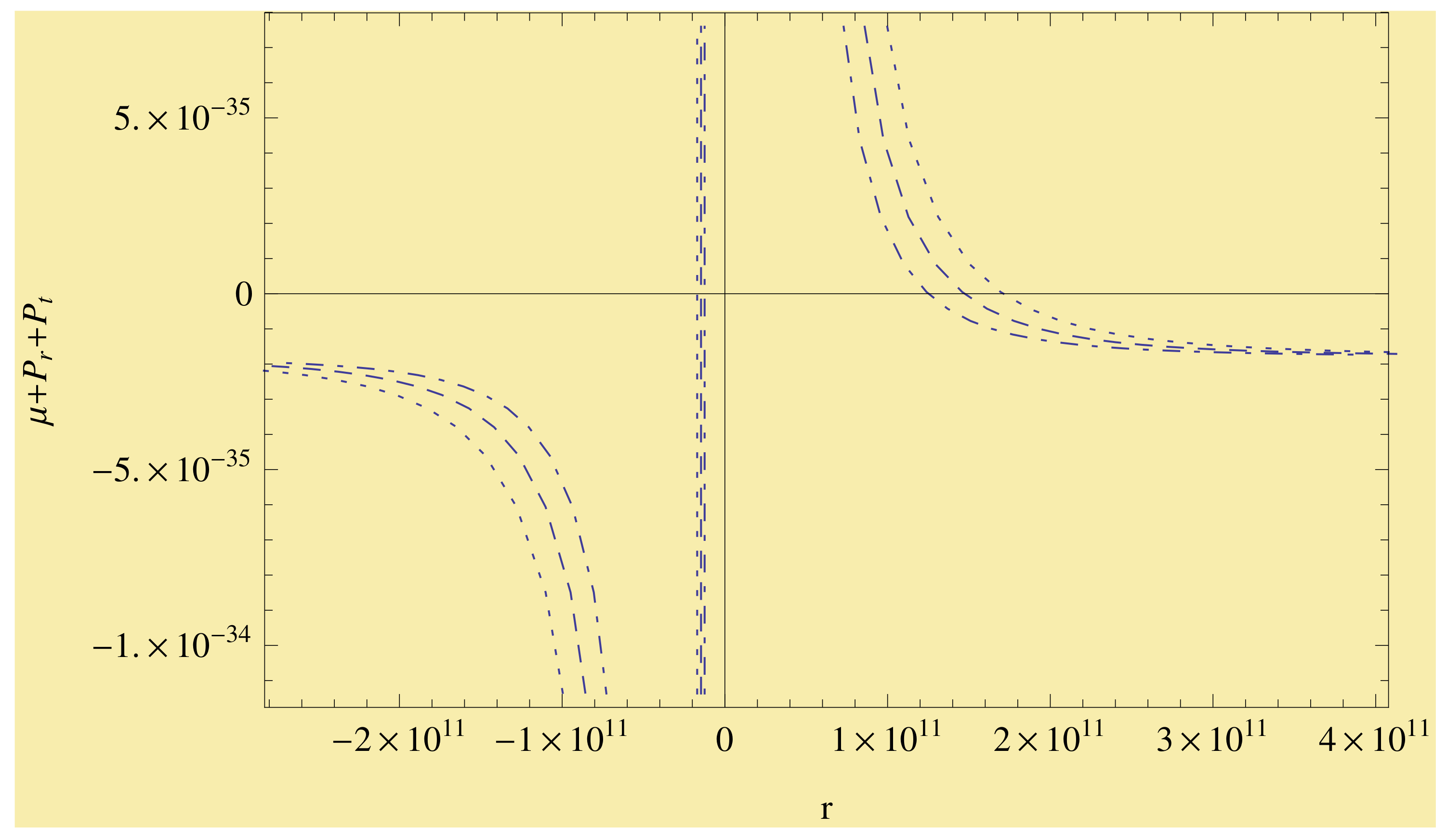
34)–(37) with respect to stiff HSS generation functions. I can see from
Figure 2,
Figure 3 and
Figure 4 that the energy conditions are violated for the majority of the zonal parameters. Only a few regions can be observed that support the viability of the energy conditions. It is worth mentioning that the observable effects of dark energy are well known to violate the strong energy conditions. Therefore, our results could be helpful to understand the dark energy problem as well as quantum or cosmological scenarios [
57,
58,
59].
6. Conclusions
The present paper aimed to understand the modeling of hyperbolically symmetric solutions in the presence of the cosmological constant. I have considered spatially hyperbolical spacetime, which is assumed to be coupled with locally anisotropic fluid configurations. Under a co-moving frame of reference and cosmological constant, I have presented field equations and Bianchi identities. With the help of two formalisms (i.e., Misner-Sharp and Tolman) for the calculation of the mass function, I have computed theoretical relations between total quantity matter and structural variables. The orthogonal splitting is used to decompose the curvature tensor into scalar variables. Four structure scalars are calculated. This led us to understand the Tolman mass through and .
Finally, I propose a generic framework that allows every diagonally symmetric hyperbolical fluid model with static backgrounds to be described by means of two generating functions. I have described the stellar models under three main categories. The first category gives cosmic solutions of hyperbollically symmetric spacetime in conformally flat backgrounds. The second describes the diagonally symmetric hyperbolical solutions for non-complex relativistic interiors. The last category is devoted to understanding the structure formation through equations of state. Thus, certain straightforward corresponding solutions are discovered, along with their physical explanations. It is necessary to address the fact that the violation of the weak energy condition () in our modeling represents the negative attitude of Tolman mass under certain circumstances of cosmological constant and matter variables, i.e., if . Despite the fact that I would anticipate the energy density to be positive based on classical physics considerations, however, the negative energy densities are frequently mentioned in extreme astrophysical and cosmic events, notably in connection with quantum issues that could occur inside the horizon with the cosmological constant.
The second-order set of partial differential equations were solved in order to describe various physical properties of the hyperbolically symmetric objects in GR by Herrera et al. [
25]. The leading correction terms obtained in the present work are embodied with
terms, stating that our solutions depend directly on the impact of generating functions,
r, and on the cosmological constant. This term could be interpreted as the non-attractive connection among the matter variables of the locally anisotropic HSS. The cosmological constant or vacuum energy density affect the impact of matter variables, introducing corrections to the results produced by Herrera et al. [
25], which could be of interest for situations described in quantum and cosmological scenarios [
57,
58,
59]. Corrections introduced by the cosmological constant produce variations in the metric coefficients as well as the generating function due to their repulsive nature for all three fluid models.
I see that there exist some exact analytical solutions for the anisotropic HSS fluid models with the introduction of a
term. Our study allows one to understand the implications of a non-zero
towards the mathematical modeling of conformally flat, non-complex as well as stiff matter HSS distributions. These results are of interest in view of the recent observational claims about a non-vanishing cosmological constant. The other consequence of introducing the cosmological constant, however, concerns the mass definition. Herrera et al. [
25] described the matter content within the HSS through the Misner-Sharp and the Tolman mass functions. Irrespective of the inclusion of the value of the
term, the positive and negative nature of the former and latter masses is never disturbed.