Linear Polarization Signatures of Particle Acceleration in High-Synchrotron-Peak Blazars
Abstract
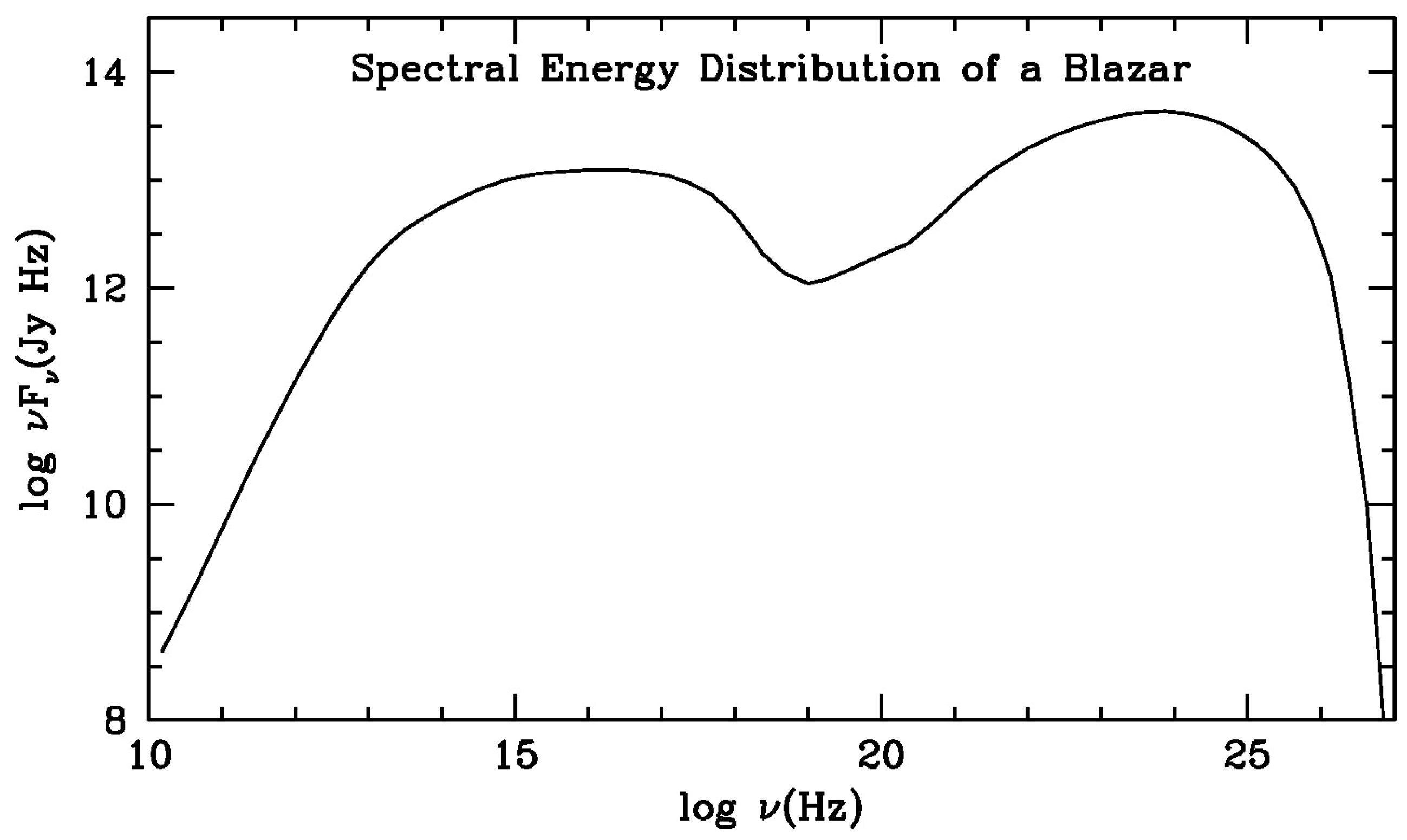
1. Introduction
2. Particle Acceleration Mechanisms in Blazars
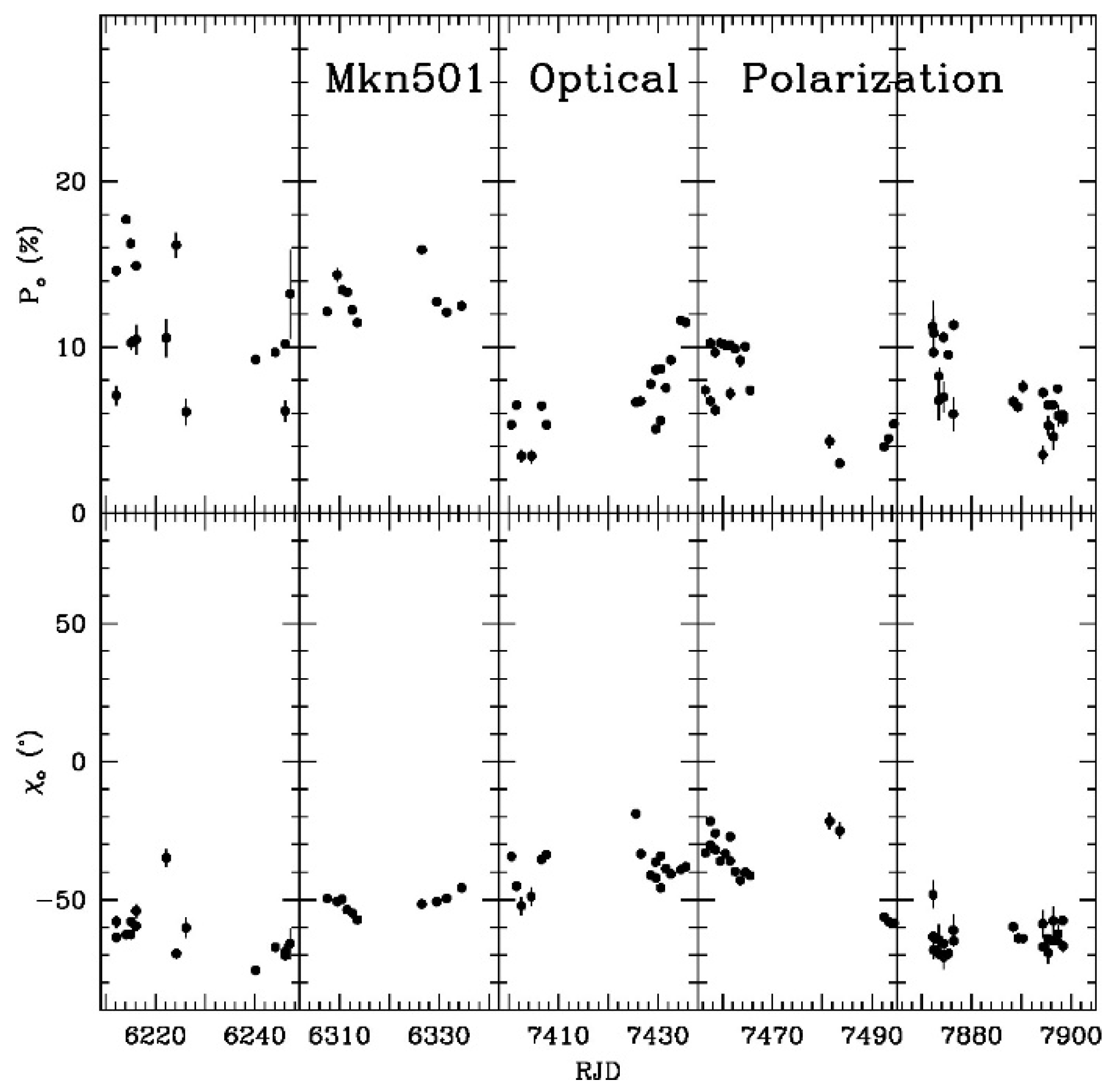
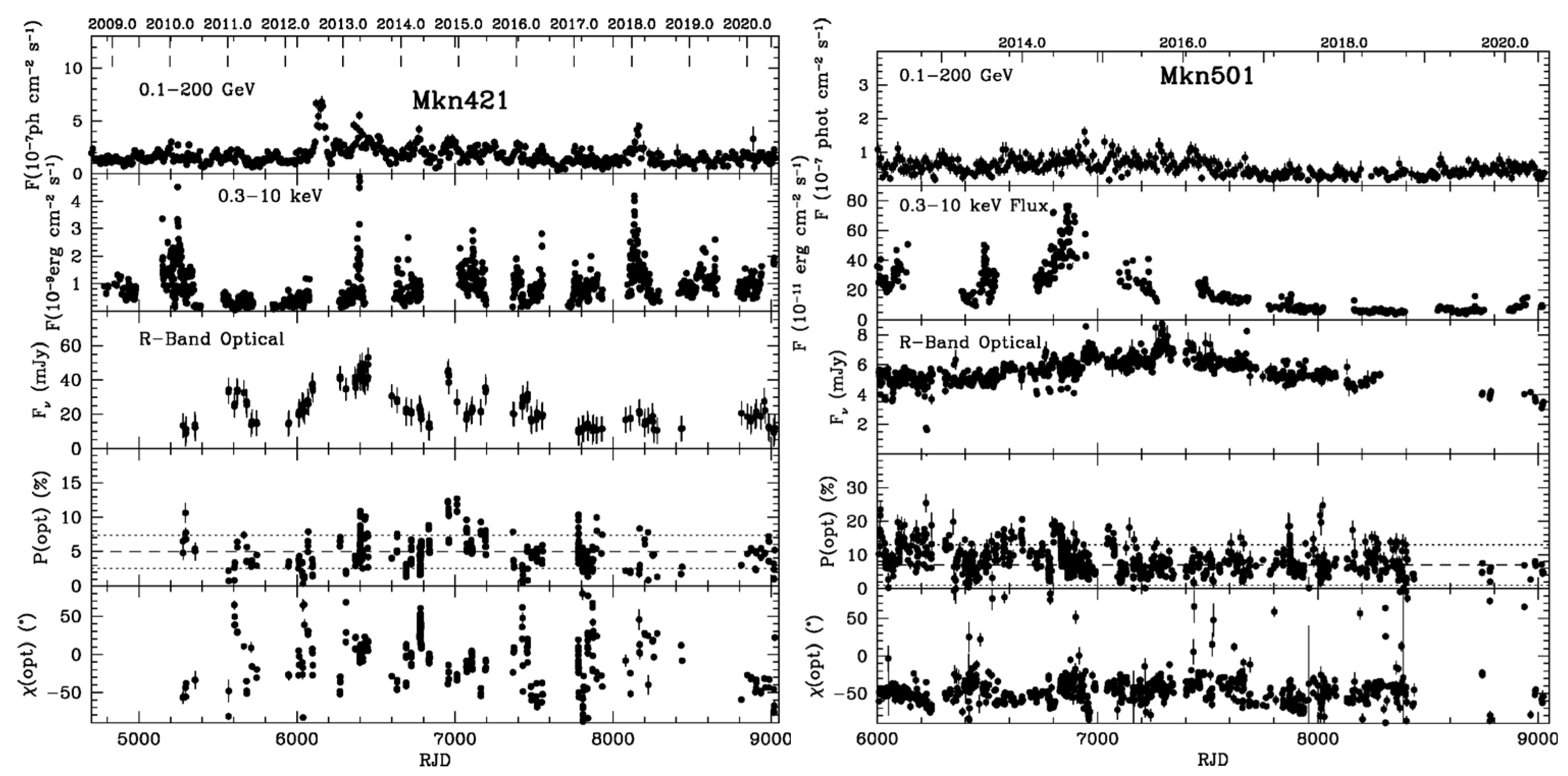
3. Observations
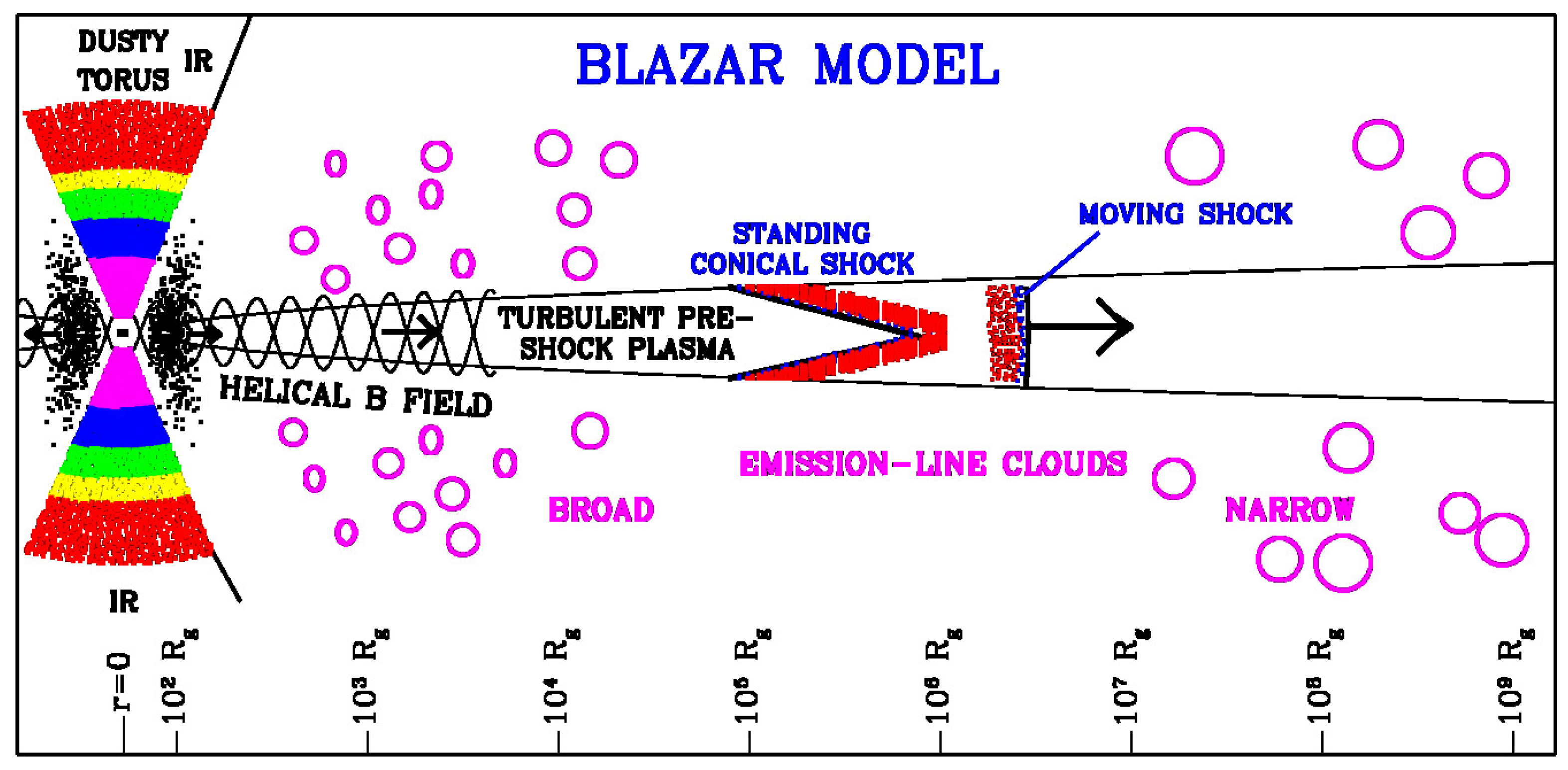
4. Turbulence Plus Shock Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Marscher, A.P.; Jorstad, S.G.; Williamson, K.E. Modeling the Time-Dependent Polarization of Blazars. Galaxies 2017, 5, 63. [Google Scholar] [CrossRef]
- Marscher, A.P.; Jorstad, S.G. Frequency and Time Dependence of Linear Polarization in Turbulent Jets of Blazars. Galaxies 2021, 9, 27. [Google Scholar] [CrossRef]
- Marscher, A.P. Turbulent, Extreme Multi-Zone Model for Simulating Flux and Polarization Variability in Blazars. Astrophys. J. 2014, 780, 87. [Google Scholar] [CrossRef]
- Lyutikov, M.; Pariev, V.I.; Gabuzda, D.C. Polarization and Structure of Relativistic Parsec-scale ANG Jets. Mon. Not. R. Astron. Soc. 2005, 360, 869–891. [Google Scholar] [CrossRef]
- Gabuzda, D.C. Evidence for Helical Magnetic Fields Associated with AGN Jets and the Action of a Cosmic Battery. Galaxies 2019, 7, 5. [Google Scholar] [CrossRef]
- Hughes, P.A.; Aller, H.D.; Aller, M.F. Polarized radio outbursts in BL Lacertae. I—Polarized emission from a compact jet. II—The flux, polarization of a piston-driven shock. Astrophys. J. 1985, 298, 296–315. [Google Scholar] [CrossRef]
- Vlahakis, N.; Königl, A. Magnetic Driving of Relativistic Outflows in Active Galactic Nuclei. 1. Interpretation of Parsec-Scale Accelerations. Astrophys. J. 2004, 605, 656–661. [Google Scholar] [CrossRef]
- Daly, R.A.; Marscher, A.P. The Gas Dynamics of Compact Relativistic Jets. Astrophys. J. 1988, 334, 552–559. [Google Scholar] [CrossRef]
- Gómez, J.L.; Marti, J.M.; Marscher, A.P.; Ibañez, J.M.; Marcaide, J.M. Parsec-Scale Synchrotron Emission from Hydrodynamic Relativistic Jets in Active Galactic Nuclei. Astrophys. J. Lett. 1995, 449, L19–L21. [Google Scholar] [CrossRef]
- Marscher, A.P. The Core of a Blazar Jet. In Extragalactic Jets Theory and Observation from Radio to Gamma Ray; Rector, T.A., DeYoung, D.S., Eds.; Astronomical Society of the Pacific Conference Series: San Francisco, CA, USA, 2008; Volume 386, pp. 437–443. [Google Scholar]
- Blandford, R.D.; Königl, A. Relativistic Jets in Compact Radio Sources. Astrophys. J. 1979, 232, 34–48. [Google Scholar] [CrossRef]
- Bell, A.R.; Schure, K.M.; Reville, B.; Giacinti, G. Cosmic-Ray Acceleration and Escape from Supernova Remnants. Mon. Not. R. Astron. Soc. 2013, 431, 415–429. [Google Scholar] [CrossRef]
- Sironi, L.; Petropoulou, M.; Giannios, D. Relativistic Jets Shine through Shocks or Magnetic Reconnection? Mon. Not. R. Astron. Soc. 2015, 450, 183–191. [Google Scholar] [CrossRef]
- Summerlin, E.J.; Baring, M.G. Diffusive Acceleration of Particles at Oblique, Relativistic, Magnetohydrodynamic Shocks. Astrophys. J. 2012, 745, 63. [Google Scholar] [CrossRef]
- Petropoulou, M.; Sironi, L. The Steady Growth of the High-Energy Spectral Cutoff in Relativistic Magnetic Reconnection. Mon. Not. R. Astron. Soc. 2015, 481, 5687–5701. [Google Scholar] [CrossRef]
- Stawarz, L.; Petrosian, V. On the Momentum Diffusion of Radiating Ultrarelativistic Electrons in a Turbulent Magnetic Field. Astrophys. J. 2008, 681, 1725–1744. [Google Scholar] [CrossRef]
- Rieger, F.M.; Duffy, P. Particle Acceleration in Relativistic Shearing Flows: Energy Spectrum. Astrophys. J. 2022, 933, 149. [Google Scholar] [CrossRef]
- Cawthorne, T.V. Polarization of Synchrotron Radiation from Conical Shock Waves. Mon. Not. R. Astron. Soc. 2006, 367, 851–859. [Google Scholar] [CrossRef]
- Cawthorne, T.V.; Jorstad, S.G.; Marscher, A.P. Evidence for Recollimation Shocks in the Core of 1803+784. Astrophys. J. 2013, 772, 14. [Google Scholar] [CrossRef]
- Zhang, H.; Li, X.; Giannios, D.; Guo, F. First-Principles Prediction of X-ray Polarization from Magnetic Reconnection in High-Frequency BL Lacertae Objects. Astrophys. J. 2021, 912, 129. [Google Scholar] [CrossRef]
- Tavecchio, F. Probing Magnetic Fields and Acceleration Mechanisms in Blazar Jets with X-Ray Polarimetry. Galaxies 2021, 9, 37. [Google Scholar] [CrossRef]
- Peirson, A.L.; Romani, R.W. The Polarization Behavior of Relativistic Synchrotron Jets. Astrophys. J. 2018, 864, 140. [Google Scholar] [CrossRef]
- Marscher, A.P.; Jorstad, S.G.; D’Arcangelo, F.D.; Smith, P.S.; Williams, G.G.; Larionov, V.M.; Oh, H.; Olmstead, A.R.; Aller, M.F.; Aller, H.D.; et al. The Inner Jet of an Active Galactic Nucleus as Revealed by a Radio to Gamma-ray Outburst. Nature 2008, 452, 966–969. [Google Scholar] [CrossRef] [PubMed]
- Marscher, A.P.; Jorstad, S.G.; Larionov, V.M.; Aller, M.F.; Aller, H.D.; Lähteenmäki, A.; Agudo, I.; Smith, P.S.; Gurwell, M.; Hagen-Thorn, V.A.; et al. Probing the Inner Jet of the Quasar PKS 1510-089 with Multi-waveband Monitoring during Strong Gamma-ray Activity. Astrophys. J. Lett. 2010, 710, L126–L131. [Google Scholar] [CrossRef]
- Bodo, G.; Tavecchio, F.; Sironi, L. Kink-Driven Magnetic Reconnection in Relativistic Jets: Consequences for X-ray Polarimetry of BL Lacs. Mon. Not. R. Astron. Soc. 2021, 501, 2836–2847. [Google Scholar] [CrossRef]
- Dong, L.; Zhang, H.; Giannios, D. Kink Instabilities in Relativistic Jets Can Drive Quasi-Periodic Radiation Signatures. Mon. Not. R. Astron. Soc. 2020, 494, 1817–1825. [Google Scholar] [CrossRef]
- Jorstad, S.G.; Marscher, A.P.; Raiteri, C.M.; Villata, M.; Weaver, Z.R.; Zhang, H.; Dong, L.; Gómez, J.L.; Perel, M.V.; Savchenko, S.S.; et al. Rapid Periodic Oscillations in the Relativistic Jet of BL Lacertae. Nature 2022, 609, 265–268. [Google Scholar] [CrossRef]
- Williamson, K.E.; Jorstad, S.G.; Marscher, A.P.; Larionov, V.M.; Smith, P.S.; Agudo, I.; Arkharov, A.A.; Blinov, D.A.; Casadio, C.; Efimova, N.V.; et al. Comprehensive Monitoring of Gamma-ray Bright Blazars: Statistical Study of Optical, X-ray, and Gamma-ray Spectral Slopes. Astrophys. J. 2014, 789, 135. [Google Scholar] [CrossRef]
- Weisskopf, M.C.; Soffitta, P.; Baldini, L.; Ramsey, B.D.; O’Dell, S.L.; Romani, R.W.; Matt, G.; Deininger, W.D.; Baumgartner, W.H.; Bellazzini, R.; et al. The Imaging X-Ray Polarimetry Explorer (IXPE): Pre-Launch. J. Astron. Telesc. Instrum. Syst. 2022, 8, 026002. [Google Scholar] [CrossRef]
- DiGesu, L.; Donnarumma, I.; Tavecchio, F.; Agudo, I.; Barnounan, T.; Cibrario, N.; Di Lalla, N.; Di Marco, A.; Escudero, J.; Errando, M.; et al. The X-Ray Polarization View of Mrk 421 in an Average Flux State as Observed by the Imaging X-Ray Polarimetry Explorer. Astrophys. J. Lett. 2022, 938, L7. [Google Scholar] [CrossRef]
- Liodakis, I.; Marscher, A.P.; Agudo, I.; Berdyugin, A.V.; Bernardos, M.I.; Bonnoli, G.; Borman, G.A.; Casadio, C.; Casanova, V.; Cavazzuti, E.; et al. Polarized Blazar X-Rays Imply Particle Acceleration in Shocks. Nature 2022, 611, 677–681. [Google Scholar] [CrossRef]
- Weaver, Z.R.; Jorstad, S.G.; Marscher, A.P.; Morozova, D.A.; Troitsky, I.S.; Agudo, I.; Gómez, J.L.; Lähteenmäki, A.; Tammi, J.; Tornikoski, M. Kinematics of Parsec-Scale Jets of Gamma-Ray Bright Blazars at 43 GHz during Ten Years of the VLBA-BU-BLAZAR Program. Astrophys. J. Suppl. 2022, 260, 12. [Google Scholar] [CrossRef]
- Blazar Research at Boston University: 1959+650. Available online: https://www.bu.edu/blazars/VLBA_GLAST/1959.html (accessed on 30 September 2022).
- Marscher, A.P.; Gear, W.K. Models for High-Frequency Radio Outbursts in Extragalactic Sources with Application to the Early 1983 Millimeter to Infrared Flare of 3C273. Astrophys. J. 1985, 298, 114–127. [Google Scholar] [CrossRef]
- Weaver, Z.R.; Williamson, K.E.; Jorstad, S.G.; Marscher, A.P.; Larionov, V.M.; Raiteri, C.M.; Villata, M.; Acosta-Pulido, J.A.; Bachev, R.; Baida, G.V.; et al. Multi-wavelength Variability of BL Lacertae Measured with High Time Resolution. Astrophys. J. 2020, 900, 137. [Google Scholar] [CrossRef]
- Albert, A.; Alfaro, R.; Alvarez, C.; Camacho, J.A.; Arteaga-Velázquez, J.C.; Arunbabu, K.P.; Rojas, D.A.; Solares, H.A.; Baghmanyan, V.; Belmont-Moreno, E.; et al. Long-term Spectra of the Blazars Mrk 421 and Mrk 501 at TeV Energies Seen by HAWC. Astrophys. J. 2022, 929, 125. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Agudo, I.; Ajello, M.; Aller, H.D.; Aller, M.F.; Angelakis, E.; Arkharov, A.A.; Axelsson, M.; Bach, U.; et al. The Spectral Energy Distribution of Fermi Bright Blazars. Astrophys. J. 2010, 716, 30–70. [Google Scholar] [CrossRef]
- Blandford, R.D.; Znajek, R. Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 1977, 179, 433–456. [Google Scholar] [CrossRef]
- McKinney, J.C.; Narayan, R. Disc-jet Coupling in Black Hole Accretion Systems I. General Relativistic Magnetohydrodynamical Models. Mon. Not. R. Astron. Soc. 2007, 375, 513–530. [Google Scholar] [CrossRef]
- Tchekhovskoy, A.; Narayan, R.; McKinney, J.C. Efficient Generation of Jets from Magnetically Arrested Accretion on a Rapidly Spinning Black Hole. Mon. Not. R. Astron. Soc. 2011, 418, L79–L83. [Google Scholar] [CrossRef]
- Meier, D.L.; Koide, S.; Uchida, Y. Magnetohydrodynamic Production of Relativistic Jets. Science 2001, 291, 84–92. [Google Scholar] [CrossRef]
- Vlahakis, N. Disk-Jet Connection. In Blazar Variability Workshop II: Entering the GLAST Era; Miller, H.R., Marshall, K., Webb, J.R., Aller, M.F., Eds.; Astronomical Society of the Pacific: San Francisco, CA, USA, 2006; Volume 350, pp. 169–177. [Google Scholar]
- Zamaninasab, M.; Clausen-Brown, E.; Savolainen, T.; Tchekhovskoy, A. Dynamically Important Magnetic Fields near Accreting Supermassive Black Holes. Nature 2014, 510, 126–128. [Google Scholar] [CrossRef]
- Nalewajko, K.; Begelman, M.C. The Effect of Poloidal Velocity Shear on the Local Development of Current-Driven Instabilities. Mon. Not. R. Astron. Soc. 2012, 427, 2480–2486. [Google Scholar] [CrossRef]
- Tavecchio, F.; Landoni, M.; Sironi, L.; Coppi, P. Probing Dissipation Mechanisms in BL Lac Jets through X-ray Polarimetry. Mon. Not. R. Astron. Soc. 2018, 480, 2872–2880. [Google Scholar] [CrossRef]
- Burn, B.J. On the Depolarization of Discrete Radio Sources by Faraday Dispersion. Mon. Not. R. Astron. Soc. 1966, 133, 67–83. [Google Scholar] [CrossRef]
- Jones, T.W. Polarization as a Probe of Magnetic Field and Plasma Properties of Compact Radio Sources—Simulation of Relativistic Jets. Astrophys. J. 1988, 332, 678–695. [Google Scholar] [CrossRef]
- Webb, J.R.; Arroyave, V.; Laurence, D.; Revesz, S.; Bhatta, G.; Hollingsworth, H.; Dahlla, S.; Howard, E.; Cioffi, M. The Nature of Micro-Variability in Blazars. Galaxies 2021, 9, 114. [Google Scholar] [CrossRef]
- Smith, P.S.; Montiel, E.; Rightley, S.; Turner, J.; Schmidt, G.D.; Jannuzi, B.T. Coordinated Fermi/Optical Monitoring of Blazars and the Great 2009 September Gamma-Ray Flare of 3C 454.3. In Proceedings of the 2009 Fermi Symposium, eConf Proceedings C091122, Washington, DC, USA, 2–5 November 2009. [Google Scholar]
- Zhang, H.; Fang, K.; Li, H.; Giannios, D.; Böttcher, M.; Buson, S. Probing the Emission Mechanism and Magnetic Field of Neutrino Blazars with Multiwavelength Polarization Signatures. Astrophys. J. 2019, 876, 109. [Google Scholar] [CrossRef]
- Peirson, A.L.; Romani, R.W. The Polarization Behavior of Relativistic Synchrotron Self-Compton Jets. Astrophys. J. 2019, 856, 76. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marscher, A.P.; Jorstad, S.G. Linear Polarization Signatures of Particle Acceleration in High-Synchrotron-Peak Blazars. Universe 2022, 8, 644. https://doi.org/10.3390/universe8120644
Marscher AP, Jorstad SG. Linear Polarization Signatures of Particle Acceleration in High-Synchrotron-Peak Blazars. Universe. 2022; 8(12):644. https://doi.org/10.3390/universe8120644
Chicago/Turabian StyleMarscher, Alan P., and Svetlana G. Jorstad. 2022. "Linear Polarization Signatures of Particle Acceleration in High-Synchrotron-Peak Blazars" Universe 8, no. 12: 644. https://doi.org/10.3390/universe8120644
APA StyleMarscher, A. P., & Jorstad, S. G. (2022). Linear Polarization Signatures of Particle Acceleration in High-Synchrotron-Peak Blazars. Universe, 8(12), 644. https://doi.org/10.3390/universe8120644