Abstract
Active Galactic Nuclei (AGNs) and their relativistic jets belong to the most promising class of ultra-high-energy cosmic ray (UHECR) accelerators. This compact review summarises basic experimental findings by recent instruments, and discusses possible interpretations and astrophysical constraints on source energetics. Particular attention is given to potential sites and mechanisms of UHECR acceleration in AGNs, including gap-type particle acceleration close to the black hole, as well as first-order Fermi acceleration at trans-relativistic shocks and stochastic shear particle acceleration in large-scale jets. It is argued that the last two represent the most promising mechanisms given our current understanding, and that nearby FR I type radio galaxies provide a suitable environment for UHECR acceleration.
1. Introduction
The energy spectrum of cosmic rays runs over more than ten orders of magnitudes, from GeV energies to ∼ eV. While supernova remnants are believed to be the most probable sources of cosmic rays at lower energies (i.e., up to the ‘knee’ at ∼ eV) [1,2], the origin of ultra-high-energy cosmic rays (UHECRs, eV = 1 EeV) is much less understood. While thought to be of extragalactic origin [3], the real astrophysical sources are still to be deciphered. Possible candidate sources include Active Galactic Nuclei (AGNs) and their relativistic jets, starburst galaxies (SBGs) and gamma-ray bursts, as well as accretion shocks around clusters of galaxies, see, e.g., ref. [4]. The present review will focus on the relevance of AGNs, and highlight some of the recent developments in the field, including a compact discussion of particle acceleration in the relativistic jets of AGNs. As such it draws on an earlier review [5], extending and updating its perspectives.
Jetted AGNs [6] have for long be considered as promising UHECR emitters. As the most powerful, persistent sources in the Universe, they are in principle capable to satisfy the physics constraints (e.g., size, energetics) on putative UHECR emitters, see, e.g., ref. [7]. Since UHECRs lose energy during propagation by inelastic collisions with CMB photons, possible AGN sources have to be relatively nearby (i.e., within a few hundred Mpc)1 in order to be able to account for the highest cosmic-ray energies observed. In recent years, particular attention has thus been given to the nearest AGNs, i.e., the radio galaxies Centaurus A (Cen A), M87 and Fornax A. As shown below, these sources are indeed particularly interesting given current experimental results and theoretical considerations.
From an experimental point of view, major progress in UHECR research has been achieved over the last decade by the Pierre Auger (PA) and the Telescope Array (TA) collaborations, see, e.g., refs. [8,9] for recent experimental reports. Both collaborations run hybrid, large-scale instruments that are fully operational since 2008. The larger, PA observatory consists of 1660 surface (water tank) detectors and four fluorescence detector stations, and is located in the southern hemisphere (Mendoza, Argentina). The original TA construction, on the other hand, consists of 507 surface (scintillation counter) detectors and three fluorescence detector stations, and is located in the northern hemisphere (Utah, USA). Both instruments are "hybrid" in nature: Their surface detectors (SDs) measure air shower particles on the ground, and are sensitive to its electromagnetic, muonic and hadronic components, while the air fluorescence detectors (FDs) observe the longitudinal development of air showers in the atmosphere by the light emitted during their passage. The FDs provide a direct calorimetric measurement of the shower energy, and can thus be used to calibrate the energy scale of the SD events.
In the following, selected experimental results are briefly summarized. For comprehensive overviews and discussion of recent results the reader is also referred to refs. [10,11,12,13,14].
2. Basic Results of Current UHECR Experiments
2.1. Energy Spectrum of UHECRs
The energy spectrum of UHECRs extends up to ∼ eV, with the highest-energy event reported having an energy of about eV [15]. A comparison of current PA and TA measurements shows that up to eV a good spectral agreement between experiments, including the position of the “ankle” at eV, is achieved once the uncertainty (∼) in absolute energy scale is taken into account, see, e.g., [16] and Figure 1. Whether possible differences towards higher energies are simply caused by different instrumental systematics (including energy-dependent effects), and/or some real source differences (e.g., as the particle mean free path decreases, differences in the ‘large-scale’ structure may no longer be negligible) still remains to be studied. In general, the overall UHECR energy spectrum reveals a pronounced steepening above eV, that is compatible with a Greisen-Zatsepin-Kuzmin (GZK) cut-off [17,18], but could also be related to the maximum particle acceleration efficiency in UHECR emitting, astrophysical sources. A closer look now provides evidence for an additional spectral feature (referred to as “instep”) between eV and eV (with power-law index , where ). The spectrum becomes harder after the ankle and before eV (index p changing from ), and significantly steepens above eV (index p changing from ), cf. Figure 1. This could be interpreted as providing some indications for multiple astrophysical source contributions to the overall UHECR spectrum, such as, e.g., two extragalactic components, a soft lower-energy and a fiducial, hard (index ) higher-energy one [19].
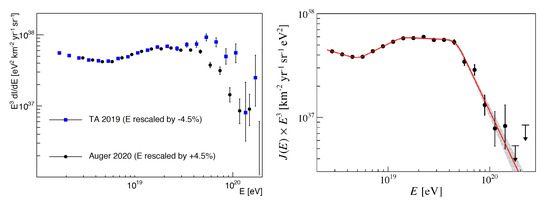
Figure 1.
Left: Energy spectrum of UHECRs as measured by the PA (Auger) and TA surface detectors, with each spectrum being adjusted for uncertainties in absolute energy scale by the same amount. Good agreement is achieved up to eV. Right: Evidence from PA data for a new spectral feature (“instep”) between and , also supported by TA data. The observed spectrum can be well fitted by a series of four power-laws. From ref. [16].
For reference, the observed UHECR spectrum roughly translates into an UHECR luminosity density (around eV) of erg/(Mpc yr) [20].
2.2. Composition of UHECRs
Upon entering the atmosphere, cosmic-ray particles initiate hadronic showers by interaction with atmospheric nuclei, cf. ref. [21] for review. The number of secondary shower particles increases up to a depth (measured in g/cm), beyond which the available energy becomes insufficient to create further particles. In general, the depth of the shower maximum is sensitive to the primary mass A and initial energy , approximately as , and hence light particles penetrate deeper in the atmosphere and exhibit a steeper lateral distribution compared to heavy nuclei. The UHECR mass composition can thus in principle be inferred from measurements of the mean, , and its dispersion (RMS), . While high-energy hadronic interaction models play an important role in this and a coherent explanation of all data still remains challenging [22], the currently favoured interpretation points to a primary mass composition that is mixed and changes with energy. In particular, a comparison of UHECR data suggests that the composition becomes lighter between eV and eV, compatible with a transition from galactic to extragalactic cosmic rays [14]. Above eV the composition seems to become heavier again, as evident from the measurements of both, the mean and its fluctuations (see Figure 2). There is evidence that protons are gradually replaced by helium, helium by nitrogen etc, possibly continuing up to iron (e.g., ref. [23]).
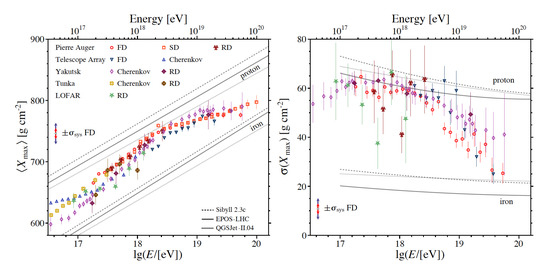
Figure 2.
Measurements of the mean (left) and its fluctuations (right) of the distribution of shower maximum as function of energy, along with predictions for proton and iron nuclei based on hadronic interaction models. There is an apparent trend for the composition to become heavier towards highest energies. Systematic uncertainties of the fluorescence (FD) measurements of TA (Telescope Array) and PA (Auger) are indicated as blue and red arrows, respectively. From ref. [14].
Note that within current systematic and statistical uncertainties, the TA and PA results appear compatible with each other. As shown below, the requirements on astrophysical accelerators become much less demanding if the composition becomes indeed heavier towards the highest energies.
2.3. Anisotropies in the Arrival Direction of UHECRs
While UHECRs are deflected in magnetic fields, significant anisotropies in their arrival directions could offer important clues as to their astrophysical origin. On large angular scales (>), for example, PA has reported strong evidence (≥) for a dipole anisotropy (∼ away from the Galactic Center) above eV with an amplitude of ≃, supporting an extragalactic origin of UHECRs [3,24]. The evidence for a growth of the amplitude with energy further supports this claim [25]. In principle, searches for possible anisotropies on intermediate scales (a few tens of degrees) could offer further, improved insights. Typically however, these anisotropy results are somewhat less significant and need thus be viewed with some caution. Nevertheless, based on an updated analysis, TA [26,27] has reported evidence for a “hot spot” in the UHECR events above eV (smeared out on circles of ) at a level of ∼ (local significance) and (global significance), respectively, (cf. also [28]). In equatorial coordinates, the TA hot spot is centered around R.A. and dec ∼, approximately in the direction of the starburst galaxy M82 ( Mpc) and the Ursa Major/Virgo supercluster ( Mpc). In addition, at lower energies a “warm spot” (∼ local significance) around R.A. and dec , approximately in the direction of the Perseus-Pisces supercluster ( Mpc), or Andromeda [29], has been reported. On the other hand, based on a constrained search PA has also reported an UHECR excess ("warm spot”) at a ∼ level above eV on an angular scale of around the Centaurus region [30,31], containing amongst other objects the radio galaxy Cen A and the starburst galaxies M83 and NGC 4945, see also Figure 3.
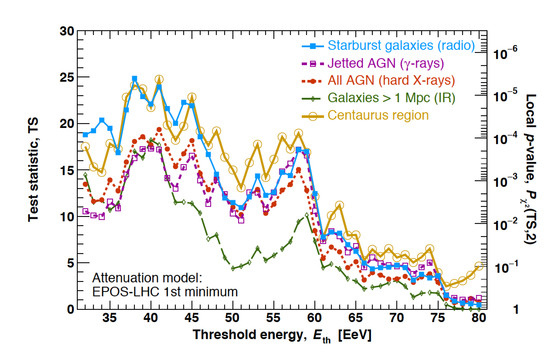
Figure 3.
Significance (test statistic) of the search for UHECR anisotropies as a function of threshold energy (in EeV) against four, complementary catalogs, including jetted AGNs and starburst galaxies (SBGs), along with the results for the Centaurus region. In general, the AGN catalogs are dominated by a contribution from Cen A, while the SBGs M83 and NGC 4945 in the Centaurus region feature prominently in the SBG model. From ref. [30].
3. On Possible Correlations of UHECRs with Matter and Known Sources
The anisotropy findings have motivated a variety of studies searching for possible correlations with matter and/or AGNs and starburst galaxies catalogs. Examples include:
3.1. On Correlations with Catalogs
In the most recent PA analysis, correlation studies of the arrival direction of PA events above 32 EeV (∼2600 events) have been performed with four different catalogs, including a catalog of jetted AGNs and a catalog of starburst galaxies (SBGs) [30,31]. Interestingly, a SBG model with search radius ∼ that attributes of the UHECR (>38 EeV) events to a catalog of 44 nearby SBGs (including NGC 4945, NGC 253, M83, NGC 1068), and the remaining to an isotropic background, appears favoured at over the hypothesis of isotropy. In comparison, a jetted AGN model with search radius of ∼ that attributes ∼ of the UHECR flux to a catalog of 26 nearby, -bright AGNs (including Cen A, M87, Mkn 421, Mkn 501 and Fornax A) is only preferred at a level, cf. Figure 3. However, although the significance is different, these findings do not (yet) provide statistically compelling evidence for a catalog preference.
From an astrophysical physical point of view, the interpretation is further complicated by the fact that (i) the UHECR luminosities of individual AGNs or SBGs is not known and thus some ad hoc proxies (e.g., average Fermi-LAT fluxes for AGNs) have to be employed and (ii) a realistic treatment of deflection in magnetic fields is not incorporated as variations from model to model remain too large to be included in the analysis. Note that even if a significant statistical association of UHECR events with SBGs (e.g., the TA hot spot with M82) were to be established, this would physically not necessarily be conclusive, as it might also be related to an echo of the past, i.e., UHECRs that were accelerated by radio galaxies and subsequently being scattered by SBGs (see Section 3.4 below) [32].
3.2. On Correlation with Matter
Following a different approach, Ding et al. [33] have recently studied the possible imprint of the (local) large-scale structure on the UHECR sky distribution. Assuming that the UHECR source density is proportional to the Cosmicflows-2 matter density field [34] and incorporating the PA-inferred chemical composition of UHECRs, they showed that the magnitude and the energy-dependence and, to some extent, also the direction of the PA dipole anisotropy above eV could in principle be reproduced in a scenario with many low power sources (following the matter distribution) instead of a few high-power ones. Their findings verify that the observed anisotropy is incompatible with a pure proton composition. Typically, in such frameworks a good reconstruction of the dipole direction is quite challenging to achieve [35]. The considered approach is advanced in that it includes the relevant energy losses and magnetic deflection (essentially in the Galactic magnetic field) via multi-particle tracking as well as fits to the (PA) mass composition. Possible caveats concern the use of a highly simplified source model (all being standard candles in terms of luminosity, composition and spectral index), the fact that prominent individual sources (e.g., Cen A, cf. above) are not included, and the assumption of a homogeneous turbulent (non-structured) extragalactic magnetic field.
3.3. On Correlation with Nearby Radio Galaxies
Using structured extragalactic magnetic field (EGMF) models with voids and filaments as inferred from MHD (ENZO) simulations, and focusing on nearby radio galaxies, de Oliveira & de Souza [36] have recently shown that the EGMF structure can dominate the arrival of UHECRs from nearby sources. In particular, while the EGMF choice does not strongly affect the UHECR flux from Cen A, Earth is found to be in a flux-suppressed position to receive UHECRs from the direction of M87, while favoured for Fornax A. With only these three sources, the PA dipole direction cannot be explained at energies below 32 EeV, but might be above these energies if the sources inject heavy nuclei. Moreover, Cen A, M87 and Fornax A are found to contribute to the excess emission associated with the detected UHECR hot spots (HS). In particular, Cen A may contribute to HS1 (by light nuclei), Fornax A to HS2 (by intermediate nuclei) and M87 to HS3 (by light to intermediate nuclei), cf. Figure 4.
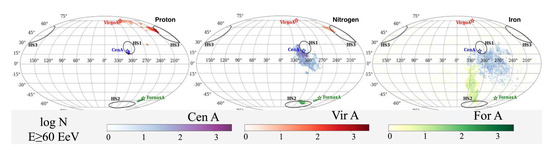
Figure 4.
Sky maps (galactic coordinates) of the arrival direction of simulated UHECR events above 60 EeV for a strong and highly structured extragalactic magnetic field (Prim), along with the locations of three excess (HS: "hot spots") regions inferred from PA and TA maps (black solid circles). From left to right for proton, nitrogen and iron. The contributions from M87 (Virgo A), Cen A and Fornax A are shown in red, blue and green, respectively. Accordingly, light nuclei from Cen A may contribute to HS1, intermediate nuclei from Fornax A to HS2 and light to intermediate nuclei from M87 to HS3. From ref. [36].
The considered model does not aim to fit the mass composition, but includes the relevant energy losses and a (CRPropa3) treatment of magnetic deflection in the Galactic and the local EGMF, as well as source specific rigidity cut-offs. The results fit into a framework where a few nearby radio galaxies are considered to dominate the UHECR flux above the ankle, cf. also [37].
3.4. An UHECR Echo from the Past?
As common in astrophysics, finding some correlation does not straightforwardly establish causality, in our case the true astrophysical sites of UHECR acceleration. This introduce a general caveat for such kind of approaches. As has been argued recently, for example, a putative correlation of UHECRs with starburst galaxies might be the echo of UHECRs originally produced in Cen A [32], see Figure 5 below. In this scenario, some of the UHECRs accelerated in Cen A, are considered to propagate directly to Earth, while others arrive later via M82 and/or M81, by being scattered and diffusively reflected in their halos. This would then imply that the present flux of UHECRs should rather be attributed to a leakage from the lobes of Cen A, with these lobes representing a reservoir of UHECRs accelerated during earlier (likely more powerful) activity episodes.
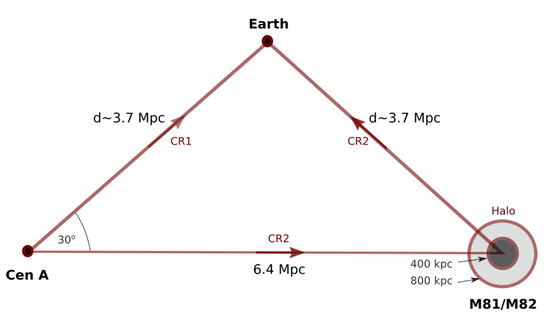
Figure 5.
Sketch of the echo model in which UHECRs, originally being accelerated in Cen A, are scattered and reflected in the spherical halo of the starburst galaxy M82 (with radius up to 800 kpc), introducing an apparent UHECR—starburst galaxy correlation. In this scenario, UHECRs arriving at Earth via M82 (CR2) are delayed by approximately 20 Myr relative to those arriving by direct propagation (CR1) from Cen A. After ref. [32].
4. Radio Galaxies as Prime UHECR Candidate Sources
Radio-loud active galaxies have for long been discussed as potential sources of the highest energy cosmic rays, e.g., refs [7,38,39,40,41,42,43,44,45]. Although active galaxies form only a small fraction (∼1–3%) of all galaxies, they are known as powerful, non-thermal emitting sources. Radio-loud Active Galaxies (or jetted AGNs, cf. [6]) are in fact characterised by multiple sites of efficient electron and putative cosmic-ray acceleration, from the vicinity of the black holes () up to multi kiloparsec-scale relativistic jets and giant lobes. While originally the more powerful Fanaroff-Riley (FR) II radio galaxies have been considered as promising UHECR accelerators, more recently the FR I radio galaxies Cen A, M87 and Fornax A have also been in the focus of attention as they are nearby and come with radio fluxes about an order of magnitude higher than other nearby radio galaxies, see also Figure 6 and Figure 7.2 For example, within ∼130 Mpc, a fraction of about ∼ galaxies in the 2MRS catalog have been identified as radio-loud; out of those only 24 galaxies have an intrinsic radio (1 GHz) luminosity greater or equal to Cen A, most of them being much more distant (>10 times) than Cen A [48].
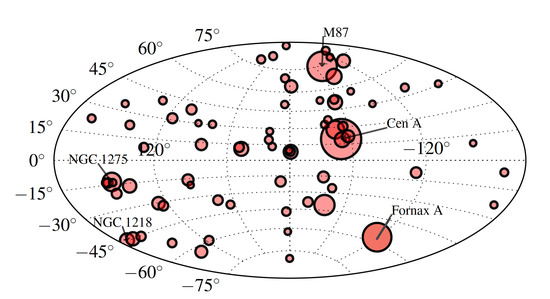
Figure 6.
Map in Galactic coordinates of the 74 radio galaxies within ∼130 Mpc, along with the locations of some prominent (FR I) sources. The circular areas are proportional to the ∼1 GHz-radio flux of the source. Adapted (with Fornax A adjusted) based on ref. [48].
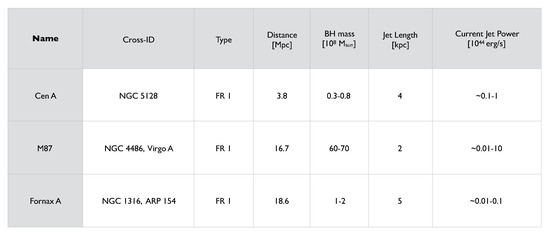
Figure 7.
The three nearest radio galaxies, considered to be UHECR prime candidate sources, along with values for their black hole mass, typical (projected) jet lengths and estimates for the “current” jet power. The latter are somewhat uncertain and model-dependent. Cross-IDs give their alternative source identifications.
For comparison and discussion, the relevant physics characteristics of the three nearest radio sources are, in the following, shortly summarized (cf. also Figure 7):
- Cen A: As the closest active galaxy to Earth ( Mpc), Centaurus A (Cen A) is one of the most prominent radio sources in the southern sky. Its inner region harbours a warped, relatively massive dust and gas disk, most likely the product of a past merger activity between a small, gas-rich spiral galaxy and a larger, elliptical one. There are in fact several lines of evidence suggesting that at least one major merger event occurred some – years ago [49]. Over time, Cen A then most likely underwent several phases of AGN activity [50,51]. Its central engine hosts a black hole of mass ≃ (0.3–0.8) [52], and currently emits a (nuclear) bolometric (photon) luminosity of erg/s [53]. At radio frequencies, Cen A is known for its peculiar morphology including a compact radio core, a sub-pc scale jet and counter-jet, a one-sided kpc-scale jet (∼4 kpc in projection), inner radio lobes as well as giant outer lobes with a length of several hundreds of kiloparsec, e.g., [54]. At high photon energies, gamma-ray observations have revealed GeV emission from the giant lobes as well as TeV emission along its large-scale jet, demonstrating the operation of efficient in situ particle acceleration [55,56,57]. VLBI observations indicate that Cen A is a non-blazar source, with its inner jet misaligned by about (12–45) and characterized by moderate bulk flow speeds ≤ c for the radio region probed [58]. EHT observations have revealed asymmetric (spine-sheath type) jet emission on scales of a few hundred Schwarzschild radii [59]. On larger scales (>100 pc), trans-relativistic jet speeds of ∼0.5–0.7 c have been inferred [60,61]. Estimates for the “current” kinetic jet power are in the range ∼– erg/s [56,62,63].
- M87: As the second closest active galaxy ( Mpc [64]), the Virgo Cluster galaxy M87 (NGC 4486) hosts one of the most massive black holes of [65,66]. Classified as low-excitation FR I source, M87 is thought to be currently accreting in a radiatively inefficient (RIAF) mode [67,68]. Common estimates for its total nuclear (disk and jet) bolometric luminosity in fact do not exceed erg/s by much [53,69,70,71]. In the radio, M87 exhibits an extended morphology including a sub-pc scale jet and counter-jet, a one-sided kpc-scale jet (∼2 kpc in projection) that is also seen in X-rays, inner lobes as well as a large-scale halo of size ∼50 kpc [69,70,72,73,74]. The X-ray emission seen in the large-scale jet of M87 provides evidence for the presence of ultra-relativistic electrons and the operation of efficient in situ acceleration [75]. Both, on sub-parsec as well as on kpc scales evidence has been found for a stratified jet structure compatible with a fast spine and a slower sheath [76,77]. There is evidence, including superluminal motion seen at optical and X-ray energies, that on larger scales (>100 pc) the jet still possesses significantly trans-relativistic (0.7 c) speeds [78,79]. Estimates for the kinetic power of the jet in M87 are somewhat uncertain and range from to erg/s [67,71,73,75]. Being at the center of a galaxy cluster, it has been argued that M87 might be repeatedly fed by accretion of satellite galaxies containing intermediate mass black holes [80]. There is evidence that accretion of a smaller galaxy has caused an important modification of its outer halo in the last Gyr [81]. On the other hand, many X-ray features (e.g., cavities) on halo-scale appear to be a result of recurrent AGN activity (on timescales probably down to ∼ yr) [82,83].
- Fornax A: Located at Mpc [84], Fornax A (NGC 1316) is the brightest member of the Fornax Cluster and a prominent merger remnant. In the optical, it resembles an elongated spheroid-type galaxy. In the radio, an S-shaped nuclear radio jet (∼5 kpc in projection) and giant double lobes spanning ∼350 kpc are seen [85]. Fornax A harbours a supermassive black hole of ≃ [86]. Given its peculiar morphology, Fornax A is thought to be shaped by a major merger about 3 Gyr ago, probably followed by some minor mergers of smaller companions [87,88,89]. There is evidence that the extended radio lobes have been formed by multiple episodes of nuclear activity on timescales of several Myr [90]. Characteristic estimates for the current jet power are in the range erg/s [90,91,92]. While Fornax A is commonly classified as an FR I source, different episodes of activity could explain some challenges as to a unique classification, e.g., the phase that shaped the lobes appears to have been more powerful compared with the activity of the central emission [90].
As shown below, jet power estimates can provide important constraints for UHECR acceleration (Section 5). Results for the current jet power are, however, not necessarily conclusive in this regard. In particular, as UHECRs are confined to magnetic fields, they might escape only slowly from the AGN environment. Since most likely many radio sources have undergone several phases of AGN activity, current FR I sources could well have seen more powerful jets in the past. If this is the case, then the history of a source becomes relevant for understanding its role as a possible UHECR accelerator. It has been argued, for example, that this particularly applies to Cen A and Fornax A where UHECR particles, accelerated in the past, could still be escaping from their giant lobes [45,93]. Note that the presence of strong magnetic fields on cluster scales might also suppress the escape of nuclear UHECRs from the Virgo Cluster (M87) [94].
For an informative, recent discussion of the role of individual FR I radio galaxies as possible UHECR sources the reader is also referred to refs. [95,96] (Cen A), [97] (Virgo A/M87), [98] (Cen B) and [45] (Fornax A), respectively.
5. Basics Physics Constraints on UHECR Candidate Sources
In general, to be considered as a realistic astrophysical candidate, a possible UHECR source has to satisfy a few basic physics requirements. For example, in order to be capable of accelerating charged particles to ultra-high energies E, the relevant particles need to remain confined within the accelerator, i.e., the particle Larmor radius has to remain smaller than the characteristic dimension L of the source (), where B is the source magnetic field strength and Z the charge number. This introduces a basic (Hillas) bound
which is often visualised by means of a B-L (or R) diagram, Figure 8, delineating potential astrophysical sources that meet this requirement. Radio galaxies typically represent suitable candidates in this regard. An improved Hillas constraint is obtained once characteristic astrophysical flow velocities, V, are properly taken into account. This relates to the fact that particle acceleration will be constrained by the accessible, motional electric field, i.e., , which gives
where . Accordingly, efficient UHECR acceleration generally requires source environments with fast flow speeds , strong magnetic fields and/or large volumes [7]. Obviously, the requirements are significantly relaxed if the composition at the highest energies would be sufficiently heavy (e.g., ).
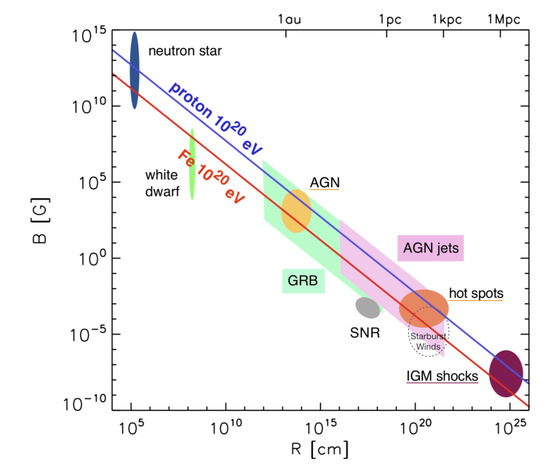
Figure 8.
Updated Hillas diagram [7], obtained by requiring the Larmor radius for a eV particle to be smaller than the characteristic source size R. The blue line and the red line show the limits for protons and iron nuclei, respectively. Shown also are astrophysical objects that can meet the requirements on source size and magnetic field B (above the respective lines). AGN (radio galaxies) typically represent suitable environments. Adapted based on ref. [4].
In general, the basic constraints above only represent necessary but not sufficient conditions for UHECR acceleration. Applications and more refined constraints have been discussed by various authors, e.g., refs. [41,99,100,101]. In particular, particle acceleration needs to proceed on a characteristic timescale (), which remains faster than both, the escape () and the relevant radiative loss () timescale, respectively. Since depends on acceleration physics, and , on individual source physics, one important outcome of this is that detailed "multi-messenger" studies of individual sources (allowing to, e.g., infer magnetic fields and flow speeds) become highly relevant again. Hence, while an individual source may formally belong to the "right" class of objects in the Hillas diagram, its true suitability can only be verified within a wider astrophysical perspective. To illustrate this, note that already the three closest FR I radio galaxies reveal a significant spread in parameters, cf. Figure 7.
The Hillas source constraint can be used to infer the magnetic power a putative accelerator needs to carry to allow for UHECR production. For collimated, non-relativistic () jetted outflows for example, . With , and L from Equation (2), one obtains
This can be extended to shock-type particle acceleration in relativistic outflows, see, e.g., ref. [101], resulting in a strong, generalized Hillas constraint on the required source power. The argument utilises (i) the requirement that particle acceleration must proceed faster than dynamical escape, i.e., that in the local, co-moving frame (primed quantities referring to the co-moving frame). If one expresses the timescale for shock acceleration in terms of the gyro-timescale, i.e., , where provides a measure for the efficiency, and uses that the dynamical timescale can be written as (with d the longitudinal length scale and the flow Lorentz factor), then maximum achievable UHECR energies in the observer’s frame can be re-expressed as . To allow for this, however, the outflow (ii) would need to carry a high enough magnetic power , where r denotes the lateral half width and . Using the relation from (i), and noting that we can approximate , where is the jet/flow half opening angle, this can be rewritten as , or
For the commonly assumed , this thus implies a lower limit on the required source luminosity for a steady relativistic () outflow to accelerate charged particles to energies E, of erg/sec. For non-relativistic shocks, where , this condition becomes even more stringent as , cf. Equation (3). In general, the situation is again much relaxed if a heavier () composition would prevail at the highest end, as suggested by the experimental findings reported in Section 2.2. In particular, the three closest FR I radio galaxies, Cen A, M87 and Fornax A could then, already in their current phase of activity, satisfy the power requirement imposed by shock acceleration, cf. Figure 7. On the other hand, since UHECRs get deflected in (Galactic) magnetic fields by , one may have to address, why, assuming (!) a conventional Fermi-type particle spectrum, we do not seem to observe a (more) pronounced anisotropy associated with protons at , cf. refs. [101,102,103].
Note that from an astrophysical point of view, the power requirement, Equation (4), disfavours starburst galaxies (SBGs) as promising UHECR accelerators. Since the winds in SBGs are comparatively slow (shock velocities less than a few ∼1000 km/s) and carry rather modest power erg/sec, cf. refs. [45,104,105,106], shock-driven UHECR acceleration in SBGs is unlikely to be efficient. Unless SBGs would be (more) frequent hosts of explosions of UHECR progenitors that match the Hillas criterion (e.g., long GRBs), this would suggest that a putative UHECR-SBG correlation (if any) is more consistently interpreted as being caused by a scattering of UHECRs originally accelerated in radio galaxies (see Section 3.4).
6. UHECR Acceleration in AGNs: Sites and Mechanisms
Radio-loud or jetted AGNs provide multiple sites for efficient particle acceleration, including the vicinity of the black hole (in so-called “vacuum” gaps), the inner (pc-scale) and outer (kpc-scale) jet, the jet termination shock (“hot spot”) in the case of powerful sources, the back-flowing region and the jet-inflated, large-scale lobes, see, e.g., Figure 9.
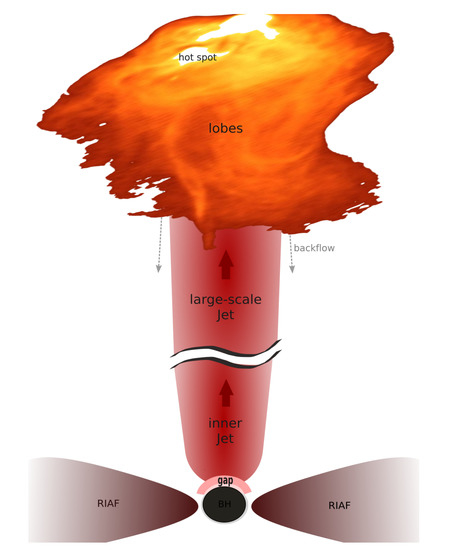
Figure 9.
Sketch: Radio galaxies or jetted AGNs provide multiple sites for cosmic particle acceleration, from the black hole vicinity (gaps) to their large-scale lobes. The preferred acceleration mechanism can change, dependent on the location within the source. Some of the mechanisms might as well work in tandem as to UHECR production.
In principle, a variety of acceleration mechanisms can be operative, from, e.g., “one-shot” type particle acceleration (by an emergent, ordered electric field component) to Fermi-type particle acceleration [107,108] based on particles repeatedly scattering off moving magnetic inhomogeneities (plasma waves) and drawing energy from the velocity changes they experience during their diffusion process, cf. Figure 10. The operating mechanism can change, dependent on the location within the source.
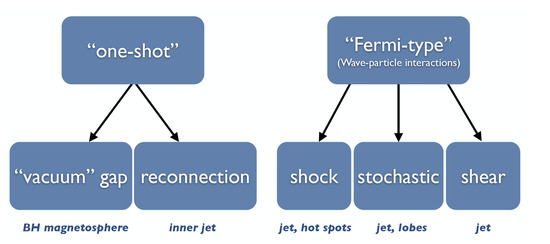
Figure 10.
Possible acceleration mechanisms and preferred sites in AGNs (not exhaustive). Sometimes the processes could be intertwined, e.g., reconnection could also be a driver for part of the turbulence required for stochastic acceleration.
In the following, three exemplary, recent scenarios will be highlighted.
6.1. Cosmic-Ray Acceleration in the Magnetospheres of Rotating Supermassive Black Holes
The vicinity of accreting, supermassive black holes is permeated by strong magnetic fields B whose strengths can reach thousands of Gauss. Fields that are dragged into rotation () by the black hole can induce an electric field, that, if not screened, can facilitate efficient particle acceleration. The possibility of UHECRs acceleration in the magnetospheres of supermassive black holes has been discussed by several authors, see, e.g., refs. [109,110,111,112,113,114,115]. In this framework, particle acceleration essentially relies on the emergence of an electric field component parallel to the magnetic field in a charge-deficient (“gap”) region close to a rotating black hole, cf. also ref. [116] for a related review. This could occur either around the so-called null surface across which the Goldreich-Julian charge density, , required to screen the electric field, changes sign, or at the stagnation surface that separates MHD in- and outflows, see Figure 11.
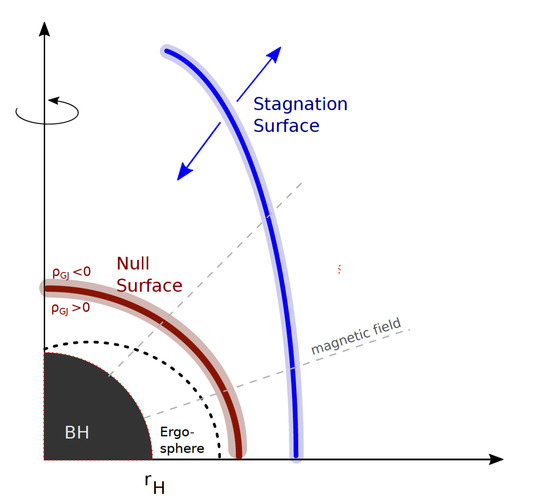
Figure 11.
Illustration of possible locations of charge-deficient regions (gaps) around a rotating black hole in which UHECR acceleration could occur. The red line denotes the null surface across which the required Goldreich-Julian charge density changes sign, while the blue line delineates the stagnation surface from which stationary MHD flows start.
The maximum available voltage drop for a gap of width h around a rotating (Kerr) black hole is of the order of [117]
assuming a horizon-threading magnetic field G, a black hole of mass , field line rotation with , normalized accretion rate and a gravitational radius . This would seem to suggest that in massive () and active () galaxies, ultra-high energies eV might be accessible, provided no other limitations exist. However, charged particles moving along curved magnetic field lines will also undergo curvature radiation losses. Taking these radiative losses into account introduces a general upper limit for a particle of mass m and charge number Z, which is of the order of [117]
for curvature radii of the order of the gravitational one. Note that for low accretion rates and narrow gaps, Equation (5) will be more constraining and set the relevant limit. Note also, that Equation (6) provides an example for a process where the maximum energy no longer scales linearly with Z.
In reality, the prospects for UHECR acceleration in black hole magnetospheres are expected to be further reduced: Unless accretion rates are sufficiently low (i.e., well below ), the ambient soft photon environment will facilitate efficient pair production in the gap (if gaps form at all, cf. [118,119]), leading to gap sizes , thereby significantly reducing the particle energies achievable, cf. Equation (5). On the other hand, if accretion rates would be very low, , as in the case of “quiescent quasars”, externally supported magnetic fields () would be much reduced as well. By hosting one of the most massive black hole () and accreting at low rates (RIAF mode), the radio galaxy M87 represents an instructive example to explore this in more details this:
Solving the system of relevant partial differential Equations (e.g., Gauss’ law, equation of particle motion, continuity equation), one can seek for self-consistent steady gap solutions [115,119], that provide insights into characteristic electric field strengths and achievable voltage drops, see, e.g., Figure 12. For example, taking an accretion rate , which is close to the mean MAD value used in Event Horizon Telescope (EHT) GRMHD simulations for M87 [68] and which corresponds to jet powers of a few times erg/s, the gap properties for M87 can be determined, see Figure 13. These gap solutions imply a voltage drop for M87 which is of the order of V, suggesting that its black hole is not an efficient UHECR proton accelerator.
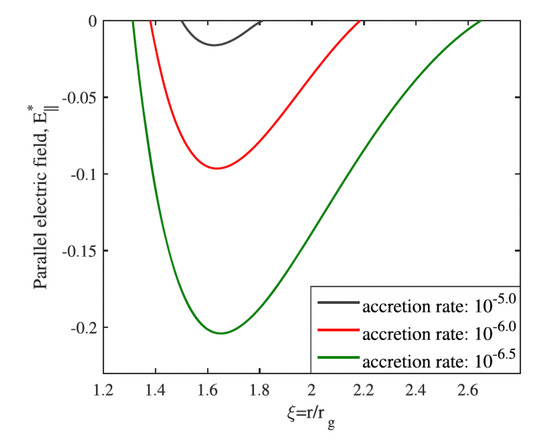
Figure 12.
Characteristic gap evolution for a rotating supermassive black hole of mass that accretes in a radiatively inefficient mode. The curves show the radial distribution of the parallel electric field component for different accretion rate. The gap width and voltage drop increase as the accretion rate drops because pair creation of energetic photons with the soft photon field becomes less efficient. Results like these can be used to evaluate the gap properties and prospects for UHECR acceleration for a particular source of interest. From ref. [115].

Figure 13.
Characteristic gap properties inferred for M87 assuming and . The columns give the extension or width h of the gap, the associated voltage drop, and the total gap power for a global current . Based on ref. [115].
These considerations reinforce the belief that in our sources of interest, efficient gap-type particle acceleration of protons to energies much beyond eV is problematic. We note that since efficient UHECR production in the black hole magnetosphere is accompanied by VHE curvature emission, gamma-ray observations could in principle allow to further constrain UHECR acceleration in under-luminous or "passive” AGNs, e.g., [110,120].
6.2. Shear Particle Acceleration in the Large-Scale Jets of AGNs
The large-scale jets in AGNs are efficient electron accelerators as evidenced by the detection of extended, non-thermal X-ray emission along their kpc-scale jets. The currently most favoured mechanism for producing the observed X-ray emission is electron synchrotron radiation, see, e.g., ref. [121,122] for a discussion. In M87, the radio-X-ray spectral characteristics in fact preclude an inverse Compton (CMB up-scattering by low energy electrons) origin [75], while in the case of Cen A the recent detection of extended VHE emission (due to up-scattering of dust by very energetic electrons) has verified the X-ray synchrotron interpretation and demonstrated the presence of ultra-relativistic electrons with Lorentz factors along its kpc-scale jet [57]. Given the short synchrotron cooling timescale and cooling length, kpc, of these electrons, the operation of a distributed acceleration mechanism is required to keep electrons energized and to account for the extended emission. Stochastic (2nd order Fermi) and shear particle acceleration are among the most promising acceleration mechanisms in this regard [123,124,125,126], cf. Figure 10. It seems then natural to suppose that these mechanisms could also facilitate the acceleration of protons and hadrons to high energies. Given the reduced energy losses and photo-disintegration, large-scale jets may in fact represent the most promising sites of UHECR acceleration. As has been argued in Section 5, however, to adequately assess the UHECR potential of a given source eventually requires a wider, multi-messenger approach. Insights from multi-wavelength SED modelling, for example, can be used to constrain key physical parameters of the jet (e.g., magnetic field strength, flow speed), cf. [126], and thereby inform our understanding.
In general, AGN jets are expected to exhibit some internal jet stratification and velocity shearing. A fast-spine, slower-sheath structure, for example, may already be introduced close to the black hole, and be related to an ergospheric-driven (Blandford-Znajek) jet surrounded by a disk-driven (Blandford-Payne) outflow, cf. ref. [127] for a review. As the jet continues to propagate, instabilities and mixing will continue to modify its shape and bulk velocity structure [128]. Limb-brightened features, different velocity and polarization pattern, for example, are observable signatures typically attributed to such flow structures, see, e.g., refs. [77,129].
Fast shear flows are conducive to efficient particle acceleration by a variety of means, see, e.g., ref. [130] for an introduction and review. Prominent scenarios include Fermi-type shear particle acceleration in non-gradual (discontinuous), e.g., refs. [131,132,133,134,135], and gradual (continuous), e.g., refs. [123,126,130,136,137,138,139,140,141,142], jet velocity shear flows. Particle acceleration in this framework basically draws on the kinematic flow velocity difference () that a particles experiences as it moves across the jet shear. AGN jets may be seeded with protons and heavier nuclei by, e.g., internal entrainment from stars intercepted by the jet, e.g., [62,143], or by the pick-up of Galactic type (SNR accelerated) cosmic rays permeating its halo environment, e.g., [133,134], cf. Figure 14.
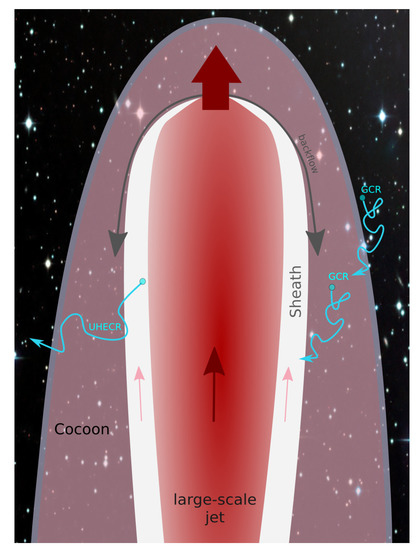
Figure 14.
Sketch of an UHECR model for AGN jets, in which some fraction of galactic-type cosmic rays (GCR) permeating the halo are swept up by the jet (“injected”) and shear-accelerated to ultra-high energies in its jet-sheath structure. Stochastic (2nd order Fermi) acceleration by turbulence in the cocoon and first-order Fermi acceleration by shocks in back-flowing regions may further add to particle energisation.
Non-gradual shear particle acceleration distribution would remain quasi-isotropic near a shear discontinuity (e.g., a flow velocity “jump”), the mean fractional energy change for a CR particle crossing and re-crossing the velocity shear (full cycle) is given by, e.g., [107,136]
similar to what is expected for the first Fermi cycle at relativistic shocks [144]. This might suggest that cosmic-ray seed particles could be boosted to very high energies in a velocity shear that is highly relativistic (, cf. [133,135]), while for a non-relativistic shear flow () only modest gains are obtained. In reality the situation is likely to be more complex: For relativistic flow velocities (), the emerging anisotropy of the particle distribution has to be appropriately modelled and taken into account. For repeated shear crossings, the principal effects of this is a reduction in efficiency, see, e.g., refs. [131,132]. Formally, this corresponds to a multiplication of the rhs of Equation (7) by an efficiency factor significantly below unity.
Knowing the average energy change, the characteristic acceleration timescale can then be approximated by
where here denotes the mean cycle time (into and out of the shear). Note that, depending on the considered set-up, e.g., for non-gradual shear at a jet side boundary, might actually be dominated by the turbulence properties in the cocoon, i.e., by the (diffusion) time a CR particle needs to return to the jet boundary shear [134]. If the transition layer becomes larger, particle scattering will occur within the shear layer, facilitating gradual shear particle acceleration within it, see, e.g., refs. [126,130,136,137,138,139,140]. On larger scales, this may generically be the case as shear flows are generally prone to shear-driven Kelvin-Helmholtz type instabilities. Simple stability considerations then suggest that to account for the observed structures, the shearing layers in large-scale AGN jets should encompass a sizeable fraction () of the jet radius [125]. In a microscopic picture [145], gradual shear acceleration can be viewed as a stochastic, second-order () Fermi-type particle acceleration process, in which the common scattering center speed, , is replaced by an effective velocity, , determined by the shear flow profile, i.e., by the characteristic flow velocity change sampled over the mean free path of the particle. In the case of a continuous (non-relativistic) shear flow for example, one has , see also ref. [130] for a discussion. This implies a characteristic, fractional energy change scaling as
If we again write the characteristic acceleration timescale as , then , i.e., in contrast to classical first-order Fermi (shock) or non-gradual shear acceleration, the acceleration timescale for gradual shear particle acceleration is inversely proportional to the particle mean free path . This seemingly unusual behaviour relates to the fact that as a particle increases its energy (), its mean free path increase as well (typically, ), so that a higher effective velocity is experienced.
To illustrate the potential of fast shearing flows for UHECR acceleration, three selected applications are highlighted in the following:
- Non-gradual shear particle acceleration in trans-relativistic FR I type jets: Kimura et al. [134] have reproduced the observed UHECR spectrum in a scenario that considers non-gradual shear particle acceleration in large-scale FR I jets, see Figure 15. The reference model assumes that Galactic-type cosmic rays (with, e.g., CR proton densities comparable to our Galaxy) are picked up, re-cycled and re-accelerated to UHE energies in a mildly relativistic jet (, G) surrounded by a narrow shear layer (). Their Monte Carlo simulations suggest that UHECRs escaping the source, possess a rather hard energy spectrum (). The chemical compositions at UHE energies (relative abundance ratio) is somewhat more complex, as different particle species (i) have different injection thresholds into the acceleration process ( TeV). Achievable maximum energy, EeV, are limited by the jet size (by ) and (via in , cf. Equation (8)) dominated by the diffusion process (assumed turbulence properties) in the cocoon. These numbers are in principle compatible with requirements on source energetics for FR I type sources, cf. also Equation (4). Given an FR I number density of – Mpc (cf. footnote 2) for example, an average source luminosity – erg/s would be needed to account for the observed UHECR luminosity erg/(Mpc yr) [20]. Moreover, possible anisotropy constraints are relaxed, partly due to suitable UHECR spectral shapes, as well as a high source number density (multi-FR I source contributions) with heavy composition. The results shown are, however, sensitive to the chosen cocoon properties (i.e., the assumed cocoon size and turbulence scale) and, in particular, dependent on a narrow velocity transition layer (defining the energy threshold for CR injection). Enlarging to satisfy jet stability constraints [125], for example, is likely to affect the outcome. Nevertheless, these simulations illustrate that non-gradual shear acceleration in an ensemble of FR I’s (and not only FR II’s) could in principle play an important role in UHECR acceleration.
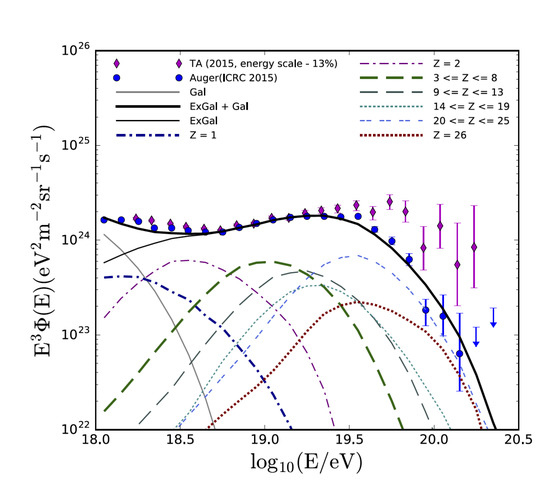 Figure 15. Reconstruction of the observed UHECR spectrum in a multi-FR I source scenario, assuming as reference a mildly relativistic () jet of width kpc surrounded by a narrow transition layer of width pc ( mG). The chemical composition at the highest energies is dominated by intermediate and heavy nuclei. From ref. [134].
Figure 15. Reconstruction of the observed UHECR spectrum in a multi-FR I source scenario, assuming as reference a mildly relativistic () jet of width kpc surrounded by a narrow transition layer of width pc ( mG). The chemical composition at the highest energies is dominated by intermediate and heavy nuclei. From ref. [134]. - Non-gradual shear particle acceleration in large-scale FR II type jets: Powerful AGN jets can remain significantly relativistic () on large scales, allowing for a substantial particle energy change per cycle if strong flow gradients are experienced over the mean free path of a particle, cf. Equation (7). In fact, given suitable conditions, significant -type boosts are possible across quasi-narrow shears, in which case only a few cycles (“shots”) would be needed to boost Galactic-type cosmic rays to UHE energies (sometimes referred to as “espresso” acceleration, e.g., ref. [133]). In this context, Mbarek & Caprioli [135,146] have recently studied the recycling of energetic cosmic rays in a relativistic () large-scale jet by following their test particle trajectories in a simulated (PLUTO) 3d-MHD jet environment, assuming a homogeneous ambient medium setup, see, e.g., Figure 16.
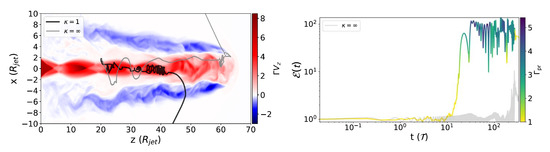 Figure 16. Left: Two-dimensional projection of exemplary trajectories of energetic particles, injected with initial Larmor radius into the simulated MHD jet environment. Right: Evolution of the relative energy gain of these particles, in terms of their initial relativistic gyro-period , colour-coded with the Lorentz factor probed. In 3d, the particle following the grey trajectory, only experiences, in the absence of scattering (), some moderate velocity differences (hence, gains) towards the end, and eventually becomes unconfined (escapes) as the initial jet magnetic field is assumed to decrease, approximately as along the jet, and a toroidal field scaling and has been employed. The particle following the black trajectory undergoes strong spatial (Bohm) diffusion (), experiences the fast jet spine and significantly gains energy (by up to a factor of ∼100) in these interactions. From ref. [135] (©AAS. Reproduced with permission).Given the fact that MHD jet simulations generally come with limited resolution (i.e., here of the order , where is the jet radius), a suitable (sub-grid) prescription needs to be designed to explore the effect of unresolved turbulence on the cosmic-ray transport. In the considered example, a gyro-dependent spatial diffusion coefficient , with the Larmor radius, has been employed (with momentum-diffusion being neglected), exploring cases where , with corresponding to Bohm diffusion, and implying no diffusion/scattering. The results show that incorporation of particle scattering (spatial diffusion) generally allows more particles to reach higher energies by probing the jet spine, making acceleration more efficient and resulting in a hardening of the injection spectrum. These features appear akin to what is expected in gradual- and non-gradual shear particle acceleration. To adequately assess the implications, an extension of the simulation framework to more general conditions will be helpful. As of now, comparison appears limited to, e.g., gyro-dependent pitch-angle diffusion, and rather high-power ( erg/s), significantly magnetized () FR II type jets. Nevertheless, these results already illustrate that for sufficiently large mean free paths multiple energy-boosts can occur in the environment of relativistic jets, allowing to push particle energies beyond what, e.g., stochastic or gradual shear acceleration alone might achieve.
Figure 16. Left: Two-dimensional projection of exemplary trajectories of energetic particles, injected with initial Larmor radius into the simulated MHD jet environment. Right: Evolution of the relative energy gain of these particles, in terms of their initial relativistic gyro-period , colour-coded with the Lorentz factor probed. In 3d, the particle following the grey trajectory, only experiences, in the absence of scattering (), some moderate velocity differences (hence, gains) towards the end, and eventually becomes unconfined (escapes) as the initial jet magnetic field is assumed to decrease, approximately as along the jet, and a toroidal field scaling and has been employed. The particle following the black trajectory undergoes strong spatial (Bohm) diffusion (), experiences the fast jet spine and significantly gains energy (by up to a factor of ∼100) in these interactions. From ref. [135] (©AAS. Reproduced with permission).Given the fact that MHD jet simulations generally come with limited resolution (i.e., here of the order , where is the jet radius), a suitable (sub-grid) prescription needs to be designed to explore the effect of unresolved turbulence on the cosmic-ray transport. In the considered example, a gyro-dependent spatial diffusion coefficient , with the Larmor radius, has been employed (with momentum-diffusion being neglected), exploring cases where , with corresponding to Bohm diffusion, and implying no diffusion/scattering. The results show that incorporation of particle scattering (spatial diffusion) generally allows more particles to reach higher energies by probing the jet spine, making acceleration more efficient and resulting in a hardening of the injection spectrum. These features appear akin to what is expected in gradual- and non-gradual shear particle acceleration. To adequately assess the implications, an extension of the simulation framework to more general conditions will be helpful. As of now, comparison appears limited to, e.g., gyro-dependent pitch-angle diffusion, and rather high-power ( erg/s), significantly magnetized () FR II type jets. Nevertheless, these results already illustrate that for sufficiently large mean free paths multiple energy-boosts can occur in the environment of relativistic jets, allowing to push particle energies beyond what, e.g., stochastic or gradual shear acceleration alone might achieve. - Gradual shear particle acceleration in relativistic AGN jets: On large scales, the shearing layers around relativistic jets are likely to encompass a sizeable fraction of the jet radius, e.g., [125]. Acceleration of electrons in such shearing flows has been proposed to account for the extended X-ray synchrotron emission that requires the maintenance of ultra-relativistic electrons () on kpc-scales, e.g., refs. [123,126]. In order to compete with diffusive escape, efficient shear acceleration typically requires sufficiently relativistic flow speeds, i.e., bulk Lorentz factors of some few [130,138,139]. At mildly relativistic speeds, intrinsic particle spectra become rather soft and sensitive to the underlying shear flow profile [142]. It seems natural to suppose that the underlying shear acceleration mechanism can be operative not only on electrons but also on cosmic rays. In principle, by modelling their multi-wavelength large-scale jet emission, improved constraints on the parameter space of individual sources can be obtained, thereby allowing a more precise classification [126]. Still, for a first orientation, a Hillas type approach (Section 5) may be chosen, requiring the properties of a potential UHECR source to be such as (i) to allow UHECRs to be confined within the shear, (ii) to enable particle acceleration to overcome radiative cooling (e.g., ) and (iii) to operate within the lifetime () of the system. Figure 17 shows an example, adjusted to (mildly relativistic) large-scale AGN jets, assuming a linearly decreasing flow profile with on the jet axis. A shear-width to jet length ratio has been employed.
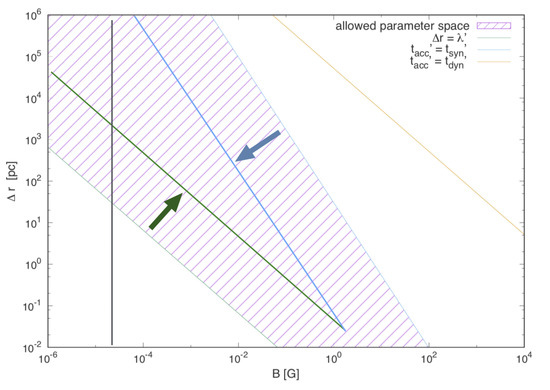 Figure 17. Allowed (shaded) parameter range, i.e., magnetic field strength B, shear layer width , to facilitate gradual shear acceleration of protons in (mildly relativistic) large-scale AGN jets, and to comply with confinement and synchrotron loss constraints. A Kolmogorov-type scaling for the particle mean free path () has been assumed. While for protons, EeV energies are well achievable, shear acceleration of protons to EeV in mildly relativistic jet flows appears quite restricted (to the parameter space confined by the arrows). Following ref. [130].Figure 17 suggests that shear acceleration of protons to energies ∼ eV can in principle be achieved for a quite plausible range of parameters, cf. also refs. [123,126,138,139] The vertical (black) line, for example, denotes the regime for a Cen A type source (G, cf. [57]), where the presence of a shear width of several tens of parsec would be sufficient. However, proton acceleration to ∼ eV in mildly relativistic shearing flows would seem to be less likely (requiring large, extended shears and higher magnetic fields). Since higher energies are possible either, in faster flows or for heavier particles, this would then suggest that current Cen A type (FR I) sources are contributors of heavy UHECRs, while ∼100 EeV protons would have to be associated with an earlier, more powerful (faster jet, FR II type) stage. This could possibly be linked to an evolutionary scenario where during the lifetime of a radio galaxy (at least for some of the nearby), basic characteristics could change FR class from FR II to FR I. In a simple leaky-box approach for gradual shear acceleration, UHECRs escaping their source, can have a relatively hard spectrum, approaching [130]. The spectrum is expected to be more complex, though, if non-gradual shear acceleration becomes operative toward higher energies.
Figure 17. Allowed (shaded) parameter range, i.e., magnetic field strength B, shear layer width , to facilitate gradual shear acceleration of protons in (mildly relativistic) large-scale AGN jets, and to comply with confinement and synchrotron loss constraints. A Kolmogorov-type scaling for the particle mean free path () has been assumed. While for protons, EeV energies are well achievable, shear acceleration of protons to EeV in mildly relativistic jet flows appears quite restricted (to the parameter space confined by the arrows). Following ref. [130].Figure 17 suggests that shear acceleration of protons to energies ∼ eV can in principle be achieved for a quite plausible range of parameters, cf. also refs. [123,126,138,139] The vertical (black) line, for example, denotes the regime for a Cen A type source (G, cf. [57]), where the presence of a shear width of several tens of parsec would be sufficient. However, proton acceleration to ∼ eV in mildly relativistic shearing flows would seem to be less likely (requiring large, extended shears and higher magnetic fields). Since higher energies are possible either, in faster flows or for heavier particles, this would then suggest that current Cen A type (FR I) sources are contributors of heavy UHECRs, while ∼100 EeV protons would have to be associated with an earlier, more powerful (faster jet, FR II type) stage. This could possibly be linked to an evolutionary scenario where during the lifetime of a radio galaxy (at least for some of the nearby), basic characteristics could change FR class from FR II to FR I. In a simple leaky-box approach for gradual shear acceleration, UHECRs escaping their source, can have a relatively hard spectrum, approaching [130]. The spectrum is expected to be more complex, though, if non-gradual shear acceleration becomes operative toward higher energies.
6.3. Shock Acceleration of UHECRs in AGN Jets
Following the general considerations above (e.g., Equation (2)), relativistic speeds are seemingly conducive for efficient UHECR acceleration. This, however, does not necessarily apply to diffusive shock acceleration. In fact, in many circumstances, particle acceleration at highly relativistic shocks has turned out to be problematic, see, e.g., refs. [147,148,149,150] for review. This is partly due to the fact that ultra-relativistic (magnetized) shocks are generically perpendicular (i.e., with downstream magnetic field quasi perpendicular to the shock normal, thus preventing particles from diffusing back upstream) and that the isotropization of particles ahead of the shock is no longer guaranteed (i.e., there is not enough time to growth turbulence on scales ). The situation is much more relaxed for mildly relativistic shock speeds, and this has led to the proposal that UHECR acceleration preferentially occurs at multiple (mildly relativistic) shocks in the back-flow regions surrounding the large-scale jets of radio galaxies, instead of at jet termination shocks [151]. Diffusive particle acceleration at trans-relativistic shocks is accompanied by an acceleration timescale approximately scaling as , where is the spatial diffusion coefficient. For typical numbers, the shock would have propagated a distance of up to a few kilo-parsecs if protons would be accelerated to EeV. Multiple shocks can in principle provide multiple opportunities for efficient particle acceleration, and also produce particle spectra harder (flatter) than the canonical (single-shock) power-law with index 2–2.3, e.g., [152,153]. The latter introduces some flexibility to account for the observed UHECR spectrum as suggested by some models [154].
The multiple shock-model has been motivated by 2D- and 3D-hydrodynamical simulations of light (density contrast –), powerful (∼ erg/s; more akin to FR II) jets in cluster environments, where significant back-flows have been found (e.g., see also [155,156]). Along these, multiple, moderately strong shocks have been seen to form, cf. Figure 18 for illustration.
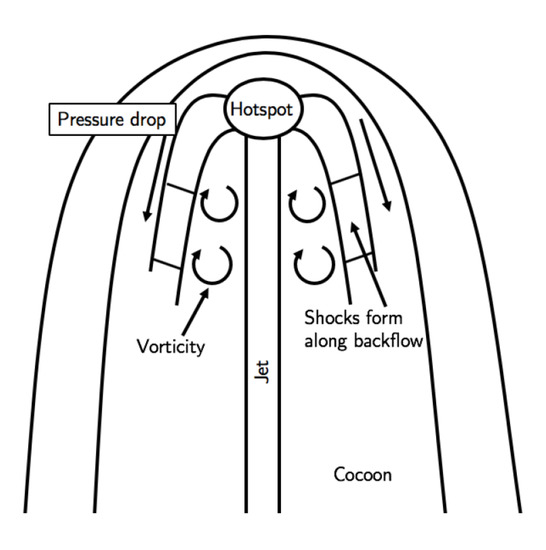
Figure 18.
Sketch of the considered scenario, where multiple (mildly relativistic) shocks in fast back-flows surrounding the large-scale jets of radio galaxies are considered to provide sites for efficient UHECR acceleration. From ref. [93].
The analysis of Lagrangian tracer particles in ref. [151] shows that about of the particles pass through a shock of Mach number , and ∼ pass through multiple shocks. Typical inferred shock speeds are of the order of c, while estimated sizes are kpc. Since in this setup, particles can only escape sidewise by diffusing across the magnetic fields, cosmic rays could reach the Hillas energy limit in a long-lived back-flow, even if Bohm diffusion () would not be achieved [157]. Assuming a reference magnetic field strength of G, for example, maximum cosmic-ray energies of eV, see Equation (2), would seem achievable. The rather large magnetic field strength employed here, could possibly be generated by magnetic field amplification as the plasma passes through the termination hot-spot into the back-flow [158]. While the general framework is clear, full high-resolution MHD simulations might be needed to validate numbers (e.g., field strengths, shock size, compression ratio) given the fact that the magnetic energy contribution would no longer seem to be negligible, and that weak shocks would be rather poor accelerators. Be it as it may, the multiple shock-scenario provides a stimulating rationale for the relevance of intermediate powerful, nearby radio galaxies in shaping the observed UHECR spectrum, see, e.g., ref. [45].
7. Conclusions and Perspectives
Current anisotropy results indicate that both, starburst galaxies and jetted AGNs could be (or host) the long-sought sources of UHECRs. While theoretical considerations suggest that starburst winds are less promising sites (by being not powerful enough), radio galaxies appear in principle capable of satisfying the relevant (Hillas-Type) requirements. In the AGN context, a variety of possible (not mutually exclusive) UHECR acceleration mechanisms have been explored in recent times. Among them, Fermi-type particle acceleration at trans-relativistic (internal) shocks and/or in shearing, relativistic jet flows appear most promising. In general, nearby FR I type radio galaxies (or restarted jets in close-by galaxies) could provide suitable environments in this regard. From a theoretical (particle acceleration) and phenomenological (UHECR anisotropy) point of view, insights from multi-messenger astrophysics [159] become important to obtain a more detailed picture, and to adequately assess the potential of specific source candidates. If the UHECR composition would become heavier (with, e.g., ) towards highest energies, as indicated by the recent Pierre Auger results, nearby FR I’s, such as Cen A, M87 and Fornax A, could probably meet the minimum power requirement already in activity phases comparable to the current ones. Since UHECRs are likely to escape rather slowly from their source environment, a significant proton contribution (if any) might possibly be related to a higher source stage in the past. There are indications, for example, that the giant lobe evolution in Cen A has been shaped by an enhanced activity in the past, making these lobes a potential reservoir of UHECR protons.
Further experimental constraints on the chemical composition and anisotropies of UHECRs, along with physically-motivated propagation studies will be important to eventually conclude about the astrophysical sources of UHECRs.
Funding
This research was funded by the German Science Foundation (DFG) under RI 1187/8-1.
Acknowledgments
I am grateful for inspiring discussion on UHECRs with Denis Allard and Sergey Ostapchenko during the 18th Rencontres du Vietnam Workshop. I have much benefited from insights provided by Felix Aharonian and Tony Bell. I also grateful to thank Andrew Taylor and Jonathan Biteau for helpful comments on the manuscript. I would like to thank Kumiko Kotera, Caina de Oliveira, James Matthews, Rostom Mbarek, Khota Murase and Sjoert van Velzen for allowance to use figures from their papers. Funding by a DFG Fellowship RI 1187/8-1 is gratefully acknowledged.
Conflicts of Interest
The author declares no conflict of interest.
Notes
| 1 | This so-called GZK horizon is longest ( Mpc) for 100 EeV protons and heavy nuclei (e.g., iron), but can be much shorter for intermediate masses (e.g., Mpc for helium and Mpc for silicon). |
| 2 | Characteristic (local) number densities are of the order – Mpc for FR I and – Mpc for FR II radio galaxies, cf. [46,47]. Cen A is the closest ( Mpc) FR I, while Pictor A is one of the closest (, Mpc) FR II radio galaxies. There are not many FR II sources known within the GZK horizon. |
References
- Bell, A.R. Cosmic ray acceleration. Astropart. Phys. 2013, 43, 56–70. [Google Scholar] [CrossRef]
- Blasi, P. The origin of galactic cosmic rays. A&ARv 2013, 21, 70. [Google Scholar] [CrossRef]
- Pierre Auger Collaboration; Aab, A.; Abreu, P.; Aglietta, M.; Samarai, I.A.; Albuquerque, I.F.M.; Allekotte, I.; Almela, A.; Alvarez Castillo, J.; Alvarez-Muñiz, J.; et al. Observation of a large-scale anisotropy in the arrival directions of cosmic rays above 8×1018 eV. Science 2017, 357, 1266–1270. [Google Scholar] [CrossRef]
- Kotera, K.; Olinto, A.V. The Astrophysics of Ultrahigh-Energy Cosmic Rays. ARA&A 2011, 49, 119–153. [Google Scholar] [CrossRef]
- Rieger, F. UHE Cosmic Rays and AGN Jets. High Energy Phenomena in Relativistic Outflows VII. arXiv 2019, arXiv:astro-ph.HE/1911.04171. [Google Scholar]
- Padovani, P. On the two main classes of active galactic nuclei. Nat. Astron. 2017, 1, 194. [Google Scholar] [CrossRef]
- Hillas, A.M. The Origin of Ultra-High-Energy Cosmic Rays. ARA&A 1984, 22, 425–444. [Google Scholar] [CrossRef]
- Array, T.; Abbasi, R.; Abu-Zayyad, T.; Allen, M.; Arai, Y.; Arimura, R.; Barcikowski, E.; Belz, J.; Bergman, D.; Blake, S.; et al. Highlights from the Telescope Array experiment. In Proceedings of the 37th International Cosmic Ray Conference, Berlin, Germany, 12–23 July 2021; p. 12. [Google Scholar]
- Novotný, V.; The Pierre Auger Collaboration; Abreu, P.; Aglietta, M.; Albury, J.M.; Allekotte, I.; Almela, A.; Alvarez-Muniz, J.; Alves Batista, R.; Anastasi, G.A.; et al. Energy spectrum of cosmic rays measured using the Pierre Auger Observatory. In Proceedings of the 37th International Cosmic Ray Conference, Berlin, Germany, 12–23 July 2021; p. 324. [Google Scholar]
- Aloisio, R. Acceleration and propagation of ultra high energy cosmic rays. PTEP 2017, 12A102, 115. [Google Scholar] [CrossRef]
- Kachelriess, M.; Semikoz, D.V. Cosmic Ray Models. arXiv 2019, arXiv:1904.08160. [Google Scholar] [CrossRef]
- Anchordoqui, L.A. Ultra-high-energy cosmic rays. Phys. Rep. 2019, 801, 1–93. [Google Scholar] [CrossRef]
- Kachelriess, M. Extragalactic cosmic rays. In Proceedings of the 37th International Cosmic Ray Conference, Berlin, Germany, 12–23 July 2021; p. 18. [Google Scholar]
- Coleman, A.; Eser, J.; Mayotte, E.; Sarazin, F.; Schröder, F.G.; Soldin, D.; Venters, T.M.; Aloisio, R.; Alvarez-Muñiz, J.; Alves Batista, R.; et al. Ultra-High-Energy Cosmic Rays: The Intersection of the Cosmic and Energy Frontiers. arXiv 2022, arXiv:2205.05845. [Google Scholar] [CrossRef]
- Bird, D.J.; Corbato, S.C.; Dai, H.Y.; Elbert, J.W.; Green, K.D.; Huang, M.A.; Kieda, D.B.; Ko, S.; Larsen, C.G.; Loh, E.C.; et al. Detection of a Cosmic Ray with Measured Energy Well beyond the Expected Spectral Cutoff due to Cosmic Microwave Radiation. ApJ 1995, 441, 144. [Google Scholar] [CrossRef]
- Tsunesada, Y.; Array, T.; Abbasi, R.; Abu-Zayyad, T.; Allen, M.; Arai, Y.; Arimura, R.; Barcikowski, E.; Belz, J.; Bergman, D.; et al. Joint analysis of the energy spectrum of ultra-high-energy cosmic rays as measured at the Pierre Auger Observatory and the Telescope Array. In Proceedings of the 37th International Cosmic Ray Conference, Berlin, Germany, 12–23 July 2021; p. 337. [Google Scholar]
- Greisen, K. End to the Cosmic-Ray Spectrum? PRL 1966, 16, 748–750. [Google Scholar] [CrossRef]
- Zatsepin, G.T.; Kuz’min, V.A. Upper Limit of the Spectrum of Cosmic Rays. Sov. J. Exp. Theor. Phys. Lett. 1966, 4, 78. [Google Scholar]
- Guido, E.; The Pierre Auger Collaboration; Abreu, P.; Aglietta, M.; Albury, J.M.; Allekotte, I.; Almela, A.; Alvarez-Muniz, J.; Alves Batista, R.; Anastasi, G.A.; et al. Combined fit of the energy spectrum and mass composition across the ankle with the data measured at the Pierre Auger Observatory. In Proceedings of the 37th International Cosmic Ray Conference, Berlin, Germany, 12–23 July 2021; p. 311. [Google Scholar]
- Murase, K.; Fukugita, M. Energetics of high-energy cosmic radiations. Phys. Rev. D 2019, 99, 063012. [Google Scholar] [CrossRef]
- Engel, R.; Heck, D.; Pierog, T. Extensive Air Showers and Hadronic Interactions at High Energy. ARNPS 2011, 61, 467–489. [Google Scholar] [CrossRef]
- Ostapchenko, S. High energy cosmic ray interactions and UHECR composition problem. Eur. Phys. J. Web Conf. 2019, 210, 02001. [Google Scholar] [CrossRef][Green Version]
- Alves Batista, R.; Biteau, J.; Bustamante, M.; Dolag, K.; Engel, R.; Fang, K.; Kampert, K.H.; Kostunin, D.; Mostafa, M.; Murase, K.; et al. Open questions in cosmic-ray research at ultrahigh energies. Front. Astron. Space Sci. 2019, 6, 23. [Google Scholar] [CrossRef]
- de Almeida, R.; The Pierre Auger Collaboration; Abreu, P.; Aglietta, M.; Albury, J.M.; Allekotte, I.; Almela, A.; Alvarez-Muniz, J.; Alves Batista, R.; Anastasi, G.A.; et al. Large-scale and multipolar anisotropies of cosmic rays detected at the Pierre Auger Observatory with energies above 4 EeV. In Proceedings of the 37th International Cosmic Ray Conference, Berlin, Germany, 12–23 July 2021; p. 335. [Google Scholar]
- Aab, A.; Abreu, P.; Aglietta, M.; Albuquerque, I.F.M.; Albury, J.M.; Allekotte, I.; Almela, A.; Alvarez Castillo, J.; Alvarez-Muñiz, J.; Anastasi, G.A.; et al. Large-scale Cosmic-Ray Anisotropies above 4 EeV Measured by the Pierre Auger Observatory. ApJ 2018, 868, 4. [Google Scholar] [CrossRef]
- Kim, J.; Ivanov, D.; Kawata, K.; Sagawa, H.; Thomson, G. Hotspot Update, and a new Excess of Events on the Sky Seen by the Telescope Array Experiment. In Proceedings of the 37th International Cosmic Ray Conference, Berlin, Germany, 12–23 July 2021; p. 328. [Google Scholar]
- Tkachev, I.; Fujii, T.; Ivanov, D.; Jui, C.C.H.; Kawata, K.; Kim, J.H.; Kuznetsov, M.Y.; Nonaka, T.; Ogio, S.; Rubtsov, G.I.; et al. Telescope Array anisotropy summary. In Proceedings of the 37th International Cosmic Ray Conference, Berlin, Germany, 12–23 July 2021; p. 392. [Google Scholar]
- Matthews, J.; Telescope Array Collaboration. Highlights from the Telescope Array Experiment. In Proceedings of the 35th International Cosmic Ray Conference (ICRC2017), Busan, Republic of Korea, 12–20 July 2017; Volume 301, p. 1096. [Google Scholar]
- Zirakashvili, V.N.; Ptuskin, V.S.; Rogovaya, S.I. Ultra high energy cosmic rays from past activity of Andromeda galaxy. arXiv 2022, arXiv:2211.04522. [Google Scholar] [CrossRef]
- Biteau, J.; The Pierre Auger Collaboration; Abreu, P.; Aglietta, M.; Albury, J.M.; Allekotte, I.; Almela, A.; Alvarez-Muniz, J.; Alves Batista, R.; Anastasi, G.A.; et al. The ultra-high-energy cosmic-ray sky above 32 EeV viewed from the Pierre Auger Observatory. In Proceedings of the 37th International Cosmic Ray Conference, Berlin, Germany, 12–23 July 2021; p. 307. [Google Scholar]
- The Pierre Auger Collaboration; Abreu, P.; Aglietta, M.; Albury, J.M.; Allekotte, I.; Almeida Cheminant, K.; Almela, A.; Alvarez-Muñiz, J.; Alves Batista, R.; Ammerman Yebra, J.; et al. Arrival Directions of Cosmic Rays above 32 EeV from Phase One of the Pierre Auger Observatory. arXiv 2022, arXiv:2206.13492. [Google Scholar]
- Bell, A.R.; Matthews, J.H. Echoes of the past: Ultra-high-energy cosmic rays accelerated by radio galaxies, scattered by starburst galaxies. MNRAS 2022, 511, 448–456. [Google Scholar] [CrossRef]
- Ding, C.; Globus, N.; Farrar, G.R. The Imprint of Large-scale Structure on the Ultrahigh-energy Cosmic-Ray Sky. ApJL 2021, 913, L13. [Google Scholar] [CrossRef]
- Hoffman, Y.; Carlesi, E.; Pomarède, D.; Tully, R.B.; Courtois, H.M.; Gottlöber, S.; Libeskind, N.I.; Sorce, J.G.; Yepes, G. The quasi-linear nearby Universe. Nat. Astron. 2018, 2, 680–687. [Google Scholar] [CrossRef]
- Allard, D.; Aublin, J.; Baret, B.; Parizot, E. What can be learnt from UHECR anisotropies observations? Paper I: Large-scale anisotropies and composition features. arXiv 2021, arXiv:2110.10761. [Google Scholar]
- de Oliveira, C.; de Souza, V. Magnetically Induced Anisotropies in the Arrival Directions of Ultra-high-energy Cosmic Rays from Nearby Radio Galaxies. ApJ 2022, 925, 42. [Google Scholar] [CrossRef]
- Eichmann, B.; Kachelrieß, M.; Oikonomou, F. Explaining the UHECR spectrum, composition and large-scale anisotropies with radio galaxies. JCAP 2022, 2022, 6. [Google Scholar] [CrossRef]
- Brecher, K.; Burbidge, G.R. Extragalactic Cosmic Rays. ApJ 1972, 174, 253. [Google Scholar] [CrossRef]
- Takahara, F. On the Origin of Highest Energy Cosmic Rays. Prog. Theor. Phys. 1990, 83, 1071–1075. [Google Scholar] [CrossRef]
- Rachen, J.P.; Biermann, P.L. Extragalactic ultra-high energy cosmic rays. I. Contribution from hot spots in FR-II radio galaxies. A&A 1993, 272, 161–175. [Google Scholar]
- Blandford, R.D. Acceleration of Ultra High Energy Cosmic Rays. Phys. Scr. Vol. T 2000, 85, 191–194. [Google Scholar] [CrossRef]
- Rieger, F.M. Cosmic Ray Acceleration in Active Galactic Nuclei - On Centaurus A as a possible UHECR Source. arXiv 2009, arXiv:0911.4004. [Google Scholar]
- Hardcastle, M.J. Which radio galaxies can make the highest energy cosmic rays? MNRAS 2010, 405, 2810–2816. [Google Scholar] [CrossRef]
- Biermann, P.L.; de Souza, V. Centaurus A: The Extragalactic Source of Cosmic Rays with Energies above the Knee. ApJ 2012, 746, 72. [Google Scholar] [CrossRef]
- Matthews, J.H.; Bell, A.R.; Blundell, K.M.; Araudo, A.T. Fornax A, Centaurus A, and other radio galaxies as sources of ultrahigh energy cosmic rays. MNRAS 2018, 479, L76–L80. [Google Scholar] [CrossRef]
- Padovani, P.; Miller, N.; Kellermann, K.I.; Mainieri, V.; Rosati, P.; Tozzi, P. The VLA Survey of Chandra Deep Field South. V. Evolution and Luminosity Functions of Sub-millijansky Radio Sources and the Issue of Radio Emission in Radio-quiet Active Galactic Nuclei. ApJ 2011, 740, 20. [Google Scholar] [CrossRef]
- Prescott, M.; Mauch, T.; Jarvis, M.J.; McAlpine, K.; Smith, D.J.B.; Fine, S.; Johnston, R.; Hardcastle, M.J.; Baldry, I.K.; Brough, S.; et al. Galaxy Furthermore, Mass Assembly (GAMA): The 325 MHz radio luminosity function of AGN and star-forming galaxies. MNRAS 2016, 457, 730–744. [Google Scholar] [CrossRef]
- van Velzen, S.; Falcke, H.; Schellart, P.; Nierstenhöfer, N.; Kampert, K.H. Radio galaxies of the local universe. All-sky catalog, luminosity functions, and clustering. A&A 2012, 544, A18. [Google Scholar] [CrossRef]
- Israel, F.P. Centaurus A—NGC 5128. A&ARv 1998, 8, 237–278. [Google Scholar] [CrossRef]
- Saikia, D.J.; Jamrozy, M. Recurrent activity in Active Galactic Nuclei. Bull. Astron. Soc. India 2009, 37, 63–89. [Google Scholar]
- Struve, C.; Oosterloo, T.A.; Morganti, R.; Saripalli, L. Centaurus A: Morphology and kinematics of the atomic hydrogen. A&A 2010, 515, A67. [Google Scholar] [CrossRef]
- Neumayer, N. The Supermassive Black Hole at the Heart of Centaurus A: Revealed by the Kinematics of Gas and Stars. PASA 2010, 27, 449–456. [Google Scholar] [CrossRef]
- Whysong, D.; Antonucci, R. Thermal Emission as a Test for Hidden Nuclei in Nearby Radio Galaxies. ApJ 2004, 602, 116–122. [Google Scholar] [CrossRef]
- Feain, I.J.; Cornwell, T.J.; Ekers, R.D.; Calabretta, M.R.; Norris, R.P.; Johnston-Hollitt, M.; Ott, J.; Lindley, E.; Gaensler, B.M.; Murphy, T.; et al. The Radio Continuum Structure of Centaurus A at 1.4 GHz. ApJ 2011, 740, 17. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Ajello, M.; Atwood, W.B.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Baughman, B.M.; Bechtol, K.; et al. Fermi Gamma-Ray Imaging of a Radio Galaxy. Science 2010, 328, 725. [Google Scholar] [CrossRef]
- Yang, R.Z.; Sahakyan, N.; de Ona Wilhelmi, E.; Aharonian, F.; Rieger, F. Deep observation of the giant radio lobes of Centaurus A with the Fermi Large Area Telescope. A&A 2012, 542, A19. [Google Scholar] [CrossRef]
- H. E. S. S. Collaboration; Abdalla, H.; Adam, R.; Aharonian, F.; Ait Benkhali, F.; Angüner, E.O.; Arakawa, M.; Arcaro, C.; Armand, C.; Ashkar, H.; et al. Resolving acceleration to very high energies along the jet of Centaurus A. Nature 2020, 582, 356–359. [Google Scholar] [CrossRef]
- Müller, C.; Kadler, M.; Ojha, R.; Perucho, M.; Großberger, C.; Ros, E.; Wilms, J.; Blanchard, J.; Böck, M.; Carpenter, B.; et al. TANAMI monitoring of Centaurus A: The complex dynamics in the inner parsec of an extragalactic jet. A&A 2014, 569, A115. [Google Scholar] [CrossRef]
- Janssen, M.; Falcke, H.; Kadler, M.; Ros, E.; Wielgus, M.; Akiyama, K.; Baloković, M.; Blackburn, L.; Bouman, K.L.; Chael, A.; et al. Event Horizon Telescope observations of the jet launching and collimation in Centaurus A. Nat. Astron. 2021, 5, 1017–1028. [Google Scholar] [CrossRef]
- Hardcastle, M.J.; Worrall, D.M.; Kraft, R.P.; Forman, W.R.; Jones, C.; Murray, S.S. Radio and X-Ray Observations of the Jet in Centaurus A. ApJ 2003, 593, 169–183. [Google Scholar] [CrossRef]
- Snios, B.; Wykes, S.; Nulsen, P.E.J.; Kraft, R.P.; Meyer, E.T.; Birkinshaw, M.; Worrall, D.M.; Hardcastle, M.J.; Roediger, E.; Forman, W.R.; et al. Variability and Proper Motion of X-Ray Knots in the Jet of Centaurus A. ApJ 2019, 871, 248. [Google Scholar] [CrossRef]
- Wykes, S.; Hardcastle, M.J.; Karakas, A.I.; Vink, J.S. Internal entrainment and the origin of jet-related broad-band emission in Centaurus A. MNRAS 2015, 447, 1001–1013. [Google Scholar] [CrossRef]
- Sun, X.n.; Yang, R.z.; Mckinley, B.; Aharonian, F. Giant lobes of Centaurus A as seen in radio and gamma-ray images obtained with the Fermi-LAT and Planck satellites. A&A 2016, 595, A29. [Google Scholar] [CrossRef]
- Bird, S.; Harris, W.E.; Blakeslee, J.P.; Flynn, C. The inner halo of M 87: A first direct view of the red-giant population. A&A 2010, 524, A71. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; et al. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. ApJL 2019, 875, L1. [Google Scholar] [CrossRef]
- Broderick, A.E.; Pesce, D.W.; Tiede, P.; Pu, H.Y.; Gold, R.; Anantua, R.; Britzen, S.; Ceccobello, C.; Chatterjee, K.; Chen, Y.; et al. The Photon Ring in M87*. arXiv 2022, arXiv:2208.09004. [Google Scholar] [CrossRef]
- Reynolds, C.S.; Di Matteo, T.; Fabian, A.C.; Hwang, U.; Canizares, C.R. The ‘quiescent’ black hole in M87. MNRAS 1996, 283, L111–L116. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; et al. First M87 Event Horizon Telescope Results. V. Physical Origin of the Asymmetric Ring. ApJL 2019, 875, L5. [Google Scholar] [CrossRef]
- Biretta, J.A.; Stern, C.P.; Harris, D.E. The Radio to X-ray Spectrum of the M87 Jet and Nucleus. AJ 1991, 101, 1632. [Google Scholar] [CrossRef]
- Owen, F.N.; Eilek, J.A.; Kassim, N.E. M87 at 90 Centimeters: A Different Picture. ApJ 2000, 543, 611–619. [Google Scholar] [CrossRef]
- Prieto, M.A.; Fernández-Ontiveros, J.A.; Markoff, S.; Espada, D.; González-Martín, O. The central parsecs of M87: Jet emission and an elusive accretion disc. MNRAS 2016, 457, 3801–3816. [Google Scholar] [CrossRef]
- Marshall, H.L.; Miller, B.P.; Davis, D.S.; Perlman, E.S.; Wise, M.; Canizares, C.R.; Harris, D.E. A High-Resolution X-Ray Image of the Jet in M87. ApJ 2002, 564, 683–687. [Google Scholar] [CrossRef]
- de Gasperin, F.; Orrú, E.; Murgia, M.; Merloni, A.; Falcke, H.; Beck, R.; Beswick, R.; Bîrzan, L.; Bonafede, A.; Brüggen, M.; et al. M 87 at metre wavelengths: The LOFAR picture. A&A 2012, 547, A56. [Google Scholar] [CrossRef]
- Walker, R.C.; Hardee, P.E.; Davies, F.B.; Ly, C.; Junor, W. The Structure and Dynamics of the Subparsec Jet in M87 Based on 50 VLBA Observations over 17 Years at 43 GHz. ApJ 2018, 855, 128. [Google Scholar] [CrossRef]
- Sun, X.N.; Yang, R.Z.; Rieger, F.M.; Liu, R.Y.; Aharonian, F. Energy distribution of relativistic electrons in the kiloparsec scale jet of M 87 with Chandra. A&A 2018, 612, A106. [Google Scholar] [CrossRef]
- Perlman, E.S.; Biretta, J.A.; Zhou, F.; Sparks, W.B.; Macchetto, F.D. Optical and Radio Polarimetry of the M87 Jet at 0.2” Resolution. AJ 1999, 117, 2185–2198. [Google Scholar] [CrossRef]
- Mertens, F.; Lobanov, A.P.; Walker, R.C.; Hardee, P.E. Kinematics of the jet in M 87 on scales of 100-1000 Schwarzschild radii. A&A 2016, 595, A54. [Google Scholar] [CrossRef]
- Meyer, E.T.; Sparks, W.B.; Biretta, J.A.; Anderson, J.; Sohn, S.T.; van der Marel, R.P.; Norman, C.; Nakamura, M. Optical Proper Motion Measurements of the M87 Jet: New Results from the Hubble Space Telescope. ApJL 2013, 774, L21. [Google Scholar] [CrossRef]
- Snios, B.; Nulsen, P.E.J.; Kraft, R.P.; Cheung, C.C.; Meyer, E.T.; Forman, W.R.; Jones, C.; Murray, S.S. Detection of Superluminal Motion in the X-Ray Jet of M87. ApJ 2019, 879, 8. [Google Scholar] [CrossRef]
- Safarzadeh, M.; Loeb, A.; Reid, M. Constraining a black hole companion for M87* through imaging by the Event Horizon Telescope. MNRAS 2019, 488, L90–L93. [Google Scholar] [CrossRef]
- Longobardi, A.; Arnaboldi, M.; Gerhard, O.; Mihos, J.C. The build-up of the cD halo of M 87: Evidence for accretion in the last Gyr. A&A 2015, 579, L3. [Google Scholar] [CrossRef]
- Forman, W.; Nulsen, P.; Heinz, S.; Owen, F.; Eilek, J.; Vikhlinin, A.; Markevitch, M.; Kraft, R.; Churazov, E.; Jones, C. Reflections of Active Galactic Nucleus Outbursts in the Gaseous Atmosphere of M87. ApJ 2005, 635, 894–906. [Google Scholar] [CrossRef]
- Forman, W.; Churazov, E.; Jones, C.; Heinz, S.; Kraft, R.; Vikhlinin, A. Partitioning the Outburst Energy of a Low Eddington Accretion Rate AGN at the Center of an Elliptical Galaxy: The Recent 12 Myr History of the Supermassive Black Hole in M87. ApJ 2017, 844, 122. [Google Scholar] [CrossRef]
- Cantiello, M.; Grado, A.; Blakeslee, J.P.; Raimondo, G.; Di Rico, G.; Limatola, L.; Brocato, E.; Della Valle, M.; Gilmozzi, R. The distance to NGC 1316 (Fornax A): Yet another curious case. A&A 2013, 552, A106. [Google Scholar] [CrossRef]
- Geldzahler, B.J.; Fomalont, E.B. Radio observations of the jet in Fornax A. AJ 1984, 89, 1650–1657. [Google Scholar] [CrossRef]
- Nowak, N.; Saglia, R.P.; Thomas, J.; Bender, R.; Davies, R.I.; Gebhardt, K. The supermassive black hole of FornaxA. MNRAS 2008, 391, 1629–1649. [Google Scholar] [CrossRef]
- Mackie, G.; Fabbiano, G. Evolution of Gas and Stars in the Merger Galaxy NGC 1316 (Fornax A). AJ 1998, 115, 514–524. [Google Scholar] [CrossRef]
- Goudfrooij, P.; Mack, J.; Kissler-Patig, M.; Meylan, G.; Minniti, D. Kinematics, ages and metallicities of star clusters in NGC 1316: A 3-Gyr-old merger remnant. MNRAS 2001, 322, 643–657. [Google Scholar] [CrossRef]
- Iodice, E.; Spavone, M.; Capaccioli, M.; Peletier, R.F.; Richtler, T.; Hilker, M.; Mieske, S.; Limatola, L.; Grado, A.; Napolitano, N.R.; et al. The Fornax Deep Survey with VST. II. Fornax A: A Two-phase Assembly Caught in the Act. ApJ 2017, 839, 21. [Google Scholar] [CrossRef]
- Maccagni, F.M.; Murgia, M.; Serra, P.; Govoni, F.; Morokuma-Matsui, K.; Kleiner, D.; Buchner, S.; Józsa, G.I.G.; Kamphuis, P.; Makhathini, S.; et al. The flickering nuclear activity of Fornax A. A&A 2020, 634, A9. [Google Scholar] [CrossRef]
- Balmaverde, B.; Baldi, R.D.; Capetti, A. The accretion mechanism in low-power radio galaxies. A&A 2008, 486, 119–130. [Google Scholar] [CrossRef]
- Russell, H.R.; McNamara, B.R.; Edge, A.C.; Hogan, M.T.; Main, R.A.; Vantyghem, A.N. Radiative efficiency, variability and Bondi accretion on to massive black holes: The transition from radio AGN to quasars in brightest cluster galaxies. MNRAS 2013, 432, 530–553. [Google Scholar] [CrossRef]
- Matthews, J.H.; Bell, A.R.; Araudo, A.T.; Blundell, K.M. Cosmic ray acceleration to ultrahigh energy in radio galaxies. Eur. Phys. J. Web Conf. 2019, 210, 04002. [Google Scholar] [CrossRef][Green Version]
- Biteau, J.; Marafico, S.; Kerfis, Y.; Deligny, O. Cosmographic model of the astroparticle skies. In Proceedings of the 37th International Cosmic Ray Conference, Berlin, Germany, 12–23 July 2021; p. 1012. [Google Scholar] [CrossRef]
- Eichmann, B.; Rachen, J.P.; Merten, L.; van Vliet, A.; Becker Tjus, J. Ultra-high-energy cosmic rays from radio galaxies. JCAP 2018, 2018, 36. [Google Scholar] [CrossRef]
- Wykes, S.; Taylor, A.M.; Bray, J.D.; Hardcastle, M.J.; Hillas, M. UHECR propagation from Centaurus A. Nucl. Part. Phys. Proc. 2018, 297–299, 234–241. [Google Scholar] [CrossRef][Green Version]
- Kobzar, O.; Hnatyk, B.; Marchenko, V.; Sushchov, O. Search for ultra high-energy cosmic rays from radiogalaxy Virgo A. MNRAS 2019, 484, 1790–1799. [Google Scholar] [CrossRef]
- Fraija, N.; Araya, M.; Galván-Gámez, A.; de Diego, J.A. Analysis of Fermi-LAT observations, UHECRs and neutrinos from the radio galaxy Centaurus B. JCAP 2019, 2019, 23. [Google Scholar] [CrossRef]
- Norman, C.A.; Melrose, D.B.; Achterberg, A. The Origin of Cosmic Rays above 1018.5 eV. ApJ 1995, 454, 60. [Google Scholar] [CrossRef]
- Aharonian, F.A.; Belyanin, A.A.; Derishev, E.V.; Kocharovsky, V.V.; Kocharovsky, V.V. Constraints on the extremely high-energy cosmic ray accelerators from classical electrodynamics. Phys. Rev. D 2002, 66, 023005. [Google Scholar] [CrossRef]
- Lemoine, M.; Waxman, E. Anisotropy vs. chemical composition at ultra-high energies. JCAP 2009, 2009, 9. [Google Scholar] [CrossRef]
- Liu, R.Y.; Taylor, A.M.; Lemoine, M.; Wang, X.Y.; Waxman, E. Constraints on the Source of Ultra-high-energy Cosmic Rays Using Anisotropy versus Chemical Composition. ApJ 2013, 776, 88. [Google Scholar] [CrossRef][Green Version]
- Lemoine, M. On Ultra-High Rigidity Cosmic Rays. In Proceedings of the Ultra-High Energy Cosmic Rays (UHECR2016), Paris, France, 8–12 October 2018; p. 011004. [Google Scholar] [CrossRef][Green Version]
- Heckman, T.M.; Thompson, T.A. Galactic Winds and the Role Played by Massive Stars. arXiv 2017, arXiv:1701.09062. [Google Scholar]
- Romero, G.E.; Müller, A.L.; Roth, M. Particle acceleration in the superwinds of starburst galaxies. A&A 2018, 616, A57. [Google Scholar] [CrossRef]
- Zhang, D. A Review of the Theory of Galactic Winds Driven by Stellar Feedback. Galaxies 2018, 6, 114. [Google Scholar] [CrossRef]
- Rieger, F.M.; Bosch-Ramon, V.; Duffy, P. Fermi acceleration in astrophysical jets. Ap&SS 2007, 309, 119–125. [Google Scholar] [CrossRef]
- Lemoine, M. Generalized Fermi acceleration. Phys. Rev. D 2019, 99, 083006. [Google Scholar] [CrossRef]
- Boldt, E.; Ghosh, P. Cosmic rays from remnants of quasars? MNRAS 1999, 307, 491–494. [Google Scholar] [CrossRef][Green Version]
- Levinson, A. Particle Acceleration and Curvature TeV Emission by Rotating, Supermassive Black Holes. Phys. Rev. Lett. 2000, 85, 912–915. [Google Scholar] [CrossRef]
- Neronov, A.Y.; Semikoz, D.V.; Tkachev, I.I. Ultra-high energy cosmic ray production in the polar cap regions of black hole magnetospheres. New J. Phys. 2009, 11, 065015. [Google Scholar] [CrossRef]
- Rieger, F.M. Nonthermal Processes in Black Hole-Jet Magnetospheres. Int. J. Mod. Phys. D 2011, 20, 1547–1596. [Google Scholar] [CrossRef]
- Ptitsyna, K.; Neronov, A. Particle acceleration in the vacuum gaps in black hole magnetospheres. A&A 2016, 593, A8. [Google Scholar] [CrossRef]
- Moncada, R.J.; Colon, R.A.; Guerra, J.J.; O’Dowd, M.J.; Anchordoqui, L.A. Ultrahigh energy cosmic ray nuclei from remnants of dead quasars. J. High Energy Astrophys. 2017, 13, 32–45. [Google Scholar] [CrossRef]
- Katsoulakos, G.; Rieger, F.M. Gap-type Particle Acceleration in the Magnetospheres of Rotating Supermassive Black Holes. ApJ 2020, 895, 99. [Google Scholar] [CrossRef]
- Rieger, F.; Levinson, A. Radio Galaxies at VHE Energies. Galaxies 2018, 6, 116. [Google Scholar] [CrossRef]
- Katsoulakos, G.; Rieger, F.M. Magnetospheric Gamma-Ray Emission in Active Galactic Nuclei. ApJ 2018, 852, 112. [Google Scholar] [CrossRef]
- Levinson, A.; Rieger, F. Variable TeV Emission as a Manifestation of Jet Formation in M87? ApJ 2011, 730, 123. [Google Scholar] [CrossRef]
- Hirotani, K.; Pu, H.Y.; Lin, L.C.C.; Chang, H.K.; Inoue, M.; Kong, A.K.H.; Matsushita, S.; Tam, P.H.T. Lepton Acceleration in the Vicinity of the Event Horizon: High-energy and Very-high-energy Emissions from Rotating Black Holes with Various Masses. ApJ 2016, 833, 142. [Google Scholar] [CrossRef]
- Pedaletti, G.; Wagner, S.J.; Rieger, F.M. Very High Energy γ-ray Emission from Passive Supermassive Black Holes: Constraints for NGC 1399. ApJ 2011, 738, 142. [Google Scholar] [CrossRef][Green Version]
- Georganopoulos, M.; Meyer, E.; Perlman, E. Recent Progress in Understanding the Large Scale Jets of Powerful Quasars. Galaxies 2016, 4, 65. [Google Scholar] [CrossRef]
- Breiding, P.; Meyer, E.T.; Georganopoulos, M.; Keenan, M.E.; DeNigris, N.S.; Hewitt, J. Fermi Non-detections of Four X-Ray Jet Sources and Implications for the IC/CMB Mechanism. ApJ 2017, 849, 95. [Google Scholar] [CrossRef]
- Liu, R.Y.; Rieger, F.M.; Aharonian, F.A. Particle Acceleration in Mildly Relativistic Shearing Flows: The Interplay of Systematic and Stochastic Effects, and the Origin of the Extended High-energy Emission in AGN Jets. ApJ 2017, 842, 39. [Google Scholar] [CrossRef]
- Tavecchio, F. Constraining the shear acceleration model for the X-ray emission of large-scale extragalactic jets. MNRAS 2021, 501, 6199–6207. [Google Scholar] [CrossRef]
- Rieger, F.M.; Duffy, P. Turbulence and Particle Acceleration in Shearing Flows. ApJL 2021, 907, L2. [Google Scholar] [CrossRef]
- Wang, J.S.; Reville, B.; Liu, R.Y.; Rieger, F.M.; Aharonian, F.A. Particle acceleration in shearing flows: The case for large-scale jets. MNRAS 2021, 505, 1334–1341. [Google Scholar] [CrossRef]
- Mizuno, Y. GRMHD Simulations and Modeling for Jet Formation and Acceleration Region in AGNs. Universe 2022, 8, 85. [Google Scholar] [CrossRef]
- Perucho, M. Dissipative Processes and Their Role in the Evolution of Radio Galaxies. Galaxies 2019, 7, 70. [Google Scholar] [CrossRef]
- Kim, J.Y.; Krichbaum, T.P.; Lu, R.S.; Ros, E.; Bach, U.; Bremer, M.; de Vicente, P.; Lindqvist, M.; Zensus, J.A. The limb-brightened jet of M87 down to the 7 Schwarzschild radii scale. A&A 2018, 616, A188. [Google Scholar] [CrossRef]
- Rieger, F.M. An Introduction to Particle Acceleration in Shearing Flows. Galaxies 2019, 7, 3. [Google Scholar] [CrossRef]
- Ostrowski, M. Acceleration of ultra-high energy cosmic ray particles in relativistic jets in extragalactic radio sources. A&A 1998, 335, 134–144. [Google Scholar]
- Ostrowski, M. On possible ‘cosmic ray cocoons’ of relativistic jets. MNRAS 2000, 312, 579–584. [Google Scholar] [CrossRef][Green Version]
- Caprioli, D. “Espresso” Acceleration of Ultra-high-energy Cosmic Rays. ApJL 2015, 811, L38. [Google Scholar] [CrossRef]
- Kimura, S.S.; Murase, K.; Zhang, B.T. Ultrahigh-energy cosmic-ray nuclei from black hole jets: Recycling galactic cosmic rays through shear acceleration. Phys. Rev. D 2018, 97, 023026. [Google Scholar] [CrossRef]
- Mbarek, R.; Caprioli, D. Espresso and Stochastic Acceleration of Ultra-high-energy Cosmic Rays in Relativistic Jets. ApJ 2021, 921, 85. [Google Scholar] [CrossRef]
- Rieger, F.M.; Duffy, P. Shear Acceleration in Relativistic Astrophysical Jets. ApJ 2004, 617, 155–161. [Google Scholar] [CrossRef]
- Rieger, F.M.; Duffy, P. Shear Acceleration in Expanding Flows. ApJ 2016, 833, 34. [Google Scholar] [CrossRef]
- Webb, G.M.; Barghouty, A.F.; Hu, Q.; le Roux, J.A. Particle Acceleration Due to Cosmic-ray Viscosity and Fluid Shear in Astrophysical Jets. ApJ 2018, 855, 31. [Google Scholar] [CrossRef]
- Webb, G.M.; Al-Nussirat, S.; Mostafavi, P.; Barghouty, A.F.; Li, G.; le Roux, J.A.; Zank, G.P. Particle Acceleration by Cosmic Ray Viscosity in Radio-jet Shear Flows. ApJ 2019, 881, 123. [Google Scholar] [CrossRef]
- Webb, G.M.; Mostafavi, P.; Al-Nussirat, S.; Barghouty, A.F.; Li, G.; le Roux, J.A.; Zank, G.P. Cosmic-Ray Acceleration in Radio-jet Shear Flows: Scattering Inside and Outside the Jet. ApJ 2020, 894, 95. [Google Scholar] [CrossRef]
- Merten, L.; Boughelilba, M.; Reimer, A.; Da Vela, P.; Vorobiov, S.; Tavecchio, F.; Bonnoli, G.; Lundquist, J.P.; Righi, C. Scrutinizing FR 0 radio galaxies as ultra-high-energy cosmic ray source candidates. Astropart. Phys. 2021, 128, 102564. [Google Scholar] [CrossRef]
- Rieger, F.M.; Duffy, P. Particle Acceleration in Relativistic Shearing Flows: Energy Spectrum. ApJ 2022, 933, 149. [Google Scholar] [CrossRef]
- Bosch-Ramon, V.; Perucho, M.; Barkov, M.V. Clouds and red giants interacting with the base of AGN jets. A&A 2012, 539, A69. [Google Scholar] [CrossRef]
- Gallant, Y.A.; Achterberg, A. Ultra-high-energy cosmic ray acceleration by relativistic blast waves. MNRAS 1999, 305, L6–L10. [Google Scholar] [CrossRef]
- Rieger, F.M.; Duffy, P. A Microscopic Analysis of Shear Acceleration. ApJ 2006, 652, 1044–1049. [Google Scholar] [CrossRef]
- Mbarek, R.; Caprioli, D. Bottom-up Acceleration of Ultra-high-energy Cosmic Rays in the Jets of Active Galactic Nuclei. ApJ 2019, 886, 8. [Google Scholar] [CrossRef]
- Lemoine, M.; Pelletier, G. On electromagnetic instabilities at ultra-relativistic shock waves. MNRAS 2010, 402, 321–334. [Google Scholar] [CrossRef]
- Sironi, L.; Spitkovsky, A. Particle Acceleration in Relativistic Magnetized Collisionless Electron-Ion Shocks. ApJ 2011, 726, 75. [Google Scholar] [CrossRef]
- Bell, A.R.; Araudo, A.T.; Matthews, J.H.; Blundell, K.M. Cosmic-ray acceleration by relativistic shocks: Limits and estimates. MNRAS 2018, 473, 2364–2371. [Google Scholar] [CrossRef]
- Vanthieghem, A.; Lemoine, M.; Plotnikov, I.; Grassi, A.; Grech, M.; Gremillet, L.; Pelletier, G. Physics and Phenomenology of Weakly Magnetized, Relativistic Astrophysical Shock Waves. Galaxies 2020, 8, 33. [Google Scholar] [CrossRef]
- Matthews, J.H.; Bell, A.R.; Blundell, K.M.; Araudo, A.T. Ultrahigh energy cosmic rays from shocks in the lobes of powerful radio galaxies. MNRAS 2019, 482, 4303–4321. [Google Scholar] [CrossRef]
- Pope, M.H.; Melrose, D.B. Diffusive shock acceleration by multiple shock fronts with differing properties. PASA 1994, 11, 175–179. [Google Scholar] [CrossRef]
- Gieseler, U.D.J.; Jones, T.W. First order Fermi acceleration at multiple oblique shocks. A&A 2000, 357, 1133–1136. [Google Scholar]
- Aab, A.; Abreu, P.; Aglietta, M.; Samarai, I.A.; Albuquerque, I.F.M.; Allekotte, I.; Almela, A.; Alvarez Castillo, J.; Alvarez-Muñiz, J.; Anastasi, G.A.; et al. Combined fit of spectrum and composition data as measured by the Pierre Auger Observatory. JCAP 2017, 2017, 38. [Google Scholar] [CrossRef]
- Perucho, M.; Martí, J.M. A numerical simulation of the evolution and fate of a Fanaroff-Riley type I jet. The case of 3C 31. MNRAS 2007, 382, 526–542. [Google Scholar] [CrossRef]
- Perucho, M.; Martí, J.M.; Quilis, V. Long-term FRII jet evolution: Clues from three-dimensional simulations. MNRAS 2019, 482, 3718–3735. [Google Scholar] [CrossRef]
- Bell, A.R.; Matthews, J.H.; Blundell, K.M.; Araudo, A.T. Cosmic ray acceleration in hydromagnetic flux tubes. MNRAS 2019, 487, 4571–4579. [Google Scholar] [CrossRef]
- Araudo, A.T.; Bell, A.R.; Blundell, K.M.; Matthews, J.H. On the maximum energy of non-thermal particles in the primary hotspot of Cygnus A. MNRAS 2018, 473, 3500–3506. [Google Scholar] [CrossRef]
- Mészáros, P.; Fox, D.B.; Hanna, C.; Murase, K. Multi-messenger astrophysics. Nat. Rev. Phys. 2019, 1, 585–599. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).