Exploring Gauge Theories with Adjoint Matter on the Lattice
Abstract
1. Introduction
2. Supersymmetric Yang–Mills Theory
2.1. The Particle Spectrum of Supersymmetric Yang–Mills Theory
2.2. Zero-Temperature Phases and the Gluino Condensate
2.3. Phase Transitions in Supersymmetric Yang–Mills Theory
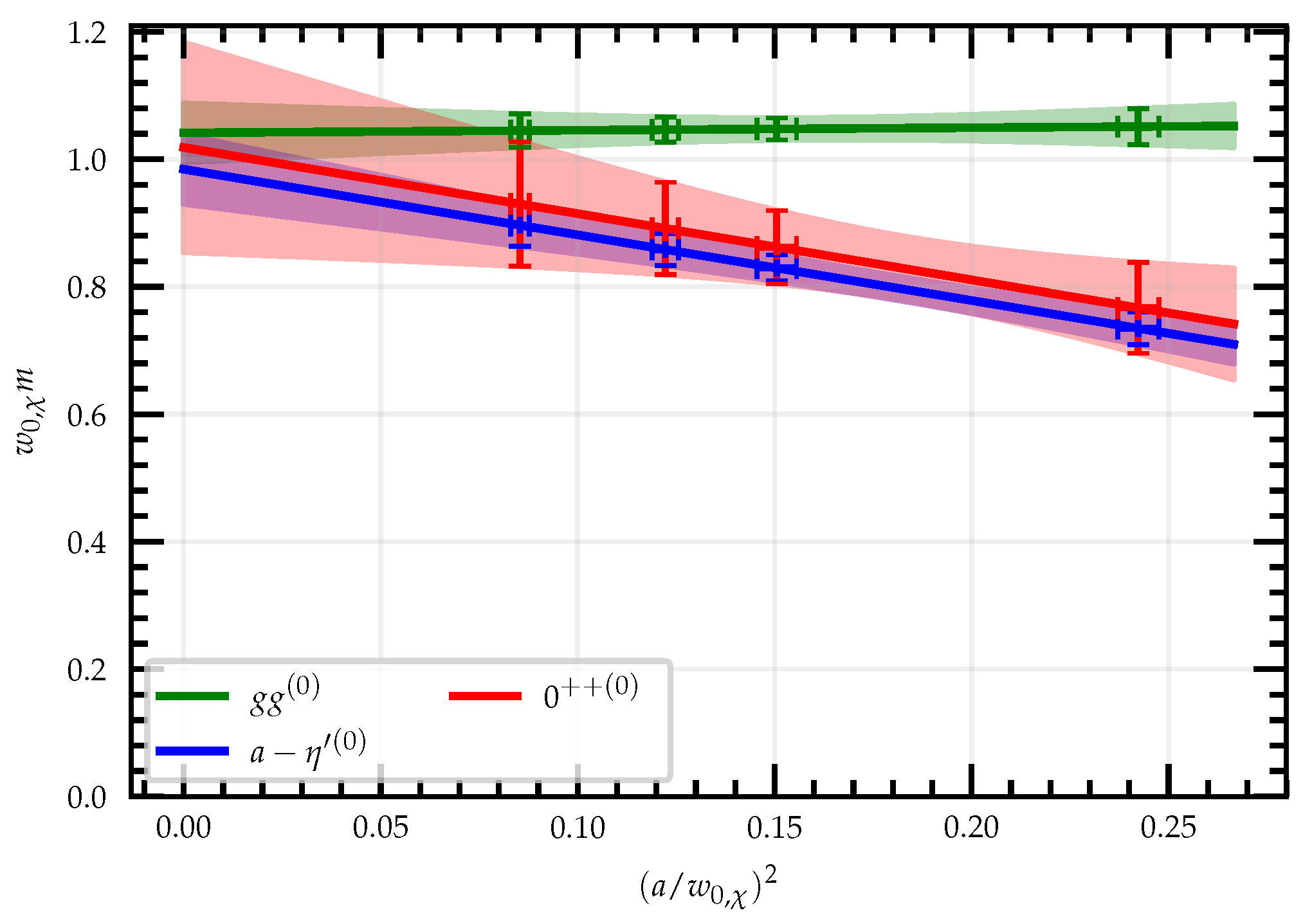
2.4. Compactified Theory
3. Towards the Conformal Window with Fermions in the Adjoint Representation
3.1. Two Dirac Flavors: Minimal Walking Technicolor
3.2. Theories between Two Dirac Flavors and Supersymmetric Yang–Mills Theory
3.3. Combining Adjoint and Fundamental Fermion Fields
4. Towards Supersymmetric QCD and Extended Supersymmetry
5. Adjoint Dark Matter
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Novikov, V.A.; Shifman, M.A.; Vainshtein, A.I.; Zakharov, V.I. Exact Gell-Mann-Low function of supersymmetric Yang-Mills theories from instanton calculus. Nucl. Phys. B 1983, 229, 381–393. [Google Scholar] [CrossRef]
- Hollowood, T.J.; Khoze, V.V.; Lee, W.J.; Mattis, M.P. Breakdown of cluster decomposition in instanton calculations of the gluino condensate. Nucl. Phys. B 2000, 570, 241–266. [Google Scholar] [CrossRef][Green Version]
- Veneziano, G.; Yankielowicz, S. An effective Lagrangian for the pure N = 1 supersymmetric Yang-Mills theory. Phys. Lett. B 1982, 113, 231. [Google Scholar] [CrossRef]
- Farrar, G.R.; Gabadadze, G.; Schwetz, M. On the effective action of N = 1 supersymmetric Yang-Mills theory. Phys. Rev. D 1998, 58, 015009. [Google Scholar] [CrossRef]
- Farrar, G.R.; Gabadadze, G.; Schwetz, M. The spectrum of softly broken N = 1 supersymmetric Yang-Mills theory. Phys. Rev. D 1999, 60, 035002. [Google Scholar] [CrossRef]
- Witten, E. Constraints on supersymmetry breaking. Nucl. Phys. B 1982, 202, 253. [Google Scholar] [CrossRef]
- Amati, D.; Konishi, K.; Meurice, Y.; Rossi, G.C.; Veneziano, G. Nonperturbative aspects in supersymmetric gauge theories. Phys. Rep. 1988, 162, 169–248. [Google Scholar] [CrossRef]
- Curci, G.; Veneziano, G. Supersymmetry and the lattice: A reconciliation? Nucl. Phys. B 1987, 292, 555–572. [Google Scholar] [CrossRef]
- Suzuki, H. Supersymmetry, chiral symmetry and the generalized BRS transformation in lattice formulations of 4D N = 1 SYM. Nucl. Phys. B 2012, 861, 290–320. [Google Scholar] [CrossRef]
- Ginsparg, P.H.; Wilson, K.G. A remnant of chiral symmetry on the lattice. Phys. Rev. D 1982, 25, 2649. [Google Scholar] [CrossRef]
- Feo, A.; Merlatti, P.; Sannino, F. Information on the super Yang-Mills spectrum. Phys. Rev. D 2004, 70, 096004. [Google Scholar] [CrossRef]
- Münster, G.; Stüwe, H. The mass of the adjoint pion in N = 1 supersymmetric Yang-Mills theory. J. High Energy Phys. 2014, 05, 034. [Google Scholar] [CrossRef]
- Ali, S.; Gerber, H.; Montvay, I.; Münster, G.; Piemonte, S.; Scior, P.; Bergner, G. Analysis of Ward identities in supersymmetric Yang-Mills theory. Eur. Phys. J. C 2018, 78, 404. [Google Scholar] [CrossRef]
- Sommer, R. A New way to set the energy scale in lattice gauge theories and its applications to the static force and αs in SU(2) Yang-Mills theory. Nucl. Phys. B 1994, 411, 839–854. [Google Scholar] [CrossRef]
- Borsányi, S.; Dürr, S.; Fodor, Z.; Hoelbling, C.; Katz, S.D.; Krieg, S.; Kurth, T.; Lellouch, L.; Lippert, T.; McNeile, C.; et al. High-precision scale setting in lattice QCD. J. High Energy Phys. 2012, 9, 10. [Google Scholar] [CrossRef]
- Montvay, I. An algorithm for gluinos on the lattice. Nucl. Phys. B 1996, 466, 259–284. [Google Scholar] [CrossRef]
- Donini, A.; Guagnelli, M.; Hernandez, P.; Vladikas, A. Towards N = 1 super Yang-Mills on the lattice. Nucl. Phys. B 1998, 523, 529–552. [Google Scholar] [CrossRef]
- Campos, I.; Kirchner, R.; Montvay, I.; Westphalen, J.; Feo, A.; Luckmann, S.; Münster, G.; Spanderen, K. Monte Carlo simulation of SU(2) Yang-Mills theory with light gluinos. Eur. Phys. J. C 1999, 11, 507–527. [Google Scholar] [CrossRef]
- Cerdeno, D.G.; Knauf, A.; Louis, J. A Note on effective N = 1 superYang-Mills theories versus lattice results. Eur. Phys. J. C 2003, 31, 415–420. [Google Scholar] [CrossRef]
- Demmouche, K.; Farchioni, F.; Ferling, A.; Montvay, I.; Münster, G.; Scholz, E.E.; Wuilloud, J. Simulation of 4d N = 1 supersymmetric Yang-Mills theory with Symanzik improved gauge action and stout smearing. Eur. Phys. J. C 2010, 69, 147–157. [Google Scholar] [CrossRef]
- Bergner, G.; Berheide, T.; Münster, G.; Özugurel, U.D.; Sandbrink, D.; Montvay, I. The gluino-glue particle and finite size effects in supersymmetric Yang-Mills theory. J. High Energy Phys. 2012, 9, 108. [Google Scholar] [CrossRef]
- Bergner, G.; Giudice, P.; Münster, G.; Montvay, I.; Piemonte, S. The light bound states of supersymmetric SU(2) Yang-Mills theory. J. High Energy Phys. 2016, 3, 80. [Google Scholar] [CrossRef]
- Ali, S.; Bergner, G.; Gerber, H.; Kuberski, S.; Montvay, I.; Münster, G.; Piemonte, S.; Scior, P. Variational analysis of low-lying states in supersymmetric Yang-Mills theory. J. High Energy Phys. 2019, 4, 150. [Google Scholar] [CrossRef]
- Feo, A.; Kirchner, R.; Luckmann, S.; Montvay, I.; Münster, G. Numerical simulations of dynamical gluinos in SU(3) Yang-Mills theory: First results. Nucl. Phys. B Proc. Suppl. 2000, 83, 661–663. [Google Scholar] [CrossRef]
- Ali, S.; Bergner, G.; Gerber, H.; Giudice, P.; Montvay, I.; Münster, G.; Piemonte, S.; Scior, P. The light bound states of N = 1 supersymmetric SU(3) Yang-Mills theory on the lattice. J. High Energy Phys. 2018, 3, 113. [Google Scholar] [CrossRef]
- Ali, S.; Bergner, G.; Gerber, H.; Montvay, I.; Münster, G.; Piemonte, S.; Scior, P. Numerical results for the lightest bound states in N = 1 supersymmetric SU(3) Yang-Mills theory. Phys. Rev. Lett. 2019, 122, 221601. [Google Scholar] [CrossRef]
- Ali, S.; Bergner, G.; Gerber, H.; Montvay, I.; Münster, G.; Piemonte, S.; Scior, P. Continuum extrapolation of Ward identities in N = 1 supersymmetric SU(3) Yang-Mills theory. Eur. Phys. J. C 2020, 80, 548. [Google Scholar] [CrossRef]
- Steinhauser, M.; Sternbeck, A.; Wellegehausen, B.; Wipf, A. N = 1 Super-Yang-Mills theory on the lattice with twisted mass fermions. J. High Energy Phys. 2021, 1, 154. [Google Scholar] [CrossRef]
- Butti, P.; García Pérez, M.; González-Arroyo, A.; Ishikawa, K.I.; Okawa, M. Scale setting for large-N SUSY Yang-Mills on the lattice. J. High Energy Phys. 2022, 7, 74. [Google Scholar] [CrossRef]
- Ziegler, F.P.G.; Della Morte, M.; Jäger, B.; Sannino, F.; Tsang, J.T. One flavour QCD as an analogue computer for SUSY. PoS 2022, LATTICE2021, 225. [Google Scholar] [CrossRef]
- Bergner, G.; Wuilloud, J. Acceleration of the Arnoldi method and real eigenvalues of the non-Hermitian Wilson-Dirac operator. Comput. Phys. Commun. 2012, 183, 299–304. [Google Scholar] [CrossRef][Green Version]
- Kirchner, R.; Montvay, I.; Westphalen, J.; Luckmann, S.; Spanderen, K. Evidence for discrete chiral symmetry breaking in N = 1 supersymmetric Yang-Mills theory. Phys. Lett. B 1999, 446, 209–215. [Google Scholar] [CrossRef]
- Lüscher, M. Properties and uses of the Wilson flow in lattice QCD. J. High Energy Phys. 2014, 8, 71, Erratum in J. High Energy Phys. 2014, 3, 92. [Google Scholar] [CrossRef]
- Bergner, G.; López, C.; Piemonte, S. Study of center and chiral symmetry realization in thermal N = 1 super Yang-Mills theory using the gradient flow. Phys. Rev. D 2019, 100, 074501. [Google Scholar] [CrossRef]
- Fleming, G.T.; Kogut, J.B.; Vranas, P.M. Super Yang-Mills on the lattice with domain wall fermions. Phys. Rev. D 2001, 64, 034510. [Google Scholar] [CrossRef]
- Endres, M.G. Dynamical simulation of N = 1 supersymmetric Yang-Mills theory with domain wall fermions. Phys. Rev. D 2009, 79, 094503. [Google Scholar] [CrossRef]
- Giedt, J.; Brower, R.; Catterall, S.; Fleming, G.T.; Vranas, P. Lattice super-Yang-Mills using domain wall fermions in the chiral limit. Phys. Rev. D 2009, 79, 025015. [Google Scholar] [CrossRef]
- Kim, S.W.; Fukaya, H.; Hashimoto, S.; Matsufuru, H.; Nishimura, J.; Onogi, T. Lattice study of 4d N = 1 super Yang-Mills theory with dynamical overlap gluino. PoS 2011, LATTICE2011, 69. [Google Scholar] [CrossRef][Green Version]
- Kogut, J.B.; Polonyi, J.; Wyld, H.W.; Sinclair, D.K. Hierarchical mass scales in lattice gauge theories with dynamical light fermions. Phys. Rev. Lett. 1985, 54, 1980. [Google Scholar] [CrossRef]
- Karsch, F.; Lütgemeier, M. Deconfinement and chiral symmetry restoration in an SU(3) gauge theory with adjoint fermions. Nucl. Phys. B 1999, 550, 449–464. [Google Scholar] [CrossRef][Green Version]
- Engels, J.; Holtmann, S.; Schulze, T. Scaling and Goldstone effects in a QCD with two flavors of adjoint quarks. Nucl. Phys. B 2005, 724, 357–379. [Google Scholar] [CrossRef][Green Version]
- Bergner, G.; Giudice, P.; Münster, G.; Piemonte, S.; Sandbrink, D. Phase structure of the N = 1 supersymmetric Yang-Mills theory at finite temperature. J. High Energy Phys. 2014, 11, 49. [Google Scholar] [CrossRef]
- Witten, E. Branes and the dynamics of QCD. Nucl. Phys. B 1997, 507, 658–690. [Google Scholar] [CrossRef]
- Campos, A.; Holland, K.; Wiese, U.J. Complete wetting in supersymmetric QCD or why QCD strings can end on domain walls. Phys. Rev. Lett. 1998, 81, 2420–2423. [Google Scholar] [CrossRef]
- Dunne, G.V.; Tanizaki, Y.; Ünsal, M. Quantum distillation of Hilbert spaces, semi-classics and anomaly matching. J. High Energy Phys. 2018, 08, 068. [Google Scholar] [CrossRef]
- Shifman, M.; Yung, A. Supersymmetric solitons and how they help us understand non-Abelian gauge theories. Rev. Mod. Phys. 2007, 79, 1139. [Google Scholar] [CrossRef]
- Ünsal, M. Abelian duality, confinement, and chiral symmetry breaking in QCD(adj). Phys. Rev. Lett. 2008, 100, 032005. [Google Scholar] [CrossRef]
- Misumi, T.; Kanazawa, T. Adjoint QCD on R3 × S1 with twisted fermionic boundary conditions. J. High Energy Phys. 2014, 6, 181. [Google Scholar] [CrossRef]
- Aitken, K.; Cherman, A.; Poppitz, E.; Yaffe, L.G. QCD on a small circle. Phys. Rev. D 2017, 96, 096022. [Google Scholar] [CrossRef]
- Bergner, G.; Piemonte, S. Compactified N = 1 supersymmetric Yang-Mills theory on the lattice: Continuity and the disappearance of the deconfinement transition. J. High Energy Phys. 2014, 12, 133. [Google Scholar] [CrossRef]
- Bergner, G.; Giudice, P.; Münster, G.; Piemonte, S. Witten index and phase diagram of compactified N = 1 supersymmetric Yang-Mills theory on the lattice. arXiv 2016, arXiv:1510.05926. [Google Scholar] [CrossRef]
- Bergner, G.; Piemonte, S.; Ünsal, M. Adiabatic continuity and confinement in supersymmetric Yang-Mills theory on the lattice. J. High Energy Phys. 2018, 11, 92. [Google Scholar] [CrossRef]
- Cossu, G.; Hatanaka, H.; Hosotani, Y.; Noaki, J.I. Polyakov loops and the Hosotani mechanism on the lattice. Phys. Rev. D 2014, 89, 094509. [Google Scholar] [CrossRef]
- Peskin, M.E.; Takeuchi, T. A new constraint on a strongly interacting Higgs sector. Phys. Rev. Lett. 1990, 65, 964–967. [Google Scholar] [CrossRef]
- Hill, C.T.; Simmons, E.H. Strong dynamics and electroweak symmetry breaking. Phys. Rep. 2003, 381, 235–402, Erratum in Phys. Rep. 2004, 390, 553–554. [Google Scholar] [CrossRef]
- Cacciapaglia, G.; Pica, C.; Sannino, F. Fundamental composite dynamics: A review. Phys. Rep. 2020, 877, 1–70. [Google Scholar] [CrossRef]
- Caswell, W.E. Asymptotic behavior of nonabelian gauge theories to two loop order. Phys. Rev. Lett. 1974, 33, 244. [Google Scholar] [CrossRef]
- Dietrich, D.D.; Sannino, F. Conformal window of SU(N) gauge theories with fermions in higher dimensional representations. Phys. Rev. D 2007, 75, 085018. [Google Scholar] [CrossRef]
- Banks, T.; Zaks, A. On the phase structure of vector-like gauge theories with massless fermions. Nucl. Phys. B 1982, 196, 189–204. [Google Scholar] [CrossRef]
- Catterall, S.; Sannino, F. Minimal walking on the lattice. Phys. Rev. D 2007, 76, 034504. [Google Scholar] [CrossRef]
- Catterall, S.; Giedt, J.; Sannino, F.; Schneible, J. Phase diagram of SU(2) with 2 flavors of dynamical adjoint quarks. J. High Energy Phys. 2008, 11, 9. [Google Scholar] [CrossRef]
- Hietanen, A.; Rantaharju, J.; Rummukainen, K.; Tuominen, K. Minimal Technicolor on the lattice. Nucl. Phys. A 2009, 820, 191C–194C. [Google Scholar] [CrossRef]
- DeGrand, T.; Shamir, Y.; Svetitsky, B. Infrared fixed point in SU(2) gauge theory with adjoint fermions. Phys. Rev. D 2011, 83, 074507. [Google Scholar] [CrossRef]
- Patella, A. A precise determination of the psibar-psi anomalous dimension in conformal gauge theories. Phys. Rev. D 2012, 86, 025006. [Google Scholar] [CrossRef]
- Rantaharju, J.; Rantalaiho, T.; Rummukainen, K.; Tuominen, K. Running coupling in SU(2) gauge theory with two adjoint fermions. Phys. Rev. D 2016, 93, 094509. [Google Scholar] [CrossRef]
- Bergner, G.; Giudice, P.; Münster, G.; Montvay, I.; Piemonte, S. Spectrum and mass anomalous dimension of SU(2) adjoint QCD with two Dirac flavors. Phys. Rev. D 2017, 96, 034504. [Google Scholar] [CrossRef]
- Yamawaki, K.; Bando, M.; Matumoto, K. Scale invariant technicolor model and a technidilaton. Phys. Rev. Lett. 1986, 56, 1335. [Google Scholar] [CrossRef] [PubMed]
- Golterman, M.; Shamir, Y. Low-energy effective action for pions and a dilatonic meson. Phys. Rev. D 2016, 94, 054502. [Google Scholar] [CrossRef]
- Catterall, S.; Galvez, R.; Ünsal, M. Realization of center symmetry in two adjoint flavor large-N Yang-Mills. J. High Energy Phys. 2010, 8, 10. [Google Scholar] [CrossRef]
- Bringoltz, B.; Koren, M.; Sharpe, S.R. Large-N reduction in QCD with two adjoint Dirac fermions. Phys. Rev. D 2012, 85, 094504. [Google Scholar] [CrossRef]
- García Pérez, M.; González-Arroyo, A.; Keegan, L.; Okawa, M. Mass anomalous dimension of Adjoint QCD at large N from twisted volume reduction. J. High Energy Phys. 2015, 8, 34. [Google Scholar] [CrossRef]
- Bergner, G.; Piemonte, S. Running coupling from gluon and ghost propagators in the Landau gauge: Yang-Mills theories with adjoint fermions. Phys. Rev. D 2018, 97, 074510. [Google Scholar] [CrossRef]
- Athenodorou, A.; Bennett, E.; Bergner, G.; Lucini, B. Infrared regime of SU(2) with one adjoint Dirac flavor. Phys. Rev. D 2015, 91, 114508. [Google Scholar] [CrossRef]
- Bergner, G.; Giudice, P.; Münster, G.; Scior, P.; Montvay, I.; Piemonte, S. Low energy properties of SU(2) gauge theory with Nf = 3/2 flavours of adjoint fermions. J. High Energy Phys. 2018, 1, 119. [Google Scholar] [CrossRef]
- Anber, M.M.; Poppitz, E. Two-flavor adjoint QCD. Phys. Rev. D 2018, 98, 034026. [Google Scholar] [CrossRef]
- Bi, Z.; Grebe, A.; Kanwar, G.; Ledwith, P.; Murphy, D.; Wagman, M.L. Lattice analysis of SU(2) with 1 adjoint Dirac flavor. arXiv 2019, arXiv:1912.11723. [Google Scholar] [CrossRef]
- Athenodorou, A.; Bennett, E.; Bergner, G.; Lucini, B. Investigating the conformal behavior of SU(2) with one adjoint Dirac flavor. Phys. Rev. D 2021, 104, 074519. [Google Scholar] [CrossRef]
- Bergner, G.; López, J.C.; Piemonte, S.; Calero, I.S. Lattice simulations of adjoint QCD with one Dirac overlap fermion. Phys. Rev. D 2022, 106, 094507. [Google Scholar] [CrossRef]
- Ryttov, T.A.; Sannino, F. Ultra Minimal Technicolor and its dark matter TIMP. Phys. Rev. D 2008, 78, 115010. [Google Scholar] [CrossRef]
- Cacciapaglia, G.; Sannino, F. Fundamental composite (Goldstone) Higgs dynamics. J. High Energy Phys. 2014, 4, 111. [Google Scholar] [CrossRef]
- Kanazawa, T.; Ünsal, M. Quantum distillation in QCD. Phys. Rev. D 2020, 102, 034013. [Google Scholar] [CrossRef]
- Ayyar, V.; DeGrand, T.; Golterman, M.; Hackett, D.C.; Jay, W.I.; Neil, E.T.; Shamir, Y.; Svetitsky, B. Spectroscopy of SU(4) composite Higgs theory with two distinct fermion representations. Phys. Rev. D 2018, 97, 074505. [Google Scholar] [CrossRef]
- Cossu, G.; Del Debbio, L.; Panero, M.; Preti, D. Strong dynamics with matter in multiple representations: SU(4) gauge theory with fundamental and sextet fermions. Eur. Phys. J. C 2019, 79, 638. [Google Scholar] [CrossRef]
- DeGrand, T.; Golterman, M.; Neil, E.T.; Shamir, Y. One-loop chiral perturbation theory with two fermion representations. Phys. Rev. D 2016, 94, 025020. [Google Scholar] [CrossRef]
- Bergner, G.; Piemonte, S. Lattice simulations of a gauge theory with mixed adjoint-fundamental matter. Phys. Rev. D 2021, 103, 014503. [Google Scholar] [CrossRef]
- Terning, J. Modern Supersymmetry: Dynamics and Duality; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Elliott, J.W.; Giedt, J.; Moore, G.D. Lattice four-dimensional N = 4 SYM is practical. Phys. Rev. D 2008, 78, 081701. [Google Scholar] [CrossRef]
- Giedt, J. Progress in four-dimensional lattice supersymmetry. Int. J. Mod. Phys. A 2009, 24, 4045–4095. [Google Scholar] [CrossRef]
- Costa, M.; Panagopoulos, H. Supersymmetric QCD on the lattice: An exploratory study. Phys. Rev. D 2017, 96, 034507. [Google Scholar] [CrossRef]
- Wellegehausen, B.; Wipf, A. N = 1 supersymmetric SU(3) gauge theory—Towards simulations of Super-QCD. arXiv 2018, arXiv:1811.01784. [Google Scholar] [CrossRef]
- Bergner, G.; Piemonte, S. Supersymmetric and conformal theories on the lattice: From super Yang-Mills towards super QCD. arXiv 2019, arXiv:1811.01797. [Google Scholar] [CrossRef]
- Catterall, S.; Kaplan, D.B.; Ünsal, M. Exact lattice supersymmetry. Phys. Rep. 2009, 484, 71–130. [Google Scholar] [CrossRef]
- Kribs, G.D.; Neil, E.T. Review of strongly-coupled composite dark matter models and lattice simulations. Int. J. Mod. Phys. A 2016, 31, 1643004. [Google Scholar] [CrossRef]
- Cline, J.M. Dark atoms and composite dark matter. SciPost Phys. Lect. Notes 2022, 52, 1. [Google Scholar] [CrossRef]
- Boddy, K.K.; Feng, J.L.; Kaplinghat, M.; Shadmi, Y.; Tait, T.M.P. Strongly interacting dark matter: Self-interactions and keV lines. Phys. Rev. D 2014, 90, 095016. [Google Scholar] [CrossRef]
- Contino, R.; Mitridate, A.; Podo, A.; Redi, M. Gluequark dark matter. J. High Energy Phys. 2019, 2, 187. [Google Scholar] [CrossRef]
- Reichert, M.; Sannino, F.; Wang, Z.W.; Zhang, C. Dark confinement and chiral phase transitions: Gravitational waves vs matter representations. J. High Energy Phys. 2022, 1, 003. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bergner, G.; Münster, G.; Piemonte, S. Exploring Gauge Theories with Adjoint Matter on the Lattice. Universe 2022, 8, 617. https://doi.org/10.3390/universe8120617
Bergner G, Münster G, Piemonte S. Exploring Gauge Theories with Adjoint Matter on the Lattice. Universe. 2022; 8(12):617. https://doi.org/10.3390/universe8120617
Chicago/Turabian StyleBergner, Georg, Gernot Münster, and Stefano Piemonte. 2022. "Exploring Gauge Theories with Adjoint Matter on the Lattice" Universe 8, no. 12: 617. https://doi.org/10.3390/universe8120617
APA StyleBergner, G., Münster, G., & Piemonte, S. (2022). Exploring Gauge Theories with Adjoint Matter on the Lattice. Universe, 8(12), 617. https://doi.org/10.3390/universe8120617







