A Correction Algorithm of the Sampling Effect and Its Application in High-Precision Astrometry
Abstract
1. Introduction
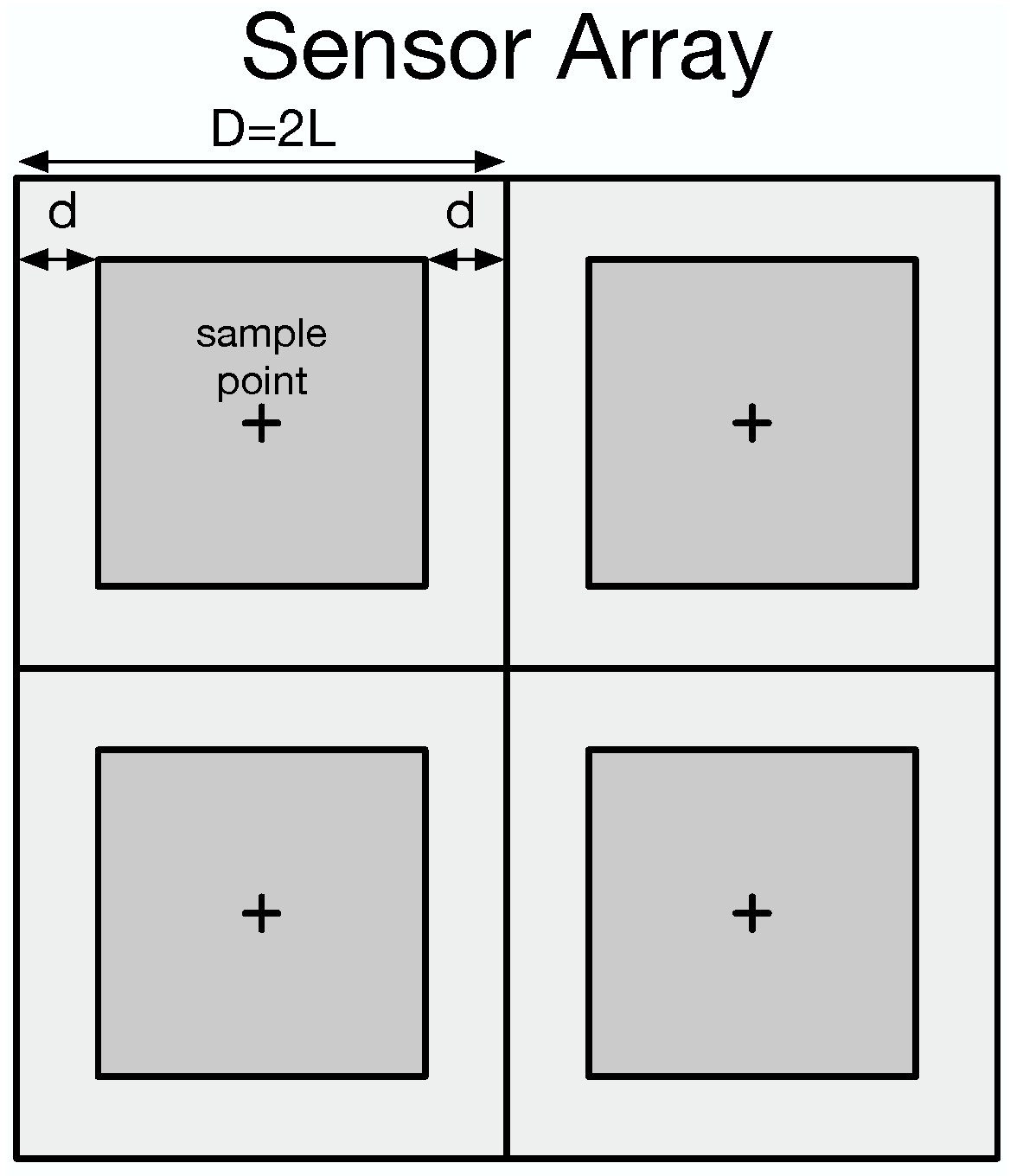
2. Models for Image Sensors and Sampling Process
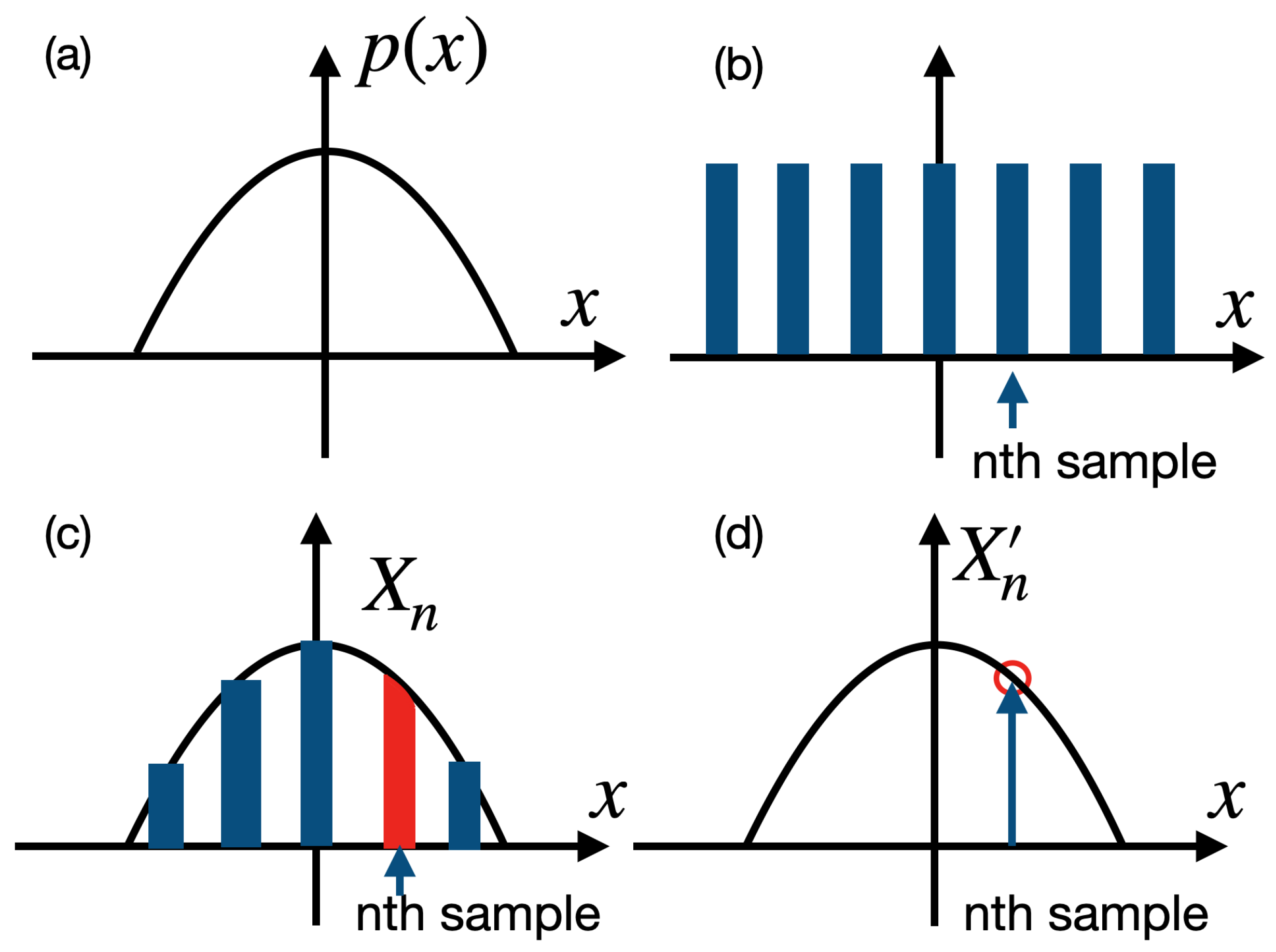
2.1. Models for Integral Sampling Process
2.2. Practical Method for Integral Sampling Correction
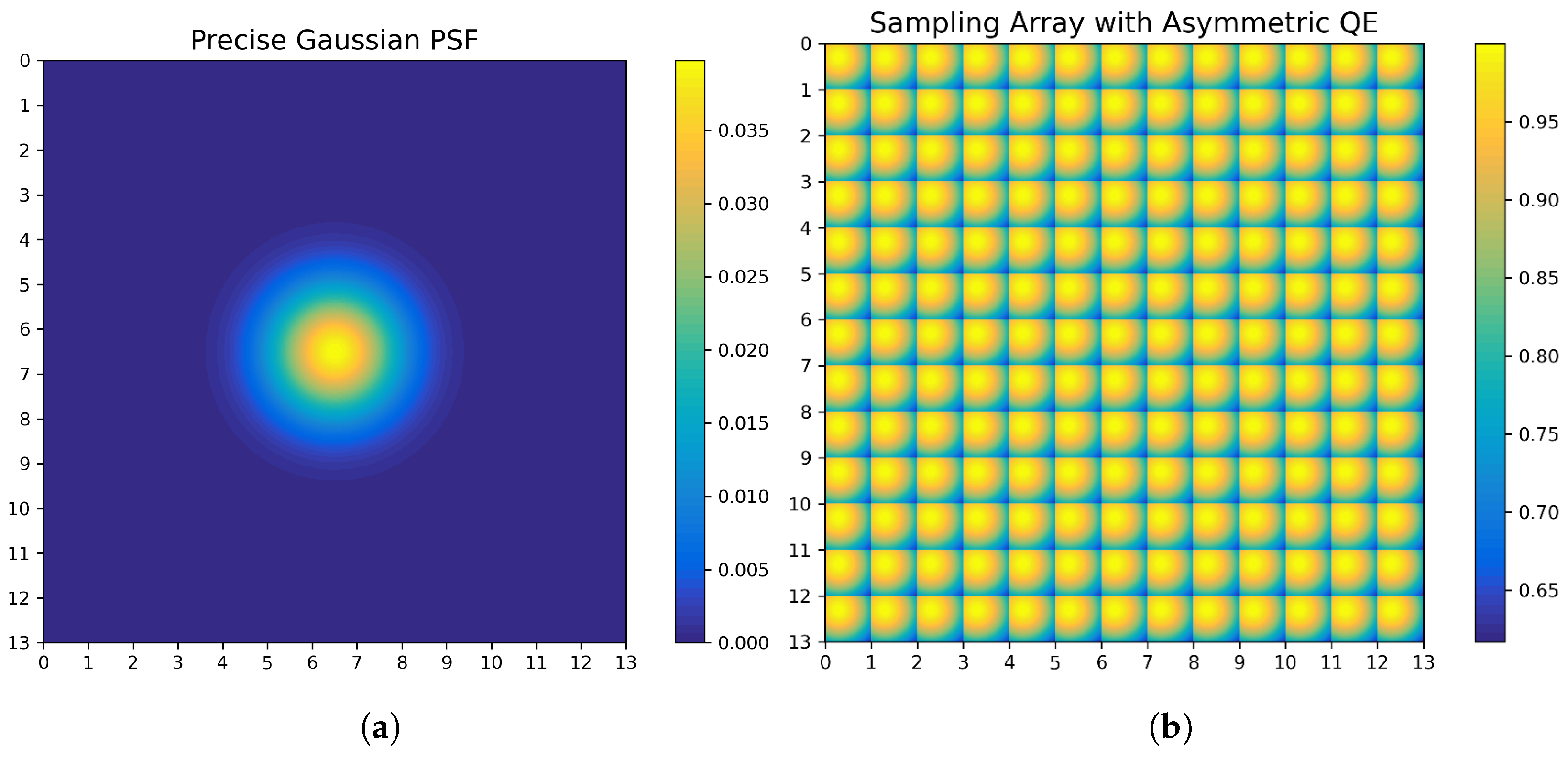
2.3. Models for Intra-Pixel Sensitivity and Its Correction Algorithm
2.4. Spatial Frequency Constraints
3. Simulations and Applications
3.1. Reconstructions for Ideal Integral Sampler
3.2. Reconstructions for the Integral Sampler with Asymmetric QE
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Schöller, M.; Wilhelm, R.; Koehler, B. Modeling the imaging process in optical stellar interferometers. Astron. Astrophys. Suppl. Ser. 2000, 144, 541–552. [Google Scholar] [CrossRef][Green Version]
- Ghaderpour, E. Least-squares Wavelet and Cross-wavelet Analyses of VLBI Baseline Length and Temperature Time Series: Fortaleza–Hartebeesthoek–Westford–Wettzell. Publ. Astron. Soc. Pac. 2021, 133, 014502. [Google Scholar] [CrossRef]
- Mena, F.; Olivares, P.; Bugueño, M.; Molina, G.; Araya, M. On the Quality of Deep Representations for Kepler Light Curves Using Variational Auto-Encoders. Signals 2021, 2, 706–728. [Google Scholar] [CrossRef]
- Malbet, F.; Boehm, C.; Krone-Martins, A.; Amorim, A.; Anglada-Escudé, G.; Brandeker, A.; Courbin, F.; Enßlin, T.; Falcão, A.; Freese, K.; et al. Faint objects in motion: The new frontier of high precision astrometry. Exp. Astron. 2021, 51, 845–886. [Google Scholar] [CrossRef]
- Fliegel, K. Modeling and Measurement of Image Sensor Characteristics. Radioengineering 2004, 13, 27–34. [Google Scholar]
- Boreman, G.D. Modulation transfer function in optical and electro-optical systems. Russ. Chem. Rev. 2001, 71, 159–179. [Google Scholar]
- Feltz, J.C.; Karim, M.A. Modulation transfer function of charge-coupled devices. Appl. Opt. 1990, 29, 717–722. [Google Scholar] [CrossRef] [PubMed]
- Sukumar., V.; Hess, H.L.; Noren, K.V.; Donohoe, G.; Ay, S. Imaging system MTF- modeling with modulation functions. In Proceedings of the 2008 34th Annual Conference of IEEE Industrial Electronics, Orlando, FL, USA, 10–13 November 2008; pp. 1748–1753. [Google Scholar] [CrossRef]
- Vorobiev, D.; Ninkov, Z.; Caldwell, D.; Mochnacki, S. Direct measurement of the intra-pixel response function of the Kepler Space Telescope’s CCDs. In Proceedings of the Space Telescopes and Instrumentation 2018: Optical, Infrared, and Millimeter Wave; Lystrup, M., MacEwen, H.A., Fazio, G.G., Batalha, N., Siegler, N., Tong, E.C., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2018; Volume 10698, pp. 1585–1598. [Google Scholar] [CrossRef]
- Krishnamurthy, A.; Villasenor, J.; Seager, S.; Ricker, G.; Vanderspek, R. Precision characterization of the TESS CCD detectors: Quantum efficiency, charge blooming and undershoot effects. Acta Astronaut. 2019, 160, 46–55. [Google Scholar] [CrossRef]
- Hardy, T.; Baril, M.R.; Pazder, J.; Stilburn, J.S. Intra-pixel response of infrared detector arrays for JWST. In Proceedings of the High Energy, Optical, and Infrared Detectors for Astronomy III; Dorn, D.A., Holland, A.D., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2008; Volume 7021, pp. 711–722. [Google Scholar] [CrossRef]
- Hardy, T.; Willot, C.; Pazder, J. Intra-pixel response of the new JWST infrared detector arrays. In Proceedings of the High Energy, Optical, and Infrared Detectors for Astronomy VI; Holland, A.D., Beletic, J., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2014; Volume 9154, pp. 750–761. [Google Scholar] [CrossRef]
- Robberto, M.; Baggett, S.M.; Hilbert, B.; MacKenty, J.W.; Kimble, R.A.; Hill, R.J.; Cottingham, D.A.; Delo, G.; Johnson, S.D.; Landsman, W.; et al. The infrared detectors for the wide field camera 3 on HST. In Proceedings of the Optical and Infrared Detectors for Astronomy; Garnett, J.D., Beletic, J.W., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2004; Volume 5499, pp. 15–22. [Google Scholar] [CrossRef]
- Toyozumi, H.; Ashley, M.C.B. Intra-Pixel Sensitivity Variation and Charge Transfer Inefficiency—Results of CCD Scans. Publ. Astron. Soc. Aust. 2005, 22, 257–266. [Google Scholar] [CrossRef][Green Version]
- Mahato, S.B.; de Ridder, J.; Meynants, G.; Raskin, G.; van Winckel, H. Measuring Intra-Pixel Sensitivity Variations of a CMOS Image Sensor. IEEE Sens. J. 2018, 18, 2722–2728. [Google Scholar] [CrossRef]
- Ketchazo, C.; Viale, T.; Boulade, O.; de la Barrière, F.; Dubreuil, D.; Mugnier, L.; Moreau, V.; Guérineau, N.; Mulet, P.; Druart, G.; et al. Intrapixel measurement techniques on large focal plane arrays for astronomical applications: A comparative study. In Proceedings of the International Conference on Space Optics—ICSO 2016, Biarritz, France, 18–21 October 2016; Cugny, B., Karafolas, N., Sodnik, Z., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2017; Volume 10562, p. 105623D. [Google Scholar] [CrossRef][Green Version]
- Willemin, M.; Blanc, N.; Lang, G.; Lauxtermann, S.; Schwider, P.; Seitz, P.; Wäny, M. Optical characterization methods for solid-state image sensors. Opt. Lasers Eng. 2001, 36, 185–194. [Google Scholar] [CrossRef]
- Takacs, P.Z.; Kotov, I.; Frank, J.; O’Connor, P.; Radeka, V.; Lawrence, D.M. PSF and MTF measurement methods for thick CCD sensor characterization. In Proceedings of the High Energy, Optical, and Infrared Detectors for Astronomy IV; Holland, A.D., Dorn, D.A., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2010; Volume 7742, p. 774207. [Google Scholar] [CrossRef]
- Zhong, L.; Li, X.; Zhu, M.; Hu, Z.; Chen, F. Improved Intra-Pixel Sensitivity Characterization Based on Diffusion and Coupling Model for Infrared Focal Plane Array Photodetector. Sensors 2021, 21, 8195. [Google Scholar] [CrossRef] [PubMed]
- Mahato, S.; De Ridder, J.; Meynants, G.; Raskin, G.; Van Winckel, H. A novel technique to characterize the spatial intra-pixel sensitivity variations in a CMOS image sensor. In Proceedings of the 2017 15th IEEE International New Circuits and Systems Conference (NEWCAS), Strasbourg, France, 25–28 June 2017; pp. 361–364. [Google Scholar] [CrossRef]
- Li, J.; Liu, Z.; Liu, F. Using sub-resolution features for self-compensation of the modulation transfer function in remote sensing. Opt. Express 2017, 25, 4018–4037. [Google Scholar] [CrossRef]
- Choi, H.; Kim, J.P.; Song, M.G.; Kim, W.C.; Park, N.C.; Park, Y.P.; Park, K.S. Effects of motion of an imaging system and optical image stabilizer on the modulation transfer function. Opt. Express 2008, 16, 21132–21141. [Google Scholar] [CrossRef]
- Barnard, K.J.; Boreman, G.D. Modulation transfer function of hexagonal staring focal plane arrays. Opt. Eng. 1991, 30, 1915–1919. [Google Scholar] [CrossRef]
- Vitek, S.; Hozman, J. Modeling of Imaging Systems in Matlab. Radioengineering 2003, 12, 55–57. [Google Scholar]
- Park, S.K.; Schowengerdt, R.A.; Kaczynski, M.A. Modulation-transfer-function analysis for sampled image systems. Appl. Opt. 1984, 23, 2572. [Google Scholar] [CrossRef] [PubMed]
- Shannon, C. Communication in the Presence of Noise. Proc. IRE 1949, 37, 10–21. [Google Scholar] [CrossRef]
- Boreman; Glenn, D. Oversampling requirements for pixelated-imager systems. Opt. Eng. 1999, 38, 782–785. [Google Scholar] [CrossRef]
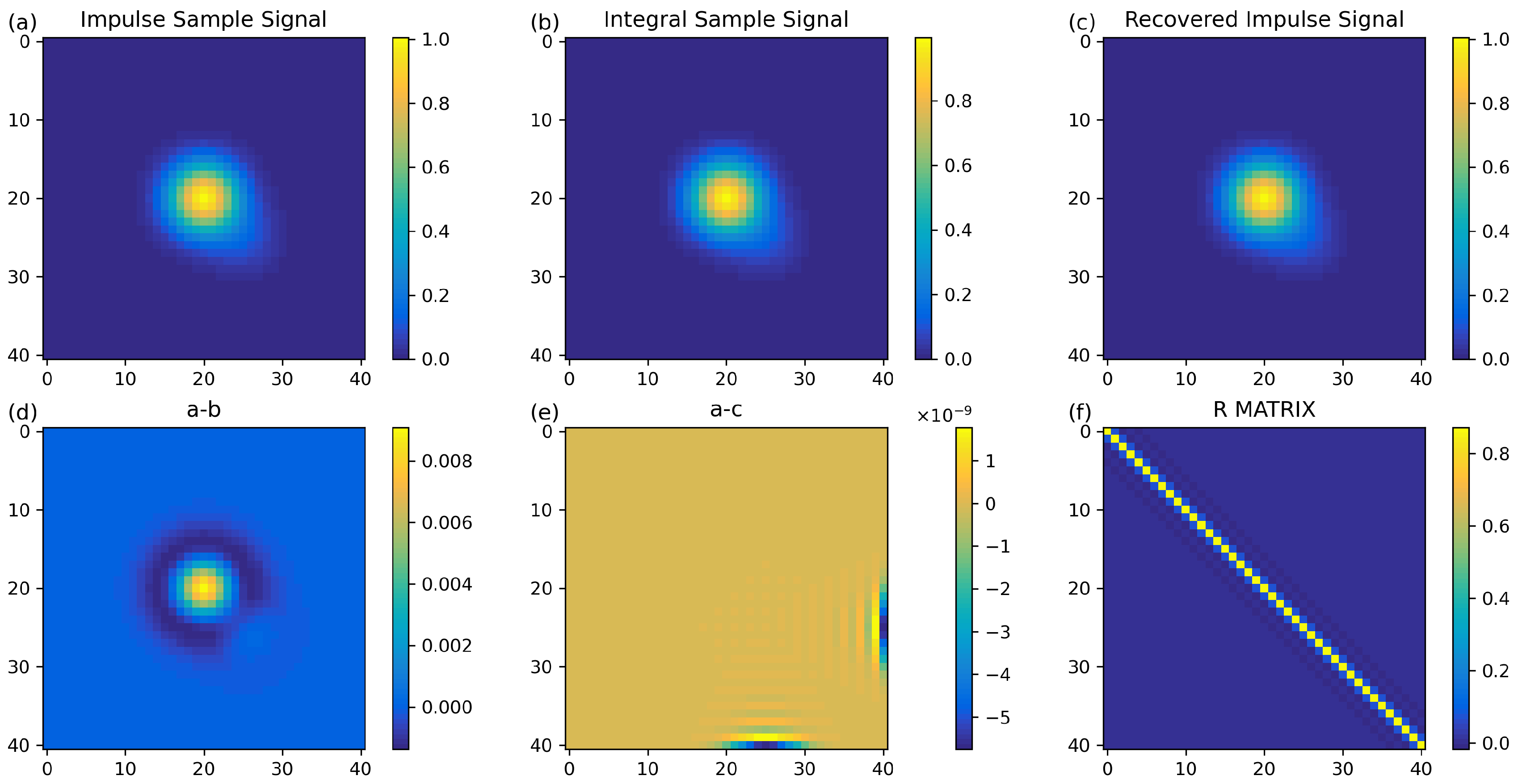



| Barycenter | X (Pixel) | Y (Pixel) | Relative Error |
|---|---|---|---|
| Ideal | 6.5000 | 6.5000 | |
| Uniform Integral Sampler | 6.5050 | 6.5050 | |
| Asymmetric Integral Sampler | 6.5211 | 6.5211 |
| Barycenter | X (Pixel) | Y (Pixel) | Relative Error |
|---|---|---|---|
| Ideal Centroid | 6.5000 | 6.5000 | |
| Recovered Uniform Integral Sampler | 6.5051 | 6.5051 |
| Position (Pixel) | X | std (X) | Y | std (Y) |
|---|---|---|---|---|
| Ideal position | 29.474 | 0.290 | 29.514 | 0.281 |
| Uniform integral sampler | 29.475 | 0.288 | 29.513 | 0.281 |
| Asymmetric integral sampler | 29.491 | 0.289 | 29.529 | 0.281 |
| Fixed integral sampler | 29.475 | 0.289 | 29.513 | 0.281 |
| Position (Pixel) | X | std (X) | Y | std (Y) |
|---|---|---|---|---|
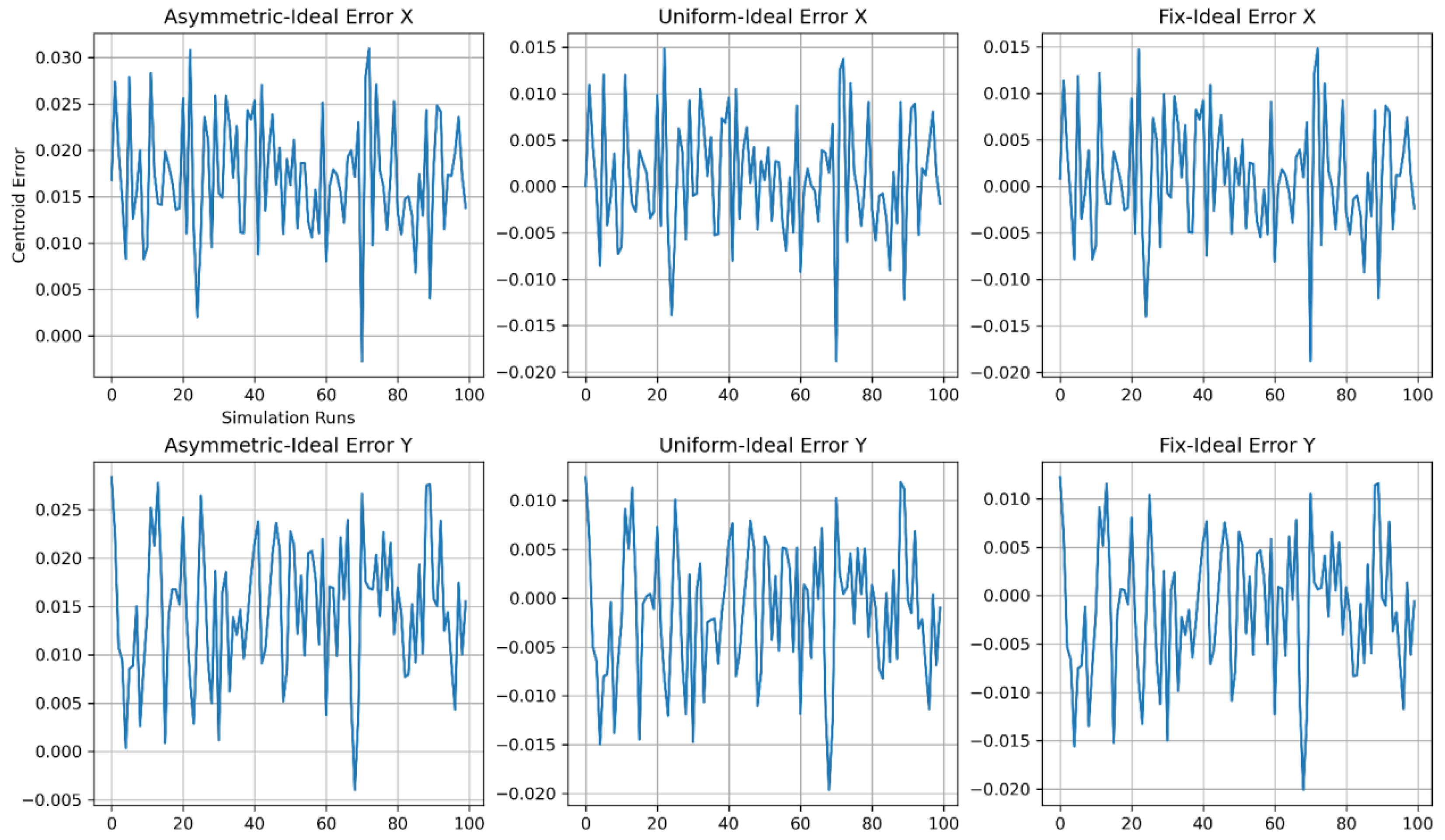
| Uniform error | 0.001 | 0.006 | −0.001 | 0.007 |
| Asymmetric error | 0.017 | 0.006 | 0.015 | 0.007 |
| Fixed error | 0.001 | 0.006 | −0.001 | 0.007 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Zhou, J. A Correction Algorithm of the Sampling Effect and Its Application in High-Precision Astrometry. Universe 2022, 8, 593. https://doi.org/10.3390/universe8110593
Sun Y, Zhou J. A Correction Algorithm of the Sampling Effect and Its Application in High-Precision Astrometry. Universe. 2022; 8(11):593. https://doi.org/10.3390/universe8110593
Chicago/Turabian StyleSun, Yunqi, and Jianfeng Zhou. 2022. "A Correction Algorithm of the Sampling Effect and Its Application in High-Precision Astrometry" Universe 8, no. 11: 593. https://doi.org/10.3390/universe8110593
APA StyleSun, Y., & Zhou, J. (2022). A Correction Algorithm of the Sampling Effect and Its Application in High-Precision Astrometry. Universe, 8(11), 593. https://doi.org/10.3390/universe8110593






