Construction of Exact Solutions for Gilson–Pickering Model Using Two Different Approaches

Abstract

In this paper, the extended simple equation method (ESEM) and the generalized Riccati equation mapping (GREM) method are applied to the nonlinear third-order Gilson–Pickering (GP) model to obtain a variety of new exact wave solutions. With the suitable selection of parameters involved in the model, some familiar physical governing models such as the Camassa–Holm (CH) equation, the Fornberg–Whitham (FW) equation, and the Rosenau–Hyman (RH) equation are obtained. The graphical representation of solutions under different constraints shows the dark, bright, combined dark–bright, periodic, singular, and kink soliton. For the graphical representation, 3D plots, contour plots, and 2D plots of some acquired solutions are illustrated. The obtained wave solutions motivate researchers to enhance their theories to the best of their capacities and to utilize the outcomes in other nonlinear cases. The executed methods are shown to be practical and straightforward for approaching the considered equation and may be utilized to study abundant types of NLEEs arising in physics, engineering, and applied sciences.

1. Introduction

Differential equations in our daily lives govern many physical phenomena. In particular, nonlinear partial differential equations (NLPDEs) play a vital role in nonlinear science. Several natural wonders appear in biological and applied studies, such as fluid mechanics, hydrodynamics, mathematical physics, optics, birefringent fibers, elastic media, chemical reactions, cosmology, ecology, quantum mechanics, geology, plasma physics, wave propagation, and shallow water, can be interpreted by NLPDEs [1,2,3,4,5,6,7,8,9,10,11,12].

Researchers, mathematicians, and physicists have worked on NLPDEs for many decades due to their wide range of applications in daily life. For the last few decades, NLPDEs have been a vital matter of contention for exploration. As we know that natural physical phenomena are complex in nature, to illustrate the diverse quantitative and qualitative exposures of NLPDEs, numerous mathematical approaches have been invented and explained in the literature, such as the extended hyperbolic function method [13], Sardar subequation method [14,15], ${\varphi }^6$ model expansion techniques [16], $exp(-\varphi (\xi \left)\right)$ expansion, first integral and Sin–Gordon methods [17], $(G^{\prime }/G)$ expansion method [18], extended auxiliary equation method [19], generalized Kudryashov method [20], tanh method [21], extended simple equation method [22,23], generalized Riccati equation mapping method [24], modified F expansion method [25], etc. A direct approach for the exact solutions of nonlinear partial differential equations (NLPDEs) has been suggested by using the rational function transformation [26], applying Bäcklund transformations of the linear form [27], Hirota’s bilinear method [28] as a mathematical tool for the systematic and computational approach to the soliton solutions of NLPDEs, the improved Hirota bilinear method (HBM) [29], a double subequation method [30] for constructing complexion solutions of nonlinear partial differential equations (NLPDEs), and refinements of the transformation of inequalities for zero-balanced hypergeometric functions [31].

The Gilson–Pickering model is of supreme value due to its unique characteristic of providing the foundation for different governed models, also discussed for specific values of the parameters. The bifurcation behavior of the GP model [32] has a certain curiosity to investigate and explore its salient features through some analytical approaches, which has not been considered before in the literature.

The primary purpose behind the research in this paper is to explore the variety of exact and advanced solutions of the Gilson–Pickering equation using two different analytical approaches, i.e., the extended simple equation method (ESEM) [22,23] and the generalized Riccati equation mapping (GREM) method [24]. These methods are vital in finding exact solutions for NLEEs in engineering and mathematical physics. We keenly focus on the fundamental role of the proposed methods to establish the new families of accurate solutions following the nonlinear third-order Gilson–Pickering equation [32].

$$q_t+2\alpha q_x-\beta q{q}_x-\gamma q_x{q}_{xx}-\omega q_{xxt}-\epsilon q{q}_{xxx}=0,$$

(1)

where $\alpha ,\beta ,\gamma ,\omega$, and $\epsilon$ are constants. The following governed physical models are associated with the suitable selection of parameters $\alpha ,\beta$:

When $\alpha =0.5$, $\beta =-1$, $\gamma =3$, $\omega =1$, Equation (1) is transformed into the Fornberg–Whitham (FW) equation [33,34], i.e.,

$$q_t+q_x+q{q}_x-3q_x{q}_{xx}-q_{xxt}-\epsilon q{q}_{xxx}=0.$$

(2)

When $\alpha =0$, $\beta =1$, $\gamma =3$, $\omega =0$, Equation (1) converts into the Rosenau–Hyman equation [35,36], i.e.,

$$q_t-q{q}_x-3q_x{q}_{xx}-\epsilon q{q}_{xx}=0.$$

(3)

When $\beta =-1$, $\gamma =2$, $\omega =1$, Equation (1) becomes the Fuchssteiner–Fokas–Camassa–Holm (FFCH) equation [37,38] as

$$q_t+2\alpha q_x+q{q}_x-2q_x{q}_{xx}-q_{xxt}-\epsilon q{q}_{xxx}=0.$$

(4)

This paper is organized as follows: Section 2 addresses the methodology of the ESEM. In Section 3, the description of the GREM method is given. Section 4 discusses the application of the ESEM to the GP equation, and Section 5 presents the solutions of the GP equation by using the GREM method. Section 6 explains the physical interpretation of some solutions. Finally, in Section 7, the conclusion is presented.

2. Methodology of Extended Simple Equation Method

To solve Equation (1), the following steps are used:

Step 1: 

Let the PDE have the form

$$\begin{array}{c}\hfill Q_1(v,v_{xx},v_{xz},v_{xt},v_{xy},v_{xtt},\dots )=0.\end{array}$$

(5)

Step 2: 

Consider the wave transformation:

$$\begin{array}{c}\hfill v=V\left(\varrho \right),\varrho =x-ϵt,\end{array}$$

(6)

which transforms PDE (5) into the following ODE:

$$\begin{array}{c}\hfill Q_2(V,V^{\prime },V^{″},\dots )=0.\end{array}$$

(7)

Step 3: 

Consider that Equation (7) has a solution of the form

$$\begin{array}{c}\hfill R\left(\varrho \right)=\sum _{j=-N}^N{A}_j{\mathrm{\Phi }}^j\left(\varrho \right).\end{array}$$

(8)

Step 4: 

Let $\mathrm{\Phi }$ satisfy the DE of the form

$$\begin{array}{c}\hfill {\mathrm{\Phi }}^{\prime }=c_0+c_1\mathrm{\Phi }+c_2{\mathrm{\Phi }}^2+c_3{\mathrm{\Phi }}^3.\end{array}$$

(9)

Step 5: 

Equation (9) has the following solutions [22,23]:

If $c_3=0$,

$$\begin{array}{c}\hfill \mathrm{\Phi }\left(\varrho \right)=-\frac{c_1-\sqrt{4c_0{c}_2-c_1^2}tan(\frac{\sqrt{4c_0{c}_2-c_1^2}}{2}(\varrho +{\varrho }_0))}{2c_2},4c_0{c}_2>c_1^2.\end{array}$$

(10)

If $c_0=0$, $c_3=0$, then

$$\begin{array}{ccc}\hfill \mathrm{\Phi }& =& \frac{c_1{e}^{c_1(\varrho +{\varrho }_0)}}{1-c_2{e}^{c_1(\varrho +{\varrho }_0)}},c_1>0,\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill \mathrm{\Phi }& =& \frac{-c_1{e}^{c_1(\varrho +{\varrho }_0)}}{1+c_2{e}^{c_1(\varrho +{\varrho }_0)}},c_1<0.\hfill \end{array}$$

(12)

If $c_1=0$, $c_3=0$, then

$$\begin{array}{c}\hfill \mathrm{\Phi }=\frac{\sqrt{c_0{c}_2}}{c_2}tan\left(\sqrt{c_0{c}_2}(\varrho +{\varrho }_0)\right),c_0{c}_2>0,\end{array}$$

(13)

$$\begin{array}{c}\hfill \mathrm{\Phi }=-\frac{\sqrt{-c_0{c}_2}}{c_2}tanh\left(\sqrt{-c_0{c}_2}(\varrho +{\varrho }_0)\right),c_0{c}_2<0.\end{array}$$

(14)

Using Equation (8) with Equation (9) in Equation (7) and after simplification, the values of the constant parameters are found. Taking these constants and the $\mathrm{\Phi }\left(\varrho \right)$ values in Equation (8), we obtain the solution of Equation (5).

3. Methodology of Generalized Riccati Equation Mapping Method

In this method, the first two steps are same as in the ESEM.

Step 3: 

Let the solution for Equation (7) have the form

$$\begin{array}{c}\hfill Q\left(\varrho \right)=a_0+\sum _{j=1}^N{a}_j{\mathrm{\Phi }}^j\left(\varrho \right)+\sum _{j=1}^N{b}_j{\mathrm{\Phi }}^{-j}\left(\varrho \right).\end{array}$$

(15)

Let $\mathrm{\Phi }\left(\varrho \right)$ satisfy the DE:

$$\begin{array}{c}\hfill {\mathrm{\Phi }}^{\prime }=u+v\mathrm{\Phi }+w{\mathrm{\Phi }}^2,\end{array}$$

(16)

where u, v, and w are arbitrary constants. Using Equation (15) with Equation (16) in Equation (7) and comparing all the coefficients of $\mathrm{\Phi }$ imply a system of equations, from which the constants involved in the supposed solution (15) are determined. Taking these obtained values of the constants with the following known solutions of the generalized Riccati Equation (16), the soliton solutions for ODE (7) can be easily calculated.

The following twenty-seven solutions of Equation (16) are used for ODE (7).

Type 1: 

When $v^2-4uw>0$ and $vw$ or $uw\ne 0$, the solutions of Equation (16) are given as

$$\begin{array}{ccc}\hfill {\mathrm{\Phi }}_1& =& -\frac{\sqrt{v^2-4uw}tanh\left(\frac{1}{2}\varrho \sqrt{v^2-4uw}\right)+v}{2w},\hfill \\ \hfill {\mathrm{\Phi }}_2& =& -\frac{\sqrt{v^2-4uw}coth\left(\frac{1}{2}\varrho \sqrt{v^2-4uw}\right)+v}{2w},\hfill \\ \hfill {\mathrm{\Phi }}_3& =& -\frac{\sqrt{v^2-4uw}\left(tanh\left(\varrho \sqrt{v^2-4uw}\right)\pm \mathrm{isech}\left(\varrho \sqrt{v^2-4uw}\right)\right)+v}{2w},\hfill \\ \hfill {\mathrm{\Phi }}_4& =& -\frac{\sqrt{v^2-4uw}\left(coth\left(\varrho \sqrt{v^2-4uw}\right)\pm \csc \mathrm{h}\left(\varrho \sqrt{v^2-4uw}\right)\right)+v}{2w},\hfill \\ \hfill {\mathrm{\Phi }}_5& =& -\frac{\sqrt{v^2-4uw}\left(tanh\left(\frac{1}{4}\varrho \sqrt{v^2-4uw}\right)\pm coth\left(\frac{1}{4}\varrho \sqrt{v^2-4uw}\right)\right)+2v}{4w},\hfill \\ \hfill {\mathrm{\Phi }}_6& =& \frac{\frac{\sqrt{\left(A^2+B^2\right)\left(v^2-4uw\right)}-A\sqrt{v^2-4uw}cosh\left(\varrho \sqrt{v^2-4uw}\right)}{Asinh\left(\varrho \sqrt{v^2-4uw}\right)+B}-v}{2w},\hfill \\ \hfill {\mathrm{\Phi }}_7& =& \frac{-\frac{\sqrt{\left(B^2-A^2\right)\left(v^2-4uw\right)}+A\sqrt{v^2-4uw}cosh\left(\varrho \sqrt{v^2-4uw}\right)}{Asinh\left(\varrho \sqrt{v^2-4uw}\right)+B}-v}{2w},\hfill \end{array}$$

where A and B are two non-zero real constants that satisfy $B^2-A^2>0.$

$$\begin{array}{ccc}\hfill {\mathrm{\Phi }}_8& =& \frac{2ucosh\left(\frac{1}{2}\varrho \sqrt{v^2-4uw}\right)}{\sqrt{v^2-4uw}sinh\left(\frac{1}{2}\varrho \sqrt{v^2-4uw}\right)-vcosh\left(\frac{1}{2}\varrho \sqrt{v^2-4uw}\right)},\hfill \\ \hfill {\mathrm{\Phi }}_9& =& -\frac{2usinh\left(\frac{1}{2}\varrho \sqrt{v^2-4uw}\right)}{vsinh\left(\frac{1}{2}\varrho \sqrt{v^2-4uw}\right)-\sqrt{v^2-4uw}cosh\left(\frac{1}{2}\varrho \sqrt{v^2-4uw}\right)},\hfill \\ \hfill {\mathrm{\Phi }}_{10}& =& \frac{2ucosh\left(\frac{1}{2}\varrho \sqrt{v^2-4uw}\right)}{\sqrt{v^2-4uw}sinh\left(\varrho \sqrt{v^2-4uw}\right)-\left(vcosh\left(\varrho \sqrt{v^2-4uw}\right)\pm i\sqrt{v^2-4uw}\right)},\hfill \\ \hfill {\mathrm{\Phi }}_{11}& =& \frac{2usinh\left(\frac{1}{2}\varrho \sqrt{v^2-4uw}\right)}{\left(\sqrt{v^2-4uw}cosh\left(\varrho \sqrt{v^2-4uw}\right)\pm \sqrt{v^2-4uw}\right)-vsinh\left(\varrho \sqrt{v^2-4uw}\right)},\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\mathrm{\Phi }}_{12}& =& \frac{4usinh\left(\frac{1}{4}\varrho \sqrt{v^2-4uw}\right)cosh\left(\frac{1}{4}\varrho \sqrt{v^2-4uw}\right)}{(-2\sqrt{v^2-4uw}{\cos \mathrm{h}}^2\left(\frac{1}{4}\varrho \sqrt{v^2-4uw}\right)-2vsinh\left(\frac{1}{4}\varrho \sqrt{v^2-4uw}\right)cosh\left(\frac{1}{4}\varrho \sqrt{v^2-4uw}\right)-\sqrt{v^2-4uw}}.\hfill \end{array}$$

Type 2: 

When $v^2-4uw<0$ and $vw$ or $uw\ne 0$, the solutions of Equation (16) are given as

$$\begin{array}{ccc}\hfill {\mathrm{\Phi }}_{13}& =& \frac{\sqrt{4uw-v^2}tan\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)-v}{2w},\hfill \\ \hfill {\mathrm{\Phi }}_{14}& =& -\frac{\sqrt{4uw-v^2}cot\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)+v}{2w},\hfill \\ \hfill {\mathrm{\Phi }}_{15}& =& \frac{\sqrt{4uw-v^2}\left(tan\left(\varrho \sqrt{4uw-v^2}\right)\pm sec\left(\varrho \sqrt{4uw-v^2}\right)\right)-v}{2w},\hfill \\ \hfill {\mathrm{\Phi }}_{16}& =& -\frac{\sqrt{4uw-v^2}\left(cot\left(\varrho \sqrt{4uw-v^2}\right)\pm csc\left(\varrho \sqrt{4uw-v^2}\right)\right)+v}{2w},\hfill \\ \hfill {\mathrm{\Phi }}_{17}& =& \frac{\sqrt{4uw-v^2}\left(tan\left(\frac{1}{4}\varrho \sqrt{4uw-v^2}\right)-coth\left(\frac{1}{4}\varrho \sqrt{4uw-v^2}\right)\right)-2v}{4w},\hfill \\ \hfill {\mathrm{\Phi }}_{18}& =& \frac{\frac{\pm \sqrt{\left(A^2-B^2\right)\left(4uw-v^2\right)}-A\sqrt{4uw-v^2}cos\left(\varrho \sqrt{4uw-v^2}\right)}{Asinh\left(\varrho \sqrt{4uw-v^2}\right)+B}-v}{2w},\hfill \\ \hfill {\mathrm{\Phi }}_{19}& =& \frac{-\frac{\pm \sqrt{\left(A^2-B^2\right)\left(4uw-v^2\right)}+A\sqrt{4uw-v^2}cos\left(\varrho \sqrt{4uw-v^2}\right)}{Asin\left(\varrho \sqrt{4uw-v^2}\right)+B}-v}{2w},\hfill \end{array}$$

where A and B are two non-zero real constants that satisfy $A^2-B^2>0.$

$$\begin{array}{ccc}\hfill {\mathrm{\Phi }}_{20}& =& -\frac{2ucos\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)}{\sqrt{4uw-v^2}sin\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)+vcos\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)},\hfill \\ \hfill {\mathrm{\Phi }}_{21}& =& \frac{2usin\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)}{\sqrt{4uw-v^2}cos\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)-vsin\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)},\hfill \\ \hfill {\mathrm{\Phi }}_{22}& =& -\frac{2ucos\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)}{\sqrt{4uw-v^2}sin\left(\varrho \sqrt{4uw-v^2}\right)+\left(vcos\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)\pm \sqrt{4uw-v^2}\right)},\hfill \\ \hfill {\mathrm{\Phi }}_{23}& =& \frac{2usin\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)}{\left(\sqrt{4uw-v^2}cos\left(\varrho \sqrt{4uw-v^2}\right)\pm \sqrt{4uw-v^2}\right)-vsin\left(\varrho \sqrt{4uw-v^2}\right)},\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\mathrm{\Phi }}_{24}& =& \frac{4usin\left(\frac{1}{4}\varrho \sqrt{4uw-v^2}\right)cos\left(\frac{1}{4}\varrho \sqrt{4uw-v^2}\right)}{2\sqrt{4uw-v^2}{\cos }^2\left(\varrho \sqrt{\frac{1}{4}\left(4uw-v^2\right)}\right)-2vsin\left(\frac{1}{4}\varrho \sqrt{4uw-v^2}\right)cos\left(\frac{1}{4}\varrho \sqrt{4uw-v^2}\right)-\sqrt{4uw-v^2}}.\hfill \end{array}$$

Type 3: 

When $u=0$ and $wv\ne 0$, the solutions of Equation (16) are given as

$$\begin{array}{ccc}\hfill {\mathrm{\Phi }}_{25}& =& -\frac{v.d}{w(d-sinh(v.\varrho )+cosh(v.\varrho \left)\right)},\hfill \\ \hfill {\mathrm{\Phi }}_{26}& =& -\frac{v(sinh(v\varrho )+cosh(v\varrho \left)\right)}{w(d+sinh(v\varrho )+cosh(v\varrho \left)\right)},\hfill \end{array}$$

where d is an arbitrary constant.

Type 4: 

When $w\ne 0$ and $u=v=0$, the only solution of Equation (16) is

$${\mathrm{\Phi }}_{27}=-\frac{1}{w\varrho +c},$$

where c is an arbitrary constant.

Using the transformation given in Equation (6) in Equation (1), we have

$$(2\alpha -ϵ)Q^{\prime }+\omega ϵQ^{‴}-ϵQ{Q}^{‴}-\beta Q{Q}^{\prime }-\gamma Q{Q}^{″}=0.$$

(17)

Integrating Equation (17) once, we obtain

$$-\epsilon Q{Q}^{″}+\omega ϵQ^{″}+\frac{1}{2}(ϵ-\gamma ){\left(Q^{\prime }\right)}^2+(2\alpha -ϵ)Q-\frac{1}{2}\beta Q^2=L,$$

(18)

where L is the constant of integration. Balancing between the highest derivative and the nonlinear term, Equation (18) provides $M=2$.

4. Application of Extended Simple Equation Method

In this section, the extended simple equation method is applied to derive the solution of Equation (1).

Let the general form of the solution of Equation (18) be

$$Q\left(\varrho \right)=A_2\mathrm{\Phi }{\left(\varrho \right)}^2+A_1\mathrm{\Phi }\left(\varrho \right)+\frac{A_{-2}}{\mathrm{\Phi }{\left(\varrho \right)}^2}+\frac{A_{-1}}{\mathrm{\Phi }\left(\varrho \right)}+A_0.$$

(19)

Using Equation (19) with Equation (9) in Equation (18) and after simplification, the following cases arise:

Case 1: 

If $c_3=0,4c_0{c}_2-c_1^2>0.$

Family-I:

$$\begin{array}{ccc}& & L=\frac{\left(A_0{c}_1-A_{-1}{c}_2\right)\left(-A_{-1}\beta c_1^2+6A_0\beta c_0{c}_1-2A_{-1}\beta c_0{c}_2+A_{-1}{c}_1^4\epsilon -8A_{-1}{c}_0{c}_2{c}_1^2\epsilon +16A_{-1}{c}_0^2{c}_2^2\epsilon \right)}{12c_0{c}_1^2},\hfill \\ & & A_{-2}=\frac{A_{-1}{c}_0}{c_1},A_1=0,A_2=0,\omega =\frac{A_{-1}\beta +A_{-1}{c}_1^2(-\epsilon )+12A_0{c}_0{c}_1\epsilon -8A_{-1}{c}_0{c}_2\epsilon }{12c_0{c}_1ϵ},\gamma =-2\epsilon ,\hfill \\ & & \alpha =\frac{-A_{-1}\beta c_1^2+12A_0\beta c_0{c}_1-8A_{-1}\beta c_0{c}_2+A_{-1}{c}_1^4\epsilon -8A_{-1}{c}_0{c}_2{c}_1^2\epsilon +16A_{-1}{c}_0^2{c}_2^2\epsilon +12c_0{c}_1ϵ}{24c_0{c}_1}.\hfill \end{array}$$

(20)

$$\begin{array}{ccc}& & Q_1=\frac{4A_{-1}{c}_0{c}_2^2}{c_1\left(c_1-\sqrt{4c_0{c}_2-c_1^2}tan\left(\frac{1}{2}\sqrt{4c_0{c}_2-c_1^2}\left(\varrho +{\varrho }_0\right)\right)\right){}^2}+A_0\hfill \\ & & -\frac{2A_{-1}{c}_2}{c_1-\sqrt{4c_0{c}_2-c_1^2}tan\left(\frac{1}{2}\sqrt{4c_0{c}_2-c_1^2}\left(\varrho +{\varrho }_0\right)\right)}.\hfill \end{array}$$

(21)

Family-II:

$$\begin{array}{ccc}& & L=\frac{\beta \left(A_0^2{c}_2-A_1{A}_0{c}_1+A_1^2{c}_0\right)}{2c_2},\omega =\frac{A_1\beta c_1-2A_0\beta c_2}{2c_2\left(c_1^2-4c_0{c}_2\right)ϵ},\epsilon =-\frac{\beta }{c_1^2-4c_0{c}_2},\hfill \\ & & A_2=0,A_{-1}=0,A_{-2}=0,\gamma =\frac{3\beta }{c_1^2-4c_0{c}_2},\alpha =\frac{A_1(-\beta )c_1+2A_0\beta c_2+2c_2ϵ}{4c_2}.\hfill \end{array}$$

(22)

$$\begin{array}{c}\hfill Q_2=A_0-\frac{A_1\left(c_1-\sqrt{4c_0{c}_2-c_1^2}tan\left(\frac{1}{2}\sqrt{4c_0{c}_2-c_1^2}\left(\varrho +{\varrho }_0\right)\right)\right)}{2c_2}.\end{array}$$

(23)

Family-III:

$$\begin{array}{ccc}& & L=\frac{\beta \left(A_{-1}^2{c}_2-A_0{A}_{-1}{c}_1+A_0^2{c}_0\right)}{2c_0},\omega =\frac{\beta \left(2A_0{c}_0-A_{-1}{c}_1\right)}{8c_0^2{c}_2ϵ-2c_0{c}_1^2ϵ},\epsilon =-\frac{\beta }{c_1^2-4c_0{c}_2},\hfill \\ & & A_1=0,A_2=0,A_{-2}=0,\gamma =\frac{3\beta }{c_1^2-4c_0{c}_2},\alpha =\frac{2A_0\beta c_0-A_{-1}\beta c_1+2c_0ϵ}{4c_0}.\hfill \end{array}$$

(24)

$$\begin{array}{c}\hfill Q_3=A_0-\frac{2A_{-1}{c}_2}{c_1-\sqrt{4c_0{c}_2-c_1^2}tan\left(\frac{1}{2}\sqrt{4c_0{c}_2-c_1^2}\left(\varrho +{\varrho }_0\right)\right)}.\end{array}$$

(25)

Case 2: 

If $c_0=0$, $c_3=0$.

Family-I:

$$\begin{array}{ccc}& & L=\frac{1}{2}\left(A_{-1}{c}_2-A_0{c}_1\right)\left(-3A_0{c}_1\epsilon +3A_{-1}{c}_2\epsilon +2c_1\omega ϵ\right),A_{-2}=0,A_1=0,A_2=0,\hfill \\ & & \beta =c_1^2\epsilon ,\alpha =\frac{1}{2}\left(2A_0{c}_1^2\epsilon -2A_{-1}{c}_2{c}_1\epsilon +c_1^2\omega (-ϵ)+ϵ\right),\gamma =-2\epsilon \hfill \end{array}$$

(26)

$$\begin{array}{ccc}\hfill Q_4& =& \frac{A_{-1}{e}^{-c_1\left(\varrho +{\varrho }_0\right)}\left(1-c_2{e}^{c_1\left(\varrho +{\varrho }_0\right)}\right)}{c_1}+A_0,c_1>0.\hfill \end{array}$$

(27)

$$\begin{array}{ccc}\hfill Q_5& =& A_0-\frac{A_{-1}{e}^{-c_1\left(\varrho +{\varrho }_0\right)}\left(c_2{e}^{c_1\left(\varrho +{\varrho }_0\right)}+1\right)}{c_1},c_1<0.\hfill \end{array}$$

(28)

Family-II:

$$\begin{array}{ccc}& & L=\frac{1}{2}\left(A_{-1}{c}_2-2A_0{c}_1\right)\left(-6A_0{c}_1\epsilon +3A_{-1}{c}_2\epsilon +4c_1\omega ϵ\right),A_{-2}=\frac{A_{-1}{c}_1}{2c_2},A_1=0,A_2=0,\hfill \\ & & \alpha =\frac{1}{2}\left(8A_0{c}_1^2\epsilon -4A_{-1}{c}_2{c}_1\epsilon -4c_1^2\omega ϵ+ϵ\right),\beta =4c_1^2\epsilon ,\gamma =-2\epsilon .\hfill \end{array}$$

(29)

$$\begin{array}{ccc}& & Q_6=\frac{A_{-1}{e}^{-c_1\left(\varrho +{\varrho }_0\right)}\left(1-c_2{e}^{c_1\left(\varrho +{\varrho }_0\right)}\right)}{c_1}{A}_0\hfill \end{array}$$

$$\begin{array}{ccc}& & +\frac{A_{-1}{e}^{-2c_1\left(\varrho +{\varrho }_0\right)}\left(1-c_2{e}^{c_1\left(\varrho +{\varrho }_0\right)}\right){}^2}{2c_1{c}_2},c_1>0.\hfill \\ & & Q_7=\frac{A_{-1}{e}^{-2c_1\left(\varrho +{\varrho }_0\right)}\left(c_2{e}^{c_1\left(\varrho +{\varrho }_0\right)}+1\right){}^2}{2c_1{c}_2}\hfill \end{array}$$

(30)

$$\begin{array}{ccc}& & -\frac{A_{-1}{e}^{-c_1\left(\varrho +{\varrho }_0\right)}\left(c_2{e}^{c_1\left(\varrho +{\varrho }_0\right)}+1\right)}{c_1}+A_0,c_1<0.\hfill \end{array}$$

(31)

Family-III:

$$\begin{array}{ccc}& & L=\frac{8A_0^2{c}_1^2{c}_2\epsilon -A_0{A}_1{c}_1^3\epsilon }{4c_2},\alpha =\frac{A_1{c}_1^3(-\epsilon )+16A_0{c}_2{c}_1^2\epsilon +4c_2ϵ}{8c_2},\hfill \\ & & A_{-1}=0,A_{-2}=0,A_2=\frac{A_1{c}_2}{c_1},\beta =4c_1^2\epsilon ,\gamma =-2\epsilon ,\omega =\frac{\epsilon \left(A_1{c}_1+4A_0{c}_2\right)}{4c_2ϵ}.\hfill \end{array}$$

(32)

$$\begin{array}{c}\hfill Q_8=\frac{A_1{c}_1{c}_2{e}^{2c_1\left(\varrho +{\varrho }_0\right)}}{\left(1-c_2{e}^{c_1\left(\varrho +{\varrho }_0\right)}\right){}^2}+A_0+\frac{A_1{c}_1{e}^{c_1\left(\varrho +{\varrho }_0\right)}}{1-c_2{e}^{c_1\left(\varrho +{\varrho }_0\right)}},c_1>0.\end{array}$$

(33)

$$\begin{array}{c}\hfill Q_9=\frac{A_1{c}_1{c}_2{e}^{2c_1\left(\varrho +{\varrho }_0\right)}}{\left(c_2{e}^{c_1\left(\varrho +{\varrho }_0\right)}+1\right){}^2}+A_0-\frac{A_1{c}_1{e}^{c_1\left(\varrho +{\varrho }_0\right)}}{c_2{e}^{c_1\left(\varrho +{\varrho }_0\right)}+1},c_1<0.\end{array}$$

(34)

Case 3: 

If $c_3=0$, $c_1=0$.

Family-I:

$$\begin{array}{ccc}& & L=2\left(A_0^2{c}_0{c}_2\epsilon +A_1^2{c}_0^2\epsilon \right),\alpha =\frac{1}{2}\left(4A_0{c}_0{c}_2\epsilon +ϵ\right),\omega =\frac{A_0\epsilon }{ϵ},\hfill \\ & & A_2=0,A_{-1}=0,A_{-2}=0,\gamma =-3\epsilon ,\beta =4c_0{c}_2\epsilon .\hfill \end{array}$$

(35)

$$\begin{array}{ccc}\hfill Q_{10}& =& \frac{A_1\sqrt{c_0{c}_2}tan\left(\sqrt{c_0{c}_2}\left(\varrho +{\varrho }_0\right)\right)}{c_2}+A_0,c_0{c}_2>0.\hfill \end{array}$$

(36)

$$\begin{array}{ccc}\hfill Q_{11}& =& A_0-\frac{A_1\sqrt{-c_0{c}_2}tanh\left(\sqrt{-c_0{c}_2}\left(\varrho +{\varrho }_0\right)\right)}{c_2},c_0{c}_2<0.\hfill \end{array}$$

(37)

Family-II:

$$\begin{array}{ccc}& & A_{-2}=0,L=8\left(A_0^2{c}_0{c}_2\epsilon +4A_1^2{c}_0^2\epsilon \right),\alpha =\frac{1}{2}\left(16A_0{c}_0{c}_2\epsilon +ϵ\right),\hfill \\ & & A_2=0,A_{-1}=-\frac{A_1{c}_0}{c_2},\gamma =-3\epsilon ,\beta =16c_0{c}_2\epsilon ,\omega =\frac{A_0\epsilon }{ϵ}.\hfill \end{array}$$

(38)

$$\begin{array}{ccc}& & Q_{12}=A_0-\frac{A_1{c}_{0}cot\left(\sqrt{c_0{c}_2}\left(\varrho +{\varrho }_0\right)\right)}{\sqrt{c_0{c}_2}}\hfill \end{array}$$

$$\begin{array}{ccc}& & +\frac{A_1\sqrt{c_0{c}_2}tan\left(\sqrt{c_0{c}_2}\left(\varrho +{\varrho }_0\right)\right)}{c_2},c_0{c}_2>0.\hfill \\ & & Q_{13}=A_0+\frac{A_1{c}_{0}coth\left(\sqrt{-c_0{c}_2}\left(\varrho +{\varrho }_0\right)\right)}{\sqrt{-c_0{c}_2}}\hfill \end{array}$$

(39)

$$\begin{array}{ccc}& & -\frac{A_1\sqrt{-c_0{c}_2}tanh\left(\sqrt{-c_0{c}_2}\left(\varrho +{\varrho }_0\right)\right)}{c_2},c_0{c}_2<0.\hfill \end{array}$$

(40)

Family-III:

$$\begin{array}{ccc}& & L=-4A_0^2{c}_0{c}_2\epsilon ,\alpha =\frac{1}{2}\left(ϵ-8A_0{c}_0{c}_2\epsilon \right),\gamma =-3\epsilon ,\hfill \\ & & A_2=0,A_{-1}=\frac{A_1{c}_0}{c_2},A_{-2}=0,\beta =-8c_0{c}_2\epsilon ,\omega =\frac{A_0\epsilon }{ϵ}.\hfill \end{array}$$

(41)

$$\begin{array}{ccc}& & Q_{14}=A_0+\frac{A_1{c}_{0}cot\left(\sqrt{c_0{c}_2}\left(\varrho +{\varrho }_0\right)\right)}{\sqrt{c_0{c}_2}}\hfill \end{array}$$

$$\begin{array}{ccc}& & +\frac{A_1\sqrt{c_0{c}_2}tan\left(\sqrt{c_0{c}_2}\left(\varrho +{\varrho }_0\right)\right)}{c_2},c_0{c}_2>0.\hfill \\ & & Q_{15}=A_0-\frac{A_1{c}_{0}coth\left(\sqrt{-c_0{c}_2}\left(\varrho +{\varrho }_0\right)\right)}{\sqrt{-c_0{c}_2}}\hfill \end{array}$$

(42)

$$\begin{array}{ccc}& & -\frac{A_1\sqrt{-c_0{c}_2}tanh\left(\sqrt{-c_0{c}_2}\left(\varrho +{\varrho }_0\right)\right)}{c_2},c_0{c}_2<0.\hfill \end{array}$$

(43)

5. Application of Generalized Riccati Equation Mapping Method:

We have the general form of the solution of Equation (18):

$$Q\left(\varrho \right)=a_2{\mathrm{\Phi }}^2+a_1\mathrm{\Phi }+a_0+\frac{b_2}{{\mathrm{\Phi }}^2}+\frac{b_1}{\mathrm{\Phi }}.$$

(44)

Suppose $\mathrm{\Phi }\left(\varrho \right)$ satisfies the DE:

$${\mathrm{\Phi }}^{\prime }\left(\varrho \right)=u+v\mathrm{\Phi }+w{\mathrm{\Phi }}^2.$$

(45)

Using Equation (44) along with Equation (45) in Equation (18) and after simplification for the constants, we obtain

$$\begin{array}{ccc}& & L=\frac{\left(a_{0}v-a_{1}u\right)\left(-2a_1{v}^2\omega ϵ-12a_0^2\epsilon vw+12a_{0}vw\omega ϵ\right)}{2a_{1}v}\hfill \\ & & -\frac{\left(a_{0}v-a_{1}u\right)\left(-3a_1^2\epsilon uv+12a_0{a}_1\epsilon uw+4a_{1}uw\omega ϵ+3a_0{a}_1\epsilon v^2\right)}{2a_{1}v},\hfill \\ & & \alpha =\frac{a_1{v}^3\omega (-ϵ)-12a_0^2\epsilon v^{2}w+12a_0{v}^{2}w\omega ϵ+a_{1}vϵ}{2a_{1}v}\hfill \\ & & -\frac{-4a_1^2\epsilon u^{2}w-2a_1^2\epsilon u{v}^2+16a_0{a}_1\epsilon uvw+8a_{1}uvw\omega ϵ+2a_0{a}_1\epsilon v^3}{2a_{1}v},\hfill \\ & & \beta =\frac{8a_1\epsilon uw+a_1\epsilon v^2-12a_0\epsilon vw+12vw\omega ϵ}{a_1},\gamma =-2\epsilon .\hfill \end{array}$$

(46)

Now, taking these constant values and depending on the solutions of Equation (45), the following new soliton wave solutions are obtained:

Type 1: 

When $v^2-4uw>0$ and $vw$ or $uw\ne 0$, the solutions of Equation (18) are

$$\begin{array}{ccc}\hfill Q_{16}& =& \frac{a_1{\left(\sqrt{v^2-4uw}tanh\left(\frac{1}{2}\varrho \sqrt{v^2-4uw}\right)+v\right)}^2}{4vw}-\frac{a_1\left(\sqrt{v^2-4uw}tanh\left(\frac{1}{2}\varrho \sqrt{v^2-4uw}\right)+v\right)}{2w}+a_0,\hfill \\ \hfill Q_{17}& =& \frac{a_1{\left(\sqrt{v^2-4uw}coth\left(\frac{1}{2}\varrho \sqrt{v^2-4uw}\right)+v\right)}^2}{4vw}-\frac{a_1\left(\sqrt{v^2-4uw}coth\left(\frac{1}{2}\varrho \sqrt{v^2-4uw}\right)+v\right)}{2w}+a_0,\hfill \\ \hfill Q_{18}& =& \frac{a_1{\left(\sqrt{v^2-4uw}\left(tanh\left(\varrho \sqrt{v^2-4uw}\right)\pm \mathrm{isech}\left(\varrho \sqrt{v^2-4uw}\right)\right)+v\right)}^2}{4vw}\hfill \\ & & -\frac{a_1\left(\sqrt{v^2-4uw}\left(tanh\left(\varrho \sqrt{v^2-4uw}\right)\pm \mathrm{isech}\left(\varrho \sqrt{v^2-4uw}\right)\right)+v\right)}{2w}+a_0,\hfill \\ \hfill Q_{19}& =& \frac{a_1{\left(\sqrt{v^2-4uw}\left(coth\left(\varrho \sqrt{v^2-4uw}\right)\pm \csc \mathrm{h}\left(\sqrt{v^2-4uw}\right)\right)+v\right)}^2}{4vw}\hfill \\ & & -\frac{a_1\left(\sqrt{v^2-4uw}\left(coth\left(\varrho \sqrt{v^2-4uw}\right)\pm \csc \mathrm{h}\left(\sqrt{v^2-4uw}\right)\right)+v\right)}{2w}+a_0,\hfill \\ \hfill Q_{20}& =& \frac{a_1{\left(\sqrt{v^2-4uw}\left(tanh\left(\frac{1}{4}\varrho \sqrt{v^2-4uw}\right)\pm coth\left(\frac{1}{4}\varrho \sqrt{v^2-4uw}\right)\right)+2v\right)}^2}{16vw}\hfill \\ & & -\frac{a_1\left(\sqrt{v^2-4uw}\left(tanh\left(\frac{1}{4}\varrho \sqrt{v^2-4uw}\right)\pm coth\left(\frac{1}{4}\varrho \sqrt{v^2-4uw}\right)\right)+2v\right)}{4w}+a_0,\hfill \\ \hfill Q_{21}& =& \frac{a_1{\left(\frac{\sqrt{\left(A^2+B^2\right)\left(v^2-4uw\right)}-A\sqrt{v^2-4uw}cosh\left(\varrho \sqrt{v^2-4uw}\right)}{Asinh\left(\varrho \sqrt{v^2-4uw}\right)+B}-v\right)}^2}{4vw}\hfill \\ & & +\frac{a_1\left(\frac{\sqrt{\left(A^2+B^2\right)\left(v^2-4uw\right)}-A\sqrt{v^2-4uw}cosh\left(\varrho \sqrt{v^2-4uw}\right)}{Asinh\left(\varrho \sqrt{v^2-4uw}\right)+B}-v\right)}{2w}+a_0,\hfill \\ \hfill Q_{22}& =& \frac{a_1{\left(-\frac{\sqrt{\left(B^2-A^2\right)\left(v^2-4uw\right)}+A\sqrt{v^2-4uw}cosh\left(\varrho \sqrt{v^2-4uw}\right)}{Asinh\left(\varrho \sqrt{v^2-4uw}\right)+B}-v\right)}^2}{4vw}\hfill \\ & & +\frac{a_1\left(-\frac{\sqrt{\left(B^2-A^2\right)\left(v^2-4uw\right)}+A\sqrt{v^2-4uw}cosh\left(\varrho \sqrt{v^2-4uw}\right)}{Asinh\left(\varrho \sqrt{v^2-4uw}\right)+B}-v\right)}{2w}+a_0,\hfill \end{array}$$

where A and B are two non-zero real constants that satisfy $B^2-A^2>0.$

$$\begin{array}{ccc}\hfill Q_{23}& =& \frac{4a_1{u}^{2}w{cosh}^2\left(\frac{1}{2}\varrho \sqrt{v^2-4uw}\right)}{v{\left(\sqrt{v^2-4uw}sinh\left(\frac{1}{2}\varrho \sqrt{v^2-4uw}\right)-vcosh\left(\frac{1}{2}\varrho \sqrt{v^2-4uw}\right)\right)}^2}\hfill \\ & & +\frac{2a_{1}ucosh\left(\frac{1}{2}\varrho \sqrt{v^2-4uw}\right)}{\sqrt{v^2-4uw}sinh\left(\frac{1}{2}\varrho \sqrt{v^2-4uw}\right)-vcosh\left(\frac{1}{2}\varrho \sqrt{v^2-4uw}\right)}+a_0,\hfill \\ \hfill Q_{24}& =& \frac{4a_1{u}^{2}w{sinh}^2\left(\frac{1}{2}\varrho \sqrt{v^2-4uw}\right)}{v{\left(vsinh\left(\frac{1}{2}\varrho \sqrt{v^2-4uw}\right)-\sqrt{v^2-4uw}cosh\left(\frac{1}{2}\varrho \sqrt{v^2-4uw}\right)\right)}^2}\hfill \\ & & -\frac{2a_{1}usinh\left(\frac{1}{2}\varrho \sqrt{v^2-4uw}\right)}{vsinh\left(\frac{1}{2}\varrho \sqrt{v^2-4uw}\right)-\sqrt{v^2-4uw}cosh\left(\frac{1}{2}\varrho \sqrt{v^2-4uw}\right)}+a_0,\hfill \\ \hfill Q_{25}& =& \frac{4a_1{u}^{2}w{cosh}^2\left(\frac{1}{2}\varrho \sqrt{v^2-4uw}\right)}{v{\left(\sqrt{v^2-4uw}sinh\left(\varrho \sqrt{v^2-4uw}\right)-\left(vcosh\left(\varrho \sqrt{v^2-4uw}\right)\pm i\sqrt{v^2-4uw}\right)\right)}^2}\hfill \\ & & +\frac{2a_{1}ucosh\left(\frac{1}{2}\varrho \sqrt{v^2-4uw}\right)}{\sqrt{v^2-4uw}sinh\left(\varrho \sqrt{v^2-4uw}\right)-\left(vcosh\left(\varrho \sqrt{v^2-4uw}\right)\pm i\sqrt{v^2-4uw}\right)}+a_0,\hfill \\ \hfill Q_{26}& =& \frac{4a_1{u}^{2}w{sinh}^2\left(\frac{1}{2}\varrho \sqrt{v^2-4uw}\right)}{v{\left(\left(\sqrt{v^2-4uw}cosh\left(\varrho \sqrt{v^2-4uw}\right)\pm \sqrt{v^2-4uw}\right)-vsinh\left(\varrho \sqrt{v^2-4uw}\right)\right)}^2}\hfill \\ & & +\frac{2a_{1}usinh\left(\frac{1}{2}\varrho \sqrt{v^2-4uw}\right)}{\left(\sqrt{v^2-4uw}cosh\left(\varrho \sqrt{v^2-4uw}\right)\pm \sqrt{v^2-4uw}\right)-vsinh\left(\varrho \sqrt{v^2-4uw}\right)}+a_0,\hfill \end{array}$$

$$\begin{array}{c}\hfill Q_{27}=\frac{4usinh\left(\frac{1}{4}\varrho \sqrt{v^2-4uw}\right)cosh\left(\frac{1}{4}\varrho \sqrt{v^2-4uw}\right)}{2\sqrt{v^2-4uw}{\mathrm{Cos}\mathrm{h}}^2\left(\frac{1}{4}\varrho \sqrt{v^2-4uw}\right)-2vsinh\left(\frac{1}{4}\varrho \sqrt{v^2-4uw}\right)cosh\left(\frac{1}{4}\varrho \sqrt{v^2-4uw}\right)-\sqrt{v^2-4uw}}.\end{array}$$

Type 2: 

When $v^2-4uw<0$ and $vw$ or $uw\ne 0$, the solutions of Equation (18) are

$$\begin{array}{ccc}\hfill Q_{28}& =& \frac{a_1{\left(\sqrt{4uw-v^2}tan\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)-v\right)}^2}{4vw}+\hfill \\ & & \frac{a_1\left(\sqrt{4uw-v^2}tan\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)-v\right)}{2w}+a_0,\hfill \\ \hfill Q_{29}& =& \frac{a_1{\left(\sqrt{4uw-v^2}cot\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)+v\right)}^2}{4vw}-\frac{a_1\left(\sqrt{4uw-v^2}cot\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)+v\right)}{2w}+a_0,\hfill \\ \hfill Q_{30}& =& \frac{a_1{\left(\sqrt{4uw-v^2}\left(tan\left(\varrho \sqrt{4uw-v^2}\right)\pm sec\left(\varrho \sqrt{4uw-v^2}\right)\right)-v\right)}^2}{4vw}\hfill \\ & & +\frac{a_1\left(\sqrt{4uw-v^2}\left(tan\left(\varrho \sqrt{4uw-v^2}\right)\pm sec\left(\varrho \sqrt{4uw-v^2}\right)\right)-v\right)}{2w}+a_0,\hfill \\ \hfill Q_{31}& =& \frac{a_1{\left(\sqrt{4uw-v^2}\left(cot\left(\varrho \sqrt{4uw-v^2}\right)\pm csc\left(\varrho \sqrt{4uw-v^2}\right)\right)+v\right)}^2}{4vw}\hfill \\ & & -\frac{a_1\left(\sqrt{4uw-v^2}\left(cot\left(\varrho \sqrt{4uw-v^2}\right)\pm csc\left(\varrho \sqrt{4uw-v^2}\right)\right)+v\right)}{2w}+a_0,\hfill \\ \hfill Q_{32}& =& \frac{a_1\left(\sqrt{4uw-v^2}\left(tan\left(\frac{1}{4}\varrho \sqrt{4uw-v^2}\right)-coth\left(\frac{1}{4}\varrho \sqrt{4uw-v^2}\right)\right)-2v\right)}{4w}\hfill \\ & & +\frac{a_1{\left(\sqrt{4uw-v^2}\left(tan\left(\frac{1}{4}\varrho \sqrt{4uw-v^2}\right)-coth\left(\frac{1}{4}\varrho \sqrt{4uw-v^2}\right)\right)-2v\right)}^2}{16vw}+a_0,\hfill \\ \hfill Q_{33}& =& \frac{a_1{\left(\frac{\pm \sqrt{\left(A^2-B^2\right)\left(4uw-v^2\right)}-A\sqrt{4uw-v^2}cos\left(\varrho \sqrt{4uw-v^2}\right)}{Asinh\left(\varrho \sqrt{4uw-v^2}\right)+B}-v\right)}^2}{4vw}\hfill \\ & & +\frac{a_1\left(\frac{\pm \sqrt{\left(A^2-B^2\right)\left(4uw-v^2\right)}-A\sqrt{4uw-v^2}cos\left(\varrho \sqrt{4uw-v^2}\right)}{Asinh\left(\varrho \sqrt{4uw-v^2}\right)+B}-v\right)}{2w}+a_0,\hfill \\ \hfill Q_{34}& =& \frac{a_1{\left(-\frac{\pm \sqrt{\left(A^2-B^2\right)\left(4uw-v^2\right)}+A\sqrt{4uw-v^2}cos\left(\varrho \sqrt{4uw-v^2}\right)}{Asin\left(\varrho \sqrt{4uw-v^2}\right)+B}-v\right)}^2}{4vw}\hfill \\ & & +\frac{a_1\left(-\frac{\pm \sqrt{\left(A^2-B^2\right)\left(4uw-v^2\right)}+A\sqrt{4uw-v^2}cos\left(\varrho \sqrt{4uw-v^2}\right)}{Asin\left(\varrho \sqrt{4uw-v^2}\right)+B}-v\right)}{2w}+a_0,\hfill \end{array}$$

where A and B are two non-zero real constants that satisfy $A^2-B^2>0.$

$$\begin{array}{ccc}\hfill Q_{35}& =& \frac{4a_1{u}^{2}w{cos}^2\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)}{v{\left(\sqrt{4uw-v^2}sin\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)+vcos\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)\right)}^2}\hfill \\ & & -\frac{2a_{1}ucos\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)}{\sqrt{4uw-v^2}sin\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)+vcos\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)}+a_0,\hfill \\ \hfill Q_{36}& =& \frac{4a_1{u}^{2}w{sin}^2\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)}{v{\left(\sqrt{4uw-v^2}cos\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)-vsin\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)\right)}^2}\hfill \\ & & +\frac{2a_{1}usin\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)}{\sqrt{4uw-v^2}cos\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)-vsin\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)}+a_0,\hfill \\ \hfill Q_{37}& =& \frac{4a_1{u}^{2}w{cos}^2\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)}{v{\left(\sqrt{4uw-v^2}sin\left(\varrho \sqrt{4uw-v^2}\right)+\left(vcos\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)\pm \sqrt{4uw-v^2}\right)\right)}^2}\hfill \\ & & -\frac{2a_{1}ucos\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)}{\sqrt{4uw-v^2}sin\left(\varrho \sqrt{4uw-v^2}\right)+\left(vcos\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)\pm \sqrt{4uw-v^2}\right)}+a_0,\hfill \\ \hfill Q_{38}& =& \frac{4a_1{u}^{2}w{sin}^2\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)}{v{\left(\left(\sqrt{4uw-v^2}cos\left(\varrho \sqrt{4uw-v^2}\right)\pm \sqrt{4uw-v^2}\right)-vsin\left(\varrho \sqrt{4uw-v^2}\right)\right)}^2}\hfill \\ & & +\frac{2a_{1}usin\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)}{\left(\sqrt{4uw-v^2}cos\left(\varrho \sqrt{4uw-v^2}\right)\pm \sqrt{4uw-v^2}\right)-vsin\left(\varrho \sqrt{4uw-v^2}\right)}+a_0,\hfill \\ \hfill Q_{39}& =& a_0+\frac{2usin\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)\left(2v\sqrt{4uw-v^2}{\cos }^2\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)-v\sqrt{4uw-v^2}\right.}{v{\left(-2\sqrt{4uw-v^2}{\cos }^2\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)+vsin\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)+\sqrt{4uw-v^2}\right)}^2}\hfill \\ & & -\frac{2usin\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)\left.\left(v^2-2uw\right)sin\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)\right)a_1}{v{\left(-2\sqrt{4uw-v^2}{\cos }^2\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)+vsin\left(\frac{1}{2}\varrho \sqrt{4uw-v^2}\right)+\sqrt{4uw-v^2}\right)}^2}.\hfill \end{array}$$

Type 3: 

When $u=0$ and $wv\ne 0$, the solutions of Equation (18) are

$$\begin{array}{ccc}\hfill Q_{40}& =& \frac{a_1{(v.d)}^2}{vw{(d-sinh(v.\varrho )+cosh(v.\varrho ))}^2}\hfill \\ & & -\frac{a_{1}v.d}{w(d-sinh(v.\varrho )+cosh(v.\varrho \left)\right)}+a_0,\hfill \\ \hfill Q_{41}& =& \frac{a_{1}v{(sinh\left(v\varrho \right)+cosh\left(v\varrho \right))}^2}{w{(d+sinh\left(v\varrho \right)+cosh\left(v\varrho \right))}^2}\hfill \\ & & -\frac{a_{1}v(sinh\left(v\varrho \right)+cosh\left(v\varrho \right))}{w(d+sinh(v\varrho )+cosh(v\varrho \left)\right)}+a_0.\hfill \end{array}$$

Type 4: 

When $w\ne 0$ and $u=v=0$, the only solution of Equation (18) is

$$\begin{array}{ccc}\hfill Q_{42}& =& \frac{a_{1}w}{v{(c+w\varrho )}^2}-\frac{a_1}{c+w\varrho }+a_0.\hfill \end{array}$$

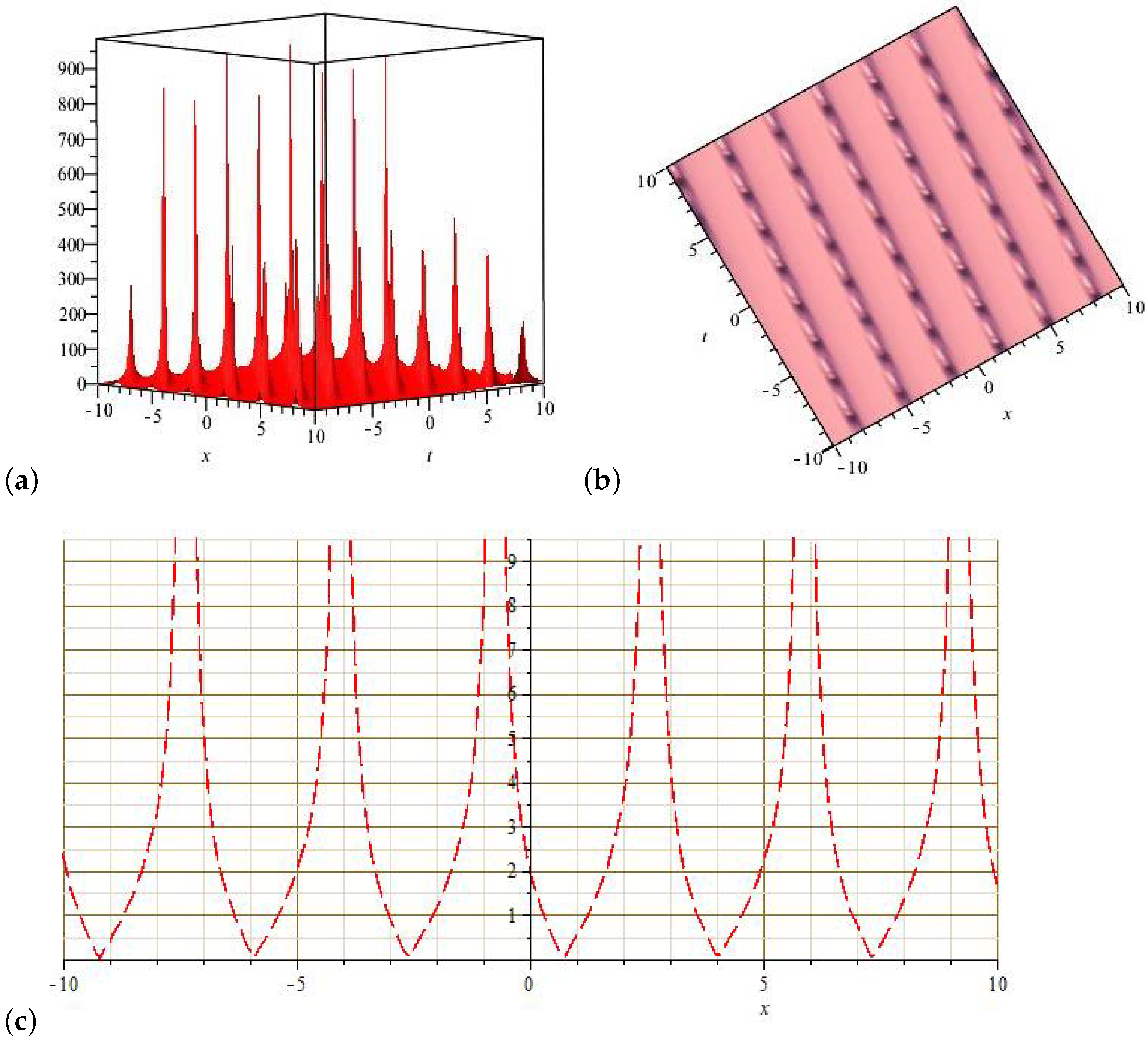
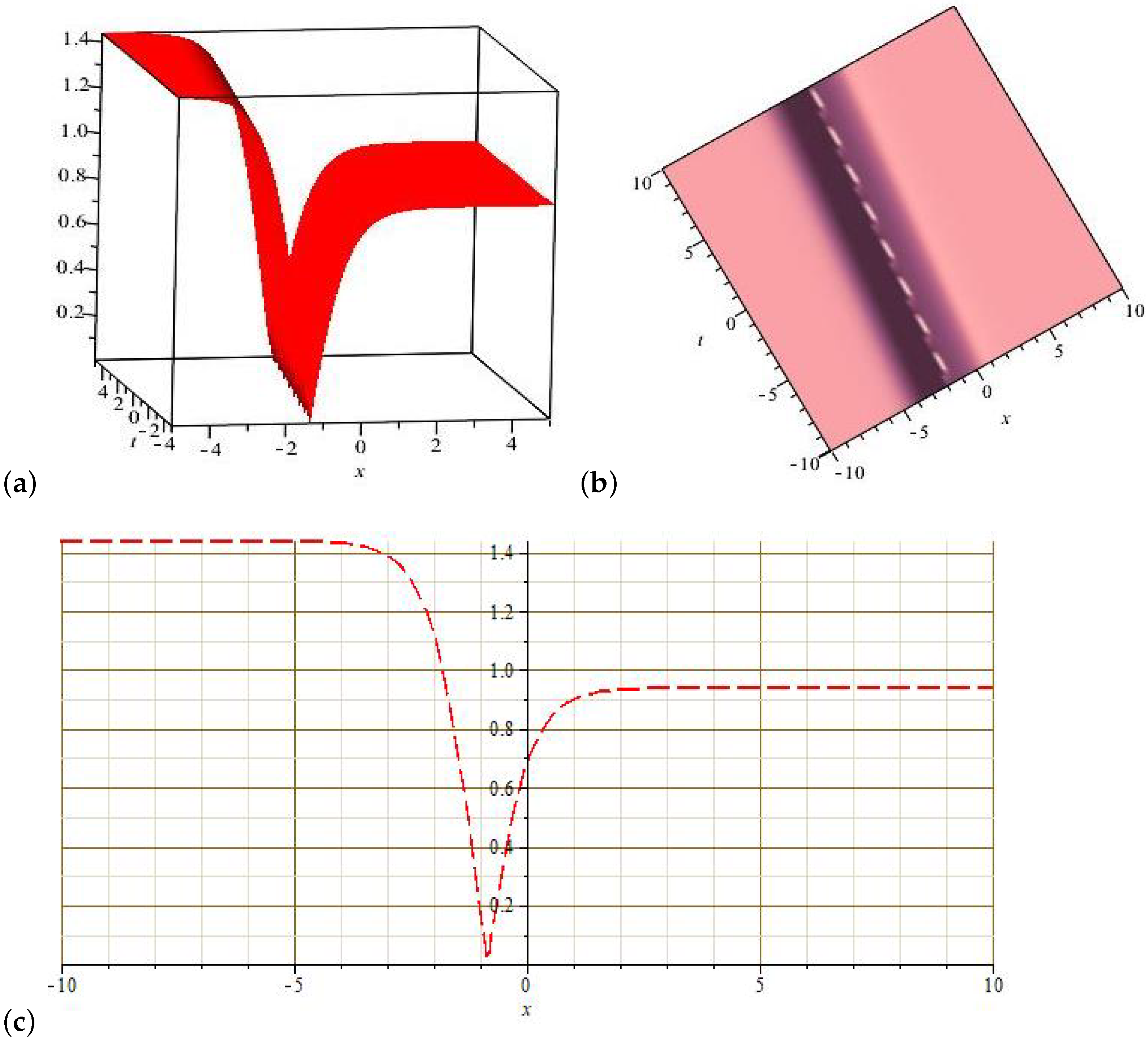
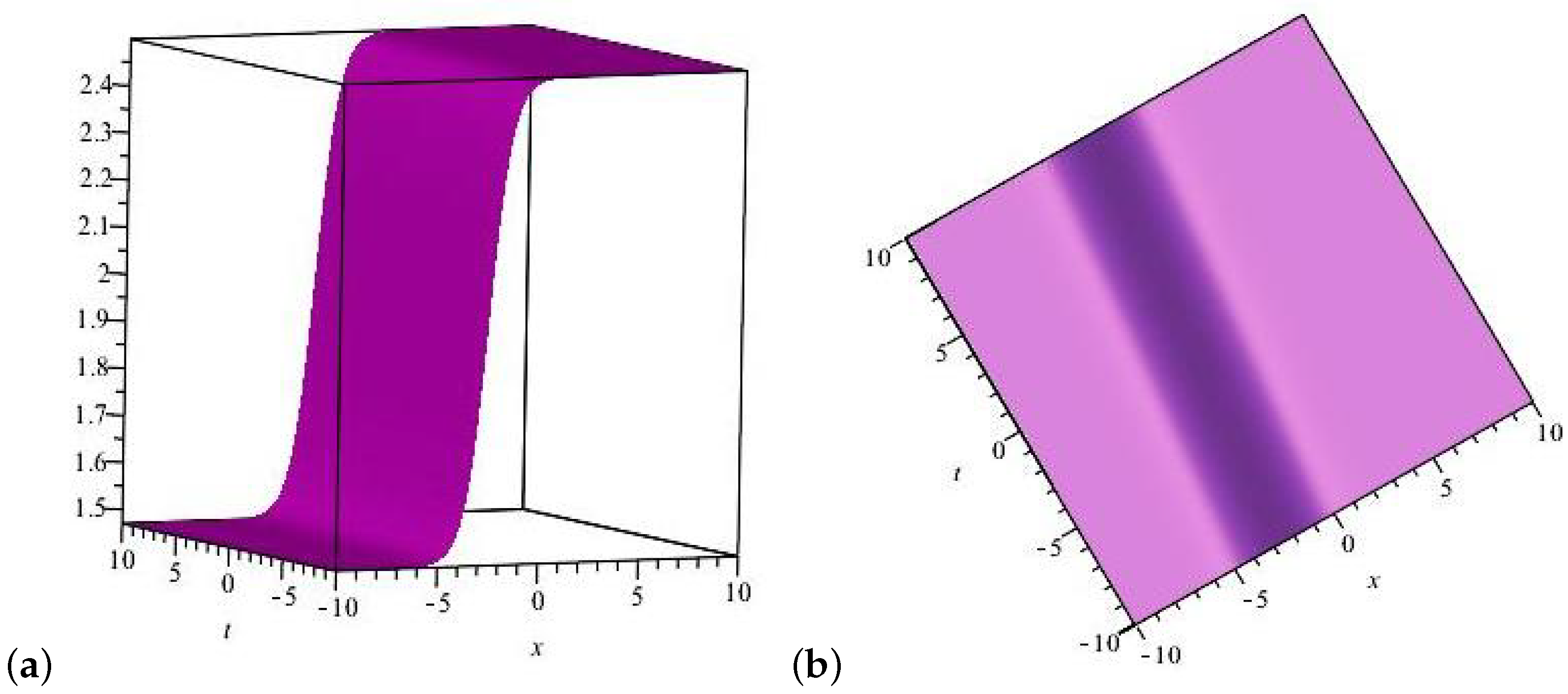
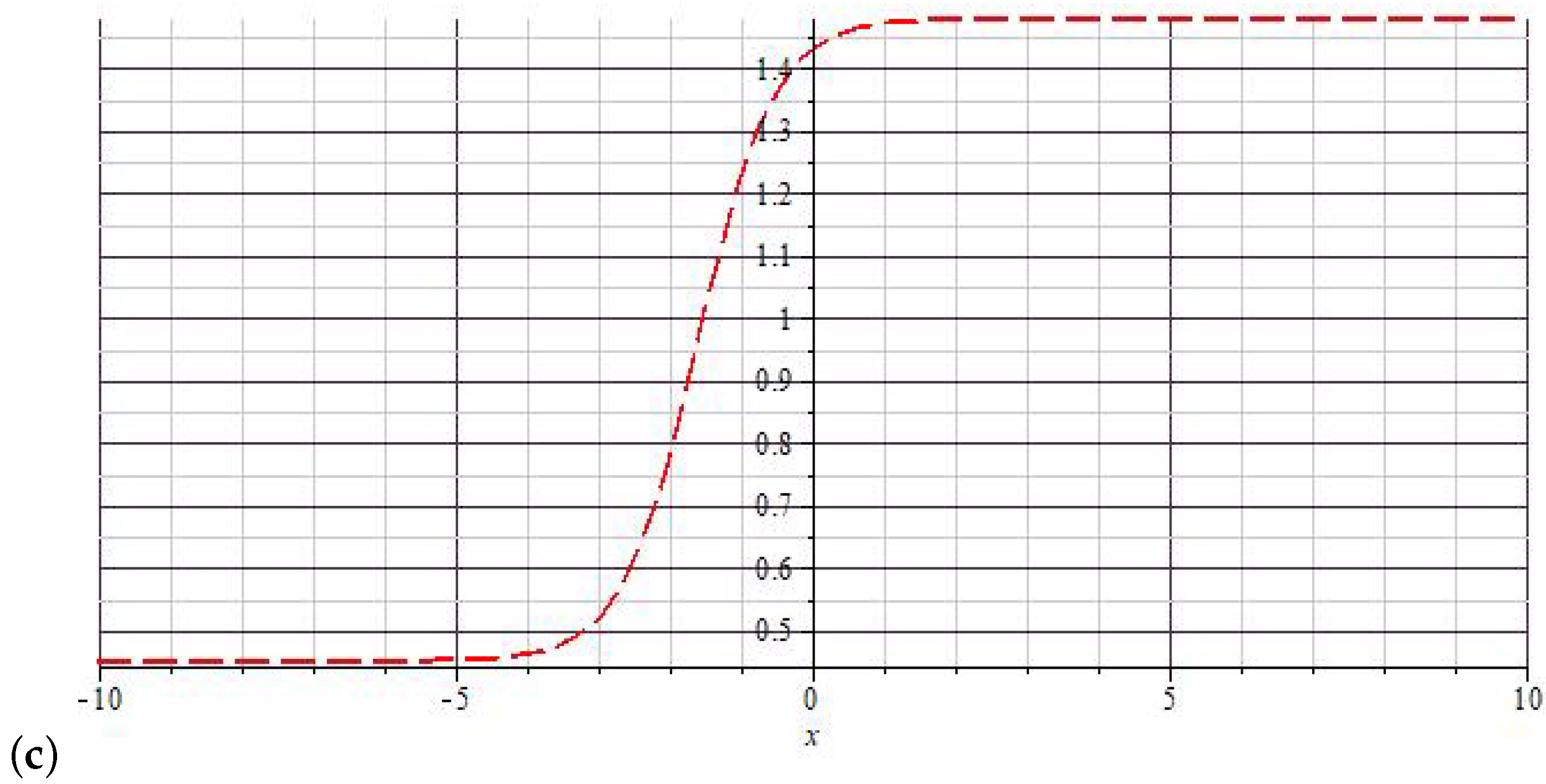
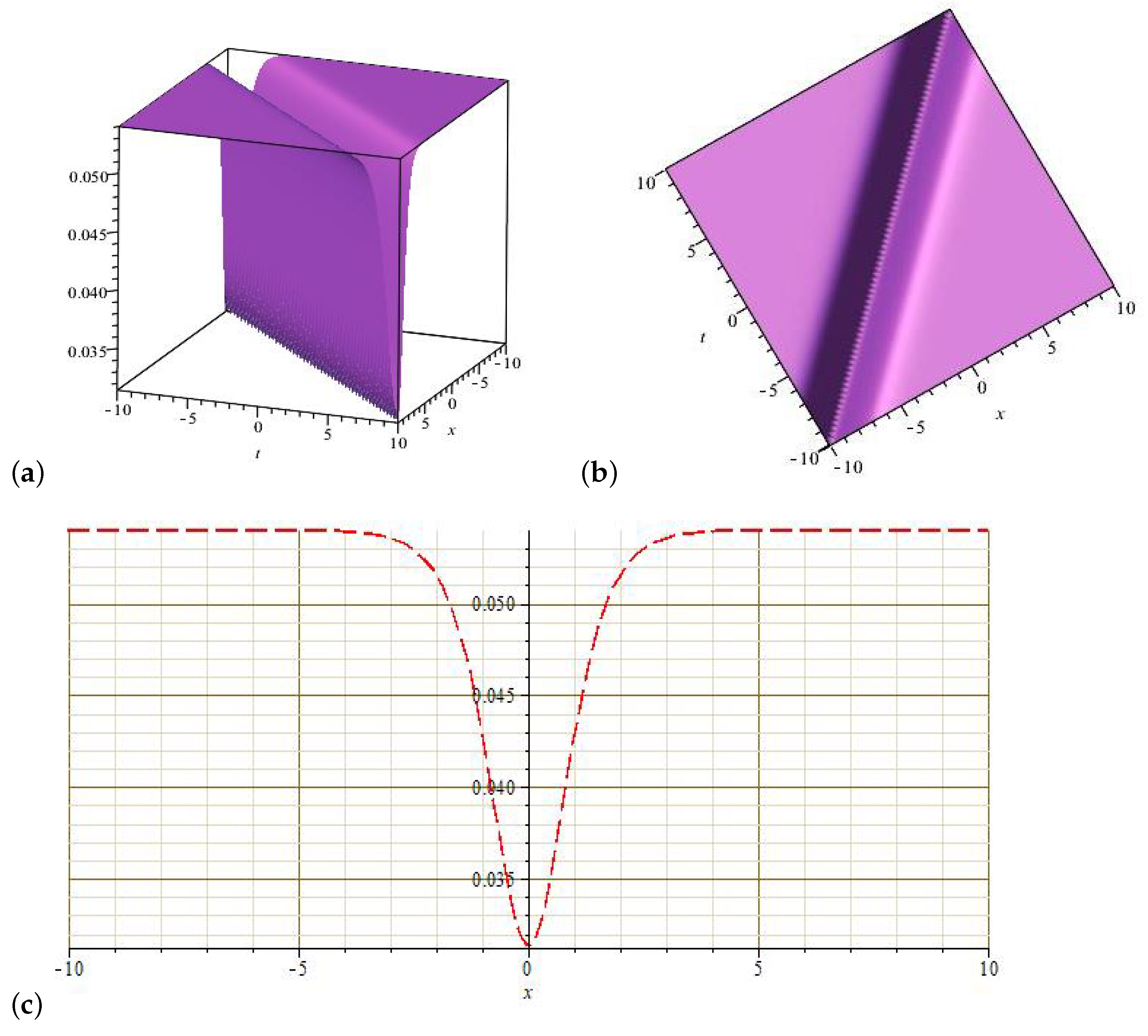
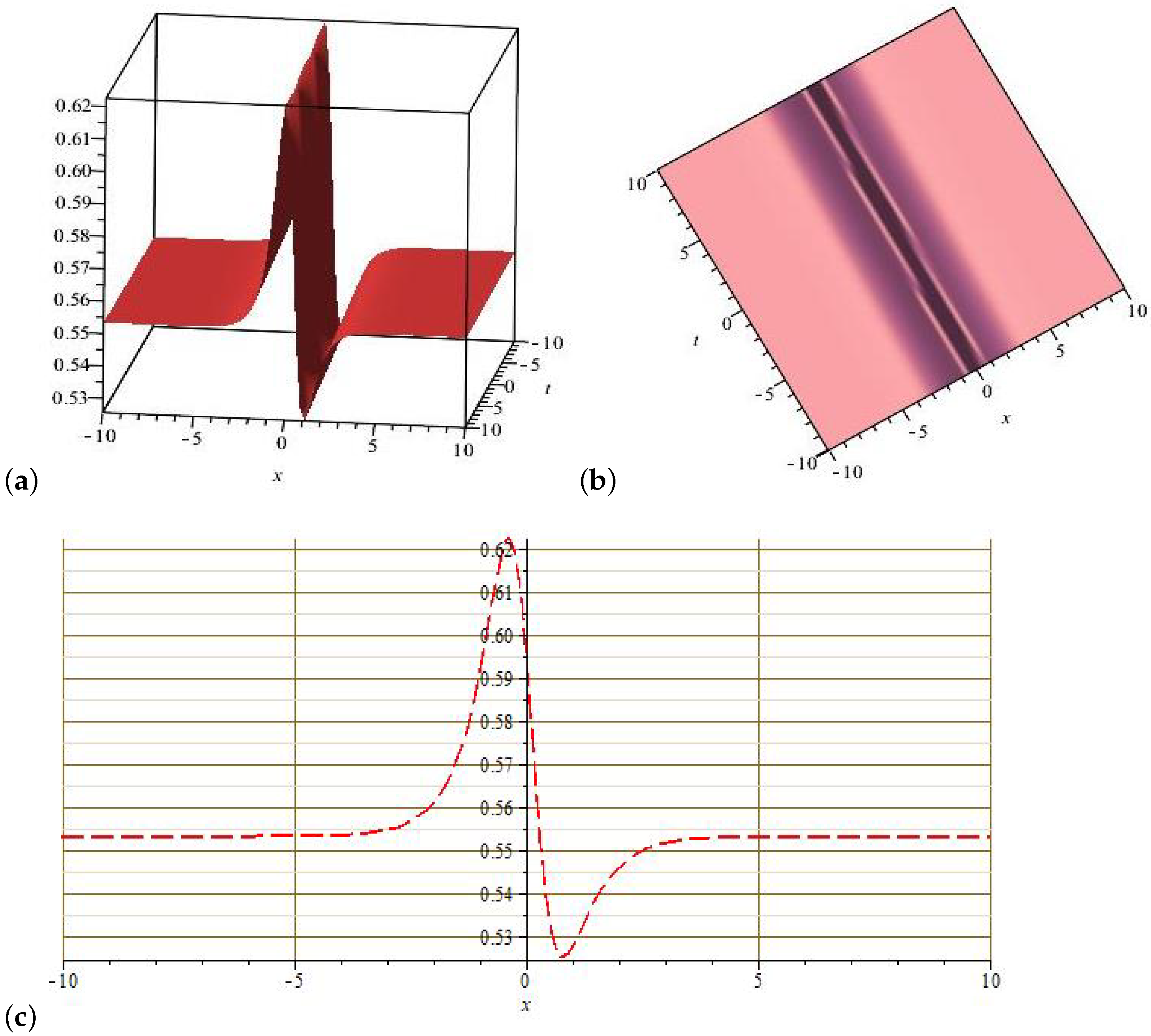
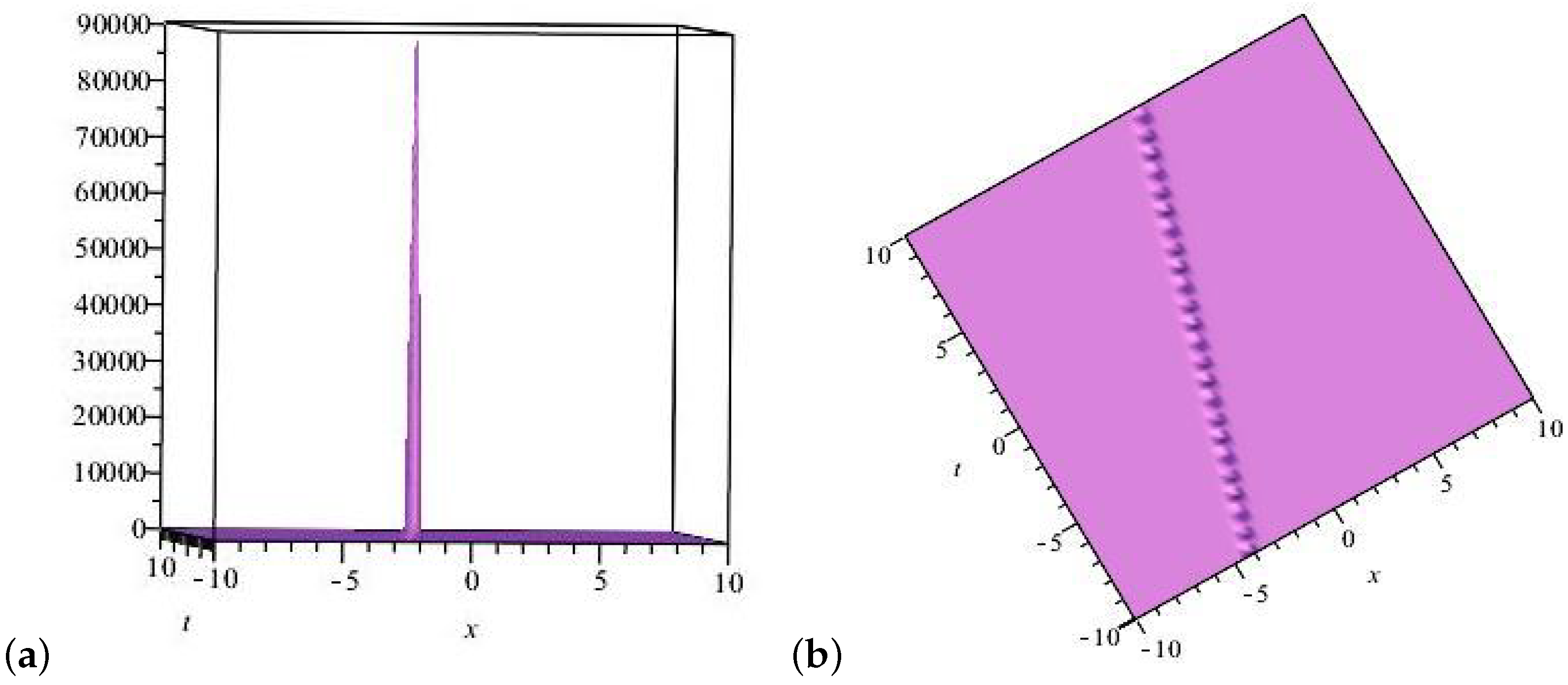
6. Results and Discussion

This paper sought the exact soliton solutions of the GP equation using the GREM method. The 2D, 3D, and contour plots were interpreted to show some obtained solutions’ specific dynamic and physical behavior for different parameter values. A family of dark, singular, kink, and periodic solitons were displayed for a set of values. Maple 18 was utilized to view the physical behavior of the GP equation.

Figure 1 illustrates the periodic wave structure of $|Q_3\left(\varrho \right)|$ for suitable values of constants involving $A_{-1}=1.67$, $c_1=0.61$, $ϵ=0.1$, $c_2=1.26$, ${\varrho }_0=1.06$, $A_0=0.25$, $c_0=0.79$.

Figure 1. Graphical view of $|Q_3\left(\varrho \right)|$ for $A_{-1}=1.67$, $c_1=0.61$, $ϵ=0.1$, $c_2=1.26$, ${\varrho }_0=1.06$, $A_0=0.25$, $c_0=0.79$: (a) 3D plot, (b) contour plot, and (c) 2D plot at $t=0$.

Figure 2 shows that the structure of $|Q_{11}\left(\varrho \right)|$ is the dark soliton for $A_1=1.5$, $c_1=-1.61$, $c_0=-0.79$, $ϵ=0.1$, $c_2=1.26$, ${\varrho }_0=1.06$, and $A_0=0.25$.

Figure 2. Graphical view of $|Q_{11}\left(\varrho \right)|$ for $A_1=1.5$, $c_1=0.61$, $c_0=-0.79$, $A_0=0.25$, ${\varrho }_0=1.06$, $c_2=1.26$ and $ϵ=0.1$: (a) 3D plot, (b) contour plot, and (c) 2D plot at $t=0$.

The graphical structure of $|Q_{13}\left(\varrho \right)|$ is the kink-type soliton for $A_1=0.69$, $c_0=0.7$, $ϵ=0.1$, $c_2=-1.26$, $A_0=0.45$, ${\varrho }_0=1.6$ and given in Figure 3.

Figure 3. Graphical view of $|Q_{13}\left(\varrho \right)|$ for $A_1=0.69$, $c_0=0.7$, $ϵ=0.1$, $c_2=-1.26$, $A_0=0.45$ and ${\varrho }_0=1.6$: (a) 3D plot, (b) contour plot, and (c) 2D plot at $t=0$.

The graph of the result given $|Q_{16}\left(\varrho \right)|$ describes the dark soliton of GP-model and is illustrated in Figure 4 for $a_0=0.06$, $a_1=0.04$, $v=2$, $ϵ=0.7$, $w=1$, $u=0.3$

Figure 4. Graphical view of $|Q_{16}\left(\varrho \right)|$ for $a_1=0.04$, $v=2$, $ϵ=1$, $a_0=0.06$, $w=0.7$, $u=0.3$: (a) 3D plot, (b) contour plot, and (c) 2D plot at $t=0$.

Figure 5 shows that the depiction of $|Q_{18}\left(\varrho \right)|$ provides the dark–bright soliton shape using $a_0=0.3$, $a_1=1.47$, $B=0.69$, $ϵ=0.7$.

Figure 5. Graphical view of $|Q_{18}\left(\varrho \right)|$ for $a_1=0.07$, $v=0.9$, $w=-0.7$, $u=0.6$, $a_0=0.6$, $ϵ=0.03$: (a) 3D plot, (b) contour plot, and (c) 2D plot at $t=0$.

For the physical description of $|Q_{22}\left(\varrho \right)|$ with $a_0=0.47$, $b_1=0.69$, $ϵ=0.7$, the graphical representation is given in Figure 6, which illustrates the singular soliton. Furthermore, all 2D graphs are shown with t = 0.

Figure 6. Graphical view of $|Q_{22}\left(\varrho \right)|$ for $a_0=0.3$, $a_1=1.47$, $B=0.69$, $u=0.7$, $ϵ=0.1$, $v=-1.26$, $w=0.2$, $A=0.43$: (a) 3D plot, (b) contour plot, and (c) 2D plot at $t=0$.

It is noted that the solutions in [32] possess a bell-shaped wave, a periodic wave, and a shock wave, while in the present paper, singular, periodic, dark, combined dark–bright, and kink-type solitons were observed.

7. Conclusions

In this article, new exact soliton wave solutions were calculated for the Gilson–Pickering model by applying the extended simple equation method and the Riccati equation method. Several computational wave solitons were formulated by the techniques used. These solutions were checked for accuracy by substituting them in the original equation. Some solutions were represented in diverse sketches to describe the dynamical and physical characterizations of the waves, providing singular, periodic, bright, dark, kink-type, singular-kink, V-shaped, and shock wave soliton solutions. Our contribution and novelty were established by comparing its solutions with the previously published results. The solutions indicate that the proposed methodology promises to authorize us the ability to address an extensive class of NLEEs arising in mathematical physics. The soliton solutions obtained in the present study are just one example of solutions that can have the potential to enable the understanding and methodical analysis of the NLEE used widely in science and engineering.