Abstract
In this scientific research article, the new Kudryashov method and the tanh-coth method, which have not been applied before, are employed to construct analytical and soliton solutions of the -dimensional Hirota–Maccari system. The -dimensional Hirota–Maccari system is a special kind of nonlinear Schrödinger equation (NLSEs) that models the motion of isolated waves localized in a small part of space, and is used in such various fields as fiber optics telecommunication systems, nonlinear optics, plasma physics, and hydrodynamics. In addition, the Hirota–Maccari system defines the dynamical characters of femtosecond soliton pulse propagation in single-mode fibers. Analytical solutions of the model are successfully acquired with the assistance of symbolic computation utilizing these methods. Finally, 3D, 2D, and contour graphs of solutions are depicted at specific values of parameters. It is shown that the new Kudryashov method and the tanh-coth method are uncomplicated, very effective, easily applicable, reliable, and indeed vital mathematical tools in solving nonlinear models.
1. Introduction
Nonlinear evolution equations play an important role in the study of nonlinearity in physical phenomena in many areas of the natural and engineering sciences, such as population models, nonlinear optics, fluid mechanics, solid-state physics, plasma physics, etc. [,,,,,,,,,,,]. Because searching the analytical and soliton solutions for nonlinear evolution equations (NLEEs) is a considerable undertaking in examining of the dynamics of these phenomena, a variety of approaches have been produced to examine analytical and soliton solutions for NLEEs, such as the Weiss–Tabor–Carnevale method [], Jacobi elliptic function expansion method [], enhanced Kudryashov method [,], modified extended tanh expansion scheme [,], the modified extended tanh expansion method enhanced with new Riccati solutions [], generalized exponential rational function method [], extended sinh-Gordon equation expansion method [], sech-csch function method [], -expansion scheme [], Bernoulli sub-equation function method [], Riccati–Bernoulli sub-ODE method [], Nucci’s reduction method [], Sardar subequation method [], Darboux transformation method [,], -expansion method [], rational sine-Gordon expansion method [], modified exponential function method [], p-Laplacian operator [], Daubechies wavelet technique [], and many more.
It is possible to add several dozen more to the methods mentioned above, and each method has its unique advantages and disadvantages. Among the factors that determine the use of a method according to the purpose of the researcher are the suitability of the method to the model being applied, whether the applied method responds to the goal, whether it is easy to use, whether it requires more technically equipped calculation tools, and whether it allows for obtaining more and more different solution functions. At this point, our aim in using the new Kudryashov and tanh-coth methods that we discuss in the study is not to obtain a large number of soliton solutions; rather, our interest is because these methods can be easily applied for both nonlinear partial differential equation (NLPDE), a fractional form of NLPDE, a system of NLPDEs, and high-order optical problems; moreover, they require little processing and are effective methods that provide basic soliton types (bright, dark, singular). As is known, the application of many of the methods for obtaining solutions to NLPDE problems requires long processing, takes a lot of time, and may involve complex situations. For certain problems, the results cannot be obtained even when the methods are effectively applied. At this point, the new Kudryashov and tanh-coth methods presented in this study provide researchers with the opportunity to get an idea of whether many problems to be investigated produce soliton solutions or not, and allowing researchers to turn to other methods to obtain different soliton solutions if they wish.
In this study, we consider the (2 + 1)-dimensional Hirota–Maccari system introduced by Maccari []:
where , , and are the complex and real scalar fields, the functions of the independent coordinates and t. The (2 + 1)-dimensional Hirota–Maccari system represents the motion of isolated waves localized in a small part of space, that is, the interaction of large-amplitude lower-hybrid waves with finite-frequency density perturbations in various fields such as hydrodynamic, plasma physics, nonlinear optics, and more. The (2 + 1)-dimensional Hirota–Maccari system was obtained from the well-recognized two-dimensional generalizations of the KdV equation [,]. If we consider that , Equation (1) is converted to the -dimensional Hirota equation []. Over the past two decades, many authors have successfully examined the Hirota–Maccari system, applying diverse techniques to evaluate and acquire analytic and soliton solutions. Methods which have been presented include the improved -expansion method and general projective Riccati equation method [], the extended trial equation method and generalized Kudryashov method [], the extended sinh-Gordon equation expansion method [], the expansion method and addendum to Kudryashov’s method [], the Weierstrass elliptic function expansion method [], and the -expansion method [].
The present study is laid out as follows. In Section 2, the mathematical analysis of the (2 + 1)-dimensional Hirota–Maccari system is provided and the new Kudryashov method is structured and applied to this model. In Section 3, the tanh-coth method is presented and applied, then the analytical and soliton solutions of the (2 + 1)-dimensional Hirota–Maccari system are acquired using the proposed method. The consequences of this acquisition are noted in Section 4, and our conclusions are presented in Section 5.
2. Obtaining the Nonlinear Ordinary Differential form of Equation (1) and the Description of the New Kudryashov Method
If we use the following wave transformations, then we acquire the explicit and analytical traveling wave solutions of Equation (1):
where , r, and are the coefficients of the spatial variable x which is the frequency of the wave, the spatial variable y, the temporal variable t which represents time, and the velocity of the wave, respectively. In addition, , and are nonzero arbitrary real values. Substituting Equation (2) into the second segment of Equation (1), the following relation is acquired:
Again, substituting Equation (2) into the first segment of Equation (1) by considering Equation (3), then classifying the real and imaginary parts of the obtained Equation, provides the following nonlinear ordinary differential equation (NODE) in Equation (4) and the relation in Equation (5):
Now, the principal steps of the new Kudryashov method [,,] are proposed as follows. Presume that Equation (6) is the solution of Equation (4):
in which are calculated real constants. The function fulfils the next first-order differential equation
in which and are nonzero values to be determined later. In this case, the solution of Equation (7) can be provided as follows:
where a is a nonzero real constant.
Application of the New Kudryashov Method to the Hirota–Maccari System
In this section, the new Kudryashov method is efficiently applied to the (2 + 1)-dimensional Hirota–Maccari system in Equation (1). With the help of the homogeneous balance rule and in Equation (4), is acquired. Thus, Equation (6) can be transformed as follows:
By substituting Equation (9) into Equation (4) when considering Equation (7) and equating the coefficients of to zero, the following system of algebraic equations is obtained:
When this algebraic system is solved using computer algebra software, the following solution set is generated:
where , and . Substituting Equation (10) into Equations (9) and (8) together with Equation (2), we obtain the next solutions for Equation (1):
in which . The graph (Figure 1) of Equation (11) for various parameters is given below.
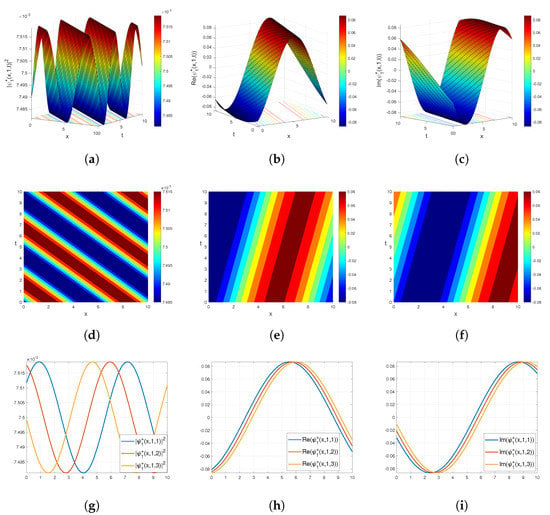
Figure 1.
3D plots of in Equation (12): (a) the graph of the square of the modulus; (b) the graph of the real part; and (c) the graph of the imaginary part. Contour plots of in Equation (12): (d) the graph of the square of the modulus; (e) the graph of the real part; and (f) the graph of the imaginary part. 2D plots of in Equation (12): (g) the graph of the square of the modulus; (h) the graph of the real part; and (i) the graph of the imaginary part of for the parameters and .
Case 2:
Inserting Equation (14) into Equation (9) and Equation (8) by taking into account the wave transformation Equation (2), we have the next solutions for Equation (1):
in which . The graph (Figure 2) of Equation (15) for various parameters is given below.
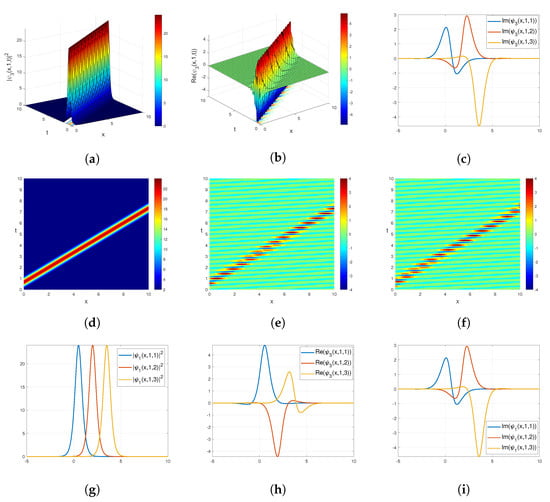
Figure 2.
3D plots of in Equation (16): (a) the graph of the square of the modulus; (b) the graph of the real part; and (c) the graph of the imaginary part. Contour plots of in Equation (16): (d) the graph of the square of the modulus; (e) the graph of the real part; and (f) the graph of the imaginary part. 2D plots of in Equation (16): (g) the graph of the square of the modulus; (h) the graph of the real part; and (i) the graph of the imaginary part of in Equation (16) for the parameters and .
3. Description and Application of the Tanh-Coth Method
3.1. Description of the Tanh-Coth Method
In this section, the principal steps of the tanh-coth method discovered by Wazwaz [] are provided. We first contemplate a general form of the nonlinear partial differential equation
To seek the travelling wave solution of Equation (17) utilizing , Equation (17) can be transformed into an ordinary differential equation (ODE):
where , etc. A new independent variable,
is formed, and the derivative is changed:
Herein, is defined as the wave number.
The tanh-coth method [] permits the use of the finite expansion
and
in which N is a positive integer. By substituting Equations (22) and (23) into Equation (4), Equation (4) can be transformed into an algebraic equation in powers of . To compute the parameter N, the highest order linear terms are balanced with the highest order nonlinear terms in the resulting equation. Then, by collecting all the coefficients of powers of in the obtained algebraic equation and vanishing them to these coefficients, we acquire a system of algebraic equations involving , and . After determining these parameters, a closed analytical solution form is obtained.
3.2. Application of the Tanh-Coth Method to the Hirota–Maccari System
The tanh-coth method is efficiently implemented in the -dimensional Hirota–Maccari system in Equation (1). With the assistance of the homogeneous balance rule between and in Equation (3), can be determined. Therefore, Equation (22) is transformed as follows:
By inserting Equation (24) into Equation (4) while taking account of Equation (23) and approving all the coefficients of to zero, the following system of algebraic equations is obtained:
Solving the algebraic system using a computer algebra system produces the following solution sets:
where , and . Substituting Equation (25) into Equations (24) and (19) by taking account of the wave transformation Equation (2), we have the next solutions for Equation (1):
in which and , , and are the same as in Equation (25).
where , and . By substituting Equation (28) into Equations (24) and (19) while taking account of the wave transformation Equation (2), we have the soliton solutions for Equation (1):
in which and , , and are the same as in Equation (28).
Case 3:
Substituting Equation (31) into Equations (24) and (19) by taking account of Equation (2), we have the soliton solutions for Equation (1):
where and and are the same as in Equation (31).
Below, we provide reviews of functions previously obtained between Equations (26) and (35) for certain special values and asymptotic cases. Equations (26), (29), (32), and (34) take the following forms.
If we consider in Equations (26), (29), (32), and (34), for all solution functions we have the following asymptotic behavior:
Taking into account in Equations (27), (30), (33) and (35), the following asymptotic equations can be written:
In Equations (44) and (45), , are real values in which . Let us consider Figure 3 and Equation (29). Figure 3 represents the various graphical simulations of in Equation (29). From Figure 3a,g, the following asymptotic approach is obtained:
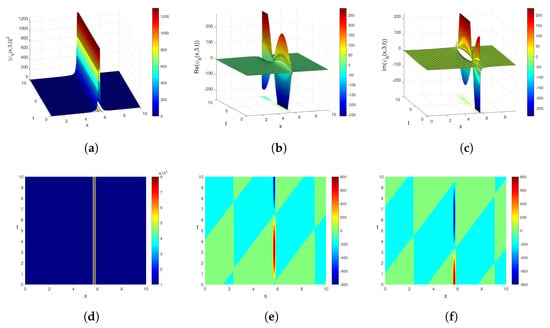
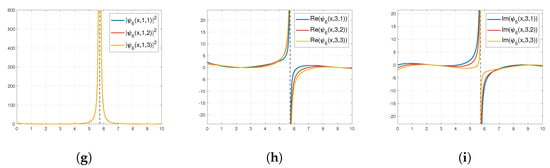
Figure 3.
3D plots of in Equation (31): (a) the graph of the square of the modulus; (b) the graph of the real part; and (c) the graph of the imaginary part. Contour plots of in Equation (31): (d) the graph of the square of the modulus; (e) the graph of the real part; and (f) the graph of the imaginary part. 2D plots of in Equation (31): (g) the graph of the square of the modulus; (h) the graph of the real part; and (i) the graph of the imaginary part for , , and .
4. Results and Discussion
In physical studies, solitary waves are beneficial for comprehending nonlinear models [,,,,]. Bright solitons, periodic solitons, singular solitons, and other types of solitons have been utilized to understand whether nonlinear models in fields such as nonlinear optics, plasmas, and fluid dynamics are stable or unstable. From Figure 1, Figure 2 and Figure 3, it can be seen that these methods can be utilized for searching the nonlinear complex equation and nonlinear equation systems in optical soliton structures. In Figure 1, we depict the 3D, 2D, and contour plots for the modulus and the real and imaginary parts of for the values , and . The graph of indicates the periodic bright and dark solitons. In Figure 2, we depict the 3D, 2D, and contour plots for the modulus and the real and imaginary parts of for the values and . The plot of indicates the bright soliton. In Figure 3, we present the 3D, 2D, and contour plots for the modulus and the real and imaginary parts of for the values and, . The graph of the solution indicates the singular soliton. We to emphasize that in Figure 3a, Figure 1a and Figure 2a, 3D graphs were drawn for in Equation (11), in Equation (15), and in Equation (29), respectively. However, the graphs of in Equation (12), in Equation (16), and in Equation (30), which are scalar field functions, are not plotted separately because of the differences in amplitude according to Equation (3); nonetheless, all are of the same type graphically. In addition, we emphasize that all soliton solutions obtained within the scope of this article provide the main equation, Equation (1), that we have investigated.
5. Conclusions
In this work, we used the new Kudryashov and tanh-coth methods to investigate the existence of analytical and soliton solutions for the -dimensional Hirota–Maccari system. As a result, singular, bright, and periodic soliton solutions of the model were successfully captured. The 3D, 2D, and contour plots of the obtained soliton solution show the correct parameter values. We strongly believe that the solution resulting from this study can contribute and add value to the research in this area of the literature, especially considering that the system, higher order, and dispersive nonlinear partial differential equations involve complex and unique challenges, and the method selection gains importance at this point. In this study, we understood well that the presented methods have proven to be efficient and robust approaches that acquire successful results when analyzing and investigating soliton solutions of different nonlinear models.
Author Contributions
N.O., A.S., M.O. and M.B. contributed equally to the writing of this paper. All authors read and approved the final manuscript.
Funding
This research received no external funding.
Data Availability Statement
All data generated or analyzed during this study are included in this article.
Conflicts of Interest
The authors declare that there is no conflict of interest.
References
- Manton, N.; Sutcliffe, P. Topological Solitons; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Campos, J.G.F.; Mohammadi, A. Interaction between kinks and antikinks with double long-range tails. Phys. Lett. B 2021, 818, 136361. [Google Scholar]
- Blinov, P.A.; Gani, T.V.; Gani, V.A. Deformations of kink tails. Ann. Phys. 2022, 437, 168739. [Google Scholar]
- Belendryasova, E.; Gani, V.A.; Zloshchastiev, K.G. Kink solutions in logarithmic scalar field theory: Excitation spectra, scattering, and decay of bions. Phys. Lett. B 2021, 823, 136776. [Google Scholar]
- Manton, N.S. Forces between kinks and antikinks with long-range tails. J. Phys. A Math. Theor. 2019, 52, 065401. [Google Scholar]
- Campos, J.G.; Mohammadi, A. Wobbling double sine-Gordon kinks. J. High Energy Phys. 2021, 67, 1–20. [Google Scholar]
- Gani, V.A.; Marjaneh, A.M.; Blinov, P.A. Explicit kinks in higher-order field theories. Phys. Rev. D 2020, 101, 125017. [Google Scholar]
- Gani, V.A.; Moradi Marjaneh, A.; Saadatmand, D. Multi-kink scattering in the double sine-Gordon model. Eur. Phys. J. C 2019, 79, 620. [Google Scholar]
- Zhong, Y.; Du, X.L.; Jiang, Z.C.; Liu, Y.X.; Wang, Y.Q. Collision of two kinks with inner structure. J. High Energy Phys. 2020, 2020, 153. [Google Scholar]
- Saadatmand, D.; Marjaneh, A.M. Scattering of the asymmetric ϕ6 kinks from a PT-symmetric perturbation: Creation of multiple pairs of kink-antikink from phonons. Eur. Phys. J. B 2022, 95, 144. [Google Scholar]
- Gani, V.A.; Moradi Marjaneh, A. Asymmetric kink solutions of hyperbolically deformed model. J. Phys. Conf. Ser. 2020, 1690, 012096. [Google Scholar]
- Marjaneh, A.M.; Askari, A.; Saadatmand, D.; Dmitriev, S.V. Extreme values of elastic strain and energy in sine-Gordon multi-kink collisions. Eur. Phys. J. B 2018, 91, 22. [Google Scholar]
- Kudryashov, N.A. Exact solutions of the generalized Kuramoto-Sivashinsky equation. Phys. Lett. A 1990, 147, 287–291. [Google Scholar]
- Muniyappan, A.; Amirthani, S.; Chandrika, P.; Biswas, A.; Yildirim, Y.; Alshehri, H.M.; Al-Bogami, D.H. Dark solitons with anti–cubic and generalized anti–cubic nonlinearities in an optical fiber. Optik 2022, 255, 168641. [Google Scholar]
- Arnous, A.H.; Biswas, A.; Yildirim, Y.; Zhou, Q.; Liu, W.; Alshomrani, A.S.; Alshehri, H.M. Cubic–quartic optical soliton perturbation with complex Ginzburg–Landau equation by the enhanced Kudryashov’s method. Chaos Soliton Fract. 2022, 155, 111748. [Google Scholar]
- Arnous, A.H.; Zhou, Q.; Biswas, A.; Guggilla, P.; Khan, S.; Yildirim, Y.; Alshomrani, A.S.; Alshehri, H.M. Optical solitons in fiber Bragg gratings with cubic–quartic dispersive reflectivity by enhanced Kudryashov’s approach. Phys. Lett. A 2022, 422, 127797. [Google Scholar]
- Ozdemir, N.; Esen, H.; Secer, A.; Bayram, M.; Yusuf, A.; Sulaiman, T.A. Optical Soliton Solutions to Chen Lee Liu model by the modified extended tanh expansion scheme. Optik 2021, 245, 167643. [Google Scholar]
- Cinar, M.; Onder, I.; Secer, A.; Sulaiman, T.A.; Yusuf, A.; Bayram, M. Optical solitons of the (2 + 1)-dimensional Biswas–Milovic equation using modified extended tanh-function method. Optik 2021, 245, 167631. [Google Scholar]
- Ozisik, M. On the optical soliton solution of the (1 + 1)- dimensional perturbed NLSE in optical nano-fibers. Optik 2022, 250, 168233. [Google Scholar]
- Mohamed, M.S.; Akinyemi, L.; Najati, S.A.; Elagan, S.K. Abundant solitary wave solutions of the Chen–Lee–Liu equation via a novel analytical technique. Opt. Quant. Electron. 2022, 54, 141. [Google Scholar]
- Yel, G.; Cattani, C.; Baskonus, H.M.; Gao, W. On the complex simulations with dark–bright to the Hirota–Maccari system. J. Comput. Nonlinear Dyn. 2021, 16, 061005. [Google Scholar]
- Alquran, M.; Ali, M.; Jaradat, I.; Al-Ali, N. Changes in the physical structures for new versions of the Degasperis-Procesi-Camassa-Holm model. Chin. J. Phys. 2021, 71, 85–94. [Google Scholar]
- Bekhouche, F.; Alquran, M.; Komashynska, I. Explicit Rational Solutions for Time-Space Fractional Nonlinear Equation Describing the Propagation of Bidirectional Waves in Low-Pass Electrical Lines. Rom. J. Phys. 2021, 66, 7–8. [Google Scholar]
- Causanilles, F.S.V.; Baskonus, H.M.; Guirao, J.L.G.; Bermúdez, G.R. Some Important Points of the Josephson Effect via Two Superconductors in Complex Bases. Mathematics 2022, 10, 2591. [Google Scholar]
- Yang, X.F.; Deng, Z.C.; Wei, Y. A Riccati-Bernoulli sub-ODE method for nonlinear partial differential equations and its application. Adv. Differ. Equ. 2015, 1, 117. [Google Scholar]
- Hashemi, M.S. A novel approach to find exact solutions of fractional evolution equations with non-singular kernel derivative. Chaos Soliton Fract. 2021, 152, 111367. [Google Scholar]
- Onder, I.; Secer, A.; Ozisik, M.; Bayram, M. On the optical soliton solutions of Kundu-Mukherjee-Naskar equation via two different analytical methods. Optik 2022, 257, 168761. [Google Scholar]
- Guo, L.; Zhang, Y.; Xu, S.; Wu, Z.; He, J. The higher order rogue wave solutions of the Gerdjikov–Ivanov equation. Phys. Scr. 2014, 89, 035501. [Google Scholar]
- Ling, L.; Feng, B.F.; Zhu, Z. General soliton solutions to a coupled Fokas–Lenells equation. Nonlinear Anal.-Real 2018, 40, 185–214. [Google Scholar]
- Durur, H.; Yokus, A. Exact solutions of (2 + 1)-Ablowitz-Kaup-Newell-Segur equation. Appl. Math. Nonlinear Sci. 2021, 6, 381–386. [Google Scholar]
- Chen, Q.; Baskonus, H.M.; Gao, W.; Ilhan, E. Soliton theory and modulation instability analysis: The Ivancevic option pricing model in economy. Alex. Eng. J. 2022, 61, 7843–7851. [Google Scholar]
- Zhirong, G.; Daniyal, M.A. Optimal solution of fractional differential equations in solving the relief of college students’ mental obstacles. Appl. Math. Nonlinear sci. 2021, 7, 353–360. [Google Scholar]
- Hu, S.; Meng, Q.; Xu, D.; Hasan, H. The optimal solution of feature decomposition based on the mathematical model of nonlinear landscape garden features. Appl. Math. Nonlinear Sci. 2021, 7, 751–760. [Google Scholar]
- Maccari, A. A generalized Hirota equation in 2 + 1 dimensions. J. Math. Phys. 1998, 39, 6547–6551. [Google Scholar]
- Maccari, A. The Kadomtsev–Petviashvili equation as a source of integrable model equations. J. Math. Phys. 1996, 37, 6207–6212. [Google Scholar]
- Zhao, H. Applications of the generalized algebraic method to special-type nonlinear equations. Chaos Soliton Fract. 2008, 36, 359–369. [Google Scholar]
- Raza, N.; Jhangeer, A.; Rezazadeh, H.; Bekir, A. Explicit solutions of the (2 + 1)-dimensional Hirota–Maccari system arising in nonlinear optics. Int. J. Mod. Phys. B 2019, 33, 1950360. [Google Scholar]
- Demiray, S.T.; Pandir, Y.; Bulut, H. All exact traveling wave solutions of Hirota equation and Hirota–Maccari system. Optik 2016, 127, 1848–1859. [Google Scholar]
- Irshad, A.; Ahmed, N.; Khan, U.; Mohyud-Din, S.T.; Khan, I.; Sherif, E.S.M. Optical Solutions of Schrödinger Equation Using Extended Sinh–Gordon Equation Expansion Method. Front. Phys. 2020, 8, 73. [Google Scholar]
- Alotaibi, H. Traveling wave solutions to the nonlinear evolution equation using expansion method and addendum to Kudryashov’s method. Symmetry 2021, 13, 2126. [Google Scholar]
- Chen, Y.; Yan, Z. The Weierstrass elliptic function expansion method and its applications in nonlinear wave equations. Chaos Soliton Fract. 2006, 29, 948–964. [Google Scholar]
- Yokus, A.; Baskonus, H.M. Dynamics of traveling wave solutions arising in fiber optic communication of some nonlinear models. Soft Comput. 2022, 26, 13605–13614. [Google Scholar]
- Kudryashov, N.A. Method for finding highly dispersive optical solitons of nonlinear differential equations. Optik 2020, 206, 163550. [Google Scholar]
- Ozisik, M.; Secer, A.; Bayram, M.; Aydin, H. An encyclopedia of Kudryashov’s integrability approaches applicable to optoelectronic devices. Optik 2022, 265, 169499. [Google Scholar]
- Rezazadeh, H.; Ullah, N.; Akinyemi, L.; Shah, A.; Mirhosseini-Alizamin, S.M.; Chu, Y.M.; Ahmad, H. Optical soliton solutions of the generalized non-autonomous nonlinear Schrödinger equations by the new Kudryashov’s method. Results Phys. 2021, 24, 104179. [Google Scholar]
- Wazwaz, A.M. The tanh–coth method for solitons and kink solutions for nonlinear parabolic equations. Appl. Math. Comput. 2007, 188, 1467–1475. [Google Scholar]
- Kudryashov, N.A. On types of nonlinear nonintegrable equations with exact solutions. Phys. Lett. A 1991, 155, 269–275. [Google Scholar]
- Kudryashov, N.A. Simplest equation method to look for exact solutions of nonlinear differential equations. Chaos Soliton Fract. 2005, 24, 1217–1231. [Google Scholar]
- Kudryashov, N.A. One method for finding exact solutions of nonlinear differential equations. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 2248–2253. [Google Scholar]
- Arshed, S.; Raza, N.; Javid, A.; Baskonus, H.M. Chiral solitons of (2 + 1)-Dimensional Stochastic Chiral Nonlinear Schrodinger Equation. Int. J. Geom. Methods M. 2022, 19, 2250149-3991. [Google Scholar]
- Baskonus, H.M.; Wei, G. Investigation of optical solitons to the nonlinear complex Kundu–Eckhaus and Zakharov–Kuznetsov–Benjamin–Bona–Mahony equations in conformable. Opt. Quant. Electron. 2022, 54, 388. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).