Abstract
The origin of gamma-ray flares of blazars is still an open issue in jet physics. In this work, we reproduce the multiwavelength spectral energy distribution (SED) of flat-spectrum radio quasars 3C 454.3 under a one-zone leptonic scenario, investigate the variation of the physical parameters in different activity states, and analyze the possible origin of its -ray outburst. Based on the analysis of multiwavelength quasi-simultaneous observations of 3C 454.3 during MJD 55,400–56,000, we consider that the radiation includes synchrotron (Syn), synchrotron self-Compton (SSC), and external Compton (EC) radiations by the simulation, and the seed photons of the external Compton component mainly comes from the broad-line region and dusty molecular torus. The model results show that: (1) We can well reproduce the multiwavelength quasi-simultaneity SED of 3C 454.3 in various activity states by using a one-zone Syn+SSC+EC model. (2) By comparing the physical model parameters of the bright and the quiescent states, we suggest that this -ray flaring activity is more likely to be caused by the increase in the doppler factor.
1. Introduction
Radio-loud active galactic nucleus (AGNs) are usually assumed to exhibit jets [1,2]. Blazars are the most active objects in AGNs, and they often display extreme observational properties, such as rapid variability, apparent super-luminal motion, flat or inverted radio spectrum, high polarization, non-thermal emission, and very small angle between jet and observation line sight [3,4,5,6]. Blazars are usually classified as BL Lacertae (BL Lac) objects or flat-spectrum radio quasars (FSRQs). The broadband spectral energy distribution (SED) of blazars has a prominent double-humps structure in diagram, which is generally considered to be dominated by non-thermal emissions from jets [7,8,9,10]. In the framework of the leptonic model, it is widely suggested that the low-energy humps in the radio to soft X-ray bands are generated by synchrotron radiation (Syn) of relativistic electrons, and the high-energy humps from MeV to TeV energies are usually explained by inverse Compton (IC) scattering process [11,12,13,14]. According to the origin of seed photons, the inverse Compton process can be divided into synchrotron self-Compton (SSC) process from the same electron populations inside the jet and external Compton process (EC) from outside the jet [15,16]. These external photons are generally provided by the accretion disc [15,17], broad-line region (BLR) [18], and dusty molecular torus (MT) [19]. According to the peak frequencies of low-energy synchrotron radiation (), the blazars can be divided into high-synchrotron-peaked (HSP; ), intermediate-synchrotron-peaked (ISP; ), and low-synchrotron peaked (LSP; ) sources [3,14]. The SSC model of jets is widely used to explain the HSP BL Lac objects, while the FSRQs are usually better explained by the SSC+EC radiation model [20,21].
The source 3C 454.3 is a well-known -ray detected bright FSRQ at redshift [22], and its central black hole has a mass estimated to be [23]. This source was extensively studied in the multi-band over the last two decades, making it an ideal object for our multiwavelength study [24,25]. Historically, the source was detected above 100 MeV by EGRET [26] and in the softer -ray bands by OSSE [27] and COMPTEL [28]. It is worth noting that 3C 454.3 experienced an exceptional bright -ray flare in 2010 that propelled its radiation flux over (∼) by Fermi-LAT and making it one of the brightest -ray sources in the all-sky [29]. Researching the multi-wavelength SED under different activity states is significant for understanding the origin of -ray outbursts (e.g., [21,30,31,32,33,34,35,36]). Zhang et al. [21] used the synchrotron+synchrotron-self-Compton model to simulate multiwavelength SEDs in high and low states of GeV-TeV BL Lac objects for analyzing and constraining jet physical model parameters. Sahakyan & Giommi [37] conducted a long-term multifrequency study on transient -ray source NVSS J154419-064913 by 12 years of data and fitted it in different states (i.e., low, average, and high state) with the one-zone synchrotron/SSC model. The origins of -ray and X-ray outbursts were explained by analyzing the model parameters under different activity states [37]. Paliya et al. [38] analyzed the near-simultaneous SED data of two Fermi bright blazars in different periods in the subdivision, obtained relevant physical parameters by fitting them with a third-order polynomial, analyzed the evolution of SED peaks and the correlation of Compton dominance parameters with the -ray flux activity, and proposed several possible origins of -ray flares. However, to understand the more profound nature of the outbursts and their physical mechanism, one should apply various physically motivated models rather than a phenomenological mathematical model.
Based on the proposed methods and the questions to be addressed, we consider further investigating the multiwavelength radiation mechanism of 3C 454.3 under different activity states and the implicating origins of -ray outbursts. By analyzing the research of Ref. [39] on the multi-frequency variability of 3C 454.3 in an extended period, we selected the period of MJD 55,400–56,000, which contains the high and low states, for consideration. Moreover, a one-zone Syn+SSC+EC leptonic radiation model will be used in our SED fitting and analysis, in which the external soft photons mainly originate from the BLR and MT and are upscattered by interacting with the non-thermal electron population. This paper is organized as follows. In Section 2, data reduction and analysis are presented. The model and the effects of changes in the parameters are described in Section 3. Section 4 gives the results. Finally, the discussion and conclusion are presented in Section 5. The following cosmology is considered throughout: the Hubble constant to be km s Mpc, the matter energy density to be , the radiation energy density to be , and the dimensionless cosmological constant to be [40].
2. Data Reduction and Analysis
2.1. Fermi -ray Data
Using the Fermi data server1, the newest Pass 8 data of 3C 454.3 are acquired. We analyzed 0.1–300 (evclass = 128 and evtype = 3) data taken with the Large Area Telescope of the Fermi Gamma-ray Space Telescope mission (Fermi-LAT) between 23 July 2010 and 14 March 2012 (MJD 55,400–56,000) to yield one day binned -ray light curves and spectra. Then we give a brief description of the light curve, energy spectrum analysis, and data reduction procedure, respectively.
The standard unbinned-likelihood data reduction procedure2 is used for our variability analysis. The event data were extracted by gtselect while selecting the source region centered on the coordinates of 3C 454.3 with the radius of the search region of interest (ROI) of . Their photon indexes and normalized parameters are left free to vary during the model fitting for sources lying within from the center of the ROI. For sources lying outside from the center of the ROI, their parameters are kept fixed to the 4FGL catalog values [41]. The normalization of diffuse background components is kept free during the model fitting. Additionally, the recommended quality cuts, (DATA_QUAL==1)(LAT_CONFIG==1), and a zenith angle cut at are applied to eliminate the Earth’s limb events. The good time intervals were selected with the task gtmktime. A count map of ROI was created by gtbin, and the exposure map was generated by gtltcube and gtexpmap. The Galactic diffuse emission component and the isotropic background templates3 were also used with P8R3-SOURCE-V3 and iso-P8R3-SOURCE-V3-v1.txt, respectively, and the XML files were created by the user-contributed tool make4FGLxml.py. The diffuse source responses were created by gtdiffrsp and the flux was obtained by running the task gtlike. The significance of the -ray detection was quantified using maximum likelihood test statistic , where L is the ratio of the likelihood values for models with and without a -ray point object. The threshold of the TS value is set to be 10 in this work.
On the basis of more than 12 years of -ray observations from the Fermi Science Support Center (FSSC) and the updated Fermi P8R34 data, we calculated the -ray photon spectrum of the Fermi-LAT for 3C 454.3 using (v11r5p3), the open source Python package [42]. We used the corresponding instrument response function of , the galactic interstellar emission model (i.e., ), and a new isotropic spectral template () [41,43].
2.2. Swift Data
The Swift satellite with three instruments on board, the UV and Optical Telescope (UVOT; [44]), the X-ray Telescope (XRT; [45]) sensitive to the 0.3–10 band, and the Burst Alert Telescope (BAT; [46]) sensitive to the 15–150 band is an ideal instrument for simultaneous/quasi-simultaneous observation of blazars in the X-ray, Optical, and UV bands. The XRT data were taken both in photon counting mode (PC) or windowed timing mode (WT) with the single exposure ranging from 0.22 to 14.35 ks for a total exposure of ∼. The data from 23 July 2010 to 14 March 2012 were retrieved from the High Energy Astrophysics Science Archive Research Center (HEASARC) website5, and we followed standard threads6 to analyze the data from level . All Swift data were reduced with HEASoft 6.26.1. The task xrtpipeline was run, with a source region file selected by a central circularity with a radius of ∼20 pixels (47 arcsec) and a background region file selected for an annular ring with an inner radius of ∼51 pixels (120 arcsec) and outer radius of ∼85 pixels (200 arcsec). The light curves and spectra were generated by xselect with level data from the WT mode and PC mode, respectively. The source spectra were grouped by grppha with a minimum of 20 photons per bin for WT mode spectra and at least 10 photons per bin for PC mode spectra. In the reduction of X-ray spectra, the response matrix file swxwt0to2s6_20131212v015.rmf for WT mode and swxpc0to12s6_20130101v014.rmf for PC mode were used and the standard ancillary response files were created by xrtmkarf. Fixing the neutral hydrogen column density (), the grouped spectra are fitted with the package xspec 12.10.1. The energy spectra of X-rays were fitted by a redshifted power law (zPL) model , E stands for the X-ray photon energy, and z stands for the redshift (See Table A1 for details). Galactic absorption (i.e., in Milky Way) is included in all these spectral models (i.e., tbabs × zPL, where tbabs are the absorption due to the interstellar-medium). Still, zPL does not include intrinsic absorption at the redshift of the source, where the redshift is cosmological.
Simultaneously with XRT, 3C 454.3 was observed with the UVOT instrument in six filters, V (500–), B (380–), U (300–), UVW1 (220–), UVM2 (200–), and UVW2 (180–). Following the recommended threads7, uvotsource in HEASoft 6.26.1 was run with a source circular region radius of 5 arcsec and a background file with a 20-arcsec circular radius. We adopted the extinction , and the results of Ref. [47] were applied here with 0.173, 0.229, 0.275, 0.394, 0.457, and 0.481 mag corresponding to the V, B, U, UVW1, UVM2, and UVW2 bands. In addition, we also obtained the variability data before the period of MJD 55,400 from Ref. [39] for comparison.
2.3. Other Data
We can collect a large amount of multiwavelength data from the ASI Space Science Data Center (SSDC), which combines radio to -ray (even TeV) band data from several missions, external services (e.g., NASA/IPAC Extragalactic Database, The Sloan Digital Sky Survey, The United States Naval Observatory) and experiments together with catalogs and archival data8 (e.g., [14,48,49,50,51]). In this work, SSDC data after 2008 are used as a reference because the high-energy data of the photon spectrum had few data points due to the limited detection sensitivity.
2.4. Multiwavelength Light Curves during Outburst
The multiwavelength light curves of 3C 454.3 during 2010 June to 2012 March are shown in Figure 1.
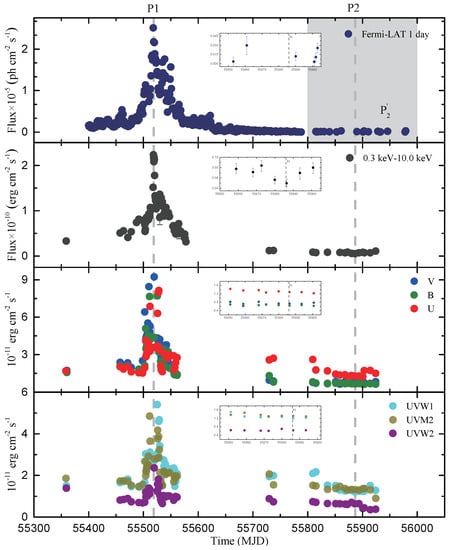
Figure 1.
Multiwavelength light curves for 3C 454.3 from June 2010 to March 2012. The data in the first panel were extracted from Fermi-LAT, the data in the second panel are from Swift/XRT, the data in the third and fourth panels are from Swift/UVOT. The gray dashed lines in each panel correspond to different epochs: P1 and P2 defined in Section 2.4. An enlarged view of the nearby P2 epochs is shown in the inset of each panel.
In order to determine the time of maximum flux in the flare epoch, the multiple Gaussian profile function can be used to fit the observed light curve [52,53]:
where , , , and are the offset constant, the intensity, position of the peak, and standard deviation of the ith Gaussian component, respectively.

Table 1.
The multiple gaussians profile function fitting results of X-ray and -ray flare period near the highest flux points.
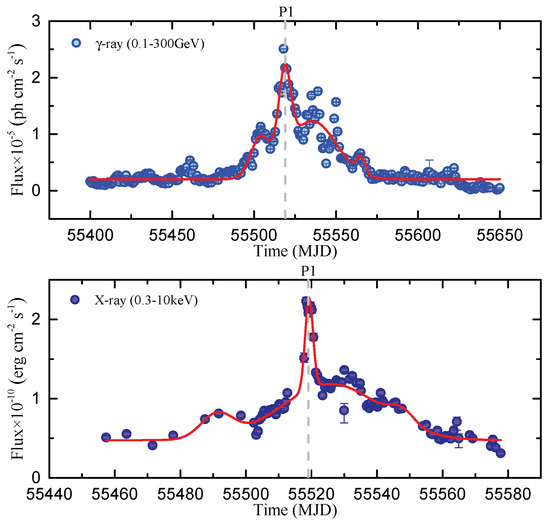
Figure 2.
Diagram of a combination of multiple gaussians profile function fitting -ray and X-ray light curve during flare periods. The gray dashed lines in each panel correspond to the P1 epoch.
Based on the fitting results shown in Figure 2, the bright X-ray flaring state of 3C 454.3 is around MJD 55,519.27, and the highest X-ray flux is corresponding to MJD 55,519.10. The bright -ray flaring state of 3C 454.3 is around MJD 55,518.72. In addition, on 55,519, the highest X-ray flux corresponds to the -ray flux of , which is closer to the multiple Gaussian profile function fitting value. The flares in different bands are nearly correlated or appear with small lags in Figure 1.
To investigate the nature of the multiwavelength emission from 3C 454.3 in Figure 1 and Figure 2, data from the following periods are considered:
- Period 1 (P1): MJD 55,519 corresponding to the period when the highest multiwavelength flux was observed, so it is taken as the bright states.
- Period 2 (P2): MJD 55,886 corresponding to the period when the lowest X-ray flux was observed, and the -ray and optical/UV bands flux are also relatively low at this time, so we take it as the quiescent states.
- Period (): In the P2, the Fermi -ray spectra that we obtain are all upper limits. Therefore, in order to make the fitting of -rays energy spectrum in the quiescent states more reliable, we considered merging the photons in the period before and after the P2 to make the average gamma-ray energy spectrum of 55,800 to 56,000 (we denote it as ), which is used to constrain the model parameter range of -ray energy spectrum in the quiescent states.
3. Modelling the SED of 3C 454.3
3.1. Model
In this study, a traditional one-zone Syn+SSC+EC model was adopted to fit SED of 3C 454.3, which has been widely implemented in the field of blazars [8,12,56]. The model assumes that the radiation region is a homogeneous spherical blob with radius surrounding an uniform magnetic field , and that the radiation region moves relativistically with the bulk Lorentz factor along the jet [20,21,57].
The electron energy distribution (EED) is described by a broken power-law distribution with the form:
where is the normalization of the particle distribution, is the broken electron Lorentz factor, and represent the indices of the electron distribution below and above , the parameters and are the minimum and maximum electron Lorentz factors. The quantities with a prime represent are calculated in the co-moving coordinate system. Interestingly, represents the energies of the particles as it undergoes a balance between escape and cooling process [13,57,58,59].
The synchrotron radiation peak frequency of a single electron is [60]:
where is the Larmor frequency of relativistic electrons.
Assuming an isotropic distribution of electrons, the theoretical synchrotron emissivity can be calculated by convolving the solution with the isotropic synchrotron emission power:
where is the single electron synchrotron emissivity averaged over an isotropic distribution of pitch angles [20,21,61,62].
In the spherical geometry structure, the synchrotron intensity is given by the transfer equation:
where is the absorption coefficient [20,21,63].
Similar to , the IC emissivity is:
In the SSC scenario, the relativistic electrons interact with synchrotron radiation photons through the IC scattering. The SSC emissivity is calculated by [20,21]:
where is the frequency of the incident photons emitted by the synchrotron radiation, , is the spectrum produced by scattering monochromatic photons of frequency with a single electron.
Then, we can obtain the SSC emission intensity [13,60]:
The IC peak frequency is [60]:
In the EC scenario, the seed photons originate from the external radiation field (e.g., the BLR and MT), and the relativistic electrons interact with external radiation photons through the IC scattering. The EC intensity is given by [12,56,64,65,66,67]:
where is the frequency of the incident photons emitted by the external radiation; is external photon field, and [68]; is the temperature of an isotropic black body, and , is the maximum frequency of seed photon in the space, which is expressed as in the case of BLR; In the case of MT, it is expressed as , where in our calculations; is the Stefan-Boltzmann constant; is the Boltzmann constant.
We can calculate the energy density of the external photon field () according to [64,66,69,70,71,72]:
where is the characteristic distance of the BLR () and MT (); is the luminosity of the BLR () or MT (), and ; is an effective scattering depth of the surrounding medium including the BLR () and MT (); is the accretion disk luminosity.
Base on the above, the total observed flux density can be calculated by [12,21,56,60]:
where is the luminosity distance, , is the minimum variability time-scale, z is the redshift of the source, and is the absorption optical depth due to the interaction of very high-energy gamma-ray photons with the photons from the extragalactic background light (EBL) [73].
3.2. Effects of Changes in the Parameters
To understand the variation of spectral behaviors observed from blazar jets, it is critical to meticulously research the particle spectral parameters associated with the jet radiation region and the jet parameters associated with the observation of theoretical photon spectra [13,14].
There are altogether 13 free parameters in our model: , , ,, , , , , , , , and . To centralize the influence of the individual parameter shift, we change only one parameter and keep the others fixed. We adopt , , , , , , , , , , , and as a baseline of the theoretical SED. The changes in the theoretical photon spectrum by varying the individual parameters are shown in Figure 3 and Figure 4.
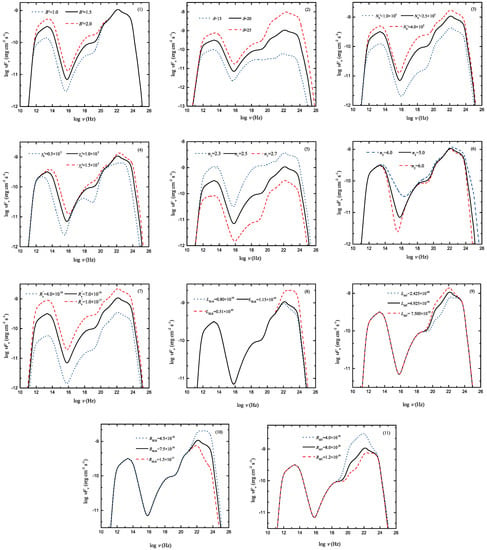
Figure 3.
Theoretical SED for various parameter changes. (1) the magnetic field strength ; (2) the Doppler factor ; (3) the normalization constant ; (4) the broken electron Lorentz factor ; (5) the spectral index of the lower-energy segment before ; (6) the spectral index of the high-energy segment after ; (7) the radius of the radiation zone ; (8) the luminosity of the broad-line region; (9) the luminosity of the dusty molecular torus; (10) the characteristic distance of the broad-line region; (11) the characteristic distance of the the dusty molecular torus.
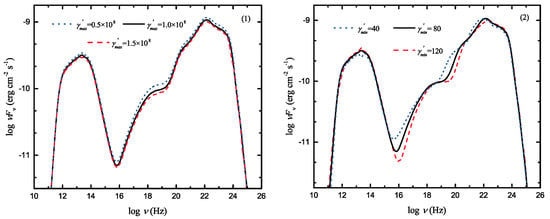
Figure 4.
SED of models with different and values for 3C 454.3.
We note that: (1) has little effect on the shape of the high-energy -ray photon spectrum; (2) the intensity of the photon spectrum becomes higher when the increase; (3) the intensity of the photon spectrum is proportional to the for synchrotron and EC component; (4) the shape of the photon spectrum variates when the higher. With the increase of , the peak frequency of photon spectrum moves higher and the spectral intensity increases; (5) when increases, the photon spectrum intensity decreases, and the amplitude of the X-ray band changes significantly; (6) the effect of the on the spectral shape is mainly concentrated in the high energy tail of low-energy components of the photon spectrum, it has little effect on other bands; (7) the intensity of the photon spectrum has a particular influence on the change; the more significant the is, the higher its intensity is; (8) when the luminosity of the external radiation field increases, the intensity of the high-energy components of the photon spectrum increases; (9) when the characteristic distance of the external radiation field is larger in scale, the intensity of the photon spectrum in the high-energy components decreases; (10) the and have little effect on the overall spectral shape of the photon spectrum. Among all parameter changes, , , and have an immense influence on the overall spectral shape of theoretical SEDs. While , , and parameters are mainly reflected in their effects on the amplitude of the intensity of photon spectrum. The , , and mainly affect the amplitude of the intensity of the photon spectrum at high energy.
Based on the above simulation, we consider reproducing multiwavelength SED of 3C 454.3 in different activity states P1, P2 and . In general, the possible causes of the high energy -ray flares are: (1) an increase in the energy density of the external radiation field ; (2) an increase in the Doppler factor in jet; (3) the hardened distribution of radiated electrons leads to the change of ; (4) an increase in the number of relativistic electrons [38,74,75,76,77]. Therefore, we consider two strategies in the fitting to research the multiwavelength radiation property in different active states.
- In the first strategy, we adjust the values of all the free parameters according to the -minimum technique [12,14,78], so that the theoretical photon spectrum can conform well to the multiwavelength observation data in P1, P2 and states. In the specific fitting, is given by adjusting , , , and .
- In the second strategy, we consider fixing the parameters (, , , and ) related to the external radiation field and the insensitive parameters (, ) in Figure 4 to reduce the free parameters. The parameters , , and are restricted by the following relations: , , , and in the fitting process [79]. Only the parameters (, , , , , , ) related to the physical conditions of the jet radiation region were adjusted to test whether the multiwavelength SEDs can be fitted on this basis. In order to better compare parameters in different activity states, we introduce the average state simultaneous data of 3C 454.3 in Ref. [80].
4. Results
As described in the previous section, we first reproduce the multiwavelength quasi-simultaneous SEDs of 3C 454.3 in P1, P2 and using the first strategy. In SED fitting, we ignore the radio data and the upper limit of energy. The optimal fitting results of parameters are shown in Figure 5 and Figure 6 and Table 2.
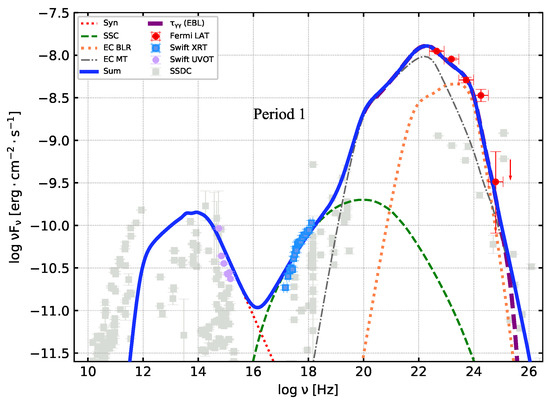
Figure 5.
Modeling of multiwavelength SEDs of 3C 454.3 during the bright states (P1). The arrow indicates the energetic upper limit of Fermi-LAT. The model is described in the text and the parameters are given in Table 2.
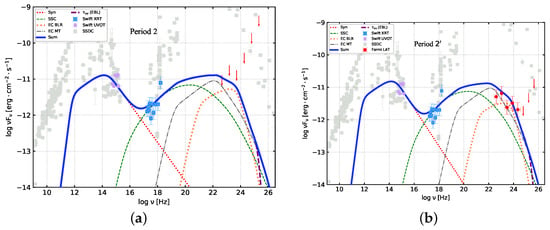
Figure 6.
Modeling of multiwavelength SEDs of 3C 454.3 during the quiescent states (P2 (a) and (b)). The symbols and lines are the same as shown in Figure 5.

Table 2.
Parameters of modelling of the multiwavelength SED of 3C 454.3 within a one-zone Syn+SSC+EC scenario during P1, P2 and .
It can be seen that (1) The one-zone Syn+SSC+EC leptonic model can well reproduce the multiwavelength quasi-simultaneous SEDs of 3C 454.3 in P1, P2 and ; (2) the jet radiation region parameters , , and have certain variations in all free parameters in the two periods; (3) Compared with P2 and , the Doppler factor increases during the bright states. This indicates that the variation of bulk Lorentz factor in the radiation region may have a certain effect on the flare activity; (4) The magnetic field strength in the bright states (P1) is lower than that in the quiescent states (P2 and ); (5) When the parameters of the external radiation field are taken as free parameters, the values of the energy density of BLR in different states are , , and , respectively. The energy density of MT is , , and , respectively.
Then, we employ the second strategy to reproduce the multi-band quasi-simultaneous SEDs of different activity states (e.g., the P1, the P2, the , and the average states) of 3C 454.3 with fixed partly parameters. In accordance with the restricting method of Ref. [56], the values of fixed parameters are estimated as follows. (1) The radius of the radiation zone in the jet frame could be bounded with the minimum variability time-scale and redshift with , where the intraday variation of Fermi -ray band was determined for 3C 454.3 [82]. (2) The minimum electron Lorentz factor and the maximum electron Lorentz factor [83] is assumed in this work without any considerable effect on the fundamental results according to Figure 3.
The SED modelling results are shown in Figure 7 and the corresponding parameters are presented in Table 3.
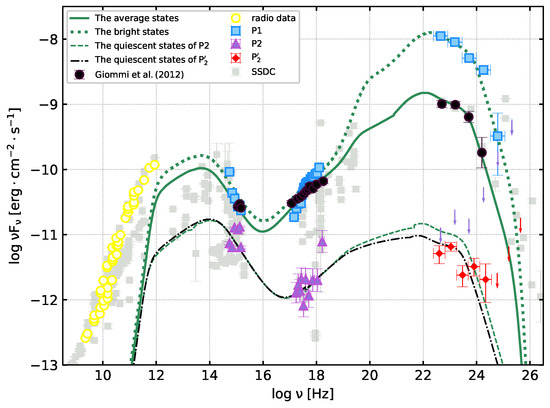
Figure 7.
Modeling the multiwavelength SEDs of 3C 454.3 in different active states with fixed partly parameters. The model is presented in the text and the parameters are given in Table 3.

Table 3.
Parameters of the multiwavelength SEDs of 3C 454.3 in different activity states modeling with fixed partly parameter.
It can be seen that (1) The Doppler factor significantly increases in the bright period (P1) compared with the quiescent period (, ). (2) The magnetic field strength in the jet radiation region decreases gradually from the quiescent state to the average state and then to the bright state. (3) The SED parameters , , and have small changes under different active states. (4) The energy density of BLR and MT are and , respectively.
Combining the strategy 1 and 2, we obtain that the Doppler factor and the magnetic field change obviously in different active states. In the bright period, is increases significantly and is lower than in the quiescent period.
5. Conclusions and Discussion
In this paper, we reproduce the multiwavelength simultaneous/quasi-simultaneous SEDs of 3C 454.3 in different activity states by investigating the broad-band emission in MJD 55,400–56,000. By analyzing the differences of physical model parameters in the bright states (P1), the average states, and the quiescent states (P2, ) or fixing some parameters to research the effects of other parameters on SED simulation, we can explain the possible causes of -ray flare.
In general, under the framework of the leptonic scenario of the blazars, we consider that the non-thermal electron populations are isotropically distributed in the co-moving coordinate system of the radiation region. According to the studies of Refs. [14,84], as well as Equations (3) and (9), we can find the relation between the peak frequency of the SED component and the physical parameters of the jet radiation region as follows:
According to the above formula and the SED simulation result in Section 4, we found that: (1) in the bright states (P1) is greater than 0.56 in the quiescent states (), and is the dominant factor among all parameters in Figure 7. (2) By comparing P1 with in Table 3, the decreases in the bright period. This change may indicate the conversion of magnetic energy, which converts the energy of the magnetic field into the energy of the relativistic particle, and is therefore accompanied by an efficient particle acceleration [38,85,86]. Combining the results of strategies 1 and 2, we suggest that this -ray flaring activity is more likely to be caused by the Doppler factor increases.
In addition, there are also compelling observations implying the existence of more than one dissipation zones in the jet, and studies have shown that blazar flares can be well explained under multi-zone models based on geometric structure (e.g., [35,87,88,89]). The multi-zone models has advantages over the one-zone model in explaining the phenomenon of orphan flare in multi-band light variability and radio observations. They will acquire smaller magnetic field strengths and more precise dissipation distances in Refs. [35,89]. Our aim in this paper is to use a relatively general and simple one-zone leptonic model to analyze the multiwavelength SEDs of the 3C454.3 in different active states and to explain the origin of the outbursts. We are considering introducing the multi-zone model into future work.
Author Contributions
Formal analysis, Y.F. and S.H.; Software, Y.F., R.Z. and S.G.; Data curation, R.Z., S.G. and Y.F.; Writing—original draft, Y.F. and R.Z.; writing—review and editing, Y.F. and S.H.; supervision, S.H.; Funding acquisition, S.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Natural Science Foundation of China under grant (11873035), the Natural Science Foundation of Shandong province (JQ201702).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
https://fermi.gsfc.nasa.gov/; https://heasarc.gsfc.nasa.gov/; https://tools.ssdc.asi.it/SED/, accessed on 21 August 2022.
Acknowledgments
We acknowledge the use of data, analysis tools, and services from the Open Universe platform, the ASI Space Science Data Center (SSDC), the Astrophysics Science Archive Research Center (HEASARC), the Fermi Science Tools, the Astrophysics Data System (ADS), and the National Extra-galactic Database (NED).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
The X-ray Energy Spectra Fitted Results by zPL (tbabs × zpowerlw ).
Table A1.
The X-ray Energy Spectra Fitted Results by zPL (tbabs × zpowerlw ).
| Parameter 1 | P1 (Obsid:00035030136) | P2 (Obsid:00035030215) |
|---|---|---|
| 15.66/(8) |
1 Considering the interstellar medium absorption model tbabs in the fitting, the hydrogen column density was adopted as [39] in these fits. Here the chi-square , and denote the photon index of X-ray and normalization factor in the zPL fits, respectively [55]. Fitting parameters and goodness evaluations were obtained from xspec 12.10.1 (https://heasarc.gsfc.nasa.gov/xanadu/xspec/, accessed on 21 August 2022), an X-ray spectrum fitting program. N is the number of data points. are the degrees of freedom.
Notes
| 1 | http://fermi.gsfc.nasa.gov/ssc/data/, accessed on 21 August 2022 |
| 2 | http://fermi.gsfc.nasa.gov/ssc/data/analysis/documentation/, accessed on 21 August 2022 |
| 3 | https://fermi.gsfc.nasa.gov/ssc/data/access/lat/BackgroundModels.html, accessed on 21 August 2022 |
| 4 | https://fermi.gsfc.nasa.gov/ssc/data/access/, accessed on 21 August 2022 |
| 5 | https://heasarc.gsfc.nasa.gov/db-perl/W3Browse/w3browse.pl, accessed on 21 August 2022 |
| 6 | https://www.swift.ac.uk/analysis/xrt/index.php, accessed on 21 August 2022 |
| 7 | https://www.swift.ac.uk/analysis/uvot/index.php, accessed on 21 August 2022 |
| 8 | https://tools.ssdc.asi.it/SED/, accessed on 21 August 2022 |
References
- Urry, C.M.; Padovani, P. Unified Schemes for Radio-Loud Active Galactic Nuclei. Publ. Astron. Soc. Pac. 1995, 107, 803. [Google Scholar] [CrossRef]
- Ghisellini, G.; Maraschi, L.; Dondi, L. Diagnostics of Inverse-Compton models for the γ-ray emission of 3C 279 and MKN 421. Astron. Astrophys. Suppl. 1996, 120, 503–506. [Google Scholar]
- Abdo, A.A.; Ackermann, M.; Agudo, I.; Ajello, M.; Aller, H.D.; Aller, M.F.; Angelakis, E.; Arkharov, A.A.; Axelsson, M.; Bach, U.; et al. The Spectral Energy Distribution of Fermi Bright Blazars. Astrophys. J. 2010, 716, 30–70. [Google Scholar] [CrossRef]
- Fossati, G.; Maraschi, L.; Celotti, A.; Comastri, A.; Ghisellini, G. A unifying view of the spectral energy distributions of blazars. Mon. Not. R. Astron. Soc. 1998, 299, 433–448. [Google Scholar] [CrossRef]
- Ulrich, M.H.; Maraschi, L.; Urry, C.M. Variability of Active Galactic Nuclei. Ann. Rev. Astron. Astrophys. 1997, 35, 445–502. [Google Scholar] [CrossRef]
- Hovatta, T.; Lindfors, E. Relativistic Jets of Blazars. New. Astron. Rev. 2019, 87, 101541. [Google Scholar] [CrossRef]
- Dermer, C.; Finke, J.; Menon, G. Multiwavelength synchrotron/Compton spectral analysis of TeV blazars and FSRQs: A new approach. In Proceedings of the Blazar Variability across the Electromagnetic Spectrum, Palaiseau, France, 22–25 April 2008; p. 19. [Google Scholar]
- Ghisellini, G.; Tavecchio, F.; Foschini, L.; Ghirlanda, G.; Maraschi, L.; Celotti, A. General physical properties of bright Fermi blazars. Mon. Not. R. Astron. Soc. 2010, 402, 497–518. [Google Scholar] [CrossRef]
- Tavecchio, F.; Ghisellini, G.; Ghirlanda, G.; Foschini, L.; Maraschi, L. TeV BL Lac objects at the dawn of the Fermi era. Mon. Not. R. Astron. Soc. 2010, 401, 1570–1586. [Google Scholar] [CrossRef]
- Kang, S.J.; Wu, Q.; Zheng, Y.G.; Yin, Y.; Song, J.L.; Zou, H.; Feng, J.C.; Dong, A.J.; Wu, Z.Z.; Zhang, Z.B.; et al. On the intrinsic shape of the gamma-ray spectrum for Fermi blazars. Res. Astron. Astrophys. 2018, 18, 056. [Google Scholar] [CrossRef]
- Maraschi, L.; Ghisellini, G.; Celotti, A. A Jet Model for the Gamma-ray–Emitting Blazar 3C 279. Astrophys. J. Lett. 1992, 397, L5. [Google Scholar] [CrossRef]
- Kang, S.J.; Chen, L.; Wu, Q. Constraints on the Minimum Electron Lorentz Factor and Matter Content of Jets for a Sample of Bright Fermi Blazars. Astrophys. J. Suppl. Ser. 2014, 215, 5. [Google Scholar] [CrossRef]
- Zheng, Y.G.; Kang, S.J.; Yang, C.Y.; Bai, J.M. Particle Acceleration and Synchrotron Self-Compton Emission in Blazar Jets. I. An Application to Quiescent Emission. Astrophys. J. 2019, 873, 7. [Google Scholar] [CrossRef]
- Zhou, R.X.; Zheng, Y.G.; Zhu, K.R.; Kang, S.J. The Intrinsic Properties of Multiwavelength Energy Spectra for Fermi Teraelectronvolt Blazars. Astrophys. J. 2021, 915, 59. [Google Scholar] [CrossRef]
- Dermer, C.D.; Schlickeiser, R. Model for the High-Energy Emission from Blazars. Astrophys. J. 1993, 416, 458. [Google Scholar] [CrossRef]
- Sikora, M.; Begelman, M.C.; Rees, M.J. Comptonization of Diffuse Ambient Radiation by a Relativistic Jet: The Source of Gamma rays from Blazars? Astrophys. J. 1994, 421, 153. [Google Scholar] [CrossRef]
- Dermer, C.D.; Cerruti, M.; Lott, B.; Boisson, C.; Zech, A. Equipartition Gamma-ray Blazars and the Location of the Gamma-ray Emission Site in 3C 279. Astrophys. J. 2014, 782, 82. [Google Scholar] [CrossRef]
- Ghisellini, G.; Madau, P. On the origin of the gamma-ray emission in blazars. Mon. Not. R. Astron. Soc. 1996, 280, 67–76. [Google Scholar] [CrossRef]
- Błażejowski, M.; Sikora, M.; Moderski, R.; Madejski, G.M. Comptonization of Infrared Radiation from Hot Dust by Relativistic Jets in Quasars. Astrophys. J. 2000, 545, 107–116. [Google Scholar] [CrossRef]
- Zhang, J. A synchrotron self-Compton scenario for the very high energy γ-ray emission of the intermediate BL Lacertae object W Comae. Res. Astron. Astrophys. 2009, 9, 777–782. [Google Scholar] [CrossRef]
- Zhang, J.; Liang, E.W.; Zhang, S.N.; Bai, J.M. Radiation Mechanisms and Physical Properties of GeV-TeV BL Lac Objects. Astrophys. J. 2012, 752, 157. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Ajello, M.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Battelino, M.; et al. Early Fermi Gamma-ray Space Telescope Observations of the Quasar 3C 454.3. Astrophys. J. 2009, 699, 817–823. [Google Scholar] [CrossRef]
- Woo, J.H.; Urry, C.M. Active Galactic Nucleus Black Hole Masses and Bolometric Luminosities. Astrophys. J. 2002, 579, 530–544. [Google Scholar] [CrossRef]
- Giommi, P.; Blustin, A.J.; Capalbi, M.; Colafrancesco, S.; Cucchiara, A.; Fuhrmann, L.; Krimm, H.A.; Marchili, N.; Massaro, E.; Perri, M.; et al. Swift and infra-red observations of the blazar 3C 454.3 during the giant X-ray flare of May 2005. Astron. Astrophys. 2006, 456, 911–916. [Google Scholar] [CrossRef]
- Vercellone, S.; Striani, E.; Vittorini, V.; Donnarumma, I.; Pacciani, L.; Pucella, G.; Tavani, M.; Raiteri, C.M.; Villata, M.; Romano, P.; et al. The Brightest Gamma-ray Flaring Blazar in the Sky: AGILE and Multi-wavelength Observations of 3C 454.3 During 2010 November. Astrophys. J. Lett. 2011, 736, L38. [Google Scholar] [CrossRef]
- Hartman, R.C.; Bertsch, D.L.; Bloom, S.D.; Chen, A.W.; Deines-Jones, P.; Esposito, J.A.; Fichtel, C.E.; Friedlander, D.P.; Hunter, S.D.; McDonald, L.M.; et al. The Third EGRET Catalog of High-Energy Gamma-ray Sources. Astrophys. J. Suppl. Ser. 1999, 123, 79–202. [Google Scholar] [CrossRef]
- McNaron-Brown, K.; Johnson, W.N.; Jung, G.V.; Kinzer, R.L.; Kurfess, J.D.; Strickman, M.S.; Dermer, C.D.; Grabelsky, D.A.; Purcell, W.R.; Ulmer, M.P.; et al. OSSE Observations of Blazars. Astrophys. J. 1995, 451, 575. [Google Scholar] [CrossRef]
- Zhang, S.; Collmar, W.; Schönfelder, V. COMPTEL observations of the γ-ray blazars 3C 454.3 and CTA 102 during the CGRO mission. Astron. Astrophys. 2005, 444, 767–775. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Ajello, M.; Allafort, A.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bellazzini, R.; Berenji, B.; et al. Fermi Gamma-ray Space Telescope Observations of the Gamma-ray Outburst from 3C454.3 in November 2010. Astrophys. J. Lett. 2011, 733, L26. [Google Scholar] [CrossRef]
- Dermer, C.D.; Sturner, S.J.; Schlickeiser, R. Multiwavelength Spectral Modeling of Blazars. In Proceedings of the American Astronomical Society Meeting Abstracts, Rome, Italy, 28 August–8 September 1995; Volume 187, p. 46.02. [Google Scholar]
- Macomb, D.J.; Akerlof, C.W.; Aller, H.D.; Aller, M.F.; Bertsch, D.L.; Bruhweiler, F.; Buckley, J.H.; Carter-Lewis, D.A.; Cawley, M.F.; Cheng, K.P.; et al. Multiwavelength Observations of Markarian 421 during a TeV/X-ray Flare. Astrophys. J. Lett. 1995, 449, L99. [Google Scholar] [CrossRef][Green Version]
- Chen, X.; Fossati, G.; Liang, E.P.; Böttcher, M. Time-dependent simulations of multiwavelength variability of the blazar Mrk 421 with a Monte Carlo multizone code. Mon. Not. R. Astron. Soc. 2011, 416, 2368–2387. [Google Scholar] [CrossRef]
- Gaur, H.; Gupta, A.C.; Wiita, P.J. Multiwavelength Variability of the Blazars Mrk 421 and 3C 454.3 in the High State. Astron. J. 2012, 143, 23. [Google Scholar] [CrossRef]
- Finke, J. Modeling Fermi Large Area Telescope and Multiwavelength Data from Blazars. arXiv 2016, arXiv:1602.05965. [Google Scholar]
- Zheng, Y.G.; Yang, C.Y.; Zhang, L.; Wang, J.C. Discerning the Gamma-ray-emitting Region in the Flat Spectrum Radio Quasars. Astrophys. J. Suppl. Ser. 2017, 228, 1. [Google Scholar] [CrossRef]
- Malik, Z.; Shah, Z.; Sahayanathan, S.; Iqbal, N.; Manzoor, A. Multiwavelength study of blazar 4C + 01.02 during its long-term flaring activity in 2014-2017. Mon. Not. R. Astron. Soc. 2022, 514, 4259–4269. [Google Scholar] [CrossRef]
- Sahakyan, N.; Giommi, P. The strange case of the transient HBL blazar 4FGL J1544.3-0649. Mon. Not. R. Astron. Soc. 2021, 502, 836–844. [Google Scholar] [CrossRef]
- Paliya, V.S.; Böttcher, M.; Gurwell, M.; Stalin, C.S. On the Origin of Gamma-ray Flares from Bright Fermi Blazars. Astrophys. J. Suppl. Ser. 2021, 257, 37. [Google Scholar] [CrossRef]
- Sahakyan, N. Modelling the broad-band emission of 3C 454.3. Mon. Not. R. Astron. Soc. 2021, 504, 5074–5086. [Google Scholar] [CrossRef]
- Planck Collaboration; Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; et al. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar] [CrossRef]
- Abdollahi, S.; Acero, F.; Ackermann, M.; Ajello, M.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; et al. Fermi Large Area Telescope Fourth Source Catalog. Astrophys. J. Suppl. Ser. 2020, 247, 33. [Google Scholar] [CrossRef]
- Wood, M.; Caputo, R.; Charles, E.; Di Mauro, M.; Magill, J.; Perkins, J.S.; Fermi-LAT Collaboration. Fermipy: An open-source Python package for analysis of Fermi-LAT Data. In Proceedings of the 35th International Cosmic ray Conference (ICRC2017), Busan, Korea, 12–20 July 2017; Volume 301, p. 824. [Google Scholar]
- Zhu, K.R.; Kang, S.J.; Zhou, R.X.; Zheng, Y.G. Searching for TeV Candidates in 4LAC High-synchrotron- peaked Frequency BL Lac Objects. Astrophys. J. 2021, 916, 93. [Google Scholar] [CrossRef]
- Roming, P.W.A.; Kennedy, T.E.; Mason, K.O.; Nousek, J.A.; Ahr, L.; Bingham, R.E.; Broos, P.S.; Carter, M.J.; Hancock, B.K.; Huckle, H.E.; et al. The Swift Ultra-Violet/Optical Telescope. Space Sci. Rev. 2005, 120, 95–142. [Google Scholar] [CrossRef]
- Burrows, D.N.; Hill, J.E.; Nousek, J.A.; Kennea, J.A.; Wells, A.; Osborne, J.P.; Abbey, A.F.; Beardmore, A.; Mukerjee, K.; Short, A.D.T.; et al. The Swift X-ray Telescope. Space Sci. Rev. 2005, 120, 165–195. [Google Scholar] [CrossRef]
- Barthelmy, S.D.; Barbier, L.M.; Cummings, J.R.; Fenimore, E.E.; Gehrels, N.; Hullinger, D.; Krimm, H.A.; Markwardt, C.B.; Palmer, D.M.; Parsons, A.; et al. The Burst Alert Telescope (BAT) on the SWIFT Midex Mission. Space Sci. Rev. 2005, 120, 143–164. [Google Scholar] [CrossRef]
- Raiteri, C.M.; Stamerra, A.; Villata, M.; Larionov, V.M.; Acosta-Pulido, J.A.; Arévalo, M.J.; Arkharov, A.A.; Bachev, R.; Benítez, E.; Bozhilov, V.V.; et al. The WEBT campaign on the BL Lac object PG 1553+113 in 2013. An analysis of the enigmatic synchrotron emission. Mon. Not. R. Astron. Soc. 2015, 454, 353–367. [Google Scholar] [CrossRef]
- Stratta, G.; Capalbi, M.; Giommi, P.; Primavera, R.; Cutini, S.; Gasparrini, D. The ASDC SED Builder Tool description and Tutorial. arXiv 2011, arXiv:1103.0749. [Google Scholar]
- Aharonian, F.A.; Akhperjanian, A.G.; Barrio, J.A.; Bernlöhr, K.; Bolz, O.; Börst, H.; Bojahr, H.; Contreras, J.L.; Cortina, J.; Denninghoff, S.; et al. Reanalysis of the high energy cutoff of the 1997 Mkn 501 TeV energy spectrum. Astron. Astrophys. 2001, 366, 62–67. [Google Scholar] [CrossRef]
- Aharonian, F.; Akhperjanian, A.; Beilicke, M.; Bernlöhr, K.; Börst, H.G.; Bojahr, H.; Bolz, O.; Coarasa, T.; Contreras, J.L.; Cortina, J.; et al. Detection of TeV gamma-rays from the BL Lac 1ES 1959+650 in its low states and during a major outburst in 2002. Astron. Astrophys. 2003, 406, L9–L13. [Google Scholar] [CrossRef][Green Version]
- Lin, C.; Fan, J.H. Spectral energy distributions for TeV blazars. Res. Astron. Astrophys. 2018, 18, 120. [Google Scholar] [CrossRef]
- Norris, J.P.; Nemiroff, R.J.; Bonnell, J.T.; Scargle, J.D.; Kouveliotou, C.; Paciesas, W.S.; Meegan, C.A.; Fishman, G.J. Attributes of Pulses in Long Bright Gamma-ray Bursts. Astrophys. J. 1996, 459, 393. [Google Scholar] [CrossRef]
- Xu, J.; Hu, S.; Webb, J.R.; Bhatta, G.; Jiang, Y.; Chen, X.; Alexeeva, S.; Li, Y. Statistical Analysis of Microvariability Properties of the Blazar S5 0716+714. Astrophys. J. 2019, 884, 92. [Google Scholar] [CrossRef]
- Ivezić, Ž.; Connelly, A.J.; VanderPlas, J.T.; Gray, A. Statistics, Data Mining, and Machine Learning in Astronomy; Princeton University Press: Princeton, NJ, USA, 2014. [Google Scholar]
- Huang, S.; Hu, S.; Yin, H.; Chen, X.; Alexeeva, S.; Gao, D.; Jiang, Y. A Possible Tidal Disruption Event Candidate in the Black Hole Binary System of OJ 287. Astrophys. J. 2021, 920, 12. [Google Scholar] [CrossRef]
- Kang, S.J.; Zheng, Y.G.; Wu, Q.; Chen, L.; Yin, Y. On the origin of GeV spectral break for Fermi blazars: 3C 454.3. Mon. Not. R. Astron. Soc. 2021, 502, 5875–5881. [Google Scholar] [CrossRef]
- Tavecchio, F.; Maraschi, L.; Ghisellini, G. Constraints on the Physical Parameters of TeV Blazars. Astrophys. J. 1998, 509, 608–619. [Google Scholar] [CrossRef]
- Kino, M.; Takahara, F.; Kusunose, M. Energetics of TeV Blazars and Physical Constraints on Their Emission Regions. Astrophys. J. 2002, 564, 97–107. [Google Scholar] [CrossRef][Green Version]
- Finke, J.D. Compton Dominance and the Blazar Sequence. Astrophys. J. 2013, 763, 134. [Google Scholar] [CrossRef]
- Rybicki, G.B.; Lightman, A.P. Radiative Processes in Astrophysics; John Wiley & Sons: Hoboken, NJ, USA, 1979. [Google Scholar]
- Crusius, A.; Schlickeiser, R. Synchrotron radiation in random magnetic fields. Astron. Astrophys. 1986, 164, L16–L18. [Google Scholar]
- Ghisellini, G.; Celotti, A.; Fossati, G.; Maraschi, L.; Comastri, A. A theoretical unifying scheme for gamma-ray bright blazars. Mon. Not. R. Astron. Soc. 1998, 301, 451–468. [Google Scholar] [CrossRef]
- Ghisellini, G.; Svensson, R. The synchrotron and cyclo-synchrotron absorption cross-section. Mon. Not. R. Astron. Soc. 1991, 252, 313–318. [Google Scholar] [CrossRef]
- Inoue, S.; Takahara, F. Electron Acceleration and Gamma-ray Emission from Blazars. Astrophys. J. 1996, 463, 555. [Google Scholar] [CrossRef]
- Dermer, C.D.; Finke, J.D.; Krug, H.; Böttcher, M. Gamma-ray Studies of Blazars: Synchro-Compton Analysis of Flat Spectrum Radio Quasars. Astrophys. J. 2009, 692, 32–46. [Google Scholar] [CrossRef]
- Ghisellini, G.; Tavecchio, F. Canonical high-power blazars. Mon. Not. R. Astron. Soc. 2009, 397, 985–1002. [Google Scholar] [CrossRef]
- Ghisellini, G.; Tavecchio, F. The blazar sequence: A new perspective. Mon. Not. R. Astron. Soc. 2008, 387, 1669–1680. [Google Scholar] [CrossRef]
- Chen, L.; Bai, J.M. Implications for the Blazar Sequence and Inverse Compton Models from Fermi Bright Blazars. Astrophys. J. 2011, 735, 108. [Google Scholar] [CrossRef][Green Version]
- Sikora, M.; Stawarz, Ł.; Moderski, R.; Nalewajko, K.; Madejski, G.M. Constraining Emission Models of Luminous Blazar Sources. Astrophys. J. 2009, 704, 38–50. [Google Scholar] [CrossRef]
- Hayashida, M.; Madejski, G.M.; Nalewajko, K.; Sikora, M.; Wehrle, A.E.; Ogle, P.; Collmar, W.; Larsson, S.; Fukazawa, Y.; Itoh, R.; et al. The Structure and Emission Model of the Relativistic Jet in the Quasar 3C 279 Inferred from Radio to High-energy γ-ray Observations in 2008-2010. Astrophys. J. 2012, 754, 114. [Google Scholar] [CrossRef]
- Lewis, T.R.; Finke, J.D.; Becker, P.A. A Steady-state Spectral Model for Electron Acceleration and Cooling in Blazar Jets: Application to 3C 279. Astrophys. J. 2018, 853, 6. [Google Scholar] [CrossRef]
- Ghisellini, G. Radiative Processes in High Energy Astrophysics; Springer: Berlin/Heidelberg, Germany, 2013; Volume 873. [Google Scholar] [CrossRef]
- Franceschini, A.; Rodighiero, G.; Vaccari, M. Extragalactic optical-infrared background radiation, its time evolution and the cosmic photon-photon opacity. Astron. Astrophys. 2008, 487, 837–852. [Google Scholar] [CrossRef]
- Camenzind, M.; Krockenberger, M. The lighthouse effect of relativistic jets in blazars. A geometric originof intraday variability. Astron. Astrophys. 1992, 255, 59–62. [Google Scholar]
- Gopal-Krishna.; Wiita, P.J. Swinging jets and the variability of active nuclei. Astron. Astrophys. 1992, 259, 109–117. [Google Scholar]
- Wagner, S.J.; Camenzind, M.; Dreissigacker, O.; Borgeest, U.; Britzen, S.; Brinkmann, W.; Hopp, U.; Schramm, K.J.; von Linde, J. Simultaneous optical and gamma-ray flaring in PKS 0420-014. Implications for emission processes and rotating jet models. Astron. Astrophys. 1995, 298, 688. [Google Scholar]
- Marscher, A.P.; Gear, W.K. Models for high-frequency radio outbursts in extragalactic sources, with application to the early 1983 millimeter-to-infrared flare of 3C 273. Astrophys. J. 1985, 298, 114–127. [Google Scholar] [CrossRef]
- Mankuzhiyil, N.; Ansoldi, S.; Persic, M.; Tavecchio, F. The Environment and Distribution of Emitting Electrons as a Function of Source Activity in Markarian 421. Astrophys. J. 2011, 733, 14. [Google Scholar] [CrossRef]
- Paliya, V.S.; Domínguez, A.; Ajello, M.; Olmo-García, A.; Hartmann, D. The Central Engines of Fermi Blazars. Astrophys. J. Suppl. Ser. 2021, 253, 46. [Google Scholar] [CrossRef]
- Giommi, P.; Polenta, G.; Lähteenmäki, A.; Thompson, D.J.; Capalbi, M.; Cutini, S.; Gasparrini, D.; González-Nuevo, J.; León-Tavares, J.; López-Caniego, M.; et al. Simultaneous Planck, Swift, and Fermi observations of X-ray and γ-ray selected blazars. Astron. Astrophys. 2012, 541, A160. [Google Scholar] [CrossRef]
- Aleksić, J.; Ansoldi, S.; Antonelli, L.A.; Antoranz, P.; Babic, A.; Bangale, P.; Barres de Almeida, U.; Barrio, J.A.; Becerra González, J.; Bednarek, W.; et al. MAGIC long-term study of the distant TeV blazar PKS 1424+240 in a multiwavelength context. Astron. Astrophys. 2014, 567, A135. [Google Scholar] [CrossRef]
- Weaver, Z.R.; Balonek, T.J.; Jorstad, S.G.; Marscher, A.P.; Larionov, V.M.; Smith, P.S.; Boni, S.J.; Borman, G.A.; Chapman, K.J.; Jenks, L.G.; et al. The 2016 June Optical and Gamma-ray Outburst and Optical Microvariability of the Blazar 3C 454.3. Astrophys. J. 2019, 875, 15. [Google Scholar] [CrossRef]
- Kang, S.J.; Zheng, Y.G.; Wu, Q.; Chen, L. On the origin of the soft photons of the high-synchrotron-peaked blazar PKS 1424+240. Mon. Not. R. Astron. Soc. 2016, 461, 1862–1867. [Google Scholar] [CrossRef]
- Sobacchi, E.; Lyubarsky, Y.E. On the magnetization and the radiative efficiency of BL Lac jets. Mon. Not. R. Astron. Soc. 2019, 484, 1192–1201. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, X.; Böttcher, M.; Guo, F.; Li, H. Polarization Swings Reveal Magnetic Energy Dissipation in Blazars. Astrophys. J. 2015, 804, 58. [Google Scholar] [CrossRef]
- Böttcher, M.; Baring, M.G. Multi-wavelength Variability Signatures of Relativistic Shocks in Blazar Jets. Astrophys. J. 2019, 887, 133. [Google Scholar] [CrossRef]
- Lefa, E.; Aharonian, F.A.; Rieger, F.M. “Leading Blob” Model in a Stochastic Acceleration Scenario: The Case of the 2009 Flare of Mkn 501. Astrophys. J. Lett. 2011, 743, L19. [Google Scholar] [CrossRef][Green Version]
- Aguilar-Ruiz, E.; Fraija, N.; Galván-Gámez, A.; Benítez, E. A two-zone model as origin of hard TeV spectrum in extreme BL lacs. Mon. Not. R. Astron. Soc. 2022, 512, 1557–1566. [Google Scholar] [CrossRef]
- Wang, Z.R.; Liu, R.Y.; Petropoulou, M.; Oikonomou, F.; Xue, R.; Wang, X.Y. Unified model for orphan and multiwavelength blazar flares. Phy. Rev. D. 2022, 105, 023005. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).