Longitudinal Variations in Equatorial Ionospheric TEC from GPS, Global Ionosphere Map and International Reference Ionosphere-2016 during the Descending and Minimum Phases of Solar Cycle 24
Abstract
1. Introduction
2. Materials and Methods
3. Results
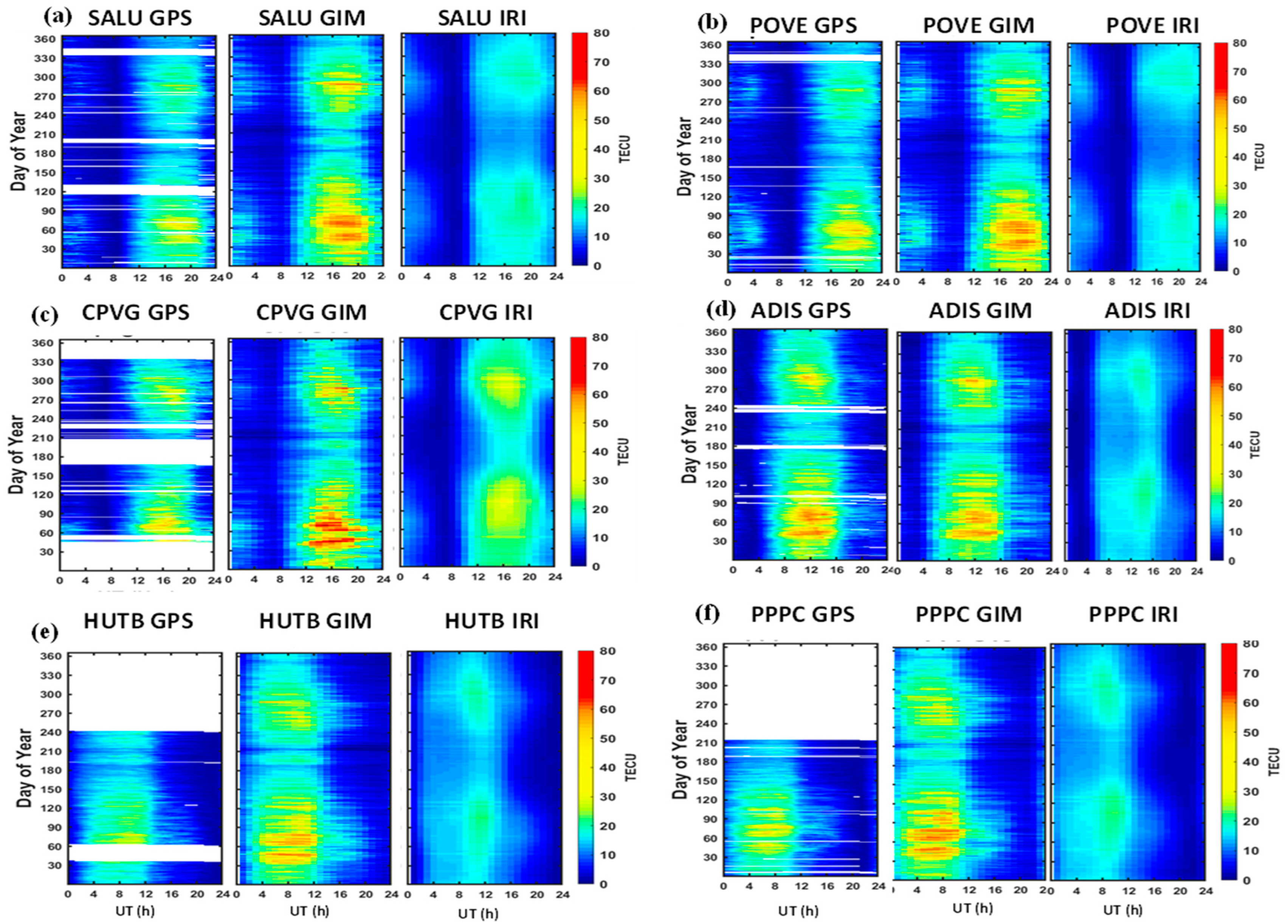
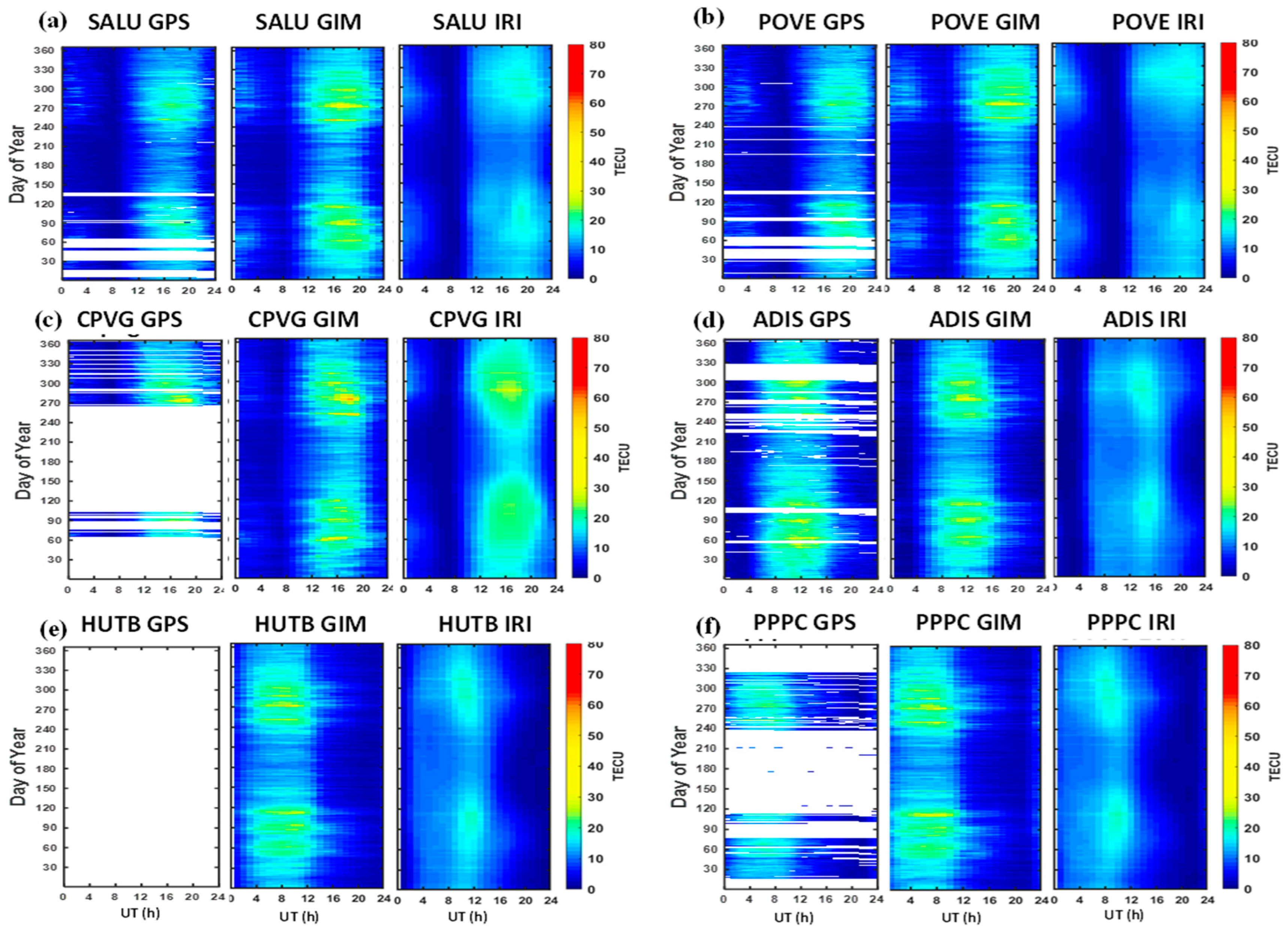
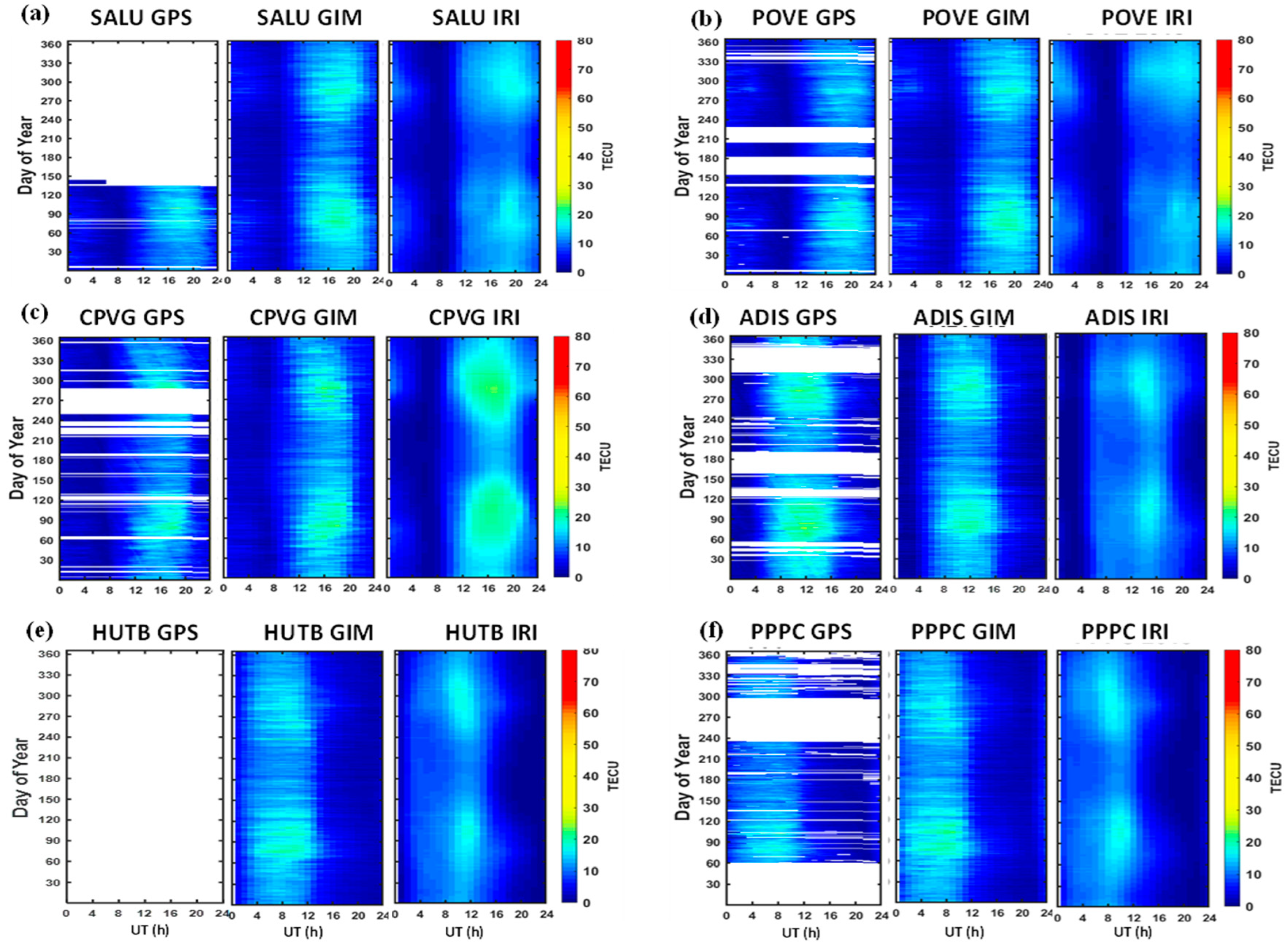
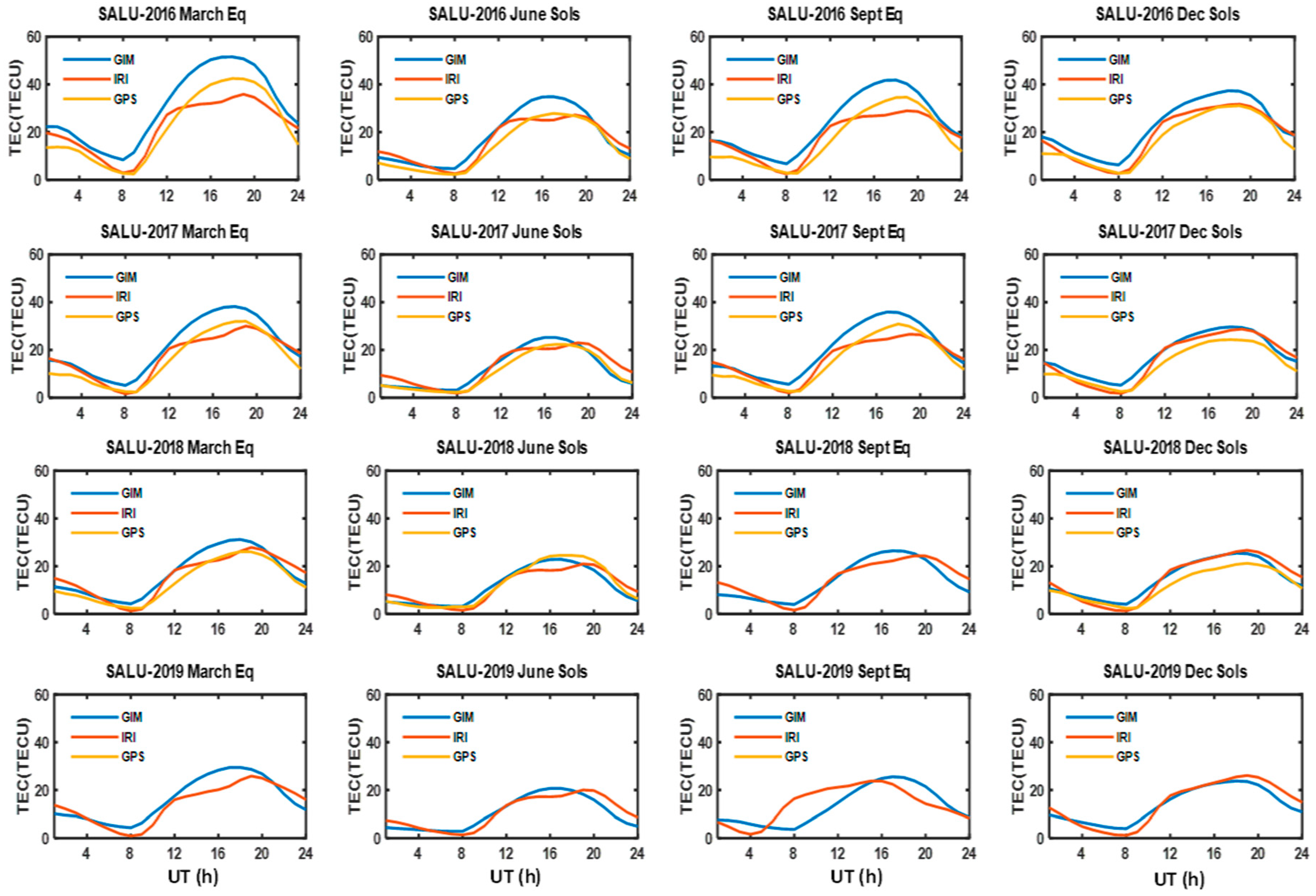
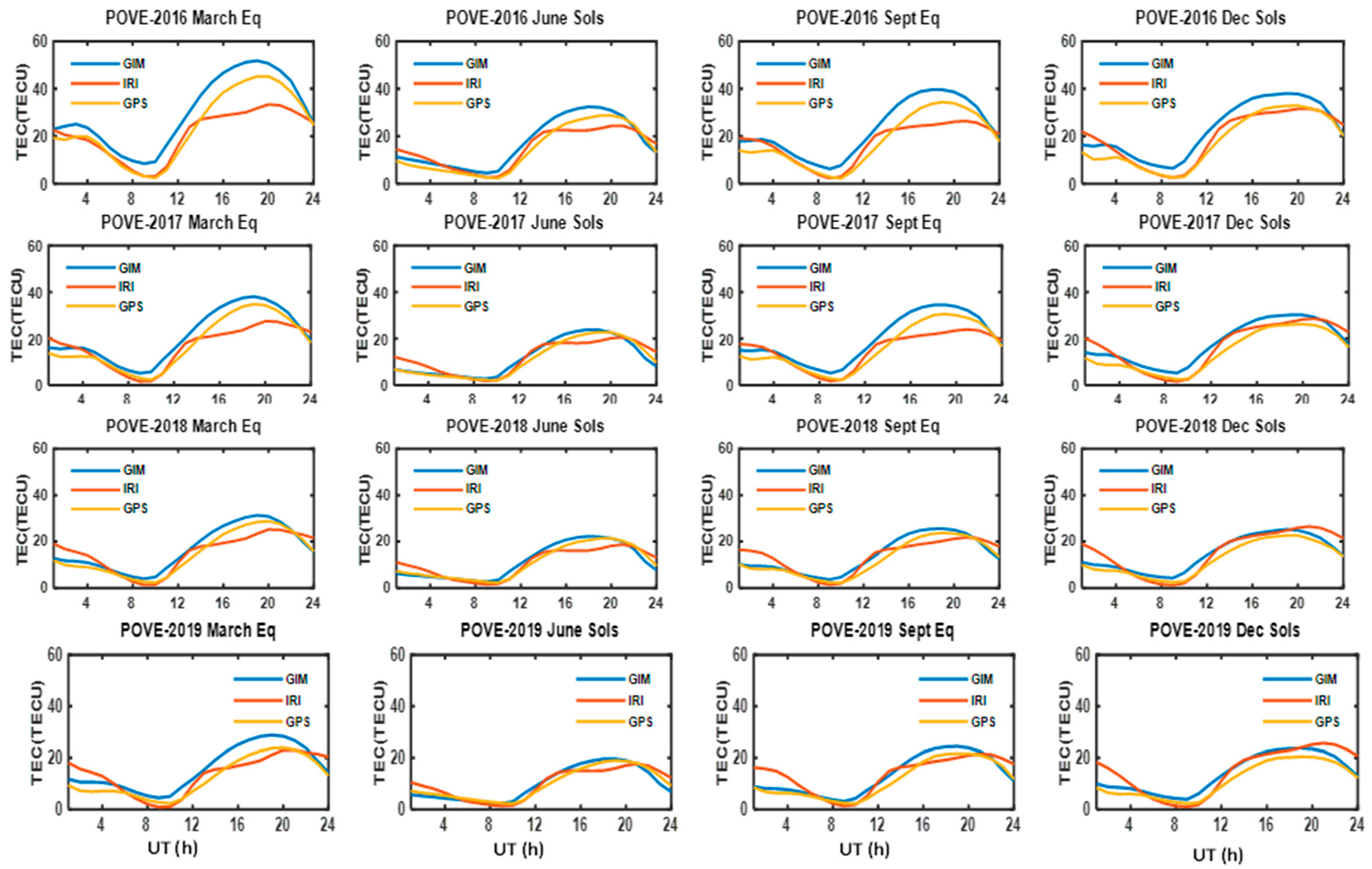
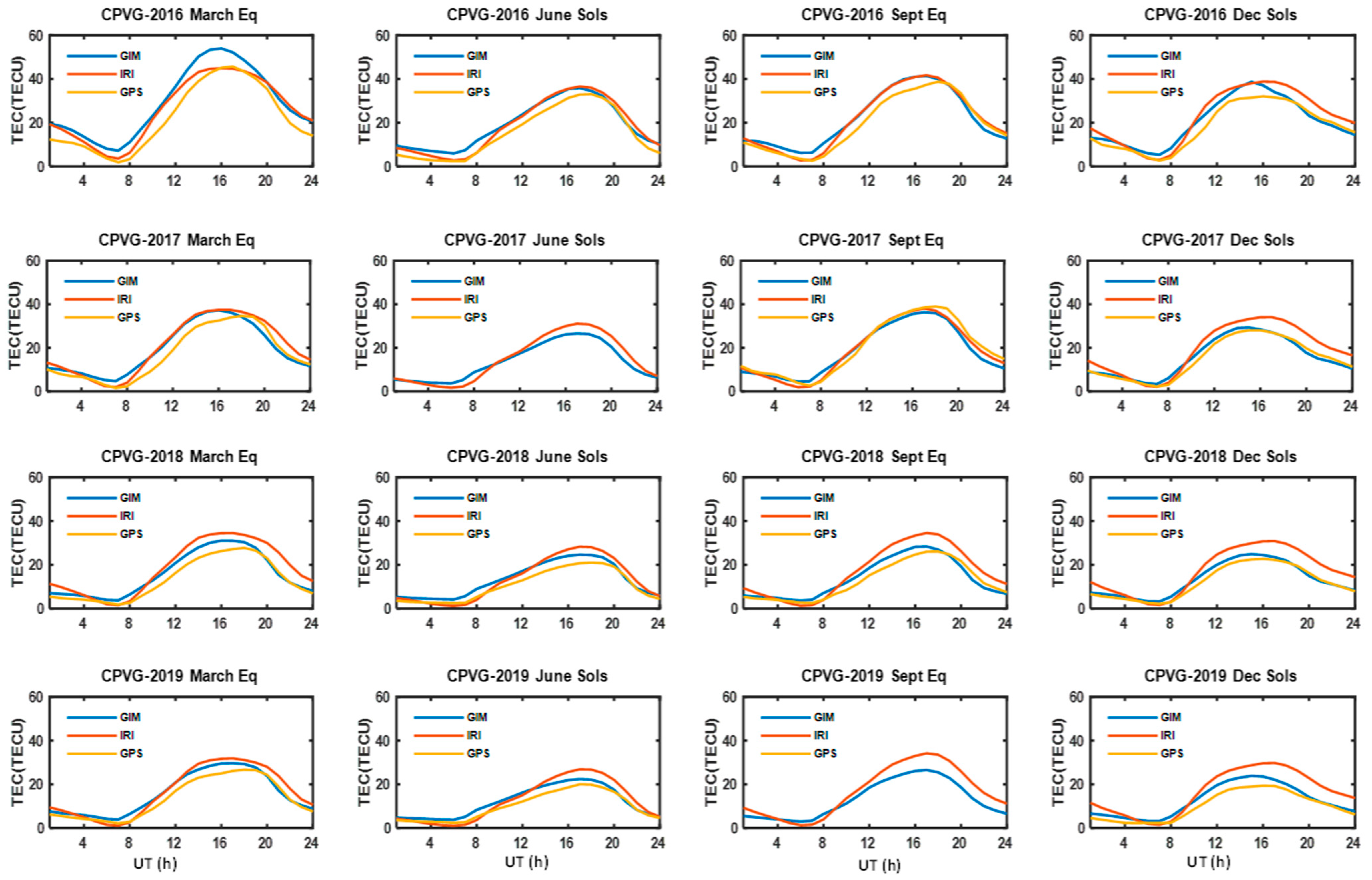
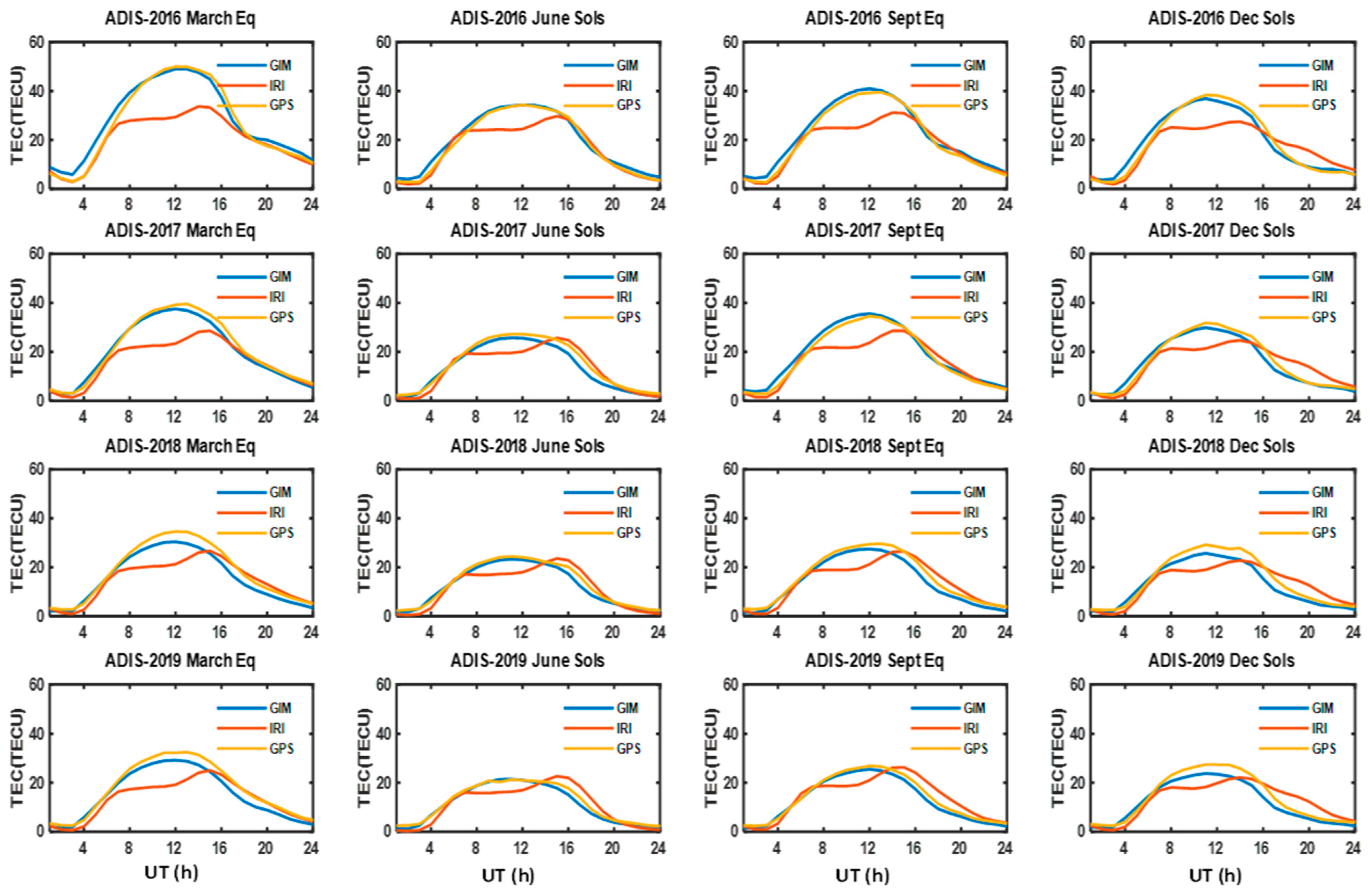
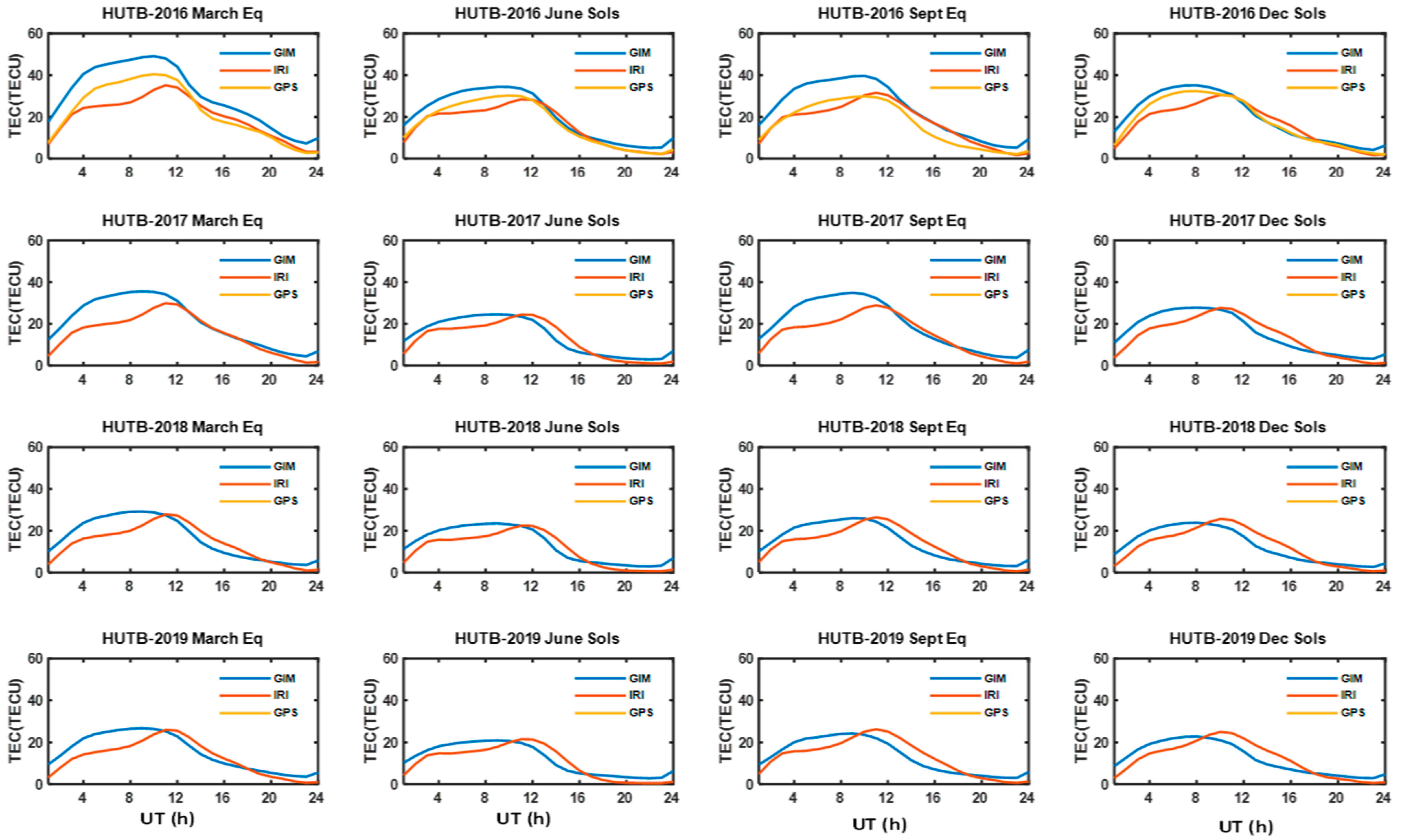
3.1. Diurnal Variations
3.2. Seasonal Variations
3.3. RMSE Estimation
3.4. Longitudinal Variations
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Reddybattula, K.D.; Panda, S.K. Performance analysis of quiet and disturbed time ionospheric TEC responses from GPS-based observations, IGS-GIM, IRI-2016 and SPIM/IRI-Plas 2017 models over the low latitude Indian region. Adv. Space Res. 2019, 64, 2026–2045. [Google Scholar] [CrossRef]
- Mallika, I.L.; Venkata Ratnam, D.; Raman, S.; Sivavaraprasad, G. Machine learning algorithm to forecast ionospheric time delays using Global Navigation satellite system observations. Acta Astronaut. 2020, 173, 221–231. [Google Scholar] [CrossRef]
- Koons, H.C.; Mazur, J.E.; Selesnick, R.S.; Blake, J.B.; Fennell, J.F.; Roeder, J.L.; Anderson, P.C. The impact of the space environment on space system. In Proceedings of the 6th Spacecraft Charging Technology Conference, AFRL Science Center, Hanscom AFB, MA, USA, 2–6 November 1998; AFRL-VS-TR-200015782000. pp. 7–11. [Google Scholar]
- Jee, G.; Schunk, R.W.; Scherliess, L. Analysis of TEC data from the TOPEX/Poseidon mission. J. Geophys. Res. 2004, 109, A01301. [Google Scholar] [CrossRef]
- Maruyama, T.; Ma, G.; Nakamura, M. Signature of TEC storm on 6 November 2001 derived from dense GPS receiver network and ionosonde chain over Japan. J. Geophys. Res. 2004, 109, A10302. [Google Scholar] [CrossRef]
- Codrescu, M.V.; Palo, S.E.; Zhang, X.; Fuller-Rowell, T.J.; Poppe, C. TEC climatology derived from TOPEX/POSEIDON measurements. J. Atmos. Sol. 1999, 61, 281–298. [Google Scholar] [CrossRef]
- Ogwala, A.; Somoye, E.O.; Ogunmodimu, O.; Adeniji-Adele, R.A.; Onori, E.O.; Oyedokun, O. Diurnal, seasonal and solar cycle variation in total electron content and comparison with IRI-2016 model at Birnin Kebbi. Ann. Geophys. 2019, 37, 775–789. [Google Scholar] [CrossRef]
- Bagiya, M.S.; Joshi, H.P.; Iyer, K.N.; Aggarwal, M.; Ravin-Dran, S.; Pathan, B.M. TEC variations during low solar activity period (2005–2007) near the Equatorial Ionization Anomaly Crest region in India. Ann. Geophys. 2009, 27, 1047–1057. [Google Scholar] [CrossRef]
- Tariku, Y.A. Pattern of GPS-TEC variability over low-latitude regions (African sector) during the deep solar minimum (2008 to 2009) and solar maximum (2012 to 2013) phases. Earth Planets Space 2015, 67, 35. [Google Scholar] [CrossRef]
- Torr, M.R.; Torr, D.G. The seasonal behavior of the F2 layer of the ionosphere. J. Atmos. Terr. Phys. 1973, 35, 2237. [Google Scholar] [CrossRef]
- Wanninger, L. Effects of the equatorial ionosphere on GPS. GPS World 1993, 2, 48. [Google Scholar]
- Fedrizzi, M.; de Paula, E.R.; Kantor, I.J.; Langley, R.B.; Santos, M.C.; Komjathy, A. Mapping the Low-Latitude Ionosphere with GPS. GPS WORLD 2002, 13, 41–47. [Google Scholar]
- Rama Rao, P.V.S.; Krishna, S.G.; Niranjan, K.; Prasad, D.S.V.V.D. Study of temporal and spatial characteristics of L-band scintillation over the Indian low-latitude region and their possible effects on GPS navigation. Ann. Geophys. 2006, 24, 1567–1580. [Google Scholar] [CrossRef]
- Wu, C.C.; Liou, K.; Shan, S.J.; Tseng, C.L. Variation of ionospheric total electron content in Taiwan region of the equatorial anomaly from 1994–2003. Adv. Space Res. 2008, 41, 611–616. [Google Scholar] [CrossRef]
- Ayorinde, T.T.; Rabiu, A.B.; Amory-Mazaudier, C. Inter-hourly variability of Total Electron Content during the quiet condition over Nigeria within the Equatorial Ionization Anomaly region. J. Atmos. Solar Terr. Phys. 2016, 145, 21–33. [Google Scholar] [CrossRef]
- Klobuchar, J.A. Ionospheric Time-Delay Algorithm for Single-Frequency GPS Users. IEEE Trans. Aerosp. Electron. Syst. 1987, AES-23, 325–331. [Google Scholar] [CrossRef]
- Komjathy, A.; Langley, R.; Bilitza, D. Ingesting GPS-derived data into the IRI for single frequency radar altimeter ionospheric delay corrections. Adv. Space Res. 1998, 22, 793–802. [Google Scholar] [CrossRef]
- Bolaji, O.S.; Adeniyi, J.O.; Radicella, S.M.; Doherty, P.H. Variability of total electron content over an equatorial West African station during low solar activity. Radio Sci. 2012, 47, RS1001. [Google Scholar] [CrossRef]
- Alizadeh, M.M.; Wijaya, D.D.; Hobiger, T.; Weber, R.; Schuh, H. Ionospheric effects on microwave signals. In Atmospheric Effect in Space Geodesy; Springer Atmospheric, Sciences; Bohm, J., Schuh, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Bilitza, D.; Altadill, D.; Truhlik, V.; Shubin, V.; Galkin, I.; Reinisch, B.; Huang, X. International reference ionosphere 2016: From ionospheric climate to real-time weather predictions. Space Weather 2017, 15, 418–429. [Google Scholar] [CrossRef]
- Hernandez-Pajares, M.; Juan, J.M.; Sanz, J.; Orus, R.; Garcia-Rigo, A.; Feltens, J.; Komjathy, A.; Schaer, S.C.; Krankowski, A. The IGS VTEC maps: A reliable source of ionospheric information since 1998. J. Geod. 2009, 83, 263–275. [Google Scholar] [CrossRef]
- Schaer, S. Mapping and Predicting the Earth’s Ionosphere Using the Global Positioning System. Ph.D. Thesis, Bern University of Bern, Bern, Switzerland, 1999. [Google Scholar]
- Bilitza, D.; Pezzopane, M.; Truhlik, V.; Altadill, D.; Reinisch, B.W.; Pignalberi, A. The International Reference Ionosphere model: A review and description of an ionospheric benchmark. Rev. Geophys. 2022, 60, e2022RG000792. [Google Scholar] [CrossRef]
- Rama Rao, P.V.S.; Krishna, S.G.; Prasad, J.V.; Prasad, S.N.V.S.; Prasad, D.S.V.V.D.; Niranjan, K. Geomagnetic storm effects on GPS based navigation. Ann. Geophys. 2009, 27, 2101–2110. [Google Scholar] [CrossRef]
- D’ujanga, F.M.; Opio, P.; Twinomugisha, F. Variation of total electron content with solar activity during the ascending phase of solar cycle 24 observed at Makerere University, Kampala. Ionos. Space Weather. Longit. Depend. Low. Atmos. 2016, 220, 263. [Google Scholar]
- Balan, N.; Liu, L.; Le, H. A brief review of the equatorial ionization anomaly and ionospheric irregularities. Earth Planet. Phys. 2018, 2, 257–275. [Google Scholar] [CrossRef]
- Ogwala, A.; Somoye, E.O.; Panda, S.K.; Ogunmodimu, O.; Onori, E.O.; Sharma, S.K.; Okoh, D.; Oyedokun, O.J. Total electron content at equatorial and low-, middle and high-latitudes in the African longitude sector and its comparison with IRI-2016 and IRI-Plas 2017 models. Adv. Space Res. 2021, 68, 2160–2176. [Google Scholar] [CrossRef]
- Kumar, S.; Tan, E.L.; Murti, D.S. Impacts of solar activity on performance of the IRI-2012 model predictions from low to mid latitudes. Earth Planets Space 2015, 67, 42. [Google Scholar] [CrossRef]
- Bhuyan, P.K.; Borah, R.R. TEC derived from GPS network in India and comparison with the IRI. Adv. Space Res. 2007, 39, 830–840. [Google Scholar] [CrossRef]
- Alcay, S.; Oztan, G.; Selvi, H.Z. Comparison of IRI_PLAS and IRI_2012 Model Predictions with GPS-TEC Measurements in Different Latitude Regions. Ann. Geophys. 2017, 60, G0549. [Google Scholar] [CrossRef]
- Atıcı, R. Comparison of GPS TEC with modelled values from IRI 2016 and IRI-PLAS over Istanbul, Turkey. Astrophys. Space Sci. 2018, 363, 231. [Google Scholar] [CrossRef]
- Sharma, S.K.; Ansari, K.; Panda, S.K. Analysis of Ionospheric TEC Variation over Manama, Bahrain, and Comparison with IRI- 2012 and IRI-2016 Models. Arab. J. Sci. Eng. 2018, 43, 3823–3830. [Google Scholar] [CrossRef]
- Ansari, K.; Park, K.-D.; Panda, S.K. Empirical Orthogonal Function analysis and modeling of ionospheric TEC over South Korean region. Acta Astronaut. 2019, 161, 313–324. [Google Scholar] [CrossRef]
- Reddybattula, K.D.; Panda, S.K.; Ansari, K.; Peddi, V.S.R. Analysis of ionospheric TEC from GPS, GIM and global ionosphere models during moderate, strong, and extreme geomagnetic storms over Indian region. Acta Astronaut. 2019, 161, 283–292. [Google Scholar] [CrossRef]
- Tariku, Y.A. Performance evaluation of the IRI 2016 and IRI-Plas 2017 models over central Asian mid-latitude regions in the descending phase of solar cycle 24. Adv. Space Res. 2019, 64, 1065–1077. [Google Scholar] [CrossRef]
- Tariku, Y.A. Testing the improvement of performance of the IRI model in the estimation of TEC over the mid-latitude American regions. Adv. Space Res. 2019, 63, 2066–2074. [Google Scholar] [CrossRef]
- Dabbakuti, J.R.K.K.; Peesapati, R.; Panda, S.K.; Thummala, S. Modeling and analysis of ionospheric TEC variability from GPS–TEC measurements using SSA model during 24th solar cycle. Acta Astronaut. 2021, 178, 24–35. [Google Scholar] [CrossRef]
- Bolaji, O.; Oyeyemi, E.; Adewale, A.O.; Wu, Q.; Okoh, D.; Doherty, P.H.; Kaka, R.O.; Abbas, M.; Owolabi, C.; Jidele, P.A. Assessment of IRI-2012, NeQuick-2 and IRI-Plas 2015 models with observed equatorial ionization anomaly in Africa during 2009 sudden stratospheric warming event. J. Atmos. Sol.-Terr. Phys. 2017, 164, 203–214. [Google Scholar] [CrossRef]
- Nogueira, P.A.B.; Abdu, M.A.; Souza, J.R.; Bailey, G.J.; Batista, I.S.; Shume, E.B.; Denardini, C.M. Longitudinal variation in Global Navigation Satellite Systems TEC and topside ion density over South American sector associated with the four-peaked wave structures. J. Geophys. Res. Space Phys. 2013, 118, 7940–7953. [Google Scholar] [CrossRef]
- Akala, A.O.; Seemala, G.K.; Doherty, P.H.; Valladares, C.E.; Carrano, C.S.; Espinoza, J.; Oluyo, K.S. Comparison of equatorial GPS-TEC observations over an African station and an American station during the minimum and ascending phases of solar cycle 24. Ann. Geophys. 2013, 31, 2085. [Google Scholar] [CrossRef]
- Oryema, B.; Jurua, E.; D’ujanga, F.M.; Ssebiyonga, N. Investigation of TEC variations over the magnetic equatorial and equatorial anomaly regions of the African sector. Adv. Space Res. 2015, 56, 1939–1950. [Google Scholar] [CrossRef]
- Zhong, J.; Lei, J.; Wang, W.; Burns, A.G.; Yue, X.; Dou, X. Longitudinal variations of topside ionospheric and plasmaspheric TEC. J. Geophys. Res. Space Phys. 2017, 122, 6737–6760. [Google Scholar] [CrossRef]
- Olwendo, O.J.; Yamazaki, Y.; Cilliers, P.J.; Baki, P.; Doherty, P. A study on the variability of ionospheric total electron content over east African low latitude region and storm time ionspheric variations. Radio Sci. 2016, 51, 1503–1518. [Google Scholar] [CrossRef]
- Seemala, G.; Valladares, C. Statistics of total electron content depletions observed over the South American continent for the year 2008. Radio Sci. 2011, 46, 1–14. [Google Scholar] [CrossRef]
- Valladares, C.E.; Villalobos, J.; Hei, M.A.; Sheehan, R.; Basu, S.; Mackenzie, E.; Doherty, P.H.; Rios, V.H. Simultaneous observation of travelling ionospheric disturbances in the northern and southern hermisphere. Ann. Geophys. 2009, 27, 1501–1508. [Google Scholar] [CrossRef]
- Sardon, E.; Zarraoa, N. Estimation of total electron using GPS data: How stable are the differential satellite and receiver instrumental biases? Radio Sci. 1997, 32, 1899–1910. [Google Scholar] [CrossRef]
- Arikan, F.; Nayir, H.; Sezen, U.; Arikan, O. Estimation of single station interfrequency receiver biase using GPS-TEC. Radio Sci. 2008, 43, RS4004. [Google Scholar] [CrossRef]
- Galkin, I.; Fron, A.; Reinisch, B.; Hernandez-Pajere, M.; Krankwoski, A.; Nava, B.; Bilitza, D.; Kotulak, K.; Flisek, P.; Li, Z. Global Monitoring of the ionospheric weather by GIRO and GNSS Data Fusion. Atmosphere 2022, 13, 371. [Google Scholar] [CrossRef]
- Oyedokun, O.J.; Akala, A.O.; Oyeyemi, E.O. Characterization of African equatorial ionization anomaly (EIA) during maximum phase of solar cycle 24. J. Geophys. Res. Space Phys. 2020, 125, e2019JA027066. [Google Scholar] [CrossRef]
- Somoye, E.; Akala, A. Comparison of diurnal, seasonal and latitudinal effect of MUF VR and NmF2 VR during some solar cycle epochs. Adv. Space Res. 2011, 47, 2182–2187. [Google Scholar] [CrossRef]
- Aggarwal, M.; Bardhan, A.; Sharma, D.K. Equinoctial asymmetry in ionosphere over Indian region during 2006–2013 using COSMIC measurements. Adv. Space Res. 2017, 60, 999–1014. [Google Scholar] [CrossRef]
- Balan, N.; Otsuka, Y.; Bailey, G.; Fukao, S. Equinoctial asymmetries in the ionosphere and thermosphere observed by the MU radar. J. Geophys. Res. 1998, 103, 9481–9495. [Google Scholar] [CrossRef]
- Bailey, G.J.; Su, Y.Z.; Oryama, K.-I. Yearly variations in the low-latitude topside ionosphere. Ann. Geophys. 2000, 18, 789–798. [Google Scholar] [CrossRef]
- Pezzopane, M.; Del Corpo, A.; Piersanti, M.; Cesaroni, C.; Pignalberi, A.; Matteo, S.D.; Spogli, L.; Vellante, M.; Heilig, B. On some features characterizing the plasmasphere–magnetosphere–ionosphere system during the geomagnetic storm of 27 May 2017. Earth Planets Space 2019, 71, 77. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Wang, W.; Ning, B.; Pirog, O.M.; Kurkin, V.I. Solar activity variations of the ionospheric peak electron density. J. Geophys. Res. 2006, 111, A08304. [Google Scholar] [CrossRef]
- Forbes, J.M.; Bruinsma, S.; Lemoine, F.G. Solar rotation effects on the thermospheres of Mars and Earth. Science 2006, 312, 1366–1368. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Wang, W.; Chen, Y.; Le, H. Solar activity effects on the ionosphere: A brief review, Space Physics and Space Weather Geophysics. Chin. Sci. Bull. 2011, 56, 1202–1211. [Google Scholar] [CrossRef]
- Panda, S.K.; Haralambous, H.; Mefe, M.; Dabbakuti, J.R.K.K.; Tariku, Y.A. Ionospheric ans plasmaspheric electron contents from space-time collated digisonde, COSMIC, GPS observations and model assessments. Acta Astronaut. 2021, 179, 619–635. [Google Scholar] [CrossRef]
- Tsai, H.-F.; Liu, J.-Y.; Tsai, W.-H.; Liu, C.-H.; Tseng, C.-L.; Wu, C.-C. Seasonal variations of the ionospheric TEC in Asian equatorial anomaly regions. J. Geophys. Res. 2001, 106, 30363–30369. [Google Scholar]
- Ma, R.; Xu, J.; Liao, H. The features and a possible mechanism of semiannual variation in the peak electron density of the low latitude F2 Layer. J. Atmos. Sol. Terr. Phys. 2003, 65, 47–57. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, L.; Wan, W.; Ren, Z. Equinoctial asymmetry in solar activity variations of NmF2 and TEC. Ann. Geophys. 2012, 30, 613–622. [Google Scholar] [CrossRef]
- Kawamura, S.; Balan, N.; Otsuka, Y.; Fukao, S. Annual and semiannual variations of themidlatitude ionosphere under low solar activity. J. Geophys. Res. 2002, 107, 1166. [Google Scholar]
- Yizengaw, E.; Zesta, E.; Moldwin, M.B.; Damtie, B.; Mebrahtu, A.; Valladares, C.E.; Pfaff, R.F. Longitudinal differences of ionospheric vertical density distribution and equatorial electrodynamics. J. Geophys. Res. 2012, 117, A07312. [Google Scholar] [CrossRef]
- Potula, B.S.; Chu, Y.-H.; Uma, G.; Hsia, H.-P.; Wu, K.-H. A global comparative study on the ionospheric measurements between COSMIC radio occultation technique and IRI model. J. Geophys. Res. 2011, 116, A02310. [Google Scholar] [CrossRef]
- Klimenko, M.V.; Klimenko, V.V.; Bessarab, F.S.; Zakharenkova, I.E.; Vesnin, A.M.; Ratovsky, K.G.; Galkin, I.A.; Chernyak, I.V.; Yasyukevich, Y.V.; Koren’kova, N.A. Diurnal and longitudinal variations in the earth’s ionosphere in the period of solstice in conditions of a deep minimum of solar activity. Cosm. Res. 2016, 54, 8–19. [Google Scholar] [CrossRef]
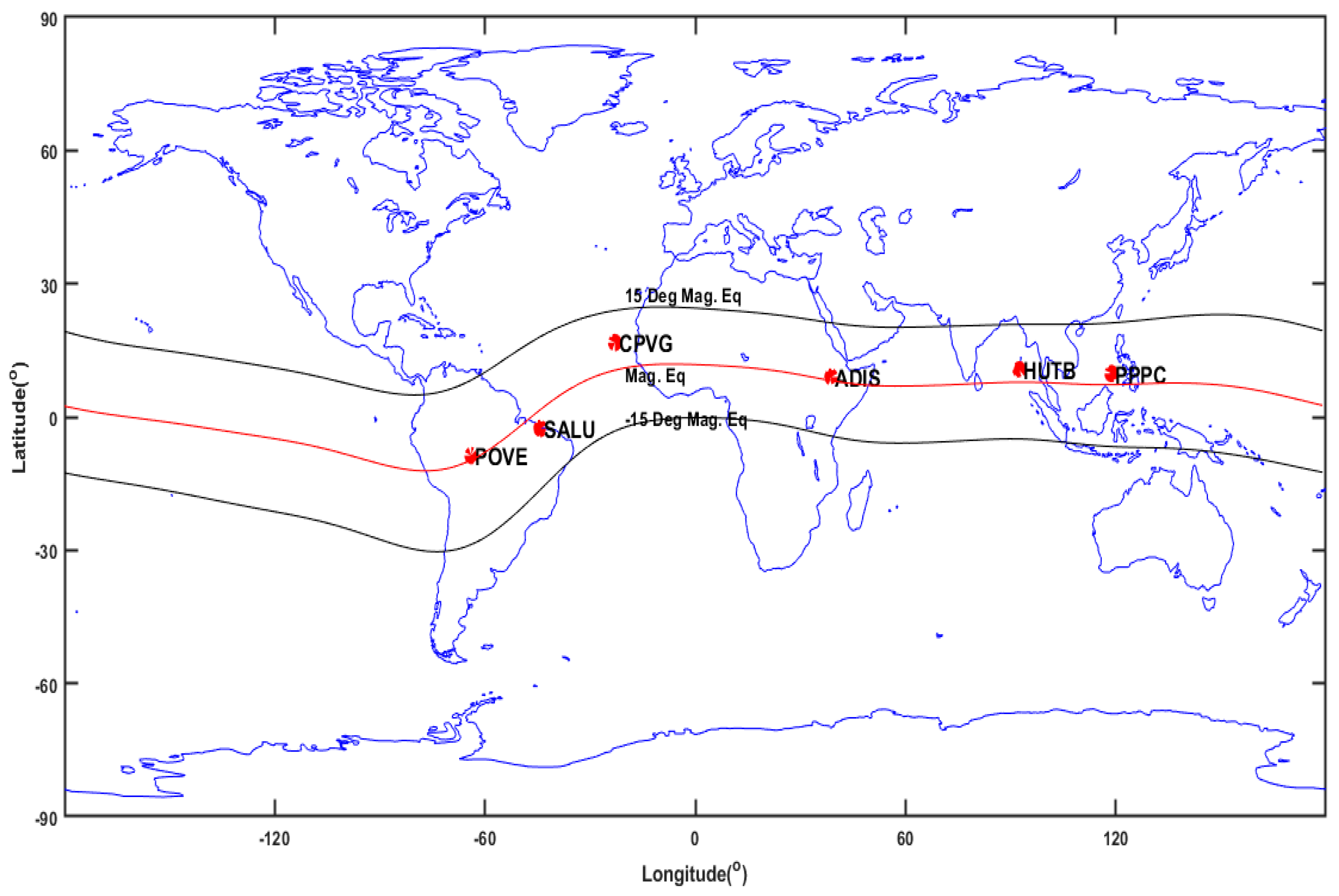


| Longitude Sector | Station Code | Location | Geographic Lat. | Geographic Long. | Magnetic Lat. |
|---|---|---|---|---|---|
| American | SALU | Sao Luis, Brazil | −2.59° | −44.21° | −0.25° |
| POVE | Porto Velho, Brazil | −8.7° | −63.9° | 2.87° | |
| African | CPVG | Cape Verde | 16.73° | −22.94° | 4.94° |
| ADIS | Addis Ababa University, Ethiopia | 9.02° | 38.81° | 0.16° | |
| Asian | HUTB | Hutbay, Nicobar Islands | 10.62° | 92.51° | 2.28° |
| PPPC | Puerto Princesa, Phillipines | 9.77° | 118.74° | 1.93° |
| Station ID | Years | March Equinox | June Solstice | September Equinox | December Solstice |
|---|---|---|---|---|---|
| SALU | 2016 | 8.50 | 4.70 | 6.64 | 5.70 |
| 2017 | 5.42 | 2.30 | 4.88 | 4.23 | |
| 2018 | 3.85 | 1.96 | - | 3.36 | |
| 2019 | - | - | - | - | |
| POVE | 2016 | 6.55 | 3.50 | 5.46 | 5.44 |
| 2017 | 3.79 | 1.79 | 4.18 | 4.07 | |
| 2018 | 2.63 | 1.79 | 2.29 | 2.65 | |
| 2019 | 4.03 | 1.58 | 2.33 | 2.82 | |
| CPVG | 2016 | 7.39 | 3.86 | 3.91 | 3.56 |
| 2017 | 3.92 | - | 3.16 | 1.78 | |
| 2018 | 3.09 | 2.96 | 2.50 | 1.75 | |
| 2019 | 2.75 | 2.46 | - | 2.90 | |
| ADIS | 2016 | 2.90 | 1.56 | 1.85 | 2.15 |
| 2017 | 1.77 | 2.00 | 1.63 | 1.81 | |
| 2018 | 2.96 | 1.39 | 2.14 | 2.70 | |
| 2019 | 2.82 | 1.22 | 1.36 | 2.71 | |
| HUTB | 2016 | 8.05 | 3.96 | 7.51 | 2.78 |
| 2017 | - | - | - | - | |
| 2018 | - | - | - | - | |
| 2019 | - | - | - | - | |
| PPPC | 2016 | 7.70 | 5.21 | 13.42 | 2.50 |
| 2017 | 6.02 | 3.84 | 3.24 | 2.21 | |
| 2018 | 3.15 | 2.81 | 4.40 | 3.38 | |
| 2019 | 2.82 | 2.01 | 4.50 | 3.48 |
| Station ID | Year | March Equinox | June Solstice | September Equinox | December Solstice |
|---|---|---|---|---|---|
| SALU | 2016 | 4.94 | 3.14 | 4.19 | 2.83 |
| 2017 | 3.45 | 2.90 | 3.05 | 3.48 | |
| 2018 | 3.29 | 2.76 | - | 3.86 | |
| 2019 | - | - | - | - | |
| POVE | 2016 | 6.44 | 3.26 | 4.54 | 3.50 |
| 2017 | 4.76 | 2.82 | 4.17 | 3.85 | |
| 2018 | 3.89 | 2.37 | 3.58 | 4.36 | |
| 2019 | 4.02 | 1.92 | 4.02 | 4.92 | |
| CPVG | 2016 | 5.01 | 3.31 | 3.16 | 5.23 |
| 2017 | 4.16 | - | 2.01 | 4.88 | |
| 2018 | 6.10 | 3.86 | 5.43 | 5.91 | |
| 2019 | 3.94 | 3.88 | - | 7.34 | |
| ADIS | 2016 | 9.87 | 4.17 | 5.81 | 6.33 |
| 2017 | 7.34 | 3.50 | 4.74 | 4.79 | |
| 2018 | 5.95 | 3.32 | 4.21 | 4.67 | |
| 2019 | 6.27 | 2.95 | 3.46 | 4.63 | |
| HUTB | 2016 | 5.31 | 2.76 | 3.37 | 3.52 |
| 2017 | - | - | - | - | |
| 2018 | - | - | - | - | |
| 2019 | - | - | - | - | |
| PPPC | 2016 | 5.57 | 2.01 | 6.64 | 3.59 |
| 2017 | 2.96 | 3.44 | 3.86 | 1.69 | |
| 2018 | 2.56 | 2.07 | 3.44 | 3.18 | |
| 2019 | 2.78 | 2.34 | 4.49 | 3.79 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ogwala, A.; Oyedokun, O.J.; Ogunmodimu, O.; Akala, A.O.; Ali, M.A.; Jamjareegulgarn, P.; Panda, S.K. Longitudinal Variations in Equatorial Ionospheric TEC from GPS, Global Ionosphere Map and International Reference Ionosphere-2016 during the Descending and Minimum Phases of Solar Cycle 24. Universe 2022, 8, 575. https://doi.org/10.3390/universe8110575
Ogwala A, Oyedokun OJ, Ogunmodimu O, Akala AO, Ali MA, Jamjareegulgarn P, Panda SK. Longitudinal Variations in Equatorial Ionospheric TEC from GPS, Global Ionosphere Map and International Reference Ionosphere-2016 during the Descending and Minimum Phases of Solar Cycle 24. Universe. 2022; 8(11):575. https://doi.org/10.3390/universe8110575
Chicago/Turabian StyleOgwala, Aghogho, Oluwole Johnson Oyedokun, Olugbenga Ogunmodimu, Andrew Ovie Akala, Masood Ashraf Ali, Punyawi Jamjareegulgarn, and Sampad Kumar Panda. 2022. "Longitudinal Variations in Equatorial Ionospheric TEC from GPS, Global Ionosphere Map and International Reference Ionosphere-2016 during the Descending and Minimum Phases of Solar Cycle 24" Universe 8, no. 11: 575. https://doi.org/10.3390/universe8110575
APA StyleOgwala, A., Oyedokun, O. J., Ogunmodimu, O., Akala, A. O., Ali, M. A., Jamjareegulgarn, P., & Panda, S. K. (2022). Longitudinal Variations in Equatorial Ionospheric TEC from GPS, Global Ionosphere Map and International Reference Ionosphere-2016 during the Descending and Minimum Phases of Solar Cycle 24. Universe, 8(11), 575. https://doi.org/10.3390/universe8110575






