Experimentum crucis for Electromagnetic Response of Metals to Evanescent Waves and the Casimir Puzzle

Abstract

It is well known that the Casimir force calculated at large separations using the Lifshitz theory differs by a factor of 2 for metals described by the Drude or plasma models. We argue that this difference is entirely determined by the contribution of transverse electric (s) evanescent waves. Taking into account that there is a lack of experimental information on the electromagnetic response of metals to low-frequency evanescent waves, we propose an experiment on measuring the magnetic field of an oscillating magnetic dipole spaced in a vacuum above a thick metallic plate. According to our results, the lateral components of this field are governed by the transverse electric evanescent waves and may vary by orders of magnitude depending on the model describing the permittivity of the plates used in calculations and the oscillation frequency of the magnetic dipole. Measuring the lateral component of the magnetic field for typical parameters of the magnetic dipole designed in the form of a 1-mm coil, one could either validate or disprove the applicability of the Drude model as a response function of metal in the range of low-frequency evanescent waves. This will elucidate the roots of the Casimir puzzle lying in the fact that the theoretical predictions of the Lifshitz theory using the Drude model are in contradiction with the high-precision measurements of the Casimir force at separations exceeding 150 nm. Possible implications of the suggested experiment for a wide range of topics in optics and condensed matter physics dealing with evanescent waves are discussed.

1. Introduction

Casimir’s discovery [1] that two parallel uncharged ideal-metal planes attract each other marked the beginning of active research and led to new concepts and far-reaching implications in both fundamental and applied physics (see, e.g., the monographs [2,3,4,5]). The Casimir force results from zero-point and thermal (if the planes are kept at nonzero temperature) fluctuations of the electromagnetic field. On ideal-metal planes the tangential component of electric field and the normal component of magnetic induction vanish leading to the discrete oscillation frequencies. A finite difference between the infinite free energies in the presence and in the absence of the planes determines the finite Casimir free energy per unit area. The derivative of this free energy with respect to the separation between the planes with a minus sign is the Casimir force.

The Lifshitz theory generalized the Casimir force for two thick material plates (semispaces) in thermal equilibrium with the environment [6,7,8]. In this case, the electromagnetic response of the plate materials is given by the standard continuity boundary conditions formulated in terms of the frequency-dependent dielectric permittivity and (for magnetic plates) magnetic permeability. The Lifshitz theory treats the van der Waals force as a particular case of the Casimir force at separations of a few nanometers where one can neglect the effects of relativistic retardation. During the last two decades the Lifshitz theory was generalized for material bodies of arbitrary shape [9,10,11].

The interest in measuring the Casimir force was rekindled by the experiment of [12] (an unaccounted systematic error which was present in this experiment was corrected by its author in [13]). The beginning of the 21st century was marked by performing several high-precision experiments on measuring the Casimir force between metallic test bodies. These experiments were made by means of a micromechanical torsional oscillator [14,15,16,17,18,19] and an atomic force microscope [20,21,22,23,24,25,26] at the separation distances exceeding 150 nm. A comparison between the measurement data and theoretical predictions of the Lifshitz theory showed that these predictions are experimentally excluded if the electromagnetic response of metals (Au, Ni) at low frequencies is described by the well-established Drude model which takes the proper account of the relaxation properties of conduction electrons [14,15,16,17,18,19,20,21,22,23,24,25,26]. If, however, the response of metals at low frequencies is described by the dissipationless plasma model—a very good agreement between the measurement data and theoretical predictions was revealed [14,15,16,17,18,19,20,21,22,23,24,25,26].

For distances below 100 nm, a comparison between the Lifshitz theory and the measurement data demonstrated good agreement (see, e.g., [27,28,29,30]). Analysis made it apparent that the problem is related to the low-frequency contribution to the Casimir force, which is determined by conduction electrons [31,32,33]. At separations below 100 nm the major contribution to the Casimir force is given by the core electrons whereas with increasing separation the role of conduction electrons progressively increases. Thus, it is very surprising that the Drude model does not work at large separations because it provides a well-established description of collisions of conduction electrons which are responsible for the resistance of metals (Ohm’s law).

No less surprise is the fact that, for metals with perfect crystal lattices described by the Drude model, the Casimir entropy goes with vanishing temperature to the negative quantity which depends on the parameters of a system, such as the separation between the plates and the plasma frequency, i.e., the Nernst heat theorem is violated [34,35,36,37]. If the experimentally consistent plasma model is used, the Nernst heat theorem is satisfied [34,35,36,37] in spite of the fact that this model disregards the dissipation of conduction electrons, which plays an important role at low frequencies. To satisfy the Nernst heat theorem with the Drude model, it was suggested to take into account a nonzero residual relaxation at zero temperature, which exists for crystal lattices with defects [38,39,40]. It was noted, however, that the perfect crystal lattice is an equilibrium system with the nondegenerate ground state so that the Nernst heat theorem must be satisfied in this case [41]. Moreover, in equilibrium there must be no defects [42]. The unresolved problems of disagreement between the theoretical predictions of the Lifshitz theory and measurement data, on the one hand, and the requirements of thermodynamics, on the other hand, were named the Casimir puzzle [43,44,45].

During the last 20 years, many attempts to resolve the Casimir puzzle have been undertaken based on the assumptions that there might be some unaccounted systematic effects in the performed experiments or inaccuracies in the comparison between the measurement data and theoretical predictions (see [4,46,47,48] for review). These efforts, although they did not resolve the Casimir puzzle, have had a profound impact on future investigations of the problem. Specifically, it was underlined that, in the frequency region of the anomalous skin effect, the concept of the dielectric permittivity depending only on frequency used in the standard Lifshitz theory loses its meaning and one has to take into account the effects of spatial dispersion [42,49,50,51,52,53,54,55]. In doing so, the reflection coefficients entering the Lifshitz formula for the Casimir pressure are expressed via the nonlocal surface impedances [49,52]. This approach allowed some progress in resolution of thermodynamic part of the Casimir puzzle [53,54] but did not remove the contradiction between experiment and theory because for metallic test bodies corrections to the Casimir pressure due to spatial nonlocality in the region of the anomalous skin effect turned out to be too small [51,52].

To find a solution for both components of the Casimir puzzle, recently the phenomenological spatially nonlocal dielectric permittivities have been proposed [56,57,58], which almost coincide with the permittivity of the standard Drude model for the propagating waves satisfying the condition $k_{\perp }<\omega /c$ where $k_{\perp }$ is the magnitude of the wave vector projection on the plane of Casimir plates and $\omega$ is the frequency. The suggested permittivities, however, can deviate from the Drude model significantly for the evanescent waves which obey the inequality $k_{\perp }>\omega /c$ and, thus, are characterized by a pure imaginary $k_z$. Allowing for only real $k_z$, one can say that the evanescent waves are off the mass shell in the free space. It was shown that the Lifshitz theory using the permittivities of this kind is in agreement with the Nernst heat theorem [59] and with the measurement data of all high-precision experiments on measuring the Casimir force [56,57,58]. Thus, we can say that the nonlocal permittivities, proposed for metals in [56,57,58], are to some extent analogous to the permittivities of graphene, which are also spatially nonlocal but were derived on the basis of first principles of quantum electrodynamics at nonzero temperature using the formalism of polarization tensor [60,61]. It was shown that, for graphene described by these permittivities, there is no Casimir puzzle, i.e., the Lifshitz theory is consistent with both the experimental results [62,63] and the requirements of thermodynamics [64,65].

The proposed phenomenological permittivities [56,57,58] take into account the dissipation of conduction electrons in metals and leave almost unchanged the transverse magnetic (p) reflection coefficient as compared to the standard Drude model. As to the transverse electric (s) reflection coefficient, its value at zero frequency becomes nonzero for both propagating and evanescent waves as it holds if the plasma model is used (recall that for evanescent waves the transverse electric reflection coefficient calculated using the Drude model vanishes at zero frequency). Keeping in mind that the suggested nonlocal permittivities are of entirely phenomenological character, it is desirable to determine their possible role in some physical phenomena other than the Casimir effect.

The direct measurement of the s-type reflection coefficient in the range of evanescent waves cannot be performed because all conventional methods (for example, ellipsometry) are designed for propagating waves. Nevertheless, the evanescent fields are actively discussed in the literature in relation to the possibility to overcome the diffraction limit in optics [66]. Although the physics of surface plasmon polaritons [67] provides a considerable body of data related to the region of rather large $k_{\perp }$, it is restricted to only the transverse magnetic (p) reflection coefficient. The widely used techniques of total internal reflection and frustrated total internal reflection give the possibility to test the reflection properties in the region of $k_{\perp }$ only slightly exceeding $\omega /c$. This is connected to the fact that there are no transparent media with sufficiently large index of refraction (see the long-performed experiments [68,69,70]). The method of nano frustrated total internal reflection exploits the illumination of a nanoparticle of size $R\sim 1/k_{\perp }$ placed near the material surface under investigation. This approach is employed in the near-field optical microscopy, which allows exceeding of the standard resolution limit using the evanescent waves [66,71]. The near-field optical microscopes, however, are mostly employed in various technological applications [71] and are more sensitive to the p-polarized electromagnetic field [72].

In this paper, we suggest the Experimentum crucis, which can reliably select between different response functions of metals to the low-frequency electromagnetic field in the area of evanescent waves. To do so, we consider an oscillating magnetic dipole spaced at a distance of a few millimeters from a metallic plate. The electric field of this dipole is negligibly small as compared to the magnetic one. We obtain explicit expressions for the latter via the transverse electric (s) reflection coefficient of the plate without specifying its form. According to our results, the lateral field components are fully determined by the contribution of extremely evanescent waves $(k_{\perp }\gg \omega /c)$, whereas the contribution of propagating waves is negligibly small. The components of the magnetic field are calculated as functions of lateral separation from the dipole for different oscillation frequencies using the dielectric permittivities of metal described by the Drude model, plasma model, and the spatially nonlocal model of [56,57,58,59]. It is shown that the lateral field components, which are fully determined by reflections on the plate, strongly depend on the model of used dielectric permittivity. For example, the lateral field component computed using the Drude model is smaller by up to a factor of ${10}^4$ than that computed using the plasma model or the spatially nonlocal model of [56,57,58,59]. Thus, by measuring the field of oscillating magnetic dipole spaced near a metallic plate, one can probe the response function of metal in the range of evanescent waves.

The above results are used to propose the Experimentum crucis for the Casimir puzzle. For this purpose, we consider the Casimir pressure at large separations between the plates. It is demonstrated that the differences in theoretical predictions obtained using the Drude model, plasma model and the spatially nonlocal model of [56,57,58,59] are fully determined by different contributions from the evanescent waves to the transverse electric (s) reflection coefficient. Possible parameters of the experiment, which could determine the response function of metals to the extremely evanescent waves, are suggested. The role of this experiment not only for the Casimir physics, but for a wide range of topics in optics and condensed matter physics is discussed.

The brief presentation of the part of obtained results related to the lateral component of the field of magnetic dipole is published in the form of a letter in [73].

The paper is organized as follows. In Section 2, it is shown that the conflict between experiment and theory in the Casimir physics is determined by a contribution from the evanescent waves. Section 3 contains the derivation of the field of oscillating magnetic dipole spaced near a metallic plate. In Section 4, we compute the dipole field for different frequencies and find how the contribution from the evanescent waves depends on the response function of a metal. Section 5 suggests the Experimentum crucis for the Casimir puzzle. In Section 6 and Section 7, the reader will find a discussion and our conclusions. Appendix A and Appendix B contain some necessary details about the mathematical derivations.

2. Role of Evanescent Waves in the Conflict between Experiment and Theory in Casimir Physics

It has long been known that the Casimir pressure between two thick material plates (semispaces) maintained at separation a at temperature T in thermal equilibrium with the environment is given by the Lifshitz formula which can be written in two mathematically equivalent representations. The representation that has enjoyed the widest application is in terms of the pure imaginary discrete Matsubara frequencies, ${\omega }_l=i{\xi }_l=2\pi i{k}_{B}Tl/\hslash$ with $l=0,1,2,\dots$ [4,5,6,7,8]

$$P(a,T)=-\frac{k_{B}T}{\pi }\sum _{l=0}^{\infty }{\phantom{\sum }}^{\prime }{\int }_0^{\infty }d{k}_{\perp }{q}_l{k}_{\perp }\sum _{\alpha }\frac{r_{\alpha }^2(i{\xi }_l,k_{\perp })e^{-2a{q}_l}}{1-r_{\alpha }^2(i{\xi }_l,k_{\perp })e^{-2a{q}_l}},$$

(1)

where the magnitude of the lateral wave vector component $k_{\perp }={(k_x^2+k_y^2)}^{1/2}$ was already defined in Section 1, $q_l={(k_{\perp }^2+{\xi }_l^2/c^2)}^{1/2}$, the prime on the summation sign in l divides the term with $l=0$ by 2, $k_B$ is the Boltzmann constant, and the sum in $\alpha$ is over the transverse magnetic (TM or p) and transverse electric (TE or s) polarizations of the electromagnetic field. The respective reflection coefficients are given by:

$$r_{\mathrm{TM}}(i{\xi }_l,k_{\perp })=\frac{{\epsilon }_l{q}_l-p_l}{{\epsilon }_l{q}_l+p_l},r_{\mathrm{TE}}(i{\xi }_l,k_{\perp })=\frac{q_l-p_l}{q_l+p_l},$$

(2)

where ${\epsilon }_l\equiv \epsilon \left(i{\xi }_l\right)$ is the dielectric permittivity of the plates calculated at the Matsubara frequencies and $p_l=p_l\left(k_{\perp }\right)={(k_{\perp }^2+{\epsilon }_l{\xi }_l^2/c^2)}^{1/2}$. The signs of the coefficients (2) are chosen in such a way that in the limiting case of ideal metal planes $r_{\mathrm{TM}}=1$ and $r_{\mathrm{TE}}=-1$.

Another representation of the Lifshitz formula is in terms or real frequencies [4,5,6,7]. It expresses the Casimir pressure as the sum of contributions from the propagating and evanescent waves,

$$P(a,T)=P^{\mathrm{prop}}(a,T)+P^{\mathrm{evan}}(a,T),$$

(3)

where

$$P^{\mathrm{prop}}(a,T)=-\frac{\hslash }{2{\pi }^2}{\int }_0^{\infty }d\omega coth\frac{\hslash \omega }{2k_{B}T}{\int }_0^{k_0}d{k}_{\perp }{k}_{\perp }\sum _{\alpha }\mathrm{Im}\left[q\frac{r_{\alpha }^2(\omega ,k_{\perp })e^{-2aq}}{1-r_{\alpha }^2(\omega ,k_{\perp })e^{-2aq}}\right]$$

(4)

and

$$P^{\mathrm{evan}}(a,T)=-\frac{\hslash }{2{\pi }^2}{\int }_0^{\infty }d\omega coth\frac{\hslash \omega }{2k_{B}T}{\int }_{k_0}^{\infty }d{k}_{\perp }{k}_{\perp }q\sum _{\alpha }\mathrm{Im}\frac{r_{\alpha }^2(\omega ,k_{\perp })e^{-2aq}}{1-r_{\alpha }^2(\omega ,k_{\perp })e^{-2aq}}.$$

(5)

Here, $q=q(\omega ,k_{\perp })={(k_{\perp }^2-k_0^2)}^{1/2}$, $k_0=\omega /c$ and the reflection coefficients (2) with $p=p(\omega ,k_{\perp })={[k_{\perp }^2-\epsilon \left(\omega \right)k_0^2]}^{1/2}$ can be transformed into the familiar Fresnel coefficients [74]

$$r_{\mathrm{TM}}(\omega ,k_{\perp })=\frac{\epsilon \left(\omega \right)q-p}{\epsilon \left(\omega \right)q+p}=\frac{\epsilon \left(\omega \right)\tilde{q}-\tilde{p}}{\epsilon \left(\omega \right)\tilde{q}+\tilde{p}},r_{\mathrm{TE}}(\omega ,k_{\perp })=\frac{q-p}{q+p}=\frac{\tilde{q}-\tilde{p}}{\tilde{q}+\tilde{p}},$$

(6)

where

$$\tilde{q}=\tilde{q}(\omega ,k_{\perp })={(k_0^2-k_{\perp }^2)}^{1/2},\tilde{p}=\tilde{p}(\omega ,k_{\perp })={[\epsilon \left(\omega \right)k_0^2-k_{\perp }^2]}^{1/2}.$$

(7)

Note that $\tilde{q}=iq$ and $\tilde{p}=ip$. Because of this, Equation (4), expressing the contribution of propagating waves in the Casimir pressure, contains the rapidly oscillating function $exp\left(2ia\tilde{q}\right)$ and is not convenient for numerical computations.The contribution of evanescent waves (5) does not have this disadvantage (different aspects of evanescent waves with respect to the Casimir force are considered in [31,32,75,76,77]).

The problems arising in the Casimir physics become more pronounced in the limit of large separations (high temperatures) satisfying the condition $T\gg \hslash c/\left(2a{k}_B\right)$. In fact, at room temperature $T=300$K this limit occurs at separations exceeding $6\mathsf{\mu }$m. In the case of large separations, (1) and (4), (5) become much simplified. Thus, in (1) the total result is given by the zero-frequency term with $l=0$ along, whereas all terms with $l⩾1$ are exponentially small

$$P(a,T)=-\frac{k_{B}T}{2\pi }{\int }_0^{\infty }d{k}_{\perp }{k}_{\perp }^2\sum _{\alpha }\frac{r_{\alpha }^2(0,k_{\perp })e^{-2a{k}_{\perp }}}{1-r_{\alpha }^2(0,k_{\perp })e^{-2a{k}_{\perp }}}.$$

(8)

The condition of large separations can be identically rewritten in the form $\hslash {\omega }_c\ll 2k_{B}T$, where ${\omega }_c=c/\left(2a\right)$ is the characteristic frequency giving the major contribution to the Casimir pressure. Because of this, in the limiting case of large separations one can use the inequality $\hslash \omega \ll 2k_{B}T$ and replace $coth(\hslash \omega /2k_{B}T)$ in (4) and (5) with the first expansion term in powers of the small parameter

$$coth\frac{\hslash \omega }{2k_{B}T}\approx \frac{2k_{B}T}{\hslash \omega }.$$

(9)

Then, (4) and (5) take the form:

$$P^{\mathrm{prop}}(a,T)=\frac{k_{B}T}{{\pi }^2}{\int }_0^{\infty }\frac{d\omega }{\omega }{\int }_0^{k_0}d{k}_{\perp }{k}_{\perp }\tilde{q}\sum _{\alpha }\mathrm{Re}\frac{r_{\alpha }^2(\omega ,k_{\perp })e^{2ia\tilde{q}}}{1-r_{\alpha }^2(\omega ,k_{\perp })e^{2ia\tilde{q}}},$$

(10)

and

$$P^{\mathrm{evan}}(a,T)=-\frac{k_{B}T}{{\pi }^2}{\int }_0^{\infty }\frac{d\omega }{\omega }{\int }_{k_0}^{\infty }d{k}_{\perp }{k}_{\perp }q\sum _{\alpha }\mathrm{Im}\frac{r_{\alpha }^2(\omega ,k_{\perp })e^{-2aq}}{1-r_{\alpha }^2(\omega ,k_{\perp })e^{-2aq}}.$$

(11)

The quantity (8) can be easily calculated using the dielectric permittivities of the Drude and plasma models,

$${\epsilon }_D\left(\omega \right)=1-\frac{{\omega }_p^2}{\omega (\omega +i\gamma )},{\epsilon }_{pl}\left(\omega \right)=1-\frac{{\omega }_p^2}{{\omega }^2},$$

(12)

where ${\omega }_p$ is the plasma frequency and $\gamma$ is the relaxation parameter. Substituting (12) in (2), one obtains the values of the reflection coefficients at zero Matsubara frequency for the Drude and plasma models:

$$r_{D,\mathrm{TM}}(0,k_{\perp })=1,r_{D,\mathrm{TE}}(0,k_{\perp })=0$$

(13)

and

$$r_{pl,\mathrm{TM}}(0,k_{\perp })=1,r_{pl,\mathrm{TE}}(0,k_{\perp })=\frac{c{k}_{\perp }-\sqrt{c^2{k}_{\perp }^2+{\omega }_p^2}}{c{k}_{\perp }+\sqrt{c^2{k}_{\perp }^2+{\omega }_p^2}},$$

(14)

respectively.

Then, substituting (13) and (14) in (8), one finds the following different results [4]:

$$P_D(a,T)=-\frac{k_{B}T}{8\pi a^3}\zeta \left(3\right),P_{pl}(a,T)=-\frac{k_{B}T}{4\pi a^3}\zeta \left(3\right),$$

(15)

where $\zeta \left(z\right)$ is the Riemann zeta function. Note that differences between the theoretical predictions for the thermal Casimir force using the Drude and plasma models were discussed long ago in [78] and [79], respectively.

Now we consider what the relative role of the propagating and evanescent waves in the Casimir pressures is (15). Let us start with the pressures calculated using the Drude model. For the TE polarization of the electromagnetic field, this question was solved in [33,80] using (10) and (11). It was shown that

$$P_{D,\mathrm{TE}}^{\mathrm{prop}}(a,T)=-\frac{k_{B}T}{8\pi a^3}\zeta \left(3\right),P_{D,\mathrm{TE}}^{\mathrm{evan}}(a,T)=\frac{k_{B}T}{8\pi a^3}\zeta \left(3\right).$$

(16)

Thus, the contribution of evanescent waves leads to the repulsive Casimir force and cancels the contribution of propagating waves with the result $P_{D,\mathrm{TE}}=0$. As for the TM mode, numerical computations performed for the evanescent waves using (11) result in the attractive Casimir pressure whose magnitude is negligibly small as compared to $P_{D,\mathrm{TE}}^{\mathrm{evan}}$ in (16). Then, using the first equality in (15) for the total pressure, one can conclude that:

$$P_{D,\mathrm{TM}}^{\mathrm{prop}}(a,T)=-\frac{k_{B}T}{8\pi a^3}\zeta \left(3\right),P_{D,\mathrm{TM}}^{\mathrm{evan}}(a,T)=0.$$

(17)

We are coming now to the Casimir pressure calculated using the plasma model. It is given by the second equality in (15). The contributions of evanescent waves (11) to this result for both the TM and TE modes are equal to zero because the dielectric permittivity ${\epsilon }_{pl}\left(\omega \right)$ in (12) and the reflection coefficients in (6) are the real-valued functions. In regard to the propagating waves, the TM and TE modes contribute to (10) equally because at large separations the characteristic frequency ${\omega }_c$ goes to zero and the TM and TE reflection coefficients (16) go to 1 and −1, respectively, if the plasma model is used in calculations.

As a result, taking into account the second equality in (15), one obtains:

$$P_{pl,\mathrm{TE}}^{\mathrm{prop}}(a,T)=-\frac{k_{B}T}{8\pi a^3}\zeta \left(3\right),P_{pl,\mathrm{TE}}^{\mathrm{evan}}(a,T)=0$$

(18)

and

$$P_{pl,\mathrm{TM}}^{\mathrm{prop}}(a,T)=-\frac{k_{B}T}{8\pi a^3}\zeta \left(3\right),P_{pl,\mathrm{TM}}^{\mathrm{evan}}(a,T)=0.$$

(19)

From (16)–(19), we conclude that, at large separations between metallic plates, both the TM and TE modes make equal contributions to the Casimir pressures determined by the propagating waves irrespective of whether the Drude or the plasma model is used in calculations. As is seen from (17) and (19), the TM mode also makes equal (zeroth) contributions to the Casimir pressures computed using either the Drude or the plasma model.

Thus, according to (16) and (18), the heart of the problem is in the TE contribution to the Casimir pressure determined by the low-frequency evanescent waves. This contribution essentially depends on the model of dielectric permittivity used. However, as discussed in Section 1, the required experimental data concerning the dielectric response of metal to the evanescent waves are few.

Before proceeding to the proposed experiment which could supply us with these data, we briefly dwell on the phenomenological spatially nonlocal dielectric permittivity suggested in [56,57,58,59]. This permittivity combines the merits of the Drude model by taking into account the dissipation of conduction electrons and of the plasma model by bringing the Lifshitz theory in agreement with experiments on measuring the Casimir force and with the requirements of thermodynamics.

In the spatially nonlocal case it is convenient to express the reflection coefficients in terms of the surface impedances $Z_{\alpha }(\omega ,k_{\perp })$. Thus, the TE reflection coefficient of our interest is given by [49,81]:

$$r_{\mathrm{TE}}(\omega ,k_{\perp })=\frac{q{Z}_{\mathrm{TE}}(\omega ,k_{\perp })+i{k}_0}{q{Z}_{\mathrm{TE}}(\omega ,k_{\perp })-i{k}_0},$$

(20)

where in the approximation of specular reflection the TE impedance is expressed via the transverse dielectric permittivity ${\epsilon }^{\mathrm{Tr}}(\omega ,k)$ as [49,82]:

$$Z_{\mathrm{TE}}(\omega ,k_{\perp })=\frac{i{k}_0}{\pi }{\int }_{-\infty }^{\infty }\frac{d{k}_z}{k_0^2{\epsilon }^{\mathrm{Tr}}(\omega ,k)-k^2}.$$

(21)

Here, $k_z$ is the wave vector component perpendicular to the plate and $k^2=k_{\perp }^2+k_z^2$. Recall that in the presence of spatial dispersion the response of metals to perpendicular and parallel to k electric fields is described by the transverse—${\epsilon }^{\mathrm{Tr}}(\omega ,k)$—and longitudinal—${\epsilon }^{\mathrm{L}}(\omega ,k)$—dielectric permittivities [74,81]. In so doing, the TM impedance and respective TM reflection coefficient are expressed via both of them.

In [58], the following transverse dielectric permittivity was suggested to describe the response of metals to the low-frequency electromagnetic field:

$${\epsilon }^{\mathrm{Tr}}(\omega ,k)=1-\frac{{\omega }_p^2}{\omega (\omega +i\gamma )}\left(1+i\frac{v^{\mathrm{Tr}}k}{\omega }\right),$$

(22)

where $k=\left|k\right|$, the value of $v^{\mathrm{Tr}}=1.5v_{\mathrm{F}}$, and $v_{\mathrm{F}}$ is the Fermi velocity. This permittivity brings theoretical predictions of the Lifshitz theory in good agreement with the experimental data of all high-precision measurements of the Casimir force. In so doing, the theoretical predictions are scarcely affected by the form of ${\epsilon }^{\mathrm{L}}(\omega ,k)$.

The distinctive feature of the permittivity (22) is that for the propagating waves satisfying a condition $k_{\perp }<k_0$ it differs little from the standard Drude model in (12). This is because for the propagating waves the magnitude of an addition to unity in the parentheses of (22) becomes negligibly small:

$$\frac{v^{\mathrm{Tr}}k}{\omega }=\frac{v^{\mathrm{Tr}}}{c}\frac{k}{k_0}=\frac{v^{\mathrm{Tr}}}{c}\ll 1.$$

(23)

As to extremely evanescent waves for which $k_{\perp }\gg k_0$, the permittivity (22) may significantly deviate from the Drude model.

It should be noted that the permittivity (22) is of entirely phenomenological character and does not lay claim that it is generally applicable. Specifically, the imaginary part of ${\epsilon }^{\mathrm{Tr}}$ is positive under the condition $k<\gamma /v^{\mathrm{Tr}}$. For good metals, such as Au or Cu, this condition is satisfied for $a\sim 1/\left(2k\right)>v^{\mathrm{Tr}}/\left(2\gamma \right)$, i.e., at separations exceeding a few tens of nanometers (we recall that the high-precision experiments of [14,15,16,17,18,19,20,21,22,23,24,25,26] were performed at much larger separations).

Below, we consider the experimental test for the response of metals in the area of evanescent waves unrelated to the Casimir effect which may give additional information regarding the validity of dielectric functions (12) and (22) in this area.

3. Field of Oscillating Magnetic Dipole near a Metallic Plate

We consider the field of an oscillating magnetic dipole situated above a thick metallic plate and show that it bears a close analogy to the Casimir pressure at large separation between two metallic plates discussed in the previous section.

Let the magnetic moment of our dipole be directed along the z axis which is perpendicular to the surface of metallic plate situated in the $(x,y)$ plane (see Figure 1):

$$m=(0,0,m_0{e}^{-i{\omega }_{d}t}).$$

(24)

The dipole with the oscillation frequency ${\omega }_d$ is spaced in a vacuum at height h above the plate. It is assumed that h is much larger than the dipole size.

Let us consider first the electromagnetic field of the magnetic dipole (24) in free space, i.e., in the absence of a conducting plate. Under a condition that the wavelength ${\lambda }_d=2\pi c/{\omega }_d$ is much larger than the dipole size the solution of this problem is contained in [83] (§ 72, problem 1). All fields considered below depend on t as $exp(-i{\omega }_{d}t)$. The monochromatic components of the magnetic field can be represented in the form:

$$\begin{array}{ccc}& & H_x({\omega }_d,r)=-m_0\frac{xz}{r^2}\left(\frac{k_d^2}{r}+3i\frac{k_d}{r^2}-\frac{3}{r^3}\right)e^{i{k}_{d}r},\hfill \\ & & H_y({\omega }_d,r)=-m_0\frac{yz}{r^2}\left(\frac{k_d^2}{r}+3i\frac{k_d}{r^2}-\frac{3}{r^3}\right)e^{i{k}_{d}r},\hfill \\ & & H_z({\omega }_d,r)=m_0\left[\frac{k_d^2}{r}+i\frac{k_d}{r^2}-\frac{1}{r^3}-\frac{z^2}{r^2}\left(\frac{k_d^2}{r}+3i\frac{k_d}{r^2}-\frac{3}{r^3}\right)\right]e^{i{k}_{d}r},\hfill \end{array}$$

(25)

where the radius-vector $r=(x,y,z)$ is directed from the magnetic dipole to the observation point, $r=\left|r\right|$, $k_d={\omega }_d/c$, and the Gaussian system of units is used. In a similar way, the monochromatic components of the electric field are given by

$$E({\omega }_d,r)=i{m}_0{k}_d\left(i\frac{k_d}{r^2}-\frac{1}{r^3}\right)e^{i{k}_{d}r}\left(\begin{array}{c}\hfill y\\ \hfill -x\\ \hfill 0\end{array}\right).$$

(26)

Below, we consider the quasistationary case of low oscillation frequencies ${\omega }_d$ and large ${\lambda }_d\gg r$. In this case, the magnitudes of components of the electric field (26) are smaller than those of the magnetic field (25) by the factor of:

$$k_{d}r=\frac{{\omega }_{d}r}{c}=\frac{2\pi r}{{\lambda }_d}\ll 1.$$

(27)

Taking into account that in the configuration of suggested experiment $k_{d}r\lesssim {10}^{-9}$ (see Section 5), one can safely neglect by the electric field as compared to the magnetic one.

Below we also use the Fourier expansion of the field of magnetic dipole (25) in plane waves $exp\left(i{k}_{\perp }{r}_{\perp }\right)$ where $k_{\perp }=(k_x,k_y)$ and $r_{\perp }=(x,y)$,

$$H({\omega }_d,r)=\frac{1}{{\left(2\pi \right)}^2}\int d{k}_{\perp }{e}^{i{k}_{\perp }{r}_{\perp }}H({\omega }_d,k_{\perp },z).$$

(28)

It should be recalled that the third component of the wave vector, $k_z$, is not independent but is expressed via $k_x$ and $k_y$ by the dispersion relation $k_z^2\equiv {\tilde{q}}_d^2=k_d^2-k_{\perp }^2$, see the first equality in (7), following from the Maxwell equations.

The explicit expressions for the components of the Fourier transform $H({\omega }_d,k_{\perp },z)$ are (see the Appendix A where these expressions are proven):

$$\begin{array}{ccc}& & H_{x\left(y\right)}({\omega }_d,k_{\perp },z)=-2\pi i{m}_0{k}_{x\left(y\right)}\mathrm{sign}\left(z\right)e^{i{\tilde{q}}_d\left|z\right|},\hfill \\ & & H_z({\omega }_d,k_{\perp },z)=2\pi i{m}_0\frac{k_{\perp }^2}{{\tilde{q}}_d}{e}^{i{\tilde{q}}_d\left|z\right|}.\hfill \end{array}$$

(29)

Now we find the field of the magnetic dipole in the presence of a thick metallic plate (see Figure 1). We do not specify the explicit form of the reflection coefficients $r_{\alpha }({\omega }_d,k_{\perp })$ to take into account both cases of spatially local and nonlocal response of the plate to the electromagnetic field.

In fact in our case the reflected wave is fully determined by only the TE reflection coefficient $\alpha =\mathrm{TE}$. As was shown above, the electric field of our magnetic dipole is negligibly small in comparison with the magnetic one. At the same time, the magnetic field of the TM-polarized wave is perpendicular to the plane of incidence, i.e., parallel to the surface of metallic plate. Thus, it is not reflected from this plate.

The magnetic field of magnetic dipole in a vacuum in the domain above the metallic plate can be calculated most simply by the method of images [84,85,86]. As shown in the Appendix B, the same result can be obtained using the method of the Green tensor. To apply the method of images, we use the coordinate system illustrated in Figure 1 where the magnetic dipole is positioned at the point $x=y=0$, $z=h$ and the fictitious (image) dipole is in the point $x=y=0$, $z=-h$. The magnetic moment of the image dipole is in opposition to the real one and its magnitude depends on the reflectivity properties of the metallic plate. In the domain above the plate the resulting magnetic field is found as a superposition of the fields of real and image dipoles. Using (29), we find the Fourier transform of the resulting magnetic field in the presence of a plate:

$$\begin{array}{ccc}& & H_{x\left(y\right)}^{\left(p\right)}({\omega }_d,k_{\perp },z)=-2\pi i{m}_0{k}_{x\left(y\right)}\left[r_{\mathrm{TE}}({\omega }_d,k_{\perp })e^{i{\tilde{q}}_d(z+h)}+\mathrm{sign}(z-h)e^{i{\tilde{q}}_d|z-h|}\right],\hfill \\ & & H_z^{\left(p\right)}({\omega }_d,k_{\perp },z)=2\pi i{m}_0\frac{k_{\perp }^2}{{\tilde{q}}_d}\left[r_{\mathrm{TE}}({\omega }_d,k_{\perp })e^{i{\tilde{q}}_d(z+h)}+e^{i{\tilde{q}}_d|z-h|}\right],\hfill \end{array}$$

(30)

where the first terms on the right-hand side are related to the image dipole and the second to the real dipole.

The presence of only TE reflection coefficient in (30) is explained by the fact that the TE polarized field has a nonzero component of magnetic field perpendicular to the surface. Note that for the oscillating electric dipole the magnetic field is negligibly small, as compared to the electric one, and, vice versa, the TM polarized field has a nonzero component of the electric field perpendicular to the surface.

Now we substitute (30) into (28) and represent the total magnetic field above the plate in the form:

$$H^{\left(p\right)}({\omega }_d,r)=H^{\left(R\right)}({\omega }_d,r)+H({\omega }_d,r).$$

(31)

Here, $H({\omega }_d,r)$ is the monochromatic field (25) of real magnetic dipole where z should be replaced with $z-h$ and $H^{\left(R\right)}({\omega }_d,r)$ is the monochromatic field of the image dipole given by:

$$\begin{array}{ccc}& & H_{x\left(y\right)}^{\left(R\right)}({\omega }_d,r)=-\frac{i}{2\pi }{m}_0\int d{k}_{\perp }{r}_{\mathrm{TE}}({\omega }_d,k_{\perp })k_{x\left(y\right)}{e}^{i[k_{\perp }{r}_{\perp }+{\tilde{q}}_d(z+h)]},\hfill \\ & & H_z^{\left(R\right)}({\omega }_d,r)=\frac{i}{2\pi }{m}_0\int d{k}_{\perp }{r}_{\mathrm{TE}}({\omega }_d,k_{\perp })\frac{k_{\perp }^2}{{\tilde{q}}_d}{e}^{i[k_{\perp }{r}_{\perp }+{\tilde{q}}_d(z+h)]}.\hfill \end{array}$$

(32)

The integrals in (32) can be calculated as is described in Appendix A for the case of magnetic dipole in the absence of a plate. Thus, using the polar coordinates defined in (A2) and (A3), the x-component, $H_x^{\left(R\right)}$, is rewritten as:

$$H_x^{\left(R\right)}({\omega }_d,r)=-\frac{i}{2\pi }{m}_0{\int }_0^{\infty }d{k}_{\perp }{k}_{\perp }^2{r}_{\mathrm{TE}}({\omega }_d,k_{\perp })e^{i{\tilde{q}}_d(z+h)}{\int }_0^{2\pi }d\psi cos\psi e^{i{k}_{\perp }\rho cos(\psi -\phi )}.$$

(33)

Substituting here (A5), one finds:

$$H_x^{\left(R\right)}({\omega }_d,r)=\frac{m_{0}x}{\rho }{\int }_0^{\infty }d{k}_{\perp }{k}_{\perp }^2{J}_1\left(k_{\perp }\rho \right)r_{\mathrm{TE}}({\omega }_d,k_{\perp })e^{i{\tilde{q}}_d(z+h)}.$$

(34)

Likewise, the y-component in (32), $H_y^{\left(R\right)}$, is expressed as:

$$H_y^{\left(R\right)}({\omega }_d,r)=\frac{m_{0}y}{\rho }{\int }_0^{\infty }d{k}_{\perp }{k}_{\perp }^2{J}_1\left(k_{\perp }\rho \right)r_{\mathrm{TE}}({\omega }_d,k_{\perp })e^{i{\tilde{q}}_d(z+h)}.$$

(35)

Using the polar coordinates, for the z-component in (32) we obtain:

$$H_z^{\left(R\right)}({\omega }_d,r)=\frac{i{m}_0}{2\pi }{\int }_0^{\infty }d{k}_{\perp }\frac{k_{\perp }^3}{{\tilde{q}}_d}{r}_{\mathrm{TE}}({\omega }_d,k_{\perp })e^{i{\tilde{q}}_d(z+h)}{\int }_0^{2\pi }d\psi e^{i{k}_{\perp }\rho cos(\psi -\phi )}.$$

(36)

Then, applying (A12), we rewrite (36) as:

$$H_z^{\left(R\right)}({\omega }_d,r)=i{m}_0{\int }_0^{\infty }d{k}_{\perp }\frac{k_{\perp }^3{J}_0\left(k_{\perp }\rho \right)}{{\tilde{q}}_d}{r}_{\mathrm{TE}}({\omega }_d,k_{\perp })e^{i{\tilde{q}}_d(z+h)}.$$

(37)

Needless to say that both the propagating ($k_{\perp }<k_d$) and evanescent ($k_{\perp }>k_d$) waves contribute to (34), (35), and (37). However, in the region $r\ll {\lambda }_d$ under consideration here one can neglect by the phase in the exponential factors under the integrals. Then, the contribution of propagating waves in the reflected field, as compared to the contribution of evanescent ones, is suppressed by the factor ${\left(k_{d}h\right)}^3={(2\pi h/{\lambda }_d)}^3$. In the configuration of suggested experiment $h\sim r$ and ${\left(k_{d}h\right)}^3\sim {10}^{-27}$ (see Section 5). This means that the contribution of propagating waves to (34), (35), and (37) does not play any role and one can replace the lower integration limit in these equations with $k_d$. The results of numerical computations confirm this conclusion.

Finally, we write out the full components of the monochromatic field (31) of the magnetic dipole in the presence of metallic plate in a form convenient for computations:

$$\begin{array}{c}{H}_x^{\left(p\right)}({\omega }_d,r)=\frac{m_{0}x}{\rho }{\int }_{k_d}^{\infty }d{k}_{\perp }{k}_{\perp }^2{J}_1\left(k_{\perp }\rho \right)r_{\mathrm{TE}}({\omega }_d,k_{\perp })e^{-\sqrt{k_{\perp }^2-k_d^2}(z+h)}\\ -m_0\frac{x(z-h)}{r^2}\left(\frac{k_d^2}{r}+3i\frac{k_d}{r^2}-\frac{3}{r^3}\right)e^{i{k}_{d}r},\end{array}$$

(38)

$$\begin{array}{ccc}& & H_z^{\left(p\right)}({\omega }_d,r)=m_0{\int }_{k_d}^{\infty }d{k}_{\perp }\frac{k_{\perp }^3}{\sqrt{k_{\perp }^2-k_d^2}}{J}_0\left(k_{\perp }\rho \right)r_{\mathrm{TE}}({\omega }_d,k_{\perp })e^{-\sqrt{k_{\perp }^2-k_d^2}(z+h)}\hfill \\ & & +m_0\left[\frac{k_d^2}{r}+i\frac{k_d}{r^2}-\frac{1}{r^3}-\frac{{(z-h)}^2}{r^2}\left(\frac{k_d^2}{r}+3i\frac{k_d}{r^2}-\frac{3}{r^3}\right)\right]e^{i{k}_{d}r}.\hfill \end{array}$$

(39)

The expression for $H_y^{\left(p\right)}({\omega }_d,r)$ is similar to (38) where x is replaced with y.

In fact, (34), (35) and (37) have much in common with (10) and (11) presenting the contributions of propagating and evanescent waves to the Casimir pressure between two parallel metallic plates at large separations. At first glance (10) and (11) are quite different from the components of magnetic field (38) and (39) because the former are presented as the integrals over real frequencies whereas the latter are measured as the function of dipole oscillation frequency ${\omega }_d$. Moreover, (10) and (11) contain the second power of the factor $r_{\alpha }{e}^{-aq}$ and take into account multiple reflections on two surfaces whereas (38) and (39) describe the single reflection on one surface.

What is in common, however, is the role of the TE-polarized evanescent waves in both cases. The contribution of evanescent waves to the Casimir force at large separations is given by (11). In the case of magnetic field of an oscillating magnetic dipole located above metallic plate, the contribution of evanescent waves is given by the first terms in (38) and (39). By using the dimensionless variables $v=2a\sqrt{k_{\perp }^2-k_0^2}$ in (11) and $v=(z+h)\sqrt{k_{\perp }^2-k_d^2}$ in (38) and (39), one can see that the values of the Casimir force and of the dipole magnetic field are determined by one and the same integration domain $v\sim 1$. The lateral components of the field of magnetic dipole in the presence of metallic plate computed at $z=h$ are determined by the TE-polarized evanescent waves alone. If we replace the lower integration limit $k_d$ in (38) and (39) with 0, this does not influence the obtained results, i.e., the propagating waves do not contribute to them. According to Section 2, the contribution of propagating waves (10) to the Casimir pressure is common for both polarizations and for any model of dielectric permittivity used. The TM-polarized evanescent waves do not contribute to the Casimir pressure irrespective of the used dielectric function. Thus, again, only the contribution of TE-polarized evanescent waves eventually determines the value of the total pressure which is different for different models of the dielectric permittivity. This means that by measuring magnetic field of the magnetic dipole with fixed oscillation frequency spaced near a metallic plate one can test the response of metals to the TE-polarized evanescent waves in the wide region of real frequencies contributing to the magnetic field and simultaneously to the Casimir pressure. The obtained results can be used to resolve the Casimir puzzle.

4. Influence of the Response Function in the Evanescent Domain on the Field of Magnetic Dipole near Metallic Plate

Here, we perform numerical computations of the dipole field (38) and (39) for different oscillator frequencies and different models of the dielectric permittivity. Taking into account that an impact of metal on the dipole field is performed through the reflected field in (31), it is advantageous to make all computations at the dipole height $z=h$. At this height, the lateral component (38) of the dipole field coincides with that of the reflected field whereas the relative role of reflected field in z-component (39) is maximized.

As a metal of the plate, we consider Cu with the Drude parameters ${\omega }_p=1.12\times {10}^{16}$rad/s and ${\gamma }_p=1.38\times {10}^{13}$rad/s [87]. The oscillation frequencies of the magnetic dipole should be chosen so as to gain sufficient reflectance and simultaneously large enough deviation between theoretical predictions obtained using the Drude and plasma models.

To estimate the corresponding parameters, one can use the spatially local reflection coefficients (6). We introduce a new variable,

$$w=h{q}_d=h\sqrt{k_{\perp }^2-k_d^2},$$

(40)

and rewrite the TE reflection coefficient defined in (6) as:

$$r_{\mathrm{TE}}({\omega }_d,k_{\perp })=\frac{w-\sqrt{w^2-K\left({\omega }_d\right)}}{w+\sqrt{w^2-K\left({\omega }_d\right)}},$$

(41)

where

$$K\left({\omega }_d\right)=[\epsilon \left({\omega }_d\right)-1]\frac{{\omega }_d^2}{{\omega }_h^2}$$

(42)

and ${\omega }_h=c/h$.

The major contribution to $\left|K\right({\omega }_d\left)\right|$ computed in the region of small frequencies under consideration here using the dielectric permittivity of the Drude model is given by its imaginary part,

$$|K\left({\omega }_d\right)|=\frac{\gamma {\omega }_p^2{\omega }_d}{({\omega }_d^2+{\gamma }^2){\omega }_h^2}\approx \frac{{\omega }_p^2{\omega }_d}{\gamma {\omega }_h^2}.$$

(43)

If $\left|K\right({\omega }_d\left)\right|\gg 1$, the reflections on a metallic surface occur much as in the case when the plasma model is used. If $\left|K\right({\omega }_d\left)\right|$ is much less than unity, only a small fraction of the magnetic field is reflected from the surface. Thus, for our purposes, it would be best to choose

$$|K\left({\omega }_d\right)|\approx \frac{{\omega }_p^2{\omega }_d}{\gamma {\omega }_h^2}⩽1,{\omega }_d⩽\Omega \equiv \frac{\gamma {\omega }_h^2}{{\omega }_p^2}.$$

(44)

For the Drude parameters of Cu indicated above and the typical value of $h=1$cm (see Section 5), one obtains ${\Omega }_{\mathrm{Cu}}\approx 100$rad/s. Based on this result, the computations below are performed for the oscillation frequencies of magnetic dipole equal to 0.2, 2, 10, 20, and 100 rad/s.

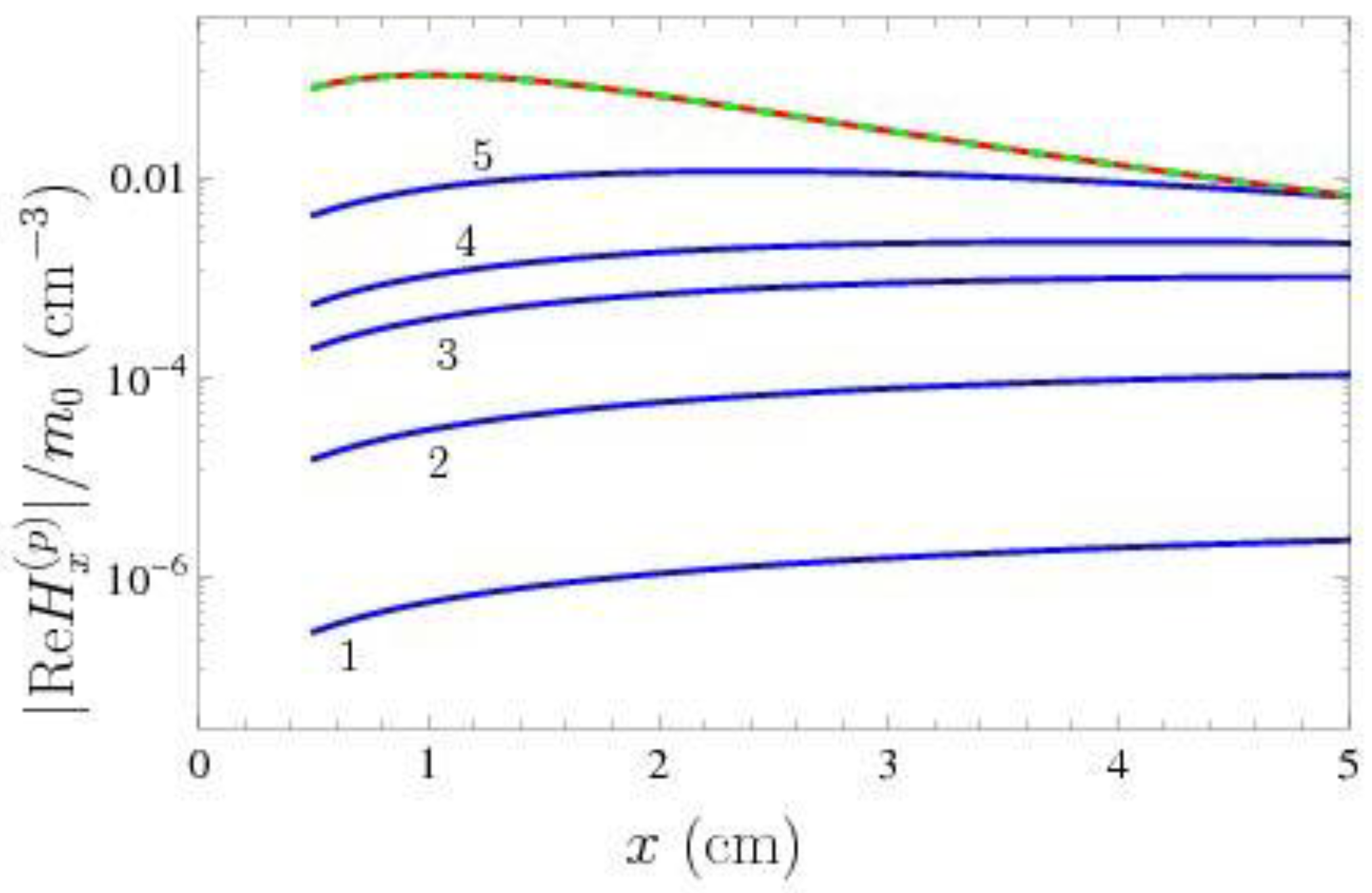
In Figure 2, we present the computational results for $|\mathrm{Re}{H}_x^{\left(p\right)}|$ normalized to $m_0$ as a function of separation from the magnetic dipole along the x-axis. In this case, one should put in (38) $r=(x,0,h)$ and $\rho =x$. We recall that all computations are performed at $z=h=1$cm. Thus, only the reflected field contributes to the result, i.e., $H_x^{\left(p\right)}$ = $H_x^{\left(R\right)}$. The solid lines labeled 1, 2, 3, 4, and 5 are computed using the Drude model and the Fresnel reflection coefficient $r_{\mathrm{TE}}$ defined in (6) for the dipole oscillation frequencies equal to 0.2, 2, 10, 20, and 100 rad/s, respectively. The top solid line is computed using the plasma model and the coefficient $r_{\mathrm{TE}}$ defined in (6). Under the condition (27) it does not depend on the value of $\omega$. The top dashed line overlapping with the solid one is computed using the spatially nonlocal dielectric permittivity (22) and the impedance reflection coefficient (20). The Fermi velocity $v_{\mathrm{F}}^{\mathrm{Cu}}=1.6\times {10}^6$m/s was determined under an assumption of the spherical Fermi surface. The top dashed line is also independent on the value of ${\omega }_d$ as well as in the case of the top solid line plotted for the plasma model.

From Figure 2, one can see that, as expected, the difference between the values of $|\mathrm{Re}{H}_x^{\left(p\right)}|$ computed using the Drude and plasma models increases with decreasing oscillation frequency of the magnetic dipole. This difference reaches several orders of magnitude and can be observed experimentally (see Section 5).

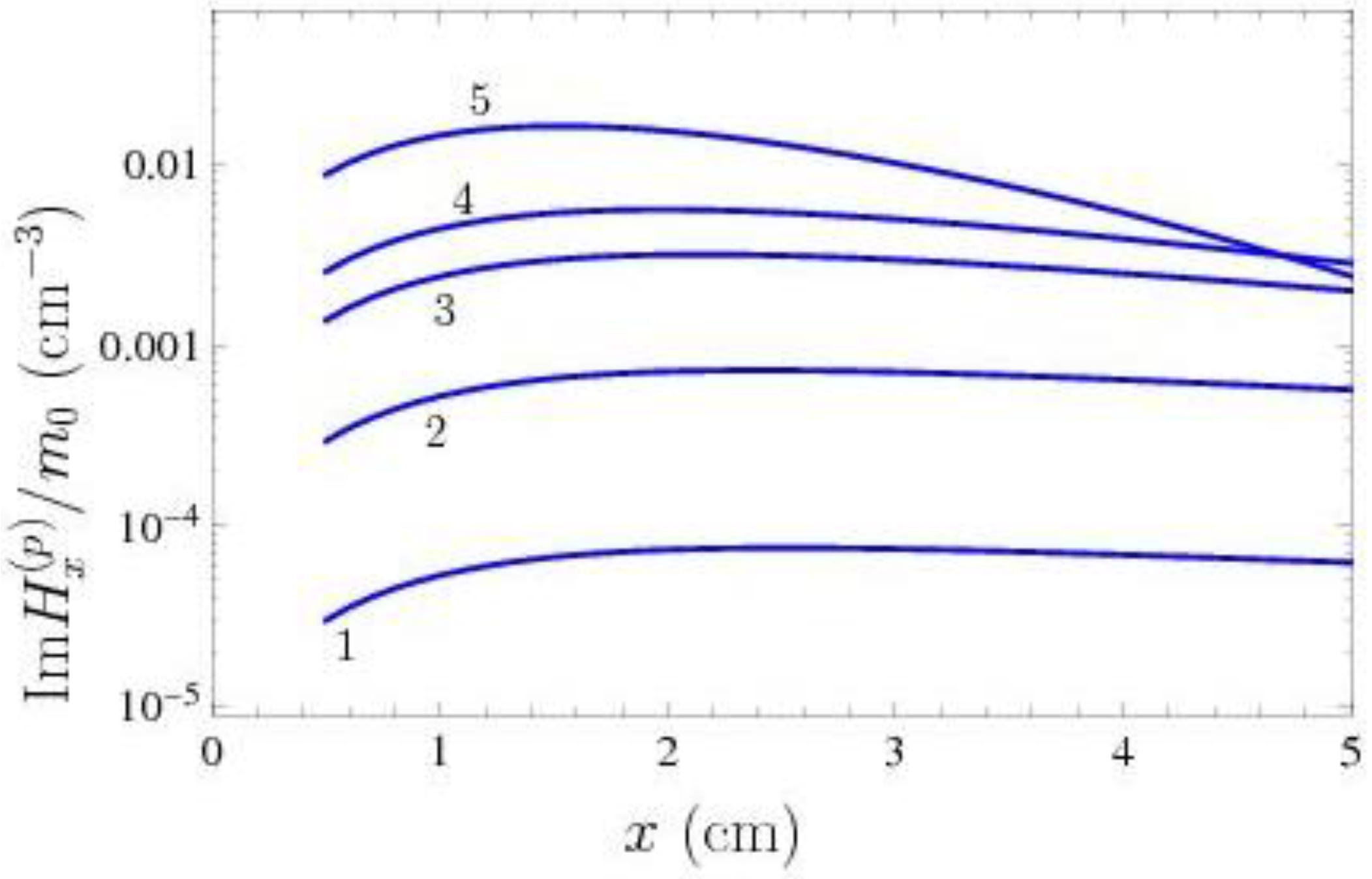
Similar results for the imaginary part of $H_x^{\left(p\right)}$ = $H_x^{\left(R\right)}$ normalized to $m_0$ are shown in Figure 3. Here, again, the lines labeled 1, 2, 3, 4, and 5 are computed by (38) using the Drude model for the dipole oscillation frequencies of 0.2, 2, 10, 20, and 100 rad/s, respectively. For the plasma model, the reflection coefficient $r_{\mathrm{TE}}$ in (38) is real so that the obtained result is $\mathrm{Im}{H}_x^{\left(p\right)}/m_0=0$. If the spatially nonlocal dielectric permittivity defined in (22) is used in computations, the obtained values of $\mathrm{Im}{H}_x^{\left(p\right)}/m_0$ are by ten orders of magnitudes smaller than those shown by the line labeled 1 in Figure 3.

By comparing Figure 3 with Figure 2, it is seen that $\mathrm{Im}{H}_x^{\left(p\right)}$ is much greater than $|\mathrm{Re}{H}_x^{\left(p\right)}|$ for each value of oscillation frequency if the Drude model is used in computations. If, however, the plasma or spatially nonlocal models are used, the magnitude of the real part, $|\mathrm{Re}{H}_x^{\left(p\right)}|$, is far in excess of $\mathrm{Im}{H}_x^{\left(p\right)}$ which is either equal to zero or negligibly small.

For completeness, we also consider the component $H_z^{\left(p\right)}$ given in (39) which contains both contributions of the source dipole field and its part reflected from the plate. The computational results for $|\mathrm{Re}{H}_z^{\left(p\right)}|$ at $z=h=1$cm normalized to $m_0$ as the function of separation from the magnetic dipole along the x-axis are presented in Figure 4. The solid line is obtained for ${\omega }_d=100$rad/s using the Drude model and another solid line overlapping with the short-dashed one, which does not depend on frequency, is found by means of the plasma model and the spatially nonlocal model (22). For comparison purposes, the long-dashed line shows the quantity $|\mathrm{Re}{H}_z|/m_0$ computed in the absence of metallic plate for a magnetic dipole in free space. It is also frequency-independent for the frequency region under consideration.

From Figure 4, it is seen that, at separations exceeding 2 cm, there is a considerable deviation between the theoretical predictions of the Drude model, on the one hand, and the plasma and our spatially nonlocal models, on the other hand. This deviation takes the largest value at $x=5$cm. It is seen also that at large separations the impact of metallic plate on theoretical predictions obtained using the Drude model is far less than can be obtained when the plasma or spatially non-local models are used. Because of this, the measurement of the z-component of magnetic field can be considered as complementary to the measurement of the lateral component (according to Figure 2 for ${\omega }_d=100$rad/s the largest deviation between different theoretical predictions for the lateral component occurs at $x=1$cm).

In the inset to Figure 4, we also plot the ratio of $\mathrm{Re}{H}_z^{\left(R\right)}$ to $\mathrm{Re}{H}_z$ as the function of separation where the first quantity characterizes the reflected field and the second one is for the dipole field in free space in the absence of metallic plate. The solid line is computed using the Drude model and another solid line overlapping with the dashed one is found by means of the plasma and spatially nonlocal models. According to the inset, the quantity $\mathrm{Re}{H}_z^{\left(R\right)}$ determined by the reflected field changes its sign with separation if it is computed using the plasma model and the spatially nonlocal model (22) but preserves its sign if the Drude model is used in computations. Some computational results for $\mathrm{Im}{H}_z$ are presented in Section 5.

It is also interesting to illustrate the dependence on separation of the total field magnitude:

$$\tilde{H}({\omega }_d,r)=\sqrt{{|H_x^{\left(p\right)}({\omega }_d,r)|}^2+{|H_z^{\left(p\right)}({\omega }_d,r)|}^2}.$$

(45)

In Figure 5, the quantity $\tilde{H}(\omega ,r)$ normalized to $m_0$ is shown as the function of separation from the magnetic dipole by the solid lines labeled 1 and 2, which are computed using the Drude model for the dipole oscillation frequencies of 0.2 and 100 rad/s, respectively. Another solid line overlapping with the dashed one is computed employing the plasma and the spatially nonlocal models. These lines do not depend on the value of oscillation frequency.

From Figure 5, it is seen that at separations of 2.67 and 4.85 cm the theoretical predictions of all three models coincide for the dipole oscillation frequency equal to 100 and 0.2 rad/s, respectively. At these separations, there are, however, significant deviations between the theoretical predictions of the Drude mode, on the one hand, and the plasma and spatially nonlocal models, on the other hand, if the oscillation frequencies of 0.2 and 100 rad/s are used, respectively.

In the inset to Figure 5, we plot as a function of separation the ratio of the reflected,

$$\tilde{H}{\phantom{H}}^{\left(R\right)}({\omega }_d,r)=\sqrt{{|H_x^{\left(R\right)}({\omega }_d,r)|}^2+{|H_z^{\left(R\right)}({\omega }_d,r)|}^2},$$

(46)

to the total (45) magnitudes of the field. The solid lines 1 and 2 are computed using the Drude model for the dipole oscillation frequencies of 0.2 and 100 rad/s, respectively, whereas another solid line overlapping with the dashed one using the plasma and the spatially nonlocal models. As is seen from the inset, for the oscillation frequency of 0.2 rad/s the quantity $\tilde{H}{\phantom{H}}^{\left(R\right)}/\tilde{H}$ is separation-independent. The largest difference between the theoretical predictions is reached at 5 cm for the dipole oscillation frequency of 100 rad/s.

The above computations are for a plate made of copper. The obtained results are, however, applicable to any metallic material with appropriately chosen frequencies of the magnetic dipole. Thus, for the plate made of B-doped Si in the metallic state used in the experiment of [88], it holds: ${\omega }_p^{\mathrm{Si}}=7.0\times {10}^{14}$rad/s and ${\gamma }_p^{\mathrm{Si}}=1.5\times {10}^{14}$rad/s. Then, using (44), one obtains ${\Omega }_{\mathrm{Si}}=2.75\times {10}^5$rad/s. Because of this, by choosing the dipole oscillation frequencies in the same proportion to ${\Omega }_{\mathrm{Si}}$ as above to ${\Omega }_{\mathrm{Cu}}$, i.e., ${\Omega }_{\mathrm{Si}}/500$, ${\Omega }_{\mathrm{Si}}/50$, ${\Omega }_{\mathrm{Si}}/10$, ${\Omega }_{\mathrm{Si}}/5$, and ${\Omega }_{\mathrm{Si}}$, one arrives to the same computational results as were obtained for a copper plate. This means that Figure 2, Figure 3, Figure 4 and Figure 5 plotted for the case of Cu plate are also valid for a B-doped Si plate if the oscillation frequencies of the magnetic dipole 0.2, 2, 10, 20, and 100 rad/s are replaced with $5.5\times {10}^2$, $5.5\times {10}^3$, $2.75\times {10}^4$, $5.5\times {10}^4$, $2.75\times {10}^5$rad/s, respectively.

5. Experimentum crucis for the Casimir Puzzle

The oscillating magnetic dipole with a magnetic moment (24) is generated by an alternating current $I_{0}exp(-i{\omega }_{d}t)$ through a circular turn or a small coil. In this case,

$$m_0=\frac{1}{c}\pi N{I}_0{R}^2,$$

(47)

where R is the turn radius and N is the number of turns. In accordance to Figure 1, the loop should be located in the plane $z=h$ with a center at the point $(0,0,h)$. The surface of the metallic plate is in the plane $z=0$. As shown in Section 3, if the magnetic field is measured at the points with coordinates $(x,0,h)$, i.e., along the line parallel to the x-axis at height h, its lateral component is completely determined by reflections from the surface of a metal [see (38)].

For a qualitative estimation of the coil parameters, we can consider the case of total reflection, $r_{\mathrm{TE}}=-1$, which is close to metal plate described by the plasma model. Then the Fourier transform of the x-component of the magnetic field is obtained from (30) where the second term does not contribute because $z=h$. As a result, under the condition (27), the x-component of the field is given by the last term on the right-hand side of (25) where one should replace z with $z+h=2h$,

$$H_x^{\left(p\right)}\left(x\right)=\frac{6m_{0}xh}{{(x^2+4h^2)}^{5/2}}=\frac{m_0}{h^3}\frac{6\tilde{x}}{{(4+{\tilde{x}}^2)}^{5/2}}.$$

(48)

here, $\tilde{x}=x/h$.

The scale factor $m_0/h^3$ in (48) determines the field magnitude. Thus, in order to have the greater field, one has to use larger $m_0$, i.e., the larger current, turn radius, and the number of turns, but smaller distance h between the magnetic dipole and the metallic plate. These conditions are somewhat contradictory. The calculations made in Section 3 assume that both h and the distance x between the source and the observation point are large in comparison with the dipole size. This means that, in order to decrease h, one should decrease the dipole size accordingly. For too-small coils, however, it would be difficult to ensure large currents and the number of turns.

In the literature, one can find examples of small coils manufactured by the methods of mini- [89] and micro- [90,91] technologies (micro-electromagnets for atom manipulation have long been created [92]). The coils of such kind contain of about 10 turns with a radius of 1 mm and have height of about 1 mm. These coils are able to support the current up to $I_0=3\times {10}^9$statA (this is equal to 1 A in SI). The respective magnetic dipole moment computed by (47) is equal to:

$$m_0=3.14\times {10}^{-2}\mathrm{e}\mathrm{r}\mathrm{g}/\mathrm{O}\mathrm{e}=3.14\times {10}^{-5}{\mathrm{A}\mathrm{m}}^2.$$

(49)

For estimation of the produced lateral field, we put $x=h=10$mm so that $\tilde{x}=1$. Then (48) leads to:

$$H_x^{\left(p\right)}=3.36\times {10}^{-3}\mathrm{O}\mathrm{e}=3.36\times {10}^{-7}\mathrm{T}=0.27\mathrm{A}/\mathrm{m}.$$

(50)

By using the value of $m_0$ from (49), one can see that the obtained field is in a very good agreement with the top line in Figure 2 at $x=1$cm which was computed using the plasma model and the spatially nonlocal model of [58].

Thus, the numerical data in Figure 2, Figure 3, Figure 4 and Figure 5 in combination with the value of $m_0$ in (49) can be used for the calculation of the magnetic field produced by the oscillating magnetic dipole at different separations and oscillation frequencies depending on the used model of electromagnetic response of metal to the low-frequency evanescent waves. As an example, if the Drude model is used and the dipole oscillation frequency is equal to 100 rad/s (see the line 5 in Figure 2), one has:

$$|\mathrm{Re}{H}_x^{\left(p\right)}|\lesssim 3.36\times {10}^{-4}\mathrm{O}\mathrm{e}=3.36\times {10}^{-8}\mathrm{T}=0.027\mathrm{A}/\mathrm{m},$$

(51)

i.e., by more than an order of magnitude smaller field than for the plasma model in the separation region from 1 to 2 cm. In this case, the parameter $k_{0}r$ defined in (27) is of the order of ${10}^{-9}$. The Drude model predicts all the more damping of the lateral magnetic field for smaller oscillation frequencies (see the lines 1–4 in Figure 2).

The obtained values of the magnetic field are quite measurable. Using different methods and laboratory techniques, the presently available limit for the magnetic field resolution is down to ${10}^{-13}$T [93,94,95]. This resolution is already reached [96,97] by means of traditional search coil magnetometers consisting of several micro induction coils [98,99]. The same sensitivity is provided by the SQUID magnetometers [100,101,102]. Some novel types of magnetometers using the magnetoresistance and magnetoelectric effects, as well as the optically pumped atomic magnetometers, possess an even higher resolution when measuring alternating magnetic fields (see [94,103] for a review). In the proposed experiment one should measure the magnetic fields of the order of tens of nT which are by several orders of magnitude larger than the resolution limit of currently available magnetic sensors. Therefore, the systematic effects, i.e., from the industrial or thermal noise, although deserve careful attention, should not be a crucial problem. Based on this, measuring the magnetic field of an oscillating magnetic dipole can be considered the Experimentum crucis, which can provide valuable information concerning the electromagnetic response of metals to the evanescent waves of low frequency. Depending on the magnitude of measured magnetic field, one will have the possibility to clearly discriminate between the description of metal in the range of evanescent waves by means of the Drude model, as the first option, or by means of the plasma model or spatially nonlocal model as the second option.

Direct demonstration of an inadequacy of the Drude model in the range of low-frequency evanescent waves by means of an experiment performed in the area of classical electrodynamic phenomena would be of great help to resolution of the Casimir puzzle discussed in Section 1 and Section 2. The Casimir effect is the quantum phenomenon dealing with the concept of a quantum vacuum. As indicated above, the high precision experiments of [14,15,16,17,18,19,20,21,22,23,24,25,26], measuring the Casimir force, have already demonstrated that the theoretical predictions of the Lifshitz theory obtained using the Drude model at separations exceeding 150 nm are excluded by the measurement data. An independent confirmation of a conclusion that the Drude model does not work in the area of evanescent waves would also be of prime importance for several divisions of optics and condensed matter physics dealing with evanescent waves.

Keeping in mind subsequent experiments, in addition to the computational results presented in Section 4, here we report the real and imaginary parts of $H_x^{\left(p\right)}$ and $H_z^{\left(p\right)}$ computed as the functions of dipole frequency for the above parameters of the experimental configuration, [i.e., for the value of $m_0$ defined in (49), $z=h=1$ cm, $y=0$] with different response functions of a metal and for several values of the separation x between the dipole and the point of observation. The computations are performed using (38) and (39) for a copper plate.

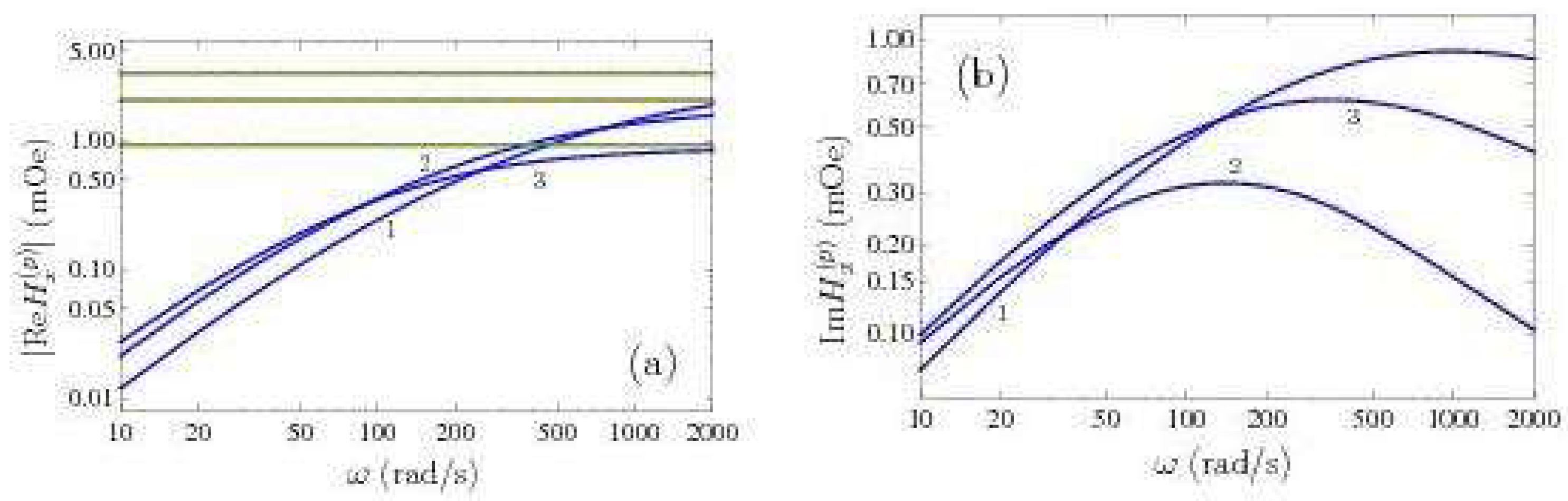
In Figure 6a, we plot the computational results for $|\mathrm{Re}{H}_x^{\left(p\right)}|$ = $|\mathrm{Re}{H}_x^{\left(R\right)}|$ as a function of dipole oscillation frequency. The solid lines labeled 1, 2, and 3 are computed by using the Drude model at separations from the magnetic dipole equal to x = 10, 20, and 30 mm, respectively. The computational results obtained using the plasma model and the spatially nonlocal model (22) at 10, 20, and 30 mm are shown by the three solid lines and overlapping with them dashed lines counted from the top to bottom, respectively. In Figure 6b, similar computational results obtained using the Drude model for $|\mathrm{Im}{H}_x^{\left(p\right)}|$ = $|\mathrm{Im}{H}_x^{\left(R\right)}|$ are presented with the same notations. If the plasma model is used in computations, one arrives to $\mathrm{Im}{H}_x^{\left(p\right)}=0$. As to the spatially nonlocal dielectric permittivity (22), it gives $\mathrm{Im}{H}_x^{\left(p\right)}$ that is smaller by the factor of ${10}^{-8}$ comparing to those shown in Figure 6b.

As one can see from Figure 6a, different theoretical predictions for $|\mathrm{Re}{H}_x^{\left(p\right)}|$ can differ significantly. For $x=10$ mm and ${\omega }_d=10$ rad/s the field computed using the plasma model is 280 times larger than that for the Drude model. For the Drude model, the magnitude of $\mathrm{Re}{H}_x^{\left(p\right)}$ increases with the frequency but stays constant for the plasma model. Although the difference between predictions of these models is reduced, for ${\omega }_d=100$ rad/s the predictions still differ by a factor of 14 which is sufficient for the experimental discrimination. As to Figure 6b, the values of $\mathrm{Im}{H}_x^{\left(p\right)}$ shown by any line computed using the Drude model are much outside the theoretical predictions based on the plasma and spatially nonlocal models where $\mathrm{Im}{H}_x^{\left(p\right)}$ vanishes or nearly vanishes.

In Figure 7a, using the same values of all experimental parameters, we plot the computational results for $|\mathrm{Re}{H}_z^{\left(p\right)}|$ as a function of the oscillation frequency of the magnetic dipole. The results obtained using the Drude and plasma (or the spatially nonlocal) models are shown by the three pairs of solid and solid-dashed lines, respectively. These pairs are labeled as 1, 2, and 3 for separations from the magnetic dipole equal to 30, 40, and 50 mm, respectively. The choice of separations, which is different from that in Figure 6, is caused by the fact that at larger separations one obtains greater differences between the z-components of magnetic field computed using different models of the dielectric permittivity (see Figure 4). The computational results for $|\mathrm{Im}{H}_z^{\left(p\right)}|$ obtained using the Drude model are shown in Figure 7b with the same notations. In common with above, the plasma model leads to $\mathrm{Im}{H}_z^{\left(p\right)}=0$ and the magnitudes of $\mathrm{Im}{H}_z^{\left(p\right)}$ computed using the spatially nonlocal model (22) are much below those shown in Figure 7b.

As is seen in Figure 7a, the theoretical predictions for $|\mathrm{Re}{H}_z^{\left(p\right)}|$ obtained using the Drude and plasma models are not so much different as for $|\mathrm{Re}{H}_x^{\left(p\right)}|$. This is caused by a contribution to the z-component of the dipole field in the absence of metallic plate. Thus, measuring the lateral component of the magnetic field is preferable for a clear discrimination between different models of the dielectric permittivity. It should be noted, however, that the imaginary part of the field can be determined by simultaneous measurements of the field magnitude and the phase shift. In doing so, if some nonzero phase shift relative to the magnetic moment is registered, this would be in favor of the Drude model. From Figure 7b, one can also see that $\mathrm{Im}{H}_z^{\left(p\right)}$, computed using the Drude model, possesses an interesting property by changing its sign from positive to negative at the dipole oscillation frequencies equal to 29.4, 58.9, and 162.8 rad/s when the measurements are performed at separations from the dipole of 50, 40, and 30 mm, respectively.

6. Discussion

In the foregoing, we have demonstrated that the longstanding problem of a disagreement between the theoretical predictions of fundamental Lifshitz theory and numerous high-precision experiments on measuring the Casimir force at separations exceeding 150 nm is determined by the role of TE-polarized low-frequency evanescent waves. The analysis of literature sources shows that the electromagnetic response of metals to the evanescent waves of this type has not yet been sufficiently explored experimentally. Taking into account that the predictions of the Lifshitz theory come into conflict with the measurement data when the low-frequency electromagnetic response of metals is described by the well-established Drude model taking into account the relaxation properties of conduction electrons, it is very desirable to independently verify whether or not this model is applicable in the range of low-frequency evanescent waves.

In this paper, we have derived an expression for the electromagnetic field of an oscillating magnetic dipole spaced above a thick metallic plate. According to our results obtained under the reasonable experimental conditions, the lateral components of magnetic field of this dipole are entirely determined by the TE-polarized evanescent waves, whereas the electric field turns out to be negligibly small. The derivation was performed both by the method of images and using the Green tensor of the boundary problem in the general case of a spatially nonlocal electromagnetic response of the plate metal with the coinciding results.

The real and imaginary parts of the components of magnetic field above the copper plate were computed by describing the electromagnetic response of copper using the dissipative Drude model, dissipationless plasma model and the spatially nonlocal phenomenological dielectric permittivity of [58] which takes into account the relaxation properties of conduction electrons and simultaneously brings the theoretical predictions of the Lifshitz theory in agreement with all high-precision experiments on measuring the Casimir force. It was shown that for the typical parameters of the magnetic dipole designed in the form of 1-mm coil the lateral components of magnetic field computed using the Drude model, as the first option, and the plasma model or the spatially nonlocal model of [58], as the second option, differ by up to several orders of magnitude depending on the oscillation frequency of the dipole. In doing so, the magnitudes of the field component remain quite measurable using the available laboratory techniques. Based on this, we have proposed an experiment which can independently either validate or disprove an applicability of the Drude model in the range of low-frequency TE-polarized evanescent waves.

The suggested experiment would elucidate the roots of the Casimir puzzle by making clear whether a disagreement between the theoretical predictions and the measurement data is caused by an inadequacy of the Drude model in the range of evanescent waves or by some other problems. Because of this, it could be called the Experimentum crucis. Based on the studies of the Casimir force in graphene systems, one could argue in favor of the inadequacy of the Drude model. The point is that the spatially nonlocal response of graphene was derived on the basis of first principles of quantum electrodynamics via the formalism of the polarization tensor [60,61]. As mentioned in Section 1, using the respective nonlocal dielectric functions, the theoretical predictions of the Lifshitz theory were shown to be in perfect agreement with the requirements of thermodynamics [64,65] and with experiments on measuring the Casimir force in graphene systems [62,63].

7. Conclusions

According to our results, the suggested experiment will be capable of clearly discriminating between the magnetic fields computed using the Drude and plasma models but not between the fields computed using the plasma model and the spatially nonlocal permittivity of [58]. The latter, in any case, does not claim a complete description of the electromagnetic response of metals but can be considered as an example that, through the spatial nonlocality, in the framework of the Lifshitz theory it is possible to reach an agreement with the requirements of thermodynamics and the measurement data of high-precision experiments having a regard for the relaxation properties of conduction electrons (see also [104], which considers other nonlocal permittivities with the same aim).

To conclude, the fundamental theoretical description of the response of metals to both the propagating and evanescent waves could be derived in the future using the methods of quantum field theory [105], as was already done for graphene. The first steps in this direction were made in [106]. In the meantime, the results of the proposed Experimentum crucis may not only shed light on the Casimir puzzle, but also find applications in a number of topics in optics and condensed matter physics which deal with evanescent waves including studies on surface plasmon polaritons, near-field optical microscopy, total internal reflection and many others.