Magnetized and Magnetically Charged Particles Motion around Regular Bardeen Black Hole in 4D Einstein Gauss–Bonnet Gravity
Abstract
1. Introduction
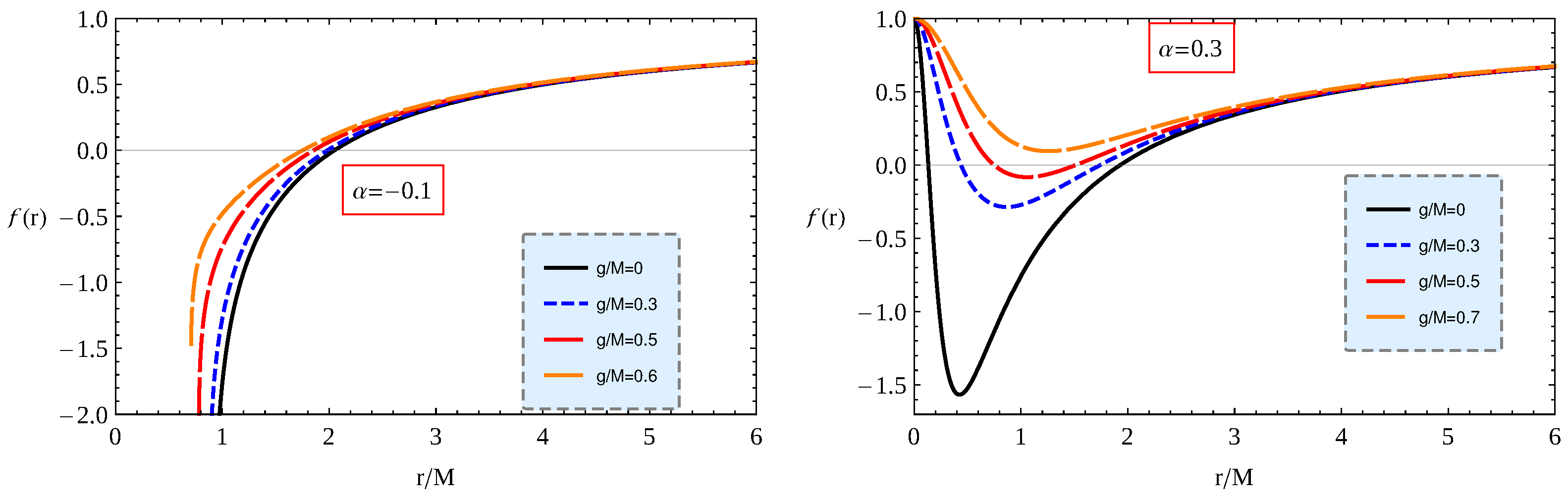
2. Regular Bardeen BH in 4D EGB Gravity
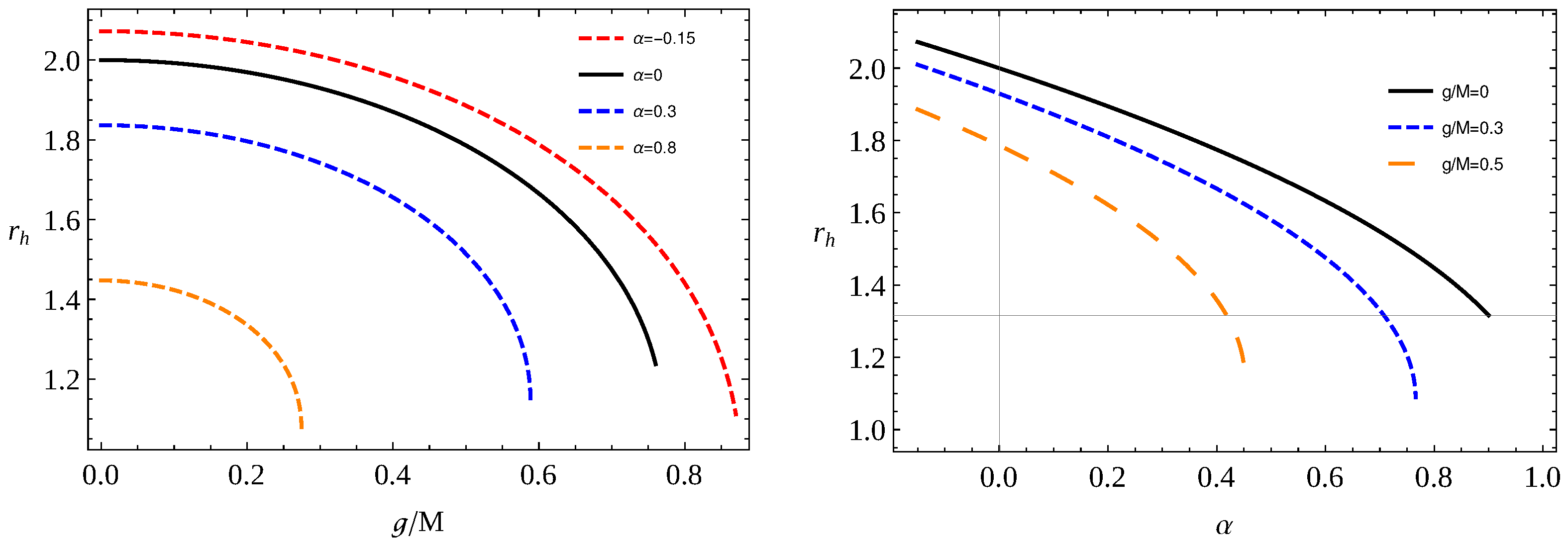
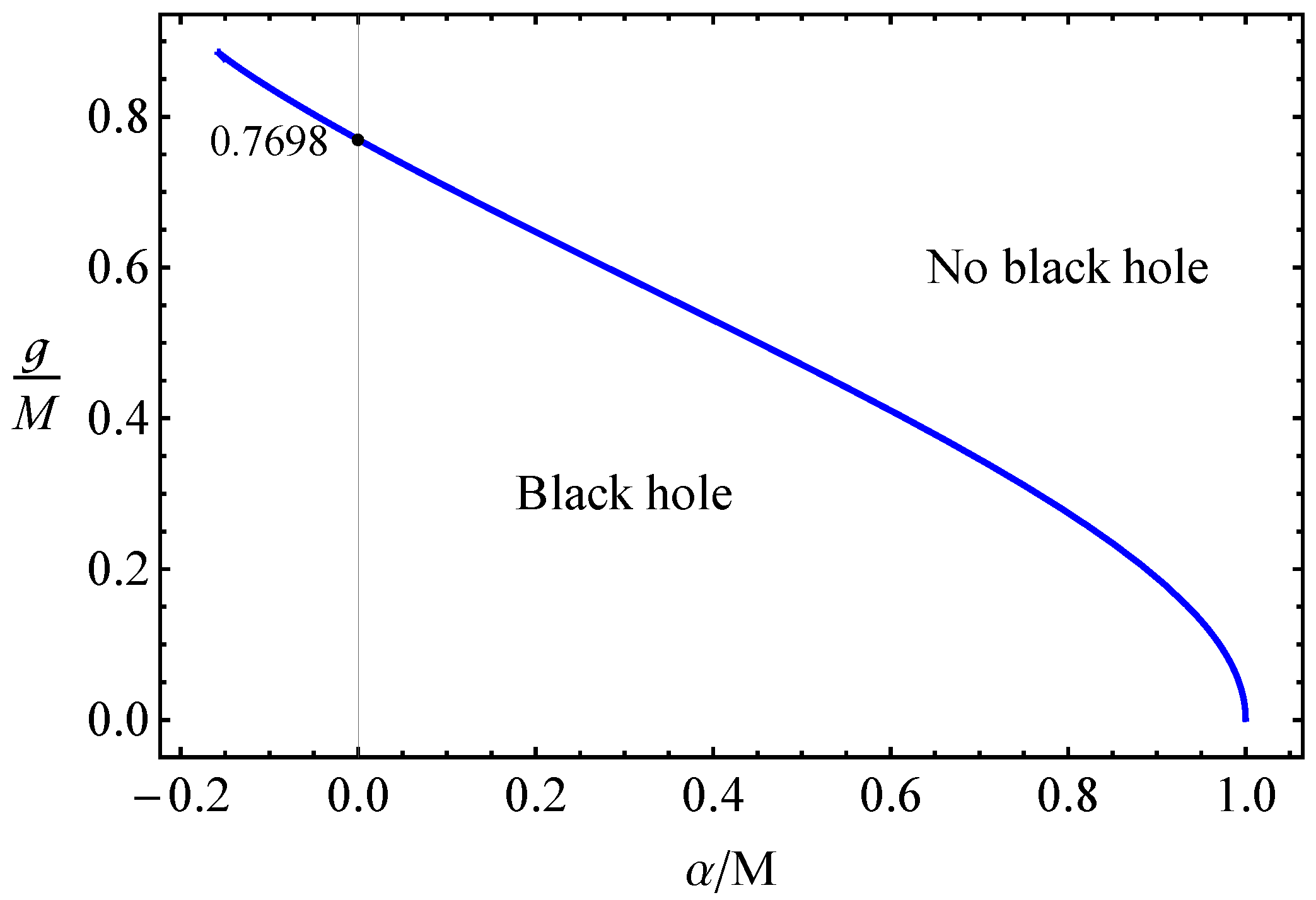
2.1. Event Horizon Structure of the Regular Bardeen BH in 4D-EGB Gravity
- (i)
- There are two (inner and outer) event horizons corresponding to the values of magnetic charge ;
- (ii)
- There is one event horizon corresponding to the value of magnetic charge and one has the extremely charged regular Bardeen BH;
- (iii)
- There is no event horizon corresponding to the values of magnetic charge, and one deals with a no-horizon strong gravitating regular object.
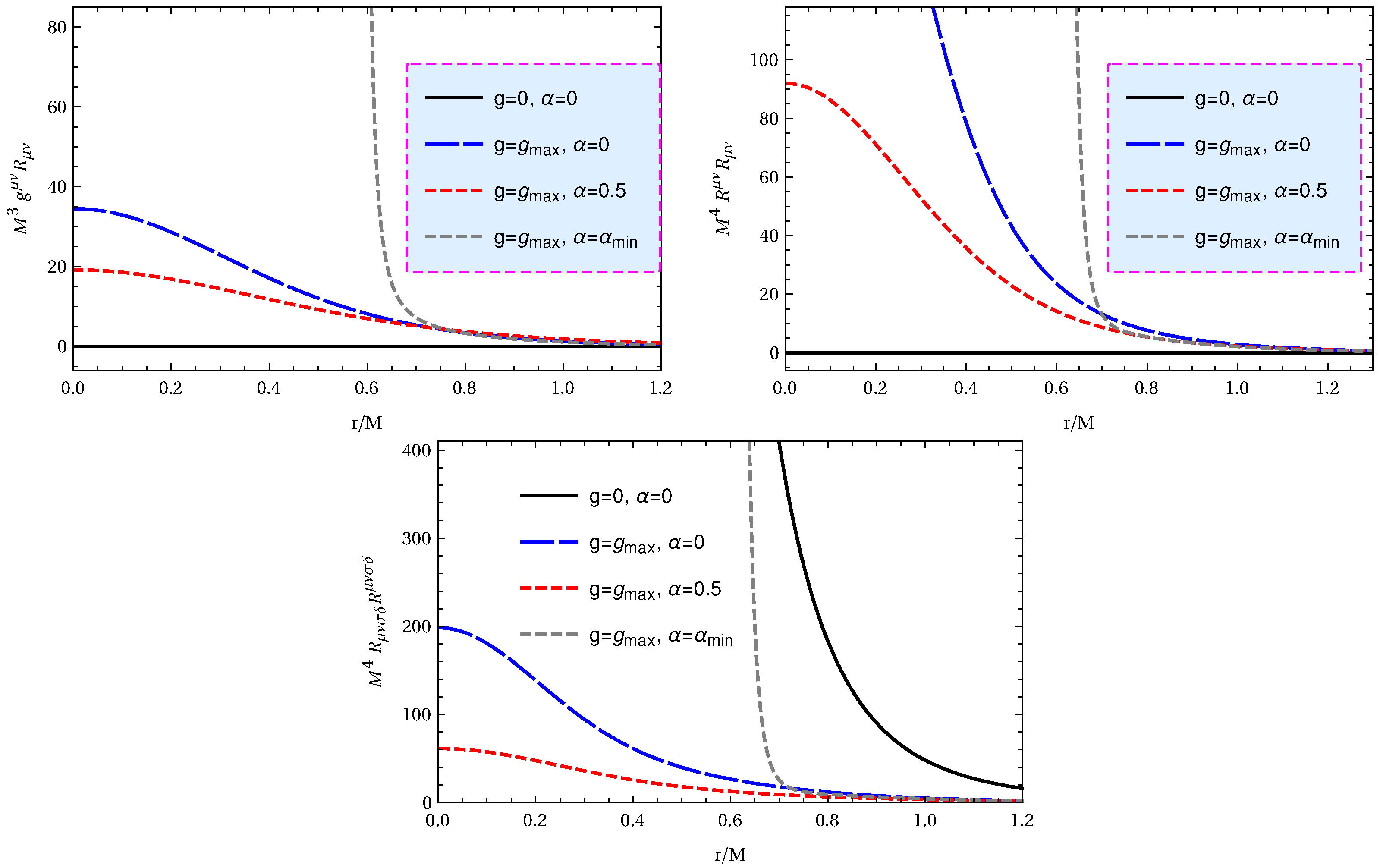
2.2. Curvature Scalars
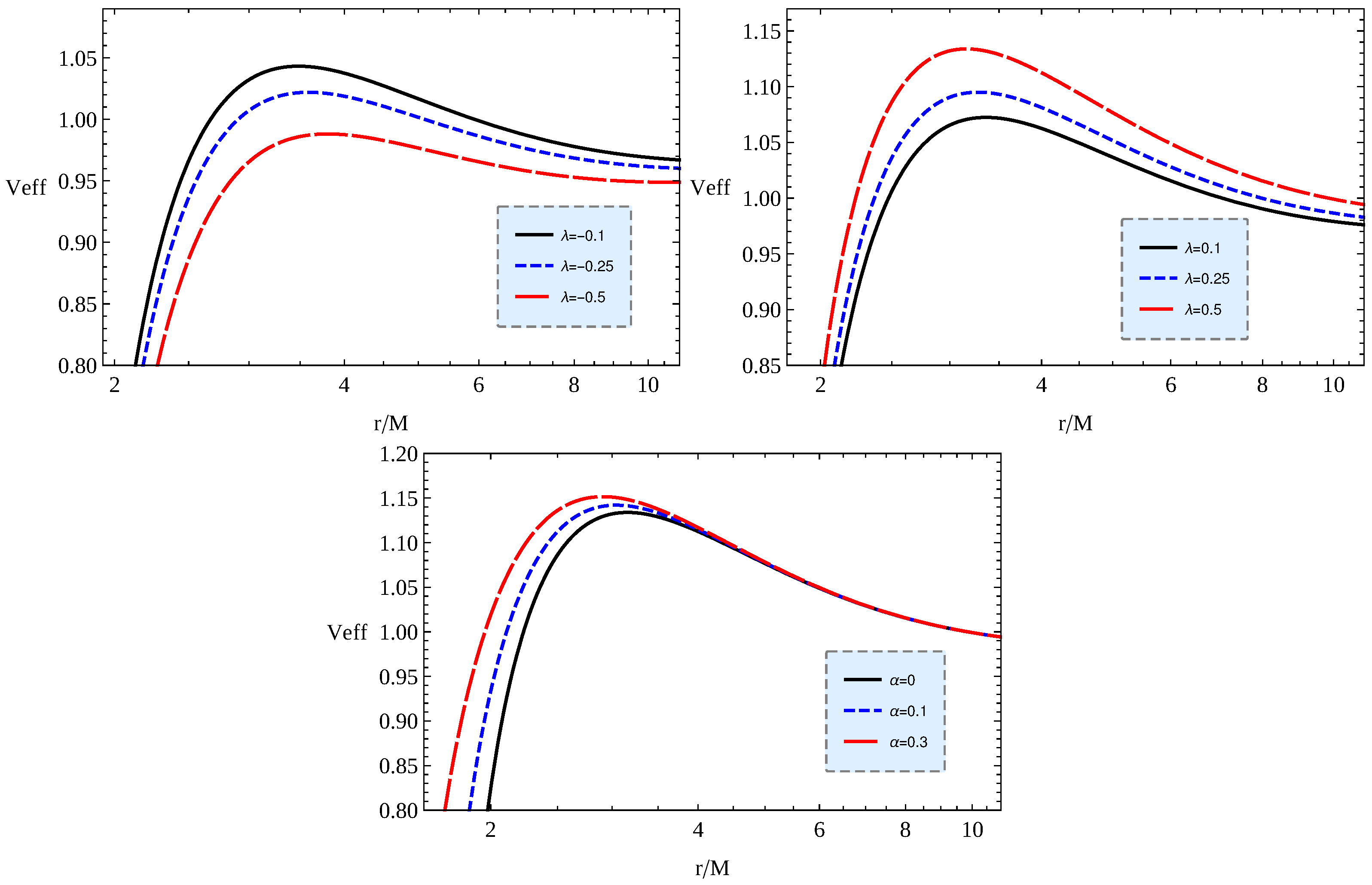
3. Magnetized Particles Motion
3.1. Equation of Motion
- We assume the direction of the magnetic dipole moment is parallel to the equatorial plane and the magnetic field. In fact, the direction of the magnetic dipole moment of the magnetized particle should be along the direction of the magnetic field lines in order to provide equilibrium in interaction with maximum energy.
- The first assumption implies that the magnetic dipole has only radial components .
- For simplicity, the motion could be considered in the proper observer frame, which is convenient to avoid a relative motion problem.
- Again, for simplicity of calculations, the value of dipole moment magnitude is assumed to be constant.
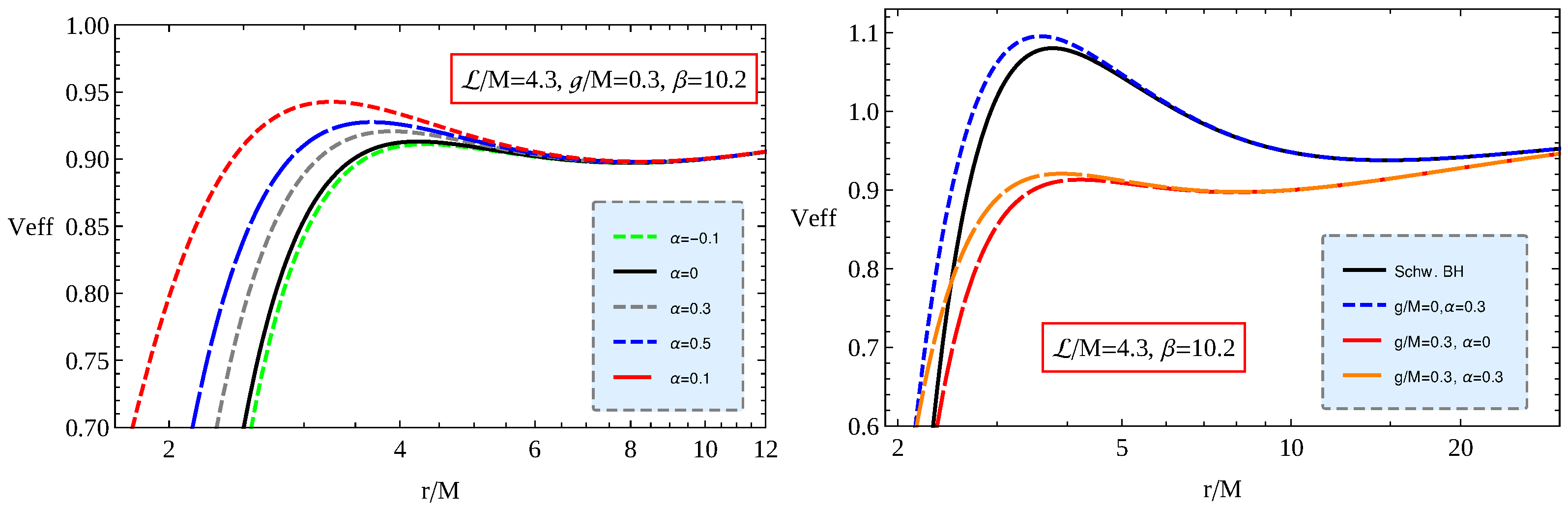
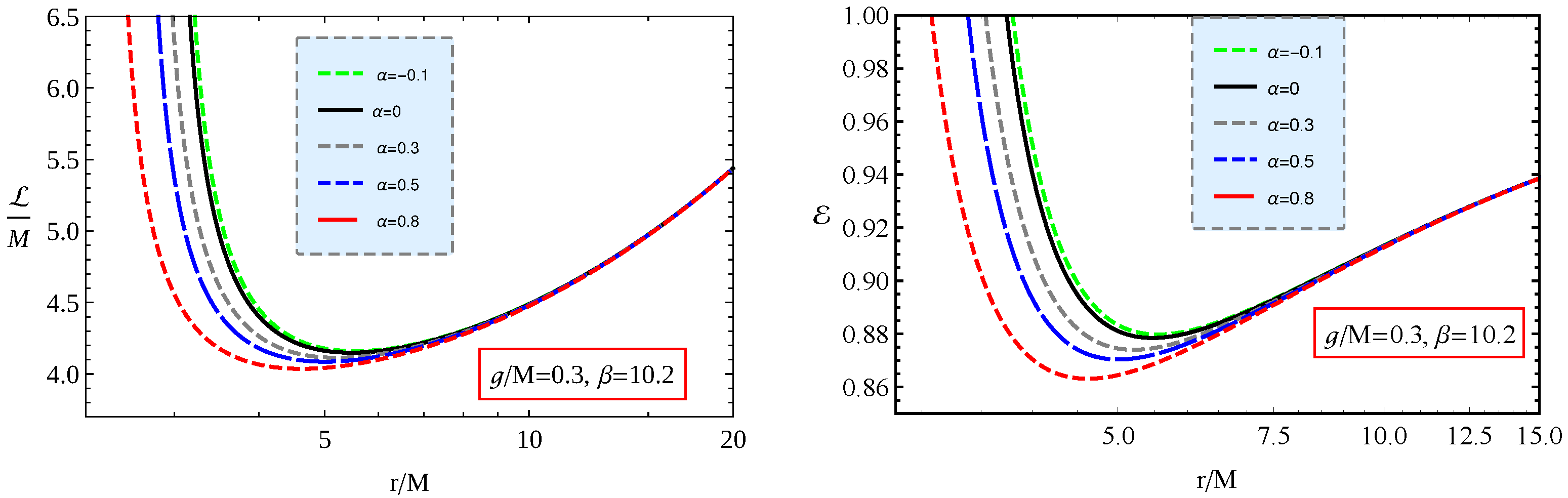
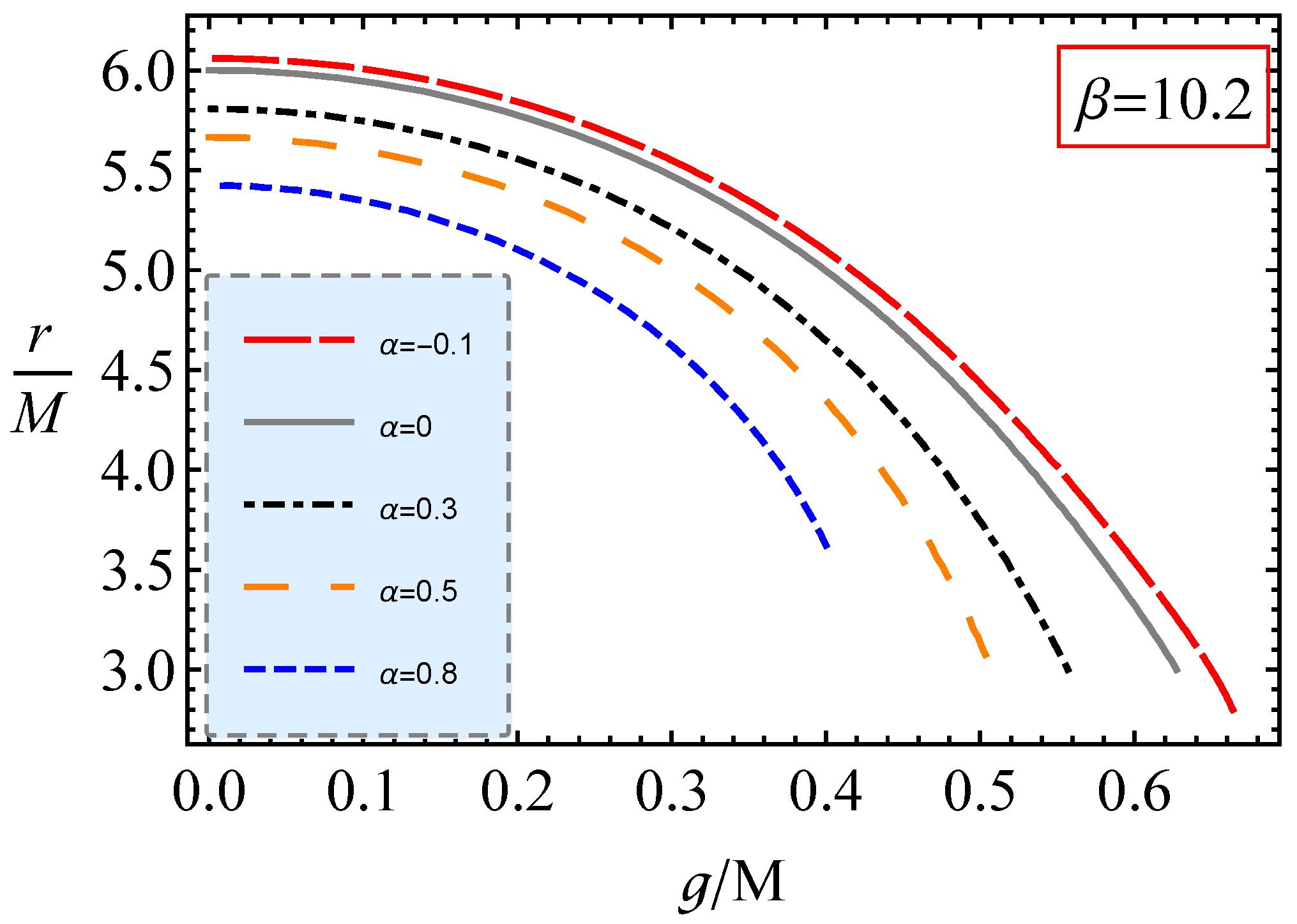
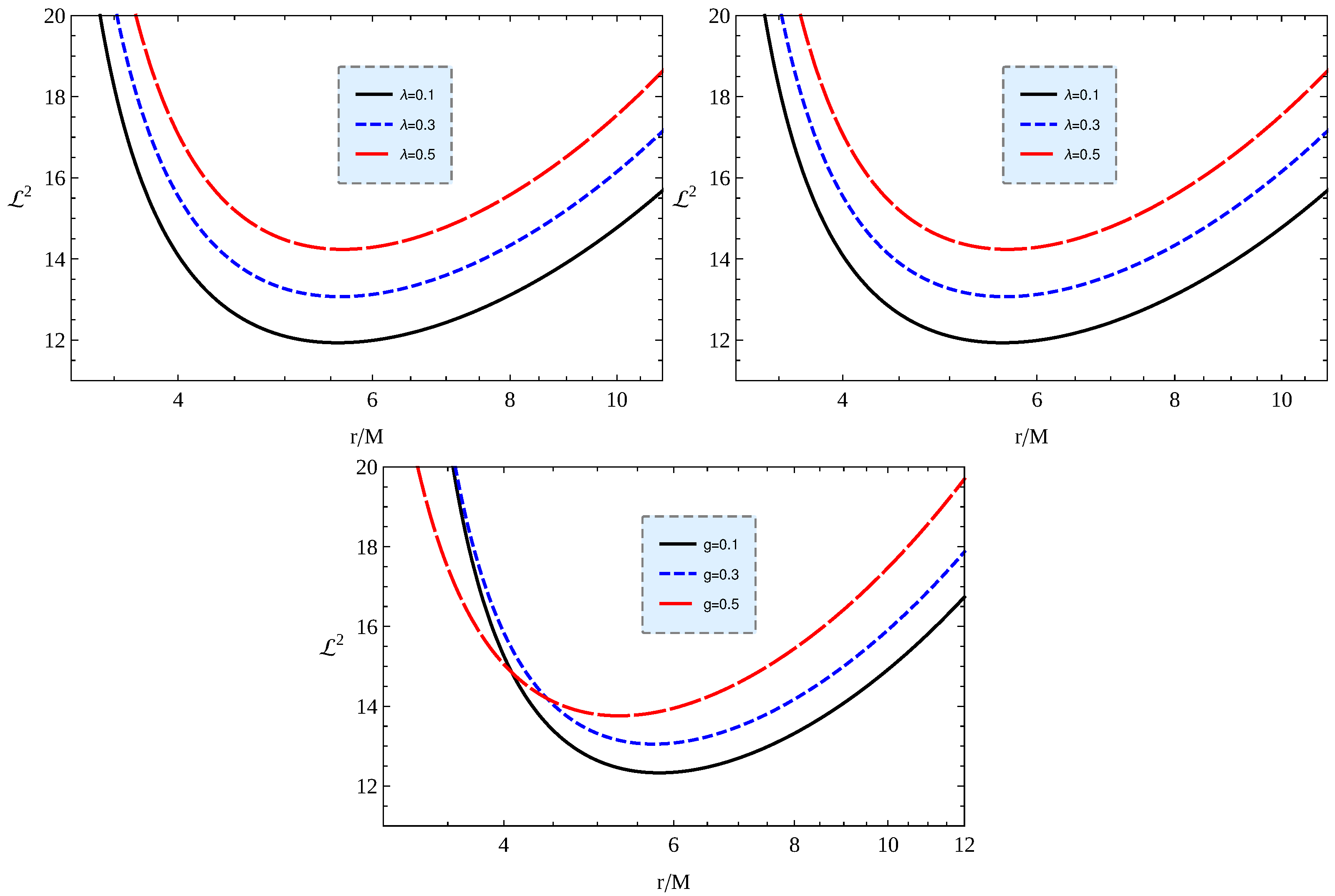
3.2. Stable Circular Orbits
4. Magnetically Charged Particles Motion
5. Particles Collisions near Bardeen BH in 4D EGB Gravity
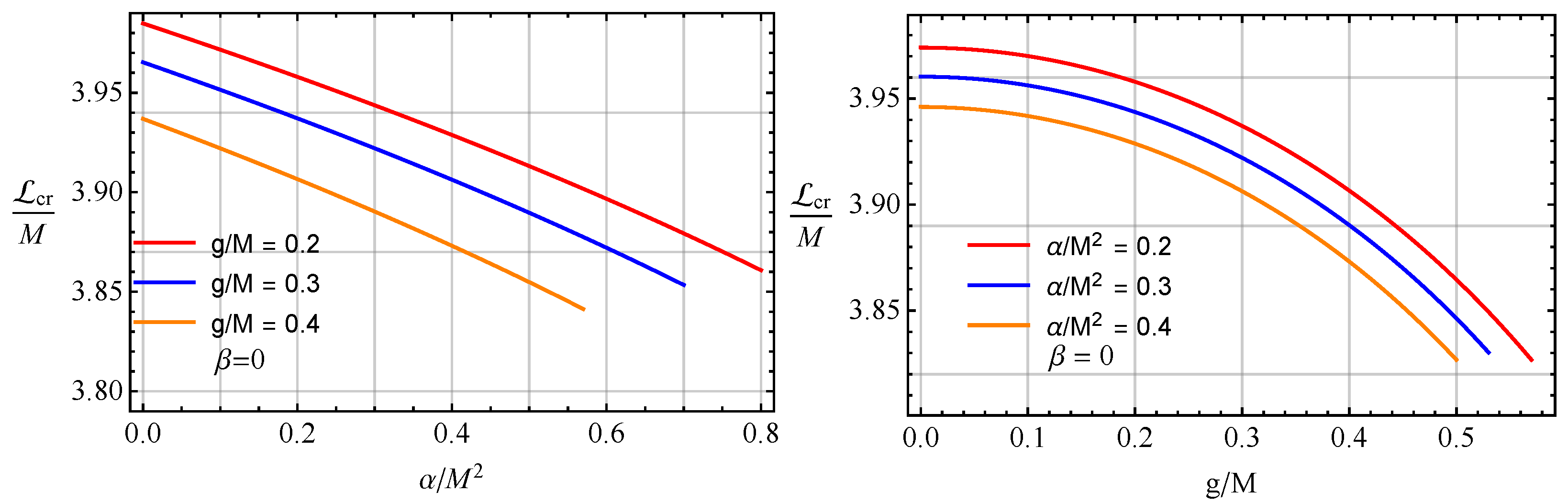
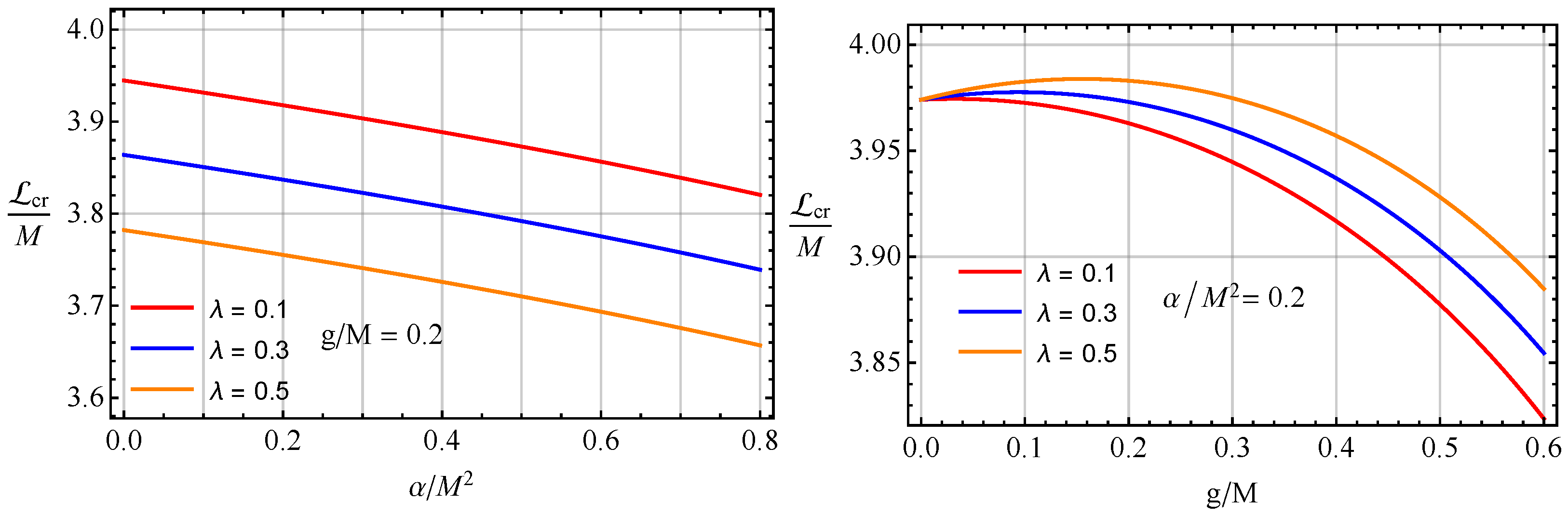
5.1. Critic Angular Momentum
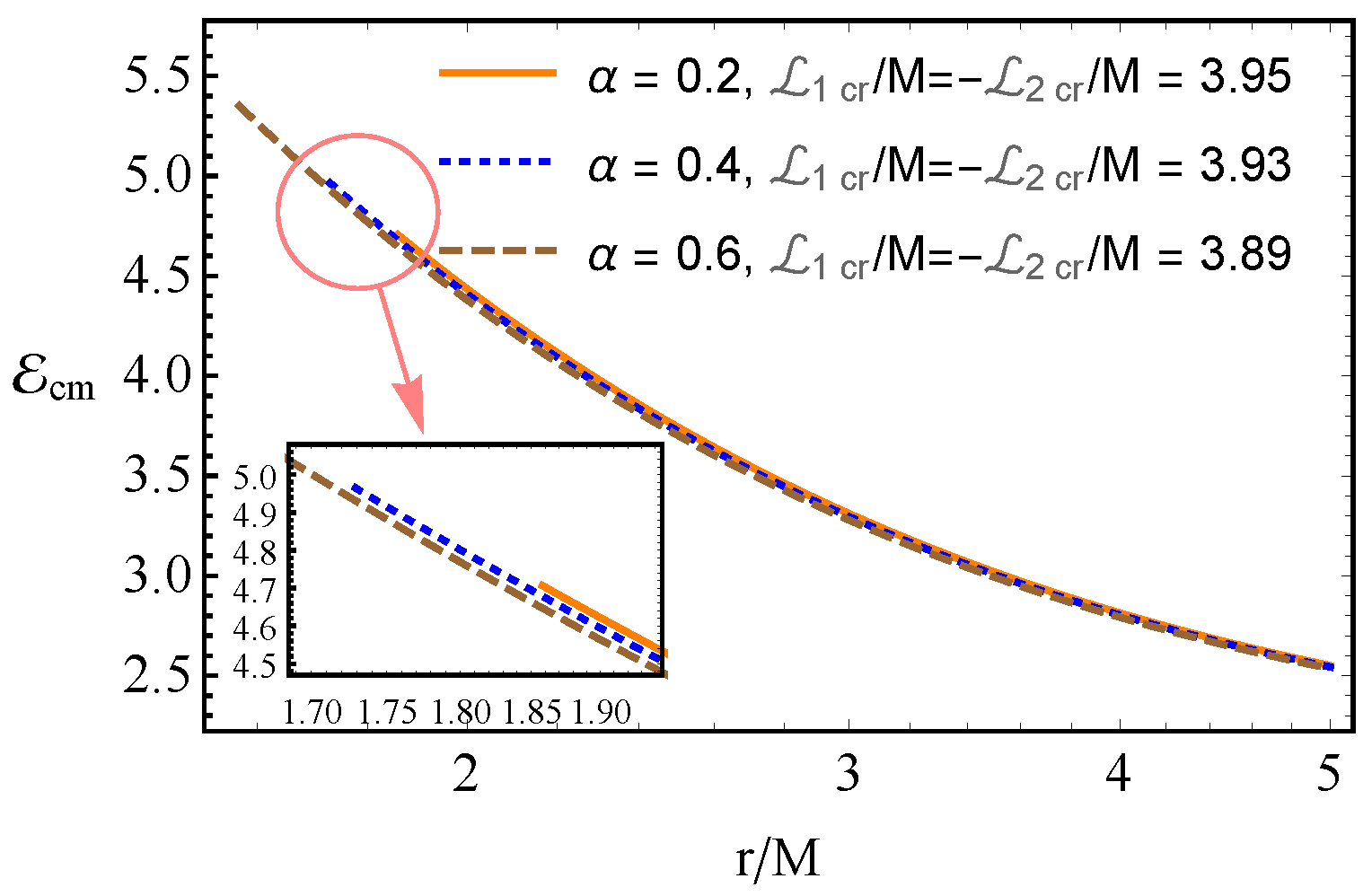
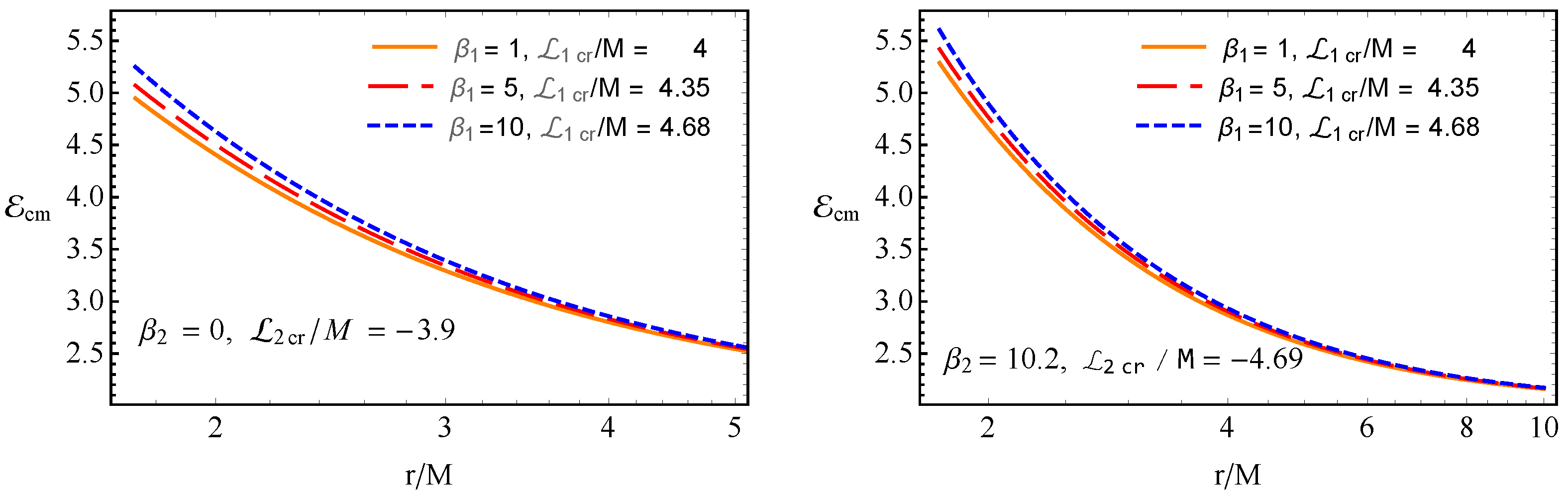
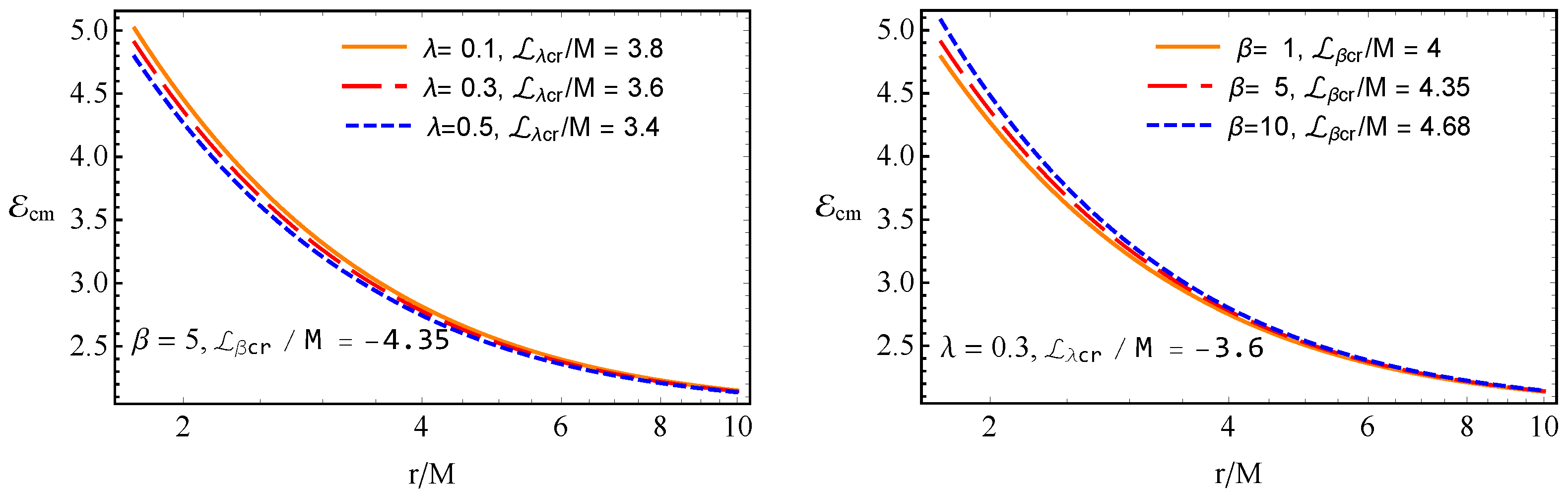
5.2. Center of Mass Energy of Collisions of Particles
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Tests of General Relativity with GW150914. Phys. Rev. Lett. 2016, 116, 221101. [Google Scholar] [CrossRef] [PubMed]
- Akiyama, K.; et al.; [The Event Horizon Telescope Collaboration] First M87 Event Horizon Telescope Results. II. Array and Instrumentation. Astrophys. J. Lett. 2019, 875, L2. [Google Scholar] [CrossRef]
- Akiyama, K.; et al.; [The Event Horizon Telescope Collaboration] First M87 Event Horizon Telescope Results. III. Data Processing and Calibration. Astrophys. J. Lett. 2019, 875, L3. [Google Scholar] [CrossRef]
- Lovelock, D. The Einstein Tensor and Its Generalizations. J. Math. Phys. 1971, 12, 498–501. [Google Scholar] [CrossRef]
- Glavan, D.; Lin, C. Einstein-Gauss-Bonnet Gravity in Four-Dimensional Spacetime. Phys. Rev. Lett. 2020, 124, 081301. [Google Scholar] [CrossRef]
- Malafarina, D.; Toshmatov, B.; Dadhich, N. Dust collapse in 4D Einstein-Gauss-Bonnet gravity. arXiv 2020, arXiv:2004.07089. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Zhang, S.J.; Li, P.C.; Guo, M. Superradiance and stability of the novel 4D charged Einstein-Gauss-Bonnet black hole. arXiv 2020, arXiv:2004.03141. [Google Scholar]
- Aguilar-Pérez, G.; Cruz, M.; Lepe, S.; Moran-Rivera, I. Hairy black hole stability under odd parity perturbations in the Einstein-Gauss-Bonnet model. arXiv 2019, arXiv:1907.06168. [Google Scholar]
- Zhang, Y.P.; Wei, S.W.; Liu, Y.X. Spinning test particle in four-dimensional Einstein-Gauss-Bonnet Black Hole. Universe 2020, 6, 103. [Google Scholar] [CrossRef]
- Guo, M.; Li, P.C. The innermost stable circular orbit and shadow in the novel 4D Einstein-Gauss-Bonnet gravity. arXiv 2020, arXiv:2003.02523. [Google Scholar]
- Kumar, R.; Ghosh, S.G. Rotating black holes in 4D Einstein-Gauss-Bonnet gravity and its shadow. J. Cosmol. Astropart. Phys. 2020, 2020, 053. [Google Scholar] [CrossRef]
- Mishra, A.K. Quasinormal modes and Strong Cosmic Censorship in the novel 4D Einstein-Gauss-Bonnet gravity. arXiv 2020, arXiv:2004.01243. [Google Scholar]
- Churilova, M.S. Quasinormal modes of the Dirac field in the novel 4D Einstein-Gauss-Bonnet gravity. arXiv 2020, arXiv:2004.00513. [Google Scholar]
- Aragón, A.; Bécar, R.; González, P.A.; Vásquez, Y. Perturbative and nonperturbative quasinormal modes of 4D Einstein-Gauss-Bonnet black holes. arXiv 2020, arXiv:2004.05632. [Google Scholar] [CrossRef]
- Islam, S.U.; Kumar, R.; Ghosh, S.G. Gravitational lensing by black holes in 4D Einstein-Gauss-Bonnet gravity. arXiv 2020, arXiv:2004.01038. [Google Scholar] [CrossRef]
- Abdujabbarov, A.; Atamurotov, F.; Dadhich, N.; Ahmedov, B.; Stuchlík, Z. Energetics and optical properties of 6-dimensional rotating black hole in pure Gauss-Bonnet gravity. Eur. Phys. J. C 2015, 75, 399. [Google Scholar] [CrossRef]
- Wei, S.W.; Liu, Y.X. Testing the nature of Gauss-Bonnet gravity by four-dimensional rotating black hole shadow. arXiv 2020, arXiv:2003.07769. [Google Scholar] [CrossRef]
- Heydari-Fard, M.; Heydari-Fard, M.; Sepangi, H.R. Bending of light in novel 4D Gauss-Bonnet-de Sitter black holes by Rindler-Ishak method. arXiv 2020, arXiv:2004.02140. [Google Scholar] [CrossRef]
- Hegde, K.; Naveena Kumara, A.; Rizwan, C.L.A.; Ajith, K.M.; Sabir Ali, M. Thermodynamics, Phase Transition and Joule Thomson Expansion of novel 4-D Gauss Bonnet AdS Black Hole. arXiv 2020, arXiv:2003.08778. [Google Scholar]
- Mansoori, S.A.H. Thermodynamic geometry of the novel 4-D Gauss Bonnet AdS Black Hole. arXiv 2020, arXiv:2003.13382. [Google Scholar]
- Wei, S.W.; Liu, Y.X. Extended thermodynamics and microstructures of four-dimensional charged Gauss-Bonnet black hole in AdS space. arXiv 2020, arXiv:2003.14275. [Google Scholar] [CrossRef]
- Naveena Kumara, A.; Rizwan, C.L.A.; Hegde, K.; Sabir Ali, M.; Ajith, K.K. Rotating 4D Gauss-Bonnet black hole as particle accelerator. arXiv 2020, arXiv:2004.04521. [Google Scholar] [CrossRef]
- Li, S.L.; Wu, P.; Yu, H. Stability of the Einstein Static Universe in 4D Gauss-Bonnet Gravity. arXiv 2020, arXiv:2004.02080. [Google Scholar]
- Abdujabbarov, A.; Rayimbaev, J.; Turimov, B.; Atamurotov, F. Dynamics of magnetized particles around 4-D Einstein Gauss-Bonnet black hole. Phys. Dark Universe 2020, 30, 100715. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, R. Bardeen black holes in the novel 4D Einstein-Gauss-Bonnet gravity. arXiv 2020, arXiv:2003.13104. [Google Scholar]
- Gurses, M.; Cagri Sisman, T.; Tekin, B. Is there a novel Einstein-Gauss-Bonnet theory in four dimensions? arXiv 2020, arXiv:2004.03390. [Google Scholar] [CrossRef]
- Arrechea, J.; Delhom, A.; Jiménez-Cano, A.R. Yet another comment on four-dimensional Einstein-Gauss-Bonnet gravity. arXiv 2020, arXiv:2004.12998. [Google Scholar]
- Tian, S.X.; Zhu, Z.H. Comment on “Einstein-Gauss-Bonnet Gravity in Four-Dimensional Spacetime”. arXiv 2020, arXiv:2004.09954. [Google Scholar]
- Bonifacio, J.; Hinterbichler, K.; Johnson, L.A. Amplitudes and 4D Gauss-Bonnet Theory. arXiv 2020, arXiv:2004.10716. [Google Scholar] [CrossRef]
- Bambi, C. Testing the Kerr nature of stellar-mass black hole candidates by combining the continuum-fitting method and the power estimate of transient ballistic jets. Phys. Rev. D 2012, 85, 043002. [Google Scholar] [CrossRef]
- Bambi, C.; Jiang, J.; Steiner, J.F. Testing the no-hair theorem with the continuum-fitting and the iron line methods: A short review. Class. Quantum Gravity 2016, 33, 064001. [Google Scholar] [CrossRef]
- Zhou, M.; Cao, Z.; Abdikamalov, A.; Ayzenberg, D.; Bambi, C.; Modesto, L.; Nampalliwar, S. Testing conformal gravity with the supermassive black hole in 1H0707-495. Phys. Rev. D 2018, 98, 024007. [Google Scholar] [CrossRef]
- Tripathi, A.; Yan, J.; Yang, Y.; Yan, Y.; Garnham, M.; Yao, Y.; Li, S.; Ding, Z.; Abdikamalov, A.B.; Ayzenberg, D.; et al. Constraints on the spacetime metric around seven “bare” AGN using X-ray reflection spectroscopy. arXiv 2019, arXiv:1901.03064. [Google Scholar] [CrossRef]
- Bambi, C. Black Holes: A Laboratory for Testing Strong Gravity; Springer: Singapore, 2017. [Google Scholar]
- Chandrasekhar, S. The Mathematical Theory of Black Holes; Oxford University Press: New York, NY, USA, 1998. [Google Scholar]
- Wald, R.M. Black hole in a uniform magnetic field. Phys. Rev. D 1974, 10, 1680–1685. [Google Scholar] [CrossRef]
- Aliev, A.N.; Galtsov, D.V.; Petukhov, V.I. Negative absorption near a magnetized black hole—Black hole masers. Astrophys. Space Sci. 1986, 124, 137–157. [Google Scholar] [CrossRef]
- Aliev, A.N.; Gal’tsov, D.V. REVIEWS OF TOPICAL PROBLEMS: “Magnetized” black holes. Sov. Phys. Uspekhi 1989, 32, 75–92. [Google Scholar] [CrossRef]
- Aliev, A.N.; Özdemir, N. Motion of charged particles around a rotating black hole in a magnetic field. Mon. Not. R. Astron. Soc. 2002, 336, 241–248. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Schee, J.; Abdujabbarov, A. Ultra-high-energy collisions of particles in the field of near-extreme Kehagias-Sfetsos naked singularities and their appearance to distant observers. Phys. Rev. D 2014, 89, 104048. [Google Scholar] [CrossRef]
- Abdujabbarov, A.; Ahmedov, B. Test particle motion around a black hole in a braneworld. Phys. Rev. D 2010, 81, 044022. [Google Scholar] [CrossRef]
- Abdujabbarov, A.; Ahmedov, B.; Hakimov, A. Particle motion around black hole in Hořava-Lifshitz gravity. Phys. Rev. D 2011, 83, 044053. [Google Scholar] [CrossRef]
- Abdujabbarov, A.A.; Ahmedov, B.J.; Shaymatov, S.R.; Rakhmatov, A.S. Penrose process in Kerr-Taub-NUT spacetime. Astrophys. Space Sci. 2011, 334, 237–241. [Google Scholar] [CrossRef]
- Abdujabbarov, A.A.; Ahmedov, B.J.; Kagramanova, V.G. Particle motion and electromagnetic fields of rotating compact gravitating objects with gravitomagnetic charge. Gen. Relativ. Gravit. 2008, 40, 2515–2532. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M. Acceleration of the charged particles due to chaotic scattering in the combined black hole gravitational field and asymptotically uniform magnetic field. Eur. Phys. J. C 2016, 76, 32. [Google Scholar] [CrossRef]
- Kovář, J.; Kopáček, O.; Karas, V.; Stuchlík, Z. Off-equatorial orbits in strong gravitational fields near compact objects II: Halo motion around magnetic compact stars and magnetized black holes. Class. Quantum Gravity 2010, 27, 135006. [Google Scholar] [CrossRef]
- Kovář, J.; Slaný, P.; Cremaschini, C.; Stuchlík, Z.; Karas, V.; Trova, A. Electrically charged matter in rigid rotation around magnetized black hole. Phys. Rev. D 2014, 90, 044029. [Google Scholar] [CrossRef]
- Rayimbaev, J.; Tadjimuratov, P. Can modified gravity silence radio-loud pulsars? Phys. Rev. D 2020, 102, 024019. [Google Scholar] [CrossRef]
- Rayimbaev, J.; Turimov, B.; Palvanov, S. Plasma magnetosphere of slowly rotating magnetized neutron star in branewold. Int. J. Mod. Phys. Conf. Ser. 2019, 49, 1960019. [Google Scholar] [CrossRef]
- Rayimbaev, J.; Turimov, B.; Marcos, F.; Palvanov, S.; Rakhmatov, A. Particle acceleration and electromagnetic field of deformed neutron stars. Mod. Phys. Lett. A 2020, 35, 2050056. [Google Scholar] [CrossRef]
- Rayimbaev, J.; Turimov, B.; Ahmedov, B. Braneworld effects in plasma magnetosphere of a slowly rotating magnetized neutron star. Int. J. Mod. Phys. D 2019, 28, 1950128. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M.; Kovář, J.; Slaný, P.; Tursunov, A. Influence of Cosmic Repulsion and Magnetic Fields on Accretion Disks Rotating around Kerr Black Holes. Universe 2020, 6, 26. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M.; Tursunov, A. Penrose Process: Its Variants and Astrophysical Applications. Universe 2021, 7, 416. [Google Scholar] [CrossRef]
- de Felice, F.; Sorge, F. Magnetized orbits around a Schwarzschild black hole. Class. Quantum Gravity 2003, 20, 469–481. [Google Scholar] [CrossRef]
- de Felice, F.; Sorge, F.; Zilio, S. Magnetized orbits around a Kerr black hole. Class. Quantum Gravity 2004, 21, 961–973. [Google Scholar] [CrossRef]
- Rayimbaev, J.R. Magnetized particle motion around non-Schwarzschild black hole immersed in an external uniform magnetic field. Astrophys. Space Sci. 2016, 361, 288. [Google Scholar] [CrossRef]
- Toshmatov, B.; Abdujabbarov, A.; Ahmedov, B.; Stuchlík, Z. Motion and high energy collision of magnetized particles around a Hořava-Lifshitz black hole. Astrophys. Space Sci. 2015, 360, 19. [Google Scholar] [CrossRef]
- Abdujabbarov, A.; Ahmedov, B.; Rahimov, O.; Salikhbaev, U. Magnetized particle motion and acceleration around a Schwarzschild black hole in a magnetic field. Phys. Scr. 2014, 89, 084008. [Google Scholar] [CrossRef]
- Rahimov, O.G.; Abdujabbarov, A.A.; Ahmedov, B.J. Magnetized particle capture cross section for braneworld black hole. Astrophys. Space Sci. 2011, 335, 499–504. [Google Scholar] [CrossRef][Green Version]
- Haydarov, K.; Rayimbaev, J.; Abdujabbarov, A.; Palvanov, S.; Begmatova, D. Magnetized particle motion around magnetized Schwarzschild-MOG black hole. Eur. Phys. J. C 2020, 80, 399. [Google Scholar] [CrossRef]
- Narzilloev, B.; Rayimbaev, J.; Shaymatov, S.; Abdujabbarov, A.; Ahmedov, B.; Bambi, C. Can the dynamics of test particles around charged stringy black holes mimic the spin of Kerr black holes? Phys. Rev. D 2020, 102, 044013. [Google Scholar] [CrossRef]
- Rayimbaev, J.; Figueroa, M.; Stuchlík, Z.; Juraev, B. Test particle orbits around regular black holes in general relativity combined with nonlinear electrodynamics. Phys. Rev. D 2020, 101, 104045. [Google Scholar] [CrossRef]
- Turimov, B.; Rayimbaev, J.; Abdujabbarov, A.; Ahmedov, B.; Stuchlík, Z.C.V. Test particle motion around a black hole in Einstein-Maxwell-scalar theory. Phys. Rev. D 2020, 102, 064052. [Google Scholar] [CrossRef]
- Vrba, J.; Abdujabbarov, A.; Kološ, M.; Ahmedov, B.; Stuchlík, Z.; Rayimbaev, J. Charged and magnetized particles motion in the field of generic singular black holes governed by general relativity coupled to nonlinear electrodynamics. Phys. Rev. D 2020, 101, 124039. [Google Scholar] [CrossRef]
- Vrba, J.; Abdujabbarov, A.; Tursunov, A.; Ahmedov, B.; Stuchlík, Z. Particle motion around generic black holes coupled to non-linear electrodynamics. Eur. Phys. J. C 2019, 79, 778. [Google Scholar] [CrossRef]
- Bardeen, J. Non-singular general-relativistic gravitational collapse. In Proceedings of the GR5, Tbilisi, Georgia, 9–13 September 1968; DeWitt, C., DeWitt, B., Eds.; Gordon and Breach: Tbilisi, Georgia, 1968; p. 174. [Google Scholar]
- Narzilloev, B.; Rayimbaev, J.; Shaymatov, S.; Abdujabbarov, A.; Ahmedov, B.; Bambi, C. Dynamics of test particles around a Bardeen black hole surrounded by perfect fluid dark matter. Phys. Rev. D 2020, 102, 104062. [Google Scholar] [CrossRef]
- Juraeva, N.; Rayimbaev, J.; Abdujabbarov, A.; Ahmedov, B.; Palvanov, S. Distinguishing magnetically and electrically charged Reissner–Nordström black holes by magnetized particle motion. Eur. Phys. J. C 2021, 81, 124078. [Google Scholar] [CrossRef]
- Rayimbaev, J.; Abdujabbarov, A.; Jamil, M.; Han, W.B. Dynamics of magnetized particles around Einstein-Æther black hole with uniform magnetic field. Nucl. Phys. B 2021, 966, 115364. [Google Scholar] [CrossRef]
- Mori, K.; Gotthelf, E.V.; Zhang, S.; An, H.; Baganoff, F.K.; Barrière, N.M.; Beloborodov, A.M.; Boggs, S.E.; Christensen, F.E.; Craig, W.W.; et al. NuSTAR Discovery of a 3.76 s Transient Magnetar Near Sagittarius A*. Astron. J. Lett. 2013, 770, L23. [Google Scholar] [CrossRef]
- Bañados, M.; Silk, J.; West, S.M. Kerr Black Holes as Particle Accelerators to Arbitrarily High Energy. Phys. Rev. Lett. 2009, 103, 111102. [Google Scholar] [CrossRef]
- Frolov, V.P. Weakly magnetized black holes as particle accelerators. Phys. Rev. D 2012, 85, 024020. [Google Scholar] [CrossRef]
- Grib, A.A.; Pavlov, Y.V. On particle collisions near rotating black holes. Gravit. Cosmol. 2011, 17, 42–46. [Google Scholar] [CrossRef]
- Grib, A.A.; Pavlov, Y.V. On particle collisions in the gravitational field of the Kerr black hole. Astropart. Phys. 2011, 34, 581–586. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rayimbaev, J.; Bardiev, D.; Abdulxamidov, F.; Abdujabbarov, A.; Ahmedov, B. Magnetized and Magnetically Charged Particles Motion around Regular Bardeen Black Hole in 4D Einstein Gauss–Bonnet Gravity. Universe 2022, 8, 549. https://doi.org/10.3390/universe8100549
Rayimbaev J, Bardiev D, Abdulxamidov F, Abdujabbarov A, Ahmedov B. Magnetized and Magnetically Charged Particles Motion around Regular Bardeen Black Hole in 4D Einstein Gauss–Bonnet Gravity. Universe. 2022; 8(10):549. https://doi.org/10.3390/universe8100549
Chicago/Turabian StyleRayimbaev, Javlon, Dilshodbek Bardiev, Farrux Abdulxamidov, Ahmadjon Abdujabbarov, and Bobomurat Ahmedov. 2022. "Magnetized and Magnetically Charged Particles Motion around Regular Bardeen Black Hole in 4D Einstein Gauss–Bonnet Gravity" Universe 8, no. 10: 549. https://doi.org/10.3390/universe8100549
APA StyleRayimbaev, J., Bardiev, D., Abdulxamidov, F., Abdujabbarov, A., & Ahmedov, B. (2022). Magnetized and Magnetically Charged Particles Motion around Regular Bardeen Black Hole in 4D Einstein Gauss–Bonnet Gravity. Universe, 8(10), 549. https://doi.org/10.3390/universe8100549








