Outliers in Spectral Time Lag-Selected Gamma Ray Bursts

Abstract

It is possible that astrophysical samples are polluted by some outliers, which might belong to a different sub-class. By removing the outliers, the underlying statistical features may be revealed. A more reliable correlation can be used as a standard candle relationship for cosmological study. We present outlier searching for gamma ray bursts with the Partitioning Around Medoids (PAM) method. In this work, we choose three parameters from the sample, with all of them having rest-frame spectral time lag (${\tau }_{\mathrm{lag},\mathrm{i}}$). In most cases, the outliers are GRBs 980425B and 030528A. Linear regression is carried out for the sample without the outliers. Some of them have passed hypothesis testing, while others have not. However, even for the passed sample, the correlation is not very significant. More parameter combinations should be considered in future work.

1. Introduction

Gamma ray bursts (GRBs) are astronomical phenomena detected at high energies. Classification and correlation seeking may reveal the underlying physics. GRBs can be classified as long GRBs (LGRBs) and short GRBs (SGRBs). SGRBs are likely associated with compact binary coalescence events involving at least one neutron star [1,2]. Massive stellar collapse is believed to generate the LGRBs [3,4,5]. However, there is no clear criterion for this classification. Some GRBs could not be decisively classified in either class. On the other hand, it is still possible that GRBs can be classified into more groups, such as intermediate class giant flares from soft gamma ray repeaters. Outlier detection belongs to classification analysis. The outliers may belong to an individual group.

There are various cluster analysis techniques, such as k-means, K-medoids, hierarchical clustering, neural network clustering, and kernel principal component analysis [6,7,8]. Modak [9] conducted fuzzy clustering on GRBs from the final Burst and Transient Source Experiment (BATSE) catalog and confirmed three groups. Partitioning Around Medoids (PAM) is the most prominent method of K-medoids. We use the Euclidean distance as the similarity measurement. The outliers are far away from the other data. We analyze the outliers and seek the underlying linear correlation between different properties.

The data are based on the collection of Wang et al. [10]. We collect a full sample including prompt emission, afterglow and host galaxy properties. We choose arbitrary three parameters based on the rest-frame spectral time lag ${\tau }_{\mathrm{lag},\mathrm{i}}$ to find the outliers, i.e., each combination of the physical parameters containing ${\tau }_{\mathrm{lag},\mathrm{i}}$, trying to find any possible clues for the classification.

Spectral time lag is the time arrival difference between different energy bands for the prompt emission light curves of GRBs. Spectral lag was first introduced by Norris et al. [11]. A cross-correlation function (CCF) can be used to quantify such an effect since the pulse peaks at different energy bands are delayed. The method is widely used to calculate spectral lag [12]. A positive spectral lag is when the high-energy photons arrive before the low-energy photons, while a negative spectral lag is the opposite. Prompt intrinsic spectral evolution or the curvature effect of relativistically moving shocked shells is used to explain the observed spectral lag [13,14].

Spectral time lag has been found to be correlated to several other quantities. The bolometric peak luminosity and spectral lag have an anti-correlation found by Norris et al. [15], later confirmed by Ukwatta et al. [12], Norris [16], Gehrels et al. [17]. Therefore, the lag is an indicator of both GRB peak luminosity and time history morphology, with short-lag and variable bursts having greater luminosities than long-lag and smooth bursts [16,18,19]. The peak luminosity and spectral lag relation can be viewed as being closely related to the peak luminosity and the variability relationship. Variability should be inversely proportional to spectral lag, i.e., larger variability jets exhibit shorter spectral lags [20]. Using the internal shock model, the peak luminosity–spectral lag relation and the peak luminosity–variability relation can be caused by changes in observer’s viewing angle with respect to the jet axis [21]. Bright GRBs are expected to have a larger Lorentz factor and smaller viewing angles, meaning that the observer is viewing the GRB jet on the axis. The spectral lag should be small due to the smaller emitting region [21]. Chen et al. [22] showed the distribution of spectral time lags in GRBs. The distribution of spectral time lags in LGRBs is apparently different from SGRBs, which implies different physical mechanisms. Yi et al. [23] confirmed this result. Zhang et al. [24] also studied the spectral time lag of SGRBs and found that the lags of the majority of SGRBs are so small that they are negligible or not measurable. Shao et al. [19] carried out a systematic study of the spectral time lag properties of 50 single-pulsed GRBs detected by Fermi. Shao et al. [19] provided a new measurement, which is independent of energy channel selections, and the new results favored the relativistic geometric effects for the origin of spectral time lag. Lu et al. [25] found the spectral time lags are closely related to spectral evolution within the pulse. However, all of the statistics related to the lags do not have very high significance. In this work, we try to find if there are outliers and to see whether the statistics become more significant without the outliers. We want to find more reliable correlations than the previous works. We hope to use the reliable correlations as a standard candle and to constrain the cosmological parameters.

This paper is organized as follows. Section 2 outlines the statistical methods. Section 3 discusses the PAM results. Section 4 is the conclusion and discussions.

2. Statistical Methods

The parameters and samples are from our previous work [10]. We collected all the possible data for 6289 GRBs in a big catalog [10], of which 165 GRBs were selected, as they contained the required parameters. The parameters we used in this work include ${\tau }_{\mathrm{lag},\mathrm{i}}$ (rest-frame spectral time lag, in units of $\mathrm{ms}{\mathrm{MeV}}^{-1}$), $T_{50,\mathrm{i}}$ (duration of 25% to 75% $\gamma$-ray fluence in rest-frame), $T_{90,\mathrm{i}}$ (duration of 5% to 95% $\gamma$-ray fluence in rest-frame), $T_{\mathrm{R}45,\mathrm{i}}$ (defined in [26]), $variabilit{y}_2$ (light curve variability from the definition of Reichart et al. [26]), $L_{\mathrm{pk},52}$ (peak luminosity of 1 $\mathrm{s}$ time bin in rest-frame 1–${10}^4$$\mathrm{keV}$ energy band, in units of ${10}^{52}\mathrm{erg}{\mathrm{s}}^{-1}$), $E_{\mathrm{iso},52}$ (isotropic $\gamma$ ray energy in rest-frame 1–${10}^4$$\mathrm{keV}$ energy band, in units of ${10}^{52}\mathrm{ergs}$), ${\alpha }_{\mathrm{Band}}$ (low-energy spectral index of the Band model), ${\beta }_{\mathrm{Band}}$ (high-energy spectral index of the Band model), $E_{\mathrm{p},\mathrm{Band},\mathrm{i}}$ (rest-frame spectral peak energy of the Band model, $\mathrm{keV}$), $E_{\mathrm{p},\mathrm{i}}$ (rest-frame spectral peak energy of the Band model and cutoff power law model, $\mathrm{keV}$), ${\alpha }_{\mathrm{cpl}}$ (low-energy spectral index of cutoff power law model), $log{t}_{\mathrm{burst},\mathrm{i}}$ (rest-frame central engine active duration in logarithm, in units of $\mathrm{s}$) (defined in [27]), $t_{\mathrm{radio},\mathrm{pk},\mathrm{i}}$ (rest-frame peak time in radio band, in units of $\mathrm{s}$), ${\beta }_{\mathrm{X}11\mathrm{hr}}$ (index in X-ray band at 11 h related to the trigger time), age (in units of $\mathrm{Myr}$), $A_{\mathrm{V}}$ (dust extinction), host galaxy offset (the distance from GRB location to the centre of its host galaxy, in units of $\mathrm{kpc}$), Mag (absolute magnitude in AB system at rest 3.6 $\mathsf{\mu }$m wavelength), $logSSFR$ (specific star formation rate in logarithm, in units of ${\mathrm{Gyr}}^{-1}$), and $N_{\mathrm{H}}$ (column density of hydrogen, in units of ${10}^{21}{\mathrm{cm}}^{-2}$). We used the label “i” to mark the parameters in the rest-frame. We chose three parameters, including ${\tau }_{\mathrm{lag},\mathrm{i}}$, for PAM analysis. For the spectral time lag, because the energy band is different for different instruments, we divided the spectral time lag by the difference of two energy band central values to get a unified quantity, which can be seen in Table 1 of Wang et al. [10]. For example, the spectral time lag for GRB 980425B is 1.46 ± 0.18 $\mathrm{s}$ between 50–100 $\mathrm{keV}$ and 25–50 $\mathrm{keV}$[20], and the redshift is 0.0085. The central value of ${\tau }_{\mathrm{lag},\mathrm{i}}$ is $\frac{1.46}{1+0.0085}·(\frac{50+100}{2}-\frac{25+50}{2})·{10}^6=38605\mathrm{ms}{\mathrm{MeV}}^{-1}$. The error of ${\tau }_{\mathrm{lag},\mathrm{i}}$ is $\frac{0.18}{1+0.0085}·(\frac{50+100}{2}-\frac{25+50}{2})·{10}^6=4760\mathrm{ms}{\mathrm{MeV}}^{-1}$. Similar to the suggestion in Foley et al. [28], we removed the ${\tau }_{\mathrm{lag},\mathrm{i}}$ for GRB 060218 because GRB 060218 has extremely large lag, and it is an X-ray flash rather than a typical GRB.

For the spectral parameters, the spectra are mainly fitted by three models: the Band model, the cutoff power law (CPL) model and the simple power law (SPL) model [29]. The Band model is a smoothly joint broken power law with the definition [30]:

$$N\left(E\right)=\{\begin{array}{cc}A{\left(\frac{E}{100\mathrm{keV}}\right)}^{\alpha }{e}^{-\frac{E}{E_0}},\hfill & \hfill E<(\alpha -\beta )E_0,\\ A{\left(\frac{E}{100\mathrm{keV}}\right)}^{\beta }{\left[\frac{(\alpha -\beta )E_0}{100\mathrm{keV}}\right]}^{\alpha -\beta }{e}^{\beta -\alpha },\hfill & \hfill E\ge (\alpha -\beta )E_0,\end{array}$$

(1)

where $\alpha$ is the low-energy photon index, $\beta$ is the high-energy photon index, A is the coefficient for normalization, E is the energy of the photons, and $E_0$ is the break energy. Mostly, we used $E_{\mathrm{p}}$ instead of $E_0$. $E_{\mathrm{p}}$ is the peak energy in the spectrum of $E^{2}N$, and $E_{\mathrm{p}}=(2+\alpha )E_0$.

In the previous work [10], we used ${\alpha }_{\mathrm{Band}}$, ${\beta }_{\mathrm{Band}}$ and $E_{\mathrm{p},\mathrm{Band}}$ as Band function spectral parameters. ${\alpha }_{\mathrm{cpl}}$ and $E_{\mathrm{p},\mathrm{cpl}}$ were used to mark CPL model spectrum parameters. The formula of SPL model is $N\left(E\right)=A{E}^{{\alpha }_{\mathrm{spl}}}$. In this paper, we used $-{\alpha }_{\mathrm{Band}}$, $-{\beta }_{\mathrm{Band}}$ and $-{\alpha }_{\mathrm{cpl}}$ to stand for the opposite of spectral indices, as they become mostly positive numbers by adding the `−’ sign.

Cluster analysis divides data into clusters that are meaningful, useful, or both. Cluster analysis is the study of techniques for finding the most representative cluster prototypes. A cluster is a set of objects in which each object is more similar to the prototype that defines the cluster than to the prototype of any other clusters. There are a number of such techniques, but two of the most prominent are K-means and K-medoids. The K-medoids method is more robust than others in terms of outliers. The outliers are the smallest groups with a few points in this paper. Partitioning Around Medoids (PAM) is the most prominent method of K-medoids. In this paper, we use the PAM method of K-medoids for outlier detection [31]. In order to avoid the influence of different units, we apply data standardization to all the parameters. We use the R language function Nbclust to calculate the best cluster number. The detailed processes are the following:

• We calculate the best cluster number K and choose K initial centroids, where K is a user-specified parameter, namely, the number of clusters desired. In this paper, the K is 2 or 3;
• We use the Euclidean distance as a similarity measurement. We calculate the Euclidean distance to the initial centroids of each point;
• Each point is then assigned to the closest centroid, and each collection of points assigned to a centroid is a cluster;
• For every cluster, we calculate the Euclidean distance sum to the centroid of each point, which are assigned to this centroid. Then, we obtain the sum of each cluster;
• For every cluster, we choose one point to update the centroid;
• Points are assigned to the updated centroids;
• For every cluster, we calculate the Euclidean distance sum to the updated centroid of each point, which are assigned to this updated centroid. Then, we get the sum of all the clusters;
• If the sum of all the clusters in the seventh step is smaller than the fourth step, we update the centroids;
• We repeat the assignments and update steps until no point changes clusters, or equivalently, until the centroids remain the same.

We tried all three parameter combinations including ${\tau }_{\mathrm{lag},\mathrm{i}}$. For every combination, we used PAM method for outlier detection firstly. If we found outliers, we conducted linear regression among the three parameters including ${\tau }_{\mathrm{lag},\mathrm{i}}$ without outliers. Some combinations have obvious outliers and significant correlations, as shown in Section 3.1. Some combinations only have obvious outliers, but no significant correlations can be found, as shown in Section 3.2. Some combinations have no obvious outliers and no significant correlations, and we do not show these results. We also consider all the error bars using the MC method [32]. The results are shown in the next section.

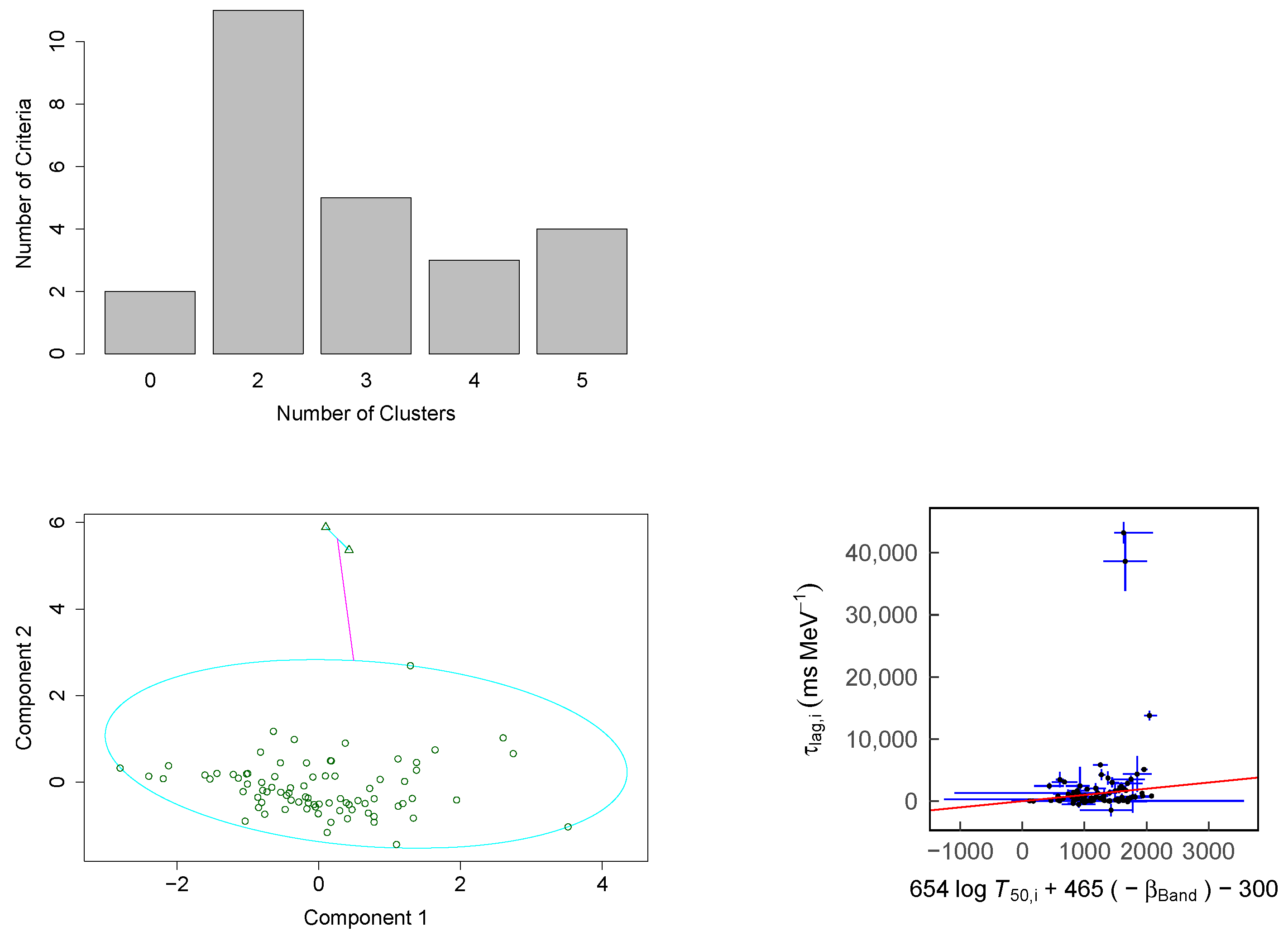
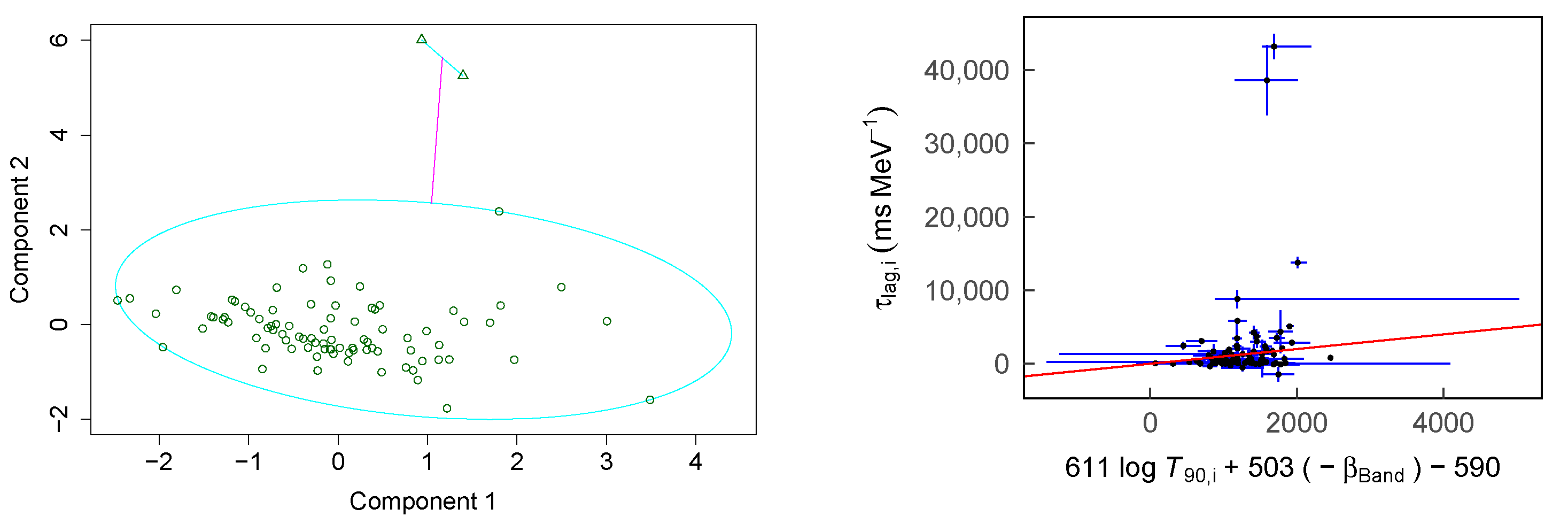
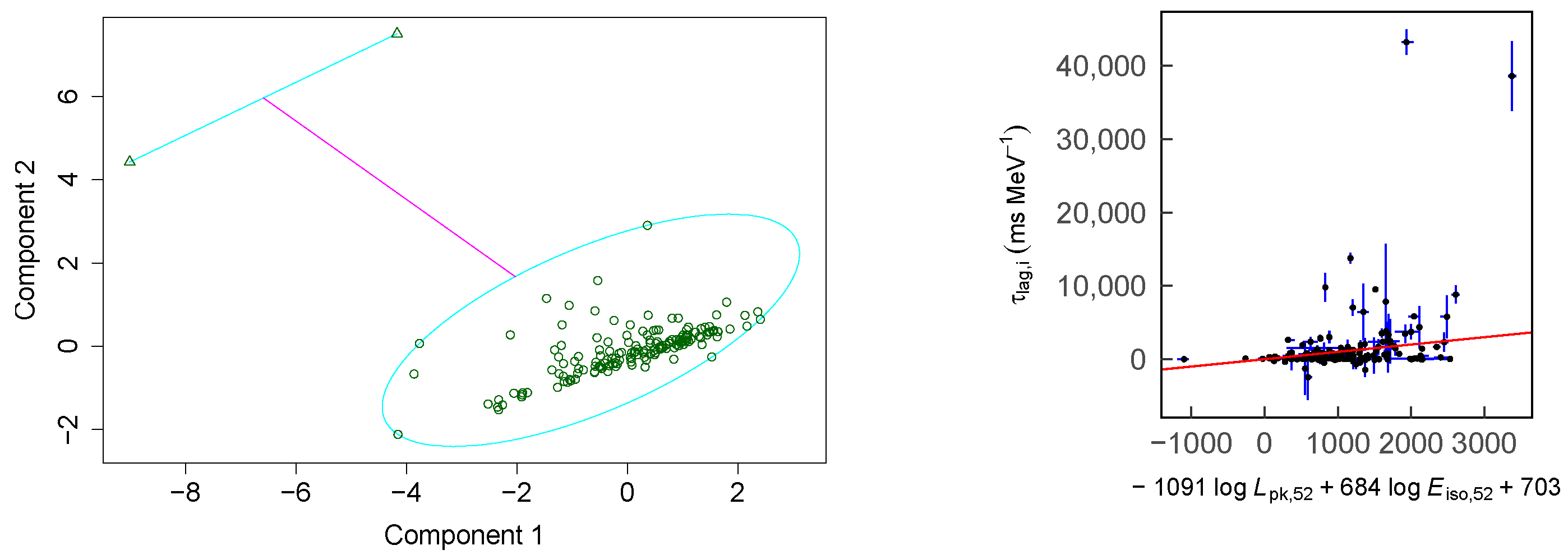
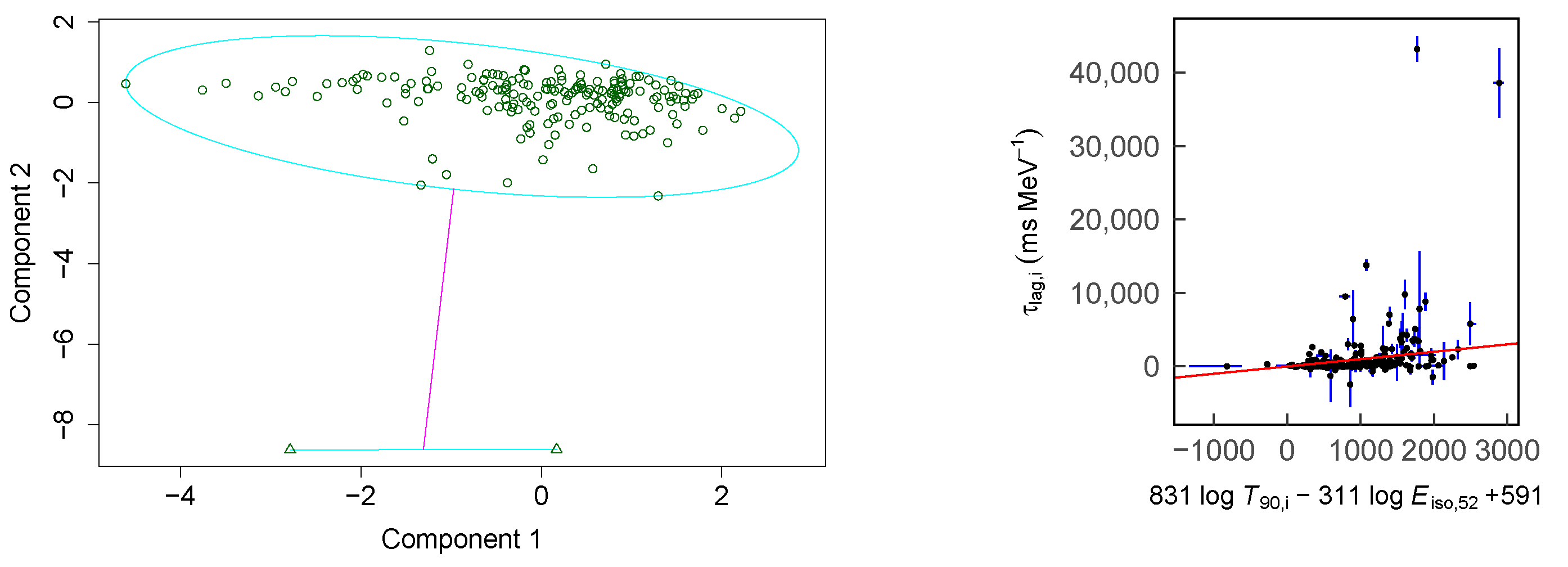
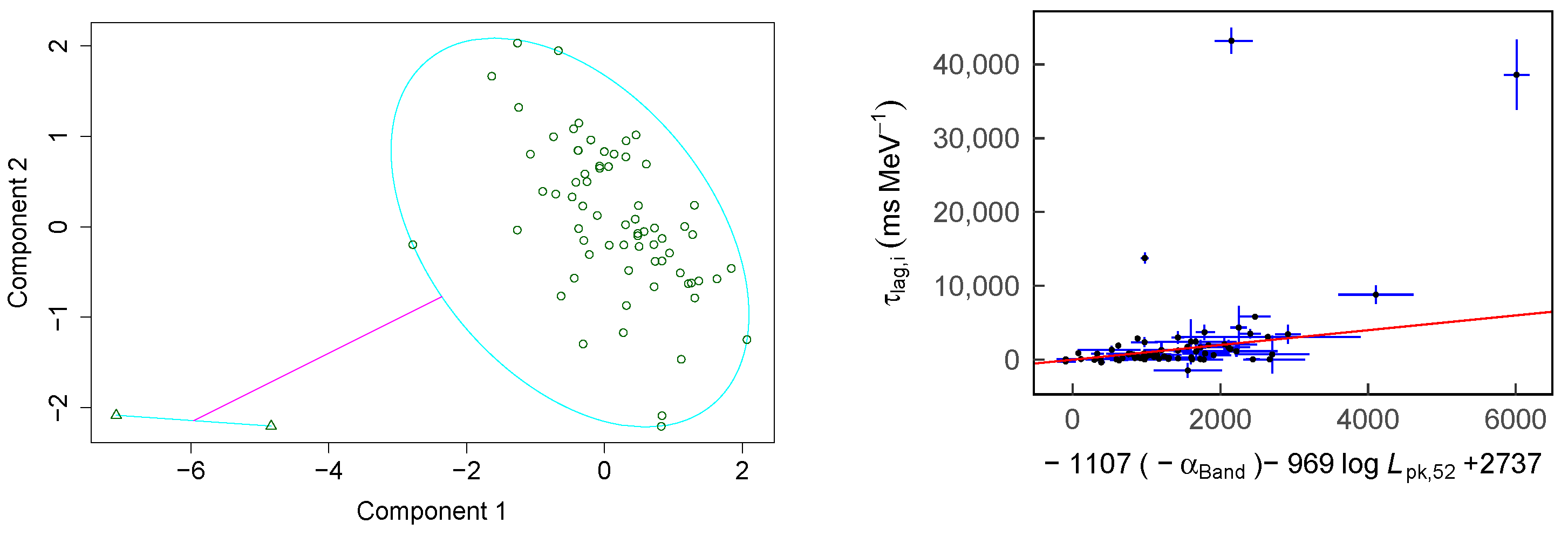
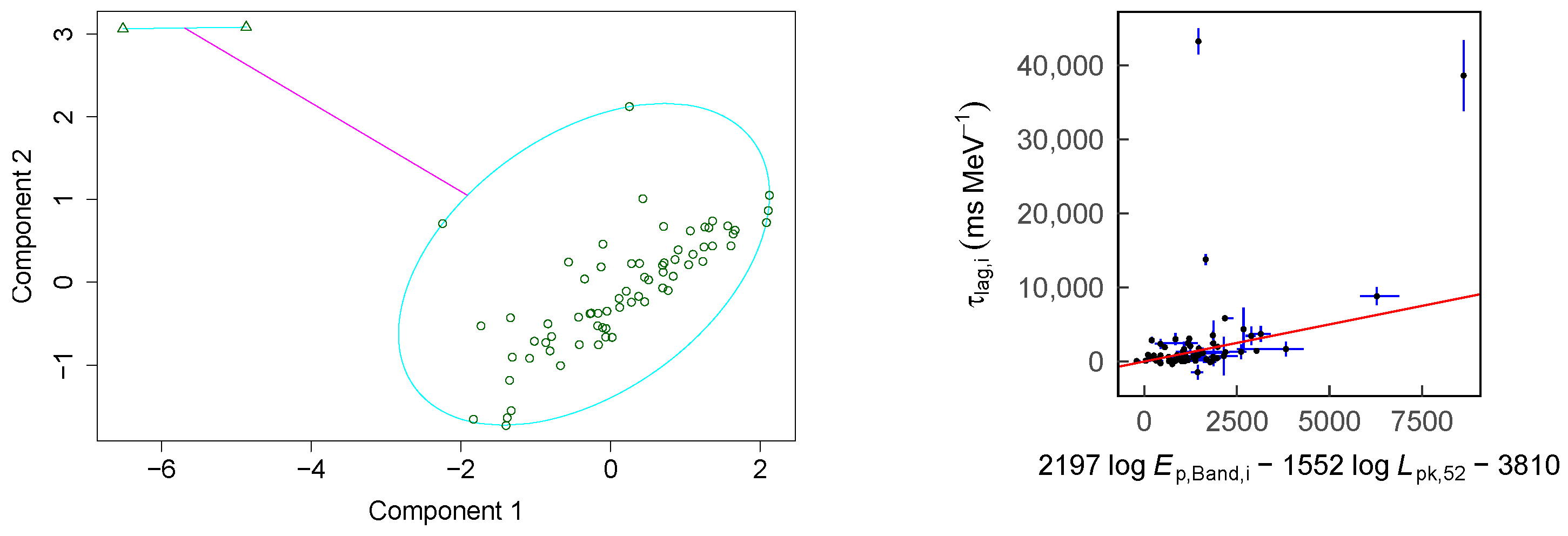
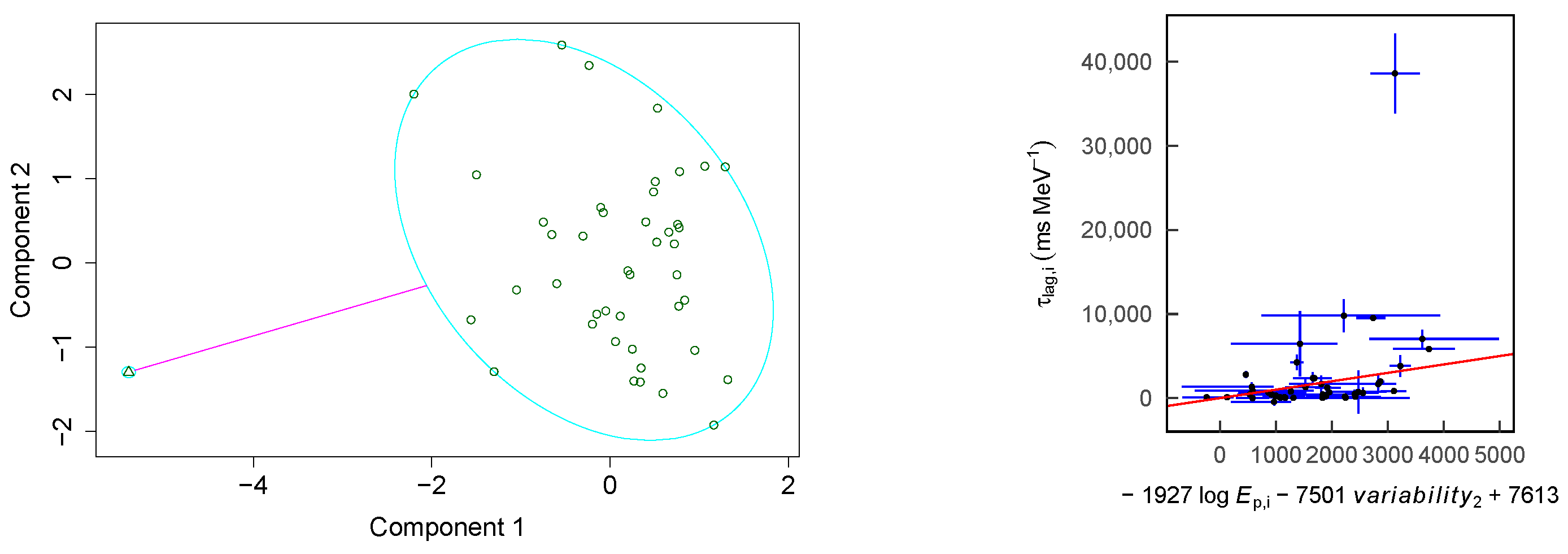
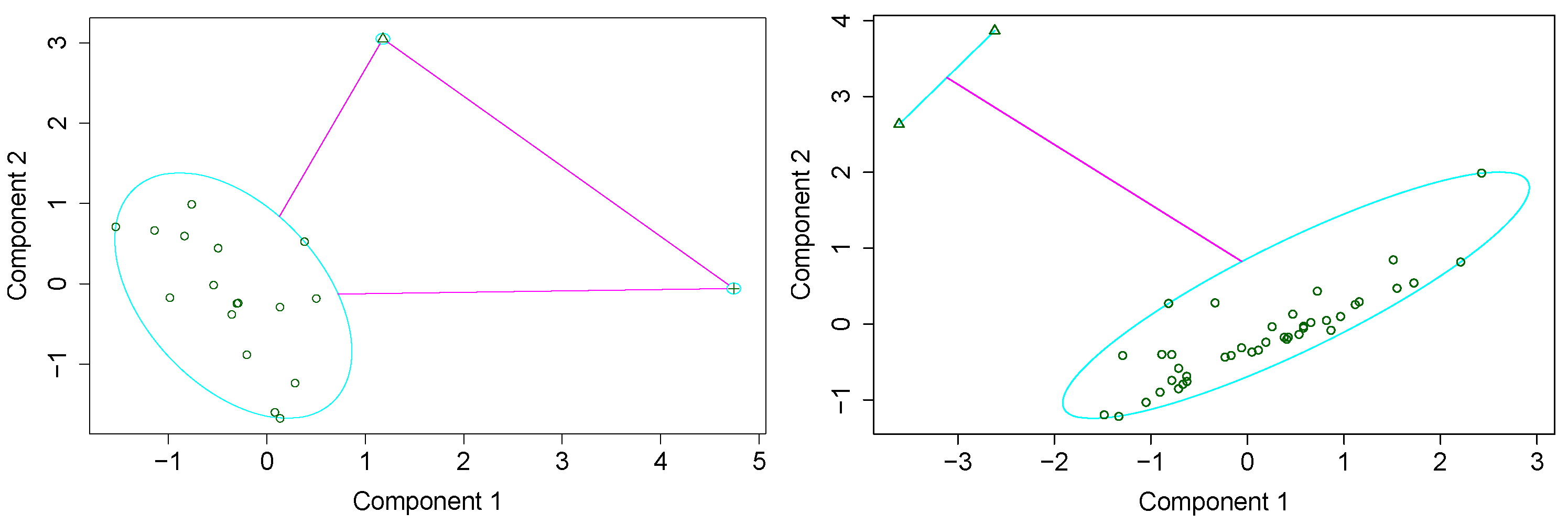
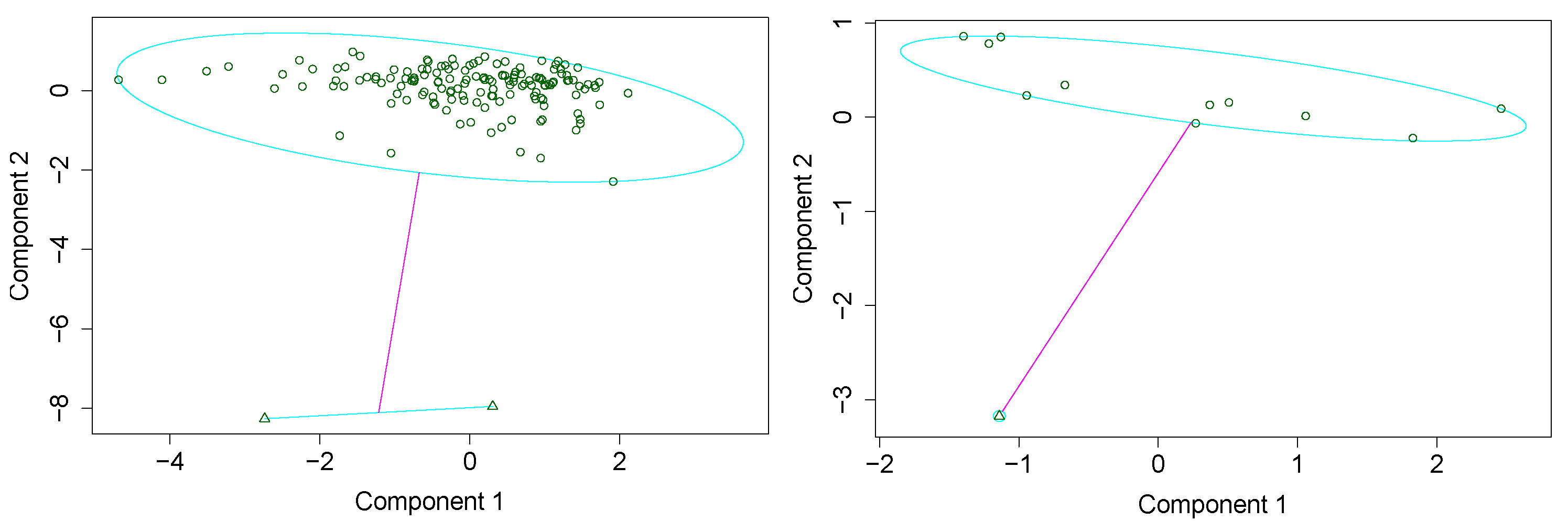
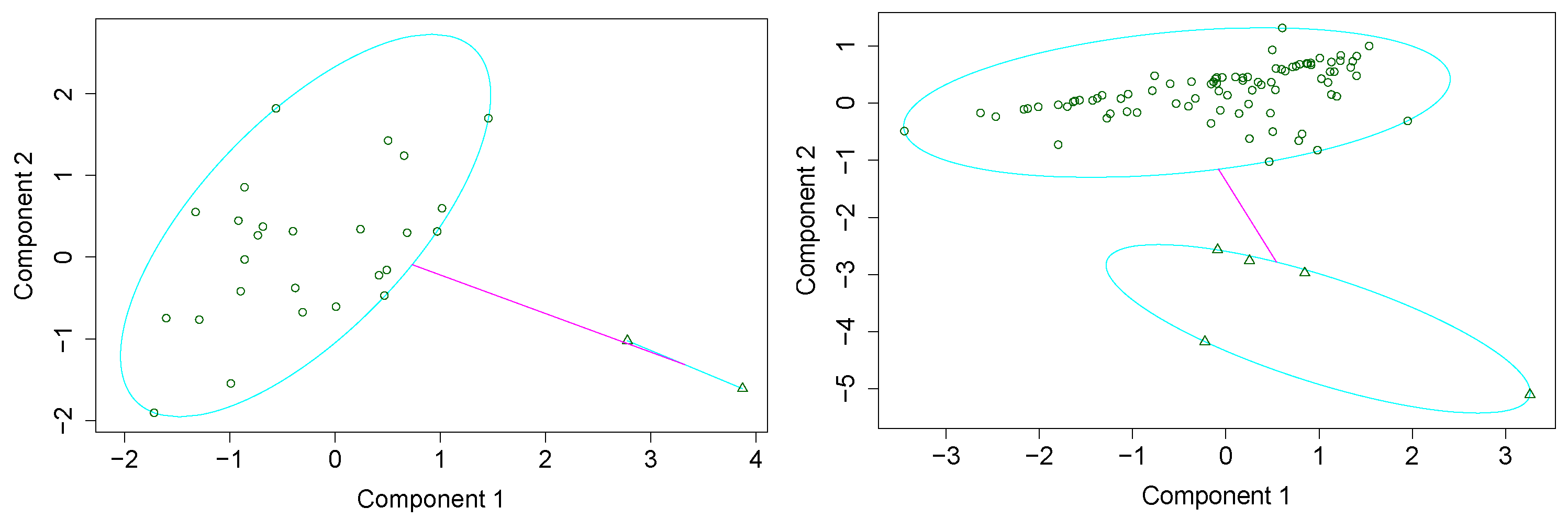
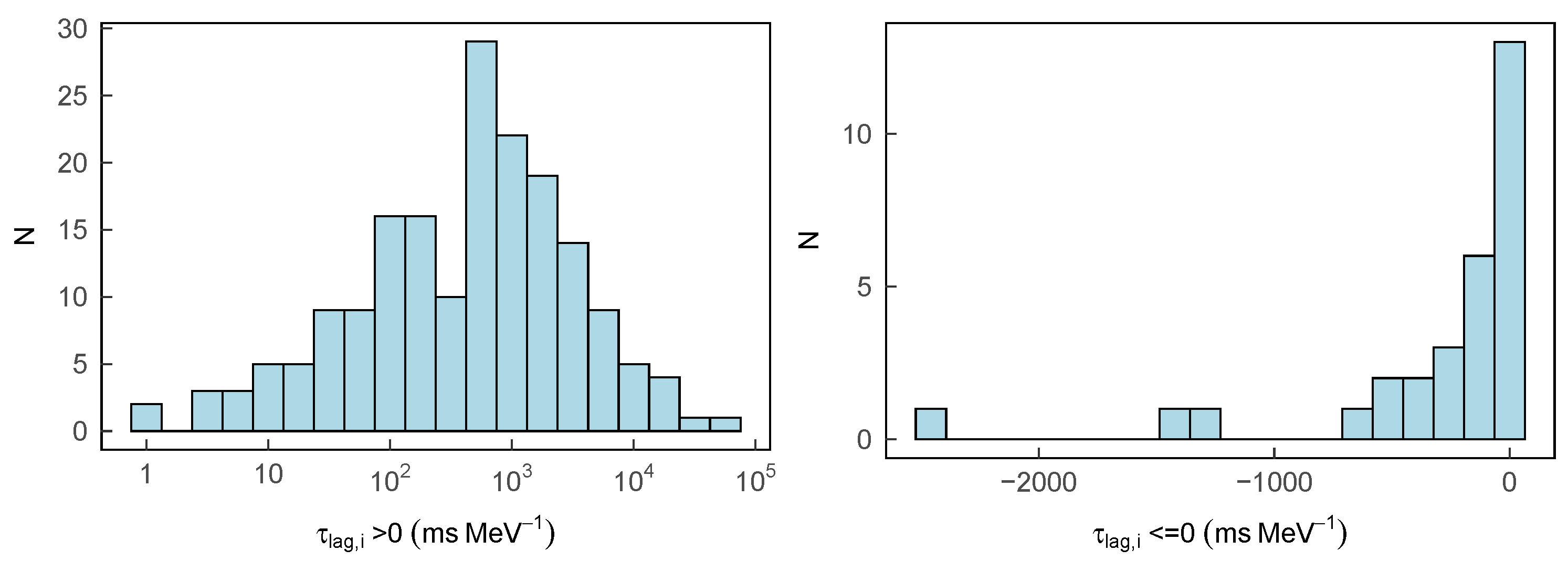
3. PAM Results

We tried all the three combinations including ${\tau }_{\mathrm{lag},\mathrm{i}}$ with the PAM method. The data selection criterion was that the sample should have at least 10 GRBs. We used the R language Nbclust package to calculate the best cluster number. The Nbclust package provides 30 indices for determining the number of clusters, such as the Krzanowski–Lai (KL) index [33], the Davies–Bouldin (DB) index [34], and so on. Charrad et al. [35] showed more details regarding the Nbclust package. As shown in the upper panel of Figure 1, number 2 has the maximum criteria. Therefore, the cluster number should be 2. However, the cluster number of Figures 9 and 10 is 3, as shown in Figure 9. Except for Figures 9 and 10, the cluster number of other figures is 2 with the Nbclust package. We did not show the others in this paper. We found 191 combinations with obvious outliers. Though the PAM method can find the outliers, the rest of the sample in the PAM plot does not show any meaningful message on the correlation or the clustering. Therefore, some independent statistics should be applied to check the statistical property for the rest of the sample. Linear regression is carried out with outliers removed. Only 8 combinations have passed the hypothesis testing, which are displayed in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8. However, for the passed combinations, the correlation is not very significant. We use the adjusted $R^2$ to measure the goodness of the regression model. It indicates the percentage of variance explained considering the parameter freedom. We also showed a small part of cluster plots with obvious outliers but not passing the hypothesis testing in Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14. These figures include all the outliers. In other words, the cluster plots with repeated outliers are not displayed in this paper.

3.1. Remarkable Linear Regression Results without Outliers

The outlier analysis can be apparently shown in the figures. We list the results with remarkable linear regression results in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8.

Figure 1 and Figure 2 show the outliers in the diagram of ${\tau }_{\mathrm{lag},\mathrm{i}}$, $T_{90,\mathrm{i}}$ (and $T_{50,\mathrm{i}}$) and ${\beta }_{\mathrm{Band}}$, respectively. Both $T_{90,\mathrm{i}}$ and $T_{50,\mathrm{i}}$ indicate the duration of the GRBs. Therefore, these two analyses have similar behavior. GRBs 980425B and 030528A are the two outliers, which can be clearly seen from these two figures. The spectral time lag for GRB 030528A is 12.5 ± 0.5 $\mathrm{s}$ between 100–300 $\mathrm{keV}$ and 25–50 $\mathrm{keV}$[36]. The spectral time lag for GRB 980425B is 1.46 ± 0.18 $\mathrm{s}$ between 50–100 $\mathrm{keV}$ and 25–50 $\mathrm{keV}$[20]. Because the energy band is different, we divide the spectral time lag by the difference of two energy band central values. ${\tau }_{\mathrm{lag},\mathrm{i}}$ for these two GRBs are 43,215 ± 1729 $\mathrm{ms}{\mathrm{MeV}}^{-1}$ and 38,605 ± 4760 $\mathrm{ms}{\mathrm{MeV}}^{-1}$, respectively, which are much larger than other GRBs. The detailed data for all the samples can be seen in [10]. Notice GRB 980425B is the familiar burst, which is generally called GRB 980425 (see [10] for the explanation). From the right panels of these two figures, one can see the two outliers have extraordinarily large lags, which should be the reason why they are classified as outliers. From the linear regression results, one can see the spectral time lag is proportional to duration of GRBs and anti-correlated to the spectral index $\beta$.

Without the two outliers, one finds ${\tau }_{\mathrm{lag},\mathrm{i}}=(-{1091}_{-164}^{+152})\times log{L}_{\mathrm{pk},52}+\left({684}_{-129}^{+118}\right)\times log{E}_{\mathrm{iso},52}+\left({703}_{-85}^{+37}\right)$. Considering $L_{\mathrm{pk},52}\sim E_{\mathrm{iso},52}/T_{90}$, this relationship is actually showing that the lag is anti-correlated to the total energy, i.e., with higher total energy, the lag is shorter.

The indication from Figure 3 is identified in Figure 4. It directly shows the proportional correlation to $T_{90}$ and the anti-correlation to $E_{\mathrm{iso},52}$.

Figure 5 introduces a new parameter, the spectral index $\alpha$. The lag is positively correlated to $\alpha$, i.e., with bigger $\alpha$, the lag is larger. Remember the anti-correlation to $\beta$ as shown in Figure 1 and Figure 2, i.e., with smaller $\beta$, the lag is larger. Notice that in general, $\alpha >0$, and $\beta <0$, which means the sharper the slope of the spectrum, the larger the lag. This is confirmed in Figure 6, where again ${\tau }_{\mathrm{lag},\mathrm{i}}$ is anti-correlated to $\beta$.

Figure 7 shows a positive correlation between the lag and the peak energy of GRBs. Another new correlation is shown in Figure 8, which is the anti-correlation between the lag and the variability. Because GRB 030528A does not have the value of $variabilit{y}_2$, we just have one outlier as shown in Figure 8. Both of them have larger adjusted $R^2$, indicating that the correlation is more reliable.

3.2. Remarkable Outliers without Significant Linear Regression

Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14 show the remarkable outliers without significant linear regression (with p-value greater than 0.05), which are clearly obvious. In some of these figures (e.g., right panel of Figure 10 and Figure 11), one can see that the sample without outliers shows apparent linear correlations. However, one cannot deduce an intrinsic correlation of the physical parameters, as the PAM method only identifies the outliers into apparent large distances.

From these figures, we found more outliers for different combinations of three parameters. The outliers are GRBs 980425B, 010921A, 030528A, 031203A, 050416A, 060502A, 060604A, 060605A, 060607A, 080319B, 080721A, 081221A, 090926A, 091127A, 100621A, and 130408A in different cases.

We also show the distribution of ${\tau }_{\mathrm{lag},\mathrm{i}}$ in Figure 15; the outliers are not obvious. Though the quantities are clearly larger for these GRBs, from the distribution itself, they could be inside a single distribution function. Only when they are combined with other parameters do the outliers become obvious. To show the distribution more obviously, we choose the logarithmic scale. However, to avoid the negative numbers, we put them in an independent panel, as shown in Figure 15. We also did not consider the error bars in the distribution, as that may arise the positive-negative value problem.

4. Discussion and Conclusions

By performing the PAM method on the GRB data, we expect to find some outliers. By removing the outliers, we then expect to find inner correlations with the remaining sample. In this work, we chose the spectral time lag selected sample together with other parameters, and we found that, in most cases, the outliers are GRBs 980425B and 030528A. This is mainly because they are the two GRBs with the largest spectral lags. However, there are also other outliers in other combinations. That means the value of the lag is not the only criterion. In some combinations of other two parameters, there are weak correlations obtained by removing the outliers, while there are also others having no correlations. As there are no strong correlations, we can not get very conclusive results from those correlations yet. We expect more combinations can reveal some underline correlations. Once we find tighter correlations, some of those correlations could be used as standard candle relations and could be used for more reliable cosmological studies.

It is interesting that the outliers are always GRBs 980425B and 030528A for those combinations having correlations (see Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8), while the others have more outliers. The reason for this is not clear yet. GRBs 980425B and 030528A both have very large ${\tau }_{\mathrm{lag},\mathrm{i}}$. In Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14, most outliers are not GRBs 980425B and 030528A. This is because not all the combinations include GRBs 980425B and 030528A. On the other hand, GRB 980425B is a low-luminosity burst [37], and GRB 030528A is an X-ray-rich burst [38]. They are both special GRBs.

With the accumulated data, one can perform both classification and correlation analysis on the data. One can also first classify the GRBs into several subgroups and look for the correlation for each subgroup. These processes may reveal the underlying nature. Outlier analysis is similar to the classification, while to find the outliers, which is the minority in the whole sample. Those outliers may indicate some special feature of the selected GRBs, which may reveal an independent origin (but much smaller samples), or a very different radiation mechanism. More outlier criteria (more parameter combinations) may reveal that in different aspects. For example, the soft $\gamma$ ray repeaters may lie in the sample of conventional GRBs from compact binary mergers or the collapse of massive stars and may be classified as outliers with a certain set of correctly selected parameters. If the outliers are real strangers, one may want to remove them from the whole sample. By omitting the outliers, the remaining sample may obey some laws, which can also be used to study the physics of GRBs. With the remaining sample, one may want to do a similar classification and correlation analysis. In the future, more comprehensive study, new patterns might be revealed.