1. Introduction
As we know, the astronomical observations on the luminosity–redshift relation of distant Type Ia supernovas [
1,
2] in the late 90’s gave the world a striking surprise that the universe is experiencing an accelerated expansion. This mysterious power is the so-called dark energy (DE), which has the feature of negative pressure and its equation of state (EoS)
, where
is its pressure and
is the density. It motivates the further observations and theoretical researches. Over the last twenty years, with the enhancement of observational accuracy [
3,
4,
5], measurements indicate that the current energy density in the universe is composed of 68.3% dark energy, 26.8% dark matter (DM) and 4.9% baryons; meanwhile, the relative constraints on cosmological quantities were developed from different aspects [
6,
7,
8,
9]. Until now, the
CDM model is still a decent explanation to the accelerated expansion, which has a constant equation of state (EoS)
as a candidate of DE in accordance with the observations. However, the
CDM model is not so perfect to unify all problems, such as reconciling the cosmological constant problem, the age problem and the coincidence problem [
10,
11,
12,
13,
14]. Then, phenomenally a vast of scalar field models have been researched to replace the cosmological constant
, while generally in those models pressure and energy density are expressed by certain forms of kinetic and potential in terms of a scalar and its derivative to time, such as, quintessence, phantom, k-essence and Dirac-Born-Infeld models, etc. [
15,
16,
17,
18,
19,
20,
21].
However, all the above models face the singularity problem, such as phantom field DE in classical Einstein cosmology, which leads to the Big Rip singularity for the fluids with
[
22]. Following the classical Einstein cosmology (EC), based on quantum geometry, loop quantum gravity (LQG) was developed as a background-independent, non-perturbative approach to quantum gravity, and has been applied as loop quantum cosmology (LQC), which adds a modified term
to the classical Friedmann equation [
23], as well as some other forms, as in [
24,
25]. Within the framework of LQC, this provides us with a novel means of researching the big bang singularity and the black hole singularity [
26,
27]. In LQC, the future singularities in the classical phantom models are avoided, instead, by a recollapsing universe, where a bounce universe in an oscillatory regime occurs when the total energy density reaches a Plankton value [
28,
29,
30,
31,
32,
33,
34]. In the case of constant EoS of DE [
35,
36], the bounce appears periodically forever, and the Hubble rate
H, with its derivative
, are bounded; in the case of a certain form of scalar field models with a variable EoS of DE [
29,
30,
37], the bounce has an infinite frequency of oscillations at a finite time in future, which leads to a diverge of
, and then the curvature singularity occurs for
. The dynamical properties of the phase space are also studied [
35,
37,
38]. In recent years, [
32] investigated the inflation in the LQC-modified scalar-tensor theory and [
39,
40] focused on the generalised EoS in LQC with interactions between DM and DE.
Originating from k-inflation [
41,
42,
43,
44], the k-essence model could be viewed as a generalization of the quintessence model, which has a canonical Lagrangian
. The k-essence model provides a variety of non-canonical Lagrangian terms, i.e.,
[
45,
46,
47], such as
,
,
and so on, which are used as the pressure of the dark energy [
48,
49,
50,
51,
52]. The action is described by a single scalar field
, and a canonical kinetic energy
. Some modified kinetic terms have been discussed, such as
and
[
45,
48,
49,
53,
54,
55,
56,
57]. The potential
takes many forms, such as
,
,
and so on [
58].
From the matter clustering properties, dark matter (DM) and dark energy (DE) are not the same substance; however there is research on the interactions between them, even some nonlinear interaction forms [
59,
60,
61,
62,
63,
64,
65,
66,
67], which could provide a mechanism by which to generate acceleration and alleviate the coincidence problem. A theoretical explanation of the transition of the DE Eos from
to
has also been presented. With the interaction between DM and DE,
and
do not separately satisfy independent conservation laws. Furthermore, a cosmological evolution system with DE, DM and unparticle with three kinds of interactions are researched in [
68].
In this work, since the k-essence DE models are not widely discussed in the frame of LQC, on the basis of our previous work [
69], we research the dynamical stabilities of the phase space of two kinds k-essence DE models in the framework of LQC, especially interactions between DM and DE. The first model is of
, where
,
, and
[
67,
69], together with a certain kind of interaction
Q. Another is of
, where
,
[
50,
51], together with interaction
Q. We investigate the possible cosmological behavior of these models in Friedmann–Robertson–Walker–Lemaître (FRWL) spacetime by performing a phase-space and stability analysis. The theory is based on [
70,
71], judging the stability of the critical points by their eigenvalues, whereas, in this model, for the convenience of calculation, the method using the determinant and trace of the Jacobian matrix of the autonomous differential equations is used [
72]. Some cosmological quantities will be calculated for each critical point, such as the dark energy density parameter
, the equation of state (EoS) parameter
of dark energy, and the deceleration parameter
q, to compare these with the case in Einstein cosmology without a loop quantum effect and the effect of interaction
Q. The effect of interaction
Q will be shown in the dynamical system for each model in LQC. In addition, for each model, a periodical bounce universe will be formed by setting suitable initial values in the dynamical system, in which both the Hubble rate and its derivative
are bounded. That is to say, both the Big Rip singularity and the curvature singularity are avoided. Throughout this paper, we work with a flat, homogeneous, and isotropic FRWL spacetime with a signature
and in units
.
This paper is organized as follows: in the next section, we will discuss the phase space analysis of k-essence dark energy models with Lagrangian
in the LQC framework with interaction
, where six critical points will be discussed. In the third section, we will choose another Lagrangian
in the model and proceed with the discussion using another set of phase variables, where ten critical points are discussed. For both models, the critical points in LQC are in accordance with the EC, which could be viewed as a generalization of EC [
51,
69]. However, compared with EC, in LQC the evolutions of the cosmological quantities are quite different in the early time universe; additionally, the evolution of the Hubble rate is bounded and oscillates forever. Finally, we close with a few concluding remarks in the fifth section.
2. Model I: in Loop Quantum Cosmology
In a flat universe, the effectively modified Friedmann equation in the framework of LQC is given by [
29,
30]
where
H is the Hubble parameter,
is the total energy density and
,
are the energy densities of dark energy and dark matter, respectively. The constant
is the critical loop quantum density, where
is the dimensionless Barbero–Immirzi parameter. Usually,
[
29,
35], and the LQC goes back to EC when
or
. Considering the interaction between DM and DE, the conservative equation of the total energy density
is represented as
From (
1), one can obtain the modified Raychaudhuri equation as
In this section, against the background of LQC, we consider a k-essence dark energy model with Lagrangian
as the pressure of the scalar field, while the energy density
. Then, the density parameter
, the EoS parameters
,
and the deceleration parameter
q are, respectively, given by
where
and
. And according to
, it has
.
The equation of motion for the k-essence field is given by
where
. Equations (
3) and (
5) are usually transformed into an autonomous dynamical system when performing the phase-space and stability analysis. By setting the phase variables:
where
by Equation (
1), and using Equation (
12), the modified Friedmann Equation (
1) and Raychaudhuri Equation (
5) become
Then, the autonomous dynamical system of the phase variables is:
where the prime denotes for the derivative to
and the parameter
. In this work, we chose
(
k is a constant), then
and
simultaneously became constants. As a result, the 4-dim system became a 3-dim system made by
.
By choosing
and
, the autonomous system was:
for
; while, for
, the system was
which has two parameters, i.e., the potential one
s and the coupling one
. If
, as no loop quantum gravity modification, the dynamical system goes back to the classical k-essence case, as in [
69]. Meanwhile, the cosmological quantities (
7)–(10) can be rewritten by the phase variables as:
The corresponding critical points
for
are
While, for
, the critical points are:
The six critical points above are shown in
Table 1, in which we also present the necessary conditions for their existences, as well as the corresponding cosmological quantities
,
and
q in form of parameters
s and
at each critical point. With these cosmological quantities, we could investigate the final state of the universe and discuss whether an acceleration phase exists. The existences are based on the physical meaning of
x,
y and
z, and
for
,
and
; however,
for
,
and
. They also require
and
according to the definition. Thus,
and
are excluded by the existence requirement. Meanwhile,
, and
are needed to accelerate expansion. From the viewpoint of LQC, all critical points have
, while
and
are as same as in EC [
67,
69], which implies that the loop quantum gravity effect vanishes and the EC dominates the whole universe in the late-time universe.
The stability of each point, except
and
, is analysed by the three eigenvalues
,
,
of the
Jacobian matrix as in [
29,
37,
38] for the 3-dim system:
Point : , , ,
Point : , , ,
Point : , , ,
Point : , , ,
where .
Points
and
each have three real eigenvalues, which implies
for stability. However, points
and
, have a real eigenvalue
and a pair of quadratic eigenvalues
and
, which indicates the decomposition of an 1-dim subspace and a 2-dim subspace. The stability requires that the single real eigenvalue
; meanwhile, the 2-dim subspace requires a determinant larger than zero and trace of less than zero, i.e.,
and
, without determining whether
and
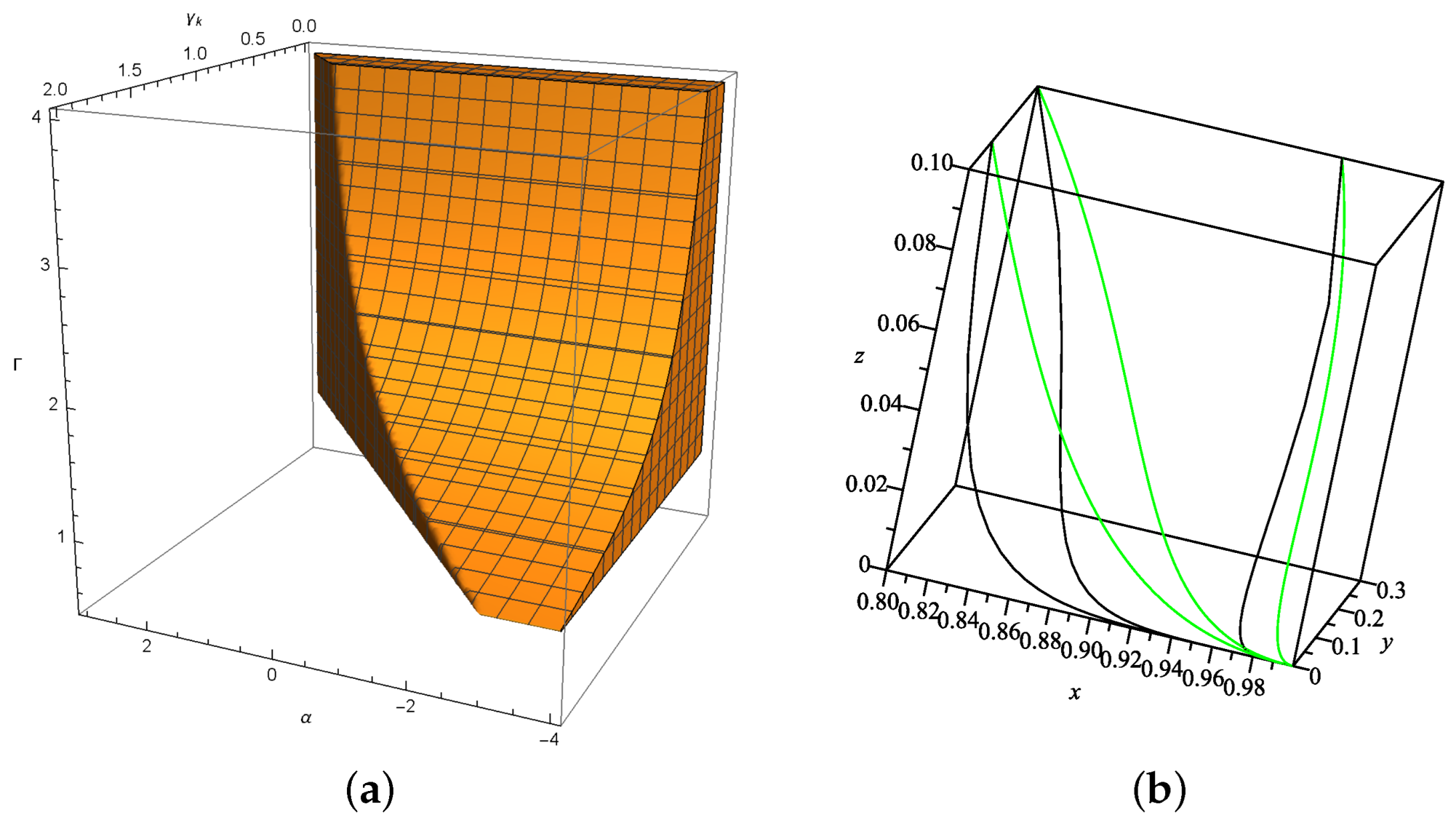
are real numbers or complex ones. Additionally, constrained by the existence, stability,
and the accelerating expansion requirement
, the corresponding value ranges for parameters
and
s are depicted in
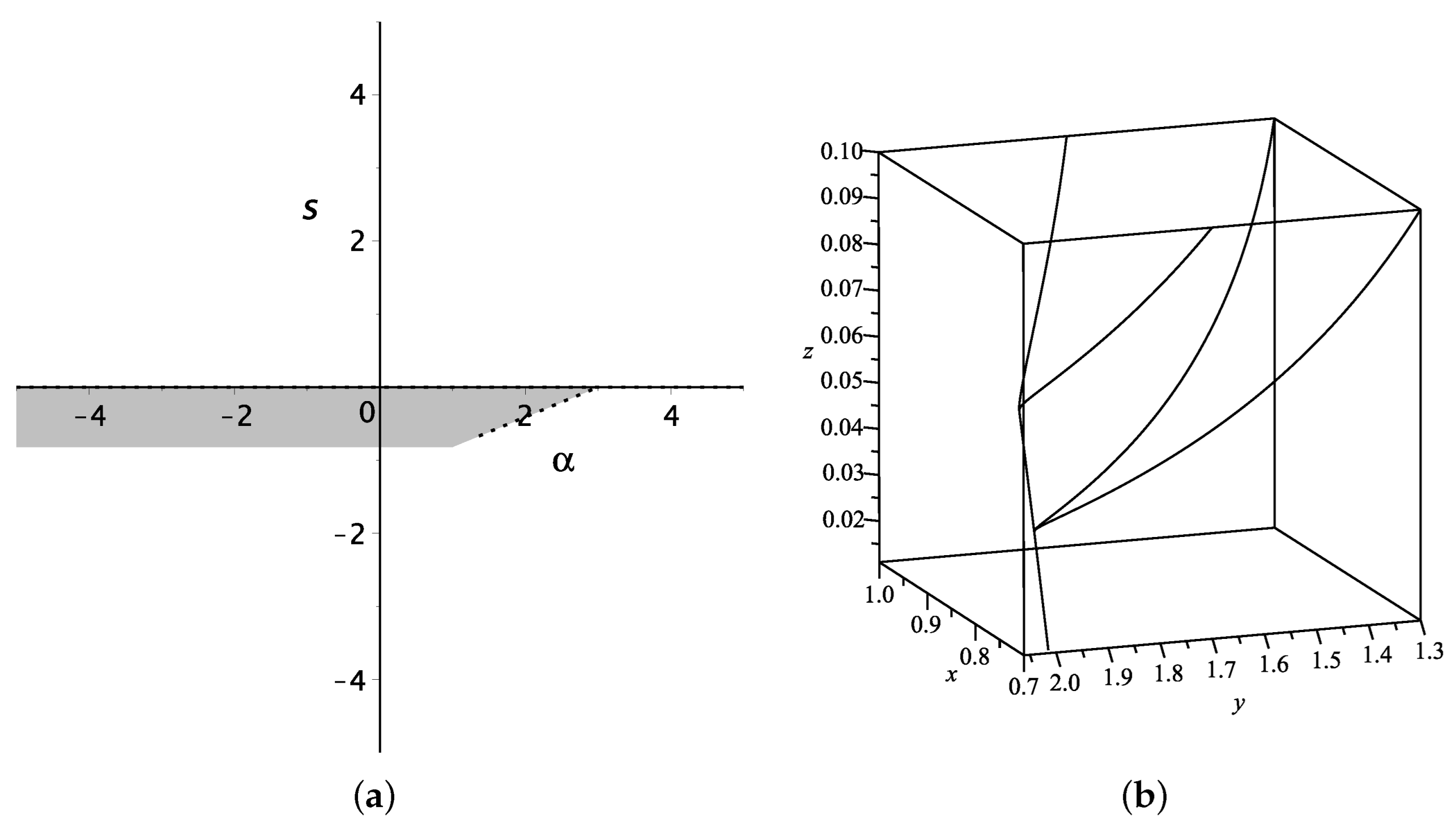
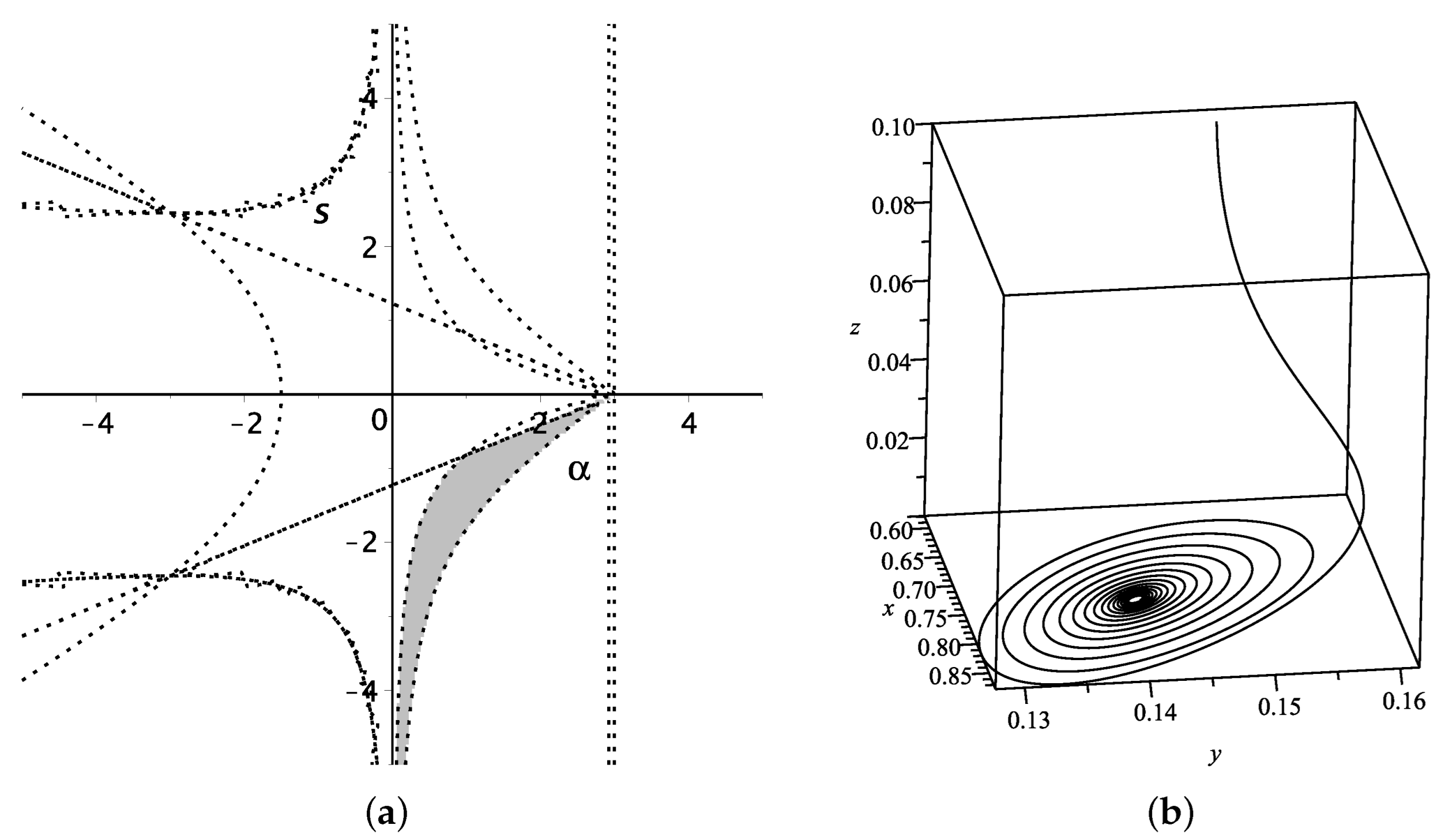
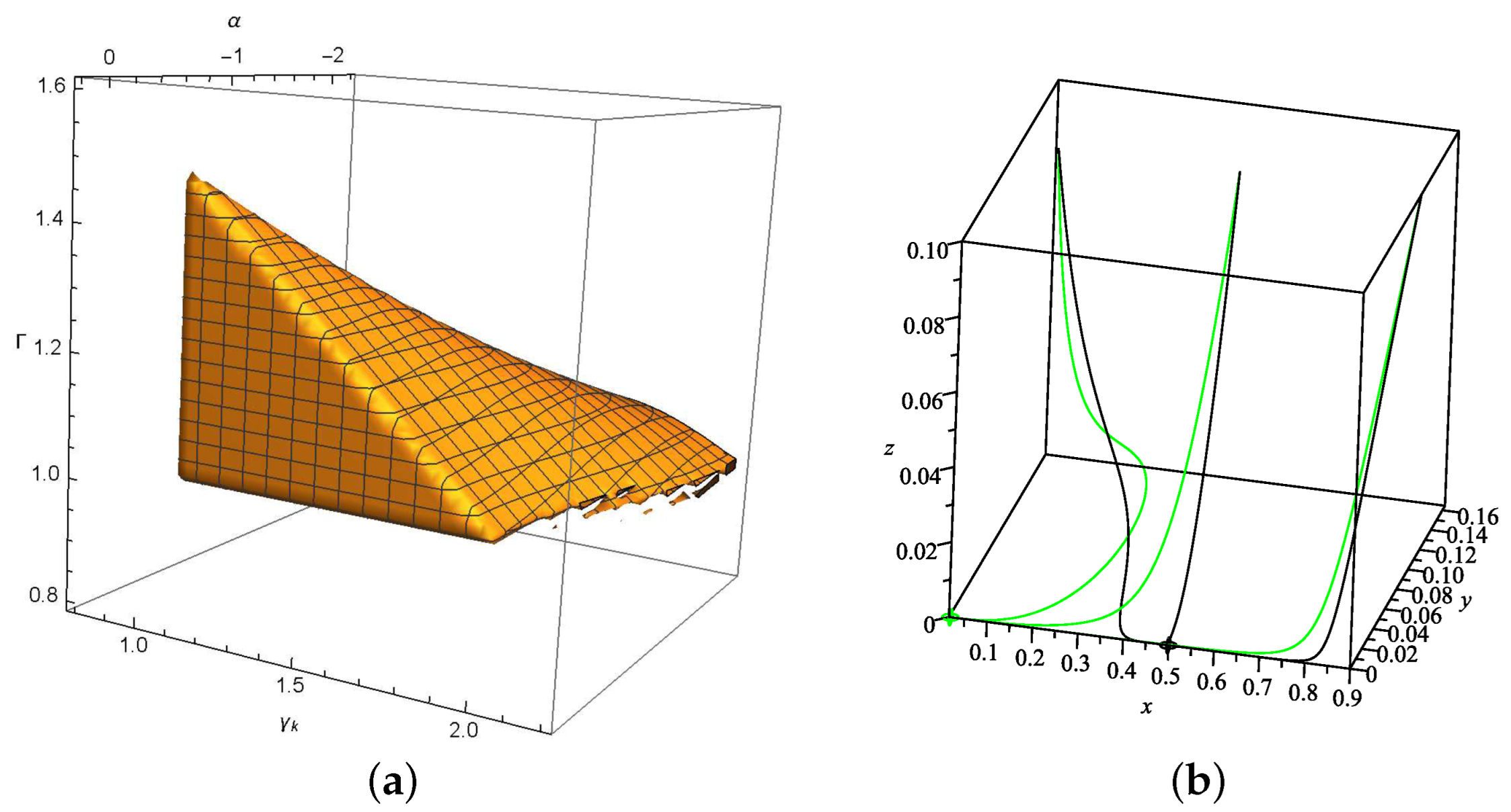
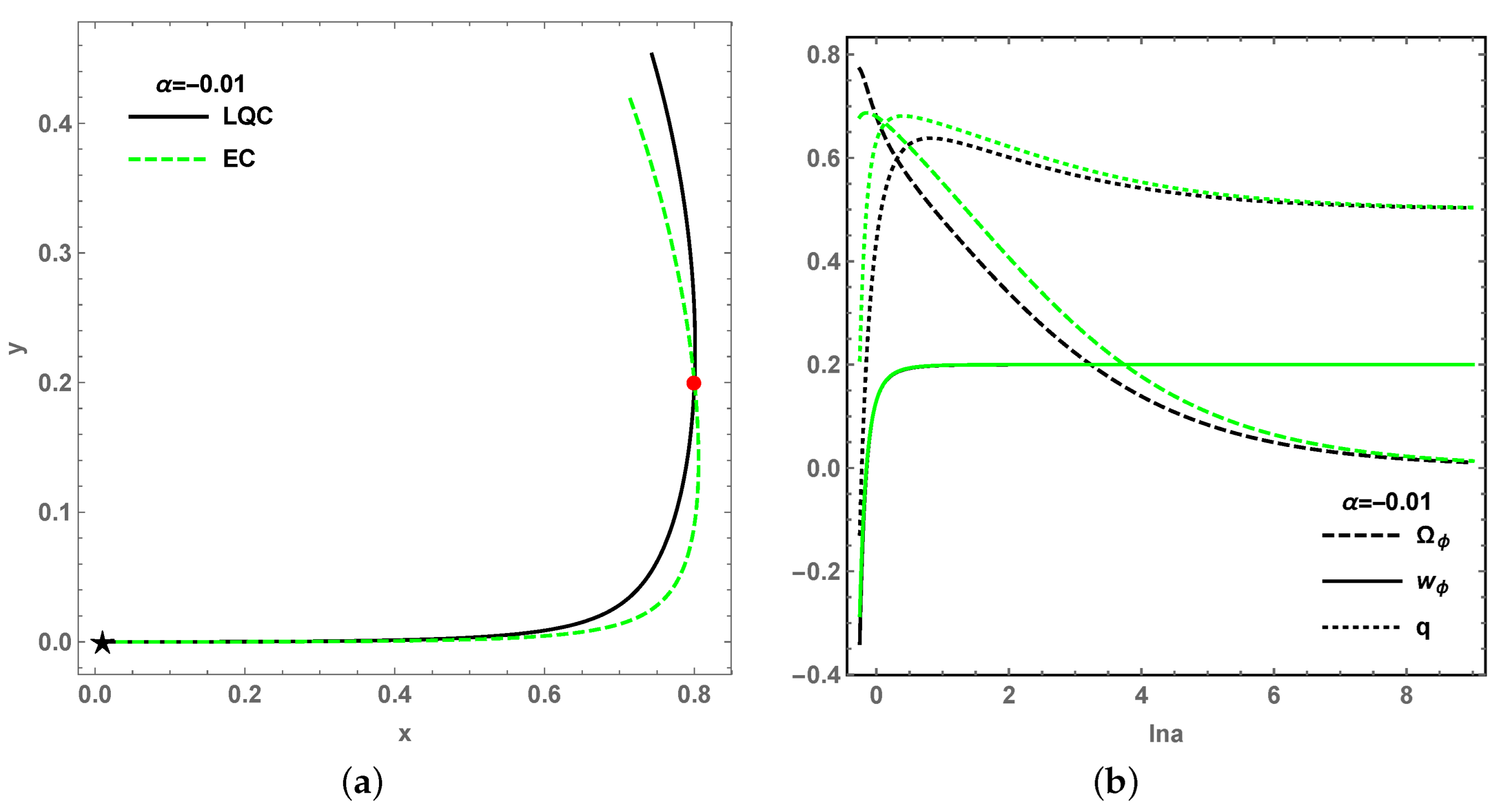
Figure 1a for
and
Figure 2a for
. Meanwhile, with the observational constrains of
in [
59],
in [
60], and
in [
5], together with the expressions of
for each stable point in
Table 1, parameters
and
s are constrained in certain values, i.e.,
for
and
for
. To make comparisons with different coupling parameter values
, we set
in Model I. Since the properties for
are symmetrical to
, we only show the evolutional trajectories in the 3-dim phase space around
(
,
) in
Figure 1b and
(
,
) in
Figure 2b. With suitable parameter values, all trajectories around
and
drop down from
to
, and converge to the attractors
and
on
x-
y plane, respectively.
Then, we will make two kinds of comparisons: the first one is between LQC and EC from the perspective of trajectories in phase space, and the second one is the effects on the evolution of cosmological quantities for different values of
s and
. First, compared with the former work in EC [
69], there is no difference in the form of
and
for each critical point in LQC, and
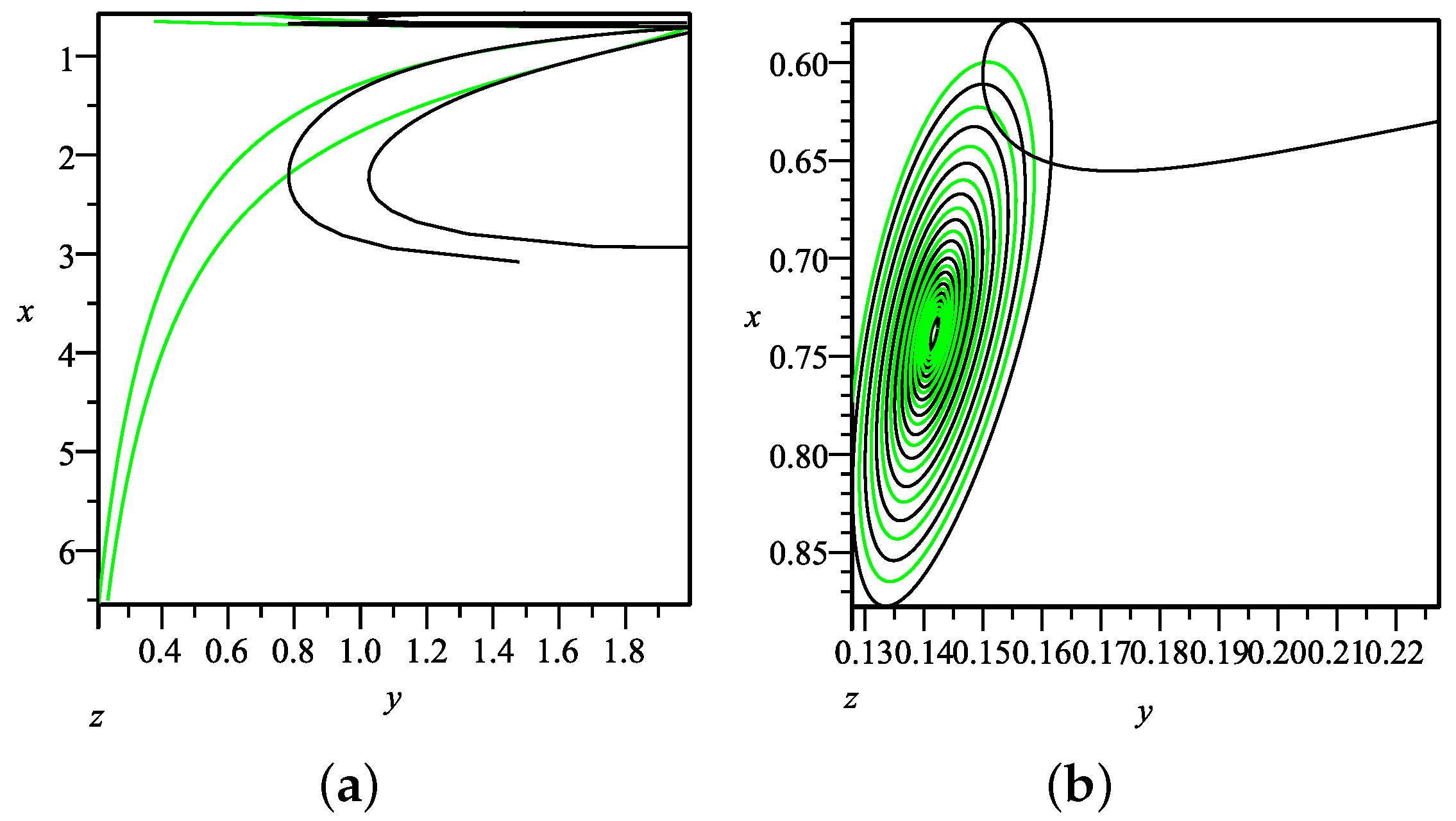
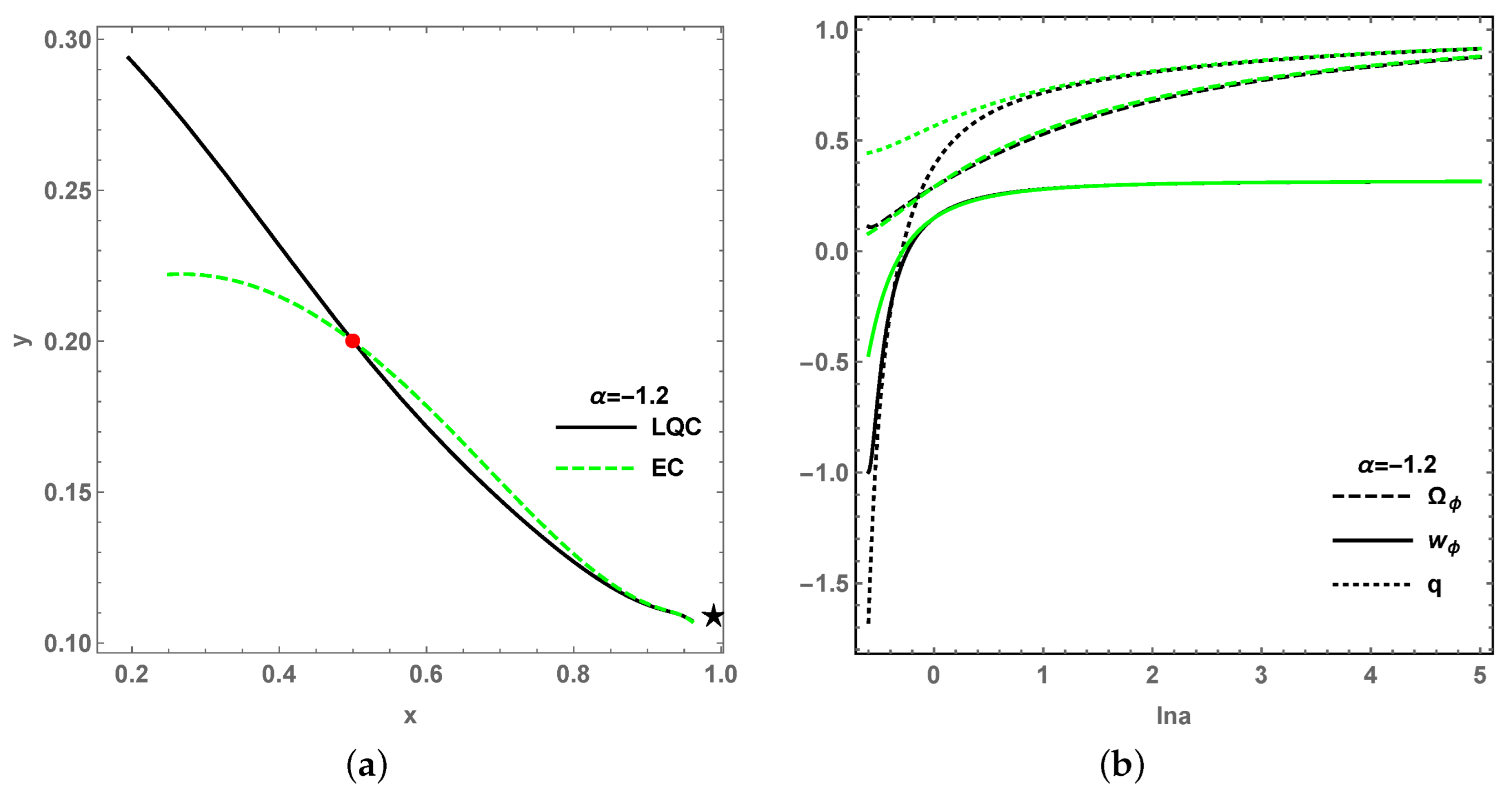
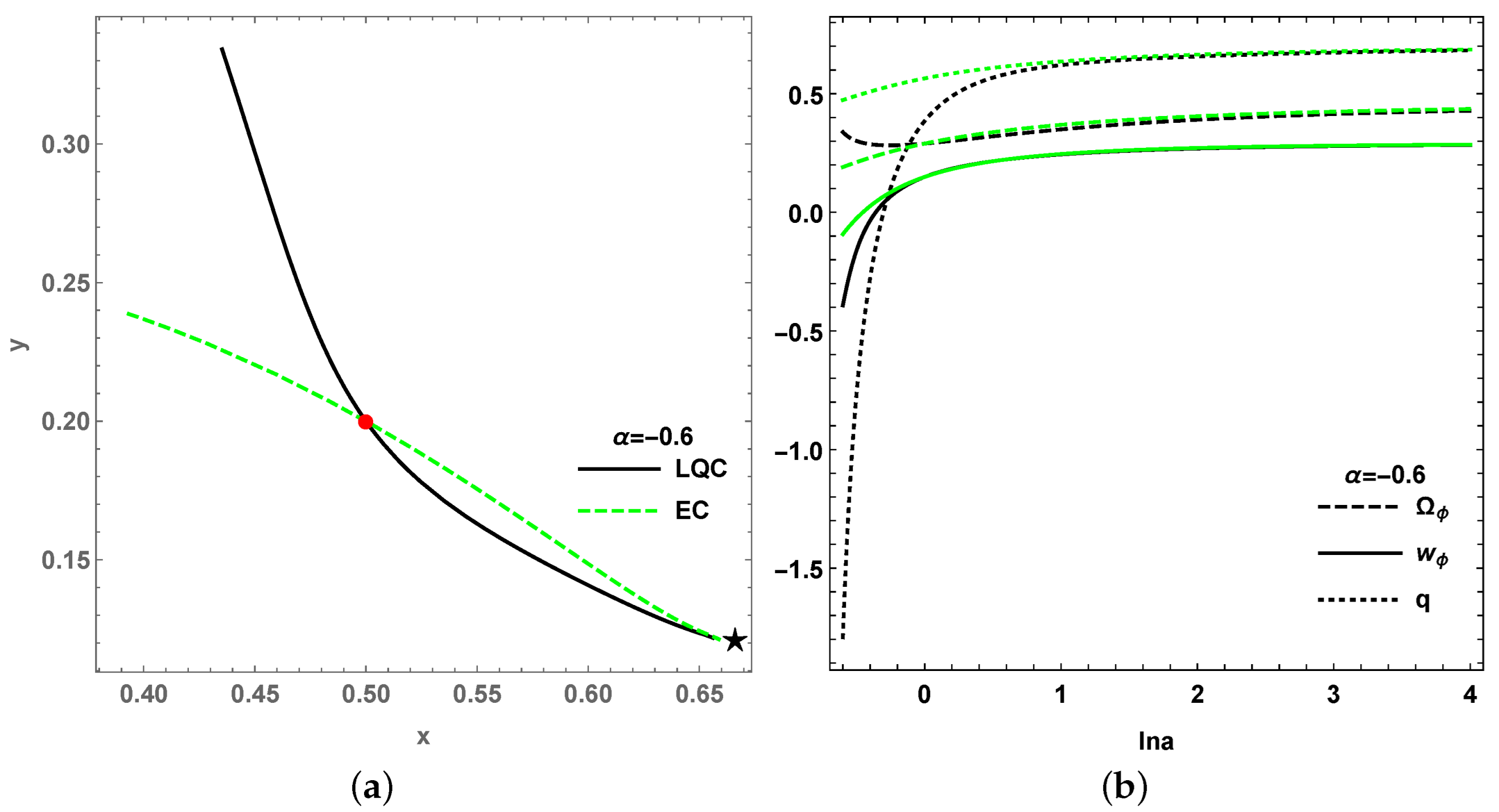
for all critical points, which indicates that the final states of the universe are scarcely effected in the LQC. However, the early universe is effected in LQC model, which is shown by the projection of evolutional trajectories from the 3-dim phase space onto
x-
y phase plane for the past, i.e.,
,
, as in
Figure 3, where the trajectories of LQC further separate from the EC ones due to the effect of the LQC phase variable
z as
. As a result, the evolution of each cosmological quantity of LQC varies from that of EC in the early universe, but reaches an identical and stable value in the future, as shown in
Figure 4 and
Figure 5. (It is interesting that the oscillation of
in
Figure 5 is due to the long period spiral around
, as in
Figure 2b; however,
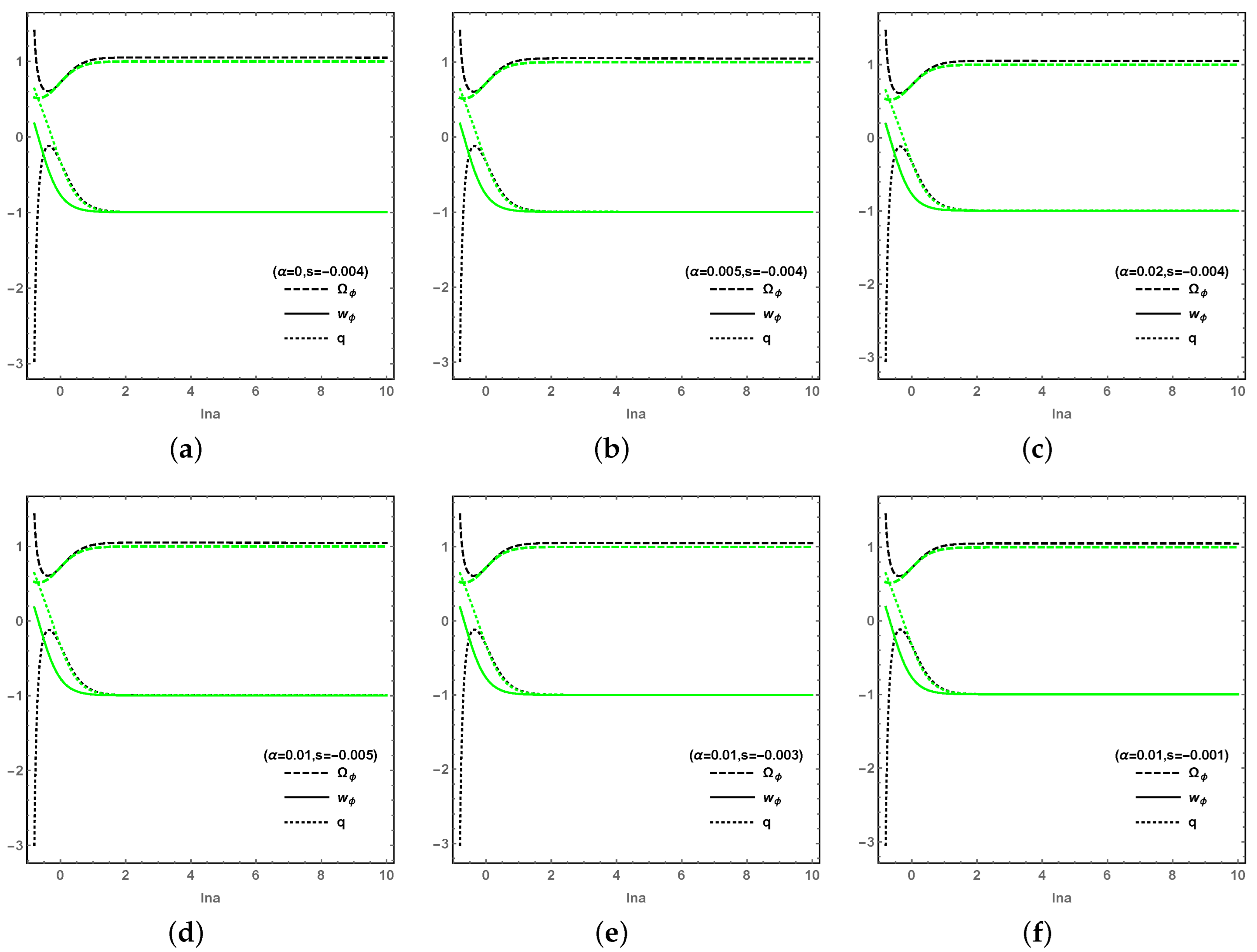
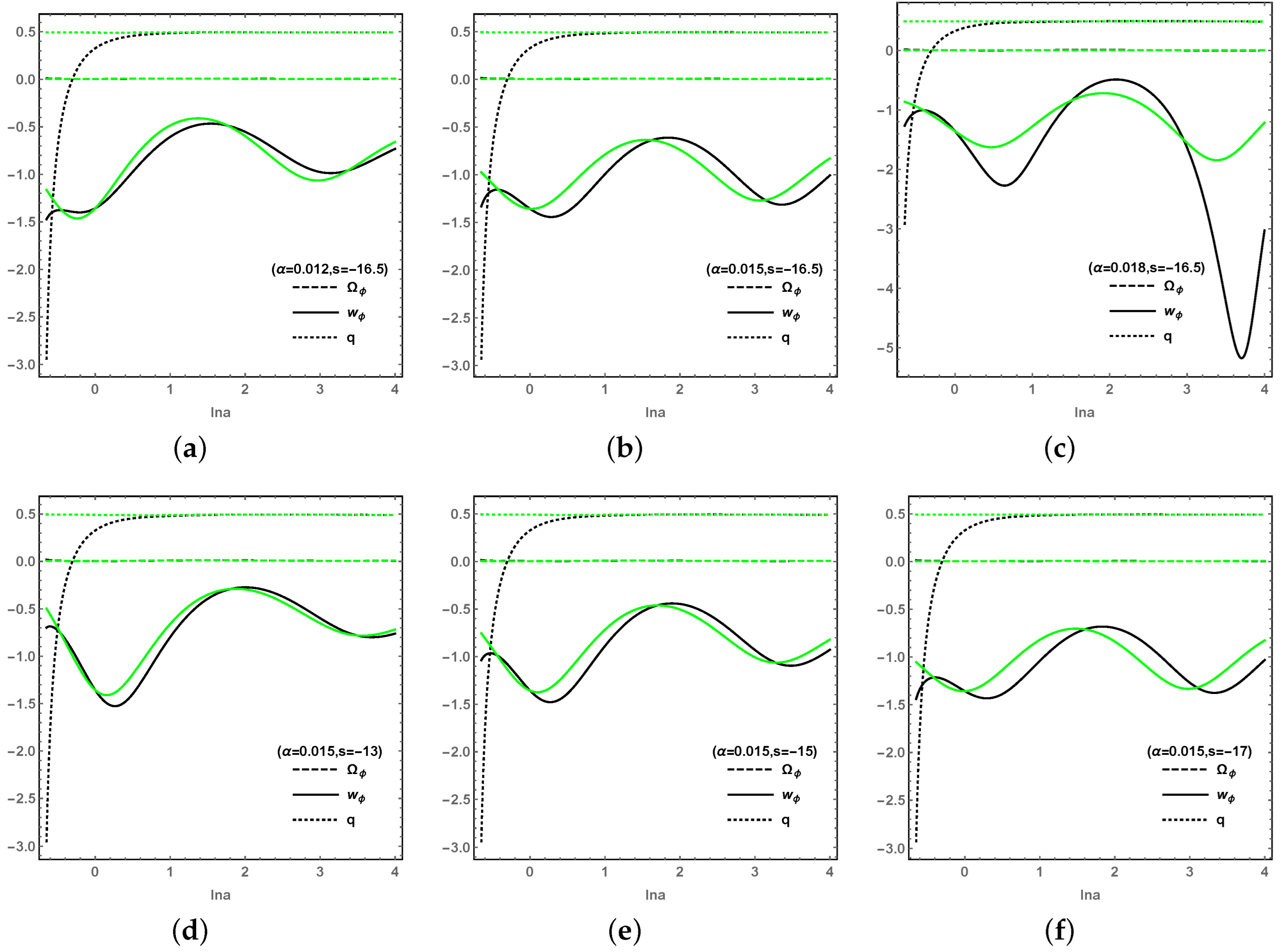
finally reach an identical and stable value in both LQC and EC for a longer period.) Second,
Figure 4 shows that the coupling parameter
and the potential parameter
s have little effect on the evolution of the cosmological quantities. From
Figure 5, the effects of
and
s on the cosmological quantities
and
q are not obvious, but the EoS of DE
is sensitive to both the coupling parameter
and the potential parameter
s. It is worth noting that, without the observational constrains on
and
s, the evolution curves of each cosmological quantity obviously vary with larger values of
and
s.
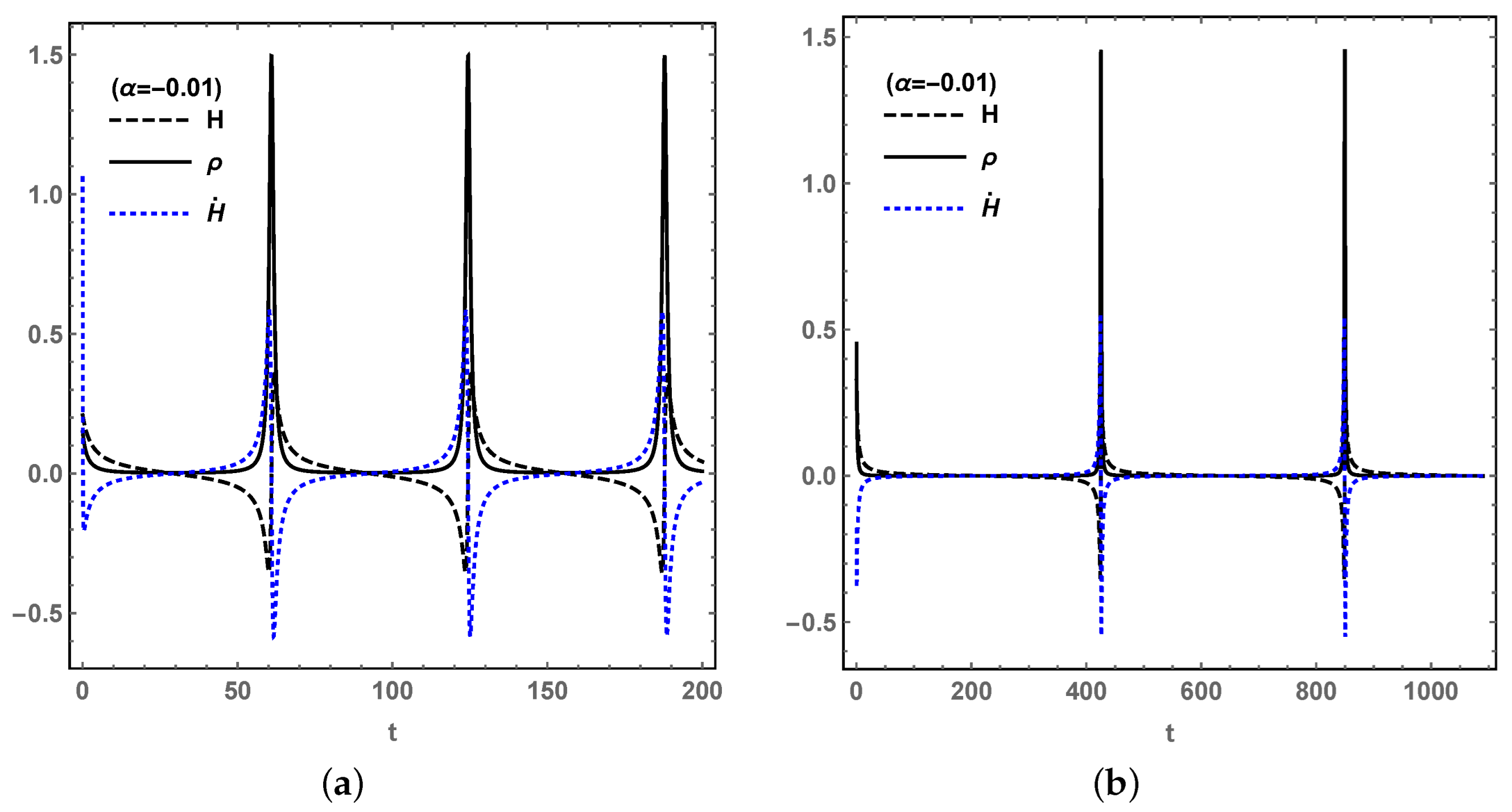
It is well known that the LQC could lead to a bouncing solution [
35,
36], which helps to avoid singularities. We drew the evolutions of
H,
and
in
Figure 6 and
Figure 7 for
and
, respectively, which are based on another autonomous dynamical system composed of the derivative of
,
,
H and
with respect to
t, as in [
29,
30]:
We set the initial value of
,
,
and
under the conditions of the initial loop quantum gravity effect, as
, i.e.,
. Then,
from Equation (
1). For
,
as
were obtained by the definition; while,
and
were obtained for
around the stable point
. For another stable point
,
as
by the definition, while
and
for
around the stable point
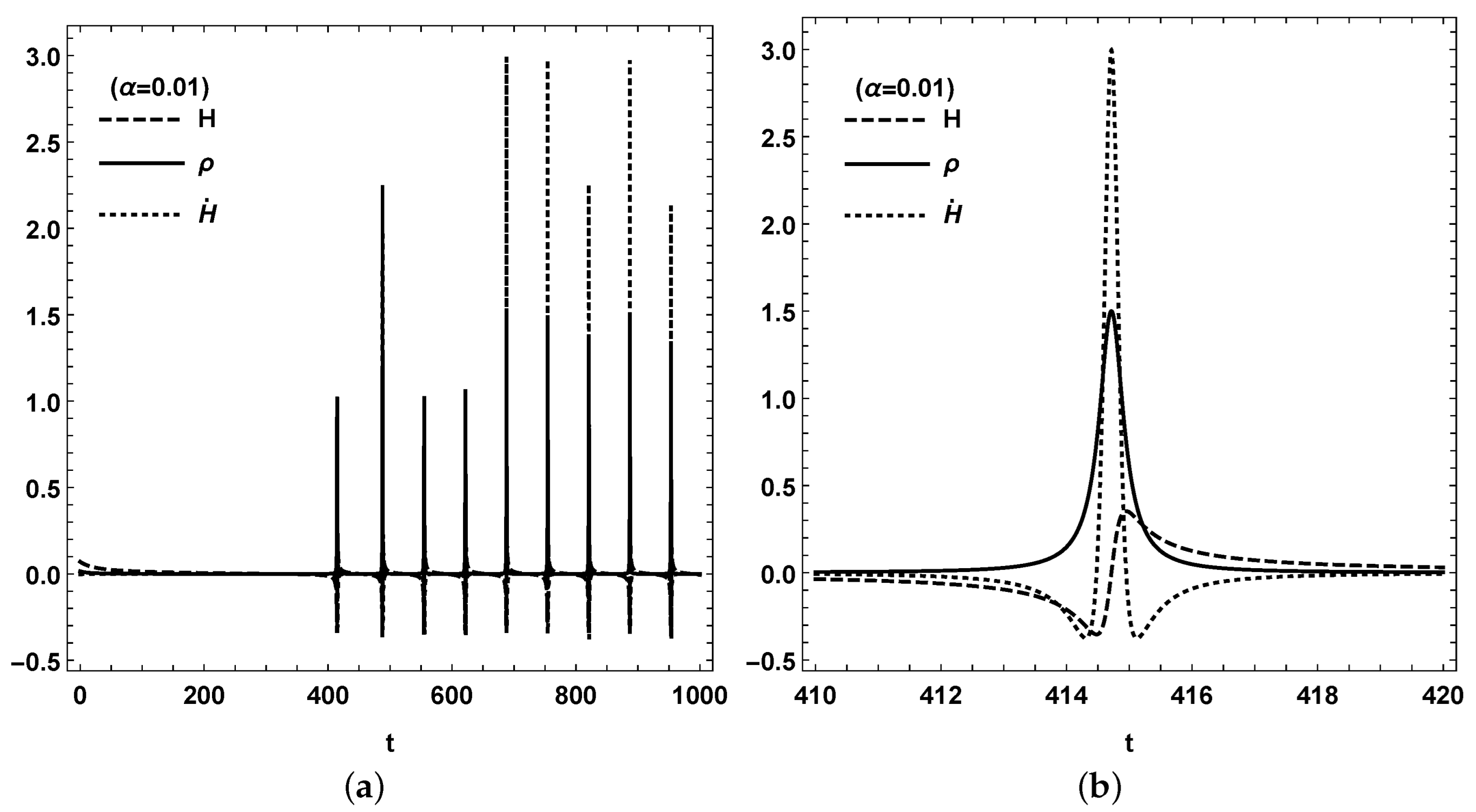
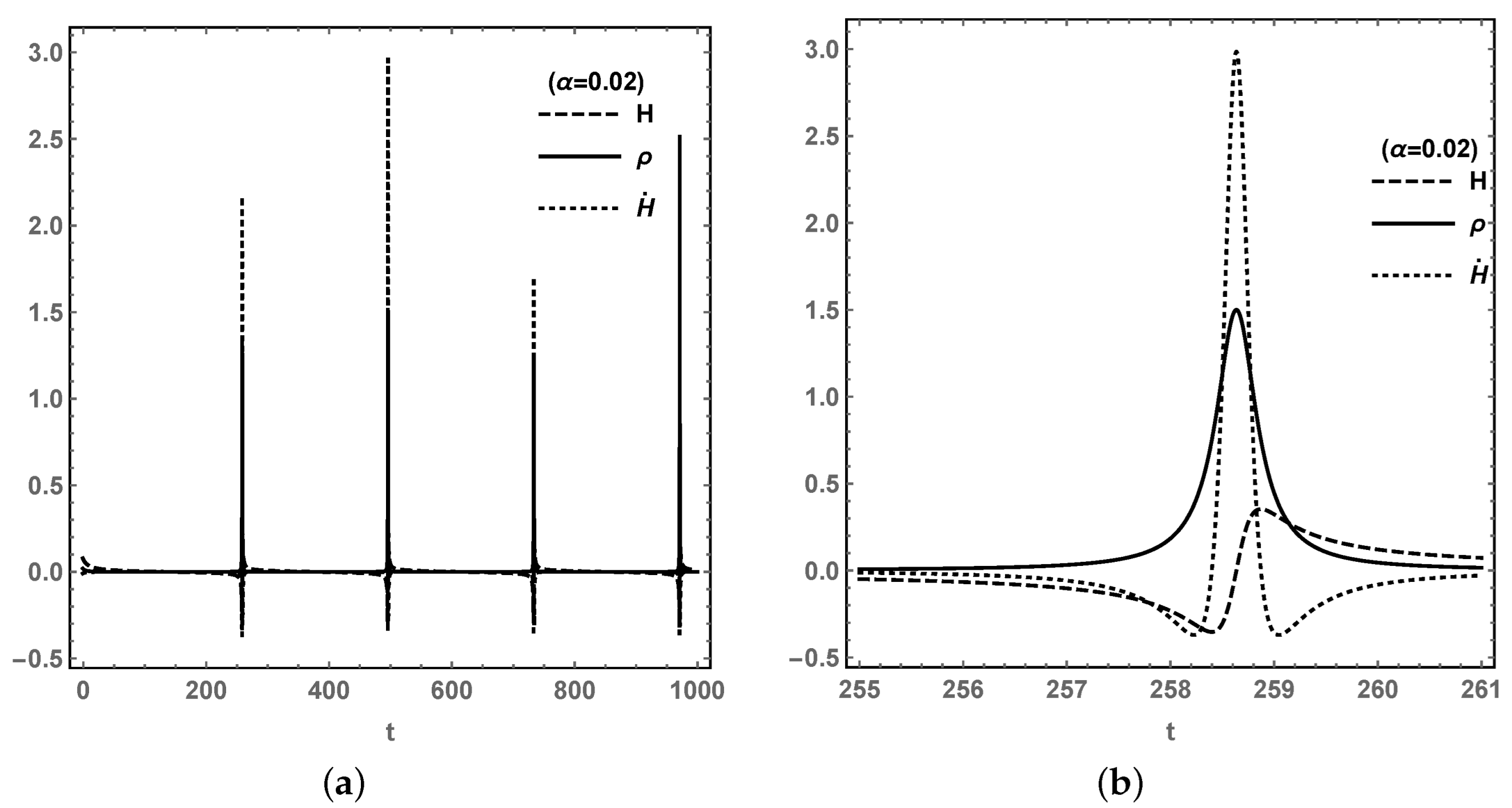
. In both cases, the bouncing is terminal, which indicates that the LQC effect acts not only in the early universe but also in future; then, the Big Rip singularity will not appear in future. In addition, the bounce appears periodically forever and the Hubble rate
H with its derivative
are bounded; then, the curvature singularity is avoided for
. From
Figure 6b and
Figure 7b, when
reaches the maximum
, the Hubble rate becomes zero for Equation (
1), and
also reaches its maximum. On the left-hand side of the bouncing,
is the universe expanding backwards, while on the right-hand side, the universe keeps expanding for
. It can be concluded that, in future, although each of the cosmological quantities reach a stable value at the stable point, the total energy density
oscillates, which leads to the bounce in
H and
as a recollapse universe.
3. Model II: in Loop Quantum Cosmology
In this section, we consider another kind of k-essence dark energy model with Lagrangian
then the energy density and the corresponding cosmological quantities, such as the DE density parameter
, the decelerating parameter
q, and the EoS parameters, are given by
According to the method in [
50,
51], in (
40) we let
, by setting the phase variables as
Then, the general autonomous dynamical system of the phase variables with three parameters
,
,
and interaction
Q is as follows,
where
,
,
. In [
73], this provides a novel setting of phase variables based on a special
, as in [
57]. Whereas, in this work, by setting
and
, the three variables
,
and
become constants. The interaction is
, as in model I, then
in (
46). For
, the above equations go back to the case in Einstein cosmology, as in [
50,
51]. By solving the equations above, we obtain eight critical points. For existence,
,
and
are required by definition. It is also constrained by
for physical meaning in the late-time universe, and
for accelerating expansion. The details are listed in
Table 2. In this case, the cosmological quantities expressed by the phase variables are as follows:
The eight critical points for
are:
where
and
.
only exists for the coupling parameter
. It is very interesting that, under the action of the interaction
Q, the system has four extra critical points
,
,
and
, and they are only for
as non-zero interaction between DE and DM. From the perspective of LQC, unlike other critical points, this has
in
and
, which indicates that the loop quantum effect still exists in the final states, corresponding to these two points. However, from the requirement
, the existences of
and
contradict the physical meaning. That is to say,
and
are out of discussion, though
is mathematically stable, as discussed later.
The stability of the dynamical system around each critical point is analysed by the eigenvalues
,
,
and
of the
Jacobian matrix, as in [
38]:
Point : , , , ;
Point : , , , ;
Point : , 0, , ;
Point : , , , ;
Point : , , , ;
Point : , , , ;
Point : , , , ;
Point : , , , .
Among those critical points, only
and
satisfy both the existence and stability properties (
is supposed to be equivalently infinitesimal in the calculation of the eigenvalues of
and
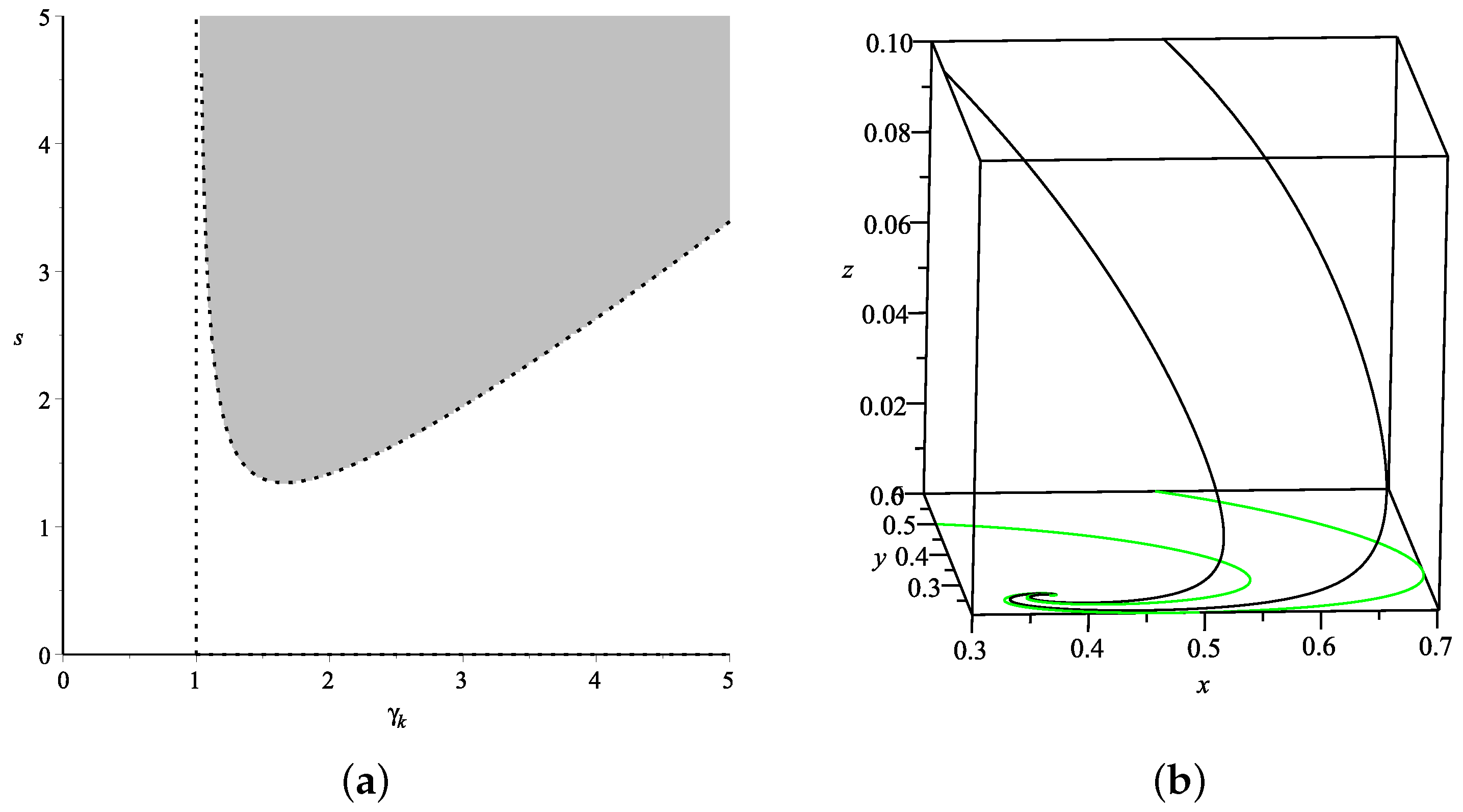
). We plotted the value region for parameters
,
and
in
Figure 8a and
Figure 9a, together with the dynamical evolution in the 3-dim phase space of
with each initial points and parameter values in
Figure 8b and
Figure 9b. In Model II, the stability condition and physical properties of some parameters move the value range of the parameter
out of the constrain
for some stable points. Since
is not effected by the coupling parameter
, the trajectories of
and
start from the same initial point and then converge to the same stable point
, but the process differs according to the effect of interaction.
means the universe is dominated by DE, and (
,
) means the DE is composed by kinetics totally. As
is effected by the coupling parameter
, the trajectories with
and
start from the same initial point but converge to different stable points. The DE density parameter
is affected by the interaction between DE and DM, i.e., the universe is composed of both DE and DM.
By using the symmetry analysis in [
50,
51] for specific Lagrangian
, the 3-dim dynamical system is reduced to a 2-dim one in EC. In this work, the analogous analysis acts in the frame of LQC to reduce the 4-dim system to a 3-dim one. With
as an independent variable instesd of
, the equations of
,
,
and
are rewritten as
If we consider
,
X,
and
as the independent variables (
is composed of
and
X), it has the transformation:
,
,
,
. Since
, by the transformation above, the Hubble parameter should hold the transformation
. However, to leave Equations (
62) invariant requires
. The relation of
n and
can be written as
, then
as a result; further, the symmetry allows for a reduction in the dynamical system from four variables into three, as follows:
where
. As a result, the system (
46) reduced to the following 3-dim form with three parameters of
,
s and coupling parameter
as follows:
Then, there are two new critical points
and
:
is found in these two critical points, which indicates that the LQC effect disappears in the late-time universe. However, for both of the critical points containing
with
inside, the expressions cannot be analytical. As a result, the stability analysis by the Jacobian matrix cannot proceed (the interaction
diminishes the coupling parameter
by substituting
into (
67)), instead we will take certain parameter values for later calculation. Using the expression (
70),
is not effected by the coupling parameter
, while the interaction effects
, as in (71). These two critical points are in accordance with [
51], in EC for the no interaction case, i.e.,
. In LQC, by setting
,
is lucky to have the analytical form
, which is expressed by parameters
and
s, by substituting
and
into (
66):
With the analytical form of
, the stability can be discussed using the eigenvalues of the
Jacobian matrix of the system, as shown below:
in which
. We calculated the value ranges of parameters
and
under the condition of existence, physical meanings and stabilities for
, which are listed in
Table 3 and depicted in
Figure 10a. By setting
and
, from
Figure 10b, which shows that
has the same stability for both EC and LQC, which indicates that the late-time universe of LQC is in accordance with EC and the loop quantum effects vanish in the late-time universe.
After discussing the critical point
of the analytical form above, we research the general forms
and
, which are non-analytical, below. Here, we set
,
and
, i.e.,
, as in [
51], to compare EC and LQC. In this case,
and
; then,
becomes the only parameter. Numerically, point
with the eigenvalues
behaves as follows:
Compared with [
51] in EC,
and
are the same as the ones in EC and, in this work, the stability condition requires
to make the critical point stable by
< 0; while, in [
51]
of no interaction means that this point is a saddle point.
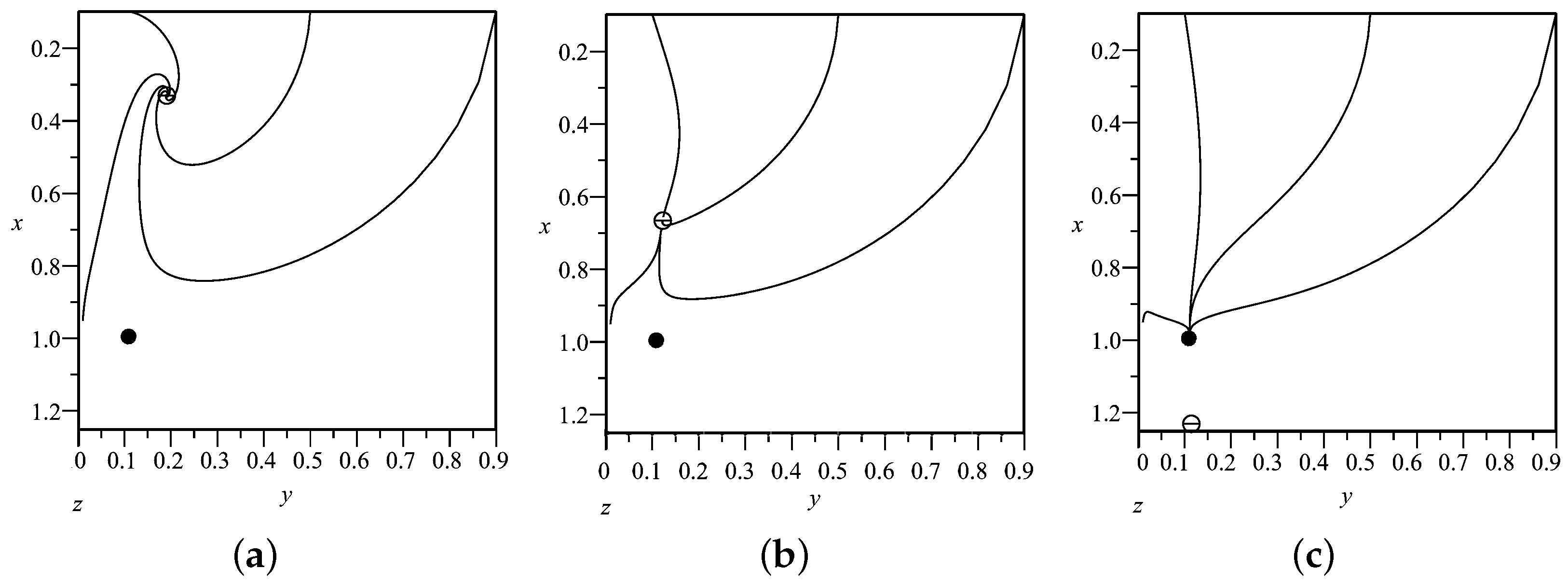
Figure 11 shows the effect of coupling parameter
. Although
has no effects on the location of the critical point
, it effects the stability, i.e., from
Figure 11a–c
becomes a stable point from a saddle point by changing the value of the coupling parameter
. Conversely, for
, by setting
, this is the stable point
, in accordance with [
51] in EC; then, by changing
from 0 to
, it becomes an unstable point. It can be concluded that coupling parameter
effects the stability of the critical points
and
. Further, from
Table 2, the critical points
and
cannot be stable simultaneously under the stability condition.
Based on all four stable points
,
,
and
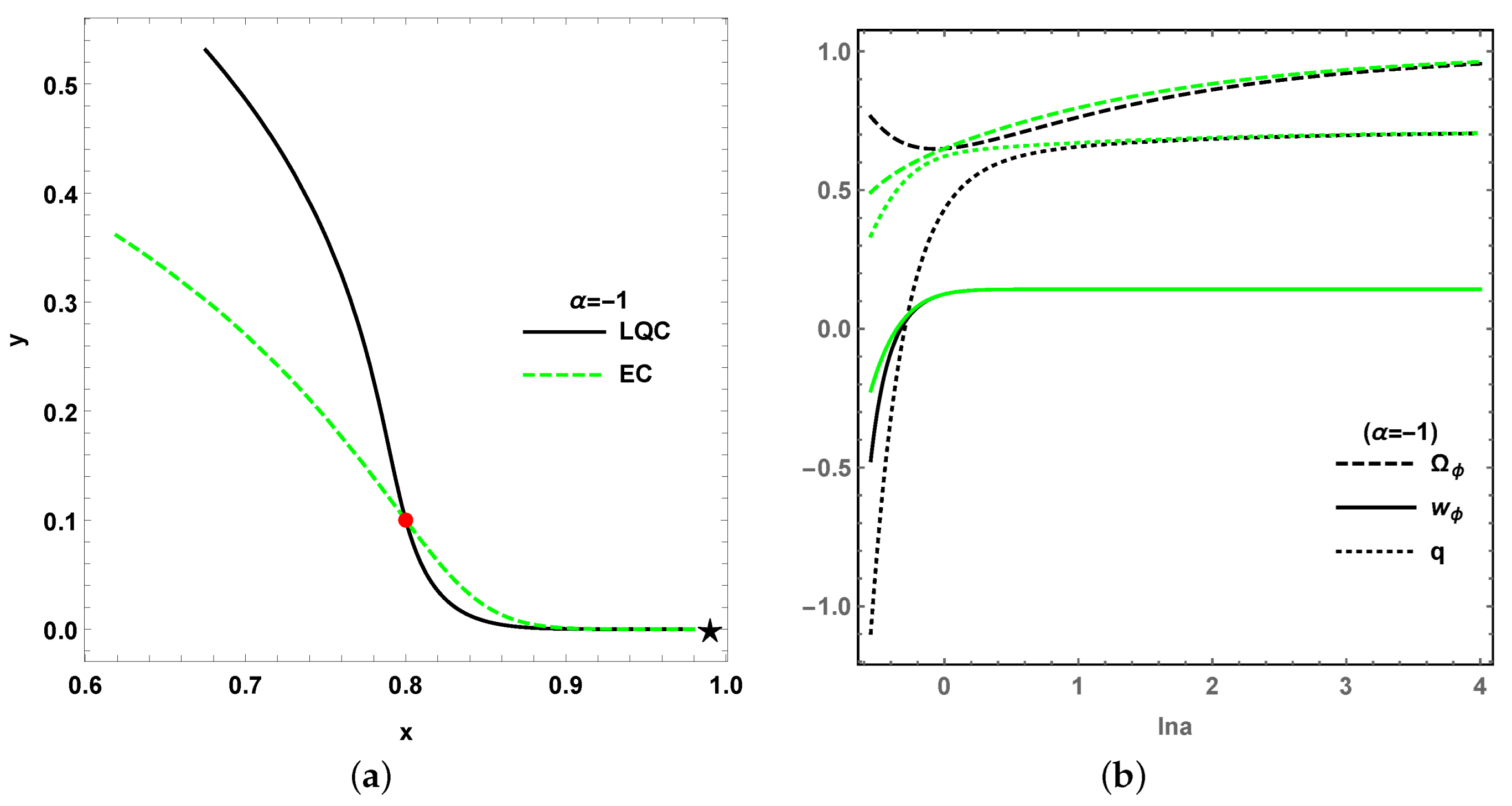
in model II above, to delineate between the effect of LQC and classical EC, the evolution trajectories for both LQC and EC are projected onto the
x-
y phase plane, as shown in
Figure 12a,
Figure 13a,
Figure 14a and
Figure 15a. It can be seen that the dynamical evolutionary trajectories for both LQC and EC, starting from the same initial points around stable points, comply with each other in the late-time universe. However, the trajectories for the early universe as
bifurcate from each other. As a result, the values of cosmological quantities in LQC are varied from EC in the early universe, as the loop quantum gravity effect is obvious; however, for the late-time universe with the diminishing of loop quantum effect, the evolutions of the cosmological quantities show no difference from LQC to EC, as depicted in
Figure 12b,
Figure 13b,
Figure 14b and
Figure 15b.
Finally, we discuss the evolution of
,
H and
, choosing certain parameter values and initial values in another dynamical system, formed as in Model I, as below:
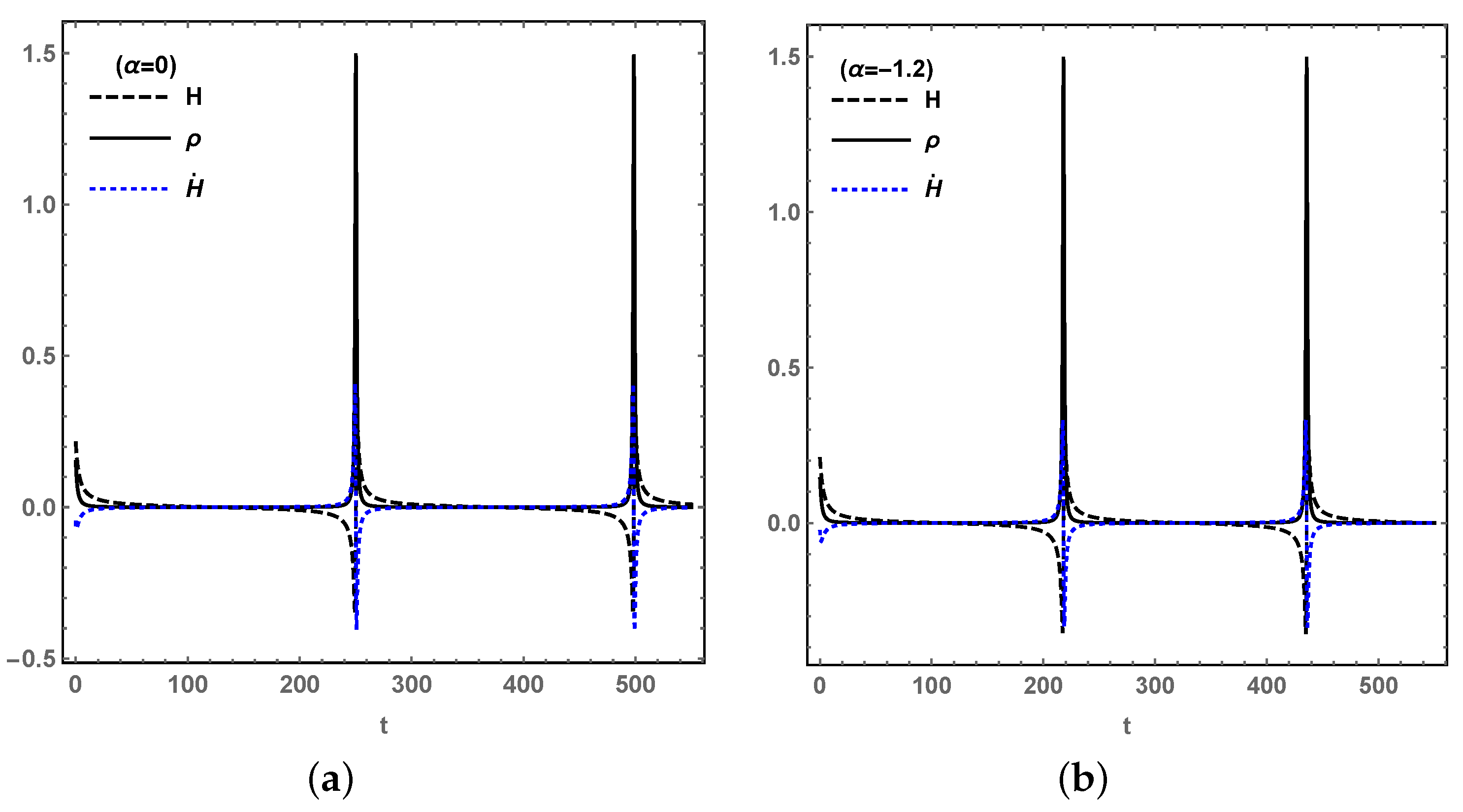
With the effect of LQC on cosmological evolution, we can predict that the future universe will experience an oscillating processes, which avoidd the Big Rip singularity and curvature singularity as
H and
are bounded.
Figure 16 is based on
for different initial values of
and
, from which the bouncing period is prolonged by larger values of
and
.
Figure 17a is based on
for no interaction, i.e.,
, while
Figure 17b is based on
for coupling parameter
, which shows that
has little effect on the bouncing. The initial values of
and
based on definition (
45).