Abstract
We reanalyze in a simple and comprehensive manner the recently released SH0ES data for the determination of . We focus on testing the homogeneity of the Cepheid+SnIa sample and the robustness of the results in the presence of new degrees of freedom in the modeling of Cepheids and SnIa. We thus focus on the four modeling parameters of the analysis: the fiducial luminosity of SnIa and Cepheids and the two parameters ( and ) standardizing Cepheid luminosities with period and metallicity. After reproducing the SH0ES baseline model results, we allow for a transition of the value of any one of these parameters at a given distance or cosmic time , thus adding a single degree of freedom in the analysis. When the SnIa absolute magnitude is allowed to have a transition at Mpc (about 160 Myrs ago), the best-fit value of the Hubble parameter drops from km s Mpc to km s Mpc in full consistency with the Planck value. Additionally, the best-fit SnIa absolute magnitude for drops to the Planck inverse distance ladder value , while the low distance best fit parameter remains close to the original distance ladder calibrated value . Similar hints for a transition behavior is found for the other three main parameters of the analysis (, and ) at the same critical distance Mpc, even though in that case, the best-fit value of is not significantly affected. When the inverse distance ladder constraint on is included in the analysis, the uncertainties for reduce dramatically ( km s Mpc), and the transition model is strongly preferred over the baseline SH0ES model (, ) according to the AIC and BIC model selection criteria.
1. Introduction
1.1. The Current Status of the Hubble Tension and Its Four Assumptions
Measurements of the Hubble constant using observations of type Ia supernovae (SnIa) with Cepheid calibrators by the SH0ES team has led to a best-fit value km s Mpc [1] (hereafter R21). This highly precise but not necessarily accurate measurement is consistent with a wide range of other less precise local measurements of using alternative SnIa calibrators [2,3,4,5], gravitational lensing [6,7,8,9], gravitational waves [10,11,12,13,14], gamma-ray bursts as standardizable candles [15,16,17,18,19], quasars as distant standard candles [20], type II supernovae [21,22], ray attenuation [23], etc. (for recent reviews, see Refs. [24,25]). This measurement is based on two simple assumptions:
- There are no significant systematic errors in the measurements of the properties (period, and metallicity) and luminosities of Cepheid calibrators and SnIa.
- The physical laws involved and the calibration properties of Cepheids and SnIa in all the rungs of the distance ladder are well understood and modeled properly.
This measurement, however, is at tension (Hubble tension) with the corresponding measurement from Planck observations of the CMB angular power spectrum (early time inverse distance ladder measurement) km s Mpc [26] (see also Refs. [24,25,27,28,29,30,31,32,33,34] for relevant recent reviews). This inverse distance ladder measurement is also based on two basic assumptions:
- The scale of the sound horizon at the last scattering surface is the one calculated in the context of the standard cosmological model with the known degrees of freedom (cold dark matter, baryons and radiation) and thus, it is a reliable distance calibrator.
- The evolution of the Hubble free expansion rate from the time of recombination (redshift ) until the present time () is the one predicted by the standard CDM model as defined by the best-fit Planck parameters (Planck18CDM) [26,35].
A wide range of approaches have been implemented in efforts to explain this Hubble tension (for reviews, see Refs. [24,25,27,34,36,37,38,39]). These approaches introduce new degrees of freedom that violate at least one of the above four assumptions and may be classified in accordance with the particular assumption that they are designed to violate.
Thus, early time sound horizon models introduce new degrees of freedom at the time just before recombination (e.g., early dark energy [36,40,41,42,43,44,45,46,47,48,49,50,51,52], radiation [53,54,55,56] or modified gravity [57,58,59,60,61,62]) to change the expansion rate at that time and thus decrease the sound horizon scale (early time distance calibrator) to increase , which is degenerate with , to a value consistent with local measurements.
The mechanism proposed by these models attempts to decrease the scale of the sound horizon at recombination, which can be calculated as
where the recombination redshift corresponds to time ; , and denote the densities for baryon, cold dark matter and radiation (photons), respectively; and is the sound speed in the photon–baryon fluid. The angular scale of the sound horizon is measured by the peak locations of the CMB perturbations angular power spectrum and may be expressed in terms of as
where is the comoving angular diameter distance to last scattering (at redshift ) and is the dimensionless normalized Hubble parameter, which for a flat CDM model is given by
Equation (2) indicates that there is a degeneracy between , and , given the measured value of . A decrease in would lead to an increase in the predicted value of (early time models), and a late time deformation of could lead to an increase in the denominator of Equation (2), leading also to an increase in (late time models).
Early dark energy models have the problem of predicting the stronger growth of perturbations than implied by dynamical probes, such as redshift space distortion (RSD) and weak lensing (WL) data and thus may worsen the − growth tension [63,64,65,66,67,68,69,70,71,72] and reduce consistency with growth data and with other cosmological probes and conjectures [38,39,47,48,49,72,73,74,75,76]. Thus, a compelling and full resolution of the Hubble tension may require multiple (or other) modifications beyond the scale of the sound horizon predicted by CDM cosmology. Even though these models are severely constrained by various cosmological observables, they currently constitute the most widely studied class of models [42,43,44,50,77,78].
Late time deformation models introduce new degrees of freedom (e.g., modified gravity [79,80,81,82], dynamical late dark energy [83,84,85,86,87,88,89,90,91,92,93,94,95,96], or interacting dark energy with matter [85,97,98,99,100,101]) to deform at redshifts so that the present time value of increases and becomes consistent with the local measurements. This class of models is even more severely constrained [84,102,103,104,105,106,107,108,109,110,111,112] by other cosmological observables (SnIa, BAO and growth of perturbations probes), which tightly constrain any deformation [35] from the Planck18/CDM shape of .
The third approach to the resolution of the Hubble tension is based on a search for possible unaccounted systematic effects, including possible issues in modeling the Cepheid data, such as non-standard dust-induced color correction [113], the impact of outliers [114,115,116], blending effects, SnIa color properties [117], robustness of the constancy of the SnIa absolute magnitude in the Hubble flow [67,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134], etc. There is currently a debate about the importance of these potential systematic effects [135,136,137,138]. Additionally, the possibility for redshift evolution of the Hubble constant was studied by Ref. [139]. In [139], the Hubble tension was analyzed with a binned analysis on the Pantheon sample of SNe Ia through a multidimensional MCMC analysis. Finally, the need for new standardizable candles with redshift values far beyond the SnIa () was studied (see Refs. [15,16,17,18,19] for gamma-ray bursts and Refs. [140,141] for quasars).
A fourth approach related to the previous one is based on a possible change of the physical laws (e.g., a gravitational transition [142,143]) during the past () when the light of the Cepheid calibrator hosts was emitted [143,144,145,146,147,148,149,150,151,152]. In this context, new degrees of freedom should be allowed for the modeling of either Cepheid calibrators and/or SnIa to allow for the possibility of this physics change. If these degrees of freedom are shown not to be excited by the data, then this approach would also be severely constrained. It is possible, however, that nontrivial values of these new parameters are favored by the data, while, at the same time, the best-fit value of shifts to a value consistent with the inverse distance ladder measurements of using the sound horizon at recombination as the calibrator. In this case [146], this class of models would be favored, especially in view of the severe constraints that have been imposed on the other three approaches.
The possible new degrees of freedom that could be allowed in the Cepheid+SnIa modeling analysis are clearly infinite, but the actual choices to be implemented in a generalized analysis may be guided by three principles: simplicity, physical motivation, and improvement of the quality of fit to the data.
In a recent analysis [146], using a previous release of the SH0ES data [153,154,155], we showed that a physically motivated new degree of freedom in the Cepheid calibrator analysis allowing for a transition in one of the Cepheid modeling parameters or is mildly favored by the data and can lead to a reduced best fit value of . Here, we extend that analysis in a detailed and comprehensive manner to a wider range of transition degrees of freedom using the latest publicly available SH0ES data described in R21.
1.2. The New SH0ES Cepheid+SnIa Data
The new Cepheid+SnIa data release and analysis from the SH0ES collaboration in R21 includes a significant increase of the sample of SnIa calibrators from 19 in Ref. [153] to 42. These SnIa reside in 37 hosts observed between 1980 and 2021 in a redshift range (see Table 1 for a more detailed comparison of the latest SH0ES data release with previous updates). These SnIa are calibrated using Cepheids in the SnIa host galaxies. In turn, Cepheid luminosities are calibrated using geometric methods in calibrator nearby galaxies (anchors). These anchor galaxies include the megamaser host NGC42581, the Milky Way (MW) where distances are measured with several parallaxes, and the Large Magellanic Cloud (LMC) where distances are measured via detached eclipsing binaries [154] as well as two supporting anchor galaxies ( [157] and the Small Magellanic Cloud (SMC). These supporting galaxies are pure Cepheid hosts and do not host SnIa but host large and well measured Cepheid samples. However, geometric measurements of their distances are not so reliable and thus are not directly used in the analysis2. The calibrated SnIa in the Hubble flow () are used to measure due to to their high precision (5% in distance per source) and high luminosity which allows deep reach and thus reduces the impact of local velocity flows.

Table 1.
A comparison of the latest SH0ES data release (R21) with previous data updates.
The new SH0ES data release includes a factor of 3 increase in the sample of Cepheids within NGC4258. In total it has 2150 Cepheids in SnIa hosts3, 980 Cepheids in anchors or supporting galaxies4, 42 SnIa (with total 77 lightcurve dataset measurements) in 37 Cepheid+SnIa hosts with redshifts and 277 SnIa in the Hubble flow in the redshift range . In addition 8 anchor based constraints (with uncertainties included) constrain the following Cepheid modeling parameters: (the Cepheid absolute magnitude zeropoint), (the slope of the Cepheid Period-Luminosity P-L relation), (the slope of the Cepheid Metallicity-Luminosity M-L relation), a zeropoint parameter used to refine the Cepheid P-L relation by describing the difference between the ground and HST zeropoints in LMC Cepheids (zp is set to 0 for HST observations), the distance moduli of the anchors NGC4258 and LMC and a dummy parameter we call X which has been included in the R21 data release and is set to 0 with uncertainty 5.
The parameters that fit with these data include the four modeling parameters , , , (the SnIa absolute magnitude), the 37 distance moduli of SnIa/Cepheid hosts, the distance moduli to the 2 anchors (NGC4258, LMC) and to the supporting Cepheid host M31, the zeropoint of the Cepheid P-L relation in the LMC ground observations, the Hubble parameter, and the dummy parameter mentioned above (tightly constrained to 0). This is a total of 47 parameters (46 if the dummy parameter X is ignored).
In addition to these parameters, there are other modeling parameters such as the color and shape correction slopes of SnIa (usually denoted as and ) as well as the Wesenheit dust extinction parameter , which were incorporated in the released SnIa and Cepheid apparent magnitudes and thus cannot be used as independent parameters in the analysis, in contrast to the previous data release.
The provided R21 Cepheid Wesenheit dust-corrected dereddened apparent magnitudes are connected with the Wesenheit dust extinction parameter as [158] (see also Refs. [153,154])
where is the observed apparent magnitude in the near-infrared H (F160W) band, and V (F555W) and I (F814W) are the optical mean apparent magnitudes in the corresponding bands. The empirical parameter is also called ’the reddening-free “Wesenheit” color ratio’ and is different from , which can be derived from a dust law (e.g., the Fitzpatrick law [159]). The parameter corrects for both dust and intrinsic variations applied to observed blackbody colors .
The provided in R21 SnIa apparent magnitudes , standardized using light curve color c and shape corrections, are defined as
where is the peak apparent magnitude, is the SnIa distance modulus, while the B-band absolute magnitude, , and correction coefficients and are fit directly using the SnIa data. The latest SH0ES data release provides the measured values of and for Cepheid and SnIa, respectively, which are also used in the corresponding analysis, while the parameters , and were fit previously and independently by the SH0ES team to provide the values of and .
1.3. The Prospect of New Degrees of Freedom in the SH0ES Data Analysis
The homogeneity of the SH0ES data with respect to the parameters , and were analyzed in previous studies with some interesting results. In particular, using the data of the previous SH0ES data release [153,154,155], it was shown [146] (see also [113] for a relevant study) that if the parameter is allowed to vary among Cepheid and SnIa hosts, then the fit quality is significantly improved, and the best-fit value of is lowered to a level consistent with the inverse distance ladder best fit. In addition, a more recent analysis allowed the parameter to have a different value in Hubble flow SnIa ( for ) compared to calibrating SnIa ( for ). A reanalysis allowing for this new degree of freedom indicated a tension between the the two best-fit values ( and ) at a level of up to [117].
Motivated by these hints for inhomogeneities in the SH0ES data, in what follows, we introduce new degrees of freedom in the analysis that are designed to probe the origin of these inhomogeneities. We thus accept three of the four above-mentioned assumptions that have led to the Hubble tension and test the validity of the fourth assumption. In particular, we keep the following assumptions:
- There are no significant systematics in the SH0ES data, and thus they are reliable.
- The CMB sound horizon scale used as a calibrator in the inverse distance ladder approach is correctly obtained in the standard model using the known particles.
- The Hubble expansion history from the time of recombination up to (or even ) used in the inverse distance ladder measurement of is provided correctly by the standard Planck18CDM cosmological model.
As discussed above, there are several studies in the literature that support the validity of these assumptions (e.g., [45,104]). If these assumptions are valid, then the most probable source of the Hubble tension is the violation of the fourth assumption stated above, namely ‘the physical laws involved and the calibration properties of Cepheids and SnIa in all the rungs of the distance ladder are well understood and modeled properly’.
If this assumption is violated, then the modeling of Cepheids+SnIa should be modified to take into account possible changes of physics by introducing new degrees of freedom that were suppressed in the original (baseline) SH0ES analysis. In the context of this approach, if these degrees of freedom are properly introduced in the analysis, then the best-fit value of will become consistent with the corresponding inverse distance ladder value of km s Mpc.
In an effort to pursue this approach for the resolution of the Hubble tension, we address the following questions:
- How can new degrees of freedom (new parameters) be included in the SH0ES data analysis for the determination of ?
- What are the new degrees of freedom that can expose internal tensions and inhomogeneities in the Cepheid/SnIa data?
- What new degrees of freedom can lead to a best-fit value of that is consistent with Planck?
The main goal of the present analysis is to address these questions. The new degree of freedom we allow and investigate is a transition of any one of the four Cepheid/SnIa modeling parameters at a specific distance or equivalently (in the context of the cosmological principle) at a given cosmic time such that , where is the present cosmic time (age of the universe). In the context of this new degree of freedom, we reanalyze the SH0ES data to find how the quality of fit to the data and the best-fit value of change when the new degree of freedom is excited. The possible introduction of new constraints included in the analysis is also considered.
The structure of this paper is the following: in the next Section 2, we describe the standard analysis of the SH0ES Cepheid+SnIa data in a detailed and comprehensive manner, stressing some details of the released dataset that are not described in R21. We also describe some tension between the values of the best-fit Cepheid modeling parameters and obtained in anchor or pure Cepheid host galaxies and the corresponding mean values obtained in SnIa host galaxies. In Section 3, we present our generalized analysis with new degrees of freedom that allow a transition of the main modeling parameters at specific distances (cosmic times of radiation emission). We also investigate the effect of the inverse distance ladder constraint on [149,160,161] for both the baseline SH0ES analysis and for our analysis involving the transition degree of freedom. Finally, in Section 4, we conclude and discuss the implications of our results and the possible extensions of our analysis.
2. The New SH0ES Data and Their Standard Analysis: Hints for Intrinsic Tensions
2.1. The Original Baseline SH0ES Analysis: A Comprehensive Presentation
The main equations used to model the Cepheid SnIa measured apparent magnitudes with parameters that include are described as follows:
- The equation that connects the measured Wesenheit magnitude of the jth Cepheid in the ith galaxy with the host distance moduli and the modeling parameters , and is of the following form6where is the inferred distance modulus to the galaxy, is the zeropoint Cepheid absolute magnitude of a period Cepheid (d for days), and − are the slope parameters that represent the dependence of magnitude on both period and metallicity. The is a measure of the metallicity of the Cepheid. The usual bracket shorthand notation for the metallicity represents the Cepheid metal abundance compared to that of the SunHere, O and H are the number of oxygen and hydrogen atoms per unit of volume, respectively. The unit often used for metallicity is the dex (decimal exponent) defined as . Additionally, the bracket shorthand notation for the period is used as (P in units of days)
- The color- and shape-corrected SnIa B-band peak magnitude in the ith host is connected with the distance modulus of the ith host and with the SnIa absolute magnitude as shown in Equation (5), i.e.,The distance modulus is connected with the luminosity distance in aswhere in a flat universewhere is the Hubble free luminosity distance, which is independent of .
- Using Equations (9)–(11), it is easy to show that that is connected with the SnIa absolute magnitude and the Hubble free luminosity distance asIn the context of the cosmographic expansion of valid for , we havewhere and are the deceleration and jerk parameters, respectively. Thus, Equations (12) and (13) lead to the equation that connects with the SnIa absolute magnitude , which may be expressed aswhere we have introduced the parameter as defined in the SH0ES analysis [153].
Thus, the basic modeling equations used in the SH0ES analysis for the measurement of are Equations (6), (9) and (14). In these equations, the input data are the measured apparent magnitudes (luminosities) of Cepheids and the SnIa apparent magnitudes (in Cepheid+SnIa hosts and in the Hubble flow). The parameters to be fit using a maximum likelihood method are the distance moduli (of the anchors and supporting hosts, the Cepheid+SnIa hosts and Hubble flow SnIa), the four modeling parameters (, , and ), the Hubble constant , the zeropoint of the Cepheid P-L relation in the LMC ground measurements and the dummy parameter X. This is a total of 47 parameters. The actual data were released by the SH0ES team as a .fits file in the form of a column vector Y with 3492 entries, which include 8 constraints on the parameters obtained from measurements in anchor galaxies where the distance moduli are measured directly with geometric methods.
The entries of the provided Y data column vector do not include the pure measured apparent magnitudes. Instead, its entries are residuals defined by subtracting specific quantities. In particular, we have the following:
- The Cepheid Wesenheit magnitudes are presented as residuals with respect to a fiducial P-L term aswhere is a fiducial Cepheid P-L slope. As a result of this definition, the derived best-fit slope is actually a residual slope .
- The residual Cepheid Wesenheit magnitudes of the Cepheids in the anchors N4258, LMC and the supporting pure Cepheid host SMC (non SnIa hosts), are presented after subtracting a corresponding fiducial distance modulus obtained with geometric methods7.
- The SnIa standardized apparent magnitudes in the Hubble flow are presented as residuals after subtracting the Hubble free luminosity distance with cosmographic expansion (see Equation (13)).
Thus, the released data vector Y has the following form
 |
The eight external anchor constraints on the parameters that appear in this vector are the following:
The parameters to be fit using the Y vector data may also be expressed as a vector q with 47 entries of the following form
| q = | 47 parameters |
Using the column vectors Y and q, Equations (6), (9) and (14) and the constraints stated above can be expressed in matrix multiplication form as
with , the matrix of measurements (data vector), , the matrix of parameters and , a model (or design) matrix which has 3492 rows corresponding to the entries of the data vector and 47 columns corresponding to the entries of the parameter vector . The model matrix also includes some data (Cepheid period and metallicity), and in the context of this baseline, the modeling of data has the form
 |
The system (17) has 3492 equations and 47 unknown parameter values. Thus, it is overdetermined and at best, it can be used in the context of the maximum likelihood analysis to find the best-fit parameter values that have maximum likelihood and thus minimum . For the definition of , the measurement error matrix (covariance matrix) is needed and provided in the data release as a square matrix with dimension 8. In Appendix A, we present the schematic form of the matrix , which also includes the standard uncertainties of the constraints as diagonal elements. Using the covariance matrix that quantifies the data uncertainties and their correlation, the statistic may be constructed as
The numerical minimization of in the presence of 47 parameters that need to be fit would be very computationally demanding, even with the use of Markov chain Monte Carlo (MCMC) methods. Fortunately, the linear form of the system (17) allows the analytical minimization of and the simultaneous analytic evaluation of the uncertainty of each parameter. In Appendix B, we show that the analytic minimization of of Equation (18) leads to the best-fit parameter maximum likelihood vector9
The standard errors for the parameters in are obtained as the square roots of the 47 diagonal elements of the transformed error matrix
For example the best fit of the parameter10 is obtained as the 47th entry of the best fit parameter vector and the corresponding standard error is the element of the error matrix. Using Equations (19) and (20) and the latest released data of the SH0ES team presented in R21 we find full agreement with all values of the best fit parameters. For example for we find (after implementing error propagation) km s Mpc fully in agreement with the published result of R21.
In Table 2, we show the best-fit values and uncertainties for all 47 parameters of the vector , including the four Cepheid modeling parameters (, , and ) along with the best-fit value of for the baseline SH0ES model. The corresponding best-fit values and uncertainties with an additional constraint on from the inverse distance ladder are also included and discussed in detail in the next section. The agreement with the corresponding results of R21 (left three columns) is excellent.

Table 2.
Best-fit parameter values in the absence and in the presence of the inverse distance ladder constraint for baseline model.
Before closing this subsection, we review a few points that are not mentioned in R21 but are useful for the reproduction of the results and the analysis:
- The number of entries of the parameter vector is 47 and not 46 as implied in R21 due to the extra dummy parameter X, which is included in the released data , and but not mentioned in R21.
- The entry referred as in R21 in the parameter vector should be because it is actually the residual () as stated above and not the original slope of the P-L relation (its best-fit value is ).
- The number of constraints shown in the definition of the vector in R21 is five, while in the actual released data , and , we found the eight constraints defined above.
2.2. Homogeneity of the Cepheid Modeling Parameters
Before generalizing the model matrix with new degrees of freedom and/or constraints, it is interesting to test the self-consistency of the assumed universal modeling parameters and of the Cepheids. These parameters can be obtained separately for each one of the Cepheid hosts11 by fitting linear relations.
In particular, in order to obtain the best-fit P-L slope of the Cepheid host, we fit the data (where is the period in units of days of the Cepheid in the host) with a linear relation of the form
with parameters to be fit in each host (intercept and slope). These equations may be expressed as a matrix equation of the form
with as the vector of measurements, as the vector of parameters and as the model (or design) matrix. These are defined as
The analytically (along the lines of the previous subsection and of Appendix B) obtained minimum of
with respect to the slope and intercept leads to the best-fit values and standard errors for these parameters. For all Cepheids, we adopt the covariance matrix of standard errors of the magnitude measurements from R21.
Thus, the analytic minimization of of Equation (24) leads to the best-fit parameter maximum likelihood vector
The standard errors for slope and intercept in are obtained as the square roots of the two diagonal elements of the error matrix
A similar analysis was implemented for the other Cepheid modeling parameter, the metallicity slopes . In this case, the linear fit considered was of the form
The best-fit values of the slopes and for each of the 40 Cepheid hosts are shown in Figure 1 and Figure 2 in terms of the host distance, respectively. The actual Cepheid data in each host with the best-fit and straight lines are shown in Figure A2 and Figure A3 in Appendix C for each of the 40 Cepheid hosts i. The slopes shown in Figure A4 for each host in sequence of increasing uncertainties, is in excellent agreement with the corresponding Figure 10 shown in R2112. The corresponding numerical values of the best fit and are shown in Table A1.
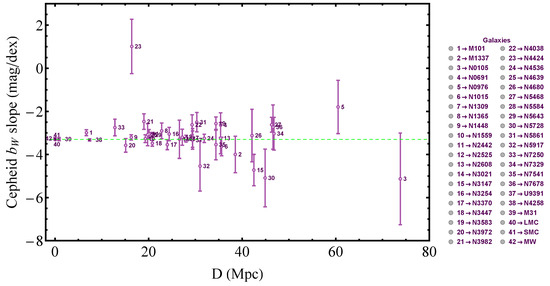
Figure 1.
Independently fitted slopes of the Cepheid P-L relations. Here, we ignored non-diagonal terms of the covariance as was done in R21 in the corresponding Figure 10. There is a consistent trend of most non-anchor hosts having a best-fit absolute slope that is smaller than corresponding best fit of the anchor hosts (above the dotted line). The dotted line corresponds to the best-fit value of in the context of the baseline SH0ES analysis as shown in Table 2.
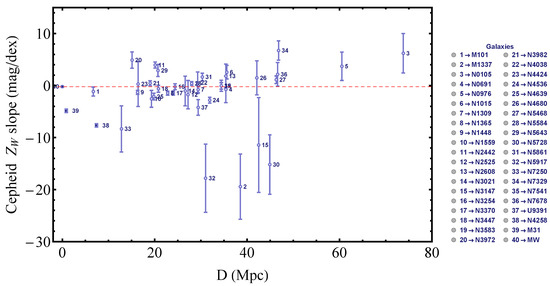
Figure 2.
Independently fitted metallicity slopes in terms of the distance of the Cepheid host. Clearly, the spread of many points is larger than the corresponding uncertainties indicating either inhomogeneities of the sample or underestimation of the uncertainties. In fact, there seems to be a trend of most absolute slopes being larger than the corresponding slope of the Milky Way (MW) (below the dotted line). The dotted line corresponds to the best-fit value of in the context of the baseline SH0ES analysis as shown in Table 2.
Some inhomogeneities are visible in the distance distribution of both the individual Cepheid slopes in Figure 1 and Figure 2 as well as in Figure A4. For example, in Figure 1 and Figure A4, there is a consistent trend of most non-anchor hosts having an absolute best-fit slope that is smaller than the corresponding best-fit of the anchor hosts (above the dotted line). Similarly, in Figure 2, there seems to be a trend of most absolute slopes being larger than the corresponding slope of the Milky Way (MW) (below the dotted line).
A careful inspection of Figure 1 and Figure 2 indicates that the scatter is significantly larger than the standard uncertainties of the slopes. Indeed, a fit to a universal slope for of the form
leads to a minimum per degree of freedom ()13 (with a best-fit ) while would be expected for an acceptable fit. Additionally, for , we find (), which is more reasonable but still larger than 1, indicating a relatively poor quality of fit to a universal slope.
There are two possible causes for this poor quality of fit to universal slopes: either many of the uncertainties of the individual host slopes were underestimated, or the universal slope model is not appropriate. In view of the fact that the uncertainties of the Cepheid periods and metallicities are not included in the fit because they were not provided by R21 released data, we make the working hypothesis that the uncertainties are underestimated, and thus we add a scatter error adjusted so that . Thus for , we have
For , we must set , which is significantly larger than most uncertainties of individual host slopes. Similarly, for we must set , which is comparable to or smaller than most uncertainties of individual host slopes as shown in Table A1.
In order to quantify possible inhomogeneities of Cepheid hosts and slopes, we split each sample of slopes in two bins: a low-distance bin with Cepheid host distances D smaller than a critical distance , and a high-distance bin with . Given , for each bin, we find the best-fit slope and its standard error using the maximum likelihood method. For example, for a low distance bin, we minimize
where is the number of hosts in the low-distance bin and is the additional uncertainty (scatter error) chosen in each bin so that so that the fit becomes consistent with a constant in each bin. Thus, we find the best-fit low-distance bin slope and its standard error and similarly for the high distance bin , and for the slopes , . Thus for each , we obtain two best-fit slopes (one for each bin) and their standard errors. The level of consistency between the two binned slopes at each determines the level of homogeneity and self consistency of the full sample. The results for the best-fit binned slopes for and are shown in Figure 3 and Figure 4, respectively, as functions of the dividing critical distance .
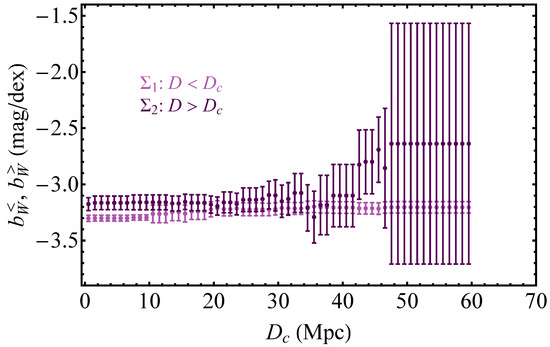
Figure 3.
Binned Cepheid P-L slopes and for the high-distance bin () and the low distance bin (), respectively. In each bin, was used and adjusted so that . Notice that for Mpc, the high–low-distance bins are statistically consistent with each other due to small number of Cepheids in the high-distance bin, but the difference of their slope best-fit values is maximized.
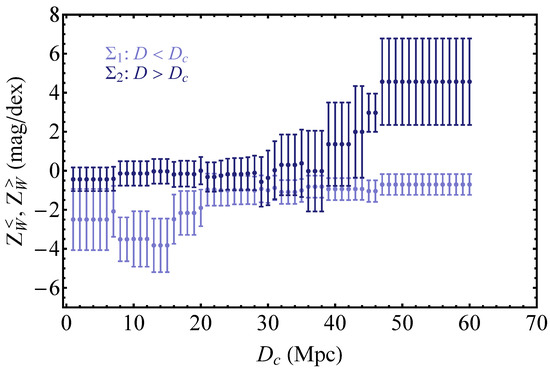
Figure 4.
Binned Cepheid metallicity slopes and for the high-distance bin () and the low-distance bin (), respectively. In each bin, the additional scattering uncertainty was used and adjusted so that . For Mpc, the difference between the best-fit bin slopes is maximized, and the tension between them is larger than (see also Figure 5).
Interestingly, for a range of , there is a mild tension between the best-fit values of the high- and low-distance bins, which reaches levels of , especially for the metallicity slopes . For both and , the absolute value of the difference between the high- and low-distance bin slopes is maximized for Mpc. For the case of , this difference is significant statistically, as it exceeds the level of . The level of statistical consistency between high- and low-distance bins for both slopes and is shown in Figure 5. In the range of between 40 Mpc and 50 Mpc and also between 10 Mpc and 20 Mpc, it is shown that in the case of , the -distance
between the best-fit binned metallicity slopes can reach a level beyond (see Figure 4 and Figure 5).
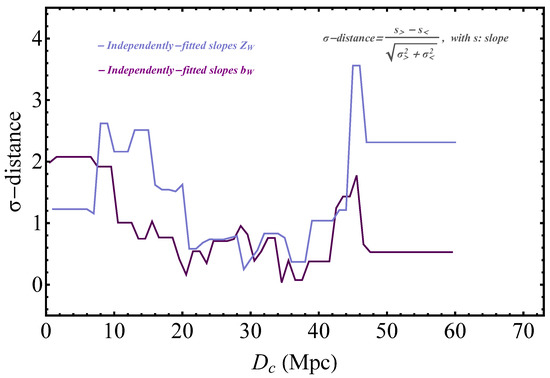
Figure 5.
The distance between the best-fit high-distance bin () and low-distance bin slopes ( and ) defined in Equation (31) for and similarly for .
An additional test of possible intrinsic tensions of the Cepheid properties in the SH0ES Cepheid sample is obtained by comparing the probability distributions of the Cepheid period and metallicity for the full sample of the 3130 Cepheid with high- and low-distance subsamples. In Figure 6 and Figure 7, we show histograms of the probability distributions of the Cepheid period and metallicity for the whole Cepheid sample and for the high- () and low-distance () subsamples for Mpc. The two subsamples for each observable are clearly inconsistent with each other and with the full sample. This is demonstrated visually and also through the Kolmogorov–Smirnov consistency test, which quantifies the inconsistency and gives a p-value very close to 0 for the three sample pairs. However, as communicated to us by members of the SH0ES team (private communication), this inconsistency can be justified by observational selection effects and does not necessarily indicate a physics change at Mpc. For example, bright Cepheids have longer periods and they are more easily observed at high distances. Thus, it is expected that there will be higher period (brighter) Cepheids observed at higher distances. Other variables, such as the time span of the observations, also play a role. For more distant galaxies, there is a trend to allow a longer window of observations so that longer period Cepheids can be found. Additionally, the star formation history of the galaxies dictates if one will have very long-period Cepheids which come from massive, short-lived stars. However, even though the observed inconsistency in the Cepheid properties probability distributions may be explained using observational biases and anticipated galactic properties, it may also be a hint of interesting new physics and/or systematic effects.
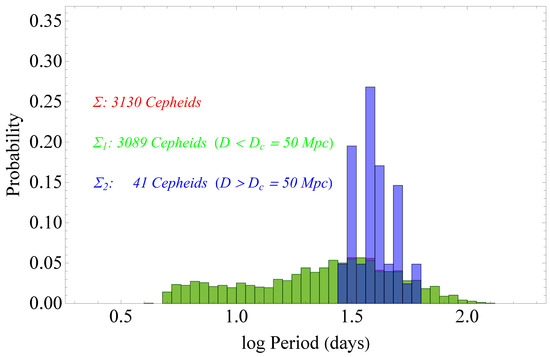
Figure 6.
Probability distributions of the Cepheid period for the whole Cepheid sample and for the high () and low distance () subsamples for Mpc. Due to the small number of Cepheids in the Mpc bin (41), the probability distribution of the full sample (3130 Cepheids) is almost identical to the probability distribution of the Mpc bin, and thus the light green bars overlap with the red bars.
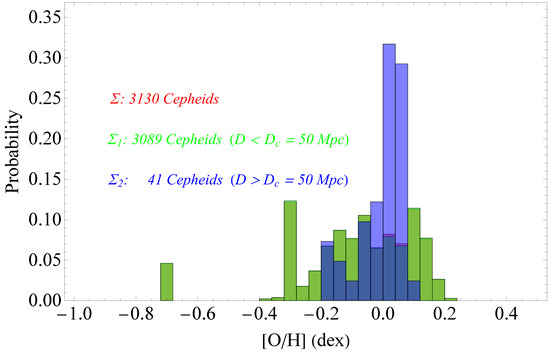
Figure 7.
Probability distributions of the Cepheid metallicity for the whole Cepheid sample and for the high () and low distance () subsamples for Mpc. Due to the small number of Cepheids in the Mpc bin (41), the probability distribution of the full sample (3130 Cepheids) is almost identical to the probability distribution of the Mpc bin, and thus the light green bars overlap with the red bars.
In view of the above level of mild inhomogeneities identified is the SH0ES data; it would be interesting to extend the SH0ES modeling of the Cepheids and SnIa with new degrees of freedom that can model the data, taking into account these inhomogeneities. This is the goal of the next section.
3. Generalized Analysis: New Degrees of Freedom Allowing for a Physics Transition
An obvious generalization of the SH0ES analysis described in Section 2.1 which models the Cepheid-SnIa luminosities using four main parameters is to allow for a transition of any one of these parameters at a particular distance or equivalently cosmic time when radiation is emitted. Such a transition could be either a result of a sudden change in a physics constant (e.g., the gravitational constant) during the last 200 Myrs in the context, e.g., of a first-order phase transition or a result of the presence of an unknown systematic.
Another modification of the standard SH0ES analysis in R21 would be to extend the number of constraints imposed on the data vector taking into account other cosmological data, such as the inverse distance ladder estimate of [149,160,161]. Both of these generalizations will be implemented in the present section.
3.1. Allowing for a Transition of a Cepheid Calibration Parameter
A transition of one of the Cepheid calibration parameters can be implemented by replacing one of the four modeling parameters in the vector by two corresponding parameters: one for high and one for low distances (recent cosmic times). Thus, in this approach, the number of parameters and entries in the parameter vector increases by one, from 47 to 48. Since one of the entries of is replaced by two entries, the corresponding column of the modeling matrix should be replaced by two columns. The high distance parameter column should be similar to the original column it replaced, but with zeros in the entries, corresponding to low-distance data (or constraints), and the reverse should happen for the low-distance parameter column. This process is demonstrated in the following schematic diagram, where the parameter is replaced by the two parameters (or ) and (or ), and the j column of is replaced by the j and corresponding columns, which have zeros in the low- or high-distance data (or constraint) entries.
In this manner, if the parameter was to be split to and for example, Equation (6) would be replaced by
and similarly for splittings of each of the other three parameters, , and . In (34), D is a distance that may be assigned to every entry of the data vector (Cepheids, SnIa and constraints). Notice that the splitting of any parameter to high- and low-distance versions does not affect the form of the data vector and the covariance matrix of the data. In order to properly place the 0 entries of each one of the new columns, a distance must be assigned to every entry of . We specified this distance for each host using the literature resources or the best-fit distance moduli of each host. These distances along with other useful properties of the Cepheids used in our analysis are shown in Table 3.

Table 3.
Properties of the Cepheid hosts considered in the analysis.
We thus considered four generalizations of the baseline SH0ES analysis, each one corresponding to a high–low-distance split of each of the four modeling parameters. For each generalization, we obtained the best-fit values and uncertainties of all 48 parameters of the generalized parameter vector for several values of the critical distance , which defined in each case the high–low-distance data bins. The best-fit values with uncertainties for the high–low D split parameter (green and blue points) and for (red points), for each generalization considered, is shown in Figure 8, Figure 9, Figure 10 and Figure 11 in terms of . Dotted lines correspond to the SH0ES R21 best fit and to the Planck18/CDM best fit for . The following comments can be made based on the results of Figure 8, Figure 9, Figure 10 and Figure 11.
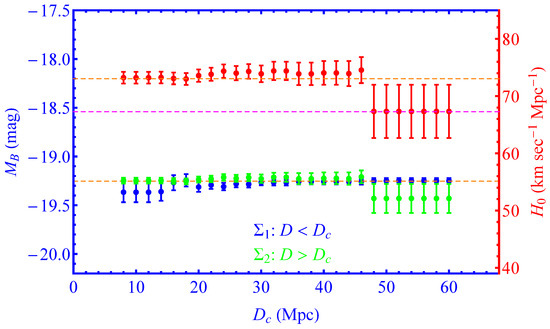
Figure 8.
The best-fit values with uncertainties for the high–low D bin of SnIa absolute magnitude (green and blue points) and for (red points). This generalization of the SH0ES baseline analysis allows for a transition of . The best-fit parameter values as shown as functions of the critical transition . Dotted lines correspond to the SH0ES R21 best fit and to the Planck18/CDM best fit for .
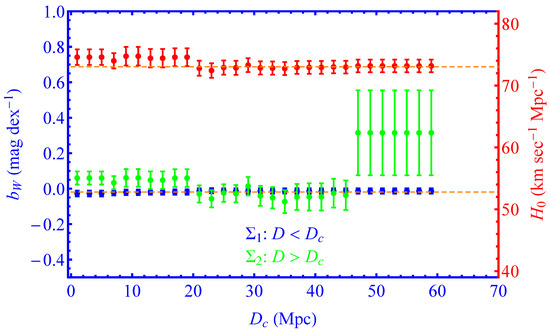
Figure 9.
Same as Figure 8 in an analysis generalization, where the parameter is allowed to have a transition at a distance . Notice the sharp increase in the difference between best-fit parameters high of D and low D bin for Mpc.
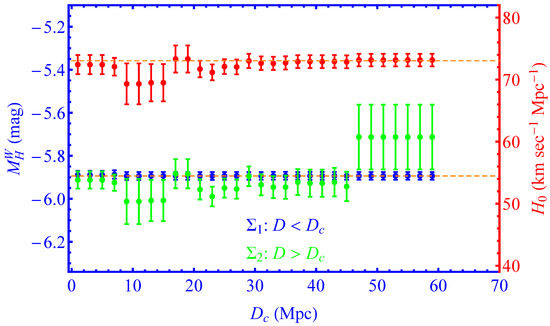
Figure 10.
Same as Figure 8 in an analysis generalization, where the parameter is allowed to have a transition at a distance . Notice the sharp increase in the difference between best-fit parameters of high D and low D bin for Mpc.
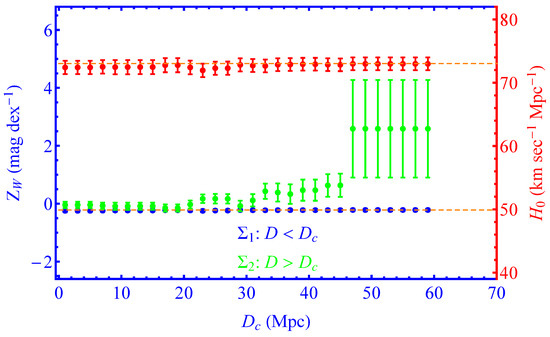
Figure 11.
Same as Figure 8 in an analysis generalization where the parameter is allowed to have a transition at a distance . Notice the sharp increase in the difference between best fit parameters of high D and low D bin for Mpc. The best-fit value of the Hubble parameter (red points) is not significantly affected by this type of degree of freedom perhaps due to the indirect connection of with .
- When the SnIa absolute magnitude is allowed to change at ( transition) and for , the best-fit value of drops spontaneously to the best-fit Planck18/CDM value, albeit with larger uncertainty (see Figure 8 and second row of Table 4). This remarkable result appears with no prior or other information from the inverse distance ladder results. Clearly, there are increased uncertainties of the best-fit parameter values for this range of because the most distant usable Cepheid hosts are at distances Mpc (N7329), Mpc (N0976) and Mpc (N0105) and only two of them are at distance beyond 47 Mpc. These hosts (N0975 and N0105) have a total of 41 Cepheids and 4 SnIa. Due to the large uncertainties involved, there is a neutral model preference for this transition degree of freedom at Mpc (the small drop of by is balanced by the additional parameter of the model). This, however, changes dramatically if the inverse distance ladder constraint on is included in the vector as discussed below.
 Table 4. A model comparison (baseline vs transitions) and best-fit parameter values in the absence (top five rows) and in the presence (last two rows) of the inverse distance ladder constraint. Notice that in the presence of the inverse distance ladder constraint and the transition degree of freedom, the best-fit value of is identical to the inverse distance ladder result of the completed SDSS-IV extended BAO survey [35].
Table 4. A model comparison (baseline vs transitions) and best-fit parameter values in the absence (top five rows) and in the presence (last two rows) of the inverse distance ladder constraint. Notice that in the presence of the inverse distance ladder constraint and the transition degree of freedom, the best-fit value of is identical to the inverse distance ladder result of the completed SDSS-IV extended BAO survey [35]. - For all four modeling parameters considered, there is a sharp increase in the absolute difference between the high–low-distance best-fit parameter values for Mpc. The statistical significance of this split, however, is low due to the relatively small number of available Cepheids at Mpc.
- The best-fit value of changes significantly when the SnIa absolute magnitude is allowed to make a transition at Mpc but is not significantly affected if the three Cepheid modeling parameters , and are allowed to make a transition at any distance. This is probably due to the large uncertainties involved and due to the fact that is only indirectly connected with the three Cepheid modeling parameters.
- Each one of the transition degrees of freedom mildly reduces , thus improving the fit to the data, but these transition models are not strongly preferred by the model selection criteria, which penalize the extra parameter implied by these models. This is demonstrated in Figure 12 and Figure 13, which show the values of , and of the four transition models with respect to the baseline SH0ES model for various transition distances. As discussed below, this changes dramatically if the inverse distance ladder constraint on is introduced in the analysis.
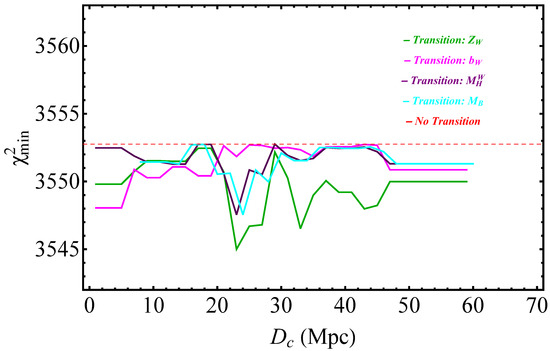 Figure 12. The values of in terms of for the four transition models considered with respect to the SH0ES baseline model. No inverse distance ladder constraint on is used for either the baseline or the transition models. The small improvement of the fit to the data is not enough to justify any model preference.
Figure 12. The values of in terms of for the four transition models considered with respect to the SH0ES baseline model. No inverse distance ladder constraint on is used for either the baseline or the transition models. The small improvement of the fit to the data is not enough to justify any model preference.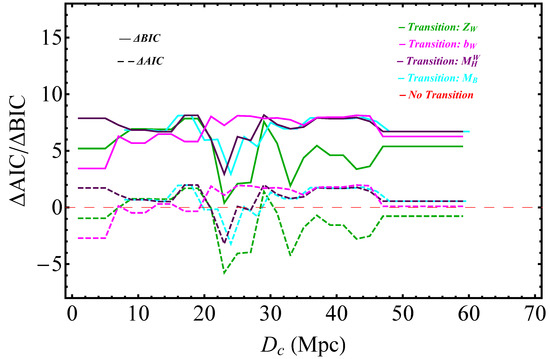 Figure 13. The values of and in terms of for the four transition models considered with respect to the SH0ES baseline model. No inverse distance ladder constraint on is used for either the baseline or the transition models. The small improvement of the fit to the data is not enough to justify any model preference. In fact, the BIC which strongly penalizes any additional parameter mildly disfavors the transition models.
Figure 13. The values of and in terms of for the four transition models considered with respect to the SH0ES baseline model. No inverse distance ladder constraint on is used for either the baseline or the transition models. The small improvement of the fit to the data is not enough to justify any model preference. In fact, the BIC which strongly penalizes any additional parameter mildly disfavors the transition models.
3.2. The Effect of the Inverse Distance Ladder Constraint
In view of the spontaneous transition of the SnIa absolute magnitude that appears to lead to a Hubble tension resolution, while being mildly favored by the SH0ES data () without any inverse distance ladder information included in the fit, the following question arises:
How does the level of preference for the transition model (compared to the SH0ES baseline model) change if an additional constraint is included in the analysis obtained from the inverse distance ladder best fit for ?
The inverse distance ladder constraint on is [149,160,161]
In order to address this question, we modify the analysis by adding one more constraint to the data vector: after entry 3215, which corresponds to the 8th constraint, we add the value −19.401 for the constraint. We also add a line to the model matrix after line 3215 with all entries set to zero except the entry at column 43 corresponding to the parameter . A column after column 43 is added in to accommodate the high distance parameter as described above. The new constraint is assigned a large distance (larger than the distance of the most distant SnIa of the sample) so that it only affects the high-distance parameter (the entry at line 3216 column 43 of is set to 0 for all , while the entry at column 44 of the same line is set to 1 for all ). To accommodate the corresponding uncertainty of the new constraint, we also add a line at the covariance matrix after line 3215 with a single nonzero entry at the diagonal equal to . Thus, after the implementation of the constraint in the transition model, the vector has 3493 entries, the model matrix has dimensions , the parameter vector has 48 entries, and the covariance matrix matrix has dimensions . In a similar way, we may implement the constraint (35) in the SH0ES model without allowing for the additional transition degree of freedom and implement model selection criteria to compare the baseline with the transition model in the presence of the inverse distance ladder constraint.
The new constraints on and on the parameters , emerging from this modified modeling analysis are shown in Figure 14 in terms of . The corresponding quality of fit expressed via the value of and model selection [162,163] expressed via the AIC [164] and BIC criteria is shown in Figure 15. The definitions and properties of the AIC and BIC criteria are described in Appendix D.
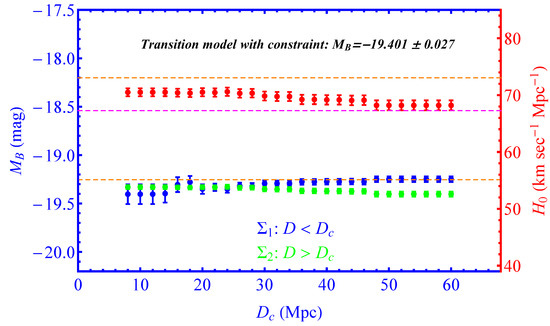
Figure 14.
The new constraints on and on the parameters , emerging after implementing the inverse distance ladder constraint (35) on the high-distance bin of the transition model.
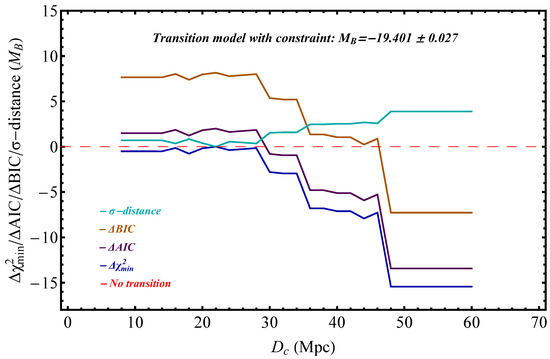
Figure 15.
Model selection criteria of the transition model with respect to the baseline SH0ES model in the presence of the inverse distance ladder constraint (35). The -distance between the low-distance best-fit and the high-distance is also plotted in terms of . Clearly, the transition model is strongly preferred with respect to the SH0ES baseline (no transition) model, especially for transition distances Mpc.
Clearly, the transition degree of freedom at Mpc which is mildly preferred by the data, even in the absence of the inverse distance ladder constraint, is strongly preferred by the data in the presence of the constraint while the -distance between the low-distance best-fit parameter and the high distance reaches a level close to . These results are described in more detail in Table 4. The full list of the best-fit values of all the parameters of the vector for the SH0ES baseline model with and without the inverse distance ladder constraint in the data vector is shown in Table 2 along with the corresponding uncertainties.
The following comments can be made on the results shown in Table 4.
- In the presence of the inverse distance ladder constraint, the model with the transition degree of freedom at Mpc is strongly preferred over the baseline model as indicated by the model selection criteria, despite the additional parameter it involves (comparison of the last two rows of Table 4).
- The transition degree of freedom, when allowed in each of the other three modeling parameters, does not lead to a spontaneous resolution of the Hubble tension since the best-fit value of is not significantly affected. However, it does induce an increased absolute difference between the best-fit values of the high-distance and low-distance parameters, which, however, is not statistically significant due to the large uncertainties of the bin with Mpc (see also Figure 9, Figure 10 and Figure 11).
The above comments indicate that interesting physical and or systematic effects may be taking place at distances at or beyond 50 Mpc in the SH0ES data, and therefore more and better quality Cepheid/SnIa data are needed at these distances to clarify the issue. This point is further enhanced by the recent study of Ref. [117], indicating that SnIa in the Hubble flow (at distances Mpc) appear to have different color calibration properties than SnIa in Cepheid hosts (at distances Mpc).
The hints for a transition in the SnIa absolute luminosity and magnitude are also demonstrated in Figure 16, where we show the mean14 SnIa absolute magnitude for each Cepheid+SnIa host i is obtained from the equation
where is the measured apparent magnitude of the SnIa, and are the best-fit distance host distance moduli obtained using the SH0ES baseline model (left panel of Figure 16) and the transition model (right panel), which allows (but does not enforce) an transition at Mpc. Notice that when the transition degree of freedom is allowed in the analysis, the best-fit values of for the more distant hosts N0976 ( Mpc) and N0105 ( Mpc) spontaneously drop to the inverse distance ladder calibrated value range.
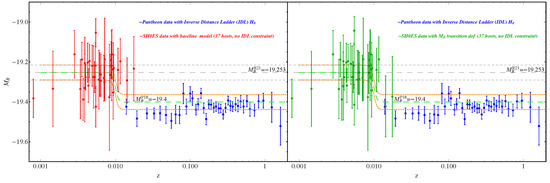
Figure 16.
The mean SnIa absolute magnitude for each Cepheid+SnIa host i obtained from Equation (36), obtained using the SH0ES baseline model (left panel) and the transition model (right panel), which allows (but does not enforce) an transition at Mpc. Notice that when the transition degree of freedom is allowed in the analysis, the best-fit values of for the more distant hosts N0976 ( Mpc) and N0105 ( Mpc) spontaneously drop to the inverse distance ladder calibrated value range (green points with ).
The inverse distance ladder calibrated values of the absolute magnitudes of SnIa in the Hubble flow are obtained by assuming km s Mpc and using the following equation
where is the Hubble free luminosity distance in the context of Planck18/CDM and are the binned corrected SnIa apparent magnitudes of the Pantheon sample. The corresponding binned Cepheid+SnIa host values of obtained assuming the baseline Sh0ES model (red points) and the transition model ( Mpc, green points) are shown in Figure 17 along with the inverse distance ladder calibrated binned of the Hubble flow SnIa of the Pantheon dataset (blue points). When the transition dof is allowed, the data excite it, and a hint for a transition appears (the green data point of the transition model is clearly below the red point corresponding to the constant SH0ES baseline model), even though the statistical significance of the indicated transition is low due to the small number of Cepheids (41) included in the last bin with Mpc,75 Mpc].
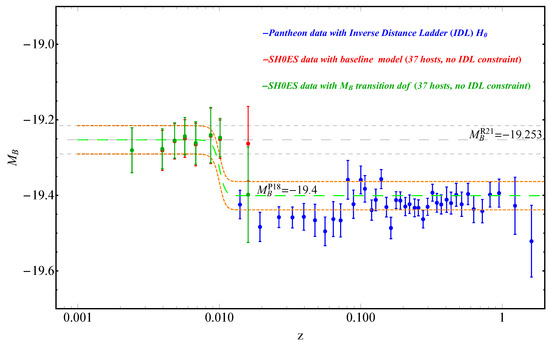
Figure 17.
The binned (5 host bins with 2 hosts in last bin where ) Cepheid+SnIa host values of obtained assuming the baseline SH0ES model (red points) and the transition model ( Mpc, green points) are shown along with the inverse distance ladder calibrated binned of the Hubble flow SnIa of the Pantheon dataset (blue points). When the transition dof is allowed, the data excite it, and a hint of a transition appears (the green data point of the transition model is clearly below the red point corresponding to the constant SH0ES baseline model).
4. Conclusions
We described a general framework for the generalization of the Cepheid+SnIa modeling in the new SH0ES data. Such a modeling generalization approach is motivated by the increased statistical significance of the Hubble tension and may hint toward new degrees of freedom favored by the data. Such degrees of freedom may be attributed to either new physics or to unknown systematics hidden in the data.
In the present analysis, we focused on a particular type of new modeling degree of freedom, allowing for the transition of any one of the four Cepheid/SnIa modeling parameters at a distance . However, our analysis can be easily extended to different degrees of freedom with physical motivation. Examples include possible modeling parameter dependence on properties other than distance (e.g., dust extinction and color and stretch calibration properties). In addition, other degrees of freedom that could be excited by the data could involve the modeling parameters that have been absorbed in the R21 SH0ES data, such as the Cepheid dust extinction parameter and the color and stretch SnIa calibration parameters and . These degrees of freedom may also be probed and excited by the fit to the data if allowed by the modeling [117].
We demonstrated that our proposed transition degrees of freedom are mildly excited by the SH0ES data, and in the case of the SnIa absolute magnitude transition degree of freedom at Mpc, the best-fit value of shifts spontaneously to a value almost identical to the Planck18/CDM best-fit value, thus annihilating the Hubble tension. However, the high-distance bin in this case involves only 41 Cepheids and 4 SnIa, and therefore, the best-fit value of , which effectively also fixes , involves significant uncertainties.
In the presence of the inverse distance ladder constraint on the high-distance bin parameter of the transition model and on the single parameter of the SH0ES model, the uncertainties reduce dramatically. The Hubble tension is fully resolved only in the presence of the transition degree of freedom at Mpc. This transition model is also strongly selected over the baseline SH0ES model with the constraint, by both model selection criteria AIC and BIC, despite the penalty imposed by AIC and especially BIC on the additional parameter involved in the new modeling. This behavior along with other recent studies [117] hints toward the need of more detailed Cepheid+SnIa calibrating data at distances Mpc, i.e., at the high end of rung two on the distance ladder.
Our comprehensively described generalized modeling approach opens a new direction in the understanding of the Hubble tension and may be extended by the introduction of a wide range of new degrees of freedom in the SH0ES data analysis and also by the introduction of new constraints motivated by other cosmological data. Such extensions could, for example, involve more distance bins in the distance dependence of the four main modeling parameters. In that case, the relevant column of the modeling matrix would have to be replaced by more than two columns (one for each distance bin). Such bins could also be defined not in terms of distance, but in terms of other Cepheid/SnIa properties (e.g., Cepheid metallicity or period and/or SnIa light curve color or stretch). In addition, other parameters beyond the four basic modeling parameters may be considered, including the dust extinction parameter and/or the SnIa light curve color and stretch parameters. Additionally, similar modeling generalizations may be implemented on different distance calibrator data used for the measurement of , such as the TRGB data [165].
Physical motivation is an important factor for the evaluation of any new modeling degree of freedom, especially if it is favored by the data. A transition of the SnIa luminosity at a particular recent cosmic time could be induced by a sudden change of the value of a fundamental physics constant, e.g., the gravitational constant in the context of a recent first-order phase transition [166,167,168] to a new vacuum of a scalar–tensor theory, or in the context of a generalization of the symmetron screening mechanism [143]. A similar first-order transition was implemented in early dark energy models [169], attempting to change the last scattering sound horizon scale without affecting other well-constrained cosmological observables. Thus, even though no relevant detailed analysis has been performed so far, there are physical mechanisms that could potentially induce the SnIa luminosity transition degree of freedom.
The emerging new puzzles challenging our standard models may soon pave the way to exciting discoveries of new physical laws. The path to these discoveries goes through the deep and objective understanding of the true information that is hidden in the cosmological data. The present analysis may be a step in that direction.
Author Contributions
Conceptualization: L.P.; methodology: L.P. and F.S.; software: L.P. and F.S.; data curation: F.S.; investigation: F.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Hellenic Foundation for Research and Innovation (HFRI-Progect No: 789).
Data Availability Statement
The numerical analysis files for the reproduction of the figures can be found in the A reanalysis of the SH0ES data for GitHub repository, https://github.com/FOTEINISKARA/A-reanalysis-of-the-SH0ES-data-for-H_0, (accessed on 23 August 2022) under the MIT license.
Acknowledgments
We thank Adam Riess, Dan Scolnic, Eoin Colgain, and Radoslaw Wojtak for useful comments.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Covariance Matrix
A schematic form of the non-diagonal covariance matrix used in our analysis is shown below. The symbols indicate the (non-diagonal in general) covariance submatrix within the i host, while the symbols indicate submatrices that correlate the uncertainties between different hosts.
 |
Appendix B. Analytic Minimization of χ 2
The proof of Equations (19) and (20) that lead to the best-fit parameter values and their uncertainties through the analytic minimization of may be sketched as follows15:
Using the matrix of measurements (data vector) , the matrix of parameters and the equation (or design) matrix with the measurement error matrix (covariance matrix) , the statistic is expressed as
The is minimized with respect to the parameters by solving the equation
Thus, the maximum-likelihood parameters are given as
We tested the validity of this equation numerically by calculating for the SH0ES baseline model and showing that, indeed, it has a minimum at the analytically predicted parameter values provided by (A3). This is demonstrated in Figure A1, where we show with the rest of the parameters fixed at their analytically predicted best-fit values. As expected, the minimum is obtained at the analytically predicted value of .
The standard errors squared of the parameters in are given as the diagonal elements of the transformed covariance matrix
or
Thus,
The standard errors provided by the equation for the SH0ES baseline model are consistent and almost identical to the published results of R21.
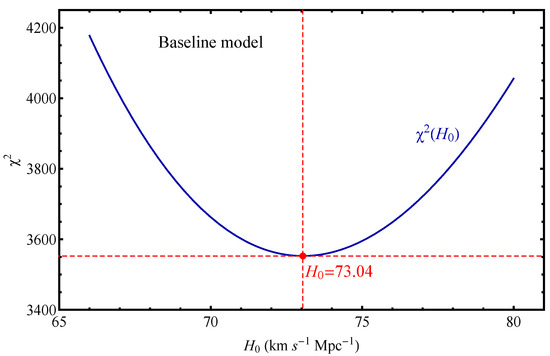
Figure A1.
The form of ) for the SH0ES baseline model has a minimum at the analytically predicted value of provided by (A3) (the rest of the parameters are fixed at their analytically predicted best-fit values).
Appendix C. Reanalysis of Individual Cepheid Slope Data
We use the released Cepheid P-L data () to find the best-fit slope in each one of the 40 Cepheid hosts, where the 3130 Cepheid magnitudes are distributed. We thus reproduce Figure 9 and 10 of R21. Since the released Cepheid magnitude data do not include outliers, we focus on the reproduction of the black points of Figure 10 of R21. Our motivation for this attempt includes the following:
- It is evident by inspection of Figure 10 of R21 (see also Figure A4 below) that most of the better measured slopes have a smaller absolute slope than the corresponding slopes obtained from anchors+MW hosts. This makes it interesting to further test the homogeneity of these measurements and their consistency with the assumption of a global value of for both anchors and SnIa hosts.
- Most of the measurements that include outliers (red points of Figure 10 of R21) tend to amplify the above-mentioned effect, i.e., they have smaller absolute slopes than the slopes obtained from the anchors.
- The slope corresponding to the host N4424 is missing from Figure 10 of R21, while the host M1337 appears to show extreme behavior of the outliers.
Based on the above motivation, we recalculated all the slopes of the Cepheid hosts and also extended the analysis to metallicity slopes for the Cepheids of each hosts. The individual metallicity slopes for each host were obtained for the first time in our analysis and thus, no direct comparison can be made with R21 for these slopes.
The Cepheid magnitude period and magnitude metallicity data used to calculate the corresponding best-fit slopes and are shown in Figure A2 and Figure A3 for each host along with the best-fit straight lines from which the individual best-fit and were obtained. The numerical values of the derived best-fit slopes along with the corresponding uncertainties are shown in Table A1.
The derived best-fit slopes for each host along with their standard errors (obtained using Equations (25) and (26) ) are shown in Figure A4 (purple points) along with the corresponding points of Figure 10 of R21 (green points).
The best-fit values of the slopes we obtained using the raw Cepheid data are consistent with Figure 10 of R21 as shown in Figure A4. The agreement with the results of R21 is excellent, except for three points. Two slopes corresponding to the hosts N4038 and N1365 are slightly shifted in our analysis compared to R21, due a small disagreement in the best-fit slope and a typo of R21 in transferring the correct slope to Figure 10.
In addition, the slope corresponding to the host N4424 is missing in Figure 10 of R21. In the plot of R21 (their Figure 9, where the magnitudes decrease upward on the vertical axis) corresponding to N4424, the indicated best fit line is the green line shown in the upper right inset plot of Figure A4 corresponding to the green point. The correct best fit, however, corresponds to the purple line of the upper right inset plot with the slope given by the purple point pointed by the arrow.
Thus, our Figure A4 is in excellent agreement with Figure 10 of R21 with the exception of three points, where our plot corrects the corresponding plot of R21. In any case, we stress that these three points do not play a significant role in our conclusion about the inhomogeneities of and discussed in Section 2.2.
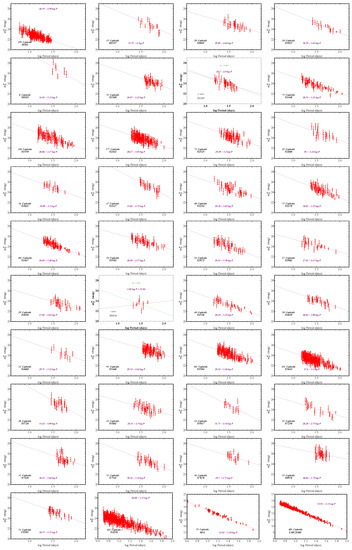
Figure A2.
Fitting individual slopes of the , P-L relations for 40 Cepheid hosts: 37 SnIa+Cepheid hosts, 2 anchors (N4258+LMC/SMC) and the pure Cepheid host M31. In the case of the SnIa+Cepheid host N4424, our fit (purple line) is not in agreement with the fit of R21 (green line). In all other cases, the agreement is very good.
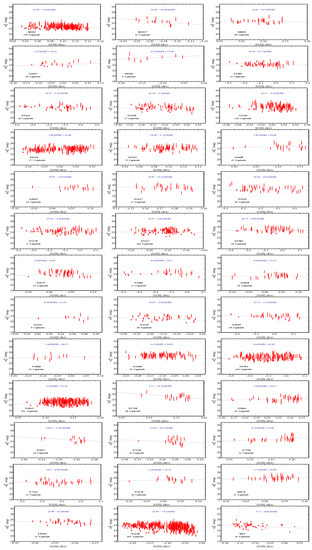
Figure A3.
Fitting individual slopes of the metallicity relations to Cepheid data for the hosts where individual Cepheid metallicity data were provided by R21 (only an average metallicity was provided for LMC/SMC and thus these Cepheid hosts are not included in the plot). Thus, the 39 hosts shown correspond to the 37 SnIa+Cepheid hosts, the anchor N4258 and the pure Cepheid host M31.
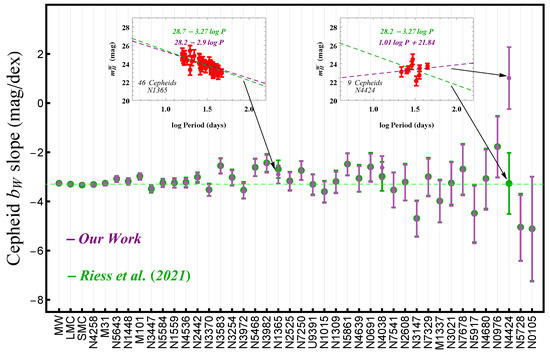
Figure A4.
Independently-fitted slopes of the P-L relations (without background covariance of any pair of Cepheids as was done in R21, i.e., taking into account only diagonal terms of the covariance matrix). The points in green are the corresponding points shown in Figure 10 of R21 (obtained using plot digitizer). Our fits are in excellent agreement with R21, with the exception of 3 points corresponding to hosts N4424, N4038 and N1365. For N4424, there is no point shown in Figure 10 of R21 but in the corresponding plot of R21 (their Figure 9, where the magnitudes decrease upward on the vertical axis), the indicated best-fit line is the green line shown in the upper right inset plot corresponding to the green point. The correct best-fit, however, corresponds to the purple line of the upper right inset plot with slope given by the purple point pointed by the arrow. Similarly, the best-fit line corresponding to N1365 shown in the upper left inset plot is identical to our purple point and not to the green point. For the Milky Way (MW), we used directly the values provided in R21 obtained from Gaia EDR3+HST.

Table A1.
The best-fit individual slopes and with their standard errors and scatter uncertainties . The scatter uncertainty ensures that the model of a universal best-fit slope becomes an acceptable model with , as described in Section 2.2. The number of hosts in the Table is , including the Milky Way (MW). For LMC and SMC, the metallicities are not provided individually for each Cepheid in R21, and thus no slope could be estimated in our analysis.
Table A1.
The best-fit individual slopes and with their standard errors and scatter uncertainties . The scatter uncertainty ensures that the model of a universal best-fit slope becomes an acceptable model with , as described in Section 2.2. The number of hosts in the Table is , including the Milky Way (MW). For LMC and SMC, the metallicities are not provided individually for each Cepheid in R21, and thus no slope could be estimated in our analysis.
| Galaxy | |||||||
|---|---|---|---|---|---|---|---|
| [Mpc] | [mag/dex] | [mag/dex] | [mag/dex] | [mag/dex] | [mag/dex] | [mag/dex] | |
| M101 | 6.71 | −2.99 | 0.14 | 0.18 | −1.14 | 0.86 | 3.2 |
| M1337 | 38.53 | −4. | 0.85 | 0.18 | −19.44 | 6.27 | 3.2 |
| N0691 | 35.4 | −2.64 | 0.57 | 0.18 | −0.73 | 2.54 | 3.2 |
| N1015 | 35.6 | −3.63 | 0.43 | 0.18 | 2.57 | 1.3 | 3.2 |
| N0105 | 73.8 | −5.13 | 2.13 | 0.18 | 6.21 | 3.8 | 3.2 |
| N1309 | 29.4 | −3.23 | 0.44 | 0.18 | −0.77 | 0.59 | 3.2 |
| N1365 | 22.8 | −2.9 | 0.37 | 0.18 | −1.45 | 0.39 | 3.2 |
| N1448 | 16.3 | −3.21 | 0.12 | 0.18 | −1.3 | 0.39 | 3.2 |
| N1559 | 19.3 | −3.27 | 0.18 | 0.18 | −2.55 | 1.62 | 3.2 |
| N2442 | 20.1 | −3.05 | 0.2 | 0.18 | 3.94 | 0.58 | 3.2 |
| N2525 | 27.2 | −3.2 | 0.37 | 0.18 | −1.75 | 2.74 | 3.2 |
| N2608 | 35.4 | −3.24 | 0.73 | 0.18 | 1.82 | 2.33 | 3.2 |
| N3021 | 26.6 | −3.3 | 0.89 | 0.18 | −1.03 | 2.85 | 3.2 |
| N3147 | 42.5 | −4.72 | 0.73 | 0.18 | −11.43 | 9.13 | 3.2 |
| N3254 | 24.4 | −3.05 | 0.31 | 0.18 | −0.22 | 0.57 | 3.2 |
| N3370 | 24 | −3.55 | 0.23 | 0.18 | −1.46 | 0.4 | 3.2 |
| N3447 | 20.8 | −3.48 | 0.13 | 0.18 | −0.62 | 0.66 | 3.2 |
| N3583 | 34.4 | −2.57 | 0.31 | 0.18 | −0.06 | 0.62 | 3.2 |
| N3972 | 15.1 | −3.58 | 0.32 | 0.18 | 4.9 | 1.58 | 3.2 |
| N3982 | 19 | −2.47 | 0.36 | 0.18 | 0.46 | 0.47 | 3.2 |
| N4038 | 29.3 | −2.63 | 0.47 | 0.18 | 0.54 | 2.07 | 3.2 |
| N4424 | 16.4 | 1.01 | 1.26 | 0.18 | 0.29 | 4.33 | 3.2 |
| N4536 | 31.9 | −3.25 | 0.19 | 0.18 | −2.82 | 0.56 | 3.2 |
| N4639 | 19.8 | −3.08 | 0.51 | 0.18 | −2.12 | 0.64 | 3.2 |
| N4680 | 42.1 | −3.12 | 1.22 | 0.18 | 1.48 | 3.27 | 3.2 |
| N5468 | 46.3 | −2.62 | 0.35 | 0.18 | 1.12 | 0.74 | 3.2 |
| N5584 | 28 | −3.26 | 0.16 | 0.18 | 0.4 | 0.36 | 3.2 |
| N5643 | 20.7 | −3.1 | 0.12 | 0.18 | 2.9 | 1.17 | 3.2 |
| N5728 | 44.9 | −5.09 | 1.34 | 0.18 | −15.19 | 5.71 | 3.2 |
| N5861 | 30.3 | −2.5 | 0.45 | 0.18 | 1.65 | 0.72 | 3.2 |
| N5917 | 31 | −4.54 | 1.17 | 0.18 | −17.82 | 6.56 | 3.2 |
| N7250 | 12.8 | −2.75 | 0.39 | 0.18 | −8.33 | 4.44 | 3.2 |
| N7329 | 46.8 | −3.04 | 0.76 | 0.18 | 6.74 | 1.86 | 3.2 |
| N7541 | 34.4 | −3.54 | 0.71 | 0.18 | −0.04 | 1.08 | 3.2 |
| N7678 | 46.6 | −2.73 | 1.03 | 0.18 | 2.16 | 2.27 | 3.2 |
| N0976 | 60.5 | −1.79 | 1.24 | 0.18 | 3.71 | 2.73 | 3.2 |
| U9391 | 29.4 | −3.33 | 0.43 | 0.18 | −4.2 | 1.51 | 3.2 |
| N4258 | 7.4 | −3.32 | 0.06 | 0.18 | −7.67 | 0.31 | 3.2 |
| M31 | 0.86 | −3.29 | 0.07 | 0.18 | −4.85 | 0.35 | 3.2 |
| LMC | 0.05 | −3.31 | 0.017 | 0.18 | − | − | 3.2 |
| SMC | 0.06 | −3.31 | 0.017 | 0.18 | − | − | 3.2 |
| MW | 0 | −3.26 | 0.05 | 0.18 | −0.2 | 0.12 | 3.2 |
Note: (a) Distances from https://ned.ipac.caltech.edu/, (accessed on 23 August 2022). (b) No individual Cepheid metallicities were provided for LMC and SMC in R21 and thus we could not estimate the slope ZW for these hosts. (c) For the Milky Way (MW), we directly used the values provided in R21 obtained from Gaia EDR3+HST.
Appendix D. Model Selection Criteria
Various methods for model selection have been developed and model comparison techniques have been used [162,163,170,171]. The reduced is a very popular method for model comparison. This is defined by
where is the minimum , and is typically the number of degrees of freedom (N is the number of datapoints used in the fit and M is the number of free parameters) for each model.
The model selection methods, such as the Akaike information criterion (AIC) [164] and the Bayesian information criterion (BIC) [172] that penalize models with additional parameters are used. For a model with M parameters and a dataset with N total observations, these are defined through the relations [163,170,171]
where (e.g., [173,174]) is the maximum likelihood of the model under consideration.
The “preferred model” is the one which minimizes AIC and BIC. The absolute values of the AIC and BIC are not informative. Only the relative values between different competing models are relevant. Hence when comparing one model versus the baseline SH0ES, we can use the model differences AIC and BIC.
The differences AIC and BIC with respect to the baseline SH0ES model are defined as
where the subindex i refers to value of AIC (BIC) for the model i and () is the value of AIC (BIC) for the baseline SH0ES model. Note that a positive value of AIC or BIC means a preference for the baseline SH0ES model.
According to the calibrated Jeffreys’ scales [175] showed in the Table A2 (see also Refs. [170,174,176,177,178]), a range of means that the two comparable models have about the same support from the data, a range means this support is considerably less for the model with the larger , while for , the model with the larger has no support, i.e., the model is practically irrelevant. Similarly, for two competing models a range is regarded as weak evidence, and a range is regarded as positive evidence, while for , the evidence is strong against the model with the larger value.
We attribute the difference between AIC and BIC for the models in consideration of the fact that the BIC penalizes additional parameters more strongly than the AIC as inferred by Equations (A10) and (A11) for the used dataset with (see Refs. [170,171,179].

Table A2.
The interpretation of differences and according to the calibrated Jeffreys’ scale [175] (see also Refs. [170,174,176,177,178]). However, it should be noted that the Jeffreys’ scale has to be interpreted with care [174] because it has been shown to lead to diverse qualitative conclusions.
Table A2.
The interpretation of differences and according to the calibrated Jeffreys’ scale [175] (see also Refs. [170,174,176,177,178]). However, it should be noted that the Jeffreys’ scale has to be interpreted with care [174] because it has been shown to lead to diverse qualitative conclusions.
| Level of empirical support for the model with the smaller | Evidence against the model with the larger | ||||||
| 0–2 | 4–7 | >10 | 0–2 | 2–6 | 6–10 | >10 | |
| Substantial | Strong | Very strong | Weak | Positive | Strong | Very strong | |
Appendix E
Here, we present in a comprehensive and concise manner the 3130 Cepheid data that appear in the vector and in the modeling matrix . The sequence is the same as the one appearing in the top 3130 entries of the vector released in the form of fits files by R21. Even though no new information is presented in the following Table A3, compared to the released fits files of R21, the concise presentation of these data may make them more useful in various applications and studies.

Table A3.
Data for 3130 Cepheids in the host SnIa host galaxies and in the anchor or supporting galaxies N4258, M31, LMC, SMC from fits files in R21. An electronic version of the complete table is available in the A reanalysis of the SH0ES data for GitHub repository, https://github.com/FOTEINISKARA/A-reanalysis-of-the-SH0ES-data-for-H_0 (accessed on 23 August 2022) under the MIT license.
Table A3.
Data for 3130 Cepheids in the host SnIa host galaxies and in the anchor or supporting galaxies N4258, M31, LMC, SMC from fits files in R21. An electronic version of the complete table is available in the A reanalysis of the SH0ES data for GitHub repository, https://github.com/FOTEINISKARA/A-reanalysis-of-the-SH0ES-data-for-H_0 (accessed on 23 August 2022) under the MIT license.
| Galaxy | Ranking | [P] | [O/H] | ||
|---|---|---|---|---|---|
| in Vector Y | [mag] | [mag] | [dex] | [dex] | |
| M1337 | 1 | 27.52 | 0.39 | 0.45 | −0.2 |
| M1337 | 2 | 28.05 | 0.47 | 0.65 | −0.19 |
| M1337 | 3 | 26.56 | 0.35 | 0.6 | −0.2 |
| M1337 | 4 | 26.97 | 0.27 | 0.78 | −0.2 |
| M1337 | 5 | 27.01 | 0.47 | 0.72 | −0.18 |
| M1337 | 6 | 26.29 | 0.5 | 0.9 | −0.17 |
| M1337 | 7 | 26.12 | 0.6 | 0.89 | −0.17 |
| M1337 | 8 | 26.94 | 0.45 | 0.75 | −0.17 |
| M1337 | 9 | 27.78 | 0.61 | 0.69 | −0.16 |
| M1337 | 10 | 26.17 | 0.55 | 0.7 | −0.14 |
| M1337 | 11 | 26.63 | 0.65 | 0.49 | −0.22 |
| M1337 | 12 | 27.4 | 0.39 | 0.85 | −0.19 |
| M1337 | 13 | 27.26 | 0.53 | 0.52 | −0.22 |
| M1337 | 14 | 27.34 | 0.34 | 0.85 | −0.17 |
| M1337 | 15 | 27 | 0.54 | 0.7 | −0.19 |
| N0691 | 1 | 26.59 | 0.57 | 0.4 | 0.09 |
| N0691 | 2 | 27.1 | 0.46 | 0.61 | 0.06 |
| N0691 | 3 | 26.79 | 0.47 | 0.71 | 0.04 |
| N0691 | 4 | 26.83 | 0.5 | 0.78 | 0.14 |
| N0691 | 5 | 26.23 | 0.44 | 0.51 | 0.05 |
| N0691 | 6 | 27.16 | 0.48 | 0.63 | 0.1 |
| N0691 | 7 | 26.89 | 0.46 | 0.7 | 0.03 |
| N0691 | 8 | 26.75 | 0.59 | 0.43 | 0.03 |
| N0691 | 9 | 27.11 | 0.28 | 0.88 | 0.04 |
| N0691 | 10 | 26.99 | 0.68 | 0.62 | 0.1 |
| N0691 | 11 | 27.6 | 0.35 | 0.81 | 0.07 |
| N0691 | 12 | 27.33 | 0.38 | 0.75 | 0.08 |
| N0691 | 13 | 26.6 | 0.53 | 0.54 | 0.14 |
| N0691 | 14 | 26.34 | 0.45 | 0.74 | 0.09 |
| N0691 | 15 | 26.91 | 0.3 | 0.96 | 0.11 |
| N0691 | 16 | 26.79 | 0.49 | 0.84 | 0.13 |
| N0691 | 17 | 27.08 | 0.48 | 0.63 | 0.1 |
| N0691 | 18 | 27.07 | 0.59 | 0.63 | 0.1 |
| N0691 | 19 | 26.69 | 0.63 | 0.53 | 0.07 |
| N0691 | 20 | 27.94 | 0.58 | 0.49 | 0.11 |
| N0691 | 21 | 26.15 | 0.62 | 0.48 | 0.12 |
| N0691 | 22 | 26.46 | 0.43 | 0.74 | 0.11 |
| N0691 | 23 | 27.16 | 0.6 | 0.42 | 0.14 |
| N0691 | 24 | 26.96 | 0.38 | 0.8 | 0.14 |
| N0691 | 25 | 26.59 | 0.44 | 0.65 | 0.04 |
| N0691 | 26 | 26.61 | 0.52 | 0.5 | 0.09 |
| N0691 | 27 | 26.21 | 0.6 | 0.62 | 0.11 |
| N0691 | 28 | 27.42 | 0.65 | 0.65 | 0.1 |
| … | … | … | … | … | … |
Notes
| 1 | At a distance [156], NGC4258 is the closest galaxy, beyond the Local Group with a geometric distance measurement. |
| 2 | A differential distance measurement of the SMC with respect to the LMC is used and thus LMC+SMC are considered in a unified manner in the released data. |
| 3 | 45 Cepheids in N1365 are mentioned in R21 but there are 46 in the fits files of the released dataset at Github repository: PantheonPlusSH0ES/DataRelease (accessed on 25 June 2022). |
| 4 | A total of 3130 Cepheids have been released in the data fits files but 3129 are mentioned in R21 (see Table 3). These data are also shown concisely in Table A3 of Appendix E and may be download in electronic form. |
| 5 | This parameter is not defined in R21 but is included in the data release fits files. We thank A. Riess for clarifying this point. |
| 6 | For Cepheids in the LMC/SMC anchor observed from the ground, the zeropoint parameter is added on the RHS, and thus Equation (6) becomes to allow for a different P-L zeropoint between ground and HST observations. |
| 7 | In the case of SMC, a differential distance with respect to LMC is used. |
| 8 | The , and matrices have been made publicly available as fits files by the SH0ES team at Github repository: PantheonPlusSH0ES/DataRelease (accessed on 25 June 2022). |
| 9 | The results for the parameters in are the same as the results obtained using the numerical minimization of (see the absolute matching of the results in the numerical analysis file “Baseline1 structure of system” in the A reanalysis of the SH0ES data for H0 GitHub repository (accessed on 23 August 2022)). |
| 10 | We use the standard notation which is important in the error propagation to . |
| 11 | 37 SnIa/Cepheid hosts and 3 pure Cepheid hosts of which 2 are anchors (N4258 and LMC) |
| 12 | As discussed in Appendix C, two slopes corresponding to the hosts N4038 and N1365 are slightly shifted in our analysis compared to R21 due a small disagreement in the best-fit slope and a typo of R21 in transferring the correct slope to Figure 10, while the slope corresponding to the host N4424 is missing in Figure 10 of R21. |
| 13 | The number of degrees of freedom is for and for . The smaller number of N for is due to the fact that metallicities were not provided for individual Cepheids in the LMC and SMS in R21, and thus, we evaluated a smaller number of slopes for . See also Table A1. The points shown in the plot Figure 1 include the two additional points corresponding to MW and SMC (which is degenerate with LMC). |
| 14 | Some hosts have more than one SnIa and more than one light curve and thus, averaging with proper uncertainties was implemented in these cases. |
| 15 | For more details see https://people.duke.edu/~hpgavin/SystemID/CourseNotes/linear-least-squres.pdf (accessed on 28 June 2022). |
References
- Riess, A.G.; Yuan, W.; Macri, L.M.; Scolnic, D.; Brout, D.; Casertano, S.; Jones, D.O.; Murakami, Y.; Anand, G.S.; Breuval, L.; et al. A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km s-1 Mpc-1 Uncertainty from the Hubble Space Telescope and the SH0ES Team. Astrophys. J. Lett. 2022, 934, L7. [Google Scholar] [CrossRef]
- Freedman, W.L. Measurements of the Hubble Constant: Tensions in Perspective. arXiv 2021, arXiv:2106.15656. [Google Scholar] [CrossRef]
- Gómez-Valent, A.; Amendola, L. H0 from cosmic chronometers and Type Ia supernovae, with Gaussian Processes and the novel Weighted Polynomial Regression method. J. Cosmol. Astropart. Phys. 2018, 04, 051. [Google Scholar] [CrossRef]
- Pesce, D.; Braatz, J.A.; Reid, M.J.; Riess, A.G.; Scolnic, D.; Condon, J.J.; Gao, F.; Henkel, C.; Impellizzeri, C.M.V.; Kuo, C.Y.; et al. The Megamaser Cosmology Project. XIII. Combined Hubble constant constraints. Astrophys. J. Lett. 2020, 891, L1. [Google Scholar] [CrossRef]
- Freedman, W.L.; Madore, B.F.; Hoyt, T.; Jang, I.S.; Beaton, R.; Lee, M.G.; Monson, A.; Neeley, J.; Rich, J. Calibration of the Tip of the Red Giant Branch (TRGB). arXiv 2020, arXiv:2002.01550. [Google Scholar]
- Wong, K.C.; Suyu, S.H.; Chen, G.C.-F.; E Rusu, C.; Millon, M.; Sluse, D.; Bonvin, V.; Fassnacht, C.D.; Taubenberger, S.; Auger, M.W.; et al. H0LiCOW – XIII. A 2.4 per cent measurement of H0 from lensed quasars: 5.3σ tension between early- and late-Universe probes. Mon. Not. Roy. Astron. Soc. 2020, 498, 1420–1439. [Google Scholar] [CrossRef]
- Chen, G.C.F.; Fassnacht, C.; Suyu, S.H.; E Rusu, C.; Chan, J.H.H.; Wong, K.C.; Auger, M.W.; Hilbert, S.; Bonvin, V.; Birrer, S.; et al. A SHARP view of H0LiCOW: H0 from three time-delay gravitational lens systems with adaptive optics imaging. Mon. Not. Roy. Astron. Soc. 2019, 490, 1743–1773. [Google Scholar] [CrossRef]
- Birrer, S.; Shajib, A.J.; Galan, A.; Millon, M.; Treu, T.; Agnello, A.; Auger, M.; Chen, G.C.-F.; Christensen, L.; Van de Vyvere, L.; et al. TDCOSMO - IV. Hierarchical time-delay cosmography – joint inference of the Hubble constant and galaxy density profiles. Astron. Astrophys. 2020, 643, A165. [Google Scholar] [CrossRef]
- Birrer, S.; Treu, T.; E Rusu, C.; Bonvin, V.; Fassnacht, C.; Chan, J.H.H.; Agnello, A.; Shajib, A.J.; Chen, G.C.-F.; Auger, M.; et al. Cosmographic analysis of the doubly imaged quasar SDSS 1206+4332 and a new measurement of the Hubble constant. Mon. Not. Roy. Astron. Soc. 2019, 484, 4726. [Google Scholar] [CrossRef]
- Fishbach, M.; Gray, R.; Hernandez, I.M.; Qi, H.; Sur, A.; Acernese, F.; Aiello, L.; Allocca, A.; Aloy, M.A.; Amato, A.; et al. A Standard Siren Measurement of the Hubble Constant from GW170817 without the Electromagnetic Counterpart. Astrophys. J. Lett. 2019, 871, L13. [Google Scholar] [CrossRef]
- Hotokezaka, K.; Nakar, E.; Gottlieb, O.; Nissanke, S.; Masuda, K.; Hallinan, G.; Mooley, K.P.; Deller, A.T. A Hubble constant measurement from superluminal motion of the jet in GW170817. Nature Astron. 2019, 3, 940–944. [Google Scholar] [CrossRef]
- Abbott, B.P.; Shajib, A.J.; Galan, A.; Millon, M.; Treu, T.; Agnello, A.; Auger, M.; Chen, G.C.-F.; Christensen, L.; Collett, T.; et al. A gravitational-wave standard siren measurement of the Hubble constant. Nature 2017, 551, 85–88. [Google Scholar] [CrossRef]
- Palmese, A.; Devicente, J.; Pereira, M.E.S.; Annis, J.; Hartley, W.; Herner, K.; Soares-Santos, M.; Crocce, M.; Huterer, D.; Magaña Hernandez, I.; et al. A statistical standard siren measurement of the Hubble constant from the LIGO/Virgo gravitational wave compact object merger GW190814 and Dark Energy Survey galaxies. Astrophys. J. Lett. 2020, 900, L33. [Google Scholar] [CrossRef]
- Soares-Santos, M.; Palmese, A.; Hartley, W.; Annis, J.; Garcia-Bellido, J.; Lahav, O.; Doctor, Z.; Fishbach, M.; Holz, D.E.; Lin, H.; et al. First Measurement of the Hubble Constant from a Dark Standard Siren using the Dark Energy Survey Galaxies and the LIGO/Virgo Binary–Black-hole Merger GW170814. Astrophys. J. Lett. 2019, 876, L7. [Google Scholar] [CrossRef]
- Cao, S.; Dainotti, M.; Ratra, B. Standardizing Platinum Dainotti-correlated gamma-ray bursts, and using them with standardized Amati-correlated gamma-ray bursts to constrain cosmological model parameters. Mon. Not. Roy. Astron. Soc. 2022, 512, 439–454. [Google Scholar] [CrossRef]
- Cao, S.; Dainotti, M.; Ratra, B. Gamma-ray burst data strongly favor the three-parameter fundamental plane (Dainotti) correlation relation over the two-parameter one. Mon. Not. R. Astron. Soc. 2022, 516, 1386–1405. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Sarracino, G.; Capozziello, S. Gamma-Ray Bursts, Supernovae Ia and Baryon Acoustic Oscillations: A binned cosmological analysis. Publ. Astron. Soc. Jpn. 2022, 74, 1095–1113. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Nielson, V.; Sarracino, G.; Rinaldi, E.; Nagataki, S.; Capozziello, S.; Gnedin, O.Y.; Bargiacchi, G. Optical and X-ray GRB Fundamental Planes as cosmological distance indicators. Mon. Not. Roy. Astron. Soc. 2022, 514, 1828–1856. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Cardone, V.F.; Piedipalumbo, E.; Capozziello, S. Slope evolution of GRB correlations and cosmology. Mon. Not. Roy. Astron. Soc. 2013, 436, 82. [Google Scholar] [CrossRef]
- Risaliti, G.; Lusso, E. Cosmological constraints from the Hubble diagram of quasars at high redshifts. Nat. Astron. 2019, 3, 272–277. [Google Scholar] [CrossRef]
- de Jaeger, T.; Galbany, L.; Riess, A.G.; Stahl, B.E.; Shappee, B.J.; Filippenko, A.V.; Zheng, W. A 5% measurement of the Hubble constant from Type II supernovae. Mon. Not. R. Astron. Soc. 2020, 514, 4620–4628. [Google Scholar] [CrossRef]
- de Jaeger, T.; Stahl, B.; Zheng, W.; Filippenko, A.; Riess, A.; Galbany, L. A measurement of the Hubble constant from Type II supernovae. Mon. Not. R. Astron. Soc. 2020, 496, 3402–3411. [Google Scholar] [CrossRef]
- Domínguez, A.; Wojtak, R.; Finke, J.; Ajello, M.; Helgason, K.; Prada, F.; Desai, A.; Paliya, V.; Marcotulli, L.; Hartmann, D. A new measurement of the Hubble constant and matter content of the Universe using extragalactic background light γ-ray attenuation. Astrophys. J. 2019, 885, 137. [Google Scholar] [CrossRef]
- Di Valentino, E.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the realm of the Hubble tension—a review of solutions. Class. Quant. Grav. 2021, 38, 153001. [Google Scholar] [CrossRef]
- Perivolaropoulos, L.; Skara, F. Challenges for ΛCDM: An update. New Astron. Rev. 2022, 95, 101659. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.I.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6, Erratum Astron. Astrophys. 2021, 652, C4. [Google Scholar] [CrossRef]
- Abdalla, E.; Abellán, G.F.; Aboubrahim, A.; Agnello, A.; Akarsu, O.; Akrami, Y.; Alestas, G.; Aloni, D.; Amendola, L.; Anchordoqui, L.A.; et al. Cosmology intertwined: A review of the particle physics, astrophysics, and cosmology associated with the cosmological tensions and anomalies. JHEAp 2022, 34, 49–211. [Google Scholar] [CrossRef]
- Shah, P.; Lemos, P.; Lahav, O. A buyer’s guide to the Hubble constant. Astron. Astrophys. Rev. 2021, 29, 9. [Google Scholar] [CrossRef]
- Knox, L.; Millea, M. The Hubble Hunter’s Guide. arXiv 2019, arXiv:1908.03663. [Google Scholar]
- Vagnozzi, S. New physics in light of the H0 tension: An alternative view. Phys. Rev. D 2020, 102, 023518. [Google Scholar] [CrossRef]
- Ishak, M. Testing General Relativity in Cosmology. Living Rev. Rel. 2019, 22, 1. [Google Scholar] [CrossRef] [PubMed]
- Mörtsell, E.; Dhawan, S. Does the Hubble constant tension call for new physics? JCAP 2018, 1809, 025. [Google Scholar] [CrossRef]
- Huterer, D.; Shafer, D.L. Dark energy two decades after: Observables, probes, consistency tests. Rept. Prog. Phys. 2018, 81, 016901. [Google Scholar] [CrossRef]
- Bernal, J.L.; Verde, L.; Riess, A.G. The trouble with H0. JCAP 2016, 1610, 019. [Google Scholar] [CrossRef]
- Alam, S.; Aubert, M.; Avila, S.; Balland, C.; Bautista, J.E.; Bershady, M.A.; Bizyaev, D.; Blanton, M.R.; Bolton, A.S.; Bovy, J.; et al. Completed SDSS-IV extended Baryon Oscillation Spectroscopic Survey: Cosmological implications from two decades of spectroscopic surveys at the Apache Point Observatory. Phys. Rev. D 2021, 103, 083533. [Google Scholar] [CrossRef]
- Verde, L.; Treu, T.; Riess, A.G. Tensions between the Early and the Late Universe. Nature Astron. 2019, 3, 891. [Google Scholar] [CrossRef]
- Schöneberg, N.; Franco Abellán, G.; Pérez Sánchez, A.; Witte, S.J.; Poulin, V.; Lesgourgues, J. The H0 Olympics: A fair ranking of proposed models. arXiv 2021, arXiv:2107.10291. [Google Scholar] [CrossRef]
- Krishnan, C.; Colgáin, E.O.; Ruchika; Sen, A.A.; Sheikh-Jabbari, M.M.; Yang, T. Is there an early Universe solution to Hubble tension? Phys. Rev. D 2020, 102, 103525. [Google Scholar] [CrossRef]
- Jedamzik, K.; Pogosian, L.; Zhao, G.B. Why reducing the cosmic sound horizon can not fully resolve the Hubble tension. arXiv 2020, arXiv:2010.04158. [Google Scholar]
- Poulin, V.; Smith, T.L.; Karwal, T.; Kamionkowski, M. Early Dark Energy Can Resolve The Hubble Tension. Phys. Rev. Lett. 2019, 122, 221301. [Google Scholar] [CrossRef]
- Niedermann, F.; Sloth, M.S. New early dark energy. Phys. Rev. D 2021, 103, L041303. [Google Scholar] [CrossRef]
- Smith, T.L.; Lucca, M.; Poulin, V.; Abellan, G.F.; Balkenhol, L.; Benabed, K.; Galli, S.; Murgia, R. Hints of Early Dark Energy in Planck, SPT, and ACT data: New physics or systematics? arXiv 2022, arXiv:2202.09379. [Google Scholar] [CrossRef]
- Smith, T.L.; Poulin, V.; Bernal, J.L.; Boddy, K.K.; Kamionkowski, M.; Murgia, R. Early dark energy is not excluded by current large-scale structure data. arXiv 2020, arXiv:2009.10740. [Google Scholar] [CrossRef]
- Chudaykin, A.; Gorbunov, D.; Nedelko, N. Combined analysis of Planck and SPTPol data favors the early dark energy models. J. Cosmol. Astropart. Phys. 2020, 08, 013. [Google Scholar] [CrossRef]
- Fondi, E.; Melchiorri, A.; Pagano, L. No evidence for EDE from Planck data in extended scenarios. Astrophys. J. Lett. 2022, 931, L18. [Google Scholar]
- Sabla, V.I.; Caldwell, R.R. The Microphysics of Early Dark Energy. arXiv 2022, arXiv:2202.08291. [Google Scholar] [CrossRef]
- Herold, L.; Ferreira, E.G.M.; Komatsu, E. New Constraint on Early Dark Energy from Planck and BOSS Data Using the Profile Likelihood. Astrophys. J. Lett. 2022, 929, L16. [Google Scholar] [CrossRef]
- McDonough, E.; Lin, M.X.; Hill, J.C.; Hu, W.; Zhou, S. Early dark sector, the Hubble tension, and the swampland. Phys. Rev. D 2022, 106, 043525. [Google Scholar] [CrossRef]
- Hill, J.C.; McDonough, E.; Toomey, M.W.; Alexander, S. Early Dark Energy Does Not Restore Cosmological Concordance. arXiv 2020, arXiv:2003.07355. [Google Scholar] [CrossRef]
- Sakstein, J.; Trodden, M. Early Dark Energy from Massive Neutrinos as a Natural Resolution of the Hubble Tension. Phys. Rev. Lett. 2020, 124, 161301. [Google Scholar] [CrossRef]
- Niedermann, F.; Sloth, M.S. New Early Dark Energy is compatible with current LSS data. arXiv 2020, arXiv:2009.00006. [Google Scholar] [CrossRef]
- Rezazadeh, K.; Ashoorioon, A.; Grin, D. Cascading Dark Energy. arXiv 2022, arXiv:2208.07631. [Google Scholar]
- Green, D.; Amin, M.A.; Meyers, J.; Wallisch, B.; Abazajian, K.N.; Abidi, M.; Adshead, P.; Ahmed, Z.; Ansarinejad, B.; Armstrong, R.; et al. Messengers from the Early Universe: Cosmic Neutrinos and Other Light Relics. Bull. Am. Astron. Soc. 2019, 51, 159. [Google Scholar]
- Schöneberg, N.; Franco Abellán, G. A step in the right direction? Analyzing the Wess Zumino Dark Radiation solution to the Hubble tension. arXiv 2022, arXiv:2206.11276. [Google Scholar]
- Seto, O.; Toda, Y. Comparing early dark energy and extra radiation solutions to the Hubble tension with BBN. arXiv 2021, arXiv:2101.03740. [Google Scholar] [CrossRef]
- Carrillo González, M.; Liang, Q.; Sakstein, J.; Trodden, M. Neutrino-Assisted Early Dark Energy: Theory and Cosmology. arXiv 2020, arXiv:2011.09895. [Google Scholar] [CrossRef]
- Braglia, M.; Ballardini, M.; Finelli, F.; Koyama, K. Early modified gravity in light of the H0 tension and LSS data. Phys. Rev. D 2021, 103, 043528. [Google Scholar] [CrossRef]
- Abadi, T.; Kovetz, E.D. Can conformally coupled modified gravity solve the Hubble tension? Phys. Rev. D 2021, 103, 023530. [Google Scholar] [CrossRef]
- Renk, J.; Zumalacárregui, M.; Montanari, F.; Barreira, A. Galileon gravity in light of ISW, CMB, BAO and H0 data. J. Cosmol. Astropart. Phys. 2017, 1710, 020. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Integral F(R) gravity and saddle point condition as a remedy for the H0-tension. Nucl. Phys. B 2022, 980, 115850. [Google Scholar] [CrossRef]
- Lin, M.X.; Raveri, M.; Hu, W. Phenomenology of Modified Gravity at Recombination. Phys. Rev. 2019, D99, 043514. [Google Scholar] [CrossRef]
- Saridakis, E.N.; Lazkoz, R.; Salzano, V.; Moniz, P.V.; Capozziello, S.; Jiménez, J.B.; De Laurentis, M.; Olmo, G.J. Modified Gravity and Cosmology: An Update by the CANTATA Network. arXiv 2021, arXiv:2105.12582. [Google Scholar]
- Benisty, D. Quantifying the S8 tension with the Redshift Space Distortion data set. Phys. Dark Univ. 2021, 31, 100766. [Google Scholar] [CrossRef]
- Heymans, C.; Tröster, T.; Asgari, M.; Blake, C.; Hildebrandt, H.; Joachimi, B.; Kuijken, K.; Lin, C.-A.; Sánchez, A.G.; Busch, J.L.V.D.; et al. KiDS-1000 Cosmology: Multi-probe weak gravitational lensing and spectroscopic galaxy clustering constraints. Astron. Astrophys. 2021, 646, A140. [Google Scholar] [CrossRef]
- Kazantzidis, L.; Perivolaropoulos, L. Evolution of the fσ8 tension with the Planck15/ΛCDM determination and implications for modified gravity theories. Phys. Rev. D 2018, 97, 103503. [Google Scholar] [CrossRef]
- Joudaki, S.; Blake, C.; Johnson, A.; Amon, A.; Asgari, M.; Choi, A.; Erben, T.; Glazebrook, K.; Harnois-Déraps, J.; Heymans, C.; et al. KiDS-450 + 2dFLenS: Cosmological parameter constraints from weak gravitational lensing tomography and overlapping redshift-space galaxy clustering. Mon. Not. Roy. Astron. Soc. 2018, 474, 4894–4924. [Google Scholar] [CrossRef]
- Kazantzidis, L.; Perivolaropoulos, L. σ8 Tension.Is Gravity Getting Weaker at Low z? Observational Evidence and Theoretical Implications. In Modified Gravity and Cosmology; Springer: Cham, Switzerland, 2019; pp. 507–537. [Google Scholar] [CrossRef]
- Skara, F.; Perivolaropoulos, L. Tension of the EG statistic and redshift space distortion data with the Planck - ΛCDM model and implications for weakening gravity. Phys. Rev. D 2020, 101, 063521. [Google Scholar] [CrossRef]
- Avila, F.; Bernui, A.; Bonilla, A.; Nunes, R.C. Inferring S8(z) and γ(z) with cosmic growth rate measurements using machine learning. Eur. Phys. J. C 2022, 82, 594. [Google Scholar] [CrossRef]
- Köhlinger, F.; Viola, M.; Joachimi, B.; Hoekstra, H.; Van Uitert, E.; Hildebrandt, H.; Choi, A.; Erben, T.; Heymans, C.; Joudaki, S.; et al. KiDS-450: The tomographic weak lensing power spectrum and constraints on cosmological parameters. Mon. Not. Roy. Astron. Soc. 2017, 471, 4412–4435. [Google Scholar] [CrossRef]
- Nunes, R.C.; Vagnozzi, S. Arbitrating the S8 discrepancy with growth rate measurements from redshift-space distortions. Mon. Not. Roy. Astron. Soc. 2021, 505, 5427–5437. [Google Scholar] [CrossRef]
- Clark, S.J.; Vattis, K.; Fan, J.; Koushiappas, S.M. The H0 and S8 tensions necessitate early and late time changes to ΛCDM. arXiv 2021, arXiv:2110.09562. [Google Scholar]
- Ivanov, M.M.; McDonough, E.; Hill, J.C.; Simonović, M.; Toomey, M.W.; Alexander, S.; Zaldarriaga, M. Constraining Early Dark Energy with Large-Scale Structure. Phys. Rev. D 2020, 102, 103502. [Google Scholar] [CrossRef]
- Hill, J.C.; Calabrese, E.; Aiola, S.; Battaglia, N.; Bolliet, B.; Choi, S.K.; Devlin, M.J.; Duivenvoorden, A.J.; Dunkley, J.; Ferraro, S.; et al. Atacama Cosmology Telescope: Constraints on prerecombination early dark energy. Phys. Rev. D 2022, 105, 123536. [Google Scholar] [CrossRef]
- Vagnozzi, S. Consistency tests of ΛCDM from the early integrated Sachs-Wolfe effect: Implications for early-time new physics and the Hubble tension. Phys. Rev. D 2021, 104, 063524. [Google Scholar] [CrossRef]
- Philcox, O.H.E.; Farren, G.S.; Sherwin, B.D.; Baxter, E.J.; Brout, D.J. Determining the Hubble Constant without the Sound Horizon: A 3.6% Constraint on H0 from Galaxy Surveys, CMB Lensing and Supernovae. arXiv 2022, arXiv:2204.02984. [Google Scholar] [CrossRef]
- Chudaykin, A.; Gorbunov, D.; Nedelko, N. Exploring an early dark energy solution to the Hubble tension with Planck and SPTPol data. Phys. Rev. D 2021, 103, 043529. [Google Scholar] [CrossRef]
- Reeves, A.; Herold, L.; Vagnozzi, S.; Sherwin, B.D.; Ferreira, E.G.M. Restoring cosmological concordance with early dark energy and massive neutrinos? arXiv 2022, arXiv:2207.01501. [Google Scholar]
- Solà Peracaula, J.; Gómez-Valent, A.; de Cruz Pérez, J.; Moreno-Pulido, C. Brans–Dicke cosmology with a Λ-term: A possible solution to ΛCDM tensions. Class. Quant. Grav. 2020, 37, 245003. [Google Scholar] [CrossRef]
- Braglia, M.; Ballardini, M.; Emond, W.T.; Finelli, F.; Gumrukcuoglu, A.E.; Koyama, K.; Paoletti, D. Larger value for H0 by an evolving gravitational constant. Phys. Rev. D 2020, 102, 023529. [Google Scholar] [CrossRef]
- Pogosian, L.; Raveri, M.; Koyama, K.; Martinelli, M.; Silvestri, A.; Zhao, G.B. Imprints of cosmological tensions in reconstructed gravity. arXiv 2021, arXiv:2107.12992. [Google Scholar]
- Bahamonde, S.; Dialektopoulos, K.F.; Escamilla-Rivera, C.; Farrugia, G.; Gakis, V.; Hendry, M.; Hohmann, M.; Said, J.L.; Mifsud, J.; Di Valentino, E. Teleparallel Gravity: From Theory to Cosmology. arXiv 2021, arXiv:2106.13793. [Google Scholar]
- Di Valentino, E.; Mukherjee, A.; Sen, A.A. Dark Energy with Phantom Crossing and the H0 Tension. Entropy 2021, 23, 404. [Google Scholar] [CrossRef] [PubMed]
- Alestas, G.; Kazantzidis, L.; Perivolaropoulos, L. H0 Tension, Phantom Dark Energy and Cosmological Parameter Degeneracies. Phys. Rev. D 2020, 101, 123516. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Mena, O.; Vagnozzi, S. Nonminimal dark sector physics and cosmological tensions. Phys. Rev. D 2020, 101, 063502. [Google Scholar] [CrossRef]
- Pan, S.; Yang, W.; Di Valentino, E.; Shafieloo, A.; Chakraborty, S. Reconciling H0 tension in a six parameter space? J. Cosmol. Astropart. Phys. 2020, 06, 062. [Google Scholar] [CrossRef]
- Li, X.; Shafieloo, A. A Simple Phenomenological Emergent Dark Energy Model can Resolve the Hubble Tension. Astrophys. J. Lett. 2019, 883, L3. [Google Scholar] [CrossRef]
- Zhao, G.B.; Raveri, M.; Pogosian, L.; Wang, Y.; Crittenden, R.G.; Handley, W.; Percival, W.J.; Beutler, F.; Brinkmann, J.; Chuang, C.-H.; et al. Dynamical dark energy in light of the latest observations. Nature Astron. 2017, 1, 627–632. [Google Scholar] [CrossRef]
- Keeley, R.E.; Joudaki, S.; Kaplinghat, M.; Kirkby, D. Implications of a transition in the dark energy equation of state for the H0 and σ8 tensions. J. Cosmol. Astropart. Phys. 2019, 12, 035. [Google Scholar] [CrossRef]
- Sola Peracaula, J.; Gomez-Valent, A.; de Cruz Pérez, J. Signs of Dynamical Dark Energy in Current Observations. Phys. Dark Univ. 2019, 25, 100311. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Di Valentino, E.; Saridakis, E.N.; Chakraborty, S. Observational constraints on one-parameter dynamical dark-energy parametrizations and the H0 tension. Phys. Rev. 2019, D99, 043543. [Google Scholar] [CrossRef]
- Krishnan, C.; Colgáin, E.O.; Sheikh-Jabbari, M.M.; Yang, T. Running Hubble Tension and a H0 Diagnostic. Phys. Rev. D 2021, 103, 103509. [Google Scholar] [CrossRef]
- Dainotti, M.G.; De Simone, B.; Schiavone, T.; Montani, G.; Rinaldi, E.; Lambiase, G. On the Hubble constant tension in the SNe Ia Pantheon sample. Astrophys. J. 2021, 912, 150. [Google Scholar] [CrossRef]
- Colgáin, E.O.; Sheikh-Jabbari, M.M.; Solomon, R.; Bargiacchi, G.; Capozziello, S.; Dainotti, M.G.; Stojkovic, D. Revealing intrinsic flat ΛCDM biases with standardizable candles. Phys. Rev. D 2022, 106, L041301. [Google Scholar] [CrossRef]
- Colgáin, E.O.; Sheikh-Jabbari, M.M.; Solomon, R.; Dainotti, M.G.; Stojkovic, D. Putting Flat ΛCDM In The (Redshift) Bin. arXiv 2022, arXiv:2206.11447. [Google Scholar]
- Zhou, Z.; Liu, G.; Xu, L. Can late dark energy restore the Cosmic concordance? arXiv 2021, arXiv:2105.04258. [Google Scholar]
- Di Valentino, E.; Melchiorri, A.; Mena, O.; Vagnozzi, S. Interacting dark energy in the early 2020s: A promising solution to the H0 and cosmic shear tensions. Phys. Dark Univ. 2020, 30, 100666. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Di Valentino, E.; Nunes, R.C.; Vagnozzi, S.; Mota, D.F. Tale of stable interacting dark energy, observational signatures, and the H0 tension. J. Cosmol. Astropart. Phys. 2018, 1809, 019. [Google Scholar] [CrossRef]
- Vattis, K.; Koushiappas, S.M.; Loeb, A. Dark matter decaying in the late Universe can relieve the H0 tension. Phys. Rev. 2019, D99, 121302. [Google Scholar] [CrossRef]
- Yang, W.; Mukherjee, A.; Di Valentino, E.; Pan, S. Interacting dark energy with time varying equation of state and the H0 tension. Phys. Rev. 2018, D98, 123527. [Google Scholar] [CrossRef]
- Ghosh, S.; Khatri, R.; Roy, T.S. Can dark neutrino interactions phase out the Hubble tension? Phys. Rev. D 2020, 102, 123544. [Google Scholar] [CrossRef]
- Brieden, S.; Gil-Marín, H.; Verde, L. Model-agnostic interpretation of 10 billion years of cosmic evolution traced by BOSS and eBOSS data. J. Cosmol. Astropart. Phys. 2022, 08, 024. [Google Scholar] [CrossRef]
- Alestas, G.; Perivolaropoulos, L. Late time approaches to the Hubble tension deforming H(z), worsen the growth tension. Mon. Not. Roy. Astron. Soc. 2021, 504, 3956. [Google Scholar] [CrossRef]
- Keeley, R.E.; Shafieloo, A. Ruling Out New Physics at Low Redshift as a solution to the H0 Tension. arXiv 2022, arXiv:2206.08440. [Google Scholar]
- Clark, S.J.; Vattis, K.; Koushiappas, S.M. CMB constraints on late-universe decaying dark matter as a solution to the H0 tension. arXiv 2020, arXiv:2006.03678. [Google Scholar]
- Chen, A.; Huterer, D.; Lee, S.; Ferté, A.; Weaverdyck, N.; Alves, O.; Leonard, C.D.; MacCrann, N.; Raveri, M.; Porredon, A.; et al. Constraints on dark matter to dark radiation conversion in the late universe with DES-Y1 and external data. Phys. Rev. D 2021, 103, 123528. [Google Scholar] [CrossRef]
- Anchordoqui, L.A.; Barger, V.; Marfatia, D.; Soriano, J.F. Decay of multiple dark matter particles to dark radiation in different epochs does not alleviate the Hubble tension. Phys. Rev. D 2022, 105, 103512. [Google Scholar] [CrossRef]
- Mau, S.; Nadler, E.O.; Wechsler, R.H.; Drlica-Wagner, A.; Bechtol, K.; Green, G.; Huterer, D.; Li, T.S.; Mao, Y.-Y.; Martínez-Vázquez, C.E.; et al. Milky Way Satellite Census. IV. Constraints on Decaying Dark Matter from Observations of Milky Way Satellite Galaxies. Astrophys. J. 2022, 932, 128. [Google Scholar] [CrossRef]
- Cai, R.G.; Guo, Z.K.; Wang, S.J.; Yu, W.W.; Zhou, Y. No-go guide for the Hubble tension: Matter perturbations. arXiv 2020, arXiv:2202.12214. [Google Scholar]
- Heisenberg, L.; Villarrubia-Rojo, H.; Zosso, J. Can late-time extensions solve the H0 and σ8 tensions? Phys. Rev. D 2022, 106, 043503. [Google Scholar] [CrossRef]
- Vagnozzi, S.; Pacucci, F.; Loeb, A. Implications for the Hubble tension from the ages of the oldest astrophysical objects. JHEAp 2022, 36, 27–35. [Google Scholar] [CrossRef]
- Davari, Z.; Khosravi, N. Can decaying dark matter scenarios alleviate both H0 and σ8 tensions? arXiv 2020, arXiv:2203.09439. [Google Scholar] [CrossRef]
- Mortsell, E.; Goobar, A.; Johansson, J.; Dhawan, S. The Hubble Tension Bites the Dust: Sensitivity of the Hubble Constant Determination to Cepheid Color Calibration. arXiv 2021, arXiv:2105.11461. [Google Scholar]
- Efstathiou, G. H0 Revisited. Mon. Not. Roy. Astron. Soc. 2014, 440, 1138–1152. [Google Scholar] [CrossRef]
- Efstathiou, G. A Lockdown Perspective on the Hubble Tension (with comments from the SH0ES team). arXiv 2020, arXiv:2007.10716. [Google Scholar]
- Efstathiou, G. To H0 or not to H0? arXiv 2021, arXiv:2103.08723. [Google Scholar] [CrossRef]
- Wojtak, R.; Hjorth, J. Intrinsic tension in the supernova sector of the local Hubble constant measurement and its implications. arXiv 2022, arXiv:2206.08160. [Google Scholar] [CrossRef]
- Benisty, D.; Mifsud, J.; Said, J.L.; Staicova, D. On the Robustness of the Constancy of the Supernova Absolute Magnitude: Non-parametric Reconstruction & Bayesian approaches. arXiv 2022, arXiv:2202.04677. [Google Scholar]
- Martinelli, M.; Tutusaus, I. CMB tensions with low-redshift H0 and S8 measurements: Impact of a redshift-dependent type-Ia supernovae intrinsic luminosity. Symmetry 2019, 11, 986. [Google Scholar] [CrossRef]
- Tinsley, B.M. Evolution of the Stars and Gas in Galaxies. Astroph. J. 1968, 151, 547. [Google Scholar] [CrossRef]
- Kang, Y.; Lee, Y.W.; Kim, Y.L.; Chung, C.; Ree, C.H. Early-type Host Galaxies of Type Ia Supernovae. II. Evidence for Luminosity Evolution in Supernova Cosmology. Astrophys. J. 2020, 889, 8. [Google Scholar] [CrossRef]
- Rose, B.M.; Garnavich, P.M.; Berg, M.A. Think Global, Act Local: The Influence of Environment Age and Host Mass on Type Ia Supernova Light Curves. Astrophys. J. 2019, 874, 32. [Google Scholar] [CrossRef]
- Jones, D.O.; Riess, A.G.; Scolnic, D.M.; Pan, Y.-C.; Johnson, E.; Coulter, D.A.; Dettman, K.; Foley, M.; Foley, R.J.; Huber, M.E.; et al. Should Type Ia Supernova Distances be Corrected for their Local Environments? Astrophys. J. 2018, 867, 108. [Google Scholar] [CrossRef]
- Rigault, M.; Brinnel, V.; Aldering, G.; Antilogus, P.; Aragon, C.; Bailey, S.; Baltay, C.; Barbary, K.; Bongard, S.; Boone, K.; et al. Strong Dependence of Type Ia Supernova Standardization on the Local Specific Star Formation Rate. Astron. Astrophys. 2020, 644, A176. [Google Scholar] [CrossRef]
- Kim, Y.L.; Smith, M.; Sullivan, M.; Lee, Y.W. Environmental Dependence of Type Ia Supernova Luminosities from a Sample without a Local-Global Difference in Host Star Formation. Astroph. J. 2018, 854, 24. [Google Scholar] [CrossRef]
- Colgáin, E.O. A hint of matter underdensity at low z? J. Cosmol. Astropart. Phys. 2019, 09, 006. [Google Scholar] [CrossRef]
- Kazantzidis, L.; Perivolaropoulos, L. Hints of a Local Matter Underdensity or Modified Gravity in the Low z Pantheon data. Phys. Rev. D 2020, 102, 023520. [Google Scholar] [CrossRef]
- Sapone, D.; Nesseris, S.; Bengaly, C.A.P. Is there any measurable redshift dependence on the SN Ia absolute magnitude? Phys. Dark Univ. 2021, 32, 100814. [Google Scholar] [CrossRef]
- Koo, H.; Shafieloo, A.; Keeley, R.E.; L’Huillier, B. Model-independent Constraints on Type Ia Supernova Light-curve Hyperparameters and Reconstructions of the Expansion History of the Universe. Astrophys. J. 2020, 899, 9. [Google Scholar] [CrossRef]
- Kazantzidis, L.; Koo, H.; Nesseris, S.; Perivolaropoulos, L.; Shafieloo, A. Hints for possible low redshift oscillation around the best-fitting ΛCDM model in the expansion history of the Universe. Mon. Not. Roy. Astron. Soc. 2021, 501, 3421–3426. [Google Scholar] [CrossRef]
- Luković, V.V.; Haridasu, B.S.; Vittorio, N. Exploring the evidence for a large local void with supernovae Ia data. Mon. Not. Roy. Astron. Soc. 2020, 491, 2075–2087. [Google Scholar] [CrossRef]
- Tutusaus, I.; Lamine, B.; Blanchard, A. Model-independent cosmic acceleration and redshift-dependent intrinsic luminosity in type-Ia supernovae. Astron. Astrophys. 2019, 625, A15. [Google Scholar] [CrossRef]
- Tutusaus, I.; Lamine, B.; Dupays, A.; Blanchard, A. Is cosmic acceleration proven by local cosmological probes? Astron. Astrophys. 2017, 602, A73. [Google Scholar] [CrossRef]
- Drell, P.S.; Loredo, T.J.; Wasserman, I. Type Ia supernovae, evolution, and the cosmological constant. Astrophys. J. 2000, 530, 593. [Google Scholar] [CrossRef]
- Kenworthy, W.D.; Scolnic, D.; Riess, A. The Local Perspective on the Hubble Tension: Local Structure Does Not Impact Measurement of the Hubble Constant. Astrophys. J. 2019, 875, 145. [Google Scholar] [CrossRef]
- Riess, A.G.; Breuval, L.; Yuan, W.; Casertano, S.; Macri, L.M.; Scolnic, D.; Cantat-Gaudin, T.; Anderson, R.I.; Reyes, M.C. Cluster Cepheids with High Precision Gaia Parallaxes, Low Zeropoint Uncertainties, and Hubble Space Telescope Photometry. arXiv 2022, arXiv:2208.01045. [Google Scholar]
- Yuan, W.; Macri, L.M.; Riess, A.G.; Brink, T.G.; Casertano, S.; Filippenko, A.V.; Hoffmann, S.L.; Huang, C.D.; Scolnic, D. Absolute Calibration of Cepheid Period-Luminosity Relations in NGC 4258. arXiv 2022, arXiv:2203.06681. [Google Scholar]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.; Bucciarelli, B.; Lattanzi, M.G.; MacKenty, J.W.; Bowers, J.B.; Zheng, W.; Filippenko, A.V.; et al. Milky Way Cepheid Standards for Measuring Cosmic Distances and Application to Gaia DR2: Implications for the Hubble Constant. Astrophys. J. 2018, 861, 126. [Google Scholar] [CrossRef]
- Dainotti, M.G.; De Simone, B.; Schiavone, T.; Montani, G.; Rinaldi, E.; Lambiase, G.; Bogdan, M.; Ugale, S. On the Evolution of the Hubble Constant with the SNe Ia Pantheon Sample and Baryon Acoustic Oscillations: A Feasibility Study for GRB-Cosmology in 2030. Galaxies 2022, 10, 24. [Google Scholar] [CrossRef]
- Bargiacchi, G.; Benetti, M.; Capozziello, S.; Lusso, E.; Risaliti, G.; Signorini, M. Quasar cosmology: Dark energy evolution and spatial curvature. arXiv 2021, arXiv:2111.02420. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Bardiacchi, G.; Lenart, A.L.; Capozziello, S.; Colgain, E.O.; Solomon, R.; Stojkovic, D.; Sheikh-Jabbari, M.M. Quasar Standardization: Overcoming Selection Biases and Redshift Evolution. Astrophys. J. 2022, 931, 106. [Google Scholar] [CrossRef]
- Khosravi, N.; Farhang, M. Phenomenological gravitational phase transition: Early and late modifications. Phys. Rev. D 2022, 105, 063505. [Google Scholar] [CrossRef]
- Perivolaropoulos, L.; Skara, F. Gravitational transitions via the explicitly broken symmetron screening mechanism. arXiv 2022, arXiv:2203.10374. [Google Scholar] [CrossRef]
- Alestas, G.; Camarena, D.; Di Valentino, E.; Kazantzidis, L.; Marra, V.; Nesseris, S.; Perivolaropoulos, L. Late-transition versus smooth H(z)-deformation models for the resolution of the Hubble crisis. Phys. Rev. D 2022, 105, 063538. [Google Scholar] [CrossRef]
- Desmond, H.; Jain, B.; Sakstein, J. Local resolution of the Hubble tension: The impact of screened fifth forces on the cosmic distance ladder. Phys. Rev. 2019, D100, 043537. [Google Scholar] [CrossRef]
- Perivolaropoulos, L.; Skara, F. Hubble tension or a transition of the Cepheid SnIa calibrator parameters? Phys. Rev. D 2021, 104, 123511. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Did the Universe experience a pressure non-crushing type cosmological singularity in the recent past? Europhys. Lett. 2022, 137, 39001. [Google Scholar] [CrossRef]
- Alestas, G.; Kazantzidis, L.; Perivolaropoulos, L. w-M phantom transition at zt<0.1 as a resolution of the Hubble tension. Phys. Rev. D 2021, 103, 083517. [Google Scholar] [CrossRef]
- Marra, V.; Perivolaropoulos, L. A rapid transition of Geff at zt≃0.01 as a possible solution of the Hubble and growth tensions. Phys. Rev. D 2021, 104, L021303. [Google Scholar] [CrossRef]
- Alestas, G.; Antoniou, I.; Perivolaropoulos, L. Hints for a gravitational constant transition in Tully-Fisher data. arXiv 2021, arXiv:2104.14481. [Google Scholar]
- Perivolaropoulos, L. Is the Hubble Crisis Connected with the Extinction of Dinosaurs? Universe 2022, 8, 263. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Dissimilar donuts in the sky? Effects of a pressure singularity on the circular photon orbits and shadow of a cosmological black hole. Europhys. Lett. 2022, 139, 59003. [Google Scholar] [CrossRef]
- Riess, A.G.; Macri, L.; Hoffmann, S.L.; Scolnic, D.; Casertano, S.; Filippenko, A.V.; Tucker, B.E.; Reid, M.J.; Jones, D.O.; Silverman, J.M.; et al. A 2.4% Determination of the Local Value of the Hubble Constant. Astrophys. J. 2016, 826, 56. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.M.; Scolnic, D. Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of the Hubble Constant and Stronger Evidence for Physics beyond ΛCDM. Astrophys. J. 2019, 876, 85. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Bowers, J.B.; Macri, L.; Zinn, J.C.; Scolnic, D. Cosmic Distances Calibrated to 1% Precision with Gaia EDR3 Parallaxes and Hubble Space Telescope Photometry of 75 Milky Way Cepheids Confirm Tension with ΛCDM. Astrophys. J. Lett. 2021, 908, L6. [Google Scholar] [CrossRef]
- Reid, M.; Pesce, D.; Riess, A. An Improved Distance to NGC 4258 and its Implications for the Hubble Constant. Astrophys. J. Lett. 2019, 886, L27. [Google Scholar] [CrossRef]
- Li, S.; Riess, A.G.; Busch, M.P.; Casertano, S.; Macri, L.M.; Yuan, W. A sub-2% Distance to M31 from Photometrically Homogeneous Near-Infrared Cepheid Period-Luminosity Relations Measured with the Hubble Space Telescope. arXiv 2021, arXiv:2107.08029. [Google Scholar] [CrossRef]
- Madore, B.F. The period-luminosity relation. IV. Intrinsic relations and reddenings for the Large Magellanic Cloud Cepheids. Astroph. J. 1982, 253, 575–579. [Google Scholar] [CrossRef]
- Fitzpatrick, E.L. Correcting for the effects of interstellar extinction. Publ. Astron. Soc. Pac. 1999, 111, 63–75. [Google Scholar] [CrossRef]
- Camarena, D.; Marra, V. On the use of the local prior on the absolute magnitude of Type Ia supernovae in cosmological inference. Mon. Not. Roy. Astron. Soc. 2021, 504, 5164–5171. [Google Scholar] [CrossRef]
- Gómez-Valent, A. Measuring the sound horizon and absolute magnitude of SNIa by maximizing the consistency between low-redshift data sets. Phys. Rev. D 2022, 105, 043528. [Google Scholar] [CrossRef]
- Kerscher, M.; Weller, J. On Model Selection in Cosmology. SciPost Phys. Lect. Notes 2019, 9, 1. [Google Scholar] [CrossRef]
- Liddle, A.R. Information criteria for astrophysical model selection. Mon. Not. Roy. Astron. Soc. 2007, 377, L74–L78. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Freedman, W.L.; Madore, B.F.; Hatt, D.; Hoyt, T.J.; Jang, I.S.; Beaton, R.L.; Burns, C.R.; Lee, M.G.; Monson, A.J.; Neeley, J.R.; et al. The Carnegie-Chicago Hubble Program. VIII. An Independent Determination of the Hubble Constant Based on the Tip of the Red Giant Branch. arXiv 2019, arXiv:1907.05922. [Google Scholar] [CrossRef]
- Coleman, S.R. The Fate of the False Vacuum. 1. Semiclassical Theory. Phys. Rev. D 1977, 15, 2929–2936, Erratum in Phys. Rev. D 1977, 16, 1248. [Google Scholar] [CrossRef]
- Callan, C.G., Jr.; Coleman, S.R. The Fate of the False Vacuum. 2. First Quantum Corrections. Phys. Rev. D 1977, 16, 1762–1768. [Google Scholar] [CrossRef]
- Patwardhan, A.V.; Fuller, G.M. Late-time vacuum phase transitions: Connecting sub-eV scale physics with cosmological structure formation. Phys. Rev. D 2014, 90, 063009. [Google Scholar] [CrossRef]
- Niedermann, F.; Sloth, M.S. Resolving the Hubble tension with new early dark energy. Phys. Rev. D 2020, 102, 063527. [Google Scholar] [CrossRef]
- Liddle, A.R. How many cosmological parameters? Mon. Not. Roy. Astron. Soc. 2004, 351, L49–L53. [Google Scholar] [CrossRef]
- Arevalo, F.; Cid, A.; Moya, J. AIC and BIC for cosmological interacting scenarios. Eur. Phys. J. 2017, C77, 565. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the Dimension of a Model. Annals Statist. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- John, M.V.; Narlikar, J.V. Comparison of cosmological models using bayesian theory. Phys. Rev. D 2002, 65, 043506. [Google Scholar] [CrossRef]
- Nesseris, S.; Garcia-Bellido, J. Is the Jeffreys’ scale a reliable tool for Bayesian model comparison in cosmology? J. Cosmol. Astropart. Phys. 2013, 8, 36. [Google Scholar] [CrossRef]
- Jeffreys, H. Theory of Probability, 3rd ed.; Oxford University Press: Oxford, UK, 1961. [Google Scholar]
- Bonilla Rivera, A.; García-Farieta, J.E. Exploring the Dark Universe: Constraints on dynamical Dark Energy models from CMB, BAO and growth rate measurements. Int. J. Mod. Phys. D 2019, 28, 1950118. [Google Scholar] [CrossRef]
- Pérez-Romero, J.; Nesseris, S. Cosmological constraints and comparison of viable f(R) models. Phys. Rev. D 2018, 97, 023525. [Google Scholar] [CrossRef]
- Camarena, D.; Marra, V. Impact of the cosmic variance on H0 on cosmological analyses. Phys. Rev. D 2018, 98, 023537. [Google Scholar] [CrossRef]
- Rezaei, M.; Malekjani, M.; Sola, J. Can dark energy be expressed as a power series of the Hubble parameter? Phys. Rev. D 2019, 100, 023539. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).