Estimating the Cosmological Constant from Shadows of Kerr–de Sitter Black Holes
Abstract
:1. Introduction
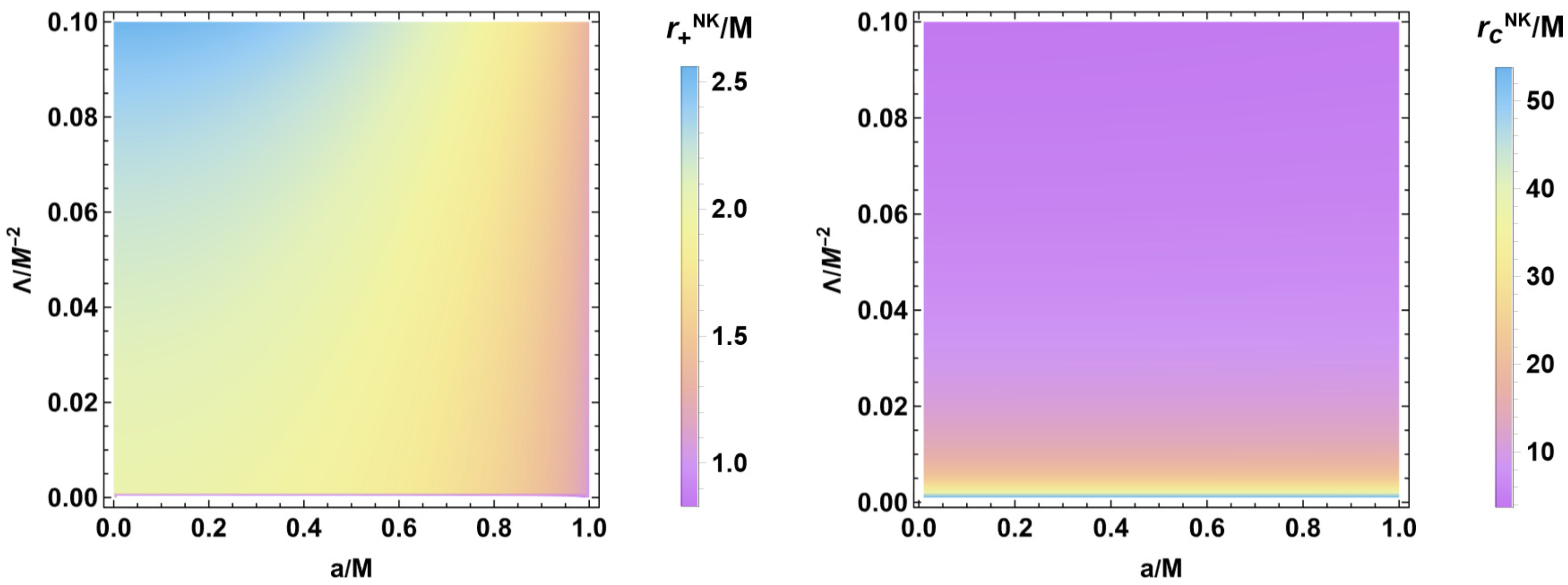
2. Kerr–de Sitter Black Holes
2.1. A New Kerr–De Sitter Black Hole
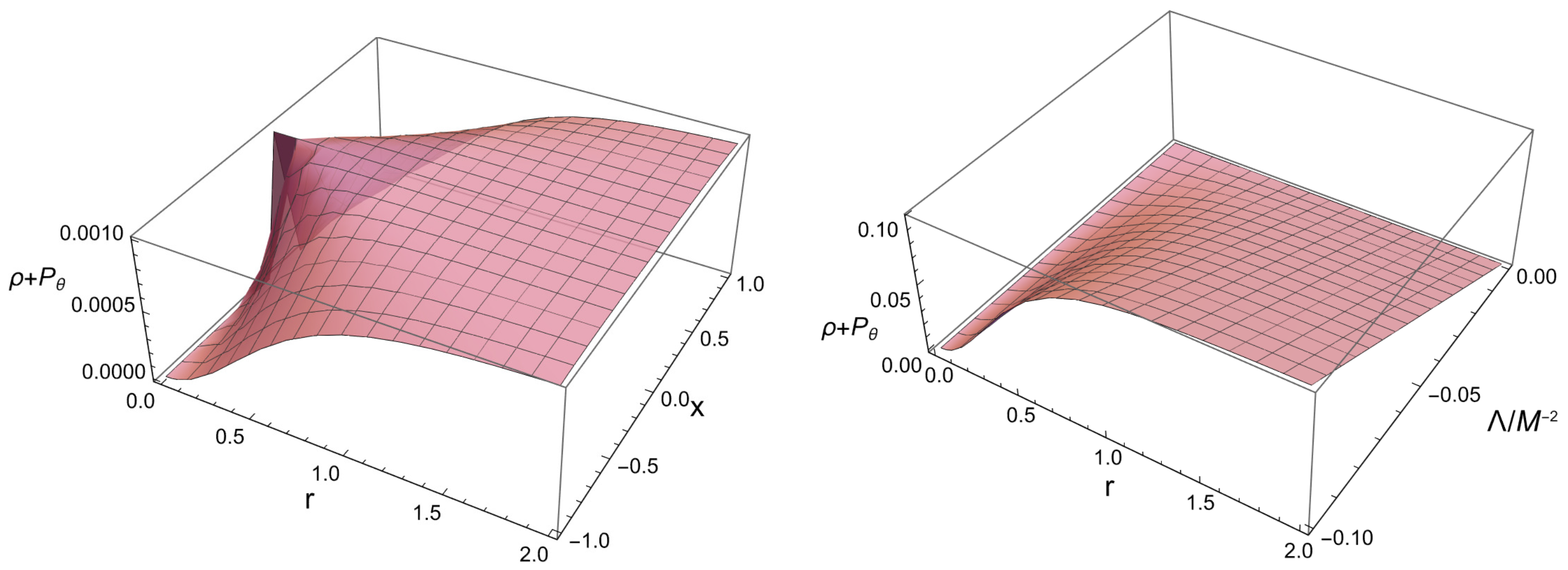
Energy Conditions
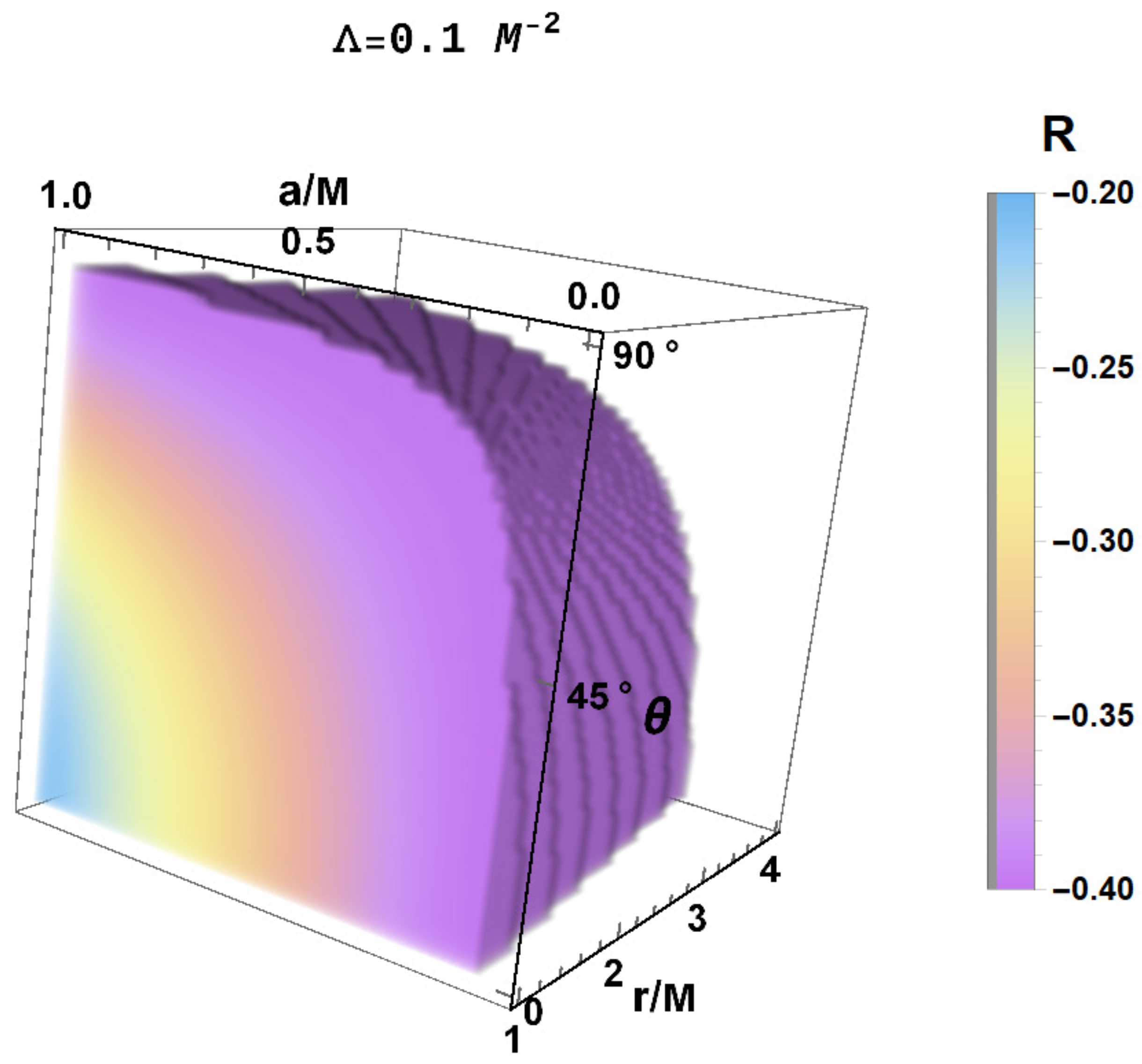
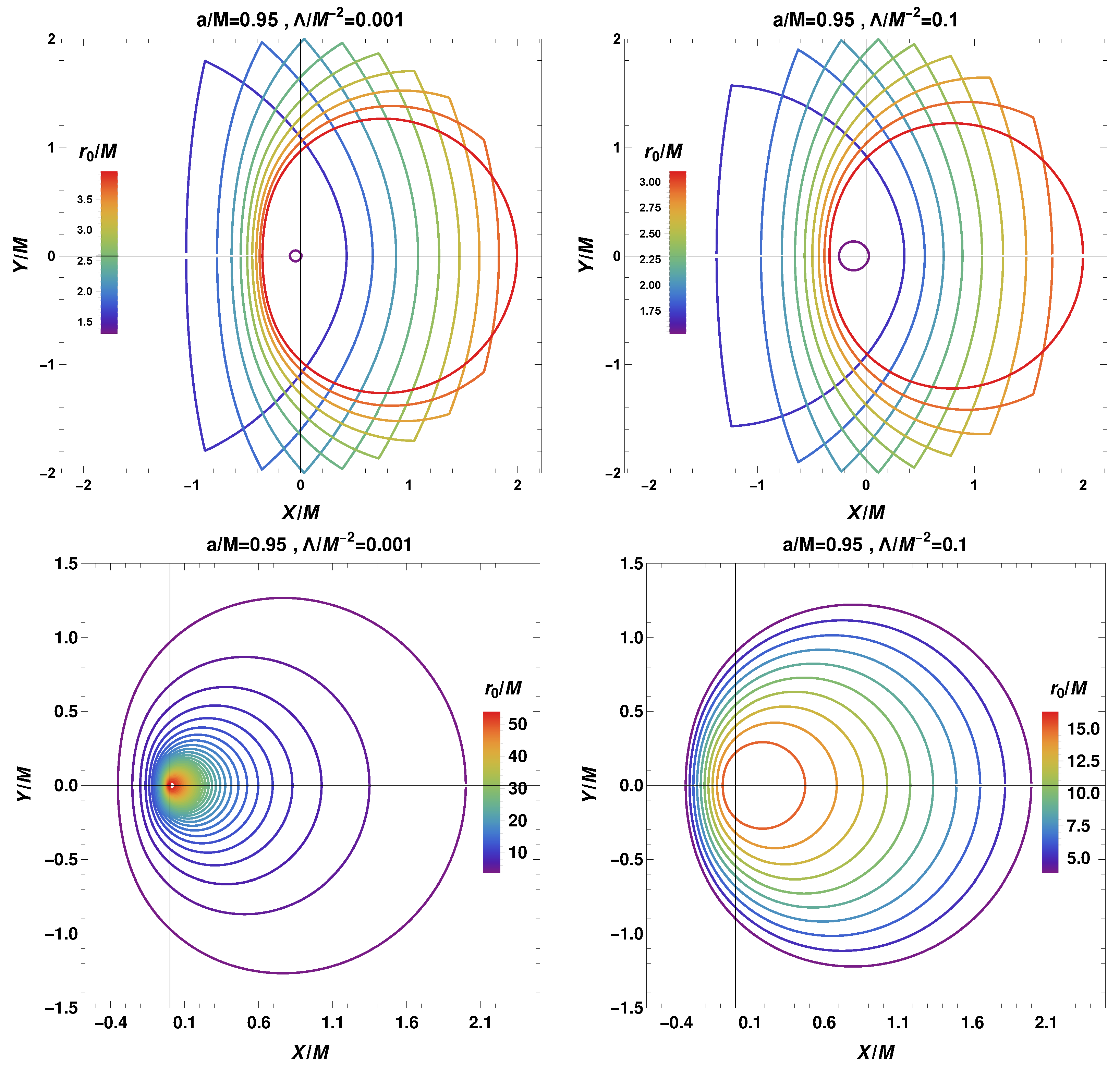
3. Photon Region and Shadow in Asymptotic de Sitter Spacetime
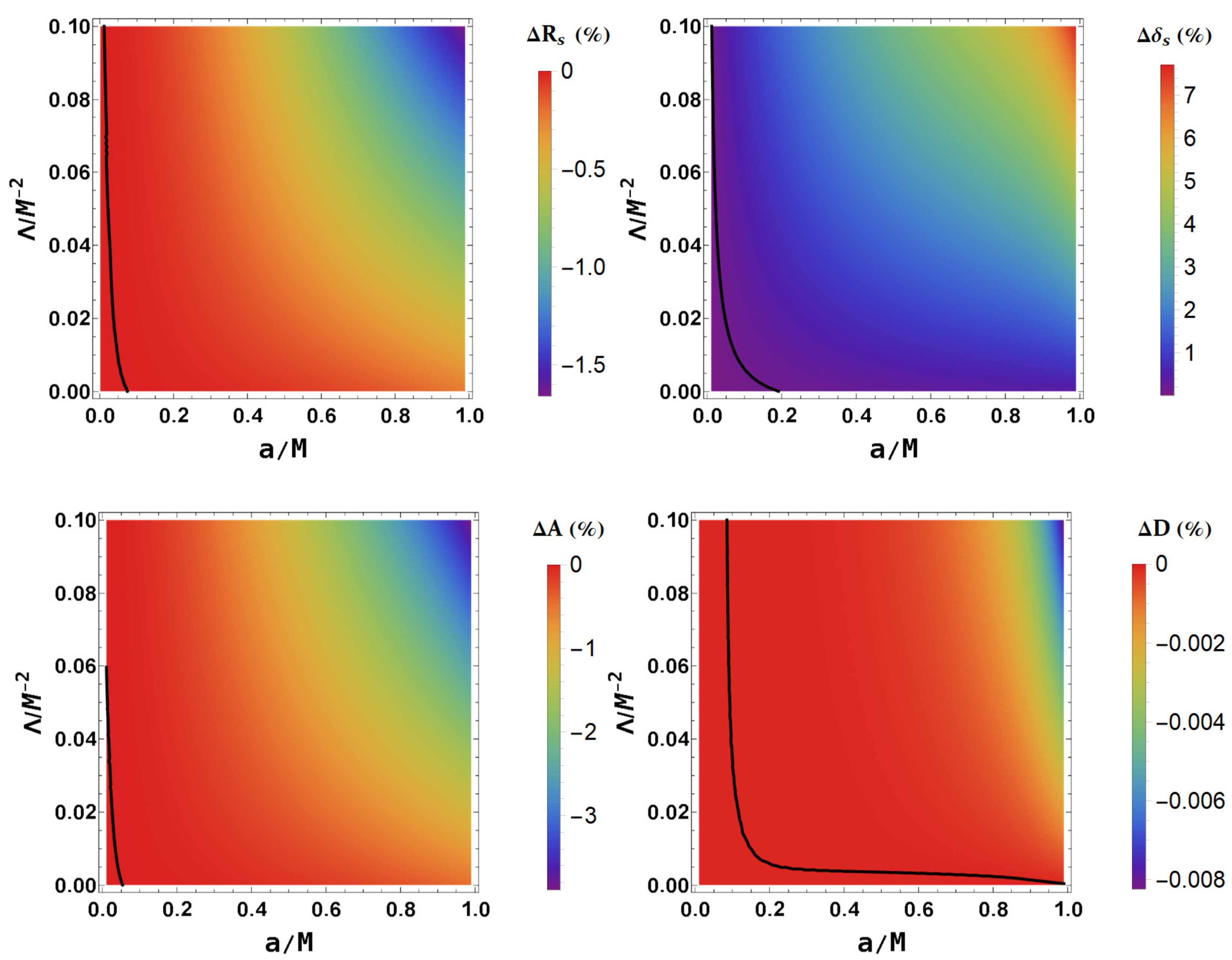
4. Parameter Estimation and Relative Difference of Shadow Observables
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| GR | General Relativity |
| MoGs | Modified Theories of Gravity |
References
- Bardeen, J.M. Timelike and Null Geodesics in the Kerr Metric; Les Houches Summer School of Theoretical Physics: Black Holes; Gordon and Breach Science Publishers, Inc.: Newark, NJ, USA, 1973. [Google Scholar]
- Falcke, H.; Melia, F.; Agol, E. Viewing the shadow of the black hole at the galactic center. Astrophys. J. Lett. 2000, 528, L13. [Google Scholar] [CrossRef] [Green Version]
- Synge, J.L. The Escape of Photons from Gravitationally Intense Stars. Mon. Not. Roy. Astron. Soc. 1966, 131, 463–466. [Google Scholar] [CrossRef]
- Luminet, J.P. Image of a spherical black hole with thin accretion disk. Astron. Astrophys. 1979, 75, 228–235. [Google Scholar]
- Teo, E. Spherical orbits around a Kerr black hole. Gen. Rel. Grav. 2021, 53, 10. [Google Scholar] [CrossRef]
- De Vries, A. The apparent shape of a rotating charged black hole, closed photon orbits and the bifurcation set A4. Class. Quantum Gravity 2000, 17, 123–144. [Google Scholar] [CrossRef]
- Bambi, C.; Yoshida, N. Shape and position of the shadow in the δ = 2 Tomimatsu-Sato space-time. Class. Quantum Gravity 2010, 27, 205006. [Google Scholar] [CrossRef] [Green Version]
- Amarilla, L.; Eiroa, E.F.; Giribet, G. Null geodesics and shadow of a rotating black hole in extended Chern-Simons modified gravity. Phys. Rev. D 2010, 81, 124045. [Google Scholar] [CrossRef] [Green Version]
- Amarilla, L.; Eiroa, E.F. Shadow of a rotating braneworld black hole. Phys. Rev. D 2012, 85, 064019. [Google Scholar] [CrossRef] [Green Version]
- Amarilla, L.; Eiroa, E.F. Shadow of a Kaluza-Klein rotating dilaton black hole. Phys. Rev. D 2013, 87, 044057. [Google Scholar] [CrossRef] [Green Version]
- Abdujabbarov, A.; Atamurotov, F.; Kucukakca, Y.; Ahmedov, B.; Camci, U. Shadow of Kerr-Taub-NUT black hole. Astrophys. Space Sci. 2013, 344, 429–435. [Google Scholar] [CrossRef]
- Yumoto, A.; Nitta, D.; Chiba, T.; Sugiyama, N. Shadows of Multi-Black Holes: Analytic Exploration. Phys. Rev. D 2012, 86, 103001. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Bambi, C. Measuring the Kerr spin parameter of regular black holes from their shadow. JCAP 2014, 01, 041. [Google Scholar] [CrossRef] [Green Version]
- Kumar, R.; Ghosh, S.G. Black Hole Parameter Estimation from Its Shadow. Astrophys. J. 2020, 892, 78. [Google Scholar] [CrossRef]
- Kumar, R.; Kumar, A.; Ghosh, S.G. Testing Rotating Regular Metrics as Candidates for Astrophysical Black Holes. Astrophys. J. 2020, 896, 89. [Google Scholar] [CrossRef]
- Kumar, R.; Ghosh, S.G.; Wang, A. Shadow cast and deflection of light by charged rotating regular black holes. Phys. Rev. D 2019, 100, 124024. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, S.G.; Amir, M.; Maharaj, S.D. Ergosphere and shadow of a rotating regular black hole. Nucl. Phys. B 2020, 957, 115088. [Google Scholar] [CrossRef]
- Amir, M.; Ali, M.S.; Maharaj, S.D. Rotating five-dimensional electrically charged Bardeen regular black holes. Class. Quantum Gravity 2020, 37, 145014. [Google Scholar] [CrossRef]
- Abdujabbarov, A.; Amir, M.; Ahmedov, B.; Ghosh, S.G. Shadow of rotating regular black holes. Phys. Rev. D 2016, 93, 104004. [Google Scholar] [CrossRef] [Green Version]
- Amir, M.; Ghosh, S.G. Shapes of rotating nonsingular black hole shadows. Phys. Rev. D 2016, 94, 024054. [Google Scholar] [CrossRef] [Green Version]
- Papnoi, U.; Atamurotov, F.; Ghosh, S.G.; Ahmedov, B. Shadow of five-dimensional rotating Myers-Perry black hole. Phys. Rev. D 2014, 90, 024073. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, F.; Singh, D.V.; Ghosh, S.G. 5D Rotating Regular Myers-Perry Black Holes and Their Shadow. arXiv 2020, arXiv:gr-qc/2008.10241. [Google Scholar]
- Ahmed, F.; Singh, D.V.; Ghosh, S.G. Five Dimensional Rotating Regular Black Holes and Shadow. arXiv 2020, arXiv:gr-qc/2002.12031. [Google Scholar]
- Amir, M.; Singh, B.P.; Ghosh, S.G. Shadows of rotating five-dimensional charged EMCS black holes. Eur. Phys. J. C 2018, 78, 399. [Google Scholar] [CrossRef] [Green Version]
- Eiroa, E.F.; Sendra, C.M. Shadow cast by rotating braneworld black holes with a cosmological constant. Eur. Phys. J. C 2018, 78, 91. [Google Scholar] [CrossRef] [Green Version]
- Vagnozzi, S.; Visinelli, L. Hunting for extra dimensions in the shadow of M87*. Phys. Rev. D 2019, 100, 024020. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, I.; Chakraborty, S.; SenGupta, S. Silhouette of M87*: A New Window to Peek into the World of Hidden Dimensions. Phys. Rev. D 2020, 101, 041301. [Google Scholar] [CrossRef] [Green Version]
- Singh, B.P.; Ghosh, S.G. Shadow of Schwarzschild–Tangherlini black holes. Ann. Phys. 2018, 395, 127–137. [Google Scholar] [CrossRef] [Green Version]
- Mizuno, Y.; Younsi, Z.; Fromm, C.M.; Porth, O.; De Laurentis, M.; Olivares, H.; Falcke, H.; Kramer, M.; Rezzolla, L. The Current Ability to Test Theories of Gravity with Black Hole Shadows. Nat. Astron. 2018, 2, 585–590. [Google Scholar] [CrossRef]
- Kumar, R.; Ghosh, S.G. Rotating black holes in 4D Einstein–Gauss–Bonnet gravity and its shadow. JCAP 2020, 07, 053. [Google Scholar] [CrossRef]
- Afrin, M.; Kumar, R.; Ghosh, S.G. Parameter estimation of hairy Kerr black holes from its shadow and constraints from M87*. Mon. Not. Roy. Astron. Soc. 2021, 504, 5927–5940. [Google Scholar] [CrossRef]
- Hioki, K.; Maeda, K.I. Measurement of the Kerr Spin Parameter by Observation of a Compact Object’s Shadow. Phys. Rev. D 2009, 80, 024042. [Google Scholar] [CrossRef] [Green Version]
- Tsupko, O.Y. Analytical calculation of black hole spin using deformation of the shadow. Phys. Rev. D 2017, 95, 104058. [Google Scholar] [CrossRef] [Green Version]
- Cunha, P.V.P.; Herdeiro, C.A.R.; Radu, E. Spontaneously Scalarized Kerr Black Holes in Extended Scalar-Tensor–Gauss–Bonnet Gravity. Phys. Rev. Lett. 2019, 123, 011101. [Google Scholar] [CrossRef] [Green Version]
- Cunha, P.V.P.; Herdeiro, C.A.R.; Radu, E. EHT constraint on the ultralight scalar hair of the M87 supermassive black hole. Universe 2019, 5, 220. [Google Scholar] [CrossRef] [Green Version]
- Khodadi, M.; Allahyari, A.; Vagnozzi, S.; Mota, D.F. Black holes with scalar hair in light of the Event Horizon Telescope. JCAP 2020, 9, 026. [Google Scholar] [CrossRef]
- Kramer, M.; Backer, D.C.; Cordes, J.M.; Lazio, T.J.W.; Stappers, B.W.; Johnston, S. Strong-field tests of gravity using pulsars and black holes. New Astron. Rev. 2004, 48, 993–1002. [Google Scholar] [CrossRef] [Green Version]
- Johannsen, T.; Psaltis, D. Testing the No-Hair Theorem with Observations in the Electromagnetic Spectrum: II. Black-Hole Images. Astrophys. J. 2010, 718, 446–454. [Google Scholar] [CrossRef] [Green Version]
- Perlick, V.; Tsupko, O.Y.; Bisnovatyi-Kogan, G.S. Black hole shadow in an expanding universe with a cosmological constant. Phys. Rev. D 2018, 97, 104062. [Google Scholar] [CrossRef] [Green Version]
- Kumar, R.; Singh, B.P.; Ali, M.S.; Ghosh, S.G. Shadows of black hole surrounded by anisotropic fluid in Rastall theory. Phys. Dark Universe 2021, 34, 100881. [Google Scholar] [CrossRef]
- Neves, J.C.S. Constraining the tidal charge of brane black holes using their shadows. Eur. Phys. J. C 2020, 80, 717. [Google Scholar] [CrossRef]
- Maluf, R.V.; Neves, J.C.S. Black holes with a cosmological constant in bumblebee gravity. Phys. Rev. D 2021, 103, 044002. [Google Scholar] [CrossRef]
- Grenzebach, A.; Perlick, V.; Lämmerzahl, C. Photon Regions and Shadows of Kerr–Newman-NUT Black Holes with a Cosmological Constant. Phys. Rev. D 2014, 89, 124004. [Google Scholar] [CrossRef] [Green Version]
- Stuchlík, Z.; Charbulák, D.; Schee, J. Light escape cones in local reference frames of Kerr–de Sitter black hole spacetimes and related black hole shadows. Eur. Phys. J. C 2018, 78, 180. [Google Scholar] [CrossRef] [Green Version]
- Charbulák, D.; Stuchlík, Z. Photon motion in Kerr-de Sitter spacetimes. Eur. Phys. J. C 2017, 77, 897. [Google Scholar] [CrossRef]
- Rindler, W.; Ishak, M. Contribution of the cosmological constant to the relativistic bending of light revisited. Phys. Rev. D 2007, 76, 043006. [Google Scholar] [CrossRef] [Green Version]
- Ovalle, J.; Contreras, E.; Stuchlik, Z. Kerr–de Sitter black hole revisited. Phys. Rev. D 2021, 103, 084016. [Google Scholar] [CrossRef]
- Carter, B. Black holes equilibrium states. Les Houches Summer School of Theoretical Physics: Black Holes; de Witt, C., de Witt, B., Eds.; Gordon and Breach Science Publishers: New York, NY, USA; London, UK; Paris, France, 1973; pp. 61–124. [Google Scholar]
- Bousso, R.; Hawking, S.W. (Anti)evaporation of Schwarzschild-de Sitter black holes. Phys. Rev. D 1998, 57, 2436–2442. [Google Scholar] [CrossRef] [Green Version]
- Galloway, G.J.; Solis, D.A. Uniqueness of de Sitter space. Class. Quantum Gravity 2007, 24, 3125–3138. [Google Scholar] [CrossRef] [Green Version]
- Bhattacharya, S. Kerr-de Sitter spacetime, Penrose process and the generalized area theorem. Phys. Rev. D 2018, 97, 084049. [Google Scholar] [CrossRef] [Green Version]
- Gibbons, G.W.; Hawking, S.W. Cosmological Event Horizons, Thermodynamics, and Particle Creation. Phys. Rev. D 1977, 15, 2738–2751. [Google Scholar] [CrossRef] [Green Version]
- Ovalle, J. Decoupling gravitational sources in general relativity: From perfect to anisotropic fluids. Phys. Rev. D 2017, 95, 104019. [Google Scholar] [CrossRef] [Green Version]
- Ovalle, J. Decoupling gravitational sources in general relativity: The extended case. Phys. Lett. B 2019, 788, 213–218. [Google Scholar] [CrossRef]
- Contreras, E.; Ovalle, J.; Casadio, R. Gravitational decoupling for axially symmetric systems and rotating black holes. Phys. Rev. D 2021, 103, 044020. [Google Scholar] [CrossRef]
- Bambi, C.; Modesto, L. Rotating regular black holes. Phys. Lett. B 2013, 721, 329–334. [Google Scholar] [CrossRef] [Green Version]
- Neves, J.C.S.; Saa, A. Regular rotating black holes and the weak energy condition. Phys. Lett. B 2014, 734, 44–48. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, S.G. A nonsingular rotating black hole. Eur. Phys. J. C 2015, 75, 532. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, S.G. Rotating black hole and quintessence. Eur. Phys. J. C 2016, 76, 222. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, S.G.; Walia, R.K. Rotating black holes in general relativity coupled to nonlinear electrodynamics. Annals Phys. 2021, 434, 168619. [Google Scholar] [CrossRef]
- Johnson, M.D.; Lupsasca, A.; Strominger, A.; Wong, G.N.; Kapec, H.D.; Narayan, R.; Chael, A.; Gammie, C.F.; Galison, P.; Palumbo, D.C.M.; et al. Universal interferometric signatures of a black hole’s photon ring. Sci. Adv. 2020, 6, eaaz1310. [Google Scholar] [CrossRef] [Green Version]
- Kumar, R.; Ghosh, S.G.; Wang, A. Gravitational deflection of light and shadow cast by rotating Kalb-Ramond black holes. Phys. Rev. D 2020, 101, 104001. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, B.P.; Ghosh, S.G. Shadow and deflection angle of rotating black hole in asymptotically safe gravity. Ann. Phys. 2020, 420, 168252. [Google Scholar] [CrossRef]
- Ghosh, S.G.; Kumar, R.; Tannukij, L.; Wongjun, P. Rotating black strings in de Rham-Gabadadze-Tolley massive gravity. Phys. Rev. D 2020, 101, 104042. [Google Scholar] [CrossRef]
- Kumar, R.; Islam, S.U.; Ghosh, S.G. Gravitational lensing by charged black hole in regularized 4D Einstein–Gauss–Bonnet gravity. Eur. Phys. J. C 2020, 80, 1128. [Google Scholar] [CrossRef]
- Islam, S.U.; Kumar, R.; Ghosh, S.G. Gravitational lensing by black holes in the 4D Einstein–Gauss–Bonnet gravity. JCAP 2020, 09, 030. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The Mathematical Theory of Black Holes; Oxford University Press: New York, NY, USA, 1985. [Google Scholar]
- Carter, B. Global structure of the Kerr family of gravitational fields. Phys. Rev. 1968, 174, 1559–1571. [Google Scholar] [CrossRef] [Green Version]
- Li, P.C.; Guo, M.; Chen, B. Shadow of a Spinning Black Hole in an Expanding Universe. Phys. Rev. D 2020, 101, 084041. [Google Scholar] [CrossRef] [Green Version]
- Kumar, R.; Ghosh, S.G. Photon ring structure of rotating regular black holes and no-horizon spacetimes. Class. Quantum Gravity 2021, 38, 8. [Google Scholar] [CrossRef]
- Roelofs, F.; Fromm, C.M.; Mizuno, Y.; Davelaar, J.; Janssen, M.; Younsi, Z.; Rezzolla, L.; Falcke, H. Black hole parameter estimation with synthetic very long baseline interferometry data from the ground and from space. Astron. Astrophys. 2021, 650, A56. [Google Scholar] [CrossRef]
- Broderick, A.E.; Tiede, P.; Pesce, D.W.; Gold, R. Measuring Spin from Relative Photon Ring Sizes. arXiv 2021, arXiv:astro-ph.HE/2105.09962. [Google Scholar]
- Broderick, A.E.; Gold, R.; Karami, M.; Preciado-Lopez, J.A.; Tiede, P.; Pu, H.; Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; et al. THEMIS: A Parameter Estimation Framework for the Event Horizon Telescope. Astrophys. J. 2020, 897, 139. [Google Scholar] [CrossRef]
- Feng, J.; Wu, Q. Constraint on the black-hole spin of M87 from the accretion-jet model. Mon. Not. Roy. Astron. Soc. 2017, 470, 612. [Google Scholar] [CrossRef] [Green Version]
- Narayan, R.; McClintock, J.E.; Shafee, R. Estimating the Spins of Stellar-Mass Black Holes by Fitting Their Continuum Spectra. AIP Conf. Proc. 2008, 968, 265–272. [Google Scholar] [CrossRef] [Green Version]
- Narayan, R. Black holes in astrophysics. New J. Phys. 2005, 7, 199. [Google Scholar] [CrossRef]
- Tsukamoto, N.; Li, Z.; Bambi, C. Constraining the spin and the deformation parameters from the black hole shadow. JCAP 2014, 06, 043. [Google Scholar] [CrossRef] [Green Version]
- Afrin, M.; Ghosh, S.G. Constraining Rotating Black Holes in Horndeski Theory with EHT Observations of M87*. arXiv 2021, arXiv:gr-qc/2110.05258. [Google Scholar]
- Ghosh, S.G.; Kumar, R.; Islam, S.U. Parameters estimation and strong gravitational lensing of nonsingular Kerr-Sen black holes. JCAP 2021, 03, 056. [Google Scholar] [CrossRef]
- Akcay, S.; Matzner, R.A. Kerr-de Sitter Universe. Class. Quant. Grav. 2011, 28, 085012. [Google Scholar] [CrossRef] [Green Version]
- Schee, J.; Stuchlik, Z. Optical phenomena in the field of braneworld Kerr black holes. Int. J. Mod. Phys. D 2009, 18, 983–1024. [Google Scholar] [CrossRef] [Green Version]
- Johannsen, T. Photon Rings around Kerr and Kerr-like Black Holes. Astrophys. J. 2013, 777, 170. [Google Scholar] [CrossRef] [Green Version]
- Abdujabbarov, A.A.; Rezzolla, L.; Ahmedov, B.J. A coordinate-independent characterization of a black hole shadow. Mon. Not. Roy. Astron. Soc. 2015, 454, 2423–2435. [Google Scholar] [CrossRef] [Green Version]
- Younsi, Z.; Zhidenko, A.; Rezzolla, L.; Konoplya, R.; Mizuno, Y. New method for shadow calculations: Application to parametrized axisymmetric black holes. Phys. Rev. D 2016, 94, 084025. [Google Scholar] [CrossRef] [Green Version]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First M87 Event Horizon Telescope Results. IV. Imaging the Central Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L4. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L1. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First M87 Event Horizon Telescope Results. VI. The Shadow and Mass of the Central Black Hole. Astrophys. J. Lett. 2019, 875, L6. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, B.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6, Erratum: Astron. Astrophys. 2021, 652, C4.. [Google Scholar] [CrossRef] [Green Version]
- Ade, P.A.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2018 results. VI. Cosmological parameters Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar] [CrossRef] [Green Version]
- Stepanian, A.; Khlghatyan, S.; Gurzadyan, V.G. Black hole shadow to probe modified gravity. Eur. Phys. J. Plus 2021, 136, 127. [Google Scholar] [CrossRef]
- Omwoyo, E.; Belich, H.; Fabris, J.C.; Velten, H. Remarks on the Black Hole Shadows in Kerr-De Sitter Space Times. arXiv 2021, arXiv:gr-qc/2112.14124. [Google Scholar]



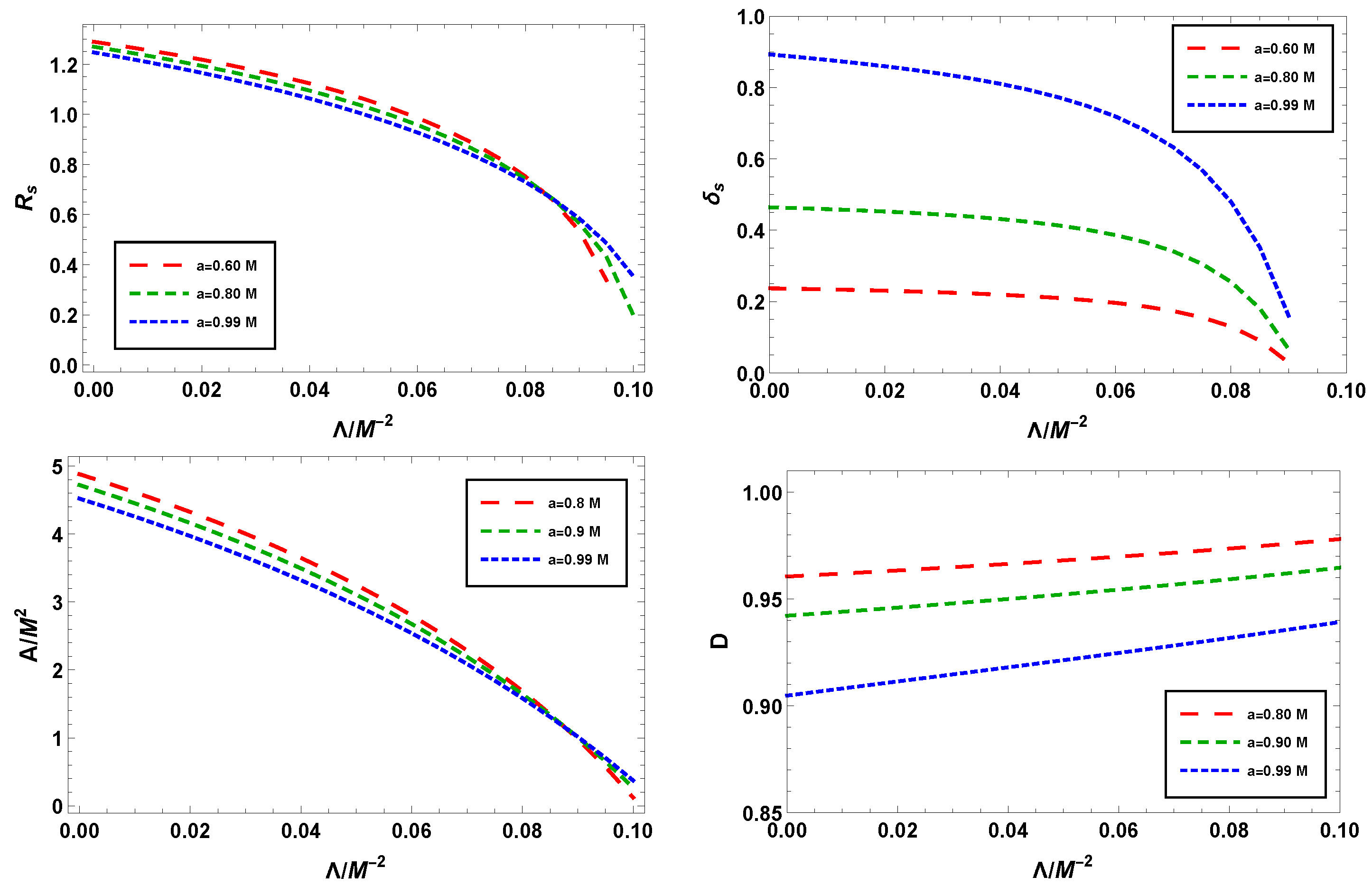
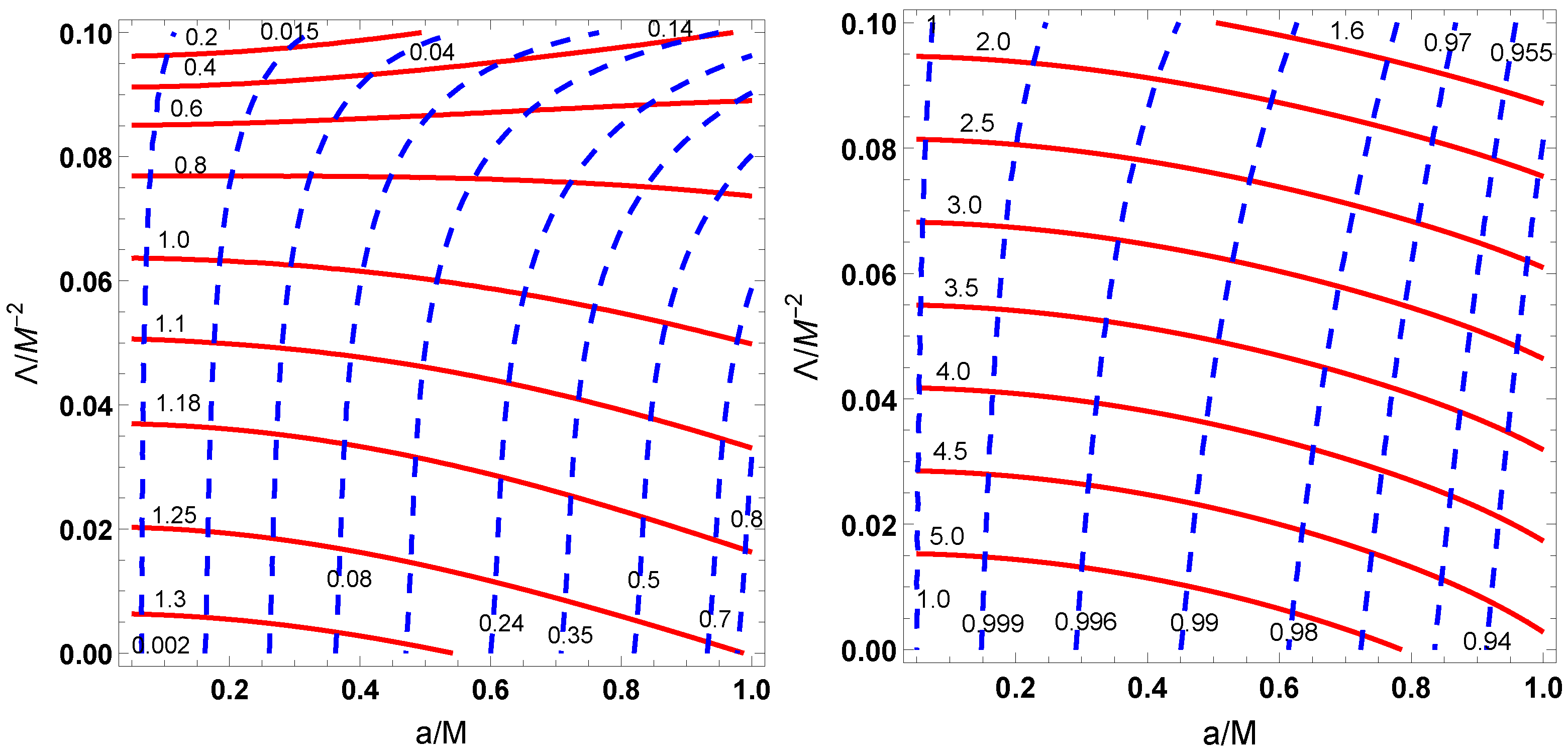
| 1.30 | 0.002 | 0.06598 | 0.00735 |
| 1.25 | 0.015 | 0.16740 | 0.02065 |
| 1.10 | 0.040 | 0.27950 | 0.05025 |
| 0.80 | 0.140 | 0.57850 | 0.07741 |
| 0.60 | 0.240 | 0.85430 | 0.08940 |
| 5.0 | 1.000 | 0.05272 | 0.01538 |
| 4.0 | 0.999 | 0.16600 | 0.04127 |
| 3.5 | 0.996 | 0.34040 | 0.05225 |
| 2.0 | 0.980 | 0.74150 | 0.08380 |
| 1.6 | 0.955 | 0.94420 | 0.08882 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Afrin, M.; Ghosh, S.G. Estimating the Cosmological Constant from Shadows of Kerr–de Sitter Black Holes. Universe 2022, 8, 52. https://doi.org/10.3390/universe8010052
Afrin M, Ghosh SG. Estimating the Cosmological Constant from Shadows of Kerr–de Sitter Black Holes. Universe. 2022; 8(1):52. https://doi.org/10.3390/universe8010052
Chicago/Turabian StyleAfrin, Misba, and Sushant G. Ghosh. 2022. "Estimating the Cosmological Constant from Shadows of Kerr–de Sitter Black Holes" Universe 8, no. 1: 52. https://doi.org/10.3390/universe8010052
APA StyleAfrin, M., & Ghosh, S. G. (2022). Estimating the Cosmological Constant from Shadows of Kerr–de Sitter Black Holes. Universe, 8(1), 52. https://doi.org/10.3390/universe8010052







