Fundamental Physics and Computation: The Computer-Theoretic Framework
Abstract
1. Introduction
2. Origins of the Concept of Computation and Its Dissemination in Physics
The Church–Turing thesis: a function is effectively calculable if and only if it is computable by a Turing machine or, equivalently, if it is specified by a recursive function.
“So I have often made the hypothesis that ultimately physics will not require a mathematical statement, that in the end the machinery will be revealed, and the laws will turn out simple, like the chequer board with all its apparent complexities” [33] (pp. 57, 58).
“This essay exploits many unpublished ideas I got from Edward Fredkin” [38] (p. 551).
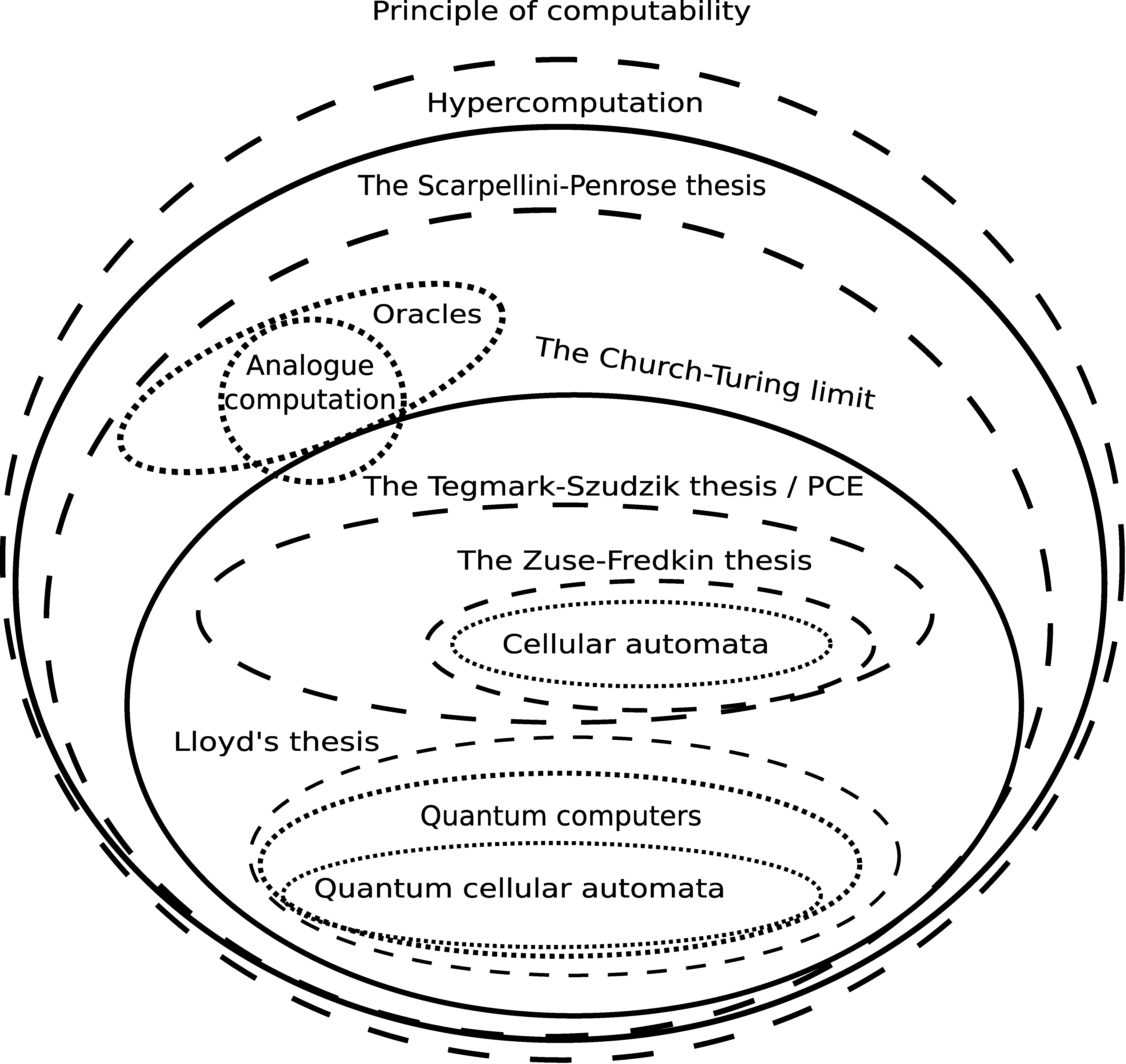
The Zuse–Fredkin thesis: the universe is a cellular automaton.
The principle of computational equivalence (PCE): “No [natural] system can ever carry out explicit computations that are more sophisticated than those carried out by cellular automata and Turing machines” [62] (p. 720).
Deutsch’s principle:“Every finitely realizable physical system can be perfectly simulated by a universal model computing machine operating by finite means” [95] (p. 99).
The Scarpellini–Penrose thesis: In the universe, physical phenomena exist that involve a computational power beyond the Turing limit.
2.1. Computational Complexity
The extended Church–Turing thesis: Every physically reasonable computational device can be simulated by a Turing machine with at most polynomial slowdown.
Feynman’s thesis: There exists a quantum computational device that cannot be simulated by a Turing machine with at most a polynomial slowdown.
2.2. A Computational Characterization of the Universe
- Computational systems. Systems that cannot go beyond the Turing machine limit.
- Supercomputational systems. Systems that have the classical computational limit of the Turing machine but can solve nondeterministic polynomial time problems in polynomial time.
- Hypercomputational systems. Systems that have a computational power beyond the Turing machine limit and can therefore solve at least one problem that is noncomputable by the Turing machine model (e.g., the halting problem).
- A computational universe.
- A supercomputational universe.
- A hypercomputational universe.
The External Reality Hypothesis (ERH): there exists an external physical reality completely independent of us humans.
The Mathematical Universe Hypothesis (MUH): our physical reality is a mathematical structure.
Computable Universe Hypothesis (CUH): the mathematical structure that is our external physical reality is defined by computable functions.
Computable Universe Hypothesis: the universe has a recursive set of states U. For each observable quantity, there is a total recursive function ϕ. is the value of that observable quantity when the universe is in state s.
3. The Link between Physics and Computer Science
4. Arguments against a Computational Universe
4.1. The Argument of Radioactive Systems
4.2. The Argument of the Continuum
4.3. The Counterargument of Evaluation
“This principle of least action does not ask to solve an equation, it just asks to evaluate the functional S at any possible path and select the extremal one” [11] (p. 252).
“But the Feynman ‘path integral’ formulation of quantum mechanics creates a revival of this idea of evaluating instead of computing” [11] (p. 252).
4.4. The Argument of Infinite Dimensions
4.5. The Argument of the Lagrangian Schema
4.6. The Argument of the Observers and the Uncertainty Principle
“A perpetual motion machine is possible if -according to the general method of physics- we view the experimenting man as a sort of deux ex machina, one who is continuously informed of the existing state of nature...”
4.7. The Argument of Physics Is More than Computation
I entirely agree that it’s likely to be fruitful to recast our conception of the world and of the laws of physics and physical processes in computational terms, and to connect fully with reality it would have to be in quantum computational terms. But computers have to be conceived as being inside the universe, subject to its laws, not somehow prior to the universe, generating its laws [7] (p. 559).
Does the theory of computation therefore coincide with physics, the study of all possible physical objects and their motions? It does not, because the theory of computation does not specify which physical system a particular program renders, and to what accuracy. That requires additional knowledge of the laws of physics [247] (p. 4342).
In fact proof and computation are, like geometry, attributes of the physical world. Different laws of physics would in general make different functions computable and therefore different mathematical assertions provable [247] (p. 4341).
The theory of computation is only a branch of physics, not vice versa, and constructor theory is the ultimate generalisation of the theory of computation [247] (p. 4342).
5. Hempel’s Dilemma and the Computational Universe
Hempel’s Dilemma: “On the one hand, we cannot rely on current physics, because we have every reason to believe that future research will overturn our present physical theories. On the other hand, if we appeal to some future finalised physics, then our ignorance of this future theory translates to an ignorance of the ontology of physicalism” [249] (p. 646).
“1. When doing physics, we only have access to finite computational resources” [250] (p. 407).
“Nothing physicists do requires use of an infinite number of bits of memory or an infinite number of steps in a computation.” [250] (p. 406).
6. The Simulated Universe Hypothesis
- (1)
- We are external observers, and there are other external observers. This kind of simulation works like a sports video game simulating an environment. It sends us information using physical phenomena that we register through our senses. Our minds are not aware of physical reality because they represent the information sent by the simulator creating a virtual reality, such as in the movie The Matrix. In this case, our mind receives the information that receives a simulation program’s agent which our mind controls in turn.
- (2)
- We are not external observers, but external observers who run the simulation process exist. This kind of simulation happens because the phenomenon of consciousness is generated by the process itself carried out by the simulator, so we are not able to access the external observers’ reality.
- (3)
- We are not external observers, and external observers who run the simulation process do not exist. This kind of simulation corresponds to the case in which the phenomenon of consciousness is generated by the process itself carried out by the simulator, and the process of simulation happens in nature by chance. We know, for example, that nuclear reactors have appeared in nature without human intervention [273]. Additionally, in this case, we are not able to access the reality where the simulation takes place.
7. The Principle of Computability and the Computer-Theoretic Framework
The principle of computability: The universe is a computational system that has a specific computational power and a specific computational complexity hierarchy associated with it.
- (1)
- Each kind of physical system can always be described by one computational model.
- (2)
- Each physical system can only be completely described by one of all the computational models.
- (3)
- Each computational model has one and only one associated computational power and complexity classes hierarchy.
- (4)
- Therefore, each kind of physical system has an associated computational power and an associated complexity classes hierarchy.
- (5)
- Therefore, computational power and complexity classes hierarchy are two physical properties.
- (6)
- The universe is a physical system.
- (7)
- Therefore, the universe is described by one computational model.
- (8)
- Therefore, the universe has one associated computational power and one associated complexity classes hierarchy.
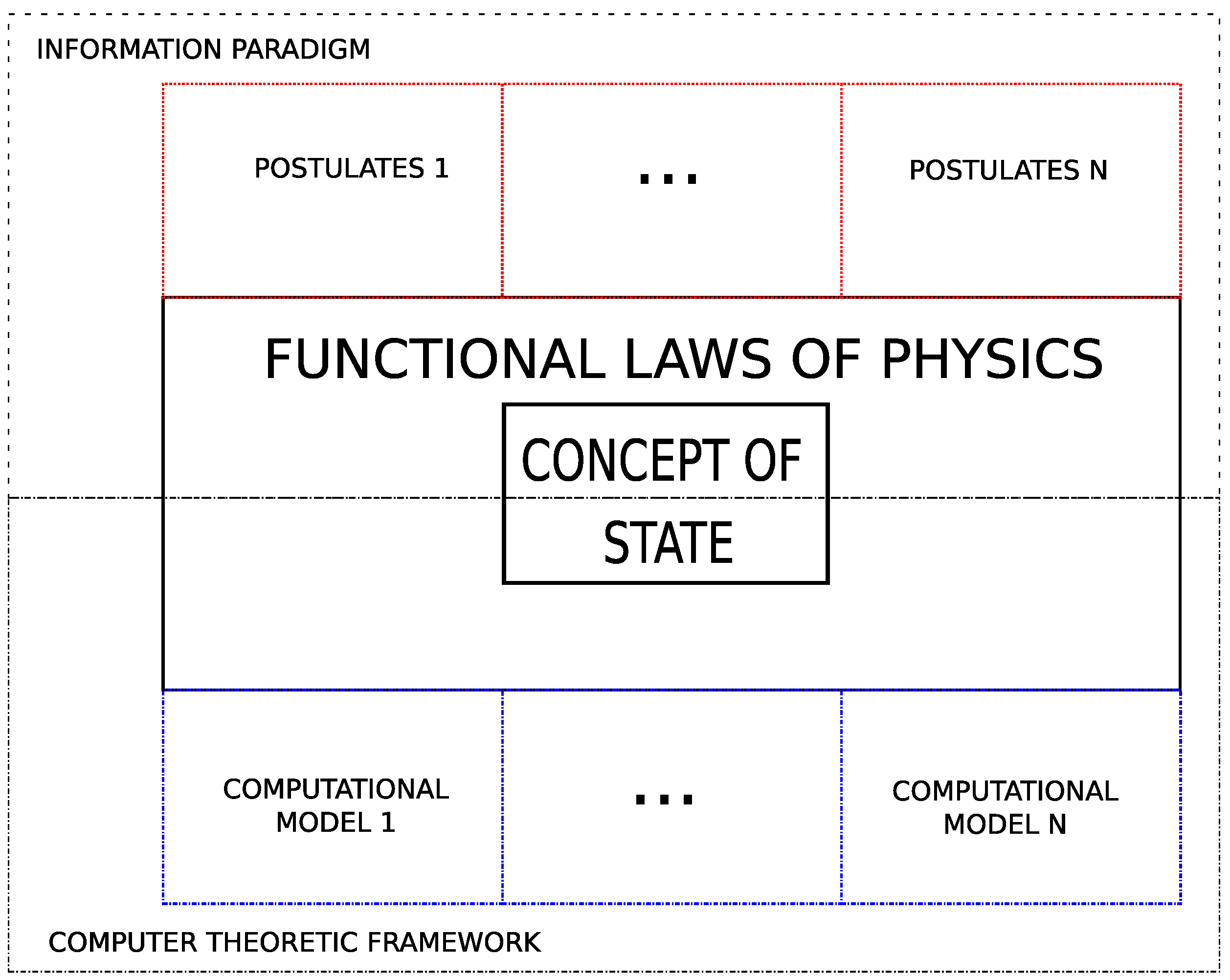
7.1. The Computer-Theoretic Framework: A New Paradigm for Fundamental Physics
7.2. The CTF and Its Formal Formulation
7.3. The Scientific Status of the CTF
7.4. Developing Theories of Fundamental Physics in the Computer-Theoretic Framework
- Units of computing. The units of computing are the elements that contain the information that defines the system’s state. A computational model can have different kinds of units of computing.
- Alphabets. Each alphabet is associated with one kind or several kinds of units of computing, which means that each element of an alphabet is a value that can be contained by a unit of computing of the kind associated with that alphabet.
- Rules of computation. The rules of computation determine how the value that contains each unit of computing changes.
- The units of computing are space. This line of research considers space as the fundamental machinery, so each unit of stating is a position of space. Both CA and QCA are examples of computational models in this line of research.
- In a computational model, the units of computing are an underlayer when they store both the particles and their spatial locations. If the units of computing are an underlayer, they cannot be identified with spatial locations. A computational model in which the units of computing are an underlayer could execute declarative programs perceived as a universe ruled by the principle of least action. Research on the holographic principle would be in this line of research.
- Finite computational models. The units of computing are a finite number, and all alphabets of the computational model have a finite number of elements.
- Countable infinite computational models. The number of the units of computing is a countable infinite number, and all alphabets of the computational model have a countable infinite number of elements.
- Uncountable infinite computational models. The number of the units of computing is an uncountable infinite number, and all alphabets of the computational model have an uncountable infinite number of elements.
- Hybrid computational models. The alphabets and the units of the computational model can have different cardinalities.
- Synchronous units of computing. The computational model has a global synchronous update signal.
- Asynchronous units of computing. The computational model does not have a global synchronous update signal, so the units of computing update their values independently of what the other units of computing do.
- Probabilistic rules of computation. The rules of computation determine how likely an element of an alphabet will be contained by the unit of stating when the units of computing update their values.
- Deterministic rules of computation. The rules of computation determine one specific value that will be contained by the units of computing when they update their values.
8. Discussion
8.1. Researching the Computability of the Universe
- Physics must determine what computational class the universe belongs to.
- Physics must determine what computational model the universe is.
8.2. Information and Computation
8.3. Is the CTF Proposing Platonic Realism?
8.4. The CTF and the Unreasonable Effectiveness of Mathematics
8.5. Cognitive Behaviour and Physics
“In chapters 1 through 5, I spoke of the independence of the physical and computational, or symbolic, descriptions of a process” [339] (p. 149).
“By mapping certain classes of physical states of the environment into computationally relevant states of a device, the transducer performs a rather special conversion: converting computationally arbitrary physical events into computational events” [339] (p. 152).
9. Conclusions
- A scientific paradigm exists, called the CTF, to develop fundamental theories of physics based on the concepts of theoretical computer science.
- The CTF highlights computational power and the computational complexity hierarchy as fundamental physical constants of the universe.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CTC | Closed Time-like Curve |
| CTF | Computer-Theoretic Framework |
| MUH | Mathematical Universe Hypothesis |
| PCE | Principle of Computational Equivalence |
| CUH | Computable Universe Hypothesis |
| CA | Cellular Automata |
| QCA | Quantum Cellular Automata |
| 1 | A function is implemented when it can generate the correct output when given an input. |
| 2 | In his article, Deutsch called this principle the Church–Turing principle, but we consider it more appropriate to use its author’s name because, as we explain in this paper, neither Church nor Turing claimed anything in their original statements about the physical world but about a framework of mathematics, the finitary point of view. |
| 3 | Subsequently, a better definition appeared [96]. |
| 4 | We have not added Deutsch’s name because he has rejected the idea that the universe is a computer in public interviews. Deutsch’s declarations can be checked in the program Closer to Truth, answering the question Is the Cosmos a Computer? [195] |
| 5 | The list of selected challenges is on the London Institute for Mathematical Sciences website: https://lims.ac.uk/23-mathematical-challenges/ (accessed on 25 August 2021). |
| 6 | To keep this explanation simple, we constrain it to the non-probabilistic formulation, but it could be formulated yet in a more general way using probabilistic functions because a non-probabilistic function can be seen as the particular case of a probabilistic function. The probabilistic function assigns to each element of the domain a subdistribution of elements of the codomain , so a non-probabilistic function can be seen as the particular case where all the subdistributions assign probability 1 to one of the elements of the codomain and 0 to the others. |
| 7 | is permitted. |
| 8 | If we were using a probabilistic framework, then the machine would compute a probabilistic function if it generated each output with the same probability as the probabilistic function. |
| 9 | The term computational space has not been used in the computability theory, but we consider that introducing this term can make various ideas more understandable and facilitate discussion of them. |
| 10 | We assume that Deutsch considers that attribute and property are equivalent. |
| 11 | Digital computers are synonymous with discreteness, and they should not be identified as binary technology because it is only one of the possible digital technologies. For example, we could have a ternary technology, which would be a digital technology, and build a ternary computer with it. |
| 12 | The increment of time is a constant quantity, so it is assumed to be a minor matter compared with duplicating or triplicating the hardware. |
References
- Svozil, K. Computational universes. Chaos Solitons Fractals 2005, 25, 845–859. [Google Scholar] [CrossRef][Green Version]
- Zenil, H. FRONT MATTER. In A Computable Universe: Understanding and Exploring Nature as Computation; World Scientific Publishing Company: Singapore, 2013; pp. i–xliv. [Google Scholar]
- Lloyd, S. Ultimate physical limits to computation. Nature 2000, 406, 1047–1054. [Google Scholar] [CrossRef]
- Lloyd, S. Computational capacity of the universe. Phys. Rev. Lett. 2002, 88, 0110141. [Google Scholar] [CrossRef]
- Margolus, N. Looking at Nature as a Computer. Int. J. Theor. Phys. 2003, 42, 309–327. [Google Scholar] [CrossRef]
- Cuffaro, M.; Fletcher, S. Introduction. In Physical Perspectives on Computation, Computational Perspectives on Physics; Cambridge University Press: Cambridge, UK, 2018; pp. 1–22. [Google Scholar]
- Deutsch, D. What is Computation? (How) Does Nature Compute? In A Computable Universe: Understanding and Exploring Nature as Computation; World Scientific Publishing Company: Singapore, 2012; pp. 551–566. [Google Scholar]
- Zenil, H. (Ed.) Irreducibility and Computational Equivalence: 10 Years After Wolfram’s A New Kind of Science; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Tong, D. The Unquantum Quantum. Sci. Am. 2012, 307, 46–49. [Google Scholar] [CrossRef] [PubMed]
- Wharton, K. The Universe is not a computer. In Questioning the Foundations of Physics; Springer: Berlin/Heidelberg, Germany, 2015; pp. 177–189. [Google Scholar]
- Longo, G.; Paul, T. The Mathematics of Computing between Logic and Physics. In Computability in Context: Computation and Logic in the Real World; World Scientific: Singapore, 2009; pp. 243–274. [Google Scholar]
- Parrondo, J.; Horowitz, J.; Sagawa, T. Thermodynamics of information. Nat. Phys. 2015, 11, 131–139. [Google Scholar] [CrossRef]
- Maruyama, K.; Nori, F.; Vedral, V. Colloquium: The physics of Maxwell’s demon and information. Rev. Mod. Phys. 2009, 81, 1–23. [Google Scholar] [CrossRef]
- Fidora, A.; Sierra, C. (Eds.) Ramon Llull: From the Ars Magna to Artificial Intelligence; Consejo Superior de Investigaciones Científicas: Madrid, Spain, 2011. [Google Scholar]
- Leibniz, G. Dissertatio de Arte Combinatoria; Sämtliche Schriften und Briefe: Berlin, Germany, 1666. [Google Scholar]
- Drake, S. Galileo and the First Mechanical Computing Device. Sci. Am. 1976, 234, 104–113. [Google Scholar] [CrossRef]
- Swade, D. Redeeming Charles Babbage’s Mechanical Computer. Sci. Am. 1993, 268, 86–91. [Google Scholar] [CrossRef]
- Corry, L. David Hilbert and the Axiomatization of Physics (1898–1918): From Grundlagen der Geometrie to Grundlagen der Physik; Archimedes: New Studies in the History and Philosophy of Science and Technology; Kluwer Academic Publishers: New York, NY, USA, 2004. [Google Scholar]
- Hilbert, D. Axiomatisches Denken. Math. Ann. 1918, 78, 405–415. [Google Scholar] [CrossRef]
- Gödel, K. Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I. Monatshefte Math. Phys. 1931, 38, 173–198. [Google Scholar] [CrossRef]
- Turing, A.M. On Computable Numbers, with an Application to the Entscheidungsproblem. Proc. Lond. Math. Soc. 1936, s2-42, 230–265. [Google Scholar] [CrossRef]
- Davis, M. Computability and Unsolvability; Dover Publications: Mineola, NY, USA, 1982. [Google Scholar]
- Sipser, M. Introduction to the Theory of Computation, 3rd ed.; Cengage Learning: Boston, MA, USA, 2012. [Google Scholar]
- Papadimitriou, C.H. Computational Complexity; Addison Wesley Longman: Cambridge, MA, USA, 1994. [Google Scholar]
- Alhazov, A.; Leporati, A.; Mauri, G.; Porreca, A.E.; Zandron, C. Space complexity equivalence of P systems with active membranes and Turing machines. Theor. Comput. Sci. 2014, 529, 69–81. [Google Scholar] [CrossRef]
- Rosen, R. Church’s thesis and its relation to the concept of realizability in biology and physics. Bull. Math. Biophys. 1962, 24, 375–393. [Google Scholar] [CrossRef]
- Wiener, N.; Rosenblueth, A. The mathematical formulation of the problem of conduction of impulses in a network of connected excitable elements, specifically in cardiac muscle. Arch. Inst. Cardiol. Méx. 1946, 16, 205–265. [Google Scholar]
- Konrad, Z. Rechender Raum. Elektron. Datenverarb. 1967, 8, 336–344. [Google Scholar]
- Konrad, Z. Rechender Raum; Friedrich Vieweg & Sohn: Braunschweig, Germany, 1969. [Google Scholar]
- Toffoli, T. Cellular Automata Mechanics; Technical Report Tech. Rep. No. 208; The University of Michigan: Ann Arbor, MI, USA, 1977. [Google Scholar]
- Toffoli, T. Computation and construction universality of reversible cellular automata. J. Comput. Syst. Sci. 1977, 15, 213–231. [Google Scholar] [CrossRef]
- Fredkin, E.; Landauer, R.; Toffoli, T. Physics of Computation. Int. J. Theor. Phys. 1982, 21, 903. [Google Scholar]
- Feynman, R. The Character of Physical Law; MIT Press: Cambridge, MA, USA, 1965. [Google Scholar]
- Hopfield, J. Feynman and Computation. In Feynman and Computation; Perseus Books Publishing: New York, NY, USA, 1998; pp. 3–6. [Google Scholar]
- Wheeler, J. Pregeometry: Motivations and Prospects. In Quantum Theory and Gravitation; Academic Press: Cambridge, MA, USA, 1980; pp. 1–11. [Google Scholar]
- Wheeler, J. Information, Physics, Quantum: The Search for Links. In Complexity, Entropy, and the Physics of Information; Addison-Wesley: Boston, MA, USA, 1990; pp. 309–336. [Google Scholar]
- Feynman, R. Simulating Physics with Computers. Int. J. Theor. Phys. 1982, 21, 467–488. [Google Scholar] [CrossRef]
- Minsky, M. Cellular Vacuum. Int. J. Theor. Phys. 1982, 21, 537–551. [Google Scholar] [CrossRef]
- Fredkin, E. Digital Mechanics. Physica D 1990, 45, 254–270. [Google Scholar] [CrossRef]
- Mainzer, K.; Chua, L. The Universe as Automaton: From Simplicity and Symmetry to Complexity; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Fredkin, E.; Toffoli, T. Conservative logic. Int. J. Theor. Phys. 1982, 21, 219–253. [Google Scholar] [CrossRef]
- Barrett, J.; de Beaudrap, N.; Hoban, M.J.; Lee, C.M. The computational landscape of general physical theories. NPJ Quantum Inf. 2019, 5, 1–10. [Google Scholar] [CrossRef]
- Toffoli, T. Physics and computation. Int. J. Theor. Phys. 1982, 21, 165–175. [Google Scholar] [CrossRef]
- Wolfram, S. Statistical mechanics of cellular automata. Rev. Mod. Phys. 1983, 55, 601–644. [Google Scholar] [CrossRef]
- Toffoli, T. Cellular automata as an alternative to (rather than an approximation of) differential equations in modeling physics. Phys. D Nonlinear Phenom. 1984, 10, 117–127. [Google Scholar] [CrossRef]
- Margolus, N. Physics-like models of computation. Physica D 1984, 10, 81–95. [Google Scholar] [CrossRef]
- Lee, T. Can time be a discrete dynamical variable? Phys. Lett. B 1983, 122, 217–220. [Google Scholar] [CrossRef]
- Lee, T.D. Difference equations as the basis of fundamental physical theories. In Old and New Problems in Fundamental Physics; Scuola Normale Superiore: Pisa, Italy, 1984; pp. 19–41. [Google Scholar]
- Lee, T. Discrete Mechanics. In How Far Are We from the Gauge Forces; Springer: New York, NY, USA, 1985; pp. 15–114. [Google Scholar]
- Svozil, K. Are quantum fields cellular automata? Phys. Lett. A 1986, 119, 153–156. [Google Scholar] [CrossRef]
- Karsten, L.H.; Smith, J. Lattice fermions: Species doubling, chiral invariance and the triangle anomaly. Nucl. Phys. B 1981, 183, 103–140. [Google Scholar] [CrossRef]
- Nielsen, H.; Ninomiya, M. Absence of neutrinos on a lattice: (I). Proof by homotopy theory. Nucl. Phys. B 1981, 185, 20–40. [Google Scholar] [CrossRef]
- Rabin, J. Perturbation theory for undoubled lattice fermions. Phys. Rev. D 1981, 24, 3218–3236. [Google Scholar] [CrossRef]
- Ilachinski, A. Cellular Automata: A Discrete Universe; World Scientific Publishing Co., Inc.: Singapore, 2001. [Google Scholar]
- Fredkin, E. A new cosmogony: On the origin of the universe. In Proceedings of the PhysComp’92: Proceedings of the Workshop on Physics and Computation, Dallas, TX, USA, 2–4 October 1992; pp. 116–121. [Google Scholar]
- Hooft, G.T. Equivalence relations between deterministic and quantum mechanical systems. J. Stat. Phys. 1988, 53, 323–344. [Google Scholar] [CrossRef]
- Hooft, G.T. Duality Between a Deterministic Cellular Automaton and a Bosonic Quantum Field Theory in 1+1 Dimensions. Found. Phys. 2013, 43. [Google Scholar] [CrossRef][Green Version]
- Hooft, G.T. The Cellular Automaton Interpretation of Quantum Mechanics; Springer International Publishing: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Hooft, G.T. Deterministic Quantum Mechanics: The Mathematical Equations. Front. Phys. 2020, 8, 253. [Google Scholar] [CrossRef]
- Hooft, G.T. Fast Vacuum Fluctuations and the Emergence of Quantum Mechanics. Found. Phys. 2021, 51, 1–24. [Google Scholar] [CrossRef]
- Hooft, G.T. The Black Hole Firewall Transformation and Realism in Quantum Mechanics. arXiv 2021, arXiv:2106.11152. [Google Scholar]
- Wolfram, S. A New Kind of Science; Wolfram Media: Champaign, IL, USA, 2002. [Google Scholar]
- Chen, K.; Bak, P. Is the universe operating at a self-organized critical state? Phys. Lett. A 1989, 140, 299–302. [Google Scholar] [CrossRef]
- Bak, P.; Chen, K.; Creutz, M. Self-organized criticality in the “Game of Life”. Nature 1989, 342, 780–782. [Google Scholar] [CrossRef]
- Guszejnov, D.; Hopkins, P.; Grudić, M. Universal scaling relations in scale-free structure formation. Mon. Not. R. Astron. Soc. 2018, 477, 5139–5149. [Google Scholar] [CrossRef]
- Grössing, G.; Zeilinger, A. Quantum Cellular Automata. Complex Syst. 1988, 2, 197–208. [Google Scholar]
- Grössing, G.; Zeilinger, A. A conservation law in quantum cellular automata. Phys. D Nonlinear Phenom. 1988, 31, 70–77. [Google Scholar] [CrossRef]
- Grössing, G.; Zeilinger, A. Structures in quantum cellular automata. Physica B+C 1988, 151, 366–369. [Google Scholar] [CrossRef]
- Fussy, S.; Grössing, G.; Schwabl, H.; Scrinzi, A. Nonlocal computation in quantum cellular automata. Phys. Rev. A 1993, 48, 3470–3477. [Google Scholar] [CrossRef] [PubMed]
- Meyer, D.A. From quantum cellular automata to quantum lattice gases. J. Stat. Phys. 1996, 85, 551–574. [Google Scholar] [CrossRef]
- Meyer, D. On the absence of homogeneous scalar unitary cellular automata. Phys. Lett. A 1996, 223, 337–340. [Google Scholar] [CrossRef]
- Boghosian, B.M.; Taylor, W. Quantum lattice-gas model for the many-particle Schrödinger equation in d dimensions. Phys. Rev. E 1998, 57, 54–66. [Google Scholar] [CrossRef]
- Love, P.J.; Boghosian, B.M. From Dirac to Diffusion: Decoherence in Quantum Lattice Gases. Quantum Inf. Process. 2005, 4, 335–354. [Google Scholar] [CrossRef][Green Version]
- Watrous, J. On one-dimensional quantum cellular automata. In Proceedings of the IEEE 36th Annual Symposium on Foundations of Computer Science, Milwaukee, WI, USA, 23–25 October 1995; pp. 528–537. [Google Scholar]
- Durr, C.; Santha, M. A decision procedure for unitary linear quantum cellular automata. In Proceedings of the IEEE 37th Annual Symposium on Foundations of Computer Science, Burlington, VT, USA, 14–16 October 1996; pp. 38–45. [Google Scholar]
- Dürr, C.; LêThanh, H.; Santha, M. A decision procedure for well-formed linear quantum cellular automata. Random Struct. Algorithms 1997, 11, 381–394. [Google Scholar] [CrossRef]
- McGuigan, M. Quantum Cellular Automata from Lattice Field Theories. arXiv 2003, arXiv:quant-ph/0307176. [Google Scholar]
- Arrighi, P.; Nesme, V.; Werner, R. One-Dimensional Quantum Cellular Automata over Finite, Unbounded Configurations. In Language and Automata Theory and Applications: Second International Conference; Springer: Berlin/Heidelberg, Germany, 2008; pp. 64–75. [Google Scholar]
- Richter, S.; Werner, R.F. Ergodicity of quantum cellular automata. J. Stat. Phys. 1996, 82, 963–998. [Google Scholar] [CrossRef]
- Pérez-Delgado, C.; Cheung, D. Local unitary quantum cellular automata. Phys. Rev. A 2007, 76, 032320. [Google Scholar] [CrossRef]
- D’Ariano, G.; Perinotti, P. Derivation of the Dirac equation from principles of information processing. Phys. Rev. A 2014, 90, 062106. [Google Scholar] [CrossRef]
- Bravyi, S.; Kitaev, A. Fermionic Quantum Computation. Ann. Phys. 2002, 298, 210–226. [Google Scholar] [CrossRef]
- D’Ariano, G.; Mosco, N.; Perinotti, P.; Tosini, A. Path-integral solution of the one-dimensional Dirac quantum cellular automaton. Phys. Lett. A 2014, 378, 3165–3168. [Google Scholar] [CrossRef]
- Bisio, A.; D’Ariano, G.M.; Perinotti, P.; Tosini, A. Free Quantum Field Theory from Quantum Cellular Automata. Found. Phys. 2015, 45, 1137–1152. [Google Scholar] [CrossRef]
- D’Ariano, G.; Perinotti, P. Quantum cellular automata and free quantum field theory. Front. Phys. 2016, 12, 1–11. [Google Scholar] [CrossRef]
- Mosco, N. Analytical Solutions of the Dirac Quantum Cellular Automata: Path-Sum Methods for the Solution of Quantum Walk Dynamics in Position Space. Ph.D. Thesis, Universitá degli Studi di Pavia, Pavia, Italy, 2017. [Google Scholar]
- Perinotti, P.; Poggiali, L. Scalar fermionic cellular automata on finite Cayley graphs. Phys. Rev. A 2018, 98, 052337. [Google Scholar] [CrossRef]
- Arrighi, P. An overview of quantum cellular automata. Nat. Comput. 2019, 18, 885–899. [Google Scholar] [CrossRef]
- Kripke, S. The Church-Turing “Thesis” as a Special Corollary of Gödel’s Completeness Theorem. In Computability: Turing, Gödel, Church, and Beyond; MIT Press: Cambridge, MA, USA, 2013; pp. 77–104. [Google Scholar]
- Kreisel, G. A Notion of Mechanistic Theory. Synthese 1974, 29, 11–26. [Google Scholar] [CrossRef]
- Wolfram, S. Undecidability and Intractability in Theoretical Physics. Phys. Rev. Lett. 1985, 54, 735–738. [Google Scholar] [CrossRef]
- Moore, C. Unpredictability and undecidability in dynamical systems. Phys. Rev. Lett. 1990, 64, 2354–2357. [Google Scholar] [CrossRef] [PubMed]
- Cubitt, T.; Perez-Garcia, D.; Wolf, M. Undecidability of the spectral gap. Nature 2015, 28, 207–211. [Google Scholar] [CrossRef] [PubMed]
- Cardona, R.; Miranda, E.; Peralta-Salas, D.; Presas, F. Constructing Turing complete Euler flows in dimension 3. Proc. Natl. Acad. Sci. USA 2021, 118, e2026818118. [Google Scholar] [CrossRef] [PubMed]
- Deutsch, D. Quantum Theory, the Church-Turing Principle and the Universal Quantum Computer. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1985, 400, 97–117. [Google Scholar]
- Deutsch, D.; Jozsa, R. Rapid solution of problems by quantum computation. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1992, 439, 553–558. [Google Scholar]
- Margolus, N.; Levitin, L.B. The maximum speed of dynamical evolution. Phys. D Nonlinear Phenom. 1998, 120, 188–195. [Google Scholar] [CrossRef]
- Lloyd, S. The Universe as Quantum Computer. In A Computable Universe: Understanding and Exploring Nature as Computation; World Scientific Publishing Company: Singapore, 2012; pp. 567–581. [Google Scholar]
- Pitowsky, I. The physical Church–Turing thesis and physical computational complexity. Iyyun 1990, 5, 81–99. [Google Scholar]
- Hogarth, M. Does general relativity allow an observer to view an eternity in a finite time? Found. Phys. Lett. 1992, 5, 173–181. [Google Scholar] [CrossRef]
- Hogarth, M. Non-Turing Computers and Non-Turing Computability. PSA Proc. Bienn. Meet. Philos. Sci. Assoc. 1994, 1994, 126–138. [Google Scholar] [CrossRef]
- Friedman, J.; Morris, M.S.; Novikov, I.D.; Echeverria, F.; Klinkhammer, G.; Thorne, K.S.; Yurtsever, U. Cauchy problem in spacetimes with closed timelike curves. Phys. Rev. D 1990, 42, 1915–1930. [Google Scholar] [CrossRef]
- Deutsch, D. Quantum mechanics near closed timelike lines. Phys. Rev. D 1991, 44, 3197–3217. [Google Scholar] [CrossRef]
- Brun, T. Computers with Closed Timelike Curves Can Solve Hard Problems Efficiently. Found. Phys. Lett. 2003, 16, 245–253. [Google Scholar] [CrossRef]
- Bacon, D. Quantum computational complexity in the presence of closed timelike curves. Phys. Rev. A 2004, 70, 032309. [Google Scholar] [CrossRef]
- Aaronson, S.; Watrous, J. Closed timelike curves make quantum and classical computing equivalent. Proc. R. Soc. A Math. Phys. Eng. Sci. 2009, 465, 631–647. [Google Scholar] [CrossRef]
- Aaronson, S.; Bavarian, M.; Gueltrini, G. Computability Theory of Closed Timelike Curves. arXiv 2016, arXiv:1609.05507. [Google Scholar]
- Baumeler, Ä.; Wolf, S. Computational tameness of classical non-causal models. Proc. R. Soc. A Math. Phys. Eng. Sci. 2018, 474, 20170698. [Google Scholar] [CrossRef]
- Earman, J.; Norton, J.D. Forever Is a Day: Supertasks in Pitowsky and Malament-Hogarth Spacetimes. Philos. Sci. 1993, 60, 22–42. [Google Scholar] [CrossRef]
- Etesi, G.; Németi, I. Non-Turing Computations Via Malament–Hogarth Space-Times. Int. J. Theor. Phys. 2002, 41, 341–370. [Google Scholar] [CrossRef]
- Németi, I.; Dávid, G. Relativistic computers and the Turing barrier. Appl. Math. Comput. 2006, 178, 118–142. [Google Scholar] [CrossRef]
- Ghosh, S.; Adhikary, A.; Paul, G. Revisiting integer factorization using closed timelike curves. Quantum Inf. Process. 2019, 18, 1–10. [Google Scholar] [CrossRef]
- White, H.; Vera, J.; Han, A.; Bruccoleri, A.R.; MacArthur, J. Worldline numerics applied to custom Casimir geometry generates unanticipated intersection with Alcubierre warp metric. Eur. Phys. J. C 2021, 81, 677. [Google Scholar] [CrossRef]
- Moore, C. Generalized shifts: Unpredictability and undecidability in dynamical systems. Nonlinearity 1991, 4, 199–230. [Google Scholar] [CrossRef]
- Tao, T. Finite time blowup for an averaged three-dimensional Navier-Stokes equation. J. Am. Math. Soc. 2016, 29, 601–674. [Google Scholar] [CrossRef]
- Tao, T. Searching for singularities in the Navier–Stokes equations. Nat. Rev. Phys. 2019, 1, 418–419. [Google Scholar] [CrossRef]
- Turing, A.M. Systems of Logic Based on Ordinals. Proc. Lond. Math. Soc. 1939, s2-45, 161–228. [Google Scholar] [CrossRef]
- Copeland, B. Hypercomputation. Minds Mach. 2002, 12, 461–502. [Google Scholar] [CrossRef]
- Scarpellini, B. Zwei Unentscheitbare Probleme der Analysis. Z. Math. Log. Grund. Math. 1963, 265–289. [Google Scholar] [CrossRef]
- Penrose, R. The Emperor’s New Mind; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Penrose, R. Shadows of the Mind: A Search for the Missing Science of Consciousness; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Siegelmann, H. Computation Beyond the Turing Limit. Science 1995, 268, 545–548. [Google Scholar] [CrossRef]
- Copeland, B.J.; Proudfoot, D. Alan Turing’s Forgotten Ideas in Computer Science. Sci. Am. 1999, 280, 99–103. [Google Scholar] [CrossRef]
- Davis, M. The Myth of Hypercomputation. In Alan Turing: Life and Legacy of a Great Thinker; Springer: Berlin/Heidelberg, Germany, 2004; pp. 195–211. [Google Scholar]
- Davis, M. Why there is no such discipline as hypercomputation. Appl. Math. Comput. 2006, 178, 4–7. [Google Scholar] [CrossRef]
- Nasar, A. The history of Algorithmic complexity. Math. Enthus. 2016, 13, 4. [Google Scholar] [CrossRef]
- Rabin, M. Degree of Difficulty of Computing a Function, and a Partial Ordering of Recursive Sets; Technical Report 2; Hebrew University: Jerusalem, Israel, 1960. [Google Scholar]
- Hartmanis, J.; Stearns, R.E. On the computational complexity of algorithms. Trans. Am. Math. Soc. 1965, 117, 285–306. [Google Scholar] [CrossRef]
- Goldschlager, L.M. A Universal Interconnection Pattern for Parallel Computers. J. ACM 1982, 29, 1073–1086. [Google Scholar] [CrossRef]
- Dymond, P.; Cook, S. Hardware complexity and parallel computation. In Proceedings of the 21st Annual Symposium on Foundations of Computer Science (sfcs 1980), Syracuse, NY, USA, 13–15 October 1980; pp. 360–372. [Google Scholar]
- Vergis, A.; Steiglitz, K.; Dickinson, B. The complexity of analog computation. Math. Comput. Simul. 1986, 28, 91–113. [Google Scholar] [CrossRef]
- Parberry, I. Parallel Speedup of Sequential Machines: A Defense of Parallel Computation Thesis. SIGACT News 1986, 18, 54–67. [Google Scholar] [CrossRef]
- Arora, S.; Barak, B. Computational Complexity: A Modern Approach; Cambridge University: Cambridge, UK, 2009. [Google Scholar]
- Aaronson, S.; Arkhipov, A. The Computational Complexity of Linear Optics. Theory Comput. 2013, 9, 143–252. [Google Scholar] [CrossRef]
- Akel Abrahao, R. Frontiers of Quantum Optics: Photonics Tolls, Computational Complexity, Quantum Metrology, and Quantum Correlations. Ph.D. Thesis, School of Mathematics and Physics, The University of Queensland, St. Lucia, Australia, 2020. [Google Scholar]
- Bernstein, E.; Vazirani, U. Quantum Complexity Theory. In Proceedings of the Twenty-Fifth Annual ACM Symposium on Theory of Computing, San Diego, CA, USA, 16–18 May 1993; pp. 11–20. [Google Scholar]
- Bernstein, E.; Vazirani, U. Quantum Complexity Theory. SIAM J. Comput. 1997, 26, 1411–1473. [Google Scholar] [CrossRef]
- Yao, A.C.C. Classical Physics and the Church-Turing Thesis. J. ACM 2003, 50, 100–105. [Google Scholar] [CrossRef]
- Harrow, A.; Montanaro, A. Quantum computational supremacy. Nature 2017, 549, 203–209. [Google Scholar] [CrossRef]
- Alexeev, Y.; Bacon, D.; Brown, K.R.; Calderbank, R.; Carr, L.D.; Chong, F.T.; DeMarco, B.; Englund, D.; Farhi, E.; Fefferman, B.; et al. Quantum Computer Systems for Scientific Discovery. PRX Quantum 2021, 2, 017001. [Google Scholar] [CrossRef]
- Lloyd, S. Universal quantum simulators. Science 1996, 273, 1073–1078. [Google Scholar] [CrossRef] [PubMed]
- Berry, D.; Ahokas, G.; Cleve, R.; Barry, C.S. Efficient Quantum Algorithms for Simulating Sparse Hamiltonians. Commun. Math. Phys. 2007, 270, 359–371. [Google Scholar] [CrossRef]
- Childs, A.; Su, Y.; Tran, M.C.; Wiebe, N.; Zhu, S. Theory of Trotter Error with Commutator Scaling. Phys. Rev. X 2021, 11, 011020. [Google Scholar] [CrossRef]
- Şahinoğlu, B.; Somma, R. Hamiltonian simulation in the low-energy subspace. NPJ Quantum Inf. 2021, 7, 1–5. [Google Scholar] [CrossRef]
- Ji, Z.; Natarajan, A.; Vidick, T.; Wright, J.; Yuen, H. MIP*=RE. arXiv 2020, arXiv:2001.04383. [Google Scholar] [CrossRef]
- Ji, Z.; Natarajan, A.; Vidick, T.; Wright, J.; Yuen, H. MIP* = RE. Commun. ACM 2021, 64, 131–138. [Google Scholar] [CrossRef]
- Aharonov, D.; van Dam, W.; Kempe, J.; Landau, Z.; Lloyd, S.; Regev, O. Adiabatic Quantum Computation Is Equivalent to Standard Quantum Computation. SIAM Rev. 2008, 50, 755–787. [Google Scholar] [CrossRef]
- Shepherd, D.; Bremner, M. Temporally unstructured quantum computation. Proc. R. Soc. A 2009, 465, 1413–1439. [Google Scholar] [CrossRef]
- Hoban, M.J.; Wallman, J.J.; Anwar, H.; Usher, N.; Raussendorf, R.; Browne, D.E. Measurement-Based Classical Computation. Phys. Rev. Lett. 2014, 112, 140505. [Google Scholar] [CrossRef]
- King, J.; Yarkoni, S.; Raymond, J.; Ozfidan, I.; King, A.D.; Nevisi, M.M.; Hilton, J.P.; McGeoch, C.C. Quantum Annealing amid Local Ruggedness and Global Frustration. J. Phys. Soc. Jpn. 2019, 88, 061007. [Google Scholar] [CrossRef]
- Rohde, P.P.; Motes, K.R.; Knott, P.A.; Munro, W.J. Will boson-sampling ever disprove the Extended Church-Turing thesis? arXiv 2014, arXiv:1401.2199. [Google Scholar]
- Aaronson, S.; Chen, L. Complexity-Theoretic Foundations of Quantum Supremacy Experiments. In Proceedings of the 32nd Computational Complexity Conference—CCC’17, Riga, Latvia, 6–9 July 2017. [Google Scholar]
- Gyongyosi, L.; Imre, S. A Survey on quantum computing technology. Comput. Sci. Rev. 2019, 31, 51–71. [Google Scholar] [CrossRef]
- Gyongyosi, L.; Imre, S. Dense Quantum Measurement Theory. Sci. Rep. 2019, 9, 6755. [Google Scholar] [CrossRef]
- Gyongyosi, L.; Imre, S. Scalable distributed gate-model quantum computers. Sci. Rep. 2021, 11, 5172. [Google Scholar] [CrossRef]
- Foxen, B.; Neill, C.; Dunsworth, A.; Roushan, P.; Chiaro, B.; Megrant, A.; Kelly, J.; Chen, Z.; Satzinger, K.; Barends, R.; et al. Demonstrating a Continuous Set of Two-qubit Gates for Near-term Quantum Algorithms. Phys. Rev. Lett. 2020, 125, 120504. [Google Scholar] [CrossRef] [PubMed]
- Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Nath, R.K.; Thapliyal, H.; Humble, T.S. A Review of Machine Learning Classification Using Quantum Annealing for Real-World Applications. arXiv 2021, arXiv:2106.02964. [Google Scholar] [CrossRef]
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.; Buell, D.A.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef]
- Pednault, E.; Gunnels, J.A.; Nannicini, G.; Horesh, L.; Wisnieff, R. Leveraging Secondary Storage to Simulate Deep 54-qubit Sycamore Circuits. arXiv 2019, arXiv:1910.09534. [Google Scholar]
- Zhong, H.S.; Wang, H.; Deng, Y.H.; Chen, M.C.; Peng, L.C.; Luo, Y.H.; Qin, J.; Wu, D.; Ding, X.; Hu, Y.; et al. Quantum computational advantage using photons. Science 2020, 370, 1460–1463. [Google Scholar] [CrossRef] [PubMed]
- Zhong, H.S.; Deng, Y.H.; Qin, J.; Wang, H.; Chen, M.C.; Peng, L.C.; Luo, Y.H.; Wu, D.; Gong, S.Q.; Su, H.; et al. Phase-Programmable Gaussian Boson Sampling Using Stimulated Squeezed Light. Phys. Rev. Lett. 2021, 127, 180502. [Google Scholar] [CrossRef]
- Wu, Y.; Bao, W.S.; Cao, S.; Chen, F.; Chen, M.C.; Chen, X.; Chung, T.H.; Deng, H.; Du, Y.; Fan, D.; et al. Strong Quantum Computational Advantage Using a Superconducting Quantum Processor. Phys. Rev. Lett. 2021, 127, 180501. [Google Scholar] [CrossRef]
- Uppu, R.; Pedersen, F.T.; Wang, Y.; Olesen, C.T.; Papon, C.; Zhou, X.; Midolo, L.; Scholz, S.; Wieck, A.D.; Ludwig, A.; et al. Scalable integrated single-photon source. Sci. Adv. 2020, 6, eabc8268. [Google Scholar] [CrossRef] [PubMed]
- Arrazola, J.M.; Bergholm, V.; Brádler, K.; Bromley, T.R.; Collins, M.J.; Dhand, I.; Fumagalli, A.; Gerrits, T.; Goussev, A.; Helt, L.G.; et al. Quantum circuits with many photons on a programmable nanophotonic chip. Nature 2021, 591, 54–60. [Google Scholar] [CrossRef] [PubMed]
- Albash, T.; Martin-Mayor, V.; Hen, I. Temperature Scaling Law for Quantum Annealing Optimizers. Phys. Rev. Lett. 2017, 119, 110502. [Google Scholar] [CrossRef]
- Marshall, J.; Rieffel, E.G.; Hen, I. Thermalization, Freeze-out, and Noise: Deciphering Experimental Quantum Annealers. Phys. Rev. Appl. 2017, 8, 064025. [Google Scholar] [CrossRef]
- Fang, K.; Liu, Z. No-Go Theorems for Quantum Resource Purification. Phys. Rev. Lett. 2020, 125, 060405. [Google Scholar] [CrossRef]
- Medvidović, M.; Carleo, G. Classical variational simulation of the Quantum Approximate Optimization Algorithm. NPJ Quantum Inf. 2021, 7, 1–7. [Google Scholar] [CrossRef]
- Aharonov, D.; Vazirani, U. Is Quantum Mechanics Falsifiable? A Computational Perspective on the Foundations of Quantum Mechanics. In Computability: Turing, Gödel, Church, and Beyond; MIT Press: Cambridge, MA, USA, 2013; pp. 329–349. [Google Scholar]
- Aharonov, D.; Ben-Or, M.; Eban, E.; Mahadev, U. Interactive Proofs for Quantum Computations. arXiv 2017, arXiv:1704.04487. [Google Scholar]
- Deutsch, D. Quantum Computational Networks. Proc. R. Soc. Lond. A Math. Phys. Sci. 1989, 425, 73–90. [Google Scholar]
- Chi-Chih Yao, A. Quantum circuit complexity. In Proceedings of the 1993 IEEE 34th Annual Foundations of Computer Science, Palo Alto, CA, USA, 3–5 November 1993; pp. 352–361. [Google Scholar]
- Nielsen, M. A Geometric Approach to Quantum Circuit Lower Bounds. Quantum Inf. Comput. 2006, 6, 213–262. [Google Scholar] [CrossRef]
- Nielsen, M.; Dowling, M.R.; Gu, M.; Doherty, A.C. Quantum Computation as Geometry. Science 2006, 311, 1133–1135. [Google Scholar] [CrossRef]
- Bremner, M.; Richard, J.; Dan, S.J. Classical simulation of commuting quantum computations implies collapse of the polynomial hierarchy. Proc. R. Soc. A Math. Phys. Eng. Sci. 2011, 467, 459–472. [Google Scholar] [CrossRef]
- Denef, F.; Douglas, M. Computational complexity of the landscape: Part I. Ann. Phys. 2007, 322, 1096–1142. [Google Scholar] [CrossRef]
- Denef, F.; Douglas, M.R.; Greene, B.; and Zukowski, C. Computational complexity of the landscape II—Cosmological considerations. Ann. Phys. 2018, 392, 93–127. [Google Scholar] [CrossRef]
- Harlow, D.; Hayden, P. Quantum computation vs. firewalls. J. High Energy Phys. 2013, 2013, 85. [Google Scholar] [CrossRef]
- Susskind, L. Three Lectures on Complexity and Black Holes; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Susskind, L. Computational complexity and black hole horizons. Fortschritte Phys. 2016, 64, 24–43. [Google Scholar] [CrossRef]
- Stanford, D.; Susskind, L. Complexity and shock wave geometries. Phys. Rev. D 2014, 90, 126007. [Google Scholar] [CrossRef]
- Brown, A.; Susskind, L.; Swingle, B.; Zhao, Y.; Roberts, D.A. Complexity, action, and black holes. Phys. Rev. D 2016, 93, 086006. [Google Scholar] [CrossRef]
- Brown, A.; Roberts, D.A.; Susskind, L.; Swingle, B.; Zhao, Y. Holographic Complexity Equals Bulk Action? Phys. Rev. Lett. 2016, 116, 191301. [Google Scholar] [CrossRef]
- Atia, Y.; Aharonov, D. Fast-forwarding of Hamiltonians and exponentially precise measurements. Nat. Commun. 2017, 8, 1–9. [Google Scholar] [CrossRef]
- Brown, A.; Susskind, L. Second law of quantum complexity. Phys. Rev. D 2018, 97, 086015. [Google Scholar] [CrossRef]
- Hashimoto, K.; Iizuka, N. and Sugishita, S. Time evolution of complexity in Abelian gauge theories. Phys. Rev. D 2017, 96, 126001. [Google Scholar] [CrossRef]
- Jefferson, R.; Myers, R. Circuit complexity in quantum field theory. J. High Energy Phys. 2017, 10, 1–80. [Google Scholar] [CrossRef]
- Hackl, L.; Myers, R. Circuit complexity for free fermions. J. High Energy Phys. 2017, 7, 1–71. [Google Scholar] [CrossRef]
- Guo, M.; Hernandez, J.; Myers, R.C.; Ruan, S.M. Circuit complexity for coherent states. J. High Energy Phys. 2018, 10, 85. [Google Scholar] [CrossRef]
- Caputa, P.; Magan, J. Quantum Computation as Gravity. Phys. Rev. Lett. 2019, 122, 231302. [Google Scholar] [CrossRef]
- Yosifov, A.; Filipov, L. Quantum Complexity and Chaos in Young Black Holes. Universe 2019, 5, 93. [Google Scholar] [CrossRef]
- Bueno, P.; Magán, J.; Shahbazi, C. Complexity measures in QFT and constrained geometric actions. J. High Energ. Phys. 2021, 2021, 1–55. [Google Scholar] [CrossRef]
- Copeland, J.; Sprevak, M.; Shagrir, O. Zuse’s Thesis, Gandy’s Thesis, and Penrose’s Thesis. In Physical Perspectives on Computation, Computational Perspectives on Physics; Cambridge University Press: Cambridge, UK, 2018; pp. 39–59. [Google Scholar]
- Deutsch, D. Is the Cosmos a Computer? Closer to Truth. 2016. Available online: https://www.youtube.com/watch?v=UohR3OXzXA8 (accessed on 20 April 2020).
- Lloyd, S. Universe as quantum computer. Complexity 1997, 3, 32–35. [Google Scholar] [CrossRef][Green Version]
- Lloyd, S. Programming the Universe: A Quantum Computer Scientist Takes on the Cosmos; KNOPF: New York, NY, USA, 2007. [Google Scholar]
- Tegmark, M. The Mathematical Universe. Found. Phys. 2008, 38, 101–150. [Google Scholar] [CrossRef]
- Szudzik, M. Some Applications of Recursive Functionals to the Foundations of Mathematics and Physics. Ph.D. Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 2010. [Google Scholar]
- Szudzik, M. The Computable Universe Hypothesis. In A Computable Universe; World Scientific: Singapore, 2012; pp. 479–523. [Google Scholar]
- Bournez, O.; Campagnolo, M. A Survey on Continuous Time Computations. In New Computational Paradigms: Changing Conceptions of What is Computable; Springer: New York, NY, USA, 2008; pp. 383–423. [Google Scholar]
- Soare, R. Turing oracle machines, online computing, and three displacements in computability theory. Ann. Pure Appl. Log. 2009, 160, 368–399. [Google Scholar] [CrossRef]
- Carl, M. Ordinal Computability: An Introduction to Infinitary Machines; de Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Ludwig, G. Concepts of states in physics. Found. Phys. 1990, 20, 621–633. [Google Scholar] [CrossRef]
- Rabin, M.O. Probabilistic automata. Inf. Control 1963, 6, 230–245. [Google Scholar] [CrossRef]
- Santos, E.S. Probabilistic Turing Machines and Computability. Proc. Am. Math. Soc. 1969, 22, 704–710. [Google Scholar] [CrossRef]
- Evans, M. Journal of the History of Ideas. Aristotle Newton Theory Contin. Magnit. 1955, 16, 548–557. [Google Scholar]
- Shannon, C.E. Mathematical Theory of the Differential Analyzer. J. Math. Phys. 1941, 20, 337–354. [Google Scholar] [CrossRef]
- Moore, C. Recursion theory on the reals and continuous-time computation. Theor. Comput. Sci. 1996, 162, 23–44. [Google Scholar] [CrossRef]
- Costa, J.; Loff, B.; Mycka, J. A foundation for real recursive function theory. Ann. Pure Appl. Log. 2009, 160, 255–288. [Google Scholar] [CrossRef]
- Mycka, J.; Costa, J. Real recursive functions and their hierarchy. J. Complex. 2004, 20, 835–857. [Google Scholar] [CrossRef][Green Version]
- Bournez, O.; Graça, D.; Pouly, A. Computing with polynomial ordinary differential equations. J. Complex. 2016, 36, 106–140. [Google Scholar] [CrossRef]
- Bournez, O.; Graça, D.; Pouly, A. Polynomial differential equations compute all real computable functions on computable compact intervals. J. Complex. 2007, 23, 317–335. [Google Scholar] [CrossRef]
- Ehrhard, T.; Regnier, L. The differential lambda-calculus. Theor. Comput. Sci. 2003, 309, 1–41. [Google Scholar] [CrossRef]
- Taylor, P. A Lambda Calculus for Real Analysis. J. Log. Anal. 2010, 2, 1–115. [Google Scholar] [CrossRef]
- Bournez, O.; Dershowitz, N.; Néron, P. Axiomatizing Analog Algorithms. In Pursuit of the Universal: 12th Conference on Computability in Europe; Springer: Berlin/Heidelberg, Germany, 2016; pp. 215–224. [Google Scholar]
- Brown, A.; Susskind, L. Complexity geometry of a single qubit. Phys. Rev. D 2019, 100, 046020. [Google Scholar] [CrossRef]
- Jackson, A.S. Analog Computation; McGraw-Hill: New York, NY, USA, 1960. [Google Scholar]
- Cowan, G.; Melville, R.C.; Tsividis, Y.P. A VLSI analog computer/math co-processor for a digital computer. In Proceedings of the IEEE International Conference on Solid-State Circuits 2005, San Francisco, CA, USA, 10 February 2005; Volume 1, pp. 82–586. [Google Scholar]
- Milios, J.; Clauvelin, N. A Programmable Analog Computer on a Chip. In Proceedings of the Embedded World Conference, Nuremberg, Germany, 26–28 February 2019. [Google Scholar]
- Mayr, R. Process Rewrite Systems. Inf. Comput. 2000, 156, 264–286. [Google Scholar] [CrossRef][Green Version]
- Baader, F.; Nipkow, T. Term Rewriting and All That; Cambrige University Press: Cambrige, UK, 1999. [Google Scholar]
- Weyl, H. Quantenmechanik und Gruppentheorie. Z. Phys. 1927, 46, 1–46. [Google Scholar] [CrossRef]
- Santhanam, T.S.; Tekumalla, A.R. Quantum mechanics in finite dimensions. Found. Phys. 1976, 6, 583–587. [Google Scholar] [CrossRef]
- Santhanam, T. Quantum mechanics in a finite number of dimensions. Phys. A Stat. Mech. Its Appl. 1982, 114, 445–447. [Google Scholar] [CrossRef]
- Eberbach, E.; Goldin, D.; Wegner, P. Turing’s Ideas and Models of Computation. In Alan Turing: Life and Legacy of a Great Thinker; Springer: Berlin/Heidelberg, Germany, 2004; pp. 159–194. [Google Scholar]
- Welch, P. Discrete Transfinite Computation. In Turing’s Revolution: The Impact of His Ideas about Computability; Springer International Publishing: Berlin/Heidelberg, Germany, 2015; pp. 161–185. [Google Scholar]
- Magaña-Loaiza, O.S.; De Leon, I.; Mirhosseini, M.; Fickler, R.; Safari, A.; Mick, U.; McIntyre, B.; Banzer, P.; Rodenburg, B.; Leuchs, G.; et al. Exotic looped trajectories of photons in three-slit interference. Nat. Commun. 2016, 7, 13987. [Google Scholar] [CrossRef]
- Toffoli, T. Action, or the fungibility of computation. In Feynman and Computation; Perseus Books Publishing: New York, NY, USA, 1998; pp. 348–392. [Google Scholar]
- Apt, K.R. From Logic Programming to Prolog; Prentice-Hall, Inc.: Hoboken, NJ, USA, 1996. [Google Scholar]
- Maxwell, J.C. Theory of Heat; Longman: London, UK, 1871. [Google Scholar]
- Szilard, L. On the decrease of entropy in a thermodynamic system by the intervention of intelligent beings. Syst. Res. Behav. Sci. 1964, 9, 301–310. [Google Scholar] [CrossRef]
- Brillouin, L. Maxwell’s Demon Cannot Operate: Information and Entropy. I. J. Appl. Phys. 1951, 22, 334–337. [Google Scholar] [CrossRef]
- Rex, A. Maxwell’s Demon—A Historical Review. Entropy 2017, 19, 240. [Google Scholar] [CrossRef]
- Sipper, M. Evolution of Parallel Cellular Machines: The Cellular Programming Approach; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Giacobazzi, R.; Mastroeni, I. Abstract Non-Interference: A Unifying Framework for Weakening Information-Flow. ACM Trans. Priv. Secur. 2018, 21, 1–31. [Google Scholar] [CrossRef]
- Heisenberg, W. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Phys. 1927, 43, 172–198. [Google Scholar] [CrossRef]
- Sen, D. The uncertainty relations in quantum mechanics. Curr. Sci. 2014, 107, 203–218. [Google Scholar]
- Ben-Ari, M. Principles of Concurrent and Distributed Programming, 2nd ed.; Addison Wesley: Boston, MA, USA, 2015. [Google Scholar]
- Calude, C.; Calude, E.; Svozil, K.; Yu, S. Physical versus computational complementarity. I. Int. J. Theor. Phys. 1997, 36, 1495–1523. [Google Scholar] [CrossRef][Green Version]
- Calude, C.S.; Calude, E. Automata: From Uncertainty to Quantum. In Developments in Language Theory. DLT 2001; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2295, pp. 1–14. [Google Scholar]
- Bennett, C.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. Theor. Comput. Sci. 2014, 560, 7–11. [Google Scholar] [CrossRef]
- Wigner, E. The Problem of Measurement. Am. J. Phys. 1963, 31, 6–15. [Google Scholar] [CrossRef]
- Schlosshauer, M. Decoherence, the measurement problem, and interpretations of quantum mechanics. Rev. Mod. Phys. 2005, 76, 1267–1305. [Google Scholar] [CrossRef]
- Schlosshauer, M. Quantum decoherence. Phys. Rep. 2019, 831, 1–57. [Google Scholar] [CrossRef]
- Adler, S.; Bassi, A. Is Quantum Theory Exact? Science 2009, 325, 275–276. [Google Scholar] [CrossRef]
- Deutsch, D. Constructor theory. Synthese 2013, 190, 4331–4359. [Google Scholar] [CrossRef]
- Hempel, C.G. Reduction: Ontological and linguistic facets. In Philosophy, Science, and Method: Essays in Honor of Ernest Nagel; St. Martin’s Press: New York, NY, USA, 1969; pp. 179–199. [Google Scholar]
- Bokulich, P. Hempel’s Dilemma and domains of physics. Analysis 2011, 71, 646–651. [Google Scholar] [CrossRef]
- Edis, T.; Boudry, M. Beyond Physics? On the Prospects of Finding a Meaningful Oracle. Found. Sci. 2014, 19, 403–422. [Google Scholar] [CrossRef]
- Kwon, O.; Hogan, C. Interferometric tests of Planckian quantum geometry models. Class. Quantum Gravity 2016, 33, 105004. [Google Scholar] [CrossRef]
- Richardson, J.; Kwon, O.; Gustafson, R.H.; Hogan, C.; Kamai, B.L.; McCuller, L.P.; Meyer, S.S.; Stoughton, C.; Tomlin, R.E.; Weiss, R. Interferometric Constraints on Spacelike Coherent Rotational Fluctuations. Phys. Rev. Lett. 2021, 126, 241301. [Google Scholar] [CrossRef]
- Chou, A.; Glass, H.; Gustafson, H.R.; Hogan, C.J.; Kamai, B.L.; Kwon, O.; Lanza, R.; McCuller, L.; Meyer, S.S.; Richardson, J.W.; et al. Interferometric constraints on quantum geometrical shear noise correlations. Class. Quantum Gravity 2017, 34, 165005. [Google Scholar] [CrossRef]
- Hagar, A. Discrete or Continuous?: The Quest for Fundamental Length in Modern Physics; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Chou, A.; Glass, H.; Gustafson, H.R.; Hogan, C.; Kamai, B.L.; Kwon, O.; Lanza, R.; McCuller, L.; Meyer, S.S.; Richardson, J.; et al. The Holometer: An instrument to probe Planckian quantum geometry. Class. Quantum Gravity 2017, 34, 065005. [Google Scholar] [CrossRef]
- Beggs, E.; Cortez, P.; Costa, J.; Tucker, J. Classifying the computational power of stochastic physical oracles. Int. J. Unconv. Comput. 2018, 14, 59–90. [Google Scholar]
- Beggs, E.; Costa, J.; Tucker, J. Three forms of physical measurement and their computability. Rev. Symb. Log. 2014, 7, 618–646. [Google Scholar] [CrossRef][Green Version]
- Beggs, E.; Costa, J.; Tucker, J. Axiomatizing physical experiments as oracles to algorithms. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2012, 370, 3359–3384. [Google Scholar] [CrossRef]
- Beggs, E.; Costa, J.; Tucker, J. The impact of models of a physical oracle on computational power. Math. Struct. Comput. Sci. 2012, 22, 853–879. [Google Scholar] [CrossRef]
- Beggs, E.; Tucker, J. Experimental computation of real numbers by Newtonian machines. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 2007, 463, 1541–1561. [Google Scholar] [CrossRef]
- Barnum, H.; Lee, C.M.; Selby, J.H. Oracles and Query Lower Bounds in Generalised Probabilistic Theories. Found. Phys. 2018, 48, 954–981. [Google Scholar] [CrossRef]
- Fogelin, R. The Intuitive Basis of Berkeley’s Immaterialism. Hist. Philos. Q. 1996, 13, 331–344. [Google Scholar]
- Tipler, F. The omega point as eschaton: answers to pannenberg’s questions for scientists. Zygon 1989, 24, 217–253. [Google Scholar] [CrossRef]
- Tipler, F. The Physics of Immortality; Macmillan: New York, NY, USA, 1995. [Google Scholar]
- Schmidhuber, J. A Computer Scientist’s View of Life, the Universe, and Everything. In Foundations of Computer Science: Potential—Theory—Cognition; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1997; Volume 1337, pp. 201–208. [Google Scholar]
- Bostrom, N. Are We Living in a Computer Simulation? Philos. Q. 2003, 53, 243–255. [Google Scholar] [CrossRef]
- McCabe, G. Universe creation on a computer. Stud. Hist. Philos. Sci. Part B Stud. Hist. Philos. Mod. Phys. 2005, 36, 591–625. [Google Scholar] [CrossRef][Green Version]
- Kipping, D. A Bayesian Approach to the Simulation Argument. Universe 2020, 6, 109. [Google Scholar] [CrossRef]
- Bibeau-Delisle, A.; Brassard FRS, G. Probability and consequences of living inside a computer simulation. Proc. R. Soc. A Math. Phys. Eng. Sci. 2021, 477, 20200658. [Google Scholar] [CrossRef]
- Greene, P. The Termination Risks of Simulation Science. Erkenn 2020, 85, 489–509. [Google Scholar] [CrossRef]
- Beane, S.; Davoudi, Z.; Savage, M. Constraints on the universe as a numerical simulation. Eur. Phys. J. A 2014, 50, 148. [Google Scholar] [CrossRef]
- Ringel, Z.; Kovrizhin, D. Quantized gravitational responses, the sign problem, and quantum complexity. Sci. Adv. 2017, 3, e1701758. [Google Scholar] [CrossRef]
- Meshik, A. The workings of an ancient nuclear reactor. Sci. Am. 2005, 293, 82–91. [Google Scholar] [CrossRef]
- Miguel-Tomé, S. Towards a model-theoretic framework for describing the semantic aspects of cognitive processes. Adv. Distrib. Comput. Artif. Intell. J. 2020, 8, 83–96. [Google Scholar] [CrossRef]
- Khan, F. Confirmed! We Live in a Simulation: We Must Never Doubt Elon Musk Again. 2021. Available online: https://www.scientificamerican.com/article/confirmed-we-live-in-a-simulation/ (accessed on 20 July 2021).
- Gates, J. Symbols of Power: Adinkras and the Nature of Reality. Physics World 2010, 23, 34–39. [Google Scholar] [CrossRef]
- Fredkin, E. An Introduction to Digital Philosophy. Int. J. Theor. Phys. 2003, 42, 189–247. [Google Scholar] [CrossRef]
- Wiesner, K. Nature computes: Information processing in quantum dynamical systems. Chaos Interdiscip. J. Nonlinear Sci. 2010, 20, 037114. [Google Scholar] [CrossRef]
- Copeland, J.; Sprevak, M.; Shagrir, O. Is the whole universe a computer. In The Turing Guide: Life, Work, Legacy; Oxford University Press: Oxford, UK, 2017; pp. 445–462. [Google Scholar]
- Copeland, B. The broad conception of computation. Am. Behav. Sci. 1997, 40, 690–716. [Google Scholar] [CrossRef]
- Sacks, G. Higher Recursion Theory; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Szudzik, M.P. Is Turing’s Thesis the Consequence of a More General Physical Principle. In How the World Computes; Springer: Berlin/Heidelberg, Germany, 2012; pp. 714–722. [Google Scholar]
- Hodges, W. VIII*—Truth in a Structure. Proc. Aristot. Soc. 2015, 86, 135–152. [Google Scholar] [CrossRef]
- Gandy, R. Church’s Thesis and Principles for Mechanisms. In The Kleene Symposium; Studies in Logic and the Foundations of Mathematics; Elsevier: Amsterdam, The Netherlands, 1980; Volume 101, pp. 123–148. [Google Scholar]
- Geroch, R.; Hartle, J. Computability and physical theories. Found. Phys. 1986, 16, 533–550. [Google Scholar] [CrossRef]
- Lloyd, S. Quantum-mechanical computers and uncomputability. Phys. Rev. Lett. 1993, 71, 943–946. [Google Scholar] [CrossRef]
- Garner, A. Interferometric Computation Beyond Quantum Theory. Found. Phys. 2018, 48, 886–909. [Google Scholar] [CrossRef]
- Brodsky, S.; Pauli, H.; Pinsky, S. Quantum chromodynamics and other field theories on the light cone. Phys. Rep. 1998, 301, 299–486. [Google Scholar] [CrossRef]
- Lee, D.; Lightman, A.; Ni, W.T. Conservation laws and variational principles in metric theories of gravity. Phys. Rev. D 1974, 10, 1685–1700. [Google Scholar] [CrossRef]
- Epelbaum, E.; Krebs, H.; Lähde, T.A.; Lee, D.; Meißner, U.G. Viability of Carbon-Based Life as a Function of the Light Quark Mass. Phys. Rev. Lett. 2013, 110, 112502. [Google Scholar] [CrossRef] [PubMed]
- Doran, C.F.; Faux, M.G.; Gates, S.J., Jr.; Hubsch, T.; Iga, K.M.; Landweber, G.D. Relating Doubly-Even Error-Correcting Codes, Graphs, and Irreducible Representations of N-Extended Supersymmetry. arXiv 2008, arXiv:0806.0051. [Google Scholar]
- Wendel, G.; Martínez, L.; Bojowald, M. Physical Implications of a Fundamental Period of Time. Phys. Rev. Lett. 2020, 124, 241301. [Google Scholar] [CrossRef] [PubMed]
- Neary, T.; Woods, D. Small fast universal Turing machines. Theor. Comput. Sci. 2006, 362, 171–195. [Google Scholar] [CrossRef]
- Lubachevsky, B. Efficient Parallel Simulations of Asynchronous Cellular Arrays. Complex Syst. 1987, 1, 1099–1123. [Google Scholar]
- Lubachevsky, B. Why The Results of Parallel and Serial Monte Carlo Simulations May Differ. arXiv 2011, arXiv:1104.0198. [Google Scholar]
- Nicol, D. Performance Bounds on Parallel Self-Initiating Discrete-Event Simulations. ACM Trans. Model. Comput. Simul. 1991, 1, 24–50. [Google Scholar] [CrossRef]
- Lerman, M. Degrees of Unsolvability: Local and Global Theory; Perspectives in Logic, Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Boker, U.; Dershowitz, N. Comparing Computational Power. Log. J. IGPL 2006, 14, 633–647. [Google Scholar] [CrossRef][Green Version]
- Lindsay, R. The concept of energy and its early historical development. Found. Phys. Vol. 1971, 1, 383–393. [Google Scholar] [CrossRef]
- Oliveira, A. The Ideas of Work and Energy in Mechanics. In A History of the Work Concept; History of Mechanism and Machine Science; Springer: Berlin/Heidelberg, Germany, 2014; Volume 24, pp. 65–91. [Google Scholar]
- Jammer, M. Concepts of Space: The History of Theories of Space in Physics; Harvard University Press: Cambridge, MA, USA, 1954. [Google Scholar]
- Bros, J. From Euclid’s Geometry to Minkowski’s Spacetime. In Einstein, 1905–2005; Progress in Mathematical Physics; Birkhäuser: Basel, Switzerland, 2006; Volume 47, pp. 60–119. [Google Scholar]
- Kiukas, J.; Lahti, P.; Pellonpää, J.P.; Ylinen, K. Complementary Observables in Quantum Mechanics. Found. Phys. 2019, 49, 506–531. [Google Scholar] [CrossRef]
- Frauchiger, D.; Renner, R. Quantum theory cannot consistently describe the use of itself. Nat. Commun. 2018, 9, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Bong, K.; Utreras-Alarcón, A.; Ghafari, F.; Liang, Y.C.; Tischler, N.; Cavalcanti, E.G.; Pryde, G.J.; Wiseman, H.M. A strong no-go theorem on the Wigner’s friend paradox. Nat. Phys. 2020, 16, 1199–1205. [Google Scholar] [CrossRef]
- Waaijer, M.; Neerven, J. Relational Analysis of the Frauchiger–Renner Paradox and Interaction-Free Detection of Records from the Past. Found. Phys. 2021, 51, 1–18. [Google Scholar] [CrossRef]
- Aharonov, Y.; Anandan, J.; Vaidman, L. Meaning of the wave function. Phys. Rev. A 1993, 47, 4616–4626. [Google Scholar] [CrossRef]
- Perlov, D.; Vilenkin, A. Cosmology for the Curious; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Arrighi, P.; Grattage, J. A quantum game of life. In Proceedings of the Second Symposium on Cellular Automata “Journées Automates Cellulaires” (JAC 2010), Turku, Finland, 15–17 December 2010; pp. 31–42. [Google Scholar]
- Bleh, D.; Calarco, T.; Montangero, S. Quantum Game of Life. arXiv 2012, arXiv:1010.4666. [Google Scholar] [CrossRef]
- Arrighi, P.; Grattage, J. The quantum game of life. Phys. World 2012, 25, 23–26. [Google Scholar] [CrossRef]
- Alvarez-Rodriguez, U.; Sanz, M.; Lamata, L.; Solano, E. Quantum Artificial Life in an IBM Quantum Computer. Sci. Rep. 2018, 8, 14793. [Google Scholar] [CrossRef]
- Ney, P.M.; Notarnicola, S.; Montangero, S.; Morigi, G. Entanglement in the Quantum Game of Life. arXiv 2021, arXiv:2104.14924. [Google Scholar]
- Gann, R.; Venable, J.; Friedman, E.J.; Landsberg, A.S. Behavior of coupled automata. Phys. Rev. E 2004, 69, 046116. [Google Scholar] [CrossRef]
- Wolfram, S. A Class of Models with the Potential to Represent Fundamental Physics. arXiv 2020, arXiv:2004.08210. [Google Scholar]
- Dirac, P. The Quantum Theory of the Electron. Proc. R. Soc. Lond. A 1928, 117, 610–624. [Google Scholar]
- Mastrolia, P.; Mizera, S. Feynman integrals and intersection theory. J. High Energy Phys. 2019, 2019, 139. [Google Scholar] [CrossRef]
- Frellesvig, H.; Gasparotto, F.; Laporta, S.; Mandal, M.K.; Mastrolia, P.; Mattiazzi, L.; Mizera, S. Decomposition of Feynman integrals on the maximal cut by intersection numbers. J. High Energy Phys. 2019, 2019, 153. [Google Scholar] [CrossRef]
- Renou, M.; Trillo, D.; Weilenmann, M.; Le, T.P.; Tavakoli, A.; Gisin, N.; Acín, A.; Navascués, M. Quantum theory based on real numbers can be experimentally falsified. Nature 2021, 600, 625–629. [Google Scholar] [CrossRef]
- Li, Z.D.; Mao, Y.L.; Weilenmann, M.; Tavakoli, A.; Chen, H.; Feng, L.; Yang, S.J.; Renou, M.O.; Trillo, D.; Le, T.P.; et al. Testing real quantum theory in an optical quantum network. Phys. Rev. Lett. 2021; in press. [Google Scholar]
- Chen, M.; Wang, C.; Liu, F.; Wang, J.; Ying, C.; Shang, Z.; Wu, Y.; Gong, M.; Deng, H.; Liang, F.T.; et al. Ruling out real-valued standard formalism of quantum theory. Phys. Rev. Lett. 2021; in press. [Google Scholar]
- Pour-El, M.; Richards, I. The wave equation with computable initial data such that its unique solution is not computable. Adv. Math. 1981, 39, 215–239. [Google Scholar] [CrossRef]
- Pour-El, M.; Zhong, N. The Wave Equation with Computable Initial Data Whose Unique Solution Is Nowhere Computable. Math. Log. Q. 1997, 43, 499–509. [Google Scholar] [CrossRef]
- da Costa, N.C.A.; Doria, F.A. Undecidability and incompleteness in classical mechanics. Int. J. Theor. Phys. 1991, 30, 1041–1073. [Google Scholar] [CrossRef]
- Brun, T.; Mlodinow, L. Detecting discrete spacetime via matter interferometry. Phys. Rev. D 2019, 99, 015012. [Google Scholar] [CrossRef]
- Brillouin, L. Science and Information Theory, 2nd ed.; Dover Publication: Mineola, NY, USA, 1962. [Google Scholar]
- Pawłowski, M.; Paterek, T.; Kaszlikowski, D.; Scarani, V.; Winter, A.; Żukowski, M. A new physical principle: Information causality. Nature 2009, 461, 1101–1104. [Google Scholar] [CrossRef] [PubMed]
- Chiribella, G.; D’Ariano, G.M.; Perinotti, P. Informational derivation of quantum theory. Phys. Rev. A 2011, 84, 012311. [Google Scholar] [CrossRef]
- Masanes, L.; Müller, M.P.; Augusiak, R.; Pérez-García, D. Existence of an information unit as a postulate of quantum theory. Proc. Natl. Acad. Sci. USA 2013, 110, 16373–16377. [Google Scholar] [CrossRef]
- Jannes, G. Some Comments on “The Mathematical Universe”. Found. Phys. 2009, 39, 397–406. [Google Scholar] [CrossRef]
- Franklin, J. An Aristotelian Realist Philosophy of Mathematics: Mathematics as the Science of Quantity and Structure; Palgrave Macmillan: New York, NY, USA, 2014. [Google Scholar]
- Franklin, J. Aristotelian realism. In The Philosophy of Mathematics; North-Holland Elsevier: Amsterdam, The Netherlands, 2009; pp. 101–153. [Google Scholar]
- Wigner, E.P. The Unreasonable Effectiveness of Mathematics in the Natural Sciences. Commun. Pure Appl. Math. 1960, 13, 1–14. [Google Scholar] [CrossRef]
- Hut, P.; Alford, M.; Tegmark, M. On Math, Matter and Mind. Found. Phys. 2006, 36, 765–794. [Google Scholar] [CrossRef]
- Rendell, P. Turing Machine Universality of the Game of Life; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Ellis, G. Physics and the Real World. Found. Phys. 2006, 36, 227–262. [Google Scholar] [CrossRef]
- Doyle, J. Extending Mechanics to Minds: The Mechanical Foundations of Psychology and Economics; Cambridge University Press: Cambridge, 2006. [Google Scholar]
- Miller, G.A. The cognitive revolution: A historical perspective. Trends Cogn. Sci. 2003, 7, 141–144. [Google Scholar] [CrossRef]
- Pylyshyn, Z. Computing in Cognitive Science; MIT Press: Cambridge, MA, USA, 1989. [Google Scholar]
- Bringsjord, S.; Kellett, O.; Shilliday, A.; Taylor, J.B.; Heuveln, V.; Yang, Y.; Baumes, J.; Ross, K. A new Gödelian argument for hypercomputing minds based on the busy beaver problem. Appl. Math. Comput. 2006, 176, 516–530. [Google Scholar] [CrossRef]
- Bringsjord, S.; Arkoudas, K. The modal argument for hypercomputing minds. Theor. Comput. Sci. 2004, 317, 167–190. [Google Scholar] [CrossRef][Green Version]
- Llinás, R. Brain. In “Mindwaves” as a Functional State of the Brain; Oxford University: Oxford, UK, 1987; pp. 339–358. [Google Scholar]
- Wheeler, J. Bits, Quanta, Meaning. In Problems in Theoretical Physics; University of Salerno Press: Fisciano, Italy, 1984; pp. 121–141. [Google Scholar]
- Miguel-Tomé, S. Principios Matemáticos del Comportamiento Natural. Ph.D. Thesis, Universidad de Salamanca, Salamanca, Spain, 2017. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miguel-Tomé, S.; Sánchez-Lázaro, Á.L.; Alonso-Romero, L. Fundamental Physics and Computation: The Computer-Theoretic Framework. Universe 2022, 8, 40. https://doi.org/10.3390/universe8010040
Miguel-Tomé S, Sánchez-Lázaro ÁL, Alonso-Romero L. Fundamental Physics and Computation: The Computer-Theoretic Framework. Universe. 2022; 8(1):40. https://doi.org/10.3390/universe8010040
Chicago/Turabian StyleMiguel-Tomé, Sergio, Ángel L. Sánchez-Lázaro, and Luis Alonso-Romero. 2022. "Fundamental Physics and Computation: The Computer-Theoretic Framework" Universe 8, no. 1: 40. https://doi.org/10.3390/universe8010040
APA StyleMiguel-Tomé, S., Sánchez-Lázaro, Á. L., & Alonso-Romero, L. (2022). Fundamental Physics and Computation: The Computer-Theoretic Framework. Universe, 8(1), 40. https://doi.org/10.3390/universe8010040





