Quantum Dark Solitons in the 1D Bose Gas: From Single to Double Dark-Solitons
Abstract
1. Introduction
2. Quantum Single Dark Soliton
2.1. Construction of Quantum States of Single Dark Solitons
2.2. Construction with Gaussian Weights
2.2.1. Effective Bose–Einstein Condensation in the Weak Coupling Case
2.2.2. Ansatz with the Ideal Gaussian Weights and the Mean-Field Product State
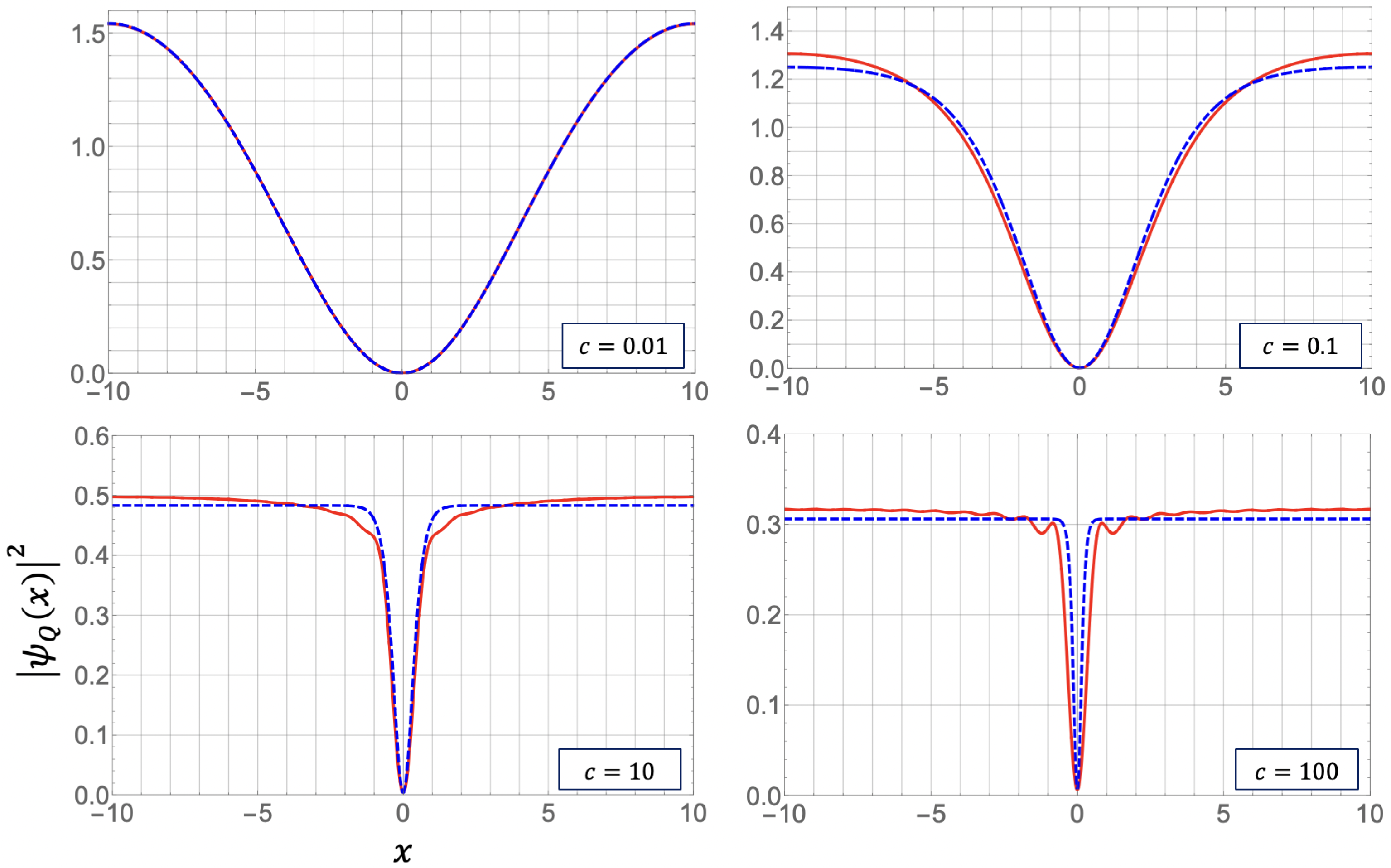
2.2.3. Numerical Study on the Validity of the Ansatz with the Ideal Gaussian Weights
3. Quantum State of a Dark Soliton with Nonzero Winding Number and the Corresponding Classical Solution
3.1. Novel Quantum State of a Single Dark Soliton with a Nonzero Winding Number
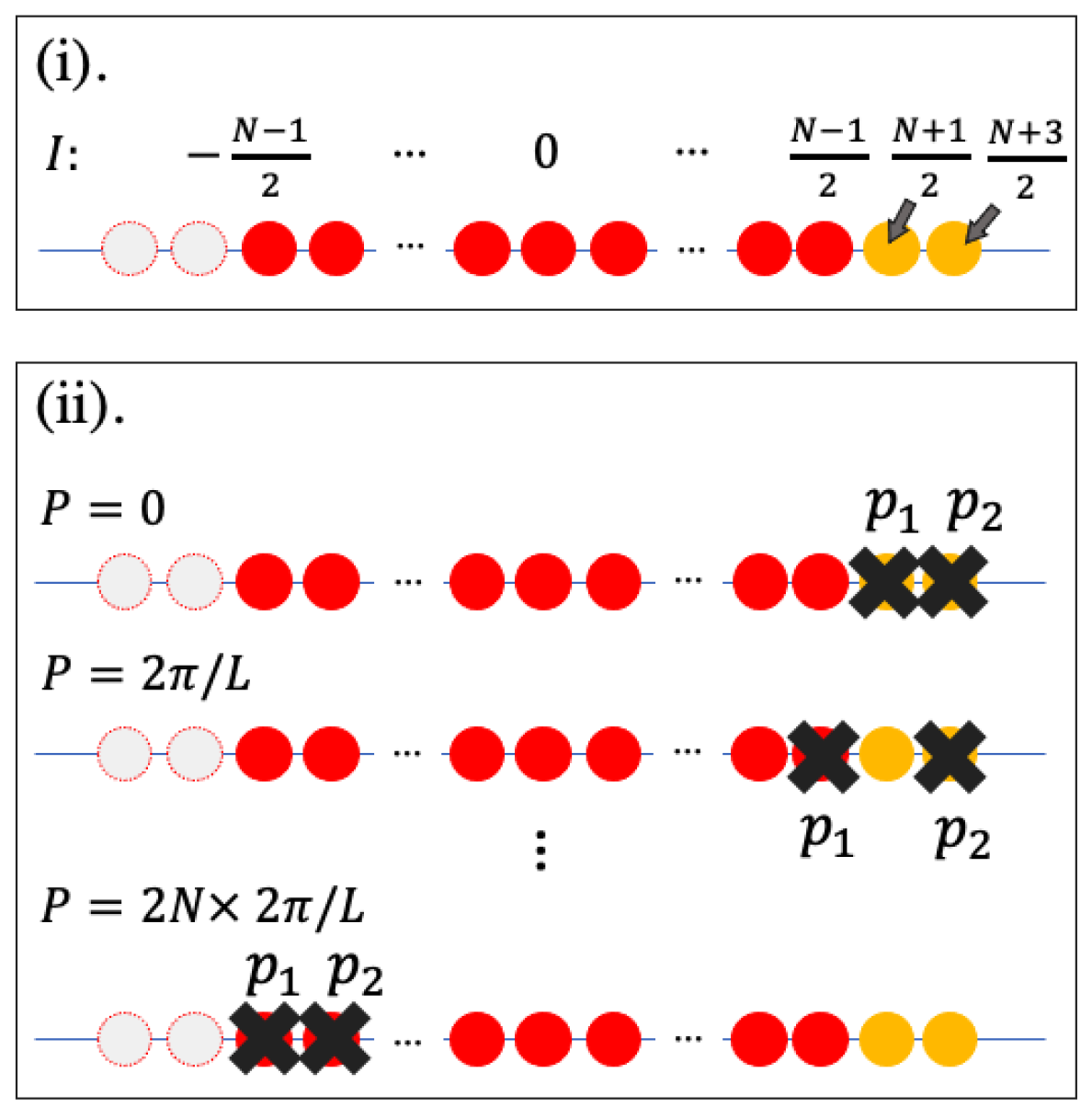
3.1.1. Construction of Quantum States with Nonzero Winding Number
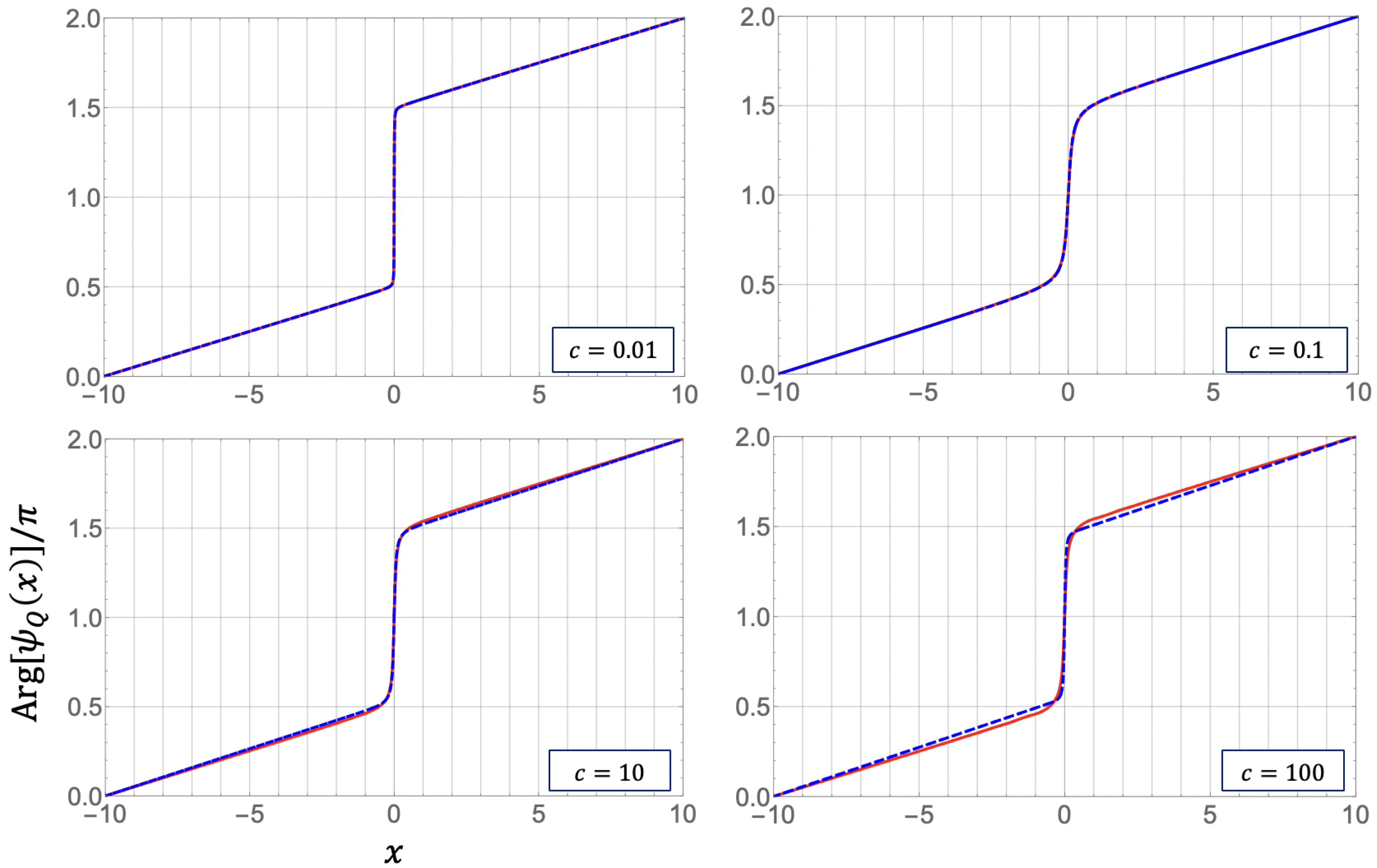
3.1.2. Profiles of the Square Amplitude and the Phase of the Matrix Element of the Field Operator
3.2. Construction of an Elliptic Multiple Dark Soliton for the GP Equation
3.2.1. Local Density and the Phase Field of an Elliptic Multiple Dark-Soliton
3.2.2. Chemical Potential and the Critical Velocity
3.3. Reduction of the Elliptic Multiple Dark-Soliton
3.3.1. Reduction of an Elliptic Multiple Dark Soliton into a Series of Single Dark-Solitons
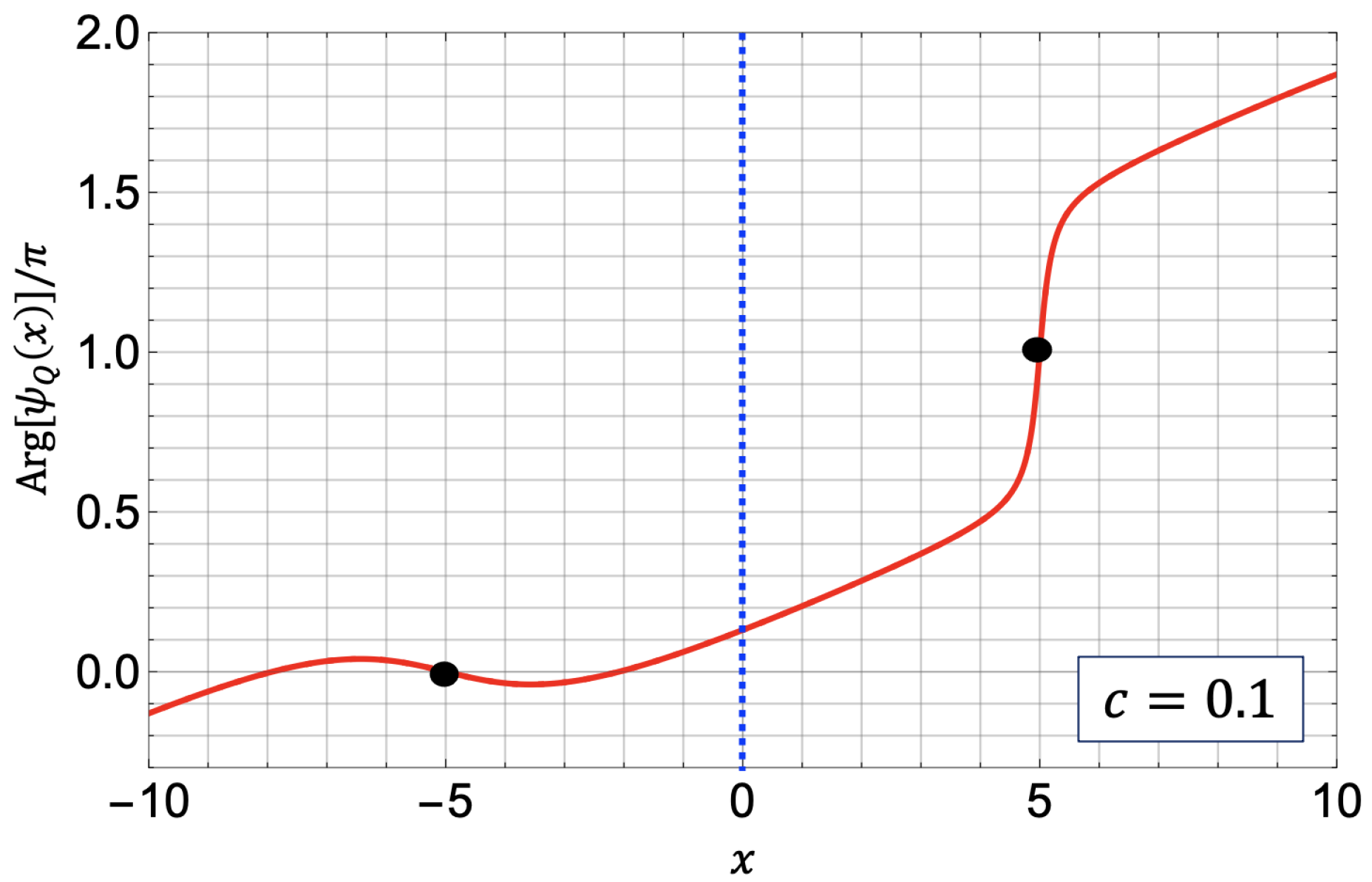
3.3.2. Abrupt Change of the Phase Profile near a Notch
3.3.3. Evaluation of Velocity in an Infinite Limit
3.3.4. Velocity for a Nonzero Winding Number
4. Quantum Double Dark Soliton
4.1. Density Profile in the Free Fermions
4.2. Quantum Double Dark Soliton with Equal Weight
4.2.1. Construction of the Quantum State for a Double Dark Soliton with Equal Weights
4.2.2. Density Profile of the Quantum Double Dark Soliton State
4.2.3. Matrix Elements of the Quantum Double Dark Soliton State
4.3. Quantum State of a Double Dark Soliton with Gaussian Weights
4.3.1. Gaussian Weights in Terms of Target Soliton Depth
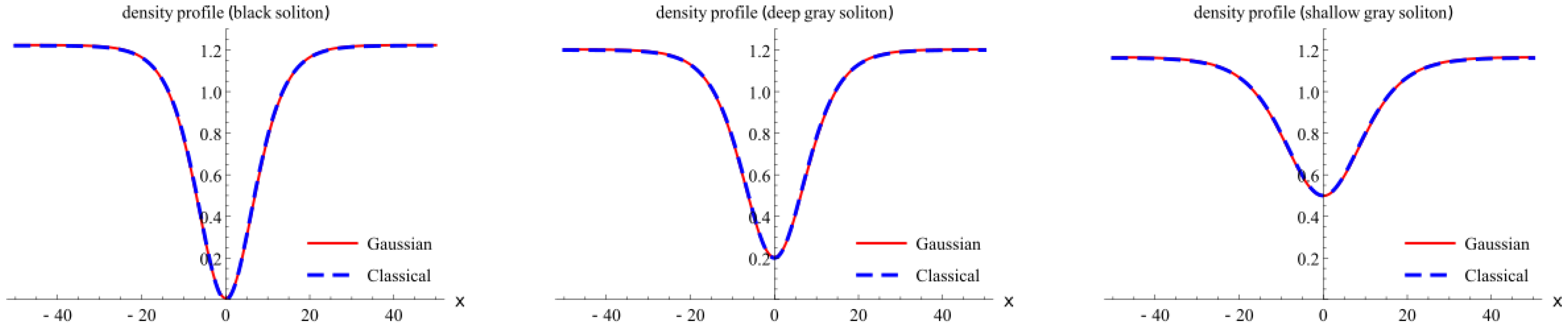
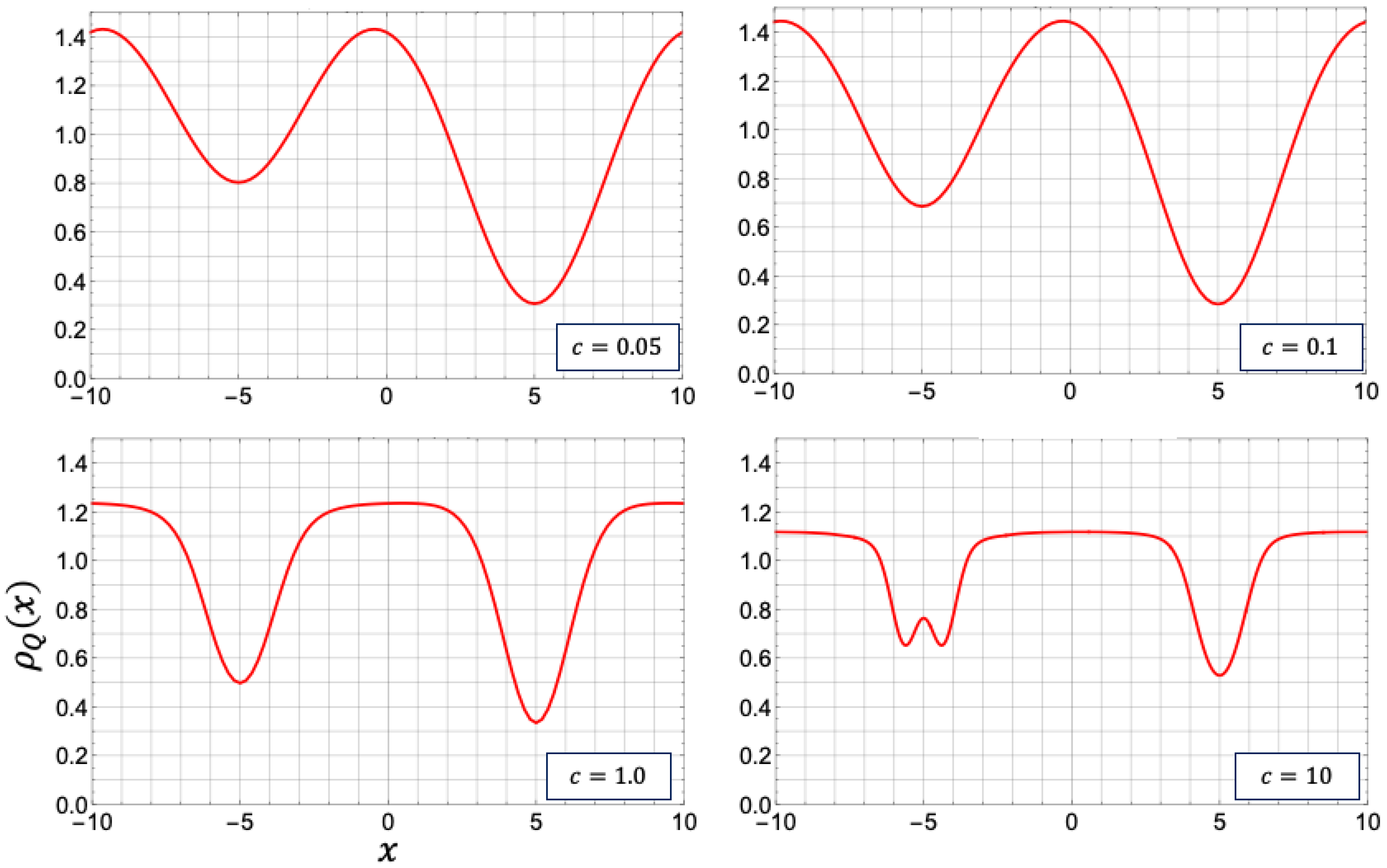
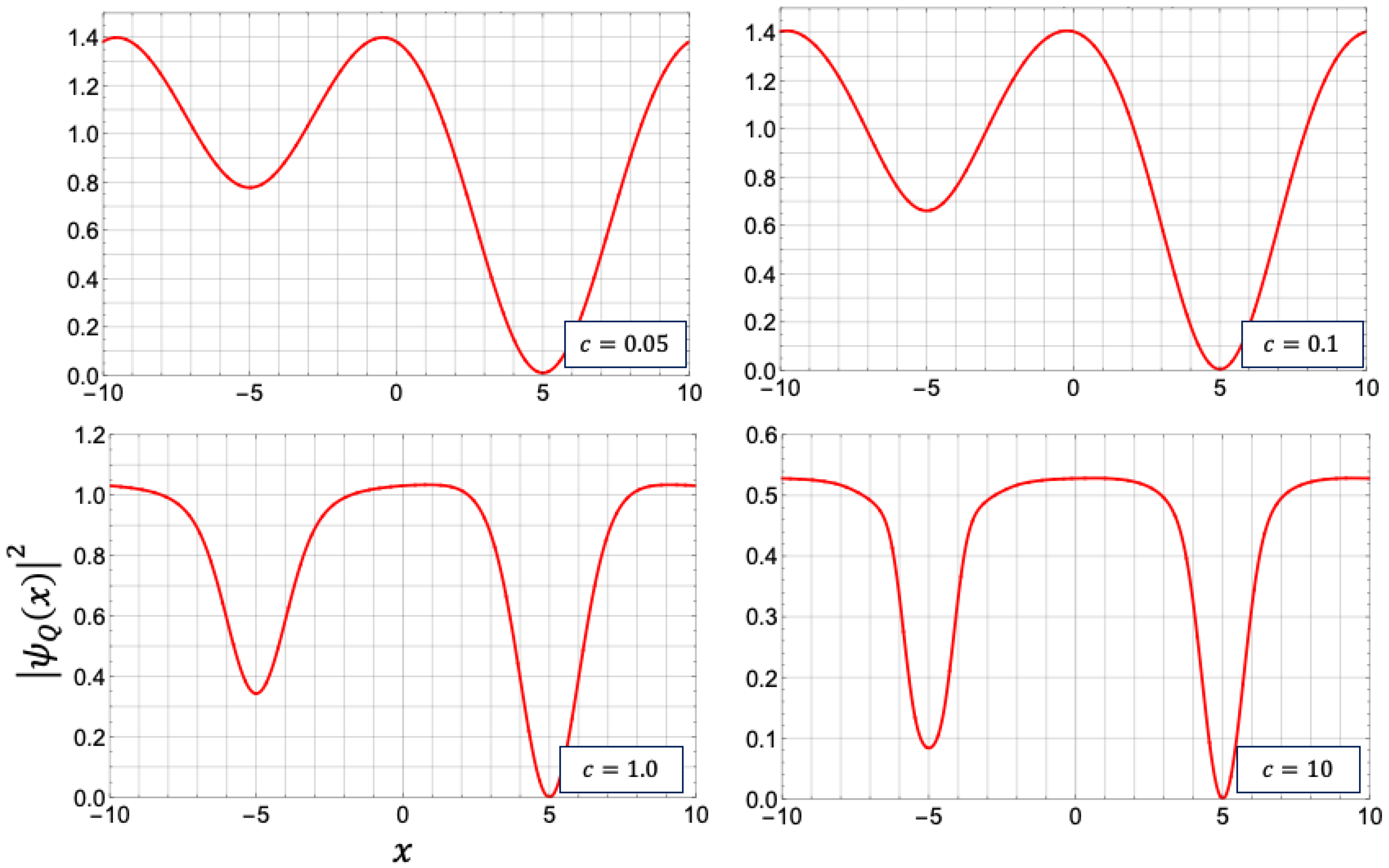
4.3.2. Profiles of Density and Square Amplitude
4.3.3. Difference between Density and Square Amplitude
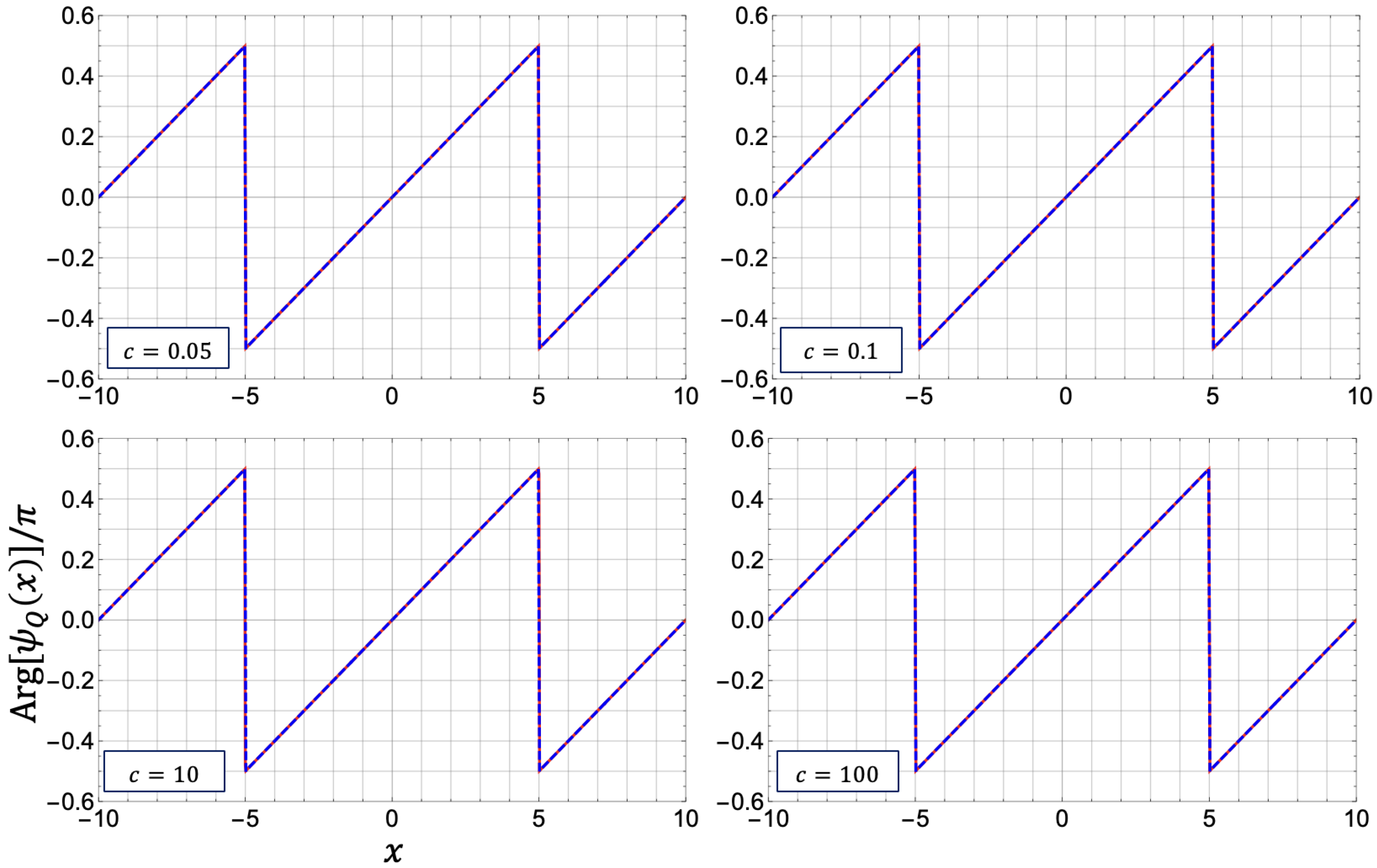
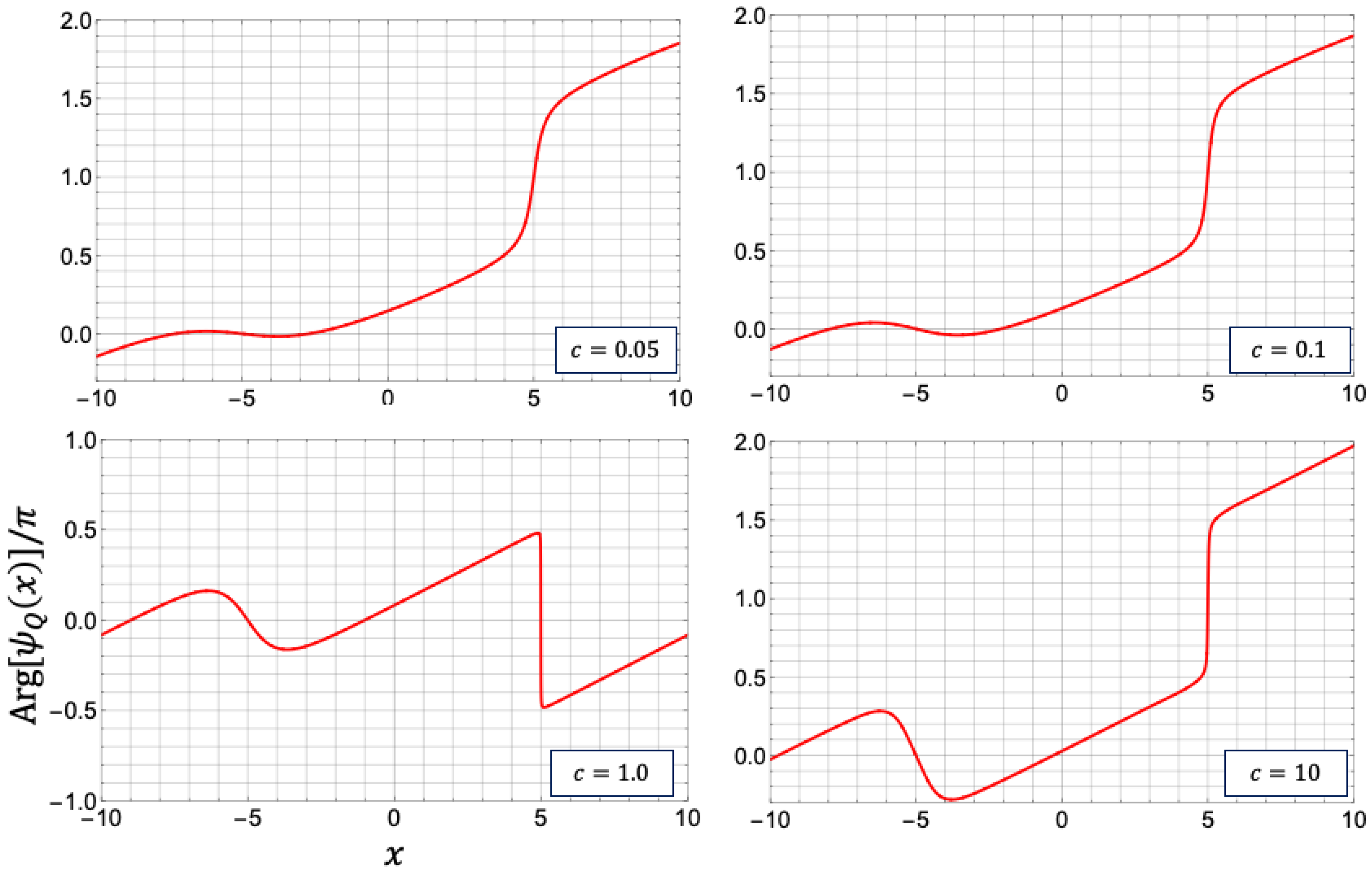
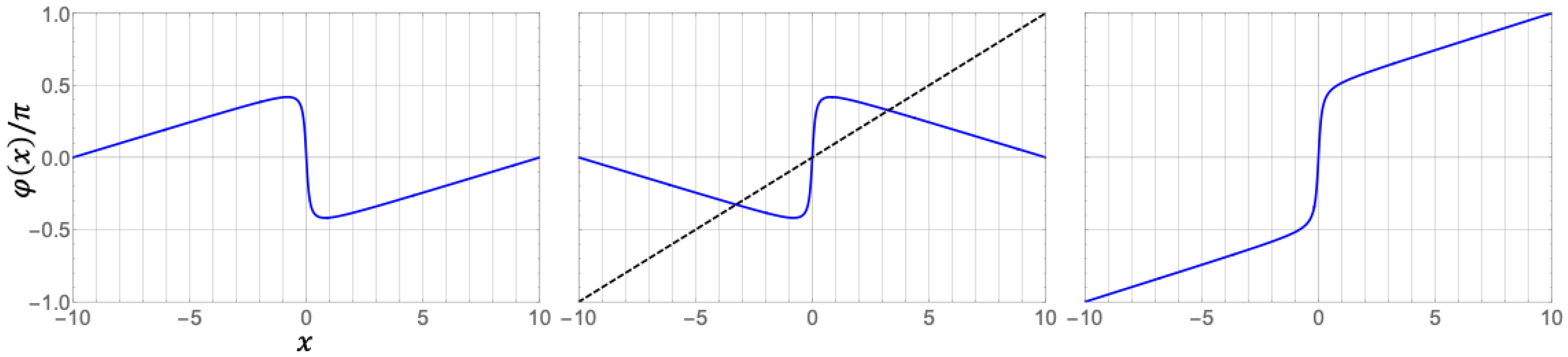
4.3.4. Phase Profile of the Quantum Double Soliton State
5. Conclusions
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pitaevskii, L.; Stringari, S. Bose–Einstein Condensation; International Series of Monographs on Physics; Clarendon Press: Oxford, UK, 2003. [Google Scholar]
- Faddeev, L.D.; Takhtajan, L.A. Hamiltonian Methods in the Theory of Solitons; Classics in Mathematics; Springer: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Tsuzuki, T. Nonlinear waves in the Pitaevskii-Gross equation. J. Low Temp. Phys. 1971, 4, 441–457. [Google Scholar] [CrossRef]
- Abdullaev, F.; Darmanyan, S.; Khabidullaev, P. Optical Solitons; Springer Series in Nonlinear Dynamics; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Burger, S.; Bongs, K.; Dettmer, S.; Ertmer, W.; Sengstock, K.; Sanpera, A.; Shlyapnikov, G.V.; Lewenstein, M. Dark Solitons in Bose–Einstein Condensates. Phys. Rev. Lett. 1999, 83, 5198–5201. [Google Scholar] [CrossRef]
- Weller, A.; Ronzheimer, J.P.; Gross, C.; Esteve, J.; Oberthaler, M.K.; Frantzeskakis, D.J.; Theocharis, G.; Kevrekidis, P.G. Experimental Observation of Oscillating and Interacting Matter Wave Dark Solitons. Phys. Rev. Lett. 2008, 101, 130401. [Google Scholar] [CrossRef] [PubMed]
- Becker, C.; Stellmer, S.; Soltan-Panahi, P.; Dörscher, S.; Baumert, M.; Richter, E.M.; Kronjäger, J.; Bongs, K.; Sengstock, K. Oscillations and interactions of dark and dark–bright solitons in Bose–Einstein condensates. Nat. Phys. 2008, 4, 496–501. [Google Scholar] [CrossRef]
- Wadachi, M.; Sakagami, M.A. Classical Soliton as a Limit of the Quantum Field Theory. J. Phys. Soc. Jpn. 1984, 53, 1933–1938. [Google Scholar] [CrossRef]
- Ishikawa, M.; Takayama, H. Solitons in a One-Dimensional Bose System with the Repulsive Delta-Function Interaction. J. Phys. Soc. Jpn. 1980, 49, 1242–1246. [Google Scholar] [CrossRef]
- Sato, J.; Kanamoto, R.; Kaminishi, E.; Deguchi, T. Exact Relaxation Dynamics of a Localized Many-Body State in the 1D Bose Gas. Phys. Rev. Lett. 2012, 108, 110401. [Google Scholar] [CrossRef]
- Sato, J.; Kanamoto, R.; Kaminishi, E.; Deguchi, T. Quantum states of dark solitons in the 1D Bose gas. New J. Phys. 2016, 18, 075008. [Google Scholar] [CrossRef]
- Syrwid, A.; Sacha, K. Lieb–Liniger model: Emergence of dark solitons in the course of measurements of particle positions. Phys. Rev. A 2015, 92, 032110. [Google Scholar] [CrossRef]
- Katsimiga, G.C.; Mistakidis, S.I.; Koutentakis, G.M.; Kevrekidis, P.G.; Schmelcher, P. Many-body dissipative flow of a confined scalar Bose–Einstein condensate driven by a Gaussian impurity. Phys. Rev. A 2018, 98, 013632. [Google Scholar] [CrossRef]
- Shamailov, S.S.; Brand, J. Quantum dark solitons in the one-dimensional Bose gas. Phys. Rev. A 2019, 99, 043632. [Google Scholar] [CrossRef]
- Kaminishi, E.; Mori, T.; Miyashita, S. Construction of quantum dark soliton in one-dimensional Bose gas. J. Phys. At. Mol. Opt. Phys. 2020, 53, 095302. [Google Scholar] [CrossRef]
- Golletz, W.; Górecki, W.; Ołdziejewski, R.; Pawłowski, K. Dark solitons revealed in Lieb–Liniger eigenstates. Phys. Rev. Res. 2020, 2, 033368. [Google Scholar] [CrossRef]
- Sotiriadis, S. Equilibration in one-dimensional quantum hydrodynamic systems. J. Phys. Math. Theor. 2017, 50, 424004. [Google Scholar] [CrossRef]
- Katsimiga, G.; Mistakidis, S.; Bersano, T.; Ome, M.; Mossman, S.; Mukherjee, K.; Schmelcher, P.; Engels, P.; Kevrekidis, P. Observation and analysis of multiple dark-antidark solitons in two-component Bose–Einstein condensates. Phys. Rev. A 2020, 102, 023301. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Shabat, A.B. Interaction between solitons in a stable medium. Sov. Phys. JETP 1973, 37, 823–828. [Google Scholar]
- Belokolos, E.; Bobenko, A.; Enol’skii, V.; Its, A.; Matveev, V. Algebro-Geometric Approach to Nonlinear Integrable Equations; Springer Series in Nonlinear Dynamics; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Morera Navarro, I.; Guilleumas, M.; Mayol, R.; Mateo, A.M.N. Bound states of dark solitons and vortices in trapped multidimensional Bose–Einstein condensates. Phys. Rev. A 2018, 98, 043612. [Google Scholar] [CrossRef]
- Liang, Z.; Zhang, Z.; Liu, W. Dynamics of a bright soliton in Bose–Einstein condensates with time-dependent atomic scattering length in an expulsive parabolic potential. Phys. Rev. Lett. 2005, 94, 050402. [Google Scholar] [CrossRef]
- Wang, D.S.; Hu, X.H.; Hu, J.; Liu, W. Quantized quasi-two-dimensional Bose–Einstein condensates with spatially modulated nonlinearity. Phys. Rev. A 2010, 81, 025604. [Google Scholar] [CrossRef]
- Wen, L.; Li, L.; Li, Z.D.; Song, S.W.; Zhang, X.F.; Liu, W. Matter rogue wave in Bose–Einstein condensates with attractive atomic interaction. Eur. Phys. J. D 2011, 64, 473–478. [Google Scholar] [CrossRef]
- Li, L.; Li, Z.; Malomed, B.A.; Mihalache, D.; Liu, W. Exact soliton solutions and nonlinear modulation instability in spinor Bose–Einstein condensates. Phys. Rev. A 2005, 72, 033611. [Google Scholar] [CrossRef]
- Lieb, E.H.; Liniger, W. Exact analysis of an interacting Bose gas. I. The general solution and the ground state. Phys. Rev. 1963, 130, 1605. [Google Scholar] [CrossRef]
- Bethe, H. Eigenvalues and eigenfunctions of the linear atom chain. Z. Phys. 1931, 71, 205–226. [Google Scholar] [CrossRef]
- Lieb, E.H. Exact Analysis of an Interacting Bose Gas. II. The Excitation Spectrum. Phys. Rev. 1963, 130, 1616. [Google Scholar] [CrossRef]
- Korepin, V.E.; Bogoliubov, N.M.; Izergin, A.G. Quantum Inverse Scattering Method and Correlation Functions; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Gaudin, M. La Fonction d’Onde de Bethe; Masson: Paris, France, 1983. [Google Scholar]
- Korepin, V.E. Calculation of norms of Bethe wave functions. Commun. Math. Phys. 1982, 86, 391–418. [Google Scholar] [CrossRef]
- Slavnov, N.A. Calculation of scalar products of wave functions and form factors in the framework of the algebraic Bethe ansatz. Teor. Mat. Fiz. 1989, 79, 232–240. [Google Scholar] [CrossRef]
- Slavnov, N.A. Nonequal-time current correlation function in a one-dimensional Bose gas. Theor. Math. Phys. 1990, 82, 273–282. [Google Scholar] [CrossRef]
- Calabrese, P.; Caux, J.S. Dynamics of the attractive 1D Bose gas: Analytical treatment from integrability. J. Stat. Mech. Theory Exp. 2007, 2007, P08032. [Google Scholar] [CrossRef][Green Version]
- Kojima, T.; Korepin, V.E.; Slavnov, N. Determinant representation for dynamical correlation functions of the quantum nonlinear Schrödinger equation. Commun. Math. Phys. 1997, 188, 657–689. [Google Scholar] [CrossRef]
- Sato, J.; Kaminishi, E.; Deguchi, T. Finite-size scaling behavior of Bose–Einstein condensation in the 1D Bose gas. arXiv 2013, arXiv:1303.2775. [Google Scholar]
- Lopes, R.; Eigen, C.; Navon, N.; Clément, D.; Smith, R.P.; Hadzibabic, Z. Quantum depletion of a homogeneous Bose–Einstein condensate. Phys. Rev. Lett. 2017, 119, 190404. [Google Scholar] [CrossRef] [PubMed]
- Kanamoto, R.; Carr, L.D.; Ueda, M. Metastable quantum phase transitions in a periodic one-dimensional Bose gas: Mean-field and Bogoliubov analyses. Phys. Rev. A 2009, 79, 063616. [Google Scholar] [CrossRef]
- Copson, E. An Introduction to the Theory of Functions of a Complex Variable; Springer Series in Nonlinear Dynamics; Oxford University Press: Oxford, UK, 1978. [Google Scholar]
- Girardeau, M. Relationship between Systems of Impenetrable Bosons and Fermions in One Dimension. J. Math. Phys. 1960, 1, 516. [Google Scholar] [CrossRef]
- Syrwid, A.; Brewczyk, M.; Gajda, M.; Sacha, K. Single-shot simulations of dynamics of quantum dark solitons. Phys. Rev. A 2016, 94, 023623. [Google Scholar] [CrossRef]
- Katsimiga, G.; Mistakidis, S.; Koutentakis, G.; Kevrekidis, P.; Schmelcher, P. Many-body quantum dynamics in the decay of bent dark solitons of Bose–Einstein condensates. New J. Phys. 2017, 19, 123012. [Google Scholar] [CrossRef]







| c | n | d | k | |||
|---|---|---|---|---|---|---|
| 0.01 | 0.830 840 | 9.670 81 | 0.680 75 | 1.446 70 | 1.753 96 | 0.982 297 |
| 0.1 | 0.903 971 | 0.00172 103 | 0.993 356 | 1.272 54 | 0.853 159 | 0.575 645 |
| 1.0 | 0.788 041 | 0.00192 928 | 1− 5.693 69 | 1.111 45 | 0.899 118 | 0.147 633 |
| 10 | 0.461 185 | 0.00419 681 | 1− 7.864 09 | 1.05 184 | 0.949 564 | −0.0188 539 |
| 100 | 0.300 536 | 0.00640 668 | 1− 2.2907 21 | 1.022 293 | 0.977 873 | −0.117 299 |
| c | d | k | |||
|---|---|---|---|---|---|
| 0.01 | 0.170 659 | 0.680 343 | 1.690 17 | 1.444 67 | 0.978 349 |
| 0.1 | 0.155 884 | 0.991 939 | 1.40 035 | 0.667 869 | 0.317 074 |
| 10 | 0.0406 314 | 1− 3.64 668 | 1.04 120 | 0.959 205 | −0.151 773 |
| 100 | 0.0475 028 | 1− 4.973 27 | 1.013 54 | 0.986 482 | −0.202 798 |
| c | k | |||
|---|---|---|---|---|
| 0.05 | 0.681 750 | 1.112 62 | 1.657 91 | 0.986 753 |
| 0.1 | 0.840 623 | 1.115 19 | 1.325 36 | 0.959 493 |
| 10 | 1 − 4.489 79 | 1.006 60 | 0.998 333 | 0.814 300 |
| 100 | 1 − 1.484 64 | 1.001 34 | 0.999 156 | 0.841 665 |
| c | k | n | |||
|---|---|---|---|---|---|
| 0.05 | 0.681 520 | 0.666918 | 1.44 586 | 1.75 158 | 0.982 197 |
| 0.1 | 0.838 694 | 0.699671 | 1.402 14 | 1.267 41 | 0.937 102 |
| 10 | 1 − 4.444 99 | 0.411534 | 1.091 57 | 0.916 966 | 0.168 885 |
| 100 | 1 − 9.964 63 | 0.267601 | 1.037 57 | 0.963 609 | 0.0630 238 |
| c | ||||||
|---|---|---|---|---|---|---|
| 0.05 | 1.41865 | 1.38161 | 0.0370444 | 0.306279 | 0.296473 | |
| 0.1 | 1.44277 | 1.40292 | 0.0398479 | 0.283943 | 0.279478 | |
| 1.0 | 1.23462 | 1.03089 | 0.203732 | 0.334114 | 0.334109 | |
| 10 | 1.11822 | 0.528072 | 0.59015 | 0.528875 | 0.528678 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kinjo, K.; Kaminishi, E.; Mori, T.; Sato, J.; Kanamoto, R.; Deguchi, T. Quantum Dark Solitons in the 1D Bose Gas: From Single to Double Dark-Solitons. Universe 2022, 8, 2. https://doi.org/10.3390/universe8010002
Kinjo K, Kaminishi E, Mori T, Sato J, Kanamoto R, Deguchi T. Quantum Dark Solitons in the 1D Bose Gas: From Single to Double Dark-Solitons. Universe. 2022; 8(1):2. https://doi.org/10.3390/universe8010002
Chicago/Turabian StyleKinjo, Kayo, Eriko Kaminishi, Takashi Mori, Jun Sato, Rina Kanamoto, and Tetsuo Deguchi. 2022. "Quantum Dark Solitons in the 1D Bose Gas: From Single to Double Dark-Solitons" Universe 8, no. 1: 2. https://doi.org/10.3390/universe8010002
APA StyleKinjo, K., Kaminishi, E., Mori, T., Sato, J., Kanamoto, R., & Deguchi, T. (2022). Quantum Dark Solitons in the 1D Bose Gas: From Single to Double Dark-Solitons. Universe, 8(1), 2. https://doi.org/10.3390/universe8010002






