Constraining the Swiss-Cheese IR-Fixed Point Cosmology with Cosmic Expansion
Abstract
1. Introduction
2. Swiss-Cheese Model and IR-Fixed Point Cosmology
2.1. Asymptotic Safety in UV and IR
2.2. AS Swiss-Cheese
2.3. Cosmic Acceleration and Coincidence Problem
3. Methodology and Numerical Results
3.1. b Constraint from and Combination
3.2. Observational Hubble Data
3.3. Matching at the Galaxy 0 Scale
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Omega and Lambda from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Knop, R.A.; Aldering, G.; Amanullah, R.; Astier, P.; Blanc, G.; Burns, M.S.; Conley, A.; Deustua, S.E.; Doi, M.; Ellis, R.; et al. Supernova Cosmology Project Collaboration. New constraints on Omega(M), Omega(lambda), and w from an independent set of eleven high-redshift supernovae observed with HST. Astrophys. J. 2003, 598, 102. [Google Scholar] [CrossRef]
- Spergel, D.N.; Bean, R.; Doré, O.; Nolta, M.R.; Bennett, C.L.; Dunkley, J.; Hinshaw, G.; Jarosik, N.; Komatsu, E.; WMAP Collaboration. Wilkinson Microwave Anisotropy Probe (WMAP) three year results: Implications for cosmology. Astrophys. J. Suppl. 2007, 170, 377. [Google Scholar] [CrossRef]
- Li, M.; Li, X.D.; Wang, S.; Wang, Y. Dark Energy. Commun. Theor. Phys. 2011, 56, 525. [Google Scholar] [CrossRef]
- Kofinas, G.; Zarikas, V. A solution of the coincidence problem based on the recent galactic core black hole energy density increase. Eur. Phys. J. C 2013, 73, 2379. [Google Scholar] [CrossRef][Green Version]
- Kofinas, G.; Zarikas, V. Solution of the dark energy and its coincidence problem based on local antigravity sources without fine-tuning or new scales. Phys. Rev. D 2018, 97, 123542. [Google Scholar] [CrossRef]
- Ellis, G.F.R.; Stoeger, W. The ’fitting problem’ in cosmology. Class. Quantum Gravity 1987, 4, 1697. [Google Scholar] [CrossRef]
- Green, S.R.; Wald, R.M. A new framework for analyzing the effects of small scale inhomogeneities in cosmology. Phys. Rev. D 2011, 83, 084020. [Google Scholar] [CrossRef]
- Buchert, T.; France, M.J.; Steiner, F. Model-independent analyses of non-Gaussianity in Planck CMB maps using Minkowski functionals. Class. Quantum Gravity 2017, 34, 094002. [Google Scholar] [CrossRef]
- Buchert, T.; Coley, A.A.; Kleinert, H.; Roukema, B.F.; Wiltshire, D.L. Observational Challenges for the Standard FLRW Model. Int. J. Mod. Phys. D 2016, 25, 1630007. [Google Scholar] [CrossRef]
- Koksbang, S.M. Light propagation in Swiss-cheese models of random close-packed Szekeres structures: Effects of anisotropy and comparisons with perturbative results. Phys. Rev. D 2017, 95, 063532. [Google Scholar] [CrossRef]
- Rasanen, S. Structure formation as an alternative to dark energy and modified gravity. EAS Publ. Ser. 2009, 36, 63. [Google Scholar] [CrossRef][Green Version]
- Niedermaier, M.; Reuter, M. The Asymptotic Safety Scenario in Quantum Gravity. Living Rev. Relativ. 2006, 9, 5. [Google Scholar] [CrossRef]
- Reuter, M.; Saueressig, F. Quantum Einstein Gravity. New J. Phys. 2012, 14, 055022. [Google Scholar] [CrossRef]
- Falls, K.; Litim, D.F.; Nikolakopoulos, K.; Rahmede, C. Further evidence for asymptotic safety of quantum gravity. Phys. Rev. D 2016, 93, 104022. [Google Scholar] [CrossRef]
- Jimenez, R.; Loeb, A. Constraining cosmological parameters based on relative galaxy ages. Astrophys. J. 2002, 573, 37. [Google Scholar] [CrossRef]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Suzuki, N.; Rubin, D.; Lidman, C.; Aldering, G.; Amanullah, R.; Barbary, K.; Barrientos, L.F.; Botyanszki, J.; Brodwin, M.; Connolly, N.; et al. The Hubble Space Telescope Cluster Supernova Survey: V. Improving the Dark Energy Constraints Above z > 1 and Building an Early-Type-Hosted Supernova Sample. Astrophys. J. 2012, 746, 85. [Google Scholar] [CrossRef]
- Amati, L.; Frontera, F.; Tavani, M.; Antonelli, A.; Costa, E.; Feroci, M.; Guidorzi, C.; Heise, J.; Masetti, N.; Montanari, E.; et al. Intrinsic spectra and energetics of BeppoSAX gamma-ray bursts with known redshifts. Astron. Astrophys. 2002, 390, 81. [Google Scholar] [CrossRef]
- Ghirlanda, G.; Ghisellini, G.; Firmani, C. Gamma Ray Bursts as standard candles to constrain the cosmological parameters. New J. Phys. 2006, 8, 123. [Google Scholar] [CrossRef]
- Basilakos, S.; Perivolaropoulos, L. Testing GRBs as Standard Candles. Mon. Not. R. Astron. Soc. 2008, 391, 411. [Google Scholar] [CrossRef]
- Wang, F.Y.; Dai, Z.G.; Liang, E.W. Gamma-ray Burst Cosmology. New Astron. Rev. 2015, 67, 1–17. [Google Scholar] [CrossRef]
- Plionis, M.; Terlevich, R.; Basilakos, S.; Bresolin, F.; Terlevich, E.; Melnick, J.; Chavez, R. A Strategy to Measure the Dark Energy Equation of State using the HII galaxy Hubble Relation & X-ray AGN Clustering: Preliminary Results. Mon. Not. R. Astron. Soc. 2011, 416, 2981. [Google Scholar] [CrossRef]
- Tsiapi, P.; Basilakos, S.; Plionis, M.; Terlevich, R.; Terlevich, E.; Moran, A.L.G.; Chavez, R.; Bresolin, F.; Arenas, D.F.; Telles, E. Cosmological Constraints Using the Newest VLT-KMOS HII Galaxies and the Full Planck CMB Spectrum. Available online: https://ui.adsabs.harvard.edu/abs/2021arXiv210701749T/abstract (accessed on 24 July 2021).
- Blake, C.; Kazin, E.A.; Beutler, F.; Davis, T.M.; Parkinson, D.; Brough, S.; Colless, M.; Contreras, C.; Couch, W.; Croom, S.; et al. The WiggleZ Dark Energy Survey: Mapping the distance-redshift relation with baryon acoustic oscillations. Mon. Not. R. Astron. Soc. 2011, 418, 1707. [Google Scholar] [CrossRef]
- de Mattia, A.; Ruhlmann-Kleider, V.; Raichoor, A.; Ross, A.J.; Tamone, A.; Zhao, C.; Alam, S.; Avila, S.; Burtin, E.; Bautista, J.; et al. The Completed SDSS-IV extended Baryon Oscillation Spectroscopic Survey: Measurement of the BAO and growth rate of structure of the emission line galaxy sample from the anisotropic power spectrum between redshift 0.6 and 1.1. Mon. Not. R. Astron. Soc. 2021, 501, 5616–5645. [Google Scholar] [CrossRef]
- Ade, P.A.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar] [CrossRef]
- Basilakos, S.; Nesseris, S. Conjoined constraints on modified gravity from the expansion history and cosmic growth. Phys. Rev. D 2017, 96, 063517. [Google Scholar] [CrossRef]
- Anagnostopoulos, F.K.; Basilakos, S.; Kofinas, G.; Zarikas, V. Constraining the Asymptotically Safe Cosmology: Cosmic acceleration without dark energy. J. Cosmol. Astropart. Phys. 2019, 1902, 053. [Google Scholar] [CrossRef]
- Anagnostopoulos, F.K.; Kofinas, G.; Zarikas, V. IR quantum gravity solves naturally cosmic acceleration and its coincidence problem. Int. J. Mod. Phys. D 2019, 28, 14. [Google Scholar] [CrossRef]
- Weinberg, S. Ultraviolet divergences in quantum theories of gravitation. In General Relativity: An Einstein Centenary Survey; Hawking, S.W., Israel, W., Eds.; Cambridge University Press: Cambridge, UK, 1979; pp. 790–831. [Google Scholar]
- Reuter, M. Nonperturbative evolution equation for quantum gravity. Phys. Rev. 1998, D57, 971–985. [Google Scholar] [CrossRef]
- Bonanno, A.; Eichhorn, A.; Gies, H.; Pawlowski, J.M.; Percacci, R.; Reuter, M.; Saueressig, F.; Vacca, G.P. Critical reflections on asymptotically safe gravity. Front. Phys. 2020, 8, 269. [Google Scholar] [CrossRef]
- Polyakov, A.M. A Few projects in string theory. arXiv 1993, arXiv:hep-th/9304146. [Google Scholar]
- Bonanno, A.; Kofinas, G.; Zarikas, V. Effective field equations and scale-dependent couplings in gravity. Phys. Rev. D 2021, 103, 104025. [Google Scholar] [CrossRef]
- Reuter, M.; Weyer, H. The Role of Background Independence for Asymptotic Safety in Quantum Einstein Gravity. Gen. Relativ. Gravit. 2009, 41, 983. [Google Scholar] [CrossRef][Green Version]
- Reuter, M.; Weyer, H. Quantum gravity at astrophysical distances? J. Cosmol. Astropart. Phys. 2004, 0412. [Google Scholar] [CrossRef]
- Reuter, M.; Weyer, H. Running Newton constant, improved gravitational actions, and galaxy rotation curves. Phys. Rev. D 2004, 70, 124028. [Google Scholar] [CrossRef]
- Bonanno, A.; Fröhlich, H.E. A new helioseismic constraint on a cosmic-time variation of G. Astrophys. J. Lett. 2020, 893, L35. [Google Scholar] [CrossRef]
- Bonanno, A.; Carloni, S. Dynamical System Analysis of Cosmologies with Running Cosmological Constant from Quantum Einstein Gravity. New J. Phys. 2012, 14, 025008. [Google Scholar] [CrossRef]
- Einstein, A.; Strauss, E.G. A generalization of the relativistic theory of gravitation. Ann. Math. 1946, 47, 731. [Google Scholar] [CrossRef]
- Israel, W. Singular hypersurfaces and thin shells in general relativity. Nuovo Cim. B 1966, 44, 1–14. [Google Scholar] [CrossRef]
- Darmois, G. Mémorial des Sciences Mathématiques, Fascicule XXV (Gauthier-Villars, Paris, 1927), Chap. V. Available online: http://www.numdam.org/item/MSM_1927__25__1_0/ (accessed on 23 July 2021).
- Baker, G.A. Bound Systems in an Expanding Universe. Available online: https://arxiv.org/pdf/astro-ph/0003152.pdf (accessed on 24 July 2021).
- Wilson, K.G.; Kogut, J.B. The Renormalization group and the epsilon expansion. Phys. Rep. 1974, 12, 75–199. [Google Scholar] [CrossRef]
- Bonanno, A.; Reuter, M. Cosmology with selfadjusting vacuum energy density from a renormalization group fixed point. Phys. Lett. B 2002, 527, 9–17. [Google Scholar] [CrossRef]
- Bonanno, A.; Reuter, M. Renormalization group improved black hole space-times. Phys. Rev. D 2000, 62, 043008. [Google Scholar] [CrossRef]
- Bonanno, A.; Casadio, R.; Platania, A. Gravitational antiscreening in stellar interiors. J. Cosmol. Astropart. Phys. 2020, 1, 22. [Google Scholar] [CrossRef]
- Bonanno, A.; Reuter, M. Entropy signature of the running cosmological constant. J. Cosmol. Astropart. Phys. 2007, 24. [Google Scholar] [CrossRef]
- Kofinas, G.; Zarikas, V. Asymptotically Safe gravity and non-singular inflationary Big Bang with vacuum birth. Phys. Rev. D 2016, 94, 103514. [Google Scholar] [CrossRef]
- Bonanno, A.; Saueressig, F. Asymptotically safe cosmology—A status report. Comptes Rendus Phys. 2017, 18, 254–264. [Google Scholar] [CrossRef]
- Platania, A. From renormalization group flows to cosmology. Front. Phys. 2020, 8, 188. [Google Scholar] [CrossRef]
- Kofinas, G.; Zarikas, V. Avoidance of singularities in asymptotically safe Quantum Einstein Gravity. J. Cosmol. Astropart. Phys. 2015, 1510, 69. [Google Scholar] [CrossRef]
- Bambi, C.; Malafarina, D.; Modesto, L. Non-singular quantum-inspired gravitational collapse. Phys. Rev. D 2013, 88, 044009. [Google Scholar] [CrossRef]
- Malafarina, D. Classical collapse to black holes and quantum bounces: A review. Universe 2017, 3, 48. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. XIII. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
- Jimenez, R.; Verde, L.; Treu, T.; Stern, D. Constraints on the equation of state of dark energy and the Hubble constant from stellar ages and the CMB. Astrophys. J. 2003, 593, 622–629. [Google Scholar] [CrossRef]
- Cao, S.; Zhang, T.J.; Wang, X.; Zhang, T. Cosmological Constraints on the Coupling Model from Observational Hubble Parameter and Baryon Acoustic Oscillation Measurements. Universe 2021, 7, 57. [Google Scholar] [CrossRef]
- Moresco, M.; Pozzetti, L.; Cimatti, A.; Jimenez, R.; Maraston, C.; Verde, L.; Thomas, D.; Citro, A.; Tojeiro, R.; Wilkinson, D. A 6% measurement of the Hubble parameter at z~0.45: Direct evidence of the epoch of cosmic re-acceleration. J. Cosmol. Astropart. Phys. 2016, 2016, 014. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, H.; Yuan, S.; Liu, S.; Zhang, T.J.; Sun, Y.C. Research in Astronomy and Astrophysics, Four new observational H(z) data from luminous red galaxies in the Sloan Digital Sky Survey data release seven. Res. Astron. Astrophys. 2014, 1221. [Google Scholar] [CrossRef]
- Moresco, M.; Verde, L.; Pozzetti, L.; Jimenez, R.; Cimatti, A. New constraints on cosmological parameters and neutrino properties using the expansion rate of the Universe to z~1.75. J. Cosmol. Astropart. Phys. 2012, 7, 53. [Google Scholar] [CrossRef]
- Gaztanaga, E.; Cabré, A.; Hui, L. Clustering of luminous red galaxies—IV. Baryon acoustic peak in the line-of-sight direction and a direct measurement of H(z). Mon. Not. R. Astron. Soc. 2009, 399, 1663–1680. [Google Scholar] [CrossRef]
- Xu, X.; Cuesta, A.J.; Padmanabhan, N.; Eisenstein, D.J.; McBride, C.K. McBride. Measuring DA and H at z = 0.35 from the SDSS DR7 LRGs using baryon acoustic oscillations. Mon. Not. R. Astron. Soc. 2013, 431, 2834–2860. [Google Scholar] [CrossRef]
- Blake, C.; Brough, S.; Colless, M.; Contreras, C.; Couch, W.; Croom, S.; Croton, D.; Davis, T.M.; Drinkwater, M.J.; Forster, K.; et al. The WiggleZ Dark Energy Survey: Joint measurements of the expansion and growth history at z < 1. Mon. Not. R. Astron. Soc. 2012, 425, 405–414. [Google Scholar] [CrossRef]
- Ratsimbazafy, A.L.; Loubser, S.I.; Crawford, S.M.; Cress, C.M.; Bassett, B.A.; Nichol, R.C.; Väisänen, P. Age-dating luminous red galaxies observed with the Southern African Large Telescope. Mon. Not. R. Astron. Soc. 2017, 467, 3239–3254. [Google Scholar] [CrossRef]
- Stern, D.; Jimenez, R.; Verde, L.; Kamionkowski, M.; Stanford, S.A. Cosmic chronometers: Constraining the equation of state of dark energy. I: H (z) measurements. J. Cosmol. Astropart. Phys. 2010, 2, 8. [Google Scholar] [CrossRef]
- Samushia, L.; Reid, B.A.; White, M.; Percival, W.J.; Cuesta, A.J.; Lombriser, L.; Manera, M.; Nichol, R.C.; Schneider, D.P.; Bizyaev, D.; et al. The clustering of galaxies in the SDSS-III DR9 Baryon Oscillation Spectroscopic Survey: Testing deviations from and general relativity using anisotropic clustering of galaxies. Mon. Not. R. Astron. Soc. 2013, 429, 1514–1528. [Google Scholar] [CrossRef]
- Moresco, M. Raising the bar: New constraints on the Hubble parameter with cosmic chronometers at z~2. Mon. Not. R. Astron. Soc. Lett. 2015, 450, L16–L20. [Google Scholar] [CrossRef]
- Delubac, T.; Bautista, J.E.; Busca, N.G.; Rich, J.; Kirkby, D.; Bailey, S.; Font-Ribera, A.; Slosar, A.; Lee, K.G.; Pieri, M.M.; et al. Baryon acoustic oscillations in the Lya forest of BOSS DR11 quasars. Astron. Astrophys. 2015, 574, A59. [Google Scholar] [CrossRef]
- Font-Ribera, A.; Kirkby, D.; Miralda-Escudé, J.; Ross, N.P.; Slosar, A.; Rich, J.; Aubourg, É.; Bailey, S.; Bhardwaj, V.; Bautista, J.; et al. Quasar-Lyman a forest cross-correlation from BOSS DR11: Baryon Acoustic Oscillations. JCAP 2014, 5, 27. [Google Scholar] [CrossRef]
- Linder, E.V.; Mitra, A. Photometric supernovae redshift systematics requirements. Phys. Rev. D 2019, 100, 043542. [Google Scholar] [CrossRef]
- Mitra, A.; Linder, E.V. Cosmology requirements on supernova photometric redshift systematics for the Rubin LSST and Roman Space Telescop. Phys. Rev. D 2021, 103, 023524. [Google Scholar] [CrossRef]
- Lau, A.W.K.; Mitra, A.; Shafiee, M.; Smoot, G. Constraining HeII reionization detection uncertainties via fast radio bursts. New Astron. 2021, 89, 101627. [Google Scholar] [CrossRef]
- Mitra, A.; Mifsud, J.; Mota, D.F.; Parkinson, D. Cosmology with the Einstein telescope: No Slip Gravity model and redshift specifications. Mon. Not. R. Astron. Soc. Lett. 2021, 502, 5563–5575. [Google Scholar] [CrossRef]
- Apostolopoulos, P.S. Szekeres models: A covariant approach. Class. Quantum Gravity 2017, 34, 095013. [Google Scholar] [CrossRef]
- Barrow, J.D.; Basilakos, S.; Saridakis, E.N. Big Bang Nucleosynthesis constraints on Barrow entropy. Phys. Lett. B. 2021, 815, 136134. [Google Scholar] [CrossRef]
- Aliferis, G.; Zarikas, V. Electroweak baryogenesis by primordial black holes in Brans-Dicke modified gravity. Phys. Rev. D. 2021, 103, 023509. [Google Scholar] [CrossRef]
- Eroshenko, Y. Mergers of primordial black holes in extreme clusters and the H0 tension. Phys. Dark Universe 2021, 32, 100833. [Google Scholar] [CrossRef]

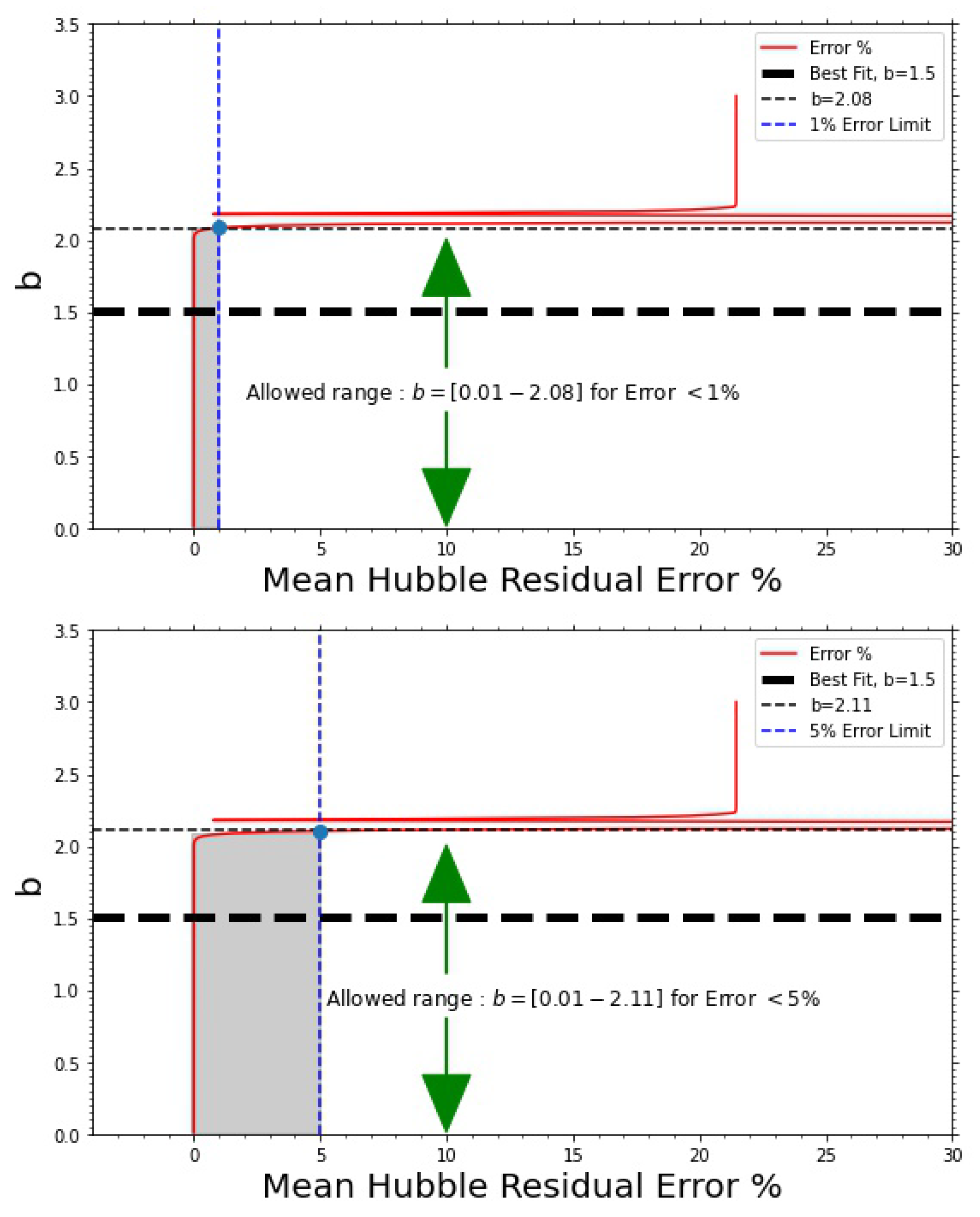
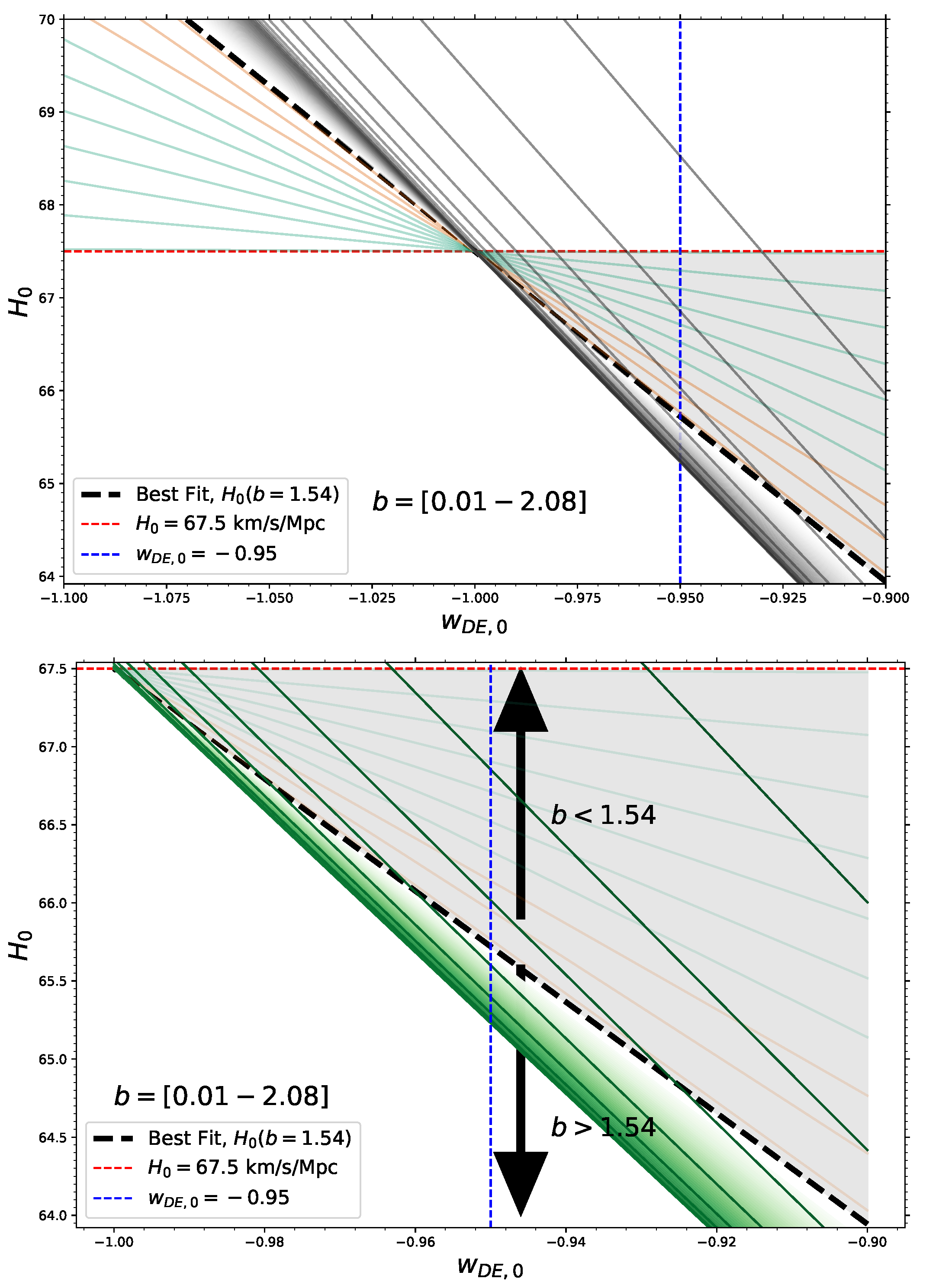

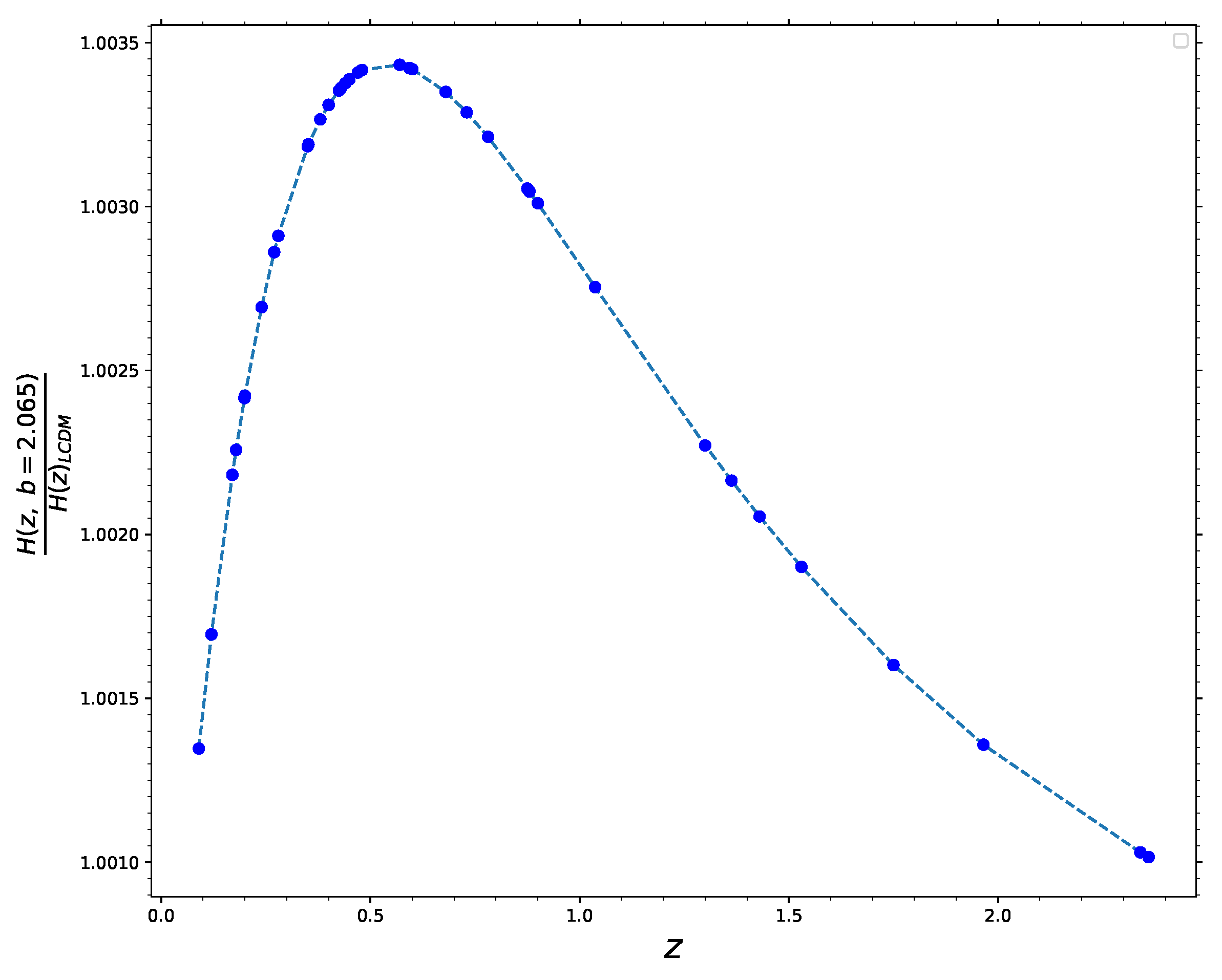
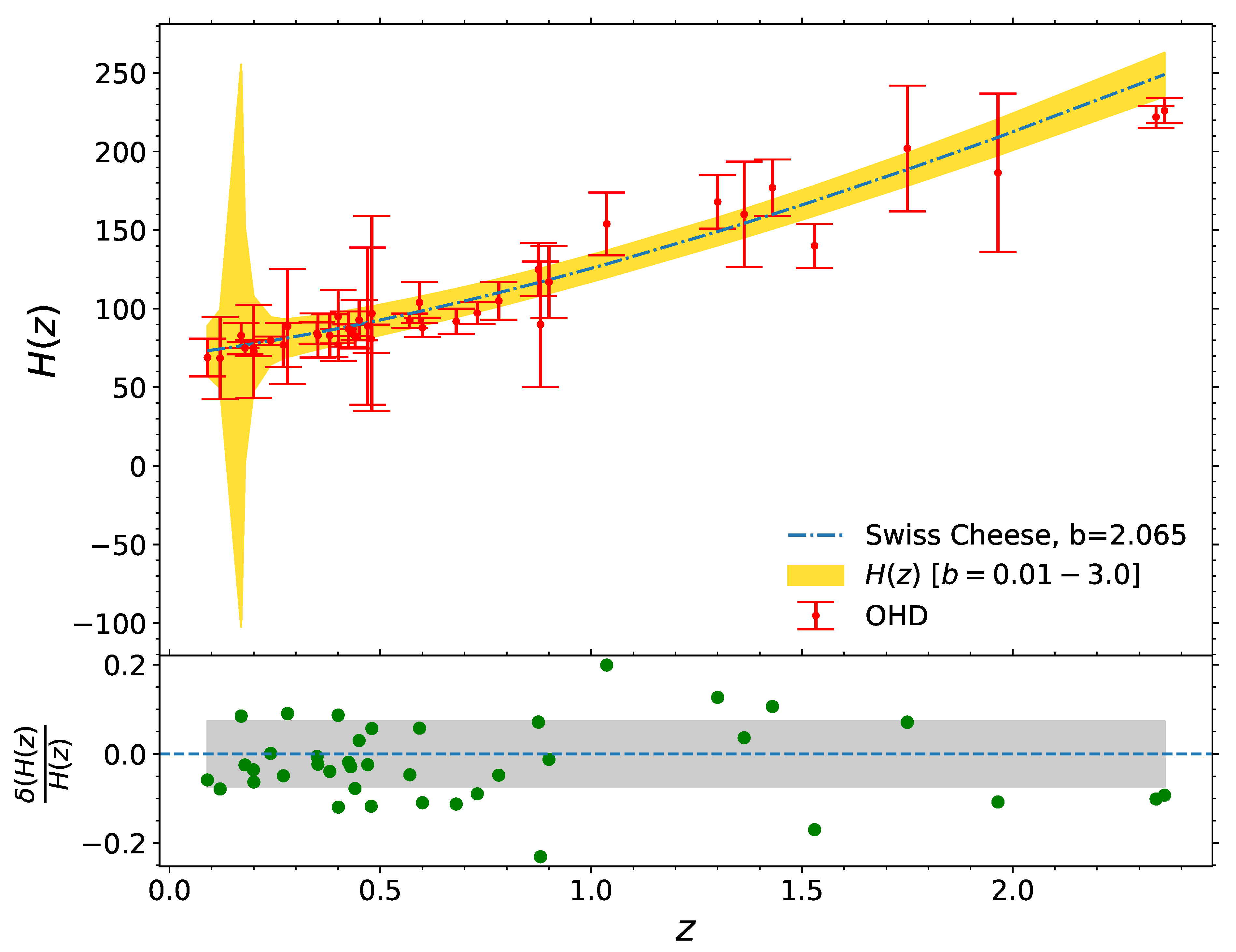
| Error % | b (from H(z)) | b (from H0 + wDE,0) |
|---|---|---|
| 1 | 2.08 | 2.07 |
| 5 | 2.11 | 2.08 |
| Error % | b (from H(z)) | b (from H0 + wDE,0) |
|---|---|---|
| 1 | 2.13 | 2.11 |
| 5 | 2.16 | 2.13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mitra, A.; Zarikas, V.; Bonanno, A.; Good, M.; Güdekli, E. Constraining the Swiss-Cheese IR-Fixed Point Cosmology with Cosmic Expansion. Universe 2021, 7, 263. https://doi.org/10.3390/universe7080263
Mitra A, Zarikas V, Bonanno A, Good M, Güdekli E. Constraining the Swiss-Cheese IR-Fixed Point Cosmology with Cosmic Expansion. Universe. 2021; 7(8):263. https://doi.org/10.3390/universe7080263
Chicago/Turabian StyleMitra, Ayan, Vasilios Zarikas, Alfio Bonanno, Michael Good, and Ertan Güdekli. 2021. "Constraining the Swiss-Cheese IR-Fixed Point Cosmology with Cosmic Expansion" Universe 7, no. 8: 263. https://doi.org/10.3390/universe7080263
APA StyleMitra, A., Zarikas, V., Bonanno, A., Good, M., & Güdekli, E. (2021). Constraining the Swiss-Cheese IR-Fixed Point Cosmology with Cosmic Expansion. Universe, 7(8), 263. https://doi.org/10.3390/universe7080263







