Decoupled Embedding Class-One Strange Stars in Self-Interacting Brans–Dicke Gravity †
Abstract
1. Introduction
2. Self-Interacting Brans–Dicke Theory
3. Gravitational Decoupling
4. Anisotropic Solutions
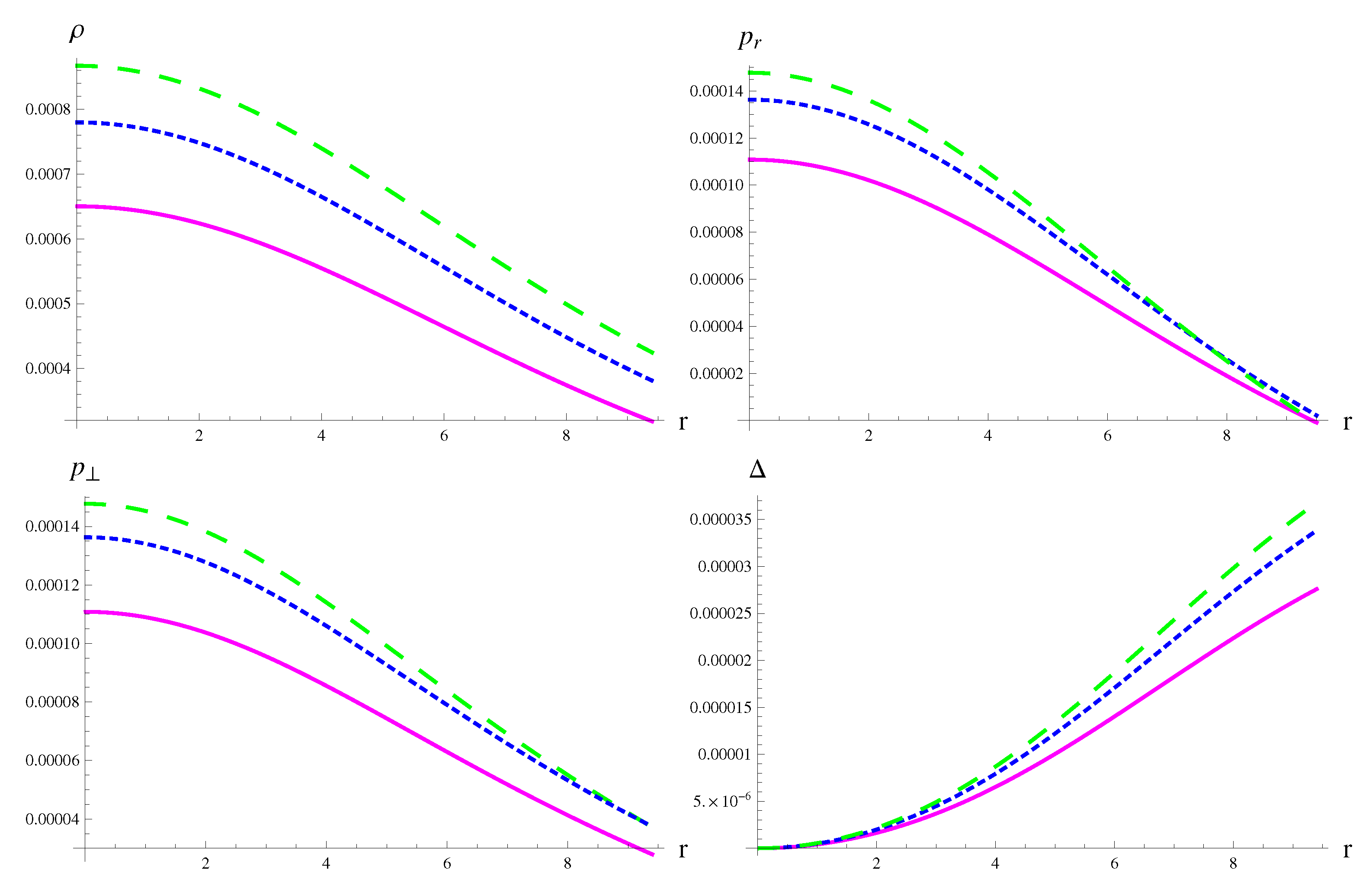
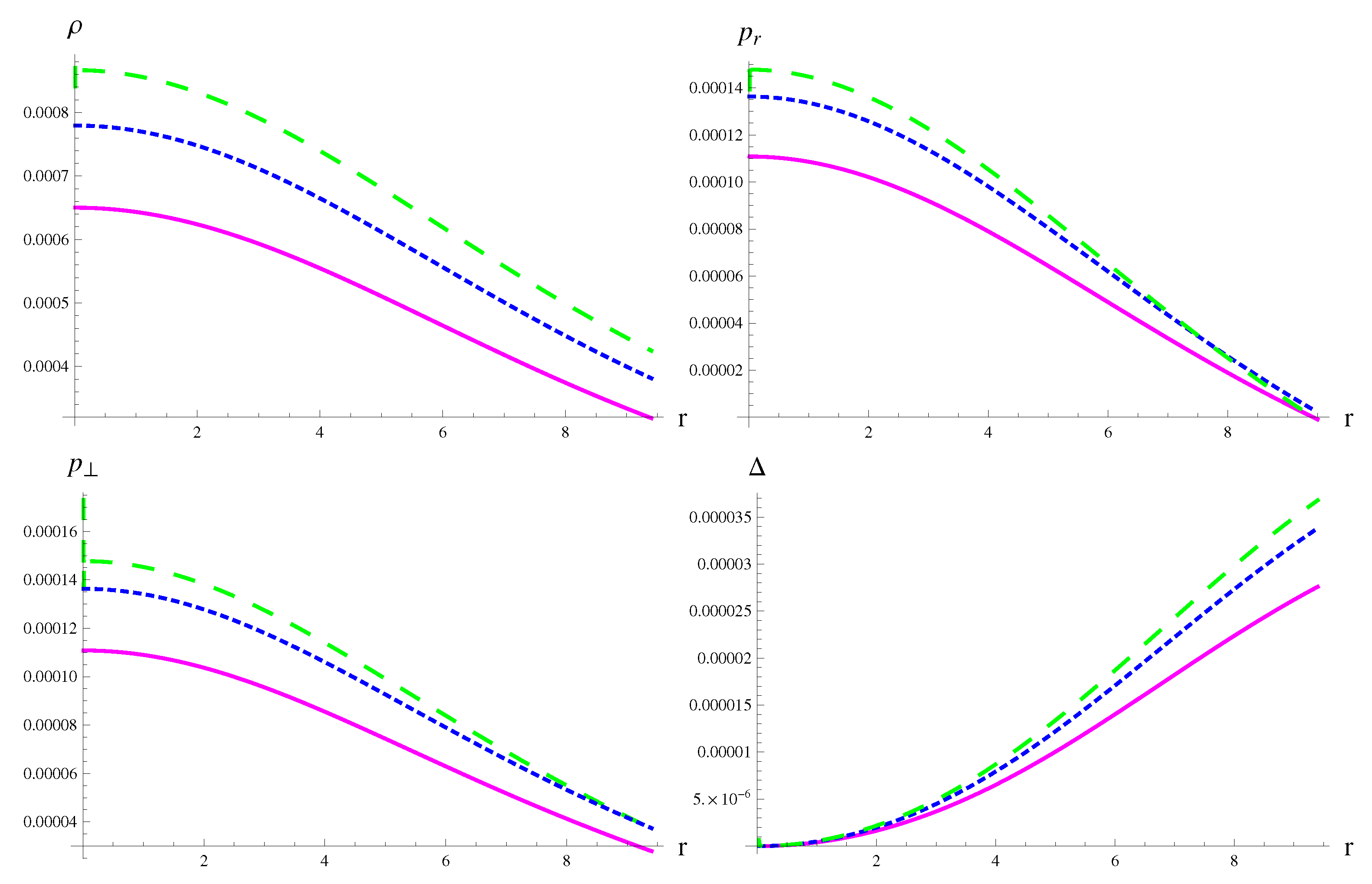
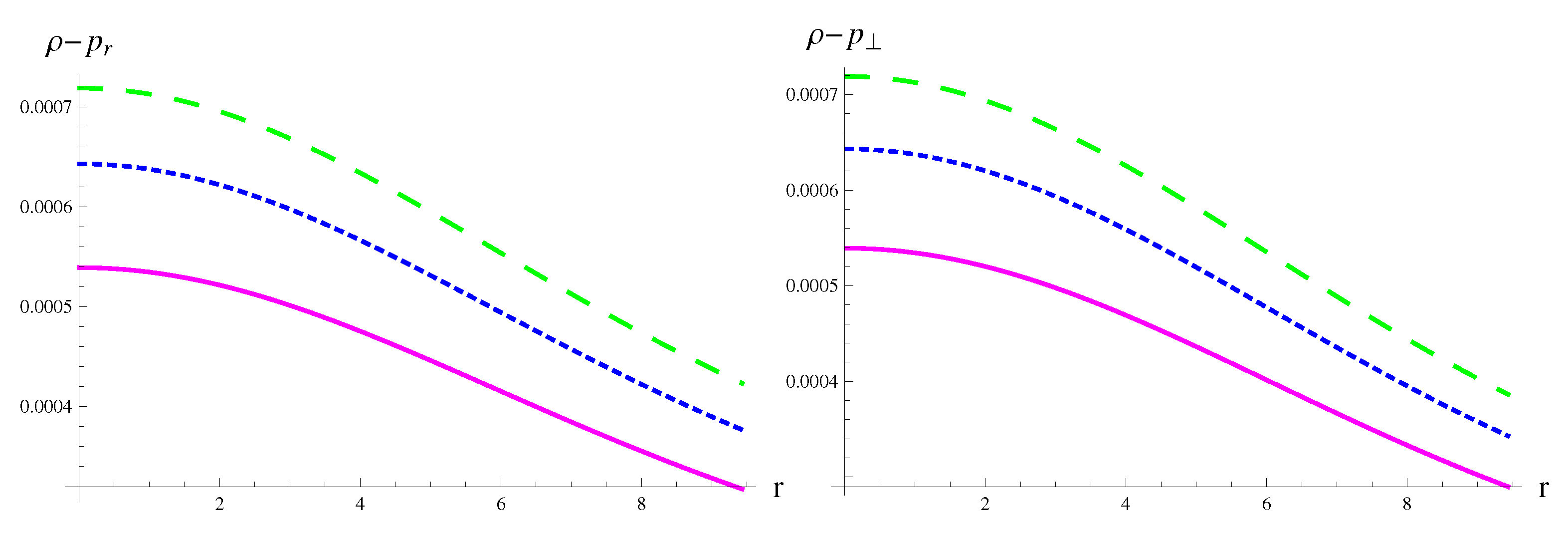
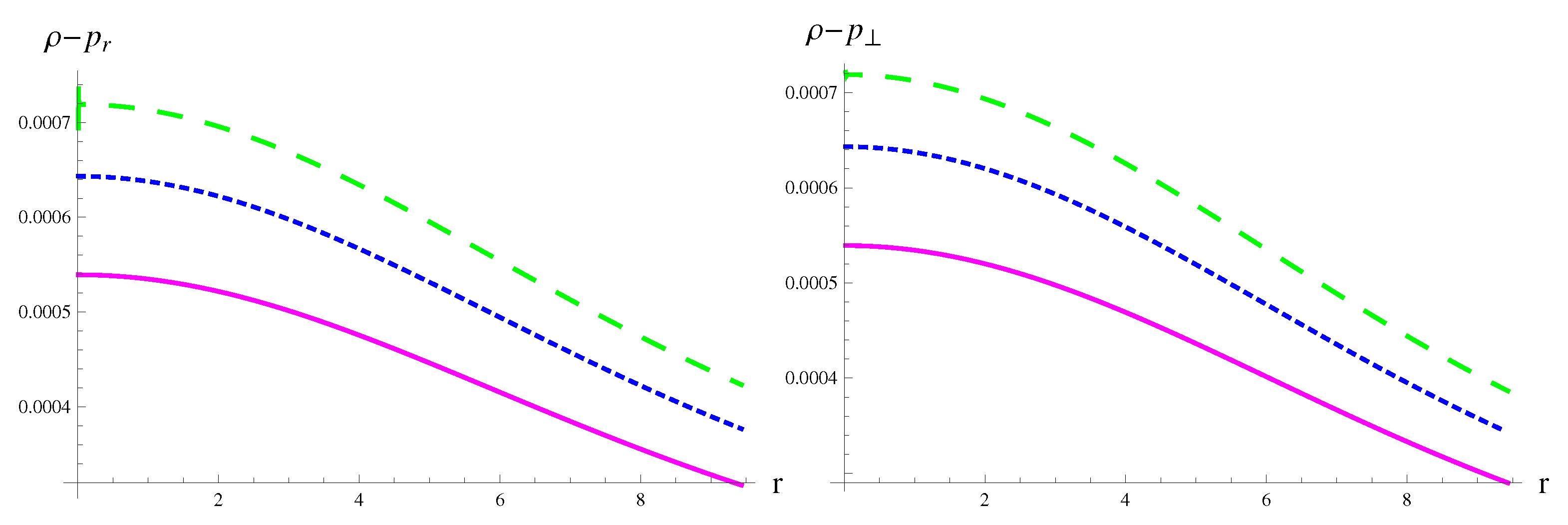
4.1. Solution I
4.2. Solution II
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Itoh, N. Hydrostatic equilibrium of hypothetical quark stars. Prog. Theor. Phys. 1970, 44, 291–292. [Google Scholar] [CrossRef]
- Witten, E. Cosmic separation of phases. Phys. Rev. D 1984, 30, 272–285. [Google Scholar] [CrossRef]
- Ofek, E.O.; Cameron, P.B.; Kasliwal, M.M.; Gal-Yam, A.; Rau, A.; Kulkarni, S.R.; Fraol, D.A.; Chandra, P.; Cenko, S.B.; Soderberg, A.M.; et al. SN2006gy: An extremely luminoue supernova in the galaxy NGC 1260. Astrophys. J. 2007, 659, L13. [Google Scholar] [CrossRef]
- Bordbar, G.H.; Peivand, A.R. Computation of the structure of a magnetized strange quark star. Res. Astron. Astrophys. 2011, 11, 851–862. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of gravitational waves from a binary neutron star inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C. et al. GW190425: Observation of a compact binary coalescence with total mass ∼3.4M⨀. Astrophys. J. Lett. 2020, 892, L3. [Google Scholar] [CrossRef]
- Haensel, P.; Zdunik, J.L.; Schaffer, R. Strange quark stars. Astron. Astrophys. 1986, 160, 121–128. [Google Scholar]
- Cheng, K.S.; Dai, Z.G.; Lu, T. Strange stars and related astrophysical phenomena. Int. J. Mod. Phys. D 1998, 7, 139–176. [Google Scholar] [CrossRef]
- Harko, T.; Mak, M.K. An exact anisotropic quark star model. Chin. J. Astron. Astrophys. 2002, 2, 248–259. [Google Scholar]
- Arbañil, J.D.V.; Malheiro, M. Stability of charged quark stars. AIP Conf. Proc. 2015, 1693, 030007. [Google Scholar]
- Bhar, P. Anisotropic compact star model: A brief study via embedding. Eur. Phys. J. C 2019, 79, 138. [Google Scholar] [CrossRef]
- Ferreira, L.F.; da Rocha, R. Nucleons and higher spin baryon resonances: An AdS/Qcd configurational entropic incursion. Phys. Rev. D 2020, 101, 106002. [Google Scholar] [CrossRef]
- Schwarzschild, K. On the gravitational field of a mass point according to Einstein’s theory. Math. Phys. 1916, 1916, 189–196. [Google Scholar]
- Herrera, L.; Santos, N.O. Local anisotropy in self-gravitating systems. Phys. Rep. 1997, 286, 53–130. [Google Scholar] [CrossRef]
- Harko, T.; Mak, M.K. Anisotropic relativistic stellar models. Annalen Phys. 2002, 11, 3–13. [Google Scholar] [CrossRef]
- Hossein, S.M.; Rahaman, F.; Naskar, J.; Kalam, M.; Ray, S. Anisotropic compact stars with variable cosmological constant. Int. J. Mod. Phys. D 2012, 21, 1250088. [Google Scholar] [CrossRef]
- Paul, B.C.; Deb, R. Relativistic solutions of anisotropic compact objects. Astrophys. Space Sci. 2014, 354, 421–430. [Google Scholar] [CrossRef]
- Ovalle, J. Decoupling gravitational sources in general relativity: From perfect to anisotropic fluids. Phys. Rev. D 2017, 95, 104019. [Google Scholar] [CrossRef]
- Ovalle, J. Decopupling gravitational sources in general relativity: The extended case. Phys. Lett. B 2019, 788, 213–218. [Google Scholar] [CrossRef]
- Ovalle, J.; Linares, F. Tolman IV solution in the Randall-Sundrum braneworld. Phys. Rev. D 2013, 88, 104026. [Google Scholar] [CrossRef]
- Ovalle, J.; Casadio, R.; da Rocha, R.; Sotomayor, A. Anisotropic solutions by gravitational decoupling. Eur. Phys. J. C 2018, 78, 122. [Google Scholar] [CrossRef]
- Gabbanelli, L.; Rincón, A.; Rubio, C. Gravitational decoupled anisotropies in compact stars. Eur. Phys. J. C 2018, 78, 370. [Google Scholar] [CrossRef]
- Estrada, M.; Tello-Ortiz, F. A new family of analytical anisotropic solutions by gravitational decoupling. Eur. Phys. J. C 2018, 133, 453. [Google Scholar] [CrossRef]
- Sharif, M.; Sadiq, S. Gravitational decoupled charged anisotropic spherical solutions. Eur. Phys. J. C 2018, 78, 410. [Google Scholar] [CrossRef]
- Gabbanelli, L.; Ovalle, J.; Sotomayor, A.; Stuchlik, Z.; Casadio, R. A causal Schwarzschild-de Sitter interior solution by gravitational decoupling. Eur. Phys. J. C 2019, 79, 486. [Google Scholar] [CrossRef]
- Contreras, E. Gravitational decoupling in 2+1 dimensional spacetime with cosmological term. Class. Quantum Gravity 2019, 36, 095004. [Google Scholar] [CrossRef]
- Contreras, E.; Bargueño, P. Extended gravitational decoupling in 2+1 dimensional spacetimes. Class. Quantum Gravity 2019, 36, 215009. [Google Scholar] [CrossRef]
- Singh, K.N.; Maurya, S.K.; Jasim, M.K.; Rahaman, F. Minimally deformed anisotropic model of class-one spacetime by gravitational decoupling. Eur. Phys. J. C 2019, 79, 851. [Google Scholar] [CrossRef]
- Hensh, S.; Stuchlik, Z. Anisotropic Tolman VII solution by gravitational decoupling. Eur. Phys. J. C 2019, 79, 834. [Google Scholar] [CrossRef]
- Sharif, M.; Ama-Tul-Mughani, Q. Study of (1+2)-dimensional charged string cloud with minimal geometric deformation. Int. J. Geom. Methods Mod. Phys. 2019, 16, 1950187. [Google Scholar] [CrossRef]
- Sharif, M.; Ama-Tul-Mughani, Q. Gravitational decoupled solutions of axial string cosmology. Mod. Phys. Lett. A 2020, 35, 2050091. [Google Scholar] [CrossRef]
- Cedeño, F.X.L.; Contreras, E. Gravitational decoupling in cosmology. Phys. Dark Universe 2020, 28, 100543. [Google Scholar] [CrossRef]
- Contreras, E.; Ovalle, J.; Casadio, R. Gravitational decoupling for axially symmetric systems and rotating black holes. Phys. Rev. D 2021, 103, 044020. [Google Scholar] [CrossRef]
- Meert, P.; da Rocha, R. Probing the minimal geometric deformation with trace and Weyl anomalies. Nucl. Phys. B 2021, 967, 115420. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The cosmological constants. Nature 1937, 139, 323. [Google Scholar] [CrossRef]
- Dirac, P.A.M. A new basis for cosmology. Proc. R. Soc. Lond. A 1938, 165, 199–208. [Google Scholar] [CrossRef]
- Brans, C.; Dicke, R.H. Mach’s principle and a relativistic theory of gravitation. Phys. Rev. 1961, 124, 925–935. [Google Scholar] [CrossRef]
- Will, C.M. Theory and experiment in gravitational physics. Living Rev. Rel. 2001, 4, 4. [Google Scholar] [CrossRef]
- Weinberg, E.J. Some problems with extended inflation. Phys. Rev. D 1989, 40, 3950. [Google Scholar] [CrossRef]
- Perivolaropoulos, L. PPN parameter γ and solar system constraints of massive Brans-Dicke theories. Phys. Rev. D 2010, 81, 047501. [Google Scholar] [CrossRef]
- Buchdahl, H.A. Static solutions of the Brans-Dicke equations. Int. J. Theor. Phys. 1972, 6, 407–412. [Google Scholar] [CrossRef]
- Bruckman, W.F.; Kazes, E. Properties of the solutions of cold ultradense configurations in the Brans-Dicke theory. Phys. Rev. D 1977, 16, 2. [Google Scholar] [CrossRef]
- Singh, T.; Rai, L.N. Stationary axially symmetric Brans-Dicke Maxwell fields. Gen. Relat. Gravit. 1979, 11, 37–43. [Google Scholar] [CrossRef]
- Krori, K.D.; Bhattacharjee, D.R. Demiański-type metric in Brans-Dicke theory. J. Math. Phys. 1982, 23, 1846–1847. [Google Scholar] [CrossRef]
- Yazadjiev, S.S.; Doneva, D.D.; Popchev, D. Slowly rotating neutron stars in scalar-tensor theories with a massive scalar field. Phys. Rev. D 2016, 93, 084038. [Google Scholar] [CrossRef]
- Doneva, D.D.; Yazadjiev, S.S. Rapidly rotating neutron stars with a massive scalar field-structure and universal relations. J. Cosmol. Astropart. Phys. 2016, 11, 019. [Google Scholar] [CrossRef]
- Staykov, K.V.; Popchev, D.; Doneva, D.D.; Yazadjiev, S.S. Static and slowly rotating neutron stars in scalar-tensor theory with a massive scalar field. Eur. Phys. J. C 2018, 78, 586. [Google Scholar] [CrossRef]
- Popchev, D.; Staykov, K.V.; Doneva, D.D.; Yazadjiev, S.S. Moment of inertia-mass universal relations for neutron stars in scalar-tensor theory with self-interacting massive scalar field. Eur. Phys. J. C 2019, 79, 178. [Google Scholar] [CrossRef]
- Sharif, M.; Majid, A. Anisotropic strange stars through embedding technique in massive Brans-Dicke gravity. Eur. Phys. J. Plus 2020, 135, 558. [Google Scholar] [CrossRef]
- Sharif, M.; Majid, A. Quark stars in massive Brans-Dicke gravity with Tolman-Kuchowicz spacetime. Universe 2020, 6, 124. [Google Scholar]
- Sharif, M.; Saba, S. Gravitational decoupled anisotropic solutions in f() gravity. Eur. Phys. J. C 2018, 78, 921. [Google Scholar] [CrossRef]
- Sharif, M.; Waseem, A. Anisotropic spherical solutions by gravitational decoupling in f() gravity. Ann. Phys. 2019, 405, 14–28. [Google Scholar] [CrossRef]
- Sharif, M.; Waseem, A. Effects of charge on gravitational decoupled anisotropic solutions in f() gravity. Chin. J. Phys. 2019, 60, 426–439. [Google Scholar] [CrossRef]
- Sharif, M.; Majid, A. Anisotropic compact stars in self-interacting Brans-Dicke gravity. Astrophys. Space Sci. 2020, 365, 42. [Google Scholar] [CrossRef]
- Sharif, M.; Majid, A. Decoupled anisotropic spheres in self-interacting Brans-Dicke gravity. Chin. J. Phys. 2020, 68, 406–418. [Google Scholar] [CrossRef]
- Maurya, S.K.; Tello-Ortiz, F. Charged anisotropic compact star in f(,T) gravity. Phys. Dark Universe 2020, 27, 100442. [Google Scholar] [CrossRef]
- Sharif, M.; Majid, A. Extended gravitaional decoupled solutions in self-interacting Brans-Dicke gravity. Phys. Dark Universe 2020, 30, 100610. [Google Scholar] [CrossRef]
- Maurya, S.K.; Errehymy, A.; Sing, K.N.; Tello-Ortiz, F.; Daoud, M. Gravitational decoupling minimal geometric deformation model in modified f(,T) gravity. Phys. Dark Universe 2020, 30, 100640. [Google Scholar] [CrossRef]
- Maurya, S.K.; Tello-Ortiz, F.; Ray, S. Decoupling gravitational sources in f(,T) gravity under class I spacetime. Phys. Dark Universe 2021, 31, 100753. [Google Scholar] [CrossRef]
- Azmat, H.; Zubair, M. An anisotropic version of Tolman VII solution in f(,T) gravity via gravitational decoupling MGD approach. Eur. Phys. J. Plus 2021, 136, 112. [Google Scholar] [CrossRef]
- Farhi, E.; Jaffe, R.L. Strange matter. Phys. Rev. D 1984, 30, 2379. [Google Scholar] [CrossRef]
- Kapusta, J.I. Finite-Temperature Field Theory, 2nd ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Karmarkar, K.R. Gravitational metrics of spherical symmetry and class one. Proc. Ind. Acad. Sci. A 1948, 27, 56. [Google Scholar] [CrossRef]
- Eisenhart, L.P. Riemannian Geometry, 1st ed.; Princeton University Press: Princeton, NJ, USA, 1926. [Google Scholar]
- Maurya, S.K.; Gupta, Y.K.; Dayanandan, B.; Jasim, M.K.; Al-jamel, A. Relativistic anisotropic models for compact star with equation of state p = f(p). Int. J. Mod. Phys. D 2017, 26, 1750002. [Google Scholar] [CrossRef]
- Baskey, L.; Das, S.; Rahaman, F. An analytical anisotropic compact stellar model of embedding class I. Mod. Phys. Lett. A 2021, 36, 2150028. [Google Scholar] [CrossRef]
- Gangopadhay, T.; Ray, S.; Xiand-Dong, L.; Jishnu, D. Strange star equation of state fits the refined mass measurement of 12 pulsaurs and predictes their radii. Mon. Not. R. Soc. 2013, 431, 3216–3221. [Google Scholar] [CrossRef]
- Atazadeh, K.; Khaleghi, A.; Sepangi, H.R.; Tavakoli, Y. Energy conditions in f() gravity and Brans-Dicke theories. Int. J. Mod. Phys. D 2009, 18, 1101–1111. [Google Scholar] [CrossRef]
- Buchdahl, H.A. General relativistic fluid spheres. Phys. Rev. 1959, 116, 1027–1034. [Google Scholar] [CrossRef]
- Ivanov, B.V. Maximum bounds on the surface redshift of anisotropic stars. Phys. Rev. D 2002, 65, 104011. [Google Scholar] [CrossRef]
- Heintzmann, H.; Hillebrandt, W. Neutron stars with an anisotropic equation of state: Mass, redshift and stability. Astron. Astrophys. 1975, 24, 51–55. [Google Scholar]
- Mustafa, G.; Hussain, I.; Shamir, M.F.; Tie-Cheng, X. Realistic and dark stellar models via embedding approach in Rastall gravity. Phys. Scr. 2021, 96, 045009. [Google Scholar] [CrossRef]

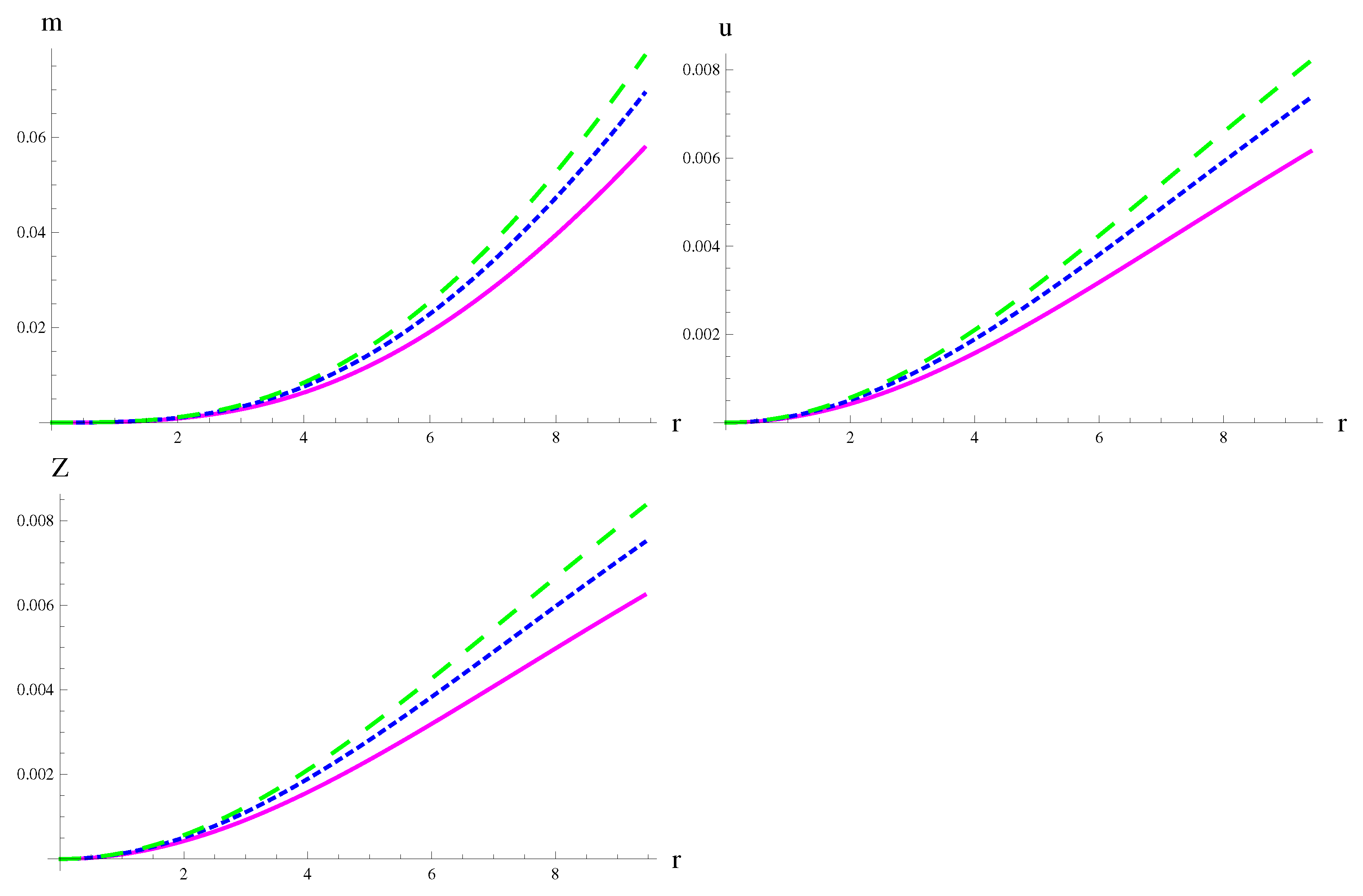

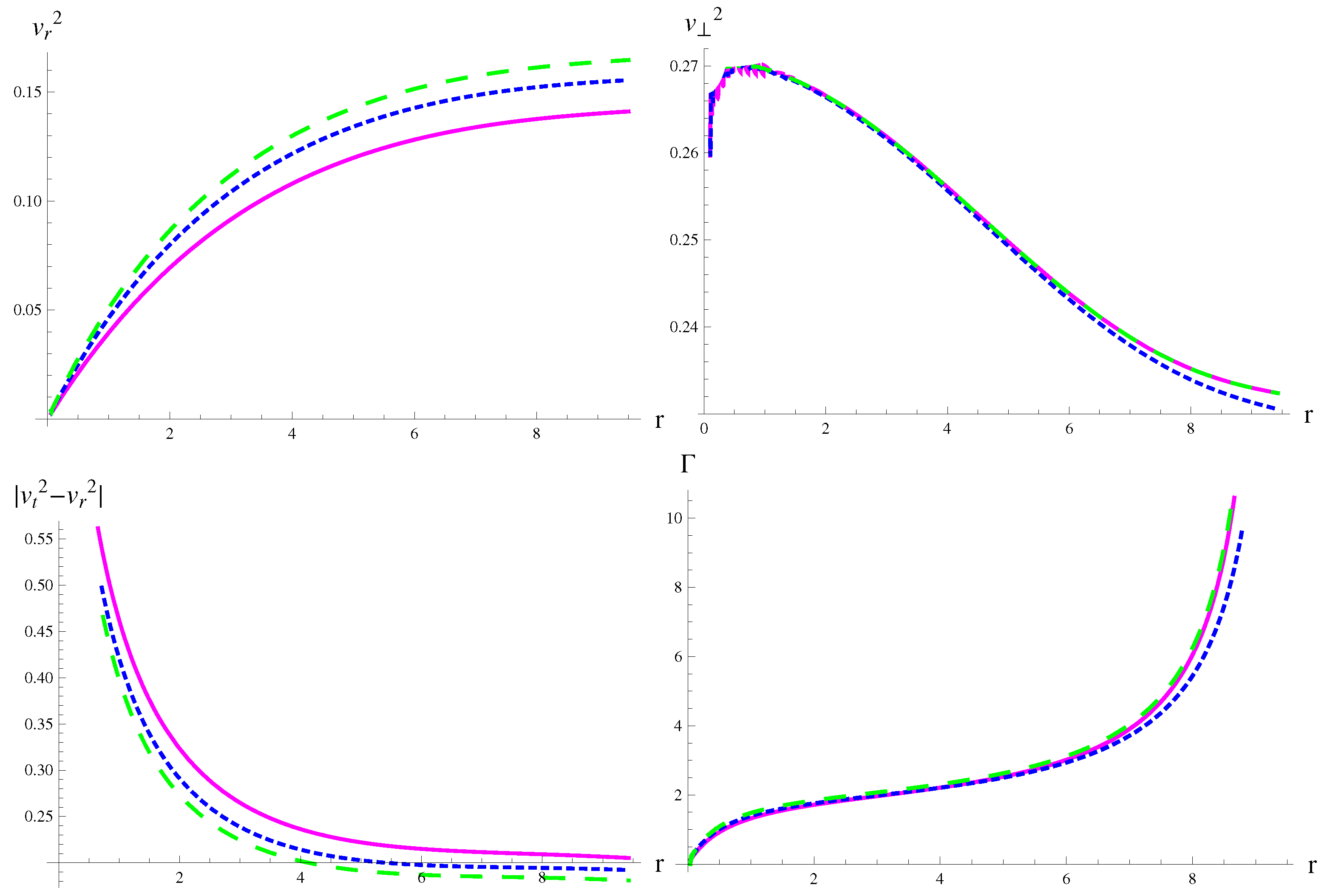
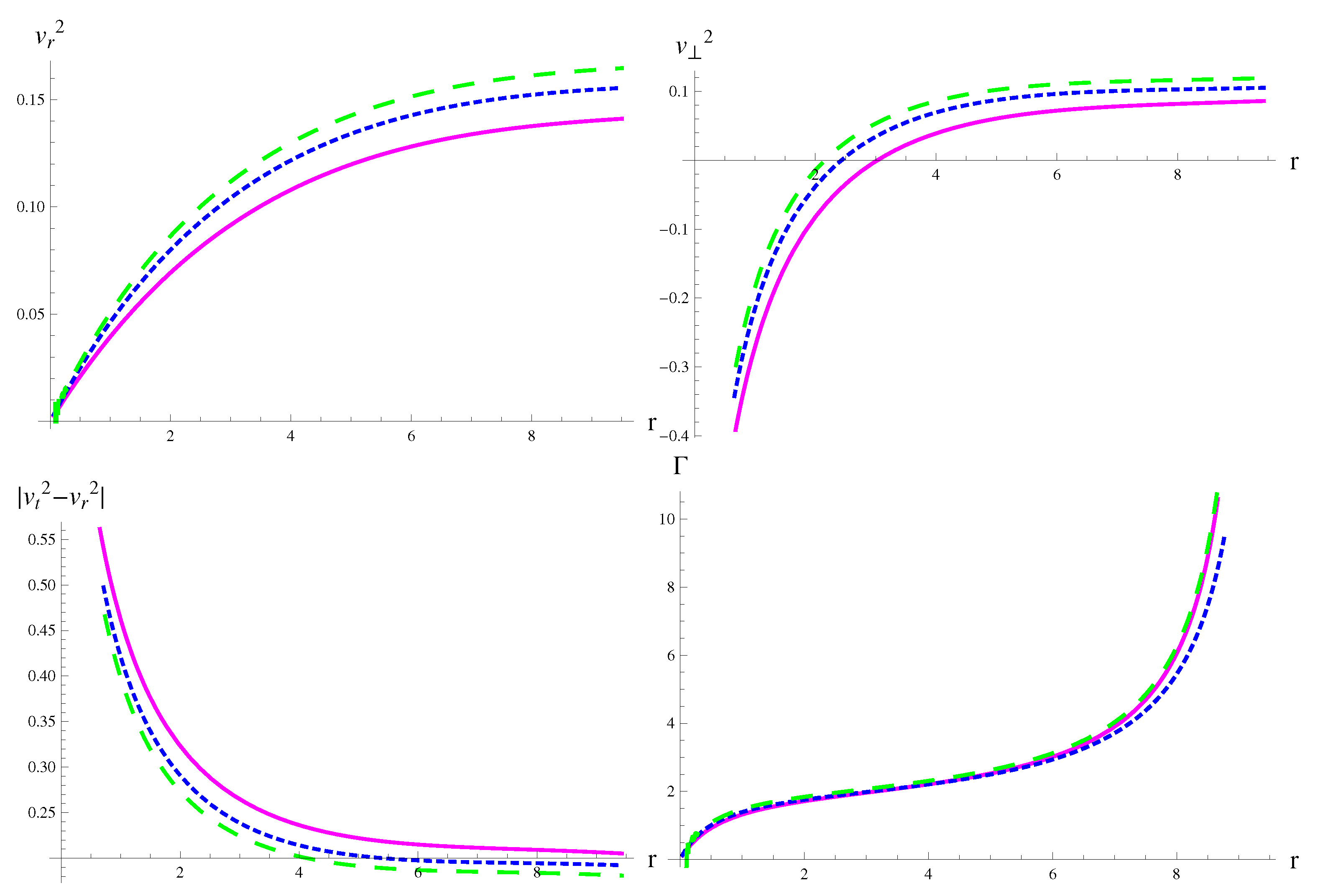
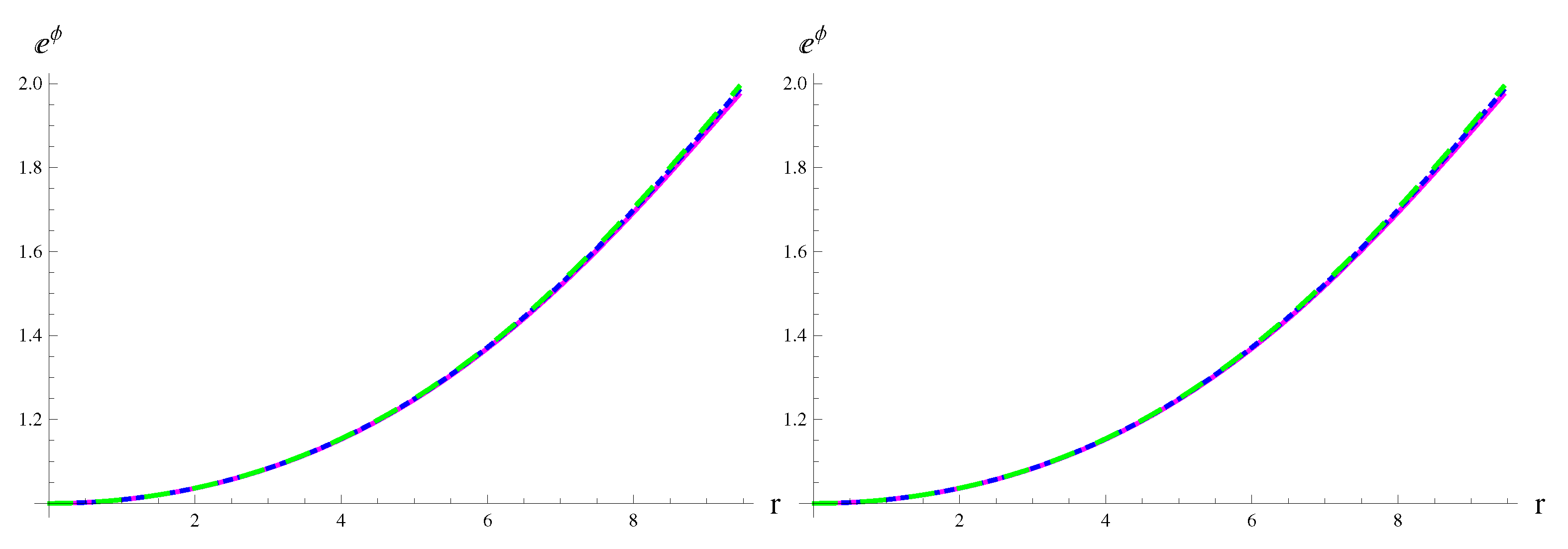
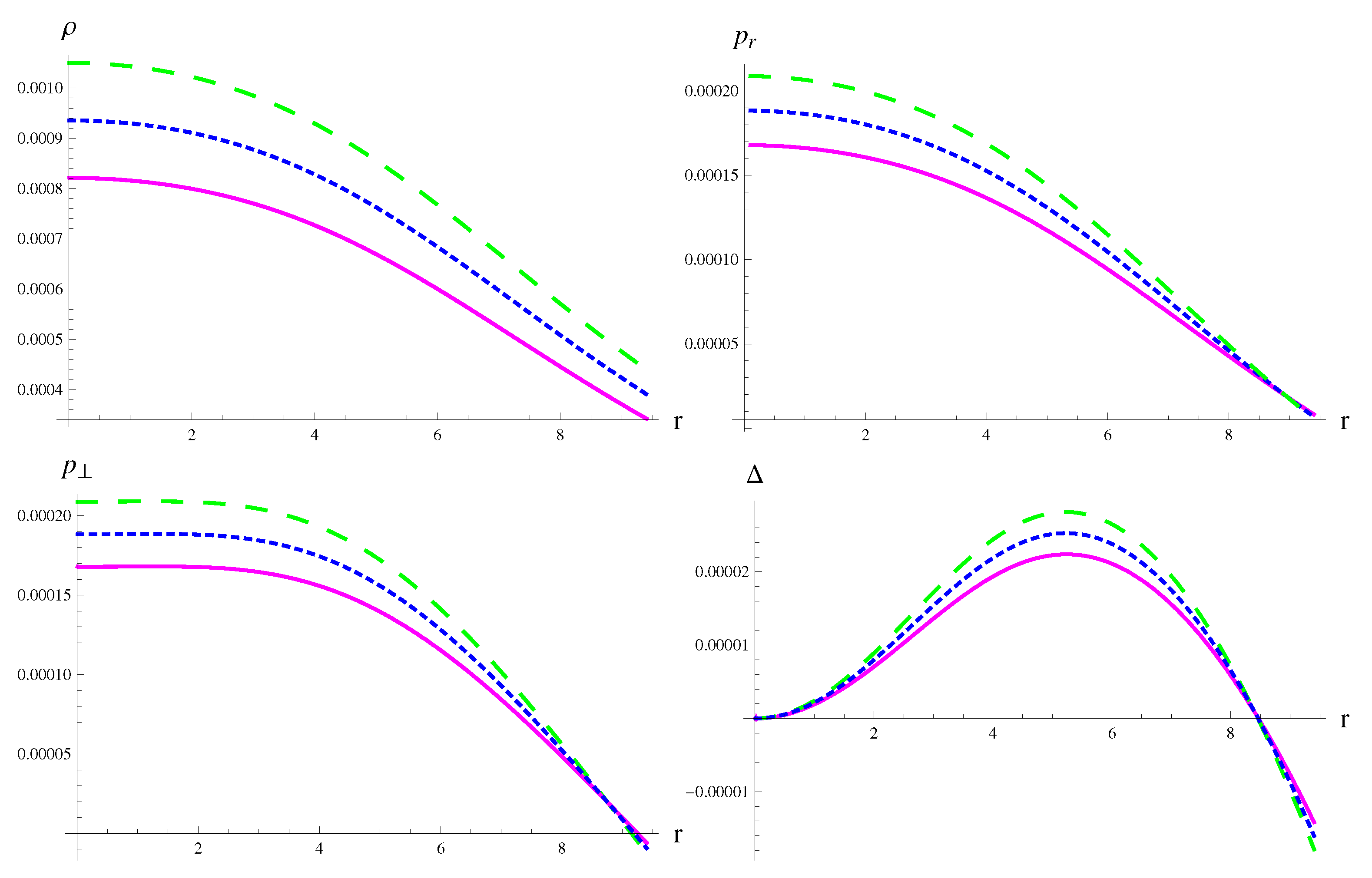
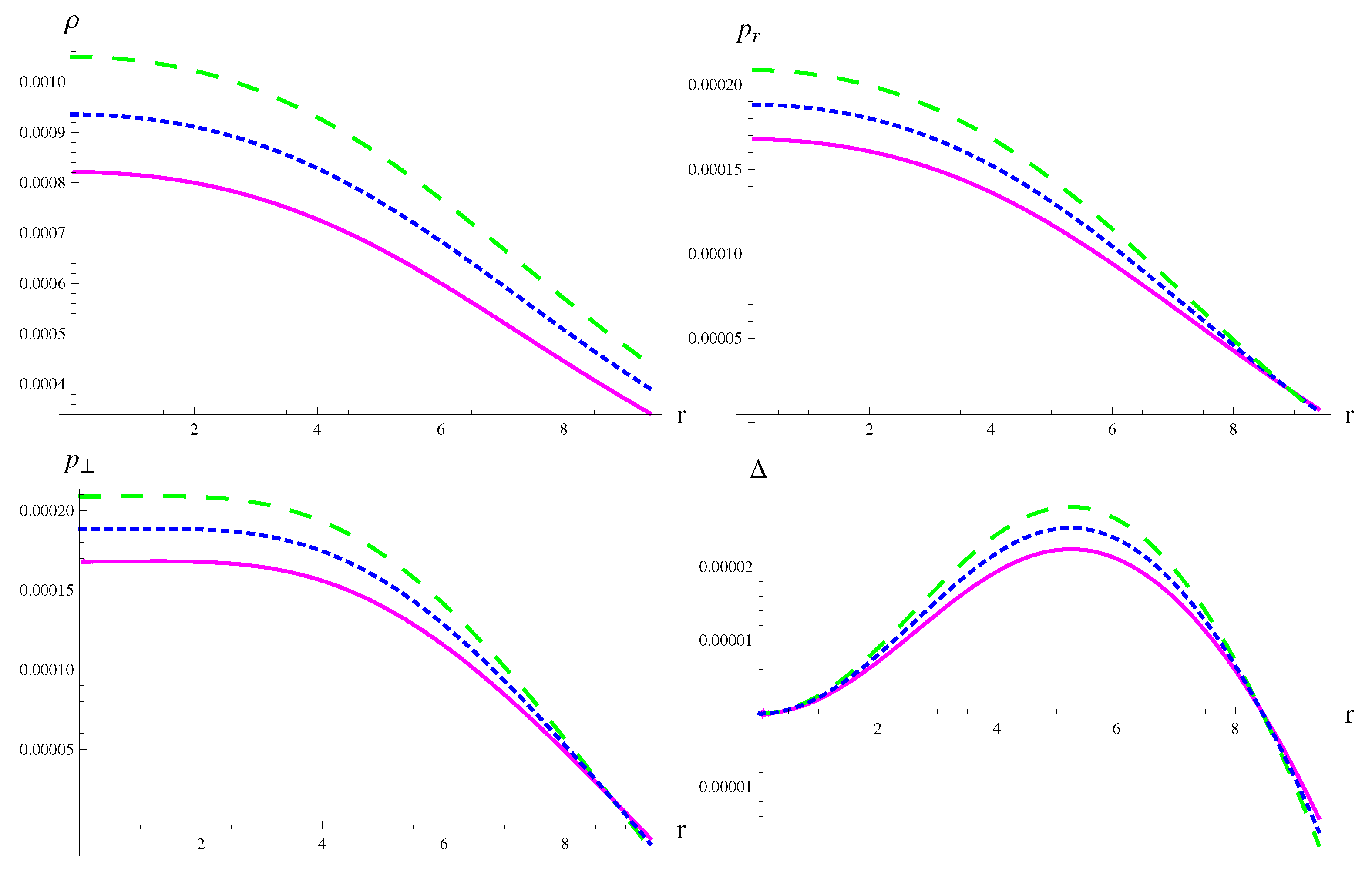

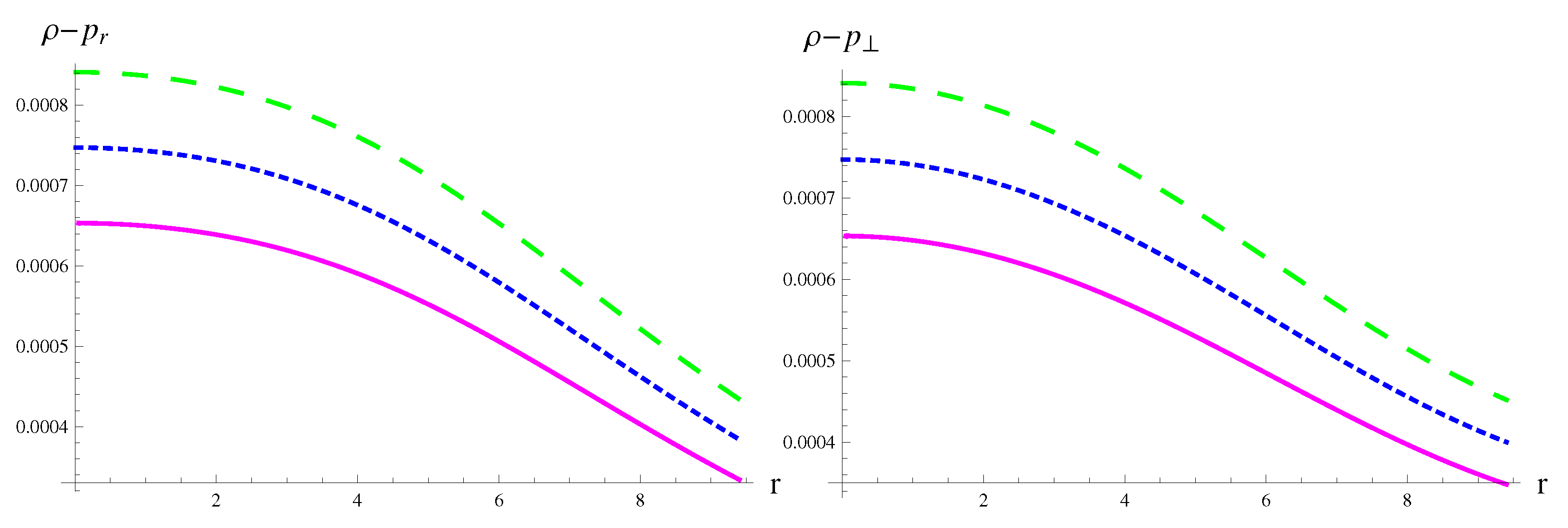
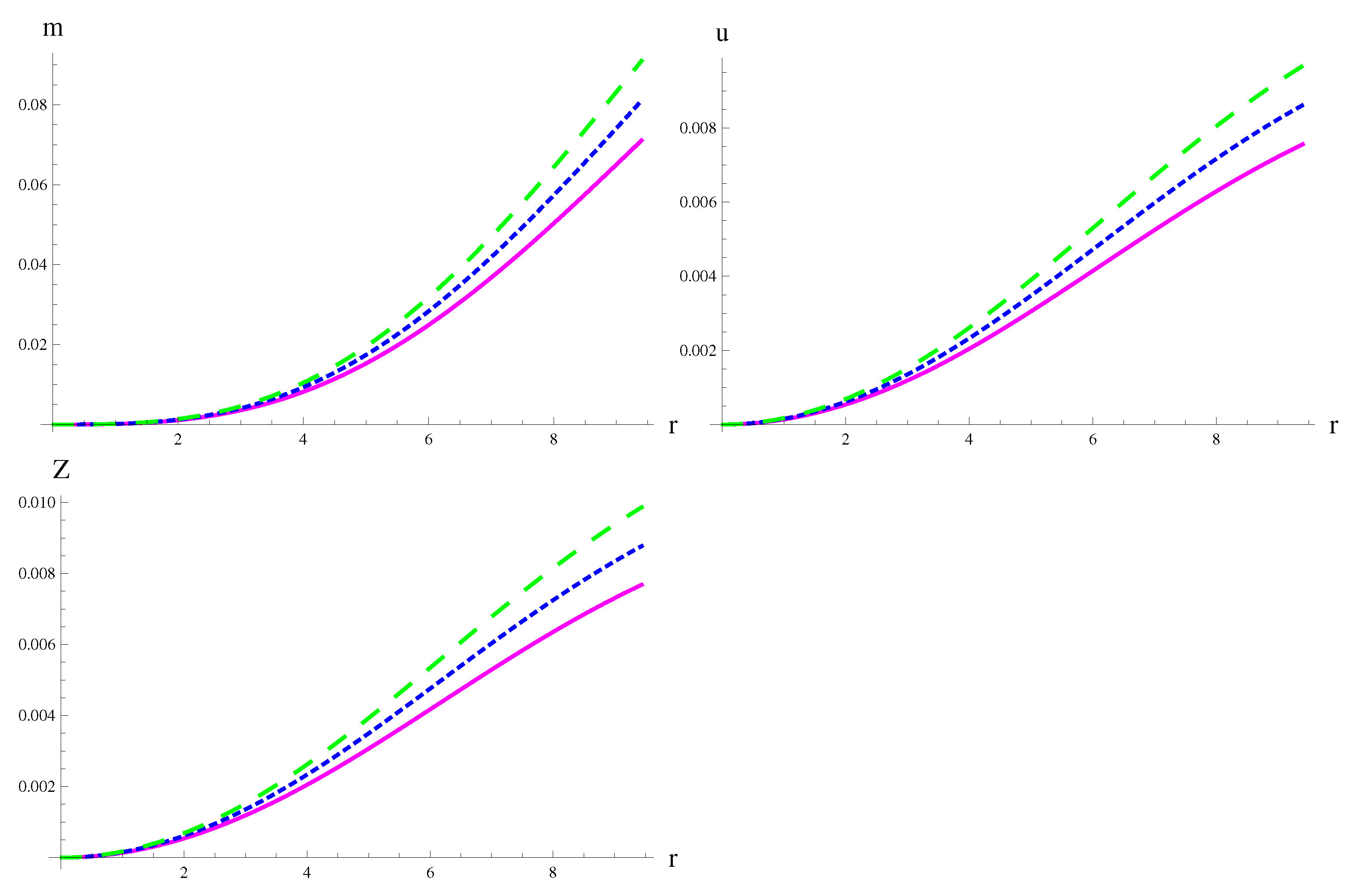
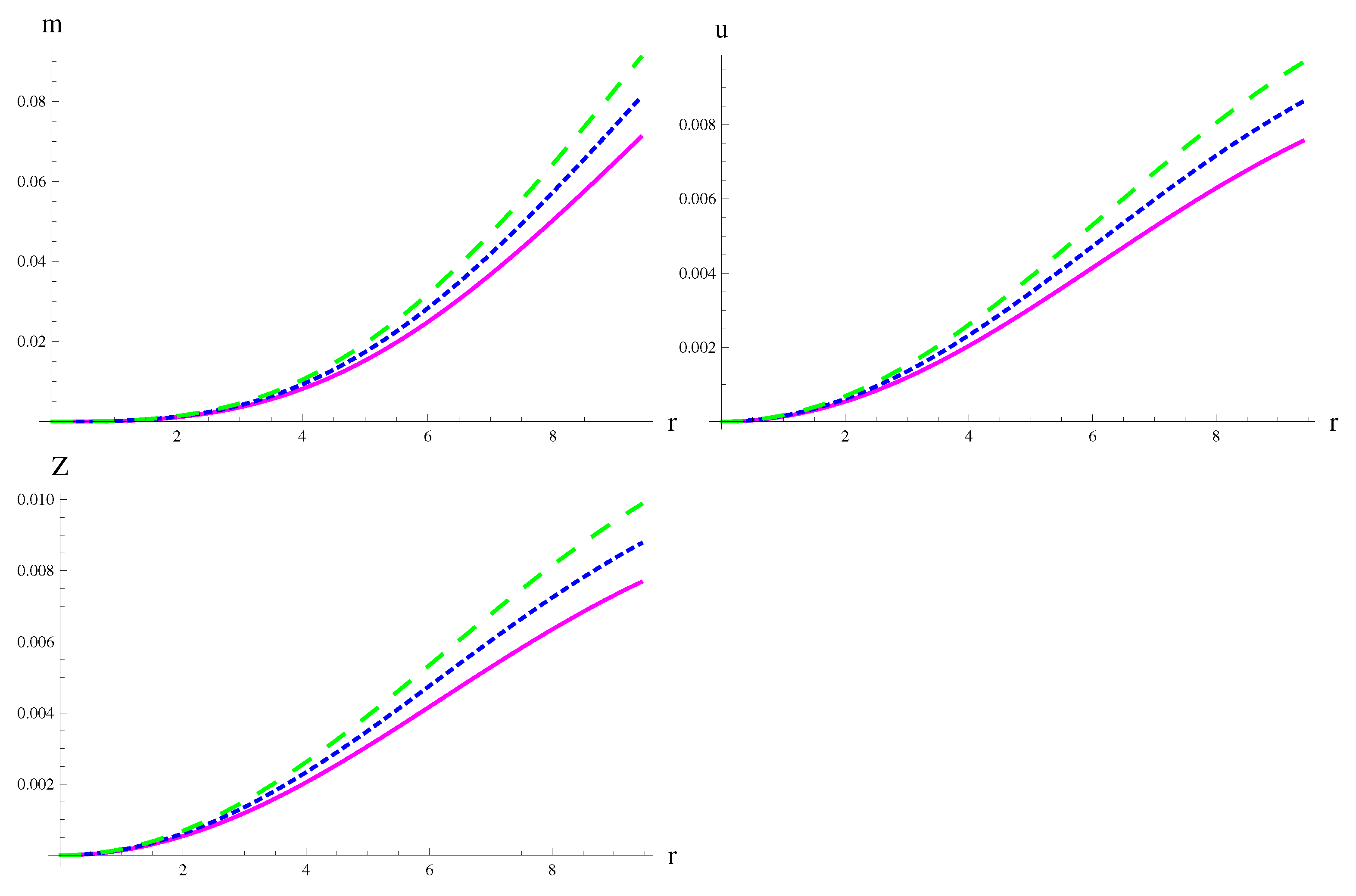
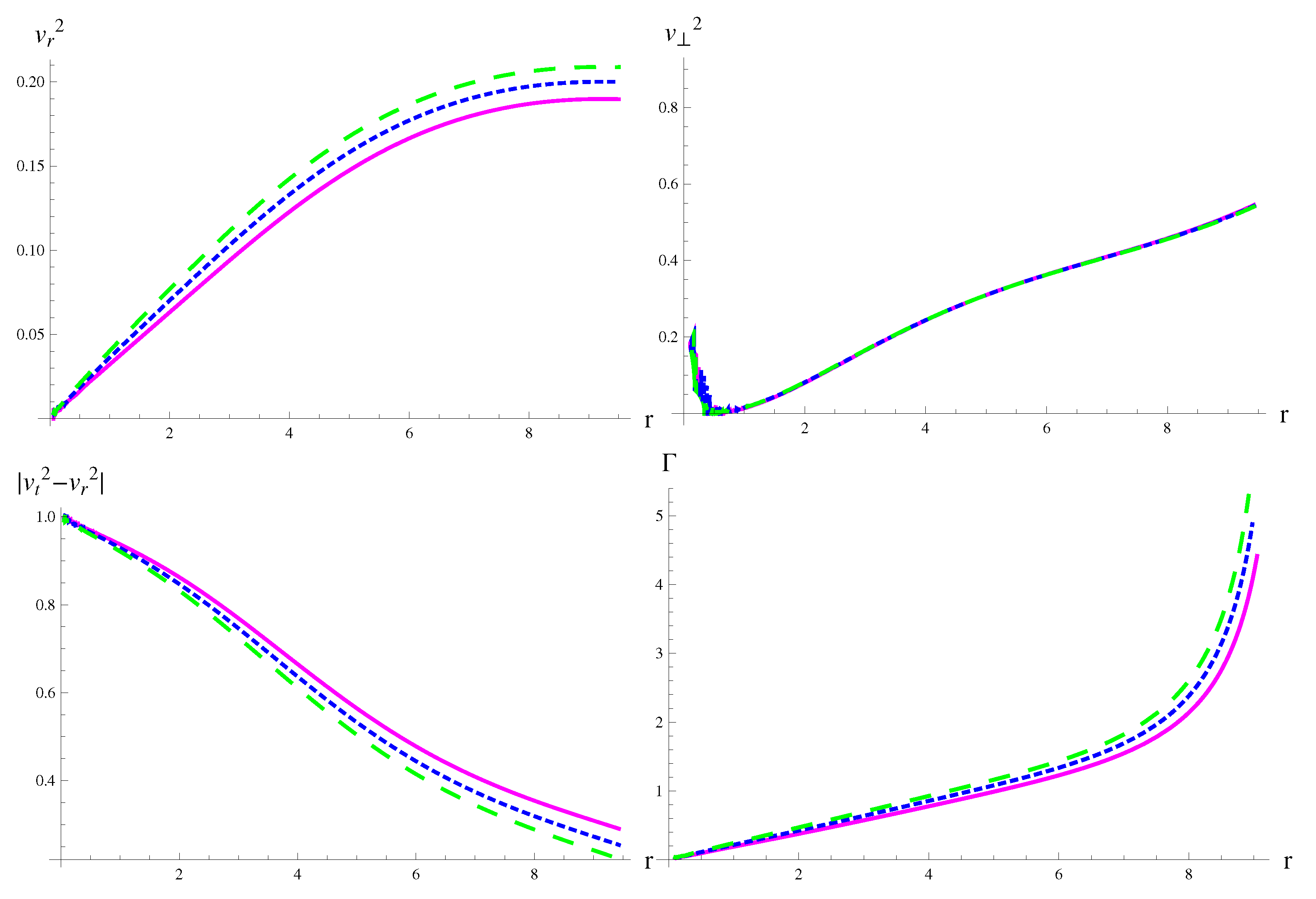
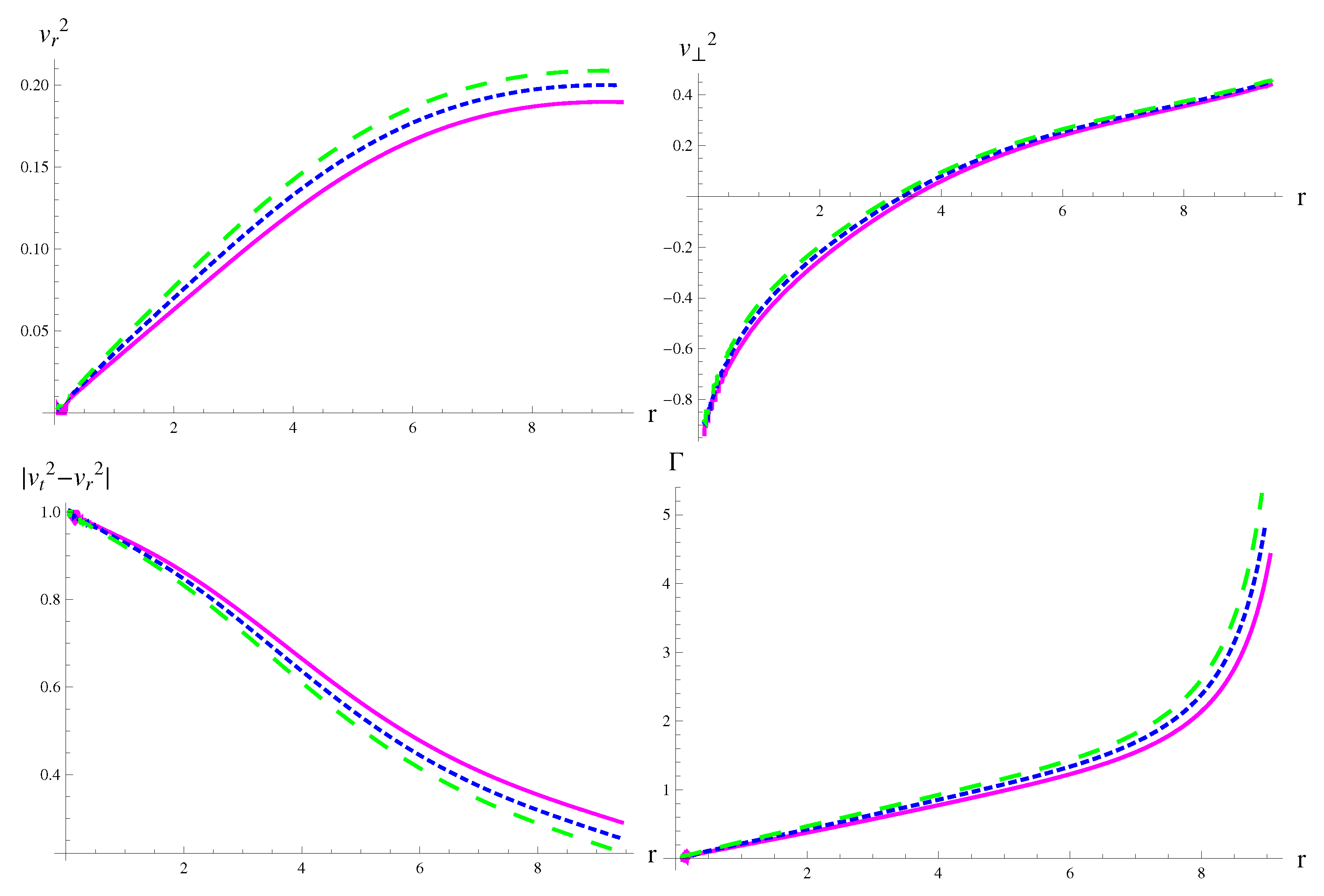
| MeV/fm | MeV/fm | MeV/fm | |
|---|---|---|---|
| 0.024 | 0.029 | 0.032 | |
| 0 | 0 | 0 |
| 0.03 | 0.034 | 0.038 | |
| 0 | 0 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharif, M.; Majid, A. Decoupled Embedding Class-One Strange Stars in Self-Interacting Brans–Dicke Gravity. Universe 2021, 7, 161. https://doi.org/10.3390/universe7060161
Sharif M, Majid A. Decoupled Embedding Class-One Strange Stars in Self-Interacting Brans–Dicke Gravity. Universe. 2021; 7(6):161. https://doi.org/10.3390/universe7060161
Chicago/Turabian StyleSharif, Muhammad, and Amal Majid. 2021. "Decoupled Embedding Class-One Strange Stars in Self-Interacting Brans–Dicke Gravity" Universe 7, no. 6: 161. https://doi.org/10.3390/universe7060161
APA StyleSharif, M., & Majid, A. (2021). Decoupled Embedding Class-One Strange Stars in Self-Interacting Brans–Dicke Gravity. Universe, 7(6), 161. https://doi.org/10.3390/universe7060161







