The de Broglie–Bohm Quantum Theory and Its Application to Quantum Cosmology
Abstract
1. Introduction
2. The de Broglie–Bohm Quantum Theory
3. The de Broglie–Bohm Theory Applied to Quantum Cosmology: Background and Perturbations
3.1. Perfect Fluids
3.2. The Canonical Scalar Field
4. Quantum Bouncing Backgrounds and Their Cosmological Perturbations
4.1. The Perfect Fluid
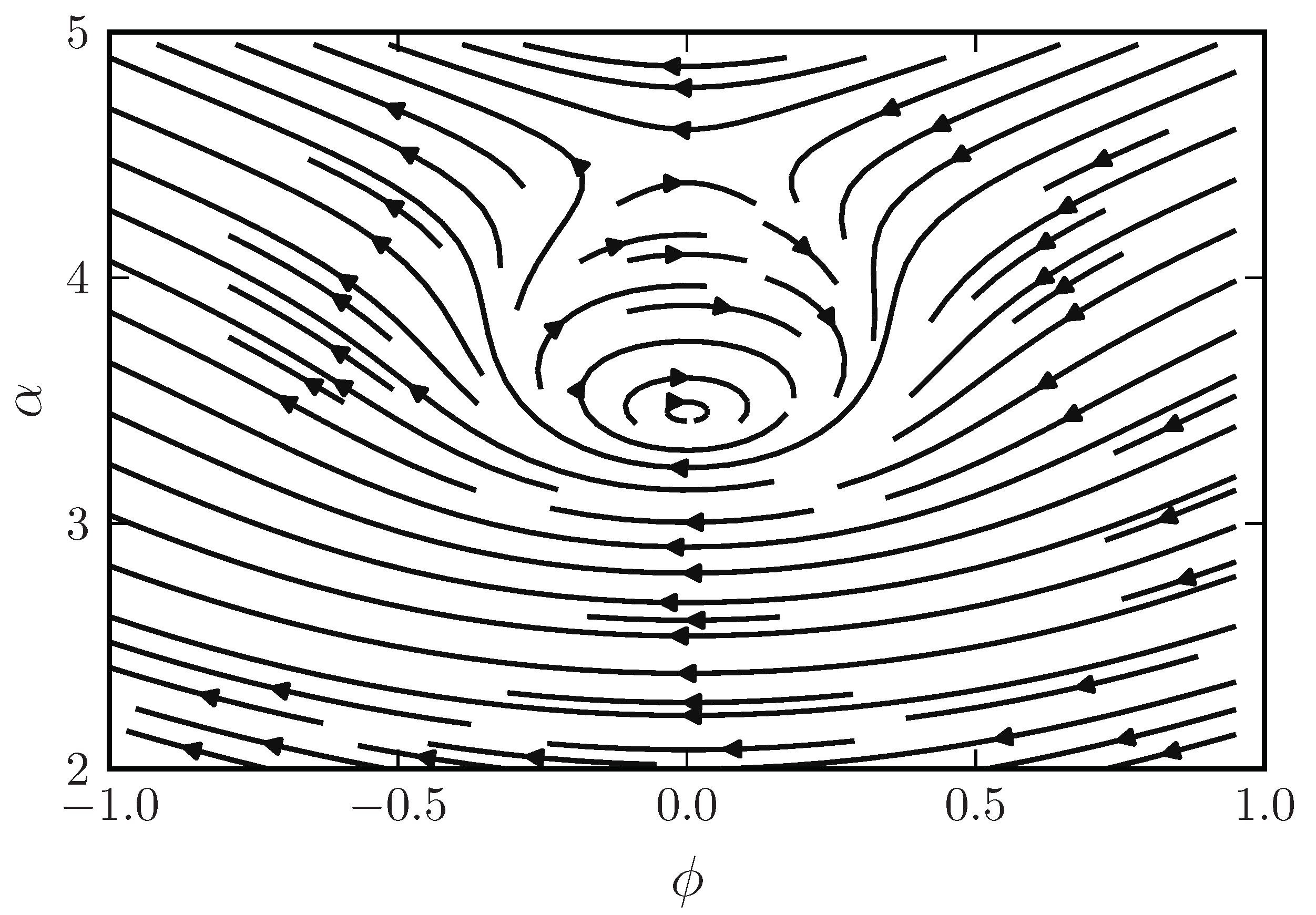
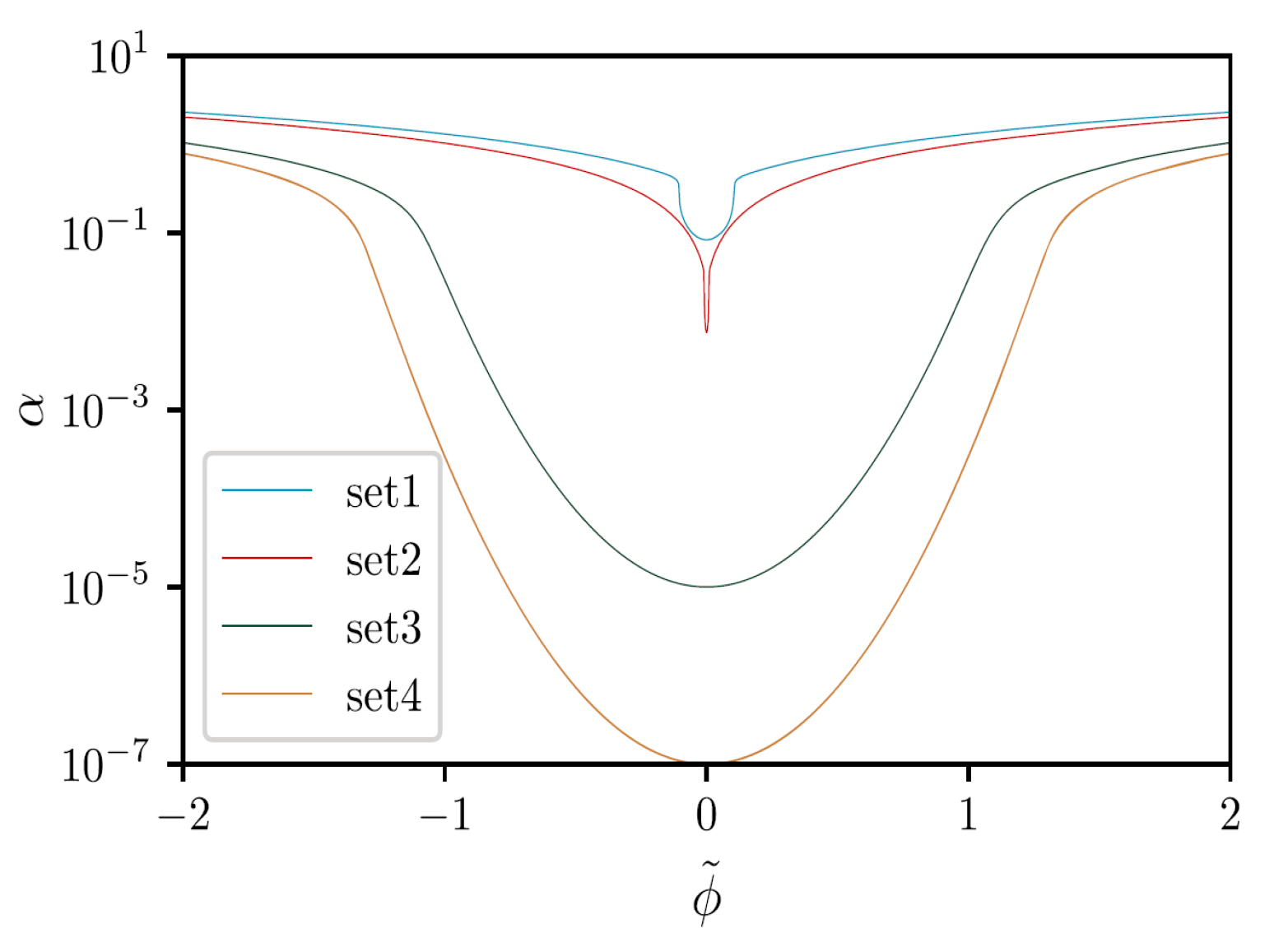
4.2. Canonical Scalar Field
- (A)
- A long classical dust contraction, which traverses a dark energy phase and realizes a stiff matter quantum bounce, directly expanding afterwards to an asymptotically dust matter expanding phase, without passing through a dark energy phase.
- (B)
- A long classical dust contraction, without traversing a dark energy phase, which realizes a stiff matter quantum bounce and expands to a dark energy phase, ending in an asymptotically dust expanding phase.
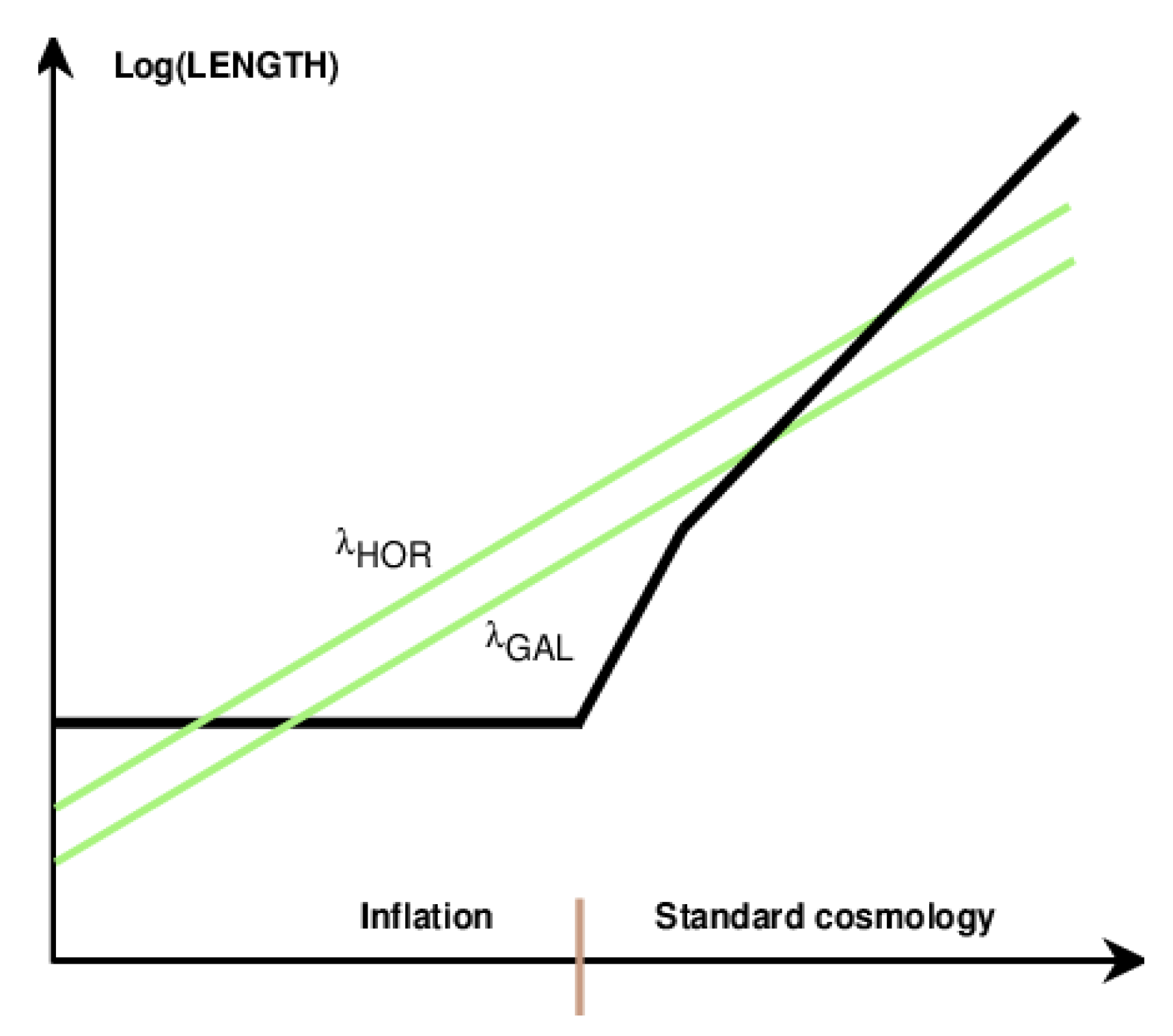
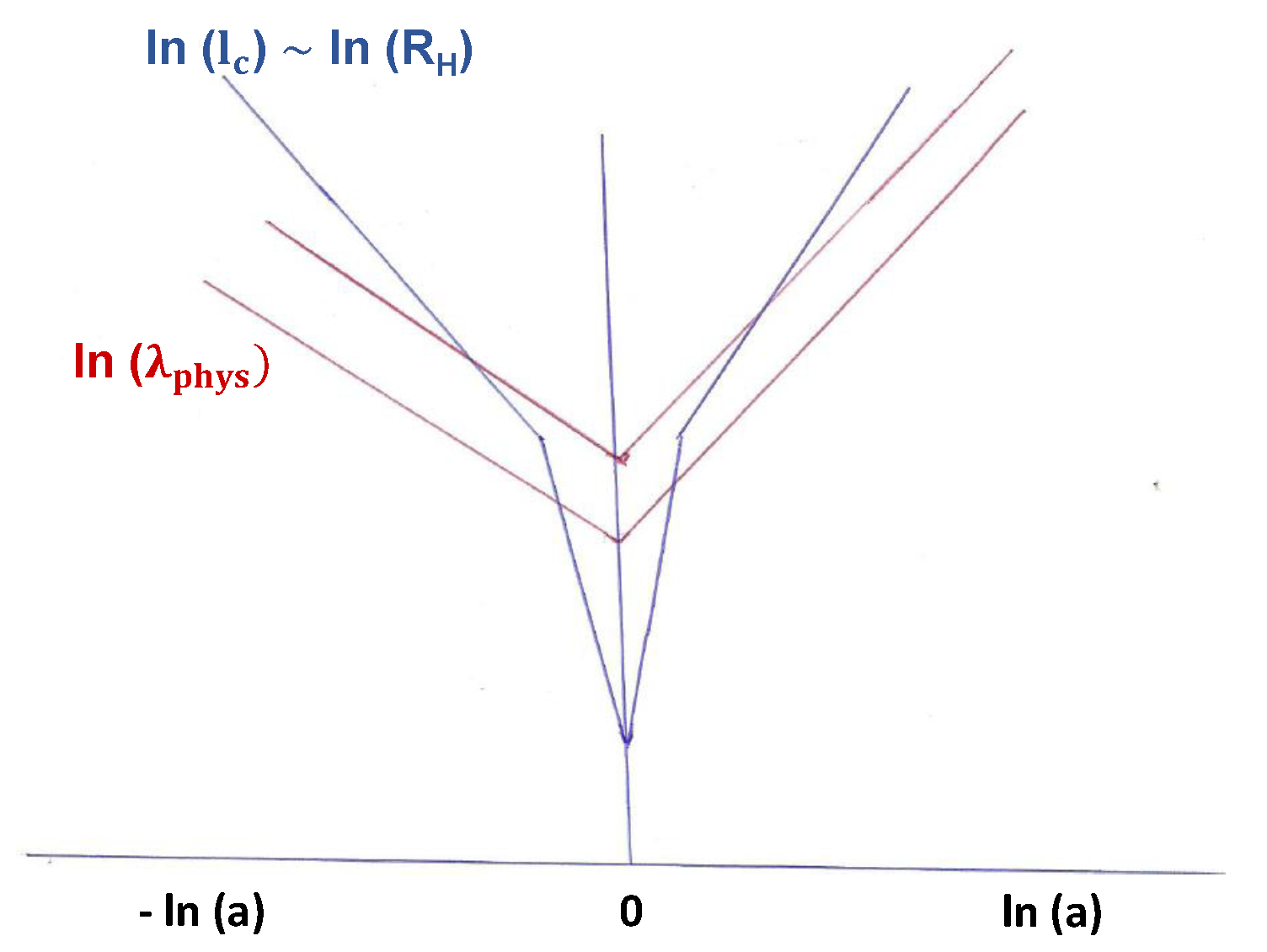
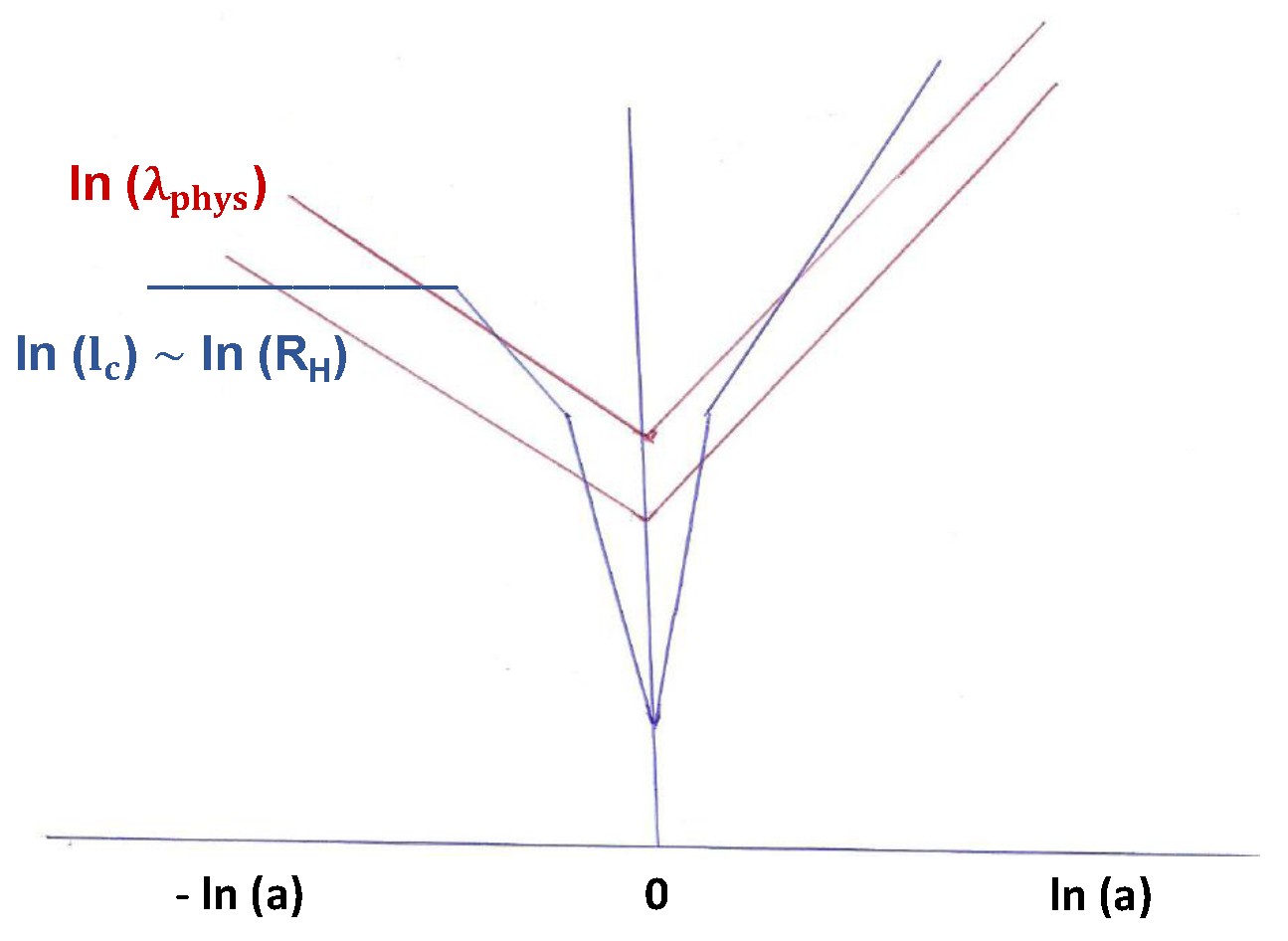
5. The Quantum-to-Classical Transition of Quantum Cosmological Perturbations
6. Discussion and Conclusions
- (1)
- The measurement problem is naturally solved, without the necessity of invoking the presence of an external agent outside the quantum physical system, which does not make sense when the physical system is the whole Universe.
- (2)
- The fact that the usual quantum equations for the wave function of the Universe that emerge from many approaches to quantum gravity do not present a Schrödinger form makes it difficult to physically interpret the wave function of the Universe, especially in probabilistic terms [65,110]. In the dBB theory, however, the wave function of the Universe yields the guidance equations, which provide the time evolution of all the quantum particles and fields present in the Universe. Hence, one can assign a nomological interpretation to , as giving the laws of motion for the quantum degrees of freedom, in the same way as Hamitonians and Lagrangians do. There is no need to talk about probabilities at this level; hence, the quantum equations for may have any form. When dealing with subsystems in the Universe, one can construct the conditional wave function to describe this subset of fields and particles, which may satisfy a Schrödinger-like equation under reasonable assumptions, and a natural probabilistic interpretation in terms of the Born rule emerges for this conditional wave function.
- (3)
- There is the so-called problem of time in quantum cosmology, as it seems that the quantum theory is timeless [110]. This issue is intimately connected with the second one. In the dBB quantum approach, the guidance equations yield a parametric evolution for the fields. Note, however, that the space-time structure that emerges from orderly stacking the fields along this parameter may be very contrived, but they can be calculated; see [111] for details. Additionally, when going to subsystems described by the conditional wave function, where a Schrödinger-like equation emerges, a time evolution for the subsystem quantum state emerges.
- (4)
- As, in the dBB theory, the Bohmian trajectories emerge, the characterization of quantum singularities becomes clear. For instance, in the quantum cosmological models discussed here, the background model is said to be non-singular if the Bohmian trajectory of the scale factor satisfies for all t.
- (5)
- The classical limit is easily obtained, either by the inspection of the quantum potential or by direct comparison between the classical and Bohmian trajectories.
- (i)
- Feature (1) yields a clear understanding of a long standing problem, which is the quantum-to-classical transition of quantum cosmological perturbations in inflation and bouncing models. This was discussed in Section 5.
- (ii)
- Feature (4) allows a simple identification of non-singular quantum models, as shown in Section 4. All of them present a regular bounce.
- (iii)
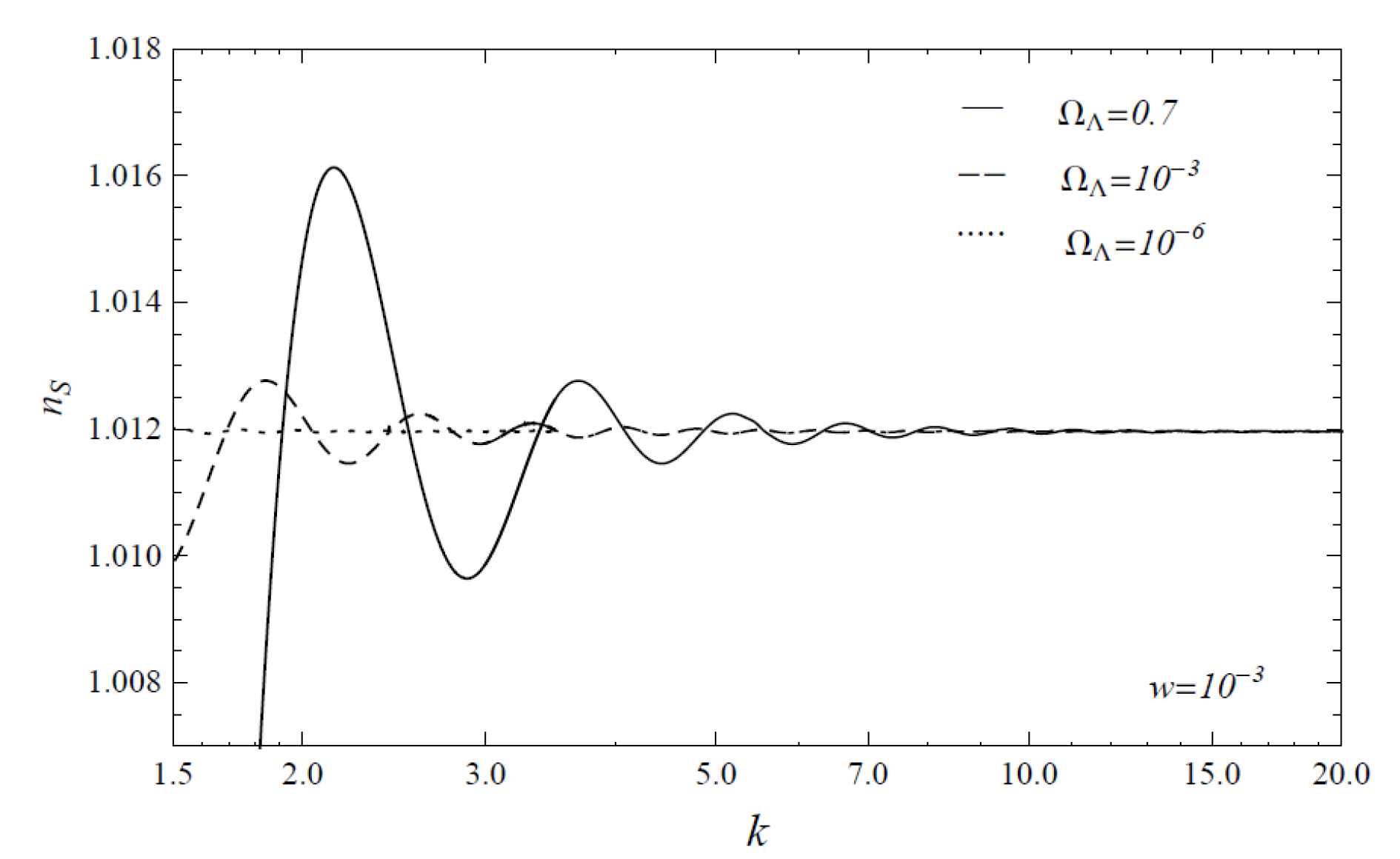
- All the features above yield simple equations for quantum perturbations in quantum backgrounds, which is not an easy task under other approaches [112]. These simple equations could be solved, providing sensible bouncing models with inhomogeneous perturbations, in which the presence of a dust fluid (dark matter?) yields an almost scale-invariant spectrum of perturbations, as observed, with the correct amplitudes. Dark energy can also be included, as in the scalar field model of Section 4. In this model, we have seen that a quantum cosmological effect becomes very relevant during the quantum bounce, leading to observable consequences which solve a conflict with observational results that cannot be solved in classical terms, rendering it a viable model to be developed.
- (iv)
- Feature (5) makes direct the evaluation of the parameter limits under which the standard classical Friedmann solution arises from a quantum Bohmian solution.
- (a)
- The angular power spectrum of the temperature–temperature correlation function, and the E and B polarization modes corresponding to the bouncing models described here, and other possibilities, must be calculated in great detail, and compared with the most recent CMB results [113], in order to differentiate these models among themselves and with inflation. Additionally, one could try to find typical fingerprints of a quantum cosmological effect, which cannot be found by other methods. One promising example is the scalar field model presented in Section 4.
- (b)
- In the analysis of more elaborate models, some new observables must be calculated. For instance, in the two-fluid model described in Section 5, one needs to calculate the entropy perturbations. In preliminary calculations [86], as the entropy effective sound velocity is given bythe large scale perturbations become super-Hubble in the dust-dominated era, when , and the short scale perturbations in the radiation-dominated era, when . Hence, in opposition to the adiabatic perturbations, the large scale entropy perturbations are very small compared to adiabatic perturbations, which is in agreement with observations, but they may be relevant at small scales. Hence, even knowing that small scale perturbations are suppressed by Silk damping, some imprint of this effect may be present. Furthermore, they may also slightly affect the spectrum index of large scale adiabatic perturbations. This is work in progress.
- (c)
- The role of dark energy in bouncing models is very important to understand. In Section 5, I presented a possible solution to the issues raised in Section 4, but there are many other possibilities. In the case that dark energy is a cosmological constant, the problem becomes more contrived, with the possibility of observational consequences. Note that bouncing models offer a unique possibility to learn about dark energy through the primordial power spectrum of cosmological perturbations, which is not the case for inflation.
- (d)
- (e)
- The dBB quantum theory, in principle, allows probability distributions that do not obey the Born rule, that are away from quantum equilibrium. It is difficult to find ordinary physical systems in this situation. In cosmology, this may not be the case. For instance, long wavelength perturbations originated from a vacuum quantum state do not relax quickly to quantum equilibrium, yielding a possible departure from quantum mechanical predictions [116]. Additionally, one could relax the conditions imposed in the conditional wave function explained in Section 5, which would lead to corrections to the effective Schrödinger equation for the perturbations in the quantum background regime and a departure from quantum equilibrium, with possible observational consequences.
“To try to stop all attempts to pass beyond the present viewpoint of quantum physics could be very dangerous for the progress of science and would furthermore be contrary to the lessons we may learn from the history of science. This teaches us, in effect, that the actual state of our knowledge is always provisional and that there must be, beyond what is actually known, immense new regions to discover”.
Funding
Acknowledgments
Conflicts of Interest
References
- Hawking, S.W.; Ellis, G.F.R. The Large Scale Structure of Space-Time; Cambridge University Press: Cambridge, UK, 1973. [Google Scholar]
- Wald, R.M. General Relativity; University of Chicago: Chicago, USA, 1984. [Google Scholar]
- Borde, A.; Vilenkin, A. Violation of the weak energy condition in inflating spacetimes. Phys. Rev. D 1997, 56, 717. [Google Scholar] [CrossRef]
- Tolman, R.C. On the theoretical requirements for a periodic behaviour of the universe. Phys. Rev. 1931, 38, 1758. [Google Scholar] [CrossRef]
- Murphy, G. Big-bang model without singularities. Phys. Rev. D 1973, 8, 4231. [Google Scholar] [CrossRef]
- Novello, M.; Salim, J.M. Nonlinear photons in the universe. Phys. Rev. D 1979, 20, 377. [Google Scholar] [CrossRef]
- Melnikov, V.; Orlov, S. Nonsingular cosmology as a quantum vacuum effect [Mass variation, conformal scalar field gauge symmetry spontaneous breakdown]. Phys. Lett. A 1979, 70, 263. [Google Scholar] [CrossRef]
- Khoury, J.; Ovrut, B.; Ovrut, B.A.; Steinhardt, P.J.; Turok, N. Ekpyrotic universe: Colliding branes and the origin of the hot big bang. Phys. Rev. D 2001, 64, 123522. [Google Scholar] [CrossRef]
- Khoury, J.; Steinhardt, P.J.; Turok, N. Designing cyclic universe models. Phys. Rev. Lett. 2004, 92, 031302. [Google Scholar] [CrossRef]
- Biswas, T.; Brandenberger, R.; Mazumdar, A.; Siegel, W. Non-perturbative gravity, the Hagedorn bounce and the cosmic microwave background. JCAP 2007, 0712, 011. [Google Scholar] [CrossRef]
- Cai, Y.F.; Brandenberger, R.; Zhang, X. Preheating a bouncing universe. JCAP 2011, 1103, 003. [Google Scholar] [CrossRef]
- Fabris, J.C.; Perez, R.S.; Bergliaffa, S.E.P.; Pinto-Neto, N. Born-Infeld-like f(R) gravity. Phys. Rev. D 2012, 86, 103525. [Google Scholar] [CrossRef]
- Cai, Y.; Easson, D.A.; Brandenberger, R. Towards a nonsingular bouncing cosmology. JCAP 2012, 8, 020. [Google Scholar] [CrossRef]
- Ijjas, A.; Steinhardt, P.J. Classically stable nonsingular cosmological bounces. Phys. Rev. Lett. 2016, 117, 121304. [Google Scholar] [CrossRef]
- Ijjas, A.; Steinhardt, P.J. A new kind of cyclic universe. Phys. Lett. B 2019, 795, 666. [Google Scholar] [CrossRef]
- Ilyas, A.; Zhu, M.; Zheng, Y.; Cai, Y.; Saridakis, E.N. DHOST bounce. JCAP 2020, 09, 002. [Google Scholar] [CrossRef]
- Novello, M.; Bergliaffa, S.E.P. Bouncing cosmologies. Phys. Rep. 2008, 463, 127. [Google Scholar] [CrossRef]
- Brandenberger, R.; Peter, P. Bouncing Cosmologies: Progress and Problems. arXiv 2016, arXiv:1603.05834. [Google Scholar] [CrossRef]
- Green, M.B.; Schwarz, J.H.; Witten, E. Superstring Theory; Cambridge University Press: Cambridge, UK, 1987; Volume 1. [Google Scholar]
- Ambjorn, J.; Goerlich, A.; Jurkiewicz, J.; Loll, R. Nonperturbative quantum gravity. Phys. Rep. 2012, 519, 127. [Google Scholar] [CrossRef]
- Ashtekar, A. Non-Perturbative Canonical Gravity; IUCAA Lecture Notes; IUCAA: Syracuse, NY, USA, 1990. [Google Scholar]
- Nagy, S. Lectures on renormalization and asymptotic safety. Ann. Phys. 2014, 350, 310–346. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. [Planck Collaboration]. Planck 2015 results-xiii. cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar]
- Cyburt, R.H.; Fields, B.D.; Olive, K.A.; Yeh, T. Big bang nucleosynthesis: Present status. Rev. Mod. Phys. 2016, 88, 015004. [Google Scholar] [CrossRef]
- Misner, C.W. Absolute zero of time. Phys. Rev. 1969, 186, 1319. [Google Scholar] [CrossRef]
- Gotay, M.J.; Demaret, J. Quantum cosmological singularities. Phys. Rev. D 1983, 28, 2402. [Google Scholar] [CrossRef]
- Tipler, F.J. Interpreting the wave function of the universe. Phys. Rep. 1986, 137, 231. [Google Scholar] [CrossRef]
- Kuchar, K.V.; Ryan, M.P. Is minisuperspace quantization valid?: Taub in mixmaster. Phys. Rev. D 1989, 40, 3982. [Google Scholar] [CrossRef]
- Halliwell, J.J. Quantum Cosmology and Baby Universes; Coleman, S., Hartle, J.B., Piran, T., Weinberg, S., Eds.; World Scientific: Singapore, 1991. [Google Scholar]
- de Barros, J.A.; Pinto-Neto, N.; Sagioro-Leal, M.A. The causal interpretation of dust and radiation fluid non-singular quantum cosmologies. Phys. Lett. A 1998, 241, 229. [Google Scholar] [CrossRef]
- Colistete, R., Jr.; Fabris, J.C.; Pinto-Neto, N. Gaussian superpositions in scalar-tensor quantum cosmological models. Phys. Rev. D 2000, 62, 083507. [Google Scholar] [CrossRef]
- Bojowald, M. Absence of a singularity in loop quantum cosmology. Phys. Rev. Lett. 2001, 86, 5227. [Google Scholar] [CrossRef] [PubMed]
- Alvarenga, F.G.; Fabris, J.C.; Lemos, N.A.; Monerat, G.A. Quantum cosmological perfect fluid models. Gen. Relat. Gravit. 2002, 34, 651. [Google Scholar] [CrossRef]
- Ashtekar, A.; Pawlowski, T.; Singh, P. Quantum nature of the big bang. Phys. Rev. Lett. 2006, 14, 141301. [Google Scholar] [CrossRef]
- Ashtekar, A.; Singh, P. Loop quantum cosmology: A status report. Class. Quant. Grav. 2011, 28, 213001. [Google Scholar] [CrossRef]
- Gielen, S.; Turok, N. Perfect quantum cosmological bounce. Phys. Rev. Lett. 2016, 117, 021301. [Google Scholar] [CrossRef] [PubMed]
- Gryb, S.; Thebault, K.P.Y. Superpositions of the cosmological constant allow for singularity resolution and unitary evolution in quantum cosmology. Phys. Lett. 2018, 784, 324. [Google Scholar] [CrossRef]
- Bojowald, M. Quantum cosmology: A review. Rep. Prog. Phys. 2015, 78, 023901. [Google Scholar] [CrossRef]
- Bohr, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 1935, 48, 696. [Google Scholar] [CrossRef]
- Heisenberg, W. The Physical Principles of the Quantum Theory; Dover: New York, NY, USA, 1949. [Google Scholar]
- von Neumann, J. Mathematical Foundations of Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 1955. [Google Scholar]
- Pais, A. ‘Subtle is the Lord... ’ The Science and the Life of Albert Einstein; Oxford University Press: Oxford, UK, 1983. [Google Scholar]
- DeWitt, B.S.; Graham, N. (Eds.) The Many-Worlds Interpretation of Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 1973. [Google Scholar]
- Ghirardi, G.C.; Rimini, A.; Weber, T. Unified dynamics for microscopic and macroscopic systems. Phys. Rev. D 1986, 34, 470. [Google Scholar] [CrossRef] [PubMed]
- Penrose, R. Quantum Implications: Essays in Honour of David Bohm; Hiley, B.J., Peat, F.D., Eds.; Routledge: London, UK, 1987. [Google Scholar]
- Kiefer, C. Conceptual issues in quantum cosmology. Lect. Notes Phys. 2000, 541, 158–187. [Google Scholar]
- Okon, E.; Sudarsky, D. Benefits of objective collapse models for cosmology and quantum gravity. Found. Phys. 2014, 44, 114. [Google Scholar] [CrossRef]
- Martin, J.; Vennin, V. Collapse models and cosmology. arXiv 2019, arXiv:1912.07429. [Google Scholar]
- Gell-Mann, M.; Hartle, J.B. Quantum Mechanics in the Light of Quantum Cosmology. arXiv 2018, arXiv:1803.04605. [Google Scholar]
- Craig, D.A.; Singh, P. Consistent probabilities in Wheeler-DeWitt quantum cosmology. Phys. Rev. D 2010, 82, 123526. [Google Scholar] [CrossRef]
- Bohm, D. A Suggested Interpretation of the Quantum Theory in Terms of “Hidden” Variables. I. Phys. Rev. 1952, 85, 166. [Google Scholar] [CrossRef]
- Holland, P.R. The Quantum Theory of Motion: An Account of the de Broglie-Bohm Causal Interpretation of Quantum Mechanichs; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Dürr, D.; Teufel, S. Bohmian Mechanics; Springer: Berlin, Germany, 2009. [Google Scholar]
- Bell, J.S. Speakable and Unspeakable in Quantum Mechanics; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Valentini, A. Signal-locality, uncertainty, and the subquantum H-theorem. I. Phys. Lett. A 1991, 156, 5–11. [Google Scholar] [CrossRef]
- Colin, S.; Valentini, A. Primordial quantum nonequilibrium and large-scale cosmic anomalies. Phys. Rev. D 2015, 92, 043520. [Google Scholar] [CrossRef]
- Bell, J.S. On the einstein podolsky rosen paradox. Physics 1994, 1, 195. [Google Scholar] [CrossRef]
- Aspect, A. Bell’s inequality test: More ideal than ever. Nature 1990, 398, 189. [Google Scholar] [CrossRef]
- Towler, M.D.; Russell, N.J.; Valentini, A. Time scales for dynamical relaxation to the Born rule. Proc. R. Soc. A 2012, 468, 990–1013. [Google Scholar] [CrossRef]
- Bohm, D.; Hiley, B.J.; Kaloyerou, P.N. Ontological basis for the quantum theory. Phys. Rep. 1987, 144 Pt 2, 349. [Google Scholar] [CrossRef]
- Duerr, D.; Goldstein, S.; Tumulka, R.; Zanghi, N. Bohmian mechanics and quantum field theory. Phys. Rev. Lett. 2004, 93, 090402. [Google Scholar] [CrossRef] [PubMed]
- Duerr, D.; Goldstein, S.; Tumulka, R.; Zanghi, N. Bell-type quantum field theories. J. Phys. A Math. Gen. 2005, 38, R1. [Google Scholar] [CrossRef]
- Struyve, W. Pilot-wave approaches to quantum field theory. J. Phys. Conf. Ser. 2011, 306, 012047. [Google Scholar] [CrossRef]
- DeWitt, B.S. Quantum theory of gravity. II. The manifestly covariant theory. Phys. Rev. 1967, 160, 1113. [Google Scholar] [CrossRef]
- Kuchar, K. Quantum Gravity 2: A Second Oxford Symposium; Isham, C.J., Penrose, R., Sciama, D.W., Eds.; Clarendon Press: Oxford, UK, 1981. [Google Scholar]
- Duerr, D.; Goldstein, R.; Zanghi, N. Bohmian Mechanics and the Meaning of the Wave Function. arXiv 1995, arXiv:quant-ph/9512031. [Google Scholar]
- Halliwell, J.J.; Hartle, J.B.; Hertog, T. What is the no-boundary wave function of the Universe? Phys. Rev. D 2019, 99, 043526. [Google Scholar] [CrossRef]
- Vilenkin, A.; Yamada, M. Tunneling wave function of the universe. Phys. Rev. D 2018, 98, 066003. [Google Scholar] [CrossRef]
- Pinto-Neto, N.; Fabris, J.C.; Toniato, J.D.; Vicente, G.S.; Vitenti, S.D.P. Vector perturbations in bouncing cosmology. Phys. Rev. D 2020, 101, 123519. [Google Scholar] [CrossRef]
- Peter, P.; Pinho, E.J.C.; Pinto-Neto, N. Tensor Perturbations in Quantum Cosmological Backgrounds. JCAP 2005, 07, 014. [Google Scholar] [CrossRef]
- Peter, P.; Pinho, E.J.C.; Pinto-Neto, N. Gravitational wave background in perfect fluid quantum cosmologies. Phys. Rev. D 2006, 73, 104017. [Google Scholar] [CrossRef]
- Mukhanov, V. Physical Foundations of Cosmology; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Peter, P.; Pinho, E.J.C.; Pinto-Neto, N. Noninflationary model with scale invariant cosmological perturbations. Phys. Rev. D 2007, 76, 023506. [Google Scholar] [CrossRef]
- Falciano, F.T.; Pinto-Neto, N.; Vitenti, S.D.P. Scalar field perturbations with arbitrary potentials in quantum backgrounds. Phys. Rev. D 2013, 87, 103514. [Google Scholar] [CrossRef]
- Falciano, F.T.; Pinto-Neto, N. Scalar perturbations in scalar field quantum cosmology. Phys. Rev. D 2009, 79, 023507. [Google Scholar] [CrossRef]
- Giulini, D.; Kiefer, C. Classical and Quantum Gravity Consistency of semiclassical gravity. Class. Quantum Grav. 1995, 12, 403. [Google Scholar] [CrossRef][Green Version]
- Agullo, I.; Ashtekar, A.; Nelson, W. Extension of the quantum theory of cosmological perturbations to the Planck era. Phys. Rev. D 2013, 87, 043507. [Google Scholar] [CrossRef]
- Barrau, A.; Jamet, P.; Martineau, K.; Moulin, F. Scalar spectra of primordial perturbations in loop quantum cosmology. Phys. Rev. D 2018, 98, 086003. [Google Scholar] [CrossRef]
- Brandenberger, R.; Wang, Z. Ekpyrotic cosmology with a zero-shear S-brane. Phys. Rev. D 2020, 101, 063522. [Google Scholar] [CrossRef]
- Pinto-Neto, N.; Santini, E.S.; Falciano, F.T. Quantization of Friedmann cosmological models with two fluids: Dust plus radiation. Phys. Lett. A 2005, 344, 131–143. [Google Scholar] [CrossRef][Green Version]
- Peter, P.; Pinto-Neto, N. Cosmology without inflation. Phys. Rev. D 2008, 78, 063506. [Google Scholar] [CrossRef]
- Vitenti, S.D.P.; Pinto-Neto, N. Large adiabatic scalar perturbations in a regular bouncing universe. Phys. Rev. D 2012, 85, 023524. [Google Scholar] [CrossRef]
- Allen, L.E.; Wands, D. Cosmological perturbations through a simple bounce. Phys. Rev. D 2004, 70, 063515. [Google Scholar] [CrossRef]
- Wilson-Ewing, E. The matter bounce scenario in loop quantum cosmology. JCAP 2013, 1303, 026. [Google Scholar] [CrossRef]
- Cheung, Y.K.E.; Kang, J.U.; Li, C. Dark matter in a bouncing universe. JCAP 2014, 11, 001. [Google Scholar] [CrossRef]
- Peter, P.; Pinto-Neto, N.; Vitenti, S.D.P. Quantum cosmological perturbations of multiple fluids. Phys. Rev. D 2016, 93, 023520. [Google Scholar] [CrossRef]
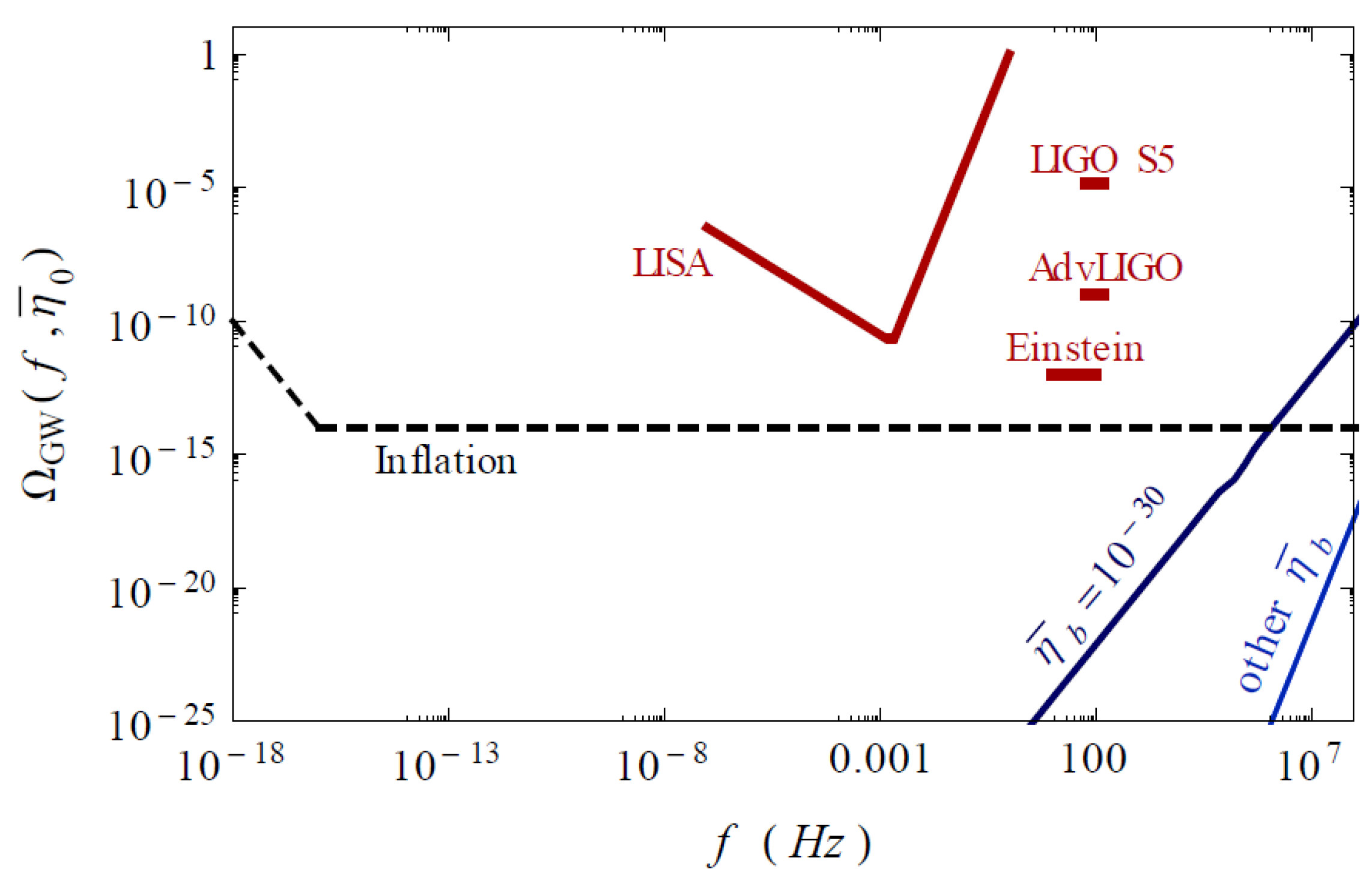
- Bessada, D.; Pinto-Neto, N.; Siffert, B.B.; Miranda, O.D. Stochastic background of relic gravitons in a bouncing quantum cosmological model. JCAP 2012, 54, 1211. [Google Scholar] [CrossRef]
- Abbott, T.M.; Aguena, M.; Alarcon, A.; Allam, S.; Allen, S.; Annis, J.; Avila, S.; Bacon, D.; Bechtol, K.; Bermeo, A.; et al. Dark Energy Survey Year 1 Results: Cosmological constraints from cluster abundances and weak lensing. Phys. Rev. D 2020, 102, 023509. [Google Scholar] [CrossRef]
- Abolfathi, B.; Aguado, D.S.; Aguilar, G.; Allende Prieto, C.; Almeida, A.; Ananna, T.T.; Anders, F.; Anderson, S.F.; Andrews, B.H.; Anguiano, B.; et al. The fourteenth data release of the sloan digital sky survey: First spectroscopic data from the extended baryon oscillation spectroscopic survey and from the second phase of the apache point observatory galactic evolution experiment. Astrophys. J. Supl. Ser. 2018, 235, 19. [Google Scholar] [CrossRef]
- Maier, R.; Pereira, S.; Pinto-Neto, N.; Siffert, B.B. Bouncing models with a cosmological constant. Phys. Rev. D 2012, 85, 023508. [Google Scholar] [CrossRef]
- Quintin, J.; Sherkatghanad, Z.; Cai, Y.-F.; Brandenberger, R.H. Evolution of cosmological perturbations and the production of non-Gaussianities through a nonsingular bounce: Indications for a no-go theorem in single field matter bounce cosmologies. Phys. Rev. D 2015, 92, 063532. [Google Scholar] [CrossRef]
- Li, Y.-B.; Quintin, J.; Wang, D.-G.; Cai, Y.-F. Matter bounce cosmology with a generalized single field: Non-Gaussianity and an extended no-go theorem. JCAP 2017, 3, 031. [Google Scholar] [CrossRef]
- Heard, I.P.C.; Wands, D. Cosmology with positive and negative exponential potentials. Class. Quantum Gravity 2002, 19, 5435. [Google Scholar] [CrossRef]
- Colin, S.; Pinto-Neto, N. Quantum matter bounce with a dark energy expanding phase. Phys. Rev. D 2017, 96, 063502. [Google Scholar] [CrossRef]
- Bacalhau, A.P.; Pinto-Neto, N.; Vitenti, S.D.P. Consistent scalar and tensor perturbation power spectra in single fluid matter bounce with dark energy era. Phys. Rev. D 2018, 97, 083517. [Google Scholar] [CrossRef]
- Lehners, J.; Steinhardt, P.J. Dark energy and the return of the phoenix universe. Phys. Rev. D 2009, 79, 063503. [Google Scholar] [CrossRef]
- Cai, Y.; Marciano, A.; Wang, D.; Wilson-Ewing, E. Bouncing Cosmologies with Dark Matter and Dark Energy. Universe 2017, 3, 1. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K.; Paul, T. From a Bounce to the Dark Energy Era with F(R) Gravity. arXiv 2020, arXiv:2009.09947. [Google Scholar] [CrossRef]
- Lyth, D.H.; Liddle, A.R. The Primordial Density Perturbation; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Weinberg, S. Cosmology; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Una’nue, A.D.; Sudarsky, D. Phenomenological analysis of quantum collapse as source of the seeds of cosmic structure. Phys. Rev. D 2008, 78, 043510. [Google Scholar] [CrossRef]
- Polarski, D.; Starobinsky, A.A. Semiclassicality and decoherence of cosmological perturbations. Class. Quantum Gravity 1996, 13, 377. [Google Scholar] [CrossRef]
- Pinto-Neto, N.; Santos, G.; Struyve, W. Quantum-to-classical transition of primordial cosmological perturbations in de Broglie-Bohm quantum theory: The bouncing scenario. Phys. Rev. D 2014, 89, 023517. [Google Scholar] [CrossRef]
- Pinto-Neto, N.; Santos, G.; Struyve, W. Pinto-Neto, N.; Santos, G.; Struyve, W. Quantum-to-classical transition of primordial cosmological perturbations in de Broglie–Bohm quantum theory. Phys. Rev. D 2012, 85, 083506. [Google Scholar] [CrossRef]
- Martin, J.; Vennin, V. Cosmic microwave background constraints cast a shadow on continuous spontaneous localization models. Phys. Rev. Lett. 2020, 124, 080402. [Google Scholar] [CrossRef]
- Leon, G.; Bengochea, G.R.; Landau, S.J. Quasi-matter bounce and inflation in the light of the CSL model. Eur. Phys. J. C 2016, 76, 407. [Google Scholar] [CrossRef]
- Martin, J.; Vennin, V. Quantum discord of cosmic inflation: Can we show that CMB anisotropies are of quantum-mechanical origin? Phys. Rev. D 2016, 93, 023505. [Google Scholar] [CrossRef]
- Leon, G.; Sudarsky, D. Origin of structure: Statistical characterization of the primordial density fluctuations and the collapse of the wave function. JCAP 2015, 6, 020. [Google Scholar] [CrossRef]
- Bini, D.; Esposito, G.; Kiefer, C.; Kraemer, M.; Pessina, F. On the modification of the cosmic microwave background anisotropy spectrum from canonical quantum gravity. Phys. Rev. D 2013, 87, 104008. [Google Scholar] [CrossRef]
- Kuchar, K.V. Time and interpretations of quantum gravity. Int. J. Mod. Phys. D 2011, 20, 3–86. [Google Scholar] [CrossRef]
- Pinto-Neto, N.; Santini, E.S. Must quantum spacetimes be Euclidean? Phys. Rev. D 1999, 59, 123517. [Google Scholar] [CrossRef]
- Halliwell, J.J.; Hawking, S.W. Origin of structure in the universe. Phys. Rev. D 1985, 31, 1777–1791. [Google Scholar] [CrossRef] [PubMed]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. Astron. Astrophys. 2020, 641, A1. [Google Scholar]
- Cai, Y.-F.; Xue, W.; Brandenberger, R.; Zhang, X. Non-Gaussianity in a matter bounce. JCAP 2009, 05, 011. [Google Scholar] [CrossRef]
- Agullo, I.; Bolliet, B.; Sreenath, V. Non-Gaussianity in loop quantum cosmology. Phys. Rev. D 2018, 97, 066021. [Google Scholar] [CrossRef]
- Vitenti, S.D.P.; Peter, P.; Valentini, A. Modeling the large-scale power deficit with smooth and discontinuous primordial spectra. Phys. Rev. D 2019, 100, 043506. [Google Scholar] [CrossRef]
- Bohm, D.; Hiley, B.J. The Undivided Universe: An Ontological Interpretation of Quantum Theory; Routledge: London, UK, 1993. [Google Scholar]
| 1 | In this section, I will name the Mukhanov–Sasaki mode of Section 4, reserving the name for the Bohmian mode that we are now discussing. |
| 2 | In inflation, this result is direct, while for bouncing models, some care must be taken with the interchange between growing and decaying modes after the bounce, but in the end, the result is the same; see [103]. |
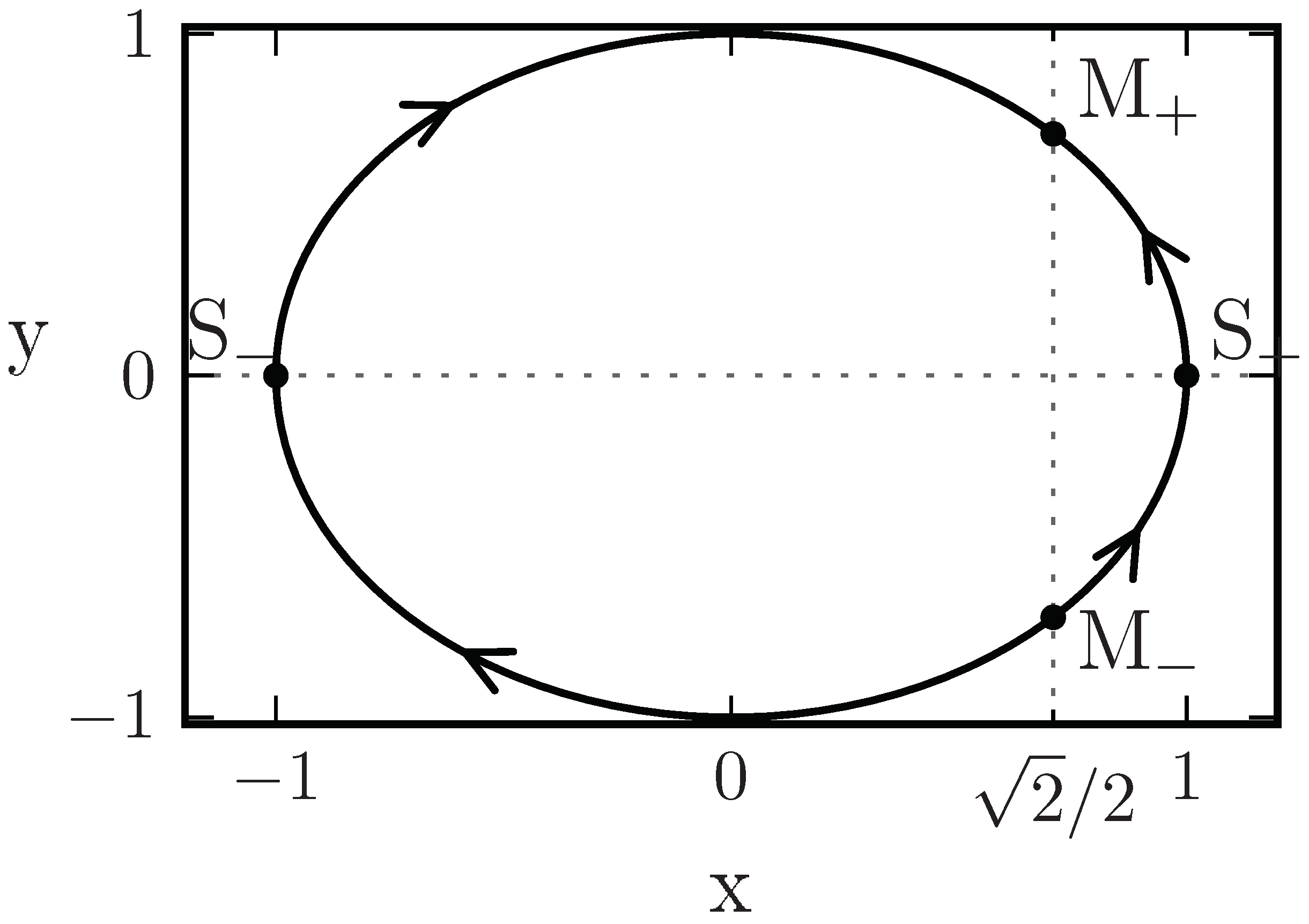
| x | y | z |
|---|---|---|
| 0 | 1 | |
| 1 | 0 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pinto-Neto, N. The de Broglie–Bohm Quantum Theory and Its Application to Quantum Cosmology. Universe 2021, 7, 134. https://doi.org/10.3390/universe7050134
Pinto-Neto N. The de Broglie–Bohm Quantum Theory and Its Application to Quantum Cosmology. Universe. 2021; 7(5):134. https://doi.org/10.3390/universe7050134
Chicago/Turabian StylePinto-Neto, Nelson. 2021. "The de Broglie–Bohm Quantum Theory and Its Application to Quantum Cosmology" Universe 7, no. 5: 134. https://doi.org/10.3390/universe7050134
APA StylePinto-Neto, N. (2021). The de Broglie–Bohm Quantum Theory and Its Application to Quantum Cosmology. Universe, 7(5), 134. https://doi.org/10.3390/universe7050134






