1. Introduction
The first terrestrial direct detection of GWs on 14 September 2015, was a milestone discovery, and it opened up an entirely new window to explore the universe. The combined effort of various scientists and engineers worldwide working on the theoretical, experimental and computational aspects of gravity made this remarkable discovery achievable. The detection of a GW signal, which necessitates measuring displacements over distances as minute as one-thousandth of the proton’s diameter, is unquestionably the essence of human knowledge and endeavour. In 1915 Albert Einstein proposed his theory of general relativity, which is the most competent theory of gravity available to date as it has passed every experimental or observational test in the last 100 years. A year later, in 1916, Einstein suggested the existence of GWs as one of the predictions of GR. According to GR, gravitational attraction is a consequence of the curvature in space-time and GWs are the ripples on the fabric of space-time that travel at the speed of light generated by the accelerating masses. The space-time metric
, in the weak-field limit, can be written as
, where
is the Minkowski metric in the flat space-time and
is the tiny perturbation around it. We get the wave equation
to the leading order in the Transverse-Traceless (TT) gauge on linearizing Einstein’s field equation in the vacuum. In the wave equation, □ is the flat space d’alembertian. Thus, it implies that the metric perturbation represents a GW that propagates at the speed of light [
1]. With the recent discovery of GWs, Einstein’s theory of GR has endured yet another round of heightened scrutiny and passed this experimental test successfully. Like electromagnetic waves, GWs in Einstein’s theory also allows two polarizations transverse to the direction of propagation. GW strain is generally minimal owing to a very weak coupling of gravity with the matter as compared to other forces. For instance, the peak GW strain during the first detection event was as small as
. Thus, it isn’t easy to detect the GWs, and hence, it took elaborate efforts over many decades to devise an experimental setup sensitive enough to observe weak GW signals directly.
The article is organized as follows. In
Section 2 we discuss main sources of gravitational radiation. In
Section 3 we present contribution of Sir Roger Penrose to understanding GWs as prediction of Einstein’s general theory of relativity. In
Section 4 we review GW detectors. In Section we present main GW measurements in the first two observational runs of the LIGO and Virgo detectors. In
Section 6 we present in detail the detections of GW signals made during the first half of the third observational run of the LIGO and Virgo detectors. In
Section 7 we present plans for future observations.
2. Gravitational-Wave Sources
The most promising candidates for ground-based GW interferometers are the binary systems consisting of BHs and NSs. The first detected GW signal originated from the merger of a binary black hole (BBH) system. Binary systems consisting of two stars radiate GWs and as a result of radiation reaction the distance between the components of the binary decreases. This results in a oscillating signal whose amplitude and frequency increases with time and which is called a chirp. The two stars eventually merge to form a single object.
A supernova explosion is also a credible source for the emission of GWs. During the lifecycle of a star, the radiation resulting from the nuclear fusion in the interior balances the inward gravitational force. A massive star dies catastrophically when it runs out of its nuclear fuel, and its core undergoes a gravitational collapse, forming possibly an NS or a BH, while the outer layers are blown apart, creating a supernova. An asymmetric collapse causes the time-varying quadrupole moment, which leads to the emission of GWs in the form of a burst. The waveform of the burst radiation is not well understood yet, and it is still a topic of research.
Another source of GW is the mountain on the crust of a rotating NS. This mountain can be as high as a few cm, induces deformation in the star, and produces a time-varying mass quadrupole moment. This deviation from the symmetry is responsible for almost a pure sinusoid GW signal with the frequency proportional to the star’s spin frequency in the source frame. This signal from an isolated NS is weaker than that originated from the binary merger, but its long-lasting nature may lead to detection with future detectors. A continuous GW from an NS will shed light on the exotic nuclear physics in the star’s core and impose a constraint on the equation of state. Despite the absence of any continuous GW, there is a spin-down limit for Crab, Vela, and several other pulsars limiting the loss of pulsars rotational kinetic energy due to the emission of GWs to a small fraction.
Finally, we discuss the stochastic GWs resulting from various physical processes that are inherently stochastic or due to the interference of different coherent signals that are too weak to be resolved individually. For example, the inflation phase of accelerated expansion in the early universe at an approximately constant Hubble rate produces stochastic GWs with quantum mechanical origin. Besides inflation, several phase transitions in the early cosmos, oscillatory motion of cosmic defects such as cosmic strings may contribute to such signals. Future third-generation ground-based detectors can identify stochastic GW background due to the unresolved binary BH and NS mergers.
The future of GW astronomy is bright because they have the potential to surprise us by exploring entirely new objects and phenomena.
3. Roger Penrose Contribution to Understanding Gravitational Waves
In the year 2020 Nobel prize in physics was awarded to Roger Penrose, Reinhard Genzel and Andrea Ghez for discovery of BHs. In particular Sir Roger Penrose was awarded for the discovery that black hole formation is a robust prediction of the general theory of relativity. This is very much related to discovery of GWs that was awarded Nobel prize in physics in 2017 because the first GW signals detected originated from merger of a BBH system. Moreover Penrose made key contributions to theoretical understanding of GWs as a prediction of GR. His results are summarized in a seminal paper published in Physical Review Letters in the year 1963 [
2]. The key mathematical tool in that paper was exploiting the conformal structure of space-time by introducing a new “unphysical” metric
assigned to space-time, which is conformal to the original physical metric
with
and according to which “infinity” is now finite and in most places regular. This new tool led to a geometrical definition of asymptotic flatness, covariant definitions of incoming and outgoing gravitational fields, simple deduction of detailed asymptotic behavior of the Riemann tensor-the “peeling-off” property, definitions of total energy-momentum and its loss by radiation with conservation laws, unification of finite and asymptotic versions of the characteristic initial value problem, and geometrical derivation of the Bondi-Metzner-Sachs asymptotic symmetry group. These fundamental results of Penrose put earlier work of Bondi, Pirani, Sachs and Trautman on GWs on a firm mathematical ground giving a mathematical proof of the existence of gravitational radiation in relativity. It is also important to note that the theory developed by Penrose applies to radiation of fields of any spin, not only to gravitational radiation!
Fundamental paper by Penrose on gravitational collapse was published in Physical Review letters in 1965 [
3]. Penrose’s research in this field was motivated by observations of quasars which emit enormous amounts of energy that could result from the collapse of a mass of millions of solar masses accompanied by a violent release of energy, possibly in the form of gravitational radiation. The key concept that Penrose introduced in his seminal paper was that of a
trapped surface. A trapped surface is a closed two-dimensional surface with the property that all light rays orthogonal to the surface converge when traced toward the future. This is contrary to a spherical surface in flat space, where outward-directed light-rays diverge. The concept of the trapped surface enabled to define gravitational collapse in geometrical terms independent of any symmetry of space-time. With this tool Penrose was able to prove mathematically that gravitational collapse is inevitable. Moreover he obtained probably the most fundamental result in GR—the inevitable occurrence of
space-time singularity as a result of gravitational collapse. The result meant that classical general theory of relativity must eventually break down. This led to extensive investigations to develop theories, often referred to as quantum gravity that could describe the final stages of gravitational collapse. Concerning space-time singularities Penrose proposed a certain very intriguing hypothesis called
cosmic censorship hypothesis [
4]. This hypothesis supposes that the singularities that arise as a result of gravitational collapse are always clothed by BH event horizon and are not visible to outside observers. Cosmic censorship hypothesis was subject of extensive research with both attempts to prove the hypothesis mathematically and studies of counterexamples to the hypothesis [
5]. Cosmic censorship can also be verified observationally. In the case of a Kerr solution the BH occurs only when
where
a is angular momentum per unit mass and
m is the mass of the BH. For
there is no black hole event horizon and singularity is “naked”, visible to distant observers. Thus measurements the parameter
a of observed BH candidates can provide insight into Penrose’s hypothesis [
6]. The measurements of the parameter
a from GW observations presented in the following sections indicate that inequality
holds.
4. Detectors
In this section, we shall briefly discuss detectors which made the observations of GWs possible. Currently, four laser interferometric detectors are operational with the desired sensitivity. Two of them are USA based detectors, known as Laser Interferometer Gravitational-Wave Observatory (LIGO), and they are located in Hanford, Washington and Livingston, Louisiana. A third detector, known as Virgo, is situated in Cascina (near Pisa) whereas, a fourth one, known as KAGRA, is located at the Kamioka mine in Japan. It is worth mentioning that LIGO and Virgo are ground-based observatories whereas KAGRA is constructed underground. There is one more detector located in Hannover, Germany and it is called GEO600. The sensitivity of this detector is too low to detect a signal because of shorter arm lengths. Nevertheless, it is used as an R & D detector with exceptional importance in testing various technologies before implementing them in LIGO or Virgo.
The quest for GW detectors began in 1957 when Felix Pirani proposed the physical existence of gravitational radiation at the Chapel Hill conference. Joe Weber, who listened to the talk of Pirani, came up with the idea of resonant bar detectors to observe GWs. Weber’s detector was a massive aluminium cylinder vibrating in its longitudinal modes and it can be considered as two test masses connected to a spring. The principle behind these detectors is coupling between GW and test masses and the electromagnetic field is used as the motion transducer.
The first laser interferometers were proposed by Gertsenshtein and Pustovoit in 1962 [
7]. and first built by Forward at Hughes Research Laboratories [
8]. Later on, Rainer Weiss studied the noise and performance of such detectors in 1972 [
9] and the continuous efforts of various scientists and engineers in different continents led to the first agreement between Massachusetts Institute of Technology (MIT) and California Institute of Technology (Caltech) for LIGO detectors in 1984. On the other hand due to the pioneering efforts of Allain Brillet in France and Adalberto Giazotto in Italy in mid 1980s the Virgo project was defined in 1989. Virgo was approved by the French National Centre for Scientific Research (CNRS), France in 1993 and then by the National Institute for Nuclear Physics (INFN), Italy in 1994.
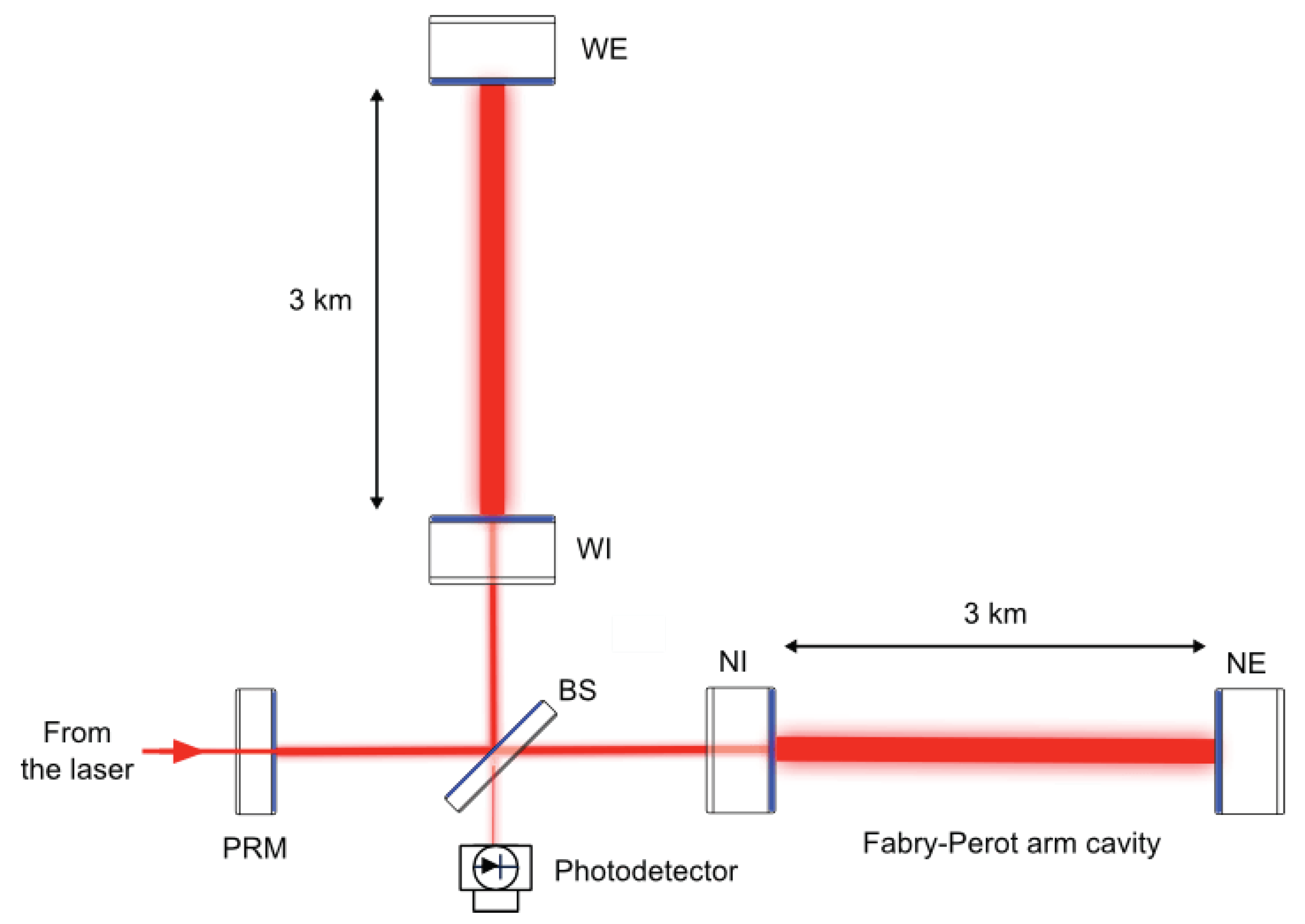
GW interferometers are motivated by the Michelson interferometers where light travelling in two arms adds up to cause an interference pattern at the output (photodetector). In GR, GWs have only two tensor polarization states (
and
) which are obtained by imposing various gauge conditions known as Transverse-Traceless (TT) gauge. The physical significance of the word transverse is that the deformations in the arms are orthogonal to the direction of propagation of the wave, whereas, traceless means that if a wave passes in the z-direction, then one arm of the detector stretches in the y-direction and the other arm shrinks in the x-direction and vice versa in such a way that the volume is not changed. The interaction of the laser interferometer with the GWs can be understood in terms of the geodesic equation and the equation of the geodesic deviation. These instruments perform near the dark fringe, which corresponds to the complete destructive interference at the output without any GW signal. The current GW interferometers are designed to detect GWs in the frequency range ∼ [10, 1000] Hz with a strain amplitude (h) of the order
. The formula below gives the expression for strain amplitude
where
L is the length of the arm and
is the change in the arm induced by a passing GW. This change in length of the arms is decoded in terms of fringes at the photodetector. The formula of strain suggests that a very long arm helps in the detection but, this is challenging for practical and economic constraints. On the other hand, if the arm is very long, GW amplitude changes with time during the round trip of light in the arms. A time average of this change will in turn scale down the sensitivity of the detector. By taking these arguments into account, the arm length for LIGO has been chosen to be 4 km and that of Virgo and KAGRA is 3 km. Although a very long arm is not feasible, one can still make the light storage time higher without extending the interferometer using a Fabry-Perot (FP) cavity. The FP cavity is a resonant cavity where the stored resonating electromagnetic field enables us to increase the effective length of the interferometer and make the apparatus more sensitive. For LIGO, this results in the bouncing of light 300 times by making the effective length of the interferometer to be 1200 km. This increased effective length reduces one important noise—the photon shot noise described below but not other sources of noise like the thermal noise.
The most phenomenal aspect of the GW interferometers is their sensitivity which allows them to detect a very feeble signals. But the hypersensitivity of these detectors also turns out to be their drawback because they are susceptible to various noise sources. A GW signal is buried under the resultant of various noises which imposes a great challenge for the scientific community to extract this signal. The noise sources dominating at the low frequency are seismic noise and thermal noise from the suspension wires. In the mid-frequency range, noise is dictated by the thermal noise of the mirrors, whereas at high frequency, the shot noise has higher influence. In the subsequent paragraphs, we shall discuss these noise sources briefly.
The sources of seismic noise are the continuous movement of the earth’s crust in a wide frequency range, bad weather or a heavy vehicle passing nearby. To reduce this noise, the Virgo detector suspends the mirror with a chain of oscillators which attenuate vibrations in all the six degrees of freedom, whereas, the LIGO detector uses a 4-stage pendulum called a ’quad’. The KAGRA detector has been constructed underground to minimize the seismic noise as well as gravity gradient noise. Another source of noise at the low frequency is the thermal noise from wires due to the random motion of molecules. To overcome this issue, the LIGO and Virgo use monolithic fused silica wires to suspend the mirrors.
In the mid-frequency range the most important are the Brownian noise and the thermoelastic noise due to irreversible thermodynamic processes triggered by thermal conductivity. These noises are reduced by introducing large and heavy (40 kg) mirrors both in LIGO and Virgo as well as low loss coating (TiO2 dopants) which reduces mechanical dissipation. The noise can be further cut down by cooling the mirrors to a low temperature and using a larger beam size on the mirror. To this end the KAGRA detector uses cryogenic mirrors.
In the high-frequency range, the noise is related to the measuring of optical power at the photodetector. The measuring of optical power is equivalent to counting the number of photons arriving during a measurement interval and the probability distribution of photons is given by the Poisson law. There is a displacement noise at the output due to the fluctuations in the number of photons which is known as shot noise. The shot noise can be reduced by increasing the power arriving at the output. Also, fringes in the photodetector become sharper with an increase in the number of photons. As photons carry momentum, an increase in the power exerts more mechanical pressure fluctuations on the mirrors and this is known as radiation pressure noise. This situation is conceptually similar to the Heisenberg microscope. It is remarkable to witness how a quantum effect due to the uncertainty principle can be crucial in the measurement of the position of a macroscopic body, like the mirror of an interferometer, which typically weighs 40 kg. To minimize the combination of shot noise and radiation pressure noise, the detectors should work at optimal power
where
c is the speed of light,
is the wavelength of the laser,
m is the mass of the mirror and
f is the frequency of the GW.
The input power of LIGO is 40 W and that of Virgo is 18 W but the formula for optimal power suggests the need of a higher power of about 360 MW for the desired sensitivity. This power crisis problem is also ironed out with the help of the FP cavity. In the LIGO detector, the power is increased to 750 kW by making 300 roundtrips in the FP cavity. whereas, the power enhancement in the Virgo is 650 kW by making 280 roundtrips. Besides using the FP cavity, the power is also recycled by placing a partial transmitting mirror between the laser and beam splitter. On the other hand, the signal is also recycled by installing a partially reflective mirror between the beam splitter and photodetector. As we have recycled both the power and the signal, the interferometer is called the Dual recycled Fabry-Perot Michelson interferometer.
Figure 1 shows a simplified optical configuration and
Figure 2 displays an aerial view of the Virgo detector which is located in Cascina, Italy.
It should also be noted that the presence of four or more detectors resolves the ambiguity in the location of the source of GW. The locus of time delay in two detectors forms an annulus. If we include the third detector, the annuli intersect at two different points, one of which is the location of the source while the other point is the mirror image of the source. On the other hand, the presence of four or more detectors gives the unique intersection and improves the sky localization.
5. First Detections of Gravitational Waves
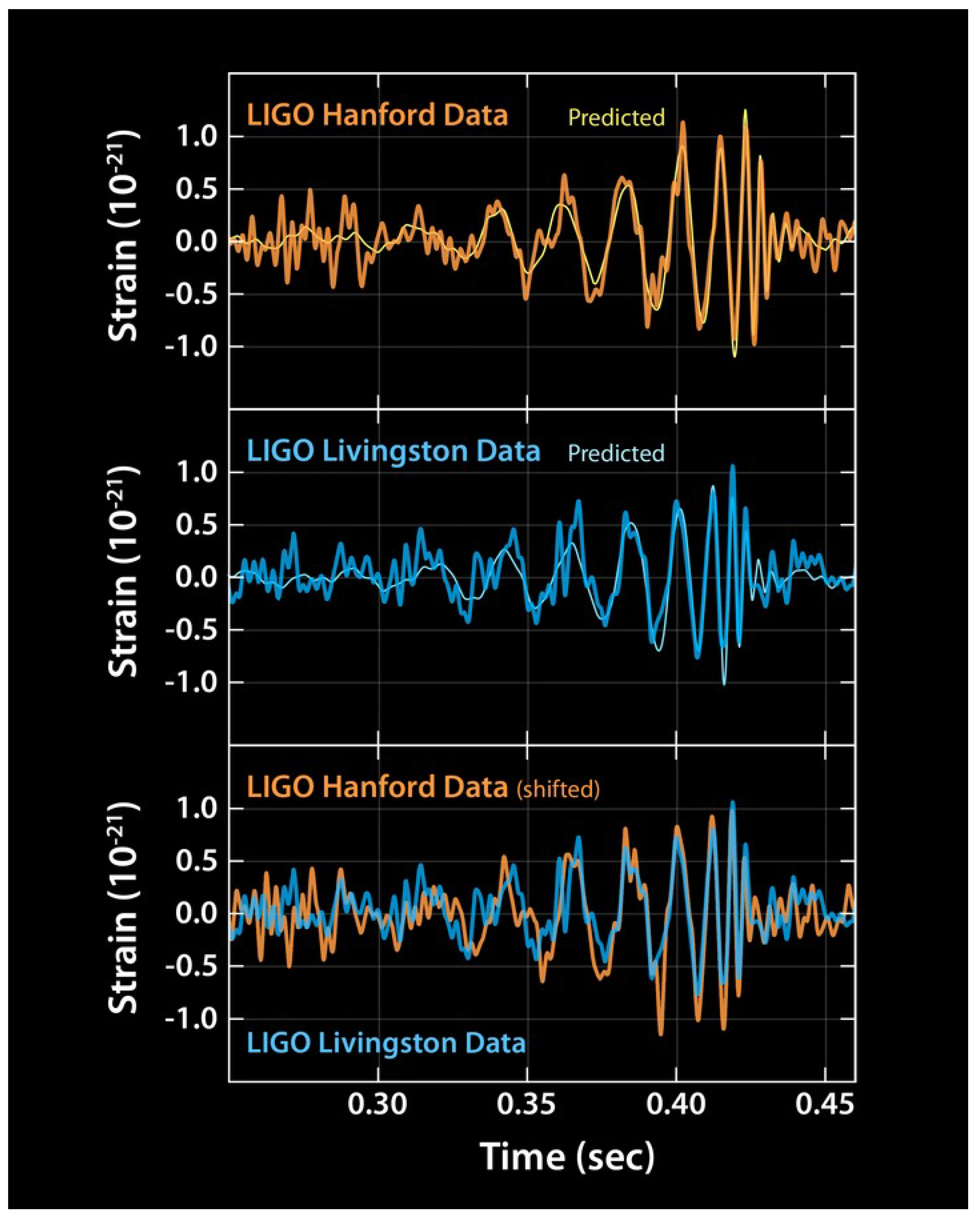
The two LIGO interferometers observed the first direct GW signal on 14 September 2015, during the first observing run (O1) that lasted from 12 September 2015, to 19 January 2016. This signal, named as GW150914, was first recorded at the LIGO Livingston Observatory (LLO) and then by LIGO Hanford Observatory (LHO) after 7 ms. An online signal search algorithm recognised the signal within 3 minutes from its arrival at the detectors. The detected signal was robust with a signal-to-noise ratio (SNR) of 24. [
10]. The use of various parameter estimation pipelines concluded it to be a GW signal that originated from the merger of two BHs with masses of
and
. The newly postmerger BH formed had a mass of
, implying that
of energy were radiated away in the form of GWs. The system was 1.3 billion light-years away from us when two BHs plunged into each other.
The observed GW signal from the two LIGO interferometers is shown in
Figure 3.
The GW150914 confirms the prediction made by GR at three different stages of the evolution of the binary:
inspiral,
merger and
ringdown. This GW event turned out to be advantageous to test the efficacy of GR in a highly nonlinear regime [
12]. The peak amplitude of GW150914 is
, which compares to a displacement of the interferometer’s arms of
m. Besides GW150914, O1 has recorded two more signals which resulted from the BBH merger.
The second observing run (O2) took place from 30 November 2016, to 25 August 2017. A significant improvement during O2 was that the Advanced Virgo detector in Europe joined the two Advanced LIGO detectors in the USA for the first time on 1 August 2017. The network of three detectors witnessed the first event together on August 14. This signal that originated from the coalescence of a BBH system was considerably similar to the event GW150914. This binary system consisted of two BHs with masses 30
and 25
and 2.7
energy released in gravitational radiation. Just three days after this BBH merger, on 17 August 2017, the LIGO-Virgo network observed a signal from the coalescence of two NSs. This event, called GW170817, was the first direct detection of a BNS system. [
13]. It was an exciting moment because, after 1.7 seconds, NASA‘s Fermi satellite recognised Short Gamma-Ray Burst called GRG170817A, an electromagnetic analogue to the BNS merger. This first-ever joint detection of gravitational and electromagnetic radiation from the same source is a marvellous occasion that marks the advent of multi-messenger astronomy [
14].
Our galaxy hosts loads of NSs and many of them exist in pairs constituting a binary system. Careful radio observations of BNS system such as Hulse-Taylor pulsars indicate that the orbit shrinks as the system evolves [
15]. The orbital dynamics is ideally consistent with calculating the loss of orbital energy due to the emission of gravitational radiation. The first indirect confirmation of GWs originated from observing the orbital period of the Hulse-Taylor binary system. For this exceptional discovery, Russell Alan Hulse and Joseph Hooton Taylor Jr. won the Nobel prize in 1993. The orbital dynamics of Hulse-Taylor binary systems, calculated using GR, predict that this system will merge in around 300 million years, giving rise to an event similar to that of GW170817. Such mergers are common throughout the universe, and hence physicists were anticipating the GW signal from the BNS merger. To summarize, the O2 run has witnessed one BNS merger and seven BBH mergers.
The discovery of GWs brought Nobel prize in Physics in the year 2017 to the three founders of the LIGO project—Rainer Weiss, Barry Barish and Kip Thorne.
6. Gravitational-Wave Observation in the First Half of the Third LIGO-Virgo Observing Run
This section presents the results of the third observation run (O3a) of LIGO and Virgo, which recorded data between 1 April 2019, 15:00 UTC and 1 October 2019, 15:00 UTC. The number of events detected in the first (O1) and second (O2) observation runs are 3 and 8 respectively whereas O3a has witnessed 39 events. This set of 50 GW events detected so far in all observing runs is known as Gravitational Wave Transient Catalogue-2 (GWTC-2) [
16]. It is also worth mentioning the new nomenclature used in GWTC-2 for the events. In any event, written like GW
, xyz represents the date and abc denotes the UTC.
The significant increase in the number of events during O3a could be feasible because of major upgrades in the detectors. At low frequency, the residual noise was still a challenge for both LLO and LHO. The source of this noise could be the static charge on the mirror and hence the discharging system was installed. The medium and high-frequency noises were lowered with the help of 40 W input power in LLO and 37 W in LHO and injecting squeezed light in both the detectors. The duty factor of LLO was 76% and that of LHO was 71 at low frequency. At medium-frequency, electronic noise was reduced by installing quantum efficiency photodiodes whereas the high-frequency noise was dealt with using an input power of 20 W and injecting squeezed light in the detector. The Virgo was operational with a duty factor of 76%. With such improvements, three detectors were functional together for 44.5% of the time whereas two of them were operational for 37.4% of the time. A single detector was working for 15% of the time and none of the detectors recorded any data for 3.2% of the total duration of observation. The BNS range of a detector is measured to be the average distance that GWs from a binary neutron star merger could be detected at a SNR of 8. Due to an increase in the sensitivity of each interferometer, the BNS range for LLO, LHO and Virgo are 135 Mpc, 108 Mpc and 45 Mpc respectively.
Once a signal is recorded in detectors, there are two ways to identify the GW sources depending on the time scale. The first method is the
low-latency method and it is used within a few minutes after the signal is recorded. The second method is called
offline re-analysis and it is performed days or months after the detection of the signal. The low-latency algorithm searches for minimally-modelled sources using five pipelines (Coherent WaveBurst [
17,
18,
19], GstLAL [
20,
21,
22], PyCBC [
23,
24,
25], MBTAOnline [
26,
27] and SPIIR [
28]) and it reported 26 out of 39 events via the Gamma-ray Coordinates Network (GCN) [
29]. The remaining 13 events were later on identified by offline re-analysis which uses three different pipelines (Coherent WaveBurst, GstLAL and PyCBC). The offline analyses are different from their low-latency analogues because they have improved template banks, better data calibration, and enhanced tuning to discard the non-stationary noise background discerned in O3a.
Before presenting the properties of the GW signals registered during the O3a run we summarize definitions of the parameters that determine the evolution of the binary systems. These parameters are chirp mass
, total mass
M, mass ratio
q, effective inspiral spin parameter
, effective precession spin parameter
, dimensionless tidal deformability parameter
. The more massive object in the binary system is called the primary component and its mass is taken to be
whereas, the mass of the lighter or secondary object is denoted by
. The total mass
M and the mass ratio
q are defined as
The mass ratio q measures asymmetricity in the system with a range where a value closer to 0 implies an asymmetric configuration.
There is a combination of individual masses known as chirp mass defined to be
The significance of the chirp mass is that in the quadrupole approximation, it determines both the amplitude and the phase modulation of the GW signal from a binary system, and it is generally better constrained than the individual masses of the binary.
The objects in the binary system may also possess individual spins. These spins are encoded in the waveform and the knowledge about individual components bears vital information regarding the evolution of the binary system. The effective inspiral spin parameter
contains information about the spin components that are perpendicular to the orbital plane. On the other hand, if there is a significant projection of the spin in the orbital plane, the orbit will precess and this precession is parametrized by effective precession spin parameter
. The analytical expressions for
is
where
and
are the spins of the primary and secondary components respectively and
is the Newtonian orbital angular momentum. The expression for
is given by
where
and
An important effect that can be helpful to differentiate between a BH and NS is the tidal deformation in an object. The external field created by the primary object induces a quadrupole deformation in its companion object. This deformation is measured in terms of tidal deformability
and in the lowest order approximation, it is given by
where
represents Love number which is dependent on the mass m and the equation of state and R is the radius of the deformed object. It is convenient to introduce a dimensionless tidal deformability parameter
defined as
For a binary system, the dominant tidal contribution to the waveform is expressed in terms of the effective dimensionless tidal deformability parameter
defined as
where
are dimensionless tidal deformability parameters for individual components. Non-spinning BHs have
, and the waveform templates use the convention that this is valid for all BHs.
In the rest of this Section we shall first describe the four most interesting observations in O3a run and then we shall summarize the properties of the remaining events reported in the GWTC-2 catalogue.
6.1. GW190412
In this subsection, we briefly introduce the GW190412 event that was recorded on 12 April 2019 at 05:30:44 UTC with an SNR of 19. This is a BBH system where the masses of primary and secondary objects are approximately 30
and 8
respectively. The source was localized within 156 deg
and its luminosity distance is found to be
Mpc with 90 % probability [
30].
For GW190412, the value of q is found to be making it a very asymmetric BBH system. There are various channels that propose the formation of such asymmetric BBH systems. One mechanism suggests that such asymmetric binary system in dense clusters may be attained by a first-generation BH merging with a higher-generation BH that has already undergone a prior merger or mergers. On the other hand, some models suggest that such an asymmetric system may be a result of massive-star collisions in young star clusters or they could be formed in the disk of active galactic nuclei. At this moment, we cannot discard or favour any particular model just based on one detection and detection of more asymmetric BBH with future sensitive detectors will give us a better understanding of the formation channel.
The analysis of waveform infers that and . The values of and are dominated by massive components because the system is highly asymmetric and this imposes a bound on the primary spin to be , whereas the secondary spin , remains unconstrained. The value of indicates no strong precession nevertheless very small values of are also disfavored. The significant spin of this system could be explained by hierarchical mergers in dynamical environments however, hierarchical mergers are predicted to be relatively rare in dynamical environments compared to first-generation mergers.
The asymmetricity in the components of GW190412 predicts a significant contribution from higher multipoles and there are strong traces of radiation. The presence of higher multipoles may break the inclination-distance degeneracy, thereby tightening constraints on inferred source inclination and luminosity distance. The inclination angle of the source is found to be radians with 90 % probability. Binary systems with asymmetric mass ratios are promising candidates to test GR and GW190412 does not show any deviation from this theory.
6.2. GW190425
In this subsection, we shall summarize the GW190425 event which was observed in the LIGO Livingston detector on 25 April 2019. with an SNR of 12.9 This event represents the merger of a binary system where the masses of the primary and secondary objects are in the range [1.61, 2.52]
and [1.12, 1.68]
respectively. The source-frame chirp mass of this system is
whereas the total mass is
with 90 % probability. Since the individual mass of both the components of the binary system is consistent with other known NSs as well as results of supernova simulations, we may consider this event to be a BNS merger [
31]. The low SNR of GW190425 does not allow us to measure the tidal deformability and this causes ambiguity in classifying the components of the binary system.
At the time of detection, LHO was temporarily offline and the SNR in the Virgo detector was below the detection threshold . Due to this, GW190425 is considered to be a single detector event and this increases the uncertainty in the sky localization of the source. The luminosity distance of the source is found to be Mpc and it is localized within 8284 deg which is approximately 16% area of the sky. This ambivalence in the localization of the source may be one of the reasons for not observing an electromagnetic counterpart.
If GW190425 is assumed to be a BNS merger, then there should be an explanation for the formation of such a massive system. One way to form such a system is to have the stellar companion of a massive NS replaced with another NS through a dynamical encounter but this process predicts a low merger rate. Another plausible mechanism suggests that the individual NS were born from low-metallicity stars. By taking possible formation channels into account as well as prior studies, the merger rate of neutron stars is foreseen to be Gpc yr. The detection of more NSs with future sensitive detectors will shed more light on the formation of such a massive system.
6.3. GW190521
The LIGO and Virgo interferometers observed an unusual GW event, GW190521, on 21 May 2019 at 03:02:29 UTC with an SNR of 14.7. This was a short duration (0.1 s) signal with a low peak frequency at 60 Hz which is in contrast to previously detected relatively longer duration and higher frequency signals. Although 60 Hz corresponds to the main power supply in the US, this was confirmed not to be an instrument noise after a careful analysis of the signal. If this signal originates from the merger of a quasi circular binary, then the mass of the primary component is
whereas that of the secondary component is
with 90 % probability. The total mass of the system is
and the presence of very massive components allows us to conclude this event to be a BBH merger. The final object formed after the merger was an intermediate mass black hole (IMBH) of
and approximately 8
energy was released in the form of GWs. It is worth mentioning that 8
is equivalent to
erg/s which is even higher than the bolometric luminosity of one of the most powerful quasars J2157-3602. For a coalescence binary system, the duration and maximum frequency of the GW signal are inversely proportional to the system’s total mass, which describes well the cause of shorter time and lower frequency of GW190521 [
32].
The luminosity distance of the source is estimated to be Gpc which corresponds to a redshift to using cosmology. The inclination of the source is nearly 90 degrees which implies that the radiation is dominated by the quadrupolar modes and higher multipoles are suppressed. The values of the effective inspiral spin parameter and the effective precession spin parameter are believed to be and respectively. This shows that the spin of individual objects is misaligned with the orbital angular momentum causing a precession of the orbit of the system. The final object was formed with a mass and spin and this is the first direct observation of an IMBH. The properties of the final object are consistent with the predictions made by GR and hence, no deviations from GR are observed.
The individual components of this GW190521 pose a challenge to the stellar theory of evolution. Stellar astrophysics predicts that stars with He core mass in the range [32, 64] can produce a BHs up to 65 after a core-collapse supernova whereas stars with He mass larger than 135 can form BHs heavier than 120 by the direct collapse without any explosion. On the other hand, theories discard the formation of BHs in the range [65, 120] because the pair-instability (PI) supernova destroys the core completely before the formation of a BH. The mass of the secondary component (66 ) can be considered to be consistent with stellar physics models if we take measurements uncertainty into account but the primary component lies in the PI gap and its probability to be below 65 M is just 0.32. To account for the existence of the primary object, various formation channels have been proposed. One of the channels suggests the merger of the massive He core star and the main sequence star in the young star cluster produces an oversized H envelope which in turn could collapse to form a BH in the PI gap. Another mechanism proposes that torque produced by gas from the AGN disk favours BH pairing and hierarchical mergers but this model predicts an EM counterpart. By considering different mechanisms, the merger rate of BH binaries similar to GW190521 is predicted to be Gpc yr.
To explain the bizarre signal GW190521, the scientific community has studied various exotic possibilities. These scenarios are head-on collision, highly eccentric merger, core-collapse supernova, primordial BHs, strong gravitational lensing by galaxies and the existence of cosmic strings. The BBH merger is considered to be the most plausible explanation for this event.
6.4. GW190814
In this subsection, we discuss the GW190814 event which was detected on 14 August 2019 at 21:10:39 UTC. The SNR of the event in the three detector network was found to be 25. This is a binary system consisting of a primary object with 22.2–24.3
and a companion compact object with a mass of 2.50–2.67
with a 90 % of confidence level. The source was localized to 18.5 deg
at a distance of
Mpc using the time delay of the signal across a network of detectors as well as amplitude and phase of the waveform in each detector [
33].
For GW190814, the value of q is found to be making it to be the most asymmetric system detected so far. The primary component of the system is conclusively a BH with a mass but, the nature of the secondary object with mass is ambiguous. This mass is larger than the maximum mass of a NS inferred by the GW170817 event or predicted by existing astrophysical models. On the other hand, the maximum mass of a known pulsar in the Milky Way is at a 68.3 % credible interval. Hence, the second object is likely to be a BH, nevertheless, its probability of being a NS is not discarded. A small value of q or a large asymmetricity also implies that the binary system will merge without an electromagnetic counterpart and any measurable tidal deformation in the second component.
The analysis of waveform infers that and with tight constraints. The values of and are dominated by massive components because the system is highly asymmetric and this imposes a bound on the primary spin to be , whereas the secondary spin , remains unconstrained.
The binary systems like GW190814 (with a low mass ratio) have never been observed before and hence, there is no confirmed conclusion about their formation mechanism. Although various channels have been proposed, young star clusters and active galactic nucleus disks turn out to be more promising hosts for GW190814-like mergers. The merger rate density of such binary systems is estimated to be 1–23 Gpc yr and their detection rate may increase with the more sensitive future detector.
The asymmetricity and significant SNR of GW190814 allow us to investigate higher multipole moments. Each subdominant multipole moment has a different angular dependence on the emission direction which in turn gives the precise measurement of the source parameters. There is strong evidence of with the orthogonal optimal SNR of in the GW190814 system. Also, a significant difference in masses of the GW190814 system helps us to test the GR. This is done using the excited higher multipole moments, looking for deviations in the spin-induced quadrupole moments of the binary components, and investigating the source dynamics of the binary through a parameterized test of gravitational waveform generation. But none of the tests anticipates any deviations from GR.
6.5. Gravitational Wave Transient Catalogue-2
The GWTC-2 catalogue contains 39 new sources detected during the O3a run. We shall summarize the key properties of these sources which are masses and spins of the components of the binary systems observed as well as their localization.
Masses. We divide the events detected into two categories depending on whether the mass of the secondary component is less or greater than three solar masses.
Sources with . The candidate events with
are assuredly anticipated to be BBHs. There are 36 events in this category in the GWTC-2 catalogue (see Table VI of [
16]). The third observation run has marked the presence of some very massive BH system.The heaviest binary system is seemingly the one associated with GW190521 described in
Section 6.3 above. Besides GW190521, three other events may have total masses above 100 solar masses: GW190519_153544, GW190602_175927, and GW190706_222641. The event GW190924_021846 is presumably the lightest O3a system in this category with a total mass of
. The mass of the secondary component is found to be
and it is likely to be the least massive object over
. For most sources identified in O3a, the mass ratio posteriors have support at unity and are compatible with identical mass mergers. An exception is a system, GW190412, described in
Section 6.1 which was the first binary discovered with a confidently asymmetric mass ratio.
Sources with . There are three events in this category. One event is GW190425 described in
Section 6.2 which is with great confidence a merger of two NSs making it the second BNS merger after the GW170817. The other event is GW190814 described in
Section 6.4; the mass of the secondary component is
, and there is an ambiguity in identifying this object. This component could either be a BH or an NS. GW190814 posses the most extreme mass ratio of all the detected sources. The third event is GW190426_152155 with the masses of the individual components of
and
. This event could have originated from an NSBH binary as the mass of the secondary component is compatible with that of previously published NSs. However, the data do not contain any information about possible tidal effects.
Spins. Most of the compact objects observed in O3a possess zero spin measures within uncertainties, but some events have exhibited a slight deviation.Two systems have a probability greater than 50% that at least one of the BHs holding dimensionless spin magnitude
. (these parameters are equivalent to the
a parameter of the Kerr solution discussed in
Section 3). These are GW190517_055101 and GW190521. The analysis of O3a results has shown the presence of positive effective inspiral spin
in 11 sources and GW190517_055101 has the highest value. There is no confident evidence of misaligned spins
, but GW190514_065416 likely has a small value of
. This implies that the spin directions of BHs in binaries do not reveal the isotropic distribution with respect to their orbital angular momenta. Concerning precession for most binaries, the posterior on
is comparable to the prior, indicating that the data is primarily equivocal about precession. There is however a clue of mild orbital precession in the systems GW190412 and GW190521.
Localization. The better sensitivity of the detectors has allowed us to identify the GW signals from larger distances as compared to O1 and O2. The farthest event, after considering for measurement uncertainties in the distance, is most plausibly GW190413_134308, with a predicted luminosity distance of Gpc. The nearest source identified in O3a is GW190425, with a suggested luminosity distance of Gpc. GW190814 is the most precisely localized event with an area of 19 deg. On the other hand, GW190424_180648 is the worst localized event with an area of 28,000 deg.
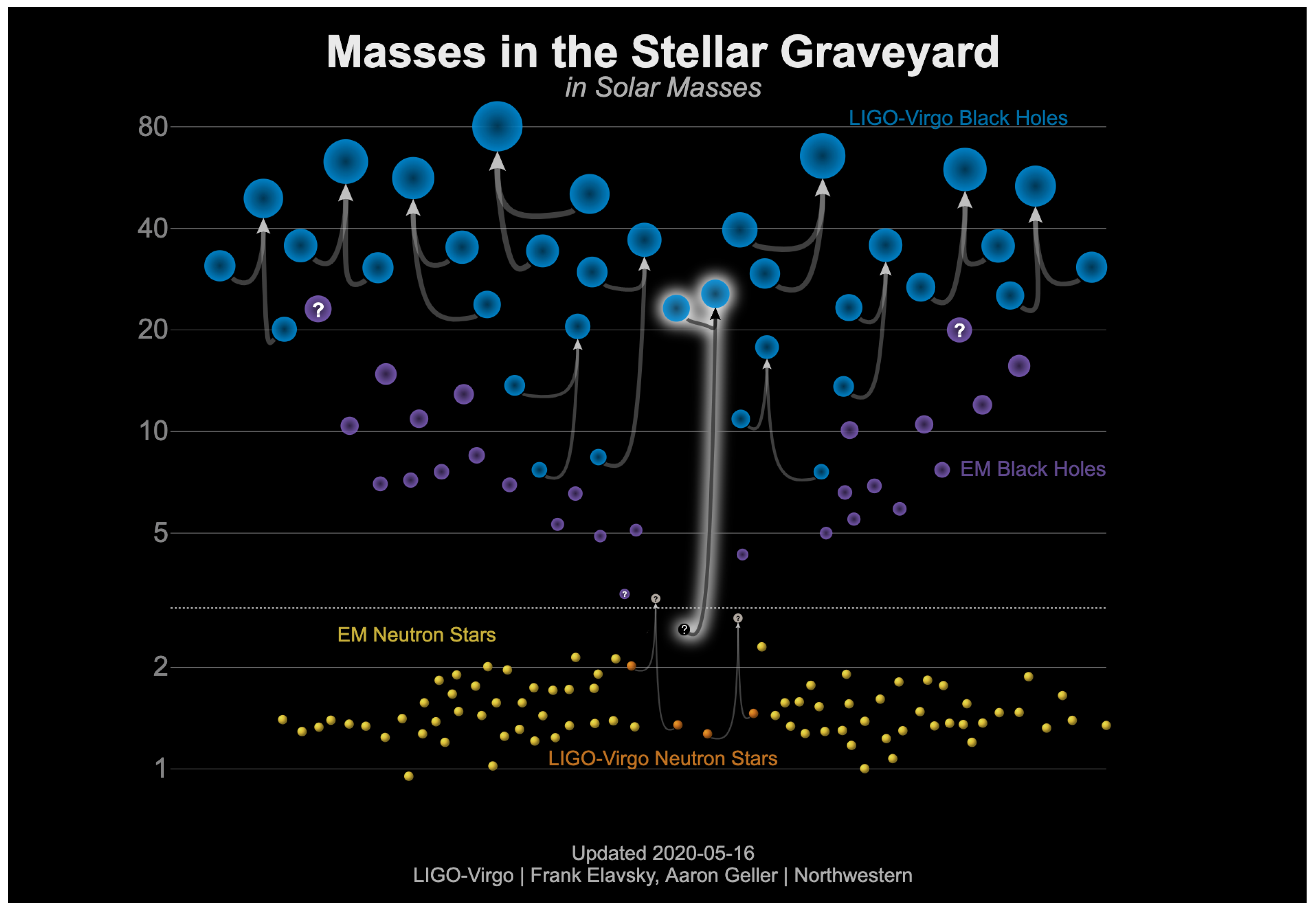
The
Figure 4 shows the masses of NS and BH observed via electromagnetic and gravitational radiation. NS measured by EM waves are represented by yellow and NS measured by GW are highlighted in orange. BH detected by EM waves are shown in purple whereas those observed by GW are represented by blue.
7. Future Detectors
The accomplishment of current detectors has inspired scientists and funding agencies to explore the cosmos by investing in future detectors with enhanced performance. We shall consider future projects in this section.
The current LIGO instruments are planned for an upgrade to LIGO A+ by 2024. One of the major improvements is the introduction of frequency-dependent light squeezing to reduce shot noise at low frequency and radiation pressure noise at high frequency. Other changes involve the replacement of mirrors that have low thermal noise in the coating and low scattered light. The Virgo detector is also going through similar changes and it is called AdV+. These improvements are expected to increase the sensitivity by a factor of 2 and hence the reachable volume in space increases by a factor of 8. With this sensitivity, we can detect 17–300 BBH/month and 1–13 BNS/month which would help in population studies and imposing constraints on the Hubble parameter. Besides LIGO A+ and AdV+, a third LIGO detector is also going to be operational in the Hingoli district, Maharashtra, India in the late 2020s. LIGO India is jointly funded by the National Science Foundation (NSF), USA, the Department of Atomic Energy (DAE) and the Department of Science and Technology (DST), Government of India. The addition of a fifth detector will help in the sky localization and increase the fraction of time that all the instruments are operating.
There are also plans for building very sophisticated third-generation detectors in 2030s by implementing advanced technologies. The European project, Einstein Telescope (ET) [
34], is planned to be an underground detector with 10 km arms. It consists of two detectors, one at low frequency for BHBH merger and the other at a higher frequency for NSNS signals. This entire setup has a triangular shape which allows us to extract the polarization of the signal just by using one observatory. The US Cosmic Explorer (CE) [
35] is an L- shaped ground-based detector with 40 km arms. Both ET and CE are expected to have 10 times higher sensitivity which means that they can record 1000 times more events as compared to current detectors.
The ground-based detectors are sensitive to stellar-mass objects in the range [1, 100]
because the frequency emitted by them lies between 5 Hz to a few kHz. But various objects in the universe emit at lower frequency and this suggests the need for a detector in space.The Laser Interferometer Space Antenna (LISA) is a space-based detector funded by European Space Agency (ESA) with a substantial contribution from the National Aeronautics and Space Administration (NASA) and it is planned to be launched in 2034 [
36]. It is a triangular-shaped detector with 2.5 million km arms and sensitive to the frequency range from around 100 mHz to around 0.1 Hz. This instrument is designed to witness the events like white dwarf binaries, the inspiral of a compact object into a massive black hole in the centre of a galaxy or massive distant black hole binaries with a long coalescence period. LISA may also be able to detect mHz stochastic GW background which could be produced by processes occurring at the TeV scale in the early Universe. With this detector, there is a hope to test the no-hair property of BHs as well as imposing constraints on dark matter candidates and modified theories of gravity.
There is also a quest for searching low-frequency GW by using a network (array) of pulsars. Pulsars are very accurate clocks with a great homogeneity in pulse profile, and little variation in frequency. A passing GW can induce a phase shift in the pulse profile and using the data from different pulsars allows us to make an indirect observation of GW. The International Pulsar Timing Array (IPTA) [
37] uses pulsars to detect lower frequency GW from slowly moving supermassive black holes at the centres of galaxies. The IPTA consists of the European Pulsar Timing Array (EPTA), NANOGrav from the US and Canada and Parkes Pulsar Timing Array (PPTA) which is an Australian collaboration.