Bouncing Quantum Cosmology
Abstract
1. Introduction
2. Bouncing Models from Quantum Cosmology
2.1. The Canonical Scalar Field
2.2. Perfect Fluids
3. Cosmological Perturbations in Quantum Bouncing Backgrounds
3.1. Perfect Fluids
3.2. The Scalar Field
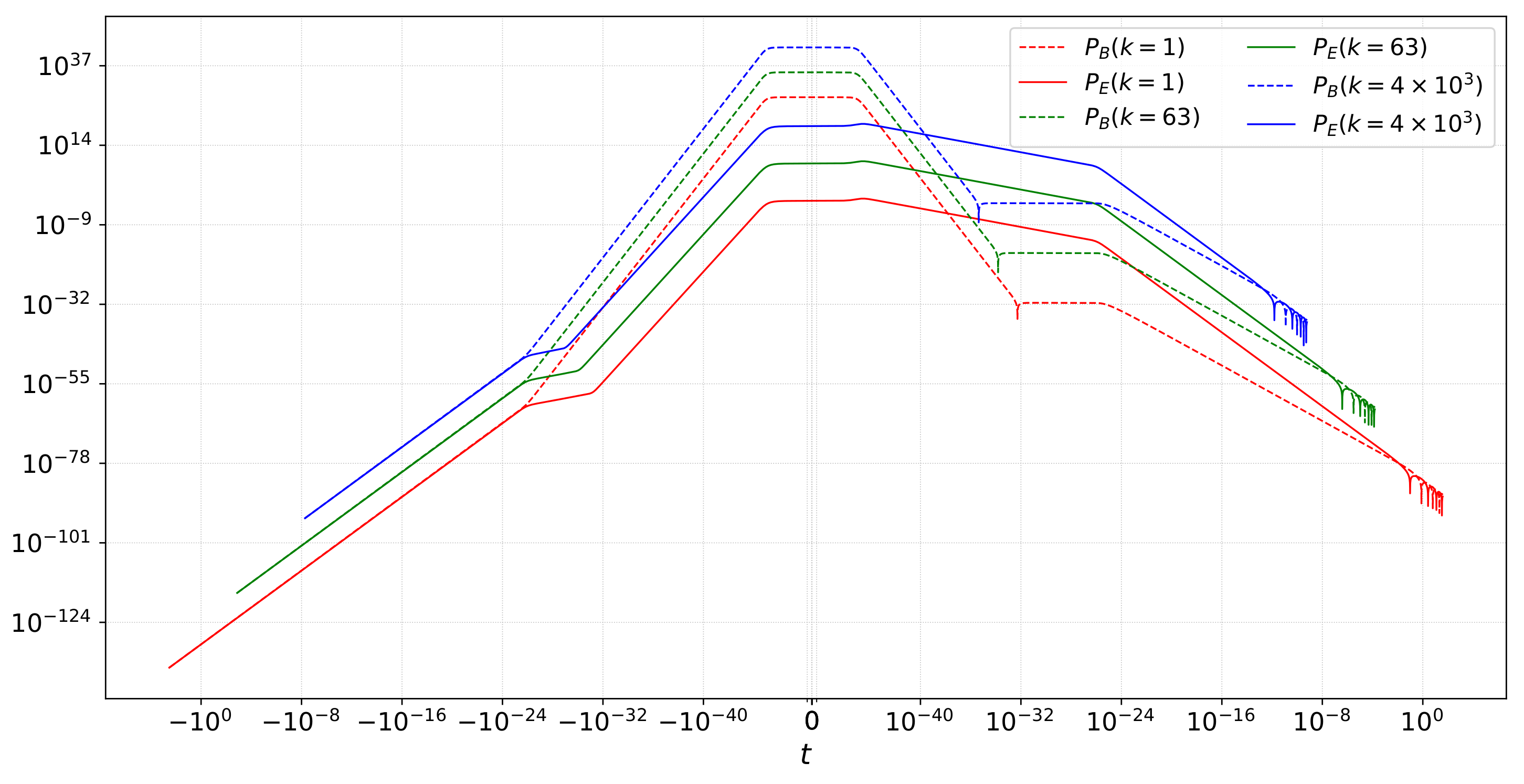
3.3. Gravitational Waves
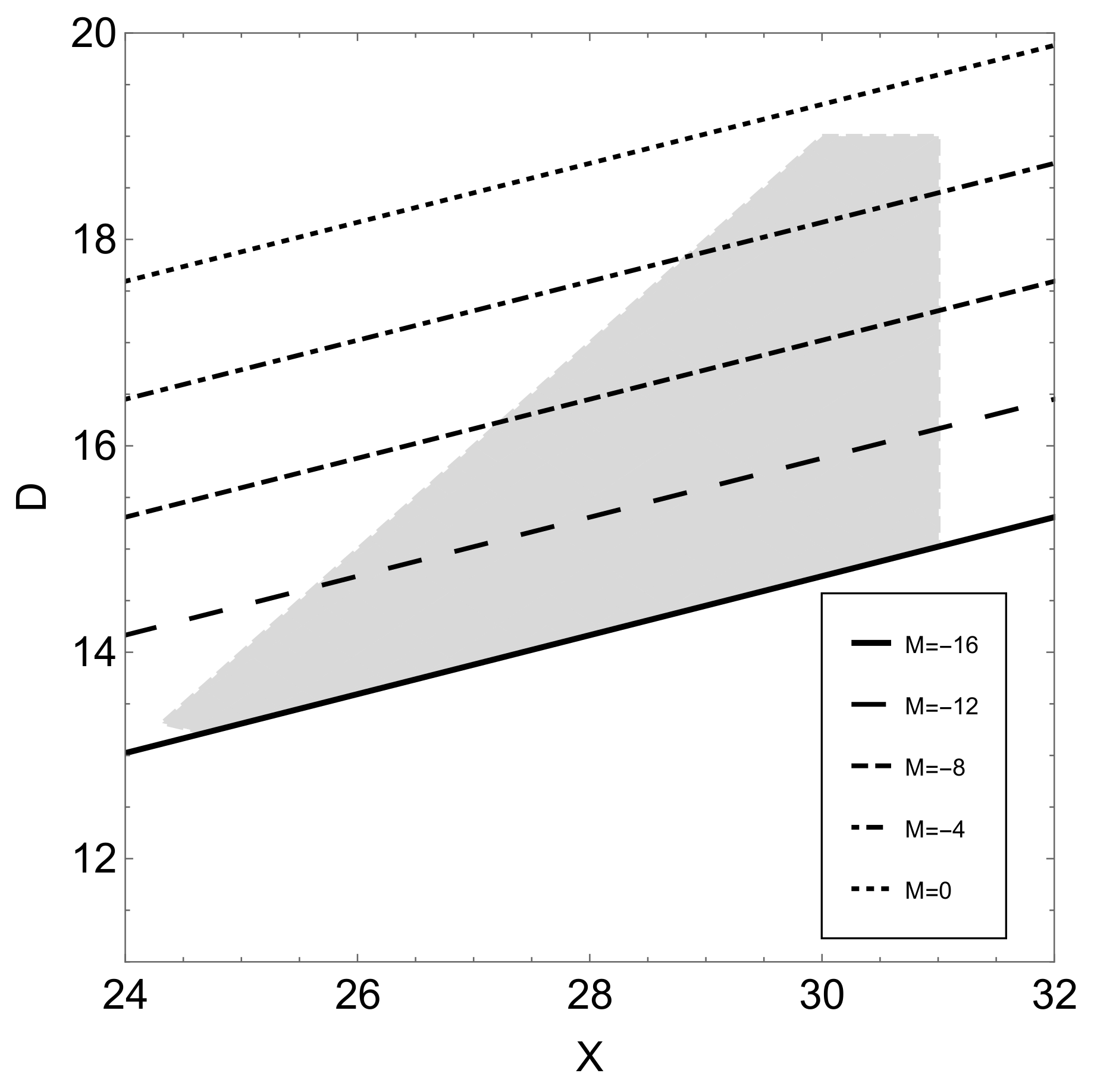
4. Bounce Stability
4.1. Scalar Perturbations
4.2. Vector Perturbations
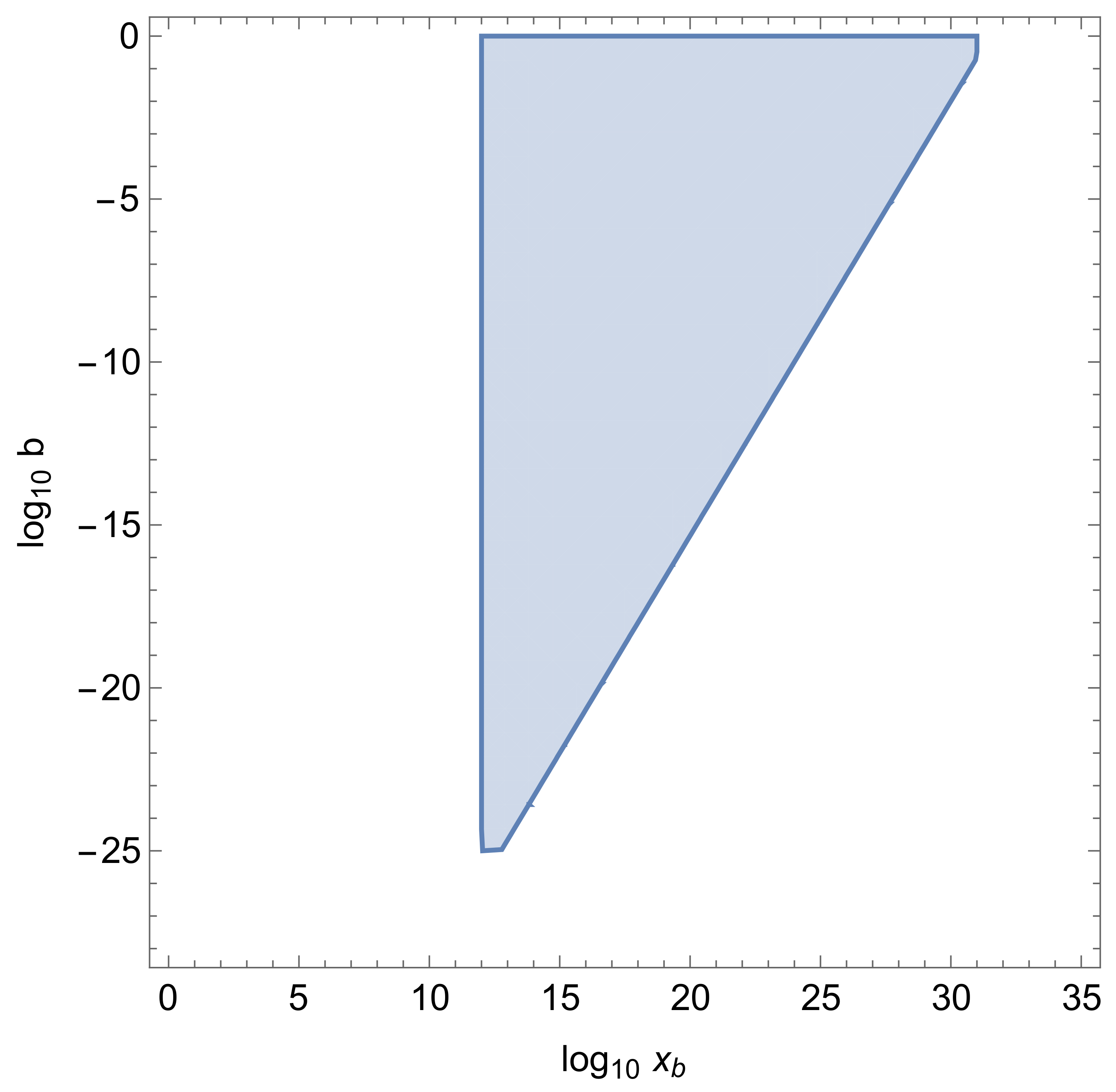
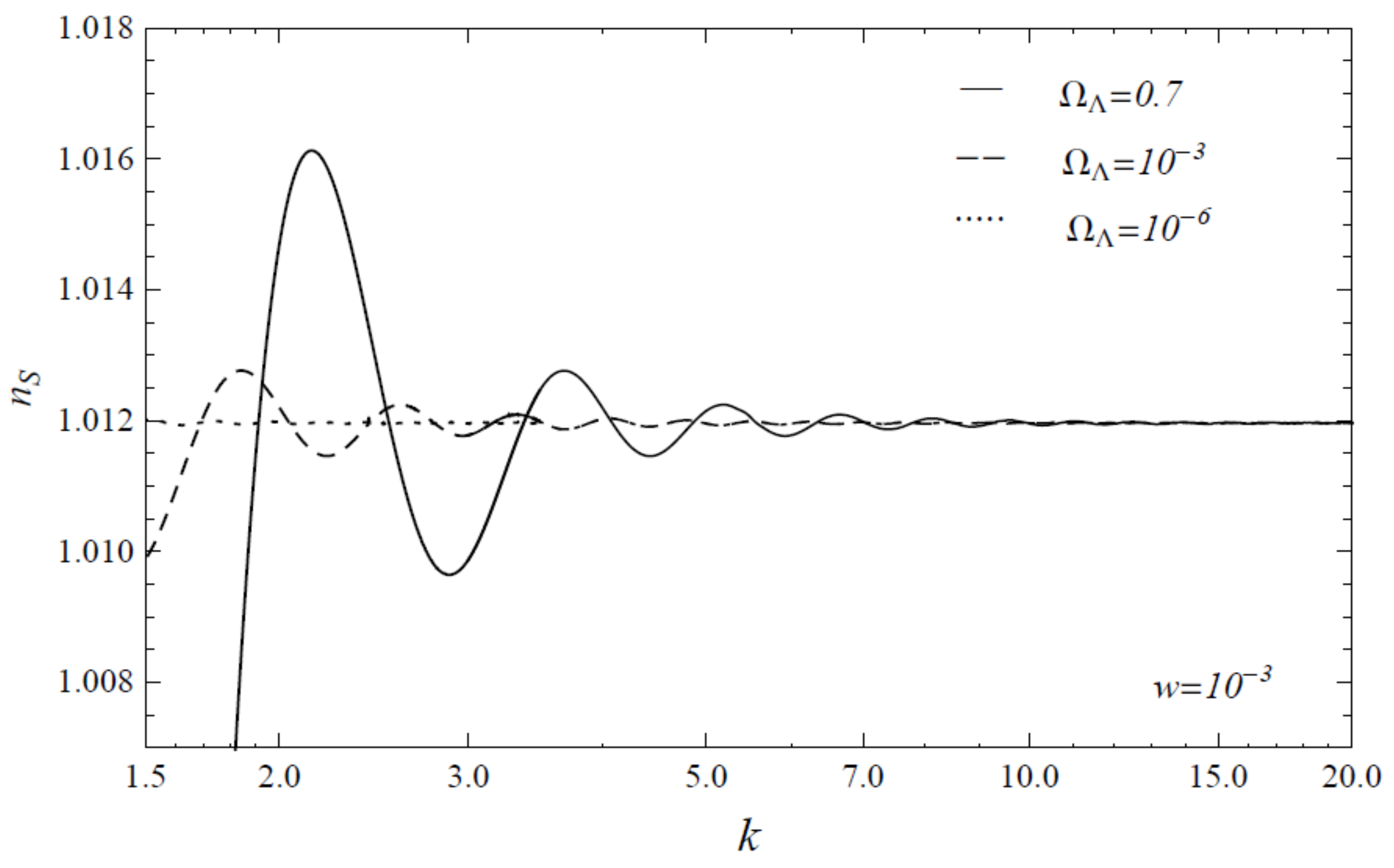
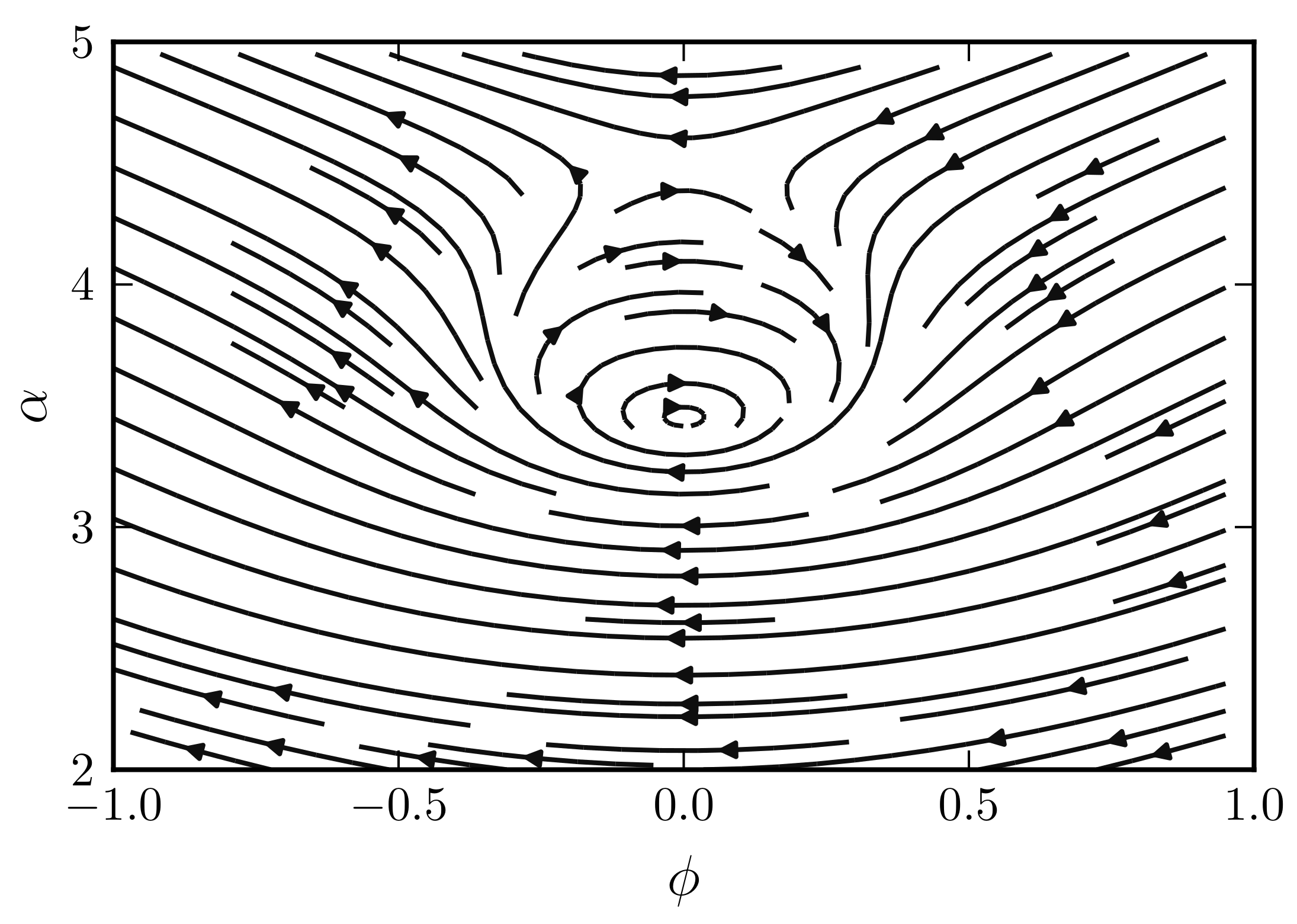
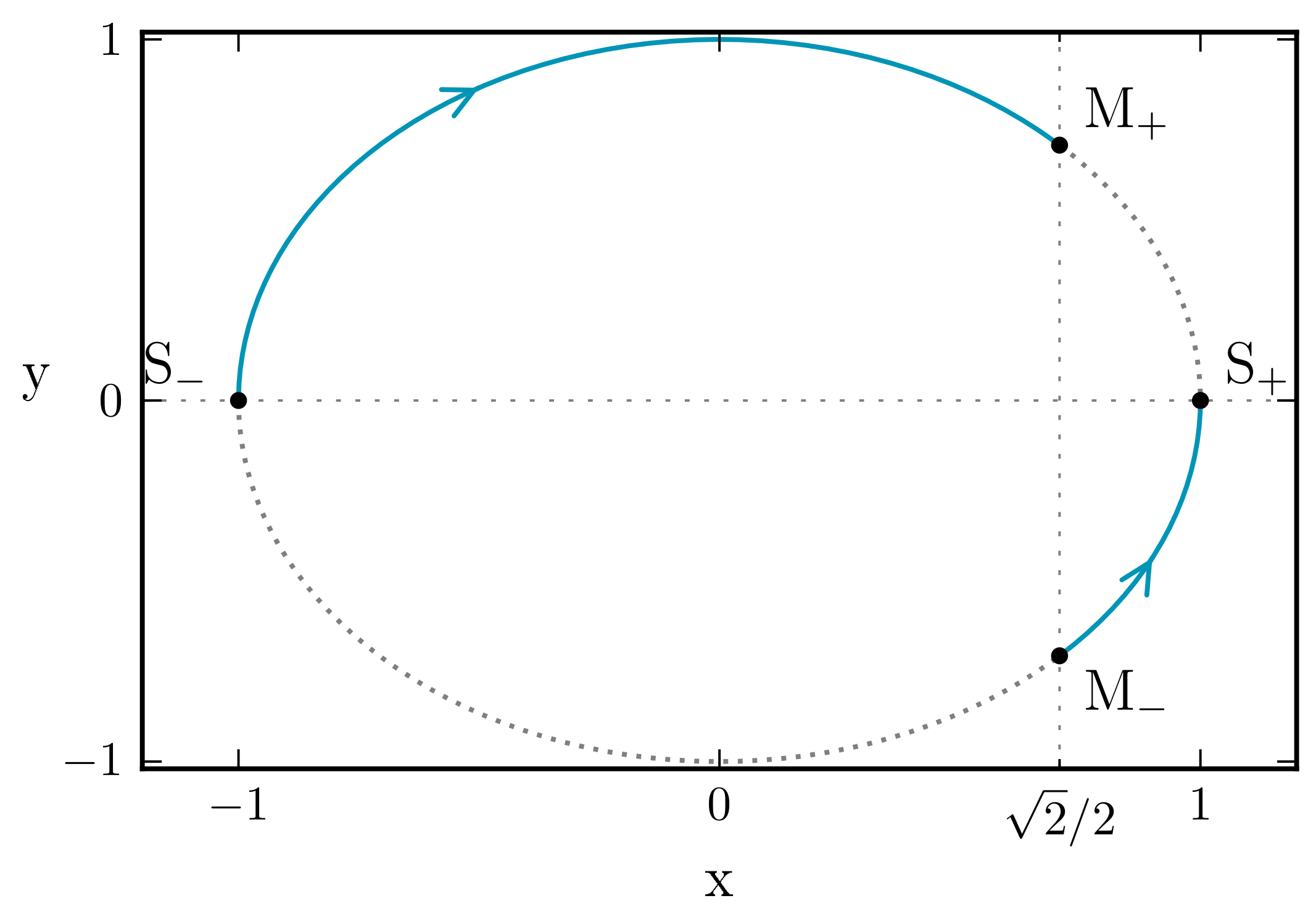
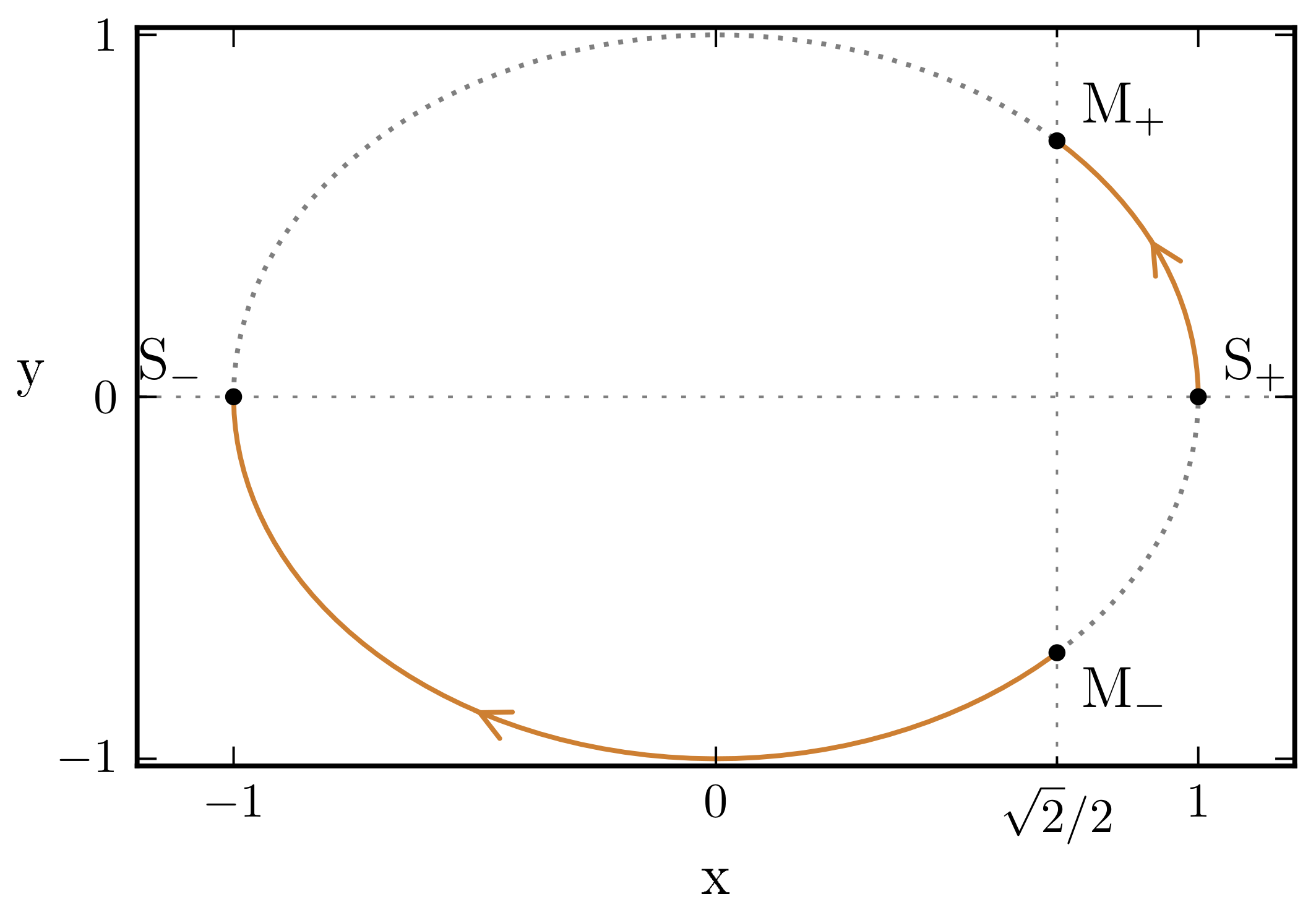
5. The Presence of Dark Energy
- (a)
- A classical dust contraction from very large scales, the initial repeller of the model, ending in a big crunch classical singularity around stiff matter domination with . The scalar field evolves smoothly from to behavior, without ever passing through a dark energy phase.
- (b)
- A classical dust contraction from very large scales, the initial repeller of the model, ending in a big crunch classical singularity around stiff matter domination with . Now the scalar field passes through a dark energy phase, evolving smoothly from to behavior, and then from to .
- (c)
- The universe emerges from a classical Big Bang singularity around stiff matter domination with , , and expands to an asymptotically dust matter domination phase, the attractor of the model. The scalar field evolves smoothly from to behavior, without ever passing through a dark energy phase. This is the time-reversed of case a.
- (d)
- The universe emerges from a classical Big Bang singularity around stiff matter domination with , , and expands to an asymptotically dust matter domination phase, the attractor of the model. Now the scalar field passes through a dark energy phase, evolving smoothly from to behavior, and then from to . This is the time-reversed of case b.
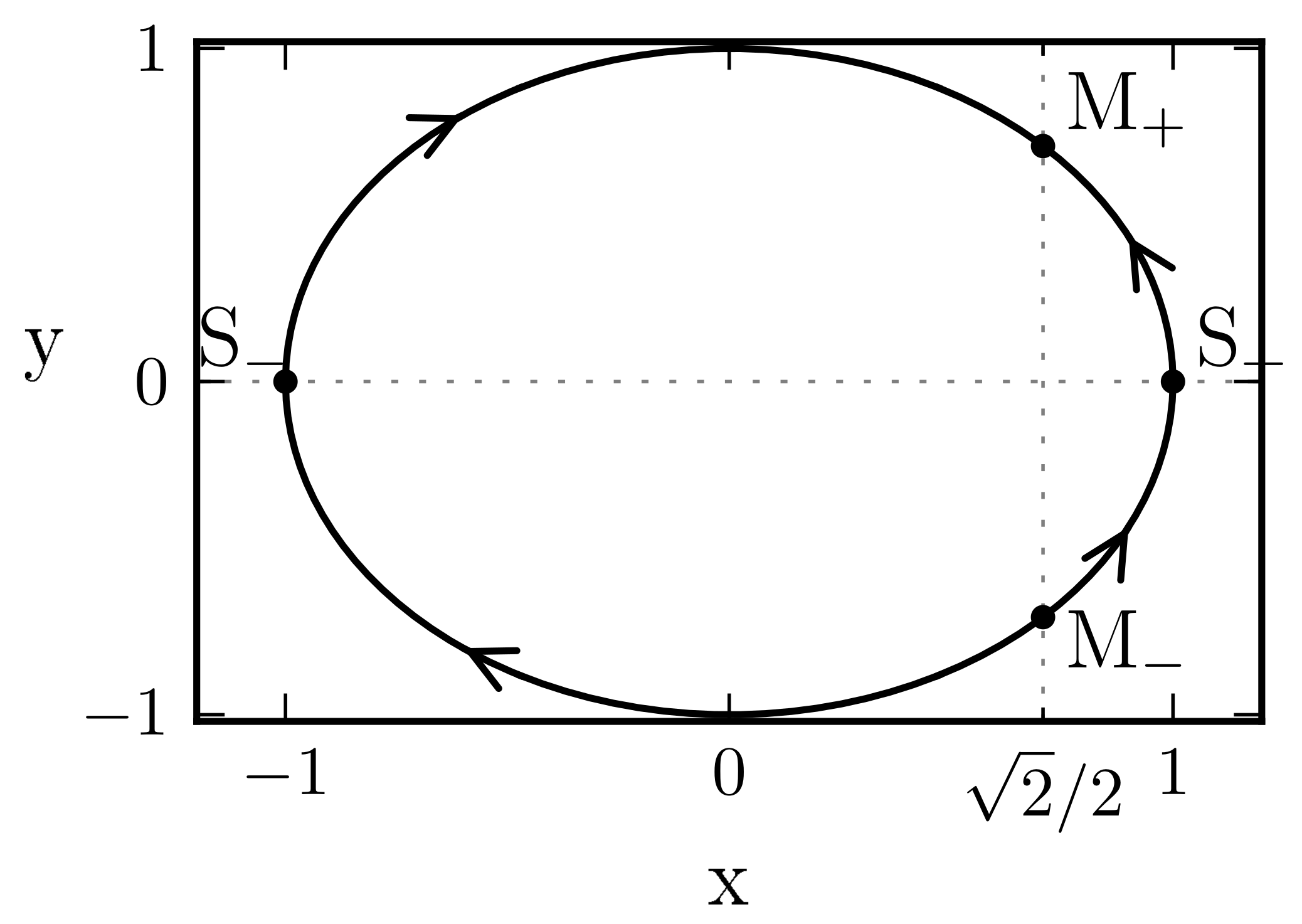
- (A)
- A classical dust contraction from very large scales, which passes through a dark energy phase up to a classical stiff matter contracting phase with . In this region, quantum effects become important, and a bounce takes place, launching the universe to a classical stiff matter expanding phase with , which then evolves to an asymptotically dust matter expanding phase, without passing through a dark energy phase.
- (B)
- A classical dust contraction from very large scales directly to a classical stiff matter contracting phase with , without ever passing through a dark energy phase. In this region, quantum effects become relevant, and a bounce takes place, launching the universe to a classical stiff matter expanding phase with , and passing through a dark energy phase before reaching the asymptotically dust matter expanding phase.
6. Baryogenesis and Magnetogenesis
6.1. Baryogenesis
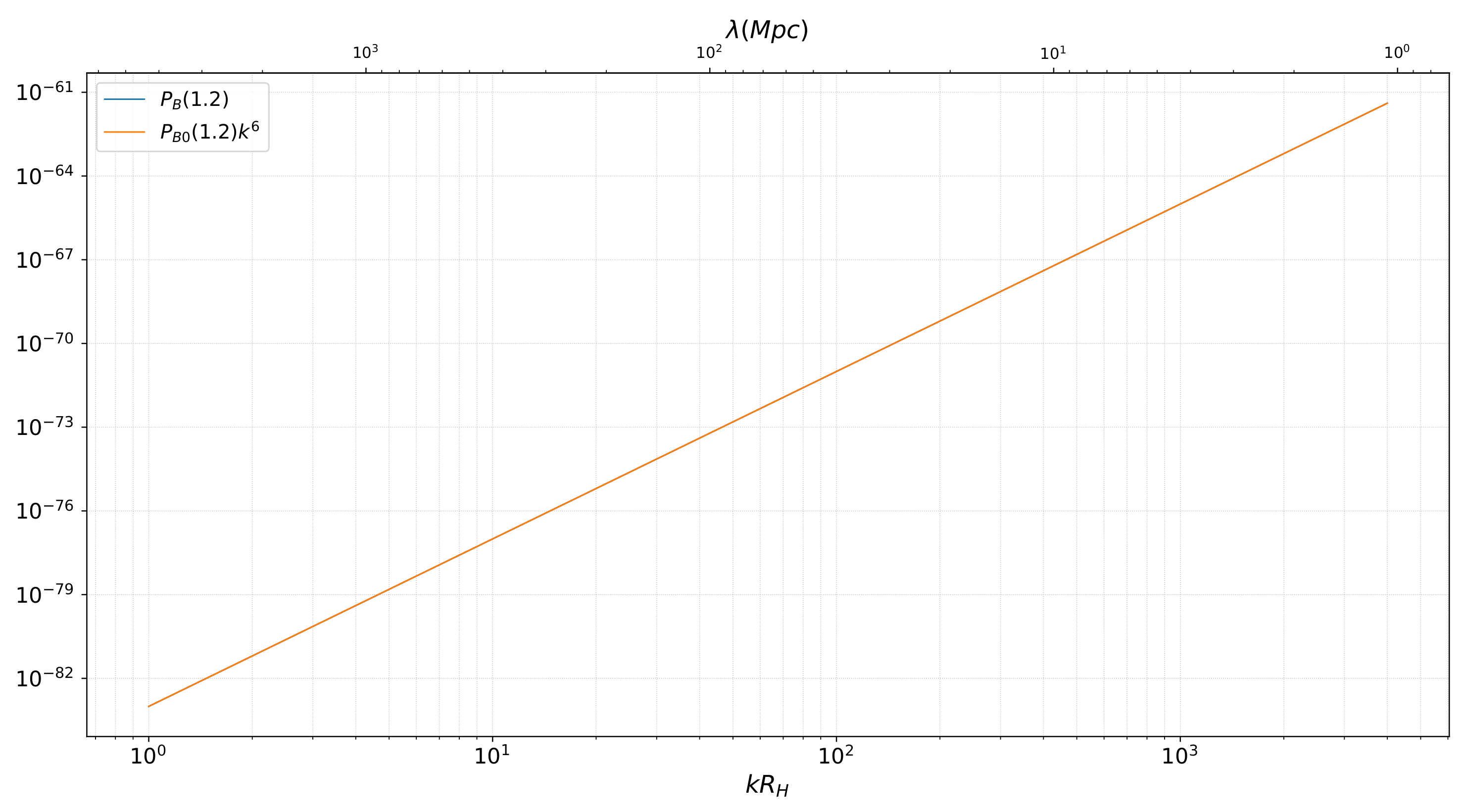
6.2. Magnetogenesis
7. Discussion and Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck Collaboration. Astron. Astrophys. 2016, A13, 594. [Google Scholar]
- Cyburt, R.H.; Fields, B.D.; Olive, K.A.; Yeh, T. Big bang nucleosynthesis: Present status. Rev. Mod. Phys. 2016, 88, 015004. [Google Scholar] [CrossRef]
- DES Collaboration. Dark Energy Survey Year 1 Results: Cosmological constraints from cluster abundances and weak lensing. Phys. Rev. D 2020, 102, 023509. [Google Scholar] [CrossRef]
- Abolfathi, B.; Aguado, D.S.; Aguilar, G.; Allende Prieto, C.; Almeida, A.; Ananna, T.T.; Anders, F.; Anderson, S.F.; Andrews, B.H.; Anguiano, B.; et al. The Fourteenth Data Release of the Sloan Digital Sky Survey: First Spectroscopic Data from the Extended Baryon Oscillation Spectroscopic Survey and from the Second Phase of the Apache Point Observatory Galactic Evolution Experiment. Astrophys. J. Suppl. Ser. 2018, 235, 19. [Google Scholar] [CrossRef]
- Hollands, S.; Wald, R.M. Essay: An alternative to inflation. Gen. Rel. Grav. 2002, 34, 2043. [Google Scholar] [CrossRef]
- Wald, R.M. The Arrow of Time and the Initial Conditions of the Universe. arXiv 2005, arXiv:gr-qc/0507094. [Google Scholar] [CrossRef]
- Fischer, A.E. Unfolding the singularities in superspace. Gen. Rel. Grav. 1983, 12, 1191. [Google Scholar] [CrossRef]
- Green, M.B.; Schwarz, J.H.; Witten, E. Superstring Theory Vol. 1; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Ambjorn, J.; Goerlich, A.; Jurkiewicz, J.; Loll, R. Nonperturbative quantum gravity. Phys. Rep. 2012, 519, 127. [Google Scholar] [CrossRef]
- Ashtekar, A. Non-Perturbative Canonical Gravity; IUCAA Lecture Notes; World Scientific: Syracuse, NY, USA, 1990. [Google Scholar]
- Nagy, S. Lectures on renormalization and asymptotic safety. Ann. Phys. 2014, 310–346. [Google Scholar] [CrossRef]
- Ashtekar, A.; Singh, P. Loop quantum cosmology: A status report. Class. Quant. Grav. 2011, 28, 213001. [Google Scholar] [CrossRef]
- Halliwell, J.J. Quantum Cosmology and Baby Universes; Coleman, S., Hartle, J.B., Piran, T., Weinberg, S., Eds.; World Scientific: Singapore, 1991. [Google Scholar]
- East, W.E.; Kleban, M.; Linde, A.; Senatore, L. Beginning inflation in an inhomogeneous universe. J. Cosmol. Astropart. Phys. 2016, 9, 010. [Google Scholar] [CrossRef]
- Ijjas, A.; Cook, W.G.; Pretorius, F.; Steinhardt, P.J.; Davies, E.Y. Robustness of slow contraction to cosmic initial conditions. J. Cosmol. Astropart. Phys. 2020, 8, 030. [Google Scholar] [CrossRef]
- Carter, B. Anthropic principle in cosmology. arXiv 2006, arXiv:gr-qc/0606117. [Google Scholar]
- Vilenkin, A.; Yamada, M. Tunneling wave function of the universe. Phys. Rev. D 2018, 98, 066003. [Google Scholar] [CrossRef]
- Halliwell, J.J.; Hartle, J.B.; Hertog, T. What is the no-boundary wave function of the Universe? Phys. Rev. D 2019, 99, 043526. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Relict gravitation radiation spectrum and initial state of the universe. JETP Lett. 1979, 30, 682. [Google Scholar]
- Guth, A. Inflationary universe: A possible solution to the horizon and flatness problems. Phys. Rev. D 1981, 23, 347. [Google Scholar] [CrossRef]
- Linde, A. A new inflationary universe scenario: A possible solution of the horizon, flatness, homogeneity, isotropy and primordial monopole problems. Phys. Lett. B 1982, 108, 389. [Google Scholar] [CrossRef]
- Mukhanov, V.; Chibisov, G. Quantum fluctuations and a nonsingular universe. JETP Lett. 1981, 33, 532. [Google Scholar]
- Planck Collaboration; Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Murphy, G. Big-bang model without singularities. Phys. Rev. D 1973, 8, 4231. [Google Scholar] [CrossRef]
- Novello, M.; Salim, J.M. Nonlinear photons in the universe. Phys. Rev. D 1979, 20, 377. [Google Scholar] [CrossRef]
- Melnikov, V.; Orlov, S. Nonsingular cosmology as a quantum vacuum effect. Phys. Lett. A 1979, 70, 263. [Google Scholar] [CrossRef]
- Khoury, J.; Ovrut, B.A.; Steinhardt, P.J.; Turok, N. Ekpyrotic universe: Colliding branes and the origin of the hot big bang. Phys. Rev. D 2001, 64, 123522. [Google Scholar] [CrossRef]
- Khoury, J.; Steinhardt, P.J.; Turok, N. Designing cyclic universe models. Phys. Rev. Lett. 2004, 92, 031302. [Google Scholar] [CrossRef]
- Biswas, T.; Brandenberger, R.; Mazumdar, A.; Siegel, W. Non-perturbative gravity, the Hagedorn bounce and the cosmic microwave background. J. Cosmol. Astropart. Phys. 2007, 712, 011. [Google Scholar] [CrossRef]
- Brandenberger, R.; Zhang, X. The matter bounce curvaton scenario. J. Cosmol. Astropart. Phys. 2011, 1103, 003. [Google Scholar]
- Fabris, J.C.; Perez, R.S.; Bergliaffa, S.E.P.; Pinto-Neto, N. Born-Infeld-like f(R) gravity. Phys. Rev. D 2012, 86, 103525. [Google Scholar] [CrossRef]
- Cai, Y.; Easson, D.A.; Brandenberger, R. Towards a nonsingular bouncing cosmology. J. Cosmol. Astropart. Phys. 2012, 8, 020. [Google Scholar] [CrossRef]
- Ilyas, A.; Zhu, M.; Zheng, Y.; Cai, Y.; Saridakis, E.N. DHOST bounce. J. Cosmol. Astropart. Phys. 2020, 9, 002. [Google Scholar] [CrossRef]
- Bojowald, M. Absence of a singularity in loop quantum cosmology. Phys. Rev. Lett. 2001, 86, 5227. [Google Scholar] [CrossRef] [PubMed]
- Ashtekar, A.; Pawlowski, T.; Singh, P. Quantum nature of the big bang. Phys. Rev. Lett. 2006, 14, 141301. [Google Scholar] [CrossRef] [PubMed]
- Gielen, S.; Turok, N. Perfect quantum cosmological bounce. Phys. Rev. Lett. 2016, 117, 021301. [Google Scholar] [CrossRef]
- Gryb, S.; Thebault, K.P.Y. Superpositions of the cosmological constant allow for singularity resolution and unitary evolution in quantum cosmology. Phys. Lett. 2018, 784, 324. [Google Scholar] [CrossRef]
- de Barros, J.A.; Pinto-Neto, N.; Sagioro-Leal, M.A. The causal interpretation of dust and radiation fluid non-singular quantum cosmologies. Phys. Lett. A 1998, 241, 229. [Google Scholar] [CrossRef]
- Alvarenga, F.G.; Fabris, J.C.; Lemos, N.A.; Monerat, G.A. Quantum cosmological perfect fluid models. Gen. Relativ. Gravit. 2002, 34, 651. [Google Scholar] [CrossRef]
- Novello, M.; Bergliaffa, S.E.P. Bouncing cosmologies. Phys. Rep. 2008, 463, 127. [Google Scholar] [CrossRef]
- Brandenberger, R.; Peter, P. Bouncing Cosmologies: Progress and Problems. arXiv 2016, arXiv:1603.05834. [Google Scholar] [CrossRef]
- Tolman, R.C. On the theoretical requirements for a periodic behaviour of the universe. Phys. Rev. 1931, 38, 1758. [Google Scholar] [CrossRef]
- Bohr, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 1935, 48, 696. [Google Scholar] [CrossRef]
- Heisenberg, W. The Physical Principles of the Quantum Theory; Dover: New York, NY, USA, 1949. [Google Scholar]
- von Neumann, J. Mathematical Foundations of Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 1955. [Google Scholar]
- Ghirardi, G.C.; Rimini, A.; Weber, T. Unified dynamics for microscopic and macroscopic systems. Phys. Rev. D 1986, 34, 470. [Google Scholar] [CrossRef]
- Penrose, R. Quantum Implications: Essays in Honour of David Bohm; Hiley, B.J., Peat, F.D., Eds.; Routledge: London, UK, 1987. [Google Scholar]
- DeWitt, B.S.; Graham, N. (Eds.) The Many-Worlds Interpretation of Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 1973. [Google Scholar]
- Bohm, D. A suggested interpretation of the quantum theory in terms of “hidden” variables. I. Phys. Rev. 1952, 85, 166. [Google Scholar] [CrossRef]
- Holland, P.R. The Quantum Theory of Motion: An Account of the de Broglie-Bohm Causal Interpretation of Quantum Mechanichs; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Dürr, D.; Teufel, S. Bohmian Mechanics; Springer: Berlin, Germany, 2009. [Google Scholar]
- Struyve, W. Pilot-wave approaches to quantum field theory. J. Phys. Conf. Ser. 2011, 306, 012047. [Google Scholar] [CrossRef]
- Vink, J.C. Quantum potential interpretation of the wave function of the universe. Nucl. Phys. B 1992, 369, 707–728. [Google Scholar] [CrossRef]
- Shtanov, Y.V. Pilot wave quantum cosmology. Phys. Rev. D 1996, 54, 2564–2570. [Google Scholar] [CrossRef] [PubMed]
- Pinto-Neto, N.; Santini, E.S. Must quantum spacetimes be Euclidean? Phys. Rev. D 1999, 59, 123517. [Google Scholar] [CrossRef]
- DeWitt, B.S. Quantum theory of gravity. II. The manifestly covariant theory. Phys. Rev. 1967, 160, 1113. [Google Scholar] [CrossRef]
- Valentini, A. Signal-locality, uncertainty, and the subquantum H-theorem. I. Phys. Lett. A 1991, 156, 5–11. [Google Scholar] [CrossRef]
- Towler, M.D.; Russell, N.J.; Valentini, A. Time scales for dynamical relaxation to the Born rule. Proc. R. Soc. A 2012, 468, 990–1013. [Google Scholar] [CrossRef]
- Norsen, T.; Struyve, W. Weak measurement and Bohmian conditional wave functions. Ann. Phys. 2014, 350, 166–178. [Google Scholar] [CrossRef][Green Version]
- Frolov, V.P.; Vilkovisky, G.A. Spherically symmetric collapse in quantum gravity. Phys. Lett. B 1981, 106, 307. [Google Scholar] [CrossRef]
- Casadio, R. Quantum gravitational fluctuations and the semiclassical limit. Int. J. Mod. Phys. D 2000, 9, 51. [Google Scholar] [CrossRef]
- Lyth, D.H.; Liddle, A.R. The Primordial Density Perturbation; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Mukhanov, V. Physical Foundations of Cosmology; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Weinberg, S. Cosmology; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- De Unánue, A.; Sudarsky, D. Phenomenological analysis of quantum collapse as source of the seeds of cosmic structure. Phys. Rev. D 2008, 78, 043510. [Google Scholar] [CrossRef]
- Pinto-Neto, N.; Santos, G.; Struyve, W. Quantum-to-classical transition of primordial cosmological perturbations in de Broglie-Bohm quantum theory. Phys. Rev. D 2012, 85, 083506. [Google Scholar] [CrossRef]
- Pinto-Neto, N.; Santos, G.; Struyve, W. Quantum-to-classical transition of primordial cosmological perturbations in de Broglie-Bohm quantum theory: The bouncing scenario. Phys. Rev. D 2014, 89, 023517. [Google Scholar] [CrossRef]
- Hawking, S.W.; Ellis, G.F.R. The Large Scale Structure of Space-Time; Cambridge University Press: Cambridge, UK, 1973. [Google Scholar]
- Colistete, R., Jr.; Fabris, J.C.; Pinto-Neto, N. Gaussian superpositions in scalar-tensor quantum cosmological models. Phys. Rev. D 2000, 62, 083507. [Google Scholar] [CrossRef]
- Pinto-Neto, N.; Santini, E.S.; Falciano, F.T. Quantization of Friedmann cosmological models with two fluids: Dust plus radiation. Phys. Lett. A 2005, 344, 131–143. [Google Scholar] [CrossRef][Green Version]
- Peter, P.; Pinto-Neto, N. Cosmology without inflation. Phys. Rev. D 2008, 78, 063506. [Google Scholar] [CrossRef]
- Halliwell, J.J.; Hawking, S. Origin of structure in the universe. Phys. Rev. D 1985, 31, 1777–1791. [Google Scholar] [CrossRef]
- Peter, P.; Pinho, E.J.C.; Pinto-Neto, N. Tensor perturbations in quantum cosmological backgrounds. J. Cosmol. Astropart. Phys. 2005, 7, 014. [Google Scholar] [CrossRef]
- Peter, P.; Pinho, E.J.C.; Pinto-Neto, N. Scalar and vector perturbations in quantum cosmological backgrounds. Phys. Rev. D 2007, 76, 023506. [Google Scholar]
- Peter, P.; Pinho, E.J.C.; Pinto-Neto, N. Gravitational wave background in perfect fluid quantum cosmologies. Phys. Rev. D 2006, 73, 104017. [Google Scholar] [CrossRef]
- Mukhanov, V.; Feldman, H.A.; Brandenberger, R.H. Theory of cosmological perturbations. Phys. Rep. 1992, 215, 203. [Google Scholar] [CrossRef]
- Allen, L.E.; Wands, D. Cosmological perturbations through a simple bounce. Phys. Rev. D 2004, 70, 063515. [Google Scholar] [CrossRef]
- Peter, P.; Pinto-Neto, N.; Vitenti, S.D.P. Quantum cosmological perturbations of multiple fluids. Phys. Rev. D 2016, 93, 023520. [Google Scholar] [CrossRef]
- Vitenti, S.D.P.; Pinto-Neto, N. Large adiabatic scalar perturbations in a regular bouncing universe. Phys. Rev. D 2012, 85, 023524. [Google Scholar] [CrossRef]
- Falciano, F.T.; Pinto-Neto, N.; Vitenti, S.D.P. Scalar field perturbations with arbitrary potentials in quantum backgrounds. Phys. Rev. D 2013, 87, 103514. [Google Scholar] [CrossRef]
- Falciano, F.T.; Pinto-Neto, N. Scalar perturbations in scalar field quantum cosmology. Phys. Rev. D 2009, 79, 023507. [Google Scholar] [CrossRef]
- Bessada, D.; Pinto-Neto, N.; Siffert, B.B.; Miranda, O.D. Stochastic background of relic gravitons in a bouncing quantum cosmological model. J. Cosmol. Astropart. Phys. 2012, 54, 1211. [Google Scholar] [CrossRef]
- Quintin, J.; Sherkatghanad, Z.; Cai, Y.-F.; Brandenberger, R.H. Evolution of cosmological perturbations and the production of non-Gaussianities through a nonsingular bounce: Indications for a no-go theorem in single field matter bounce cosmologies. Phys. Rev. D 2015, 92, 063532. [Google Scholar] [CrossRef]
- Li, Y.-B.; Quintin, J.; Wang, D.-G.; Cai, Y.-F. Matter bounce cosmology with a generalized single field: Non-Gaussianity and an extended no-go theorem. J. Cosmol. Astropart. Phys. 2017, 3, 031. [Google Scholar] [CrossRef]
- Finelli, F.; Brandenberger, R. Generation of a scale-invariant spectrum of adiabatic fluctuations in cosmological models with a contracting phase. Phys. Rev. D 2002, 65, 103522. [Google Scholar] [CrossRef]
- Pinto-Neto, N.; Vitenti, S.D.P. Comment on “Growth of covariant perturbations in the contracting phase of a bouncing universe”. Phys. Rev. D 2014, 89, 028301. [Google Scholar] [CrossRef]
- Pinto-Neto, N.; Fabris, J.C.; Toniato, J.D.; Vicente, G.S.; Vitenti, S.D.P. Vector perturbations in bouncing cosmology. Phys. Rev. D 2020, 101, 123519. [Google Scholar] [CrossRef]
- Maier, R.; Pereira, S.; Pinto-Neto, N.; Siffert, B.B. Bouncing models with a cosmological constant. Phys. Rev. D 2012, 85, 023508. [Google Scholar] [CrossRef]
- Bacalhau, A.P.; Pinto-Neto, N.; Vitenti, S.D.P. Consistent scalar and tensor perturbation power spectra in single fluid matter bounce with dark energy era. Phys. Rev. D 2018, 97, 083517. [Google Scholar] [CrossRef]
- Heard, I.P.C.; Wands, D. Cosmology with positive and negative exponential potentials. Class. Quantum Gravity 2002, 19, 5435. [Google Scholar] [CrossRef]
- Colin, S.; Pinto-Neto, N. Quantum matter bounce with a dark energy expanding phase. Phys. Rev. D 2017, 96, 063502. [Google Scholar] [CrossRef]
- Lehners, J.; Steinhardt, P.J. Dark energy and the return of the phoenix universe. Phys. Rev. D 2009, 79, 063503. [Google Scholar] [CrossRef]
- Cai, Y.; Marciano, A.; Wang, D.; Wilson-Ewing, E. Bouncing cosmologies with dark matter and dark energy. Universe 2017, 3, 1. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K.; Paul, T. From a Bounce to the Dark Energy Era with F(R) Gravity. arXiv 2020, arXiv:2009.09947. [Google Scholar] [CrossRef]
- Celani, D.; Pinto-Neto, N.; Vitenti, S.D.P. Particle creation in bouncing cosmologies. Phys. Rev. D 2017, 95, 023523. [Google Scholar] [CrossRef]
- Scardua, A.; Guimarães, L.F.; Pinto-Neto, N.; Vicente, G.S. Fermion production in bouncing cosmologies. Phys. Rev. D 2018, 98, 083505. [Google Scholar] [CrossRef]
- Olive, K.A. Review of particle physics. Chin. Phys. C 2014, 38, 090001. [Google Scholar] [CrossRef]
- Cohen, A.G.; Rujula, A.D.; Glashow, S.L. A matter-antimatter universe? Astrophys. J. 1998, 495, 539. [Google Scholar] [CrossRef]
- Sakharov, A.D. Violation of CP Invariance, Casymmetry, and baryon asymmetry of the universe. JETP Lett. 1967, 5, 24. [Google Scholar]
- Kuzmin, V.A.; Rubakov, V.A.; Shaposhnikov, M.E. On anomalous electroweak baryon-number non-conservation in the early universe. Phys. Lett. 1985, 155B, 36. [Google Scholar] [CrossRef]
- Shaposhnikov, M.E. Possible appearance of the baryon asymmetry of the universe in an electroweak theory. JETP Lett. 1986, 44, 465. [Google Scholar]
- Shaposhnikov, M.E. Baryon asymmetry of the universe in standard electroweak theory. Nucl. Phys. 1987, 287, 757. [Google Scholar] [CrossRef]
- Antunes, V.; Bediaga, I.; Novello, M. Gravitational baryogenesis without CPT violation. J. Cosmol. Astropart. Phys. 2019, 10, 076. [Google Scholar] [CrossRef]
- Cohen, A.G.; Kaplan, D.B. Thermodynamic generation of the baryon asymmetry. Phys. Lett. B 1987, 199, 251–258. [Google Scholar] [CrossRef]
- Simone, A.D.; Kobayashi, T. Cosmological aspects of spontaneous baryogenesis. J. Cosmol. Astropart. Phys. 2016, 8, 052. [Google Scholar] [CrossRef]
- Davoudiasl, H.; Kitano, R.; Kribs, G.D.; Murayama, H.; Steinhardt, P.J. Gravitational baryogenesis. Phys. Rev. Lett. 2004, 93, 201301. [Google Scholar] [CrossRef] [PubMed]
- Odintsov, S.D.; Oikonomou, V.K. Loop quantum cosmology gravitational baryogenesis. EPL Europhys. Lett. 2016, 116, 49001. [Google Scholar] [CrossRef]
- Delgado, P.C.M.; Jesus, M.B.; Pinto-Neto, N.; Mourão, T.; Vicente, G.S. Baryogenesis in cosmological models with symmetric and asymmetric quantum bounces. Phys. Rev. D 2020, 102, 063529. [Google Scholar] [CrossRef]
- Brandenburg, A.; Subramanian, K. Astrophysical magnetic fields and nonlinear dynamo theory. Phys. Rept. 2005, 417, 1. [Google Scholar] [CrossRef]
- Durrer, R.; Neronov, A. Cosmological magnetic fields: Their generation, evolution and observation. Astron. Astrophys. Rev. 2013, 21, 62. [Google Scholar] [CrossRef]
- Pogosian, L.; Zucca, A. Searching for primordial magnetic fields with CMB B-modes. Class. Quant. Grav. 2018, 35, 124004. [Google Scholar] [CrossRef]
- Turner, M.S.; Widrow, L.M. Inflation-produced, large-scale magnetic fields. Phys. Rev. D 1988, 37, 2743. [Google Scholar] [CrossRef]
- Campanelli, L.; Cea, P.; Fogli, G.L.; Tedesco, L. Inflation-produced magnetic fields in RnF2 and IF2 models. Phys. Rev. D 2008, 77, 123002. [Google Scholar] [CrossRef]
- Kunze, K.E. Completing magnetic field generation from gravitationally coupled electrodynamics with the curvaton mechanism. Phys. Rev. D 2013, 87, 063505. [Google Scholar] [CrossRef]
- Subramanian, K. The origin, evolution and signatures of primordial magnetic fields. Rept. Prog. Phys. 2016, 79, 076901. [Google Scholar] [CrossRef]
- Demozzi, V.; Mukhanov, V.; Rubinstein, H. Magnetic fields from inflation? J. Cosmol. Astropart. Phys. 2009, 908, 025. [Google Scholar] [CrossRef]
- Green, D.; Kobayashi, T. Constraints on primordial magnetic fields from inflation. J. Cosmol. Astropart. Phys. 2016, 3, 010. [Google Scholar] [CrossRef][Green Version]
- Drummond, I.; Hathrell, S. QED vacuum polarization in a background gravitational field and its effect on the velocity of photons. Phys. Rev. D 1980, 22, 343. [Google Scholar] [CrossRef]
- Frion, E.; Pinto-Neto, N.; Vitenti, S.D.P.; Bergliaffa, S.E.P. Primordial magnetogenesis in a bouncing universe. Phys. Rev. D 2020, 101, 103503. [Google Scholar] [CrossRef]
- Qian, P.; Cai, Y.-F.; Easson, D.A.; Guo, Z.-K. Magnetogenesis in bouncing cosmology. Phys. Rev. D 2016, 94, 083524. [Google Scholar] [CrossRef]
- Membiela, F.A. Primordial magnetic fields from a non-singular bouncing cosmology. Nucl. Phys. B 2014, 885, 196. [Google Scholar] [CrossRef]
- Sriramkumar, L.; Atmjeet, K.; Jain, R.K. Generation of scale invariant magnetic fields in bouncing universes. J. Cosmol. Astropart. Phys. 2015, 9, 010. [Google Scholar] [CrossRef]
- Durrer, R.; Caprini, C. Primordial magnetic fields and causality. J. Cosmol. Astropart. Phys. 2003, 11, 010. [Google Scholar] [CrossRef]
- Taylor, A.; Vovk, I.; Neronov, A. Extragalactic magnetic fields constraints from simultaneous GeV–TeV observations of blazars. Astron. Astrophys. A 2011, 144, 529. [Google Scholar] [CrossRef]
- Minoda, T.; Tashiro, H.; Takahashi, T. Insight into primordial magnetic fields from 21-cm line observation with EDGES experiment. Mon. Not. R. Astron. Soc. 2019, 488, 2001. [Google Scholar] [CrossRef]
- Belinskii, V.; Lifshitz, E.; Khalatnikov, I.M. Oscillatory approach to the singular point in relativistic cosmology. Usp. Fiz. Nauk 1970, 102, 463. [Google Scholar] [CrossRef]
- Bergeron, H.; Dapor, A.; Gazeau, J.P.; Malkiewicz, P. Smooth big bounce from affine quantization. Phys. Rev. D 2014, 89, 083522. [Google Scholar] [CrossRef]
- Cai, Y.-F.; Xue, W.; Brandenberger, R.; Zhang, X. Non-Gaussianity in a matter bounce. J. Cosmol. Astropart. Phys. 2009, 5, 011. [Google Scholar] [CrossRef]
- Agullo, I.; Bolliet, B.; Sreenath, V. Non-Gaussianity in loop quantum cosmology. Phys. Rev. D 2018, 97, 066021. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pinto-Neto, N. Bouncing Quantum Cosmology. Universe 2021, 7, 110. https://doi.org/10.3390/universe7040110
Pinto-Neto N. Bouncing Quantum Cosmology. Universe. 2021; 7(4):110. https://doi.org/10.3390/universe7040110
Chicago/Turabian StylePinto-Neto, Nelson. 2021. "Bouncing Quantum Cosmology" Universe 7, no. 4: 110. https://doi.org/10.3390/universe7040110
APA StylePinto-Neto, N. (2021). Bouncing Quantum Cosmology. Universe, 7(4), 110. https://doi.org/10.3390/universe7040110






