Van der Waals Interactions of Moving Particles with Surfaces of Cylindrical Geometry

Abstract

General nonrelativistic theory has been developed and the expressions obtained for the tangential (dissipative) and radial (conservative) image forces and van der Waals forces (vdW) acting on charged and neutral particles when they move parallel to the axis of a cylinder with circular cross-section, or in the space between coaxial cylinders. Numerical calculations of vdW forces have been performed for metal (Au) and dielectric (Si) materials of cylinders (filaments) and Cs atoms at velocities $~{10}^7\mathrm{m}/\mathrm{s}$. A remarkable result is that in the case of metal cylinders (atomic filaments and chains) the dynamic vdW potential can be repulsive for certain values of the velocity–distance parameter and the characteristic atomic frequency. In the case of a Si material, the dynamic vdW potential increases relative to the static one (by modulus) when the velocity–distance parameter $V{\omega }_0/R$ changes from zero to $~1.3$ and then tends to zero.

1. Introduction

Atom–surface interaction is a long-explored research problem of physics and adjacent areas. A particular case is the van der Waals interaction (vdW) caused by the zero-point and thermal fluctuations of the electromagnetic field and its material sources. The surface curvature is known to affect the spectrum of surface excitations (plasmons) and, accordingly, vdW forces of interaction of particles with the surfaces at distances of 1 to 10 nm [1,2,3,4]. Calculations of the vdW and Casimir–Polder potentials in cylindrical configurations (even in static case) invoke great interest [5,6] due to advances in nanotechnology, since it became possible to measure the Casimir and Casimir–Polder forces with increased precision (see Ref. [7] for a review). However, currently there are practically no relevant studies of nonequilibrium vdW interactions in cylindrical geometry. Dynamic corrections to conservative vdW forces in this case were first considered in [8]. More general calculations of the conservative and dissipative vdW forces acting on particles moving parallel to the generatrix of a cylindrical surface were carried out in [9,10]. In addition to the general theoretical importance associated with nonequilibrium vdW forces in the systems with cylindrical symmetry, studying the electromagnetic and fluctuation-electromagnetic interactions of moving charged and neutral atomic particles with cylindrical surfaces has been given a great impetus since the discovery of carbon nanotubes in 1991 [11], when a lot of theoretical teams started to work on the theoretical modelling and computer simulation of ion channeling through carbon nanotubes and capillary structures [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]. However, the role of the image forces for charged particles and vdW forces for neutral ones is underestimated due to an insufficient knowledge of the role of surface curvature at distances exceeding atomic dimensions. An interesting, but still not fully explored, feature of the image forces [16] and vdW forces [28,29,30,31] of moving particles is their velocity dependence. In particular, a particle moving near a surface, along with an attractive velocity-dependent force (an image force or vdW force in the case of charged and neutral particles, respectively), experiences a tangential dissipative (stopping) force (friction force). Both of these forces affect the particle dynamics. In contrast to the case of plane geometry [28,29,30,31], in systems with cylindrical symmetry, the velocity and curvature effects are much more complex [8,9,10,13]. Meanwhile, in the standard description of the dynamics (channeling) of charged and neutral particles in nanotubes and the capillary systems, only pairwise short-range interaction potentials between the particles and the atoms of walls are used, or continuous potentials obtained by averaging the pair potentials [13,14,15,16,17,18,19,20,21]. At channel diameters of the order of several nanometers and more, the contribution of short-range pair interactions in the main part of the cross section of the channels is close to zero, and the main role will be played by the image forces for charged particles and vdW forces (for neutral ones) with the walls of the channels. Due to this, the development of an adequate theoretical basis required in future profound studies of the channeling of charged (neutral) particles through nanotube and capillary structures is an urgent problem.

In this article, the particles are assumed to move nonrelativistically parallel to the generatrix of a concave/convex cylindrical surface, or in the space between coaxial cylindrical shells. The properties of surface materials are described by a local dielectric permittivity. Within the framework of electromagnetic fluctuation theory, we calculate the tangential (dissipative) and radial (conservative) image and vdW forces acting on particles, and the rate of their heating (for nanoparticles) when (in the general case) the particles and the cylinder walls have different local temperatures. In the limit of an infinitely large radius of cylinders, the results are reduced to those in the case of a flat surface or a plane-parallel gap. Numerical calculations of the radial and tangential vdW forces are carried out in the case of the metal (Au) and dielectric (Si) materials of the cylinders (atomic filaments and chains) and neutral Cs atoms at velocities of ~10⁷ m/s. The role of pair interactions and nonlocal effects is briefly touched upon. An intriguing result following from numerical calculations in Section 6 is that dynamic vdW potentials can be repulsive at high velocities, for certain combinations of resonance wavelengths and distances.

2. General Theory

Following [9,31], we recall the main details of the calculation of the vdW force (both its conservative and dissipative parts) and the heating rate for a neutral particle moving parallel to the generatrix of a cylindrical surface (convex and concave).

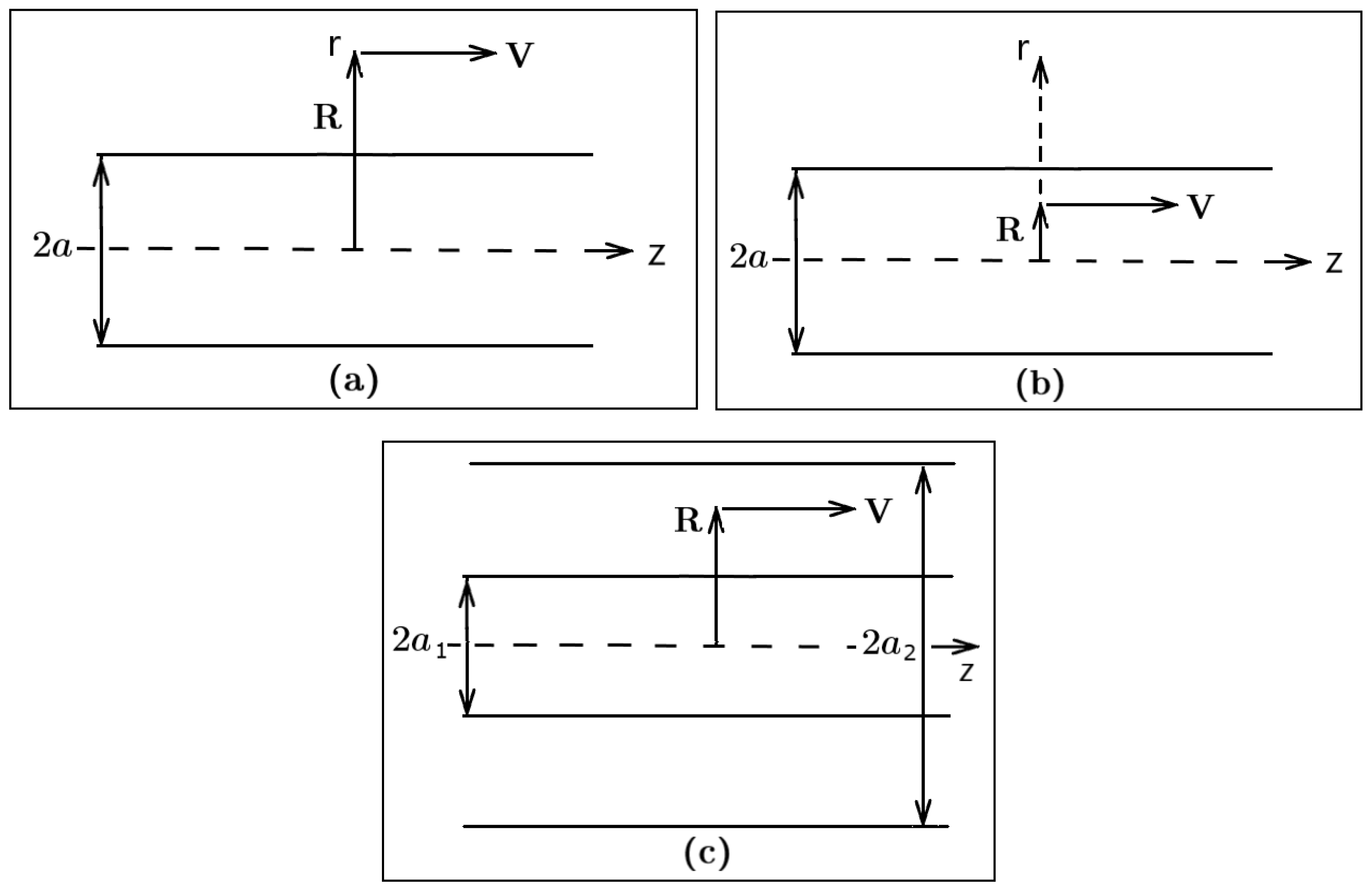
The case of a charged particle is also treated as a constituent point of the theory. Though the velocity is nonrelativistic ($V\ll c)$ and the retardation effects can be neglected, it can reach the values of order $~10V_B$ (with $V_B$ being the Bohr velocity). Figure 1 shows the cylindrical coordinate systems used and different configurations to be analyzed: convex cylindrical surface (a), cylindrical channel (b), and the case of particle motion between two coaxial cylindrical shells (c). The wall surface material is characterized by a local dielectric constant ε(ω), and the particle is characterized by the dipole polarizability α(ω). We use a cylindrical coordinate system with coordinates $\left(r,\phi ,z\right)$, where the $z$ axis is parallel to the symmetry axis of the cylinders (cylindrical shells) and their generators. The radial distance $r$ is counted off the axes of the cylinders. We further assume that an external charged or neutral particle with density $\rho \left(r,\phi ,z,t\right)$ moves along a classical trajectory with constant velocity V localized in the vacuum region outside (Figure 1a), inside (Figure 1b) or between the cylinders (Figure 1c). The instantaneous particle coordinates are $\left(R,0,z=Vt\right)$. Within the framework of the nonrelativistic approximation V << c, the main task is to find the electric field $E$ on a moving particle at the point of its instantaneous location. Since $=-\nabla \varphi$, with $\varphi$ being the electric potential, the initial problem reduces to solving the Poisson equation $\Delta \Phi =-4\pi \rho .$

2.1. Green’s Functions of Poisson’s Equation

Written in cylindrical coordinates $,\phi ,z$, the Poisson equation takes the form

$$\left(\frac{{\partial }^2}{\partial r^2}+\frac{1}{r}\frac{\partial }{\partial r}+\frac{1}{r^2}\frac{{\partial }^2}{\partial {\phi }^2}+\frac{{\partial }^2}{\partial z^2}\right)\Phi \left(r,\phi ,z,t\right)=-4\pi \rho \left(r,\phi ,z,t\right)$$

(1)

According to the symmetry of the problem, we expand both parts of (1) into the Fourier integral over the frequency $\omega$ and the wave vector $\mathit{k}$ (the direction of k is parallel to the $z$ axis) and into a Fourier series over the angle $\phi :$

$$\Phi \left(r,\phi ,z,t\right)=\frac{1}{2\pi }{\displaystyle \sum }_{n=-\infty }^{n=+\infty }\underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}\frac{d\omega }{2\pi }\underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}\frac{dk}{2\pi }{u}_n\left(\omega k;r\right)\exp \left(\mathrm{i}\left(kz-\omega t+n\phi \right)\right)$$

(2)

$$\rho \left(r,\phi ,z,t\right)=\frac{1}{2\pi }{\displaystyle \sum }_{n=-\infty }^{n=+\infty }\underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}\frac{d\omega }{2\pi }\underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}\frac{dk}{2\pi }{\rho }_n\left(\omega k;r\right)\exp \left(\mathrm{i}\left(kz-\omega t+n\phi \right)\right)$$

(3)

Substituting (2), (3) into (1) yields

$$\left(\frac{d^2}{d{r}^2}+\frac{1}{r}\frac{d}{dr}-\frac{n^2}{r^2}-k^2\right)u_n\left(\omega k,r\right)=-4\pi {\rho }_n\left(\omega k;r\right)$$

(4)

Without the loss of generality, let us consider the case shown in Figure 1a. Then, the solution to (4) should meet the boundary conditions at the surface $r=a$ of the cylinder:

$$u_n\left(\omega k;r=a+0\right)=u_n\left(\omega k;r=a-0\right),{\frac{d{u}_n}{dr}}_{r=a+0}=\epsilon \left(\omega \right){\frac{d{u}_n}{dr}}_{r=a-0}.$$

(5)

It is worth noting that Equation (4) is valid both inside and outside the cylinder, since the problem is electrostatic.

To proceed further, we first find the Green’s function $G_n\left(r,r^{\prime }\right)$ of Poisson’s Equation (4)

$$\left(\frac{d^2}{d{r}^2}+\frac{1}{r}\frac{d}{dr}-\frac{n^2}{r^2}-k^2\right)G_n\left(r,r^{\prime }\right)=\delta \left(r-r^{\prime }\right)$$

(6)

with additional conditions

$$G_n\left(r=r^{\prime }+0,r^{\prime }\right)=G_n\left(r=r^{\prime }-0,r^{\prime }\right),{\frac{d{G}_n}{dr}}_{r=r^{\prime }+0}-{\frac{d{G}_n}{dr}}_{r=r^{\prime }-0}=1,$$

(7)

and Equation (5). Then, the general solution to inhomogeneous Equation (4) that meets boundary conditions (5) and (7) reads

$$u_n\left(\omega k;r\right)=-4\pi {{\displaystyle \int }}^{}d{r}^{\prime }{G}_n\left(r,r^{\prime }\right){\rho }_n\left(\omega k;r^{\prime }\right).$$

(8)

For $r\ne r^{\prime }$, Equation (6) is a modified Bessel equation with two linearly independent solutions $I_n\left(kr\right)$ and $K_n\left(kr\right).$ We find $G_n\left(r,r^{\prime }\right)$ in Appendix A. Equations (A2), (A4), (A6) and (A7) correspond to cases (a), (b), (c) shown in Figure 1.

2.2. Image Forces on a Moving Charged Particle

The charge density $\rho$ of a moving particle with a charge $Ze$ has the form [32]

$$\rho \left(r,\phi ,z,t\right)=\frac{Ze}{r}\delta \left(r-R\right)\delta \left(\phi \right)\delta \left(z-Vt\right).$$

(9)

Using (9), the Fourier-transformed density ${\rho }_n\left(\omega k;r\right)$ is given by

$${\rho }_n\left(\omega k;r\right)=\frac{2\pi Ze}{r}\delta \left(r-R\right)\delta \left(\omega -kV\right).$$

(10)

Next, substituting (10) along with (A2), (A4) and (A6) into (8), and leaving only the terms corresponding to the induced potentials of walls, proportional to ${\Delta }_n$ and ${\stackrel{\sim }{\Delta }}_n,$ yields

$$u_n^{in}\left(\omega k;r\right)=-8{\pi }^{2}Ze\delta \left(\omega -kV\right)·\{\begin{array}{c}{\Delta }_n{K}_n\left(kr\right)K_n\left(kR\right),\\ {\stackrel{\sim }{\Delta }}_n{I}_n\left(kr\right)I_n\left(kR\right),\\ \frac{1}{D}\left[{\Delta }_{n,1}{K}_n\left(kr\right)K_n\left(kR\right)+{\stackrel{\sim }{\Delta }}_{n,2}{I}_n\left(kr\right)I_n\left(kR\right)\right]\end{array}$$

(11)

Here, and in the similar expressions below (namely, (14), (16), (30)) the upper, middle and lower expressions after the curly brace correspond to cases (a), (b), (c) in Figure 1, namely external configuration ($r>a$), internal configuration ($0<r<a$), and configuration between coaxial cylinders, ($a_1<r<a_2$). The functions ${\Delta }_n$, ${\stackrel{\sim }{\Delta }}_n$ and ${\Delta }_{n,1},{\Delta }_{n,2}$ are defined in (A3), (A5) and after Equation (A7), $D=1-{\Delta }_{n,1}{\stackrel{\sim }{\Delta }}_{n,2}$.

The induced Fourier-components $E_{r,n}^{in}\left(\omega k;r\right)$ of the electric field $E\left(r,\phi ,z,t\right)$ are obtained using Equation (2) and identity $E=-\nabla \varphi$

$$\begin{gathered} E_{r,n}^{in}\left(\omega k;r\right)=-\frac{d}{dr}{u}_n\left(\omega k;r\right),E_{\phi ,n}^{in}\left(\omega k;r\right)=-\frac{in}{r}{u}_n\left(\omega k;r\right) \\ {E}_{z,n}^{in}\left(\omega k;r\right)=-ik{u}_n\left(\omega k;r\right). \end{gathered}$$

(12)

The force on a charged particle is then $\mathit{F}=Ze{\mathit{E}}^{in}$ with the electric field ${\mathit{E}}^{in}$ obtained by the direct Fourier-transform using (12) and (11). Substituting Fourier-components (12) into the integral expression for ${\mathit{E}}^{in}$ taken with instantaneous coordinates ($R,0,Vt)$ of the particle, integrating by frequency $\omega$ and using the analytical properties of ${\Delta }_n$, ${\stackrel{\sim }{\Delta }}_n$ (even real components and odd imaginary ones) one obtains

$$F_R=2\frac{{\left(Ze\right)}^2}{\pi }{\sum }_{n=-\infty }^{\infty }{{\displaystyle \int }}_0^{\infty }dkk{f}_n^{\left(R\right)}\left(kR,kV\right),$$

(13)

$$f_n^{\left(R\right)}\left(x,y\right)=\{\begin{array}{c}{K}_n\left(x\right)K_n^{\prime }\left(x\right)\mathrm{Re}{\Delta }_n\left(y\right)\\ I_n\left(x\right)I_n^{\prime }\left(x\right)\mathrm{Re}{\stackrel{\sim }{\Delta }}_n\left(y\right)\\ K_n\left(x\right)K_n^{\prime }\left(x\right)\mathrm{Re}\left(\frac{{\Delta }_{n,1}\left(y\right)}{D}\right)+I_n\left(x\right)I_n^{\prime }\left(x\right)\mathrm{Re}\left(\frac{{\stackrel{\sim }{\Delta }}_{n,2}\left(y\right)}{D}\right)\end{array}$$

(14)

$$F_z=-2\frac{{\left(Ze\right)}^2}{\pi }{\displaystyle \sum }_{n=-\infty }^{\infty }{{\displaystyle \int }}_0^{\infty }dkk{f}_n^{\left(z\right)}\left(kR,kV\right),$$

(15)

$$f_n^{\left(z\right)}\left(x,y\right)=\{\begin{array}{c}{K}_n^2\left(x\right)\mathrm{Im}{\Delta }_n\left(y\right)\\ I_n^2\left(x\right)\mathrm{Im}{\stackrel{\sim }{\Delta }}_n\left(y\right)\\ K_n^2\left(x\right)\mathrm{Im}\left(\frac{{\Delta }_{n,1}\left(y\right)}{D}\right)+I_n^2\left(x\right)\mathrm{Im}\left(\frac{{\stackrel{\sim }{\Delta }}_{n,2}\left(y\right)}{D}\right)\end{array}.$$

(16)

In (14), the Bessel functions with a prime denote their derivatives with respect to the total argument $x=kR.$ The force component $F_{\mathsf{\phi }}$ turns out to be zero, as expected from the symmetry. Equations (13)–(16) completely coincide with [16], where the authors considered the case of a charged particle moving inside a cylindrical channel.

2.3. VdW Forces on a Moving Neutral Particle

In the case of a neutral particle (an atom) with a fluctuating dipole moment $d\left(t\right)$, the charge density is $\rho =-\mathrm{div}P$ with $P\left(r,\phi ,z,t\right)=\frac{1}{r}\mathsf{\delta }\left(r-R\right)\mathsf{\delta }\left(\phi \right)\mathsf{\delta }\left(z-Vt\right)d\left(t\right)$ being the polarization vector. Then, the Fourier-transform ${\rho }_{\mathrm{n}}\left(\omega k;r\right)$ has the form

$${\rho }_n\left(\omega k;r\right)=\left[\frac{{\delta }^{\prime }\left(r-R\right)}{r}{d}_r\left({\omega }^{-}\right)+\frac{\mathrm{i}n}{r^2}\delta \left(r-R\right)d_{\phi }\left({\omega }^{-}\right)+\frac{\mathrm{i}k}{r}\delta \left(r-R\right)d_z\left({\omega }^{-}\right)\right],$$

(17)

where ${\omega }^{-}=\omega -kV.$ The induced Fourier-component $u_n^{in}\left(\omega k;r\right)$ in this case is calculated by subsituting (27) and the induced components of $G_n\left(r,r^{\prime }\right)$ from (A2), (A4), (A6), (A7) into (8). The resulting expressions are as follows.

(i)

external configuration, $r>a$ (Figure 1a)

$$u_n^{in}\left(\omega k;r\right)=4\pi {\Delta }_n{K}_n\left(kr\right)\left[-K_n^{\prime }\left(kR\right)\left|k\right|d_r\left({\omega }^{-}\right)+\frac{\mathrm{i}n}{R}{K}_n\left(kR\right)d_{\phi }\left({\omega }^{-}\right)+\mathrm{i}k{K}_n\left(kR\right)d_z\left({\omega }^{-}\right)\right]$$

(18)

(ii)

internal configuration, $0<r<a$ (Figure 1b)

$$u_n^{in}\left(\omega k;r\right)=4\pi {\stackrel{\sim }{\Delta }}_n{I}_n\left(kr\right)\left[-I_n^{\prime }\left(kR\right)\left|k\right|d_r\left({\omega }^{-}\right)+\frac{\mathrm{i}n}{R}{I}_n\left(kR\right)d_{\phi }\left({\omega }^{-}\right)+ik{I}_n\left(kR\right)d_z\left({\omega }^{-}\right)\right]$$

(19)

(iii)

configuration between coaxial cylinders, $a_1<r<a_2$ (Figure 1c)

$$\begin{array}{l}{u}_n^{in}\left(\omega k;r\right)=\frac{4\pi {\Delta }_{n,1}}{D}{K}_n\left(kr\right)\left[-K_n^{\prime }\left(kR\right)\left|k\right|d_r\left({\omega }^{-}\right)+\frac{\mathrm{i}n}{R}{K}_n\left(kR\right)d_{\phi }\left({\omega }^{-}\right)+ik{K}_n\left(kR\right)d_z\left({\omega }^{-}\right)\right]\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{4\pi {\stackrel{\sim }{\Delta }}_{n,2}}{D}{I}_n\left(kr\right)\left[-I_n^{\prime }\left(kR\right)\left|k\right|d_r\left({\omega }^{-}\right)+\frac{\mathrm{i}n}{R}{I}_n\left(kR\right)d_{\phi }\left({\omega }^{-}\right)+ik{I}_n\left(kR\right)d_z\left({\omega }^{-}\right)\right]\end{array}$$

(20)

One can see that Equation (20) is a sum of (18) and (19) taken with the factor $D^{-1}={\left(1-{\Delta }_{n,1}{\stackrel{\sim }{\Delta }}_{n,2}\right)}^{-1}$. To find vdW forces acting on a particle, we use the expressions [31,33]

$$F_r=\langle {\nabla }_r\left(d^{sp}{E}^{in}\right)\rangle +\langle {\nabla }_r\left(d^{in}{E}^{sp}\right)\rangle ,$$

(21)

$$F_z=\langle {\nabla }_z\left(d^{sp}{E}^{in}\right)\rangle +\langle {\nabla }_z\left(d^{in}{E}^{sp}\right)\rangle ,$$

(22)

with standard definitions of the induced and spontaneous components of the dipole moment and the electric field. Instead of using (21), when calculating the radial (conservative) force component $F_r$, it is simpler to find first the conservative potential (vdW energy)

$$U=-\frac{1}{2}\langle \left(d^{sp}{E}^{in}\right)\rangle -\frac{1}{2}\langle \left(d^{in}{E}^{sp}\right)\rangle$$

(23)

Having determined $U$, the radial force $F_r$ is then calculated by $F_r=-\partial U/\partial r$.

Consider the first terms in (21) and (23), performing the Fourier-expansions for $d\left(\mathrm{t}\right)$ and $E^{in}\left(r,\phi ,z,t\right)$:

$${\mathbf{d}}^{sp}\left(t\right)={{\displaystyle \int }}^{}\frac{d\omega }{2\pi }{d}^{sp}\left(\omega \right)\exp \left(-i\omega t\right)$$

(24)

$${\mathit{E}}^{in}\left(r,\phi ,z,t\right)=\frac{1}{2\pi }{\displaystyle \sum }_{n=-\infty }^{\infty }\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}\frac{d\omega }{2\pi }\frac{dk}{2\pi }{\mathit{E}}_n^{in}\left(\omega k;r\right)\exp \left(i\left(kz-\omega t+n\phi \right)\right)$$

(25)

Substituting (24), (25) into (22), (23) yields

$$F_z^{\left(1\right)}=\frac{1}{{\left(2\pi \right)}^4}{{\displaystyle \sum }}^{}{{\displaystyle \int }}^{}d{\omega }^{\prime }d\omega dk\left(\mathrm{i}k\right)\langle d^{sp}\left({\omega }^{\prime }\right)E_n^{in}\left(\omega k;R\right)\rangle \exp \left(-\mathrm{i}\left(\omega +{\omega }^{\prime }-kV\right)t\right)$$

(26)

$$U^{\left(1\right)}=-\frac{1}{2{\left(2\pi \right)}^4}{{\displaystyle \sum }}^{}{{\displaystyle \int }}^{}d\omega \prime d\omega dk\langle d^{sp}\left({\omega }^{\prime }\right)E_n^{in}\left(\omega k;R\right)\rangle \exp \left(-\mathrm{i}\left(\omega +{\omega }^{\prime }-kV\right)t\right)$$

(27)

If not specified, the summation by $n$ in (25)–(27) and in what follows is carried out from $-\infty$ to $+\infty$.

The induced components of the electric field are calculated by inserting (18)–(20) into (19). The appeared correlators of the dipole moment are found using the fluctuation-dissipation relation [34]

$$\langle d_i^{sp}\left({\omega }^{\prime }\right)d_k^{sp}\left(\omega -kV\right)\rangle =2\pi \hslash {\delta }_{ik}\delta \left({\omega }^{\prime }+\omega -kV\right){\alpha }^{″}\left(\omega -kV\right)\coth \frac{\hslash \left(\omega -kV\right)}{2T_1}.$$

(28)

For all configurations shown in Figure 1, the correlators in (26), (27) can be written in the form

$$\langle d^{sp}\left({\omega }^{\prime }\right)E_n^{in}\left(\omega k;R\right)\rangle =8{\pi }^2\hslash \delta \left({\omega }^{\prime }+\omega -kV\right){\alpha }^{″}\left(\omega -kV\right)\coth \frac{\hslash \left(\omega -kV\right)}{2T_1}{k}^2{Z}_n\left(kR,\omega \right),$$

(29)

where $Z_n\left(kR,\omega \right)$ is given by

$$Z_n\left(kR,\omega \right)=\{\begin{array}{c}{S}_n\left(kR\right){\Delta }_n\left(\omega \right)\\ {\stackrel{\sim }{S}}_n\left(kR\right){\stackrel{\sim }{\Delta }}_n\left(\omega \right)\\ S_n\left(kR\right)\frac{{\Delta }_{n,1}\left(\omega \right)}{1-{\Delta }_{n,1}\left(\omega \right){\stackrel{\sim }{\Delta }}_{n,2}\left(\omega \right)}+{\stackrel{\sim }{S}}_n\left(kR\right)\frac{{\stackrel{\sim }{\Delta }}_{n,2}\left(\omega \right)}{1-{\Delta }_{n,1}\left(\omega \right){\stackrel{\sim }{\Delta }}_{n,2}\left(\omega \right)}\end{array}$$

(30)

$$S_n\left(x\right)=K_n^2\left(x\right)\left(\frac{n^2}{x^2}+1\right)+{\left(K_n^{\prime }(x\right)}^2,$$

(31)

$${\stackrel{\sim }{S}}_n\left(x\right)=I_n^2\left(x\right)\left(\frac{n^2}{x^2}+1\right)+{\left(I_n^{\prime }\left(x\right)\right)}^2.$$

(32)

Note that in (31), (32) we assume that $x=kR$. Substituting (29) into (26), (27), integrating by frequency ${\mathsf{\omega }}^{\prime }$ and making use of the transformation of integrals with allowance for the analytical properties of the functions under the integral yields

$$F_z^{\left(1\right)}=\frac{\hslash }{{\pi }^2}{{\displaystyle \int }}_0^{\infty }d\omega \underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}dk{k}^3{\alpha }^{″}\left({\omega }^{+}\right)\coth \left(\frac{\hslash {\omega }^{+}}{2T_1}\right){\displaystyle \sum }_{n=-\infty }^{\infty }\mathrm{Im}{Z}_n\left(kR,\omega \right)$$

(33)

$$U^{\left(1\right)}=-\frac{\hslash }{2{\pi }^2}{{\displaystyle \int }}_0^{\infty }d\omega \underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}dk{k}^2{\alpha }^{″}\left({\omega }^{+}\right)\coth \left(\frac{\hslash \omega }{2T_1}\right){\displaystyle \sum }_{n=-\infty }^{\infty }\mathrm{Re}{Z}_n\left(kR,\omega \right)$$

(34)

where ${\mathsf{\omega }}^{+}=\mathsf{\omega }+kV$; ${\mathsf{\alpha }}^{″}\left({\mathsf{\omega }}^{+}\right)$ and ${\mathsf{\alpha }}^{\prime }\left({\mathsf{\omega }}^{+}\right)$ in what follows are the imaginary and real parts of polarizability $\mathsf{\alpha }\left({\mathsf{\omega }}^{+}\right)$.

To find the contribution from spontaneous field $E^{sp}$ to (21)–(23), we expand $E^{sp}$ into the Fourier integral in frequency and wave vector at the particle location point $r_0\left(t\right)=\left(R,0,Vt\right):$

$$E^{sp}\left(r_0\left(t\right)\right)={{\displaystyle \int }}^{}\frac{d\omega }{2\pi }\frac{dk}{2\pi }{E}_{\omega k}^{sp}\left(R\right)\exp \left(-\mathrm{i}\left(\omega t-kV\right)\right)$$

(35)

and express the induced dipole moment $d^{in}\left(t\right)$ through $E^{sp}\left(r_0\left(t\right)\right)$:

$$d^{in}\left(t\right)={{\displaystyle \int }}^{}\frac{d\omega }{2\pi }\frac{dk}{2\pi }\alpha \left(\omega -kV\right)E_{\omega k}^{sp}\left(R\right)\exp \left(-\mathrm{i}\left(\omega -kV\right)t\right)$$

(36)

Substituting (35), (37) into (22), (23) yields

$$F_z^{\left(2\right)}=\frac{1}{{\left(2\pi \right)}^4}{{\displaystyle \int }}^{}d\omega d{\omega }^{\prime }dkd{k}^{\prime }\left(\mathrm{i}{k}^{\prime }\right)\alpha \left(\omega -kV\right)\langle E_{\omega k}^{sp}\left(R\right)E_{{\omega }^{\prime }{k}^{\prime }}^{sp}\left(R\right)\rangle \exp \left(-\mathrm{i}\left(\omega +{\omega }^{\prime }-kV\right)t\right)$$

(37)

$$U^{\left(2\right)}=-\frac{1}{2{\left(2\pi \right)}^4}{{\displaystyle \int }}^{}d\omega d{\omega }^{\prime }dkd{k}^{\prime }\alpha \left(\omega -kV\right)\langle E_{\omega k}^{sp}\left(R\right)E_{{\omega }^{\prime }{k}^{\prime }}^{sp}\left(R\right)\rangle \exp \left(-\mathrm{i}\left(\omega +{\omega }^{\prime }-kV\right)t\right)$$

(38)

Based on the theory of stationary electromagnetic fluctuations [34,35,36], the correlators in (37), (38) are worked out using the fluctuation-dissipation relation (see Appendix B):

$$\langle E_{\omega k}\left(R\right)\rangle E_{{\omega }^{\prime }{k}^{\prime }}\left(R\right)=-2\hslash {\left(2\pi \right)}^2\delta \left(\omega +{\omega }^{\prime }\right)\delta \left(k+k^{\prime }\right)\cot \mathrm{h}\frac{\hslash \omega }{2T}{\displaystyle \sum }_{n=-\infty }^{\infty }\mathrm{Im}{Z}_n\left(kR,\omega \right)$$

(39)

Substituting (39) into (37), (38), integrating by ${\omega }^{\prime }$, $k^{\prime }$ and simplifying yields

$$F_z^{\left(2\right)}=-\frac{\hslash }{{\pi }^2}{{\displaystyle \int }}_0^{\infty }d\omega \underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}dk{k}^3{\alpha }^{″}\left({\omega }^{+}\right)\coth \left(\frac{\hslash \omega }{2T_2}\right){\displaystyle \sum }_{n=-\infty }^{\infty }\mathrm{Im}{Z}_n\left(kR,\omega \right)$$

(40)

$$U^{\left(2\right)}=-\frac{\hslash }{2{\pi }^2}{{\displaystyle \int }}_0^{\infty }d\omega \underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}dk{k}^2{\alpha }^{\prime }\left({\omega }^{+}\right)\coth \left(\frac{\hslash \omega }{2T_2}\right){\displaystyle \sum }_{n=-\infty }^{\infty }\mathrm{Im}{Z}_n\left(kR,\omega \right)$$

(41)

Summing (33) with (40) and (34) with (41) results in

$$F_z=-\frac{\hslash }{{\pi }^2}{{\displaystyle \int }}_0^{\infty }d\omega \underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}dk{k}^3{\alpha }^{″}\left({\omega }^{+}\right)\left[\coth \left(\frac{\hslash \omega }{2T_2}\right)-\coth \left(\frac{\hslash {\omega }^{+}}{2T_1}\right)\right]{\displaystyle \sum }_{n=-\infty }^{\infty }\mathrm{Im}{Z}_n\left(kR,\omega \right)$$

(42)

$$U=-\frac{\hslash }{2{\pi }^2}{{\displaystyle \int }}_0^{\infty }d\omega \underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}dk{k}^2\left[{\alpha }^{\prime }\left({\omega }^{+}\right)\coth \left(\frac{\hslash \omega }{2T_2}\right){\displaystyle \sum }_{n=-\infty }^{\infty }\mathrm{Im}{Z}_n\left(kR,\omega \right)+{\alpha }^{″}\left({\omega }^{+}\right)\coth \left(\frac{\hslash {\omega }^{+}}{2T_1}\right){\displaystyle \sum }_{n=-\infty }^{\infty }\mathrm{Re}{Z}_n\left(kR,\omega \right)\right]$$

(43)

Using (43), the radial force $F_R=-\partial U/\partial R$ is then given by

$$\begin{gathered} F_R=-\frac{\hslash }{2{\pi }^2}{{\displaystyle \int }}_0^{\infty }d\omega \underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}dk{k}^3\left[{\alpha }^{\prime }\left({\omega }^{+}\right)\coth \left(\frac{\hslash \omega }{2T_2}\right){\displaystyle \sum }_{n=-\infty }^{\infty }\mathrm{Im}{Z}_n^{\prime }\left(kR,\omega \right) \\ +{\alpha }^{″}\left({\omega }^{+}\right)\coth \left(\frac{\hslash {\omega }^{+}}{2T_1}\right){\displaystyle \sum }_{n=-\infty }^{\infty }\mathrm{Re}{Z}_n\left(kR,\omega \right)\right] \end{gathered}$$

(44)

where $Z_n^{\prime }\left(kR,\omega \right)$ denotes the derivative of $Z_n\left(kR,\omega \right)$ with respect to its first argument.

Expressions (42)–(44) describe all configurations in Figure 1, when relating (a), (b), (c) to the first, second and third lines in the definition of $Z_n\left(kR,\omega \right)$ in (30). Moreover, using (42)–(44), one can also retrieve all known results [31] for friction forces, dynamic vdW forces and interaction potentials in planar configurations. This is shown in Section 3.

2.4. Heating Rate of a Neutral Particle

The heating rate $dQ/dt$ of a nanoparticle is calculated quite similar to vdW forces. The starting equation has the form [31,33]

$$dQ/dt=\langle \left({\dot{d}}^{\mathrm{sp}}{E}^{\mathrm{in}}\right)\rangle +\langle \left({\dot{d}}^{\mathrm{in}}{E}^{\mathrm{sp}}\right)\rangle ,$$

(45)

where the overdots for the dipole moments stand for time derivatives. Further calculations are very similar to those performed in Section 2.3. The resulting expression is simply obtained when substituting $\left(-{\omega }^{+}\right)$ for $k$ under the integrand in (42):

$$dQ/dt=\frac{\hslash }{{\pi }^2}{{\displaystyle \int }}_0^{\infty }d\omega \underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}dk{k}^2{\omega }^{+}{\alpha }^{″}\left({\omega }^{+}\right)\left[\coth \left(\frac{\hslash \omega }{2T_2}\right)-\coth \left(\frac{\hslash {\omega }^{+}}{2T_1}\right)\right]{\displaystyle \sum }_{n=-\infty }^{\infty }\mathrm{Im}{Z}_n\left(kR,\omega \right)$$

(46)

3. Transition from Cylindrical to Plane-Geometry Surfaces

Using (42)–(44), one can retrieve all known results for planar configurations. We consider, as an example, the friction force $F_z$. In the coordinates chosen in [31], the relevant plane-geometry result is

$$F_x=-\frac{\hslash }{{\pi }^2}{{\displaystyle \int }}_0^{\infty }d\omega \underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}d{k}_x{k}_x\underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}d{k}_y\exp \left(-2kz\right){\alpha }^{″}\left({\omega }^{+}\right)\left[\coth \left(\frac{\hslash \omega }{2T_2}\right)-\coth \left(\frac{\hslash \omega }{2T_1}\right)\right]{\Delta }^{″}\left(\omega \right)$$

(47)

In (47), in contrast to (42), the particle moves along the $x$-direction, ${\omega }^{+}=\omega +k_{x}V$, $k=\sqrt{k_x^2+k_y^2}$ $,z$ is the distance to surface, and $\Delta \left(\omega \right)=\frac{\epsilon \left(\omega \right)-1}{\epsilon \left(\omega \right)+1}$ is the p-wave reflection factor in the electrostatic limit. Performing the integration over $k_y$ in Equation (47) yields

$$F_z=-\frac{\hslash }{{\pi }^2}{{\displaystyle \int }}_0^{\infty }d\omega \underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}dk{k}^3{\alpha }^{″}\left({\omega }^{+}\right)\left[2K_0\left(2kz\right)+\frac{K_1\left(2kz\right)}{kz}\right]\left[\coth \left(\frac{\hslash \omega }{2T_2}\right)-\coth \left(\frac{\hslash {\omega }^{+}}{2T_1}\right)\right]{\Delta }^{″}\left(\omega \right)$$

(48)

Equation (48) now has a form very similar to (42). Using (30), (31) and (A3), it is easy to check that

$${\displaystyle \sum }_{n=-\infty }^{\infty }\mathrm{Im}{Z}_n\left(kR,\omega \right)={\displaystyle \sum }_{n=-\infty }^{\infty }\left[K_n^2\left(x\right)\left(\frac{n^2}{x^2}+1\right)+{\left(\frac{d{K}_n\left(x\right)}{dx}\right)}^2\right]\frac{I_n\left(y\right)}{K_n\left(y\right)}\mathrm{Im}\left(\frac{\epsilon -1}{\epsilon -\left[I_n\left(y\right)K_n\left(y\right)/I_n^{\prime }\left(y\right)K_n^{\prime }\left(y\right)\right]}\right)$$

(49)

where $x=kR,y=ka$. Taking the limit $a\to \infty ,R\to \infty ,R-a=z=\mathrm{const}$, and making use of the asymptotic relations $K_n\left(x\right)~\sqrt{\pi /2x}\exp \left(-x\right),$ $K_n^{\prime }\left(x\right)\approx -K_n\left(x\right),I_n\left(x\right)\approx I_n^{\prime }\left(x\right)~\sqrt{1/2\pi x}\exp \left(x\right)$, we see that the factor $\mathrm{Im}(\dots )$ in (49) reduces to $\mathrm{Im}\Delta \left(\omega \right)={\Delta }^{″}\left(\omega \right)$. Finally, making use of the relations [4] (for $x\to \infty ,y\to \infty ,x-y=z$)

$${\displaystyle \sum }_{n=-\infty }^{\infty }\frac{K_n^2\left(x\right)I_n\left(y\right)}{K_n\left(y\right)}=K_0\left(2\left(x-y\right)\right),{\displaystyle \sum }_{n=-\infty }^{\infty }\frac{n^2}{x^2}\frac{K_n^2\left(x\right)I_n\left(y\right)}{K_n\left(y\right)}=\frac{K_1\left(2\left(x-y\right)\right)}{2\left(x-y\right)}$$

(50)

$${\displaystyle \sum }_{n=-\infty }^{\infty }\frac{{\left(K_n^{\prime }\left(x\right)\right)}^2{I}_n\left(y\right)}{K_n\left(y\right)}=K_0\left(2\left(x-y\right)\right)+\frac{K_1\left(2\left(x-y\right)\right)}{2\left(x-y\right)},$$

(51)

we find

$${\displaystyle \sum }_{n=-\infty }^{\infty }\mathrm{Im}{Z}_n\left(kR,\omega \right)=\left[2K_0\left(2kz\right)+\frac{K_1\left(2kz\right)}{kz}\right]\mathrm{Im}\left(\frac{\epsilon -1}{\epsilon +1}\right)$$

(52)

Therefore, Equation (42) reduces to plane-geometry result (47). The identities (50) also hold valid for concave cylindrical surfaces when replacing $K_n\left(x\right)\leftrightarrow I_n\left(x\right)$ and $x-y\to y-x=z$. In this case, $Z_n\left(kR,\omega \right)$ is defined by the second-line in (30). Using (30), we can also check the result [31] for a particle moving in a plane-parallel gap. In the same way, one can verify the transformation properties of Equations (43) and (44).

4. VdW Energy and Stopping (Friction) Force

For a more detailed study of dynamic effects, we represent (43) in the form

$$U=U^{\left(0\right)}+U^{\left(1\right)},$$

(53)

$$U^{\left(0\right)}=-\frac{\hslash }{{\pi }^2}{{\displaystyle \int }}_0^{\infty }d\omega \underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}dk{k}^2\cot \mathrm{h}\left(\frac{\hslash \omega }{2T_2}\right)\mathrm{Im}\left[\alpha \left({\omega }^{+}\right){\displaystyle \sum }_{n=0}^{\infty }{ϵ}_n{Z}_n\left(kR,\omega \right)\right]$$

(54)

$$U^{\left(1\right)}=-\frac{\hslash }{{\pi }^2}{{\displaystyle \int }}_0^{\infty }d\omega \underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}dk{k}^2{\alpha }^{″}\left({\omega }^{+}\right)\left[\coth \left(\frac{\hslash \omega }{2T_1}\right)-\coth \left(\frac{\hslash \omega }{2T_2}\right)\right]{\displaystyle \sum }_{n=0}^{\infty }{ϵ}_n\mathrm{Re}{Z}_n\left(kR,\omega \right)$$

(55)

where ${ϵ}_n=1$ for $n\ne 0$, and ${ϵ}_n=$1/2 for $n=0$, and the property $Z_n\left(x,y\right)=Z_{-n}\left(x,y\right)$ is taken into account. Here, $U^{\left(0\right)}$ is the part of the vdW energy that remains nonzero at $V=0$ regardless of temperature $T_2$. The behavior of $U^{\left(1\right)}$ is more complicated. At $T_1=T_2=0$, taking into account the analytic properties of functions in (53) and making use of the identity $\underset{T\to 0}{\lim }\coth \left(x/T\right)=\mathrm{sign}\left(x\right)$, one obtains

$$U^{\left(0\right)}=-\frac{\hslash }{{\pi }^2}{{\displaystyle \int }}_0^{\infty }d\xi \underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}dk{k}^2\mathrm{Im}\left[\mathrm{i}\alpha \left(\mathrm{i}\xi +kV\right){\displaystyle \sum }_{n=0}^{\infty }{ϵ}_n{Z}_n\left(kR,\mathrm{i}\xi \right)\right]$$

(56)

$$U^{\left(1\right)}=\frac{2\hslash }{{\pi }^2}{{\displaystyle \int }}_0^{\infty }dk{k}^2\underset{0}{\overset{kV}{{\displaystyle \int }}}d\omega {\alpha }^{″}\left({\omega }^{-}\right){\displaystyle \sum }_{n=0}^{\infty }{ϵ}_n\mathrm{Re}{Z}_n\left(kR,\omega \right)$$

(57)

where ${\omega }^{-}=\omega -kV$. In the case $V=0$, Equation (55) coincides with the well-known static results [1,2,3,4,5], whereas one obtains $U^{\left(1\right)}\ne 0$ only for $V\ne 0$. To proceed further, we consider the oscillator model of atomic polarizability

$$\alpha \left(\omega \right)=\frac{\alpha \left(0\right){\omega }_0^2}{{\omega }_0^2-{\omega }^2+\mathrm{i}0\mathrm{sign}\left(\mathsf{\omega }\right)}=\mathrm{P}\frac{\alpha \left(0\right){\omega }_0^2}{{\omega }_0^2-{\omega }^2}+\mathrm{i}\frac{\pi \alpha \left(0\right){\omega }_0}{2}\left[\delta \left(\omega -{\omega }_0\right)-\delta \left(\omega +{\omega }_0\right)\right]$$

(58)

with $\alpha \left(0\right)$ and ${\omega }_0$ being the static polarizability and resonance frequency. Substituting (58) into (56), (57) and simplifying, yields

$$U^{\left(0\right)}=-\frac{2\hslash \alpha \left(0\right){\omega }_0^2}{{\pi }^2}{{\displaystyle \int }}_0^{\infty }d\omega \underset{0}{\overset{+\infty }{{\displaystyle \int }}}dk{k}^2\frac{\left({\omega }_0^2+{\omega }^2-k^2{V}^2\right)}{\left[{\left({\omega }_0^2+{\omega }^2-k^2{V}^2\right)}^2+4{\omega }^2{k}^2{V}^2\right]}{\displaystyle \sum }_{n=0}^{\infty }{ϵ}_n{Z}_n\left(kR,\mathrm{i}\omega \right)$$

(59)

$$U^{\left(1\right)}=-\frac{\hslash {\omega }_0\alpha \left(0\right)}{\pi }{{\displaystyle \int }}_{{\omega }_0/V}^{\infty }dk{k}^2{\displaystyle \sum }_{n=0}^{\infty }{ϵ}_n\mathrm{Re}{Z}_n\left(kR,kV-{\omega }_0\right)$$

(60)

In the case of a flat surface at $V\ne 0$, Equations (56) and (59) reduce to [28,29,30]. The plane-geometry equivalent of (60) was first obtained in Ref. [30]. The analysis performed in [30] showed that $U^{\left(0\right)}$ has a $V^2-$poportional (attractive) correction to the energy at small $V$. At larger velocities, $U^{\left(0\right)}$ reaches a maximum and then tends to zero. An intriguing fact (in the case of a flat surface) is that $U^{\left(1\right)}$ can be positive at a certain choice of the atomic frequency ${\omega }_0$ and the plasma frequency of the metal, but the resulting potential remains attractive. However, for metallized cylindrical filaments, channels and atomic chains, as we will see in Section 5, the total potential can be repulsive. In contrast to this, for dielectric (nonconducting) surfaces the resulting vdW potential proves to be attractive (as usual).

For $V=0$ and $T_2\ne 0$, using the standard transformation of the integration contour to the complex plane for $U^{\left(0\right)}$, Equation (53) takes the known form (Equation (22) in [3])

$$U^{\left(0\right)}=-\frac{4T_2}{\pi }{\displaystyle \sum }_{m=0}^{\infty }{ϵ}_m\alpha \left(\mathrm{i}{\xi }_m\right)\underset{0}{\overset{+\infty }{{\displaystyle \int }}}dk{k}^2{\displaystyle \sum }_{n=0}^{\infty }{ϵ}_n{Z}_n\left(kR,\mathrm{i}{\xi }_m\right)$$

(61)

with ${\xi }_m=\frac{2\pi m{T}_2}{\hslash }$.

As for the stopping force (42) at $T_1=T_2=0$, we obtain

$$F_z=\frac{2\hslash }{{\pi }^2}{{\displaystyle \int }}_0^{\infty }dk{k}^3\underset{0}{\overset{kV}{{\displaystyle \int }}}d\omega {\alpha }^{″}\left(\omega -kV\right){\displaystyle \sum }_{n=0}^{\infty }{ϵ}_n\mathrm{Im}{Z}_n\left(kR,\omega \right)$$

(62)

Inserting (58) into (62) yields

$$F_z=-\frac{\hslash {\omega }_0\alpha \left(0\right)}{\pi }{{\displaystyle \int }}_{{\omega }_0/V}^{\infty }dk{k}^3{\displaystyle \sum }_{n=0}^{\infty }{ϵ}_n\mathrm{Im}{Z}_n\left(kR,kV-{\omega }_0\right)$$

(63)

It is worthwhile noting that function $Z_n\left(kR,\omega \right)$ has an exponentially decaying asymptotics at large $kR$. Then, according to (63), the force $F_z$ becomes negligibly small at $V\ll {\omega }_{0}R$. If ${\omega }_0~{10}^{15}{s}^{-1}$ (for atoms) and $R~10nm$, this implies $V\ll {10}^{7}m/s$. The corresponding quantum friction limit [37] for atoms is retrieved when using Equation (61) with a more precise definition of the dressed atomic polarizability [38]. We neglect here corrections with respect to the local equilibrium case and spatial dispersion [39,40,41,42].

The case of the friction force $F_z$ acting on nanoparticles with a linear velocity dependence (at nonzero temperature and $V\ll {\omega }_{0}R$) follows from (42) when expanding ${\alpha }^{″}\left({\omega }^{+}\right)$ and $\cot \mathrm{h}\left(\frac{\hslash {\omega }^{+}}{2T_1}\right)$ in powers of $\left(kV\right)$, retaining the first-order expansion terms:

$$F_z=-\frac{4\hslash V}{{\pi }^2}{{\displaystyle \int }}_0^{\infty }d\omega \left\{\frac{\partial {\alpha }^{″}\left(\omega \right)}{\partial \omega }\left[\coth \left(\frac{\hslash \omega }{2T_2}\right)-\coth \left(\frac{\hslash \omega }{2T_1}\right)\right]+{\alpha }^{″}\left(\omega \right)\left(-\frac{\partial }{\partial \omega }\right)\coth \left(\frac{\hslash \omega }{2T_1}\right)\right\}\underset{0}{\overset{\infty }{{\displaystyle \int }}}dk{k}^4{\displaystyle \sum }_{n=0}^{\infty }{ϵ}_n\mathrm{Im}{Z}_n\left(kR,\omega \right)$$

(64)

For $T_1=T_2=T$, Equation (64) reduces to

$$F_z=-\frac{4\hslash V}{{\pi }^2}{{\displaystyle \int }}_0^{\infty }d\omega {\alpha }^{″}\left(\omega \right){\sin \mathrm{h}}^{-2}\left(\hslash \omega /2T\right)\underset{0}{\overset{\infty }{{\displaystyle \int }}}dk{k}^4{\displaystyle \sum }_{n=0}^{\infty }{ϵ}_n\mathrm{Im}{Z}_n\left(kR,\omega \right)$$

(65)

The validity of (64), (65) is restricted by the velocities $V\ll 3.9·{10}^{6}m/s$ for $R=10\mathrm{nm}$, $T=300K$, since the characteristic frequency here is ${\omega }_0~k_{B}T/\hslash$. At higher velocities and (or) R, T values, the nonretarded relativistic consideration is required.

5. Interactions with Cylindrical Filaments and Atomic Chains

In the case of configuration shown in Figure 1a, as follows from the general formulas the main contribution to the $k$–integrals comes from the wave vectors $k\le 1/R$. Therefore, for an atom at large distance $R$ compared to the radius $a$ of the cylinder, we have $a\ll R$ and $ka\ll 1.\mathrm{Therefore},$ we can expand ${\Delta }_n$ in powers of $ka$. Then, taking into account the asymptotics of cylindrical functions for small values of the argument ($z\ll 1$) [43]

$$I_0\left(z\right)\cong 1+\frac{z^2}{4},I_n\left(z\right)\cong \frac{1}{\Gamma \left(n+1\right)}{\left(\frac{z}{2}\right)}^n,n=1,2\dots ,$$

(66)

$$K_0\left(z\right)\cong -\ln \left(\frac{\gamma z}{2}\right),K_n\left(z\right)\cong \frac{\Gamma \left(n\right)}{2}{\left(\frac{2}{z}\right)}^n,n=1,2\dots$$

(67)

where $\gamma =e^{0.577}$ (with 0.577 being the Euler–Mascheroni constant), it is sufficient to retain only the first two terms in the sums by $n$, including ${\Delta }_0\left(\omega \right)$ and ${\Delta }_1\left(\omega \right)$. Using (11) and (66), (67) yields

$${\Delta }_0\left(\omega \right)=\frac{{\left(ka\right)}^2}{4}\frac{\epsilon -1}{1+\epsilon \frac{{\left(ka\right)}^2}{2}\ln \left(2/\gamma ka\right)}$$

(68)

$${\Delta }_1\left(\omega \right)=\frac{{\left(ka\right)}^2}{2}\frac{\epsilon -1}{\epsilon +1}$$

(69)

For $n\ge 2,$ other functions ${\Delta }_n\left(\omega \right)$ and $Z_n\left(kR,\omega \right)$ in (49) can be neglected since they contain higher powers of $ka$.

In the case of a dielectric filament (except strongly polar ones with large $\epsilon$), one can neglect the term with $\epsilon$ in (68). Then, the sums in Equations (54)–(65) take the form

$${\displaystyle \sum }{ϵ}_n{Z}_n=0.5Z_0+Z_1=\frac{{\left(ka\right)}^2}{2}\left(\epsilon -1\right)\left[\frac{1}{2}{R}_1\left(x\right)+\frac{1}{\left(\epsilon +1\right)}{R}_2\left(x\right)\right],$$

(70)

$$R_1\left(x\right)=K_0^2\left(x\right)+K_1^2\left(x\right),$$

(71)

$$R_2\left(x\right)=K_1^2\left(x\right)+\frac{K_1^2\left(x\right)}{x^2}+{\left(d{K}_1\left(x\right)/dx\right)}^2=R_1\left(x\right)+2\left(\frac{K_1^2\left(x\right)}{x^2}+\frac{K_0\left(x\right)K_1\left(x\right)}{x}\right).$$

(72)

Note that in (70)–(72) we use $x=kR.$ For $V=0$, making use of the integral table [43]

$$\underset{0}{\overset{\infty }{{\displaystyle \int }}}dx{x}^{a-1}{K}_m\left(x\right)K_n\left(x\right)=\frac{2^{a-3}}{\mathsf{\Gamma }\left(a\right)}\mathsf{\Gamma }\left(\frac{a+m+n}{2}\right)\mathsf{\Gamma }\left(\frac{a+m-n}{2}\right)\mathsf{\Gamma }\left(\frac{a-m+n}{2}\right)\mathsf{\Gamma }\left(\frac{a-m-n}{2}\right)$$

(73)

we obtain from (56) or (61) (in the limit $T_2\to 0$) the known result [3,44]

$$U\left(R\right)=-\frac{9\hslash }{128R^3}{\left(\frac{a}{R}\right)}^2\underset{0}{\overset{\infty }{{\displaystyle \int }}}d\omega \alpha \left(\mathrm{i}\omega \right)\frac{\left(\epsilon \left(\mathrm{i}\omega \right)-1\right)\left(\epsilon \left(\mathrm{i}\omega \right)+7\right)}{\left(\epsilon \left(\mathrm{i}\omega \right)+1\right)}$$

(74)

The dynamic potentials (59), (60) can be worked out using a single-oscillator model

$$\epsilon \left(\omega \right)=a+\frac{b{\omega }_1^2}{{\omega }_1^2-{\omega }^2-\mathrm{i}\gamma \omega }$$

(75)

with parameters $a,b,{\omega }_1,\gamma$ chosen to fit the UV range of the spectrum when calculating potentials (59), (60), and the IR range when calculating friction forces (64) and (65).

When computing the interaction of an atom with a cylindrical metal filament, the contributions from (68) and (69) are essentially different since we should retain the whole denominator in (68).

In the static case ($V=0)$, using the plasma limit of the Drude permittivity $\epsilon \left(\mathrm{i}\omega \right)=1+{\omega }_p^2/{\omega }^2$ with allowance for the condition ${\left(a/R\right)}^2\ln \left(1.123R/a\right)\ll 1$ (here $1.123=2/e^{0.577})$ taking into account only the term $n=0$ in (59), and changing the order of integration (with the $\omega$ integration being the first), one obtains

$$U\left(R\right)=-\frac{\hslash \alpha \left(0\right)a}{2\sqrt{2}\pi R^4}\underset{0}{\overset{\infty }{{\displaystyle \int }}}dx{x}^3{R}_1\left(x\right){\ln }^{-\frac{1}{2}}\left(\frac{1.123xR}{a}\right)\cong -\frac{\hslash {\omega }_p\alpha \left(0\right)a}{2\sqrt{2}\pi R^4{\ln }^{1/2}\left(1.123R/a\right)}$$

(76)

This is exactly the well-known result (Equation (43) in [44]) obtained in the electrostatic approximation, using another method. The distance dependence in (76) is a surprising feature of the vdW interaction caused by the nonadditivity and plasmon spectra of a conducting filament. In the limit of high temperatures, retaining in (61) the term with $m=n=0$, we retrieve another result of [44]

$$U\left(R\right)=-\frac{\pi \alpha \left(0\right)T}{8R^3\ln \left(1.123R/a\right)}$$

(77)

For a metal filament, dynamic potentials (59), (60) can be simplified further. The resulting expression $U=U^{\left(0\right)}+U^{\left(1\right)}$ we cast in the form

$$U\left(R,V\right)=-\frac{\hslash {\omega }_0\alpha \left(0\right)}{8\pi R^3}{\left(\frac{a}{R}\right)}^2{\left(\frac{{\omega }_p}{{\omega }_0}\right)}^2\left(U_1+U_2+2U_3+2U_4\right)$$

(78)

The contributions $U_{1-4}$ are defined by Equations (A16)–(A19) in Appendix C. The terms $U_1,U_2$ correspond to terms $n=0,1$ in (59), and $U_3,U_4$–to the similar ones in (60). The static result (76) follows from (A16).

When calculating stopping force $F_z$ by means of (63), we use the Drude model $\epsilon \left(\omega \right)=1-{\omega }_p^2/\left({\omega }^2+i\gamma \omega \right)$. As shown in in Appendix C, Equation (63) takes the form

$$F_z=-\frac{\hslash \gamma \alpha \left(0\right)}{4\pi R^4}{\left(\frac{a}{R}\right)}^2{\left(\frac{{\omega }_p}{{\omega }_0}\right)}^2\left(F_1+2F_2\right)$$

(79)

with $F_1$ and $F_2$ defined in (A21) and (A22).

We now pass to the interactions of an atom with atomic chains. For dielectric chains with atomic spacing $d,$the transition is very simple, using the limit of rarified medium $\epsilon \left(\omega \right)-1=4\pi n{\alpha }_2\left(\omega \right)$, where $n\to 0$, ${\alpha }_2\left(\omega \right)$ is the polarizability of an atom of the string and $n=1/\pi a^{2}d$. Substituting these relations into (68), (69) yields

$${{\displaystyle \sum }}^{}{ϵ}_n{Z}_n=\frac{2k^2}{d}{\alpha }_2\left(\omega \right)\left[K_0^2\left(x\right)+K_1^2\left(x\right)+\frac{K_1^2\left(x\right)}{x^2}+\frac{K_0\left(x\right)K_1\left(x\right)}{x}\right]$$

(80)

Using (79) and (57) with parameters ${\alpha }_2\left(0\right)$ and ${\omega }_{02}$ of the atomic chain, and ${\omega }_{01}$ and ${\alpha }_1\left(0\right)$ of the projectile atom, Equations (60), (61) and (63) take the form

$$U^{\left(0\right)}=-\frac{\hslash {\omega }_{01}{\alpha }_1\left(0\right){\alpha }_2\left(0\right)}{2\pi d{R}^5}{\left(\frac{{\omega }_{02}}{{\omega }_{01}}\right)}^2\underset{0}{\overset{\infty }{{\displaystyle \int }}}dx{x}^4\left[R_1\left(x\right)+R_2\left(x\right)\right]f_1\left(p_1,b_{1}x\right)$$

(81)

$$U^{\left(1\right)}=\frac{\hslash {\omega }_{01}{\alpha }_1\left(0\right){\alpha }_2\left(0\right)}{\pi d{R}^5}{\left(\frac{{\omega }_{02}}{{\omega }_{01}}\right)}^2\mathrm{P}\underset{1/b_1}{\overset{\infty }{{\displaystyle \int }}}dx\frac{x^4}{\left[{\left(b_{1}x-1\right)}^2-p_1^2\right]}\left[R_1\left(x\right)+R_2\left(x\right)\right]$$

(82)

$$F_z=-\frac{\hslash {\omega }_{01}{\alpha }_1\left(0\right){\alpha }_2\left(0\right)}{2d{R}^5}\left(\frac{{\omega }_{02}R}{V}\right){\phi }_1\left(\left({\omega }_{01}+{\omega }_{02}\right)R/V\right)$$

(83)

where $f_1\left(x,y\right)$ is defined by (A15), ${\phi }_1\left(x\right)=x^5\left(R_1\left(x\right)+R_2\left(x\right)\right)$, $b_1=V/{\omega }_{01}R$, $p_1={\omega }_{02}/{\omega }_{01}$, and one should take the principal value of the integral in (82).

For a metal string, the rarefied-gas approximation is not valid due to remaining cooperative effects, giving rise to certain effective parameters of a one-dimensional plasma. Therefore, to describe the interactions between a projectile atom and a metallized atomic chain, a more adequate way is to use (78) and (79) with $a\approx d/2$ and the appropriate plasma parameters of the atomic chain. In the case of undamped plasmons $\left(\gamma \to 0^{+}\right),$ the expressions (A21) and (A22) can be simplified further and (79) reduced to (using $a=d/2):$

$$F_z\cong -\frac{\hslash {\omega }_0\alpha \left(0\right)}{4\sqrt{2}{R}^4{\ln }^{\frac{1}{2}}\left(\frac{2.246R}{a}\right)}\left(\frac{a}{R}\right)\left(\frac{{\omega }_p}{{\omega }_0}\right){\phi }_1\left(\stackrel{\sim }{b}\right)R_1\left(\stackrel{\sim }{b}\right)-\frac{\hslash {\omega }_0\alpha \left(0\right)}{4R^4}{\left(\frac{a}{R}\right)}^2{\left(\frac{{\omega }_p}{{\omega }_0}\right)}^2{\phi }_1\left(\left(1+p\right)/b\right)R_2\left(\left(1+p\right)/b\right)$$

(84)

where ${\stackrel{\sim }{b}}^{-1}=b-p{\phi }^{\frac{1}{2}}\left(2R/d\right)$, $b=V/{\omega }_{0}R$ (see Appendix C). The second term in (84) is nearly $d/R\sqrt{2}$ times (or more) less than the first one, since (usually) $\left(1+p\right)/b>\stackrel{\sim }{b}$ (note that ${\phi }_1\left(x\right)$ decays exponentially fast at $x\gg 1$). The more gentle dependence on $R\mathrm{of}$ the first term in (84), is a result of one-dimensional plasmon dispersion, similar to (76) [44].

6. Numerical Analysis

Due to the plethora of new analytical results obtained above, we will restrict ourselves by demonstrating only a few numerical examples (Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6) of the dynamic vdW potentials and stopping forces, namely the interactions of neutral atoms (in particular, Cs) with metal and dielectric filaments and atomic chains of Au, Si, and interactions with the walls of a capillary metallized with gold.

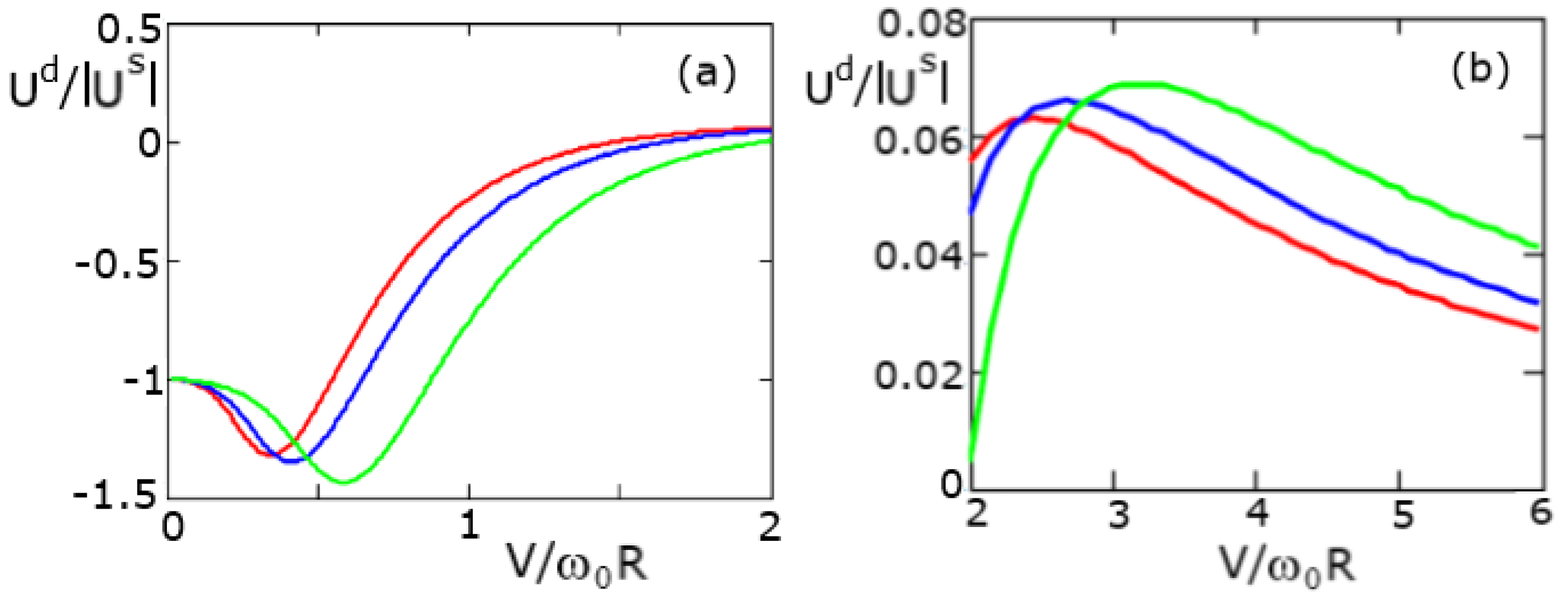
Figure 2 shows the ratio between the dynamic vdW potential $U^d$ and the modulus of the static potential $U^s$ shown as a function of the reduced velocity–distance parameter $V/{\omega }_{o}R$ for an atom in parallel motion to a metal filament, ${\omega }_o$ is the characteristic atomic frequency, ${\omega }_p$ is the metal plasma frequency. The calculations were carried out using Equation (78) with $a/R=0.1$ and ${\omega }_p/{\omega }_0=0.3,1,3$ (red, blue and green lines). The static potentials $U^s$in Figure 2 and in Figure 4 and Figure 5 were computed by the corresponding formulas for $U^d$ assuming $V=0$. It should be noted that in this velocity range, the calculations of $U^d$ are nearly independent on the choice of $\gamma$. The nonzero value of $\gamma$ simplifies calculating the integral $U_4$ in (78) by using (A19). For $\gamma =0$, the result is the same, but one should take the principal value of this integral.

The remarkable finding is that the dynamic vdW potential can be positive (repulsive) (panel (b)), though the coupling constant is an order (or more) less than that of the static potential $U^s$. At moderate velocity–distance parameters $V/{\omega }_{o}R~0.5$, the dynamic potential is attractive, and the coupling constant is 1.5 times higher than the static one.

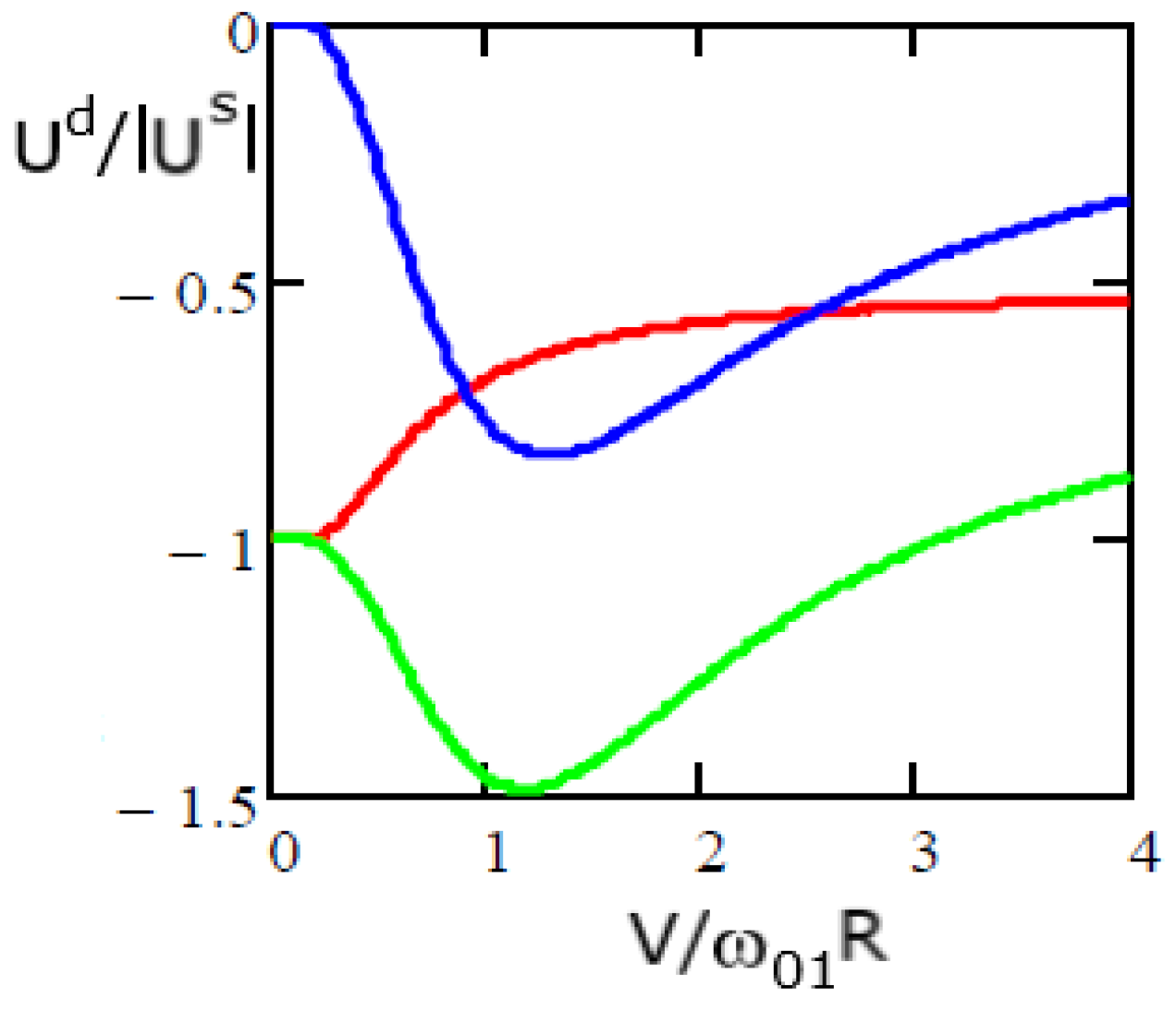
Figure 3 plots the dynamic vdW potential $U^d$ for a Cs atom as a function of distance $R$ to a metal chain of Au atoms (Equation (78) with parameters $a=d/2=0.2\mathrm{nm},{\omega }_p=9\mathrm{eV},\gamma =0.03\mathrm{eV},$ corresponding to gold. For a comparison, shown is the string continuous potential in the Moliere approximation for the Cs-Au interatomic potential $U\left(r\right)=Z_1{Z}_2{e}^2{r}^{-1}\mathsf{\Phi }\left(r/a_s\right)$ (dashed green), with $Z_1$ and $Z_2$ being the charges of the nuclei (55 and 79 for Cs and Au). Here, $\mathsf{\Phi }\left(r/a_s\right)$ is the screening function and $a_s=0.04683{\left(\sqrt{Z_1}+\sqrt{Z_2}\right)}^{-2/3}$ nm–the screening length [45]. The red and blue lines correspond to velocities of $3·{10}^7$ and $1.5·{10}^7\mathrm{m}/\mathrm{s}$. For the Cs atom, we used in (57) the values $\alpha \left(0\right)=0.057{\mathrm{nm}}^3$ and ${\omega }_0=3.89\mathrm{eV}$. Parameters ${\omega }_p$ and $\gamma$ are the same as in Figure 2. The peak structure of the red and blue curves at $R<0.5\mathrm{nm}$ is likely due to the violation of the used approximation $a/R\ll 1$. Figure 3 also demonstrates the repulsive dynamic vdW potential. In the range $0<V/{\omega }_{o}R<0.6$, the vdW interaction increases in absolute value relative to the static one (Figure 2a). This is similar to the case of a flat surface [30], but the repulsive effect was not found there. The observed feature is the pure result of the cylindrical symmetry and conductive properties of the metal filaments and atomic chains. Mathematically, the repulsion appears due to the negative contribution to the integral (A14) from the term $-y^2$ in the numerator, which is proportional to $V^2$. This leads to a change in sign in (59) and is enhanced by an increase (in absolute value) of the negative contribution to the interaction resulting from (6).

It is worthwhile noting that repulsive Casimir and Casimir–Polder forces known in so far were obtained only in static configurations of two parallel semi-infinite dielectric plates if they are separated by a dielectric fluid that is intermediate between those of the dielectric plates [46].

On the contrary, the interactions of the Cs atom with the dielectric filament and the chain (the Si chain was chosen as an example) turn out to be attractive (as in the static case). This can be seen from Figure 4 showing the ratio between the dynamic potential $U^d$ and the absolute values of the static potential $\left|U^s\right|$ for the Cs atom and the atomic chain of Si. The red and blue lines and their sum (green) were calculated using Equations (81) and (82). Both the $U^{\left(0\right)}$ and $U^{\left(1\right)}$ contributions have the negative sign, but the coupling constant of the main distance dependence $~R^{-5}$ increases in the range $0<V/{\omega }_{01}R<3$ (${\omega }_{01}=3.89\mathrm{eV}$ here means the atomic frequency of Cs).

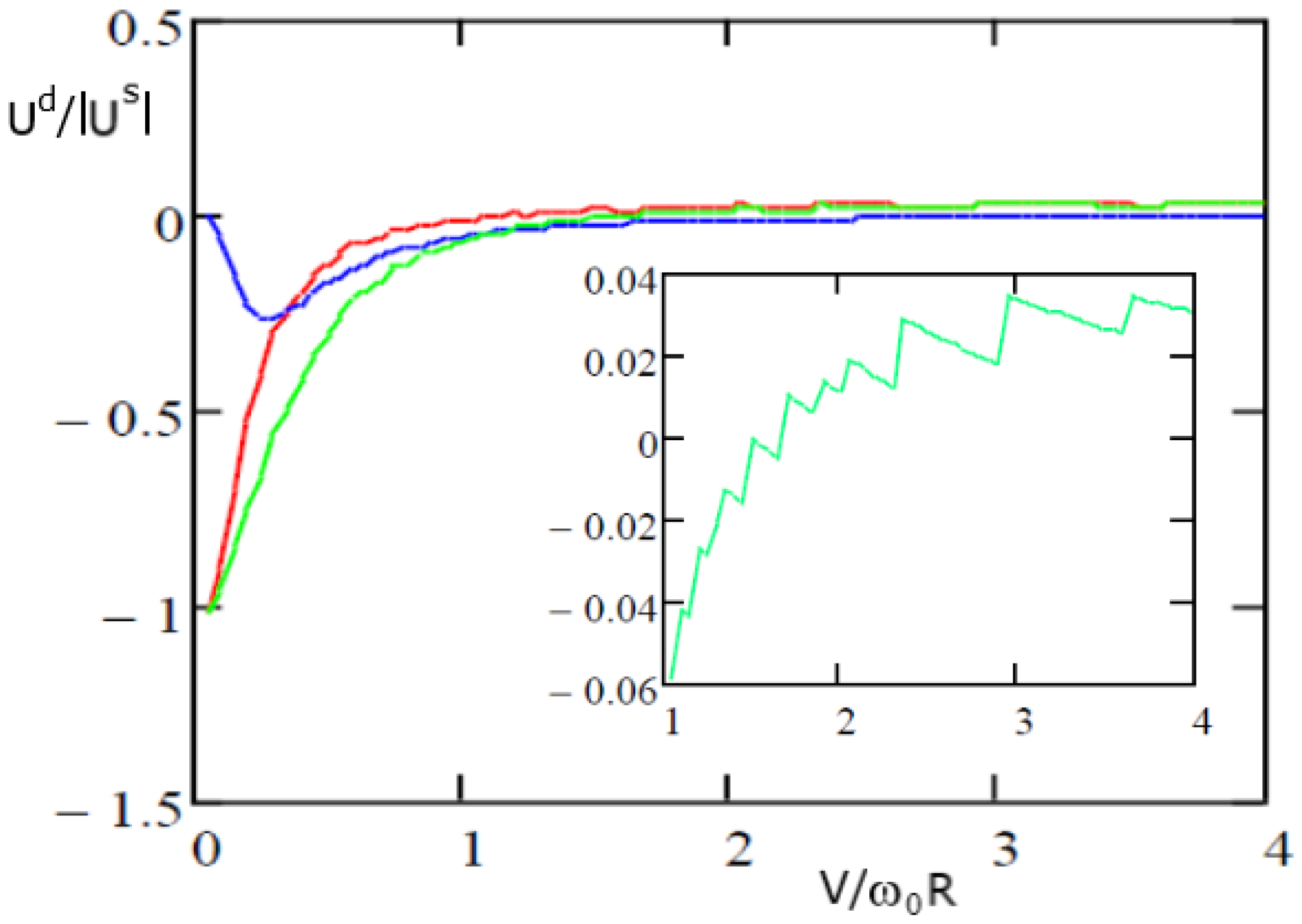
The repulsive vdW interaction also manifests itself in the case of the motion of Cs atoms inside a capillary with Au metallized walls. The results are plotted in Figure 5 with the same color convention as in Figure 4: the red and blue lines correspond to the contributions $U^{\left(0\right)}$ and $U^{\left(1\right)}$, calculated by Equations (58) and (59). The green line and the inset show the resulting potential. All parameters for the Cs atom and gold are the same as those used when plotting Figure 3. The change in the sign of the vdW potential in this case occurs close to the value $V/{\omega }_{o}R=1.5$. The toothlike structure results from the contributions of multiple harmonics in the sums of (58) and (59).

Finally, we calculated the stopping force (Equation (63)) for the Cs atom in a capillary with Au metallized walls (Figure 6).

The peak structure in Figure 6 is caused by the excitation of plasmons. This is similar to the case of the excitation of plasmons by charged particles in cylindrical channels [16].

The numerical examples presented here are illustrative, and additional analysis is required to clarify many of the subtle points of the vdW dynamic interactions that are beyond the scope of this article. Among them are the presence of many multiple resonances of the dielectric response, the transition region from the vdW to the short-range interactions with atoms of walls, the nonlocality of the dielectric permittivity, which increases at small separations, etc.

7. Conclusions

In this paper, we refined some points and developed further the nonrelativistic theory of vdW interactions; namely, we calculated the attractive potential and stopping (friction) forces between neutral ground-state atoms and cylindrical surfaces of different configurations. As a constituent part of the theory, the electromagnetic image forces for the charged particles in the systems under consideration were also calculated. The transition from the case of a cylindrical surface to a flat surface is demonstrated and the obtained expressions for image forces and vdW forces and potentials are shown to completely coincide with all known results in plane and cylindrical geometries. The formulas describing the configurations with convex, concave cylindrical surfaces and two coaxial cylinders with a particle between them are represented in a universal form. A new remarkable result is that the dynamic vdW potential can be positive (repulsive) in the case of metallized atomic chains, filaments and capillaries, providing a steering effect for the channeled neutral atoms.