Abstract
Since 1969, Lunar Laser Ranging (LLR) data have been collected by various observatories and analysed by different analysis groups. In the recent years, observations with bigger telescopes (APOLLO) and at infra-red wavelength (OCA) are carried out, resulting in a better distribution of precise LLR data over the lunar orbit and the observed retro-reflectors on the Moon. This is a great advantage for various investigations in the LLR analysis. The aim of this study is to evaluate the benefit of the new LLR data for the determination of relativistic parameters. Here, we show current results for relativistic parameters like a possible temporal variation of the gravitational constant , the equivalence principle with , and the PPN parameters and . The results show a significant improvement in the accuracy of the various parameters, mainly due to better coverage of the lunar orbit, better distribution of measurements over the lunar retro-reflectors, and last but not least, higher accuracy of the data. Within the estimated accuracies, no violation of Einstein’s theory is found and the results set improved limits for the different effects.
1. Introduction
It was 20 July 1969 when the astronauts of the Apollo 11 crew landed in the southern part of Mare Tranquillitatis on the Moon. They deployed the Apollo Lunar Surface Experiments Package, where the retro-reflector for Lunar Laser Ranging (LLR) is now the last operating part of the experiment. Until 1973, four further reflectors were deployed on the lunar surface: two reflectors by the astronauts of the Apollo 14 and 15 missions, and two reflectors mounted on the unmanned Soviet Lunokhod rovers. For more than 50 years there has been continuous measuring of the distance between observatories on the Earth and retro-reflectors on the Moon. The measurement of round trip travel times between Earth and Moon with short laser pulses is challenging. The average number of returning photons is less than one per laser pulse [1,2], mainly because of the beam divergence of the laser pulses due to the atmospheric turbulence and diffraction effects of the reflectors [3]. Further signal loss occurs in the paths of the transmitting and detection optics, in the atmosphere and due to the reflectivity of the retro-reflectors [4]. A series of single measurements over 5–15 min is used to calculate a so-called normal point (NP) [5] which is the observable in the LLR analysis. More details about the measured Earth–Moon distance are given in Section 2.
The observatories on the Earth, that were, or are, capable to range to the Moon are the Observatoire de la Côte d’Azur (OCA) in France, the McDonald observatory (MLRS) and the Apache Point Lunar Laser-ranging Operation (APOLLO) in the USA, the Lunar Ranging Experiment (LURE) of the Haleakala observatory on Hawaii, the Matera Laser Ranging Observatory (MLRO) in Italy, and the Wettzell Laser Ranging System (WLRS) in Germany. From the end of the eighties, OCA started to investigate the measurement of laser round trip travel times from the observatory to the Moon and back with laser emitting in the infrared (IR) at a wavelength , but the precision level of the detector at that time for IR measurements was insufficient for the detection of photon returns from the Moon [6]. In 2014, that problem was solved and OCA is now able to use IR and green laser light for the regular measurements. After technical renewals and improvements WLRS is also able to measure the Earth–Moon distance with IR wavelength starting in 2018 [7]. With the new technique measurements close to the new Moon and full Moon are possible. Furthermore, ranging to the retro-reflectors at lower elevation angles is possible and a better distribution of the measurements over the reflectors is achieved [1]. All that results in an improved coverage of the lunar orbit and is a big benefit in the analysis of the data and for the determination of various parameters. First tests of the universality of free-fall with IR data are promising [8].
In Germany, from the early 1980s on, the software package LUNAR (LUNar laser ranging Analysis softwaRe) has been developed to study the Earth–Moon system and to determine several related model parameters [9,10,11,12]. Research covered physical libration and orbit of the Moon, coordinates of observatories and retro-reflectors, Earth orientation parameters. With special modifications of the model and software it is possible to investigate Einstein’s theory of relativity by the determination of various parameters. Here, hard constraints for a possible violation of Einstein’s theory are given by LLR results, like the equivalence principle, variation of the gravitational constant G, and the parametrized post-Newtonian (PPN) parameters and [8,13,14]. By including the new high-precision NP measured with IR wavelength into the LLR analysis, improvements for various parameters are expected. The benefit of that NP is investigated here in more detail for the parameters related to testing Einstein’s theory. The results are compared with a previous study published in [13]. This study is based on similar conditions, but less NP in IR were evaluated in the former. In our recent study now, their effect can be addressed in detail.
2. LLR Analysis
The analysis model used in LUNAR is based on Einstein’s theory of relativity. It is fully relativistic and complete up to the first post-Newtonian () level. To take advantage of the high-precision NP that can be obtained with an accuracy of several millimetres [2], the LUNAR software has been updated continuously [15,16]. Now, the LLR analysis model takes into account, among other things, gravitational effects of the Sun and planets with the Moon as extended body, the higher-order gravitational interaction between Earth and Moon, as well as effects of the solid Earth tides on the lunar motion. The basis for the modeled lunar rotation is a 2-layer core–mantle model according to the DE430 ephemeris [17]. A recent overview of LUNAR is given in [13], a detailed description can be found in [18].
The measured laser travel time from Earth to Moon and back gives, together with the speed of light c, the length of the path (forth and back)
Figure 1 shows the principle of LLR measurements in the moving Earth–Moon system. In a weighted least-squares adjustment, the measured length of the light path is compared with the modeled length computed as
where denotes the light path between the observatory at time and the reflector at time with
and the light path between the reflector at time and the observatory at time with
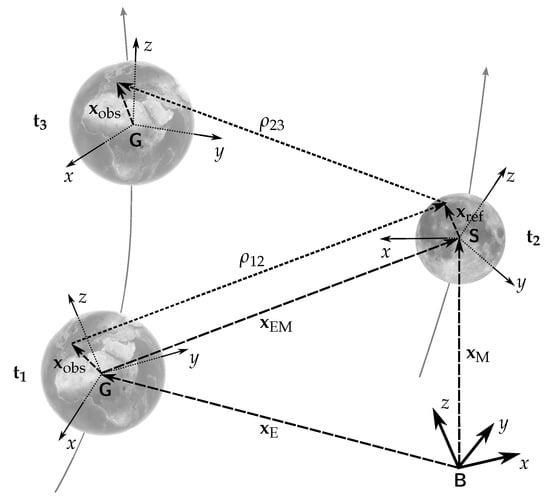
Figure 1.
Scheme of a Lunar Laser Ranging (LLR) measurement in the moving Earth–Moon system with the solar system barycenter B, geocenter G, and selenocenter S, and the transmitting time , reflection time , and detection time . The vectors are as the barycentric vector to the geocenter at time , as the barycentric vector to the selenocenter at time , as the Earth–Moon vector of the outgoing light path, as the vector from the geocenter to the observatory in the barycentric system at the times and , as vector the selenocenter-reflector in the barycentric system at the time . , as the length of outgoing and incoming light path. indicate the different reference systems of the bodies and the solar system [13].
of Equation (2) takes into account corrections of the light travel time, like the delay due to the light propagation through the gravitational potential of Sun and Earth [19,20], an atmospheric delay [21,22], a synodic modulation of the lunar orbit due to radiation pressure [23], and some time- and station-dependent biases.
For the calculation of Equations (3) and (4), the positions of the observatories and retro-reflectors are needed in an inertial reference system; here, the barycentric celestial reference system (BCRS) with the barycentric dynamical time (TDB) is selected. Therefore, in a first step, effects at the coordinates of the observatories and retro-reflectors will be considered according to the work in [24], e.g., tidal effects due to the atmosphere, ocean, and solid Earth, and the tectonic movement in the respective body-fixed reference system. In a second step, the transformations from the body-fixed systems to the BCRS are carried out. Here, the needed rotation of the Earth is modelled as defined in [15,24], the rotation of the Moon is computed simultaneously with the translation corresponding to [17]. The barycentric position and velocity vectors of Earth and Moon are derived from an ephemeris computation of the solar system bodies (all planets, the Moon and the largest asteroids). Initial values for the computation are taken from the DE430 ephemeris [17].
The measured NP serve as observations in the analysis. They are treated as uncorrelated for the stochastic model of the least squares adjustment and are weighted according to their accuracy. The adjustment is done in a Gauss–Markov model where up to 250 unknown parameters can be determined with their uncertainties. They are divided in two groups. The first group consists of the so-called Newtonian parameters, e.g., initial position, velocity, and physical libration of the Moon; parameters of the lunar interior; coordinates of LLR observatories and retro-reflectors; mass of the Earth–Moon system; precession rate; and the lunar tidal acceleration. The second group of parameters is used to perform LLR tests of the general theory of relativity. More details for those parameters are given in Section 4. As another result of the analysis one gets the post-fit residuals, of which the weighted root mean square (wrms) is given in Figure 2 for each year. Beginning in 1970 with a wrms of more than 25 cm, improvements in the measurement system lead to a decreasing wrms. Since 2006, it is about 2 cm or less.
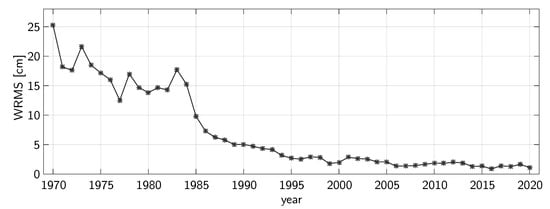
Figure 2.
Annual weighted rms (wrms) of the one-way post-fit residuals for 27,485 NP for the time span April 1970 to April 2020.
3. Distribution of the Normal Points
The distribution of LLR NP has a big impact on the determination of various parameters. Furthermore, non-uniform data distribution is one reason for correlations between solution parameters [25]. Therefore, the distribution of the LLR data is investigated in more detail below with respect to each of the observatories, retro-reflectors, and synodic angle. For the current study, NP for the period April 1970 to April 2020 were used. In a pre-analysis, all were checked for possible outliers. Outliers are defined as NP whose residuals for the Earth–Moon distance exceed a limit of a few decimetres. Where the limit lies is determined differently for each observatory because they observe with different accuracies. Sometimes NP of one or more nights are shifted by the same amount, e.g., due to calibration problems during the measurement. Then, a correction value is introduced into the analysis for this period. Furthermore, the standardized normal distribution is used for the evaluation of the outliers. If this distribution exceeds a certain value, the NP is also classified as an outlier and not included in the further analysis. After the pre-analysis, 17 NP of the current data set were identified as outliers. Thus, 27,485 NP for the period April 1970 to April 2020 are included in the investigation, 22,021 measured with green and 5464 with IR laser light.
Figure 3 shows the temporal distribution of the measured NP over the last 50 years. One can see in the legend that more than 60% of the NP were observed by OCA (42% with green and 20% with IR laser light). In the last years, only OCA and APOLLO provided regular NP, some NP also came from MLRO and WLRS. For the year 2019, 90% of the NP were measured by OCA in IR. It is clear that, with this distribution of NP, the analysis is dominated by the OCA NP. Looking at the distribution of the NP according to the respective reflectors, Figure 4 shows it for the whole time span in the left pie. Here, the clear domination of Apollo 15 is obvious. Because Apollo 15 gives the strongest reflected signal due to its large size, it was more often tracked by the observatories in the past. This was not beneficial for the data analysis. In recent years and with IR NP the situation has improved considerably. For 2019 (shown in Figure 4, right pie) all retro-reflectors were measured approximately equally often, because of the advantage of IR laser light [1]. That is also a big advantage for the analysis, especially for the determination of the lunar libration.
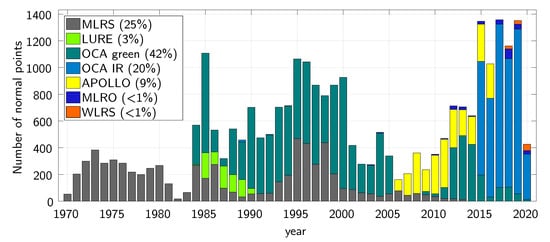
Figure 3.
Distribution of the 27,485 normal points over the the time span April 1970–April 2020. In the legend the percentages of the contribution of the respective observatories are given. The three observatories McDonald, MLRS1 and MLRS2 are linked in the analysis and listed here as MLRS.
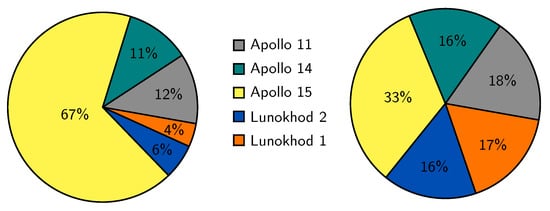
Figure 4.
Distribution of all NP as measurement to the respective reflectors for the whole data span of LLR (left) and for the year 2019 (right).
With the better performance of the measurements now also ranging near new and full Moon is possible [1] for OCA and WLRS. This leads to a better coverage of the lunar orbit over the synodic month. The synodic month is the time span, when Sun, Earth, and Moon are in the same constellation again. To illustrate the better coverage, Figure 5 shows the percentage of the NP measured for a specific angle of the synodic month. Indicated in green are the measurements with green laser light, and in red the measurements with IR laser light are given. In the past, when using only green NP there were gaps in the phases of new and full Moon. Now there are many more observations in IR and the advantage of it is obvious. The more equal distribution of the NP over the synodic month leads to a better coverage of the lunar orbit and is a big benefit for the determination of various parameters.
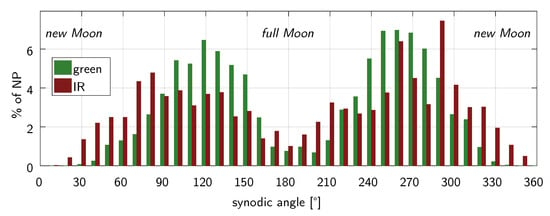
Figure 5.
Distrubution of the NP over the synodic month. Given are the percentage of NP of the total number of measurements with the specific laser color. Full and new Moon indicates the phases of the Moon.
4. Relativistic Parameters
The analysis of LLR observations is based on Einstein’s theory of relativity. Thus, the Einstein–Infeld–Hoffmann equations, the signal propagation in the gravitational field of Earth and Sun, the temporal and spatial reference systems as well as their respective transformations are formulated relativistically up to the first post-Newtonian () level [18]. By modifying the Einstein–Infeld–Hoffmann equations for the ephemeris calculation and extending it to include certain relativistic parameters, it is possible to determine and study more closely the effect of these parameters in the parameter calculation. Recent results, e.g., on the equivalence principle, Yukawa term, metric parameters, and geodetic precession, can be found in publications [8,13,14,26]. As opposed, the authors of [27,28,29] used the standard-model extension (SME) with general relativistic equations of motion, fitted parameters of the SME to LLR data and tested the Lorentz symmetry.
The various relativistic model contributions cause significant periodic variations, e.g., annual and monthly, linked to the node of the moon and combined periods in the Earth–Moon distance, through which it is possible to distinguish them from each other [30]. Due to the large distance between Earth and Moon and the effect of the bodies in the solar system, the relativistic effects in the measured Earth-Moon distance are larger than, e.g., in distance measurements to satellites (SLR) [31]. This is a great advantage of LLR. Moreover the long time span of LLR data (>50 years) is very beneficial to determine and decorrelate certain relativistic parameters.
To determine relativistic parameters in the LLR analysis, a two-step strategy is applied. In the first step, the non-relativistic Newtonian parameters of the LUNAR model are calculated in a so called standard solution. Here, the relativistic parameters are fixed to their values of Einstein’s theory. The second step then allows the estimation of individual relativistic parameters together with the Newtonian ones. If unrealistically high correlations between Newtonian and relativistic parameters are obtained in a first calculation, the corresponding Newtonian parameters can be fixed to the values of the standard solution in the further determination of the relativistic parameters.
In the following subsections, different relativistic effects are investigated, e.g., the equivalence principle, the temporal variation of the gravitational constant, and the PPN parameters and . The aim is to find out to what extent the higher precision IR NP have an impact on the estimation of the related parameters compared to the results of [13]. The analysis model in the current study and in [13] is the same, the major difference is that a shorter time span (April 1070–January 2015) with 20,856 NP and much less IR NP were used there. Due to the similar design of the two studies, the effect of the IR NP is directly visible. Table 1 gives an overview with the results in [13] and those of the current study. The basics of estimating the relativistic parameters are already given in [13] and are only briefly discussed here.

Table 1.
Values for relativistic parameters from two different estimations. In the middle column results of [13], in the right column results of the current estimation.
4.1. Equivalence Principle
The equivalence principle (EP) dates back to the 17th century when Galileo Galilei studied the acceleration of two bodies in free fall and found that in the same gravitational field it is independent of their shape, mass, and composition [32]. The second axiom of Isaac Newton states that the force F results from the multiplication of an acceleration a and the inertial mass as . In the gravitational field of the Earth, Newton’s law of gravitation is . That leads to the equivalence of the inertial mass and the gravitational mass . If the equivalence principle is valid, the ratio , which is called the weak equivalence principle (WEP), is equal to 1. The comparison of the free-fall accelerations of two bodies () leads to the test of the equivalence principle as
A violation would lead to a different acceleration of the bodies in the same gravitational field. To investigate the WEP on Earth, sensitive torsion balances and test bodies made of different compositions like beryllium and titan [33], and rubidium and potassium [34] are used. Recent results from the MICROSCOPE satellite mission confirmed the WEP at the level of [35]. From the analysis of LLR data between 1969 and 2017, the authors of [8] estimated .
In Einstein’s gravitational theory, the WEP is extended to the strong equivalence principle (SEP) due to the gravitational self-energy U of the bodies. For bodies with astronomical sizes, like Earth and Moon, the SEP can be tested [36] and parameterized with the Nordtvedt parameter by
with self energy U and mass M for the respective body and the speed of light c. In Einstein’s theory, it holds that . By analyzing the LLR data a combined test of the SEP and WEP is possible. Here, Earth and Moon are test bodies in the gravitational field of the Sun with gravitational self-energies and different composition. A violation of the EP would cause an additional acceleration of the Moon into the direction of the Sun.
For the investigation of a possible violation of the EP with LLR data there are, according to the authors of [13], two different way which leads to similar results. Here, the focus is on the determination via an additional acceleration of the Moon with the relative coordinates between Sun and Moon and the distance to the Sun, where the largest perturbation is given by
denotes the gravitational constant times the mass of the Sun. That method keeps the interaction with all other forces in the calculation of the ephemeris.
The result of [13] for the EP test was
with correlations of up to 60% with because of the dependence on the synodic angle [37]. There are also correlations of up to 60% with the X-components of the reflector coordinates. Compared to the result of this study with
the accuracy was improved and the correlations to and the reflector coordinates decreased to 40%. Here the better coverage of the LLR NP over the synodic angle, shown in Figure 5, is a clear benefit for the determination of the EP parameter.
The authors of [14] investigated a possible violation of the EP due to assumed dark matter in the galactic center which would cause an Earth–Moon range oscillation with a sidereal month period. The amplitude for such an oscillation, determined from LLR post-fit residuals, was found to be . The investigation also shows that a good orbit coverage with high precision data is more relevant for the EP test than the overall number of LLR data or a long time span. This underlines the improved values and correlations for the EP test, which shows no violation of Einstein’s theory within the given error bars.
4.2. Temporal Variation of the Gravitational Constant
From Einstein’s general theory of relativity, it follows that the gravitational constant G is a temporally and spatially invariable quantity [38]. According to the investigations of [39,40], however, the existence of alternative theories is possible, which allow a variation of the gravitational constant. One of the best known is the Brans–Dicke theory, a scalar-tensor theory. It is an extension of Einstein’s theory with additional scalar fields [39]. Recent studies in [41,42] confirm the considerations that a temporal variation of the gravitational constant in the range from to might be possible. According to the remarks in [43], there are also theories which admit so-called preferred reference systems. Furthermore, in such systems, a time dependence of G would be possible. The recent upper bounds for a non-zero value of by using LLR data come from the analysis of the ephemeris of the solar system bodies with [44] and [45]. From the analysis of MESSENGER data, the authors of [46] get an upper limit for .
The estimation of a linear and quadratic part of the gravitational constant as a function of time is done in the analysis of LLR data with
as part of the ephemeris calculation. In the standard solution, is valid. The time difference results from the current calculation time and the beginning of the LLR measurements. The partial derivatives of and needed for the adjustment in the Gauss–Markov model are calculated by numerical differentiation of the geocentric lunar ephemeris.
The results of [13] for the temporal and quadratic variation were estimated as separate parameters in two fits (where the respective other parameter was fixed to the Einsteinian value) as
For this results, the initial values of the lunar core rotation vector were fixed to their estimated standard solution values because of the high correlation of up to 94% with and . High correlations of up to 83% with some components of the station coordinates were reduced by introducing constraints on the estimated station coordinates.
The determination of and with more NP including a high number of IR NP from OCA resulted in
for the separate calculation of the two parts of G. In the current calculation, the correlations with parts of the core rotation vector were up to 70% and decreased compared to [13]. However, they were high enough to affect the determination of and , therefore they were fixed to their estimated standard solution values. The correlations with station coordinates could be reduced to up to 20% compared to [13] and no constraints were used in the calculation. Moreover, correlations with other parameters of the Earth-Moon system significantly decreased and are now at most 40% with the Z-component of the initial values of the lunar orbit. Here, the benefit of the longer data span with accurate NP leads to the improvement and a better and independent determination of the linear and quadratic part of G.
For the determination of the linear and quadratic part of G together in one parameter fit the values are
The parameters are correlated to each other with 70%. The correlations to other parameters were also higher than in the separate estimation. This leads to a less accurate determination of and . Nevertheless, the accuracies are in a similar range as for the separate estimation and the results underline the validity of Einstein’s theory in the given limits.
4.3. PPN Parameters and
In the framework of the parameterized post-Newtonian (PPN) approximation of Einstein’s theory, the parameter indicates the nonlinearity of gravity and the size of space curvature [43]. Both values are equal to 1 in this theory.
Recent analysis of MESSENGER data [46] gives a value for . From the analysis of solar system ephemeris there are values at the level of for and for . [45,47] get values of and .
From the analysis of LLR data, the authors of [13] get values for the determination of and via the Einstein–Infeld–Hoffmann equations of motion as
Both values show high correlations of up to 82% to station coordinates and the Z-component of the lunar initial velocity. Further correlations are to additional rotations between the Earth-fixed and space-fixed reference systems of up to 47%. For this reasons, the additional rotation was fixed to the values of the standard solution and the station coordinates were constraint.
In the current analysis the PPN parameters were determined to
The correlations to the station coordinates now are up to 60%, to the Z-component of the lunar initial velocity 40% and to the additional rotation 30%. All of them were reduced significantly. To make the results more comparable with those of [13], the additional rotations were nevertheless fixed to the values of the standard solution. The remaining correlations are now up to 40% with the previously mentioned parameters. Compared to the results of [13], the values of improved slightly, is on a similar level. The longer time span and IR NP are not as beneficial for the estimation of PPN parameters as for the other relativistic parameters shown, but the correlations decreased and there is still no violation of Einstein’s theory.
5. Summary and Outlook
The aim of this study was the investigation of the benefit of high-precision IR LLR measurements for determining relativistic parameters in comparison to the results of [13]. The model of the Earth–Moon system remained the same between the two calculations of relativistic parameters. The only major changes come from the longer time span of the LLR data and from many more measurements in the IR. From the previous discussions, it is clear that the IR data provide a major advantage for the LLR analysis. The accuracies of the relativistic parameters could be improved due to the better coverage of the lunar orbit and the accuracy of the data itself. Another advantage is the decorrelation of the relativistic parameters with other parameters of the Earth–Moon system. A summary of the results can be found in Table 1. So far, from the analysis of the LLR data, the assumptions of Einstein’s theory of relativity have been confirmed, now with improved limits.
An expanded network of single corner-cube retro-reflectors (CCRs) to be placed on the lunar surface near the limbs and poles from the year 2022 on will improve the existing geometry of the reflectors on the lunar surface and allows a better determination of the libration and rotation of the Moon. Such CCRs are also beneficial in terms of thermal resilience and increased return signal strength. This will improve the ranging accuracy and the resultant scientific parameters by a factor of 10 to 100 [48].
With the construction of the new LLR facility at Table Mountain Observatory (JPL’s Optical Communication Testbed Laboratory (OCTL)) in California, for the first time, it will be possible to conduct differential LLR (DLLR) with an expected range precision of less than 30 micrometers, a factor of 200 better than the current accuracy [49]. This opens new possibilities for improved analysis of the whole LLR parameter set. It is expected that the accuracy for relativistic parameters determined from DLLR data will improve by one order of magnitude, which should lead to accuracies similar to those expected from the Bepi Colombo mission [50], especially for the PPN parameters and .
The improvements on the technical side and further measurements in IR will make it possible, for example, to investigate effects related to the deep lunar interior and rotation and to determine relativistic parameters with higher accuracy. Together with improved modeling of the lunar interior and rotation in the LUNAR software, this will significantly improve many parameters determined from the analysis of the LLR data.
Author Contributions
Conceptualization, J.M.; Data curation, J.-M.T.; Formal analysis, L.B.; Funding acquisition, J.M.; Investigation, L.B.; Methodology, L.B.; Project administration, J.M.; Software, L.B.; Supervision, J.M.; Writing—original draft, L.B.; Writing—review and editing, J.M. and J.-M.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy–EXC-2123 QuantumFrontiers–390837967 and by the Deutsches Zentrum für Luft- und Raumfahrt (DLR, German Aerospace Center), Institute for Satellite Geodesy and Inertial Sensing.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All LLR NP used for this study are available from the Crustal Dynamics Data Information System (CDDIS) at NASA’s Archive for Space Geodesy Data, USA, https://cddis.nasa.gov/Data_and_Derived_Products/SLR/Lunar_laser_ranging_data.html [51].
Acknowledgments
Current LLR data were collected, archived, and distributed under the auspices of the International Laser Ranging Service (ILRS) [52]. We acknowledge with thanks that more than 50 years of processed LLR data has been obtained under the efforts of the personnel at the Observatoire de la Côte dAzur in France, the LURE Observatory in Maui, Hawaii, the McDonald Observatory in Texas, the Apache Point Observatory in New Mexico, the Matera Laser Ranging station in Italy and the Wettzell Laser Ranging Station in Germany.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chabé, J.; Courde, C.; Torre, J.M.; Bouquillon, S.; Bourgoin, A.; Aimar, M.; Albanèse, D.; Chauvineau, B.; Mariey, H.; Martinot-Lagarde, G.; et al. Recent Progress in Lunar Laser Ranging at Grasse Laser Ranging Station. Earth Space Sci. 2020, 7, e2019EA000785. [Google Scholar] [CrossRef]
- Murphy, T.W. Lunar laser ranging: The millimeter challenge. Rep. Prog. Phys. 2013, 76, 076901. [Google Scholar] [CrossRef] [PubMed]
- Murphy, T.W.; Adelberger, E.G.; Battat, J.B.R.; Hoyle, C.D.; McMillan, R.J.; Michelsen, E.L.; Samad, R.L.; Stubbs, C.W.; Swanson, H.E. Long-term degradation of optical devices on the Moon. Icarus 2010, 208, 31–35. [Google Scholar] [CrossRef]
- Müller, J.; Murphy, T.W.; Schreiber, U.; Shelus, P.J.; Torre, J.M.; Williams, J.G.; Boggs, D.H.; Bouquillon, S.; Bourgoin, A.; Hofmann, F. Lunar Laser Ranging: A tool for general relativity, lunar geophysics and Earth science. J. Geod. 2019, 93, 2195–2210. [Google Scholar] [CrossRef]
- Michelsen, E.L. Normal Point Generation and First Photon Bias Correction in APOLLO Lunar Laser Ranging. Ph.D. Thesis, University of California, San Diego, CA, USA, 2010. [Google Scholar]
- Courde, C.; Torre, J.M.; Samain, E.; Martinot-Lagarde, G.; Aimar, M.; Albanese, D.; Exertier, P.; Fienga, A.; Mariey, H.; Metris, G.; et al. Lunar laser ranging in infrared at the Grasse laser station. Astron. Astrophys. 2017, 602, A90. [Google Scholar] [CrossRef]
- Schreiber, K.U.; Eckl, J.J.; Leidig, A.; Bachem, T.; Neidhart, A.; Schüler, T. Lunar Laser Ranging: A small system approach. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 9–13 December 2019. [Google Scholar]
- Viswanathan, V.; Fienga, A.; Minazzoli, O.; Bernus, L.; Laskar, J.; Gastineau, M. The new lunar ephemeris INPOP17a and its application to fundamental physics. Mon. Not. R. Astron. Soc. 2018, 476, 1877–1888. [Google Scholar] [CrossRef]
- Egger, D. Systemanalyse der Laserentfernungsmessung. Ph.D. Thesis, Technische Universität München, München, Germany, 1985. [Google Scholar]
- Gleixner, H. Ein Beitrag zur Ephemeridenrechnung und Parameterschätzung im Erde-Mond-System. Ph.D. Thesis, Technische Universität München, München, Germany, 1986. [Google Scholar]
- Bauer, R. Bestimmung von Parametern des Erde-Mond-Systems—Ein Beitrag zur Modellerweiterung und Bewertung, Ergebnisse. Ph.D. Thesis, Technische Universität München, München, Germany, 1989. [Google Scholar]
- Müller, J. Analyse von Lasermessungen zum Mond im Rahmen Einer Post-Newton’schen Theorie. Ph.D. Thesis, Technische Universität München, München, Germany, 1991. [Google Scholar]
- Hofmann, F.; Müller, J. Relativistic tests with lunar laser ranging. Class. Quantum Gravity 2018, 35, 035015. [Google Scholar] [CrossRef]
- Zhang, M.; Müller, J.; Biskupek, L. Test of the equivalence principle for galaxy’s dark matter by lunar laser ranging. Celest. Mech. Dyn. Astron. 2020, 132, 25. [Google Scholar] [CrossRef]
- Biskupek, L. Bestimmung der Erdorientierung mit Lunar Laser Ranging. Ph.D. Thesis, Leibniz Universität Hannover, Hannover, Germany, 2015. [Google Scholar] [CrossRef]
- Hofmann, F. Lunar Laser Ranging–Verbesserte Modellierung der Monddynamik und Schätzung Relativistischer Parameter. Ph.D. Thesis, Leibniz Universität Hannover, Hannover, Germany, 2017. [Google Scholar]
- Folkner, W.M.; Williams, J.G.; Boggs, D.H.; Park, R.S.; Kuchynka, P. The Planetary and Lunar Ephemerides DE430 and DE431. In The Interplanetary Network Progress Report; Jet Propulsion Laboratory, California Institute of Technology: Passadena, CA, USA, 2014; Volume 42–196. [Google Scholar]
- Müller, J.; Biskupek, L.; Hofmann, F.; Mai, E. Lunar laser ranging and relativity. In Frontiers in Relativistic Celestial Mechanics; Kopeikin, S.M., Ed.; Walter de Gruyter: Berlin, Germany, 2014; pp. 103–156. [Google Scholar]
- Shapiro, I.I. Fourth Test of General Relativity. Phys. Rev. Lett. 1964, 13, 789–791. [Google Scholar] [CrossRef]
- Moyer, T.D. Mathematical formulation of the Double Precision Orbit Determination Program DPODP; Technical Report JPL-TR-32-1527; Jet Propulsion Laboratory, California Institute of Technology: Pasadena, CA, USA, 1971. [Google Scholar]
- Mendes, V.B.; Prates, G.; Pavlis, E.C.; Pavlis, D.E.; Lanley, R.B. Improved mapping functions for atmospheric refraction correction in SLR. Geophys. Res. Lett. 2002, 29, 1414. [Google Scholar] [CrossRef]
- Mendes, V.B.; Pavlis, E.C. High-accuracy zenith delay prediction at optical wavelengths. Geophys. Res. Lett. 2004, 31, L14602. [Google Scholar] [CrossRef]
- Vokrouhlicky, D. A Note on the Solar Radiation Perturbations of Lunar Motion. Icarus 1997, 126, 293–300. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. (Eds.) IERS Conventions 2010; Number 36 in IERS Technical Note; Verlag des Bundesamtes für Kartographie und Geodäsie: Frankfurt am Main, Germany, 2010. [Google Scholar]
- Williams, J.G.; Turyshev, S.G.; Boggs, D.H. Lunar Laser Ranging Tests of the Equivalence Principle with the Earth and Moon. Int. J. Mod. Phys. D 2009, 18, 1129–1175. [Google Scholar] [CrossRef]
- Williams, J.G.; Turyshev, S.G.; Boggs, D.H. Lunar laser ranging tests of the equivalence principle. Class. Quantum Gravity 2012, 29, 184004. [Google Scholar] [CrossRef]
- Bourgoin, A.; Hees, A.; Bouquillon, S.; Le Poncin-Lafitte, C.; Francou, G.; Angonin, M.C. Testing Lorentz Symmetry with Lunar Laser Ranging. Phys. Rev. Lett. 2016, 117, 241301. [Google Scholar] [CrossRef]
- Bourgoin, A.; Le Poncin-Lafitte, C.; Hees, A.; Bouquillon, S.; Francou, G.; Angonin, M.C. Lorentz Symmetry Violations from Matter-Gravity Couplings with Lunar Laser Ranging. Phys. Rev. Lett. 2017, 119, 201102. [Google Scholar] [CrossRef]
- Bourgoin, A.; Bouquillon, S.; Hees, A.; Le Poncin-Lafitte, C.; Bailey, Q.G.; Howard, J.J.; Angonin, M.C.; Francou, G.; Chabé, J.; Courde, C.; et al. Constraining velocity-dependent Lorentz/CPT-violations using Lunar Laser Ranging. arXiv 2020, arXiv:2011.06641. [Google Scholar]
- Müller, J.; Williams, J.G.; Turyshev, S.G. Lunar Laser Ranging Contributions to Relativity and Geodesy. In Lasers, Clocks and Drag-Free Control: Exploration of Relativistic Gravity in Space; Dittus, H., Lämmerzahl, C., Turyshev, S.G., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 349, pp. 457–472. [Google Scholar] [CrossRef]
- Müller, J.; Soffel, M.; Klioner, S.A. Geodesy and relativity. J. Geod. 2008, 82, 133–145. [Google Scholar] [CrossRef]
- Roll, P.G.; Krotkov, R.; Dicke, R.H. The equivalence of inertial and passive gravitational mass. Ann. Phys. 1964, 26, 442–517. [Google Scholar] [CrossRef]
- Schlamminger, S.; Choi, K.Y.; Wagner, T.A.; Gundlach, J.H.; Adelberger, E.G. Test of the Equivalence Principle Using a Rotating Torsion Balance. Phys. Rev. Lett. 2008, 100, 041101. [Google Scholar] [CrossRef]
- Albers, H.; Herbst, A.; Richardson, L.L.; Heine, H.; Nath, D.; Hartwig, J.; Schubert, C.; Vogt, C.; Woltmann, M.; Lämmerzahl, C.; et al. Quantum test of the Universality of Free Fall using rubidium and potassium. Eur. Phys. J. D 2020, 74, 145. [Google Scholar] [CrossRef]
- Touboul, P.; Métris, G.; Rodrigues, M.; André, Y.; Baghi, Q.; Bergé, J.; Boulanger, D.; Bremer, S.; Chhun, R.; Christophe, B.; et al. Space test of the equivalence principle: First results of the MICROSCOPE mission. Class. Quantum Gravity 2019, 36, 225006. [Google Scholar] [CrossRef]
- Nordtvedt, K. Equivalence Principle for Massive Bodies. I. Phenomenology. Phys. Rev. D 1968, 169, 1014–1016. [Google Scholar] [CrossRef]
- Müller, J.; Nordtvedt, K. Lunar laser ranging and the equivalence principle signal. Phys. Rev. D 1998, 58, 062001. [Google Scholar] [CrossRef]
- Einstein, A. Die Grundlage der allgemeinen Relativitätstheorie. Ann. Phys. 1916, 354, 769–822. [Google Scholar] [CrossRef]
- Brans, C.; Dicke, R.H. Mach’s Principle and a Relativistic Theory of Gravitation. Phys. Rev. 1961, 124, 925–935. [Google Scholar] [CrossRef]
- Peebles, P.J.; Dicke, R.H. Significance of Spatial Isotropy. Phys. Rev. 1962, 127, 629–631. [Google Scholar] [CrossRef]
- Sanders, A.; Gillies, G.; Schmutzer, E. Implications upon theory discrimination of an accurate measurement of the time rate of change of the gravitational “constant” G and other cosmological parameters. Ann. Phys. 2010, 522, 861–873. [Google Scholar] [CrossRef]
- Steinhardt, P.J.; Wesley, D. Exploring extra dimensions through observational tests of dark energy and varying Newton’s constant. arXiv 2010, arXiv:1003.2815. [Google Scholar]
- Will, C.M.; Nordtvedt, K. Conservation Laws and Preferred Frames in Relativistic Gravity. I. Preferred-Frame Theories and an Extended PPN Formalism. Astrophys. J. 1972, 177, 757–774. [Google Scholar] [CrossRef]
- Pitjeva, E.V.; Pitjev, N.P. Development of planetary ephemerides EPM and their applications. Celest. Mech. Dyn. Astron. 2014, 119, 237–256. [Google Scholar] [CrossRef]
- Fienga, A.; Laskar, J.; Exertier, P.; Manche, H.; Gastineau, M. Numerical estimation of the sensitivity of INPOP planetary ephemerides to general relativity parameters. Celest. Mech. Dyn. Astron. 2015, 123, 325–349. [Google Scholar] [CrossRef]
- Genova, A.; Mazarico, E.; Goossens, S.; Lemoine, F.G.; Neumann, G.A.; Smith, D.E.; Zuber, M.T. Solar system expansion and strong equivalence principle as seen by the NASA MESSENGER mission. Nat. Commun. 2018, 9, 289. [Google Scholar] [CrossRef] [PubMed]
- Pitjeva, E.V.; Pitjev, N.P. Relativistic effects and dark matter in the Solar system from observations of planets and spacecraft. Mon. Not. R. Astron. Soc. 2013, 432, 3431–3437. [Google Scholar] [CrossRef]
- Currie, D.G.; Dell’Agnello, S.; Delle Monache, G.O.; Behr, B.; Williams, J.G. A Lunar Laser Ranging Retroreflector Array for the 21st Century. Nucl. Phys. B 2013, 243–244, 218–228. [Google Scholar] [CrossRef]
- Turyshev, S.G.; Shao, M.; Hanh, I.; Williams, J.G.; Trahan, R. Advanced Laser Ranging for high-precision science investigations. In Proceedings of the 21st International Workshop on Laser Ranging, Canberra, Australia, 5–9 November 2018. [Google Scholar]
- Santoli, F.; Fiorenza, E.; Lefevre, C.; Lucchesi, D.M.; Lucente, M.; Magnafico, C.; Morbidini, A.; Peron, R.; Iafolla, V. ISA, a High Sensitivity Accelerometer in the Interplanetary Space. Space Sci. Rev. 2020, 216, 145. [Google Scholar] [CrossRef]
- Noll, C. The Crustal Dynamics Data Information System: A resource to support scientific analysis using space geodesy. Adv. Space Res. 2010, 45, 1421–1440. [Google Scholar] [CrossRef]
- Pearlman, M.R.; Degnan, J.J.; Bosworth, J.M. The International Laser Ranging Service. Adv. Space Res. 2002, 30, 135–143. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).