Nonthermal Radiation of the Extreme TeV Blazar 1ES 0229+200 from Electromagnetic Cascades on Infrared Photon Field
Abstract
1. Introduction
2. Peculiar Properties of Extreme TeV Blazars
- ETBs do not reveal fast (day-scale or even week-scale) or strong (flux change by an order of magnitude or more) -ray variability (the only known exception is a day-scale flare of 1ES 1218+304 [13]).
- At the same time, relatively weak and slow (if compared to other classes of blazars) -ray variability of ETBs was indeed detected. In particular, the VERITAS Collaboration finds that the blazar 1ES 0229+200 is variable on yearly timescales [12]. In the present paper we strive to explain the variability quasi-period as small as several months, at the same time explaining the absence of faster variability.
3. Models of Extreme TeV Blazar Emission and Their Difficulties
- In synchrotron self-Compton (SSC) models rays are produced as a result of inverse Compton (IC, or ) scattering of accelerated electrons on synchrotron photons radiated by the same electron population. For the case of ETBs (assuming -ray production in blobs) these models require as well as high values of minimal Lorentz factor of the primary electrons () (e.g., [12]). The last condition requires specific acceleration mechanism such as the Blandford-Znajek mechanism [17] that operates only in the immediate vicinity of the event horizon of the central black hole in the blazar. This mechanism does not chime well with the concept of particle acceleration inside a fast-moving blob that quickly escapes the central engine.
- A leptonic model presented in [18] assumes that a high value of is due to a specific preacceleration process, namely, the transfer of energy from protons to electrons. However, it is not clear why the same process does not operate in jets of other (non-extreme) blazars. This model, as well, implies .
- Another leptonic model assuming the IC process on cosmic microwave background (CMB) photons was proposed in [19]. It still suffers from the problem outlined above. In addition, the CMB energy density typically dominates very far from the central black hole, at the multi-parsec or even kiloparsec scale. Thus appears the problem of ultrarelativistic electron transport to such great distances without appreciable energy losses and/or the problem of accelerating such electrons very far from the central engine.
- Hadroleptonic models relying on production of rays, electrons and positrons in blobs via photohadronic processes (e.g., [20]) usually require .
- The proton sychrotron model (e.g., [20]) requires the acceleration of primary protons up to ∼1010 eV. The maximum energy of synchrotron photon produced by the protons is GeV, and for electrons co-accelerated with the protons MeV [21]. To produce hard (spectral index ) observable spectrum up to the energy of TeV, the bulk motion of a blob or a jet corresponding to the Doppler factor of is required. In this case, the typical observable energy of synchrotron photons emitted by electrons would be GeV, and not ∼1–10 keV typical for extreme blazars. Therefore, it is difficult to account for the low-energy SED component self-consistently.
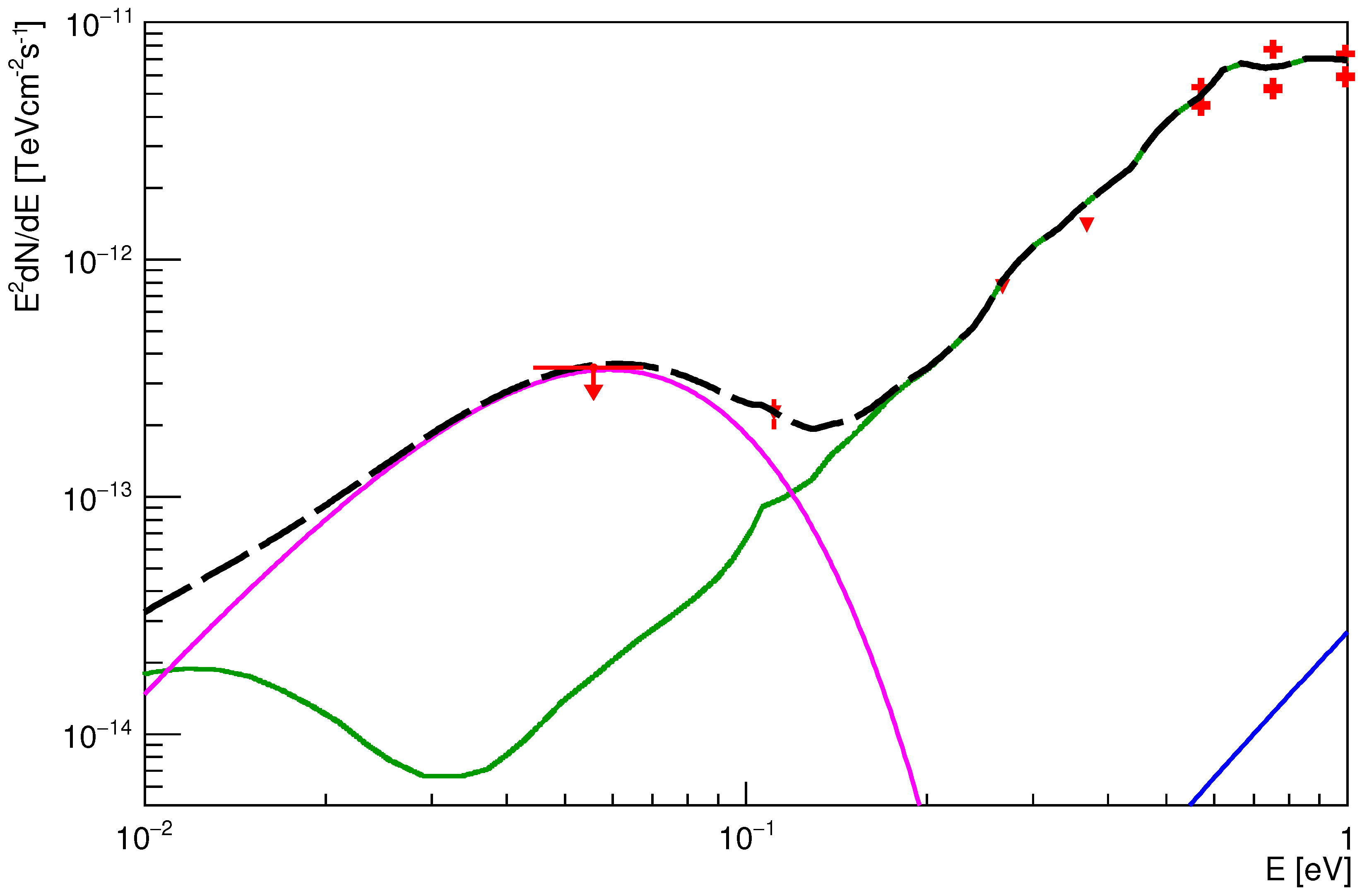
4. The Low-Energy Part of the Spectrum
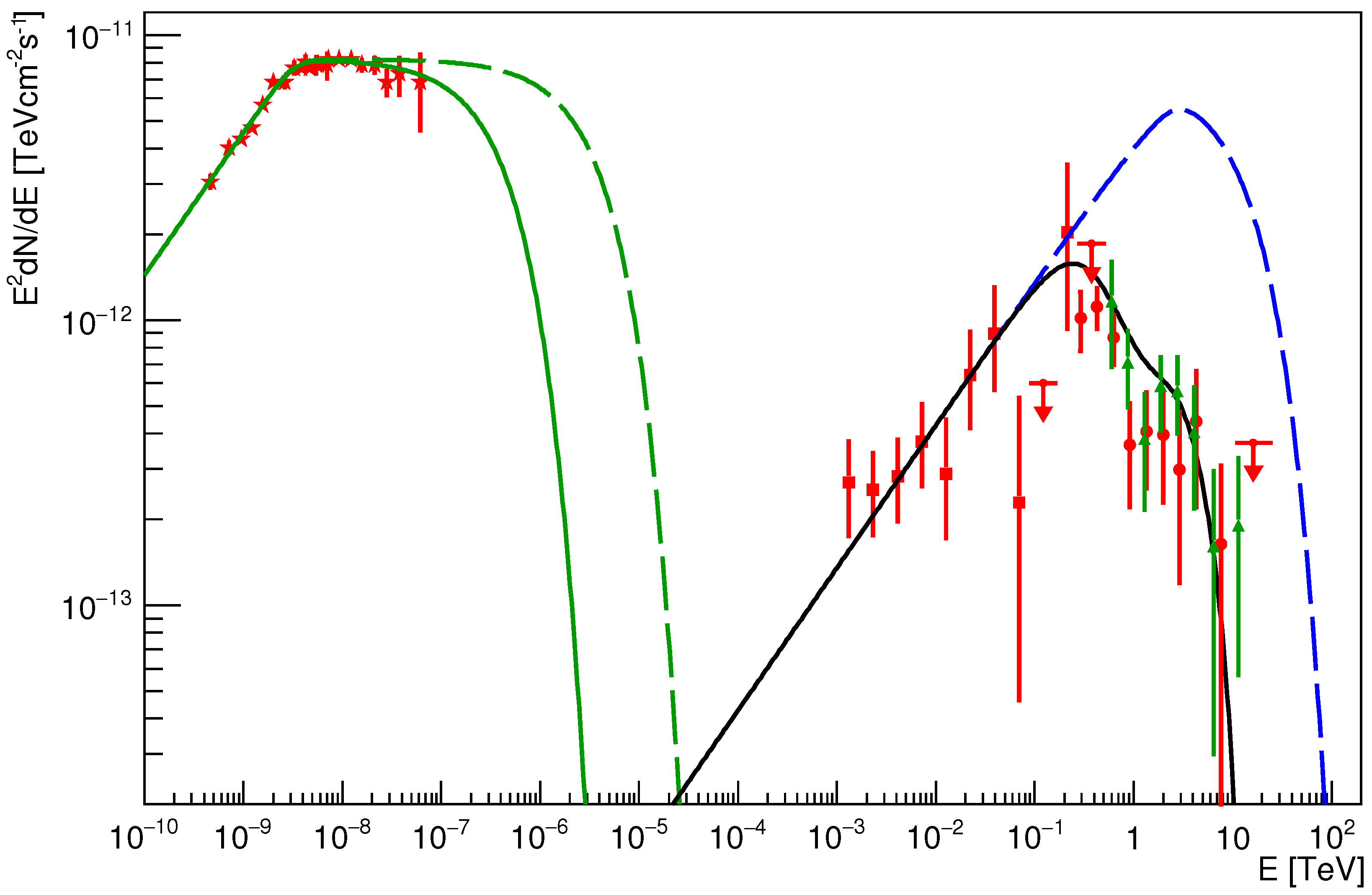
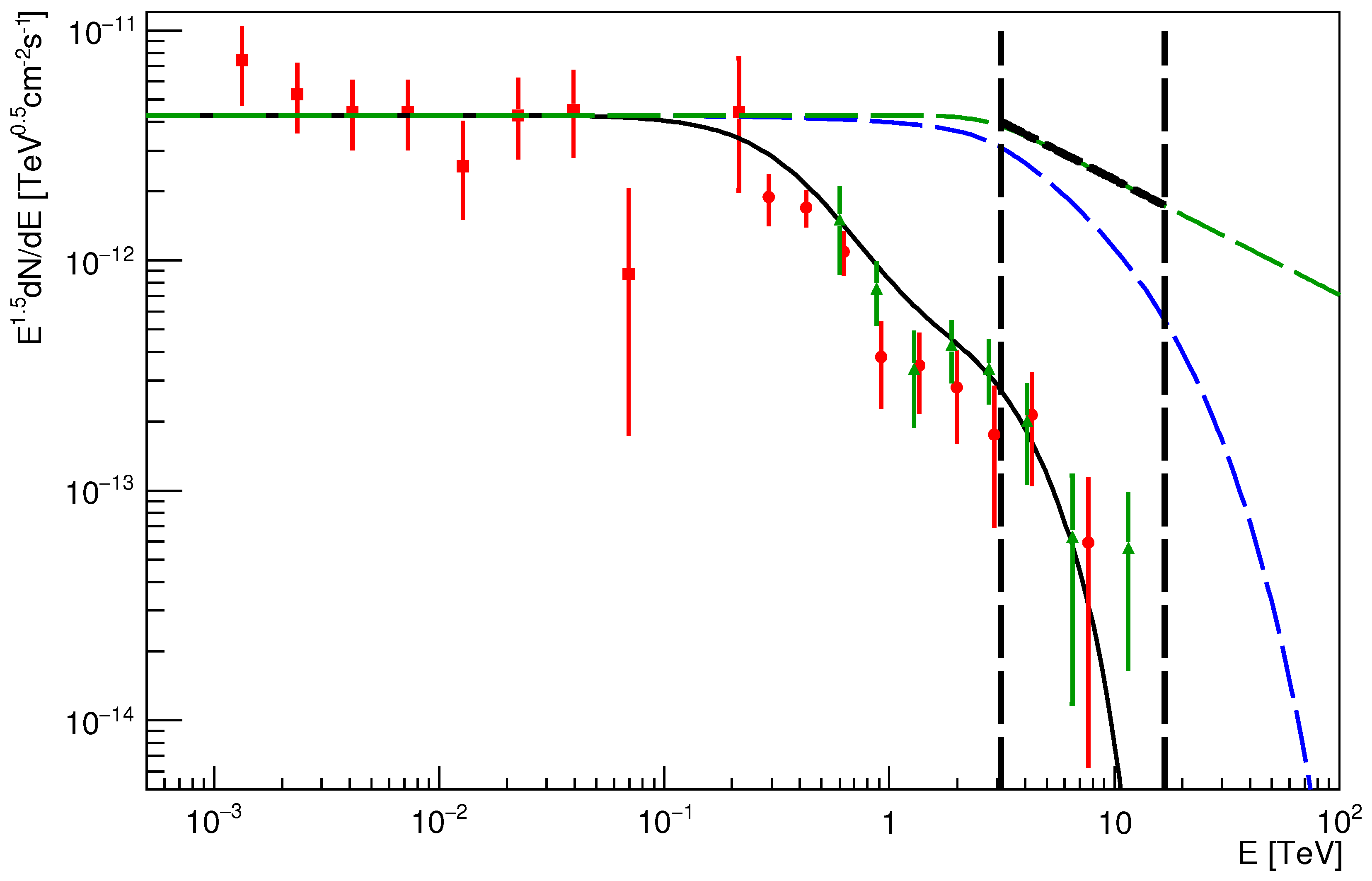
5. The High-Energy Part of the Spectrum
5.1. The Measured SED
5.2. Qualitative Considerations
5.3. The Model SED
5.4. Basic and Auxiliary Parameters
6. Discussion
6.1. Explanation of Peculiar Properties of ETBs
6.2. The Origin of the Primary Electrons
6.3. Intergalactic Electromagnetic Cascades
6.4. Additional Remarks on the Model
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | https://github.com/fermi-lat/Fermitools-conda; accessed on 20 September 2020. |
| 2 | https://github.com/fermiPy/fermipy; accessed on 20 September 2020. |
References
- Aharonian, F.; Akhperjanian, A.G.; Bazer-Bachi, A.R.; Behera, B.; Beilicke, M.; Benbow, W.; Berge, D.; Bernlöhr, K.; Boisson, C.; Bolz, O.; et al. An Exceptional Very High Energy Gamma-Ray Flare of PKS 2155-304. Astrophys. J. 2007, 664, L71–L74. [Google Scholar] [CrossRef]
- Ackermann, M.; Anantua, R.; Asano, K.; Baldini, L.; Barbiellini, G.; Bastieri, D.; Gonzalez, J.B.; Bellazzini, R.; Bissaldi, E.; Blford, R.D.; et al. Minute-Timescale >100 MeV g-Ray Variability During the Giant Outburst of Quasar 3C 279 Observed by Fermi-LAT in 2015 June. Astrophys. J. 2016, 824, L20. [Google Scholar] [CrossRef]
- Blandford, R.D.; Rees, M.J. Some comments on radiation mechanisms in Lacertids. BL Lac Objects; Wolfe, A.M., Ed.; University of Pittsburgh: Pittsburgh, PA, USA, 1978; pp. 328–341. [Google Scholar]
- Dermer, C.D.; Schlickeiser, R.; Mastichiadis, A. High-energy gamma radiation from extragalactic radio sources. Astron. Astrophys. 1992, 256, L27–L30. [Google Scholar]
- Dermer, C.D.; Schlickeiser, R. Model for the High-Energy Emission from Blazars. Astrophys. J. 1993, 416, 458. [Google Scholar] [CrossRef]
- Aharonian, F.; Akhperjanian, A.G.; Bazer-Bachi, A.R.; Beilicke, M.; Benbow, W.; Berge, D.; Bernlöhr, K.; Boisson, C.; Bolz, O.; Borrel, V.; et al. A low level of extragalactic background light as revealed by γ-rays from blazars. Nature 2006, 440, 1018–1021. [Google Scholar] [CrossRef]
- Nikishov, A.I. Absorption of high-energy photons in the Universe. Sov. Phys. JETP 1962, 14, 393. [Google Scholar]
- Gould, R.J.; Schréder, G.P. Opacity of the Universe to High-Energy Photons. Phys. Rev. 1967, 155, 1408–1411. [Google Scholar] [CrossRef]
- Dzhatdoev, T.A.; Khalikov, E.V.; Kircheva, A.P.; Lyukshin, A.A. Electromagnetic cascade masquerade: A way to mimic -axion-like particle mixing effects in blazar spectra. Astron. Astrophys. 2017, 603, A59. [Google Scholar] [CrossRef]
- Biteau, J.; Prandini, E.; Costamante, L.; Lemoine, M.; Padovani, P.; Pueschel, E.; Resconi, E.; Tavecchio, F.; Taylor, A.; Zech, A.; et al. Progress in unveiling extreme particle acceleration in persistent astrophysical jets. Nat. Astron. 2020, 4, 124–131. [Google Scholar] [CrossRef]
- Woo, J.H.; Urry, C.M.; van der Marel, R.P.; Lira, P.; Maza, J. Black Hole Masses and Host Galaxy Evolution of Radio-Loud Active Galactic Nuclei. Astrophys. J. 2005, 631, 762–772. [Google Scholar] [CrossRef]
- Aliu, E.; Archambault, S.; Arlen, T.; Aune, T.; Behera, B.; Beilicke, M.; Benbow, W.; Berger, K.; Bird, R.; Bouvier, A.; et al. A three-year multi-wavelength study of the very-high-energy-ray blazar 1ES 0229+200. Astrophys. J. 2014, 782, 13. [Google Scholar] [CrossRef]
- Acciari, V.A.; Aliu, E.; Beilicke, M.; Benbow, W.; Boltuch, D.; Böttcher, M.; Bradbury, S.M.; Bugaev, V.; Byrum, K.; Cesarini, A.; et al. Discovery of variability in the very high energy γ-ray emission of 1ES 1218+ 304 with veritas. Astrophys. J. 2010, 709, L163–L167. [Google Scholar] [CrossRef]
- Snodin, A.P.; Brandenburg, A.; Mee, A.J.; Shukurov, A. Simulating field-aligned diffusion of a cosmic ray gas. Mon. Not. R. Astron. Soc. 2006, 373, 643–652. [Google Scholar] [CrossRef]
- Berezinsky, V.S.; Bulanov, S.V.; Dogiel, V.A.; Ptuskin, V.S. Astrophysics of Cosmic Rays; Elsevier Science Publishers B.V.: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Uchiyama, Y.; Aharonian, F.A.; Tanaka, T.; Takahashi, T.; Maeda, Y. Extremely fast acceleration of cosmic rays in a supernova remnant. Nature 2007, 449, 576–578. [Google Scholar] [CrossRef] [PubMed]
- Blandford, R.D.; Znajek, R.L. Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 1977, 179, 433–456. [Google Scholar] [CrossRef]
- Zech, A.; Lemoine, M. Electron-proton co-acceleration on relativistic shocks in extreme-TeV blazars. Astron. Astrophys. 2021, 654, A96. [Google Scholar] [CrossRef]
- Böttcher, M.; Dermer, C.D.; Finke, J.D. The Hard VHE -Ray Emission in High-Redshift TeV Blazars: Comptonization of Cosmic Microwave Background Radiation in an Extended Jet? Astrophys. J. 2008, 679, L9–L12. [Google Scholar] [CrossRef]
- Cerruti, M.; Zech, A.; Boisson, C.; Inoue, S. A hadronic origin for ultra-high-frequency-peaked BL Lac objects. Mon. Not. R. Astron. Soc. 2015, 448, 910–927. [Google Scholar] [CrossRef]
- Kumar, P.; Hernández, R.A.; Bošnjak, Ž.; Barniol, D.R. Maximum synchrotron frequency for shock-accelerated particles. Mon. Not. R. Astron. Soc. 2012, 427, L40–L44. [Google Scholar] [CrossRef]
- Gehrels, N.; Chincarini, G.; Giommi, P.; Mason, K.O.; Nousek, J.A.; Wells, A.A.; White, N.E.; Barthelmy, S.D.; Burrows, D.N.; Cominsky, L.R.; et al. The Swift gamma-ray burst mission. Astrophys. J. 2004, 611, 1005–1020. [Google Scholar] [CrossRef]
- Harrison, F.A.; Craig, W.W.; Christensen, F.E.; Hailey, C.J.; Zhang, W.W.; Boggs, S.E.; Stern, D.; Cook, W.R.; Forster, K.; Giommi, P.; et al. The nuclear spectroscopic telescope array (NuSTAR) high-energy X-ray mission. Astrophys. J. 2013, 770, 103. [Google Scholar] [CrossRef]
- Costamante, L.; Bonnoli, G.; Tavecchio, F.; Ghisellini, G.; Tagliaferri, G.; Khangulyan, D. The NuSTAR view on hard-TeV BL Lacs. Mon. Not. R. Astron. Soc. 2018, 477, 4257–4268. [Google Scholar] [CrossRef]
- Wright, E.L.; Eisenhardt, P.R.M.; Mainzer, A.K.; Ressler, M.E.; Cutri, R.M.; Jarrett, T.; Kirkpatrick, J.D.; Padgett, D.; McMillan, R.S.; Skrutskie, M.; et al. The Wide-field Infrared Survey Explorer (WISE): Mission description and initial on-orbit performance. Astron. J. 2010, 140, 1868–1881. [Google Scholar] [CrossRef]
- Scarpa, R.; Urry, C.M.; Falomo, R.; Pesce, J.E.; Treves, A. The Hubble Space Telescope Survey of BL Lacertae Objects. I. Surface Brightness Profiles, Magnitudes, and Radii of Host Galaxies. Astrophys. J. 2000, 532, 740–815. [Google Scholar] [CrossRef]
- Silva, L.; Granato, G.L.; Bressan, A.; Danese, L. Modeling the Effects of Dust on Galactic Spectral Energy Distributions from the Ultraviolet to the Millimeter Band. Astrophys. J. 1998, 509, 103–117. [Google Scholar] [CrossRef]
- O’Connell, R.W. Far-Ultraviolet Radiation from Elliptical Galaxies. Annu. Rev. Astron. Astrophys. 1999, 37, 603–648. [Google Scholar] [CrossRef]
- Cappellari, M.; Renzini, A.; Greggio, L.; di Serego Alighieri, S.; Buson, L.M.; Burstein, D.; Bertola, F. The Mini–Active Galactic Nucleus at the Center of the Elliptical Galaxy NGC 4552 with Hubble Space Telescope. Astrophys. J. 1999, 519, 117–133. [Google Scholar] [CrossRef]
- Narayan, R.; McClintock, J.E.; Yi, I. A New Model for Black Hole Soft X-Ray Transients in Quiescence. Astrophys. J. 1996, 457, 821. [Google Scholar] [CrossRef]
- Shakura, N.I.; Sunyaev, R.A. Black holes in binary systems. Observational appearance. Astron. Astrophys. 1973, 500, 33–51. [Google Scholar]
- Aharonian, F.; Akhperjanian, A.G.; Barres de Almeida, U.; Bazer-Bachi, A.R.; Behera, B.; Beilicke, M.; Benbow, W.; Bernlöhr, K.; Boisson, C.; Bolz, O.; et al. New constraints on the mid-IR EBL from the HESS discovery of VHE g-rays from 1ES 0229+200. Astron. Astrophys. 2007, 475, L9–L13. [Google Scholar] [CrossRef]
- Atwood, W.B.; Abdo, A.A.; Ackermann, M.; Althouse, W.; Anderson, B.; Axelsson, M.; Baldini, L.; Ballet, J.; Band, D.L.; Barbiellini, G.; et al. The large area telescope on the Fermi gamma-ray space telescope mission. Astrophys. J. 2009, 697, 1071–1102. [Google Scholar] [CrossRef]
- Abdollahi, S.; Acero, F.; Ackermann, M.; Ajello, M.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; et al. Fermi large area telescope fourth source catalog. Astrophys. J. Suppl. Ser. 2020, 247, 33. [Google Scholar] [CrossRef]
- Wood, M.; Caputo, R.; Charles, E.; Di Mauro, M.; Magill, J.; Perkins, J.S.; Fermi-LAT Collaboration. Fermipy: An open-source Python package for analysis of Fermi-LAT Data. In Proceedings of the 35th International Cosmic Ray Conference (ICRC2017), Busan, Korea, 12–20 July 2017; Volume 301, p. 824. [Google Scholar]
- Neronov, A.; Aharonian, F.A. Production of TeV Gamma Radiation in the Vicinity of the Supermassive Black Hole in the Giant Radio Galaxy M87. Astrophys. J. 2007, 671, 85–96. [Google Scholar] [CrossRef]
- Berezinsky, V.; Kalashev, O. High-energy electromagnetic cascades in extragalactic space: Physics and features. Phys. Rev. D 2016, 94, 023007. [Google Scholar] [CrossRef]
- Blumenthal, G.R.; Gould, R.J. Bremsstrahlung, Synchrotron Radiation, and Compton Scattering of High-Energy Electrons Traversing Dilute Gases. Rev. Mod. Phys. 1970, 42, 237–271. [Google Scholar] [CrossRef]
- Khangulyan, D.; Arakawa, M.; Aharonian, F. Detection of ultra-high-energy gamma rays from the Crab Nebula: Physical implications. Mon. Not. R. Astron. Soc. 2019, 491, 3217–3224. [Google Scholar] [CrossRef]
- Kachelrieß, M.; Ostapchenko, S.; Tomàs, R. ELMAG: A Monte Carlo simulation of electromagnetic cascades on the extragalactic background light and in magnetic fields. Comput. Phys. Commun. 2012, 183, 1036–1043. [Google Scholar] [CrossRef]
- Khangulyan, D.; Aharonian, F.A.; Kelner, S.R. Simple analytical approximations for treatment of inverse Compton scattering of relativistic electrons in the blackbody radiation field. Astrophys. J. 2014, 783, 100. [Google Scholar] [CrossRef]
- Gilmore, R.C.; Somerville, R.S.; Primack, J.R.; Domínguez, A. Semi-analytic modelling of the extragalactic background light and consequences for extragalactic gamma-ray spectra. Mon. Not. R. Astron. Soc. 2012, 422, 3189–3207. [Google Scholar] [CrossRef]
- Kaufmann, S.; Wagner, S.J.; Tibolla, O.; Hauser, M. 1ES 0229+200: An extreme blazar with a very high minimum Lorentz factor. Astron. Astrophys. 2011, 534, A130. [Google Scholar] [CrossRef]
- Hirotani, K.; Pu, H.Y. Energetic gamma radiation from rapidly rotating black holes. Astrophys. J. 2016, 818, 50. [Google Scholar] [CrossRef]
- Hirotani, K.; Pu, H.Y.; Lin, L.C.C.; Chang, H.K.; Inoue, M.; Kong, A.K.H.; Matsushita, S.; Tam, P.H.T. Lepton acceleration in the vicinity of the event horizon: High-energy and very-high-energy emissions from rotating black holes with various masses. Astrophys. J. 2016, 833, 142. [Google Scholar] [CrossRef]
- Hirotani, K.; Pu, H.Y.; Lin, L.C.C.; Kong, A.K.H.; Matsushita, S.; Asada, K.; Chang, H.K.; Tam, P.H.T. Lepton Acceleration in the Vicinity of the Event Horizon: Very High Energy Emissions from Supermassive Black Holes. Astrophys. J. 2017, 845, 77. [Google Scholar] [CrossRef]
- Ochelkov, Y.P.; Usov, V.V. Curvature radiation of relativistic particles in the magnetosphere of pulsars. Astrophys. Space Sci. 1980, 69, 439–460. [Google Scholar] [CrossRef]
- Blumenthal, G.R. Energy Loss of High-Energy Cosmic Rays in Pair-Producing Collisions with Ambient Photons. Phys. Rev. 1970, 1, 1596–1602. [Google Scholar] [CrossRef]
- Kelner, S.R.; Aharonian, F.A. Energy spectra of gamma rays, electrons, and neutrinos produced at interactions of relativistic protons with low energy radiation. Phys. Rev. D 2008, 78, 034013. [Google Scholar] [CrossRef]
- Neronov, A.Y.; Semikoz, D.V.; Tkachev, I.I. Ultra-high energy cosmic ray production in the polar cap regions of black hole magnetospheres. New J. Phys. 2009, 11, 065015. [Google Scholar] [CrossRef]
- Ptitsyna, K.; Neronov, A. Particle acceleration in the vacuum gaps in black hole magnetospheres. Astron. Astrophys. 2016, 593, A8. [Google Scholar] [CrossRef]
- Aleksić, J.; Ansoldi, S.; Antonelli, L.A.; Antoranz, P.; Babic, A.; Bangale, P.; Barrio, J.A.; González, J.B.; Bednarek, W.; Bernardini, E.; et al. Black hole lightning due to particle acceleration at subhorizon scales. Science 2014, 346, 1080–1084. [Google Scholar] [CrossRef]
- Berezinsky, V.S.; Smirnov, A.Y. Cosmic neutrinos of ultra-high energies and detection possibility. Astrophys. Space Sci. 1975, 32, 461–482. [Google Scholar] [CrossRef]
- Protheroe, R.J. Effect of electron-photon cascading on the observed energy spectra of extragalactic sources of ultra-high-energy g-rays. Mon. Not. R. Astron. Soc. 1986, 221, 769–788. [Google Scholar] [CrossRef]
- Neronov, A.; Semikoz, D.V. Sensitivity of -ray telescopes for detection of magnetic fields in the intergalactic medium. Phys. Rev. D 2009, 80, 123012. [Google Scholar] [CrossRef]
- Pshirkov, M.; Tinyakov, P.; Urban, F. New Limits on Extragalactic Magnetic Fields from Rotation Measures. Phys. Rev. Lett. 2016, 116, 191302. [Google Scholar] [CrossRef]
- Neronov, A.; Vovk, I. Evidence for Strong Extragalactic Magnetic Fields from Fermi Observations of TeV Blazars. Science 2010, 328, 73–75. [Google Scholar] [CrossRef]
- Dermer, C.D.; Cavadini, M.; Razzaque, S.; Finke, J.D.; Chiang, J.; Lott, B. Time delay of cascade radiation for TeV blazars and the measurement of the intergalactic magnetic field. Astrophys. J. 2011, 733, L21. [Google Scholar] [CrossRef]
- Taylor, A.M.; Vovk, I.; Neronov, A. Extragalactic magnetic fields constraints from simultaneous GeV–TeV observations of blazars. Astron. Astrophys. 2011, 529, A144. [Google Scholar] [CrossRef]
- Arlen, T.C.; Vassilev, V.V.; Weisgarber, T.; Wakely, S.P.; Shafi, S.Y. Intergalactic magnetic fields and gamma-ray observations of extreme TeV blazars. Astrophys. J. 2014, 796, 18. [Google Scholar] [CrossRef]
- Finke, J.D.; Reyes, L.C.; Georganopoulos, M.; Reynolds, K.; Ajello, M.; Fegan, S.J.; McCann, K. Constraints on the intergalactic magnetic field with gamma-ray observations of blazars. Astrophys. J. 2015, 814, 20. [Google Scholar] [CrossRef]
- Dzhatdoev, T.; Podlesnyi, E.; Vaiman, I. Can we constrain the extragalactic magnetic field from very high energy observations of GRB 190114C? Phys. Rev. D. 2020, 102, 123017. [Google Scholar] [CrossRef]
- Aharonian, F.A.; Coppi, P.S.; Voelk, H.J. Very high energy gamma rays from active galactic nuclei: Cascading on the cosmic background radiation fields and the formation of pair halos. Astrophys. J. 1994, 423, L5. [Google Scholar] [CrossRef]
- Abramowski, A.; Aharonian, F.; Benkhali, F.A.; Akhperjanian, A.G.; Angüner, E.; Anton, G.; Backes, M.; Balenderan, S.; Balzer, A.; Barnacka, A.; et al. Search for extended γ-ray emission around AGN with HESS and Fermi-LAT. Astron. Astrophys. 2014, 562, A145. [Google Scholar] [CrossRef]
- Khalikov, E.V.; Dzhatdoev, T.A. Observable spectral and angular distributions of -rays from extragalactic ultrahigh energy cosmic ray accelerators: The case of extreme TeV blazars. Mon. Not. R. Astron. Soc. 2021, 505, 1940–1953. [Google Scholar] [CrossRef]
- Khalikov, E. Modeling Gamma-Ray SEDs and Angular Extensions of Extreme TeV Blazars from Intergalactic Proton-Initiated Cascades in Contemporary Astrophysical EGMF Models. Universe 2021, 7, 220. [Google Scholar] [CrossRef]
- Dzhatdoev, T.A.; Khalikov, E.V.; Latypova, V.S.; Podlesnyi, E.I.; Vaiman, I.A. Persistent g-ray emission of the blazar PKS 1510-089 in its low state: Fermi-LAT data analysis and theoretical modelling. arXiv 2021, arXiv:2111.07389. [Google Scholar]
- Brun, R.; Rademakers, F. ROOT—An object oriented data analysis framework. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1997, 389, 81–86. [Google Scholar] [CrossRef]

| Parameter | Meaning | Value | Units |
|---|---|---|---|
| IR photon energy | 6 × 10−2 | eV | |
| B | Magnetic field strength | 0.9 | mG |
| Maximal energy of primary electron | 100 | TeV | |
| IC SED peak dominance | 0.42 |
| Property | The Physical Reason |
|---|---|
| > 1 TeV | ≪ 1 eV → at 1 TeV ≪ 1, modest KN effects |
| > 1 keV | ≥ 100 TeV |
| Strong/fast var. absent | The absence of relativistic blobs |
| Slow/weak var. present | Variations of accretion rate/photon field |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dzhatdoev, T.; Galkin, V.; Podlesnyi, E. Nonthermal Radiation of the Extreme TeV Blazar 1ES 0229+200 from Electromagnetic Cascades on Infrared Photon Field. Universe 2021, 7, 494. https://doi.org/10.3390/universe7120494
Dzhatdoev T, Galkin V, Podlesnyi E. Nonthermal Radiation of the Extreme TeV Blazar 1ES 0229+200 from Electromagnetic Cascades on Infrared Photon Field. Universe. 2021; 7(12):494. https://doi.org/10.3390/universe7120494
Chicago/Turabian StyleDzhatdoev, Timur, Vladimir Galkin, and Egor Podlesnyi. 2021. "Nonthermal Radiation of the Extreme TeV Blazar 1ES 0229+200 from Electromagnetic Cascades on Infrared Photon Field" Universe 7, no. 12: 494. https://doi.org/10.3390/universe7120494
APA StyleDzhatdoev, T., Galkin, V., & Podlesnyi, E. (2021). Nonthermal Radiation of the Extreme TeV Blazar 1ES 0229+200 from Electromagnetic Cascades on Infrared Photon Field. Universe, 7(12), 494. https://doi.org/10.3390/universe7120494






