Interpretation of the Spectral Inhomogeneity in the 10 TV Region in Terms of a Close Source

Abstract

The description of the inhomogeneity of the cosmic ray spectrum in the region of 10 TV, which is observed in experimental data, in terms of isotropic diffusion from a single close source is considered. It is shown that such a description is possible, and the area of possible localization of the source in space and time and its energy are found. The method of penalty functions is used to account for the data on the spectrum of all particles.

1. Introduction

Galactic cosmic rays (GCRs) are largely born in supernova remnants as a result of acceleration in shock waves by the Fermi mechanism [1]. After this, GCRs propagate through the galaxy filled by dust, gas and magnetic fields with complex structures. The study of the energy and spatial distributions of GCRs makes it possible to clarify both the physics of sources of GCRs and the properties of the interstellar medium.

Some cosmic ray physics experiments (CR) [2,3,4] find evidence of variations in the CR spectrum index in the area of magnetic rigidity of about 10 TV. Let us call this the small knee. The data of the direct space experiment NUCLEON [2] allow us to resolve the single-particle structure of the small knee for each abundant primary CR component and show that this bending occurs near the same magnetic rigidity 10 TV for each nucleus regardless of Z. The data of the element-wise spectrum allow us to consider this feature in more detail and build a mathematical model to describe this phenomenon. On the other hand, data from the HAWC ground experiment [5] were recently obtained. This measured the spectrum of all particles where a deviation from the power law can also be observed.

Such an inhomogeneity in the regular CR spectrum could be due to several reasons: CR production mechanisms (for example, the acceleration limit in the envelopes of a certain type of supernova), propagation mechanisms [6], or the contribution of a single close source to the CR flux [7]. The significant sharpness of the bending in terms of the magnetic rigidity spectrum is indirect evidence that the small knee is determined by the CR acceleration limit in a single close source such as a supernova remnant. If it was the contribution of several sources, then it would be difficult to expect such a sharp bending. Therefore, in this article, we study the possibility of explaining the slight inflection of the CR spectrum through the contribution of one close source.

To test this hypothesis, as well as to localize the region of existence and age of a possible hypothetical source, the mathematical model was significantly improved to describe the spectral characteristics of CRs in terms of diffusion from a close source, first proposed by Erlykin and Wolfendale [8]. Currently, the model is quite widespread [9,10,11]; however, the existing work does not take into account the data of all the conducted experiments.

The authors have carried out an approximation of the free parameters of the model based on experimental data and constructed domains of the parameters to determine an admissible and the most probable single source. A significant difference from previous works of this type, related to the large knee of Kulikov–Christiansen CRs near 3 PeV in energy per particle, is the observation of the small knee not only in the total spectrum of all particles, but also in the spectra of individual abundant nuclei. Thus, we are dealing with the information which is much more detailed than the data currently available for the 3 PeV CR knee.

The main difference of our work from previously published works describing this spectral inhomogeneity in the approximation of a close source is the fact that we take into account all available experimental data (including element-wise spectra), both direct and indirect experiments.

2. Calculation Model

The mathematical model of the expected flux was constructed as the sum of the contribution of the close source and the galactic CR background (Figure 1):

$$F_{sum}\left(R\right)=F_{bgr}\left(R\right)+F_{star}\left(R\right),$$

where R is the magnetic rigidity.

The power-law spectrum was chosen as the galactic background $F=a_0$ and $\gamma$, where the parameters $a_0$ and $\gamma$ for each CR nucleus correspond to the slopes of the spectra, measured in the area 50 GV–3000 GV by experimental data of ATIC [12], NUCLEON [2], AMS-2 [13], CREAM [14] and TRACER [15].

The contribution of a close source is calculated by solving the diffusion equation in the flash source approximation (instantaneous in time and point in space). This approximation accurately describes the spatial localization of sources such as supernova remnants, since the distances to such sources are much larger than their sizes. The approximation works well for relatively old sources of CRs (ten thousand years or more), but can only give a qualitatively correct picture for younger supernova remnants.

The spectrum in the source is described by a double power law with a break and smooth matching of two power-law spectra at the break point:

$$Q(R,t,r)=R^{-\gamma }{(1+{(\frac{R}{R_{ref}})}^{{\omega }_0})}^{-\frac{\delta \gamma }{{\omega }_0}}\delta \left(r\right)\delta \left(t\right),$$

where R is the magnetic rigidity, $\gamma$ is the spectrum index before the bending, $\delta \gamma$ is the difference in the spectral indices before and after the bending (moreover, $\delta \gamma$ is a free parameter), ${\omega }_0$ is the bending smoothing coefficient, and $R_{ref}$ is the position of the bending with $\gamma =2$. It is assumed that the shape of the spectra is the same for all CR components, and only the integral intensity is different for different CR components.

The diffusion equation for a close source in the isotropic approximation has the form:

$$\frac{\partial N}{\partial t}-\nabla (D\nabla N)=Q(R,t,r),$$

(1)

where N is the CR concentration, Q is the source function and D is the diffusion coefficient calculated by the formula:

$$D_{xx}\left(R\right)=D_{xx0}{(\frac{R}{R_0})}^{\delta },$$

where $D_{xx0}=4.3\times {10}^{28}{\mathrm{cm}}^2{\mathrm{s}}^{-1}$, $\delta =0.395$ and $R_0=4.5\mathrm{GV}$ are parameters taken from work [6].

Since the flux of an instantaneous point source with a certain magnetic rigidity is simply expressed by Green’s function of the diffusion equation, the flux of CRs F, which satisfies Equation (1) for a point source in the approximation of an instantaneous flash with a spectrum Q (R), is calculated as:

$$F(R,t,r)=\frac{c}{4\pi }G(R,t,r)Q\left(R\right)$$

where $G(R,t,r)$ is Green’s function for three-dimensional diffusion in infinite space.

At this stage, we do not discuss the contribution of a close source to the anisotropy of GCR, since this is a rather difficult issue that requires special analysis. This contribution will depend on the superposition of the source position and the direction of the local interstellar magnetic field (since the local diffusion tensor is significantly anisotropic ($D_{\Vert }/D_{\perp }>10$) and can vary widely [16,17]). The model of diffusion transport, taking into account the change in the ratio of the components of the tensor of local ($D_{\Vert }/D_{\perp }>10$) and global diffusion ($D_{\Vert }/D_{\perp }$ ~2), will be considered in the future.

$$\mathit{b}=\sum _n{A}_n{\mathit{P}}_{n}cos(\mathit{r}{\mathit{k}}_n+{\varphi }_n)$$

(2)

3. Experimental Data Approximation

The authors used single-particle data from direct CR experiments available at the time in the rigidity range from 100 GV to 100 TV: For protons and helium, the experiments are NUCLEON [2], AMS-02 [13], ATIC [12], CREAM [14], PAMELA [18], CALET [3] and DAMPE [19], for C and O-NUCLEON [2], AMS-02 [13], ATIC [12], CREAM [14].

To calculate the spectrum of all particles, the following proposal was used: All CR components are generated in a source with the same spectrum shape; only the intensity of the CR components differs. The main contribution was made by even plentiful kernels. The background spectrum for abundant nuclei was taken from a set of experiments, NUCLEON [2], AMS-02 [13], ATIC [12], CREAM [14], PAMELA [18], and for those nuclei for which no experimental data were available, it was approximated by well-known neighboring. The intensities of protons, helium, oxygen, and carbon in the source were obtained as free parameters from the approximation of the corresponding experimental spectra, and the intensities of the other components in the source were chosen so that the relative abundance of the element in the source (the intensity normalized to the abundance of hydrogen) corresponds to the experimentally measured one in the galaxy for CR with energy above 100 GV.

Thus, summarizing the spectra of all abundant nuclei allows us to construct a model spectrum of all particles. This model makes it possible to take into account the data of the indirect HAWC experiment [5].

To search for a hypothetical close source describing the discussed spectrum inhomogeneity, it is necessary to optimize its parameters in terms of its position in space, age, and explosion energy (assuming that the CR source is a supernova remnant). To find the optimal age and distance to the source t, r, the functional was minimized:

$${\chi }^2=\sum _i{(\frac{f_i^{mod}-F_i}{{\sigma }_i})}^2,$$

where $f_i^{mod}$ represents the simulated particle flows, $F_i$ represents the experimental flows, and ${\sigma }_i$ is the corresponding experimental error; the summation was carried out over all available experimental points i of different Z-spectra of various experiments. In other words, an optimization was carried out for all available direct experiments at once, taking into account the availability of information in individual cores.

The functional also allows one to specify the position of the knee in terms of rigidity, change in the spectral slope, power of source, the values of penalty parameters, and the concentration of the nuclei of helium, carbon and oxygen (normalized to hydrogen prevalence). The penalty parameters will be discussed later.

4. Penalty Method

The indirect HAWC experiment [5] provides spectrum data of all particles. However, the experimental points have large systematic uncertainties: they greatly exceed the values of statistical uncertainties. In order to correlate the data of this experiment with the data of other experiments, we decided to apply the penalty method (two-dimensional case). This takes into account the limitations imposed on the arguments of the function by transforming the objective function of the original optimization task. In particular, the method is used in quantum chromodynamics [20].

In our case, the objective function is ${\chi }^2$. A correlation function of the form $\mu =aE+b$ is introduced, where E is the energy and a and b are the penalty parameters. Parameter a is associated with the tilt; parameter b is associated with the offset along the ordinate axis. Taking into account the correlation function, the functional ${\chi }^2$ looks like this [21]:

$${\chi }^2(\xi ,\alpha )=\sum _i\frac{{(F_i(1+{\sum }_j\frac{\partial {\mu }_i}{\partial {\alpha }_j}\Delta {\alpha }_j)-P_i\left(\xi \right))}^2}{{\delta }_i^2(1+{\sum }_j\frac{\partial {\mu }_i}{\partial {\alpha }_j}\Delta {\alpha }_j)}+\sum _i\sum _j\Delta {\alpha }_i\Delta {\alpha }_j{\left(A_s\right)}_{ij}^{-1},$$

where $\xi$ represents the arguments of the simulated flows $P_i\left(\xi \right)$, $\alpha$ is a set of penalty parameters (in our case, there are two of them), $F_i$ represents experimental flows, ${\delta }_i$ represents experimental uncertainties, and $A_s$ is the correlation matrix. The matrix itself looks like this:

$$A_s=\left[\begin{array}{cc}{\sigma }_1^2& \rho {\sigma }_1{\sigma }_2\\ \rho {\sigma }_1{\sigma }_2& {\sigma }_2^2\end{array}\right],{\sigma }_1=\frac{B}{AB-C^2},{\sigma }_2=\frac{A}{AB-C^2},\rho =\frac{-C}{AB}.$$

The coefficients A, B and C depend on the energy $E_i$ (except B) and experimental uncertainties normalized to the flow ${\sigma }_i^{rel}$:

$$A=\sum _i^n\frac{E_i^2}{{{\sigma }_i^{rel}}^2},B=\sum _i^n\frac{1}{{{\sigma }_i^{rel}}^2},C=\sum _i^n\frac{E_i}{{{\sigma }_i^{rel}}^2}$$

5. Results and Discussion

For each point in the space t, r, the value of ${\xi }^2$ was minimized according to the parameters of the energy and chemical composition of the source. The resulting surface ${\xi }^2(t,r)$ has a complicated shape with a pronounced minimum region.

The region of space t, r with the required energy of the source $W<{10}^{51}$ erg is considered acceptable, since the power of the supernova explosion according to modern concepts [22] does not exceed this value. The calculations assumed that one-tenth of the total energy of the explosion goes into the energy of CRs.

Figure 2 shows a map of the lines of the level ${\xi }^2/NDF$ (by one degree of freedom): the darker the shade, the less ${\xi }^2$. The age of the source in thousands of years is plotted along the abscissa axis, and the distance to the source in the kpc is plotted along the ordinate axis. The red winding line corresponds to the energy level $W={10}^{50}$ erg; the green one corresponds to the level $W={10}^{51}$ erg.

Figure 2 shows that the position in the space t, rof the hypothetical source is localized in a narrow region, which is an extended region of the minimum on the surface relief. The optimal position of the source in the space t, r corresponds to the region of 0.1–0.2 kpc and the age from 1 to 5 thousand years, although the hypothetical source can be located anywhere in the extended minimum region. 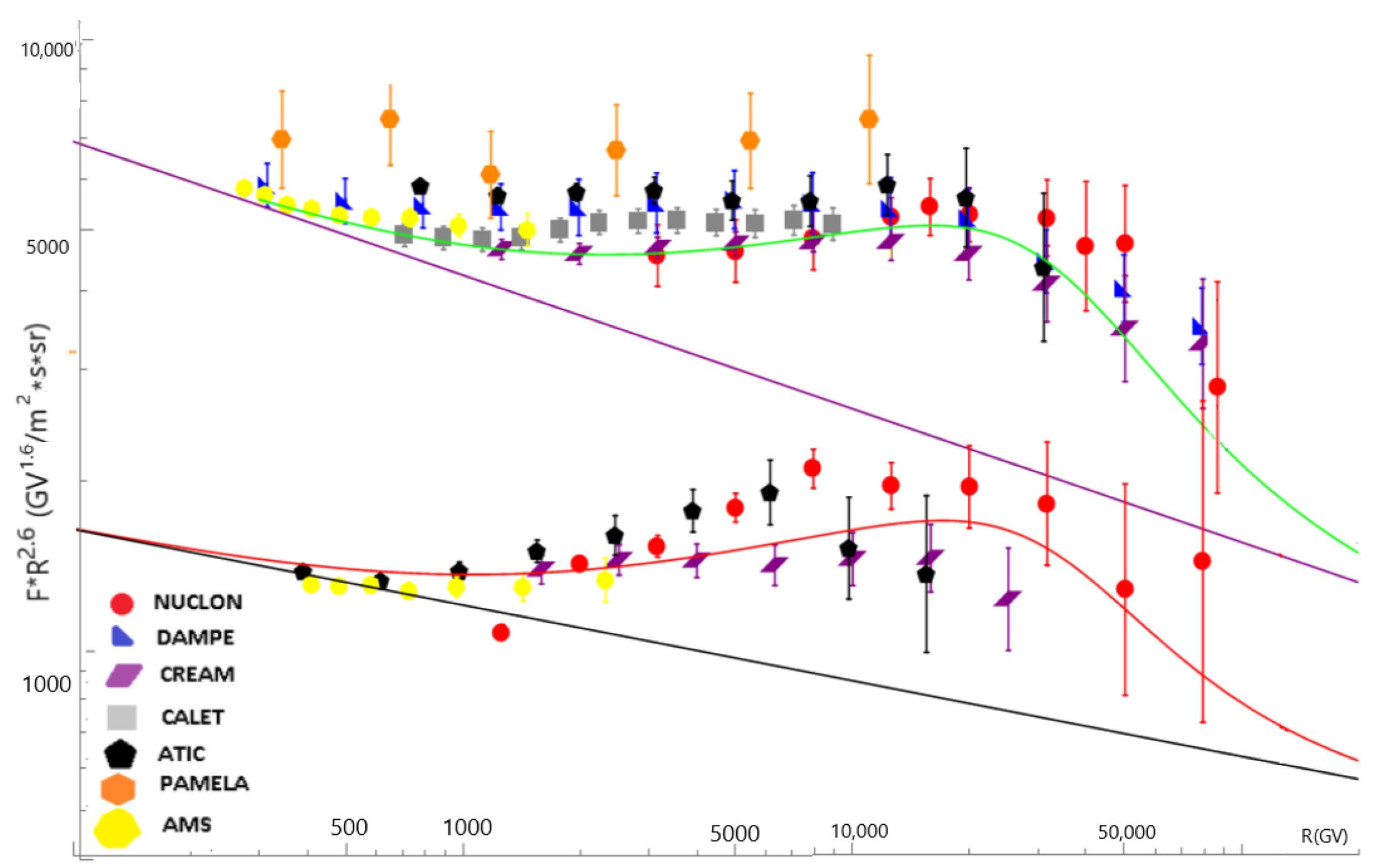The energy of the source is between ${10}^{50}$ and ${10}^{51}$ erg. The expected spectra corresponding to the source of three thousand years, 0.16 kpc, together with some experimental data used in the analysis, are shown in Figure 3 and Figure 4.

6. Conclusions

A model of the contribution of a single-point source flash to the background spectrum of CR in the approximation of diffusion without energy losses and fragmentation is proposed to explain the nature of the observed spectral inhomogeneity of CR.

This model predicts not only the element-by-element spectrum in the region of the spectral anomaly, but also the expected spectrum of all particles. The use of the penalty function method, extended for two-dimensional correlations, made it possible to use not only the data of the direct measurements NUCLEON, AMS-02, ATIC, CREAM, PAMELA, CALET, but also the data of the HAWC ground experiment, which has an extremely high statistical reliability and a large systematic error.

Said model demonstrates reasonable agreement with the experimental data of the source energy up to ${10}^{51}$ erg, localizes the position of a hypothetical source in the distance–time space in a narrow region of phase space, and also predicts the most likely area of existence of such a hypothetical source at 0.1–0.2 kpc and an age of one to five thousand years. Several supernova remnants match these criteria, including HB9 and Vela. It should be noted that the optimal source is obtained quite young, so the approximation of the source flash for its description is not very accurate, and given that the isotropic diffusion for these energies is a very rough approximation, the presented results should be considered preliminary, and in the subsequent work we assume to take into account the evolution of the supernova remnant at the Sedov–Taylor stage.

There are models that describe both anisotropy and CR spectra based on some experimental data [23] in the isotropic diffusion approximation, but the isotropic diffusion approximation for these energies is a rather rough approximation. For a more accurate description of the observed anisotropy together with the CR spectrum, it is necessary to understand the anisotropy of the diffusion coefficient tensor. This work will also be carried out in the future.

Thus, it is demonstrated that the observed spectral inhomogeneity of the CR near 10 TV in terms of magnetic rigidity through the contribution of a single remnant of a close supernova to the observed CR fluxes can be explained.