Warm Dark Matter from Higher-Dimensional Gauge Theories
Abstract
1. Introduction
2. keV WDM from Higher-Dimensional Gauge Theories
WDM Degrees of Freedom
3. Algebras with Higher-Dimensional Spinors
3.1. Superalgebra in 17 + 1 and 9-Brane WV Reduction
3.2. Superalgebra in 20 + 4 and 12-Brane WV Reduction
3.2.1. Further Reduction in Inner/Fiber Symmetry
3.2.2. Magic Star Reduction in D = 20 + 4
4. Symmetry Reduction to the Standard Model and Warm Dark Matter Disentanglement
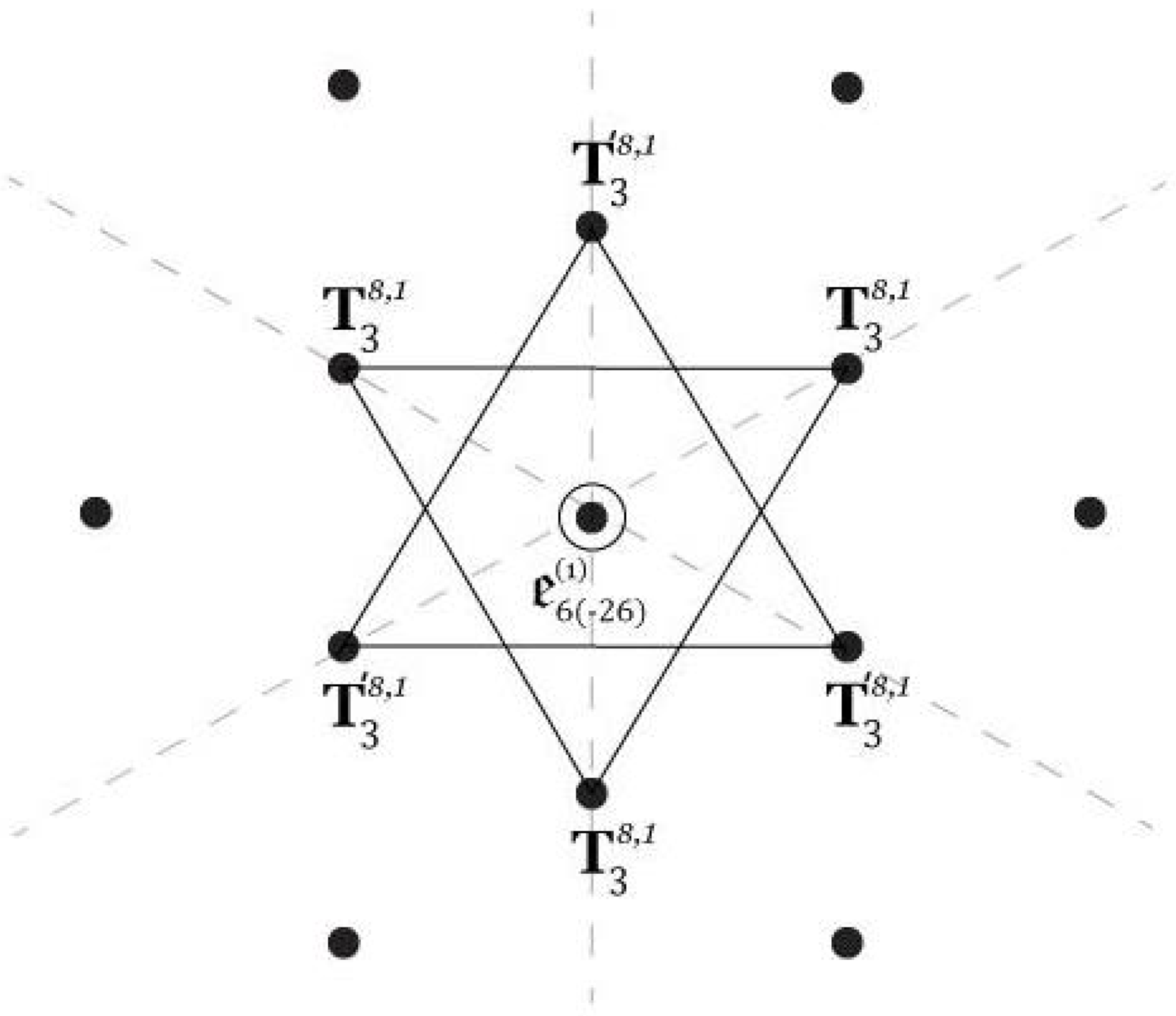
4.1. Braneworld Spinors
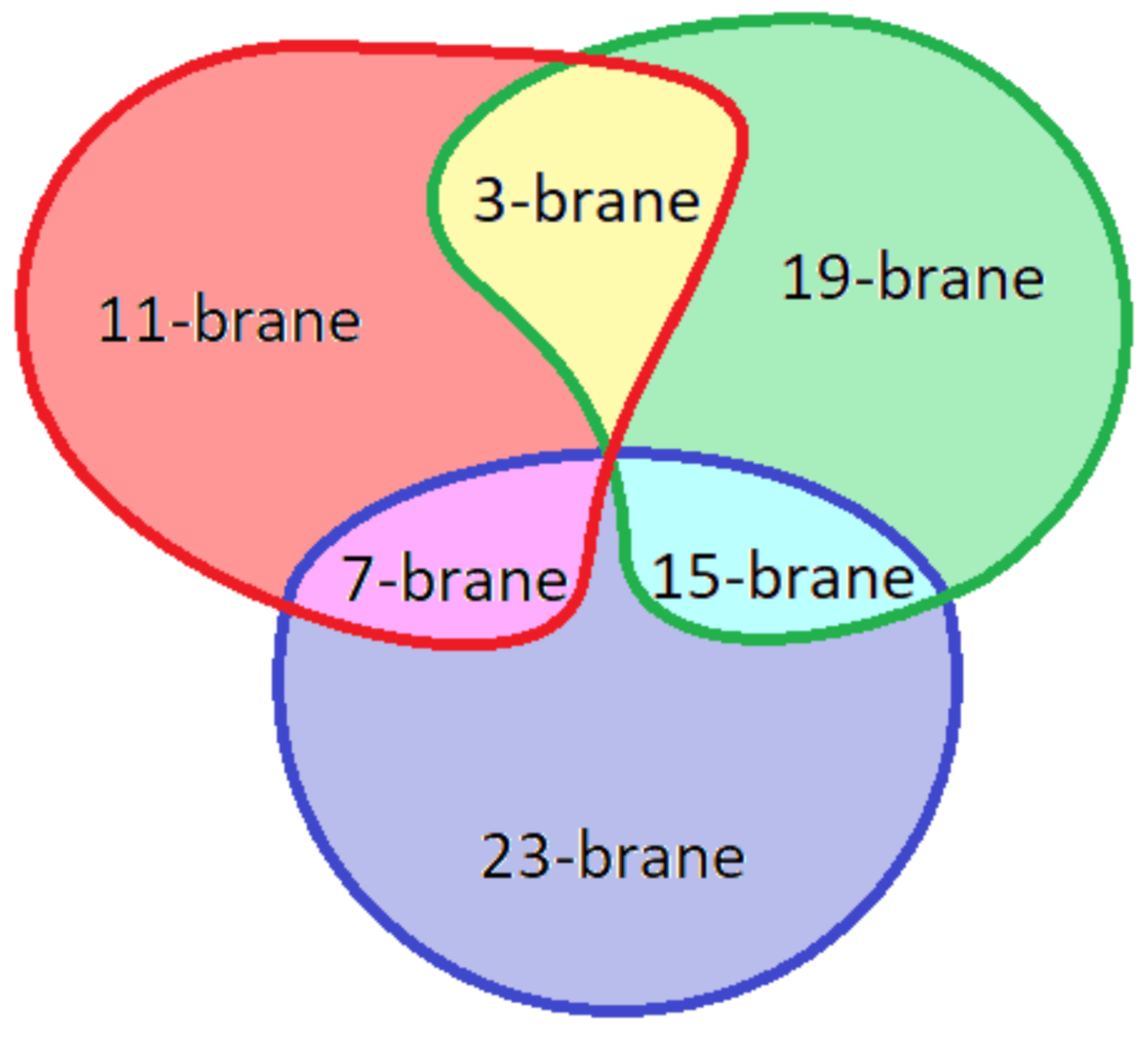
4.2. Braneworld Intersections for Warm Dark Matter beyond the Standard Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | directory of open access journals |
| WDM | warm dark matter |
| CDM | cold dark matter |
| SM | standard model |
| EP | exceptional periodicity |
| ESYM | exceptional super Yang–Mills |
| WV | worldvolume |
References
- Tikhonov, A.V.; Gottlöber, S.; Yepes, G.; Hoffman, Y. The sizes of minivoids in the local Universe: An argument in favour of a warm dark matter model? Mon. Not. RAS 2009, 399, 1611. [Google Scholar] [CrossRef]
- Zavala, J.; Jing, Y.P.; Faltenbacher, A.; Yepes, G.; Hoffman, Y.; Gottlöber, S.; Catinella, B. The velocity function in the local environment from LCDM and LWDM constrained simulations. Astrophys. J. 2009, 700, 1779. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Nusser, A. Nearby galaxies as pointers to a better theory of cosmic evolution. Nature 2010, 465, 565–569. [Google Scholar] [CrossRef]
- Kormendy, J.; Drory, N.; Bender, R.; Cornell, M.E. Bulgeless Giant Galaxies Challenge Our Picture of Galaxy Formation by Hierarchical Clustering. Astrophys. J. 2010, 723, 54. [Google Scholar] [CrossRef]
- Kormendy, J. Elliptical Galaxies and Bulges of Disc Galaxies: Summary of Progress and Outstanding Issues. In Galactic Bulges; Springer: Berlin/Heidelberg, Germany, 2016; pp. 431–477. [Google Scholar]
- Caramete, L.I.; Biermann, P.L. The catalog of nearby black hole candidates. arxiv 2011, arXiv:1107.2244. [Google Scholar]
- Wang, F.; Yang, J.; Fan, X.; Hennawi, J.F.; Barth, A.J.; Banados, E.; Bian, F.; Boutsia, K.; Connor, T.; Davies, F.B.; et al. A Luminous Quasar at Redshift 7.642. Astrophys. J. Lett. 2021, 907, L1. [Google Scholar] [CrossRef]
- de Vega, H.; Sanchez, N.G. Model independent analysis of dark matter points to a particle mass at the keV scale. Mon. Not. R. Astron. Soc. 2010, 404, 885. [Google Scholar] [CrossRef]
- de Vega, H.; Salucci, P.; Sanchez, N.G. The mass of the dark matter particle from theory and observations. New Astron. 2012, 17, 653. [Google Scholar] [CrossRef]
- de Vega, H.; Sanchez, N.G. Cosmological evolution of warm dark matter fluctuations. I. Efficient computational framework with Volterra integral equations. Phys. Rev. D 2012, 85, 043516. [Google Scholar] [CrossRef]
- de Vega, H.; Sanchez, N.G. Cosmological evolution of warm dark matter fluctuations. II. Solution from small to large scales and keV sterile neutrinos. Phys. Rev. D 2012, 85, 043517. [Google Scholar] [CrossRef]
- Destri, C.; de Vega, H.J.; Sanchez, N.G. Fermionic warm dark matter produces galaxy cores in the observed scales because of quantum mechanics. New Astron. 2013, 22, 39. [Google Scholar] [CrossRef][Green Version]
- Destri, C.; de Vega, H.J.; Sanchez, N.G. Quantum WDM fermions and gravitation determine the observed galaxy structures. Astropart. Phys. 2013, 46, 1. [Google Scholar] [CrossRef][Green Version]
- Destri, C.; de Vega, H.J.; Sanchez, N.G. Warm dark matter primordial spectra and the onset of structure formation at redshift z. Phys. Rev. D 2013, 88, 083512. [Google Scholar] [CrossRef]
- de Vega, H.; Salucci, P.; Sanchez, N.G. Observational rotation curves and density profiles versus the Thomas–Fermi galaxy structure theory. Mon. Not. R. Astron. Soc. 2014, 442, 2717. [Google Scholar] [CrossRef]
- Paduroiu, S.; Revaz, Y.; Pfenniger, D. Structure formation in warm dark matter cosmologies: Top-Bottom Upside-Down. arXiv 2015, arXiv:1506.03789. [Google Scholar]
- Paduroiu, S. Structure Formation in Warm Dark Matter Cosmologies. Ph.D. Thesis, University of Geneva, Geneva, Switzerland, 2015. [Google Scholar]
- Sanchez, N.; Paduroiu, S.; Biermann, P.L. Warm Dark Matter Astrophysics in Agreement with Observations and keV Sterile Neutrinos: Synthesis of Highlights and Conclusions of the Chalonge -de Vega Meudon Workshop 2016 In Memoriam Héctor J. de Vega. 2016. Available online: https://hal.archives-ouvertes.fr/hal-01773092 (accessed on 16 October 2021).
- Macciò, A.V.; Stinson, G.; Brook, C.B.; Wadsley, J.; Couchman, H.M.P.; Shen, S.; Gibson, B.K.; Quinn, T. Halo Expansion in Cosmological Hydro Simulations: Toward a Baryonic Solution of the Cusp/Core Problem in Massive Spirals. Astrophys. J. 2012, 744, L9. [Google Scholar] [CrossRef]
- Marinacci, F.; Pakmor, R.; Springel, V. The formation of disc galaxies in high-resolution moving-mesh cosmological simulations. Mon. Not. RAS 2014, 437, 1750. [Google Scholar] [CrossRef]
- Gao, L.; Theuns, T. Lighting the Universe with filaments. Science 2007, 317, 1527. [Google Scholar] [CrossRef] [PubMed]
- Boyarsky, A.; Drewes, M.; Lasserre, T.; Mertens, S.; Ruchayskiy, O. Sterile Neutrino Dark Matter. Prog. Part. Nucl. Phys. 2019, 104, 1–45. [Google Scholar] [CrossRef]
- Bode, P.; Ostriker, J.P.; Turok, N. Halo formation in warm dark matter models. Astrophys. J. 2001, 556, 93. [Google Scholar] [CrossRef]
- Pierpaoli, E.; Borgani, S.; Masiero, A.; Yamaguchi, M. The Formation of Cosmic Structures in a Light Gravitino Dominated Universe. Phys. Rev. D 1998, 57, 2089. [Google Scholar] [CrossRef]
- Alvarez-Gaumé, L.; Ginsparg, P.; Moore, G.; Vafa, C. An O(16) × O(16) heterotic string. Phys. Lett. B 1986, 171, 2. [Google Scholar] [CrossRef]
- Dixon, L.G.; Harvey, J.A. String theories in ten dimensions without supersymmetry. Nucl. Phys. B 1986, 274, 18. [Google Scholar] [CrossRef]
- Jedamzik, K.; Lemoine, M.; Moultaka, G. Gravitino dark matter in gauge mediated supersymmetry breaking. Phys. Rev. D 2006, 73, 1550. [Google Scholar] [CrossRef]
- Gross, C.; Lebedev, O.; Mambrini, Y. Non-Abelian gauge fields as dark matter. J. High Energy Phys. 2015, 8, 158. [Google Scholar] [CrossRef]
- McGuigan, M. Dark Horse, Dark Matter: Revisiting the SO(16)x SO(16)’ Nonsupersymmetric Model in the LHC and Dark Energy Era. arXiv 2019, arXiv:1907.01944. [Google Scholar]
- Rios, M.; Marrani, A.; Chester, D. The Geometry of Exceptional Super Yang-Mills Theories. Phys. Rev. D 2019, 99, 046004. [Google Scholar] [CrossRef]
- Rios, M.; Marrani, A.; Chester, D. Exceptional Super Yang-Mills in D = 27 + 3 and Worldvolume M-Theory. Phys. Lett. B 2020, 808, 135674. [Google Scholar] [CrossRef]
- Dodelson, S.; Widrow, L.M. Sterile neutrinos as dark matter. Phys. Rev. Lett. 1994, 72, 17–20. [Google Scholar] [CrossRef]
- Shi, X.; Fuller, G.M. New dark matter candidate: Nonthermal sterile neutrinos. Phys. Rev. Lett. 1999, 82, 2832. [Google Scholar] [CrossRef]
- Dolgov, A.D. Neutrinos in cosmology. Phys. Rep. 2002, 370, 333. [Google Scholar] [CrossRef]
- Asaka, T.; Shaposhnikov, M.; Kusenko, A. Opening a new window for warm dark matter. Phys. Lett. B 2006, 638, 401. [Google Scholar] [CrossRef]
- Boyarsky, A.; Lesgourgues, J.; Ruchayskiy, O.; Viel, M. Realistic sterile neutrino dark matter with keV mass does not contradict cosmological bounds. Phys. Rev. Lett. 2009, 102, 201304. [Google Scholar] [CrossRef] [PubMed]
- Fuller, G.M.; Kishimoto, C.T.; Kusenko, A. Heavy sterile neutrinos, entropy and relativistic energy production, and the relic neutrino background. arXiv 2011, arXiv:1110.6479. [Google Scholar]
- Lello, L.; Boyanovsky, D. Cosmological Implications of Light Sterile Neutrinos produced after the QCD Phase Transition. Phys. Rev. D 2015, 91, 063502. [Google Scholar] [CrossRef]
- Paduroiu, S. Warm Dark Matter in Numerical Simulations. 2021; submitted to Universe, MDPI. [Google Scholar]
- Colombi, S.; Dodelson, S.; Widrow, L.M. Large Scale Structure Tests of Warm Dark Matter. Astrophys. J. 1996, 458, 1. [Google Scholar] [CrossRef]
- Bezrukov, F.; Hettmansperger, H.; Lindner, M. keV sterile neutrino dark matter in gauge extensions of the standard model. Phys. Rev. D 2010, 81, 085032. [Google Scholar] [CrossRef]
- Nemevšek, M.; Senjanović, G.; Zhang, Y. Warm dark matter in low scale left-right theory. J. Cosmol. Astropart. Phys. 2012, 7, 6. [Google Scholar] [CrossRef]
- Patwardhan, A.V.; Fuller, G.M.; Kishimoto, C.T.; Kusenko, A. Diluted equilibrium sterile neutrino dark matter. Phys. Rev. D 2015, 92, 103509. [Google Scholar] [CrossRef]
- Herms, J.; Ibarra, A.; Toma, T. A new mechanism of sterile neutrino dark matter production. JCAP 2018, 6, 36. [Google Scholar] [CrossRef]
- Vafa, C. Evidence for F-Theory. Nucl. Phys. B 1996, 469, 403. [Google Scholar] [CrossRef]
- Bars, I. S-theory. Phys. Rev. D 1997, 55, 2373. [Google Scholar] [CrossRef]
- Bars, I. A case for 14 dimensions. Phys. Lett. B 1997, 403, 257. [Google Scholar] [CrossRef]
- Sezgin, E. Super Yang-Mills in (11,3) Dimensions. Phys. Lett. B 1997, 403, 265. [Google Scholar] [CrossRef][Green Version]
- Nishino, H. Supersymmetric Yang-Mills Theories in D ⩾ 12. Nucl. Phys. B 1998, 523, 450. [Google Scholar] [CrossRef]
- Rudychev, I.; Sezgin, E.; Sundell, P. Supersymmetry in dimensions beyond eleven. Nucl. Phys. Proc. Suppl. 1998, 68, 285. [Google Scholar] [CrossRef]
- Witten, E. String Theory Dynamics In Various Dimensions. Nucl. Phys. B 1995, 443, 85. [Google Scholar] [CrossRef]
- Banks, T.; Fischler, W.; Shenker, S.H.; Susskind, L. M Theory As A Matrix Model: A Conjecture. Phys. Rev. D 1995, 55, 5112. [Google Scholar] [CrossRef]
- Truini, P.; Rios, M.; Marrani, A. The Magic Star of Exceptional Periodicity. In Proceedings of the 4th Mile High Conference on Nonassociative Mathematics, Denver, CO, USA, 29 July–5 August 2017. [Google Scholar]
- Truini, P.; Marrani, A.; Rios, M. Magic Star and Exceptional Periodicity: An approach to Quantum Gravity. In Proceedings of the 32nd International Colloquium on Group Theoretical Methods in Physics, Prague, Czech Republic, 9–13 July 2018. [Google Scholar]
- Marrani, A.; Truini, P.; Rios, M. The Magic of Being Exceptional. In Proceedings of the 32nd International Colloquium on Group Theoretical Methods in Physics, Prague, Czech Republic, 9–13 July 2018. [Google Scholar]
- de Wit, B.; Van Proeyen, A. Special geometry, cubic polynomials and homogeneous quaternionic spaces. Commun. Math. Phys. 1992, 149, 307. [Google Scholar] [CrossRef]
- de Wit, B.; Vanderseypen, F.; Van Proeyen, A. Symmetry structure of special geometries. Nucl. Phys. B 1993, 400, 463. [Google Scholar] [CrossRef]
- Reig, M.; Valle, J.W.F.; Vaquera-Araujo, C.A.; Wilczek, F. A Model of Comprehensive Unification. Phys. Lett. B 2017, 774, 667. [Google Scholar] [CrossRef]
- BenTov, Y.; Zee, A. The Origin of Families and SO(18) Grand Unification. Phys. Rev. D 2016, 93, 065036. [Google Scholar] [CrossRef]
- Vinberg, E.B. The theory of Convex Homogeneous Cones. In Transaction of the Moscow Mathematical Society for the Year 1963; American Mathematical Society: Providence, RI, USA, 1963; pp. 340–403. [Google Scholar]
- Alekseevsky, D.V.; Marrani, A.; Spiro, A. Special Vinberg Cones and the Entropy of BPS Extremal Black Holes. arXiv 2021, arXiv:2107.06797. [Google Scholar] [CrossRef]
- Horava, P.; Witten, E. Heterotic and Type I String Dynamics from Eleven Dimensions. Nucl. Phys. B 1996, 460, 506. [Google Scholar] [CrossRef]
- Horava, P.; Witten, E. Eleven-Dimensional Supergravity on a Manifold with Boundary. Nucl. Phys. B 1996, 475, 94. [Google Scholar] [CrossRef]
- Horowitz, G.; Susskind, L. Bosonic M Theory. J. Math. Phys. 2001, 42, 3152–3160. [Google Scholar] [CrossRef]
- Watabiki, Y. The bosonic string and superstring models in 26 + 2 and 10 + 2 dimensional space–time, and the generalized Chern-Simons action. J. High Energy Phys. 2003, 5, 1. [Google Scholar] [CrossRef][Green Version]
- Jungman, G.; Kamionkowski, M.; Griest, K. Supersymmetric Dark Matter. Phys. Rept. 1996, 267, 195. [Google Scholar] [CrossRef]
- ATLAS Collaboration. Search for bottom-squark pair production with the ATLAS detector in final states containing Higgs bosons, bb-jets and missing transverse momentum. J. High Energy Phys. 2019, 12, 60. [Google Scholar]
- Duff, M.J.; Inami, T.; Pope, C.N.; Sezgin, E.; Stelle, K.S. Semiclassical quantization of the supermembrane. Nucl. Phys. B 1988, 297, 515. [Google Scholar] [CrossRef]
- Cederwall, M.; von Gussich, A.; Nilsson, B.E.W.; Westerberg, A. The Dirichlet super three-brane in ten-dimensional type IIB supergravity. Nucl. Phys. B 1997, 490, 163–178. [Google Scholar] [CrossRef][Green Version]
- Heckman, J.J.; Vafa, C. From F-theory GUTs to the LHC. arXiv 2008, arXiv:hep-th/0809.3452. [Google Scholar]
- Randall, L.; Sundrum, R. A Large mass hierarchy from a small extra dimension. Phys. Rev. Lett. 1999, 83, 3370–3373. [Google Scholar] [CrossRef]
- Hirayama, T. A Holographic dual of CFT with flavor on de Sitter space. J. High Energy Phys. 2006, 6, 13. [Google Scholar] [CrossRef][Green Version]
- Cheung, C.; Remmen, G.N. Twofold Symmetries of the Pure Gravity Action. J. High Energy Phys. 2017, 1, 104. [Google Scholar] [CrossRef]
- MacDowell, S.W.; Mansouri, F. Unified geometric theory of gravity and supergravity. Phys. Rev. Lett. 1977, 38, 739–742. [Google Scholar] [CrossRef]
- Gürsey, F.; Ramond, P.; Sikivie, P.A. Universal Gauge Theory Model Based on E6. Phys. Lett. B 1976, 60, 177–180. [Google Scholar] [CrossRef]
- Boyle, L. The Standard Model, The Exceptional Jordan Algebra, and Triality. arXiv 2006, arXiv:2006.16265. [Google Scholar]
- Bars, I.; Günaydin, M. Grand Unification with the Exceptional Group E8. Phys. Rev. Lett. 1980, 45, 859. [Google Scholar] [CrossRef]
- Marrani, A.; Rios, M.; Chester, D. Monstrous M-theory. arXiv 2008, arXiv:hep-th/2008.06742. [Google Scholar]
- Gaberdiel, M.R.; West, P.C. Kac-Moody algebras in perturbative string theory. J. High Energy Phys. 2002, 8, 49. [Google Scholar] [CrossRef][Green Version]
- Kostant, B. The Principle of Triality and A Distinguished Unitary Representation of SO(4,4). In Differential Geometrical Methods in Theoretical Physics; Bleuler, K., Werner, M., Eds.; NATO ASI Series (Series C: Mathematical and Physical Sciences); Springer: Dordrecht, The Netherlands, 1988; Volume 250. [Google Scholar]
- Chester, D.; Marrani, A.; Rios, M. Beyond the standard model with six-dimensional spacetime. arXiv 2020, arXiv:2002.02391. [Google Scholar]
- Aldazabal, G.; Ibanez, L.E.; Quevedo, F.; Uranga, A.M. D-Branes at Singularities: A Bottom-Up Approach to the String Embedding of the Standard Model. J. High Energy Phys. 2000, 8, 2. [Google Scholar] [CrossRef]
- Martinec, E.J. Geometrical structures of M theory. arXiv 1996, arXiv:hep-th/9608017. [Google Scholar]
- Krasnov, K. Spin(11,3), particles and octonions. arXiv 2021, arXiv:hep-th/2104.01786. [Google Scholar]
- Slansky, R. Group Theory for Unified Model Building. Phys. Rept. 1981, 79, 1–28. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paduroiu, S.; Rios, M.; Marrani, A.; Chester, D. Warm Dark Matter from Higher-Dimensional Gauge Theories. Universe 2021, 7, 462. https://doi.org/10.3390/universe7120462
Paduroiu S, Rios M, Marrani A, Chester D. Warm Dark Matter from Higher-Dimensional Gauge Theories. Universe. 2021; 7(12):462. https://doi.org/10.3390/universe7120462
Chicago/Turabian StylePaduroiu, Sinziana, Michael Rios, Alessio Marrani, and David Chester. 2021. "Warm Dark Matter from Higher-Dimensional Gauge Theories" Universe 7, no. 12: 462. https://doi.org/10.3390/universe7120462
APA StylePaduroiu, S., Rios, M., Marrani, A., & Chester, D. (2021). Warm Dark Matter from Higher-Dimensional Gauge Theories. Universe, 7(12), 462. https://doi.org/10.3390/universe7120462





