Abstract
The tremendous phenomenological success of the Standard Model (SM) suggests that its flavor structure and gauge interactions may not be arbitrary but should have a fundamental first-principle explanation. In this work, we explore how the basic distinctive properties of the SM dynamically emerge from a unified New Physics framework tying together both flavor physics and Grand Unified Theory (GUT) concepts. This framework is suggested by a novel anomaly-free supersymmetric chiral GUT containing the SM. Among the most appealing emergent properties of this theory is the Higgs-matter unification with a highly-constrained massless chiral sector featuring two universal Yukawa couplings close to the GUT scale. At the electroweak scale, the minimal SM-like effective field theory limit of this GUT represents a specific flavored three-Higgs doublet model consistent with the observed large hierarchies in the quark mass spectra and mixing already at tree level.
1. Introduction
With a handful of physical parameters such as fermion masses and gauge couplings, the Standard Model (SM) explains a huge variety of collider and low energy data spanning over several orders of magnitude for the corresponding energy scales. Its success builds strongly on the gauge principle. However, it is fundamentally incomplete as it leaves the cosmological Dark Matter and baryon asymmetry of the universe unexplained. Moreover, it neither contains mechanisms for generating the tiny neutrino masses nor explains the structure of the SM fermion families. This suggests that the SM is not the ultimate theory but an excellent effective field theory (EFT) of the subatomic world.
Since the birth of the SM in mid-1970, there have been numerous attempts to come up with a consistent first-principle explanation of the well-measured but yet totally arbitrary and rather odd properties of the SM. Among these are the remarkable proton stability, the specific structure of gauge and Yukawa interactions and the properties of the Higgs and Yukawa sectors which are intimately connected to the rather peculiar observed patterns in the neutrino and charged fermion mass spectra and generation mixings (the so-called flavor problem).
It is fairly easy to achieve unification of the gauge couplings at higher energy scales by postulating the existence of additional scalars and/or fermions belonging to incomplete representations of [1]. This is for example realized in supersymmetric (SUSY) extensions of the SM [2]. This unification is a necessary requirement to embed the SM into a larger gauge group such as as , , or [3,4,5,6,7,8,9,10,11,12,13], so-called grand unified theories (GUTs). For a recent thorough discussion of theoretical features and most important phenomenological implications of the GUTs, see e.g., Refs. [14,15,16,17,18,19,20,21]. Remarkably, in Ref. [22] it has been demonstrated that the well-known hierarchy and doublet-triplet splitting problems appear to be naturally resolved in the framework of SUSY GUT (see also Refs. [23,24]). This model also provides means for the explanation of the origin of the fermion mass hierarchy, i.e., why the third fermion family in the SM is heavier than first two [25]. Other promising scenarios designed to address the flavor problem invoke new “horizontal” symmetries at high energies; for recent studies, see e.g., Refs. [26,27,28,29,30,31,32]. For original works, where it was suggested, in particular in the context of , that the observed fermion spectrum with its hierarchies of masses and mixing angles are due to horizontal symmetry breaking hierarchy, i.e., by the flavon VEV hierarchy breaking it, see Refs. [33,34,35,36].
2. Gauge and Yukawa Structure
In general, it is rather difficult to combine both gauge symmetries and horizontal symmetries without a proliferation of unknown parameters in the Yukawa sector. Our main goal here is to find a consistent GUT framework in four spacetime dimensions, with both types of unification realized dynamically in the gauge and Yukawa sectors. For this purpose, we would like to study high-scale SUSY-based framework binding together both observed fermion families’ replication in the SM and grand unification. For this purpose, let us consider the SUSY GUT in four dimensions where the gauge symmetries of the SM originate from whereas additional group factors conveniently represent a “horizontal” gauge symmetry distinguishing the fermion families, i.e., the family symmetry1.
Note that a further constrained scenario based on has been previously studied by some of the authors in Refs. [39,40]. Indeed, promoting to , the model seems to become more compact and natural. However, it was found that the top and charm quark tree-level masses are degenerate and a strong fine-tuning in the soft SUSY breaking sector is necessary in order to induce a realistic mass splitting at one-loop level. Such fine-tuning implies a rather strong hierarchy between different soft SUSY breaking parameters that have prompted the search for a less constrained fully-gauged family symmetry such as the one considered in this work.
The subsequent symmetry breaking steps can be realized by means of the Higgs mechanism as follows:
where is the trinification group and . We adopt at this stage that theory originates from a certain large gauge group at the upper-most GUT-scale (with a single universal gauge coupling) by means of some unknown dynamics and formulate the basic criteria for phenomenological consistency of such a scenario.
The mass scales of the rank-preserving symmetry breaking steps in Equations (1) and (2) are given by the sizes of the superpotential quadratic terms implying a nearly-compressed scale hierarchy . The ⋯ in Equation (3) represent the subsequent low-scale breaking steps down to the SM gauge group triggered by soft-SUSY breaking interactions at the soft scale . The latter can be decoupled from the trinification breaking scale, i.e., , in consistency with the low-scale electroweak spontaneous symmetry breaking (EW-SSB) in the SM.
In this work, our main goal is to briefly discuss the main features of the SUSY GUT with the symmetry breaking pattern given in Equations (1)–(3) and with a particular anomaly-free superfield content summarised in Table 1. In order to build a minimal working GUT scenario in this framework, one simple way to proceed is to adopt a scheme enabling to give large masses to the majority of supermultiplets listed in Table 1 apart from those that we need for phenomenological explorations. For simplicity, we introduce an extra parity that plays a similar role to R-parity of the MSSM yielding the superpotential of the -odd superfields analogical to that of the MSSM leptonic sector with right-handed neutrinos,

Table 1.
Fundamental superfield content of the anomaly-free 4-dimensional SUSY GUT. Here, and .
Hence, an analogue of right-handed neutrino, , receives Majorana mass at some large scale , while other additional superfields , and acquire their masses upon breaking of symmetry through VEVs in scalar components of doublets. This resembles the Higgsino, (s)neutrinos’ and (s)leptons’ mass generation via the EW symmetry breaking mechanism in the conventional MSSM framework, but for the family SSB and at a larger scale, .
Provided that are -even, their VEVs are not affecting symmetry which is therefore preserved in this model and survives down to low scales. Similarly to R-parity, this symmetry provides a possible way to stabilize the lightest state among the -odd components of , and superfields. Whether or not such a state can play a role of a Dark Matter candidate remains one of the interesting topics for further studies in this model. Besides, neutrino-like states may receive a relatively small mass scale due to a seesaw-type mixing with the Majorana fermion from . Communication of such -odd sector with the SM sectors would be suppressed due to a large mass scale of family gauge bosons at tree level and due to a small loop-generated coupling to the SM Higgs boson. Apart from potentially light and decoupled -odd states, all the other fields in are well above the EW scale and their impact on the low-scale phenomenology is expected to be strongly suppressed. Thus, they can be safely integrated out below scale.
It is worth noticing here that the particle content of the considered GUT and charge assignments in Table 1 enable the superpotential mass terms to all the fundamental -even superfields except for and , providing a novel GUT framework manifestly free of the gauge and Witten anomalies.
The large representations and trigger (through their scalar VEVs) the spontaneous rank- and SUSY-preserving breaking of symmetry at scale in Equation (1), while the components of the -even -adjoint representation play a critical role in triggering the subsequent trinification SSB in Equation (2). All these fields conveniently received large masses and can be integrated out below either (large reps) or (adjoint rep) scale in the considered SUSY GUT. Taking the trinification breaking at scale as an example, the -adjoint superfields (see Table 2) originating from superfield have a universal mass term in the superpotential, which together with a cubic term triggers a rank- and SUSY-preserving VEV in one of its scalar components [40]. The SUSY-preserving breaking of a gauge symmetry implies that the D- and F-terms have to vanish separately. This means that the scalar potential has zero value in both the -symmetric and -broken vacua in the exact SUSY case. Thus, the presence of even a tiny soft-SUSY breaking effect already at the scale is needed to make these vacua non-equivalent [41], hence, enabling the trinification SSB in Equation (2). As a result, all the components of acquire a universal mass, due to D-terms and thus are integrated out below the scale.

Table 2.
Upper part: fundamental chiral superfields in the theory–components of the massless and superfields of [42]. Lower part: the corresponding components of the massive superfield . Accidental symmetries’ charges are shown in last two columns.
The remaining massless superfields and neatly unite the SM Higgs and matter (neutrino, charged lepton and quark) sectors hence imposing very specific constraints on the structure of the resulting low-energy EFT below . How does such Higgs-matter unification comply with observations? Notably, the considered SUSY GUT enables for a phenomenologically consistent splitting between the second- and third-generation quark masses already at tree level with only two distinct quark Yukawa couplings below . Let us explore this interesting phenomenon in more detail.
First of all, the SUSY theory below features a vanishing dim-3 superpotential , caused by anti-symmetry of family index contractions, where is a completely symmetric tensor [43,44], and is the totally anti-symmetric Levi-Civita pseudotensor. Since the renormalisable interactions cannot generate a non-trivial Yukawa structure in this theory, the effects of high-dimensional operators become important. In particular, the relevant part of the superpotential below scale that contains the SM matter and Higgs sectors reads
where the minimal superfield content necessary to generate two distinct Yukawa couplings below requires the presence of two different bi-fundamental -superfields of [45], and . Their VEVs, and , trigger subsequent breaking of [46] down to the trinification symmetry (1). As a result, an EFT superpotential of massless fields below reads
in terms of the massless trinification leptonic and quark superfields–components of the original massless and superfields of described in Table 2. Next, it is convenient to perform the following decomposition
such that, upon further splitting into representations, one has
Above, l, r and x represent , and triplet indices, and denote and doublet indices, respectively, i is the index, while the labels () should not be identified with left (right) chiralities at this stage (all fermionic components are L-handed Weyl spinors). In Equation (8) one can see that the model offers three up specific and three down specific Higgs doublet candidates. While by no means unique, and in fact not a preferred scenario according to the discussion in [47], a MSSM-like Higgs sector is a possible low-scale limit of the model. However, due to a non-trivial mixing structure, such doublets result from a linear combination of those in Equation (8) and cannot be promptly identified at the level of unbroken trinification. The Higgs-matter unification here implies that the Higgs doublet superfields of the EW theory are unified together with the lepton and quark -superfields in the and . Such a unification is thus enforced by the gauge symmetry of the high-scale theory and that cannot be consistently realized in the MSSM.
The effective trinification superpotential (6) contains two universal Yukawa couplings
where and . As we will demonstrate below, due to a very steep Renormalisation Group (RG) evolution of the gauge couplings in the theory at high scales and the required matching of the SM gauge couplings to their measured values at the electroweak (EW) scale, one has and . On another hand, a possible common origin of the dim-4 operators from yet unknown -scale dynamics in the superpotential (5) and a compressed hierarchy imply that suggesting the following hierarchy . It turns out that such an emergent hierarchy is consistent with the existence of an order-one top-quark Yukawa coupling given by . Besides, it leads to the observed top-charm and bottom-strange quark mass hierarchies in the SM as well as to the down-type vector-like quark mass hierarchy already at tree level, namely,
implying also a possibility for two light vector-like -quark species potentially within the reach of the LHC or future collider measurements.
The superpotential (6) possesses an accidental Abelian symmetry whose charges, W and B, are summarised in Table 2. Furthermore, the theory has an extra parity denoted as -parity defined as
where S is the spin. In the considered GUT theory, the -parity replaces the conventional R-parity and forbids triple-squark or quark-quark-squark trilinear interactions in the soft-SUSY breaking sector capable of destabilising the proton at the soft scale. Together with the baryon-number U(1)B-symmetric Yukawa sector, this ensures that only gauge interactions can trigger the proton decay, highly suppressed by a large close to .
The dim-3 superpotential of , and superfields–components of the massive chiral superfield (see Table 2, also Ref. [42])–reads
with the universal . As was mentioned above, the last rank/SUSY-preserving breaking step in Equation (2) represents the trinification breaking by means of degenerate VEVs at in the , octet superfields , , respectively [39,40]. In this case, all the components acquire large masses and hence are integrated out leaving no heavy fields in the resulting left-right (LR) symmetric SUSY EFT [47]
written in terms of the massless components of trinification bi-triplets introduced in Equation (7). The further symmetry breaking steps down to the SM and hence the masses/mixings of the and components are controlled by the structure of the soft-SUSY breaking mass terms and tri-linear interactions as well as by the tree-level Yukawa hierarchy (10).
In the LR symmetric SUSY theory, the largest amount of free parameters comes from the soft-SUSY breaking sector, namely, 17 trilinear couplings (5 involving sleptons and 12–squarks), 16 soft - and -type mass terms, 2 high-scale gaugino mass parameters (in and gauge-family sectors). In addition, there are 4 gauge couplings in the gauge sector whereas all the low-scale Yukawa couplings are matched to two universal high-scale ones defining the strongest hierarchies (10) already at tree level. The loop corrections to the Yukawa sector are controlled by the soft-SUSY breaking parameters and gauge couplings, whose number is sufficient to accommodate the measured values of the SM fermion masses and mixing angles.
3. The Unification Picture
Let us now investigate how strong the hierarchy between the soft and trinification breaking scales, , can be–the question of primary importance for a realistic low-energy theory. Provided the compressed hierarchy , the unknown -scale effects may induce significant threshold corrections to the trinification gauge couplings at scale. Indeed, the relevant gauge-kinetic dim-5 operators [46]
where C is the charge normalization, is the field strength tensor, is a non-renormalisable coupling constant, and is a linear combination of the scalar fields originating from the symmetric product of two adjoint representations , with two -reps and already utilised above. The -breaking VEVs in these fields modify the gauge coupling unification condition at scale via dim-5 threshold corrections from Equation (14) [46]
where , , are the inverse trinification structure constants, and were defined above. Provided that the family U(1)T and the hypercharge U(1)Y gauge groups remain unbroken above the EW scale, their the T- and Y-charges are related to the high-scale ones as and , respectively. The corresponding inverse structure constants are matched (at tree level) to the high-scale ones below -scale as follows: and , respectively. (Here, and are the structure constants for and U(1)A, respectively.)
We have performed a sophisticated numerical analysis of the one-loop RG flow of gauge couplings between and scales accounting for tree-level matching at intermediate scales as well as the matching to their measured counterparts at . We have demonstrated that the presence of threshold corrections to the gauge couplings at enables a perturbative universal coupling with = 10–10 GeV as well as low-scale soft-SUSY breaking down to as low as TeV, in overall consistency with the SM phenomenology. For all valid points, we have found a compressed hierarchy with as well as . One particular example for such RG flow for a valid parameter space point is shown in Figure 1. The gauge coupling evolves very fast as indicated by a steep line stretched between and scales. The threshold corrections are quite sizable in this example. We give the corresponding parameters in Table 3. Note, in an unrealistic case of a strong hierarchy , one could recover an approximate unification corresponding to -permutation symmetry in the trinification gauge sector, originally imposed in Ref. [48]. However, a small implies unacceptably small Yukawa couplings (see Equation (9)).
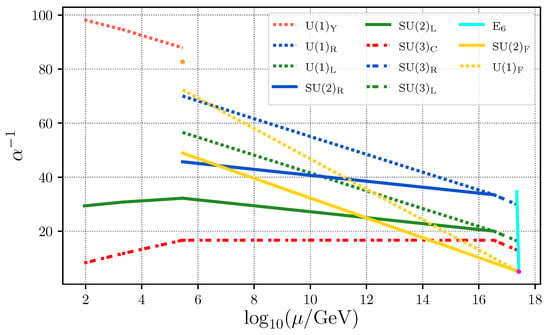
Figure 1.
An illustration of RG evolution of the gauge couplings in the considered model for a parameter space point with a low-scale soft-SUSY breaking consistent with the SM. Here, all the soft-induced symmetry breaking scales (except ) are assumed to be compressed for simplicity and are fixed to a universal value where the SM gauge symmetry emerges. The purple dot represents the universal , while the orange dot shows the value. The purple dot represents an example of a unified gauge couplings where non-perturbative effects can start playing role.

Table 3.
Benchmark points used for the running of the gauge couplings in Figure 1. The top line corresponds to a parameter space point where differ considerably whereas in the bottom line their absolute values are of the same order. Here, .
4. Quark Masses and Mixing
A simple configuration of soft-scale induced VEVs breaking the symmetry in Equation (3) down to reads
where and represent the EW-breaking Higgs up-type and down-type VEVs in the low-energy SM-like EFT, respectively, while all other VEVs are considered to be of order , for simplicity. With such a VEV setting, we can have up to six Higgs doublets in the low-energy limit of the theory. However, for the sake of simplicity, here we consider that only five Higgs doublets acquire VEVs. In this case we found that there is only one particular configuration of these VEVs with that provides the Cabibbo–Kobayashi–Maskawa (CKM) matrix and the quark mass spectrum compatible with those in the SM, i.e.,
while the u- and d-quarks as well as charged leptons and light neutrinos do not acquire masses at tree level. In the limit of small suggested by the second- and third-generation mass hierarchies (10), an approximate Cabibbo mixing arises, with the angle . Indeed, in this limit the top-bottom mixing element is well under control. Moreover, the same ratio (10) provides a strong suppression for , , and CKM elements, in agreement with measurements. In addition, small tree-level contributions to the masses and CKM from a seesaw-type mixing with the heavy vector-like quarks are present. This is similar to the model presented in Ref. [47] which we refer to for further details. Furthermore, loop contributions generate additional (small) terms to the CKM mixing entries and fermion masses. Note, the minimal scenario that is compatible with the CKM quark mixing and mass spectrum corresponds to a Three Higgs Doublet Model with ; a suitable benchmark scenario for detailed phenomenological explorations.
Note, as an interesting possibility for future studies, the fields can break not only to the trinification group but also to . The two scenarios have an intersection and the presence of adjoint which breaks trinification at a lower scale makes a difference in the associated symmetry breaking pattern and in the corresponding low-energy SM-like EFT limit. Further analysis would be necessary to conclude on which of these two breaking schemes is favored by the vacuum structure of the theory, as well as by phenomenology. Such studies should include the full RG flow analysis and the matching to the SM Higgs and flavor sectors in both scenarios.
5. Conclusions
In summary, the suggested flavored SUSY-GUT framework exhibits two-fold unification in the gauge and Yukawa sectors as a consequence of the Higgs-matter and the SM gauge couplings’ Grand Unification under . While higher-dimensional operators in the GUT theory generate the necessary splittings in the Yukawa and gauge sectors, the gauge couplings’ RG flow suggests a strongly-decoupled energy scale for the soft-SUSY breaking sector, giving rise to a consistent low-scale SM-like EFT. The latter exhibits the minimum of three light Higgs doublets for the model to be generically compatible with SM quark masses and CKM mixing. The main features of the SM fermion spectra such as the observed top-charm and bottom-strange mass hierarchies as well as a Cabibbo-type mixing in the quark sector are generated already at tree level. Other parameters of the light fermion spectra such as the small CKM mixing elements, -quark and charged lepton masses, neutrino masses and mixing should be established at higher-loop orders via a mixture of different-type seesaw mechanisms which is planned for further studies. However, it is already clear that vast phenomenological prospects offered in the proposed framework by a rich scalar, neutrino and heavy vector-like fermion sectors as well as by the gauge family interactions can be expected in the reach of future collider experiments. One of the remaining key theoretical goals for further studies is to explore the potential of the ultimate Left-Right-Color-Family gauge and Yukawa couplings’ unification through a dynamical origin of from yet unknown large gauge group at the scale.
Author Contributions
All authors contributed significantly to this work, in particular, to the model building parts. A.P.M. was also responsible for the numerical computations. All authors have read and agreed to the published version of the manuscript.
Funding
The work of APM has been performed in the framework of COST ActionCA16201 “Unraveling new physics at the LHC through the precision frontier” (PARTICLEFACE). APM is supported by the Center for Research and Development in Mathematics and Applications (CIDMA) through the Portuguese Foundation for Science and Technology (FCT - Fundação para a Ciência e a Tecnologia), references UIDB/04106/2020 and UIDP/04106/2020. APM is also supported by the project PTDC/FIS-PAR/31000/2017, the projects CERN/FIS-PAR/0027/2019, CERN/FISPAR/0002/2017 and by national funds (OE), through FCT, I.P., in the scope of the framework contract foreseen in the numbers 4, 5 and 6 of the article 23, of the Decree-Law 57/2016, of August 29, changed by Law 57/2017, of July 19. APM is also supported by the Enabling Green E-science for the Square Kilometer Array Research Infrastructure (ENGAGESKA), POCI-01-0145-FEDER-022217. R.P. is supported in part by the Swedish Research Council grants, contract numbers 621-2013-4287 and 2016-05996, as well as by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No 668679). W.P. has been supported by DFG, project nr. PO-1337/7-1.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
The authors would like to thank Ivo de Medeiros Varzielas and João Rosa for inspiring discussions at early stages of this work.
Conflicts of Interest
The authors declare no conflict of interest.
Note
| 1 | For a previous discussion of implications of non-abelian family symmetries in supersymmetric GUT model building, see e.g., Refs. [37,38]. |
References
- Calibbi, L.; Ferretti, L.; Romanino, A.; Ziegler, R. Gauge coupling unification, the GUT scale, and magic fields. Phys. Lett. B 2009, 672, 152–157. [Google Scholar] [CrossRef]
- Martin, S.P. A Supersymmetry primer. Adv. Ser. Direct. High Energy Phys. 1998, 18, 1–98. [Google Scholar] [CrossRef]
- Georgi, H.; Glashow, S.L. Unity of All Elementary Particle Forces. Phys. Rev. Lett. 1974, 32, 438–441. [Google Scholar] [CrossRef]
- Fritzsch, H.; Minkowski, P. Unified Interactions of Leptons and Hadrons. Ann. Phys. 1975, 93, 193–266. [Google Scholar] [CrossRef]
- Chanowitz, M.S.; Ellis, J.R.; Gaillard, M.K. The Price of Natural Flavor Conservation in Neutral Weak Interactions. Nucl. Phys. B 1977, 128, 506–536. [Google Scholar] [CrossRef]
- Georgi, H.; Nanopoulos, D.V. T Quark Mass in a Superunified Theory. Phys. Lett. B 1979, 82, 392–394. [Google Scholar] [CrossRef]
- Georgi, H.; Nanopoulos, D.V. Ordinary Predictions from Grand Principles: T Quark Mass in O(10). Nucl. Phys. B 1979, 155, 52–74. [Google Scholar] [CrossRef]
- Georgi, H.; Nanopoulos, D.V. Masses and Mixing in Unified Theories. Nucl. Phys. B 1979, 159, 16–28. [Google Scholar] [CrossRef]
- Georgi, H. Lie algebras in particle physics. From isospin to unified theories. Front. Phys. 1982, 54, 1–255. [Google Scholar]
- Gursey, F.; Ramond, P.; Sikivie, P. A Universal Gauge Theory Model Based on E6. Phys. Lett. B 1976, 60, 177–180. [Google Scholar] [CrossRef]
- Gursey, F.; Serdaroglu, M. E6 gauge field theory model revisited. Nuovo Cim. A 1981, 65, 337. [Google Scholar] [CrossRef]
- Achiman, Y.; Stech, B. Quark Lepton Symmetry and Mass Scales in an E6 Unified Gauge Model. Phys. Lett. B 1978, 77, 389–393. [Google Scholar] [CrossRef]
- Pati, J.C.; Salam, A. Lepton Number as the Fourth Color. Phys. Rev. D 1974, 10, 275–289, Erratum in 1975, 11, 703. [Google Scholar] [CrossRef]
- Athron, P.; King, S.F.; Miller, D.J.; Moretti, S.; Nevzorov, R.; King, S.F.; Miller, D.J.; Moretti, S.; Nevzorov, R. The Constrained E6SSM. 2008. Available online: https://arxiv.org/abs/0810.0617 (accessed on 22 November 2021).
- Hall, J.P.; King, S.F.; Nevzorov, R.; Pakvasa, S.; Sher, M.; Nevzorov, R.; Pakvasa, S.; Sher, M. Novel Higgs Decays and Dark Matter in the E(6)SSM. Phys. Rev. D 2011, 83, 075013. [Google Scholar] [CrossRef]
- Rizzo, T.G. Gauge Kinetic Mixing in the E6SSM. Phys. Rev. D 2012, 85, 055010. [Google Scholar] [CrossRef]
- Nevzorov, R. E6 inspired supersymmetric models with exact custodial symmetry. Phys. Rev. D 2013, 87, 015029. [Google Scholar] [CrossRef]
- Nevzorov, R.; Pakvasa, S. Exotic Higgs decays in the E6 inspired SUSY models. Phys. Lett. B 2014, 728, 210–215. [Google Scholar] [CrossRef]
- Nevzorov, R.; Thomas, A.W. E6 inspired composite Higgs model. Phys. Rev. D 2015, 92, 075007. [Google Scholar] [CrossRef]
- Athron, P.; Harries, D.; Nevzorov, R.; Williams, A.G. E6 Inspired SUSY Benchmarks, Dark Matter Relic Density and a 125 GeV Higgs. Phys. Lett. B 2016, 760, 19–25. [Google Scholar] [CrossRef]
- Ishihara, T.; Maekawa, N.; Takegawa, M.; Yamanaka, M. Leptogenesis in E6×U(1)A SUSY GUT model. JHEP 2016, 2, 108. [Google Scholar] [CrossRef]
- Berezhiani, Z.G.; Dvali, G.R. Possible solution of the hierarchy problem in supersymmetrical grand unification theories. Bull. Lebedev Phys. Inst. 1989, 5, 55–59. [Google Scholar]
- Berezhiani, Z.; Csaki, C.; Randall, L. Could the supersymmetric Higgs particles naturally be pseudoGoldstone bosons? Nucl. Phys. B 1995, 444, 61–91. [Google Scholar] [CrossRef]
- Dvali, G.R.; Pokorski, S. The Role of the anomalous U(1)-A for the solution of the doublet - triplet splitting problem. Phys. Rev. Lett. 1997, 78, 807–810. [Google Scholar] [CrossRef]
- Barbieri, R.; Dvali, G.R.; Strumia, A.; Berezhiani, Z.; Hall, L.J. Flavor in supersymmetric grand unification: A Democratic approach. Nucl. Phys. B 1994, 432, 49–67. [Google Scholar] [CrossRef]
- Ordell, A.; Pasechnik, R.; Serôdio, H.; Nottensteiner, F. Classification of anomaly-free 2HDMs with a gauged U(1)’ symmetry. Phys. Rev. D 2019, 100, 115038. [Google Scholar] [CrossRef]
- Cárcamo Hernández, A.E.; Kovalenko, S.; Pasechnik, R.; Schmidt, I. Sequentially loop-generated quark and lepton mass hierarchies in an extended Inert Higgs Doublet model. JHEP 2019, 6, 056. [Google Scholar] [CrossRef]
- Vien, V.V.; Long, H.N.; Cárcamo Hernández, A.E. Fermion Mass and Mixing in a Low-Scale Seesaw Model based on the S4 Flavor Symmetry. Prog. Theor. Exp. Phys. 2019, 11, 113. [Google Scholar] [CrossRef]
- Cárcamo Hernández, A.E.; Hidalgo Velásquez, Y.; Pérez-Julve, N.A. A 3-3-1 model with low scale seesaw mechanisms. Eur. Phys. J. C 2019, 79, 828. [Google Scholar] [CrossRef]
- Cárcamo Hernández, A.E.; Long, H.N.; Vien, V.V. The first Δ(27) flavor 3-3-1 model with low scale seesaw mechanism. Eur. Phys. J. C 2018, 78, 804. [Google Scholar] [CrossRef]
- Björkeroth, F.; de Medeiros Varzielas, I.; López-Ibáñez, M.L.; Melis, A.; Vives, O. Leptogenesis in Δ(27) with a Universal Texture Zero. JHEP 2019, 09, 050. [Google Scholar] [CrossRef]
- Ding, G.J.; King, S.F.; Liu, X.G.; Lu, J.N. Modular S4 and A4 Symmetries and Their Fixed Points: New Predictive Examples of Lepton Mixing. JHEP 2019, 12, 030. [Google Scholar] [CrossRef]
- Berezhiani, Z.G.; Chkareuli, J.L. Quark-leptonic families in a model with su(5) × su(3) symmetry. Sov. J. Nucl. Phys. 1983, 37, 618–626. (In Russian) [Google Scholar]
- Berezhiani, Z.G. Horizontal Symmetry and Quark-Lepton Mass Spectrum: The SU(5) × SU(3)-h Model. Phys. Lett. B 1985, 150, 177–181. [Google Scholar] [CrossRef]
- Berezhiani, Z.G.; Khlopov, M.Y. The Theory of broken gauge symmetry of families. Sov. J. Nucl. Phys. 1990, 51, 739–746. (In Russian) [Google Scholar]
- Berezhiani, Z. Unified picture of the particle and sparticle masses in SUSY GUT. Phys. Lett. B 1998, 417, 287–296. [Google Scholar] [CrossRef]
- Ross, G.G.; Vives, O. Yukawa structure, flavor and CP violation in supergravity. Phys. Rev. D 2003, 67, 095013. [Google Scholar] [CrossRef]
- Ross, G.G.; Velasco-Sevilla, L.; Vives, O. Spontaneous CP violation and nonAbelian family symmetry in SUSY. Nucl. Phys. B 2004, 692, 50–82. [Google Scholar] [CrossRef]
- Camargo-Molina, J.E.; Morais, A.P.; Ordell, A.; Pasechnik, R.; Sampaio, M.O.; Wessén, J. Reviving trinification models through an E6 -extended supersymmetric GUT. Phys. Rev. D 2017, 95, 075031. [Google Scholar] [CrossRef]
- Camargo-Molina, J.E.; Morais, A.P.; Ordell, A.; Pasechnik, R.; Wessén, J. Scale hierarchies, symmetry breaking and particle spectra in SU(3)-family extended SUSY trinification. Phys. Rev. D 2019, 99, 035041. [Google Scholar] [CrossRef]
- Witten, E. Dynamical Breaking of Supersymmetry. Nucl. Phys. B 1981, 188, 513. [Google Scholar] [CrossRef]
- Slansky, R. Group Theory for Unified Model Building. Phys. Rep. 1981, 79, 1–128. [Google Scholar] [CrossRef]
- Kephart, T.W.; Vaughn, M.T. Tensor Methods for the Exceptional Group E6. Ann. Phys. 1983, 145, 162. [Google Scholar] [CrossRef]
- Deppisch, T. E6Tensors: A Mathematica Package for E6 Tensors. Comput. Phys. Commun. 2017, 213, 130–135. [Google Scholar] [CrossRef]
- Gursey, F. Symmetry Breaking Patterns in E6. In First Workshop on Grand Unification. Birkhäuser Boston: Boston, MA, USA, 1980; p. 0039. [Google Scholar]
- Chakrabortty, J.; Raychaudhuri, A. A Note on dimension-5 operators in GUTs and their impact. Phys. Lett. B 2009, 673, 57–62. [Google Scholar] [CrossRef]
- Morais, A.P.; Pasechnik, R.; Porod, W. Prospects for new physics from gauge left-right-colour-family grand unification hypothesis. Eur. Phys. J. C 2020, 80, 1162. [Google Scholar] [CrossRef]
- Glashow, S. Fifth Workshop on Grand Unification; Kang, K., Fried, H., Frampton, F., Eds.; World Scientific: Singapore, 1984. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).