Abstract
Warm dark matter particles with masses in the keV range have been linked with the large group representations in gauge theories through a high number of species at decoupling. In this paper, we address WDM fermionic degrees of freedom from such representations. Bridging higher-dimensional particle physics theories with cosmology studies and astrophysical observations, our approach is two-folded, i.e., it includes realistic models from higher-dimensional representations and constraints from simulations tested against observations. Starting with superalgebras in exceptional periodicity theories, we discuss several symmetry reductions and we consider several representations that accommodate a high number of degrees of freedom. We isolate a model that naturally accommodates both the standard model representation and the fermionic dark matter in agreement with both large and small-scale constraints. This model considers an intersection of branes in D = 27 + 3 in a manner that provides the degrees of freedom for the standard model on one hand and 2048 fermionic degrees of freedom for dark matter, corresponding to a ∼2 keV particle mass, on the other. In this context, we discuss the theoretical implications and the observable predictions.
1. Introduction
In the past decade, having been thoroughly tested against the data from observations, the cold dark matter (CDM) model has encountered difficulties in explaining these data and has proved to be inconsistent with the observations under several aspects. Besides the two initial concerns—the large cores in galaxies and the small number of satellites—that may or may not be reconciled by introducing finely tuned baryonic processes in the simulations, there are several other points of concern at both small and large scales, e.g., the fact that the population of dwarf galaxies in voids is in contradiction with the predictions from CDM simulations [1,2,3]; the failure to replicate, in CDM simulations, the high number of pure bulgeless galaxies observed and the low number of galaxy mergers [4,5]; the formation and growth of supermassive black holes in agreement with observed distributions [6]; and the recent detection of high-redshift quasars [7].
WDM scenarios with particles in the keV range are gaining ground in explaining some of these discrepancies and many studies show the advantages that a keV dark matter model presents in explaining the observations at both small and large scales [8,9,10,11,12,13,14,15,16,17,18]. A keV WDM particle, for example, can explain the existence of cores in galaxies of varied masses, from dwarf galaxies to spirals, when considering the quantum Fermi pressure of the particles [12,13,14]. Moreover, while, for spiral galaxies, in an attempt to reconcile the CDM model with observations, the presence of the cores has been attributed to the stars and gas concentration at the center of galaxies—tentatively described by adding baryonic components in the simulations, with different studies showing different results, sometimes contradictory (e.g., [19,20])—for dwarf galaxies, which are dark matter dominated, this cannot be the case.
Furthermore, in WDM models with keV particles, stars can form early on inside the filaments, as shown in unparalleled high-resolution simulations [21] and could provide the seeds for the early formation of black holes, predictions that could be tested with more such high-resolution simulation studies.
Given the challenges that the CDM is facing and in the absence of a successful experimental detection of a CDM particle candidate, studies of warm dark matter models are highly justified both from the theoretical and numerical perspectives.
From the point of view of particle physics, the theoretical models that predict candidates for the generically called ‘warm dark matter’ are more varied than those for CDM, with different production mechanisms that translate into several intrinsic properties of the dark matter particles, reviewed in [22]. The consensus to what these particles have in common is that they possess an astronomically significant free streaming length. The free streaming length implies a cutoff in the power spectrum and a non-zero velocity dispersion. The value for these ‘quantities’ is dictated by the particular model and production mechanism and it gives a certain mass for the considered particle. In [16,17], several WDM particle models and their assumptions have been re-examined, showing how strongly model-dependent their properties are and, consequently, how weak the constraints on the particle mass from the over-simplified simulations are.
Therefore, the catch comes from the freedom WDM provides in terms of the particle candidates that are theorized in this category, mainly in the mass-velocity correspondence. Since, in reality, we can only constrain, with observations and simulations, the velocity dispersion of the particle and not the mass, other particle physics constraints have to be considered in the absence of detection experimental results.
A particular model that has been extensively used in warm dark matter simulations is the one described in [23], which implies a much higher number of degrees of freedom at decoupling than for the standard model and its supersymmetric extensions [24]. As hinted in [23], this would be possible in larger gauge groups, especially those with extra dimensions.
Several studies have looked at larger gauge group representations in relation to dark matter [25,26,27,28,29], but none that would explain the high number of degrees of freedom. In the context of the so-called exceptional super Yang Mills theories, large group representations that could allow this high number to be reached have been explored [30,31]. In this paper, we revise these results and attempt to develop and isolate models that would produce the required high number of degrees of freedom at decoupling, while preserving the standard model representations. We found that these representations favor 2048 fermionic degrees of freedom at decoupling, which corresponds to a ∼2 keV particle, which happens to be in agreement with observations.
In Section 2, we review the warm dark matter model requirement of such high degrees of freedom. In Section 3, we introduce the algebras with higher dimensional spinors and discuss several reductions in the context of exceptional periodicity. In Section 4, we discuss the WDM and SM disentanglement through braneworld intersections, isolating a mechanism through which SM degrees of freedom are isolated from WDM ones and WDM becomes neutral under the photon gauging the electromagnetic . Our conclusions are summarized in Section 5.
2. keV WDM from Higher-Dimensional Gauge Theories
Within the WDM scenario, several models with various particle production mechanisms and various properties have been previously studied. We can distinguish between thermally produced neutrinos and those coming from a non-resonant production mechanism [32,33,34,35,36] for particles in the eV–hundreds keV range that do not decay. More complex models that consider decay [37] and re-thermalization [38] have also been considered as well as quantum semi-degenerate particles with a non-negligible chemical potential [16].
However, in numerical simulations, the varied models are oversimplified, often using a ‘cutoff’ in the power spectrum as the only parameter that distinguishes WDM from CDM particles, as reviewed in [39]. The model most favored by simulation studies for a thermal relic WDM particle, which provides this ‘cutoff’ mass-velocity, is the one described in [23]. Below, we discuss this model, its assumptions and its implications.
WDM Degrees of Freedom
The particle assumed in [23] is a thermal relic particle that decouples while still relativistic, but, by equality, is nonrelativistic. The streaming speed at equality , where the effective temperature varies inversely with the scale factor. In order to have a streaming speed that is low enough to keep up with the CDM success at large scales—meaning, the formation of structures as an early enough redshift and within the observable mass scales for halos—the decrease in the effective temperature is suggested [23]. If the particle decouples with thermal abundance, must be held fixed. Therefore, to obtain a reasonable reduction in velocity, one needs to decrease the temperature and increase the mass. One way the reduction in temperature can be realized is through increasing the number of the degrees of freedom at decoupling. The example given in [23] assumes a reduction in of ∼4 and an increase in mass of , thus corresponding to 688 degrees of freedom. However, for 1 keV, the number of degrees of freedom is higher and this is usually what is indirectly used in simulations when the velocity of the WDM particle is introduced, as shown in [16,17].
Below, we remind the derivation in [23] and the discussion in [16]. As recalled in [23] (see [23] Appendix A for a detailed derivation and [16] for a detailed assessment of that derivation), for a thermal relict particle X that decouples when relativistic, the abundance relative to photons is
where is the number of relativistic species present at decoupling—degrees of freedom—and is the number of spin states of the particle. Assuming that the distribution function scales as the non-thermal distribution , for a redshift z, the velocity (in Equation (A3) [23]) is given,
The relation between the cosmological parameters and the particle’s density is
for the Hubble constant .
Therefore, for an keV particle, considering as in [23], we have the following formula for the velocity:
that gives for a 1 keV particle.
This large value for the number of degrees of freedom at decoupling is much higher than the value for the standard model, ∼107, and even the supersymmetric extension, ∼229 [24]. Other studies arbitrarily choose, in their analyses, a much more conservative value for the number of degrees of freedom of the WDM particle candidates, i.e., ∼150 for a massive neutrino [24]; ∼100 for right-handed neutrinos that would decouple before the electro-weak phase transition [40]. The number of degrees of freedom scales with the mass of the particle therefore a higher mass would correspond to a higher number of degrees of freedom (and a stronger decrease in temperature). Since this value is correlated to the mass–velocity correspondence that dictates the behavior of the WDM particle and its influence on the structure formation and evolution, we study the theoretical models where such a large number of degrees of freedom can be achieved.
While the authors in [23] do hint at larger group representations with extra dimensions in relation to the high number, they also mention that entropy-producing processes that take place after the decoupling of the particle can mimic an increase in . Indeed, trying to avoid such large group representations, [22,41,42,43] discuss the entropy generation by the out-of-equilibrium decay of heavier particles, which would allow the number of degrees of freedom of the keV particle to be similar to that used for active neutrinos [41]. Self-interactions as a possible way to reduce the number densities by self-annihilations are also discussed in [44]. However, in this paper, we look at the large gauge group representations that would naturally produce this high number of degrees of freedom, starting with the symmetry reductions in algebras with higher-dimensional spinors in exceptional periodicity theories.
3. Algebras with Higher-Dimensional Spinors
A class of algebras involving higher-dimensional spinors is studied in the so-called exceptional super Yang–Mills (ESYM) theories, firstly discussed in [30,31], in which higher-dimensional theories [45,46,47,48,49,50] beyond string/M-theory [51,52] have been considered and extended, also in relation to exceptional periodicity (EP) algebras [53,54,55]. In this section, we provide various branchings of these algebras with a number of spinor degrees of freedom of . Here, we discuss the symmetry reductions along the worldvolume (WV) of p-branes, which centrally extend the underlying chiral superalgebra and the reductions that follow the so-called Magic Star structure—named so in [53] after the star polygon geometric shape—of the corresponding EP algebra.
3.1. Superalgebra in 17 + 1 and 9-Brane WV Reduction
One of the simplest examples is based on the superalgebra obtained by setting in Equation (3.5) of [30], namely, the chiral superalgebra of ESYM in space–time dimensions, whose central extensions are given by the r.h.s. of the anticommutator
namely, by a 1-brane (fundamental string), an electric 5-brane and its dual, a magnetic 9-brane. The corresponding EP 3-graded algebra, whose semisimple, 0-graded part yields the homogeneous Lorentz algebra of space–time, is obtained by setting in (II.14) of [55], namely,
where and , respectively, denote the Majorana–Weyl (MW) semispinor in dimensions and its conjugate (note that the EP level n is understood with in [30], namely, the first non-trivial level of EP is given by therein). It should be remarked that, when the spinors are interpreted as Abelian translational generators, the non-negatively graded part of the EP algebra (6) yields the Lie algebra of the global isometry group of the homogeneous non-symmetric real special manifold in the classification cited in [56,57].
Symmetry reduction along the WV of the highest-dimensional central extension occurring in the r.h.s. of (5), namely, along the dimensional WV of the 9-brane, yields the breaking
thus yielding an inner/fiber symmetry, whose only peculiar polarization is shown in the branchings (7)–(9).
Let us recall that, in the models for family unification beyond the SM, such as the ones discussed in [58,59], one posits a further breaking of the inner symmetry,
where is used for family symmetry [58].
3.2. Superalgebra in 20 + 4 and 12-Brane WV Reduction
Another example is provided by the quasi-conformal level of the above symmetry, namely, by the the superalgebra obtained by setting in Equation (3.8) of [30], the chiral superalgebra of ESYM in space–time dimensions, whose central extensions are given by the r.h.s. of the anticommutator
namely, by a 0-brane, a 4-brane, an electric 8-brane and its dual, a magnetic 12-brane. The corresponding 5-graded EP algebra is obtained by setting in (II.16) of [55].
where and denote the MW semispinors in and dimensions, respectively. Again, when the spinors and vectors are interpreted as Abelian translational generators, the non-negatively graded part of the EP algebra (14) corresponds to the Lie algebra of the global isometry group of the homogeneous non-symmetric quaternionic Kähler manifold given by the image of the aforementioned space under the composite c·R-map [56,57].
The symmetry reduction along the WV of the highest-dimensional central extension occurring in the r.h.s. of (12), namely the dimensional WV of the 12-brane, yields the breaking
thus again yielding an inner/fiber symmetry, where and stand for the MW semispinor in dimensions and its conjugate, respectively.
3.2.1. Further Reduction in Inner/Fiber Symmetry
Through a disentangling mechanism discussed in Section 4, one copy of the encodes SM matter and the rest provides thousands of fermionic degrees of freedom.
A possible way to do this is to further break the inner/fiber symmetry down to and/or :
or
While this isolates a as a singlet of and has additional fermions, breaking further to identify the standard model and electromagnetism would lead to the additional fermions to have the same charge, therefore not be dark matter. Nevertheless, the utilization of the spinor in is later used to identify a candidate for WDM.
3.2.2. Magic Star Reduction in D = 20 + 4
Another possible symmetry reduction on the same ESYM, which is useful in order to discuss family unification beyond the SM, concerns the exploitation of the so-called Magic Star [53] decomposition of the EP algebra (13)–(14), with the EP algebra (6) posited in the center of the star-like arrangement of (generalized) roots,
as depicted in Figure 1, where denotes the Hermitian part of the special Vinberg cubic T-algebra [60,61] with elements realized as formal Hermitian matrices, whose manifestly -covariant structure reads
where and , respectively, denote the MW semispinor in 16 dimensions and its conjugate (the case and of Equation (III.1) of [55]). In addition, it is here worth recalling that the Hermitian matrix-like structure (22) corresponds to the manifestly -covariant Peirce decomposition
where the -singlet corresponds to the -singlet in (22).
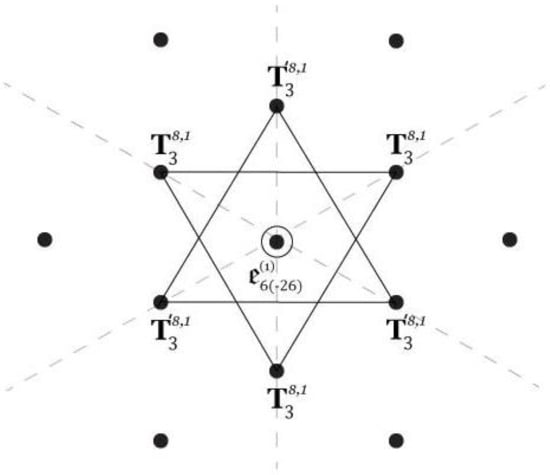
Figure 1.
A Magic Star-type projection of that contains in the center, named after the star polygon geometric shape.
4. Symmetry Reduction to the Standard Model and Warm Dark Matter Disentanglement
By studying heterotic string theory on the boundary of an 11-dimensional supergravity bulk, two gauge theories on the endpoints of an orbifold from have been found [62,63]. The anomaly cancellation requires a twelve-form, which is factorized into a 4-form and 8-form, yet these are invoked in 10- and 11-dimensional theories, implying a complete description from larger dimensions. Heterotic string theory must have an origin from or higher. While bosonic string theory exists in , heterotic string theory places 16 dimensions on an even, self-dual lattice and includes fermions. bosonic M-theory and target space–time for 2D gravity has been introduced [64,65]. How unifies the superalgebras of type I, type IIA, type IIB and heterotic theories has been articulated in [46,47,48]. The superalgebras of M-theory and F-theory can arise from nested braneworlds in , as the exceptional Yang–Mills superalgebra contains an 11-brane worldvolume with spinors [31]. Dimensional reduction also finds a 10-brane worldvolume with a 16D transverse space and includes spinors.
The Horava–Witten theory [62,63] shows how M-theory on , when compactified on , leads to type IIA and heterotic string theories, which are T-dual to type I and superstring theories. This implies that the type I superstring on naturally has a vacuum. Dark matter has been discussed in relation to nonsupersymmetric string theory [25,26,29]. While heterotic string theory leading to the supersymmetric standard model allows for supersymmetric light dark matter candidates such as neutralinos [66], light supersymmetric partners of the standard model below 1.5 TeV have not been observed [67]. The exceptional Yang–Mills superalgebras facilitate an understanding of various worldvolume constructions for M-theory and beyond, which allows for supersymmetric forms of matter beyond the standard model that are different from the superpartners or the nonsupersymmetric dark matter models..
Since the membranes discussed in this section are more complicated than those contained within M-theory itself, a brief pedagogical introduction to membranes and their relationship to gauge theory is warranted. To start, let us consider the worldline formulation of a free point particle described by the following action:
Varying this action leads to the standard geodesic equation in general relativity. Extended objects in supergravity lead to “p-brane” for arbitrary-dimensional membranes, which spans a -dimensional worldvolume and generalizes the worldline formulation above [68]. While strings are 1-branes on a worldsheet and M-theory has a 2-brane worldvolume, 3-brane worldvolumes were found in type IIB supergravity [69]. F-theory admits 3-brane phenomenology that can include the standard model with gravity [70]. Furthermore, 3-branes are intimately related to , whose isometry group is the conformal group . Additionally, supports a 4D CFT with a 3-brane on the boundary, such that can be obtained within the Randall–Sundrum model [71,72].
Before the full significance of the Yang–Mills theory for the standard model was established, the nonlinear sigma model was introduced for pions, which is a nonrenormalizable theory similar to general relativity. General relativity is equivalent to a nonlinear sigma model Lagrangian [73], which is similarly used for the bosonic sector of p-branes:
where is a -form potential sourced by the p-brane and is a scalar field with an index with respect to the target space, such as in M-theory. The bosonic p-brane Lagrangian in the static gauge leads to a Born–Infeld action,
where is the brane tension. The Born–Infeld action was introduced as an electrodynamical theory; it is the 1-loop renormalization of QED. The historical developments of transitioning from the non-renormalizable nonlinear sigma model to the renormalizable Yang–Mills theory suggest that the Yang–Mills gauge gravity theories, such as the MacDowell–Mansouri theory, will remain important for the unification of the standard model and gravity [74]. As braneworlds are intimately related to the study of gravity and beyond-the-standard-model physics is necessary for dark matter, we propose that braneworld spinors allow us to consider new dark matter candidates.
We briefly review the representation theory of the standard model as well as the most common high-energy GUT models, recalling that . allows us to consider three charts of , such that contains three charts of for a combination of GUT and conformal symmetries. The (1,0) chiral super-Poincaré algebra also exists and contains a spinor. When breaking to , the three conformal charts span (associated to a conformal braneworld symmetry), such that three distinct representations of are found, each leading to the standard model fermion representations with respect to ,
Once the bosons are unified into a single gauge group, such as or , the vector bosons are described by the Yang–Mills action.
At high energies, an conformal gauge group, axial and GUT leads to , which is also a maximal subalgebra of . An gauge theory does not need to be considered, but rather gauge theories from subalgebras. For instance, GUT contains a complex and in combination with the adjoint representation [75].
Combined with another , the total of all of these states leads to by combining the adjoint bosonic sector with the complex fermionic sector.
As shown above, the representations found within GUT stem from a single adjoint representation of ; similarly, . Recently, using to obtain the standard model spectrum has been explored [76] without using GUT. for three generations of matter has also been explored [77], although conformal spacetime symmetry was not considered. This non-supersymmetric GUT model and the supersymmetric heterotic string theory use this to make contact with three generations of matter. Since two of the authors recently found EP algebras that generalize [53], we expand the exploration of the representations associated with these algebras. Dark matter is an immediate natural candidate, as the EP algebras contain spinors for matter beyond the standard model. Superalgebras are explored to motivate braneworld intersections that naturally lead to the standard model spectrum as described above, along with additional dark matter candidates.
4.1. Braneworld Spinors
M-theory with a spinor [78] and many p-branes provides an origin for heterotic string theory and M-theory. A 2-brane, 5-brane, 10-brane, 13-brane, 18-brane and 21-brane is found from considering a superalgebra with supercharges. M-theory has a 2-brane and 5-brane, while a 21-brane was anticipated in bosonic M-theory [64]. In , a 10-brane and 18-brane allow for a (10,1) worldvolume theory and a (18,1) worldvolume theory. Breaking to various subgroups makes contact with worldvolume and transverse symmetries of interest.
in which the breaking of the spinor is also provided. The 2-brane relates to the Horowitz–Susskind [64] CFT with global symmetry and holography. The spinors in the 10-brane worldvolume only see the spinor of M-theory from components. The theory contains a spinor of a transverse , just as the superstring has an spinor of . This can be compared to the Horava–Witten theory [62,63] with , by orbifolding a spatial direction of the 10-brane. The 18-brane gives a “M-theory" that reduces to a string theory as studied in relation to Kac–Moody algebras [79]. Quasiconformal extensions of the 2-brane, 10-brane, 18-brane and global space–time motivate , , and symmetries and their EP extensions.
is the conformal symmetry of , whose exceptional Yang–Mills superalgebra admits a Hodge duality between a 3-brane and 7-brane when the 3-brane is treated as a worldvolume for space–time, generalizing the 2-brane and 5-brane. The isometry group of the 3-brane (3,3) worldvolume has conformal symmetry, which describes three generations of matter [80,81]. A transverse is used for visible matter within , where fermionic degrees of freedom can be encoded by a spinor of , leading to . Going to or allows us to consider transverse or for possible dark matter.
entails the following braneworld twistors for three generations:
Taking the 11-brane and 19-brane in , they are forced to intersect spatially via a 3-brane. The 11-brane isolates a worldvolume with a 3-brane and dual 7-brane, while the 19-brane isolates a worldvolume with a 3-brane and dual 15-brane. Our proposal is that the worldvolume theory encodes baryonic matter, while the theory encodes a dark matter sector.
EP algebras provide new dark matter models via intersected or nested higher membrane worldvolumes. In order to combine dark matter and the standard model within the same space–time worldvolume, with is of interest, as it contains in addition to various vector and spinor representations. The group combines the 4D conformal group with GUT. The compact real form of also contains , which has been studied in relation to dark matter in a different context [29].
4.2. Braneworld Intersections for Warm Dark Matter beyond the Standard Model
One candidate for describing the standard model from string theory is the utilization of D3 and D7 branes from type IIB supergravity or F-theory [82]. The central extension of minimal chiral superalgebra naturally contains a 3-brane and dual 7-brane, as well as the type IIB superalgebra [47,48]. The role of with in the context of background-independent two-time M-theory and heterotic string theory with or 1 has been mentioned in [83]. A single generation of fermions can be found via of as off-shell degrees of freedom [84]. While breaking is tempting, this makes it difficult to identify the three generations of matter with less than spinors without another consideration. Some of the authors have explored how (maximal and non-symmetric subgroup of ) naturally leads to three conformal charts, in a manner similar to how quasiconformal groups with four times are the conformal group for three generations of matter [81]. The corresponding (1,0) chiral super-Poincaré algebra in entails three generations of the standard model within of instead of 192 off-shell degrees of freedom.
Throughout this section, it is assumed that three generations of the standard model stem from a 3-brane and dual 7-brane, immersed in an 11-brane worldvolume. To go beyond the standard model and include dark matter candidates, a 15-brane is also considered. The 3-brane and 15-brane exist inside a 19-brane worldvolume. The possible p-branes in are shown in Figure 2. In particular, visible matter and dark matter are isolated on the 11-brane and 19-brane, such that they intersect on the -brane worldvolume for space–time. In this manner, the braneworld intersection identifies visible and dark matter with different forces, yet they exist within the same space–time. The theory may be isolated to for dark matter, yet reduced to for visible matter.
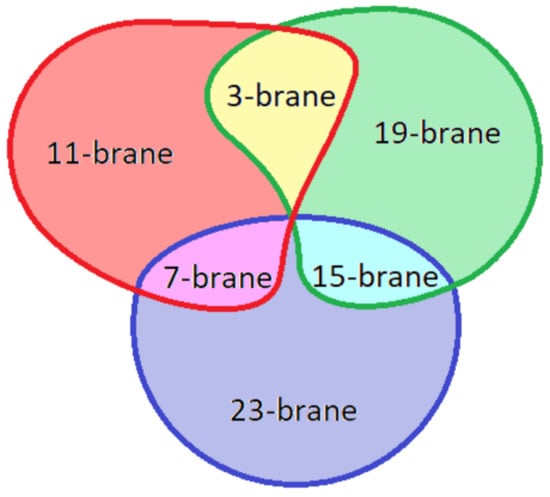
Figure 2.
The intersections of branes in . For instance, the 3-brane is dual to the 23-brane, which contains the 7-brane and 15-brane.
Here, a model via is pursued. The factor arises from the transverse symmetry of an 11-brane worldvolume in . Then, we study a braneworld intersection of the 11-brane and 19-brane in .
By restricting to the 11-brane worldvolume, the 3-brane is dual to a 7-brane. Isolating the conformal group of the 11-brane worldvolume within encodes a transverse ,
Once the 3-brane worldvolume is isolated within the 11-brane worldvolume, is found as being transverse to as the conformal worldvolume symmetry. The 3-brane within the 11-brane within has the effect of making the transverse to the 11-brane hidden with respect to the matter isolated to the 3-brane and dual 7-brane within .
On the other hand, by restricting to the 19-brane worldvolume, the 3-brane is dual to a 15-brane. Isolating the conformal group of the 19-brane worldvolume within leads to a transverse .
Once the 3-brane worldvolume is isolated within the 19-brane worldvolume, is transverse to . The 3-brane within the 19-brane in a bulk leaves the transverse to the 19-brane hidden with respect to matter isolated to the 3-brane and its dual 15-brane within .
While isolating the 3-brane in the 19-brane versus 11-brane symmetries within leads to different representations, not all representations of the fermions are identifiable. For instance, the 11-brane cannot access a 15-brane in its transverse space, such that the representations are unobservable, while the 19-brane cannot access a 7-brane in its transverse space, such that the representations are unobservable. We assume that the transverse to the 19-brane contains the electromagnetic of the standard model [85]. With the 11-brane and 19-brane intersection, the 3-brane effectively sees the following fermionic representations with respect to :
where the singlets effectively arise at low energies, since a 3-brane in an 11-brane cannot probe a transverse 15-brane immersed in , for instance. As such, since the 3-brane is the intersection of two worldvolumes, 128 visible and 2048 dark fermions are found effectively at low energy from an intersecting braneworld model that contains worldvolumes that support the commonly studied supergravities and string theories. The 2048 dark fermions come from , which cannot be probed by the containing the electromagnetic .
This number of degrees of freedom corresponds to
a ∼2 keV particle that is in agreement with observations at both large scales—galaxy formation and distribution—and small scales—cores [12,13].
5. Conclusions
In this paper, we discuss possible large gauge group representations that allow us to obtain a high number of fermionic degrees of freedom using superalgebras in the context of exceptional periodicity models and M-theory braneworlds. We find that an 11-brane and 19-brane in intersect by a 3-brane for space–time such that respective dual 7-branes and 15-branes provide both the degrees of freedom for the standard model and the ones for fermionic WDM, while preserving the ‘separation’ and the lack of interaction between SM and WDM particles. Since combines conformal symmetry with , the contains of the strong and electromagnetic forces, such that the 19-brane does not interact with light; therefore, it is dark.
In this realization, the intersecting braneworlds span , but individually span and . For , the 3-brane is dual to a 7-brane for light matter in 128 off-shell degrees of freedom. For , the 3-brane is dual to a 15-brane for dark matter. We find 2048 fermionic degrees of freedom in this representation, which correspond to ∼2 keV in the model cited in [23]. This particle spectrum is in agreement with constraints from structure formation. Moreover, a 2 keV particle influences the formation of cores in galaxies [12,13]. Several other representations have been discussed and analyzed. However, this representation has the advantage of naturally allowing for a WDM candidate that is interesting from the point of view of astrophysical constraints and also implying worldvolumes that support supergravities and string theories. The evolution of a particle produced in this manner can be discussed further. While beyond the scope of this paper, further investigations of what happens to these species once the particle decouples would provide additional constraints.
Author Contributions
S.P. and M.R. initiated this research; S.P. contributed the WDM insights and discussion, M.R. the superalgebras and brane reduction; A.M. contributed to the superalgebras and symmetry breaking; D.C. contributed the braneworld intersection and matter-multiplet phenomenology. All authors contributed to the writing of the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research study received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
S.P. would like to thank N.G. Sanchez for the invitation to submit to this special issue and for useful suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | directory of open access journals |
| WDM | warm dark matter |
| CDM | cold dark matter |
| SM | standard model |
| EP | exceptional periodicity |
| ESYM | exceptional super Yang–Mills |
| WV | worldvolume |
References
- Tikhonov, A.V.; Gottlöber, S.; Yepes, G.; Hoffman, Y. The sizes of minivoids in the local Universe: An argument in favour of a warm dark matter model? Mon. Not. RAS 2009, 399, 1611. [Google Scholar] [CrossRef]
- Zavala, J.; Jing, Y.P.; Faltenbacher, A.; Yepes, G.; Hoffman, Y.; Gottlöber, S.; Catinella, B. The velocity function in the local environment from LCDM and LWDM constrained simulations. Astrophys. J. 2009, 700, 1779. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Nusser, A. Nearby galaxies as pointers to a better theory of cosmic evolution. Nature 2010, 465, 565–569. [Google Scholar] [CrossRef]
- Kormendy, J.; Drory, N.; Bender, R.; Cornell, M.E. Bulgeless Giant Galaxies Challenge Our Picture of Galaxy Formation by Hierarchical Clustering. Astrophys. J. 2010, 723, 54. [Google Scholar] [CrossRef]
- Kormendy, J. Elliptical Galaxies and Bulges of Disc Galaxies: Summary of Progress and Outstanding Issues. In Galactic Bulges; Springer: Berlin/Heidelberg, Germany, 2016; pp. 431–477. [Google Scholar]
- Caramete, L.I.; Biermann, P.L. The catalog of nearby black hole candidates. arxiv 2011, arXiv:1107.2244. [Google Scholar]
- Wang, F.; Yang, J.; Fan, X.; Hennawi, J.F.; Barth, A.J.; Banados, E.; Bian, F.; Boutsia, K.; Connor, T.; Davies, F.B.; et al. A Luminous Quasar at Redshift 7.642. Astrophys. J. Lett. 2021, 907, L1. [Google Scholar] [CrossRef]
- de Vega, H.; Sanchez, N.G. Model independent analysis of dark matter points to a particle mass at the keV scale. Mon. Not. R. Astron. Soc. 2010, 404, 885. [Google Scholar] [CrossRef]
- de Vega, H.; Salucci, P.; Sanchez, N.G. The mass of the dark matter particle from theory and observations. New Astron. 2012, 17, 653. [Google Scholar] [CrossRef]
- de Vega, H.; Sanchez, N.G. Cosmological evolution of warm dark matter fluctuations. I. Efficient computational framework with Volterra integral equations. Phys. Rev. D 2012, 85, 043516. [Google Scholar] [CrossRef]
- de Vega, H.; Sanchez, N.G. Cosmological evolution of warm dark matter fluctuations. II. Solution from small to large scales and keV sterile neutrinos. Phys. Rev. D 2012, 85, 043517. [Google Scholar] [CrossRef]
- Destri, C.; de Vega, H.J.; Sanchez, N.G. Fermionic warm dark matter produces galaxy cores in the observed scales because of quantum mechanics. New Astron. 2013, 22, 39. [Google Scholar] [CrossRef]
- Destri, C.; de Vega, H.J.; Sanchez, N.G. Quantum WDM fermions and gravitation determine the observed galaxy structures. Astropart. Phys. 2013, 46, 1. [Google Scholar] [CrossRef][Green Version]
- Destri, C.; de Vega, H.J.; Sanchez, N.G. Warm dark matter primordial spectra and the onset of structure formation at redshift z. Phys. Rev. D 2013, 88, 083512. [Google Scholar] [CrossRef]
- de Vega, H.; Salucci, P.; Sanchez, N.G. Observational rotation curves and density profiles versus the Thomas–Fermi galaxy structure theory. Mon. Not. R. Astron. Soc. 2014, 442, 2717. [Google Scholar] [CrossRef]
- Paduroiu, S.; Revaz, Y.; Pfenniger, D. Structure formation in warm dark matter cosmologies: Top-Bottom Upside-Down. arXiv 2015, arXiv:1506.03789. [Google Scholar]
- Paduroiu, S. Structure Formation in Warm Dark Matter Cosmologies. Ph.D. Thesis, University of Geneva, Geneva, Switzerland, 2015. [Google Scholar]
- Sanchez, N.; Paduroiu, S.; Biermann, P.L. Warm Dark Matter Astrophysics in Agreement with Observations and keV Sterile Neutrinos: Synthesis of Highlights and Conclusions of the Chalonge -de Vega Meudon Workshop 2016 In Memoriam Héctor J. de Vega. 2016. Available online: https://hal.archives-ouvertes.fr/hal-01773092 (accessed on 16 October 2021).
- Macciò, A.V.; Stinson, G.; Brook, C.B.; Wadsley, J.; Couchman, H.M.P.; Shen, S.; Gibson, B.K.; Quinn, T. Halo Expansion in Cosmological Hydro Simulations: Toward a Baryonic Solution of the Cusp/Core Problem in Massive Spirals. Astrophys. J. 2012, 744, L9. [Google Scholar] [CrossRef]
- Marinacci, F.; Pakmor, R.; Springel, V. The formation of disc galaxies in high-resolution moving-mesh cosmological simulations. Mon. Not. RAS 2014, 437, 1750. [Google Scholar] [CrossRef]
- Gao, L.; Theuns, T. Lighting the Universe with filaments. Science 2007, 317, 1527. [Google Scholar] [CrossRef] [PubMed]
- Boyarsky, A.; Drewes, M.; Lasserre, T.; Mertens, S.; Ruchayskiy, O. Sterile Neutrino Dark Matter. Prog. Part. Nucl. Phys. 2019, 104, 1–45. [Google Scholar] [CrossRef]
- Bode, P.; Ostriker, J.P.; Turok, N. Halo formation in warm dark matter models. Astrophys. J. 2001, 556, 93. [Google Scholar] [CrossRef]
- Pierpaoli, E.; Borgani, S.; Masiero, A.; Yamaguchi, M. The Formation of Cosmic Structures in a Light Gravitino Dominated Universe. Phys. Rev. D 1998, 57, 2089. [Google Scholar] [CrossRef]
- Alvarez-Gaumé, L.; Ginsparg, P.; Moore, G.; Vafa, C. An O(16) × O(16) heterotic string. Phys. Lett. B 1986, 171, 2. [Google Scholar] [CrossRef]
- Dixon, L.G.; Harvey, J.A. String theories in ten dimensions without supersymmetry. Nucl. Phys. B 1986, 274, 18. [Google Scholar] [CrossRef]
- Jedamzik, K.; Lemoine, M.; Moultaka, G. Gravitino dark matter in gauge mediated supersymmetry breaking. Phys. Rev. D 2006, 73, 1550. [Google Scholar] [CrossRef]
- Gross, C.; Lebedev, O.; Mambrini, Y. Non-Abelian gauge fields as dark matter. J. High Energy Phys. 2015, 8, 158. [Google Scholar] [CrossRef]
- McGuigan, M. Dark Horse, Dark Matter: Revisiting the SO(16)x SO(16)’ Nonsupersymmetric Model in the LHC and Dark Energy Era. arXiv 2019, arXiv:1907.01944. [Google Scholar]
- Rios, M.; Marrani, A.; Chester, D. The Geometry of Exceptional Super Yang-Mills Theories. Phys. Rev. D 2019, 99, 046004. [Google Scholar] [CrossRef]
- Rios, M.; Marrani, A.; Chester, D. Exceptional Super Yang-Mills in D = 27 + 3 and Worldvolume M-Theory. Phys. Lett. B 2020, 808, 135674. [Google Scholar] [CrossRef]
- Dodelson, S.; Widrow, L.M. Sterile neutrinos as dark matter. Phys. Rev. Lett. 1994, 72, 17–20. [Google Scholar] [CrossRef]
- Shi, X.; Fuller, G.M. New dark matter candidate: Nonthermal sterile neutrinos. Phys. Rev. Lett. 1999, 82, 2832. [Google Scholar] [CrossRef]
- Dolgov, A.D. Neutrinos in cosmology. Phys. Rep. 2002, 370, 333. [Google Scholar] [CrossRef]
- Asaka, T.; Shaposhnikov, M.; Kusenko, A. Opening a new window for warm dark matter. Phys. Lett. B 2006, 638, 401. [Google Scholar] [CrossRef]
- Boyarsky, A.; Lesgourgues, J.; Ruchayskiy, O.; Viel, M. Realistic sterile neutrino dark matter with keV mass does not contradict cosmological bounds. Phys. Rev. Lett. 2009, 102, 201304. [Google Scholar] [CrossRef] [PubMed]
- Fuller, G.M.; Kishimoto, C.T.; Kusenko, A. Heavy sterile neutrinos, entropy and relativistic energy production, and the relic neutrino background. arXiv 2011, arXiv:1110.6479. [Google Scholar]
- Lello, L.; Boyanovsky, D. Cosmological Implications of Light Sterile Neutrinos produced after the QCD Phase Transition. Phys. Rev. D 2015, 91, 063502. [Google Scholar] [CrossRef]
- Paduroiu, S. Warm Dark Matter in Numerical Simulations. 2021; submitted to Universe, MDPI. [Google Scholar]
- Colombi, S.; Dodelson, S.; Widrow, L.M. Large Scale Structure Tests of Warm Dark Matter. Astrophys. J. 1996, 458, 1. [Google Scholar] [CrossRef]
- Bezrukov, F.; Hettmansperger, H.; Lindner, M. keV sterile neutrino dark matter in gauge extensions of the standard model. Phys. Rev. D 2010, 81, 085032. [Google Scholar] [CrossRef]
- Nemevšek, M.; Senjanović, G.; Zhang, Y. Warm dark matter in low scale left-right theory. J. Cosmol. Astropart. Phys. 2012, 7, 6. [Google Scholar] [CrossRef]
- Patwardhan, A.V.; Fuller, G.M.; Kishimoto, C.T.; Kusenko, A. Diluted equilibrium sterile neutrino dark matter. Phys. Rev. D 2015, 92, 103509. [Google Scholar] [CrossRef]
- Herms, J.; Ibarra, A.; Toma, T. A new mechanism of sterile neutrino dark matter production. JCAP 2018, 6, 36. [Google Scholar] [CrossRef]
- Vafa, C. Evidence for F-Theory. Nucl. Phys. B 1996, 469, 403. [Google Scholar] [CrossRef]
- Bars, I. S-theory. Phys. Rev. D 1997, 55, 2373. [Google Scholar] [CrossRef]
- Bars, I. A case for 14 dimensions. Phys. Lett. B 1997, 403, 257. [Google Scholar] [CrossRef]
- Sezgin, E. Super Yang-Mills in (11,3) Dimensions. Phys. Lett. B 1997, 403, 265. [Google Scholar] [CrossRef][Green Version]
- Nishino, H. Supersymmetric Yang-Mills Theories in D ⩾ 12. Nucl. Phys. B 1998, 523, 450. [Google Scholar] [CrossRef]
- Rudychev, I.; Sezgin, E.; Sundell, P. Supersymmetry in dimensions beyond eleven. Nucl. Phys. Proc. Suppl. 1998, 68, 285. [Google Scholar] [CrossRef]
- Witten, E. String Theory Dynamics In Various Dimensions. Nucl. Phys. B 1995, 443, 85. [Google Scholar] [CrossRef]
- Banks, T.; Fischler, W.; Shenker, S.H.; Susskind, L. M Theory As A Matrix Model: A Conjecture. Phys. Rev. D 1995, 55, 5112. [Google Scholar] [CrossRef]
- Truini, P.; Rios, M.; Marrani, A. The Magic Star of Exceptional Periodicity. In Proceedings of the 4th Mile High Conference on Nonassociative Mathematics, Denver, CO, USA, 29 July–5 August 2017. [Google Scholar]
- Truini, P.; Marrani, A.; Rios, M. Magic Star and Exceptional Periodicity: An approach to Quantum Gravity. In Proceedings of the 32nd International Colloquium on Group Theoretical Methods in Physics, Prague, Czech Republic, 9–13 July 2018. [Google Scholar]
- Marrani, A.; Truini, P.; Rios, M. The Magic of Being Exceptional. In Proceedings of the 32nd International Colloquium on Group Theoretical Methods in Physics, Prague, Czech Republic, 9–13 July 2018. [Google Scholar]
- de Wit, B.; Van Proeyen, A. Special geometry, cubic polynomials and homogeneous quaternionic spaces. Commun. Math. Phys. 1992, 149, 307. [Google Scholar] [CrossRef]
- de Wit, B.; Vanderseypen, F.; Van Proeyen, A. Symmetry structure of special geometries. Nucl. Phys. B 1993, 400, 463. [Google Scholar] [CrossRef]
- Reig, M.; Valle, J.W.F.; Vaquera-Araujo, C.A.; Wilczek, F. A Model of Comprehensive Unification. Phys. Lett. B 2017, 774, 667. [Google Scholar] [CrossRef]
- BenTov, Y.; Zee, A. The Origin of Families and SO(18) Grand Unification. Phys. Rev. D 2016, 93, 065036. [Google Scholar] [CrossRef]
- Vinberg, E.B. The theory of Convex Homogeneous Cones. In Transaction of the Moscow Mathematical Society for the Year 1963; American Mathematical Society: Providence, RI, USA, 1963; pp. 340–403. [Google Scholar]
- Alekseevsky, D.V.; Marrani, A.; Spiro, A. Special Vinberg Cones and the Entropy of BPS Extremal Black Holes. arXiv 2021, arXiv:2107.06797. [Google Scholar] [CrossRef]
- Horava, P.; Witten, E. Heterotic and Type I String Dynamics from Eleven Dimensions. Nucl. Phys. B 1996, 460, 506. [Google Scholar] [CrossRef]
- Horava, P.; Witten, E. Eleven-Dimensional Supergravity on a Manifold with Boundary. Nucl. Phys. B 1996, 475, 94. [Google Scholar] [CrossRef]
- Horowitz, G.; Susskind, L. Bosonic M Theory. J. Math. Phys. 2001, 42, 3152–3160. [Google Scholar] [CrossRef]
- Watabiki, Y. The bosonic string and superstring models in 26 + 2 and 10 + 2 dimensional space–time, and the generalized Chern-Simons action. J. High Energy Phys. 2003, 5, 1. [Google Scholar] [CrossRef][Green Version]
- Jungman, G.; Kamionkowski, M.; Griest, K. Supersymmetric Dark Matter. Phys. Rept. 1996, 267, 195. [Google Scholar] [CrossRef]
- ATLAS Collaboration. Search for bottom-squark pair production with the ATLAS detector in final states containing Higgs bosons, bb-jets and missing transverse momentum. J. High Energy Phys. 2019, 12, 60. [Google Scholar]
- Duff, M.J.; Inami, T.; Pope, C.N.; Sezgin, E.; Stelle, K.S. Semiclassical quantization of the supermembrane. Nucl. Phys. B 1988, 297, 515. [Google Scholar] [CrossRef]
- Cederwall, M.; von Gussich, A.; Nilsson, B.E.W.; Westerberg, A. The Dirichlet super three-brane in ten-dimensional type IIB supergravity. Nucl. Phys. B 1997, 490, 163–178. [Google Scholar] [CrossRef]
- Heckman, J.J.; Vafa, C. From F-theory GUTs to the LHC. arXiv 2008, arXiv:hep-th/0809.3452. [Google Scholar]
- Randall, L.; Sundrum, R. A Large mass hierarchy from a small extra dimension. Phys. Rev. Lett. 1999, 83, 3370–3373. [Google Scholar] [CrossRef]
- Hirayama, T. A Holographic dual of CFT with flavor on de Sitter space. J. High Energy Phys. 2006, 6, 13. [Google Scholar] [CrossRef][Green Version]
- Cheung, C.; Remmen, G.N. Twofold Symmetries of the Pure Gravity Action. J. High Energy Phys. 2017, 1, 104. [Google Scholar] [CrossRef]
- MacDowell, S.W.; Mansouri, F. Unified geometric theory of gravity and supergravity. Phys. Rev. Lett. 1977, 38, 739–742. [Google Scholar] [CrossRef]
- Gürsey, F.; Ramond, P.; Sikivie, P.A. Universal Gauge Theory Model Based on E6. Phys. Lett. B 1976, 60, 177–180. [Google Scholar] [CrossRef]
- Boyle, L. The Standard Model, The Exceptional Jordan Algebra, and Triality. arXiv 2006, arXiv:2006.16265. [Google Scholar]
- Bars, I.; Günaydin, M. Grand Unification with the Exceptional Group E8. Phys. Rev. Lett. 1980, 45, 859. [Google Scholar] [CrossRef]
- Marrani, A.; Rios, M.; Chester, D. Monstrous M-theory. arXiv 2008, arXiv:hep-th/2008.06742. [Google Scholar]
- Gaberdiel, M.R.; West, P.C. Kac-Moody algebras in perturbative string theory. J. High Energy Phys. 2002, 8, 49. [Google Scholar] [CrossRef][Green Version]
- Kostant, B. The Principle of Triality and A Distinguished Unitary Representation of SO(4,4). In Differential Geometrical Methods in Theoretical Physics; Bleuler, K., Werner, M., Eds.; NATO ASI Series (Series C: Mathematical and Physical Sciences); Springer: Dordrecht, The Netherlands, 1988; Volume 250. [Google Scholar]
- Chester, D.; Marrani, A.; Rios, M. Beyond the standard model with six-dimensional spacetime. arXiv 2020, arXiv:2002.02391. [Google Scholar]
- Aldazabal, G.; Ibanez, L.E.; Quevedo, F.; Uranga, A.M. D-Branes at Singularities: A Bottom-Up Approach to the String Embedding of the Standard Model. J. High Energy Phys. 2000, 8, 2. [Google Scholar] [CrossRef]
- Martinec, E.J. Geometrical structures of M theory. arXiv 1996, arXiv:hep-th/9608017. [Google Scholar]
- Krasnov, K. Spin(11,3), particles and octonions. arXiv 2021, arXiv:hep-th/2104.01786. [Google Scholar]
- Slansky, R. Group Theory for Unified Model Building. Phys. Rept. 1981, 79, 1–28. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).