The Crab Pulsar and Nebula as Seen in Gamma-Rays
Abstract
1. Introduction
2. The Crab Pulsar in Gamma-Rays: Origin of the Emission and Pair Multiplicity
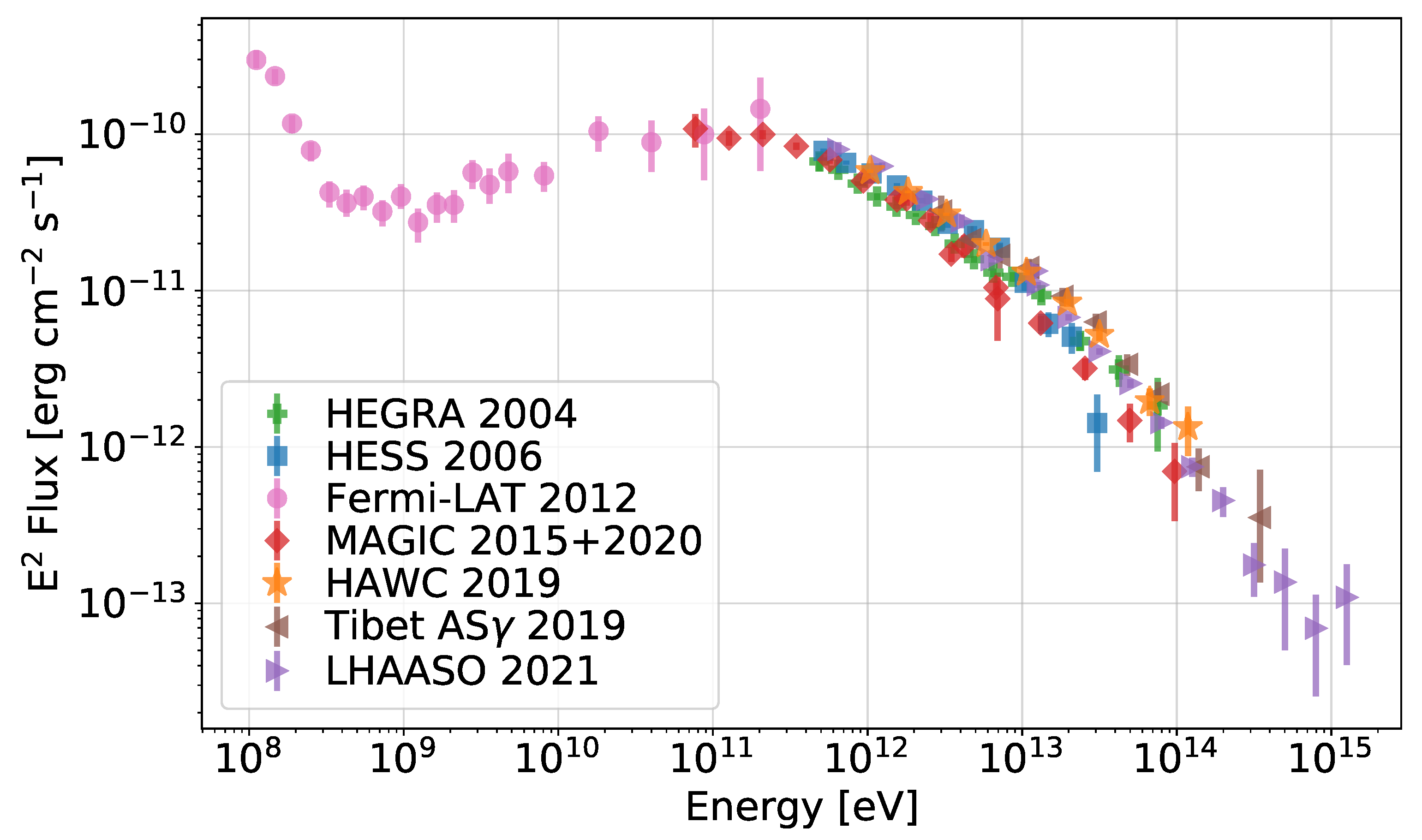
3. The Crab Nebula: What We Learn from Gamma-Rays
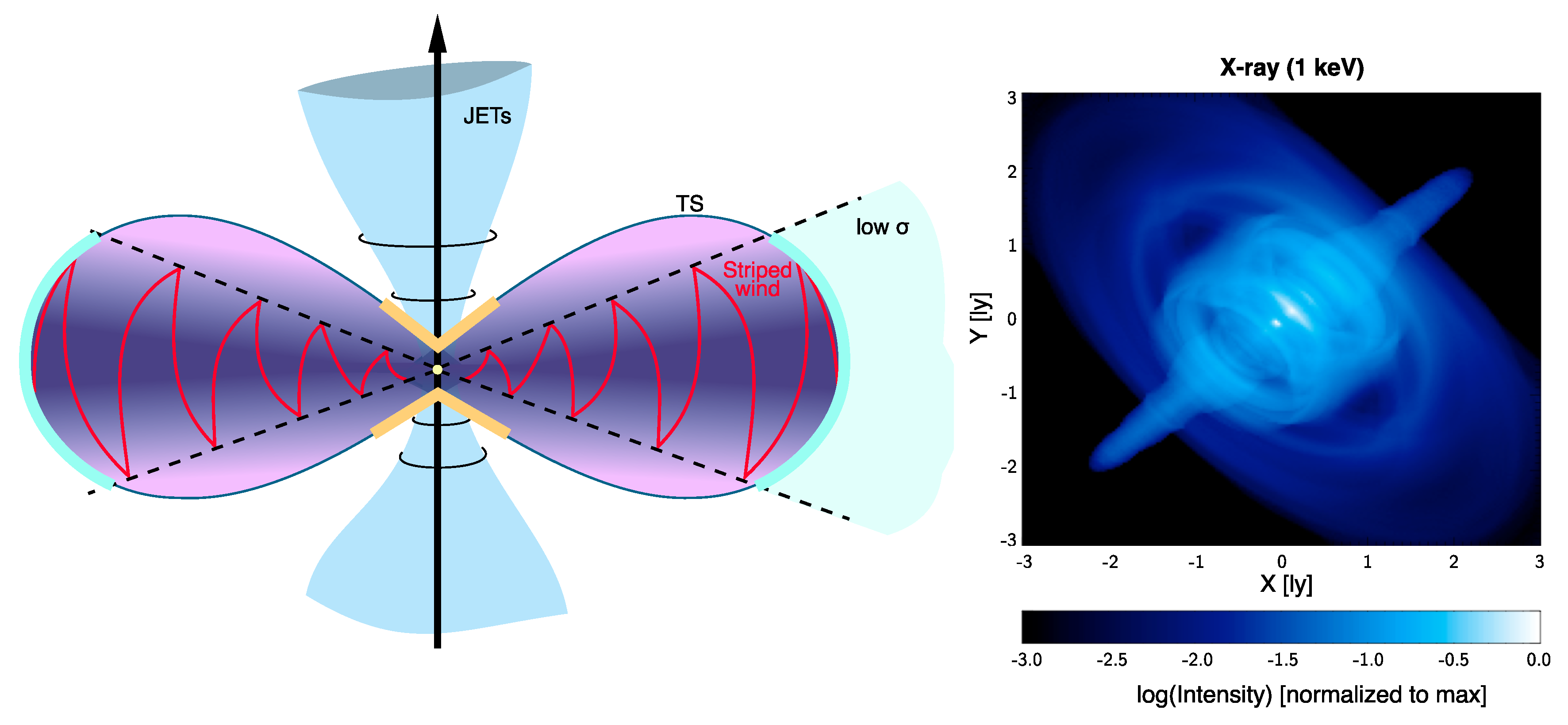
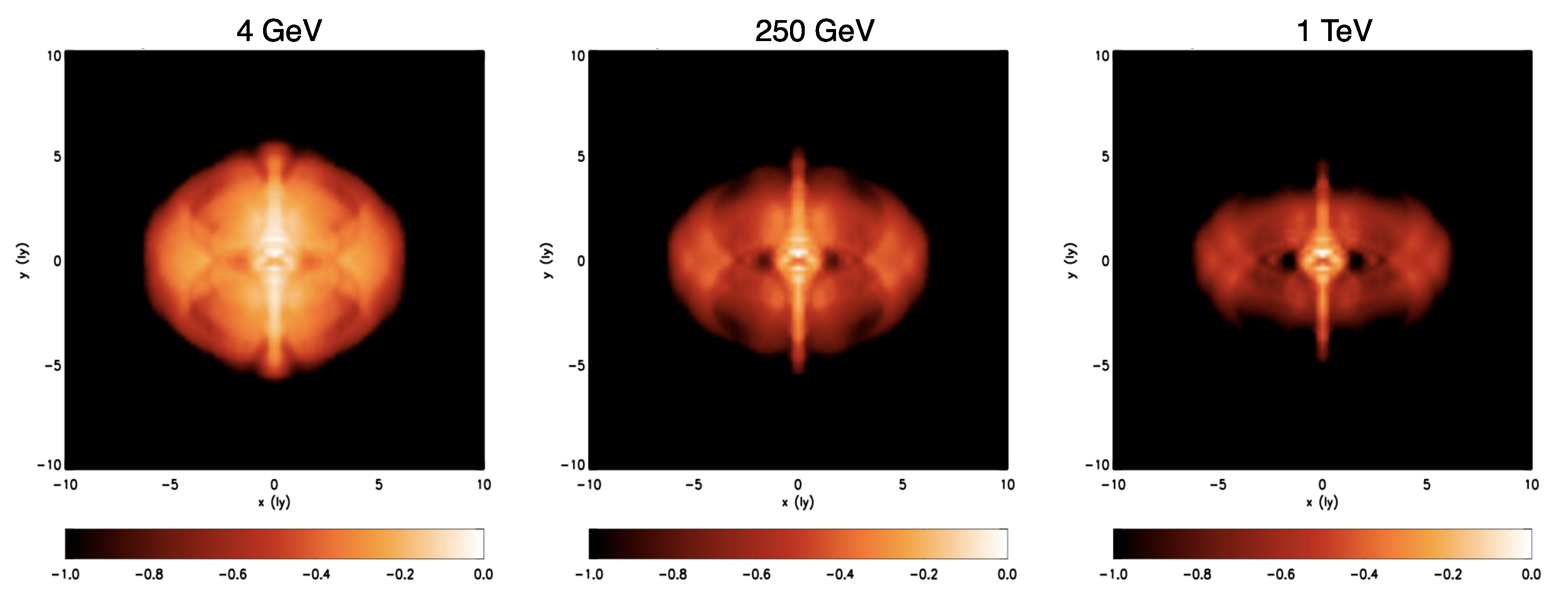
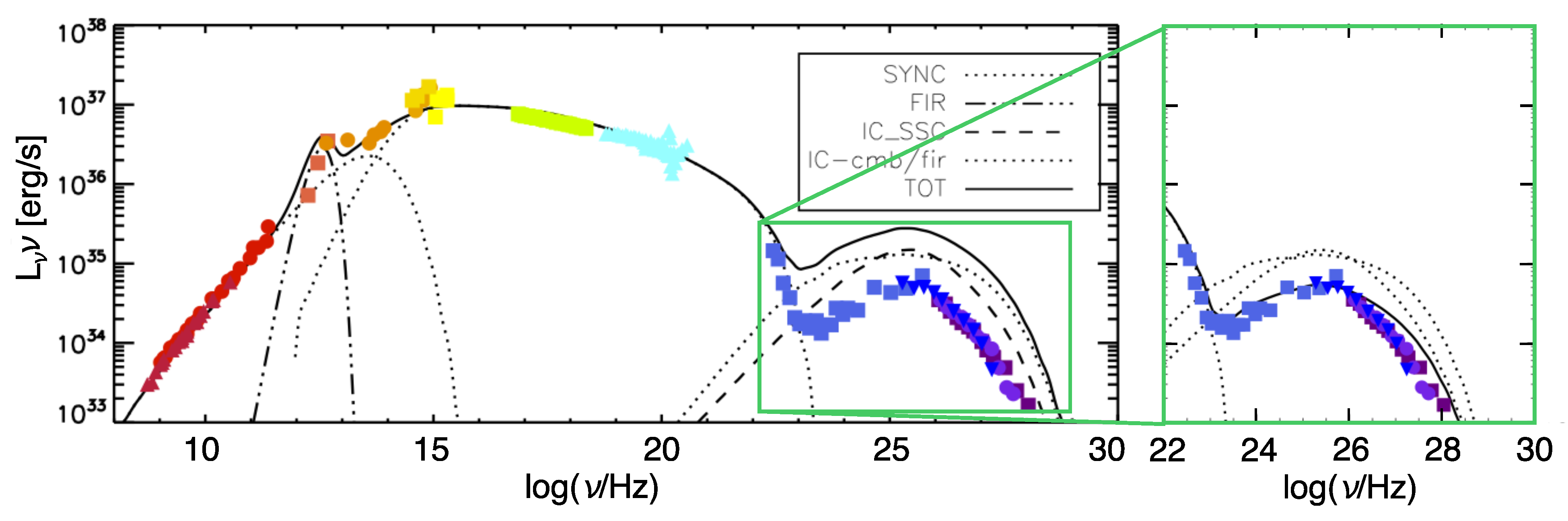
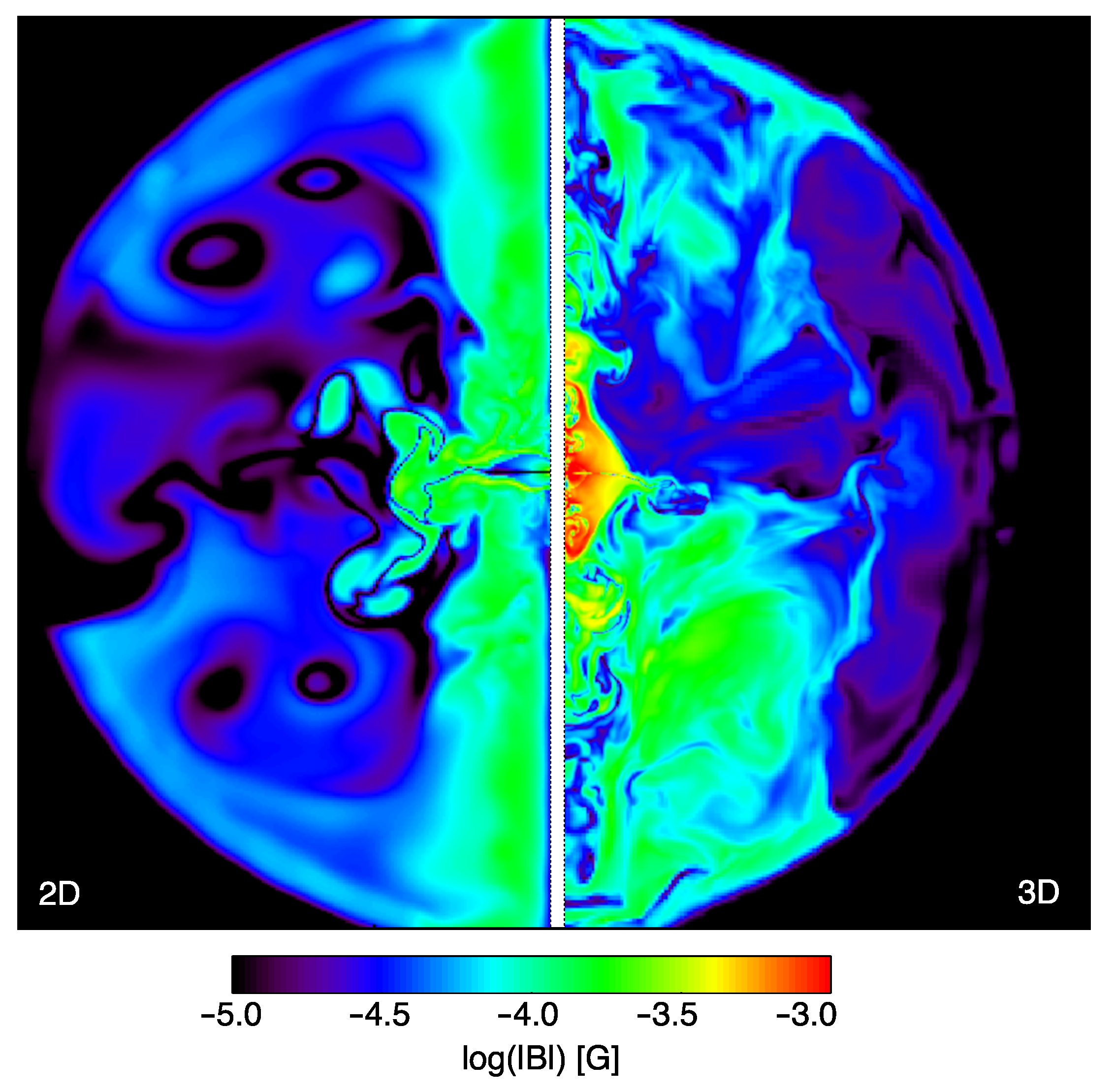
3.1. Modeling the Nebular Plasma
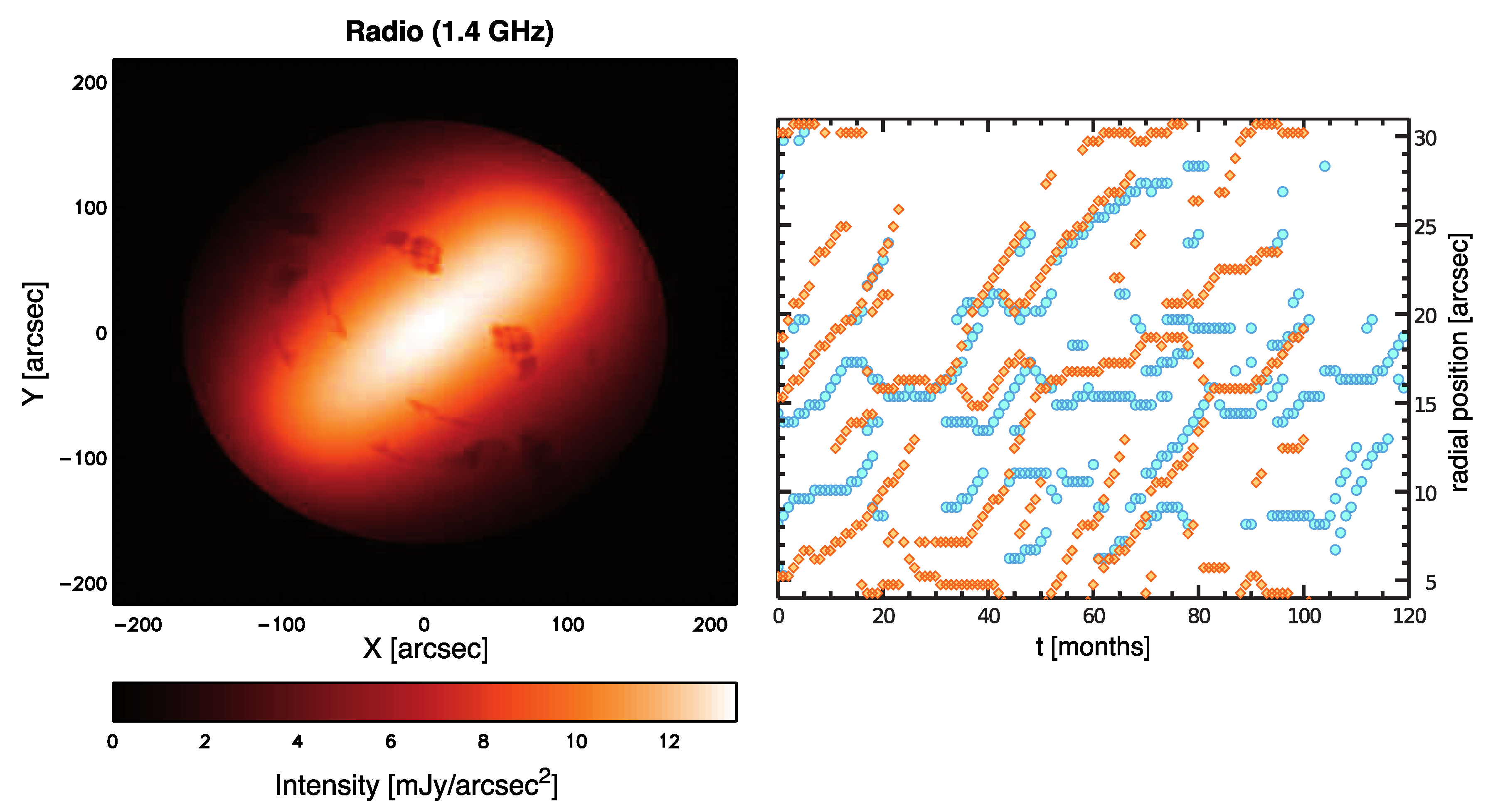
3.2. Time-Variability and Particle Acceleration
3.3. The Crab Flares and Their Implications for Particle Acceleration
3.4. Constraints on the Pulsar Wind Composition from 100 TeV Emission
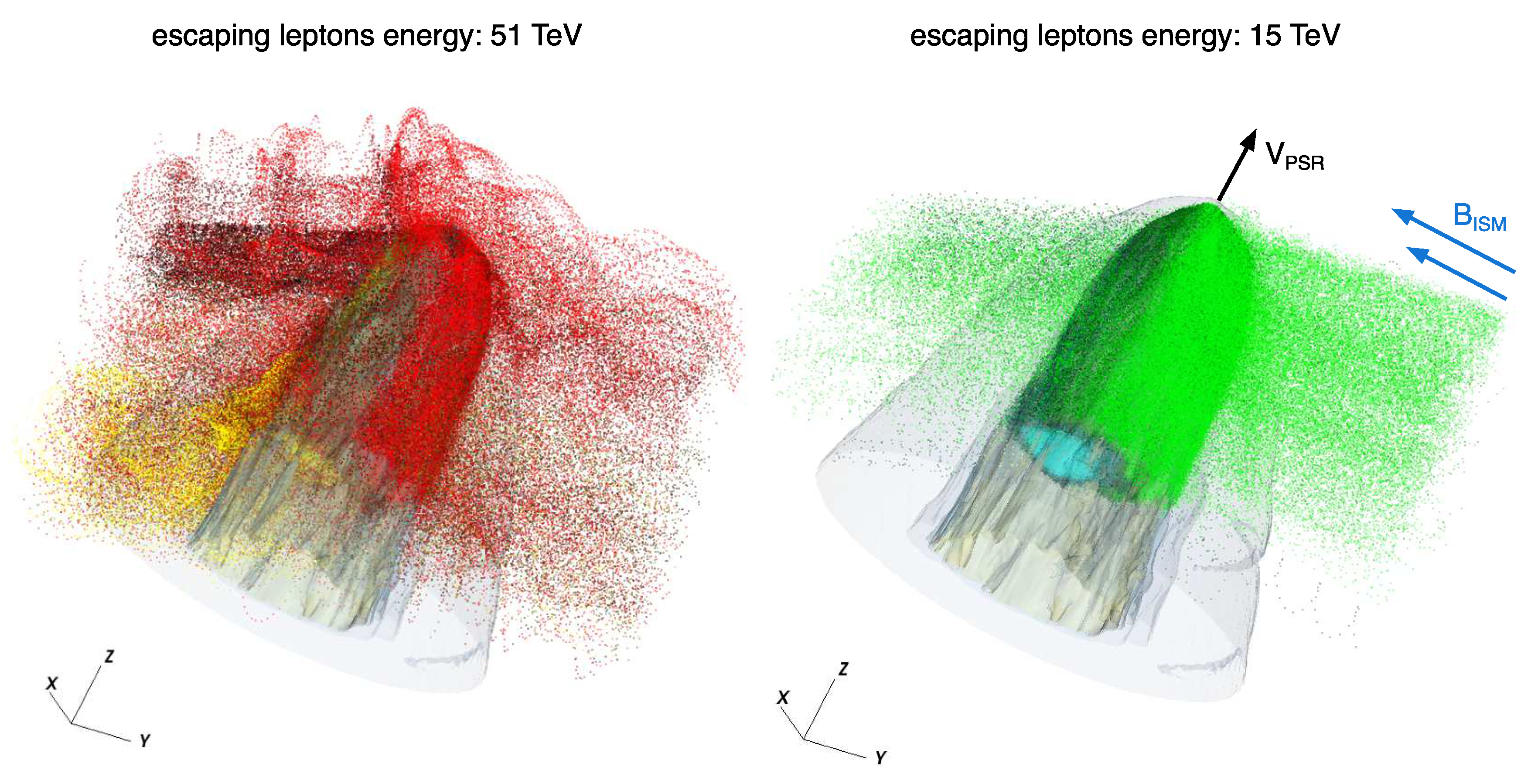
4. The Crab Nebula and the Other PWNe
5. Summary and Future Prospects
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ASTRI | Astrofisica con Specchi a Tecnologia Replicante Italiana |
| CMB | Cosmic Microwave Background |
| CTA | Cherenkov Telescope Array |
| Fermi-LAT | Fermi-Large Area Telescope |
| EHE | Extremely High Energy |
| HD | HydroDynamic |
| HE | High Energy |
| H.E.S.S. | High-Energy Stereoscopic System |
| IACT | Imaging Atmospheric Cherenkov Telescope |
| IC | Inverse Compton |
| ISM | Interstellar Medium |
| LHAASO | Large High-Altitude Air Shower Observatory |
| MAGIC | Major Atmospheric Gamma-ray Imaging Cherenkov |
| MHD | Magneto-Hydrodynamic |
| PIC | Particle In Cell |
| PSR | Pulsar |
| PW | Pulsar Wind |
| PWN | Pulsar Wind Nebula |
| SN | Supernova |
| SNR | Supernova Remnant |
| VERITAS | Very Energetic Radiation Imaging Telescope Array System |
| VHE | Very High Energy |
References
- Hester, J.J. The Crab Nebula: An astrophysical chimera. Annu. Rev. Astron. Astrophys. 2008, 46, 127–155. [Google Scholar] [CrossRef]
- Lundmark, K. Suspected New Stars Recorded in Old Chronicles and Among Recent Meridian Observations. Publ. Astron. Soc. Pac. 1921, 33, 225. [Google Scholar] [CrossRef]
- Baade, W.; Zwicky, F. On Super-novae. Proc. Natl. Acad. Sci. USA 1934, 20, 254–259. [Google Scholar] [CrossRef]
- Pacini, F. Energy Emission from a Neutron Star. Nature 1967, 216, 567–568. [Google Scholar] [CrossRef]
- Hewish, A.; Bell, S.J.; Pilkington, J.D.H.; Scott, P.F.; Collins, R.A. Observation of a Rapidly Pulsating Radio Source. Nature 1968, 217, 709–713. [Google Scholar] [CrossRef]
- Staelin, D.H.; Reifenstein, E.C. Pulsating Radio Sources near the Crab Nebula. Science 1968, 162, 1481–1483. [Google Scholar] [CrossRef]
- H. E. S. S. Collaboration; Abdalla, H.; Abramowski, A.; Aharonian, F.; Benkhali, F.A.; Angüner, E.O.; Arakawa, M.; Arrieta, M.; Aubert, P.; Backes, M.; et al. The H.E.S.S. Galactic plane survey. Astron. Astrophys. 2018, 612, A1. [Google Scholar] [CrossRef]
- Cao, Z.; Aharonian, F.A.; An, Q.; Axikegu; Bai, L.X.; Bai, Y.X.; Bao, Y.W.; Bastieri, D.; Bi, X.J.; Bi, Y.J.; et al. Ultrahigh-energy photons up to 1.4 petaelectronvolts from 12 γ-ray Galactic sources. Nature 2021, 594, 33–36. [Google Scholar] [CrossRef]
- Harding, A.K. Pulsar Polar Cap and Slot Gap Models: Confronting Fermi Data. J. Astron. Space Sci. 2013, 30, 145–152. [Google Scholar] [CrossRef]
- Zanin, R. The Crab pulsar at VHE. Eur. Phys. J. Web Conf. 2017, 136, 03003. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ajello, M.; Allafort, A.; Baldini, L.; Ballet, J.; Barbiellini, G.; Baring, M.G.; Bastieri, D.; Belfiore, A.; Bellazzini, R.; et al. The Second Fermi Large Area Telescope Catalog of Gamma-ray Pulsars. Astrophys. J. Suppl. Ser. 2013, 208, 17. [Google Scholar] [CrossRef]
- Archer, A.; Benbow, W.; Bird, R.; Brose, R.; Buchovecky, M.; Buckley, J.H.; Chromey, A.J.; Cui, W.; Falcone, A.; Feng, Q.; et al. A Search for Pulsed Very High-energy Gamma-Rays from 13 Young Pulsars in Archival VERITAS Data. Astrophys. J. 2019, 876, 95. [Google Scholar] [CrossRef]
- Melrose, D.B. Coherent emission mechanisms in astrophysical plasmas. Rev. Mod. Plasma Phys. 2017, 1, 5. [Google Scholar] [CrossRef]
- Philippov, A.; Timokhin, A.; Spitkovsky, A. Origin of Pulsar Radio Emission. Phys. Rev. Lett. 2020, 124, 245101. [Google Scholar] [CrossRef] [PubMed]
- Melrose, D.B.; Rafat, M.Z.; Mastrano, A. A rotation-driven pulsar radio emission mechanism. Mon. Not. R. Astron. Soc. 2021, 500, 4549–4559. [Google Scholar] [CrossRef]
- Romani, R.W. Gamma-ray Pulsars: Radiation Processes in the Outer Magnetosphere. Astrophys. J. 1996, 470, 469. [Google Scholar] [CrossRef]
- Caraveo, P.A. Gamma-ray Pulsar Revolution. Annu. Rev. Astron. Astrophys. 2014, 52, 211–250. [Google Scholar] [CrossRef]
- Arons, J. Pulsars as Gamma-Rays Sources: Nebular Shocks and Magnetospheric Gaps. Space Sci. Rev. 1996, 75, 235–255. [Google Scholar] [CrossRef]
- Goldreich, P.; Julian, W.H. Pulsar Electrodynamics. Astrophys. J. 1969, 157, 869. [Google Scholar] [CrossRef]
- Timokhin, A.N.; Harding, A.K. On the Maximum Pair Multiplicity of Pulsar Cascades. Astrophys. J. 2019, 871, 12. [Google Scholar] [CrossRef]
- Sturrock, P.A. A Model of Pulsars. Astrophys. J. 1971, 164, 529. [Google Scholar] [CrossRef]
- Ruderman, M.A.; Sutherland, P.G. Theory of pulsars: Polar gaps, sparks, and coherent microwave radiation. Astrophys. J. 1975, 196, 51–72. [Google Scholar] [CrossRef]
- Arons, J. Pair creation above pulsar polar caps: Geometrical structure and energetics of slot gaps. Astrophys. J. 1983, 266, 215–241. [Google Scholar] [CrossRef]
- Muslimov, A.G.; Harding, A.K. Particle Acceleration in Pair-starved Pulsars. Astrophys. J. 2004, 617, 471–479. [Google Scholar] [CrossRef][Green Version]
- Cheng, K.S.; Ho, C.; Ruderman, M. Energetic Radiation from Rapidly Spinning Pulsars. I. Outer Magnetosphere Gaps. Astrophys. J. 1986, 300, 500. [Google Scholar] [CrossRef]
- Kirk, J.G.; Skjæraasen, O.; Gallant, Y.A. Pulsed radiation from neutron star winds. Astron. Astrophys. 2002, 388, L29–L32. [Google Scholar] [CrossRef]
- Lyubarskii, Y.E. A model for the energetic emission from pulsars. Astron. Astrophys. 1996, 311, 172–178. [Google Scholar] [CrossRef]
- Watters, K.P.; Romani, R.W. The Galactic Population of Young γ-ray Pulsars. Astrophys. J. 2011, 727, 123. [Google Scholar] [CrossRef]
- Aliu, E.; Anderhub, H.; Antonelli, L.A.; Antoranz, P.; Backes, M.; Baixeras, C.; Barrio, J.A.; Bartko, H.; Bastieri, D.; Becker, J.K.; et al. Observation of Pulsed γ-rays Above 25 GeV from the Crab Pulsar with MAGIC. Science 2008, 322, 1221. [Google Scholar] [CrossRef]
- Aleksić, J.; Alvarez, E.A.; Antonelli, L.A.; Antoranz, P.; Asensio, M.; Backes, M.; Barrio, J.A.; Bastieri, D.; Becerra González, J. Observations of the Crab Pulsar between 25 and 100 GeV with the MAGIC I Telescope. Astrophys. J. 2011, 742, 43. [Google Scholar] [CrossRef]
- VERITAS Collaboration; Aliu, E.; Arlen, T.; Aune, T.; Beilicke, M.; Benbow, W.; Bouvier, A.; Bradbury, S.M.; Buckley, J.H.; Bugaev, V.; et al. Detection of Pulsed Gamma Rays Above 100 GeV from the Crab Pulsar. Science 2011, 334, 69. [Google Scholar] [CrossRef]
- Ansoldi, S.; Antonelli, L.A.; Antoranz, P.; Babic, A.; Bangale, P.; Barres de Almeida, U.; Barrio, J.A.; Becerra González, J.; Bednarek, W.; Bernardini, E.; et al. Teraelectronvolt pulsed emission from the Crab Pulsar detected by MAGIC. Astron. Astrophys. 2016, 585, A133. [Google Scholar] [CrossRef]
- Kalapotharakos, C.; Harding, A.K.; Kazanas, D.; Wadiasingh, Z. A Fundamental Plane for Gamma-ray Pulsars. Astrophys. J. Lett. 2019, 883, L4. [Google Scholar] [CrossRef]
- Cerutti, B.; Mortier, J.; Philippov, A.A. Polarized synchrotron emission from the equatorial current sheet in gamma-ray pulsars. Not. R. Astron. Soc. Lett. 2016, 463, L89–L93. [Google Scholar] [CrossRef]
- Torres, D.F.; Viganò, D.; Coti Zelati, F.; Li, J. Synchrocurvature modelling of the multifrequency non-thermal emission of pulsars. Not. R. Astron. Soc. Lett. 2019, 489, 5494–5512. [Google Scholar] [CrossRef]
- Cerutti, B.; Beloborodov, A.M. Electrodynamics of Pulsar Magnetospheres. Space Sci. Rev. 2017, 207, 111–136. [Google Scholar] [CrossRef]
- Spitkovsky, A. Time-dependent Force-free Pulsar Magnetospheres: Axisymmetric and Oblique Rotators. Astrophys. J. Lett. 2006, 648, L51–L54. [Google Scholar] [CrossRef]
- Philippov, A.A.; Spitkovsky, A. Ab Initio Pulsar Magnetosphere: Three-dimensional Particle-in-cell Simulations of Axisymmetric Pulsars. Astrophys. J. Lett. 2014, 785, L33. [Google Scholar] [CrossRef]
- Philippov, A.A.; Spitkovsky, A.; Cerutti, B. Ab Initio Pulsar Magnetosphere: Three-dimensional Particle-in-cell Simulations of Oblique Pulsars. Astrophys. J. Lett. 2015, 801, L19. [Google Scholar] [CrossRef]
- Brambilla, G.; Kalapotharakos, C.; Timokhin, A.N.; Harding, A.K.; Kazanas, D. Electron-Positron Pair Flow and Current Composition in the Pulsar Magnetosphere. Astrophys. J. 2018, 858, 81. [Google Scholar] [CrossRef]
- Chen, A.Y.; Beloborodov, A.M. Electrodynamics of Axisymmetric Pulsar Magnetosphere with Electron-Positron Discharge: A Numerical Experiment. Astrophys. J. Lett. 2014, 795, L22. [Google Scholar] [CrossRef]
- Ng, C.Y.; Romani, R.W. Pulsar Wind Tori and the Spin-Kick Connection; The AAS High Energy Astrophysics Division (HEAD): Washington, DC, USA, 2004; Volume 8, p. 16. [Google Scholar]
- Yeung, P.K.H. Inferring the origins of the pulsed γ-ray emission from the Crab pulsar with ten-year Fermi-LAT data. Astron. Astrophys. 2020, 640, A43. [Google Scholar] [CrossRef]
- Mochol, I.; Petri, J. Very high energy emission as a probe of relativistic magnetic reconnection in pulsar winds. Not. R. Astron. Soc. Lett. 2015, 449, L51–L55. [Google Scholar] [CrossRef]
- Weekes, T.C.; Cawley, M.F.; Fegan, D.J.; Gibbs, K.G.; Hillas, A.M.; Kowk, P.W.; Lamb, R.C.; Lewis, D.A.; Macomb, D.; Porter, N.A.; et al. Observation of TeV Gamma Rays from the Crab Nebula Using the Atmospheric Cerenkov Imaging Technique. Astrophys. J. 1989, 342, 379. [Google Scholar] [CrossRef]
- Nolan, P.L.; Arzoumanian, Z.; Bertsch, D.L.; Chiang, J.; Fichtel, C.E.; Fierro, J.M.; Hartman, R.C.; Hunter, S.D.; Kanbach, G.; Kniffen, D.A.; et al. Observations of the Crab Pulsar and Nebula by the EGRET Telescope on the Compton Gamma-ray Observatory. Astrophys. J. 1993, 409, 697. [Google Scholar] [CrossRef]
- De Jager, O.C.; Harding, A.K. The Expected High-Energy to Ultra–High-Energy Gamma-ray Spectrum of the Crab Nebula. Astrophys. J. 1992, 396, 161. [Google Scholar] [CrossRef]
- Atoyan, A.M.; Aharonian, F.A. On the mechanisms of gamma radiation in the Crab Nebula. Not. R. Astron. Soc. Lett. 1996, 278, 525–541. [Google Scholar] [CrossRef]
- Tavani, M.; Bulgarelli, A.; Vittorini, V.; Pellizzoni, A.; Striani, E.; Caraveo, P.; Weisskopf, M.C.; Tennant, A.; Pucella, G.; Trois, A.; et al. Discovery of Powerful Gamma-ray Flares from the Crab Nebula. Science 2011, 331, 736. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Ajello, M.; Allafort, A.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; et al. Gamma-ray Flares from the Crab Nebula. Science 2011, 331, 739. [Google Scholar] [CrossRef]
- Yeung, P.K.H.; Horns, D. Fermi Large Area Telescope observations of the fast-dimming Crab Nebula in 60–600 MeV. Astron. Astrophys. 2020, 638, A147. [Google Scholar] [CrossRef]
- Cao, Z.; Aharonian, F.; An, Q.; Axikegu; Bai, L.X.; Bai, Y.X.; Bao, Y.W.; Bastieri, D.; Bi, X.J.; Bi, Y.J.; et al. Peta-electron volt gamma-ray emission from the Crab Nebula. Science 2021, 373, 425–430. [Google Scholar] [CrossRef]
- Amato, E.; Casanova, S. On particle acceleration and transport in plasmas in the Galaxy: Theory and observations. J. Plasma Phys. 2021, 87, 845870101. [Google Scholar] [CrossRef]
- Aharonian, F.; Akhperjanian, A.; Beilicke, M.; Bernlöhr, K.; Börst, H.G.; Bojahr, H.; Bolz, O.; Coarasa, T.; Contreras, J.L.; Cortina, J.; et al. The Crab Nebula and Pulsar between 500 GeV and 80 TeV: Observations with the HEGRA Stereoscopic Air Cerenkov Telescopes. Astrophys. J. 2004, 614, 897–913. [Google Scholar] [CrossRef]
- Aharonian, F.; Akhperjanian, A.G.; Bazer-Bachi, A.R.; Beilicke, M.; Benbow, W.; Berge, D.; Bernlöhr, K.; Boisson, C.; Bolz, O.; Borrel, V.; et al. Observations of the Crab nebula with HESS. Astron. Astrophys. 2006, 457, 899–915. [Google Scholar] [CrossRef]
- Buehler, R.; Scargle, J.D.; Blandford, R.D.; Baldini, L.; Baring, M.G.; Belfiore, A.; Charles, E.; Chiang, J.; D’Ammando, F.; Dermer, C.D.; et al. Gamma-ray Activity in the Crab Nebula: The Exceptional Flare of 2011 April. Astrophys. J. 2012, 749, 26. [Google Scholar] [CrossRef]
- Aleksić, J.; Ansoldi, S.; Antonelli, L.A.; Antoranz, P.; Babic, A.; Bangale, P.; Barrio, J.A.; Becerra González, J.; Bednarek, W.; Bernardini, E.; et al. Measurement of the Crab Nebula spectrum over three decades in energy with the MAGIC telescopes. J. High Energy Astrophys. 2015, 5, 30–38. [Google Scholar] [CrossRef]
- MAGIC Collaboration; Acciari, V.A.; Ansoldi, S.; Antonelli, L.A.; Arbet Engels, A.; Baack, D.; Babić, A.; Banerjee, B.; Barres de Almeida, U.; Barrio, J.A.; et al. MAGIC very large zenith angle observations of the Crab Nebula up to 100 TeV. Astron. Astrophys. 2020, 635, A158. [Google Scholar] [CrossRef]
- Abeysekara, A.U.; Albert, A.; Alfaro, R.; Alvarez, C.; Álvarez, J.D.; Camacho, J.R.A.; Arceo, R.; Arteaga-Velázquez, J.C.; Arunbabu, K.P.; Avila Rojas, D.; et al. Measurement of the Crab Nebula Spectrum Past 100 TeV with HAWC. Astrophys. J. 2019, 881, 134. [Google Scholar] [CrossRef]
- Amenomori, M.; Bao, Y.W.; Bi, X.J.; Chen, D.; Chen, T.L.; Chen, W.Y.; Chen, X.; Chen, Y.; Cirennima; Cui, S.W.; et al. First Detection of Photons with Energy beyond 100 TeV from an Astrophysical Source. Phys. Rev. Lett. 2019, 123, 051101. [Google Scholar] [CrossRef]
- Aharonian, F.; An, Q.; Axikegu; Bai, L.X.; Bai, Y.X.; Bao, Y.W.; Bastieri, D.; Bi, X.J.; Bi, Y.J.; Cai, H.; et al. Observation of the Crab Nebula with LHAASO-KM2A—A performance study. Chin. Phys. C 2021, 45, 025002. [Google Scholar] [CrossRef]
- Kirk, J.G.; Lyubarsky, Y.; Petri, J. The Theory of Pulsar Winds and Nebulae. In Astrophysics and Space Science Library; Becker, W., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 357, p. 421. [Google Scholar] [CrossRef]
- Arons, J. Pulsar Wind Nebulae as Cosmic Pevatrons: A Current Sheet’s Tale. Space Sci. Rev. 2012, 173, 341–367. [Google Scholar] [CrossRef]
- Coroniti, F.V. Magnetically Striped Relativistic Magnetohydrodynamic Winds: The Crab Nebula Revisited. Astrophys. J. 1990, 349, 538. [Google Scholar] [CrossRef]
- Lyubarsky, Y.; Kirk, J.G. Reconnection in a Striped Pulsar Wind. Astrophys. J. 2001, 547, 437–448. [Google Scholar] [CrossRef]
- Rees, M.J.; Gunn, J.E. The origin of the magnetic field and relativistic particles in the Crab Nebula. Not. R. Astron. Soc. Lett. 1974, 167, 1–12. [Google Scholar] [CrossRef]
- Kennel, C.F.; Coroniti, F.V. Magnetohydrodynamic model of Crab nebula radiation. Astrophys. J. 1984, 283, 710–730. [Google Scholar] [CrossRef]
- Emmering, R.T.; Chevalier, R.A. Shocked Relativistic Magnetohydrodynamic Flows with Application to Pulsar Winds. Astrophys. J. 1987, 321, 334. [Google Scholar] [CrossRef]
- Begelman, M.C.; Li, Z.Y. An Axisymmetric Magnetohydrodynamic Model for the Crab Pulsar Wind Bubble. Astrophys. J. 1992, 397, 187. [Google Scholar] [CrossRef]
- Weisskopf, M.C.; Hester, J.J.; Tennant, A.F.; Elsner, R.F.; Schulz, N.S.; Marshall, H.L.; Karovska, M.; Nichols, J.S.; Swartz, D.A.; Kolodziejczak, J.J.; et al. Discovery of Spatial and Spectral Structure in the X-ray Emission from the Crab Nebula. Astrophys. J. Lett. 2000, 536, L81–L84. [Google Scholar] [CrossRef] [PubMed]
- Komissarov, S.; Lyubarsky, Y. MHD Simulations of Crab’s Jet and Torus. Virtual Astrophys. Jets 2004, 293, 107–113. [Google Scholar] [CrossRef]
- Del Zanna, L. Axisymmetric Simulations of Pulsar Wind Nebulae with a New Central-Type Scheme for Relativistic MHD. Astrophys. Space Sci. 2004, 293, 209–216. [Google Scholar] [CrossRef]
- Michel, F.C. Rotating Magnetospheres: An Exact 3-D Solution. Astrophys. J. Lett. 1973, 180, L133. [Google Scholar] [CrossRef]
- Lyubarsky, Y.E. On the structure of the inner Crab Nebula. Not. R. Astron. Soc. Lett. 2002, 329, L34–L36. [Google Scholar] [CrossRef]
- Del Zanna, L.; Volpi, D.; Amato, E.; Bucciantini, N. Simulated synchrotron emission from pulsar wind nebulae. Astron. Astrophys. 2006, 453, 621–633. [Google Scholar] [CrossRef]
- Lyutikov, M.; Komissarov, S.S.; Porth, O. The inner knot of the Crab nebula. Not. R. Astron. Soc. Lett. 2016, 456, 286–299. [Google Scholar] [CrossRef][Green Version]
- Olmi, B.; Del Zanna, L.; Amato, E.; Bandiera, R.; Bucciantini, N. On the magnetohydrodynamic modelling of the Crab nebula radio emission. Not. R. Astron. Soc. Lett. 2014, 438, 1518–1525. [Google Scholar] [CrossRef]
- Aharonian, F.A.; Akhperjanian, A.G.; Barrio, J.A.; Bernlöhr, K.; Bojahr, H.; Bolz, O.; Börst, H.; Contreras, J.L.; Cortina, J.; Denninghoff, V.; et al. Optimizing the angular resolution of the HEGRA telescope system to study the emission region of VHE gamma rays in the Crab Nebula. Astron. Astrophys. 2000, 361, 1073–1078. [Google Scholar]
- Albert, J.; Aliu, E.; Anderhub, H.; Antoranz, P.; Armada, A.; Baixeras, C.; Barrio, J.A.; Bartko, H.; Bastieri, D.; Becker, J.K.; et al. VHE γ-ray Observation of the Crab Nebula and its Pulsar with the MAGIC Telescope. Astrophys. J. 2008, 674, 1037–1055. [Google Scholar] [CrossRef]
- H. E. S. S. Collaboration. Resolving the Crab pulsar wind nebula at teraelectronvolt energies. Nat. Astron. 2020, 4, 167–173. [Google Scholar] [CrossRef]
- Volpi, D.; Del Zanna, L.; Amato, E.; Bucciantini, N. Non-thermal emission from relativistic MHD simulations of pulsar wind nebulae: From synchrotron to inverse Compton. Astron. Astrophys. 2008, 485, 337–349. [Google Scholar] [CrossRef][Green Version]
- Mestre, E.; de Oña Wilhelmi, E.; Zanin, R.; Torres, D.F.; Tibaldo, L. Prospects for the characterization of the VHE emission from the Crab nebula and pulsar with the Cherenkov Telescope Array. Not. R. Astron. Soc. Lett. 2020, 492, 708–718. [Google Scholar] [CrossRef]
- Meyer, M.; Horns, D.; Zechlin, H.S. The Crab Nebula as a standard candle in very high-energy astrophysics. Astron. Astrophys. 2010, 523, A2. [Google Scholar] [CrossRef]
- Porth, O.; Komissarov, S.S.; Keppens, R. Three-dimensional magnetohydrodynamic simulations of the Crab nebula. Not. R. Astron. Soc. Lett. 2014, 438, 278–306. [Google Scholar] [CrossRef]
- Olmi, B.; Del Zanna, L.; Amato, E.; Bucciantini, N.; Mignone, A. Multi-D magnetohydrodynamic modelling of pulsar wind nebulae: Recent progress and open questions. J. Plasma Phys. 2016, 82, 635820601. [Google Scholar] [CrossRef]
- Porth, O.; Buehler, R.; Olmi, B.; Komissarov, S.; Lamberts, A.; Amato, E.; Yuan, Y.; Rudy, A. Modelling Jets, Tori and Flares in Pulsar Wind Nebulae. Space Sci. Rev. 2017, 207, 137–174. [Google Scholar] [CrossRef]
- Olmi, B.; Bucciantini, N. Full-3D relativistic MHD simulations of bow shock pulsar wind nebulae: Dynamics. Not. R. Astron. Soc. Lett. 2019, 484, 5755–5770. [Google Scholar] [CrossRef]
- Olmi, B.; Del Zanna, L.; Amato, E.; Bucciantini, N. Constraints on particle acceleration sites in the Crab nebula from relativistic magnetohydrodynamic simulations. Not. R. Astron. Soc. Lett. 2015, 449, 3149–3159. [Google Scholar] [CrossRef][Green Version]
- Bucciantini, N.; del Zanna, L.; Amato, E.; Volpi, D. Polarization in the inner region of pulsar wind nebulae. Astron. Astrophys. 2005, 443, 519–524. [Google Scholar] [CrossRef]
- Soffitta, P.; Barcons, X.; Bellazzini, R.; Braga, J.; Costa, E.; Fraser, G.W.; Gburek, S.; Huovelin, J.; Matt, G.; Pearce, M.; et al. XIPE: The X-ray imaging polarimetry explorer. Exp. Astron. 2013, 36, 523–567. [Google Scholar] [CrossRef]
- Scargle, J.D. Activity in the Crab Nebula. Astrophys. J. 1969, 156, 401. [Google Scholar] [CrossRef]
- Hester, J.J.; Mori, K.; Burrows, D.; Gallagher, J.S.; Graham, J.R.; Halverson, M.; Kader, A.; Michel, F.C.; Scowen, P. Hubble Space Telescope and Chandra Monitoring of the Crab Synchrotron Nebula. Astrophys. J. Lett. 2002, 577, L49–L52. [Google Scholar] [CrossRef]
- Bietenholz, M.F.; Frail, D.A.; Hester, J.J. The Crab Nebula’s Moving Wisps in Radio. Astrophys. J. 2001, 560, 254–260. [Google Scholar] [CrossRef]
- Bietenholz, M.F.; Hester, J.J.; Frail, D.A.; Bartel, N. The Crab Nebula’s Wisps in Radio and Optical. Astrophys. J. 2004, 615, 794–804. [Google Scholar] [CrossRef]
- Wilson-Hodge, C.A.; Cherry, M.L.; Case, G.L.; Baumgartner, W.H.; Beklen, E.; Narayana Bhat, P.; Briggs, M.S.; Camero-Arranz, A.; Chaplin, V.; Connaughton, V.; et al. When a Standard Candle Flickers. Astrophys. J. Lett. 2011, 727, L40. [Google Scholar] [CrossRef]
- Schweizer, T.; Bucciantini, N.; Idec, W.; Nilsson, K.; Tennant, A.; Weisskopf, M.C.; Zanin, R. Characterization of the optical and X-ray properties of the north-western wisps in the Crab nebula. Not. R. Astron. Soc. Lett. 2013, 433, 3325–3335. [Google Scholar] [CrossRef]
- Amato, E. The Theory of Pulsar Wind Nebulae. Int. J. Mod. Phys. Conf. Ser. 2014, 28, 60160. [Google Scholar] [CrossRef]
- Amato, E. The Theory of Pulsar Wind Nebulae: Recent Progress. arXiv 2020, arXiv:2001.04442. [Google Scholar]
- Amato, E.; Salvati, M.; Bandiera, R.; Pacini, F.; Woltjer, L. Inhomogeneous models for plerions: The surface brightness profile of the Crab Nebula. Astron. Astrophys. 2000, 359, 1107–1110. [Google Scholar]
- Bandiera, R.; Neri, R.; Cesaroni, R. The Crab Nebula at 1.3 mm. Evidence for a new synchrotron component. Astron. Astrophys. 2002, 386, 1044–1054. [Google Scholar] [CrossRef]
- Sironi, L.; Spitkovsky, A. Particle Acceleration in Relativistic Magnetized Collisionless Pair Shocks: Dependence of Shock Acceleration on Magnetic Obliquity. Astrophys. J. 2009, 698, 1523–1549. [Google Scholar] [CrossRef]
- Sironi, L.; Keshet, U.; Lemoine, M. Relativistic Shocks: Particle Acceleration and Magnetization. Space Sci. Rev. 2015, 191, 519–544. [Google Scholar] [CrossRef]
- Sironi, L.; Spitkovsky, A. Acceleration of Particles at the Termination Shock of a Relativistic Striped Wind. Astrophys. J. 2011, 741, 39. [Google Scholar] [CrossRef]
- Hoshino, M.; Arons, J.; Gallant, Y.A.; Langdon, A.B. Relativistic Magnetosonic Shock Waves in Synchrotron Sources: Shock Structure and Nonthermal Acceleration of Positrons. Astrophys. J. 1992, 390, 454. [Google Scholar] [CrossRef]
- Amato, E.; Arons, J. Heating and Nonthermal Particle Acceleration in Relativistic, Transverse Magnetosonic Shock Waves in Proton-Electron-Positron Plasmas. Astrophys. J. 2006, 653, 325–338. [Google Scholar] [CrossRef]
- Bucciantini, N.; Arons, J.; Amato, E. Modelling spectral evolution of pulsar wind nebulae inside supernova remnants. Not. R. Astron. Soc. Lett. 2011, 410, 381–398. [Google Scholar] [CrossRef]
- Amato, E.; Guetta, D.; Blasi, P. Signatures of high energy protons in pulsar winds. Astron. Astrophys. 2003, 402, 827–836. [Google Scholar] [CrossRef]
- De Jager, O.C.; Harding, A.K.; Michelson, P.F.; Nel, H.I.; Nolan, P.L.; Sreekumar, P.; Thompson, D.J. Gamma-ray Observations of the Crab Nebula: A Study of the Synchro-Compton Spectrum. Astrophys. J. 1996, 457, 253. [Google Scholar] [CrossRef]
- Huang, X.; Yuan, Q.; Fan, Y.Z. A Systematic Study of Gamma-ray Flares from the Crab Nebula with Fermi-LAT. I. Flare Detection. Astrophys. J. 2021, 908, 65. [Google Scholar] [CrossRef]
- Pshirkov, M.S.; Nizamov, B.A.; Bykov, A.M.; Uvarov, Y.A. Gamma-ray flux depressions of the Crab Nebula in the high-energy range. Not. R. Astron. Soc. Lett. 2020, 496, 5227–5232. [Google Scholar] [CrossRef]
- Cerutti, B.; Uzdensky, D.A.; Begelman, M.C. Extreme Particle Acceleration in Magnetic Reconnection Layers: Application to the Gamma-ray Flares in the Crab Nebula. Astrophys. J. 2012, 746, 148. [Google Scholar] [CrossRef]
- Cerutti, B.; Werner, G.R.; Uzdensky, D.A.; Begelman, M.C. Simulations of Particle Acceleration beyond the Classical Synchrotron Burnoff Limit in Magnetic Reconnection: An Explanation of the Crab Flares. Astrophys. J. 2013, 770, 147. [Google Scholar] [CrossRef]
- Bühler, R.; Blandford, R. The surprising Crab pulsar and its nebula: A review. Rep. Prog. Phys. 2014, 77, 066901. [Google Scholar] [CrossRef]
- Cerutti, B.; Werner, G.R.; Uzdensky, D.A.; Begelman, M.C. Gamma-ray flares in the Crab Nebula: A case of relativistic reconnection? Phys. Plasmas 2014, 21, 056501. [Google Scholar] [CrossRef]
- Sironi, L.; Cerutti, B. Particle Acceleration in Pulsar Wind Nebulae: PIC Modelling. In Modelling Pulsar Wind Nebulae; Torres, D.F., Ed.; Springer: Cham, Switzerland, 2017; Volume 446, p. 247. [Google Scholar] [CrossRef]
- Comisso, L.; Sironi, L. The Interplay of Magnetically Dominated Turbulence and Magnetic Reconnection in Producing Nonthermal Particles. Astrophys. J. 2019, 886, 122. [Google Scholar] [CrossRef]
- Nalewajko, K.; Zrake, J.; Yuan, Y.; East, W.E.; Blandford, R.D. Kinetic Simulations of the Lowest-order Unstable Mode of Relativistic Magnetostatic Equilibria. Astrophys. J. 2016, 826, 115. [Google Scholar] [CrossRef]
- Yuan, Y.; Nalewajko, K.; Zrake, J.; East, W.E.; Blandford, R.D. Kinetic Study of Radiation-reaction-limited Particle Acceleration During the Relaxation of Unstable Force-free Equilibria. Astrophys. J. 2016, 828, 92. [Google Scholar] [CrossRef]
- Lyutikov, M.; Sironi, L.; Komissarov, S.S.; Porth, O. Explosive X-point collapse in relativistic magnetically dominated plasma. J. Plasma Phys. 2017, 83, 635830601. [Google Scholar] [CrossRef]
- Lyutikov, M.; Sironi, L.; Komissarov, S.S.; Porth, O. Particle acceleration in relativistic magnetic flux-merging events. J. Plasma Phys. 2017, 83, 635830602. [Google Scholar] [CrossRef][Green Version]
- Bykov, A.M.; Pavlov, G.G.; Artemyev, A.V.; Uvarov, Y.A. Twinkling pulsar wind nebulae in the synchrotron cut-off regime and the γ-ray flares in the Crab Nebula. Not. R. Astron. Soc. Lett. 2012, 421, L67–L71. [Google Scholar] [CrossRef]
- Lyutikov, M.; Balsara, D.; Matthews, C. Crab GeV flares from the corrugated termination shock. Not. R. Astron. Soc. Lett. 2012, 422, 3118–3129. [Google Scholar] [CrossRef][Green Version]
- Lemoine, M. A corrugated termination shock in pulsar wind nebulae? J. Plasma Phys. 2016, 82, 635820401. [Google Scholar] [CrossRef][Green Version]
- Cerutti, B.; Giacinti, G. A global model of particle acceleration at pulsar wind termination shocks. Astron. Astrophys. 2020, 642, A123. [Google Scholar] [CrossRef]
- Bednarek, W.; Protheroe, R.J. Gamma Rays and Neutrinos from the Crab Nebula Produced by Pulsar Accelerated Nuclei. Phys. Rev. Lett. 1997, 79, 2616–2619. [Google Scholar] [CrossRef]
- Bednarek, W.; Bartosik, M. Gamma-Rays from the pulsar wind nebulae. Astron. Astrophys. 2003, 405, 689–702. [Google Scholar] [CrossRef]
- Abeysekara, A.U.; Albert, A.; Alfaro, R.; Angeles Camacho, J.R.; Arteaga-Velázquez, J.C.; Arunbabu, K.P.; Avila Rojas, D.; Ayala Solares, H.A.; Baghmanyan, V.; Belmont-Moreno, E.; et al. Multiple Galactic Sources with Emission Above 56 TeV Detected by HAWC. Phys. Rev. Lett. 2020, 124, 021102. [Google Scholar] [CrossRef]
- Breuhaus, M.; Hahn, J.; Romoli, C.; Reville, B.; Giacinti, G.; Tuffs, R.; Hinton, J.A. Ultra-high Energy Inverse Compton Emission from Galactic Electron Accelerators. Astrophys. J. Lett. 2021, 908, L49. [Google Scholar] [CrossRef]
- Faucher-Giguère, C.A.; Kaspi, V.M. Birth and Evolution of Isolated Radio Pulsars. Astrophys. J. 2006, 643, 332–355. [Google Scholar] [CrossRef]
- Gelfand, J.D.; Slane, P.O.; Zhang, W. A Dynamical Model for the Evolution of a Pulsar Wind Nebula Inside a Nonradiative Supernova Remnant. Astrophys. J. 2009, 703, 2051–2067. [Google Scholar] [CrossRef]
- Torres, D.F.; Lin, T. Discovery and Characterization of Superefficiency in Pulsar Wind Nebulae. Astrophys. J. Lett. 2018, 864, L2. [Google Scholar] [CrossRef]
- Bandiera, R.; Bucciantini, N.; Martín, J.; Olmi, B.; Torres, D.F. Reverberation of pulsar wind nebulae (I): Impact of the medium properties and other parameters upon the extent of the compression. Not. R. Astron. Soc. Lett. 2020, 499, 2051–2062. [Google Scholar] [CrossRef]
- Temim, T.; Slane, P.; Kolb, C.; Blondin, J.; Hughes, J.P.; Bucciantini, N. Late-Time Evolution of Composite Supernova Remnants: Deep Chandra Observations and Hydrodynamical Modeling of a Crushed Pulsar Wind Nebula in SNR G327.1-1.1. Astrophys. J. 2015, 808, 100. [Google Scholar] [CrossRef]
- Acero, F.; Ackermann, M.; Ajello, M.; Albert, A.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; et al. Fermi Large Area Telescope Third Source Catalog. Astrophys. J. Suppl. Ser. 2015, 218, 23. [Google Scholar] [CrossRef]
- Adriani, O.; Barbarino, G.C.; Bazilevskaya, G.A.; Bellotti, R.; Boezio, M.; Bogomolov, E.A.; Bonechi, L.; Bongi, M.; Bonvicini, V.; Bottai, S.; et al. An anomalous positron abundance in cosmic rays with energies 1.5-100GeV. Nature 2009, 458, 607–609. [Google Scholar] [CrossRef]
- Aguilar, M.; Alberti, G.; Alpat, B.; Alvino, A.; Ambrosi, G.; Andeen, K.; Anderhub, H.; Arruda, L.; Azzarello, P.; Bachlechner, A.; et al. First Result from the Alpha Magnetic Spectrometer on the International Space Station: Precision Measurement of the Positron Fraction in Primary Cosmic Rays of 0.5-350 GeV. Phys. Rev. Lett. 2013, 110, 141102. [Google Scholar] [CrossRef] [PubMed]
- Bykov, A.M.; Amato, E.; Petrov, A.E.; Krassilchtchikov, A.M.; Levenfish, K.P. Pulsar Wind Nebulae with Bow Shocks: Non-thermal Radiation and Cosmic Ray Leptons. Space Sci. Rev. 2017, 207, 235–290. [Google Scholar] [CrossRef]
- Olmi, B.; Bucciantini, N. On the origin of jet-like features in bow shock pulsar wind nebulae. Not. R. Astron. Soc. Lett. 2019, 490, 3608–3615. [Google Scholar] [CrossRef]
- Hui, C.Y.; Becker, W. X-ray emission properties of the old pulsar PSR B2224+65. Astron. Astrophys. 2007, 467, 1209–1214. [Google Scholar] [CrossRef]
- Pavan, L.; Bordas, P.; Pühlhofer, G.; Filipović, M.D.; De Horta, A.; O’Brien, A.; Balbo, M.; Walter, R.; Bozzo, E.; Ferrigno, C.; et al. The long helical jet of the Lighthouse nebula, IGR J11014-6103. Astron. Astrophys. 2014, 562, A122. [Google Scholar] [CrossRef]
- De Vries, M.; Romani, R.W. PSR J2030+4415’s Remarkable Bow Shock, PWN, and Filament. Astrophys. J. Lett. 2020, 896, L7. [Google Scholar] [CrossRef]
- Kim, S.I.; Hui, C.Y.; Lee, J.; Oh, K.; Lin, L.C.C.; Takata, J. A deep X-ray spectral imaging of the bow-shock pulsar wind nebula associated with PSR B1929+10. Astron. Astrophys. 2020, 637, L7. [Google Scholar] [CrossRef]
- Zhang, S.; Zhu, Z.; Li, H.; Pasham, D.; Li, Z.; Clavel, M.; Baganoff, F.K.; Perez, K.; Mori, K.; Hailey, C.J. NuSTAR and Chandra Observations of the Galactic Center Nonthermal X-ray Filament G0.13-0.11: A Pulsar-wind-nebula-driven Magnetic Filament. Astrophys. J. 2020, 893, 3. [Google Scholar] [CrossRef]
- Wang, Q.D. X-ray Jet, Counter-jet, and Trail of the Fast-moving Pulsar PSR B2224+65. Res. Notes Am. Astron. Soc. 2021, 5, 5. [Google Scholar] [CrossRef]
- Abeysekara, A.U.; Albert, A.; Alfaro, R.; Alvarez, C.; Álvarez, J.D.; Arceo, R.; Arteaga-Velázquez, J.C.; Avila Rojas, D.; Ayala Solares, H.A.; Barber, A.S.; et al. Extended gamma-ray sources around pulsars constrain the origin of the positron flux at Earth. Science 2017, 358, 911–914. [Google Scholar] [CrossRef] [PubMed]
- Evoli, C.; Linden, T.; Morlino, G. Self-generated cosmic-ray confinement in TeV halos: Implications for TeV γ-ray emission and the positron excess. Phys. Rev. D 2018, 98, 063017. [Google Scholar] [CrossRef]
- Fang, K.; Bi, X.J.; Yin, P.F. Possible origin of the slow-diffusion region around Geminga. Not. R. Astron. Soc. Lett. 2019, 488, 4074–4080. [Google Scholar] [CrossRef]
- Sudoh, T.; Linden, T.; Beacom, J.F. TeV halos are everywhere: Prospects for new discoveries. Phys. Rev. D 2019, 100, 043016. [Google Scholar] [CrossRef]
- Giacinti, G.; Mitchell, A.M.W.; López-Coto, R.; Joshi, V.; Parsons, R.D.; Hinton, J.A. Halo fraction in TeV-bright pulsar wind nebulae. Astron. Astrophys. 2020, 636, A113. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amato, E.; Olmi, B. The Crab Pulsar and Nebula as Seen in Gamma-Rays. Universe 2021, 7, 448. https://doi.org/10.3390/universe7110448
Amato E, Olmi B. The Crab Pulsar and Nebula as Seen in Gamma-Rays. Universe. 2021; 7(11):448. https://doi.org/10.3390/universe7110448
Chicago/Turabian StyleAmato, Elena, and Barbara Olmi. 2021. "The Crab Pulsar and Nebula as Seen in Gamma-Rays" Universe 7, no. 11: 448. https://doi.org/10.3390/universe7110448
APA StyleAmato, E., & Olmi, B. (2021). The Crab Pulsar and Nebula as Seen in Gamma-Rays. Universe, 7(11), 448. https://doi.org/10.3390/universe7110448





