1. Introduction
Quasi-periodic oscillations (QPOs) of X-ray power spectral density have been observed at low (Hz) and high (kHz) frequencies and were discovered in the eighties [
1,
2]. Quasi-period oscillations have also been observed in supermassive black hole light curves and, recently, the source went through burst alert telescope (BAT) onboard Swift. Their importance is due to the fact that QPOs, peak features in the X-rays observed from stellar-mass BHs and neutron stars, are likely to arise from quite near the compact object itself and exhibit frequencies that scale inversely with the black hole mass, which allows us to probe and study the nature of accretion in highly curved space–time (for a review, see for example [
3]).
One of the first QPO models is the relativistic precession model (RPM) that identifies the twin-peak QPO frequencies with the Keplerian and periastron frequencies. In the past years, the RPM has served to explain the twin-peak QPOs in several LMXBs. However, this model has some difficulties explaining the relatively large observed high frequencies of QPO amplitudes and inferred existence of preferred orbits. To modify this model, the high frequencies QPOs (two-picks) are considered as the resonances between oscillation modes of the accreted fluid—the well-known ratio 3:2 epicyclic resonance model—identify the resonant frequencies with frequencies of radial and vertical epicyclic axisymmetric modes of disc oscillations. The correlation is a cost of resonant corrections to these frequencies. The secret of this 3:2 ratio has still not been clearly revealed, and the oscillations occur only in certain states of luminosity, and hardness.
In this paper, we are motivated by the success of the above models, and we assume the QPOs are caused by the fundamental epicyclic frequencies associated with orbital motion of the matter in the accretion disc and their combinations.
We present our work on the background of a distorted, deformed compact object which is static and axisymmetric. This background is the simplest generalization of the so-called
-metric up to quadrupole moments [
4]. This metric has two parameters, aside from the central object’s mass; namely the distortion parameter and the deformation parameter, where in the absence of one or the other, one can recover either the
-metric or distorted Schwarzschild metric [
5]. From a dynamical point of view, these parameters can be seen as perturbation parameters of the Schwarzschild space–time. We explain this metric briefly in
Section 2. In this respect, the first static and axially symmetric solution with arbitrary quadrupole moment are described by Weyl [
6]. Later, Erez and Rosen introduced a static solution with arbitrary quadrupole in prolate spheroidal coordinates [
7]. Then, Zipoy and Voorhees introduced an equivalent form [
8,
9] and, later on, by representing this metric in terms of a new parameter
, which is known as
-metric [
10]. This area of study has been discussed extensively in the literature and generalized in many respects [
11,
12,
13,
14], among many others.
There are several motives to study the circular motion of particles in this background. In the relativistic astrophysical study, it is assumed that astrophysical compact objects are described by the Schwarzschild or Kerr space–times. However, besides these setups, others can imitate a black hole’s properties, such as the electromagnetic signature. Thus, it is also possible that some astrophysical observations cannot be fitted within the general theory of relativity by using the Schwarzschild or Kerr metric [
15]. Moreover, the astrophysical systems are not always isolated as they are surrounded by different kinds of matter and radiation. In a more realistic scenario, the rotation should be taken into account; however, the possibility of observed resonant oscillations when they occur in the inner parts of accretion flow has been directly demonstrated, even if the source of radiation is steady and perfectly axisymmetric [
16]. Therefore, this work could serve to constitute a reasonable model of a real situation that arises in the vicinity of this compact object, where it is not always isolated, with the possibility of analytic analysis through exercising parameters of the model where they can be treated as the degrees of freedom of the system and link the model to the observations.
In this paper, we also investigate dynamics of test particles in this background. This discussion can approximate a diluted astrophysical plasma’s complex dynamics, where they can be located around the system.
The paper’s organization is as follows:
Section 2 presents the background object and a study of the motion of test particles in this background.
Section 3 explains epicyclic frequencies and stable circular geodesics. The parametric resonances are presented in
Section 4. Finally, the conclusions are summarized in
Section 5.
Throughout this work, we use the signature and geometric unit system , unless otherwise specified. Latin indices run from 1 to 3, while Greek ones take values from 0 to 3.
2. Space–Time of a Distorted, Deformed Compact Object
In this work, we consider generalized
-metric, which has
-metric as the seed metric and considers the existence of a static and axially symmetric external distribution of matter in its vicinity up to quadrupole. By its construction, this metric is only valid locally [
5]. The metric has this form
where
,
,
, and
.
M is a parameter that can be identified as the mass of the body generating the field, which is expressed in the dimension of length. The function
plays the role of gravitational potential, and the function
is obtained by an integration of the explicit form of the function
. These are given by
This metric contains three parameters, namely the total mass,
deformation parameter, and
distortion parameter, which are taken to be relatively small and connected to the central object and the presence of external mass distribution, respectively. In the case of
, it turns to the
-metric, and in the case of
, the Schwarzschild metric is recovered. This metric may associate the observable effects to these parameters as new physical degrees of freedom. The relation between the prolate spheroidal coordinates
and the Schwarzschild coordinates
is given by
In addition, the related kinematic quantities in this background, specific energy, angular momentum, and Keplerian orbital frequency, respectively, read as
where
Furthermore, by analyzing the effective potential, we can have general properties of the dynamics of a particle in this background. The effective potential in the equatorial plane is given by this relation [
4]:
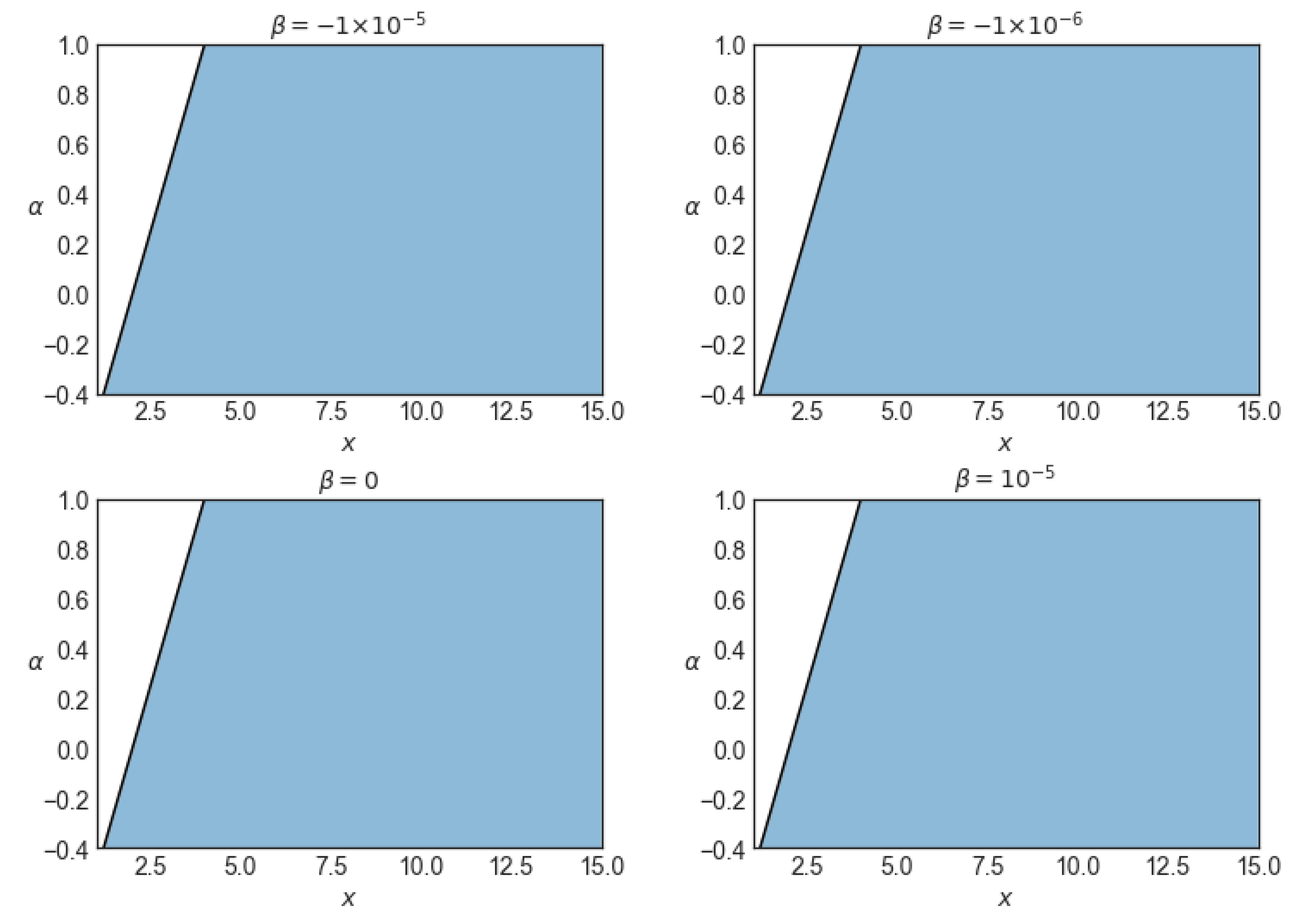
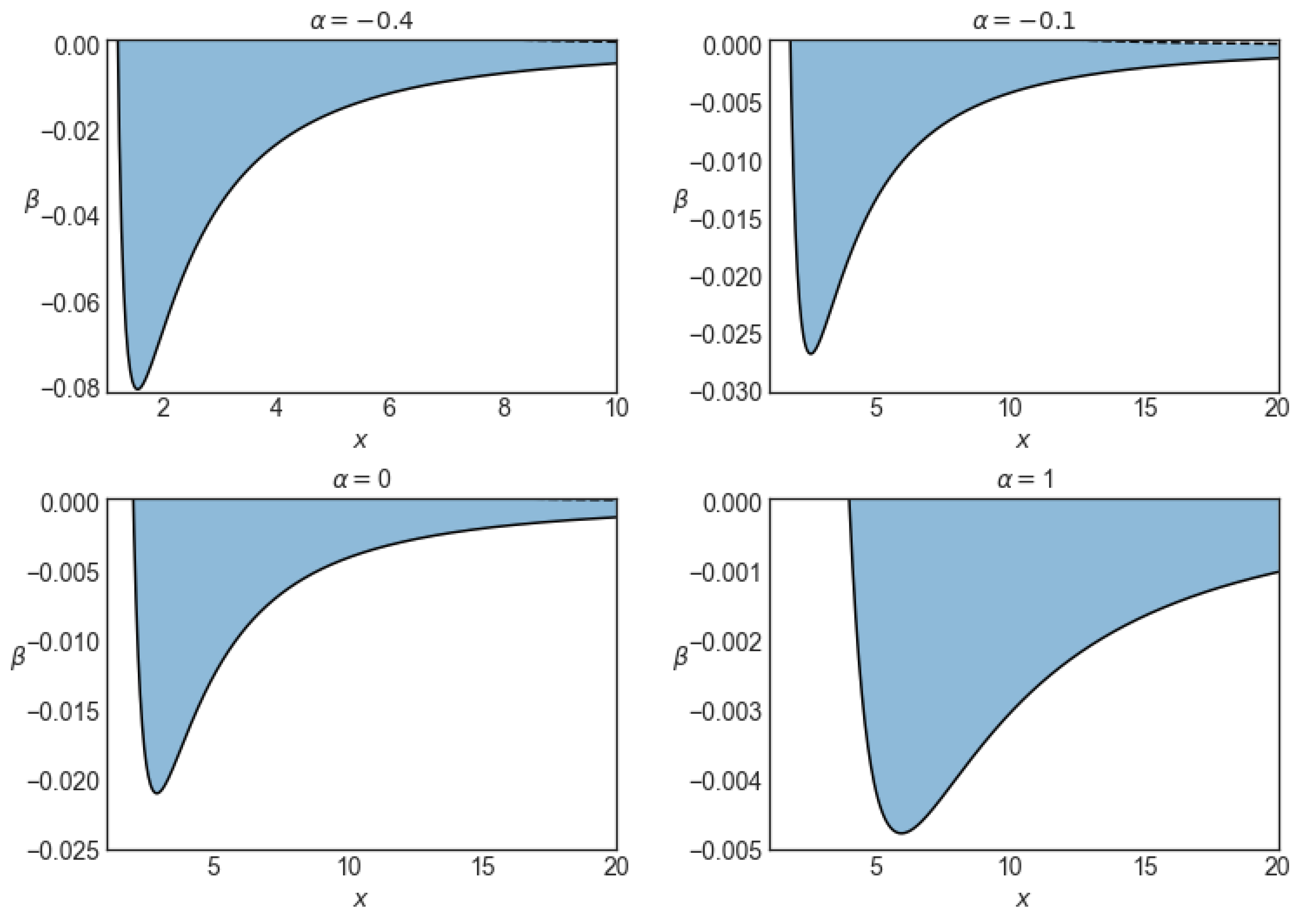
The domain of existence of the circular orbits in the equatorial plane is plotted in
Figure 1 and
Figure 2. In
Figure 1, this domain is plotted in the (
)-plane in terms of the distorted parameter
, while in
Figure 2 this region is plotted in the (
)-plane for a range of values of the deformation parameter
.
Following the standard procedure using effective potential, possible types of orbits, in general, dependent on the parameters , , L, , and . However, in what follows, we only discussed bounded timelike trajectories as we are interested in studying oscillation of particle for a small perturbation of the orbit; however, the test particles’ motion can be chaotic in this background for some combinations of parameters and .
Figure 3 corresponds to the existence of both initial conditions on inner and outer boundaries, where particles trapped in some region form a toroidal shape around the central object. The trajectories for some choices of the parameters are plotted, where a rapid inspection shows that the trajectories of the particle noticeably change when the parameters change.
3. Epicyclic Frequencies and Stability of Circular Geodesics
In the accretion disc processes, a variety of oscillatory motions are generally expected. In this regard, circular and quasi-circular orbits seem to be crucial. In the study of the relativistic accretion disc, three frequencies are relevant. The Keplerian orbital frequency , radial frequency , and the vertical frequency . A resonance between these frequencies can be a source of quasi-periodic oscillations that leads to chaotic and quasi-periodic variability in X-ray fluxes observations in many galactic objects.
In the relativistic precession model (RPM) of QPO, it is assumed that this oscillation caused by the epicyclic frequencies associated with the quasi-Keplerian motion in the accretion discs. In RPM, the upper frequency is defined as the Keplerian frequency and the lower frequency is defined as the periastron frequency, i.e., . Their correlations are obtained by varying the radius of the associated circular orbit in a reasonable range. Within this framework, it is usually assumed that the variable components of the observed X-ray signal are placed in a bright localized spot or blob orbiting the compact object on a slightly eccentric orbit. Therefore, because of the relativistic effects, the observed radiation is supposed to be periodically modulated.
To study the stability of circular geodesics in the equatorial plane, we start by considering the geodesic equation for a test particle
and substitute
as we are in the equatorial plane. To describe the more general class of orbits that slightly deviate from the circular geodesics in the equatorial plane
, we consider this diffeomorphism
. If we write the geodesic equation for this perturbation, by considering terms up to linear order in
, we obtain [
17]
where
where the 4-velocity for the circular orbits in the equatorial plane is
. Then, integration of the Equation (
11) for the
t and
components leads to
where, in the first equation,
can be taken
t or
, and
This system of equations describes the free radial phase and vertical oscillations of a particle around the circular geodesics
1. The sign of frequencies
and
determine the dynamics and leads to having a circular orbit that is either stable or unstable. Indeed, even a tiny perturbation can cause a strong deviation from the unperturbed path.
In the Schwarzschild solution, these frequencies in spheroidal coordinates are given by
In Schwarzschild space–time, the stability of the circular orbits is determined only by the radial epicyclic frequency, since the vertical frequency coincides with the orbital frequency
. As is seen from the Equation (
19), the vertical epicyclic frequency is a monotonically decreasing function of
x, and we have
, and there also exists a periapsis shift for bounded quasi-elliptic trajectory, implying the effect of relativistic precession that changes the radius of the orbit [
19]. Indeed, the ordering between frequencies contributes to the possible resonances that may occur in a given background. Furthermore, the behavior of the frequencies helps us to distinguish possible trajectories around a stable circular orbit.
These epicyclic frequencies in the background of a distorted and deformed compact object are written as
where
where
S is given as before
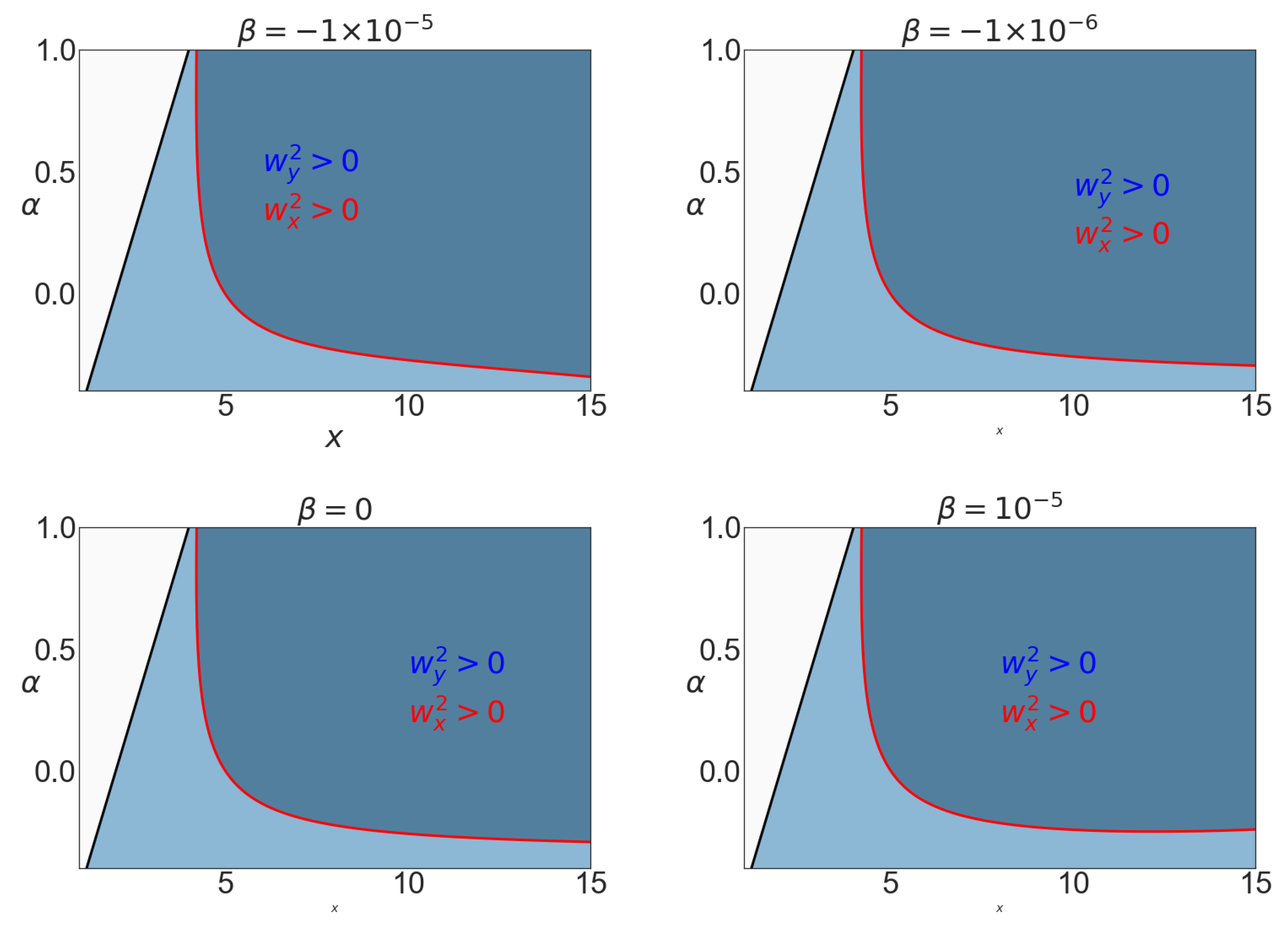
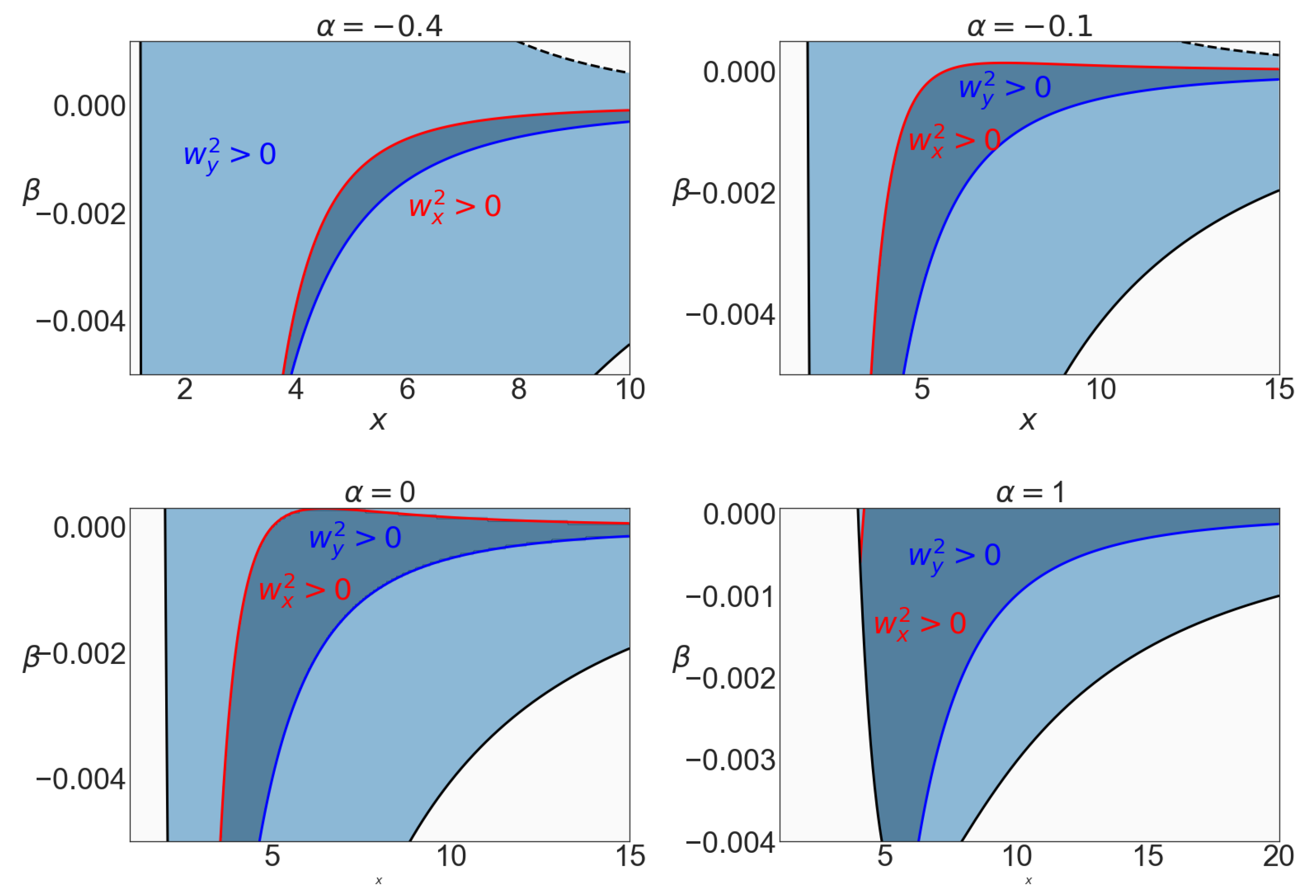
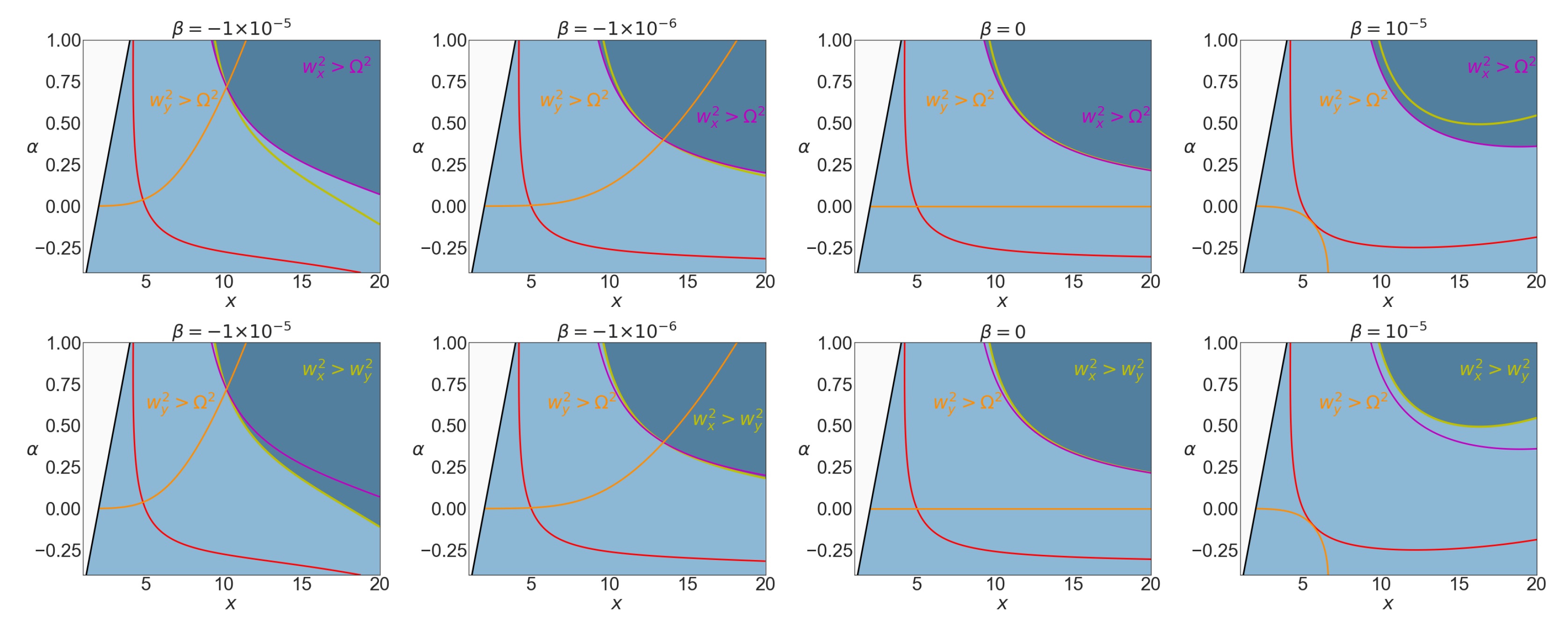
Note that these frequencies are measured regarding the proper time of a comoving observer. The signs of these fundamental frequencies provide a natural condition of having the valid domain of existence of circular and quasi-circular orbits. We explore these frequencies and the valid region more perspicaciously on
Figure 4 and
Figure 5.
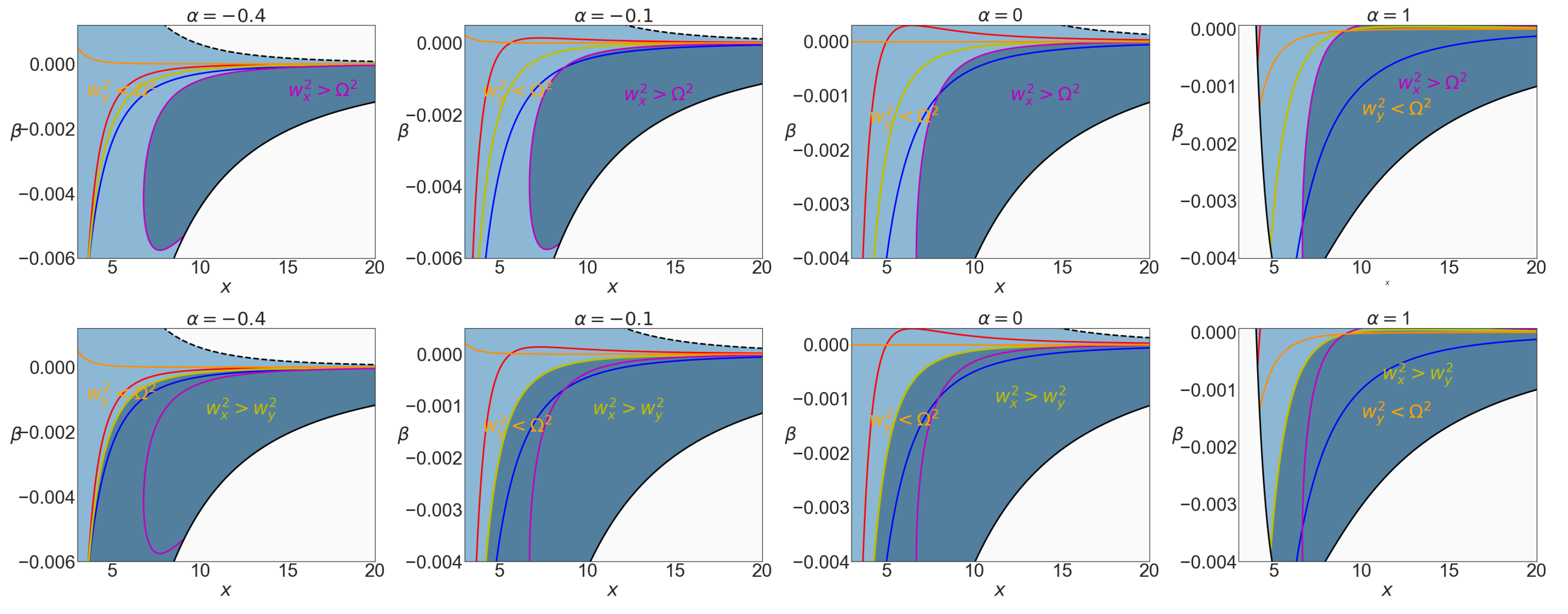
In
Figure 4, the region of stability of the timelike circular geodesics is plotted in the
-plane for different values of the distortion parameter
, and in
Figure 5, in the
-plane for different values of the deformation parameter
. In
Figure 4, as the sign of radial frequency suggests: outside the red curve and in the blue region the timelike geodesics are unstable for radial perturbations but stable for the vertical ones. In
Figure 5, both the curves
and
are depicted. The dark region is then bounded by these two curves and shows the stable domain. Comparing these two figures shows that the effect of parameter
is more profound than
. However, increasing
tends to shrink the range of
in the valid region.
The interesting situation in this background, contrary to the Schwarzschild case, is the various ordering possibilities that arise among frequencies. For analyzing the order of magnitude of these frequencies, we analyze the frequency ratio
These parameters and are not independent of each other; fixing one of them restricts the other’s domain. For example, for a small enough parameter , we have this range of orders for parameter
In
Figure 6, the different epicyclic frequencies in the (
)-plane for different values and signs of the distortion parameter
are plotted. In addition, curves of
,
and
are specified. Moreover, in the first row, the dark area represents where
, and in the second row, it represents where
. We illustrated both in one panel to ensure it would be easy to compare and analyze the behavior of different regions. In
Figure 7, the different epicyclic frequencies are also presented in the (
)-plane for different values of the deformation parameter
. In fact, this ordering is influenced by the signs and values of both parameters
and
.
By considering
Figure 6 and
Figure 7, we can extract interesting information about the order of the epicyclic frequencies in this background: in
Figure 6, in the
-plane, if we are interested in the order of the frequencies above the red line where
and
are both positives, we see that the ordering change after intersections. One appears when the red curve crossing the orange curve and the other one when the three yellow, pink, and orange curves cross each other, namely where we have
.
Thus, the first possibility is above the red curve, where there is no intersection point, then we have
. On the contrary, if a crossing point between the red and the orange appears, both situations
and
are possible. However, the existence of the second crossing point makes the order among the three frequencies even more varied. In the following, we present the order for different cases concerning different situations. In the second row of
Figure 6, we can extract three different orderings:
- (i)
from the red curve to the pink curve: ;
- (ii)
from the pink line to the yellow line: ;
- (iii)
from the yellow line to the top: .
In addition, for several different regions appear:
- (i)
above the red curve and below the orange, three regions present:
- (a)
below the pink and the yellow: ;
- (b)
above the yellow and below the pink (small area): ;
- (c)
above the yellow and the pink: .
- (ii)
above the red curve and the orange one, three regions appear:
- (a)
below the pink and the yellow: ;
- (b)
above the pink and below the yellow (small area): ;
- (c)
above the yellow and the pink: .
One can conclude the same results also by using
Figure 7.
4. Parametric Resonances
Before the twin-peak HF QPOs were discovered in microquasars, this existence and ratio, also their rational ratio due to the resonances in quasi-Keplerian accretion discs, was expected [
20,
21]. Apparently, this fact is well supported by observations. In addition, this 3:2 ratio as the ratio of
:
is seen most often in the twin HF QPOs in the LMXB containing microquasars.
In this section, we study this phenomena by means of parametric resonance and following the standard procedure utilizing the Mathieu’s equation [
22]. This equation is a linear second-order ODE, which differs from the one corresponding to a harmonic oscillator in the existence of a periodic and sinusoidal forcing of the stiffness coefficient as
, and is given by
where
is the amplitude of the excitation (forcing) term,
is its excited frequency, and
is the natural, unexcited frequency.
It is well known that this setup performs free oscillation around the stable equilibrium case. If the stiffness term contains the parametric excitation, i.e., , the motion can stay bounded, which is referred to as stable, otherwise the motion becomes unbounded and is referred to as unstable.
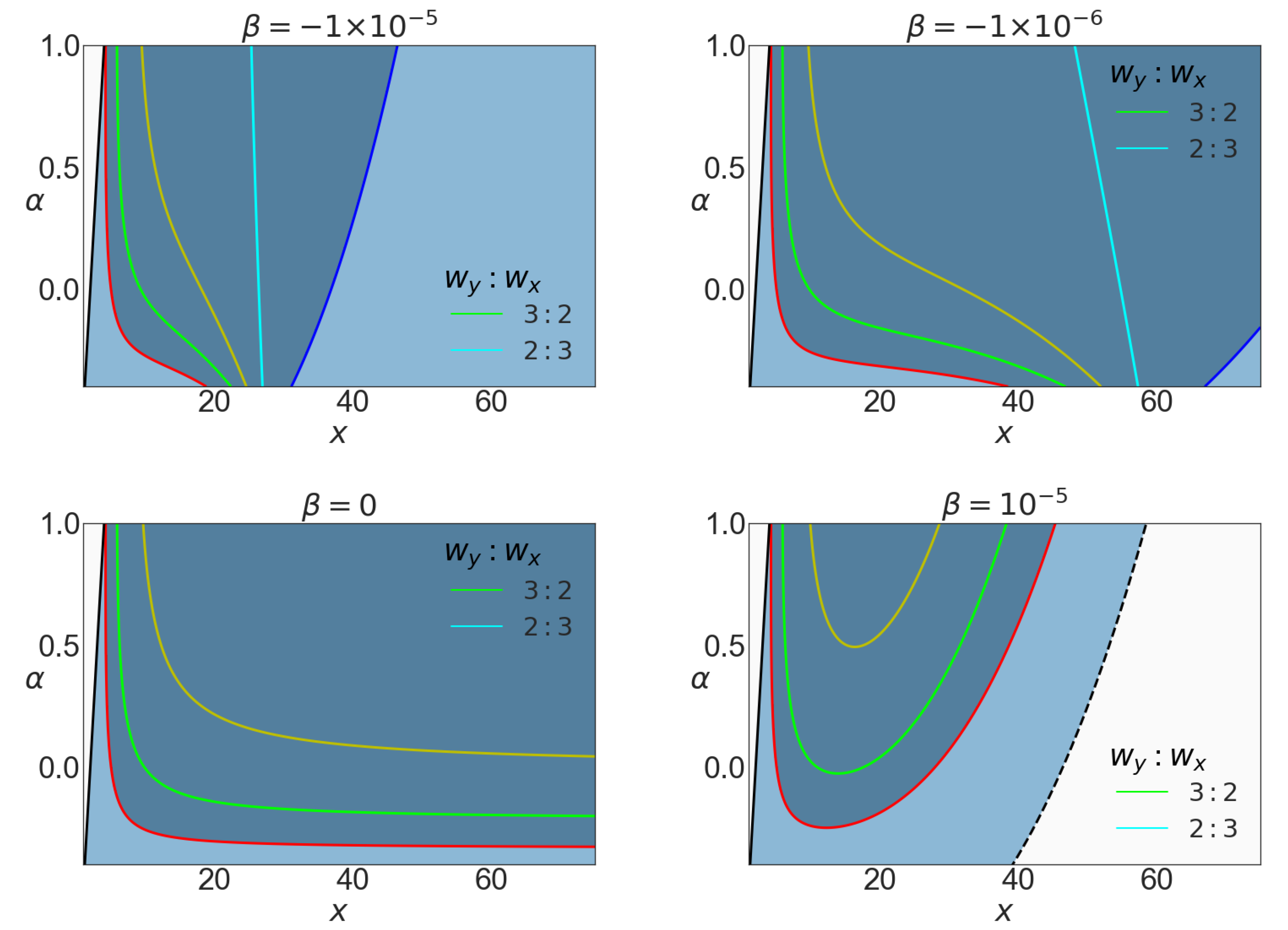
The resonance excitation arises for special values of frequencies. In contrast to the standard resonance epicyclic model, the oscillating test particles in this background allow both frequency ratios
:
:2 and
:
:3, which can be relevant in other observed data, such as in different twin frequencies observed in the microquasar GRS
(see, for example [
23]). In
Figure 8 and
Figure 9, these resonance ratio for some chosen parameters are depicted. We can see that the 3:2 resonance in the physical range is always present, while it is not the case for this ratio 2:3. For instance, for a positive value of
, in the possible range for
, the 2:3 resonance ration is not possible.
The QPO models are based on the frequencies of the quasi-circular geodesic motion. However, we should mention that considering nongeodesic effects, such as fluid pressure, can modify these models. In QPO models, one can identify the upper and lower frequencies with different combinations of and such as , or , which can also produce the 3:2 ratio.
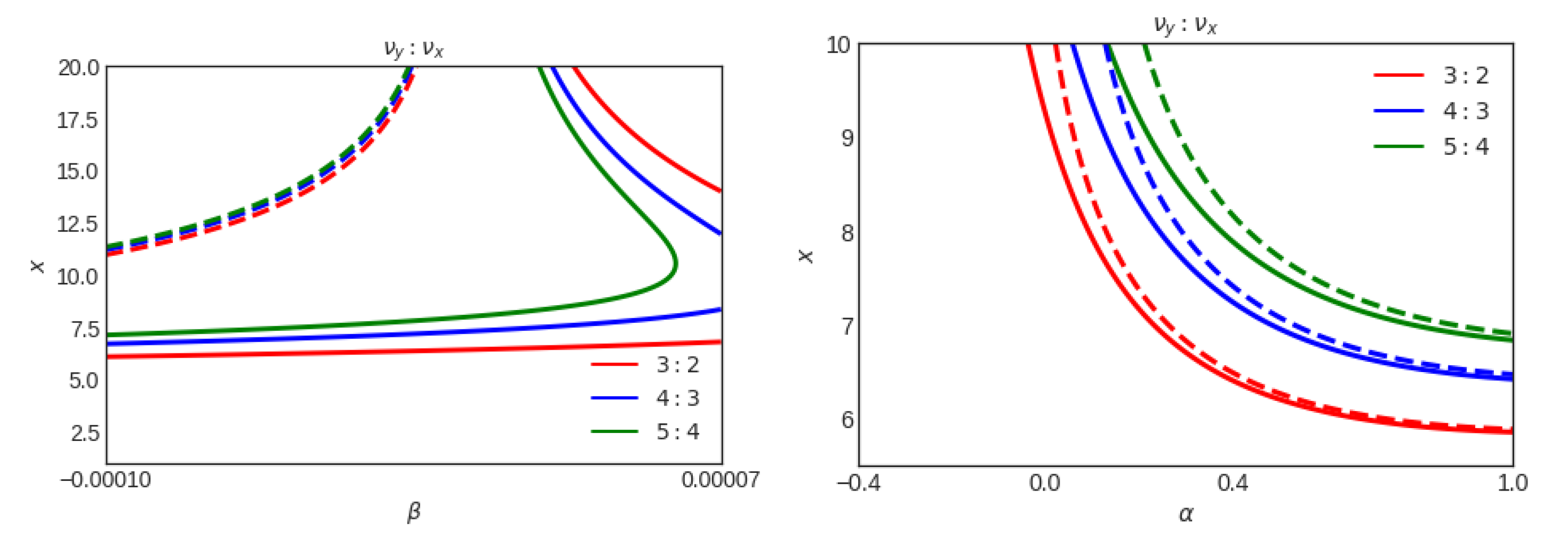
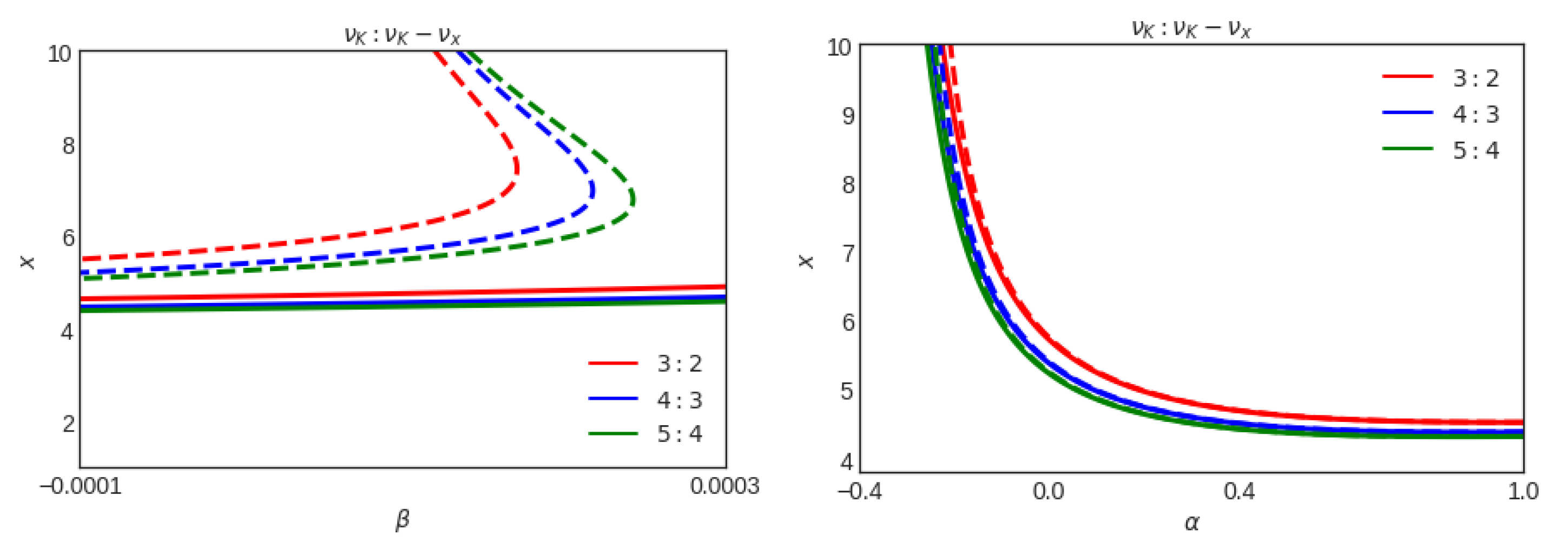
In
Figure 10 and
Figure 11, the location of the three ratios
={(3:2), (4:3), (5:4)} are plotted. In
Figure 10, we consider one of the models so-called EP and study the resonance between the vertical epicyclic frequency,
, and the radial one
with respect to
, and for two chosen values of
, also with respect to
, and are presented for two chosen values of
. In
Figure 11, the plots present the RP model, which is one of the promising models and shows the resonance between the Keplerian epicyclic frequency
and the periastron frequency
. In both figures, in the first row, we see that two radii satisfy the ratios
, and
. Moreover, increasing
tends to push the radius of the resonances outward. In the second row, the behavior of the radius is not sensitive to the value of
and is monotonically decreasing with the parameter
.
In addition, in
Figure 10 and
Figure 11, the ratios of epicyclic frequencies at the maximum of
are depicted. We see that the curves take their minimum at different radii depending on the choice of
. In all cases, the positive and negative values of
almost take their maximum at the same ratios; however, further analysis reveals that this radius is smaller for its negative values. In addition, the maximum depend on the ratio; for example, we see that as this ratio becomes larger, the maximum shifted in the smaller radius.
We also presented the result of fitting the oscillation frequencies to the observed frequencies data for the three microquasars GRS
, XTE
, and GRO
in
Figure 12. While considering rotation may modify the radial profiles of the vertical and horizontal frequencies, these preliminary results show that the fitting can be conducted even for the fast rotating microquasar as GRS
and GRO
. In fact, the work in progress shows that the positive
can play the role of the corotating Kerr, and its negative value the role of counter-rotating case in the part closer to the central object. However, we focus on the fitting in the case of a relatively slowly rotating XTE 1550 − 564 source, which is more compatible with our setup. As it shows, the parameter
is a more contributing factor. For vanishing
, the result is in good agreement with previous studies [
24,
25]. Further analysis reveals that we have a better fit for
. In addition, we expect to have a better fit for positive values of
. As a result, in
Figure 12, we see that there is a good agreement with the data for the ratio 3:2, which is the actual frequencies of the twin HF QPOs observed in this microquasars, and confirm the efficiency of the model. In general, the current results are encouraging and show improved accuracy in estimated parameters when attempting to fit the data.
5. Summary and Conclusions
This work investigated the dynamics of particles and quasi-periodic oscillation by studying the fundamental frequencies of circular motion around a deformed compact object up to the quadrupole. The metric is static, axisymmetric, and contains the distortion parameter
related to the surrounding matter and deformation parameter
linked to the central object, which are briefly explained in
Section 2. The dependency of these two parameters is reflected in the motion and epicyclic frequencies of particles that cause strong deviation from the corresponding quantities in the Schwarzschild case. In this respect, one can explore different orderings among fundamental frequencies and various possibilities to reproduce the ratio of 3:2, as well as other ratios via different combinations of parameters, which is not the case in either the Schwarzschild or in
-metric.
In general, the resonant phenomena of the radial and vertical oscillations at their frequency ratio 3:2 for different parameters can be adequately related to the frequencies of the twin 3:2 HF QPOs observed in the microquasars GRS , XTE , and GRO , especially for . The effect of parameters on the radial and vertical frequencies around a stable equatorial orbit is substantial. Moreover, different combinations can link to producing different effects of compact objects. In fact, this model may cover a variety of exciting applications in general relativity, gravitational waves and astrophysics.
A further step of this work can be considering rotation that leads to modifying the radial profiles of the vertical and radial frequencies, which is a work in progress. In addition, the magnetic field can serve as a fundamental input in this system to model more real astrophysical systems. One can also extend this work from a single particle to a complex system, such as accretion discs. Moreover, this model could serve as the initial conditions in future numerical simulations.