Dynamics of Charged Particles Moving around Kerr Black Hole with Inductive Charge and External Magnetic Field
Abstract
1. Introduction
2. Kerr Black Hole Immersed in External Magnetic Field
3. Effective Potential and Stable Circular Orbits
4. Numerical Investigations
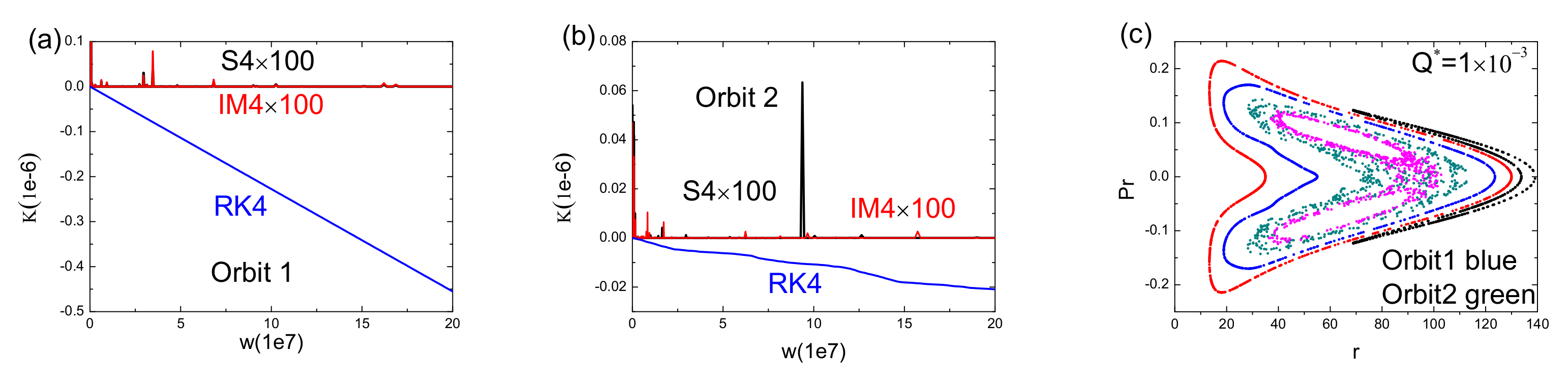
4.1. Explicit Symplectic Integrators
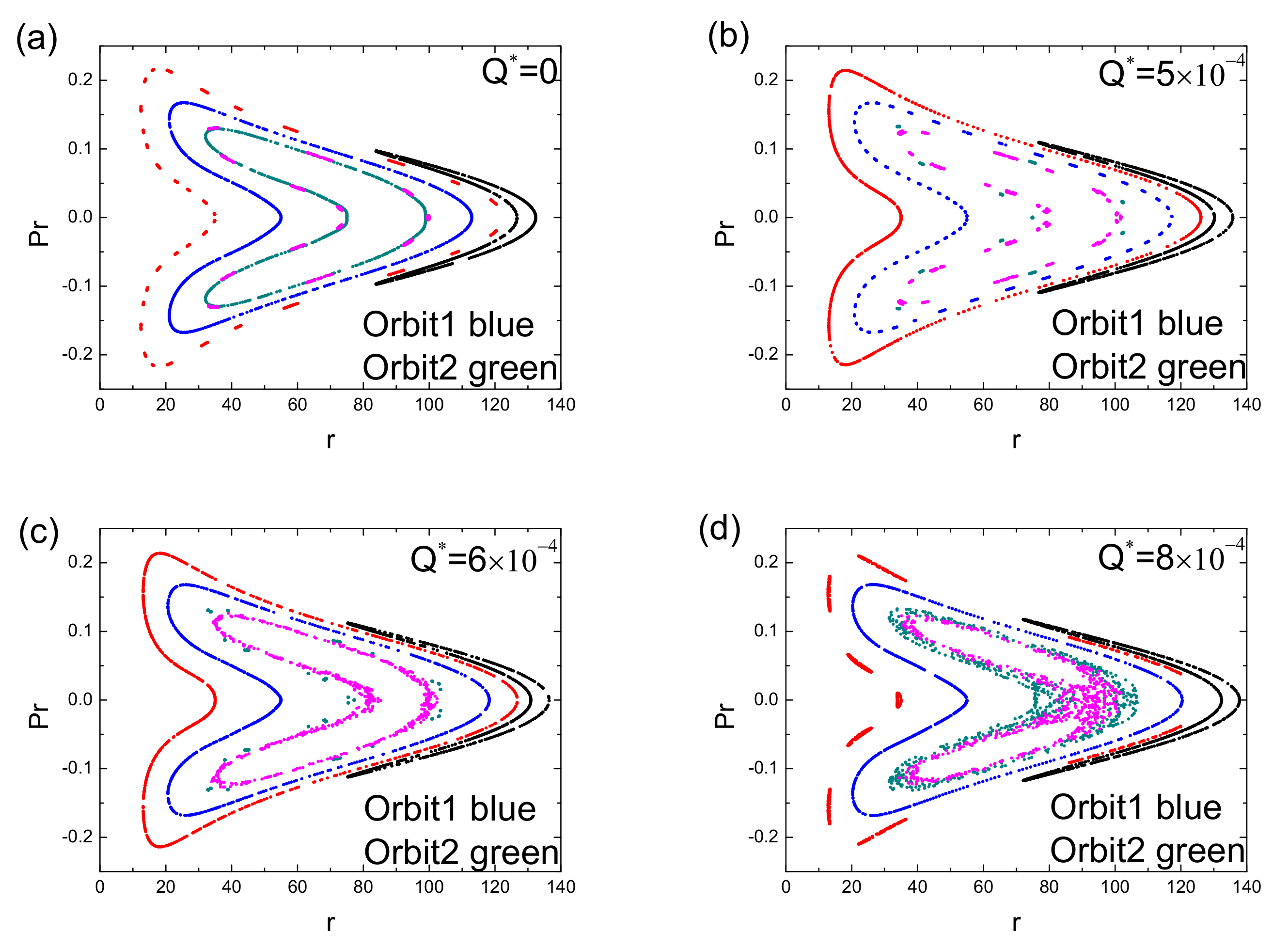
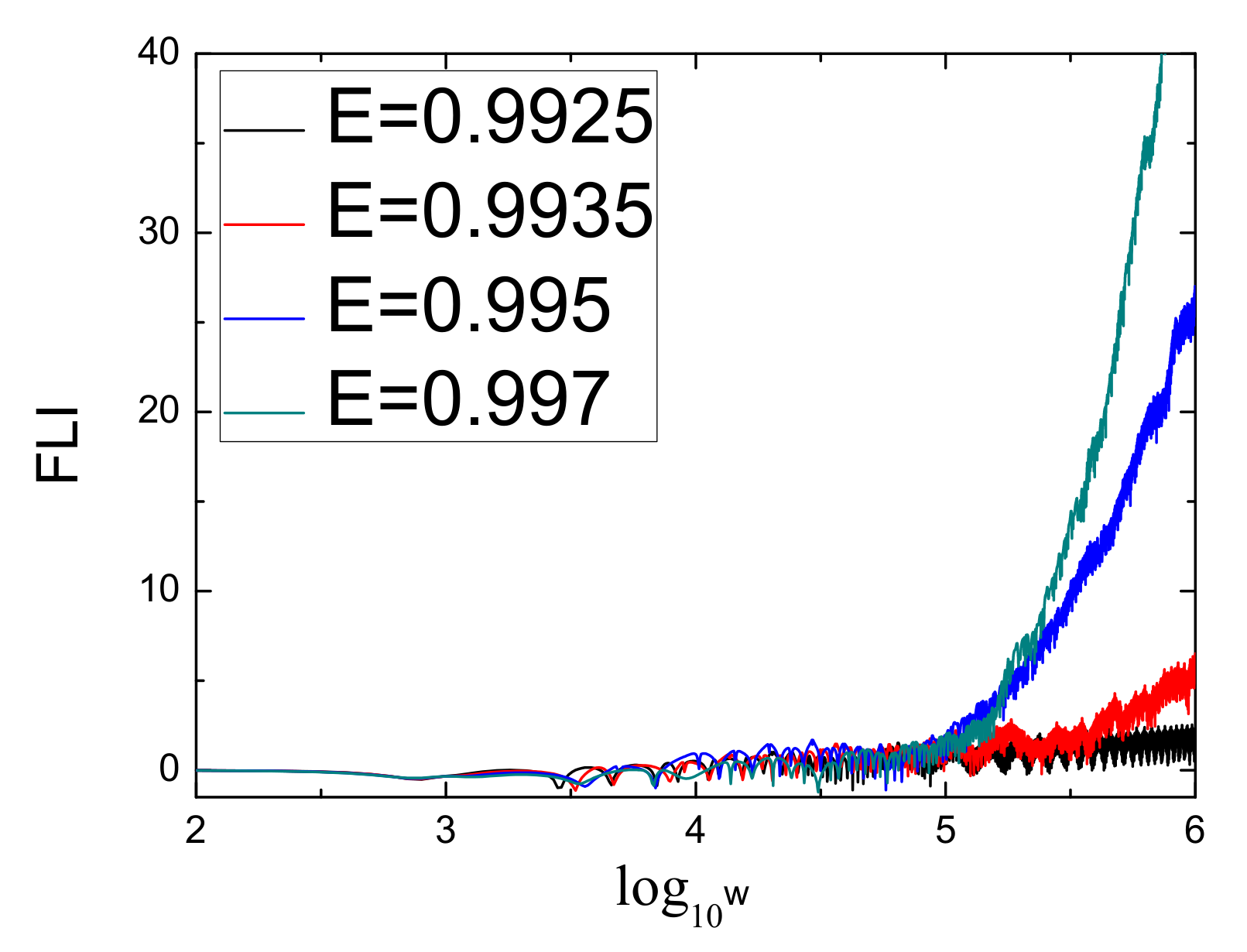
4.2. Dynamics of Generic Orbits
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First M87 Event Horizon Telescope Results. IV. Imaging the Central Supermassive Black Hole. Astrophys. J. 2019, 875, L4. [Google Scholar]
- Carter, B. Global Structure of the Kerr Family of Gravitational Fields. Phys. Rev. 1968, 174, 1559. [Google Scholar] [CrossRef]
- Eatough, R.P.; Falcke, H.; Karuppusamy, R.; Lee, K.J.; Champion, D.J.; Keane, E.F.; Desvignes, G.; Schnitzeler, D.H.F.M.; Spitler, L.G.; Kramer, M.; et al. A strong magnetic field around the supermassive black hole at the centre of the Galaxy. Nature 2013, 501, 391–394. [Google Scholar] [CrossRef] [PubMed]
- Wald, R.M. Black hole in a uniform magnetic field. Phys. Rev. D 1974, 6, 1068. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M. Acceleration of the charged particles due to chaotic scattering in the combined black hole gravitational field and asymptotically uniform magnetic field. Eur. Phys. J. C 2016, 76, 32. [Google Scholar] [CrossRef]
- Tursunov, A.; Stuchlík, Z.; Kološ, M. Circular orbits and related quasiharmonic oscillatory motion of charged particles around weakly magnetized rotating black holes. Phys. Rev. D 2016, 93, 084012. [Google Scholar] [CrossRef]
- Rayimbaev, J.R. Magnetized particle motion around non-Schwarzschild black hole immersed in an external uniform magnetic field. Astrophys. Space Sci. 2016, 361, 288. [Google Scholar] [CrossRef]
- Bambi, C.; Barausse, E. Final stages of accretion onto non-Kerr compact objects. Phys. Rev. D 2011, 84, 084034. [Google Scholar] [CrossRef]
- Chowdhury, A.N.; Patil, M.; Malafarina, D.; Joshi, P.S. Circular geodesics and accretion disks in the Janis-Newman-Winicour and gamma metric spacetimes. Phys. Rev. D 2012, 85, 104031. [Google Scholar] [CrossRef]
- Liang, E.P.T. Equatorial circular orbits of some static gravitational fields with naked singularities. Phys. Rev. D 1974, 9, 3257. [Google Scholar] [CrossRef]
- Aliev, A.; <i>o</i>¨zdemir, N. Motion of charged particles around a rotating black hole in a magnetic field. Mon. Not. R. Astron. Soc. 2002, 336, 241–248. [Google Scholar] [CrossRef]
- Takahashi, M.; Koyama, H. Chaotic motion of charged particles in an electromagnetic field surrounding a rotating black hole. Astrophys. J. 2009, 693, 472. [Google Scholar] [CrossRef]
- Pradhan, P.; Majumdar, P. Circular orbits in extremal Reissner-Nordstrom spacetime. Phys. Lett. A 2011, 375, 474–479. [Google Scholar] [CrossRef]
- Gladush, V.D.; Galadgyi, M.V. Some peculiarities of motion of neutral and charged test particles in the field of a spherically symmetric charged object in general relativity. Gen. Relat. Gravit. 2011, 43, 1347–1363. [Google Scholar] [CrossRef][Green Version]
- Pugliese, D.; Quevedo, H.; Ruffini, R. Circular motion of neutral test particles in Reissner-Nordstrom spacetime. Phys. Rev. D 2011, 83, 024021. [Google Scholar] [CrossRef]
- Pugliese, D.; Quevedo, H.; Ruffini, R. Equatorial circular motion in Kerr spacetime. Phys. Rev. D 2011, 84, 044030. [Google Scholar] [CrossRef]
- Pugliese, D.; Quevedo, H.; Ruffini, R. Motion of charged test particles in Reissner-Nordstrom spacetime. Phys. Rev. D 2011, 83, 104052. [Google Scholar] [CrossRef]
- Stuchl<i>i</i>´k, Z.; Kolo<i>s</i>˘, M. String loops in the field of braneworld spherically symmetric black holes and naked singularities. J. Cosmol. Astropart. Phys. 2012, 10, 8. [Google Scholar]
- Patil, M.; Joshi, P.S. Acceleration of particles by Janis-Newman-Winicour singularities. Phys. Rev. D 2012, 85, 104014. [Google Scholar] [CrossRef]
- Kopáček, O.; Karas, V. Inducing chaos by breaking axial symmetry in a black hole magnetosphere. Astrophys. J. 2014, 787, 117. [Google Scholar] [CrossRef]
- Lim, Y.-K. Motion of charged particles around a magnetized/electrified black hole. Phys. Rev. D 2015, 91, 024048. [Google Scholar] [CrossRef]
- Kolos, M.; Stuchlík, Z.; Tursunov, A. Quasi-harmonic oscillatory motion of charged particles around a Schwarzschild black hole immersed in a uniform magnetic field. Class. Quantum Gravity 2015, 32, 165009. [Google Scholar] [CrossRef]
- Panis, R.; Kološ, M.; Stuchlík, Z. Determination of chaotic behaviour in time series generated by charged particle motion around magnetized Schwarzschild black holes. Eur. Phys. C 2019, 79, 479. [Google Scholar] [CrossRef]
- Bokhari, A.H.; Rayimbaev, J.; Ahmedov, B. Test particles dynamics around deformed Reissner-Nordström black hole. Phys. Rev. D 2020, 102, 124078. [Google Scholar] [CrossRef]
- Igata, T.; Ishihara, H.; Takamori, Y. Stable Bound Orbits of Massless Particles around a Black Ring. Phys. Rev. D 2013, 87, 104005. [Google Scholar] [CrossRef]
- Igata, T. Stable bound orbits in six-dimensional Myers-Perry black holes. Phys. Rev. D 2015, 92, 024002. [Google Scholar] [CrossRef]
- Rincón, Á.; Panotopoulos, G.; Lopes, I.; Cruz, N. ISCOs and OSCOs in the Presence of a Positive Cosmological Constant in Massive Gravity. Universe 2021, 7, 278. [Google Scholar] [CrossRef]
- Schroven, K.; Grunau, S. The ISCO of charged particles in Reissner-Nordström, Kerr–Newman and Kerr-Sen spacetime. Phys. Rev. D 2021, 103, 024016. [Google Scholar] [CrossRef]
- Koch, B.; Saueressig, F. Black holes within asymptotic safety. Int. J. Modern Phys. A 2014, 29, 1430011. [Google Scholar] [CrossRef]
- Cristopher, G.; Benjamin, K. Improved Reissner-Nordström-(A)dS Black Hole in Asymptotic Safety. Int. J. Modern Phys. A 2016, 31, 1650141. [Google Scholar]
- Koch, B.; Reyes, I.A.; Rincoén, Á. A scale dependent black hole in three-dimensional space-time. Class. Quantum Gravity 2016, 33, 225010. [Google Scholar] [CrossRef]
- Brans, C.; Dicke, R.H. Mach’s Principle and a Relativistic Theory of Gravitation. Phys. Rev. 1961, 124, 925. [Google Scholar] [CrossRef]
- Brans, C. Mach’s Principle and a Relativistic Theory of Gravitation. II. Phys. Rev. 1961, 125, 2194. [Google Scholar] [CrossRef]
- Bonanno, A.; Reuter, M. Renormalization group improved black hole spacetimes. Phys. Rev. D 2000, 62, 043008. [Google Scholar] [CrossRef]
- Rincó, Á.; Panotopoulos, G. Quasinormal modes of scale dependent black holes in (1+2)-dimensional Einstein-power-Maxwell theory. Phys. Rev. D 2018, 97, 024027. [Google Scholar] [CrossRef]
- Hackmann, E.; Xu, H. Charged particle motion in Kerr–Newmann space-times. Phys. Rev. D 2013, 87, 124030. [Google Scholar] [CrossRef]
- Esteban, E.P.; Ramos, E. Rotating black hole in an external electromagnetic field. Phys. Rev. D 1988, 38, 2963. [Google Scholar] [CrossRef]
- Esteban, E.P.; Medina, I.R. Accretion onto black holes in external magnetic fields. Phys. Rev. D 1990, 42, 307. [Google Scholar] [CrossRef]
- Karas, V.; Vokrouhlicky, D. Chaotic motion of test particles in the Ernst space-time. Gen. Relat. Gravit. 1992, 24, 729–743. [Google Scholar] [CrossRef]
- Nakamura, Y.; Ishizuka, T. Motion of a Charged Particle Around a Black Hole Permeated by Magnetic Field and its Chaotic Characters. Astrophys. Space Sci. 1993, 210, 105–108. [Google Scholar] [CrossRef]
- Kopáček, O.; Karas, V.; Kovář, J.; Stuchlík, Z. Transition from regular to chaotic circulation in magnetized coronae near compact objects. Astrophys. J. 2010, 722, 1240. [Google Scholar] [CrossRef]
- Liu, L.; Wu, X.; Huang, G.Q.; Liu, F. Higher order explicit symmetric integrators for inseparable forms of coordinates and momenta. Mon. Not. R. Astron. Soc. 2016, 459, 1968–1976. [Google Scholar] [CrossRef][Green Version]
- Kopáček, O.; Karas, V. Near-horizon Structure of Escape Zones of Electrically Charged Particles around Weakly Magnetized Rotating Black Hole. Astrophys. J. 2018, 853, 53. [Google Scholar] [CrossRef]
- Li, D.; Wu, X. Chaotic motion of neutral and charged particles in a magnetized Ernst-Schwarzschild spacetime. Eur. Phys. J. Plus. 2019, 134, 96. [Google Scholar] [CrossRef]
- Stuchlí, Z.; Kološ, M.; Kovář, J.; Slaný, P.; Tursunov, A. Influence of Cosmic Repulsion and Magnetic Fields on Accretion Disks Rotating around Kerr Black Holes. Universe 2020, 6, 26. [Google Scholar] [CrossRef]
- Yi, M.; Wu, X. Dynamics of charged particles around a magnetically deformed Schwarzschild black hole. Phys. Scr. 2020, 95, 085008. [Google Scholar] [CrossRef]
- Swope, W.C.; Andersen, H.C.; Berens, P.H.; Wilson, K.R. A computer simulation method for the calculation of equilibrium constants for the formation of physical clusters of molecules: Application to small water clusters. J. Chem. Phys. 1982, 76, 637–649. [Google Scholar] [CrossRef]
- Wisdom, J. The origin of the Kirkwood gaps-A mapping for asteroidal motion near the 3/1 commensurability. Astron. J. 1982, 87, 577–593. [Google Scholar] [CrossRef]
- Ruth, R.D. A canonical integration technique. IEEE Trans. Nuclear Sci. 1983, 30, 2669–2671. [Google Scholar] [CrossRef]
- Forest, E.; Ruth, R.D. Fourth-order symplectic integration. Phys. D 1990, 43, 105–117. [Google Scholar] [CrossRef]
- Wisdom, J.; Holman, M. Symplectic maps for the n-body problem. Astron. J. 1991, 102, 1528–1538. [Google Scholar] [CrossRef]
- Chambers, J.E.; Murison, M.A. Pseudo-High-Order Symplectic Integrators. Astron. J. 2000, 19, 425. [Google Scholar] [CrossRef]
- Laskar, J.; Robutel, P. High order symplectic integrators for perturbed Hamiltonian systems. Celest. Mech. Dyn. Astronomy 2001, 80, 39L. [Google Scholar] [CrossRef]
- Kopáček, O.; Karas, V.; Kovář, J.; Stuchlík, Z. Application of a symplectic integrator in a non-integrable relativistic system. arXiv 2016, arXiv:1601.01262. [Google Scholar]
- Feng, K. Symplectic geometry and numerical methods in fluid dynamics. Lecture Notes Phys. 1986, 264, 1–7. [Google Scholar]
- Brown, J.D. Midpoint rule as a variational-symplectic integrator: Hamiltonian systems. Phys. Rev. D 2006, 73, 024001. [Google Scholar] [CrossRef]
- Seyrich, J.; Lukes-Gerakopoulos, G. Symmetric integrator for nonintegrable Hamiltonian relativistic systems. Phys. Rev. D 2012, 86, 124013. [Google Scholar] [CrossRef]
- Seyrich, J. Gauss collocation methods for efficient structure preserving integration of post-Newtonian equations of motion. Phys. Rev. D 2013, 87, 084064. [Google Scholar] [CrossRef]
- Preto, M.; Saha, P. On post-Newtonian orbits and the Galactic-center stars. Astrophys. J. 2009, 703, 1743. [Google Scholar] [CrossRef]
- Lubich, C.; Walther, B.; Brügmann, B. Symplectic integration of post-Newtonian equations of motion with spin. Phys. Rev. D 2010, 81, 104025. [Google Scholar] [CrossRef]
- Zhong, S.Y.; Wu, X.; Liu, S.Q.; Deng, X.F. Global symplectic structure-preserving integrators for spinning compact binaries. Phys. Rev. D 2010, 82, 124040. [Google Scholar] [CrossRef]
- Mei, L.; Ju, M.; Wu, X.; Liu, S. Dynamics of spin effects of compact binaries. Mon. Not. R. Astron. Soc. 2013, 435, 2246–2255. [Google Scholar] [CrossRef]
- Mei, L.; Wu, X.; Liu, F. On preference of Yoshida construction over Forest-Ruth fourth-order symplectic algorithm. Eur. Phys. J. C 2013, 73, 2413. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, W.; Liu, F.Y.; Wu, X. Construction of Explicit Symplectic Integrators in General Relativity. I. Schwarzschild Black Holes. Astrophys. J. 2021, 907, 66. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, W.; Liu, F.Y.; Wu, X. Construction of Explicit Symplectic Integrators in General Relativity. II. Reissner-Nordström Black Holes. Astrophys. J. 2021, 909, 22. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, W.; Liu, F.Y.; Wu, X. Construction of Explicit Symplectic Integrators in General Relativity. III. Reissner-Nordström-(anti)-de Sitter Black Holes. Astrophys. J. Suppl. Ser. 2021, 254, 8. [Google Scholar] [CrossRef]
- Wu, X.; Wang, Y.; Sun, W.; Liu, F.Y. Construction of Explicit Symplectic Integrators in General Relativity. IV. Kerr Black Holes. Astrophys. J. 2021, 914, 63. [Google Scholar] [CrossRef]
- Sun, W.; Wang, Y.; Liu, F.Y.; Wu, X. Applying explicit symplectic integrator to study chaos of charged particles around magnetized Kerr black hole. Eur. Phys. J. C 2021, 81, 785. [Google Scholar] [CrossRef]
- Newman, E.T.; Couch, E.; Chinnapared, K.; Exton, A.; Prakash, A.; Torrence, R. Metric of a Rotating, Charged Mass. J. Math. Phys. 1965, 6, 918–919. [Google Scholar] [CrossRef]
- Kovář, J.; Kopáček, O.; Karas, V.; Stuchlák, Z. Off-equatorial orbits in strong gravitational fields near compact objects—II: Halo motion around magnetic compact stars and magnetized black holes. Class. Quantum Gravity 2010, 27, 135006. [Google Scholar] [CrossRef]
- Zajaček, M.; Tursunov, A.; Eckart, A.; Britzen, S.; Hackmann, E.; Karas, V.; Stuchlík, Z.; Czerny, B.J. Anton Zensus. Constraining the charge of the Galactic centre black hole. J. Phys. Conf. Ser. 2019, 1258, 012031. [Google Scholar] [CrossRef]
- Yoshida, H. Construction of higher order symplectic integrators. Phys. Lett. A 1990, 150, 262–268. [Google Scholar] [CrossRef]
- Mikkola, S. Practical symplectic methods with time transformation for the few-body problem. Celest. Mech. Dyn. Astronomy 1997, 67, 145–165. [Google Scholar] [CrossRef]
- Wu, X.; Huang, T.Y.; Zhang, H. Lyapunov indices with two nearby trajectories in a curved spacetime. Phys. Rev. D 2006, 74, 083001. [Google Scholar] [CrossRef]
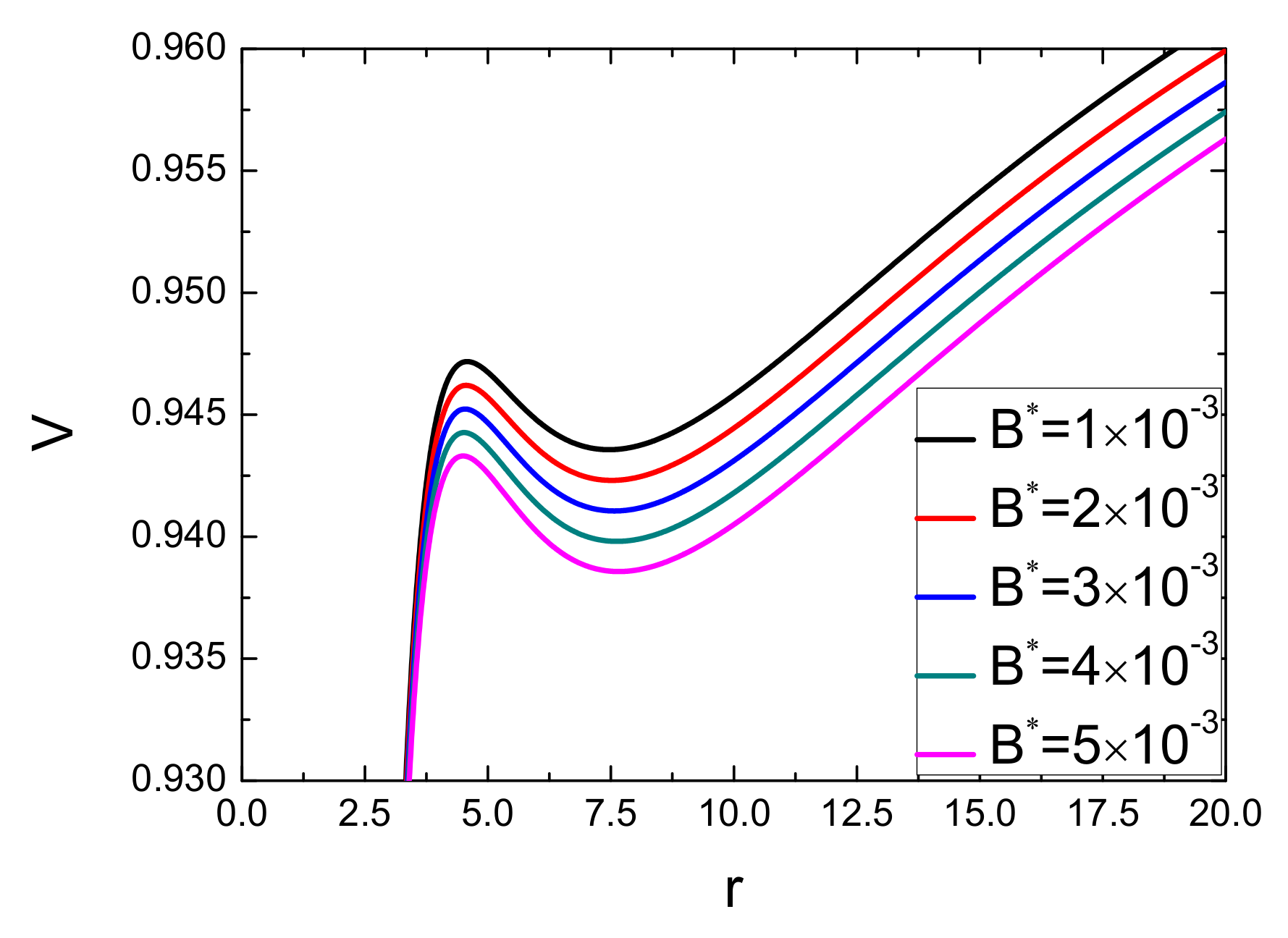
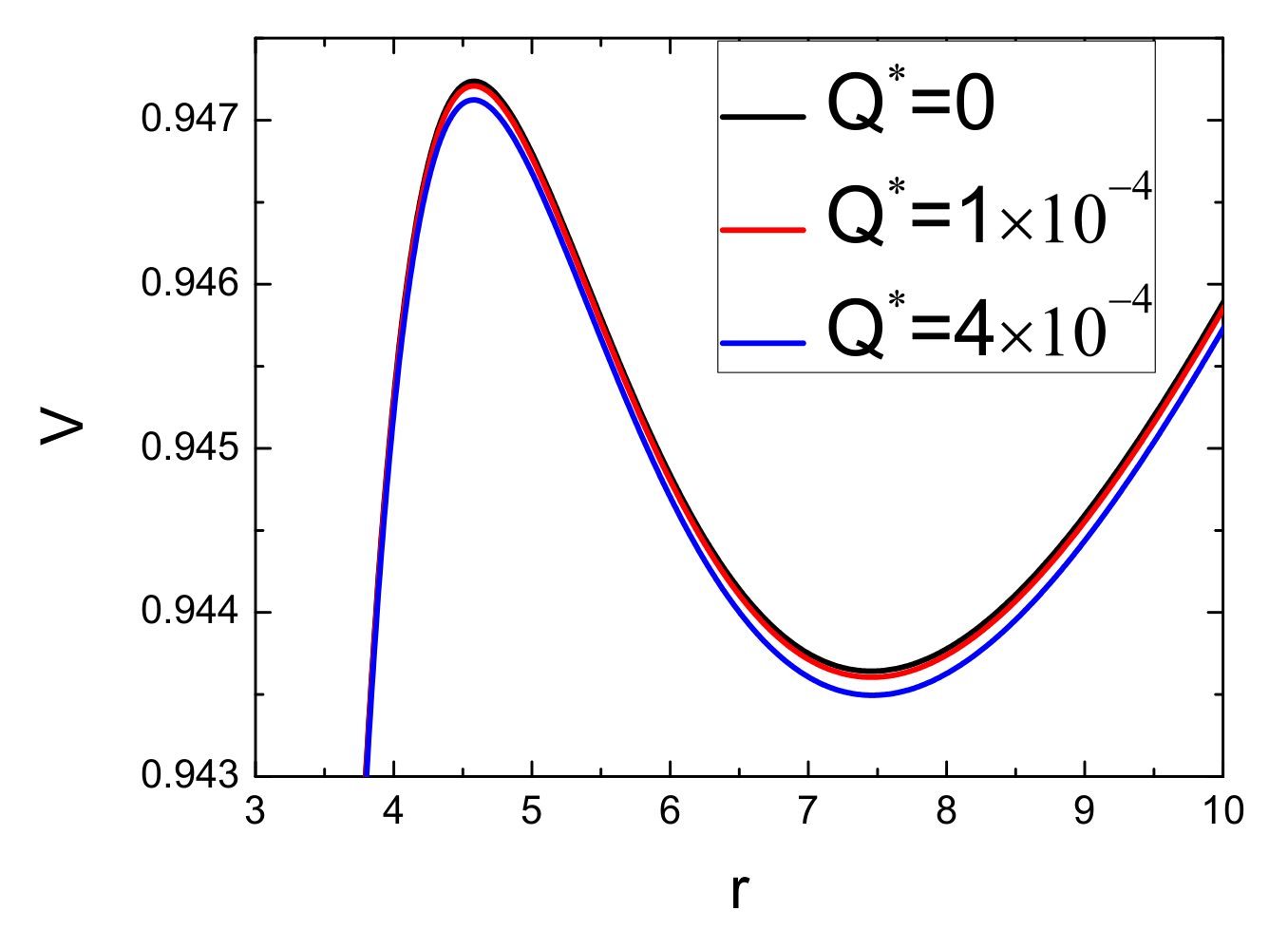
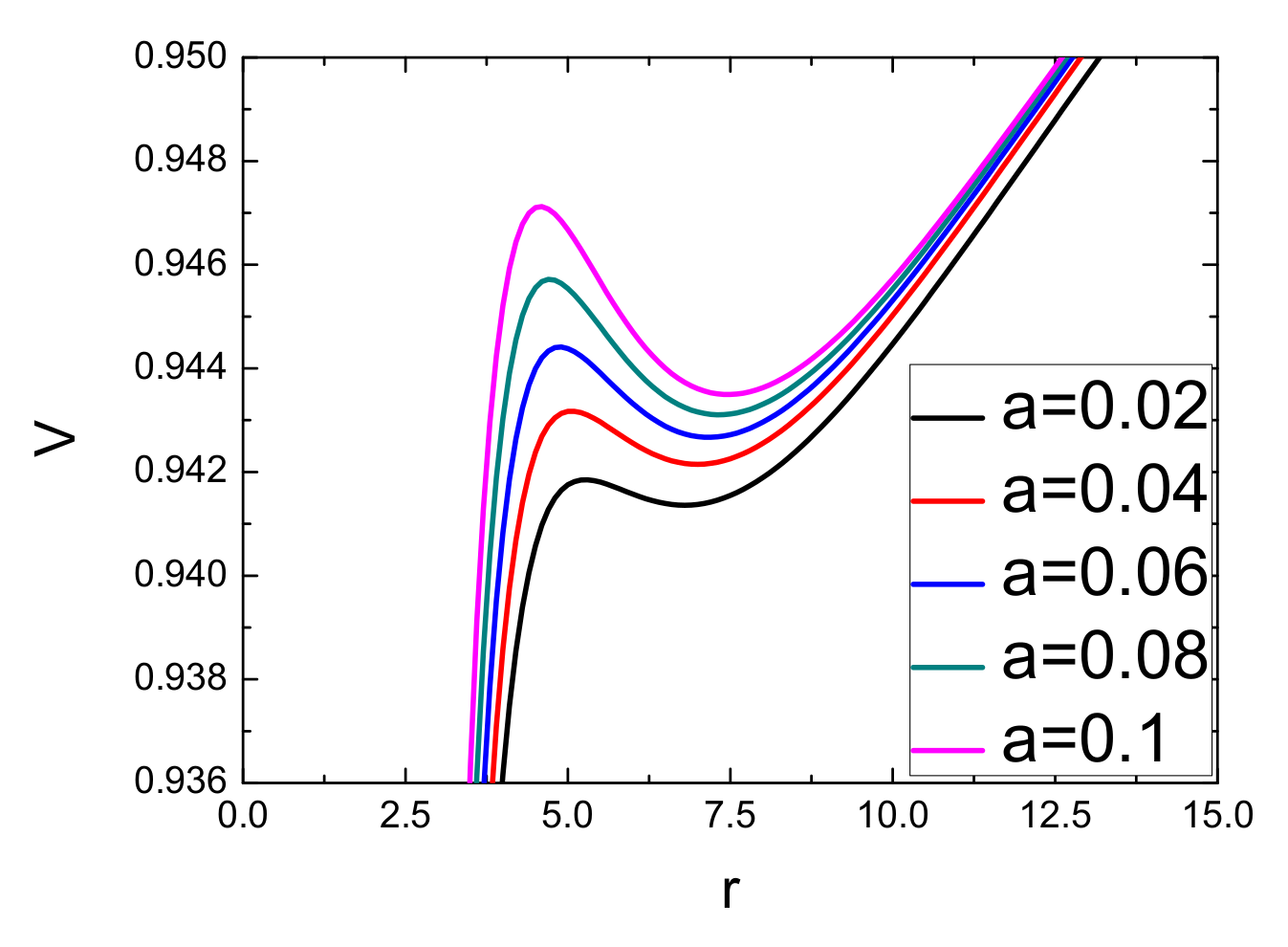
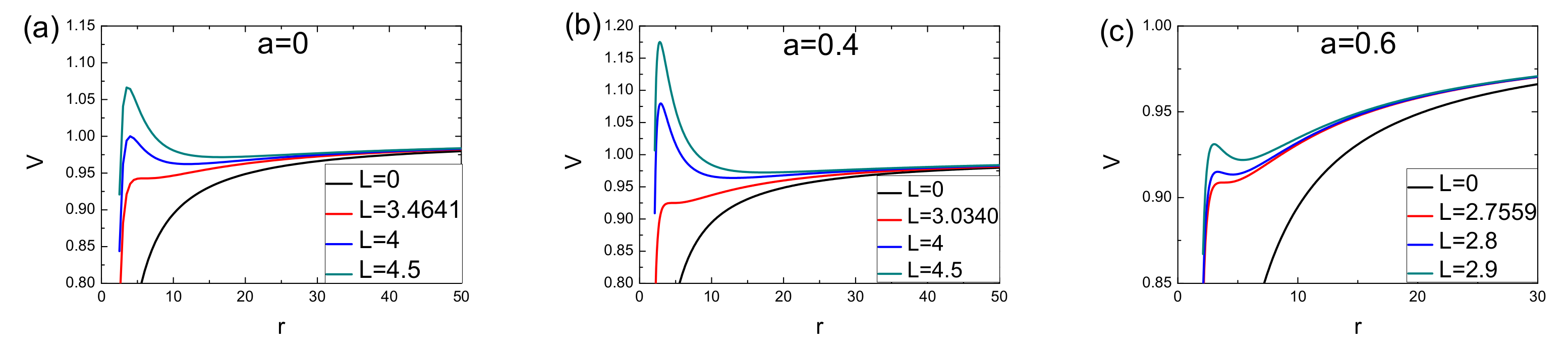




| Parameter | ||||
| R | 7.4595 | 7.5165 | 7.5693 | 7.6177 |
| Parameter | ||||
| R | 7.6618 | 7.7013 | 7.7365 | 7.7673 |
| 7.4559 | 7.5129 | |
| 7.4577 | 7.5147 | |
| 7.4631 | 7.5201 |
| a | L | R |
|---|---|---|
| 3.4641 | 6 | |
| 0 | 4.0 | 12 |
| 4.5 | 16.5876 | |
| 3.2640 | 5.3294 | |
| 0.2 | 4.0 | 12.5329 |
| 4.5 | 16.9761 | |
| 3.0340 | 4.6143 | |
| 0.4 | 4.0 | 12.9954 |
| 4.5 | 17.3336 | |
| 2.7559 | 3.8290 | |
| 0.6 | 2.8 | 4.5721 |
| 2.9 | 5.4096 |
| DO | RO | DO | RO | DO | RO | |
|---|---|---|---|---|---|---|
| R | 5.2406 | 6.4737 | 5.0411 | 6.1176 | 4.7844 | 5.8262 |
| L | 3.1794 | −3.8201 | 3.1433 | −4.0808 | 3.1311 | −4.3879 |
| E | 0.9078 | 0.9879 | 0.8885 | 1.0406 | 0.8726 | 1.10173 |
| DO | RO | DO | RO | DO | RO | |
|---|---|---|---|---|---|---|
| R | 5.3276 | 6.599 | 5.3275 | 6.6193 | 5.3274 | 6.6043 |
| L | 3.2224 | −3.7282 | 3.2209 | −3.7265 | 3.2194 | −3.7247 |
| E | 0.9226 | 0.9688 | 0.9222 | 0.9683 | 0.9217 | 0.9679 |
| DO | RO | DO | RO | DO | RO | |
|---|---|---|---|---|---|---|
| R | 5.3641 | 6.6713 | 5.2534 | 6.4653 | 5.0411 | 6.1218 |
| L | 3.2641 | −3.6434 | 3.1912 | −3.8343 | 3.1546 | −4.0954 |
| E | 0.9354 | 0.9485 | 0.9112 | 0.9917 | 0.8918 | 1.0445 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Wu, X.; Wang, Y.; Deng, C.; Liu, B.; Liang, E. Dynamics of Charged Particles Moving around Kerr Black Hole with Inductive Charge and External Magnetic Field. Universe 2021, 7, 410. https://doi.org/10.3390/universe7110410
Sun X, Wu X, Wang Y, Deng C, Liu B, Liang E. Dynamics of Charged Particles Moving around Kerr Black Hole with Inductive Charge and External Magnetic Field. Universe. 2021; 7(11):410. https://doi.org/10.3390/universe7110410
Chicago/Turabian StyleSun, Xin, Xin Wu, Yu Wang, Chen Deng, Baorong Liu, and Enwei Liang. 2021. "Dynamics of Charged Particles Moving around Kerr Black Hole with Inductive Charge and External Magnetic Field" Universe 7, no. 11: 410. https://doi.org/10.3390/universe7110410
APA StyleSun, X., Wu, X., Wang, Y., Deng, C., Liu, B., & Liang, E. (2021). Dynamics of Charged Particles Moving around Kerr Black Hole with Inductive Charge and External Magnetic Field. Universe, 7(11), 410. https://doi.org/10.3390/universe7110410






