Abstract
After giving a short overview of previous results on constraining of Extended Gravity by stellar orbits, we discuss the Schwarzschild orbital precession of S2 star assuming the congruence with predictions of General Relativity (GR). At the moment, the S2 star trajectory is remarkably fitted with the first post-Newtonian approximation of GR. In particular, both Keck and VLT (GRAVITY) teams declared that the gravitational redshift near its pericenter passage for the S2 star orbit corresponds to theoretical estimates found with the first post-Newtonian (pN) approximation. In 2020, the GRAVITY Collaboration detected the orbital precession of the S2 star around the supermassive black hole (SMBH) at the Galactic Center and showed that it is close to the GR prediction. Based on this observational fact, we evaluated parameters of the Extended Gravity theories with the Schwarzschild precession of the S2 star. Using the mentioned method, we estimate the orbital precession angles for some Extended Gravity models including power-law , general Yukawa-like corrections, scalar–tensor gravity, and non-local gravity theories formulated in both metric and Palatini formalism. In this consideration, we assume that a gravitational field is spherically symmetric, therefore, alternative theories of gravity could be described only with a few parameters. Specifically, considering the orbital precession, we estimate the range of parameters of these Extended Gravity models for which the orbital precession is like in GR. Then we compare these results with our previous results, which were obtained by fitting the simulated orbits of S2 star to its observed astrometric positions. In case of power-law , generic Yukawa-like correction, scalar–tensor gravity and non-local gravity theories, we were able to obtain a prograde orbital precession, like in GR. According to these results, the method is a useful tool to evaluate parameters of the gravitational potential at the Galactic Center.
1. Introduction
Several modified gravity theories have been proposed as possible extensions of Einstein’s theory of gravity [1]. Among their main motivations, there is the possibility to explain cosmological and astrophysical data at different scales without introducing dark energy and dark matter, but just taking into account further degrees of freedom of the gravitational field emerging from geometric corrections [2]. They have to explain different observations ranging from solar systems, neutron stars, binary pulsars, spiral and eliptical galaxies, and clusters of galaxies up to the large-scale structure of the universe and the observed accelerated dynamics [3,4,5,6]. A number of alternative gravity theories have been proposed (see, e.g., [2,7,8,9,10] for reviews). In recent years, theories of “massive gravity” have also attracted a lot of attention (see, e.g., [11,12] and references therein and citations of these papers), especially after a creation of massive gravity models without pathologies such Boulware–Deser ghosts [13,14,15,16]. Different alternative approaches for the weak field limit starting from fourth-order theories of gravity, like , have been proposed and discussed [17,18,19,20,21,22,23,24,25,26]. The alternative theories of gravity were discussed from the field-theoretical point of view by Petrov et al. in the book [27]. Furthermore, some experimental limits related to Extended Theories of Gravity are reported in the literature [28,29,30,31].
In this discussion, stellar dynamics acquires a special role because it allows us to investigate gravitational potentials of self-gravitating structures considering stellar motions. In particular, S-stars are the bright stars which move around the Galactic Center [32,33,34,35,36,37,38,39,40,41,42,43,44] where Sgr A* is located, which is a compact bright radio source. One of the brightest among S stars with a high eccentricity is called S2 [34,38].
The conventional model for the Galactic Center consists of the supermassive black hole with mass around and an extended mass distribution formed with stellar cluster and dark matter. A total mass of bulk distribution inside a spherical shell where trajectories of bright stars are located must be much smaller than the black hole mass, otherwise, theoretical fits significantly differ from observational data. Recently, GRAVITY Collaboration [45,46] and the Keck group [47] evaluated relativistic redshifts of spectral lines for the S2 star near its periapsis passage in May 2018, and the redshifts were consistent with theoretical estimates done in the first post-Newtonian correction for the redshifts.
Some time ago, Ruffini, Argüelles Rueda [48] proposed a dark matter distribution having a dense core and a diluted halo. Later, the dark matter distribution was called the RAR-model. Recently, Becerra-Vergara et al. [49] claimed that this model provides a better fit of trajectories of bright stars in comparison with the supermassive black hole model. The properties of bright star trajectories in the gravitational field of a dense core in the RAR-model have been considered in [50] and it was concluded that the gravitational field determined from the RAR model is the harmonic oscillator potential. In this case, trajectories of stars are ellipses with centers at the origin and their periods are the same, so they do not depend on semi-major axes, therefore, it was concluded that these properties are not consistent with existing observational data.
In the case of small velocities of stars (in units of speed of light) and great radial coordinates (in Schwarzschild radius units) the orbital precession occurs due to relativistic effects and due to extended mass distribution because we have perturbations of the Newtonian potential in both cases. In the first case, precession results in a prograde pericentre shift, and in the second case in a retrograde shift [51], respectively. In both cases, the result will be rosette shaped orbits [52]. Weinberg et al. [53] demonstrated that the lowest order relativistic effects, i.e., the prograde precession, could be detectable if the astrometric precision would reach a few tenths of mass.
In our previous papers, we constrained different Extended Gravity theories using astronomical data for the S2 orbit [24,54,55,56,57,58,59,60,61,62], fundamental plane of elliptical galaxies [63,64,65] and barionic Tully–Fischer relation of spiral galaxies [66]. In this paper, we evaluate parameters of the following theories of gravity: power-law , Yukawa, Sanders, Palatini and non-local gravity by Schwarzschild precession of S2 star. We assume that the orbital precession of the S2 star is equal to the GR prediction per orbital period. We use this assumption because the GRAVITY Collaboration detected the orbital precession of the S2 star around the SMBH [44] and showed that it is close to the corresponding prediction of GR.
It is important to investigate gravity in the vicinity of very massive compact objects because the environment around these objects is drastically different from that in the Solar System framework. The precession of the S2 star is a unique opportunity to test gravity at the sub-parsec scale of a few thousand AU. Gravity is relatively well constrained at short ranges (especially at sub-mm scale) by experimental tests [67]; however, for long ranges (e.g., at sub-parsec scale), further tests are still needed (see Figures 9 and 10 from [67] for different ranges). It is worth stressing that a phenomenological approach can be useful in this context. The precession of the S2 star is an excellent opportunity to test theories of gravity. Furthermore, we use the Schwarzschild precession because it is a new observational result for our Galactic Center and we are interested to learn alternative theory parameters that correspond to the Schwarzschild precession for S2 star.
We organized the paper in the following way. In Section 2, we presented basic theoretical models for power-law , Yukawa, Sanders, Palatini and non-local gravity theories. In Section 3, we evaluate parameters of these theories of gravity by Schwarzschild precession of S2 star and discussed the obtained results. The concluding remarks are given in Section 4.
2. Theory
Let us summarize the theoretical models that we want to investigate by S2 star orbits moving around Sgr A*.
2.1. Power-Law Gravity
gravity is a straightforward extension of GR where, instead of the Hilbert–Einstein action, linear in the Ricci scalar R, one considers a generic function of it [17,18,19,68,69,70,71]. A power-law is obtained by replacing the scalar curvature R with = in the gravity Lagrangian [69,70]. Clearly, for , GR is recovered. It is interesting to stress that n can be any positive real number so that, as soon as , with , little deviations from GR can be considered. In the weak field limit, a gravitational potential of the form.
can be found [69,70]. Here, is the scale-length parameter and it is related to the boundary conditions and the mass of the system and is a universal parameter related to the power n. It is possible to demonstrate that the relation
holds [70]. For the case n = 1 and = 0, the Newtonian potential is recovered.
Being n any positive real number, it is always possible to recast the power-law function as
If we assume a small deviation with respect to GR, that is , it is possible to re-write a first-order Taylor expansion as
In this way, one can control the magnitude of the corrections with respect to the Einstein gravity.
2.2. General Yukawa-Like Corrections
Yukawa-like potentials deviate from the standard Newtonian gravitational potential due to the presence of decreasing exponential terms [72,73,74,75,76,77]. Adelberger et al. [67] reviewed experiments and constraints on the Yukawa term for the short ranges. In the case of the longer distances parameters of Yukawa gravity potential are given for clusters of galaxies [78,79] and for rotation curves of spiral galaxies [74]. Other studies of long-range Yukawa-like modifications of gravity can be found in [73,80,81,82,83,84,85]. It is worth noticing that Yukawa-like corrections naturally emerge in the weak field limit derived by analytic Taylor expansions of gravity
Specifically, expanding with respect to , that is, around the Minkowskian background [86], it is possible to obtain [2,75]:
where is the range of interaction and is a universal constant. In the case , the Yukawa potential reduces to the Newtonian one.
The Yukawa-like correction coming from gravity can be used to fix the coefficients in the expansion (5) and, eventually, to match the observations [87]. For the expansion up to the second order, we have 2 parameters to fix [88]. The relations between , and and parameters are , [88].
2.3. Scalar–Tensor Gravity and Sanders Potential
The above approach can be improved by adding a scalar field into dynamics in order to match the observations according to the Sanders prescriptions for flat rotation curves of galaxies (see [86] and references therein). We can start from the action
where is the scalar field. It can be approximated as (see [86] for more details) and the function with its partial derivatives (, , , and ) and can be substituted by their corresponding Taylor series. So, in the case of , we obtain [86]:
where Ricci scalar R is approximated as (see [86] for more details). The lowest order of field equations gives [86]:
In order to evaluate parameters of Sanders gravity, we can set the value of the derivatives of the Taylor expansion as without losing generality (see [86] for more details). Setting the gravitational constant as:
where is the gravitational constant as measured at infinity and by imposing , the Yukawa gravity potential in the weak field limit gets the following form [86]:
The obtained form represents a Sanders-like gravity potential [75,89] adopted to fit flat rotation curves of spiral galaxies. It can be written in the following form [88]:
2.4. Modified Palatini Gravity Model
In the Palatini approach, the metric and the connection are considered as independent fields. Metric and Palatini approaches are equivalent in the case of the linear Einstein–Hilbert action, but this is not so for extended gravities, and in particular for gravity [90]. The Palatini approach leads to second order differential field equations, while the metric approach leads to fourth order coupled differential equations. A hybrid metric-Palatini theory, , where the standard GR term R is metric while the term is metric-affine, is also possible. For a review, see [91,92,93,94,95,96]. As discussed in [92], it is always possible to reduce a hybrid metric-Palatini model to a scalar–tensor one where the scalar field can be related to the the first derivative of the term.
In the weak field limit, the scalar field behaves as , where M is the mass of the system and r is the interaction length. The leading parameters for hybrid Palatini gravity are and and our aim is to evaluate them. The modified gravitational potential can be written in the following form:
so that it can be considered as a Yukawa-like potential.
The parameter represents a scaling parameter for gravity interaction and and we measure the parameter in AU (AU is the astronomical unit) 1, is dimensionless. Non-vanishing and would indicate a potential deviation from GR.
2.5. Non-Local Gravity Model
Non-local theories of gravity have recently showed that they can suitably represent the behavior of gravitational interaction at both ultraviolet and infrared scales. This behavior could be important because it manages to describe gravitation phenomena without the need for dark matter and dark energy at different astrophysical scales. The non-locality is introduced by the inverse of the d’Alembert operator. In the references [96,97,98], the authors studied the dynamics of the non-local theory and its Newtonian limit. See also [99,100] for a discussion.
It is possible to show that the weak-field limit of this theory has the free parameters, and (see [60] for more details). We take specific values for = 1 (to obtain the Newtonian limit), and constrain the parameter space of the and parameters. The weak field potential for non-local gravity reads:
where non-local corrections are evident, where G is the Newtonian constant, M is the black hole mass.
3. Results and Discussion
In this section, we first give a short overview of our previous results regarding the study of the extending theories of gravity by the observed orbit of the S2 star, and then we will evaluate parameters of , Yukawa, Sanders, Palatini and non-local gravity theories with the Schwarzschild precession of the S2 star, i.e., by assuming that the orbital precession of the S2 star is equal to the corresponding theoretical quantity calculated in GR. In all studied cases, we confirmed that these gravity parameters must be very close to those corresponding to the Newtonian limit of the gravity theory. It is rather natural since all bounded orbits of bright stars are very close to ellipses and its foci are located at the Galactic Center, therefore, the gravitational potential should be Newtonian.
In order to calculate the precession of the S2 star in modified gravity, we assume that the weak field potential does not differ significantly from the Newtonian potential. The used perturbing potential is of the form:
and it can be used for calculating the precession angle according to the Equation (30) from paper [52]:
where r is related to z via: and
For our calculation we used the results presented in [39], according to which mass of the SMBH of the Milky Way is , semi-major axis of the S2 star orbit is , and its eccentricity .
Figure 1 shows the simulated orbits of S2 star in GR. The lower panel represents an enlarged part of the upper panel. GR predicts that pericenter of S2 star should advance by per orbital revolution [35]. Since we assume that the orbital precession of the S2 star is equal to the theoretical quantity calculated in GR, the orbits of S2-star will be very close to the orbit in Figure 1 for all study cases. We tested the sensitivity and stability of the presented results for Schwarzschild precession of () by their comparison with the results for slightly different values of Schwarzschild precession: () and (). We found that the calculations are stable under small perturbations of Schwarzschild precession.
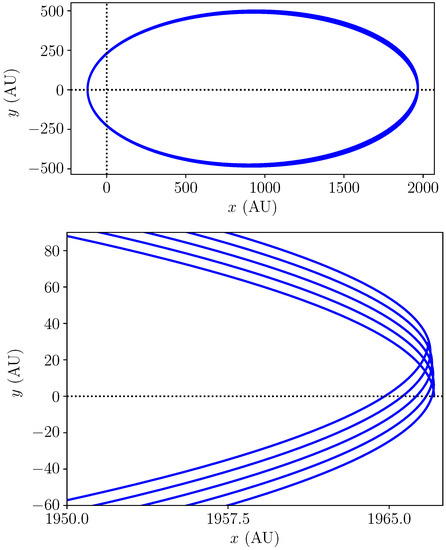
Figure 1.
The simulated orbits of S2-star in GR. Lower panel represents enlarged part of the upper panel where the obtained values of orbital precession angle is per orbital period.
Figure 2 shows the precession per orbital period for – parameter space in the case of gravity potential (1). Locations in – parameter space where precession angle is the same as in GR are designated by white dashed line. The upper panel shows the results obtained for , while the lower panel corresponds to the negative values of . In our previous papers regarding gravity [24,55], we showed that when parameter was approaching zero, we could recover the Keplerian orbit for S2 star. Our fitting indicated [24,55] that optimal value for was around 0.01. The obtained results showed that, in contrast to GR, gravity gives retrograde direction of the precession of the S2 orbit for the values .
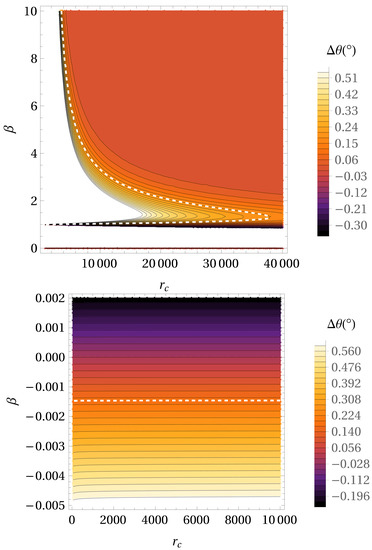
Figure 2.
The precession per orbital period for – parameter space in the case of gravity potential. With a decreasing value of angle of precession, colors are darker. Locations in parameter space where precession angle has the same value as in GR () are designated by white dashed line. Lower panel represents the same like the upper panel, but for more extended region of – parameter space.
However, as it can be seen from the upper panel of Figure 2, for the values (which are not theoretically justified since when , according to the expression (2), so it cannot be incorporated into the theory. In case when parameter is close to (see lower panel of Figure 2), we can also obtain precession like in GR. This value of is theoretically justified since it can be obtained from Equation (2) for . Regarding , it is not possible to obtain the reliable estimate without an additional independent astronomical data set. That is why we believe that gravity could be also considered as a candidate to explain S2-like star orbit, because now findings of the GRAVITY collaboration [44] indicate that precession is in the same direction like in GR case.
In our previous studies regarding the Yukawa gravity [54,57,58,62,88], we have two parameters to constrain. We used the orbit of the S2 star around the Galactic Centre to test and constrain theory of gravity. In [54], we investigated parameters and , and in [88] we investigated values of , . We find the minimal values of the reduced in order to estimate and assuming and in that way we reconstruct models up to the second order [54,88]. Figure 3 shows the precession per orbital period for – parameter space in the case of Yukawa gravity potential. Locations in the – parameter space where precession angle is the same as in GR are designated by white dashed line. From our previous findings [54,88] we conclude that the most probable parameter for Yukawa gravity in the case of the S2 star, is around 5000 AU–7000 AU and that the current observations do not enable us to obtain the reliable constraints on the universal constant . Now, with this new strategy, we obtained higher value for parameter , around 21,000 AU. For vanishing parameter , we recover the Keplerian orbit of S2 star. In the case of the S2 star orbit we obtained the orbital precession in positive direction like in GR. For Yukawa gravity parameters we obtain the following conclusion: it is not possible to get a reliable constraint for based only on the requirement that precession angle is like in GR, and so we need an additional astronomical data set; for the obtained values for are between 21,000 AU and 22,000 AU, while for the , the corresponding values are smaller ( AU), as it can be also seen from Table 2 in [58]. If we consider additional parameters in our model, i.e., that bulk distribution of matter (includes stellar cluster, interstellar gas distribution and dark matter) exists near SMBH in our Galactic Center, we will obtain a lower value for parameter (see paper [62] for more details).
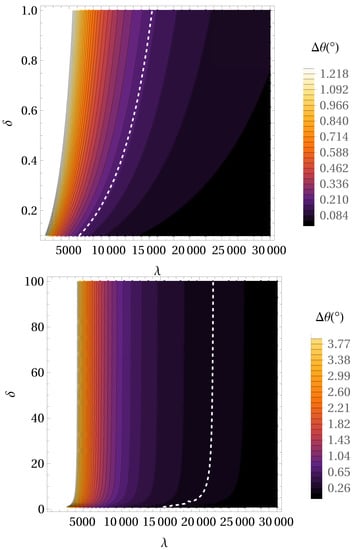
Figure 3.
The precession per orbital period for – parameter space in the case of Yukawa gravity potential. With a decreasing value of angle of precession colors are darker. Locations in parameter space where precession angle has the same value as in GR () are designated by white dashed line. Lower panel represents the same like the upper panel, but for a more extended region of – parameter space.
We studied Sanders gravity [88] and we compared the observed and simulated S2 star orbits around the Galactic Centre in order to constrain the parameters of gravitational potential derived from gravity, i.e., Sanders-like potential. We fitted the NTT/VLT astrometric observations of S2 star. The precession of S2 star orbit obtained for the best fit parameter values ( = 0.00018 and = AU) has the positive direction, as in GR. Figure 4 shows the precession per orbital period for – parameter space in the case of Sanders gravity potential. Locations in parameter space where precession angle is the same as in GR are designated by white dashed line. In our previous paper [88], we obtained much larger orbital precession of S2 star in Sanders-like gravity than the corresponding value predicted by GR. Now, with new strategy we obtained new values for parameters of Sanders gravity: is between 0 and 1/3 (vertical asymptote in the upper panel of Figure 4 is 1/3, as follows from Equation (12)) and is between 0 and 0.3 (in AU units). From Equation (12), we can see that for or , or , the Sanders potential is reducing to the Newtonian one. If we want to evaluate we need additional independent astronomical data set. As it can be seen from the lower panel of Figure 4, for obtaining precession like in GR, absolute value of cannot be lower than ≈ 0.00065 AU, which corresponds to 0.16.
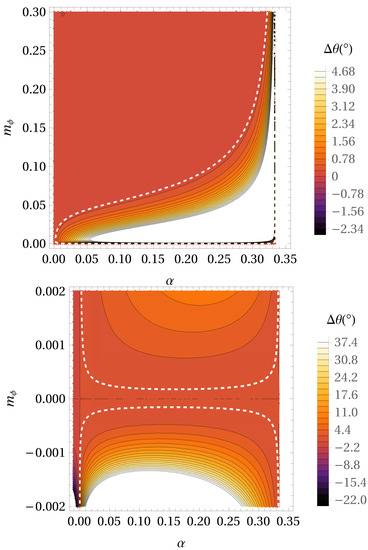
Figure 4.
The precession per orbital period for – parameter space in the case of Sanders gravity potential. With a decreasing value of angle of precession colors are darker. Locations in parameter space where precession angle has the same value as in GR () are designated by white dashed line. Lower panel represents the same like the upper panel, but for positive values of parameter.
In our previous paper regarding hybrid Palatini gravity [56] using the observed positions of S2 star, we constrained the hybrid modified gravity parameters. We obtained following results: the range of values for parameter is between and ; the range of is between AU and AU; the precession of the S2 star orbit in hybrid Palatini gravity has the same direction as in GR, but the upper limit in magnitude is much bigger than GR. Figure 5 shows the precession per orbital period for – parameter space in the case of hybrid Palatini gravity potential. Locations in – parameter space where precession angle is the same as in GR are designated by white dashed line. According the obtained figures, we can evaluate parameters of hybrid Palatini gravity. We obtained that is between (vertical asymptote in upper panel of Figure 5) and 0, which follows from Equation (13) and is between AU and 0.1 AU. If = 0 Palatini potential reduces to Newtonian. Like in the previous case, if we want to evaluate values of we need additional independent astronomical data set.
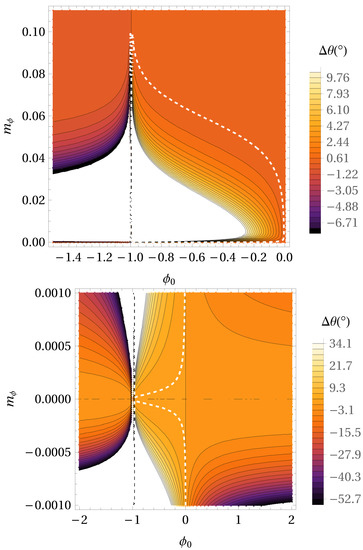
Figure 5.
The precession per orbital period for – parameter space in the case of Hybrid Palatini gravity potential. With a decreasing value of angle of precession colors are darker. Locations in parameter space where precession angle has the same value as in GR () are designated by white dashed line. Lower panel represents the same like the upper panel, but for positive values of parameter.
We studied non-local gravity in our previous paper [60], and we obtained the values for and parameters. We obtained that the most probable value for the scale parameter is approximately from 0.1 AU to 2.5 AU. We showed that it is not possible to obtain reliable estimates on the parameter of non-local gravity using only observed astrometric data for S2 star. That length scale is associated with one of the scalar fields which is not dynamical, but only plays an auxiliary role to localize the original non-local Lagrangian. The value of obtained orbital precession of the S2 star has the same order of magnitude as in GR. Figure 6 shows the precession per orbital period for – parameter space in the case of non-local modified gravity potential. As previously, the locations in – parameter space where precession angle is the same as in GR are designated by white dashed line. As it can be seen from the lower panel of Figure 6, for obtaining precession like in GR, cannot be higher than ≈0.0256 AU, while, it is not possible to obtain a unique value for without combinations of these results with some additional astronomical observations.
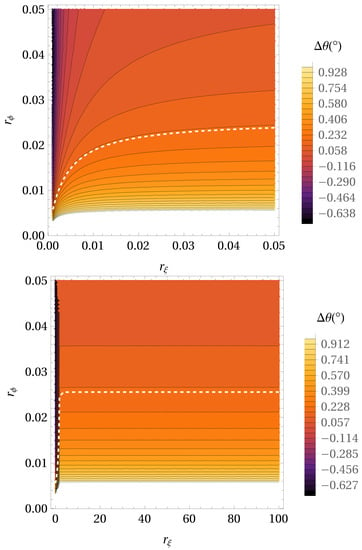
Figure 6.
The precession per orbital period for – parameter space in the case of non-local modified gravity potential. With a decreasing value of angle of precession colors are darker. Locations in parameter space where precession angle has the same value as in GR () are designated by white dashed line. Lower panel represents the same like the upper panel, but for a more extended region of – parameter space.
In this paper, we assume that the orbital precession of S2 star is equal to GR value. In our previous papers, we fitted astronomical data of the S2 star orbit, and data was with much larger uncertainties. We can notice that results differ from the previous one, and now it is much more precise. The main reason is that the GRAVITY Collaboration detected the orbital precession of the S2 star and showed that it is close to the GR prediction and direction is the same like in GR.
Lense–Thirring Precession of the S2 Star Due to Spin of Sgr A*
For the very precise calculations the Lense–Thirring (LT) precession caused by the SMBH spin should be also taken into account in the overall pN precession. In the case of the recently discovered ultra-eccentric S-stars S4711, S62, S4714 [101,102,103,104], the LT precession was studied in [102] and it was found that it is much smaller than Schwarzschild precession. Namely, the ratio between the LT precession for a rotating SMBH with dimensionless spin and the Schwarzschild precession for these stars is around 2.7, 2.3 and 0.86%, respectively [102].
In this paper, we considered the solutions of alternative theories of gravity for spherically symmetric and static gravitational field, which do not include the SMBH spin. Nevertheless, we estimated the LT precession for S2 star using the expression (10) from [102] and assuming a Kerr SMBH rotating with dimensionless spin . We also calculated the upper bound for the realistic value of the spin of Sgr A* [105]. The spin of Sgr A* was estimated ( less than 0.1) by the observed distribution of the orbital planes of the S-stars [105]. The obtained dependence of LT precession on SMBH’s spin polar angles i and for SMBH spin is presented in Figure 7.
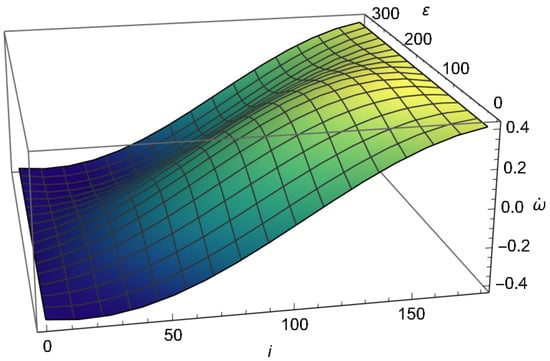
Figure 7.
The dependence of LT precession of S2 star on SMBH’s spin polar angles and for SMBH in Sgr A* with dimensionless spin . SMBH mass is taken from [102] and S2 star orbital elements from [44].
The maximum value of LT precession is obtained for the following polar angles: . For the upper bond of the realistic value of the spin of Sgr A* () LT precession of is obtained for the same values of the polar angles. Taking into account that the Schwarzschild precession of S2 star is equal to , it can be seen that the LT precession in the first case is smaller by two orders of magnitude. Therefore, in the case of S2 star, the LT precession is much smaller than in the case of the recently discovered ultra eccentric stars S4711, S62 and S4714. Having this in mind, as well as the fact that at the moment the Schwarzschild precession is detected only in the case of S2 star, in our calculations we did not take into account the LT precession.
4. Conclusions
In this paper, we evaluate parameters of the Extended Gravity theories with Schwarzschild precession of the S2 star orbit. We assume that the orbital precession of S2 star is equal to the per orbital period, i.e., the corresponding GR estimate. It is a reasonable approximation since the observed precession angle is close to this quantity [44]. We evaluate the parameters of the following extended theories of gravity: , Yukawa, Sanders, Palatini and non-local gravity. We can conclude that in all studied cases (, Yukawa, Sanders, Palatini and non-local gravity theories), depending on gravity parameters, we can recover prograde orbital precession, like in GR. This is one important condition to evaluate parameters of different modified gravities. Second condition is that value of orbital precession is per orbital period. Using these two requests we obtained following values of parameters of the extended theories of gravity:
- : if we take the conditions that the value of orbital precession is per orbital period and that it should be prograde like in GR, then .
- Yukawa potential: for , the obtained values for are between 21,000 AU and 22,000 AU, while for the , the corresponding values are smaller ( AU).
- Modified Sanders gravity: is between 0 and 1/3 (vertical asymptote). For or , or if , the Sanders potential is reducing to the Newtonian one.
- Modified Palatini gravity: is between −1 (vertical asymptote) and 0. If , the Palatini potential is reduced to the Newtonian one.
- Non-local gravity: is between 0 and 0.0256 AU.
- For all studied gravity models (described with two parameters) it is not possible to evaluate the both parameters in a unique way only from conditions that orbital precession is prograde like in GR, and that the precession angle is per orbital period. In that way, one can use the presented results to find one of the parameters of the studied gravity models, provided that the another one is evaluated in a different way.
If we compare the presented method with our previous studies, it can be seen that now the approach is different and obtained values for parameters of gravity models are not the same, but they are the same order of magnitude in both approaches and they are compatible. In our previous papers we fitted astronomical observations of the S2 star orbit, which were obtained with relatively large errors, especially in the first stage of observations (data were collecting for decades). If all orbital parameters are fixed the precision of the S2 star orbit reconstruction is about 1 mas [18], therefore, an astrometric accuracy must be much better than this value, at least, for one orbital period of S2 star. In this paper, we were not fitting observation data, we only assume that the orbital precession of S2 star is equal to the GR value because recently the GRAVITY Collaboration detected the orbital precession of the S2 star and showed that it is close to the GR prediction [44]. The Keck collaboration did not declare yet that it detected the Schwarzschild precession for S2 star.
A modified theory of gravity needs to be constrained at different scales: laboratory distances, solar systems, galaxies, binary pulsars, galactic clusters and cosmological scales. Different scales provide constraints at different stringency. The orbit of S2 star is at the sub-parsec scales (a few thousand AU), so we believe that in order to restrict the remaining parameters, one should use additional constraints at similar scales, such as solar system or binary pulsar observations. In our previous papers, we fitted astronomical data of the S2 star orbit and in this paper we assume that the orbital precession of S2 star is equal to GR value because the GRAVITY Collaboration detected the orbital precession of the S2 star and showed that it is close to the GR theoretical estimate. We hope that using this method we can evaluate parameters of alternative models for a gravitational potential at the Galactic Center.
Author Contributions
All coauthors participated in writing, calculation and discussion of obtained results. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by Ministry of Education, Science and Technological Development of the Republic of Serbia. PJ wishes to acknowledge the support by this Ministry through the project contract No. 451-03-9/2021-14/200002. SC acknowledges the support of the Istituto Nazionale di Fisica Nucleare (INFN), sezione di Napoli, iniziative specifiche QGSKY and MOONLIGHT-2.
Data Availability Statement
Not applicable.
Acknowledgments
The authors acknowledge support of Ministry of Education, Science and Technological Development of the Republic of Serbia (DB, VBJ and PJ) and the Istituto Nazionale di Fisica Nucleare (INFN) (SC). DB, VBJ and PJ also wish to thank the Center for mathematical modeling and computer simulations in physics and astrophysics of Vinča Institute of Nuclear Sciences.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| GR | General Relativity |
| pN | post-Newtonian |
| SMBH | Super massive black hole |
Note
| 1 | Since dimensions of the S2 star orbit are comparable with the Solar system size and the semi-major axis is around 970 AU, the pericenter distance is around 120 AU. |
References
- Fischbach, E.; Talmadge, C.L. The Search for Non–Newtonian Gravity; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1999; 305p. [Google Scholar]
- Capozziello, S.; Faraoni, V. Beyond Einstein Gravity: A Survey of Gravitational Theories for Cosmology and Astrophysics; Fundamental Theories of Physics; Springer: Cham, Switzerland, 2011; Volume 170. [Google Scholar]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rept. 2011, 505, 59. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-time Evolution. Phys. Rept. 2017, 692, 1. [Google Scholar] [CrossRef]
- Capozziello, S.; Laurentis, M.D. The dark matter problem from f(R) gravity viewpoint. Ann. Phys. 2012, 524, 545. [Google Scholar] [CrossRef]
- Salucci, P.; Esposito, G.; Lambiase, G.; Battista, E.; Benetti, M.; Bini, D.; Boco, L.; Sharma, G.; Bozza, V.; Buoninfante, L.; et al. Einstein, Planck and Vera Rubin: Relevant encounters between the Cosmological and the Quantum Worlds. Front. Phys. 2021, 8, 603190. [Google Scholar] [CrossRef]
- Kopeikin, S.; Vlasov, I. Parametrized post-Newtonian theory of reference frames, multipolar expansions and equations of motion in the N-body problem. Phys. Rep. 2004, 400, 209. [Google Scholar] [CrossRef]
- Clifton, T. Alternative Theories of Gravity. Ph.D. Thesis, University of Cambridge, Cambridge, UK, August 2006. [Google Scholar]
- Clifton, T.; Ferreira, P.G.; Padilla, A.; Skordis, C. Modified gravity and cosmology. Phys. Rep. 2012, 513, 1. [Google Scholar] [CrossRef]
- Capozziello, S.; de Laurentis, M. Extended Theories of Gravity. Phys. Rep. 2011, 509, 167. [Google Scholar] [CrossRef]
- Rubakov, V.A.; Tinyakov, P.G. Infrared-modified gravities and massive gravitons. Phys. Usp. 2008, 51, 759. [Google Scholar] [CrossRef]
- Babichev, E.; Deffayet, C.; Ziour, R. Recovery of general relativity in massive gravity via the Vainshtein mechanism. Phys. Rev. D 2010, 82, 104008. [Google Scholar] [CrossRef]
- De Rham, C.; Gabadadze, G. Generalization of the Fierz-Pauli action. Phys. Rev. D 2010, 82, 044020. [Google Scholar] [CrossRef]
- De Rham, C.; Gabadadze, G.; Tolley, A.J. Resummation of Massive Gravity. Phys. Rev. Lett. 2011, 106, 231101. [Google Scholar] [CrossRef]
- De Rham, C. Massive Gravity. Living Rev. Relativ. 2014, 17, 7. [Google Scholar] [CrossRef]
- De Rham, C.; Deskins, J.T.; Tolley, A.J.; Zhou, S.-Y. Massive Gravity. Rev. Mod. Phys. 2017, 89, 025004. [Google Scholar] [CrossRef]
- Zakharov, A.F.; Nucita, A.A.; Paolis, F.D.; Ingrosso, G. Solar system constraints on Rn gravity. Phys. Rev. D 2006, 74, 107101. [Google Scholar] [CrossRef]
- Zakharov, A.F.; Nucita, A.A.; Paolis, F.D.; Ingrosso, G. Apoastron shift constraints on dark matter distribution at the Galactic Center. Phys. Rev. D 2007, 76, 062001. [Google Scholar] [CrossRef]
- Martins, C.F.; Salucci, P. Analysis of rotation curves in the framework of Rn gravity. Mon. Not. R. Astron. Soc. 2007, 381, 1103. [Google Scholar] [CrossRef]
- Nucita, A.A.; Paolis, F.D.; Ingrosso, G.; Qadir, A.; Zakharov, A.F. Sgr A*: A laboratory to measure the central black hole and stellar cluster parameters. Publ. Astron. Soc. Pac. 2007, 119, 349. [Google Scholar] [CrossRef]
- Zakharov, A.F.; Capozziello, S.; Paolis, F.D.; Ingrosso, G.; Nucita, A.A. The Role of Dark Matter and Dark Energy in Cosmological Models: Theoretical Overview. Space Sci. Rev. 2009, 148, 301. [Google Scholar] [CrossRef]
- Capozziello, S.; Stabile, A.; Troisi, A. A general solution in the Newtonian limit of f(R)-gravity. Mod. Phys. Lett. A 2009, 24, 659. [Google Scholar] [CrossRef]
- Iorio, L. Galactic orbital motions in the dark matter, modified Newtonian dynamics and modified gravity scenarios. Mon. Not. R. Astron. Soc. 2010, 401, 2012. [Google Scholar] [CrossRef][Green Version]
- Borka, D.; Jovanović, P.; Borka Jovanović, V.; Zakharov, A.F. Constraints on Rn gravity from precession of orbits S2-like stars. Phys. Rev. D 2012, 85, 124004. [Google Scholar] [CrossRef]
- Dokuchaev, V.I.; Eroshenko, Y.N. Weighing of the Dark Matter at the Center of the Galaxy. JETP Lett. 2015, 101, 777. [Google Scholar] [CrossRef][Green Version]
- Dokuchaev, V.I.; Eroshenko, Y.N. Physical laboratory at the center of the Galaxy. Phys. Uspekhi 2015, 58, 772. [Google Scholar] [CrossRef]
- Petrov, A.N.; Kopeikin, S.M.; Lompay, R.R.; Tekin, B. Metric Theories of Gravity: Perturbations and Conservation Laws; De Gruyter Studies in Mathematical Physics: Berlin, Germany, 2017. [Google Scholar] [CrossRef]
- Aviles, A.; Gruber, C.; Luongo, O.; Quevedo, H. Cosmography and constraints on the equation of state of the Universe in various parametrizations. Phys. Rev. D 2012, 86, 123516. [Google Scholar] [CrossRef]
- Dunsby, P.K.S.; Luongo, O. On the theory and applications of modern cosmography. Int. J. Geom. Meth. Mod. Phys. 2016, 13, 1630002. [Google Scholar] [CrossRef]
- Capozziello, S.; Laurentis, M.D.; Luongo, O.; Ruggeri, A.C. Cosmographic Constraints and Cosmic Fluids. Galaxies 2013, 1, 216. [Google Scholar] [CrossRef]
- Capozziello, S.; D’Agostino, R.; Luongo, O. Extended gravity cosmography. Int. J. Mod. Phys. 2019, 28, 1930016. [Google Scholar] [CrossRef]
- Ghez, A.M.; Morris, M.; Becklin, E.E.; Tanner, A.; Kremenek, T. The accelerations of stars orbiting the Milky Way’s central black hole. Nature 2000, 407, 349. [Google Scholar] [CrossRef] [PubMed]
- Ghez, A.M.; Salim, S.; Weinberg, N.N.; Lu, J.R.; Do, T.; Dunn, J.K.; Matthews, K.; Morris, M.R.; Yelda, S.; Becklin, E.E.; et al. Measuring distance and properties of the Milky Way’s central supermassive black hole with stellar orbits. Astrophys. J. 2008, 689, 1044. [Google Scholar] [CrossRef]
- Gillessen, S.; Eisenhauer, F.; Fritz, T.K.; Bartko, H.; Dodds-Eden, K.; Pfuhl, O.; Ott, T.; Genzel, R. The orbit of the star S2 around SGR A* from very large telescope and Keck data. Astrophys. J. 2009, 707, L114. [Google Scholar] [CrossRef]
- Gillessen, S.; Eisenhauer, F.; Trippe, S.; Alexander, T.; Genzel, R.; Martins, F.; Ott, T. Monitoring stellar orbits around the massive black hole in the Galactic Center. Astrophys. J. 2009, 692, 1075. [Google Scholar] [CrossRef]
- Schodel, R.; Ott, T.; Genzel, R.; Hofmann, R.; Lehnert, M.; Eckart, A.; Mouawad, N.; Alexander, T.; Reid, M.J.; Lenzen, R.; et al. Closest star seen orbiting the supermassive black hole at the Centre of the Milky Way. Nature 2002, 419, 694. [Google Scholar] [CrossRef]
- Genzel, R.; Eisenhauer, F.; Gillessen, S. The Galactic Center massive black hole and nuclear star cluster. Rev. Mod. Phys. 2010, 82, 3121. [Google Scholar] [CrossRef]
- Meyer, L.; Ghez, A.M.; Schödel, R.; Yelda, S.; Boehle, A.; Lu, J.R.; Do, T.; Morris, M.R.; Becklin, E.E.; Matthews, K. The Shortest-Known-Period Star Orbiting Our Galaxy’s Supermassive Black Hole. Science 2012, 338, 84. [Google Scholar] [CrossRef]
- Gillessen, S.; Plewa, P.M.; Eisenhauer, F.; Sari, R.E.; Waisberg, I.; Habibi, M.; Pfuhl, O.; George, E.; Dexter, J.; von Fellenberg, S.; et al. An Update on Monitoring Stellar Orbits in the Galactic Center. Astrophys. J. 2017, 837, 30. [Google Scholar] [CrossRef]
- Hees, A.; Do, T.; Ghez, A.M.; Martinez, G.D.; Naoz, S.; Becklin, E.E.; Boehle, A.; Chappell, S.; Chu, D.; Dehghanfar, A.; et al. Testing General Relativity with Stellar Orbits around the Supermassive Black Hole in Our Galactic Center. Phys. Rev. Lett. 2017, 118, 211101. [Google Scholar] [CrossRef]
- Chu, D.S.; Do, T.; Hees, A.; Ghez, A.; Naoz, S.; Witzel, G.; Sakai, S.; Chappell, S.; Gautam, A.K.; Lu, J.R.; et al. Investigating the Binarity of S0-2: Implications for Its Origins and Robustness as a Probe of the Laws of Gravity around a Supermassive Black Hole. Astrophys. J. 2018, 854, 12. [Google Scholar] [CrossRef]
- Amorim, A.; Bauböck, M.; Benisty, M.; Berger, J.-P. [The GRAVITY Collaboration] Scalar field effects on the orbit of S2 star. Mon. Not. R. Astron. Soc. 2019, 489, 4606. [Google Scholar]
- Hees, A.; Do, T.; Roberts, B.M.; Ghez, A.M.; Nishiyama, S.; Bentley, R.O.; Gautam, A.K.; Jia, S.; Kara, T.; Lu, J.R.; et al. Search for a Variation of the Fine Structure Constant around the Supermassive Black Hole in Our Galactic Center. Phys. Rev. Lett. 2020, 124, 081101. [Google Scholar] [CrossRef]
- Abuter, R.; Amorim, A.; Bauböck, M.; Berger, J.P.; Bonnet, H.; Brandner, W.; Cardoso, V.; Clénet, Y.; de Zeeuw, P.T.; Dexter, J.; et al. [The GRAVITY Collaboration] Detection of the Schwarzschild precession in the orbit of the star S2 near the Galactic centre massive black hole. Astron. Astrophys. 2020, 636, L5. [Google Scholar]
- Abuter, R.; Amorim, A.; Anugu, N.; Bauböck, M.; Benisty, M.; Berger, J.P.; Blind, N.; Bonnet, H.; Brandner, W.; Buron, A.; et al. [The GRAVITY Collaboration] Detection of the gravitational redshift in the orbit of the star S2 near the Galactic centre massive black hole. Astron. Astrophys. 2018, 615, L15. [Google Scholar]
- Abuter, R.; Amorim, A.; Bauböck, M.; Berger, J.P.; Bonnet, H.; Brandner, W.; Clénet, Y.; Du Foresto, V.C.; De Zeeuw, P.T.; Dexter, J.; et al. [The GRAVITY Collaboration] A geometric distance measurement to the Galactic center black hole with 0.3% uncertainty. Astron. Astrophys. 2019, 625, L10. [Google Scholar]
- Do, T.; Hees, A.; Ghez, A.; Martinez, G.D.; Chu, D.S.; Jia, S.; Sakai, S.; Lu, J.R.; Gautam, A.K.; O’neil, K.K.; et al. Relativistic redshift of the star S0-2 orbiting the Galactic Center supermassive black hole. Science 2019, 365, 664. [Google Scholar] [CrossRef] [PubMed]
- Ruffini, R.; Argüelles, C.R.; Rueda, J.A. On the core-halo distribution of dark matter in galaxies. Mon. Not. R. Astron. Soc. 2015, 451, 622. [Google Scholar] [CrossRef]
- Becerra-Vergara, E.A.; Argüelles, C.R.; Krut, A.; Rueda, J.A.; Ruffini, R. Hinting a dark matter nature of Sgr A* via the S-stars. Mon. Not. R. Astron. Soc. 2021, 505, L64. [Google Scholar] [CrossRef]
- Zakharov, A.F. Testing the Galactic Centre potential with S-stars. Mon. Not. R. Astron. Soc. Lett. 2021. [Google Scholar] [CrossRef]
- Rubilar, G.F.; Eckart, A. Periastron shifts of stellar orbits near the Galactic Center. Astron. Astrophys. 2001, 374, 95. [Google Scholar] [CrossRef]
- Adkins, G.S.; McDonnell, J. Orbital precession due to central-force perturbations. Phys. Rev. D 2007, 75, 082001. [Google Scholar] [CrossRef]
- Weinberg, N.N.; Milosavljević, M.; Ghez, A.M. Stellar dynamics at the Galactic Center with an extremely large telescope. Astrophys. J. 2005, 622, 878. [Google Scholar] [CrossRef]
- Borka, D.; Jovanović, P.; Borka Jovanović, V.; Zakharov, A.F. Constraining the range of Yukawa gravity interaction from S2 star orbits. J. Cosmol. Astropart. P. 2013, 11, 081101. [Google Scholar] [CrossRef]
- Zakharov, A.F.; Borka, D.; Borka Jovanović, V.; Jovanović, P. Constraints on Rn gravity from precession of orbits of S2-like stars: A case of a bulk distribution of mass. Adv. Space Res. 2014, 54, 1108. [Google Scholar] [CrossRef]
- Borka, D.; Capozziello, S.; Jovanović, P.; Borka Jovanović, V. Probing hybrid modified gravity by stellar motion around Galactic Center. Astropart. Phys. 2016, 79, 41. [Google Scholar] [CrossRef]
- Zakharov, A.F.; Jovanović, P.; Borka, D.; Borka Jovanović, V. Constraining the range of Yukawa gravity interaction from S2 star orbits II: Bounds on graviton mass. J. Cosmol. Astropart. P. 2016, 5, 45. [Google Scholar] [CrossRef]
- Zakharov, A.F.; Jovanović, P.; Borka, D.; Borka Jovanović, V. Constraining the range of Yukawa gravity interaction from S2 star orbits III: Improvement expectations for graviton mass bounds. J. Cosmol. Astropart. P. 2018, 2018, 50. [Google Scholar] [CrossRef]
- Zakharov, A.F.; Jovanović, P.; Borka, D.; Borka Jovanović, V. Different Ways to Estimate Graviton Mass. Intern. J. Mod. Phys. Conf. Ser. 2018, 47, 1860096. [Google Scholar] [CrossRef]
- Dialektopoulos, K.F.; Borka, D.; Capozziello, S.; Borka Jovanović, V.; Jovanović, P. Constraining nonlocal gravity by S2 star orbits. Phys. Rev. D 2019, 99, 044053. [Google Scholar] [CrossRef]
- Borka Jovanović, V.; Jovanović, P.; Borka, D.; Capozziello, S.; Gravina, S.; D’Addio, A. Constraining scalar–tensor gravity models by S2 star orbits around the Galactic Center. Facta Univ. Ser. Phys. Chem. Tech. 2019, 17, 11–20. [Google Scholar] [CrossRef]
- Jovanović, P.; Borka, D.; Borka Jovanović, V.; Zakharov, A.F. Influence of bulk mass distribution on orbital precession of S2 star in Yukawa gravity. Eur. Phys. J. 2021, 75, 145. [Google Scholar]
- Borka Jovanović, V.; Capozziello, S.; Jovanović, P.; Borka, D. Recovering the fundamental plane of galaxies by f(R) gravity. Phys. Dark Universe 2016, 14, 73. [Google Scholar] [CrossRef]
- Capozziello, S.; Borka Jovanović, V.; Borka, D.; Jovanović, P. Constraining theories of gravity by fundamental plane of elliptical galaxies. Phys. Dark Universe 2020, 29, 100573. [Google Scholar] [CrossRef]
- Borka Jovanović, V.; Borka, D.; Jovanović, P.; Capozziello, S. Possible effects of hybrid gravity on stellar kinematics in elliptical galaxies. Eur. Phys. J. 2021, 75, 149. [Google Scholar]
- Capozziello, S.; Jovanović, P.; Borka Jovanović, V.; Borka, D. Addressing the missing matter problem in galaxies through a new fundamental gravitational radius. J. Cosmol. Astropart. P. 2017, 6, 44. [Google Scholar] [CrossRef]
- Adelberger, E.G.; Gundlach, J.H.; Heckel, B.R.; Hoedl, S.; Schlamminger, S. Torsion balance experiments: A low-energy frontier of particle physics. Prog. Part. Nucl. Phys. 2009, 62, 102. [Google Scholar] [CrossRef]
- Clifton, T.; Barrow, J.D. The power of general relativity. Phys. Rev. D 2005, 72, 103005. [Google Scholar] [CrossRef]
- Capozziello, S.; Cardone, V.F.; Troisi, A. Gravitational lensing in fourth order gravity. Phys. Rev. D 2006, 73, 104019. [Google Scholar] [CrossRef]
- Capozziello, S.; Cardone, V.F.; Troisi, A. Low surface brightness galaxy rotation curves in the low energy limit of Rn gravity: No need for dark matter? Mon. Not. R. Astron. Soc. 2007, 375, 1423. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Faraoni, V. f(R) theories of gravity. Rev. Mod. Phys. 2010, 82, 451. [Google Scholar] [CrossRef]
- Talmadge, C.; Berthias, J.-P.; Hellings, R.W.; Standish, E.M. Model-independent constraints on possible modifications of Newtonian gravity. Phys. Rev. Lett. 1988, 61, 1159. [Google Scholar] [CrossRef]
- Sereno, M.; Jetzer, P. Dark matter versus modifications of the gravitational inverse-square law: Results from planetary motion in the Solar system. Mon. Not. R. Astron. Soc. 2006, 371, 626. [Google Scholar] [CrossRef]
- Cardone, V.F.; Capozziello, S. Systematic biases on galaxy haloes parameters from Yukawa-like gravitational potentials. Mon. Not. R. Astron. Soc. 2011, 414, 1301. [Google Scholar] [CrossRef]
- Sanders, R.H. Anti-gravity and galaxy rotation curves. Astron. Astrophys. 1984, 136, L21. [Google Scholar]
- Iorio, L. Constraints on the range Λ of Yukawa-like modifications to the Newtonian inverse-square law of gravitation from Solar System planetary motions. JHEP 2007, 10, 041. [Google Scholar] [CrossRef]
- Iorio, L. Putting Yukawa-like Modified Gravity (MOG) on the test in the Solar System. Sch. Res. Exch. 2008, 2008, 238385. [Google Scholar] [CrossRef][Green Version]
- Capozziello, S.; Stabile, A.; Troisi, A. Newtonian limit of f(R) gravity. Phys. Rev. D 2007, 76, 104019. [Google Scholar] [CrossRef]
- Capozziello, S.; de Filippis, E.; Salzano, V. Modelling clusters of galaxies by f(R)-gravity. Mon. Not. R. Astron. Soc. 2009, 394, 947. [Google Scholar] [CrossRef]
- White, M.J.; Kochanek, C.S. Constraints on the long-range properties of gravity from weak gravitational lensing. Astrophys. J. 2001, 560, 539. [Google Scholar] [CrossRef]
- Amendola, L.; Quercellini, C. Skewness as a test of the equivalence principle. Phys. Rev. Lett. 2004, 92, 181102. [Google Scholar] [CrossRef] [PubMed]
- Reynaud, S.; Jaekel, M.-T. Testing the Newton law at long distances. Int. J. Mod. Phys. 2005, 20, 2294. [Google Scholar] [CrossRef]
- Sealfon, C.; Verde, L.; Jimenez, R. Limits on deviations from the inverse-square law on megaparsec scales. Phys. Rev. D 2005, 71, 083004. [Google Scholar] [CrossRef]
- Moffat, J.W. Gravitational theory, galaxy rotation curves and cosmology without dark matter. JCAP 2005, 5, 22. [Google Scholar] [CrossRef]
- Moffat, J.W. Scalar–tensor-vector gravity theory. JCAP 2006, 03, 004. [Google Scholar] [CrossRef]
- Stabile, A.; Capozziello, S. Galaxy rotation curves in f(R,ϕ) gravity. Phys. Rev. D 2013, 87, 064002. [Google Scholar] [CrossRef]
- Capozziello, S.; Harko, T.; Koivisto, T.S.; Lobo, F.S.N.; Olmo, G.J. Wormholes supported by hybrid metric-Palatini gravity. Phys. Rev. D 2012, 86, 127504. [Google Scholar] [CrossRef]
- Capozziello, S.; Borka, D.; Jovanović, P.; Borka Jovanović, V.B. Constraining Extended Gravity Models by S2 star orbits around the Galactic Centre. Phys. Rev. D 2014, 90, 044052. [Google Scholar] [CrossRef]
- Sanders, R.H. Mass discrepancies in galaxies: Dark matter and alternatives. Ann. Rev. Astron. Astrophys. 1990, 2, 1. [Google Scholar] [CrossRef]
- Olmo, G.J. Palatini Approach to Modified Gravity: f(R) Theories and Beyond. Int. J. Mod. Phys. D 2011, 20, 413. [Google Scholar] [CrossRef]
- Harko, T.; Koivisto, T.S.; Lobo, F.S.N.; Olmo, G.J. Metric-Palatini gravity unifying local constraints and late-time cosmic acceleration. Phys. Rev. D 2012, 85, 084016. [Google Scholar] [CrossRef]
- Capozziello, S.; Harko, T.; Koivisto, T.S.; Lobo, F.S.N.; Olmo, G.J. Galactic rotation curves in hybrid metric-Palatini gravity. Astropart. Phys. 2013, 35, 65. [Google Scholar] [CrossRef]
- Capozziello, S.; Harko, T.; Koivisto, T.S.; Lobo, F.S.N.; Olmo, G.J. Cosmology of hybrid metric-Palatini f(X)-gravity. JCAP 2013, 1304, 011. [Google Scholar] [CrossRef]
- Capozziello, S.; Harko, T.; Lobo, F.S.N.; Olmo, G.J. Hybrid modified gravity unifying local tests, galactic dynamics and late-time cosmic acceleration. Int. J. Mod. Phys. D 2013, 22, 1342006. [Google Scholar] [CrossRef]
- Koivisto, T.S. Cosmology of modified (but second order) gravity. AIP Conf. Proc. 2010, 1206, 79. [Google Scholar]
- Koivisto, T. Dynamics of Nonlocal Cosmology. Phys. Rev. D 2008, 77, 123513. [Google Scholar] [CrossRef]
- Koivisto, T.S. Newtonian limit of nonlocal cosmology. Phys. Rev. D 2008, 78, 123505. [Google Scholar] [CrossRef]
- Barvinsky, A.O. Aspects of Nonlocality in Quantum Field Theory, Quantum Gravity and Cosmology. Mod. Phys. Lett. A 2015, 30, 1540003. [Google Scholar] [CrossRef]
- Capozziello, S.; Capriolo, M. Gravitational waves in non-local gravity. Class. Quantum Grav. 2021, 38, 175008. [Google Scholar] [CrossRef]
- Capozziello, S.; Capriolo, M.; Nojiri, S. Considerations on gravitational waves in higher-order local and non-local gravity. Phys. Lett. B 2020, 810, 135821. [Google Scholar] [CrossRef]
- Peißker, F.; Eckart, A.; Zajaček, M.; Michal, A.; Ali, B.; Parsa, M. S62 and S4711: Indications of a Population of Faint Fast-moving Stars inside the S2 Orbit—S4711 on a 7.6 yr Orbit around Sgr A*. Astrophys. J. 2020, 899, 50. [Google Scholar] [CrossRef]
- Iorio, L. The Short-period S-stars S4711, S62, S4714 and the Lense–Thirring Effect due to the Spin of Sgr A*. Astrophys. J. 2020, 904, 186. [Google Scholar] [CrossRef]
- Iorio, L. On the 2PN Pericentre Precession in the General Theory of Relativity and the Recently Discovered Fast-Orbiting S-Stars in Sgr A*. Universe 2021, 7, 37. [Google Scholar] [CrossRef]
- Gainutdinov, R.; Baryshev, Y. Relativistic Effects in Orbital Motion of the S-Stars at the Galactic Center. Universe 2020, 6, 177. [Google Scholar] [CrossRef]
- Fragione, G.; Loeb, A. An Upper Limit on the Spin of SgrA* Based on Stellar Orbits in Its Vicinity. Astrophys. J. Lett. 2020, 901, L32. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).