Hyperons in Neutron Stars
Abstract
1. Introduction
2. Many-Body Methods
2.1. Relativistic Mean-Field Models
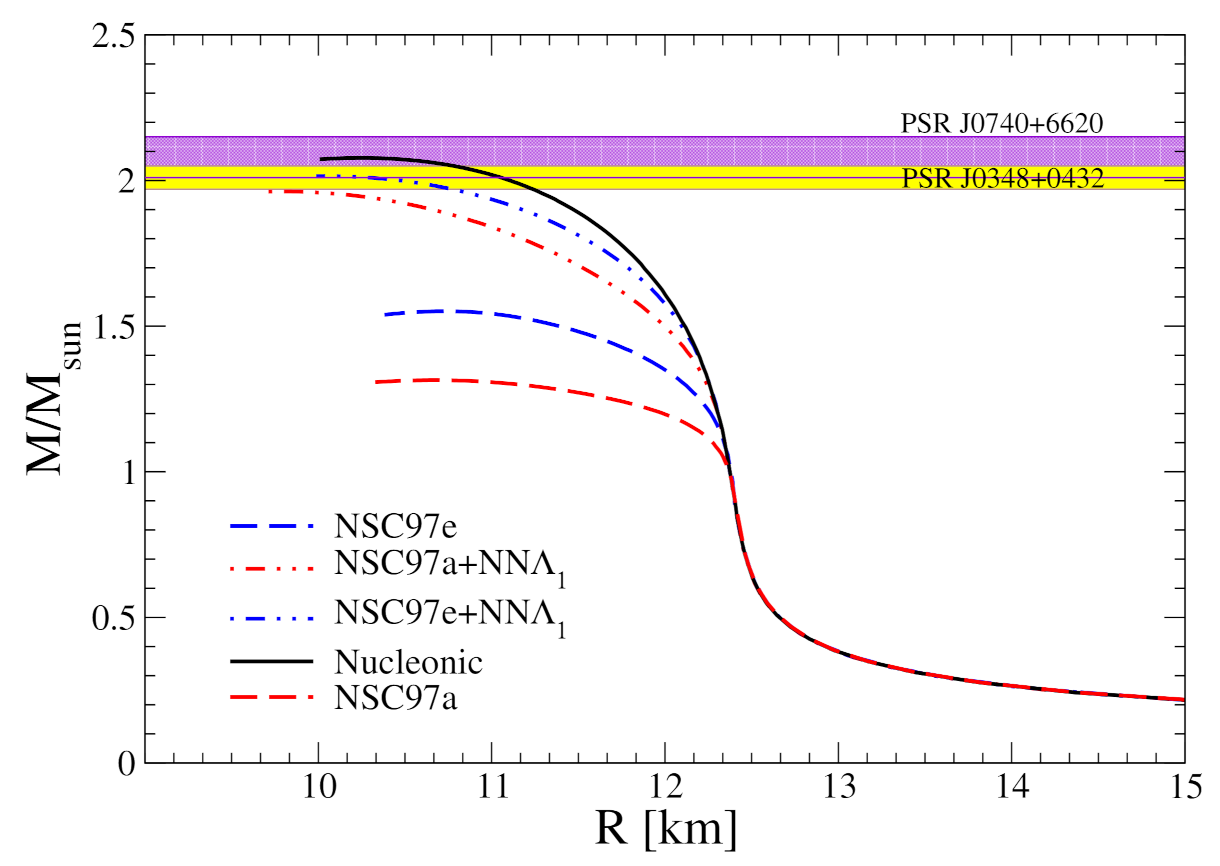
2.2. Neutron Star Structure of RMF Models
2.3. Microscopic Approaches
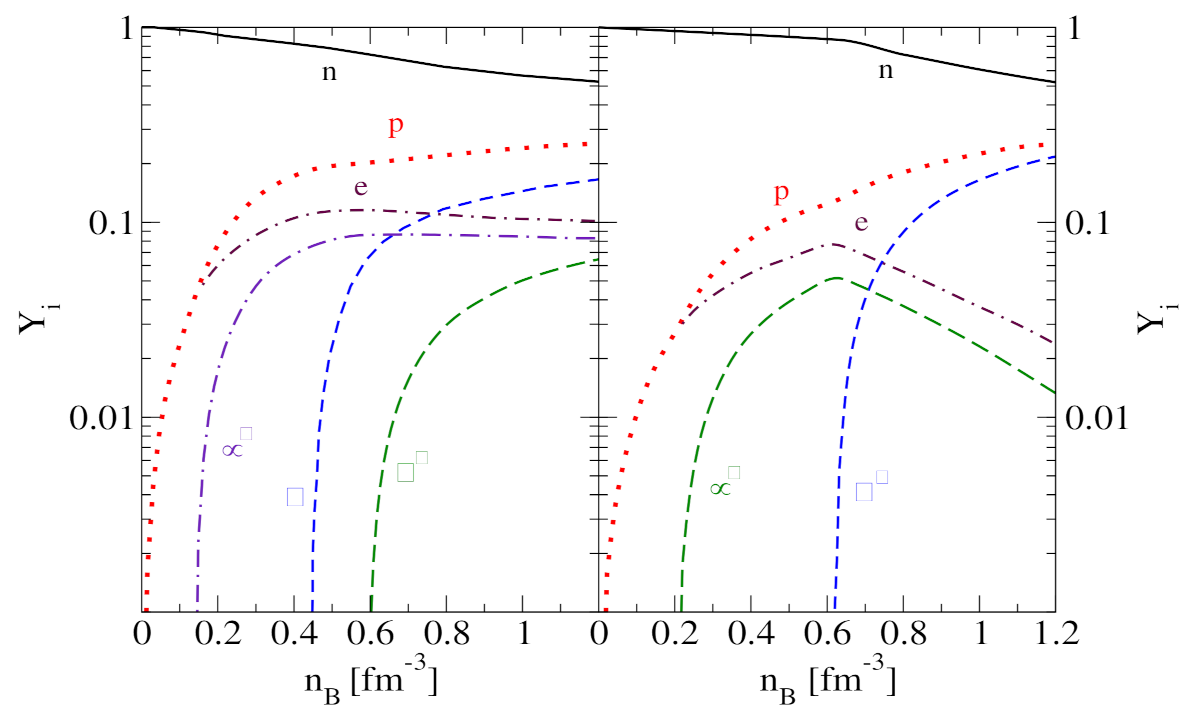
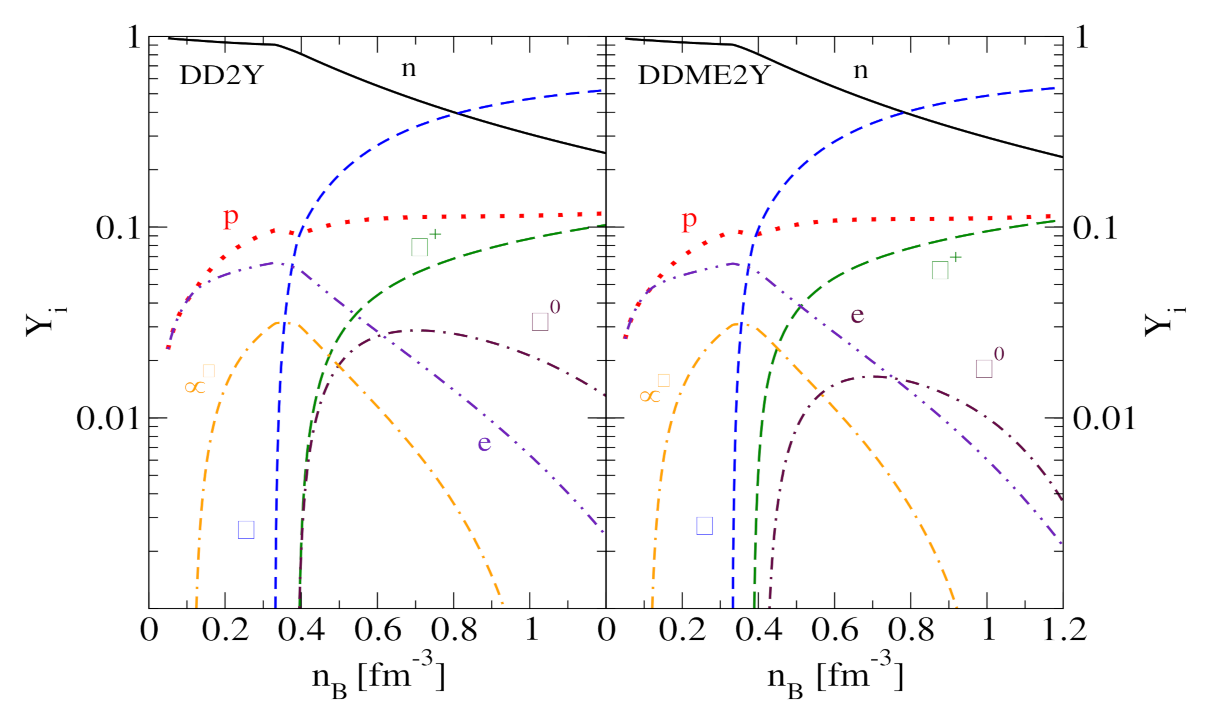
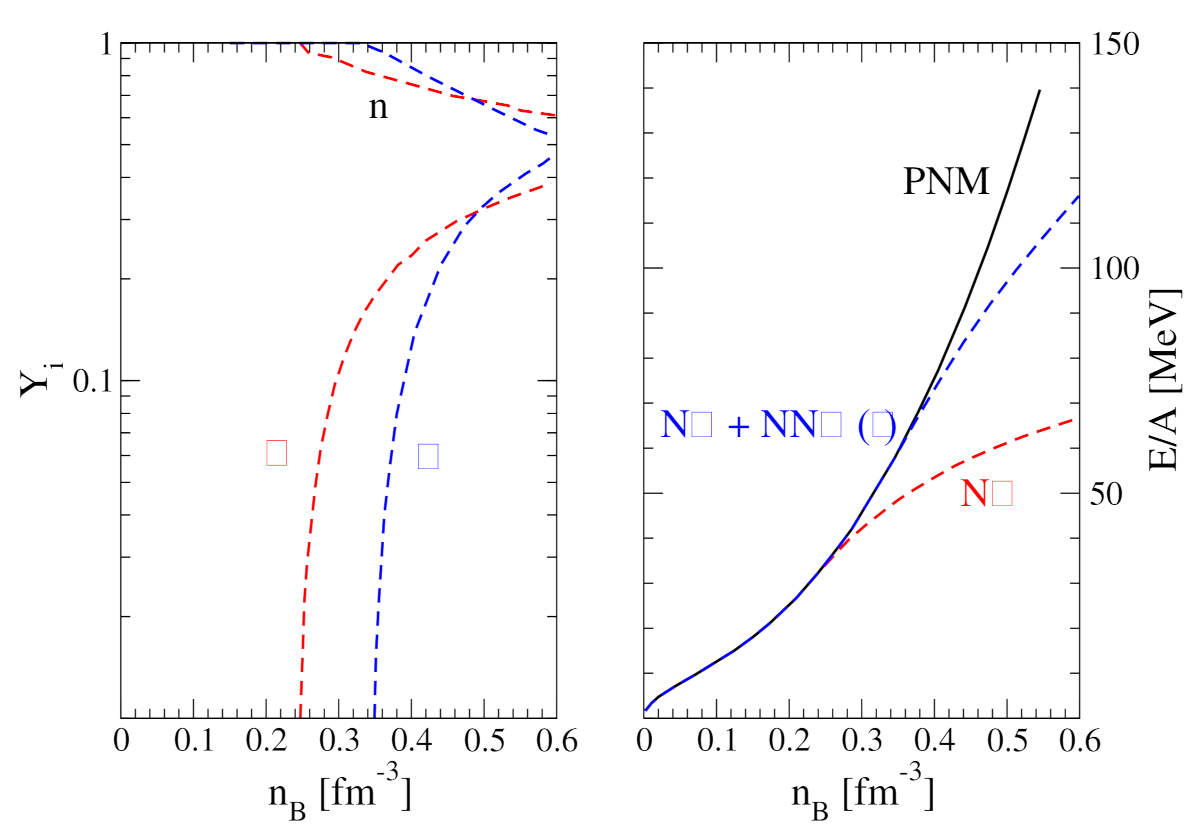
2.4. The NY and YY Interactions
2.5. Results from Microscopic Calculations
2.6. Possible Signatures of the Presence of Hyperons in Astrophysical Dynamical Systems
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rochester, G.; Butler, C. Evidence for the Existence of New Unstable Elementary Particles. Nature 1947, 160, 855–857. [Google Scholar] [CrossRef] [PubMed]
- Danysz, M.; Pniewski, J. Delayed disintegration of a heavy nuclear fragment: I. Philos. Mag. 1953, 44, 348–350. [Google Scholar] [CrossRef]
- Alexander, G.; Karshon, U.; Shapira, A.; Yekutieli, G.; Engelmann, R.; Filthuth, H.; Lughofer, W. Study of the Λ-N system in low-energy Λ-p elastic scattering. Phys. Rev. 1968, 173, 1452–1460. [Google Scholar] [CrossRef]
- Sechi-Zorn, B.; Kehoe, B.; Twitty, J.; Burnstein, R.A. Low-energy Λ-proton elastic scattering. Phys. Rev. 1968, 175, 1735–1740. [Google Scholar] [CrossRef]
- Engelmann, R.; Filthuth, H.; Hepp, V.; Kluge, E. Inelastic Σ-p-interactions at low momenta. Phys. Lett. 1966, 21, 587–589. [Google Scholar] [CrossRef]
- Eisele, F.; Filthuth, H.; Fohlisch, W.; Hepp, V.; Zech, G. Elastic Σ±p scattering at low energies. Phys. Lett. B 1971, 37, 204–206. [Google Scholar] [CrossRef]
- Khaustov, P. Evidence of Ξ hypernuclear production in the 12C(K-,K+)Be reaction. Phys. Rev. C 2000, 61, 054603. [Google Scholar] [CrossRef]
- Nakazawa, K.; Endo, Y.; Fukunaga, S.; Hoshino, K.; Hwang, S.H.; Imai, K.; Yoshida, J. The first evidence of a deeply bound state of Ξ--14N system. Progr. Theor. Exp. Phys. 2015, 2015, 033D02. [Google Scholar] [CrossRef]
- Hayakawa, S.H.; Agari, K.; Ahn, J.K.; Akaishi, T.; Akazawa, Y.; Ashikaga, S.; J-PARC E07 Collaboration. Observation of Coulomb-Assisted Nuclear Bound State of Ξ--14N System. Phys. Rev. Lett. 2021, 126, 062501. [Google Scholar] [CrossRef] [PubMed]
- Yoshimoto, M.; Ahn, J.K.; Bassalleck, B.; Ekawa, H.; Endo, Y.; Fujita, M.; Zhang, Z. First observation of a nuclear s-state of a Ξ hypernucleus, C. Prog. Theor. Exp. Phys. 2021, 7, 073D02. [Google Scholar] [CrossRef]
- Prakash, M.; Bombaci, I.; Prakash, M.; Ellis, P.J.; Lattimer, M.J.; Knorren, R. Composition and structure of protoneutron stars. Phys. Rep. 1997, 280, 1. [Google Scholar] [CrossRef]
- Oertel, M.; Hempel, M.; Klähn, T.; Typel, S. Equations of state for supernovae and compact stars. Rev. Mod. Phys. 2017, 89, 015007. [Google Scholar] [CrossRef]
- Bernuzzi, S.; Dietrich, T.; Nagar, A. Modeling the complete gravitational wave spectrum of neutron star mergers. Phys. Rev. Lett. 2015, 115, 091101. [Google Scholar] [CrossRef]
- Bauswein, A.; Janka, H.-T. Measuring Neutron-Star Properties via Gravitational Waves from Neutron-Star Mergers. Phys. Rev. Lett. 2012, 108, 011101. [Google Scholar] [CrossRef] [PubMed]
- Shibata, M.; Hotokezaka, K. Merger and Mass Ejection of Neutron-Star Binaries. Annu. Rev. Nucl. Part. Sci. 2019, 69, 41. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Cahillane, C. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Bulten, H.J. GW170817: Measurements of Neutron Star Radii and Equation of State. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Byer, R.L. GW190425: Observation of a Compact Binary Coalescence with Total Mass ∼3.4M⊙. Astrophys. J. Lett. 2020, 892, L3. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Brown, D.D. GW190814: Gravitational Waves from the Coalescence of a 23 Solar Mass Black Hole with a 2.6 Solar Mass Compact Object. Astrophys. J. Lett. 2020, 896, L44. [Google Scholar] [CrossRef]
- Glendenning, N.K. Compact Stars; Springer: New York, NY, USA, 2000. [Google Scholar]
- Bombaci, I.; Logoteta, D.; Panda, P.K.; Providência, C.; Vidaña, I. Quark matter nucleation in hot hadronic matter. Phys. Lett. B 2009, 680, 448–452. [Google Scholar] [CrossRef]
- Bombaci, I.; Logoteta, D.; Vidaña, I.; Providência, C. Quark matter nucleation in neutron stars and astrophysical implications. Eur. Phys. J. A 2016, 52, 58. [Google Scholar] [CrossRef]
- Klahn, T.; Blaschke, D.; Lastowiecki, D. Implications of the measurement of pulsars with two solar masses for quark matter in compact stars and heavy-ion collisions: A Nambu–Jona-Lasinio model case study. Phys. Rev. D 2013, 88, 085001. [Google Scholar] [CrossRef]
- Weissenborn, S.; Sagert, I.; Pagliara, G.; Hempel, M.; Schaeffner-Bielich, J. Quark matter in massive compact stars. Astophys. J. Lett. 2011, 740, L14. [Google Scholar] [CrossRef]
- Bonanno, L.; Sedrakian, A. Composition and stability of hybrid stars with hyperons and quark color-superconductivity. Astron. Astrophys. 2012, 539, A16. [Google Scholar] [CrossRef]
- Bombaci, I.; Drago, A.; Logoteta, D.; Pagliara, G.; Vidaña, I. Was GW190814 a Black Hole–Strange Quark Star System? Phys. Rev. Lett. 2021, 126, 162702. [Google Scholar] [CrossRef] [PubMed]
- Ambartsumyan, V.A.; Saakyan, G.S. The Degenerate Superdense Gas of Elementary Particles. Sov. Astron. 1960, 4, 187. [Google Scholar]
- Balberg, S.; Gal, A. An Effective Equation of State for Dense Matter with Strangeness. Nucl. Phys. A 1997, 625, 435–472. [Google Scholar] [CrossRef]
- Schaffner, U.; Mishustin, I.N. Hyperon-rich matter in neutron stars. Phys. Rev. C 1996, 53, 3. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Piekarewicz, J. Neutron radii of 208Pb and neutron stars. Phys. Rev. C 2001, 64, 062802. [Google Scholar] [CrossRef]
- Typel, S.; Wolter, H.H. Relativistic mean field calculations with density-dependent meson-nucleon coupling. Nucl. Phys. 1999, 656, 331–364. [Google Scholar] [CrossRef]
- ter Haar, B.; Malfliet, R. Nucleons, mesons and deltas in nuclear matter a relativistic Dirac-Brueckner approach. Phys. Rep. 1987, 149, 207. [Google Scholar] [CrossRef]
- Brockmann, R.; Machleidt, R. Relativistic nuclear structure. I. Nuclear matter. Phys. Rev. C 1990, 42, 1965. [Google Scholar] [CrossRef]
- Sugahara, Y.; Toki, H. Relativistic mean-field theory for unstable nuclei with non-linear σ and ω terms. Nucl. Phys. A 1994, 579, 557–572. [Google Scholar] [CrossRef]
- Lalazissis, G.A.; Konig, J.; Ring, P. New parametrization for the Lagrangian density of relativistic mean field theory. Phys. Rev. C 1997, 55, 540–543. [Google Scholar] [CrossRef]
- Providência, C.; Rabhi, A. Interplay between the symmetry energy and the strangeness content of neutron stars. Phys. Rev. C 2013, 87, 055801. [Google Scholar] [CrossRef]
- Steiner, A.; Hempel, M.; Fischer, T. Core-collapse Supernova Equations of State Based on Neutron Star Observations. Astrophys. J. 2013, 774, 17. [Google Scholar] [CrossRef]
- Fattoyev, F.J.; Horowitz, C.J.; Piekarewicz, J.; Shen, G. Relativistic effective interaction for nuclei, giant resonances, and neutron stars. Phys. Rev. C 2010, 82, 055803. [Google Scholar] [CrossRef]
- Lalazissis, G.A.; Niksic, T.; Vretenar, D.; Ring, P. New relativistic mean-field interaction with density-dependent meson-nucleon couplings. Phys. Rev. C 2005, 71, 024312. [Google Scholar] [CrossRef]
- Typel, W. Composition and thermodynamics of nuclear matter with light clusters. Phys. Rev. C 2010, 81, 015803. [Google Scholar] [CrossRef]
- Glendenning, N.K.; Moszkowski, S.A. Reconciliation of Neutron-Star Masses and Binding of the Λ in Hypernuclei. Phys. Rev. Lett. 1996, 67, 18. [Google Scholar] [CrossRef]
- Millener, D.J.; Dover, C.B.; Gal, A. Λ-nucleus single-particle potentials. Phys. Rev. C 1988, 38, 2700. [Google Scholar] [CrossRef]
- Gal, A. Strangeness nuclear physics—2010. arXiv 2010, arXiv:1008.3510. [Google Scholar] [CrossRef][Green Version]
- Gal, A.; Hungerford, E.V.; Millener, D.J. Strangeness in nuclear physics. Rev. Mod. Phys. 2016, 88, 035004. [Google Scholar] [CrossRef]
- Sugimura, H. Search for H hypernucleus by the 6Li(π-,K+) reaction at pπ- = 1.2 GeV/c. Phys. Lett. B 2014, 729, 39. [Google Scholar] [CrossRef]
- Honda, R. Missing-mass spectroscopy with the 6Li(π-,K+)X reaction to search for H. Phys. Rev. C 2017, 96, 014005. [Google Scholar] [CrossRef]
- Danysz, M.; Garbowska, K.; Pniewski, J.; Pniewski, T.; Zakrzewski, J.; Fletcher, E.R.; March, P.V. The identification of a double hyperfragment. Nucl. Phys. A 1963, 49, 121. [Google Scholar] [CrossRef]
- Prowse, D.J. The identification of a double hyperfragment. Phys. Rev. Lett. 1966, 17, 782. [Google Scholar] [CrossRef]
- Takahashi, H.; Ahn, J.K.; Akikawa, H.; Aoki, S.; Arai, K.; Bahk, S.Y.; Baik, K.M.; Bassalleck, B.; Chung, J.H.; Chung, M.S.; et al. Observation of a He Double Hypernucleus. Phys. Rev. Lett. 2001, 87, 212502. [Google Scholar] [CrossRef]
- Ahn, J.K.; Akikawa, H.; Aoki, S. Double-Λ hypernuclei observed in a hybrid emulsion experiment. Phys. Rev. C 2013, 88, 014003. [Google Scholar] [CrossRef]
- Fortin, M.; Avancini, S.S.; Providência, C.; Vidaña, I. Hypernuclei and massive neutron stars. Phys. Rev. C 2017, 95, 065803. [Google Scholar] [CrossRef]
- Danielewicz, P.; Lacey, R.; Lynch, W.G. Determination of the Equation of State of Dense Matter. Science 2002, 298, 1592. [Google Scholar] [CrossRef] [PubMed]
- Van Dalen, E.N.E.; Colucci, G.; Sedrakian, A. Constraining hypernuclear density functional with Λ-hypernuclei and compact stars. Phys. Lett. B 2014, 734, 383–387. [Google Scholar] [CrossRef]
- Papazoglou, P.; Schramm, S.; Schaffner-Bielich, J.; Stöcker, H.; Greiner, W. Chiral Lagrangian for strange hadronic matter. Phys. Rev. C 1998, 57, 5. [Google Scholar] [CrossRef]
- Papazoglou, P.; Zschiesche, D.; Schramm, S.; Schaffner-Bielich, J.; Stocker, H.; Greiner, W. Nuclei in a chiral SU(3) model. Phys. Rev. C 1999, 59, 1. [Google Scholar] [CrossRef]
- Hanauske, M.; Zschiesche, D.; Pal, S.; Schramm, S.; Stocker, H.; Greiner, W. Neutron Star Properties in a Chiral SU(3) Model. Astrophys. J. 2000, 537, 958. [Google Scholar] [CrossRef]
- Dexheimer, V.; Schramm, S. Protoneutron stars in a Chiral SU(3) Model. Astrophys. J. 2008, 683, 943. [Google Scholar] [CrossRef]
- Kubis, S.; Kutschera, M. Nuclear matter in relativistic mean field theory with isovector scalar meson. Phys. Lett. B 1997, 399, 191. [Google Scholar] [CrossRef]
- Liu, B.; Greco, V.; Baran, V.; Colonna, M.; di Toro, M. Asymmetric nuclear matter: The role of the isovector scalar channel. Phys. Rev. C 2002, 65, 045201. [Google Scholar] [CrossRef]
- Menezes, D.P.; Providência, C. δ meson effects on stellar matter. Phys. Rev. C 2004, 70, 058801. [Google Scholar] [CrossRef]
- Mi, A.J.; Zuo, W.; Li, A. The effect of the scalar-isovector meson field on hyperon-rich neutron star matter. J. Mod. Phys. E 2008, 17, 1293. [Google Scholar] [CrossRef]
- Guichon, P.A.M. A possible quark mechanism for the saturation of nuclear matter. Phys. Lett. B 1988, 200, 235. [Google Scholar] [CrossRef]
- Saito, K.; Thomas, A.W. A quark-meson coupling model for nuclear and neutron matter. Phys. Lett. B 1994, 327, 9. [Google Scholar] [CrossRef]
- Migdal, A.B. Phase transitions (π-condensation) in nuclei and neutron stars. Phys. Lett. B 1973, 45, 448. [Google Scholar] [CrossRef]
- Sawyer, R.F. Condensed π- Phase in Neutron-Star Matter. Phys. Rev. Lett. 1972, 29, 382. [Google Scholar] [CrossRef]
- Baym, G.; Flowers, E. Pion condensation in neutron star matter: Equilibrium conditions and model calculations. Nucl. Phys. A 1974, 222, 29. [Google Scholar] [CrossRef]
- Haensel, P.; Proszinsky, M. Pion condensation in cold dense matter and neutron stars. Astrophys. J. 1982, 258, 306. [Google Scholar] [CrossRef]
- Ohnishi, A.; Jido, D.; Sekihara, T.; Tsubakihara, K. Possibility of s-wave pion condensates in neutron stars revisited. Phys. Rev. C 2008, 80, 038202. [Google Scholar] [CrossRef]
- Fore, B.; Reddy, S. Pions in hot dense matter and their astrophysical implications. Phys. Rev. C 2020, 101, 035809. [Google Scholar] [CrossRef]
- Kaplan, D.B.; Nelson, A.E. Kaon condensation in dense matter. Phys. Lett. B 1992, 291, 355. [Google Scholar] [CrossRef]
- Brown, G.E.; Kubodera, K.; Rho, M.; Thorsson, V. A novel mechanism for kaon condensation in neutron star matter. Phys. Lett. B 1992, 291, 355. [Google Scholar] [CrossRef]
- Thorsson, V.; Prakash, M.; Lattimer, J.M. Composition, Structure and Evolution of Neutron Stars with Kaon Condensates. Nucl. Phys. A 1994, 572, 693. [Google Scholar] [CrossRef]
- Fujii, H.; Maruyama, T.; Muto, T.; Tatsumi, T. Equation of state with kaon condensates and neutron stars. Nucl. Phys. A 1996, 597, 645. [Google Scholar] [CrossRef]
- Li, G.Q.; Lee, C.H.; Brown, G.E. Kaon Production in Heavy-Ion Collisions and Maximum Mass of Neutron Stars. Phys. Rev. Lett. 1997, 79, 5214. [Google Scholar] [CrossRef]
- Glendenning, N.K.; Schaffner-Bielich, J. Kaon Condensation and Dynamical Nucleons in Neutron stars. Phys. Rev. Lett. 1998, 81, 4564. [Google Scholar] [CrossRef]
- Ramos, A.; Schaffner-Bielich, J.; Wambach, J. Kaon Condensation in Neutron Stars. Lect. Notes Phys. 2001, 578, 175. [Google Scholar] [CrossRef]
- Norsen, T.; Reddy, S. First order kaon condensation in neutron stars: Finite size effects in the mixed phase. Phys. Rev. C 2001, 63, 065804. [Google Scholar] [CrossRef]
- Kubis, S.; Kutschera, M. Kaon Condensates, Nuclear Symmetry Energy and Cooling of Neutron Stars. Nucl. Phys. A 2003, 720, 189–206. [Google Scholar] [CrossRef][Green Version]
- Li, A.; Burgio, G.F.; Lombardo, U. Microscopic three-body forces and kaon condensation in cold neutrino-trapped matter. Phys. Rev. C 2006, 74, 055801. [Google Scholar] [CrossRef]
- Baruah Thapa, V.; Monika, S.; Li, J.J.; Sedrakian, A. Massive Δ-resonance admixed hypernuclear stars with antikaon condensations. Phys. Rev. D 2021, 103, 063004. [Google Scholar] [CrossRef]
- Tolos, L.; Fabbietti, L. Strangeness in nuclei and neutron stars. Prog. Part. Nucl. Phys. 2020, 112, 103770. [Google Scholar] [CrossRef]
- Mishra, A.; Kumar, A.; Sanyal, S.; Dexheimer, V.; Schramm, S. Kaon properties in (proto-)neutron star matter. Eur. Phys. J. A 2010, 45, 169. [Google Scholar] [CrossRef][Green Version]
- Iliescu, M.; Bazzi, M.; Beer, G.; Bombelli, L.; Bragadireanu, A.M.; Cargnelli, M.; Curceanu, C.; Fiorini, C.; Frizzi, T.; Ghio, F.; et al. Kaon-Nucleon Strong Interaction in Kaonic Atoms: The SIDDHARTA Program. Few-Body Syst. 2013, 54, 1123. [Google Scholar] [CrossRef]
- Voskresensky, D.N. On the possibility of the condensation of the charged rho-meson field in dense isospin asymmetric baryon matter. Phys. Lett. B 1997, 392, 262. [Google Scholar] [CrossRef]
- Kolomeitsev, E.E.; Voskresensky, D.N. Relativistic mean-field models with effective hadron masses and coupling constants, and ρ-condensation. Nucl. Lett. A 2005, 759, 373. [Google Scholar] [CrossRef]
- Brown, G.E.; Rho, M. Scaling effective Lagrangians in a dense medium. Phys. Rev. Lett. 1991, 66, 2720. [Google Scholar] [CrossRef]
- Mallick, R.; Schramm, S.; Dexheimer, V.; Bhattacharyya, A. On the possibility of rho-meson condensation in neutron stars. Mon. Not. R. Astron. Soc. 2015, 449, 1347. [Google Scholar] [CrossRef]
- Sawyer, R.F. Energy shifts of excited nucleons in neutron-star matter. Astrophys. J. 1972, 176, 205. [Google Scholar] [CrossRef]
- Drago, A.; Lavagno, A.; Pagliara, G.; Pigato, D. Early appearance of Δ isobars in neutron stars. Phys. Rev. C 2014, 90, 065809. [Google Scholar] [CrossRef]
- Kolomeitsev, E.E.; Maslov, K.A.; Voskresensky, D.N. Delta isobars in relativistic mean-field models with σ-scaled hadron masses and couplings. Nucl. Phys. A 2017, 961, 106. [Google Scholar] [CrossRef]
- Xiang, H.; Guo, H. Δ excitation and its influences on neutron stars in relativistic mean field theory. Phys. Rev. C 2003, 67, 038801. [Google Scholar] [CrossRef]
- Chen, Y.J.; Guo, H.; Liu, Y. Neutrino scattering rates in neutron star matter with Δ isobars. Phys. Rev. C 2007, 75, 035806. [Google Scholar] [CrossRef]
- Schurhoff, T.; Schramm, S.; Dexheimer, V. Neutron stars with small radii—The role of delta resonances. Astrophys. J. 2010, 724, L74. [Google Scholar] [CrossRef]
- Lavagno, A. Hot and dense hadronic matter in an effective mean-field approach. Phys. Rev. C 2010, 2010 81, 044909. [Google Scholar] [CrossRef]
- Ribes, P.; Ramos, A.; Tolos, L.; Gonzalez-Boquera, C.; Centelles, M. Interplay between Δ Particles and Hyperons in Neutron Stars. Astrophys. J. 2019, 883, 168. [Google Scholar] [CrossRef]
- Motta, T.F.; Thomas, A.W.; Guichon, P.A.M. Do Delta baryons play a role in neutron stars? Phys. Lett. B 2020, 802, 135266. [Google Scholar] [CrossRef]
- Li, J.J.; Sedrakian, A.; Webers, F. Competition between delta isobars and hyperons and properties of compact stars. Phys. Lett B 2018, 783, 234. [Google Scholar] [CrossRef]
- Baldo, M.; Ferreira, L.S. The Δ potential in nuclear matter from the Argonne v28 interaction. Phys. Lett. B 1992, 268, 19–23. [Google Scholar] [CrossRef]
- Zhu, Z.Y.; Li, A.; Hu, J.N.; Sagawa, H. Δ(1232) effects in density-dependent relativistic Hartree-Fock theory and neutron stars. Phys. Rev. C 2016, 94, 045803. [Google Scholar] [CrossRef]
- Miyatsu, T.; Katayama, T.; Saito, K. Effects of Fock term, tensor coupling and baryon structure variation on a neutron star. Phys. Lett. B 2012, 709, 242. [Google Scholar] [CrossRef]
- Katayama, T.; Miyatsu, T.; Saito, K. Equation of state for massive neutron stars. Astrophys. J. 2012, 203, 22. [Google Scholar] [CrossRef][Green Version]
- Zhang, X.; Prakash, M. Hot and dense matter beyond relativistic mean field theory. Phys. Rev. C 2016, 93, 055805. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; Van Kerkwijk, M.H.; Whelan, D.G. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 1233232. [Google Scholar] [CrossRef] [PubMed]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Zhu, W.W. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2020, 4, 72–76. [Google Scholar] [CrossRef]
- Fonseca, E.; Cromartie, H.; Pennucci, T.T.; Ray, P.S.; Kirichenko, A.Y.; Ransom, S.M.; Zhu, W. Refined Mass and Geometric Measurements of the High-Mass PSR J0740+6620. Astrophys. J. Lett. 2021, 915, L12. [Google Scholar] [CrossRef]
- Demorest, P.; Pennucci, T.; Ransom, S.; Roberts, M.; Hessels, J. Shapiro delay measurement of a two solar mass neutron star. Nature 2010, 467, 1081. [Google Scholar] [CrossRef] [PubMed]
- Shapiro, I. Fourth Test of General Relativity. Phys. Rev. Lett. 1964, 13, 789–791. [Google Scholar] [CrossRef]
- Shibata, M.; Fujibayashi, S.; Hotokezaka, K.; Kiuchi, K.; Kyutoku, K.; Sekiguchi, Y.; Tanaka, M. Modeling GW170817 based on numerical relativity and its implications. Phys. Rev. D 2017, 96, 123012. [Google Scholar] [CrossRef]
- Margalit, B.; Metzger, B.D. Constraining the Maximum Mass of Neutron Stars from Multi-messenger Observations of GW170817. Astrophys. J. Lett. 2017, 850, L19. [Google Scholar] [CrossRef]
- Rezzolla, L.; Most, E.R.; Weih, L.R. Using Gravitational-wave Observations and Quasi-universal Relations to Constrain the Maximum Mass of Neutron Stars. Astrophys. J. Lett. 2017, 852, L25. [Google Scholar] [CrossRef]
- Ozel, F.; Psaltis, D.; Guver, T.; Baym, G.; Heinke, C.; Guillot, S. The Dense Matter Equation of State from Neutron Star Radius and Mass Measurements. Astrophys. J. 2016, 820, 28. [Google Scholar] [CrossRef]
- Suleimanov, V.F.; Poutanen, J.; Nättilä, J.; Kajava, J.J.E.; Revnivtsev, M.G.; Werner, K. The direct cooling tail method for X-ray burst analysis to constrain neutron star masses and radii. Mon. Not. R. Astron. Soc. 2017, 446, 906. [Google Scholar] [CrossRef]
- Bogdanov, S. The nearest millisecond pulsar revisited with the XMM-Newton: Improved mass-radius constraints for PSR J0437–4715. Astrophys. J. 2013, 762, 96. [Google Scholar] [CrossRef]
- Lattimer, J.M. The Nuclear Equation of State and Neutron Star Masses. Ann. Rev. Nucl. Part. Sci. 2012, 62, 485. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Stairs, I. The Radius of PSR J0740+6620 from NICER and XMM-Newton Data. Astrophys. J. Lett. 2021, 918, L28. [Google Scholar] [CrossRef]
- Riley, T.E. A NICER View of the Massive Pulsar PSR J0740+6620 Informed by Radio Timing and XMM-Newton Spectroscopy. Astrophys. J. Lett. 2021, 918, L27. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Soong, Y. PSR J0030+0451 Mass and Radius from NICER Data and Implications for the Properties of Neutron Star Matter. Astrophys. J. Lett. 2019, 887, L24. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Bogdanov, S.; Ray, P.S.; Ludlam, R.M.; Guillot, S.; Arzoumanian, Z.; Baker, C.L.; Bilous, A.V.; Chakrabarty, D.; et al. A NICER View of PSR J0030+0451: Millisecond Pulsar Parameter Estimation. Astrophys. J. Lett. 2019, 887, L21. [Google Scholar] [CrossRef]
- Huber, H.; Weigel, M.K.; Weber, F. Compatibility of Neutron Star Masses and Hyperon Coupling Constants. Z. Naturforsch 1999, 54a, 77. [Google Scholar] [CrossRef][Green Version]
- Tolos, L.; Ramos, A.; Centelles, M. The Equation of State for the Nucleonic and Hyperonic Core of Neutron Stars. Publ. Astron. Soc. Aust. 2017, 34, e065. [Google Scholar] [CrossRef]
- Weissenborn, S.; Chatterjee, D.; Schaffner-Bielich, J. Hyperons and massive neutron stars: The role of hyperon potentials. Nucl. Phys. A 2012, 881, 62–77. [Google Scholar] [CrossRef]
- Fortin, M.; Raduta, A.R.; Avancini, S.; Providência, C. Hyperonic stars and the nuclear symmetry energy. Phys. Rev. D 2020, 101, 034017. [Google Scholar] [CrossRef]
- Colucci, G.; Sedrakian, A. Equation of state of hypernuclear matter: Impact of hyperon–scalar-meson couplings. Phys. Rev. C 2013, 87, 055806. [Google Scholar] [CrossRef]
- Maslov, K.A.; Kolomeitsev, K.K.; Voskresensky, D.N. Solution of the Hyperon Puzzle within a Relativistic Mean-Field Model. Phys. Lett. B 2015, 748, 369. [Google Scholar] [CrossRef]
- Bednarek, I.; Haensel, P.; Zdunik, J.L.; Bejger, M.; Manka, R. Hyperons in neutron-star cores and a 2M⊙ pulsar. Astron. Astrophys. 2012, 543, A157. [Google Scholar] [CrossRef]
- Taurines, A.R.; Vasconcellos, C.A.Z.; Malheiro, M.; Chiapparini, M. Neutron Stars with Parametrized Meson Couplings. Mod. Phys. Lett. A 2000, 15, 1789. [Google Scholar] [CrossRef]
- Gomes, R.O.; Dexheimer, V.; Schramm, S.; Vasconcellos, C.A.Z. Many-body forces in the equation of state of hyperonic matter. Astrophys. J. 2015, 808, 8. [Google Scholar] [CrossRef]
- Oertel, M.; Gulminelli, F.; Providência, C.; Raduta, A.R. Hyperons in neutron stars and supernova cores. Eur. Phys. J. A 2016, 52, 50. [Google Scholar] [CrossRef]
- Yu, Z.; Ding, W.B.; Liu, N.N.; Luo, Q. Effects of temperature on the stability of protoneutron stars with hyperons. Mod. Phys. Lett. A 2012, 27, 1250008. [Google Scholar] [CrossRef]
- Fortin, M.; Raduta, A.R.; Avancini, S.; Providência, C. Thermal evolution of relativistic hyperonic compact stars with calibrated equations of state. Phys. Rev. D 2021, 103, 083004. [Google Scholar] [CrossRef]
- Tolós, L.; Cabrera, D.; Ramos, A. Strange mesons in nuclear matter at finite temperature. Phys. Rev. C 2008, 78, 045205. [Google Scholar] [CrossRef]
- Banik, S.; Hempel, M.; Bandyopadhyay, D. New Hyperon Equations of State for Supernovae and Neutron Stars in Density-dependent Hadron Field Theory. Astrophys. J. Suppl. 2014, 214, 22. [Google Scholar] [CrossRef]
- Day, B.D. Elements of the Brueckner-Goldstone Theory of Nuclear Matter. Rev. Mod. Phys. 1967, 39, 719. [Google Scholar] [CrossRef]
- Fiorilla, S.; Kaiser, N.; Weise, W. Chiral thermodynamics of nuclear matter. Nucl. Phys. A 2012, 880, 65. [Google Scholar] [CrossRef]
- Frick, T.; Müther, H. Self-consistent solution to the nuclear many-body problem at finite temperature. Phys. Rev. C 2003, 68, 034310. [Google Scholar] [CrossRef]
- Frick, T.; Müther, H.; Rios, A.; Polls, A.; Ramos, A. Correlations in hot asymmetric nuclear matter. Phys. Rev. C 2005, 71, 014313. [Google Scholar] [CrossRef]
- Reynolds, P.J.; Tobochnik, J.; Gould, H. Diffusion Quantum Monte Carlo. Comput. Phys. 1990, 4, 662–668. [Google Scholar] [CrossRef]
- Pudliner, B.S.; Pandharipande, V.R.; Carlson, J.; Pieper, S.C.; Wiringa, R.B. Quantum Monte Carlo calculations of nuclei with A<∼7. Phys. Rev. C 1997, 56, 1720. [Google Scholar] [CrossRef]
- Schmidt, K.E.; Fantoni, S. A quantum Monte Carlo method for nucleon systems. Phys. Lett. B 1999, 446, 99. [Google Scholar] [CrossRef]
- Song, H.Q.; Baldo, M.; Giansiracusa, G.; Lombardo, U. Bethe-Brueckner-Goldstone Expansion in Nuclear Matter. Phys. Rev. Lett. 1998, 81, 1584. [Google Scholar] [CrossRef]
- Holt, J.W.; Kaiser, N.; Weise, W. Density-dependent effective nucleon-nucleon interaction from chiral three-nucleon forces. Phys. Rev. C 2010, 81, 024002. [Google Scholar] [CrossRef]
- Logoteta, D. Consistent nuclear matter calculations with local three-nucleon interactions. Phys Rev. C 2019, 100, 045803. [Google Scholar] [CrossRef]
- Haftel, M.I.; Tabakin, F. Nuclear saturation and the smoothness of nucleon-nucleon potentials. Nucl. Phys. A 1970, 158, 1. [Google Scholar] [CrossRef]
- White, L.; Sammarruca, F. Solution of the Bethe-Goldstone equation without partial-wave decomposition. Phys. Rev. C. 2013, 88, 054619. [Google Scholar] [CrossRef]
- Gandolfi, S.; Illarionov, A.Y.; Schmidt, K.E.; Pederiva, F.; Fantoni, S. Quantum Monte Carlo calculation of the equation of state of neutron matter. Phys. Rev. C 2009, 79, 054005. [Google Scholar] [CrossRef]
- Anderson, J.B. Quantum chemistry by random walk. J. Chem. Phys. 1976, 65, 4121. [Google Scholar] [CrossRef]
- Carlson, J.; Gandolfi, S.; Pederiva, F.; Pieper, S.C.; Schiavilla, R.; Schmidt, K.E.; Wiringa, R.B. Quantum Monte Carlo methods for nuclear physics. Rev. Mod. Phys. 2015, 87, 1067. [Google Scholar] [CrossRef]
- Gandolfi, S. The Auxiliary Field Diffusion Monte Carlo Method for Nuclear Physics and Nuclear Astro-physics. arXiv 2007, arXiv:0712.1364. [Google Scholar]
- Lonardoni, D.; Pederiva, F.; Gandolfi, S. Accurate determination of the interaction between Λ hyperons and nucleons from auxiliary field diffusion Monte Carlo calculations. Phys. Rev. C 2014, 89, 014314. [Google Scholar] [CrossRef]
- Gandolfi, S.; Lovato, A.; Carlson, J.; Schmidt, K.E. From the lightest nuclei to the equation of state of asymmetric nuclear matter with realistic nuclear interactions. Phys. Rev. C 2014, 90, 061306. [Google Scholar] [CrossRef]
- Lynn, J.E.; Tews, I.; Carlson, J.; Gandolfi, S.; Gezerlis, A.; Schmidt, K.E.; Schwenk, A. Quantum Monte Carlo calculations of light nuclei with local chiral two- and three-nucleon interactions. Phys. Rev. C 2017, 96, 054007. [Google Scholar] [CrossRef]
- Lonardoni, D.; Tews, I.; Gandolfi, S.; Carlson, J. Nuclear and neutron-star matter from local chiral interactions. Phys. Rev. Res. 2020, 2, 022033. [Google Scholar] [CrossRef]
- Tews, I.; Gandolfi, S.; Gezerlis, A.; Schwenk, A. Quantum Monte Carlo calculations of neutron matter with chiral three-body forces. Phys. Rev. C 2016, 93, 024305. [Google Scholar] [CrossRef]
- Piarulli, M.; Bombaci, I.; Logoteta, D.; Lovato, A.; Wiringa, B. Benchmark calculations of pure neutron matter with realistic nucleon-nucleon interactions. Phys. Rev. C 2020, 101, 045801. [Google Scholar] [CrossRef]
- Nagels, M.M.; Rijken, T.A.; de Swart, J.J. Baryon-baryon scattering in a one-boson-exchange-potential approach. II. Hyperon-nucleon scattering. Phys. Rev. D 1977, 15, 2547. [Google Scholar] [CrossRef]
- Nagels, M.M.; Rijken, T.A.; de Swart, J.J. Baryon-baryon scattering in a one-boson-exchange-potential approach. III. A nucleon-nucleon and hyperon-nucleon analysis including contributions of a nonet of scalar mesons. Phys. Rev. D 1977, 20, 1633. [Google Scholar] [CrossRef]
- Maessen, P.; Rijken, T.A.; de Swart, J.J. Soft-core baryon-baryon one-boson-exchange models. II. Hyperon-nucleon potential. Phys. Rev. C 1989, 40, 2226. [Google Scholar] [CrossRef] [PubMed]
- Holzenkamp, B.; Holinde, K.; Speth, J. A meson exchange model for the hyperon-nucleon interaction. Nucl. Phys. A 1989, 500, 458. [Google Scholar] [CrossRef]
- Machleidt, R.; Holinde, K.; Elster, C. The bonn meson-exchange model for the nucleon—Nucleon interaction. Phys. Rep. 1987, 149, 1. [Google Scholar] [CrossRef]
- Haidenbauer, J.; Meissner, U.G. Jülich hyperon-nucleon model revisited. Phys. Rev. C 2005, 2005 72, 044005. [Google Scholar] [CrossRef]
- Stoks, V.G.J.; Rijken, T.A. Soft-core baryon-baryon potentials for the complete baryon octet. Phys. Rev. C 1999, 59, 3009. [Google Scholar] [CrossRef]
- Rijken, T.A.; Nagels, M.M.; Yamamoto, Y. Status of understanding the YN/YY-interactions Meson-exchange viewpoint. Nucl. Phys. C 2010, 835, 160. [Google Scholar] [CrossRef]
- Rijken, T.A.; Nagels, M.M.; Yamamoto, Y. Baryon-Baryon Interactions: Nijmegen Extended-Soft-Core Models. Prog. Theor. Phys. Suppl. 2010, 185, 14. [Google Scholar] [CrossRef]
- Nagels, M.M.; Rijken, T.A.; Yamamoto, Y. Extended-soft-core Baryon-Baryon ESC08 model III. S=-2 Hyperon-hyperon/nucleon Interaction. arXiv 2015, arXiv:1504.02634. [Google Scholar]
- Nagels, M.M.; Rijken, T.A.; Yamamoto, Y. Extended-soft-core baryon-baryon model ESC16. I. Nucleon-nucleon scattering. Phys. Rev. C 2019, 99, 044002. [Google Scholar] [CrossRef]
- Nagels, M.M.; Rijken, T.A.; Yamamoto, Y. Extended-soft-core baryon-baryon model ESC16. II. Hyperon-nucleon interactions. Phys. Rev. C 2019, 99, 044003. [Google Scholar] [CrossRef]
- Schwinger, J. A theory of the fundamental interactions. Annals Phys. 1957, 2, 407. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Levy, M. The Axial Vector Current in Beta Decay. Nuovo Cimento 1960, 16, 705. [Google Scholar] [CrossRef]
- Schwinger, J. Chiral dynamics. Phys. Lett. B 1967, 24, 473. [Google Scholar] [CrossRef]
- Weinberg, S. Nonlinear Realizations of Chiral Symmetry. Phys. Rev. 1968, 166, 1568. [Google Scholar] [CrossRef]
- Weinberg, S. Phenomenological Lagrangians. Phys. A 1979, 96, 327. [Google Scholar] [CrossRef]
- Coleman, S.; Wess, J.; Zumino, B. Structure of Phenomenological Lagrangians. I. Phys. Rev. 1969, 177, 223. [Google Scholar] [CrossRef]
- Callan, C.G.; Coleman, S.; Wess, J.; Zumino, B. Structure of Phenomenological Lagrangians. II. Phys. Rev. 1969, 177, 2247. [Google Scholar] [CrossRef]
- Georgi, H. An Effective Field Theory for Heavy Quarks at Low-energies. Phys. Lett. B 1990, 240, 447. [Google Scholar] [CrossRef]
- Jenkins, E.; Manohar, A.V. Baryon chiral perturbation theory using a heavy fermion Lagrangian. Phys. Lett. B 1991, 255, 558. [Google Scholar] [CrossRef]
- Machleidt, R.; Entem, D.R. Chiral effective field theory and nuclear forces. Phys. Rept. 2011, 503, 1. [Google Scholar] [CrossRef]
- Polinder, H.; Haidenbauer, J.; Meißner, U.G. Hyperon-nucleon interactions—A chiral effective field theory approach. Nucl. Phys. A 2006, 779, 244. [Google Scholar] [CrossRef]
- Haidenbauer, J.; Petschauer, S.; Kaiser, N.; Meissner, U.G.; Nogga, A. Hyperon-nucleon interaction at next-to-leading order in chiral effective field theory. Nucl. Phys. A 2013, 915, 24. [Google Scholar] [CrossRef]
- Haidenbauer, J.; Meissner, U.G.; Nogga, A. Hyperon-nucleon interaction at next-to-leading order in chiral effective field theory. Eur. Phys. J. A 2020, 56, 91. [Google Scholar] [CrossRef]
- Haidenbauer, J.; Meissner, U.G.; Petschauer, S. Strangeness S = −2 baryon–baryon interaction at next-to-leading order in chiral effective field theory. Nucl. Phys. A 2016, 954, 273. [Google Scholar] [CrossRef]
- Ishii, N.; Aoki, S.; Hatsuda, T. Nuclear force from lattice QCD. Phys. Rev. Lett. 2007, 99, 022001. [Google Scholar] [CrossRef] [PubMed]
- Inoue, T.; Aoki, S.; Doi, T.; Hatsuda, T.; Ikeda, Y.; Ishii, N.; Murano, K.; Nemura, H.; Sasaki, K.; HAL QCD Collaboration. Two-Baryon potentials and H-dibaryon from 3-flavor lattice QCD simulations. Nucl. Phys. A 2012, 881, 23. [Google Scholar] [CrossRef][Green Version]
- Inoue, T.; Ishii, N.; Aoki, S.; Doi, T.; Hatsuda, T.; Ikeda, Y.; Sasaki, K. Baryon-Baryon interactions in the flavor SU(3) limit from full QCD simulations on the lattice. Prog. Theor. Phys. 2010, 124, 591. [Google Scholar] [CrossRef]
- Inoue, T.; Ishii, N.; Aoki, S.; Doi, T.; Hatsuda, T.; Ikeda, Y.; Hal Qcd Collaboration. Bound H-dibaryon in flavor SU(3) limit of lattice QCD. Phys. Rev. Lett. 2011, 106, 162002. [Google Scholar] [CrossRef]
- Oka, M.; Shimizu, K.; Yazaki, K. Quark cluster model of baryon baryon interaction. Prog. Theor. Phys. Suppl. 2000, 137, 1. [Google Scholar] [CrossRef]
- Nemura, H.; Ishii, N.; Aoki, S.; Hatsuda, D. Hyperon–nucleon force from lattice QCD. Phys. Lett. B 2009, 673, 136–141. [Google Scholar] [CrossRef]
- Nemura, H.; Hal Qcd Collaboration. Baryon-Baryon Interaction in Lattice QCD. Nucl. Phys. A 2010, 835, 176–183. [Google Scholar] [CrossRef]
- Hatsuda, T.; Morita, K.; Ohnishi, A.; Sasaki, K. pΞ-Correlation in Relativistic Heavy Ion Collisions with Nucleon-Hyperon Interaction from Lattice QCD. Nucl. Phys. A 2017, 967, 856. [Google Scholar] [CrossRef]
- Takumi, I.; Aoki, S.; Doi, T.; Etminan, F.; Gongyo, S.; Hatsuda, T.; HAL QCD Collaboration. NΩ dibaryon from lattice QCD near the physical point. Phys. Lett. B 2019, 792, 284. [Google Scholar] [CrossRef]
- Sesaki, K.; Aoki, S.; Doi, T.; Gongyo, S.; Hatsuda, T.; Ikeda, Y.; HAL QCD Collaboration. ΛΛ and NΞ interactions from lattice QCD near the physical point. Nucl. Phys. A 2020, 998, 121737. [Google Scholar] [CrossRef]
- Aoki, S.; Doi, T. Lattice QCD and Baryon-Baryon Interactions: HAL QCD Method. Frontiers 2020, 8, 307. [Google Scholar] [CrossRef]
- Illa, M.; Beane, S.R.; Chang, E.; Davoudi, Z.; Detmold, W.; Murphy, D.J.; Nplqcd Collaboration. Low-energy Scattering and Effective Interactions of Two Baryons at mπ∼450 MeV from Lattice Quantum Chromodynamics. Phys. Rev. D 2021, 103, 054508. [Google Scholar] [CrossRef]
- Wagman, M.L.; Winter, F.; Chang, E.; Davoudi, Z.; Detmold, W.; Orginos, K.; Nplqcd Collaboration. Baryon-Baryon Interactions and Spin-Flavor Symmetry from Lattice Quantum Chromo-dynamics. Phys. Rev. D 2017, 96, 114510. [Google Scholar] [CrossRef]
- Baldo, M.; Burgio, G.F.; Schulze, H.J. Onset of hyperon formation in neutron star matter from Brueckner theory. Phys. Rev. C 1998, 58, 3688. [Google Scholar] [CrossRef]
- Lagaris, I.E.; Pandharipande, V.R. Phenomenological two-nucleon interaction operator. Nucl. Phys. A 1981, 359, 349. [Google Scholar] [CrossRef]
- Carlson, J.; Pandharipande, V.R.; Wiringa, B. Three-nucleon interaction in 3-, 4- and ∞-body systems. Nucl. Phys. A 1983, 401, 59–85. [Google Scholar] [CrossRef]
- Vidaña, I.; Polls, A.; Ramos, A.; Hjorth-Jensen, M.; Stoks, V.G.J. Strange nuclear matter within Brueckner-Hartree-Fock theory. Phys. Rev. C 2000, 61, 025802. [Google Scholar] [CrossRef]
- Baldo, M.; Burgio, G.F.; Schulze, H.J. Hyperon stars in the Brueckner-Bethe-Goldstone theory. Phys. Rev. C 2000, 61, 055801. [Google Scholar] [CrossRef]
- Vidaña, I.; Polls, A.; Ramos, A.; Engvik, L.; Hjorth-Jensen, M. Hyperon-hyperon interactions and properties of neutron star matter. Phys. Rev. C 2000, 62, 035801. [Google Scholar] [CrossRef]
- Schulze, H.J.; Riken, T. Maximum mass of hyperon stars with the Nijmegen ESC08 model. Phys. Rev. C 2011, 84, 035801. [Google Scholar] [CrossRef]
- Schulze, H.J.; Riken, T. Hyperon-hyperon interactions with the Nijmegen ESC08 model. Eur. Phys. J. A 2016, 52, 21. [Google Scholar] [CrossRef]
- Djapo, H.; Schaefer, B.J.; Wambach, J. Appearance of hyperons in neutron stars. Phys. Rev. C 2010, 81, 035803. [Google Scholar]
- Schulze, H.J.; Polls, A.; Ramos, A.; Vidaña, I. Maximum mass of neutron stars. Phys. Rev. C 2006, 73, 058801. [Google Scholar] [CrossRef]
- Takatsuka, T.; Nishizaki, S.; Yamamoto, Y. Necessity of extra repulsion in hypernuclear systems: Suggestion from neutron stars. Eur. Phys. J. A 2002, 13, 213. [Google Scholar] [CrossRef]
- Takatsuka, T.; Nishizaki, S.; Tamagaki, R. Three-body force as an ’extra repulsion’ suggested from hyperon-mixed neutron stars. Prog. Theor. Phys. Suppl. 2008, 174, 80. [Google Scholar] [CrossRef]
- Drischler, C.; Hebeler, K.; Schwenk, A. Chiral Interactions up to Next-to-Next-to-Next-to-Leading Order and Nuclear Saturation. Phys. Rev. Lett. 2019, 122, 042501. [Google Scholar] [CrossRef]
- Kievsky, A.; Viviani, M.; Logoteta, D.; Bombaci, I.; Girlanda, L. Correlations imposed by the unitary limit between few-nucleon systems, nuclear matter and neutron stars. Phys. Rev. Lett. 2018, 121, 072701. [Google Scholar] [CrossRef]
- Petschauer, S.; Kaiser, N.; Haidenbauer, J.; Meissner, U.G.; Weise, W. Leading three-baryon forces from SU(3) chiral effective field theory. Phys. Rev. C 2016, 93, 014001. [Google Scholar] [CrossRef]
- Van Kolck, U. Effective field theory of nuclear forces. Prog. Part. Nucl. Phys. 1999, 43, 377. [Google Scholar] [CrossRef]
- Epelbaum, E.; Nogga, A.; Glockle, W.; Kamada, K.; Meissner, U.G.; Witala, H. Three-nucleon forces from chiral effective field theory. Phys. Rev. C 2002, 66, 064001. [Google Scholar] [CrossRef]
- Bernard, V.; Epelbaum, E.; Krebs, H.; Meissner, U.G. Subleading contributions to the chiral three-nucleon force: Long-range terms. Phys. Rev. C 2008, 77, 064004. [Google Scholar] [CrossRef]
- Bernard, V.; Epelbaum, E.; Krebs, H.; Meissner, U.G. Subleading contributions to the chiral three-nucleon force II: Short-range terms and relativistic corrections. Phys. Rev. C 2011, 84, 054001. [Google Scholar] [CrossRef]
- Vidaña, I.; Logoteta, D.; Providência, C.; Polls, A.; Bombaci, I. Estimation of the effect of hyperonic three-body forces on the maximum mass of neutron stars. Europhys. Lett. 2011, 94, 11002. [Google Scholar] [CrossRef]
- Wiringa, R.B.; Stoks, V.G.J.; Schiavilla, R. Accurate nucleon-nucleon potential with charge-independence breaking. Phys. Rev. C 1995, 51, 38. [Google Scholar] [CrossRef]
- Lonardoni, D.; Lovato, A.; Gandolfi, S.; Pederiva, F. Hyperon Puzzle: Hints from Quantum Monte Carlo Calculations. Phys. Rev. Lett. 2015, 114, 092301. [Google Scholar] [CrossRef] [PubMed]
- Logoteta, D.; Vidaña, I.; Bombaci, I. Towards the solution of the “hyperon puzzle”. Eur. Phys. J. A 2019, 55, 207. [Google Scholar] [CrossRef]
- Piarulli, M.; Girlanda, L.; Schiavilla, R.; Kievsky, A.; Lovato, A.; Marcucci, L.E.; Pieper, S.C.; Viviani, M.; Wiringa, R.B. Local chiral potentials and the structure of light nuclei. Phys. Rev. C 2016, 94, 054007. [Google Scholar] [CrossRef]
- Navratil, P. Local three-nucleon interaction from chiral effective field theory. Few-Body Syst. 2007, 41, 117. [Google Scholar] [CrossRef]
- Logoteta, D.; Bombaci, I.; Kievsky, A. Nuclear matter properties from local chiral interactions with Δ isobar intermediate states. Phys. Rev. C 2016, 94, 064001. [Google Scholar] [CrossRef]
- Bombaci, I.; Logoteta, D. Equation of state of dense nuclear matter and neutron star structure from nuclear chiral interactions. Astron. Astrophys. 2018, 609, A128. [Google Scholar] [CrossRef]
- Endrizzi, A.; Logoteta, D.; Giacomazzo, B.; Bombaci, I.; Kastaun, W.; Ciolfi, R. Effects of chiral effective field theory equation of state on binary neutron star mergers. Phys. Rev. D 2018, 98, 043015. [Google Scholar] [CrossRef]
- Logoteta, D.; Perego, A.; Bombaci, I. Microscopic nuclear matter equation of state for numerical relativity simulations. Astron. Astrophys. 2021, 646, A55. [Google Scholar] [CrossRef]
- Bernuzzi, S.; Breschi, M.; Daszuta, B.; Endrizzi, A.; Logoteta, D.; Nedora, V.; Ortiz, N. Accretion-induced prompt black hole formation in asymmetric neutron star mergers, dynamical ejecta and kilonova signals. Mon. Not. R. Astron. Soc. 2020, 497, 1488–1507. [Google Scholar] [CrossRef]
- Vidaña, I.; Polls, A.; Ramos, A.; Hjorth-Jensen, M. Hyperon properties in finite nuclei using realistic YN interactions. Nucl. Phys. A 1998, 644, 201. [Google Scholar] [CrossRef]
- Haidenbauer, J.; Vidaña, I. Structure of single-Λ hypernuclei with chiral hyperon-nucleon potentials. Eur. Phys. J. A 2020, 56, 55. [Google Scholar] [CrossRef]
- Haidenbauer, J.; Kaiser, N.; Meissner, U.G.; Weise, W. Lambda-nuclear interactions and hyperon puzzle in neutron stars. Eur. Phys. J. A 2017, 53, 121. [Google Scholar] [CrossRef]
- Gerstung, D.; Kaiser, N.; Weise, W. Hyperon–nucleon three-body forces and strangeness in neutron stars. Eur. Phys. J. A 2020, 56, 175. [Google Scholar] [CrossRef]
- Petschauer, S.; Haidenbauer, J.; Meissner, U.G.; Kaiser, N.; Weise, W. Hyperons in nuclear matter from SU(3) chiral effective field theory. Eur. Phys. J. A 2016, 52, 15. [Google Scholar] [CrossRef]
- Kohno, M. Single-particle potential of the Λ-hyperon in nuclear matter with chiral effective field theory NLO interactions including effects of YNN three-baryon interactions. Phys. Rev. C 2018, 97, 035206. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Furumoto, T.; Yasutake, N.; Rijken, T.A. Hyperon mixing and universal many-body repulsion in neutron stars. Phys Rev. C 2014, 90, 045805. [Google Scholar] [CrossRef]
- Togashi, H.; Hiyama, E.; Yamamoto, Y.; Takano, M. Equation of state for neutron stars with hyperons by the variational method. Phys. Rev. C 2016, 93, 035808. [Google Scholar] [CrossRef]
- Alonso, D.; Sammarruca, F. A Microscopic calculation of asymmetric nuclear matter properties. Phys. Rev. C 2003, 67, 054301. [Google Scholar] [CrossRef]
- Van Dalen, E.N.E.; Fuchs, C.; Faessler, A. Dirac-Brueckner-Hartree-Fock calculations for isospin asymmetric nuclear matter based on improved approximation schemes. Eur. Phys. J. A 2007, 31, 29–42. [Google Scholar] [CrossRef]
- Krastev, P.G.; Sammarruca, F. Neutron star properties and the equation of state of neutron-rich matter. Phys. Rev. C 2006, 74, 025808. [Google Scholar] [CrossRef]
- Sammarruca, F. Effect of Λ hyperons on the nuclear equation of state in a Dirac-Brueckner-Hartree-Fock model. Phys. Rev. C 2009, 79, 034301. [Google Scholar] [CrossRef]
- Katayama, T.; Saito, K. Neutron stars with Hyperons in Dirac-Brueckner-Hartree-Fock approach. arXiv 2014, arXiv:1410.7166v1. [Google Scholar]
- Endrizzi, A.; Perego, A.; Fabbri, F.M.; Branca, L.; Radice, D.; Bernuzzi, S.; Giacomazzo, B.; Pederiva, F.; Lovato, A. Thermodynamics conditions of matter in the neutrino decoupling region during neutron star mergers. Eur. Phys. J. A 2020, 56, 15. [Google Scholar] [CrossRef]
- Strobel, K.; Schaab, C.; Weigel, M.K. Properties of non-rotating and rapidly rotating protoneutron stars. Astron. Astrophys. 1999, 350, 497. [Google Scholar]
- Fischer, T.; Whitehouse, S.C.; Mezzacappa, A.; Thielemann, F.K.; Liebendörfer, M. The neutrino signal from protoneutron star accretionand black hole formation. Astron. Astrophys. 2009, 499, 1. [Google Scholar] [CrossRef]
- Sekiguchi, Y.; Kiuchi, K.; Kyutoku, K.; Shibata, M. Effects of Hyperons in Binary Neutron Star Mergers. Phys. Rev. Lett. 2011, 107, 211101. [Google Scholar] [CrossRef] [PubMed]
- Radice, D.; Bernuzzi, S.; Del Pozzo, W.; Roberts, L.F.; Ott, C.D. Probing Extreme-Density Matter with Gravitational Wave Observations of Binary Neutron Star Merger Remnants. Astrophys. J. Lett. 2017, 842, L10. [Google Scholar] [CrossRef]
- Ishizuka, C.; Ohnishi, A.; Sumiyoshi, K.; Yamada, S. Finite Temperature Effects on Supernova Explosion Energy and Hyperon Composition. Prog. Theor. Phys. Suppl. 2004, 156, 152. [Google Scholar] [CrossRef]
- Sumiyoshi, K.; Ishizuka, C.; Ohnishi, A.; Yamada, S.; Suzuki, H. Emergence of hyperons in failed supernovae:trigger of the black-hole formation. Astrophys. J. Lett. 2009, 690, L43. [Google Scholar] [CrossRef]
- Peres, B.; Oertel, M.; Novak, J. Influence of pions and hyperons on stellar black hole formation. Phys. Rev. D 2013, 87, 043006. [Google Scholar] [CrossRef]
- Banik, S. Probing the metastability of protoneutron star with hyperon in core-collapse supernova. Phys. Rev. C 2014, 89, 035807. [Google Scholar] [CrossRef]
- Keil, W.; Janka, H.T. Hadronic phase transitions at supranuclear densities and the delayed collapse of newly formed neutron stars. Astron. Astrophys. 1996, 296, 145. [Google Scholar]
- Vidaña, I.; Bombaci, I.; Polls, A.; Ramos, A. Microscopic study of neutrino trapping in hyperon stars. Astron. Astrophys. 2003, 399, 687–693. [Google Scholar] [CrossRef]
- Bombaci, I. The maximum mass of a neutron star. Astron. Astrophys. 1996, 305, 871–877. [Google Scholar] [CrossRef]
- Baldo, M.; Lombardo, U.; Saperstein, É.E. Microscopic calculation of a pairing gap in semi-infinite nuclear matter. Phys. Atom. Nuclei 2000, 63, 43–54. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, L.W. Pairing effects on neutron matter equation of state and symmetry energy at subsaturation densities. Phys. Rev. C 2019, 100, 044301. [Google Scholar] [CrossRef]
- Rios, A.; Polls, A.; Dickhoff, W.H. Pairing and Short-Range Correlations in Nuclear Systems. J. Low Temp. Phys. 2017, 189, 234–249. [Google Scholar] [CrossRef]
- Gandolfi, S.; Illarionov, Y.A.; Fantoni, S.; Pederiva, F.; Schmidt, K.E. Equation of State of Superfluid Neutron Matter and the Calculation of the Pairing Gap. Phys. Rev. Lett. 2008, 101, 132501. [Google Scholar] [CrossRef]
- Drischler, C.; Kruger, T.; Hebeler, K.; Schwenk, A. Pairing in neutron matter: New uncertainty estimates and three-body forces. Phys. Rev. C 2017, 95, 024302. [Google Scholar] [CrossRef]
- Takatsuka, T.; Tamagaki, R. Superfluidity of Λ-hyperons admixed in neutron star cores. Prog. Theor. Phys. 1999, 102, 1043–1048. [Google Scholar] [CrossRef]
- Takatsuka, T.; Nishizaki, S.; Yamamoto, Y.; Tamagaki, R. Superfluidity of hyperon-mixed neutron stars. Prog. Theor. Phys. Suppl. 2002, 146, 279–288. [Google Scholar] [CrossRef][Green Version]
- Vidaña, I.; Tolos, L. Superfluidity of Σ- hyperons in β-stable neutron star matter. Phys. Rev. C 2004, 70, 028802. [Google Scholar] [CrossRef]
- Yakovlev, D.G.; Pethick, C.J. Neutron Star Cooling. Annu. Rev. Astron. Astrophys. 2004, 42, 169–210. [Google Scholar] [CrossRef]
- Potekhin, A.Y.; Pons, J.A.; Page, D. Neutron stars—Cooling and transport. Space Sci. Rev. 2015, 191, 239. [Google Scholar] [CrossRef]
- Friedman, J.L.; Ipser, J.R.; Parker, L. Rapidly rotating neutron star models. Astrophys. J. 1986, 304, 115. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Solutions of two problems in the theory of gravitational radiation. Phys. Rev. Lett. 1970, 24, 611–615. [Google Scholar] [CrossRef]
- Langer, W.D.; Cameron, A.G.W. Effects of hyperons on the vibrations of neutron stars. Astrophys. Space Sci. 1969, 5, 213–253. [Google Scholar] [CrossRef]
- Jones, P.B. Comment on ‘gravitational radiation instability in hot young neutron stars’. Phys. Rev. Lett. 2001, 86, 1384. [Google Scholar] [CrossRef]
- Haensel, P.; Levenfish, K.P.; Yakovlev, D.G. Bulk viscosity in superfluid neutron star cores. Astron. Astrophys. 2002, 381, 1080–1089. [Google Scholar] [CrossRef]
- Chatterjee, D.; Bandyopadhyay, D. Hyperon bulk viscosity in the presence of antikaon condensate. Astrophys. J. 2006, 680, 686–694. [Google Scholar] [CrossRef]
- Gusakov, M.E.; Kantor, E.M. Bulk viscosity of superfluid hyperon stars. Phys. Rev. D 2008, 78, 083006. [Google Scholar] [CrossRef]
- Sinha, M.; Bandyopadhyay, D. Hyperon bulk viscosity in strong magnetic fields. Phys. Rev. D 2009, 79, 123001. [Google Scholar] [CrossRef]
- Shternin, P.; Vidaña, I. Transport Coefficients of Hyperonic Neutron Star Cores. Universe 2021, 7, 203. [Google Scholar] [CrossRef]
- Logoteta, D.; Bombaci, I.; Providência, C.; Vidaña, I. Chiral model approach to quark matter nucleation in neutron stars. Phys. Rev. D 2012, 85, 023003. [Google Scholar] [CrossRef]
- Logoteta, D.; Providência, C.; Vidaña, I. Formation of hybrid stars from metastable hadronic stars. Phys. Rev. C 2013, 88, 055802. [Google Scholar] [CrossRef]

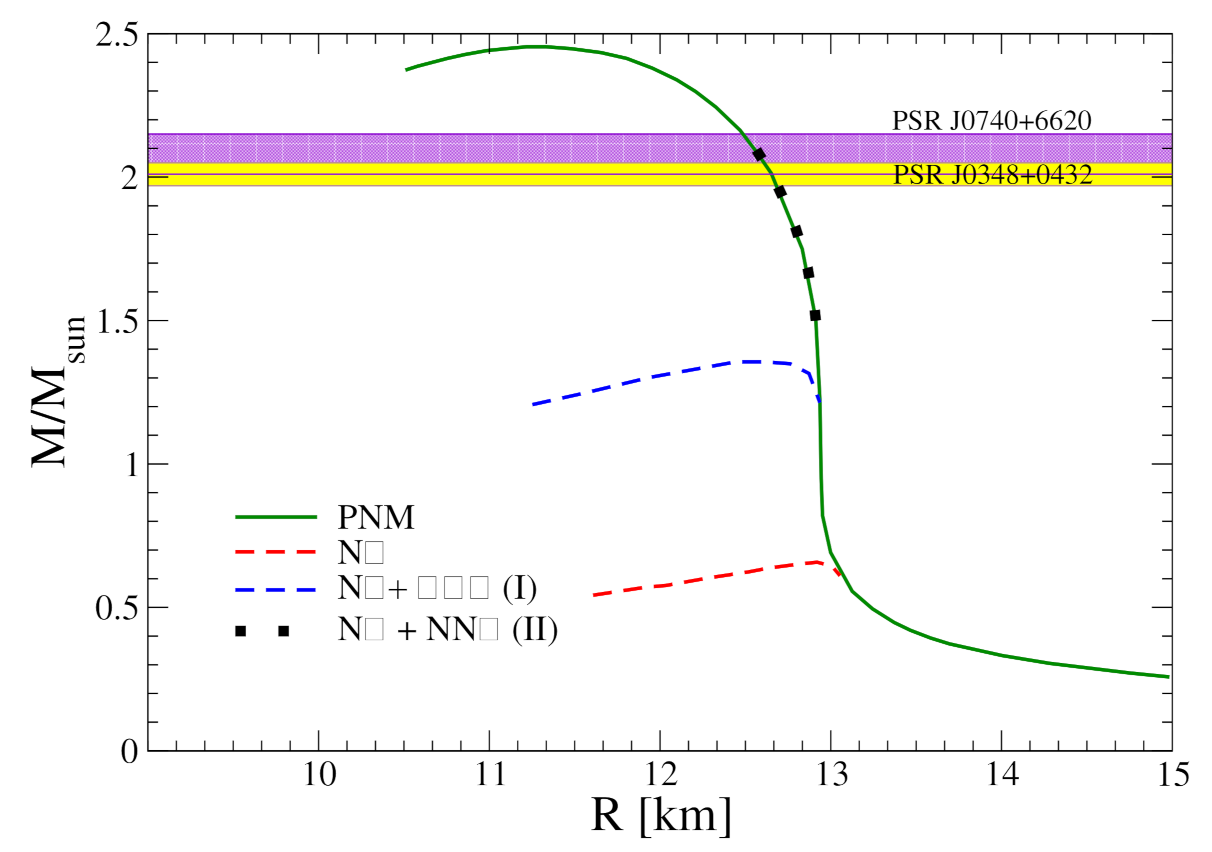
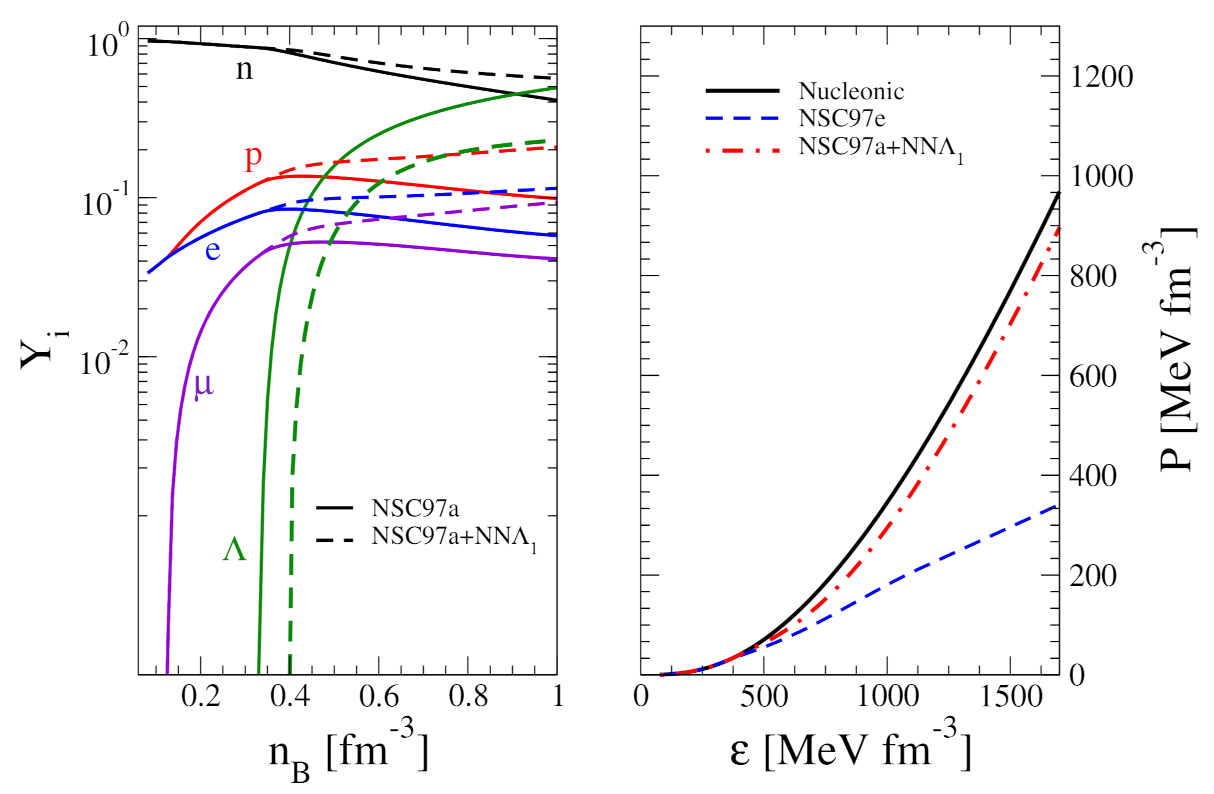
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Logoteta, D. Hyperons in Neutron Stars. Universe 2021, 7, 408. https://doi.org/10.3390/universe7110408
Logoteta D. Hyperons in Neutron Stars. Universe. 2021; 7(11):408. https://doi.org/10.3390/universe7110408
Chicago/Turabian StyleLogoteta, Domenico. 2021. "Hyperons in Neutron Stars" Universe 7, no. 11: 408. https://doi.org/10.3390/universe7110408
APA StyleLogoteta, D. (2021). Hyperons in Neutron Stars. Universe, 7(11), 408. https://doi.org/10.3390/universe7110408