Abstract
We explore the way different loop quantization prescriptions affect the formation of trapped surfaces in the gravitational collapse of a homogeneous dust cloud, with particular emphasis on the so-called scheme in which loop quantum cosmology was initially formulated. Its undesirable features in cosmological models led to the so-called improved dynamics or the scheme. While the jury is still out on the right scheme for black hole spacetimes, we show that as far as black hole formation is concerned, the scheme has another, so far unknown, serious problem. We found that in the scheme, no trapped surfaces would form for a nonsingular collapse of a homogeneous dust cloud in the marginally bound case unless the minimum nonzero area of the loops over which holonomies are computed or the Barbero–Immirzi parameter decreases almost four times from its standard value. It turns out that the trapped surfaces in the scheme for the marginally bound case are also forbidden for an arbitrary matter content as long as the collapsing interior is isometric to a spatially flat Friedmann–Lemaître–Robertson–Walker (FLRW) spacetime. We found that in contrast to the situation in the scheme, black holes can form in the scheme, as well as other lattice refinements with a mass gap determined by quantum geometry.
1. Introduction
One of the most important predictions of loop quantum cosmology (LQC) is the resolution of the curvature singularity in the Planck regime by replacing it with a quantum bounce [1,2,3,4,5]. The generic resolution of singularities has been obtained for isotropic, as well as anisotropic spacetimes [6,7,8,9,10]. The techniques developed in LQC can be readily applied to study the final state of the gravitational collapse as well, such as the gravitational collapse of a homogeneous dust cloud whose interior spacetime is described by the Lemaître–Tolman–Bondi (LTB) metric. An important question in the loop quantization program, as in any other quantization strategy, is to find a preferred quantization that is compatible with physical phenomena and rule out other possible prescriptions. This exercise has been performed in the past in isotropic cosmological spacetimes, which uniquely selects the so-called scheme or the improved dynamics [11,12] put forward in [3]. This question has also been asked regarding the static black hole spacetimes [13,14]. However, so far, there is no comparative exploration on this issue for gravitational collapse using different quantization prescriptions1. Thanks to the isometry with the FLRW spacetime for the homogeneous collapse, the physical implications of the different quantization prescriptions mathematically permitted in LQC can be examined in the context of gravitational collapse. Though the results known in cosmological spacetimes directly apply to such a simple gravitational collapse, we show that this exercise reveals a so far unknown serious problem, which is absent in the cosmological setting with one of the main loop quantization prescriptions.
Let us recall briefly two of the most well-known loop quantization prescriptions: the scheme [16] and the scheme [3]. While the scheme can follow naturally from loop quantum gravity (LQG), so far, it has been difficult to obtain the scheme. Moreover, in the cosmological setting, the scheme has several undesirable properties [11]. Firstly, in the scheme, the maximum energy density at which the bounce occurs is found to be dependent on the phase space variables whose initial conditions can be chosen such that the bounce can happen at classical densities. Secondly, in the case of noncompact manifolds, the dynamics depends on the choice of the fiducial cell used to define the symplectic structure. Finally, in the presence of matter that violates the strong energy condition, the universe recollapses at small spacetime curvatures. All of these undesirable features arise from the way the scheme is defined where measures the edge length of the holonomies and is put equal to the square root of the minimum area eigenvalue in loop quantum gravity. These problems are absent in the scheme, where one considers the physical area of the loop to determine the value of the edge length . In the context of the gravitational collapse of a dust cloud, the interior spatial manifold is compact, and the strong energy condition is not violated. Hence, two of the problems of using the scheme are eliminated. Though the problem of bounce density depending on phase space variables remains, one can engineer a small set of initial data such that the bounce density is in the Planck regime.
The strategy used in defining the and schemes in LQC has led to the introduction of various quantization prescriptions for loop quantization of static (vacuum) black hole spacetimes, which can be viewed as generalizations of the above schemes (see, for example, [13,14,17,18,19,20,21,22,23,24,25]). Investigations into singularity resolution have been carried out also for dynamical gravitational collapse spacetimes when a matter field is taken into account2 [15,28,29,30,31,32,33]. These studies mainly focused on the scheme and showed that the central singularity is generically resolved and a black hole can form when its mass is above some threshold value. In this manuscript, we studied the scheme in the simplest setting where a homogeneous dust cloud is collapsing in the marginally bound case. In order to highlight the main features of the scheme in the homogeneous gravitational collapse, we also considered other loop quantizations due to different kinds of lattice refinements, including the scheme and others parameterized in [11]. We found that although the central singularity is generically resolved and replaced with a bounce in all loop quantization schemes considered in this paper, regardless of the initial conditions and even the matter content, the scheme cannot allow for the formation of the trapped surface as long as the minimal eigenvalue of the area operator that directly determines the specific value of is given by LQG. In contrast, for other loop quantizations, including the scheme, the trapped surface can always form during the collapse of the dust cloud when the dust mass is larger than a threshold mass whose order of magnitude is dependent on the lattice refinement. We show that the trapped surface cannot form in the scheme even for arbitrary matter, which is compatible with the isometry with an FLRW interior. For a trapped surface to form in the scheme, the minimum nonzero eigenvalue of the area operator or the Barbero–Immirzi parameter must decrease almost four times. Further, such a value of a minimum nonzero area eigenvalue or the Barbero–Immirzi parameter would violate the covariant entropy bound.
In the following, we first briefly review of the homogeneous dust shell model in Section 2, including the classical Hamiltonian constraint and the matching conditions between the interior spacetime and the exterior generalized Vaidya spacetime. In Section 3, we first discuss the loop quantization of the interior collapsing spacetime in the scheme and its physical consequences. Then, we proceed with other loop quantizations including the scheme and other possible lattice refinements. In this section, we concentrate on the role of different loop quantizations on the formation of the trapped surface during the nonsingular evolution of the dust cloud. Finally, we conclude our main results in Section 4. Throughout this paper, we use the Planck units in which , while keeping Newton’s constant G explicit in our formulae.
2. Preliminaries: The Classical Dust Shell Model
In this section, we briefly review the classical dust shell model of the gravitational collapse in the marginally bound case using connection and triad variables. Our discussion parallels the one in [15], which we refer the reader to for further details.
The dust shell model applies to a homogeneous evolution of the dust cloud, which ignores the interactions between neighboring shells and thus leads to a collapse of all of the dust shells at a uniform speed. As a result, the dynamics of the whole dust cloud can be inferred from the dynamics of the outermost dust shell. The interior collapsing spacetime is described by the classical LTB metric,
where x is the radial coordinate, R is the areal radius, and is the angular part of the metric. The prime denotes the differentiation with respect to x. The function f only depends on the radial coordinate x and stands for the total energy per unit mass at . Depending on the sign of f, there exist three distinct cases: the marginally bound case with , the bound case with , and the unbound case with . In all three cases, the classical dynamical evolution is governed by:
where an overdot denotes differentiation with respect to the proper time t, denotes the energy density of the dust cloud, and , which only depends on the radial coordinate x, is the active gravitating mass enclosed within the dust sphere with radius .
In the following, we only focus on the homogeneous collapse of the dust cloud in the marginally bound case with . The homogeneous evolution of the dust cloud implies that the energy density of the dust cloud only depends on the proper time, and consequently, the areal radius takes the form . As a result, the interior LTB metric (1) reduces to the one for a spatially flat FLRW universe. Correspondingly, the dynamical equations in (2) are equivalent to the equation:
As already discussed in detail in [15], in terms of the areal radius R and its conjugate momentum, the gravitational and the matter sectors of the Hamiltonian constraint of the outermost dust shell are given respectively by:
where the angular part in the Hamiltonian constraint has already been integrated and the integration along the radial direction has been performed from the center of the dust cloud to its outermost shell (namely, the boundary surface), yielding and . In order to loop quantize the dust shell model, it is a prerequisite to express the above Hamiltonian constraint of the dust shell model in terms of the Ashtekar variables, which was first analyzed in [34] for an inhomogeneous dust cloud and later adapted to the shell model for a homogeneous dust cloud in [15]. In the dust shell model, one can identify the radial component of the densitized triad with the square of the areal radius, namely with . Then, in terms of and its conjugate momentum , which is half of the radial component of the extrinsic curvature, the Hamiltonian of the outermost shell of the dust cloud can be written as [15]:
with , and represents the mass of the dust cloud. Finally, one can recover the classical Hamiltonian constraint in the cosmological setting for the dust interior by identifying:
in which Equation (5) reduces to the familiar form in terms of the connection c and the triad p, namely:
with , and the volume of the dust interior is given by .
For a complete description of the gravitational collapse of the dust cloud, it is necessary to match the interior collapsing spacetime with an exterior spacetime. Without loss of generality, we chose the generalized Vaidya spacetime as the exterior spacetime since, in general, the dust cloud acquires an effective nonvanishing pressure after quantum gravity effects are taken into account. The generalized Vaidya spacetime in the advanced Eddington–Finkelstein coordinates takes the form [35]:
where stands for the Vaidya mass. Note that the interior spacetime (1) is glued to the exterior (8) by requiring the continuation of the first and second fundamental forms at the boundary surface . The matching conditions can be worked out explicitly by computing the first and second fundamental forms at from the interior and the exterior metrics, yielding [36]:
As a result, the boundary surface would become a trapped surface when or, equivalently, . Using the second dynamical equation in (2), the criterion for the formation of the trapped surface in the marginally bound case turns out to be . Moreover, from the detailed discussions on the expansion parameters given in [15], we can identify a black hole for in the contracting phase and a white hole for in the expanding phase. Classically, these two branches are disjoint, and one inevitably encounters a central singularity either in the past or in the future. However, after loop quantization, the expanding and contracting branches can be connected via a bounce due to quantum gravity effects, such as in the scheme [15].
3. Loop Quantizations of the Dust Shell Model
In this section, we discuss the physical implications of the loop quantizations of the dust shell model in the marginally bound case with emphasis on the question of the formation of the trapped surfaces in the scheme. Our analysis was based on the effective dynamics, which was proven via numerical simulations to faithfully capture the underlying quantum dynamics for the states sharply peaked around the classical solutions at late times [3,37,38,39].
3.1. The Scheme
The loop quantization of the classical Hamiltonian constraint was carried out in terms of the Ashtekar–Barbero connection and the densitized triad, which in the homogeneous spacetime reduce to the connection c and the triad p. The nonperturbative quantum gravity modification arises from the regularization of the field strength of the connection, which leads to a quantum difference equation, whose dynamics can be faithfully captured by an effective Hamiltonian constraint for the sharply peaked states. For the classical Hamiltonian constraint of the dust shell model given in (7), the effective Hamiltonian constraint in the scheme takes the form [2]:
Using Hamilton’s equation for the triad p and the vanishing of the effective Hamiltonian constraint, one obtains:
The quadratic term with a negative sign tells us that vanishes at a maximum energy density:
Unlike the classical theory, the central singularity is avoided in the collapse of the dust shell. Instead, the shell bounces at . Note that the maximum energy density in the scheme is not a constant, but depends explicitly on the mass of the dust cloud. When the dust mass is taken to be macroscopic, the bounce takes place at a very small spacetime curvature. This problem is well known in the cosmological setting for the scheme [2,11]. Our goal here was to investigate the formation of trapped surfaces. For this, it is sufficient to note that the square of the velocity of the outermost shell is given by:
where x is defined by:
On the other hand, from the effective Hamiltonian constraint (11), one can find:
It is important to note that the above upper and lower limits for x are constant, which do not depend on the triad p. As a result, combining (14) and (16), we found that at , the square of the velocity of the outermost dust shell attains its maximum value, which turns out to be:
where we used and , which is fixed by the black hole thermodynamics discussed in [40]. For these values of and , a trapped surface cannot form in the scheme. Can one choose other values of and such that ? In order to have a black hole form during the collapse, the factor in the denominator of (17) has to satisfy , which implies we need to decrease and/or . The freedom to choose a different depends on how is determined in the scheme. As discussed in [2], is related to the minimal nonzero eigenvalue of the area operator denoted by via:
where is the Planck length. Since is proportional to , decreasing the Barbero–Immirzi parameter does not affect the magnitude of . If the value of needs to be decreased, then one would have to change the way the minimum area of the loop over which holonomies are computed is equated with the minimum nonzero area eigenvalues in LQG. If one keeps the Barbero–Immirzi parameter unchanged, the value of has to decrease by four times. On the other hand, if is kept fixed, one needs to decrease the Barbero–Immirzi parameter by four times. However, the value of the Barbero–Immirzi parameter is determined by the black hole entropy. Though the value is generally used in LQC [40], other evaluations exist [41,42,43,44], and the lowest evaluated value is [42]. Even if one uses this value, the scheme does not allow a trapped surface formation. Interestingly, in earlier works in LQC, was chosen to be the lowest nonzero eigenvalue , but its corresponding eigenstates were argued to not yield homogeneous classical metrics [45]. Despite a lack of physical justification to examine this, even using this value of along with does not allow the formation of trapped surfaces since one finds , which is still larger than the value (). Further, such a change in the value of the Barbero–Immirzi parameter is incompatible with the covariant entropy bound. Here, we note that the value , which is currently used in the literature, leads to a maximum energy density in the scheme, which almost saturates the covariant entropy bound [46]. Any decrease in , as needed above, would not be consistent with the covariant entropy bound in LQC. Since should be a universal constant in loop quantizations, irrespective of whether one chooses the or scheme, we concluded that if trapped surfaces form in the scheme for the model discussed above, the covariant entropy bound would be violated. In conclusion, irrespective of the initial conditions, the black hole would not form during the collapse of a homogeneous dust cloud in the marginally bound case for any possibly allowed values of and that have appeared in the literature.
Remark 1.
It should be noted that the result that no trapped surface can form in the marginally bound case with the scheme can be extended to an arbitrary matter content. The effective Hamiltonian constraint for any matter content can be expressed as:
where stands for the matter Hamiltonian. It is straightforward to check from the corresponding Hamilton equations that one obtains the same expression for as given in (14) with , which takes the values in the same range shown in (16). As a result, for any matter content, the maximum velocity squared of the outermost shell of a collapsing cloud is still given by (17), which implies no trapped surface can form during the collapse and expansion of the cloud, irrespective of the initial conditions and the matter content.
3.2. The Scheme
The effective dynamics in the scheme is governed by the effective Hamiltonian constraint, which takes the form [3]:
where , and the resulting dynamics was already discussed in detail in the context of the gravitational collapse in [15]. The corresponding equation for the outermost shell takes the form:
where . As a result, the bounce in the scheme takes place in the Planck regime at a fixed maximum energy density, which does not depend on the initial conditions. Furthermore, during the evolution of the dust cloud, the velocity squared of the outermost dust shell is given by:
Therefore, at , attains its maximum value, which turns out to be:
The above equation implies that in contrast to the scheme, the dust mass would affect the formation of the trapped surface in the scheme. To be specific, we found that there exists a threshold dust mass [15]:
When the initial dust mass is larger than , the trapped surface would form during the collapse or the expansion of the dust cloud. On the other hand, if the initial dust mass is lower than , no trapped surface can form during the nonsingular evolution of the dust cloud.
3.3. Other Quantizations with Different Kinds of Lattice Refinement
In the literature, it has been sometimes argued that one can have quantization prescriptions based on lattice refinements, which are a more general case of the and schemes [47]. Though the physical derivation of such refinements remains unclear, their implications have been discussed earlier in the cosmological setting, which rules all of them out except the scheme [11]. We considered these generalizations for the formation of trapped surfaces. In this model, one deals with a generalized set of the phase space variables, which are obtained from the variables by a canonical transformation [11]:
where n is a constant, which carries the information of a particular refinement and can take any values in the range . The case corresponds to the scheme, and corresponds to the scheme. Following the ideas in loop quantization, one then polymerizes the momentum , leading to the effective Hamiltonian constraint [11]:
where only depends on n. From the effective Hamiltonian constraint, one can derive the corresponding Hamilton equations and a constraint equation for , which takes the same form as (21), but with a different maximum energy density given explicitly by:
As a result, only in the scheme, the maximum energy density does not depend on the dust mass, which agrees with the observations in [11]. For other lattice refinements including the scheme, the maximum energy density is always determined by the dust mass. On the other hand, it is straightforward to obtain the velocity squared of the outermost shell of the dust cloud for an arbitrary n, which takes the form:
Using the Hamiltonian constraint and the definition of the dust energy density, we found the maximum of the velocity squared in terms of the dust mass and the lattice refinement factor n,
which reduces to Equation (17) in the scheme and Equation (23) in the scheme. In order to form a trapped surface during the evolution of the dust cloud, one requires the maximum value of the velocity squared larger than unity, which gives rise to the condition:
Except for (the scheme), the right-hand side of the above equation gives the threshold dust mass for an arbitrary choice of n. We show the dependence of the threshold mass on the parameter n in Figure 1. Assuming that numerically, takes a value of the same order as or , we see from the figure that when n increases from to zero, the threshold mass increases rapidly and approaches infinity as n approaches zero. Thus, we found that except in the scheme, one can always choose the dust mass so that a trapped surface forms, which can be identified with a dynamical black hole or white hole. It is important to note that even though there exist values of n except that allow the formation of the trapped surface, this does not imply their viability. These quantization prescriptions would suffer from the dependence of energy density at the bounce on the phase space variables, as a result of which the bounce density can be very small for a gravitational collapse of a macroscopic dust cloud.
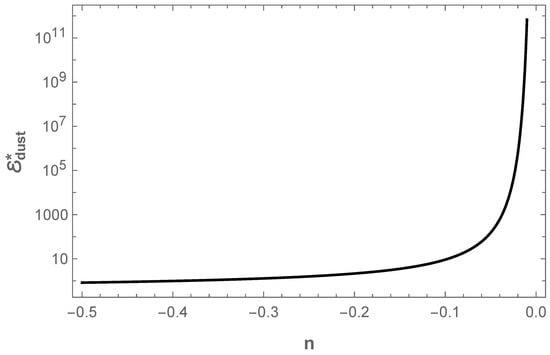
Figure 1.
In the figure, we show the qualitative relationship between the threshold mass and the parameter n by assuming that is numerically of a similar order as () or (). To be specific, in the plot, we choose the numerical value of the same as that of . The threshold mass for the formation of the trapped surface tends to be close to the Planck mass as n approaches , and it approaches infinity when n approaches zero.
4. Conclusions
The main goal of this paper was to explore whether different loop quantization prescriptions allow the formation of a black hole. Our work was based on investigating the evolution of a homogeneous dust cloud whose interior is isometric to a spatially flat FLRW spacetime. The homogeneity of the interior spacetime allowed us to use the quantization prescriptions used in LQC. In particular, we focused on the scheme and compared the results with the scheme and other possible lattice refinements. While the scheme already faces three serious challenges in the cosmological setting, two of these, the dependence of physical predictions on the choice of a fiducial cell and recollapse at late times when the strong energy condition is violated, are not relevant for the case of the gravitational collapse of a dust cloud. The third limitation is that bounce can occur at very small energy densities, but one can also choose initial conditions of the matter content such that the bounce occurs at Planckian densities. In this manuscript, our objective was not to show that this problem can be resolved for the scheme, but to add another problem to this list. In summary, the problem is that unless the minimum area gap or the Barbero–Immirzi parameter decreases by almost four times, no trapped surfaces can form in the homogeneous collapse of a dust shell or in fact any other form of matter in the scheme. This serious problem was so far unknown and in some sense shows that the existence of black holes completely rules out the scheme.
In contrast to the situation in the scheme, we found that trapped surfaces can form in the scheme, a result derived earlier in [15,30], and also for other lattice refinements parameterized by a parameter n following [11]. The central singularity for all values of n and all lattice refinements except the case of results in the formation of trapped surfaces. Unlike other values of , the formation of the trapped surfaces in the scheme only depends on the values of and the Barbero–Immirzi parameter . For all of the values of these two parameters that are allowed in the literature, we found that no trapped surface can form in the scheme. As a result, the scheme is disfavored in this context. On the other hand, for other loop quantizations, there always exists some particular threshold mass. When the dust mass is greater than this threshold value, the trapped surfaces can form during the nonsingular evolution of the dust cloud. It is remarkable to note that only in the scheme, the trapped surface would not form regardless of the dust mass, the initial radius, and even the matter content.
A few remarks regarding our main findings are in order. Firstly, the exclusion of trapped surfaces in the scheme can also be argued using Bousso’s covariant entropy bound. If this bound is satisfied, the minimal area gap cannot decrease to the value required for the formation of the trapped surface in the scheme. Secondly, though we believe that the simplest treatment of the dust collapse in the homogeneous setting does grasp some generic features of the full quantum gravity effects, including the resolution of the central singularity and the lower bounds on the dust mass for the formation of the trapped surfaces in some loop quantizations, since the scale of any finite celestial bodies cannot be compared with the universe, a homogeneous reduction that can be well justified for the entire universe may not be sufficient to describe a realistic gravitational collapse. In other words, to completely exclude the scheme, one still needs to further investigate the inhomogeneous case where the energy density also changes in the radial direction and the interactions between neighboring shells could in principle change the dynamics of the outermost shell. Thirdly, even in the homogeneous case, we only considered the marginally bound case of the dust collapse. Note that the marginally bound case could be matched to the spatially flat interior, and it was straightforward to deal with it using effective dynamics of the spatially flat isotropic model in LQC. However, an important question is whether these results hold in the presence of spatial curvature, i.e., the bound and the unbound cases. Since the spatial curvature can result in qualitatively distinct dynamics even in the classical theory, its inclusion at the quantum level for the gravitational collapse of a dust cloud can potentially give rise to a richer phenomenology. As an example, the bound case corresponds to the positively curved interior, which brings in various nontrivialities under loop quantization because of the interaction between the spatial curvature and quantum geometry effects. It can be shown that for the bound case, the scheme yields a trapped surface for different loop quantizations, but the scheme fails to give a viable macroscopic model of gravitational collapse, for the holonomy [48] and connection-based approaches [49,50], because of the lack of the classical limit [51]. These are important avenues to be investigated in the future for the bound and unbound cases and to check the robustness of the results obtained in this manuscript. Finally, our analysis leaves open the question of whether the generalizations of the and schemes, which are applied to the static black hole spacetimes, still remain valid for the collapsing spacetime. It will be interesting to apply the arguments used in this manuscript to examine the viability of such approaches.
Author Contributions
Conceptualization, P.S.; Analysis, B.-F.L., P.S.; Investigation: B.-F.L., P.S.; Project administration, P.S.; Software, B.-F.L. All authors have read and agreed to the published version of the manuscript.
Funding
NSF Grants PHY-1454832 and PHY-2110207 and the National Natural Science Foundation of China (NNSFC) with Grant No. 12005186.
Acknowledgments
This work is supported by NSF Grants PHY-1454832 and PHY-2110207 and the National Natural Science Foundation of China (NNSFC) with Grant No. 12005186.
Conflicts of Interest
The authors declare no conflict of interest.
Notes
| 1 | Recently, a question on similar lines was asked regarding a homogeneous collapse to understand the role of triad vs. gauge-covariant fluxes, but only for a specific quantization prescription (the scheme) [15]. |
| 2 | For early works taking only inverse volume modifications into account, see [26,27]. These modifications only become relevant near Planck lengths and are negligible compared to holonomy modifications [2,3]. In this work, we ignored the inverse volume modifications. |
References
- Ashtekar, A.; Pawlowski, T.; Singh, P. Quantum nature of the Big Bang. Phys. Rev. Lett. 2006, 96, 141301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ashtekar, A.; Pawlowski, T.; Singh, P. Quantum nature of the Big Bang: An analytical and numerical investigation. I. Phys. Rev. D 2006, 73, 124038. [Google Scholar] [CrossRef] [Green Version]
- Ashtekar, A.; Pawlowski, T.; Singh, P. Quantum nature of the Big Bang: Improved dynamics. Phys. Rev. D 2006, 74, 084003. [Google Scholar] [CrossRef] [Green Version]
- Ashtekar, A.; Corichi, A.; Singh, P. Robustness of key features of loop quantum cosmology. Phys. Rev. D 2010, 77, 024046. [Google Scholar] [CrossRef] [Green Version]
- Ashtekar, A.; Singh, P. Loop Quantum Cosmology: A Status Report. Class. Quant. Grav. 2011, 28, 213001. [Google Scholar] [CrossRef] [Green Version]
- Singh, P. Are loop quantum cosmos never singular? Class. Quant. Grav. 2009, 26, 125005. [Google Scholar] [CrossRef]
- Singh, P. Curvature invariants, geodesics and the strength of singularities in Bianchi-I loop quantum cosmology. Phys. Rev. 2012, 85, 104011. [Google Scholar] [CrossRef] [Green Version]
- Singh, P. Loop quantum cosmology and the fate of cosmological singularities. arXiv 2014, arXiv:1509.09182. [Google Scholar]
- Saini, S.; Singh, P. Resolution of strong singularities and geodesic completeness in loop quantum Bianchi-II spacetimes. Class. Quant. Grav. 2017, 34, 235006. [Google Scholar] [CrossRef] [Green Version]
- Saini, S.; Singh, P. Generic absence of strong singularities in loop quantum Bianchi-IX spacetimes. Class. Quant. Grav. 2018, 35, 065014. [Google Scholar] [CrossRef] [Green Version]
- Corichi, A.; Singh, P. Is loop quantization in cosmology unique? Phys. Rev. D 2008, 78, 024034. [Google Scholar] [CrossRef] [Green Version]
- Corichi, A.; Singh, P. Geometric perspective on singularity resolution and uniqueness in loop quantum cosmology. Phys. Rev. D 2009, 80, 044024. [Google Scholar] [CrossRef] [Green Version]
- Ashtekar, A.; Olmedo, J.; Singh, P. Quantum transfiguration of Kruskal black holes. Phys. Rev. Lett. 2018, 121, 241301. [Google Scholar] [CrossRef] [Green Version]
- Ashtekar, A.; Olmedo, J.; Singh, P. Quantum extension of the Kruskal spacetime. Phys. Rev. D 2018, 98, 126003. [Google Scholar] [CrossRef] [Green Version]
- Giesel, K.; Li, B.-F.; Singh, P. Non-singular quantum gravitational dynamics of an LTB dust shell model: The role of quantization prescriptions. arXiv 2021, arXiv:2107.05797. [Google Scholar]
- Ashtekar, A.; Bojowald, M.; Lewandowski, J. Mathematical structure of loop quantum cosmology. Adv. Theor. Math. Phys. 2003, 7, 233–268. [Google Scholar] [CrossRef]
- Ashtekar, A.; Bojowald, M. Quantum geometry and the Schwarzschild singularity. Class. Quant. Grav. 2005, 23, 391–411. [Google Scholar] [CrossRef] [Green Version]
- Bohmer, C.G.; Vandersloot, K. Loop quantum dynamics of the Schwarzschild interior. Phys. Rev. D 2007, 76, 104030. [Google Scholar] [CrossRef] [Green Version]
- Campiglia, M.; Gambini, R.; Pullin, J. Loop quantization of spherically symmetric midi-superspaces: The interior problem. AIP Conf. Proc. 2008, 977, 52–63. [Google Scholar]
- Gambini, R.; Pullin, J. Black holes in Loop Quantum Gravity: The complete space-time. Phys. Rev. Lett. 2008, 101, 161301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gambini, R.; Pullin, J. Loop quantization of the Schwarzschild black hole. Phys. Rev. Lett. 2013, 110, 211301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gambini, R.; Olmedo, J.; Pullin, J. Quantum black holes in loop quantum gravity. Class. Quant. Grav. 2014, 31, 095009. [Google Scholar] [CrossRef]
- Corichi, A.; Singh, P. Loop quantization of the Schwarzschild interior revisited. Class. Quant. Grav. 2016, 33, 055006. [Google Scholar] [CrossRef]
- Olmedo, J.; Saini, S.; Singh, P. From black holes to white holes: A quantum gravitational, symmetric bounce. Class. Quant. Grav. 2017, 34, 225011. [Google Scholar] [CrossRef]
- Gambini, R.; Olmedo, J.; Pullin, J. Spherically symmetric loop quantum gravity: Analysis of improved dynamics. Class. Quant. Grav. 2020, 37, 205012. [Google Scholar] [CrossRef]
- Bojowald, M.; Goswami, R.; Maartens, R.; Singh, P. Black hole mass threshold from nonsingular quantum gravitational collapse. Phys. Rev. Lett. 2005, 95, 091302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goswami, R.; Joshi, P.S.; Singh, P. Quantum evaporation of a naked singularity. Phys. Rev. Lett. 2006, 96, 031302. [Google Scholar] [CrossRef] [Green Version]
- Gambini, R.; Pullin, J.; Rastgoo, S. Quantum scalar field in quantum gravity: The vacuum in the spherically symmetric case. Class. Quant. Grav. 2009, 26, 215011. [Google Scholar] [CrossRef]
- Bambi, C.; Malafarina, D.; Modesto, L. Non-singular quantum-inspired gravitational collapse. Phys. Rev. 2013, 88, 044009. [Google Scholar] [CrossRef] [Green Version]
- Tavakoli, Y.; Marto, J.; Dapor, A. Semiclassical dynamics of horizons in spherically symmetric collapse. Int. J. Mod. Phys. D 2014, 23, 1450061. [Google Scholar] [CrossRef]
- Benitez, F.; Gambini, R.; Lehner, L.; Liebling, S.; Pullin, J. Critical collapse of a scalar field in semiclassical Loop Quantum Gravity. Phys. Rev. Lett. 2020, 124, 071301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Han, M.; Liu, H. Improved effective dynamics of Loop-Quantum-Gravity black hole and Nariai limit. arXiv 2020, arXiv:2012.05729. [Google Scholar]
- Kelly, J.G.; Santacruz, R.; Wilson-Ewing, E. Black hole collapse and bounce in effective loop quantum gravity. Class. Quant. Grav. 2020, 38, 04LT01. [Google Scholar] [CrossRef]
- Bojowald, M.; Harada, T.; Tibrewala, R. Lemaître-Tolman-Bondi collapse from the perspective of loop quantum gravity. Phys. Rev. 2008, 78, 064057. [Google Scholar] [CrossRef] [Green Version]
- Barrabès, C.; Israel, W. Thin shells in general relativity and cosmology: The lightlike limit. Phys. Rev. 1991, 43, 1129. [Google Scholar] [CrossRef]
- Goswami, R.; Joshi, P.S. Naked Singularity formation in scalar field collapse. arXiv 2004, arXiv:gr-qc/0410144. [Google Scholar]
- Singh, P. Glimpses of spacetime beyond the singularities using supercomputers. Comput. Sci. Eng. 2018, 20, 26–38. [Google Scholar] [CrossRef] [Green Version]
- Diener, P.; Gupt, B.; Singh, P. Numerical simulations of a loop quantum cosmos: Robustness of the quantum bounce and the validity of effective dynamics. Class. Quant. Grav. 2014, 31, 105015. [Google Scholar] [CrossRef]
- Diener, P.; Gupt, B.; Megevand, M.; Singh, P. Numerical evolution of squeezed and non-Gaussian states in loop quantum cosmology. Class. Quant. Grav. 2014, 31, 165006. [Google Scholar] [CrossRef] [Green Version]
- Meissner, K.A. Black-hole entropy in loop quantum gravity. Class. Quant. Grav. 2004, 21, 5245–5251. [Google Scholar] [CrossRef] [Green Version]
- Ashtekar, A.; Baez, J.; Corichi, A.; Krasnov, K. Quantum Geometry and Black Hole Entropy. Phys. Rev. Lett. 1998, 80, 904–907. [Google Scholar] [CrossRef] [Green Version]
- Dreyer, O. Quasinormal Modes, the Area Spectrum, and Black Hole Entropy. Phys. Rev. Lett. 2003, 90, 081301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Domagala, M.; Lewandowski, J. Black-hole entropy from quantum geometry. Class. Quant. Grav. 2004, 21, 5233–5243. [Google Scholar] [CrossRef] [Green Version]
- Ansari, M.H. Generic degeneracy and entropy in loop quantum gravity. Nucl. Phys. B 2008, 795, 635–644. [Google Scholar] [CrossRef] [Green Version]
- Ashtekar, A. Loop quantum cosmology: An overview. Gen. Rel. Grav. 2009, 41, 707–741. [Google Scholar] [CrossRef]
- Ashtekar, A.; Wilson-Ewing, E. Covariant entropy bound and loop quantum cosmology. Phys. Rev. 2008, 78, 064047. [Google Scholar] [CrossRef] [Green Version]
- Bojowald, M. Loop quantum cosmology and inhomogeneities. Gen. Rel. Grav. 2006, 38, 1771–1795. [Google Scholar] [CrossRef] [Green Version]
- Ashtekar, A.; Pawlowski, T.; Singh, P.; Vandersloot, K. Loop quantum cosmology of k = 1 FRW models. Phys. Rev. D 2007, 75, 024035. [Google Scholar] [CrossRef] [Green Version]
- Corichi, A.; Karami, A. Loop quantum cosmology of k = 1 FRW: A tale of two bounces. Phys. Rev. D 2011, 84, 044003. [Google Scholar] [CrossRef] [Green Version]
- Dupuy, J.L.; Singh, P. Implications of quantum ambiguities in k = 1 loop quantum cosmology: Distinct quantum turnarounds and the super-Planckian regime. Phys. Rev. D 2017, 95, 023510. [Google Scholar] [CrossRef] [Green Version]
- Li, B.-F.; Singh, P. Loop quantization prescriptions and black hole formation in the bound case. 2021; in preparation. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).