The Early Evolution of Solar Flaring Plasma Loops
Abstract
1. Introduction
2. The Analysis of Energy Balance of Coronal Plasma Loops
2.1. Transport and Accumulate Areas of Coronal Plasma Loops

2.2. Energy Input
2.3. Energy Loss
- (1)
- Cyclotron and gyro-synchrotron emission. With the magnetic field in the plasma of the accumulate area, particle accelerations due to gyration around the magnetic field lines become dominant. Cyclotron emission in thermal plasma and gyro-synchrotron emission in very hot thermal plasma will provide the main contributions of radiative energy loss. Generally, it is very complicated to calculate the total energy of cyclotron and gyrosynchrotron emission in magnetized plasma loops. In a very diluted solar plasma with thermal equilibrium distribution, we may obtain the approximation of the total energy loss released in the unit volume at all possible frequencies,is the magnetic field strength with the unit at Tesla. is at eV. is at . Here, we find that the total energy of cyclotron and gyrosynchrotron emission increases with respect to the plasma density () and temperature (), and rapidly increases with the magnetic field strength (B).
- (2)
- Bremsstrahlung emission. In thermal plasma, the accelerations due to collisions between electrons and ions may result in a bremsstrahlung emission. The total energy of the bremsstrahlung emission at all possible frequencies in unit volume can be approximated ashere, the unit of is at , and and are the density of the electrons and ions, respectively. is the plasma temperature with the unit of eV. The contribution of the thermal bremsstrahlung emission increases with respect to the plasma temperature and rapidly increases with the plasma density.
- (3)
- Excitation emission: This is the radiation produced when electrons in an excited state in atoms or ions jump down to some lower energy state (transition of the energy levels), which may form a series of line emissions. In solar coronal plasmas, this may contribute the energy loss in the unit volume per unit time:here, the unit of is eV. is the charge number of the nuclei. Equation (8) indicates that the excitation emission decreases rapidly with the increment of the plasma temperature. At the same time, it quickly increases with the charge number Z. Typically, in the plasma around the solar coronal looptop, , eV; therefore, .
- (4)
- Recombination radiation: When a free electron collides with ions, recombination may take place and may radiate photons. The energy loss of recombination radiation in unit volume solar plasma per unit time can be approximated ashere, is the ionization energy of hydrogen. For ground state of hydrogen, eV, and the typical plasma temperature (>100 eV) in the looptop is . Therefore, normally . Equation (9) indicates that the contributions of recombination radiation also decrease rapidly with the increase of plasma temperature.
2.4. The Temporal Evolution of Temperature
3. The Evolution of Coronal Plasma Loop during the Early Phase
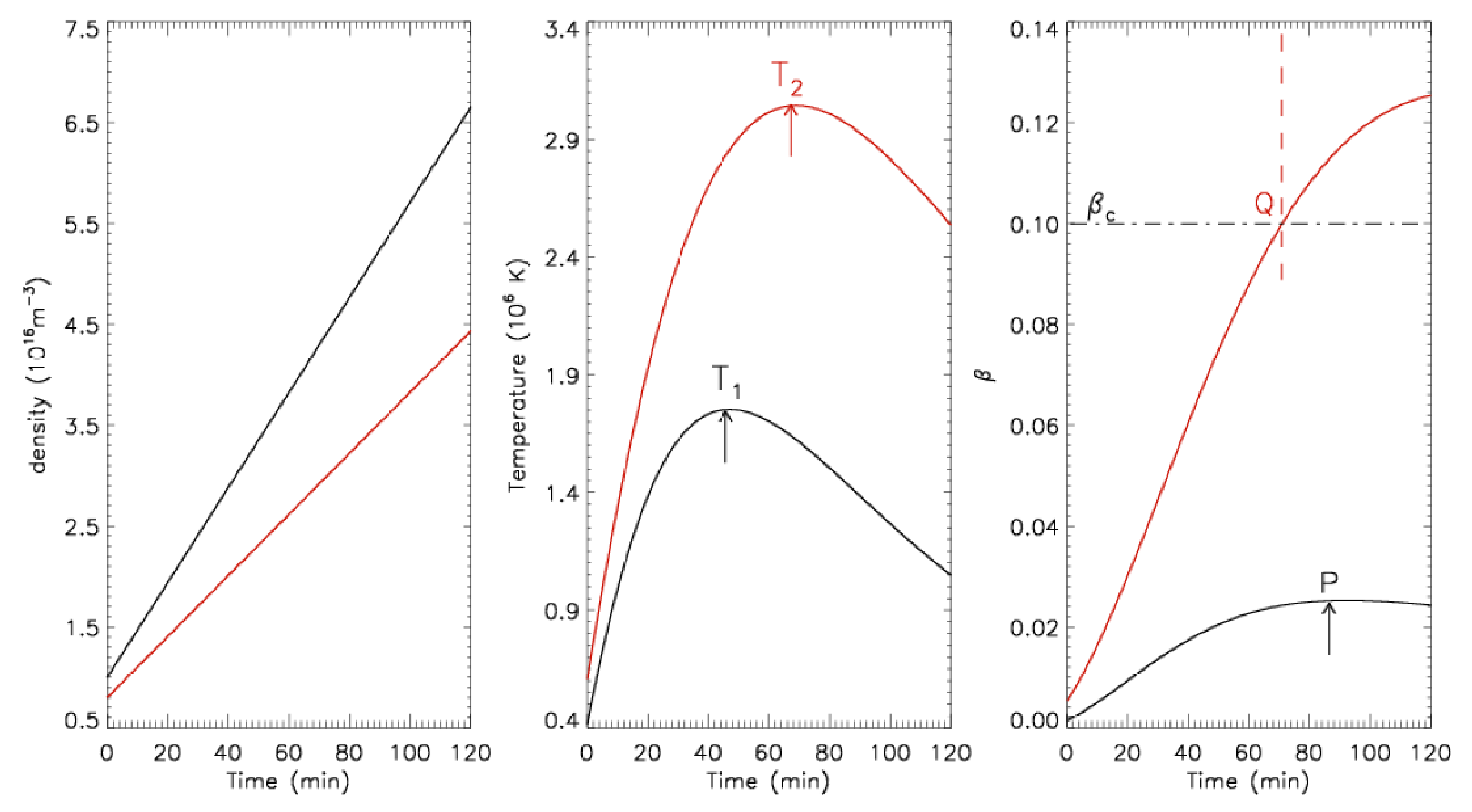
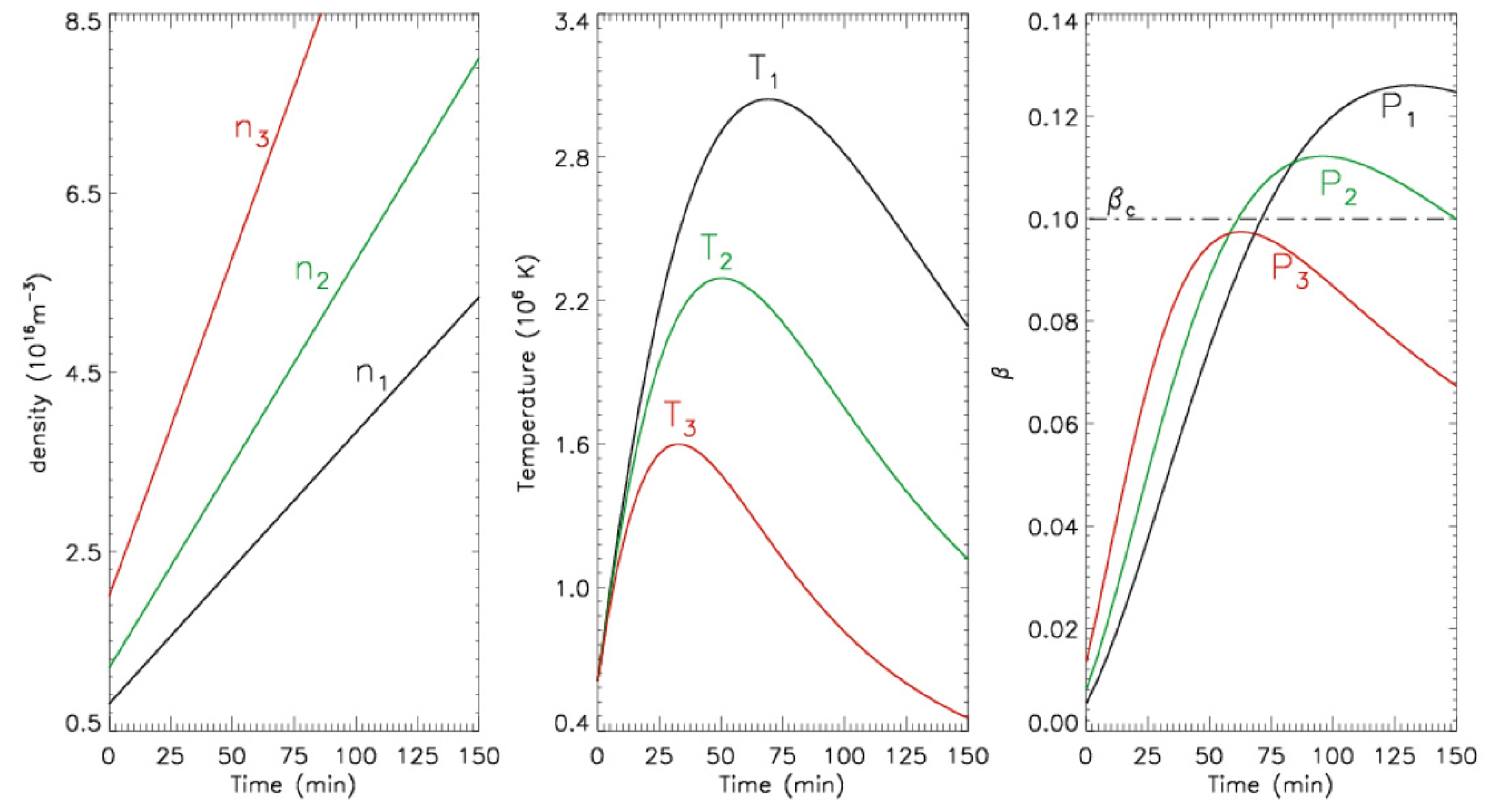
4. Conclusions
- (1)
- Solar plasma loops can be divided into two distinct areas: the transport path (from foot-points to the loop legs with considerable magnetic gradient) and the accumulate area (around the looptop). The energetic particles comprising the underlying thermal plasma can be driven by MGP process to flow upward through the transport paths and to be depositedt in the accumulate area.
- (2)
- With the deposit and accumulation of MGP upflow energetic particles, the plasma density in the accumulate area may increase the initial value several times in about one or two hours. The accumulation of the MGP upflow energetic particles around the looptop provides the material basis for the possible following flaring eruptions.
- (3)
- The plasma temperature in the accumulate area gradually increases to a maximum of several million K in several decade minutes after the formation of the loops. Then, it decreases slowly due to the enhancement of the bremsstrahlung and cyclotron radiations.
- (4)
- The value is a key parameter to show the temporal evolutionary features of a plasma loop. We find that the value of the accumulate area also gradually increases, which is driven by MGP process in the first decades of minutes. However, in fact, not all solar coronal loops can evolve into an unstable stage to produce eruptions. Most of the low, initially dense solar plasma loops with relatively strong magnetic fields tend to be stable (such as Case 1 showing in Figure 2), for the maximum value is still much smaller than the critical value . This can be demonstrated by the evolution of many quiet, or quasi-static plasma loops in the solar atmosphere [32]. On the other hand, the higher, initially diluted solar plasma loops with relatively weak magnetic fields tend to be unstable (such as in Case 2 showing in Figure 2) for values exceeding the critical value at a time of about one hour after the formation of the solar magnetized plasma loop, which may trigger ballooning instability and the following eruptions. This case can be applied to demonstrate the early evolution of flaring plasma loops [43,44].
Funding
Acknowledgments
Conflicts of Interest
References
- Del Zanna, G.; Mason, H.E. Solar active regions: SOHO/CDS and TRACE observations of quiescent coronal loops. Astron. Astrophys. 2003, 406, 1089–1103. [Google Scholar] [CrossRef]
- Reale, F. Coronal Loops: Observations and Modeling of Confined Plasma. Living Rev. Sol. Phys. 2014, 11, 1–94. [Google Scholar] [CrossRef] [PubMed]
- Deforest, C.E. On the Size of Structures in the Solar Corona. Astrophys. J. 2007, 661, 532–542. [Google Scholar] [CrossRef]
- Carmichael, H. Physics of Solar Flares; Hess, W.N., Ed.; NASA SP-50; Cambridge University Press: Washington, DC, USA, 1964; p. 451. [Google Scholar]
- Sturrock, P.A. Structure and Development of Solar Active Regions; Kiepenheuer, K.O., Ed.; Reidel: Dordrecht, The Netherlands, 1968; p. 471. [Google Scholar]
- Hirayama, T. Theoretical model of flares and prominences. Sol. Phys. 1974, 34, 323–338. [Google Scholar] [CrossRef]
- Kopp, R.A.; Pneuman, G.W. Magnetic reconnection in the corona and the loop prominence phenomenon. Sol. Phys. 1976, 50, 85–98. [Google Scholar] [CrossRef]
- Yokoyama, T.; Shibata, K. Magnetic Reconnection Coupled with Heat Conduction. Astrophys. J. 1997, 474, L61–L64. [Google Scholar] [CrossRef]
- Shibata, K.; Masuda, S.; Shimojo, M.; Hara, H.; Yokoyama, T.; Tsuneta, S.; Kosugi, T.; Ogawara, Y. Hot-Plasma Ejections Associated with Compact-Loop Solar Flares. Astrophys. J. 1995, 451, L83. [Google Scholar] [CrossRef]
- Chen, B.; Yu, S.; Reeves, K.K.; Gary, D.E. Microwave Spectral Imaging of an Erupting Magnetic Flux Rope: Implications for the Standard Solar Flare Model in Three Dimensions. Astrophys. J. 2020, 895, L50. [Google Scholar] [CrossRef]
- Tsuneta, S.; Masuda, S.; Kosugi, T.; Sato, J. Hot and Superhot Plasmas above an Impulsive Flare Loop. Astrophys. J. 1997, 478, 787–798. [Google Scholar] [CrossRef]
- Tan, B.; Yu, Z.; Huang, J.; Tan, C.; Zhang, Y. Very long-period pulsations before the onset of solar flares. Astrophys. J. 2016, 833, 206. [Google Scholar] [CrossRef]
- Chen, P.F.; Fang, C.; Ding, M.; Tang, Y.H. Flaring Loop Motion and a Unified Model for Solar Flares. Astrophys. J. 1999, 520, 853–858. [Google Scholar] [CrossRef]
- Li, L.; Zhang, J. On the brightening propagation of post-flare loops observed by trace. Astrophys. J. 2008, 690, 347–357. [Google Scholar] [CrossRef]
- Aulanier, G.; Janvier, M.; Schmieder, B. The standard flare model in three dimensions. Astron. Astrophys. 2012, 543, A110. [Google Scholar] [CrossRef]
- Cai, Q.; Feng, H.; Ye, J.; Shen, C. Dynamical and Thermal Manifestations of the Region above the Top of the Post-flare Loops: MHD Simulations. Astrophys. J. 2021, 912, 79. [Google Scholar] [CrossRef]
- Lin, J.; Soon, W.; Baliunas, S. Theories of solar eruptions: A review. New Astron. Rev. 2003, 47, 53–84. [Google Scholar] [CrossRef]
- Forbes, T.G.; Linker, J.A.; Chen, J.; Cid, C.; Kóta, J.; Lee, M.A.; Mann, G.; Mikić, Z.; Potgieter, M.S.; Schmidt, J.; et al. CME Theory and Models. Space Sci. Rev. 2006, 123, 251–302. [Google Scholar] [CrossRef]
- Kusano, K.; Bamba, Y.; Yamamoto, T.; Iida, Y.; Toriumi, S.; Asai, A. Magnetic fields structures triggering solar flares and coronal mass ejections. Astrophys. J. 2012, 760. [Google Scholar] [CrossRef]
- Tan, B. Coronal heating driven by a magnetic gradient pumping mechanism in solar plasmas. Astrophys. J. 2014, 795. [Google Scholar] [CrossRef]
- Tan, B.-L.; Yan, Y.; Li, T.; Zhang, Y.; Chen, X. Magnetic gradient: A natural driver of solar eruptions. Res. Astron. Astrophys. 2020, 20, 90. [Google Scholar] [CrossRef]
- Gelfreikh, G.B.; Pilyeva, N.A.; Ryabov, B.I. On the gradient of coronal magnetic fields from radio observations. Sol. Phys. 1997, 170, 253–264. [Google Scholar] [CrossRef]
- Mathew, S.K.; Ambastha, A. Magnetic field gradient and flare: Study of a small flare in NOAA 8038. Sol. Phys. 2000, 197, 75–84. [Google Scholar] [CrossRef]
- Joshi, J.; Lagg, A.; Hirzberger, J.; Solanki, S.; Tiwari, S.K. Vertical magnetic field gradient in the photospheric layers of sunspots. Astron. Astrophys. 2017, 599, A35. [Google Scholar] [CrossRef]
- Dulk, G.A.; McLean, D.J. Coronal magnetic fields. Sol. Phys. 1978, 57, 279–295. [Google Scholar] [CrossRef]
- Boyd, T.J.M.; Sanderson, J.J. The Physics of Plasmas; Cambridge University Press: Cambridge, UK, 2003; pp. 324–354. [Google Scholar]
- Bradshow, S.J.; Cargill, P.J. The cooling of coronal plasmas. II. Properties of the radiative phase. A&A 2005, 437, 311–317. [Google Scholar] [CrossRef]
- Bradshow, S.J.; Cargill, P.J. The cooling of coronal plasmas. III, Enthalpy transfer as a mechanism for energy loss. ApJ 2010, 717, 163–174. [Google Scholar] [CrossRef]
- Cargill, P.J.; Bradshow, S.J. The cooling of coronal plasmas. IV. Catastrophic cooling of loops. ApJ 2013, 772, 40. [Google Scholar] [CrossRef]
- Vernazza, J.E.; Avrett, E.H.; Loeser, R. Structure of the solar chromosphere. III—Models of the EUV brightness components of the quiet-sun. Astrophys. J. Suppl. Ser. 1981, 45, 635–725. [Google Scholar] [CrossRef]
- Zhang, J.; White, S.M.; Kundu, M.R. Two-Temperature Coronal Models fromSOHO/EIT Observations. Astrophys. J. 1999, 527, 977–991. [Google Scholar] [CrossRef]
- Li, X.Q.; Zhang, Z.; Smartt, R.N. Magnetic reconnection theory for coronal loop interaction. A&A 1994, 290, 963–971. [Google Scholar]
- Huang, G.; Ji, H. Microwave, Optical, EUV, and Hard X-Ray Signature of Possible Coronal Loop Interaction. Sol. Phys. 2005, 229, 227–236. [Google Scholar] [CrossRef]
- Ji, H.; Huang, G.; Wang, H. The Relaxation of Sheared Magnetic Fields: A Contracting Process. Astrophys. J. 2007, 660, 893–900. [Google Scholar] [CrossRef]
- Mei, Z.; Keppens, R.; Roussev, I.I.; Lin, J. Parametric study on kink instabilities of twisted magnetic flux ropes in the solar atmosphere. Astron. Astrophys. 2017, 609, A2. [Google Scholar] [CrossRef]
- Greenwald, M. Density limits in toroidal plasmas. Plasma Phys. Control. Fusion 2002, 44, R27–R53. [Google Scholar] [CrossRef]
- Pariat, E.; Dalmasse, K.; DeVore, C.R.; Antiochos, S.K.; Karpen, J.T. A model for straight and helical solar jets: II. Parametric study of the plasma beta. Astron. Astrophys. Suppl. Ser. 2016, 596, A36. [Google Scholar] [CrossRef]
- Strauss, H.R. Criticalβfor Toroidal Equilibrium. Phys. Rev. Lett. 1971, 26, 616–618. [Google Scholar] [CrossRef]
- La Haye, R.J.; Buttery, R.J.; Guenter, S.; Huysmans, G.T.A.; Maraschek, M.; Wilson, H.R. Dimensionless scaling of the critical beta for onset of a neoclassical tearing mode. Phys. Plasmas 2000, 7, 3349–3359. [Google Scholar] [CrossRef]
- Tsap, Y.T.; Kopylova, Y.; Stepanov, A. Ballooning instability and oscillations of coronal loops. Astron. Rep. 2006, 50, 1026–1035. [Google Scholar] [CrossRef]
- Tsap, Y.T.; Kopylova, Y.; Stepanov, A.; Melnikov, V.; Shibasaki, K. Ballooning Instability in Coronal Flare Loops. Sol. Phys. 2008, 253, 161–172. [Google Scholar] [CrossRef]
- Melnikov, V.; Shibasaki, K.; Reznikova, V. Loop-Top Nonthermal Microwave Source in Extended Solar Flaring Loops. Astrophys. J. 2002, 580, L185–L188. [Google Scholar] [CrossRef]
- Müller, D.A.N.; Hansteen, V.H.; Peter, H. Dynamics of solar coronal loops. Astron. Astrophys. 2003, 411, 605–613. [Google Scholar] [CrossRef][Green Version]
- Nindos, A.; White, S.M.; Kundu, M.R.; Gary, D. Observations and Models of a Flaring Loop. Astrophys. J. 2000, 533, 1053–1062. [Google Scholar] [CrossRef]
- Li, D.; Feng, S.; Su, W.; Huang, Y. Preflare very long-periodic pulsations observed in Hα emission before the onset of a solar flare. Astron. Astrophys. 2020, 639, L5. [Google Scholar] [CrossRef]
- Li, D.; Li, Y.; Lu, L.; Zhang, Q.; Ning, Z.; Anfinogentov, S. Observations of a Quasi-periodic Pulsation in the Coronal Loop and Microwave Flux during a Solar Preflare Phase. Astrophys. J. 2020, 893, L17. [Google Scholar] [CrossRef]
- Yan, Y.; Chen, Z.; Wang, W.; Liu, F.; Geng, L.; Chen, L.; Tan, C.; Chen, X.; Su, C.; Tan, B. Mingantu Spectral Radioheliograph for Solar and Space Weather Studies. Front. Astron. Space Sci. 2021, 8. [Google Scholar] [CrossRef]
- Lemen, J.R.; Title, A.M.; Akin, D.J.; Boerner, P.F.; Chou, C.; Drake, J.F.; Duncan, D.W.; Edwards, C.G.; Friedlaender, F.M.; Heyman, G.F.; et al. The Atmospheric Imaging Assembly (AIA) on the Solar Dynamics Observatory (SDO). Sol. Phys. 2011, 275, 17–40. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, B. The Early Evolution of Solar Flaring Plasma Loops. Universe 2021, 7, 378. https://doi.org/10.3390/universe7100378
Tan B. The Early Evolution of Solar Flaring Plasma Loops. Universe. 2021; 7(10):378. https://doi.org/10.3390/universe7100378
Chicago/Turabian StyleTan, Baolin. 2021. "The Early Evolution of Solar Flaring Plasma Loops" Universe 7, no. 10: 378. https://doi.org/10.3390/universe7100378
APA StyleTan, B. (2021). The Early Evolution of Solar Flaring Plasma Loops. Universe, 7(10), 378. https://doi.org/10.3390/universe7100378




