Abstract
We investigate the influence of repulsive vector interactions and color superconductivity on the structure of neutron stars using an extended version of the field correlator method (FCM) for the description of quark matter. The hybrid equation of state is constructed using the Maxwell description, which assumes a sharp hadron-quark phase transition. The equation of state of hadronic matter is computed for a density-dependent relativistic lagrangian treated in the mean-field approximation, with parameters given by the SW4L nuclear model. This model described the interactions among baryons in terms of , and mesons. Quark matter is assumed to be in either the CFL or the 2SC+s color superconducting phase. The possibility of sequential (hadron-quark, quark-quark) transitions in ultra-dense matter is investigated. Observed data related to massive pulsars, gravitational-wave events, and NICER are used to constrain the parameters of the extended FCM model. The successful equations of state are used to explore the mass-radius relationship, radii, and tidal deformabilities of hybrid stars. A special focus lies on investigating consequences that slow or fast conversions of quark-hadron matter have on the stability and the mass-radius relationship of hybrid stars. We find that if slow conversion should occur, a new branch of stable massive stars would exist whose members have radii that are up to 1.5 km smaller than those of conventional neutron stars of the same mass. Such objects could be possible candidates for the stellar high-mass object of the GW190425 binary system.
1. Introduction
Neutron stars (NSs) are compact stellar remnants which are born in type-II supernova explosions [1]. Within just a few minutes after birth, they turn into cold (on the nuclear scale) stellar objects with temperature of just a few MeV [2]. Their masses can be as high as ∼, and their radii range from ∼10 to ∼13 km, depending on mass. The mean density of a NS with a canonical mass of is higher than the nuclear saturation density of g cm and the density reached in the central core is expected to be several times higher than [3]. Paired with the unprecedented current progress in observational astronomy [4,5,6,7,8] these characteristic features make NSs superb astrophysical laboratories for a wide range of physical studies, which help us to understand the nature of matter subjected to most extreme conditions of pressure and density [9,10].
Traditionally, NSs are though as three-layer compact objects composed by an inner core, an outer core and a crust. Densities in the crust are lower than . Experimental nuclear physics data from terrestrial laboratories have been extremely useful to reduce the uncertainties in the low-density regime of such NS matter and its associate equation of state (EoS). The situation is different for matter with densities above , for which there is no general agreement about the structure and composition. This lack of knowledge increases with increasing central density [11,12]. Over the years, several different theoretical possibilities regarding the unknown nuclear composition have been explored, including those that take into account a possible hadron-quark phase transition (see, e.g., Refs. [10,12], and references therein). Neutron stars containing hadrons and deconfined quarks in their center are referred to as hybrid stars (HS). The situation is different for matter at densities above , for which no general agreement on the structure and composition exists. This lack of knowledge deepens with increasing density. Several different theoretical possibilities of the central composition of NSs are being explored, including some which account for a possible hadron-quark phase transition (see, for example, Refs. [10,12], and references therein). NSs containing hadrons and deconfined quarks in their centers, are known as hybrid stars (HSs).
Observations of the pulsars PSR J1614-2230 [13,14], PSR J0348+0432 [15] and PSR J0740+6620 [16] have imposed strong constraints to the EoS of matter inside NSs. In addition, the merger of two binary NSs (BNSs) known as GW170817, together with the detection of the electromagnetic radiation associated with this event, has been used to put constraints on the radius and dimensionless tidal deformability of the merging compact objects and, therefore, indirectly on their nuclear EoSs [4]. The analysis of the data from this event has been used to set new limits on the radius of a NS which is estimated to be between and km [17]. Moreover, the upper bound to the maximum-mass of cold and slowly rotating NS has been estimated to be ∼ [18]. A second BNS merger, named GW190425, has been detected by the LIGO Livingston interferometer. In this case, the inferred total mass of the NSs that merged has been estimated to be [6]. This is higher than the expected Galactic mean mass for this kind of binary systems [19]. To date, no electromagnetic counterpart associated with GW190425 has been detected (see, for example, Ref. [20], and references therein).
In 2019 the NICER collaborations have determined the mass and radius of the isolated NS PSR J0030+0451 with values of and km [21] and and km [22]. Very recently, data from NICER and XMM-Newton were used to determine the radius of PSR J0740+6620 with a value of km [8] and km [7]. These values show that the radius of PSR J0030+0451 is similar to the radius of the much more massive NS PSR J0740+6620, whose mass is [7]. This constrains the nuclear EoS to a greater degree than previously possible.
For a comprehensive study of the properties of matter in the cores of neutron stars and the EOS associated with such matter, it is necessary to resort to Quantum Chromodynamics (QCD), the theory of strong interactions. Besides quark confinement, asymptotic freedom is one of the main features of QCD, which states that matter at high density and/or temperatures exhibits a phase transition in which hadrons merge leading to the formation of a plasma of quarks and gluons. QCD has inherent computational problems that make it extremely difficult to perform analytic calculations at finite densities to be performed. For this reason, several phenomenological and/or effective models have been proposed that reproduce (some of) the key features and symmetries of the QCD Lagrangian density (see Ref. [10] and references therein).
If the hadron-quark phase transition occurs in the cores of NSs, it has been shown that the liberated quarks should form a color superconductor (CSC) [23,24,25]. This phase is characterized by the formation of quark Cooper pairs, similarly to the formation of electron Cooper pairs in ordinary condensed matter superconductivity, which is energetically favored since it lowers the energy of the Fermi sea of fermions [26]. A Cooper pair of quarks can not be a in a color singlet state as the corresponding condensate breaks the QCD local color symmetry, SU(3). Hence the notion color superconductivity. Since the pairing among the quarks is quite robust, quark matter, if existing in the cores of NSs, ought to be a CSC. In contrast to ordinary condensed matter superconductivity, however, the condensation patterns of CSC quark matter are much more complex as up to three different quark flavors and three different color states are involved in the diquark formation [24,25].
Two of the most studied color superconducting phases are the two flavor color superconducting (2SC) phase and the color-flavor-locked (CFL) phase. In the 2SC phase, only up, u, and down, d, quarks pair. The strange quark, s, has a mass that is by two orders of magnitude higher than the masses of u and d quarks. This favors the formation of the 2SC phase at intermediate densities, while at high densities, where the mass of the strange quark plays a less dominant role, the CFL phase may replace the 2SC phase. CFL is a more symmetric phase of matter in which all three quark flavors are involved in the pairing process. There is also the possibility that a phase known as 2SC+s is formed at intermediate densities, where the strange quarks are treated as a gas of free massive fermions [27]. The formation of diquarks lower the energy of the system by an amount related to the size of the CSC gap, . This quantity is a function of the chemical potential, but can be treated as a free parameter of the model [28]. This phenomenological approach is useful as it gives theoretical insight into CSC. The occurrence of each of these phases is directly related to the mass of the strange quark mass, the energy gap, and the electron chemical potential [25].
In addition to the possibility of diquarks formation in HSs, it is known that the inclusion of the repulsive vector interaction in quark models allows HSs to satisfy the constraint [29,30,31].
In this work, we study the influence of color superconductivity and of vector interactions among quarks on the composition and structure of HSs. Using an extended version of the Field Correlator Method (FCM) for the description of quark matter [32,33,34], the effects of 2SC+s and CFL superconductivity is included in the quark model in a phenomenological way. To model the hadronic phase of the hybrid EoS, we use the SW4L parametrization of the density dependent relativistic mean-field theory which includes all particles of the baryon octet as well as the resonance [35].
We assume that the surface tension at the hadron-quark interface is high so that a sharp hadron-quark phase transition occurs, which is modeled as a Maxwell transition (see Ref. [10], and references therein). In this context we analyze the possibilities of rapid versus slow conversions of matter at the hadronic and quark matter interface [36]. This phenomenon requires a modification of the traditional stability criteria of compact objects.
The paper is organized as follows. In Section 2 we provide some details of the treatment of phase transitions in HSs. Chemical and mechanical equilibrium conditions for the construction of the hybrid EoS are also given. Section 3 is devoted to the description of the hadronic model used to describe the outer cores of HSs. The model used to describe quark matter in the inner core of HSs is introduced in Section 4. The model accounts for vector interactions among quarks and the effects of color superconductivity. The results of our comprehensive analysis of quark matter parameters, phase transitions and hybrid configurations will be discussed in Section 5. Finally, a summary and discussion of our key findings are presented in Section 6.
2. Quark-Hadron Phase Transition in Neutron Stars
Properties such as the surface tension at the hadron-quark interface, , and nucleation timescale are only poorly known. These two quantities define the nature of the hadron-quark phase transition. For example, whether the hadron-quark phase transition separating both types of matter is sharp or smooth is determined by the value of the surface tension between the two phases. If the value of the surface tension is larger than a critical value of MeV fm, a (sharp) Maxwell phase transition is favored [37,38,39]. Otherwise, a (smooth) Gibbs phase transition would be expected. It is important to note that for the Gibbs formalism, the global electric charge neutrality condition leads to the appearance of geometrical structures in the mixed hadron-quark phase. This so-called pasta phase is highly dependent on the EoS used to construct the phase transition as well as on the value of (see, for example Refs. [40,41], and references therein).
Although the analysis of data from GW170817 and its electromagnetic counterpart led to the conclusion that high-mass NSs may be expected to have quark matter in their inner cores [42], there is no direct observational evidence of the occurrence of a hadron-quark phase transition in the interior of such objects. In this work, we assume that the favored transition scenario is that of a sharp hadron-quark phase transition.
Within this theoretical framework, we study two different regimes related to the nucleation timescales of the sharp phase transition: the slow and the rapid conversion. The importance of considering these different theoretical scenarios has been introduced in Ref. [36]. In that work, the authors showed the huge impact these two types of conversions have on the structure and stability of HSs against radial oscillations. The main result was that when a slow conversion rate is considered to occur inside of a HS, the star continues to remain stable against radial oscillations (i.e., the fundamental radial mode remains real valued) even beyond the gravitational mass peak, where the mass is decreasing with increasing central energy density (for details, see Ref. [43]). This finding differs drastically from the standard stability criterion established for compact stars whereupon stability of stars against radial oscillations is only possible if the mass is monotonically increasing with density.
The concept of slow and rapid conversion is linked to the relationship between two very different timescales. These are the nucleation timescale, i.e., the characteristic time during which a hadron (quark) fluid element is converted into quark (hadronic) matter, and the characteristic timescale of the oscillation of the fluid elements. As to the latter, the fluid elements located near the transition interface oscillate to regions of larger (smaller) pressures as the oscillation stretches and compresses the matter in the star. The hadron-quark conversion is slow (rapid) if the nucleation timescale is much larger (smaller) that the one associated with the oscillations at the interface separating the two phases.
The strong and weak interactions have times scales that differ from each other by many orders of magnitude ( s, s). For this reason it has been proposed that the hadron-quark deconfinement process ought to consist of two separate steps: the formation of a virtual drop of out-of--equilibrium quark matter that will subsequently reach chemical equilibrium. The characteristic time scale of this process is related to the difference between the Gibbs free energies of equilibrium and out-of--equilibrium quark matter (for a more detailed discussion, see, for example, Ref. [44]). Present results for this energy difference are strongly model dependent and inconclusive (for details, see, for example, Refs. [45,46,47,48,49]). Therefore, in this work we shall account for both theoretical possibilities and analyze the astrophysical consequences and observational differences that might help understand in detail the microphysics of the hadron-quark phase transition.
The composition of the matter in the interior of a HS is determined by the condition of -equilibrium and electric charge neutrality [50,51]. These condition imposes a relationship between the chemical potentials of the different particle species in the hadronic phase,
and in the quark phase with flavors f = u, d, s,
where and are the baryon and quark electric charges, is the neutron chemical potential, and the electron chemical potential.
To calculate the hybrid EoS within the Maxwell construction at zero temperature, , we impose the mechanical equilibrium condition that reads
Charge neutrality is imposed locally in the Maxwell formalism, i.e., each phase has to be independently electrically neutral. This condition is satisfied if , where is the pressure of the hadronic (quark) phase, which will be defined later.
3. The Hadronic Phase
To describe hadronic matter in the outer core of HSs we use the SW4L parametrization of the density dependent non-linear relativistic mean-field model [52,53,54]. This family of models have gained popularity since the density-dependent couplings allows one to account for the latest slope values of the symmetry energy consistent with experimental data [55,56]. This quantity plays a significant role for the determination of the radii of NSs [57].
For the SW4L parametrization, the interactions between baryons are described by the exchange of scalar (, ), vector (, ) and isovector () mesons. The pressure and the energy density of the model are given by
where the sum over B sums all members of the baryon octet, , as well as the resonance. The quantities denote density dependent meson–baryon coupling constants that have a functional form given by
where n is the total baryon number density. The last term in Equation (4) is the rearrangement term which guarantees the thermodynamic consistency of the model [58],
The quantity is the 3-component of isospin, and are the particle number densities of each baryon B with Fermi momentum . The effective baryon mass in Equations (4) and (5) is given by
The parameters of SW4L are presented in Table 1. These values are adjusted to the properties of nuclear matter at saturation density shown in Table 2 (for details, see Ref. [54], and references therein).

Table 1.
Parameters of the SW4L parametrization that lead to the properties of symmetric nuclear matter at saturation density shown in Table 2.

Table 2.
Energy per nucleon , nuclear compressibility , effective nucleon mass , symmetry energy , and slope of the symmetry energy of nuclear matter at saturation density, , obtained for the SW4L parametrization.
4. The Quark Phase
To describe quark matter in the inner core of cold HSs we use an extended version of the FCM model, including the effects of repulsive vector interactions among quarks and of color superconductivity.
The FCM model is based on the calculation of the amplitudes of the color electric , and color magnetic , Gaussian correlators. and are directly related with the confinement of quarks, and , contain perturbative terms related to the perturbation expansion over the strong coupling constant at a given order [32,59]. The method has been generalized to finite temperature and baryonic density using the single line approximation (SLA) which neglects, to first order, all perturbative and non-perturbative interactions of the system. In this way, it is possible to factorize the partition function into the products of one gluon and one quark (anti-quark) contributions and thus calculate the corresponding thermodynamic potential [33].
For zero-temperature HS matter, and , leaving two field correlators which can be parametrized through the large distance potential, , and the gluon condensate, . In addition, the main consequence of repulsive vector interactions for HSs is to stiffen the EoS of quark matter to obtain stellar configurations, in agreement with recent observations of massive pulsars. We also mention that the onset of quark matter in the interior of HSs is affected by this interaction.
Both vector interactions among quarks and color superconductivity are taken into account by FCM model.
4.1. Inclusion of Vector Interactions in the FCM Model
The inclusion of vector interactions among quarks modifies the SLA of the quark pressure in the following way
where
and , is the bare quark mass of a quark flavor f and T is the temperature. The effective chemical potential is given by
where is the chemical potential of a quark of flavor f, is the coupling constant of the vector interactions, and is the associated condensate.
An expression similar to the first term in Equation (9) can be deduced for the pressure of the gluons, which vanished at zero temperature. The second term is the pressure due the vector condensates given by
Taking the limit in Equation (9), we obtain a simplified expression for the total pressure of the system that reads
where , , , and
is the vacuum energy density for flavors [32].
The EoS of the system can be computed using the Euler thermodynamic relation given by
4.2. Effects of Color Superconductivity on the Quark EoS
The working hypothesis of our study is that in the inner cores of HSs deconfined up, down and strange quarks are paired in the CFL phase. However, since the mass of the strange quark is around two orders of magnitude greater than that of up and down quarks, paired up and down quark condensates should appear first, in a phase known as 2SC+s. The quark masses in the 2SC+s and CFL color superconducting phases are taken as and .
To include the effect of color superconductivity, we work to order in the diquark energy gap , which simplifies the calculation considerably [51]. In this way, it is possible to consider Equation (13) as a fictional state made of unpaired quark matter that transforms to a superconducting state once the quarks involved in the pairing reach a common Fermi momentum. Thus, analogously to what happens in BSC theory, the diquarks formed in the 2SC+s and CFL phases are conventional zero-momentum Cooper pairs.
For each quark forming a diquark, we have a contribution to the binding energy of the diquark pairing [51], where
is the mean chemical potential related to N quarks participating in the pairing. In the 2SC+s phase, four of the nine quarks (three flavors times three colors) form pairs while in the CFL phase all quarks form diquarks. The condensation terms that contribute to the pressure are given by
for the 2SC+s phase and by
in for the CFL phase.
In the case of the CFL phase, the nine quarks forming pairs give rise to a singlet and an octet state of quasi-particles (see Equation (18)) that satisfy the approximate relation [60].
Due to the breaking of the SU(3) symmetry in the subgroup , Equation (11) becomes
where the matrices are defined in color space as and
. The subscript i in Equation (19) accounts for the nine possible combinations of flavor and color, as given in Table 3. The quantities and are the chemical potentials associated with the color charges. For the 2SC+s phase, we consider because the symmetry that is broken in this phase is U(1), leaving the U(1) intact. Only u and d quarks carrying green and red colors are paired in the 2SC+s phase, while blue colored quarks do not participate in the formation of Cooper pairs. The vector condensate in that phase is .
Considering the possibility of diquark formation, Equation (13) is modified as
where is either given by Equation (17) or Equation (18), depending on which superconducting phase is being considered. The quantity is given by
or
where and are determined by minimizing Equation (20). Color charge neutrality is imposed by the conditions . The breaking of color symmetry increases the number of coupled equations that are to be solved in order to compute the quark matter EoS. The system of equations consists of nine coupled equations for the 2SC+s phase and twelve coupled equations for the CFL phase.
5. Results
The hybrid configurations studied in this work consist of an inner core, an outer core, and a crust. The latter has been modeled in out study by the Baym-Pethick-Sutherland (BPS) and Baym-Bethe-Pethick (BBP) EoSs [61,62].
The FCM model has already been used in several works to model the inner cores of HSs [34,43,63,64,65,66]. In these studies, the parameter space (, ) of the model has been analyzed by accounting for constraints from Lattice QCD simulations, the existence of pulsars, as well as the limits set by the gravitational-wave event GW170817. In our work, we expand the (, ) space by accounting for vector interactions and color superconductivity, which introduces the additional parameters and , respectively. To investigate this new parameter space spanned by , , , , we have chosen MeV and GeV, following the results presented in Ref. [34]; these values for and are qualitatively representative of the parameters space. In this way, we focus our attention on the values of and .
In this context, it should be mentioned that one of the methods used to combine and analyze different sets of data is Bayesian analysis, which analyzes the ranges of parameters using probability techniques. The application of Bayesian methods is frequently used in astrophysics (e.g., neutron star physics [67,68]), particularly when dealing with large data sets. A Bayesian analysis of the parameters of our model, however, is out of the scope of this paper.
To calculate the properties of HSs, such as gravitational mass, radius, tidal deformability and study their stability under slow and rapid conversion of hadronic matter to quark matter, we solve the relativistic hydrostatic equilibrium equation of Tolman, Oppenheimer, and Volkoff (TOV) [69,70].
5.1. Analysis of the FCM Parameter Space Spanned by , , ,
We start by analyzing the effects of varying and values on the EoSs and the mass-radius relationship (M–R) of HSs shown in Figure 1, Figure 2, Figure 3 and Figure 4. All the hybrid EoSs shown in these figures satisfy the constraints presented in [42]; besides, these EoSs have one common characteristic feature, namely that the hadron-quark transition pressure must be larger than about 200 MeV fm so that the -mass constraint condition can be satisfied.
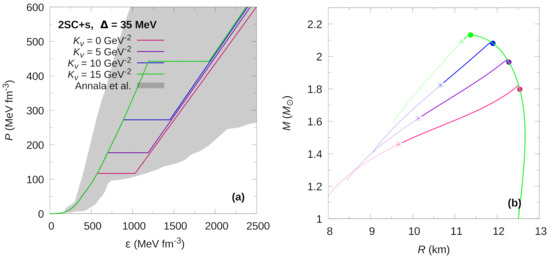
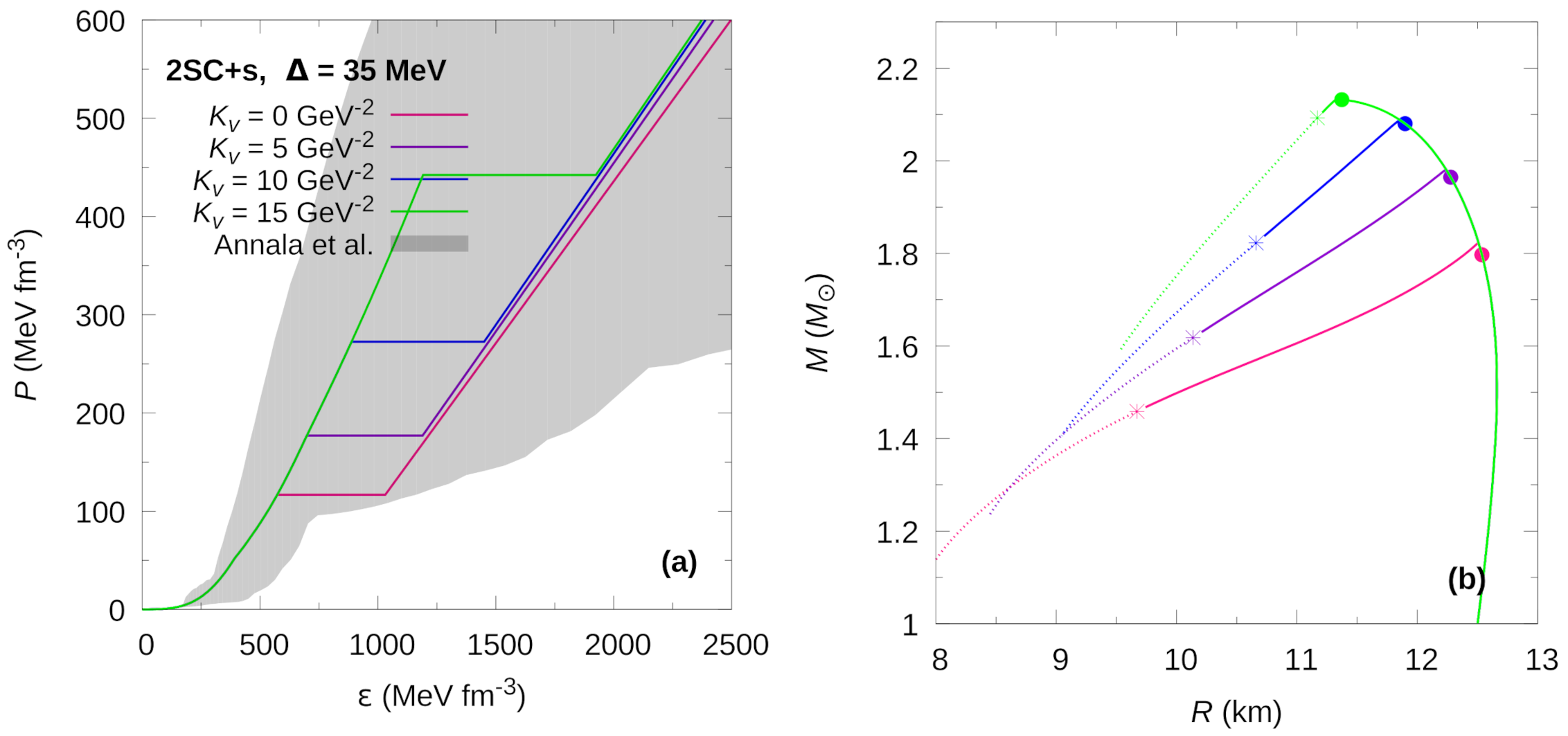
Figure 1.
(Color online) Hybrid EoS (panel (a)) and mass-radius relationship (panel (b)) for the 2SC+s phase at fixed gap value of MeV, for different values of the parameter. In panel (a), the grey region shows the constraints presented in [42]. The solid dots in panel (b) indicate the appearance of the color superconducting phase, just before the maximum mass peak. For rapid conversions, the stellar configurations to the left of each maximum mass are unstable and the existence of HSs is only marginal. For slow conversions, an extended stability branch exists. The stable configurations are shown by continuous lines. The terminal configurations are marked with asterisks.
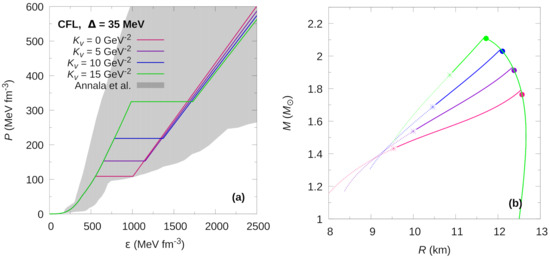
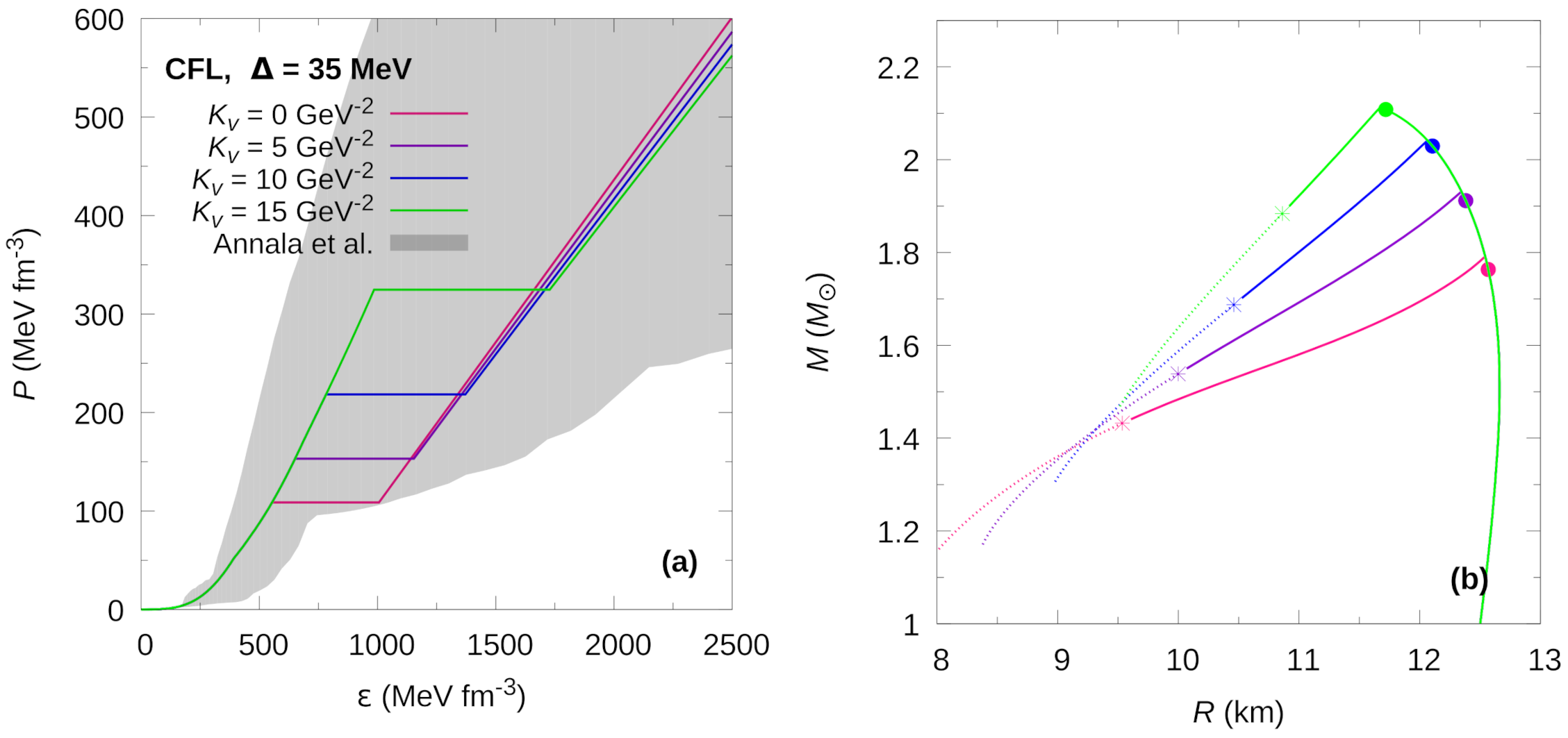
Figure 2.
Hybrid EoS (panel (a)) and mass-radius relationship (panel (b)) for the CFL phase at fixed gap value of MeV, for different values of the parameter. In panel (a), the grey region shows the constraints presented in [42]. The solid dots in panel (b) indicate the appearance of the color superconducting phase, just before the maximum mass peak. For rapid conversions, the stellar configurations to the left of each maximum mass are unstable and the existence of HSs is only marginal. For slow conversions, an extended stability branch exists. The stable configurations are shown by continuous lines. The terminal configurations are marked with asterisks.
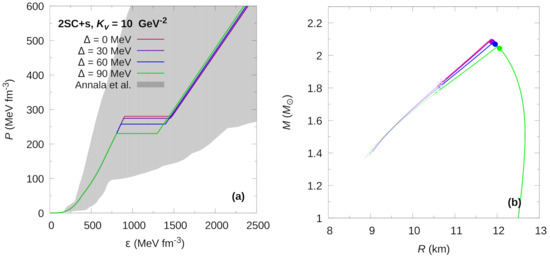
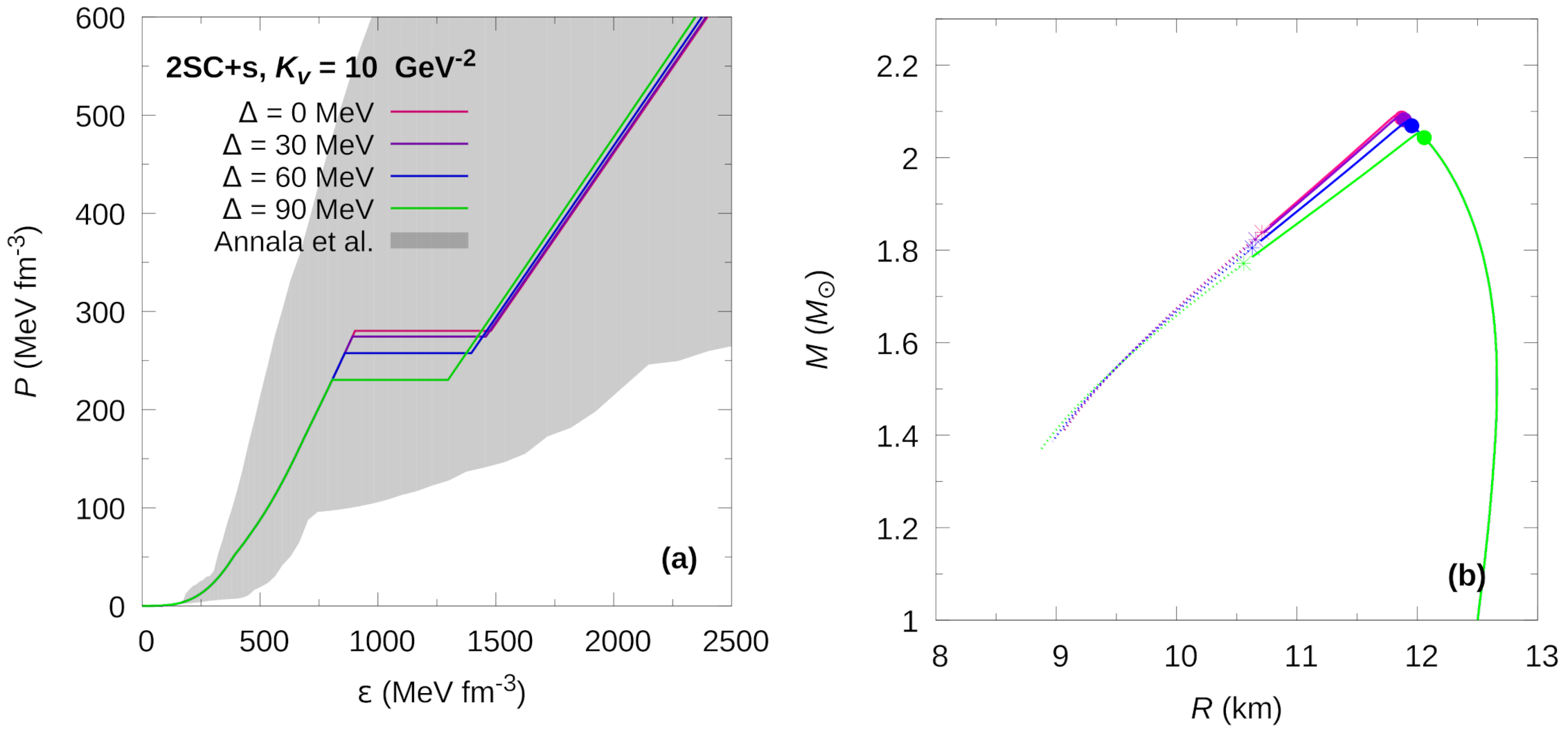
Figure 3.
Hybrid EoS (panel (a)) and mass-radius relationship (panel (b)) for the 2SC+s phase at fixed gap value of GeV, for different values of the parameter. In panel (a), the grey region shows the constraints presented in [42]. The solid dots in panel (b) indicate the appearance of the color superconducting phase, just before the maximum mass peak. For rapid conversions, the stellar configurations to the left of each maximum mass are unstable and the existence of HSs is only marginal. For slow conversions, an extended stability branch exists. The stable configurations are shown by continuous lines. The terminal configurations are marked with asterisks.
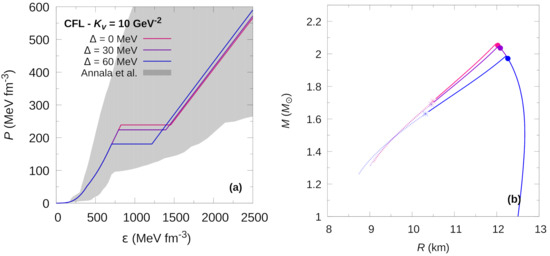
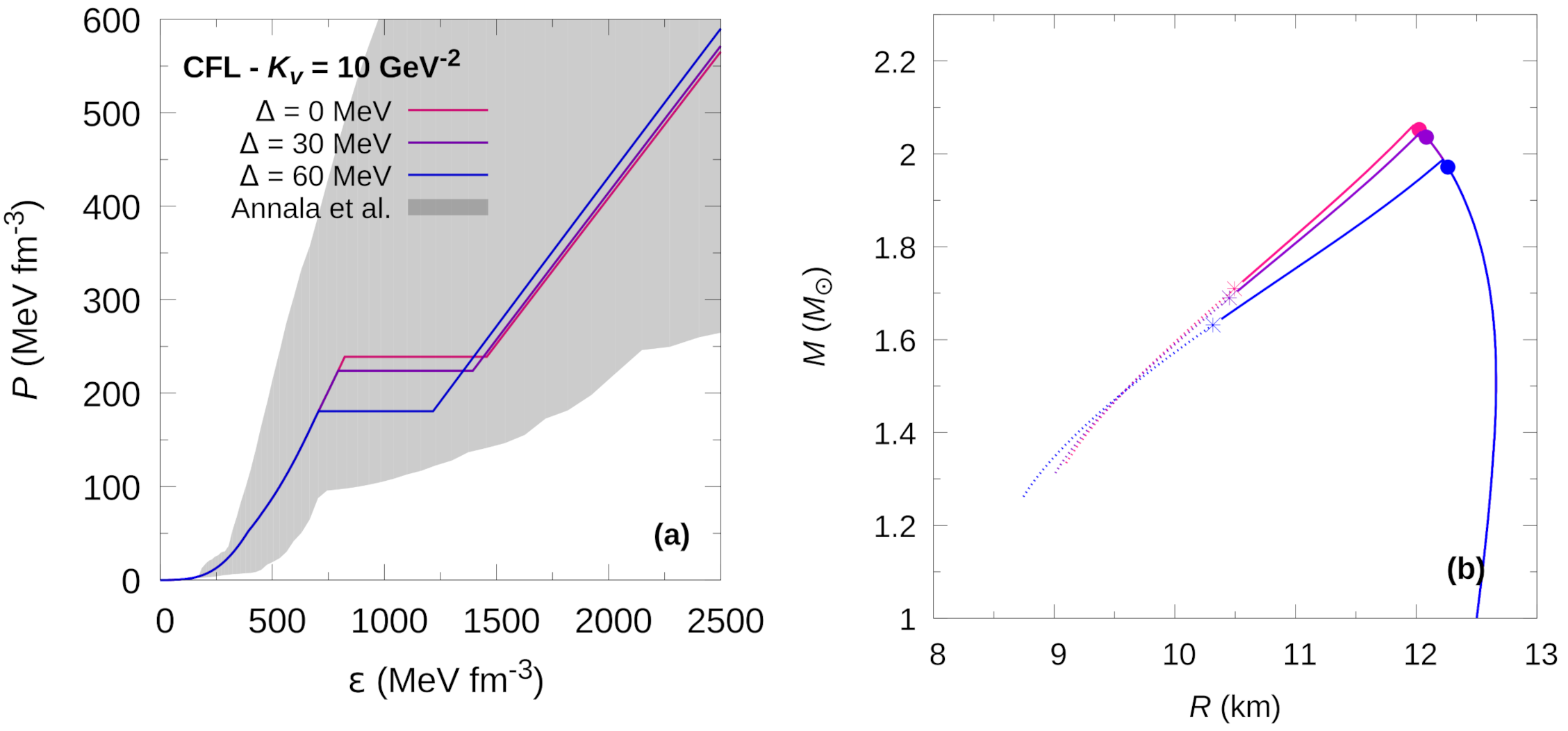
Figure 4.
(Hybrid EoS) (panel (a)) and mass-radius relationship (panel (b)) for the CFL phase at fixed gap value of GeV, for different values of the parameter. In panel (a), the grey region shows the constraints presented in [42]. The solid dots in panel (b) indicate the appearance of the color superconducting phase, just before the maximum mass peak. For rapid conversions, the stellar configurations to the left of each maximum mass are unstable and the existence of HSs is only marginal. For slow conversions, an extended stability branch exists. The stable configurations are shown by continuous lines. The terminal configurations are marked with asterisks.
This has direct implications for the appearance of quark Matter in the cores of HSs. A comprehensive study of the range of values of and (including the values of and ) shows that only a rapid conversion of hadronic matter to quark matter destabilized HSs. This finding is independent of the type of the color superconducting phase and is in agreement with the results obtained in a previous study of HSs, where quark matter was modeled with NJL-type models [71].
In Figure 1 and Figure 2 we show the hybrid EoSs and the corresponding M–R relationships of HSs computed for the 2SC+s and CFL phases. The value for the superconducting gap is MeV, and the values range from zero to 15 GeV. In panels (a), we see how the pressure at which the phase transition occurs increases and the energy density gap widens as increases. For the 2SC+s EoS (Figure 1) the increase in stiffens the EoS of the color superconducting phase, which in turn increases the speed of sound () in that phase. On the contrary, for the CFL EoS (Figure 2) we find that increasing values of lead to decreasing speeds of sound.
The solid dots shown in the M–R relationships shown in panels (b) of Figure 1 and Figure 2 mark the appearance of color superconducting quark matter cores of these stars. Most interestingly, the appearance of such matter does not destabilize the stars if the conversions from hadronic matter to quark matter proceed slowly. Instead, such stars remain stable over an extended regime in the M–R diagram. Their final termination points are marked with asterisks in Figure 1 and Figure 2).
In Figure 3 and Figure 4, we present the EoSs and M–R relationships of HSs with 2SC+s and CFL matter in their cores, but for which the value of is kept constant while the diquark energy gap taken on several different values. We can see that varying the value of in the 2SC+s phase has little impact on the hybrid EoS. For the CFL phase, however, the impact is more pronounced. In both cases, the speed of sound in the quark superconducting phase does not change significantly with changes in . An increase in leads to a somewhat smaller changes in energy density in the transition region. This effect is more noticeable in the CFL phase than in the the 2SC+s phase. The main differences appear in the transition pressure where a higher value of leads to a lower transition pressure. This, of course, has consequences for the appearance of superconducting quark cores in HSs and, in particular, reverberates on the extended stable branch of HSs, panels (b) of Figure 3 and Figure 4. One common feature is that the increase of the value of leads to a shortening of the extended branch of stable compact objects.
5.2. Astrophysical Constraints
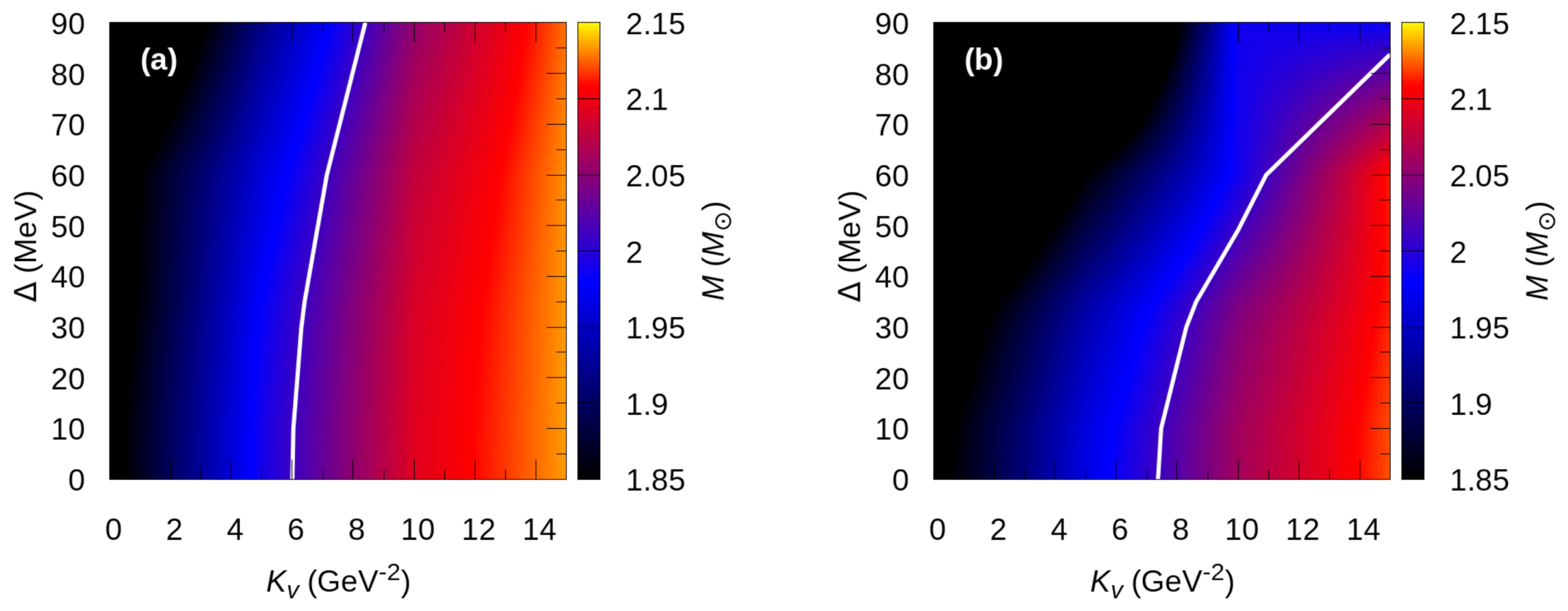
In Figure 5, we explore the maximum-mass values of HSs in the - plane. Panel (a) shows the results for 2SC+s stars while panel (b) is for CFL stars. The gravitational mass constraint imposed by PSR J1614-2230, PSR J0348+0432, and PSR J0740+6620 is shown by the white curve. It can be seen that our models satisfy this mass constraint for a wide range of and values. A combination of such values is compiled in Table 4, which will be used for subsequent investigations below. It is worth noting that HSs with MeV and GeV do not satisfy the = constraint unless vector interactions and color superconductivity are included in the model. Furthermore, the possibility of obtaining sufficiently massive HSs with color superconducting quark matter in their cores increases if increases, for a wide range of values. This is most noticeable in panel (b) for stars with a CFL core. Comparing panels (a) and (b) with each other shows that the parameter space that leads to sufficiently massive HSs with 2SC+s cores is narrower. For the 2SC+s phase, shown in panel (a), stars with (along the white curve) correspond to values that scatter around 7 GeV. This situation is quite different when the CFL phase is considered (see panel (b) in Figure 5) where it is shown that the maximum masses depend on both and rather strongly.
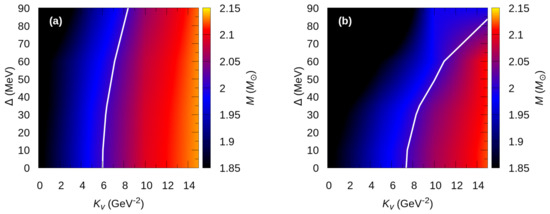
Figure 5.
(Text) Maximum mass of stars as a function of and , for the 2SC+s quark matter (panel (a)) and CFL quark matter (panel (b)). The white curve marks the maximum mass constraint .

Table 4.
Selected sets of parameters for the quark matter EoS.
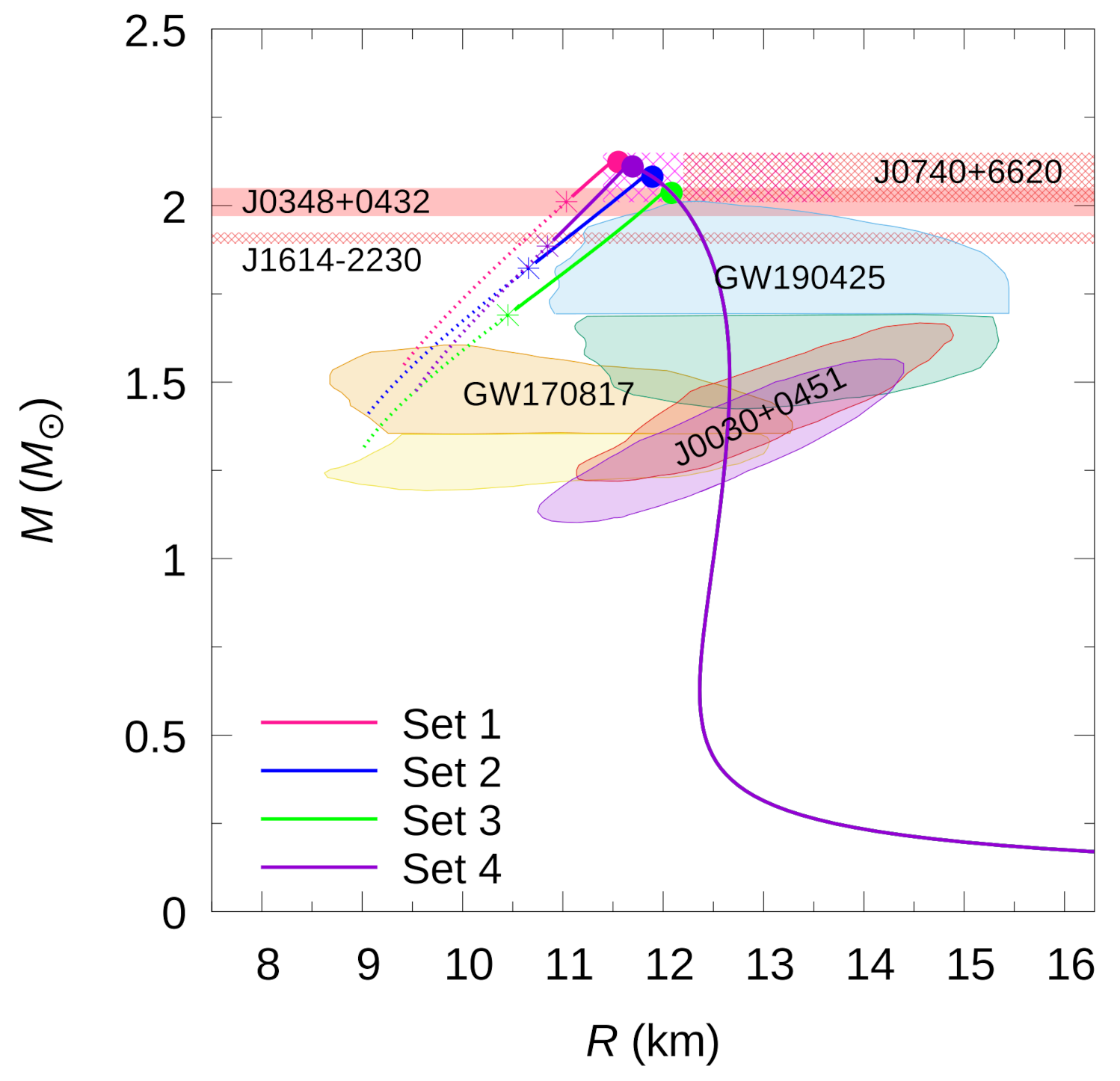
In Figure 6, we show the M-R curves that correspond to hybrid star configurations constructed with EoSs whose parameters are listed in Table 4. These curves are consistent with the mass constraint set by massive pulsars, NICER observations, as well as the NS data extracted from the gravitational-wave event GW170817 and GW190425. We see that, when assuming slow hadron-quark conversion, each model predicts the existence of high-mass twin stars. And because of this possibility, the observed pulsars could be either NSs or HSs. The radii of the latter could be up to 1.5 km smaller than those of the NSs. Furthermore, for parameter set 3 of Table 4 we find that the corresponding extended hybrid-star branch could even explain the stellar high-mass component of the GW190425 binary system [6].
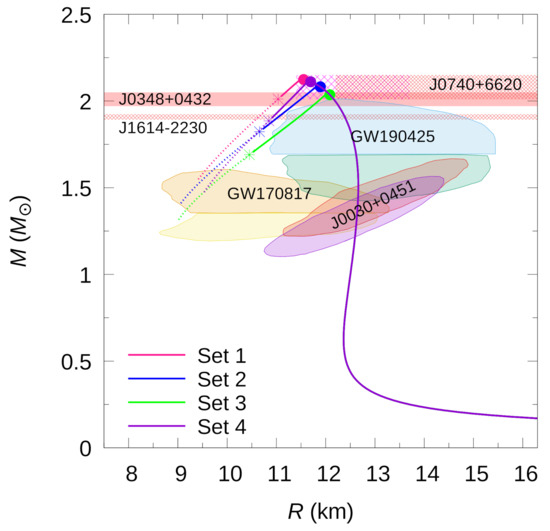
Figure 6.
(Color online) M–R relationship of the selected EoSs (Table 4) of this work. The solid dots indicate the appearance of color superconducting quark matter in HSs, which happens just before the maximum-mass peaks are reached. For a rapid conversion of matter, the stellar configurations to the left of each maximum-mass star are unstable. For slow conversions there exist extended branches of stable stars which end at the locations marked with asterisks. The shaded regions (clouds) correspond to constraints imposed by GW170817, GW190425, and NICER observations of PSR J0030+0451. The horizontal pink stripped bands, indicate constraints imposed by pulsars J0740+6620, J0348+0432, and J1614-2230.
We have also explored the possibility of sequential phase transitions between the two different quark matter EoSs, i.e., the occurrence of a transition of quark matter from the 2SC+s to the CFL phase. We find that such a sequential transition is possible, but the M–R relationships do not fulfill mass constraint. The main reasons for this is a low speed of sound of in the extended FCM EoS and a high phase transition pressure.
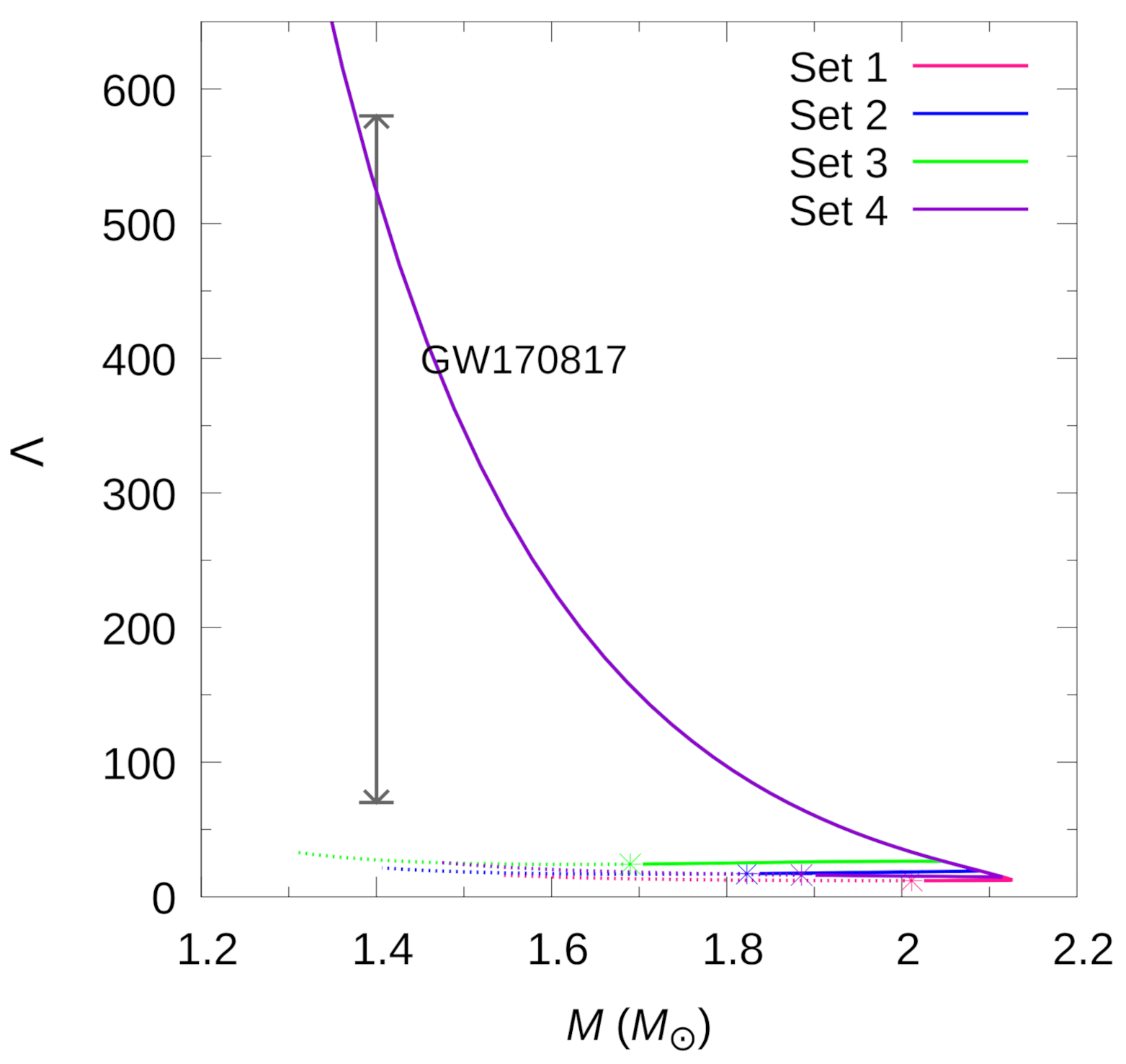
In Figure 7, we present the dimensionless tidal deformability, , as a function of gravitational mass for the stellar hybrid configurations of Figure 6. All models present pure hadronic stars for masses , and are consistent with the constraint deduced from GW170817. One also sees that the HSs along the twin stellar branch have tidal deformabilities that lie on an almost straight horizontal line. This opens up the possibility that future observations of NS mergers may help to shed light on the actual existence of twin stars and hence on the behavior of matter in the inner cores of compact objects.
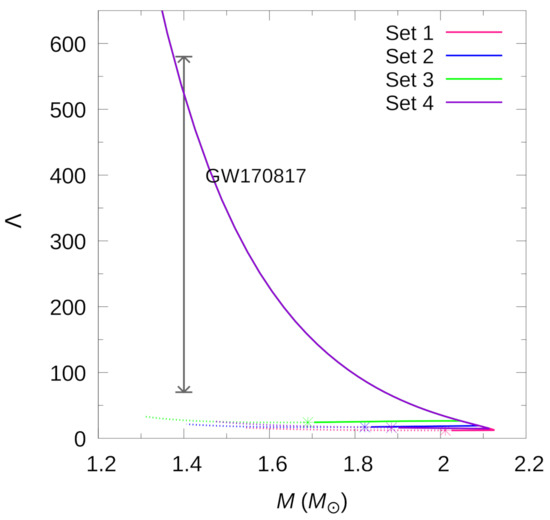
Figure 7.
(Color online) Dimensionless tidal deformability as a function of gravitational mass, with the constraint obtained from GW170817 [5]. Stable stellar configurations beyond the maximum mass have very small values of , which are almost independent of mass. The positions of the terminal stars of the twin HSs branch (obtained for slow hadron-quark conversion) are marked with asterisks.
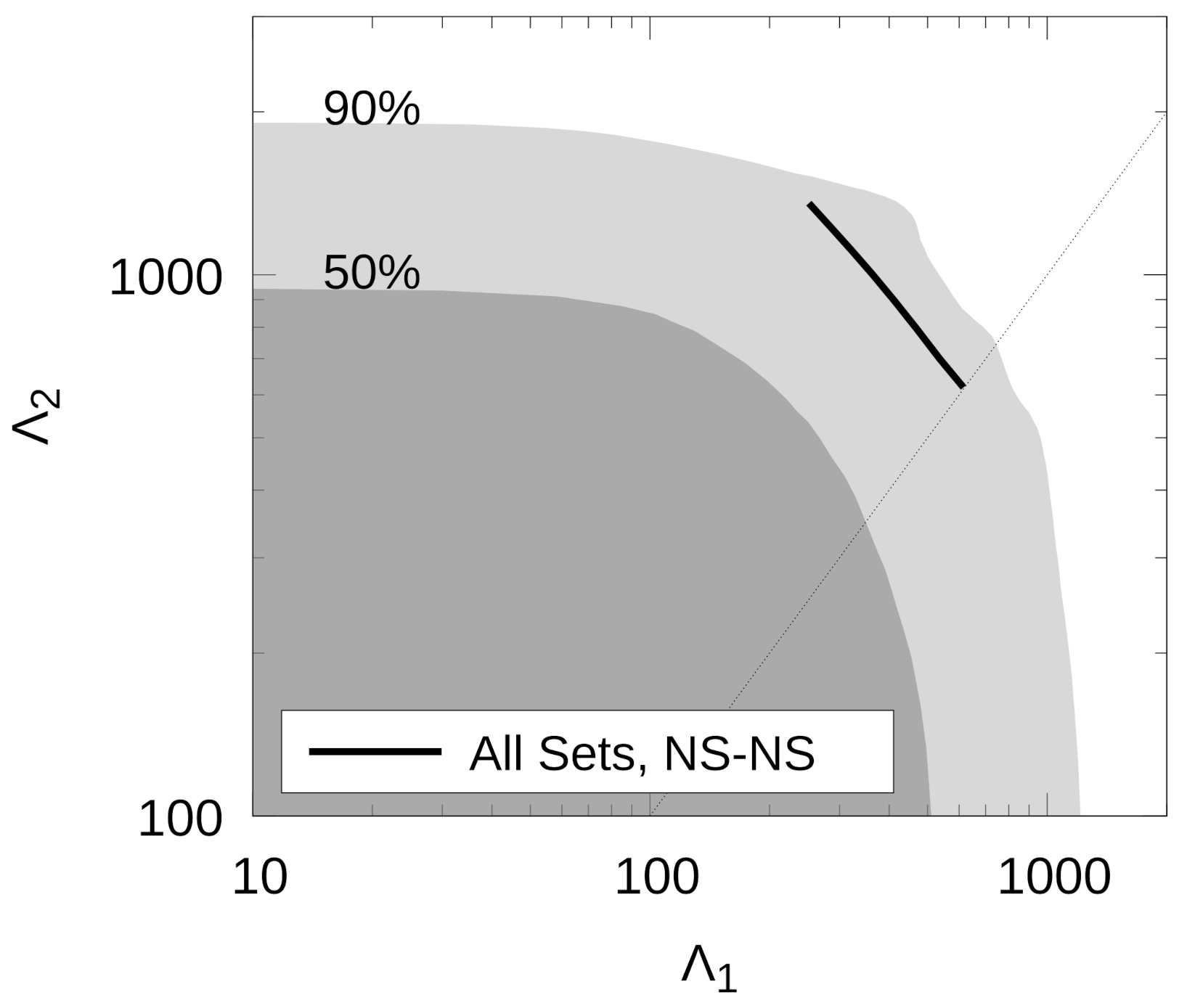
In Figure 8, we show the individual dimensionless tidal deformabilities of the hybrid configurations consistent with the observational constraints obtained after GW170817 and its electromagnetic counterpart. The black line represents the situation in which the two merging objects are purely hadronic NSs.
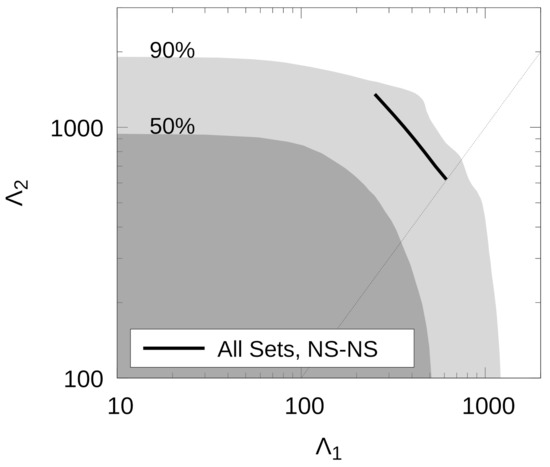
Figure 8.
Text Dimensionless tidal deformabilities and for the selected EoSs. The solid black line represents the results obtained for a purely hadronic NS-NS merger with masses consistent with data from GW170817. The dark (light) gray areas represent the 50% (90%) confidence limit of the probability contour of GW170817 and the dotted line corresponds to .
6. Summary and Conclusions
In this work, we have studied hybrid EoSs and the structure of HSs considering the effects of color superconductivity (2SC+s and CFL phases) and vector interactions in quark matter in the framework of the FCM model. Both color superconductivity and vector interactions were included in the model in a phenomenological way, taking advantage of the similarity of the FCM with the MIT bag model at the zero temperature limit. For the description of the hadronic phase, we used the SW4L parametrization of the RMF model. We have assumed a sharp hadron-quark phase transition and considered the the implications of slow versus rapid conversions of matter at the hadron-quark interface. This assumption dramatically modifies the traditional picture of stability in the M–R diagram of HSs. For instance, if we consider a soft Gibbs phase transition, instead of a Maxwell sharp transition, the extended stable branch does not exist. Since in the Gibbs case the EoS has no discontinuity or jump, the stability criterion for hybrid stars is the traditional one, in which case indicates unstable configurations and the maximum mass configuration is the last stable star in the mass-radius diagrams.
After extending the parameter space of the FCM model, we performed a systematic analysis of the parameters of this new space. The goal was to find out whether the parameters lead to equations of state that are consistent with present astrophysical observations. For this purpose we investigated the dependencies of the EoS and the M–R relationship of compact stars on the and parameters, which are related to vector interactions and color superconductivity of the extended FCM model. Fixed values were assumed for the other two parameters, and , of the model. As our investigations show, the hybrid EoSs we determined successfully satisfy the constraints set by Annala et al. [42] and by PSR J1614-2230, PSR J0348+0432, PSR J0740+6620, GW170817, GW190425, and NICER observations.
In addition, using a specific FCM model parameter set, we have shown that the inclusion of vector interactions and color superconductivity plays a central role in satisfying the mass constraint set by massive pulsars. Specifically, we found that increasing leads to a stiffer hybrid EoS, which increases the maximum stellar mass. However, this increase leads to shorter stability branches for the twin stars. In contrast, an increase in the parameter leads to softer EoSs, both for the 2SC+s and CFL phase, which lowers the maximum mass but leads to extended branches of stellar stability. In general, changes in the value of have a more pronounced effect on the system properties than changes in . An exception is the CFL phase, where changes in dominate the mass-radius relationship.
We have also explored the possibility of a sequential phase transition in HSs. We have found that although that possibility exists, the hybrid configurations obtained from these EoSs do not satisfy the restrictions imposed by massive pulsars. This is due to a low speed of sound in the quark phase and a high value of the hadron-quark transition pressure. It is worth a short discussion of this point since the authors of Refs. [72,73] obtained HSs with sequential phase transitions in the constant speed of sound framework, which fulfill the mass constraint. This was possible by using a parametric EoS for the quark phase and by fixing the hadron-quark phase transition pressure (at MeV fm) as well as the quark-quark phase transition pressure (at MeV fm). Furthermore, a high value of the speed of sound in quark matter phases () was assumed in that paper.
Massive HSs with sequential phase transitions were also obtained with Nambu-Jona-Lasinio type models of quark matter [74,75]. However, extra ingredients are needed in these models to achieve a hadron-quark followed by a quark-quark phase transition, because in these models . Besides that, an effective bag can be added to the model to lower the transition pressure, considering a large diquark coupling [74]. In these works, the transition pressures (i.e., to 60 MeV fm for the hadron-quark transition and to 130 MeV fm for the quark-quark transition) are lower than in Ref. [72]. In a recent study [31] it was shown that in NJL models a higher speed of sound can be achieved through the incorporation of higher-order repulsive interactions. This affects the size of the quark core in HSs, leading to massive hybrid configurations with extended cores of quark matter in the rapid conversion scenario.
Regarding the tidal deformability results, our models satisfy the GW170817 constraint of a star. Also the restrictions coming from the constraints in the – plane are fulfilled. In this case, the purely hadronic branch already lies, for all four parameters sets of Table 4, inside the confidence region. Remarkably, the slow hadron-quark conversion scenario, which leads to new stable hybrid-star branches, helps to satisfy astrophysical constraints (similar conclusions have already been presented in Refs. [43,54,73]).
Author Contributions
Conceptualization, D.C., A.F.R.-S., M.M., M.G.O.; methodology, A.F.R.-S., M.M., M.G.O.; investigation, D.C., A.F.R.-S., M.M., M.G.O., F.W.; writing—original draft preparation, D.C., A.F.R.-S., M.M., M.G.O.; writing—review and editing, F.W.; supervision, F.W. All authors have read and agreed to the published version of the manuscript.
Funding
D.C. is a fellow of UNLP. D.C., I.F.R.-S., M.M. and M.G.O. thank CONICET and UNLP (Argentina) for financial support under grants PIP-0714 and G157, G007. I.F.R.-S. is also partially supported by PICT 2019-0366 from ANPCyT (Argentina). I.F.R.-S., M.G.O. and F.W. are supported by the National Science Foundation (USA) under Grants PHY-2012152.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
The authors would like to thank V. Dexheimer and R. Negreiros for inviting us to submit a contribution to the Special Issue of Universe entitled “Properties and Dynamics of Neutron Stars and Proto-Neutron Stars”.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lattimer, J.M.; Prakash, M. The Physics of Neutron Stars. Science 2004, 304, 536–542. [Google Scholar] [CrossRef] [PubMed]
- Pons, J.A.; Reddy, S.; Prakash, M.; Lattimer, J.M.; Miralles, J.A. Evolution of Proto-Neutron Stars. Astrophys. J. 1999, 513, 780–804. [Google Scholar] [CrossRef]
- Potekhin, A.Y. The physics of neutron stars. Phys.-Uspekhi 2010, 53, 1235–1256. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. [The LIGO Scientific Collaboration and the Virgo Collaboration]. GW170817: Measurements of Neutron Star Radii and Equation of State. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. [The LIGO Scientific Collaboration and the Virgo Collaboration]. Properties of the binary neutron star merger GW170817. Phys. Rev. X 2019, 9, 011001. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GW190425: Observation of a Compact Binary Coalescence with Total Mass ∼ 3.4 M⊙. Astrophys. J. Lett. 2020, 892, L3. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Ray, P.S.; Bogdanov, S.; Guillot, S.; Morsink, S.M.; Bilous, A.V.; Arzoumanian, Z.; Choudhury, D.; Deneva, J.S.; et al. A NICER View of the Massive Pulsar PSR J0740+6620 Informed by Radio Timing and XMM-Newton Spectroscopy. Astrophys. J. Lett. 2021, 918, L27. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Ho, W.C.G.; Lattimer, J.M.; Loewenstein, M.; et al. The Radius of PSR J0740+6620 from NICER and XMM-Newton Data. Astrophys. J. Lett. 2021, 918, L28. [Google Scholar] [CrossRef]
- Baym, G.; Hatsuda, T.; Kojo, T.; Powell, P.D.; Song, Y.; Takatsuka, T. From hadrons to quarks in neutron stars: A review. Rept. Prog. Phys. 2018, 81, 056902. [Google Scholar] [CrossRef]
- Orsaria, M.G.; Malfatti, G.; Mariani, M.; Ranea-Sandoval, I.F.; García, F.; Spinella, W.M.; Contrera, G.A.; Lugones, G.; Weber, F. Phase transitions in neutron stars and their links to gravitational waves. J. Phys. G 2019, 46, 073002. [Google Scholar] [CrossRef]
- Weber, F. Pulsars as Astrophysical Laboratories for Nuclear and Particle Physics; Series in High Energy Physics, Cosmology and Gravitation; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar] [CrossRef]
- Weber, F. Strange quark matter and compact stars. Prog. Part. Nucl. Phys. 2005, 54, 193–288. [Google Scholar] [CrossRef]
- Demorest, P.; Pennucci, T.; Ransom, S.; Roberts, M.; Hessels, J. Shapiro Delay Measurement of A Two Solar Mass Neutron Star. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef]
- Arzoumanian, Z.; Brazier, A.; Burke-Spolaor, S.; Chamberlin, S.; Chatterjee, S.; Christy, B.; Cordes, J.M.; Cornish, N.J.; Crawford, F.; Cromartie, H.T.; et al. The NANOGrav 11-year Data Set: High-precision Timing of 45 Millisecond Pulsars. Astrophys. J. Suppl. Ser. 2018, 235, 37. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; Van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 6131. [Google Scholar] [CrossRef] [PubMed]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2020, 4, 72–76. [Google Scholar] [CrossRef]
- Tews, I.; Margueron, J.; Reddy, S. Critical examination of constraints on the equation of state of dense matter obtained from GW170817. Phys. Rev. C 2018, 98, 045804. [Google Scholar] [CrossRef]
- Shibata, M.; Zhou, E.; Kiuchi, K.; Fujibayashi, S. Constraint on the maximum mass of neutron stars using GW170817 event. Phys. Rev. D 2019, 100, 023015. [Google Scholar] [CrossRef]
- Farrow, N.; Zhu, X.J.; Thrane, E. The Mass Distribution of Galactic Double Neutron Stars. Astrophys. J. 2019, 876, 18. [Google Scholar] [CrossRef]
- Gompertz, B.P.; Cutter, R.; Steeghs, D.; Galloway, D.K.; Lyman, J.; Ulaczyk, K.; Dyer, M.J.; Ackley, K.; Dhillon, V.S.; O’Brien, P.T.; et al. Searching for electromagnetic counterparts to gravitational-wave merger events with the prototype Gravitational-Wave Optical Transient Observer (GOTO-4). Mon. Not. R. Astron. Soc. 2020, 497, 726–738. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Bogdanov, S.; Ray, P.S.; Ludlam, R.M.; Guillot, S.; Arzoumanian, Z.; Baker, C.L.; Bilous, A.V.; Chakrabarty, D.; et al. A NICER View of PSR J0030+0451: Millisecond Pulsar Parameter Estimation. Astrophys. J. Lett. 2019, 887, L21. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Harding, A.K.; Ho, W.C.G.; Lattimer, J.M.; et al. PSR J0030+0451 Mass and Radius from NICER Data and Implications for the Properties of Neutron Star Matter. Astrophys. J. Lett. 2019, 887, L24. [Google Scholar] [CrossRef]
- Rajagopal, K.; Frank Wilczek, F. The condensed matter physics of QCD. In At the Frontier of Particle Physics; World Scientific: Singapore, 2001; pp. 2061–2151. [Google Scholar]
- Alford, M.G. Color superconducting quark matter. Ann. Rev. Nucl. Part. Sci. 2001, 51, 131–160. [Google Scholar] [CrossRef]
- Alford, M.G.; Schmitt, A.; Rajagopal, K.; Schäfer, T. Color superconductivity in dense quark matter. Rev. Mod. Phys. 2008, 80, 1455–1515. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Microscopic Theory of Superconductivity. Phys. Rev. 1957, 106, 162–164. [Google Scholar] [CrossRef]
- Ranea-Sandoval, I.F.; Orsaria, M.G.; Han, S.; Weber, F.; Spinella, W.M. Color superconductivity in compact stellar hybrid configurations. Phys. Rev. C 2017, 96, 065807. [Google Scholar] [CrossRef]
- Lugones, G.; Horvath, J.E. High-density QCD pairing in compact star structure. Astron. Astrophys. 2003, 403, 173–178. [Google Scholar] [CrossRef]
- Orsaria, M.; Rodrigues, H.; Weber, F.; Contrera, G.A. Quark deconfinement in high-mass neutron stars. Phys. Rev. C 2014, 89, 015806. [Google Scholar] [CrossRef]
- Klähn, T.; Fischer, T. Vector interaction enhanced bag model for astrophysical applications. Astrophys. J. 2015, 810, 134. [Google Scholar] [CrossRef]
- Ferreira, M.; Pereira, R.C.; Providência, C. Quark matter in light neutron stars. Phys. Rev. D 2020, 102, 083030. [Google Scholar] [CrossRef]
- Simonov, Y.A.; Trusov, M.A. Deconfinement transition for nonzero baryon density in the field correlator method. JETP Lett. 2007, 85, 598–601. [Google Scholar] [CrossRef]
- Nefediev, A.V.; Simonov, Y.A.; Trusov, M.A. Deconfinement and Quark—Gluon plasma. Int. J. Mod. Phys. E 2009, 18, 549–599. [Google Scholar] [CrossRef]
- Mariani, M.; Orsaria, M.; Vucetich, H. Constant entropy hybrid stars: A first approximation of cooling evolution. Astron. Astrophys. 2017, 601, A21. [Google Scholar] [CrossRef]
- Malfatti, G.; Orsaria, M.G.; Contrera, G.A.; Weber, F.; Ranea-Sandoval, I.F. Hot quark matter and (proto-) neutron stars. Phys. Rev. C 2019, 100, 015803. [Google Scholar] [CrossRef]
- Pereira, J.P.; Flores, C.V.; Lugones, G. Phase Transition Effects on the Dynamical Stability of Hybrid Neutron Stars. Astrophys. J. 2018, 860, 12. [Google Scholar] [CrossRef]
- Voskresensky, D.; Yasuhira, M.; Tatsumi, T. Charge screening at first order phase transitions and hadron quark mixed phase. Nucl. Phys. A 2003, 723, 291–339. [Google Scholar] [CrossRef]
- Endo, T. Region of hadron-quark mixed phase in hybrid stars. Phys. Rev. C 2011, 83, 068801. [Google Scholar] [CrossRef]
- Wu, X.; Shen, H. Nuclear symmetry energy and hadron-quark mixed phase in neutron stars. Phys. Rev. C 2019, 99, 065802. [Google Scholar] [CrossRef]
- Maslov, K.; Yasutake, N.; Blaschke, D.; Ayriyan, A.; Grigorian, H.; Maruyama, T.; Tatsumi, T.; Voskresensky, D.N. Hybrid equation of state with pasta phases, and third family of compact stars. Phys. Rev. C 2019, 100, 025802. [Google Scholar] [CrossRef]
- Weber, F.; Farrell, D.; Spinella, W.M.; Malfatti, G.; Orsaria, M.G.; Contrera, G.A.; Maloney, I. Phases of Hadron-Quark Matter in (Proto) Neutron Stars. Universe 2019, 5, 169. [Google Scholar] [CrossRef]
- Annala, E.; Gorda, T.; Kurkela, A.; Nättilä, J.; Vuorinen, A. Evidence for quark-matter cores in massive neutron stars. Nat. Phys. 2020, 16, 907–910. [Google Scholar] [CrossRef]
- Mariani, M.; Orsaria, M.G.; Ranea-Sandoval, I.F.; Lugones, G. Magnetized hybrid stars: Effects of slow and rapid phase transitions at the quark-hadron interface. Mon. Not. R. Astron. Soc. 2019, 489, 4261–4277. [Google Scholar] [CrossRef]
- Bombaci, I.; Lugones, G.; Vidana, I. Effects of color superconductivity on the nucleation of quark matter in neutron stars. Astron. Astrophys. 2007, 462, 1017–1022. [Google Scholar] [CrossRef][Green Version]
- Haensel, P.; Zdunik, J.L.; Schaeffer, R. Phase transitions in dense matter and radial pulsations of neutron stars. A&A 1989, 217, 137–144. [Google Scholar]
- Bombaci, I.; Parenti, I.; Vidaña, I. Quark Deconfinement and Implications for the Radius and the Limiting Mass of Compact Stars. Astrophys. J. 2004, 614, 314–325. [Google Scholar] [CrossRef]
- Bombaci, I.; Logoteta, D.; Panda, P.K.; Providência, C.; Vidaña, I. Quark matter nucleation in hot hadronic matter. Phys. Lett. B 2009, 680, 448–452. [Google Scholar] [CrossRef]
- Lugones, G.; Grunfeld, A.G. Critical spectrum of fluctuations for deconfinement at protoneutron star cores. Phys. Rev. D 2011, 84, 085003. [Google Scholar] [CrossRef]
- Bombaci, I.; Logoteta, D.; Vidaña, I.; Providência, C. Quark matter nucleation in neutron stars and astrophysical implications. Eur. Phys. J. A 2016, 52, 58. [Google Scholar] [CrossRef]
- Glendenning, N.K. Neutron stars are giant hypernuclei? Astrophys. J. 1985, 293, 470–493. [Google Scholar] [CrossRef]
- Alford, M.; Rajagopal, K. Absence of two-flavor color-superconductivity in compact stars. J. High Energy Phys. 2002, 2002, 31. [Google Scholar] [CrossRef]
- Typel, S.; Wolter, H.H. Relativistic mean field calculations with density dependent meson nucleon coupling. Nucl. Phys. A 1999, 656, 331–364. [Google Scholar] [CrossRef]
- Spinella, W.M. A Systematic Investigation of Exotic Matter in Neutron Stars. Ph.D. Thesis, Claremont Graduate University & San Diego State University, Claremont, CA, USA, 2017. [Google Scholar]
- Malfatti, G.; Orsaria, M.G.; Ranea-Sandoval, I.F.; Contrera, G.A.; Weber, F. Delta baryons and diquark formation in the cores of neutron stars. Phys. Rev. D 2020, 102, 063008. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Lim, Y. Constraining the Symmetry Parameters of the Nuclear Interaction. Astrophys. J. 2013, 771, 51. [Google Scholar] [CrossRef]
- Lattimer, J.M. Neutron Star Mass and Radius Measurements. Universe 2019, 5, 159. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Brown, E.F.; Kim, Y.; Lynch, W.G.; Michaels, R.; Ono, A.; Piekarewicz, J.; Tsang, M.B.; Wolter, H.H. A way forward in the study of the symmetry energy: Experiment, theory, and observation. J. Phys. G Nucl. Part. Phys. 2014, 41, 093001. [Google Scholar] [CrossRef]
- Hofmann, F.; Keil, C.M.; Lenske, H. Application of the density dependent hadron field theory to neutron star matter. Phys. Rev. C 2001, 64, 025804. [Google Scholar] [CrossRef]
- Simonov, Y.; Trusov, M. Vacuum phase transition at nonzero baryon density. Phys. Lett. B 2007, 650, 36–40. [Google Scholar] [CrossRef]
- Shovkovy, I.A. Two Lectures on Color Superconductivity*. Found. Phys. 2005, 35, 1309–1358. [Google Scholar] [CrossRef]
- Baym, G.; Pethick, C.; Sutherland, P. The Ground State of Matter at High Densities: Equation of State and Stellar Models. Astrophys. J. 1971, 170, 299. [Google Scholar] [CrossRef]
- Baym, G.; Bethe, H.A.; Pethick, C.J. Neutron star matter. Nucl. Phys. A 1971, 175, 225–271. [Google Scholar] [CrossRef]
- Plumari, S.; Burgio, G.; Greco, V.; Zappala, D. Quark matter in neutron stars within the field correlator method. Phys. Rev. D 2013, 88, 083005. [Google Scholar] [CrossRef]
- Logoteta, D.; Bombaci, I. Quark deconfinement transition in neutron stars with the field correlator method. Phys. Rev. D 2013, 88, 063001. [Google Scholar] [CrossRef]
- Burgio, G.; Zappalà, D. Hybrid star structure with the Field Correlator Method. Eur. Phys. J. A 2016, 52, 1–14. [Google Scholar] [CrossRef][Green Version]
- Khanmohamadi, S.; Moshfegh, H.; Tehrani, S.A. Structure and tidal deformability of a hybrid star within the framework of the field correlator method. Phys. Rev. D 2020, 101, 123001. [Google Scholar] [CrossRef]
- Char, P.; Traversi, S.; Pagliara, G. A Bayesian Analysis on Neutron Stars within Relativistic Mean Field Models. Particles 2020, 3, 621–629. [Google Scholar] [CrossRef]
- Xie, W.J.; Li, B.A. Bayesian Inference of the Symmetry Energy of Superdense Neutron-rich Matter from Future Radius Measurements of Massive Neutron Stars. Astrophys. J. 2020, 899, 4. [Google Scholar] [CrossRef]
- Tolman, R.C. Static solutions of Einstein’s field equations for spheres of fluid. Phys. Rev. 1939, 55, 364–373. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G.M. On Massive Neutron Cores. Phys. Rev. 1939, 55, 374–381. [Google Scholar] [CrossRef]
- Ranea-Sandoval, I.F.; Han, S.; Orsaria, M.G.; Contrera, G.A.; Weber, F.; Alford, M.G. Constant-sound-speed parametrization for Nambu–Jona-Lasinio models of quark matter in hybrid stars. Phys. Rev. C 2016, 93, 045812. [Google Scholar] [CrossRef]
- Alford, M.; Sedrakian, A. Compact Stars with Sequential QCD Phase Transitions. Phys. Rev. Lett. 2017, 119, 161104. [Google Scholar] [CrossRef]
- Rodríguez, M.; Ranea-Sandoval, I.F.; Mariani, M.; Orsaria, M.G.; Malfatti, G.; Guilera, O. Hybrid stars with sequential phase transitions: The emergence of the g2 mode. J. Cosmol. Astropart. Phys. 2021, 2021, 9. [Google Scholar] [CrossRef]
- Pagliara, G.; Schaffner-Bielich, J. Stability of color-flavor-locking cores in hybrid stars. Phys. Rev. D 2008, 77, 063004. [Google Scholar] [CrossRef]
- Bonanno, L.; Sedrakian, A. Composition and stability of hybrid stars with hyperons and quark color-superconductivity. Astron. Astrophys. 2012, 539, A16. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).