Three-Dimensional MHD Modeling of Interplanetary Solar Wind Using Self-Consistent Boundary Condition Obtained from Multiple Observations and Machine Learning
Abstract
:1. Introduction
2. Materials and Methods
2.1. The MHD Numerical Model
2.2. Boundary Conditions Obtained from Multiple Observations and Machine Learning
3. Results
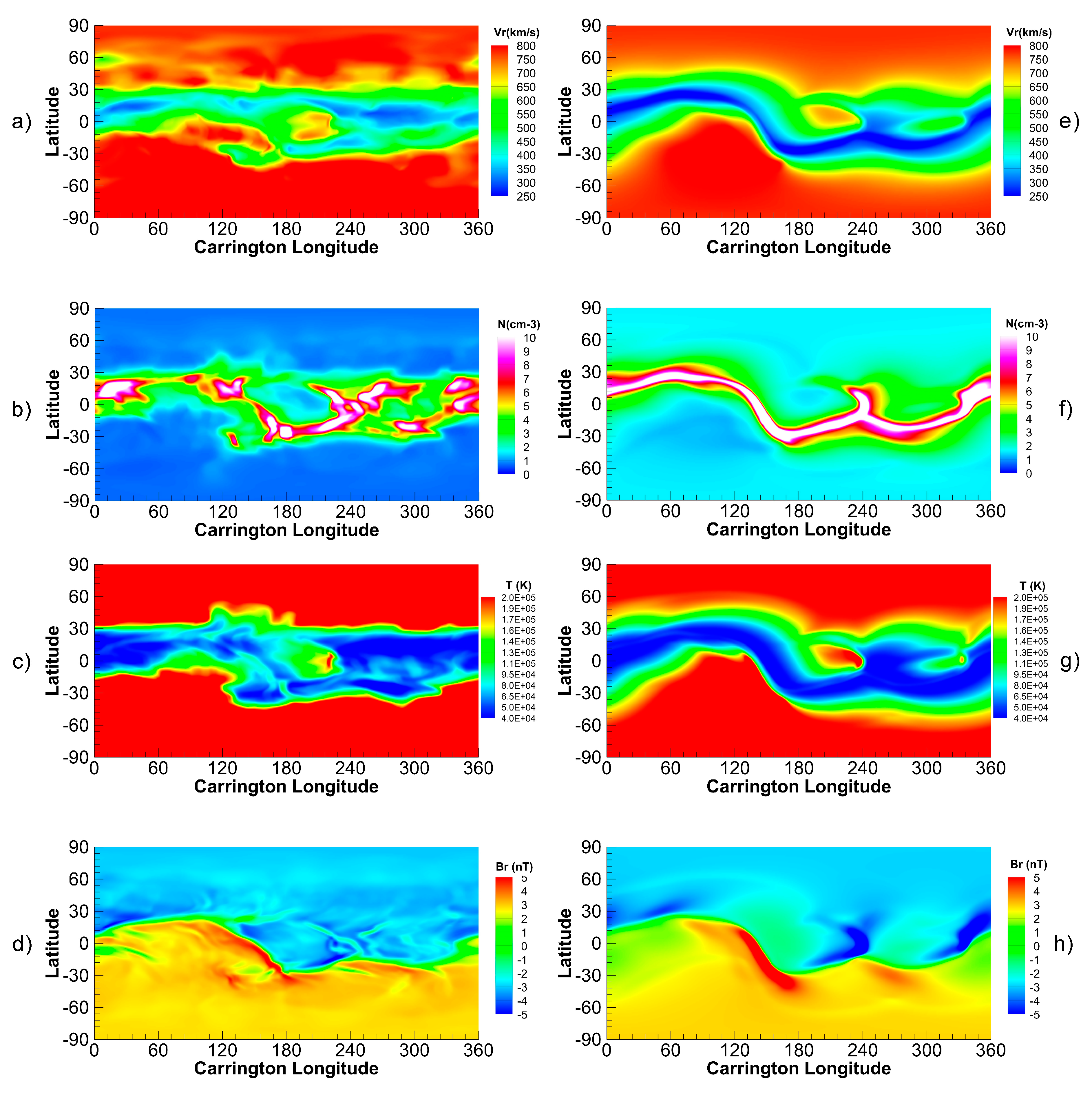
3.1. Analyses of the Modeled Solar Wind Parameters at 1AU
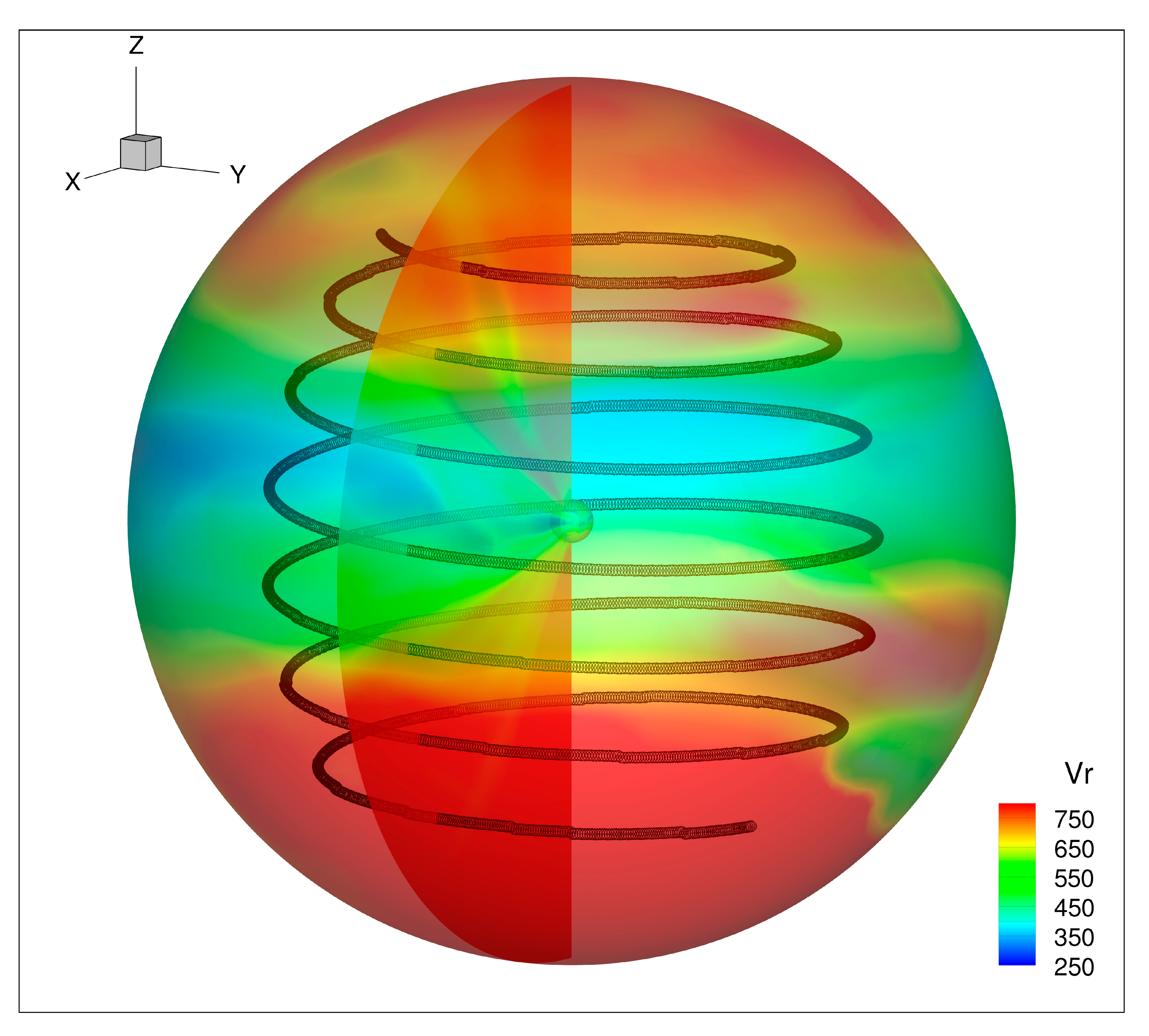
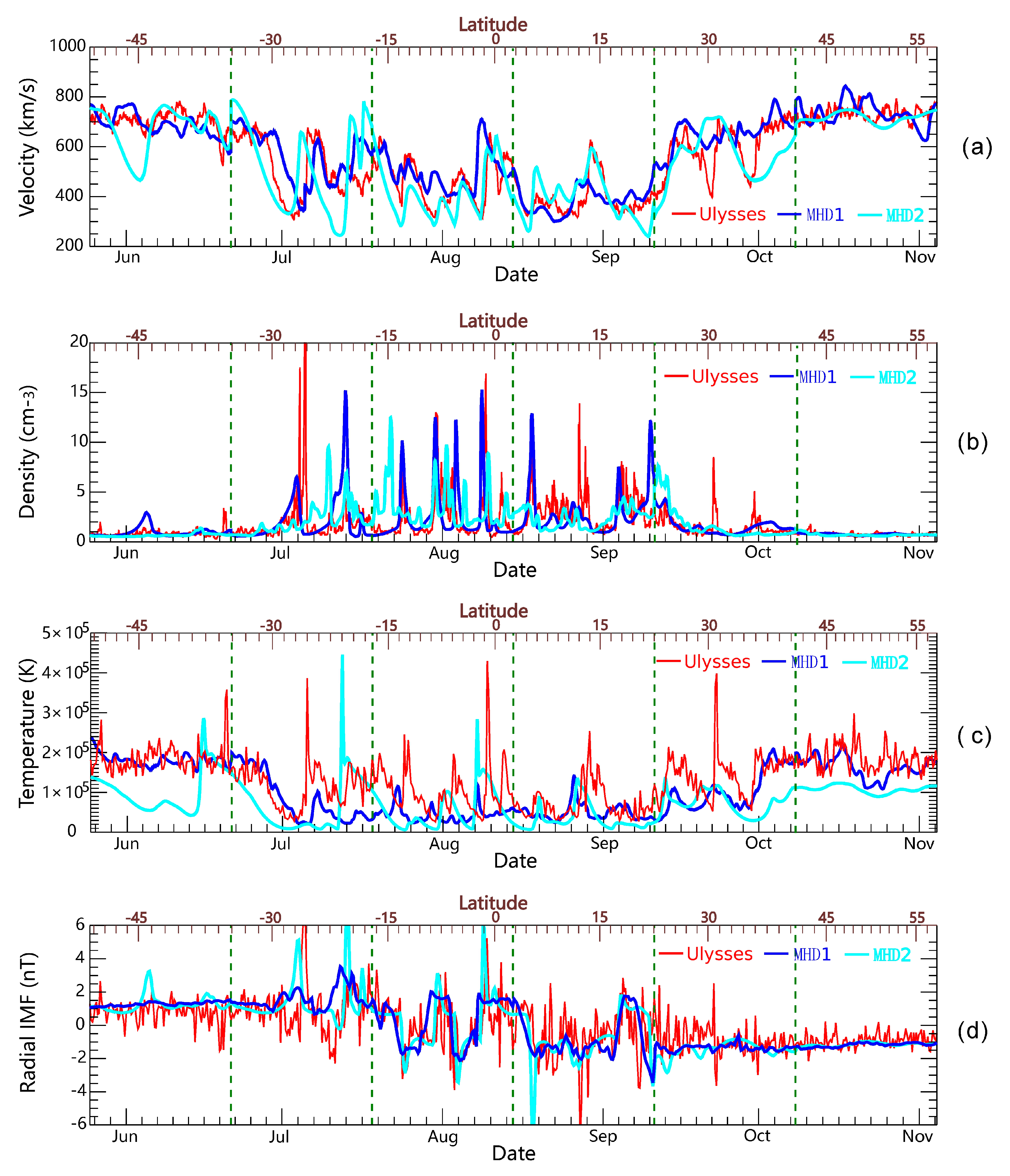
3.2. Comparison with the Ulysses Observation
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Feng, X. Magnetohydrodynamic Modeling of the Solar Corona and Heliosphere; Atmosphere, Earth, Ocean & Space; Springer: Singapore, 2020. [Google Scholar]
- Lugaz, N.; Manchester, W.B., IV; Gombosi, T.I. Numerical Simulation of the Interaction of Two Coronal Mass Ejections from Sun to Earth. Astrophys. J. 2005, 634, 651–662. [Google Scholar] [CrossRef]
- Linker, J.A.; Caplan, R.M.; Schwadron, N.; Gorby, M.; Downs, C.; Torok, T.; Lionello, R.; Wijaya, J. Coupled MHD-Focused Transport Simulations for Modeling Solar Particle Events. J. Physics Conf. Ser. 2019, 1225, 012007. [Google Scholar] [CrossRef]
- Luhmann, J.G.; Mays, M.L.; Odstrcil, D.; Li, Y.; Bain, H.; Lee, C.O.; Galvin, A.B.; Mewaldt, R.A.; Cohen, C.M.S.; Leske, R.A.; et al. Modeling solar energetic particle events using ENLIL heliosphere simulations. Space Weather 2017, 15, 934–954. [Google Scholar] [CrossRef]
- Shen, F.; Shen, C.; Wang, Y.; Feng, X.; Xiang, C. Could the collision of CMEs in the heliosphere be super-elastic? Validation through three-dimensional simulations. Geophys. Res. Lett. 2013, 40, 1457–1461. [Google Scholar] [CrossRef] [Green Version]
- Shen, F.; Shen, C.; Zhang, J.; Hess, P.; Wang, Y.; Feng, X.; Cheng, H.; Yang, Y. Evolution of the 12 July 2012 CME from the Sun to the Earth: Data-constrained three-dimensional MHD simulations. J. Geophys. Res. Space Phys. 2014, 119, 7128–7141. [Google Scholar] [CrossRef] [Green Version]
- Wijsen, N.; Aran, A.; Pomoell, J.; Poedts, S. Modelling three-dimensional transport of solar energetic protons in a corotating interaction region gen-erated with EUHFORIA. Astron. Astrophys. 2019, 622, A28. [Google Scholar] [CrossRef]
- Wei, W.; Shen, F.; Yang, Z.; Zhao, L.; Wang, Y.; Zuo, P.; Zhang, J. Modeling solar energetic particle transport in 3D background solar wind: Influences of the compression regions. J. Atmos. Sol.-Terr. Phys. 2019, 182, 155–164. [Google Scholar] [CrossRef]
- Shen, F.; Liu, Y.; Yang, Y. Numerical Research on the Effect of the Initial Parameters of a CME Flux-rope Model on Simulation Results. Astrophys. J. Suppl. Ser. 2021, 253, 12. [Google Scholar] [CrossRef]
- Tóth, G.; Sokolov, I.; Gombosi, T.; Chesney, D.R.; Clauer, C.R.; De Zeeuw, D.; Hansen, K.C.; Kane, K.J.; Manchester, W.B.; Oehmke, R.C.; et al. Space Weather Modeling Framework: A new tool for the space science community. J. Geophys. Res. Space Phys. 2005, 110, A12226. [Google Scholar] [CrossRef] [Green Version]
- Linker, J.A.; Riley, P.; Mikic, Z.; Lionello, R.; Titov, V.; Wijaya, J. CORHEL MHD Modeling in Support of Solar Dynamics Observatory. Am. Astron. Soc. Meet. 2010, 41, 876. [Google Scholar]
- Riley, P.; Linker, J.A.; Mikić, Z. An empirically-driven global MHD model of the solar corona and inner heliosphere. J. Geophys. Res. Space Phys. 2001, 106, 15889–15901. [Google Scholar] [CrossRef]
- Odstrcil, D. Modeling 3-D solar wind structure. Adv. Space Res. 2003, 32, 497–506. [Google Scholar] [CrossRef]
- Feng, X.; Wu, S.T.; Fan, Q.; Wei, F.; Yao, J. A class of TVD type combined numerical scheme for MHD equations and its application to MHD numerical simulation. Chin. J. Space Sci. 2002, 22, 200–208. [Google Scholar]
- Shen, F.; Feng, X.; Song, W. An asynchronous and parallel time-marching method: Application to three-dimensional MHD simulation of solar wind. Sci. China Ser. E: Technol. Sci. 2009, 52, 2895–2902. [Google Scholar] [CrossRef]
- Feng, X.; Xiang, C.; Zhong, D.; Zhou, Y.; Yang, L.; Ma, X. SIP-CESE MHD model of solar wind with adaptive mesh refinement of hexahedral meshes. Comput. Phys. Commun. 2014, 185, 1965–1980. [Google Scholar] [CrossRef]
- Pomoell, J.; Poedts, S. EUHFORIA: European heliospheric forecasting information asset. J. Space Weather. Space Clim. 2018, 8, A35. [Google Scholar] [CrossRef]
- Kissmann, R.; Kleimann, J.; Krebl, B.; Wiengarten, T. The CRONOS code for astrophysical MHD. Astrophys. J. Suppl. 2018, 236, 53. [Google Scholar] [CrossRef]
- Detman, T.; Smith, Z.; Dryer, M.; Fry, C.D.; Arge, C.N.; Pizzo, V. A hybrid heliospheric modeling system: Background solar wind. J. Geophys. Res. Space Phys. 2006, 111, 111.A7. [Google Scholar] [CrossRef]
- Lapenta, G.; Pierrard, V.; Keppens, R.; Markidis, S.; Poedts, S.; Šebek, O.; Trávníček, P.M.; Henri, P.; Califano, F.; Pegoraro, F.; et al. SWIFF: Space weather integrated forecasting framework. J. Space Weather. Space Clim. 2013, 3, A05. [Google Scholar] [CrossRef]
- Hayashi, K. An MHD simulation model of time-dependent co-rotating solar wind. J. Geophys. Res. Space Phys. 2012, 117, A8. [Google Scholar] [CrossRef] [Green Version]
- Wu, S.T.; Dryer, M. Comparative analyses of current three-dimensional numerical solar wind models. Sci. China Earth Sci. 2015, 58, 839–858. [Google Scholar] [CrossRef]
- Owens, M.J.; Arge, C.N.; Spence, H.; Pembroke, A. An event-based approach to validating solar wind speed predictions: High-speed enhancements in the Wang-Sheeley-Arge model. J. Geophys. Res. Space Phys. 2005, 110, 12105. [Google Scholar] [CrossRef]
- Hayashi, K.; Benevolenskaya, E.; Hoeksema, T.; Liu, Y.; Zhao, X.P. Three-Dimensional Magnetohydrodynamic Simulation of a Global Solar Corona Using a Temperature Distribution Map Obtained from SOHOEIT Measurements. Astrophys. J. Lett. 2006, 636, L165–L168. [Google Scholar] [CrossRef] [Green Version]
- Jackson, B.V.; Odstrcil, D.; Yu, H.-S.; Hick, P.P.; Buffington, A.; Mejia-Ambriz, J.C.; Kim, J.; Hong, S.; Kim, Y.; Han, J.; et al. The UCSD kinematic IPS solar wind boundary and its use in the ENLIL 3-D MHD prediction model. Space Weather 2015, 13, 104–115. [Google Scholar] [CrossRef]
- Manoharan, P.; Kim, T.; Pogorelov, N.V.; Arge, C.N.; Manoharan, P.K. Modeling solar wind with boundary conditions from interplanetary scintillations. J. Phys. Conf. Ser. 2015, 642, 012016. [Google Scholar] [CrossRef]
- Hayashi, K. Magnetohydrodynamic Simulations of the Solar Corona and Solar Wind Using a Boundary Treatment to Limit Solar Wind Mass Flux. Astrophys. J. Suppl. Ser. 2005, 161, 480–494. [Google Scholar] [CrossRef]
- Wiengarten, T.; Kleimann, J.; Fichtner, H.; Cameron, R.; Jiang, J.; Kissmann, R.; Scherer, K. MHD simulation of the inner-heliospheric magnetic field. J. Geophys. Res. Space Phys. 2013, 118, 29–44. [Google Scholar] [CrossRef] [Green Version]
- Shen, F.; Yang, Z.; Zhang, J.; Wei, W.; Feng, X. Three-dimensional MHD Simulation of Solar Wind Using a New Boundary Treatment: Comparison with In Situ Data at Earth. Astrophys. J. 2018, 866, 18. [Google Scholar] [CrossRef]
- Arge, C.N.; Odstrcil, D.; Pizzo, V.J.; Mayer, L.R. Improved Method for Specifying Solar Wind Speed Near the Sun. AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2003; Volume 679, pp. 190–193. [Google Scholar]
- Arge, C.N.; Pizzo, V.J. Improvement in the prediction of solar wind conditions using near-real time solar magnetic field updates. J. Geophys. Res. Space Phys. 2000, 105, 10465–10479. [Google Scholar] [CrossRef]
- Wang, Y.-M.; Sheeley, N. Solar wind speed and coronal flux-tube expansion. Astrophys. J. 1990, 355, 726–732. [Google Scholar] [CrossRef]
- Kim, T.K.; Pogorelov, N.V.; Arge, C.N.; Henney, C.J.; Jones-Mecholsky, S.I.; Smith, W.P.; Bale, S.D.; Bonnell, J.W.; De Wit, T.D.; Goetz, K.; et al. Predicting the Solar Wind at the Parker Solar Probe Using an Empirically Driven MHD Model. Astrophys. J. Suppl. Ser. 2020, 246, 40. [Google Scholar] [CrossRef] [Green Version]
- Odstrcil, D.; Pizzo, V.J.; Linker, J.A.; Riley, P.; Lionello, R.; Mikic, Z. Initial coupling of coronal and heliospheric numerical magnetohydrodynamic codes. J. Atmos. Sol. -Terr. Phys. 2004, 66, 1311–1320. [Google Scholar] [CrossRef]
- Everson, R.W.; Dikpati, M. An Observationally Constrained 3D Potential-field Source-surface Model for the Evolution of Longitude-dependent Coronal Structures. Astrophys. J. 2017, 850, 152. [Google Scholar] [CrossRef]
- Jones, S.I.; Davila, J.M.; Uritsky, V. Optimizing Global Coronal Magnetic Field Models Using Image-Based Constrains. Astrophys. J. 2016, 820, 113. [Google Scholar] [CrossRef] [Green Version]
- Hayashi, K.; Kojima, M.; Tokumaru, M.; Fujiki, K. MHD tomography using interplanetary scintillation measurement. J. Geophys. Res. Space Phys. 2003, 108, 1102. [Google Scholar] [CrossRef]
- Hayashi, K.; Tokumaru, M.; Fujiki, K. MHD-IPS analysis of relationship among solar wind density, temperature, and flow speed. J. Geophys. Res. Space Phys. 2016, 121, 7367–7384. [Google Scholar] [CrossRef]
- Kim, T.K.; Pogorelov, N.V.; Borovikov, S.N.; Jackson, B.V.; Yu, H.-S.; Tokumaru, M. MHD heliosphere with boundary conditions from a tomographic reconstruction using interplanetary scintillation data. J. Geophys. Res. Space Phys. 2014, 119, 7981–7997. [Google Scholar] [CrossRef]
- Tokumaru, M.; Satonaka, D.; Fujiki, K.; Hayashi, K.; Hakamada, K. Relation Between Coronal Hole Areas and Solar Wind Speeds Derived from Interplanetary Scintillation Measurements. Sol. Phys. 2017, 292, 41. [Google Scholar] [CrossRef]
- Bailey, R.L.; Reiss, M.A.; Arge, C.N.; Möstl, C.; Henney, C.J.; Owens, M.J.; Amerstorfer, U.V.; Amerstorfer, T.; Weiss, A.J.; Hinterreiter, J. Using Gradient Boosting Regression to Improve Ambient Solar Wind Model Predictions. Space Weather 2021, 19, 19. [Google Scholar] [CrossRef]
- Upendran, V.; Cheung, M.; Hanasoge, S.; Krishnamurthi, G. Solar Wind Prediction Using Deep Learning. Space Weather 2020, 18, e2020SW002478. [Google Scholar] [CrossRef]
- Yang, Y.; Shen, F. Modeling the Global Distribution of Solar Wind Parameters on the Source Surface Using Multiple Observations and the Artificial Neural Network Technique. Sol. Phys. 2019, 294, 1–22. [Google Scholar] [CrossRef]
- Feng, X.; Yang, L.; Xiang, C.; Wu, S.T.; Zhou, Y.; Zhong, D. Three-dimensional solar wind modeling from the Sun to Earth by a SIP-CESE MHD model with a six-component grid. Astrophys. J. 2010, 723, 300. [Google Scholar] [CrossRef]
- Rempel, M.; Schuessler, M.; Knoelker, M. Radiative MHD simulation of sunspot structure. Astrophys. J. 2008, 691, 812. [Google Scholar]
- Feng, X.; Wu, S.; Wei, F.; Fan, Q. A Class of TVD Type Combined Numerical Scheme for MHD Equations With a Survey About Numerical Methods in Solar Wind Simulations. Space Sci. Rev. 2003, 107, 43–53. [Google Scholar] [CrossRef]
- Parker, E.N. Dynamics of the Interplanetary Gas and Magnetic Fields. Astrophys. J. 1958, 128, 664. [Google Scholar] [CrossRef]
- Altschuler, M.D.; Newkirk, G. Magnetic fields and the structure of the solar corona. Sol. Phys. 1969, 9, 131–149. [Google Scholar] [CrossRef]
- Schatten, K.H.; Wilcox, J.M.; Ness, N.F. A model of interplanetary and coronal magnetic fields. Sol. Phys. 1969, 6, 442–455. [Google Scholar] [CrossRef] [Green Version]
- Hoeksema, J.T. Large-scale structure of the heliospheric magnetic field: 1976-1991. In Solar Wind Seven; Pergamon: Amsterdam, The Netherlands, 1992; pp. 191–196. Available online: https://doi.org/10.1016/B978-0-08-042049-3.50042-9 (accessed on 30 September 2021).
- Riley, P.; Linker, J.A.; Mikić, Z.; Lionello, R.; Ledvina, S.A.; Luhmann, J.G. A Comparison between Global Solar Magnetohydrodynamic and Potential Field Source Surface Model Results. Astrophys. J. 2006, 653, 1510–1516. [Google Scholar] [CrossRef]
- Li, H.; Feng, X.; Wei, F. Comparison of Synoptic Maps and PFSS Solutions for The Declining Phase of Solar Cycle 24. J. Geophys. Res. Space Phys. 2021, 126, 126. [Google Scholar] [CrossRef]
- Wang, Y.-M. Solar Cycle Variation of the Sun’s Low-Order Magnetic Multipoles: Heliospheric Consequences. Space Sci. Rev. 2014, 186, 387–407. [Google Scholar] [CrossRef]
- Newkirk, G.; Fisk, L.A. Variation of cosmic rays and solar wind properties with respect to the heliospheric current sheet: 1, Five-GeV protons and solar wind speed. J. Geophys. Res. Space Phys. 1985, 90, 3391. [Google Scholar] [CrossRef]
- McComas, D.J.; Elliott, H.A.; Gosling, J.T.; Skoug, R. Ulysses observations of very different heliospheric structure during the declining phase of solar activity cycle 23. Geophys. Res. Lett. 2006, 33, 33. [Google Scholar] [CrossRef]
- Hoeksema, J.T.; Wilcox, J.M.; Scherrer, P. The structure of the heliospheric current sheet: 1978–1982. J. Geophys. Res. Space Phys. 1983, 88, 9910–9918. [Google Scholar] [CrossRef]
- Hofmeister, S.J.; Veronig, A.; Temmer, M.; Vennerstrom, S.; Heber, B.; Vršnak, B. The Dependence of the Peak Velocity of High-Speed Solar Wind Streams as Measured in the Ecliptic by ACE and the STEREO satellites on the Area and Co-latitude of Their Solar Source Coronal Holes. J. Geophys. Res. Space Phys. 2018, 123, 1738–1753. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Shen, F.; Zhang, J.; Yang, Y.; Feng, X.; Richardson, I.G. Correlation Between the Magnetic Field and Plasma Parameters at 1 AU. Sol. Phys. 2018, 293, 24. [Google Scholar] [CrossRef]
- Van de Hulst, H. The electron density of the solar corona. Bull. Astron. Inst. Neth. 1950, 11, 135–150. [Google Scholar]
- Billings, D.E. A Guide to the Solar Corona; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Riley, P.; Linker, J.A.; Arge, C.N. On the role played by magnetic expansion factor in the prediction of solar wind speed. Space Weather 2015, 13, 154–169. [Google Scholar] [CrossRef]
- Gary, G.A. Plasma Beta above a Solar Active Region: Rethinking the Paradigm. Sol. Phys. 2001, 203, 71–86. [Google Scholar] [CrossRef]
- Khabarova, O.V.; Malova, H.V.; Kislov, R.A.; Zelenyi, L.M.; Obridko, V.N.; Kharshiladze, A.F.; Tokumaru, M.; Sokół, J.M.; Grzedzielski, S.; Fujiki, K. High-latitude Conic Current Sheets in the Solar Wind. Astrophys. J. 2017, 836, 108. [Google Scholar] [CrossRef]
- Kislov, R.A.; Khabarova, O.V.; Malova, H.V. Quasi-stationary Current Sheets of the Solar Origin in the Heliosphere. Astrophys. J. 2019, 875, 28. [Google Scholar] [CrossRef]
- Maiewski, E.V.; Kislov, R.A.; Khabarova, O.V.; Malova, H.V.; Popov, V.Y.; Petrukovich, A.A.; Zelenyi, L.M. Magnetohydrodynamic Modeling of the Solar Wind Key Parameters and Current Sheets in the Heli-osphere: Radial and Solar Cycle Evolution. Astrophys. J. 2020, 892, 12. [Google Scholar] [CrossRef]




| Solar Wind Parameters | Models | Correlation Coefficient | RMSE |
|---|---|---|---|
| Velocity | MHD1 | 0.84 | 81 |
| MHD2 | 0.80 | 109 | |
| Density | MHD1 | 0.35 | 4.5 |
| MHD2 | 0.27 | 5.2 | |
| Temperature | MHD1 | 0.63 | 6.0 |
| MHD2 | 0.62 | 6.2 | |
| Radial Magnetic Field | MHD1 | 0.58 | 2.5 |
| MHD2 | 0.51 | 2.8 |
| Solar Wind Parameters | Models | Correlation Coefficient | RMSE |
|---|---|---|---|
| Velocity | MHD1 | 0.84 | 83 |
| MHD2 | 0.79 | 101 | |
| Density | MHD1 | 0.40 | 2.2 |
| MHD2 | 0.30 | 2.2 | |
| Temperature | MHD1 | 0.60 | 5.8 |
| MHD2 | 0.57 | 6.3 | |
| Radial Magnetic Field | MHD1 | 0.56 | 0.9 |
| MHD2 | 0.52 | 0.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Shen, F. Three-Dimensional MHD Modeling of Interplanetary Solar Wind Using Self-Consistent Boundary Condition Obtained from Multiple Observations and Machine Learning. Universe 2021, 7, 371. https://doi.org/10.3390/universe7100371
Yang Y, Shen F. Three-Dimensional MHD Modeling of Interplanetary Solar Wind Using Self-Consistent Boundary Condition Obtained from Multiple Observations and Machine Learning. Universe. 2021; 7(10):371. https://doi.org/10.3390/universe7100371
Chicago/Turabian StyleYang, Yi, and Fang Shen. 2021. "Three-Dimensional MHD Modeling of Interplanetary Solar Wind Using Self-Consistent Boundary Condition Obtained from Multiple Observations and Machine Learning" Universe 7, no. 10: 371. https://doi.org/10.3390/universe7100371
APA StyleYang, Y., & Shen, F. (2021). Three-Dimensional MHD Modeling of Interplanetary Solar Wind Using Self-Consistent Boundary Condition Obtained from Multiple Observations and Machine Learning. Universe, 7(10), 371. https://doi.org/10.3390/universe7100371





