Hints for a Gravitational Transition in Tully–Fisher Data
Abstract
1. Introduction
- Are there hints for a transition in the evolution of the BTFR?
- What constraints can be imposed on a possible transition, using BTFR data?
- Are these constraints consistent with the level of required to address the Hubble tension?
| Method | () | Time Scale (Yr) | References | |
|---|---|---|---|---|
| Lunar ranging | 24 | [34] | ||
| Solar system | 50 | [35,36] | ||
| Pulsar timing | 1.5 | [37] | ||
| Strong Lensing | 0.6 | [38] | ||
| Orbits of binary pulsar | 22 | [39] | ||
| Ephemeris of Mercury | 7 | [40] | ||
| Exoplanetary motion | 4 | [41] | ||
| Hubble diagram SnIa | 0.1 | ∼ | [42] | |
| Pulsating white-dwarfs | 0 | [43] | ||
| Viking lander ranging | 6 | [44] | ||
| Helioseismology | [45] | |||
| Gravitational waves | 8 | [46] | ||
| Paleontology | [47] | |||
| Globular clusters | ∼ | [48] | ||
| Binary pulsar masses | ∼ | [49] | ||
| Gravitochemical heating | ∼ | [50] | ||
| Strong lensing | ∼ | [38] | ||
| Big Bang Nucleosynthesis * | [30] | |||
| Anisotropies in CMB * | [51] |
2. Search for Transitions in the Evolution of the BTFR
- We use an exclusively low z sample to search for BTFR evolution.
- We focus on a particular type of evolution: sharp transitions of the intercept and slope.
- We assign to each galaxy a randomly chosen distance obtained from a Gaussian distribution with mean equal to the measured distance and standard deviation equal to the error of the measured distance.
- We assign to each galaxy a randomly chosen obtained from a Gaussian distribution with mean equal to the measured and standard deviation equal to the error of the measured .
- For each galaxy, we use the random obtained in the previous step to calculate the corresponding BTFR , using the best-fit slope and intercept of the real full dataset (first row of Table 2). We then obtain a random for each galaxy from a Gaussian distribution with mean equal to the BTFR calculated and standard deviation equal to the error of the measured .
- We repeat the above process 100 times, thereby generating 100 homogeneous Monte Carlo samples (HMCS) based on the SPARC dataset.
3. Conclusions-Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Dataset of Galaxies Used
| Galaxy Name | D | |||||
|---|---|---|---|---|---|---|
| (km/s) | (km/s) | () | () | (Mpc) | (Mpc) | |
| D631-7 | 1.76 | 0.03 | 8.68 | 0.05 | 7.72 | 0.39 |
| DDO154 | 1.67 | 0.02 | 8.59 | 0.06 | 4.04 | 0.2 |
| DDO161 | 1.82 | 0.03 | 9.32 | 0.26 | 7.5 | 2.25 |
| DDO168 | 1.73 | 0.03 | 8.81 | 0.06 | 4.25 | 0.21 |
| DDO170 | 1.78 | 0.03 | 9.1 | 0.26 | 15.4 | 4.62 |
| ESO079-G014 | 2.24 | 0.01 | 10.48 | 0.24 | 28.7 | 7.17 |
| ESO116-G012 | 2.04 | 0.02 | 9.55 | 0.27 | 13. | 3.9 |
| ESO563-G021 | 2.5 | 0.02 | 11.27 | 0.16 | 60.8 | 9.1 |
| F568-V1 | 2.05 | 0.11 | 9.72 | 0.1 | 80.6 | 8.06 |
| F571-8 | 2.15 | 0.02 | 9.87 | 0.19 | 53.3 | 10.7 |
| F574-1 | 1.99 | 0.04 | 9.9 | 0.1 | 96.8 | 9.68 |
| F583-1 | 1.93 | 0.04 | 9.52 | 0.22 | 35.4 | 8.85 |
| IC2574 | 1.82 | 0.04 | 9.28 | 0.06 | 3.91 | 0.2 |
| IC4202 | 2.38 | 0.02 | 11.03 | 0.13 | 100.4 | 10. |
| KK98-251 | 1.53 | 0.03 | 8.29 | 0.26 | 6.8 | 2.04 |
| NGC0024 | 2.03 | 0.04 | 9.45 | 0.09 | 7.3 | 0.36 |
| NGC0055 | 1.93 | 0.03 | 9.64 | 0.08 | 2.11 | 0.11 |
| NGC0100 | 1.94 | 0.04 | 9.63 | 0.27 | 18.45 | 0.2 |
| NGC0247 | 2.02 | 0.04 | 9.78 | 0.08 | 3.7 | 0.19 |
| NGC0289 | 2.21 | 0.05 | 10.86 | 0.22 | 20.8 | 5.2 |
| NGC0300 | 1.97 | 0.09 | 9.43 | 0.08 | 2.08 | 0.1 |
| NGC0801 | 2.34 | 0.01 | 11.27 | 0.13 | 80.7 | 8.07 |
| NGC0891 | 2.33 | 0.01 | 10.88 | 0.11 | 9.91 | 0.5 |
| NGC1003 | 2.04 | 0.02 | 10.05 | 0.26 | 11.4 | 3.42 |
| NGC1090 | 2.22 | 0.02 | 10.68 | 0.23 | 37. | 9.25 |
| NGC2403 | 2.12 | 0.02 | 9.97 | 0.08 | 3.16 | 0.16 |
| NGC2683 | 2.19 | 0.03 | 10.62 | 0.11 | 9.81 | 0.49 |
| NGC2841 | 2.45 | 0.02 | 11.03 | 0.13 | 14.1 | 1.4 |
| NGC2903 | 2.27 | 0.02 | 10.65 | 0.28 | 6.6 | 1.98 |
| NGC2915 | 1.92 | 0.04 | 9. | 0.06 | 4.06 | 0.2 |
| NGC2976 | 1.93 | 0.05 | 9.28 | 0.11 | 3.58 | 0.18 |
| NGC2998 | 2.32 | 0.02 | 11.03 | 0.15 | 68.1 | 10.2 |
| NGC3109 | 1.82 | 0.03 | 8.86 | 0.06 | 1.33 | 0.07 |
| NGC3198 | 2.18 | 0.01 | 10.53 | 0.11 | 13.8 | 1.4 |
| NGC3521 | 2.33 | 0.03 | 10.68 | 0.28 | 7.7 | 2.3 |
| NGC3726 | 2.23 | 0.03 | 10.64 | 0.15 | 18. | 2.5 |
| NGC3741 | 1.7 | 0.03 | 8.41 | 0.06 | 3.21 | 0.17 |
| NGC3769 | 2.07 | 0.04 | 10.22 | 0.14 | 18. | 2.5 |
| NGC3877 | 2.23 | 0.02 | 10.58 | 0.16 | 18. | 2.5 |
| NGC3893 | 2.25 | 0.04 | 10.57 | 0.15 | 18. | 2.5 |
| NGC3917 | 2.13 | 0.02 | 10.13 | 0.15 | 18. | 2.5 |
| NGC3949 | 2.21 | 0.04 | 10.37 | 0.15 | 18. | 2.5 |
| NGC3953 | 2.34 | 0.02 | 10.87 | 0.16 | 18. | 2.5 |
| NGC3972 | 2.12 | 0.02 | 9.94 | 0.15 | 18. | 2.5 |
| NGC3992 | 2.38 | 0.02 | 11.13 | 0.13 | 23.7 | 2.3 |
| NGC4010 | 2.1 | 0.02 | 10.09 | 0.14 | 18. | 2.5 |
| NGC4013 | 2.24 | 0.02 | 10.64 | 0.16 | 18. | 2.5 |
| NGC4051 | 2.2 | 0.03 | 10.71 | 0.16 | 18. | 2.5 |
| NGC4085 | 2.12 | 0.02 | 10.1 | 0.15 | 18. | 2.5 |
| NGC4088 | 2.24 | 0.02 | 10.81 | 0.15 | 18. | 2.5 |
| NGC4100 | 2.2 | 0.02 | 10.53 | 0.15 | 18. | 2.5 |
| NGC4138 | 2.17 | 0.05 | 10.38 | 0.16 | 18. | 2.5 |
| NGC4157 | 2.27 | 0.02 | 10.8 | 0.15 | 18. | 2.5 |
| NGC4183 | 2.04 | 0.03 | 10. | 0.14 | 18. | 2.5 |
| NGC4217 | 2.26 | 0.02 | 10.66 | 0.16 | 18. | 2.5 |
| NGC4559 | 2.08 | 0.02 | 10.24 | 0.27 | 7.31 | 0.2 |
| NGC5005 | 2.42 | 0.04 | 10.96 | 0.13 | 16.9 | 1.5 |
| NGC5033 | 2.29 | 0.01 | 10.85 | 0.27 | 15.7 | 4.7 |
| NGC5055 | 2.26 | 0.03 | 10.96 | 0.1 | 9.9 | 0.5 |
| NGC5371 | 2.32 | 0.02 | 11.27 | 0.24 | 39.7 | 9.92 |
| NGC5585 | 1.96 | 0.02 | 9.57 | 0.27 | 7.06 | 2.12 |
| NGC5907 | 2.33 | 0.01 | 11.06 | 0.1 | 17.3 | 0.9 |
| NGC5985 | 2.47 | 0.02 | 11.08 | 0.24 | 50.35 | 0.2 |
| NGC6015 | 2.19 | 0.02 | 10.38 | 0.27 | 17. | 5.1 |
| NGC6195 | 2.40 | 0.03 | 11.35 | 0.13 | 127.8 | 12.8 |
| NGC6503 | 2.07 | 0.01 | 9.94 | 0.09 | 6.26 | 0.31 |
| NGC6674 | 2.38 | 0.03 | 11.18 | 0.19 | 51.2 | 10.2 |
| NGC6946 | 2.20 | 0.04 | 10.61 | 0.28 | 5.52 | 1.66 |
| NGC7331 | 2.38 | 0.01 | 11.15 | 0.13 | 14.7 | 1.5 |
| NGC7814 | 2.34 | 0.01 | 10.59 | 0.11 | 14.4 | 0.72 |
| UGC00128 | 2.12 | 0.05 | 10.2 | 0.14 | 64.5 | 9.7 |
| UGC00731 | 1.87 | 0.02 | 9.41 | 0.26 | 12.5 | 3.75 |
| UGC01281 | 1.75 | 0.03 | 8.75 | 0.06 | 5.27 | 0.1 |
| UGC02259 | 1.94 | 0.03 | 9.18 | 0.26 | 10.5 | 3.1 |
| UGC02487 | 2.52 | 0.05 | 11.43 | 0.16 | 69.1 | 10.4 |
| UGC02885 | 2.46 | 0.02 | 11.41 | 0.12 | 80.6 | 8.06 |
| UGC02916 | 2.26 | 0.04 | 10.97 | 0.15 | 65.4 | 9.8 |
| UGC02953 | 2.42 | 0.03 | 11.15 | 0.28 | 16.5 | 4.95 |
| UGC03205 | 2.34 | 0.02 | 10.84 | 0.2 | 50. | 10. |
| UGC03546 | 2.29 | 0.03 | 10.73 | 0.24 | 28.7 | 7.2 |
| UGC03580 | 2.10 | 0.02 | 10.09 | 0.23 | 20.7 | 5.2 |
| UGC04278 | 1.96 | 0.03 | 9.33 | 0.26 | 12.59 | 0.2 |
| UGC04325 | 1.96 | 0.03 | 9.28 | 0.27 | 9.6 | 2.88 |
| UGC04499 | 1.86 | 0.03 | 9.35 | 0.26 | 12.5 | 3.75 |
| UGC05253 | 2.33 | 0.04 | 11.03 | 0.23 | 22.9 | 5.72 |
| UGC05716 | 1.87 | 0.06 | 9.24 | 0.22 | 21.3 | 5.3 |
| UGC05721 | 1.9 | 0.04 | 9.01 | 0.26 | 6.18 | 1.85 |
| UGC05986 | 2.05 | 0.02 | 9.77 | 0.27 | 8.63 | 2.59 |
| UGC06399 | 1.93 | 0.03 | 9.31 | 0.14 | 18. | 2.5 |
| UGC06446 | 1.92 | 0.04 | 9.37 | 0.26 | 12. | 3.6 |
| UGC06614 | 2.3 | 0.11 | 10.96 | 0.12 | 88.7 | 8.87 |
| UGC06667 | 1.92 | 0.02 | 9.25 | 0.13 | 18. | 2.5 |
| UGC06786 | 2.34 | 0.02 | 10.64 | 0.24 | 29.3 | 7.32 |
| UGC06787 | 2.4 | 0.01 | 10.75 | 0.24 | 21.3 | 5.32 |
| UGC06818 | 1.85 | 0.04 | 9.35 | 0.13 | 18. | 2.5 |
| UGC06917 | 2.04 | 0.03 | 9.79 | 0.14 | 18. | 2.5 |
| UGC06923 | 1.90 | 0.03 | 9.4 | 0.14 | 18. | 2.5 |
| UGC06930 | 2.03 | 0.07 | 9.94 | 0.13 | 18. | 2.5 |
| UGC06983 | 2.04 | 0.03 | 9.82 | 0.13 | 18. | 2.5 |
| UGC07125 | 1.81 | 0.03 | 9.88 | 0.26 | 19.8 | 5.9 |
| UGC07151 | 1.87 | 0.02 | 9.29 | 0.08 | 6.87 | 0.34 |
| UGC07399 | 2.01 | 0.03 | 9.2 | 0.27 | 8.43 | 2.53 |
| UGC07524 | 1.9 | 0.03 | 9.55 | 0.06 | 4.74 | 0.24 |
| UGC07603 | 1.79 | 0.02 | 8.73 | 0.26 | 4.7 | 1.41 |
| UGC07690 | 1.76 | 0.06 | 8.98 | 0.27 | 8.11 | 2.43 |
| UGC08286 | 1.92 | 0.01 | 9.17 | 0.06 | 6.5 | 0.33 |
| UGC08490 | 1.9 | 0.03 | 9.17 | 0.11 | 4.65 | 0.53 |
| UGC08550 | 1.76 | 0.02 | 8.72 | 0.26 | 6.7 | 2. |
| UGC08699 | 2.26 | 0.03 | 10.48 | 0.24 | 39.3 | 9.82 |
| UGC09037 | 2.18 | 0.04 | 10.78 | 0.11 | 83.6 | 8.4 |
| UGC09133 | 2.36 | 0.04 | 11.27 | 0.19 | 57.1 | 11.4 |
| UGC10310 | 1.85 | 0.08 | 9.39 | 0.27 | 15.2 | 4.6 |
| UGC11455 | 2.43 | 0.01 | 11.31 | 0.16 | 78.6 | 11.8 |
| UGC11914 | 2.46 | 0.07 | 10.88 | 0.28 | 16.9 | 5.1 |
| UGC12506 | 2.37 | 0.03 | 11.07 | 0.11 | 100.6 | 10.1 |
| UGC12632 | 1.86 | 0.03 | 9.47 | 0.26 | 9.77 | 2.93 |
| UGCA442 | 1.75 | 0.03 | 8.62 | 0.06 | 4.35 | 0.22 |
| UGCA444 | 1.57 | 0.07 | 7.98 | 0.06 | 0.98 | 0.05 |
| 1 |
References
- Tully, R.B.; Fisher, J.R. A New method of determining distances to galaxies. Astron. Astrophys. 1977, 54, 661–673. [Google Scholar]
- Den Heijer, M.; Oosterloo, T.A.; Serra, P.; Józsa, G.I.G.; Kerp, J.; Morganti, R.; Cappellari, M.; Davis, T.A.; Duc, P.-A.; Emsellem, E.; et al. The Hully-Fisher relation of early-type galaxies. Astron. Astrophys. 2015, 581, A98. [Google Scholar] [CrossRef]
- McGaugh, S.S. The Baryonic Tully-Fisher Relation of Galaxies with Extended Rotation Curves and the Stellar Mass of Rotating Galaxies. Astrophys. J. 2005, 632, 859–871. [Google Scholar] [CrossRef]
- Aaronson, M.; Huchra, J.; Mould, J. The infrared luminosity/H I velocity-width relation and its application to the distance scale. Astroph. J. 1979, 229, 1–13. [Google Scholar] [CrossRef]
- Freeman, K.C. On the Disks of Spiral and S0 Galaxies. Astroph. J. 1970, 160, 811. [Google Scholar] [CrossRef]
- Zwaan, M.A.; van der Hulst, J.M.; de Blok, W.J.G.; McGaugh, S.S. The Tully-Fisher relation for low surface brightness galaxies—Implications for galaxy evolution. Mon. Not. R. Astron. Soc. 1995, 273, L35. [Google Scholar] [CrossRef]
- McGaugh, S.S.; de Blok, W.J.G. Testing the dark matter hypothesis with low surface brightness galaxies and other evidence. Astrophys. J. 1998, 499, 41. [Google Scholar] [CrossRef]
- Dutton, A.A. The baryonic Tully–Fisher relation and galactic outflows. Mon. Not. R. Astron. Soc. 2012, 424, 3123–3128. [Google Scholar] [CrossRef]
- Sales, L.V.; Navarro, J.F.; Oman, K.; Fattahi, A.; Ferrero, I.; Abadi, M.; Bower, R.; Crain, R.A.; Frenk, C.S.; Sawala, T.; et al. The low-mass end of the baryonic Tully–Fisher relation. Mon. Not. R. Astron. Soc. 2016, 464, 2419–2428. [Google Scholar] [CrossRef]
- Freeman, K.C. On the Origin of the Hubble Sequence. Astrophys. Space Sci. 1999, 269, 119–137. [Google Scholar] [CrossRef]
- McGaugh, S.S.; Schombert, J.M.; Bothun, G.D.; de Blok, W.J.G. The Baryonic Tully-Fisher Relation. Astrophys. J. Lett. 2000, 533, L99–L102. [Google Scholar] [CrossRef]
- Verheijen, M.A.W. The Ursa Major Cluster of Galaxies. V. H I Rotation Curve Shapes and the Tully-Fisher Relations. Astroph. J. 2001, 563, 694–715. [Google Scholar] [CrossRef]
- Zaritsky, D.; Courtois, H.; Munoz-Mateos, J.C.; Sorce, J.; Erroz-Ferrer, S.; Comerón, S.; Gadotti, D.A.; Gil de Paz, A.; Hinz, J.L.; Laurikainen, E. The Baryonic Tully-Fisher Relationship for S4G Galaxies and the ”Condensed” Baryon Fraction of Galaxies. Astron. J. 2014, 147, 134. [Google Scholar] [CrossRef]
- Schombert, J.; McGaugh, S.; Lelli, F. Using the Baryonic Tully–Fisher Relation to Measure Ho. Astron. J. 2020, 160, 71. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Bowers, J.B.; Macri, L.; Zinn, J.C.; Scolnic, D. Cosmic Distances Calibrated to 1% Precision with Gaia EDR3 Parallaxes and Hubble Space Telescope Photometry of 75 Milky Way Cepheids Confirm Tension with ΛCDM. Astrophys. J. Lett. 2021, 908, L6. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
- Perivolaropoulos, L.; Skara, F. Challenges for ΛCDM: An update. arXiv 2021, arXiv:2105.05208. [Google Scholar]
- Di Valentino, E.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the Realm of the Hubble tension—A Review of Solutions. arXiv 2021, arXiv:2103.01183. [Google Scholar]
- Kazantzidis, L.; Perivolaropoulos, L. Is gravity getting weaker at low z? Observational evidence and theoretical implications. arXiv 2019, arXiv:1907.03176. [Google Scholar]
- Alestas, G.; Kazantzidis, L.; Perivolaropoulos, L. H0 tension, phantom dark energy, and cosmological parameter degeneracies. Phys. Rev. D 2020, 101, 123516. [Google Scholar] [CrossRef]
- Alestas, G.; Perivolaropoulos, L. Late-time approaches to the Hubble tension deforming H(z), worsen the growth tension. Mon. Not. R. Astron. Soc. 2021, 504, 3956–3962. [Google Scholar] [CrossRef]
- Marra, V.; Perivolaropoulos, L. A rapid transition of Geff at zt≃0.01 as a solution of the Hubble and growth tensions. arXiv 2021, arXiv:2102.06012. [Google Scholar]
- Alestas, G.; Kazantzidis, L.; Perivolaropoulos, L. A w-M phantom transition at zt<0.1 as a resolution of the Hubble tension. arXiv 2020, arXiv:2012.13932. [Google Scholar]
- Camarena, D.; Marra, V. A new method to build the (inverse) distance ladder. Mon. Not. R. Astron. Soc. 2020, 495, 2630–2644. [Google Scholar] [CrossRef]
- Amendola, L.; Corasaniti, P.S.; Occhionero, F. Time variability of the gravitational constant and type Ia supernovae. arXiv 1999, arXiv:astro-ph/9907222. [Google Scholar]
- Gaztanaga, E.; Garcia-Berro, E.; Isern, J.; Bravo, E.; Dominguez, I. Bounds on the possible evolution of the gravitational constant from cosmological type Ia supernovae. Phys. Rev. D 2002, 65, 023506. [Google Scholar] [CrossRef]
- Wright, B.S.; Li, B. Type Ia supernovae, standardizable candles, and gravity. Phys. Rev. D 2018, 97, 083505. [Google Scholar] [CrossRef]
- Übler, H.; Förster Schreiber, N.M.; Genzel, R.; Wisnioski, E.; Wuyts, S.; Lang, P.; Naab, T.; Burkert, A.; van Dokkum, P.G.; Tacconi, L.J.; et al. The Evolution of the Tully-Fisher Relation between z ~ 2.3 and z ~ 0.9 with KMOS3D. Astroph. J. 2017, 842, 121. [Google Scholar] [CrossRef]
- Esposito-Farese, G.; Polarski, D. Scalar tensor gravity in an accelerating universe. Phys. Rev. D 2001, 63, 063504. [Google Scholar] [CrossRef]
- Alvey, J.; Sabti, N.; Escudero, M.; Fairbairn, M. Improved BBN Constraints on the Variation of the Gravitational Constant. Eur. Phys. J. C 2020, 80, 148. [Google Scholar] [CrossRef]
- Walter, F.; Brinks, E.; de Blok, W.J.G.; Bigiel, F.; Kennicutt, R.C.; Thornley, M.D.; Leroy, A. Things: The H I nearby galaxy survey. Astron. J. 2008, 136, 2563–2647. [Google Scholar] [CrossRef]
- Lelli, F.; McGaugh, S.S.; Schombert, J.M.; Desmond, H.; Katz, H. The baryonic Tully-Fisher relation for different velocity definitions and implications for galaxy angular momentum. Mon. Not. R. Astron. Soc. 2019, 484, 3267–3278. [Google Scholar] [CrossRef]
- Lelli, F.; McGaugh, S.S.; Schombert, J.M. The Small Scatter of the Baryonic Tully-Fisher Relation. Astroph. J. Lett. 2016, 816, L14. [Google Scholar] [CrossRef]
- Hofmann, F.; Müller, J. Relativistic tests with lunar laser ranging. Class. Quant. Grav. 2018, 35, 035015. [Google Scholar] [CrossRef]
- Pitjeva, E.V.; Pitjev, N.P.; Pavlov, D.A.; Turygin, C.C. Estimates of the change rate of solar mass and gravitational constant based on the dynamics of the Solar System. Astron. Astrophys. 2021, 647, A141. [Google Scholar] [CrossRef]
- Pitjeva, E.V.; Pitjev, N.P. Relativistic effects and dark matter in the Solar system from observations of planets and spacecraft. Mon. Not. R. Astron. Soc. 2013, 432, 3431. [Google Scholar] [CrossRef]
- Deller, A.T.; Verbiest, J.P.W.; Tingay, S.J.; Bailes, M. Extremely high precision VLBI astrometry of PSR J0437-4715 and implications for theories of gravity. Astrophys. J. Lett. 2008, 685, L67. [Google Scholar] [CrossRef]
- Giani, L.; Frion, E. Testing the Equivalence Principle with Strong Lensing Time Delay Variations. J. Cosmol. Astropart. Phys. 2020, 9, 8. [Google Scholar] [CrossRef]
- Zhu, W.W.; Desvignes, G.; Wex, N.; Caballero, R.N.; Champion, D.J.; Demorest, P.B.; Ellis, J.A.; Janssen, G.H.; Kramer, M.; Krieger, A.; et al. Tests of Gravitational Symmetries with Pulsar Binary J1713+0747. Mon. Not. R. Astron. Soc. 2019, 482, 3249–3260. [Google Scholar] [CrossRef]
- Genova, A.; Mazarico, E.; Goossens, S.; Lemoine, F.G.; Neumann, G.A.; Smith, D.E.; Zuber, M.T. Solar system expansion and strong equivalence principle as seen by the NASA MESSENGER mission. Nat. Commun. 2018, 9, 289. [Google Scholar] [CrossRef]
- Masuda, K.; Suto, Y. Transiting planets as a precision clock to constrain the time variation of the gravitational constant. Publ. Astron. Soc. Jap. 2016, 68, L5. [Google Scholar] [CrossRef]
- Gaztañaga, E.; Cabré, A.; Hui, L. Clustering of luminous red galaxies—IV. Baryon acoustic peak in the line-of-sight direction and a direct measurement of H(z). Mon. Not. R. Astron. Soc. 2009, 399, 1663–1680. [Google Scholar] [CrossRef]
- Córsico, A.H.; Althaus, L.G.; García-Berro, E.; Romero, A.D. An independent constraint on the secular rate of variation of the gravitational constant from pulsating white dwarfs. J. Cosmol. Astropart. Phys. 2013, 6, 32. [Google Scholar] [CrossRef]
- Hellings, R.W.; Adams, P.J.; Anderson, J.D.; Keesey, M.S.; Lau, E.L.; Standish, E.M.; Canuto, V.M.; Goldman, I. Experimental Test of the Variability of G Using Viking Lander Ranging Data. Phys. Rev. Lett. 1983, 51, 1609–1612. [Google Scholar] [CrossRef]
- Guenther, D.B.; Krauss, L.M.; Demarque, P. Testing the Constancy of the Gravitational Constant Using Helioseismology. Astrophys. J. 1998, 498, 871–876. [Google Scholar] [CrossRef]
- Vijaykumar, A.; Kapadia, S.J.; Ajith, P. Constraints on the time variation of the gravitational constant using gravitational wave observations of binary neutron stars. arXiv 2020, arXiv:2003.12832. [Google Scholar]
- Uzan, J.P. The Fundamental Constants and Their Variation: Observational Status and Theoretical Motivations. Rev. Mod. Phys. 2003, 75, 403. [Google Scholar] [CrossRef]
- Degl’Innocenti, S.; Fiorentini, G.; Raffelt, G.G.; Ricci, B.; Weiss, A. Time variation of Newton’s constant and the age of globular clusters. Astron. Astrophys. 1996, 312, 345–352. [Google Scholar]
- Thorsett, S.E. The Gravitational constant, the Chandrasekhar limit, and neutron star masses. Phys. Rev. Lett. 1996, 77, 1432–1435. [Google Scholar] [CrossRef]
- Jofre, P.; Reisenegger, A.; Fernandez, R. Constraining a possible time-variation of the gravitational constant through gravitochemical heating of neutron stars. Phys. Rev. Lett. 2006, 97, 131102. [Google Scholar] [CrossRef]
- Wu, F.; Chen, X. Cosmic microwave background with Brans-Dicke gravity II: Constraints with the WMAP and SDSS data. Phys. Rev. D 2010, 82, 083003. [Google Scholar] [CrossRef]
- Conselice, C.J.; Bundy, K.; Ellis, R.S.; Brichmann, J.; Vogt, N.P.; Phillips, A.C. Evolution of the near-infrared Tully-Fisher relation: Constraints on the relationship between the stellar and total masses of disk galaxies since z = 1. Astrophys. J. 2005, 628, 160–168. [Google Scholar] [CrossRef][Green Version]
- Kassin, S.A.; Weiner, B.J.; Faber, S.M.; Koo, D.C.; Lotz, J.M.; Diemand, J.; Harker, J.J.; Bundy, K.; Metevier, A.J.; Phillips, A.C.; et al. The Stellar Mass Tully-Fisher Relation to z = 1.2 from AEGIS. Astrophys. J. Lett. 2007, 660, L35–L38. [Google Scholar] [CrossRef][Green Version]
- Miller, S.H.; Bundy, K.; Sullivan, M.; Ellis, R.S.; Treu, T. The Assembly History of Disk Galaxies: I—The Tully-Fisher Relation to z~1.3 from Deep Exposures with DEIMOS. Astrophys. J. 2011, 741, 115. [Google Scholar] [CrossRef]
- Contini, T.; Epinat, B.; Bouché, N.; Brinchmann, J.; Boogaard, L.A.; Ventou, E.; Bacon, R.; Richard, J.; Weilbacher, P.M.; Wisotzki, L.; et al. Deep MUSE observations in the HDFS—Morpho-kinematics of distant star-forming galaxies down to 108M. Astron. Astrophys. 2016, 591, A49. [Google Scholar] [CrossRef]
- Di Teodoro, E.M.; Fraternali, F.; Miller, S.H. Flat rotation curves and low velocity dispersions in KMOS star-forming galaxies at z ∼ 1. Astron. Astrophys. 2016, 594, A77. [Google Scholar] [CrossRef]
- Molina, J.; Ibar, E.; Swinbank, A.M.; Sobral, D.; Best, P.N.; Smail, I.; Escala, A.; Cirasuolo, M. SINFONI-HiZELS: The dynamics, merger rates and metallicity gradients of ’typical’ star-forming galaxies at z = 0.8–2.2. Mon. Not. R. Astron. Soc. 2017, 466, 892–905. [Google Scholar] [CrossRef][Green Version]
- Pelliccia, D.; Tresse, L.; Epinat, B.; Ilbert, O.; Scoville, N.; Amram, P.; Lemaux, B.C.; Zamorani, G. HR-COSMOS: Kinematics of star-forming galaxies at z ∼ 0.9. Astron. Astrophys. 2017, 599, A25. [Google Scholar] [CrossRef]
- Puech, M.; Flores, H.; Hammer, F.; Yang, Y.; Neichel, B.; Lehnert, M.; Chemin, L.; Nesvadba, N.; Epinat, B.; Amram, P.; et al. IMAGES- III. The evolution of the near-infrared Tully-Fisher relation over the last 6 Gyr. Astron. Astrophys. 2008, 484, 173–187. [Google Scholar] [CrossRef]
- Puech, M.; Hammer, F.; Flores, H.; Delgado-Serrano, R.; Rodrigues, M.; Yang, Y. The baryonic content and Tully-Fisher relation at z ∼ 0.6. Astron. Astrophys. 2010, 510, A68. [Google Scholar] [CrossRef]
- Cresci, G.; Hicks, E.K.S.; Genzel, R.; Schreiber, N.M.F.; Davies, R.; Bouché, N.; Buschkamp, P.; Genel, S.; Shapiro, K.; Tacconi, L.; et al. The sins survey: Modeling the dynamics of z ∼ 2 galaxies and the high-z tully–fisher relation. Astrophys. J. 2009, 697, 115. [Google Scholar] [CrossRef]
- Gnerucci, A.; Marconi, A.; Cresci, G.; Maiolino, R.; Mannucci, F.; Calura, F.; Cimatti, A.; Cocchia, F.; Grazian, A.; Matteucci, F.; et al. Dynamical properties of AMAZE and LSD galaxies from gas kinematics and the Tully-Fisher relation at z ∼ 3. Astron. Astrophys. 2011, 528, A88. [Google Scholar] [CrossRef]
- Swinbank, M.; Sobral, D.; Smail, I.; Geach, J.; Best, P.; McCarthy, I.; Crain, R.; Theuns, T. The Properties of the Star-Forming Interstellar Medium at z = 0.84–2.23 from HiZELS-I: Mapping the Internal Dynamics and Metallicity Gradients in High-Redshift Disk Galaxies. Mon. Not. R. Astron. Soc. 2012, 426, 935. [Google Scholar] [CrossRef]
- Price, S.H.; Kriek, M.; Shapley, A.E.; Reddy, N.A.; Freeman, W.R.; Coil, A.L.; de Groot, L.; Shivaei, I.; Siana, B.; Azadi, M.; et al. The mosdef survey: Dynamical and baryonic masses and kinematic structures of star-forming galaxies at 1.4 ≤ z ≤ 2.6. Astrophys. J. 2016, 819, 80. [Google Scholar] [CrossRef]
- Tiley, A.L.; Stott, J.P.; Swinbank, A.M.; Bureau, M.; Harrison, C.M.; Bower, R.; Johnson, H.L.; Bunker, A.J.; Jarvis, M.J.; Magdis, G.; et al. The KMOS Redshift One Spectroscopic Survey (KROSS): The Tully–Fisher relation at z ∼ 1. Mon. Not. R. Astron. Soc. 2016, 460, 103–129. [Google Scholar] [CrossRef][Green Version]
- Straatman, C.M.S.; Glazebrook, K.; Kacprzak, G.G.; Labbé, I.; Nanayakkara, T.; Alcorn, L.; Cowley, M.; Kewley, L.J.; Spitler, L.R.; Tran, K.V.H.; et al. ZFIRE: The Evolution of the Stellar Mass Tully–Fisher Relation to Redshift ∼ 2.2. Astrophys. J. 2017, 839, 57. [Google Scholar] [CrossRef]
- Portinari, L.; Sommer-Larsen, J. The Tully-Fisher relation and its evolution with redshift in cosmological simulations of disc galaxy formation. Mon. Not. R. Astron. Soc. 2007, 375, 913–924. [Google Scholar] [CrossRef][Green Version]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes 3rd Edition: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Dutton, A.A.; Obreja, A.; Wang, L.; Gutcke, T.A.; Buck, T.; Udrescu, S.M.; Frings, J.; Stinson, G.S.; Kang, X.; Macciò, A.V. NIHAO XII: Galactic uniformity in a ΛCDM universe. Mon. Not. R. Astron. Soc. 2017, 467, 4937–4950. [Google Scholar] [CrossRef]
- Desmond, H. The scatter, residual correlations and curvature of the sparc baryonic Tully–Fisher relation. Mon. Not. R. Astron. Soc. Lett. 2017, 472, L35–L39. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-time Evolution. Phys. Rept. 2017, 692, 1–104. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rept. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- Clifton, T.; Ferreira, P.G.; Padilla, A.; Skordis, C. Modified Gravity and Cosmology. Phys. Rept. 2012, 513, 1–189. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics—Implications for galaxies. Astroph. J. 1983, 270, 371–383. [Google Scholar] [CrossRef]
- McGaugh, S.S. The baryonic tully–fisher relation of gas-rich galaxies as a test of ΛCDM and MOND. Astron. J. 2012, 143, 40. [Google Scholar] [CrossRef]
- Ghosh, S.; Bhadra, A.; Mukhopadhyay, A.; Sarkar, K. Baryonic Tully–Fisher Test of Grumiller’s Modified Gravity Model. Grav. Cosmol. 2021, 27, 157–162. [Google Scholar] [CrossRef]
- Blanton, M.R.; Geha, M.; West, A.A. Testing Cold Dark Matter with the Low-Mass Tully-Fisher Relation. Astroph. J. 2008, 682, 861–873. [Google Scholar] [CrossRef]
- Governato, F.; Brook, C.; Mayer, L.; Brooks, A.; Rhee, G.; Wadsley, J.; Jonsson, P.; Willman, B.; Stinson, G.; Quinn, T.; et al. Bulgeless dwarf galaxies and dark matter cores from supernova-driven outflows. Nature 2010, 463, 203–206. [Google Scholar] [CrossRef]
- Mortsell, E.; Goobar, A.; Johansson, J.; Dhawan, S. The Hubble Tension Bites the Dust: Sensitivity of the Hubble Constant Determination to Cepheid Color Calibration. arXiv 2021, arXiv:2105.11461. [Google Scholar]
- Iorio, L. Gravitational Anomalies in the Solar System? Int. J. Mod. Phys. D 2015, 24, 1530015. [Google Scholar] [CrossRef]
- Feulner, G. The faint young Sun problem. Rev. Geophys. 2012, 50, RG2006. [Google Scholar] [CrossRef]
- Amendola, L.; Marra, V.; Quartin, M. Internal robustness: Systematic search for systematic bias in SN Ia data. Mon. Not. R. Astron. Soc. 2013, 430, 1867–1879. [Google Scholar] [CrossRef]
- Heneka, C.; Marra, V.; Amendola, L. Extensive search for systematic bias in supernova Ia data. Mon. Not. R. Astron. Soc. 2014, 439, 1855–1864. [Google Scholar] [CrossRef][Green Version]
- Benedict, G.F.; McArthur, B.E.; Feast, M.W.; Barnes, T.G.; Harrison, T.E.; Patterson, R.J.; Menzies, J.W.; Bean, J.L.; Freedman, W.L. Hubble Space Telescope Fine Guidance Sensor Parallaxes of Galactic Cepheid Variable Stars: Period-Luminosity Relations. Astron. J. 2007, 133, 1810–1827, Erratum in Astron. J. 2007, 133, 2980. [Google Scholar] [CrossRef]
- Benedict, G.F.; McArthur, B.E.; Fredrick, L.W.; Harrison, T.E.; Lee, J.; Slesnick, C.L.; Rhee, J.; Patterson, R.J.; Nelan, E.; Jefferys, W.H.; et al. Astrometry with hubble space telescope: A parallax of the fundamental distance calibrator delta cephei. Astron. J. 2002, 124, 1695–1705. [Google Scholar] [CrossRef]
- Wenger, M.; Ochsenbein, F.; Egret, D.; Dubois, P.; Bonnarel, F.; Borde, S.; Genova, F.; Jasniewicz, G.; Laloë, S.; Lesteven, S.; et al. The SIMBAD astronomical database. The CDS reference database for astronomical objects. Astron. Astroph. 2000, 143, 9–22. [Google Scholar] [CrossRef]
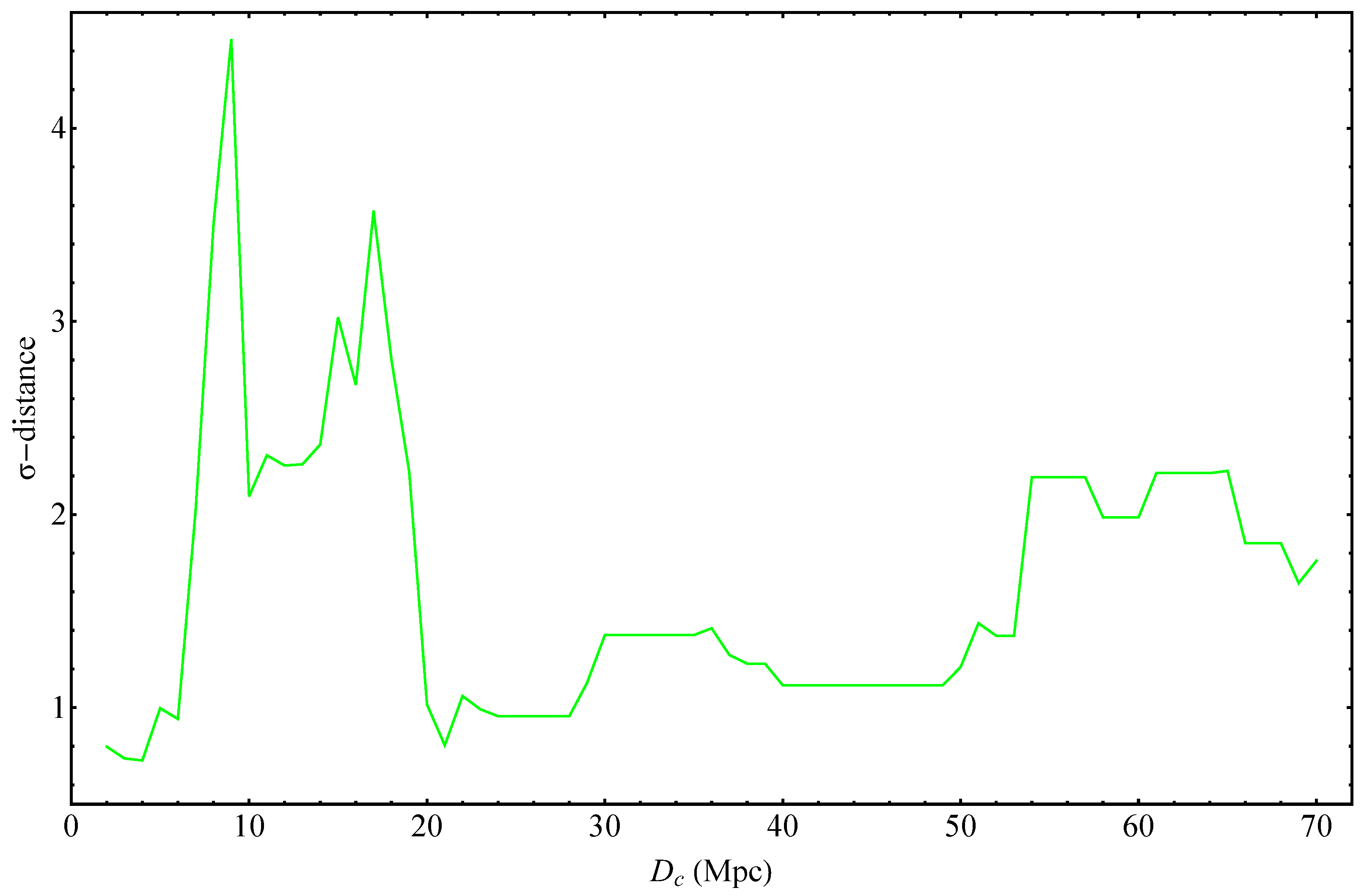
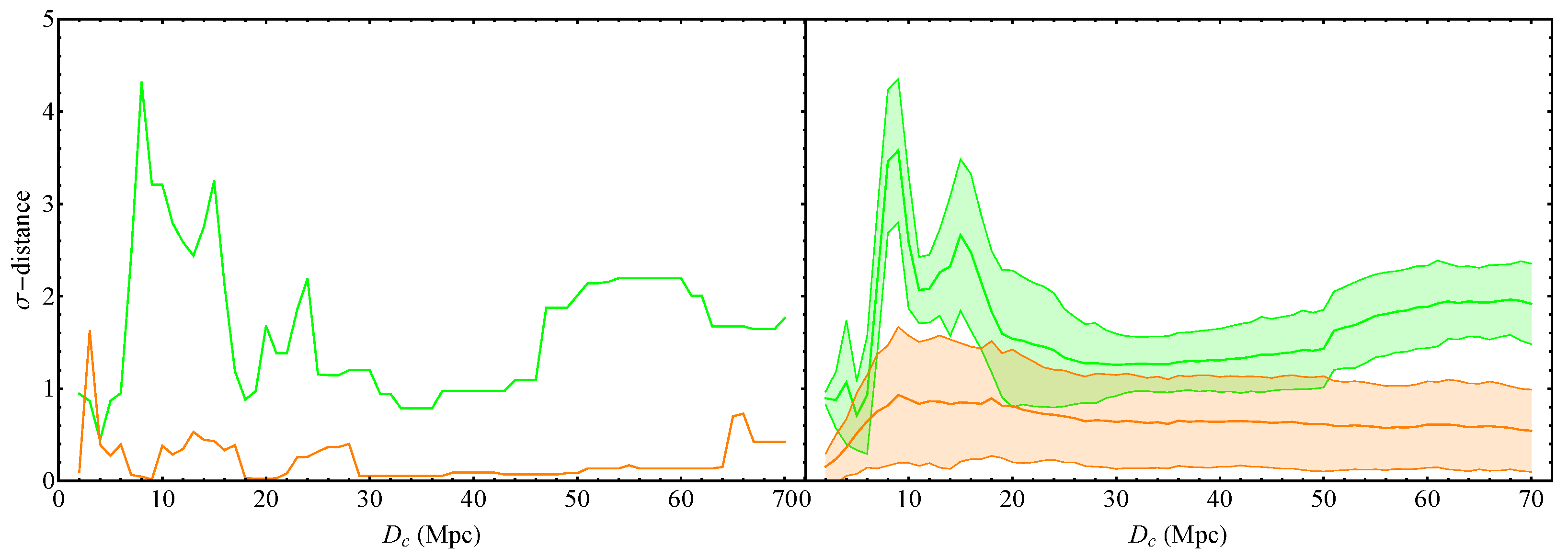
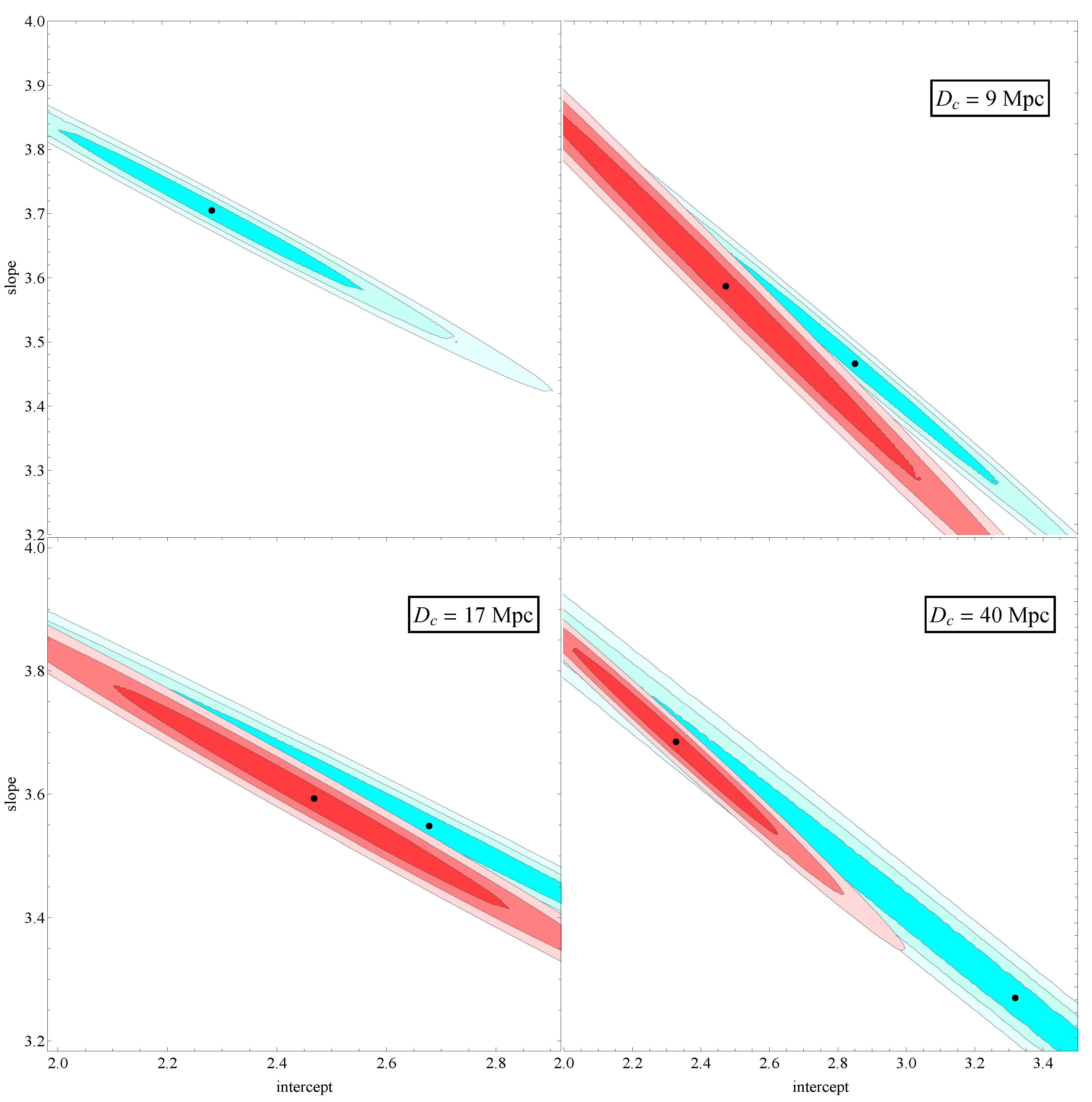
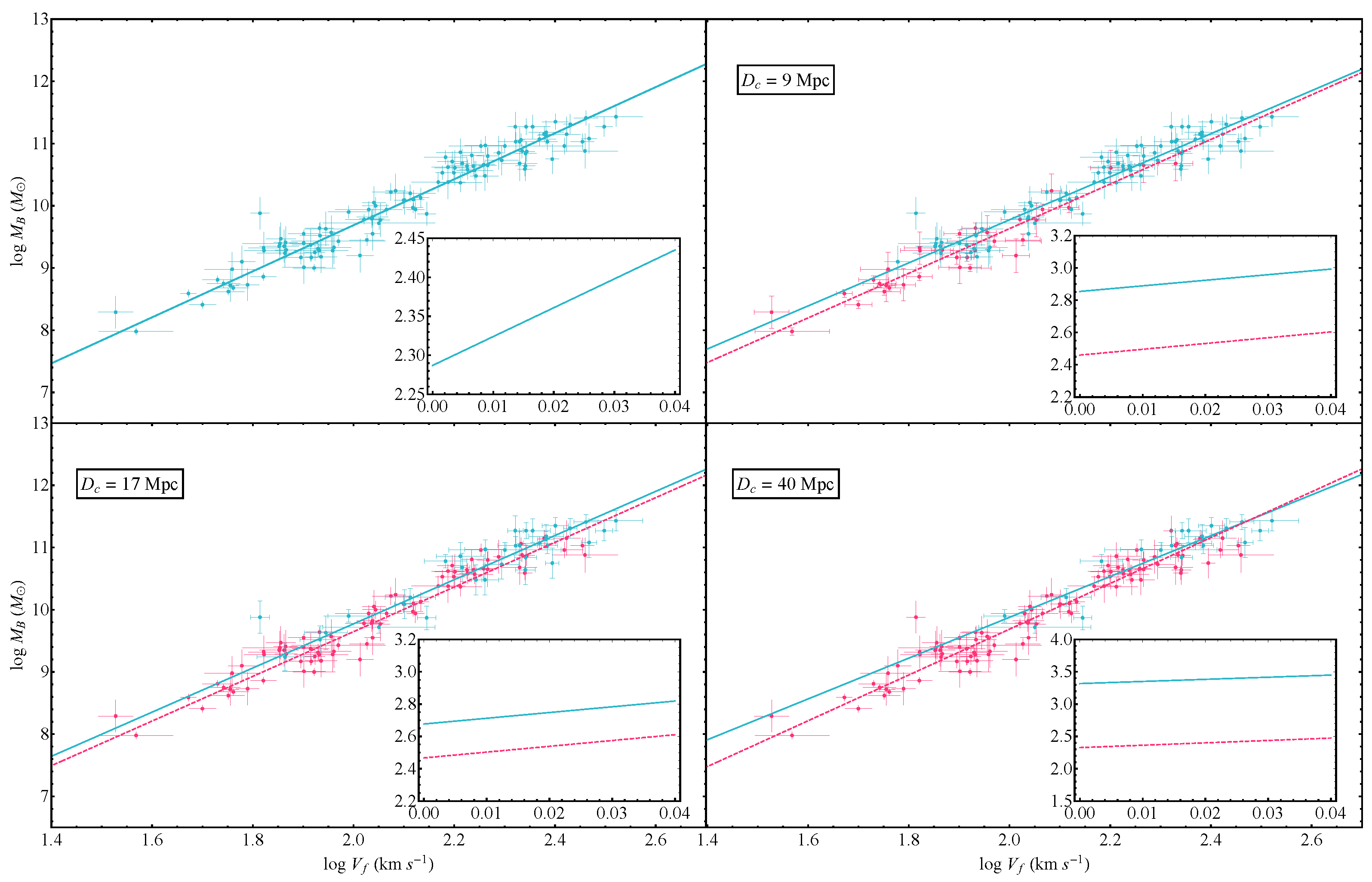
| (Mpc) | Intercept | Slope | |
|---|---|---|---|
| - | - | ||
| <9 | |||
| >9 | |||
| <17 | |||
| >17 | |||
| <40 | |||
| >40 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alestas, G.; Antoniou, I.; Perivolaropoulos, L. Hints for a Gravitational Transition in Tully–Fisher Data. Universe 2021, 7, 366. https://doi.org/10.3390/universe7100366
Alestas G, Antoniou I, Perivolaropoulos L. Hints for a Gravitational Transition in Tully–Fisher Data. Universe. 2021; 7(10):366. https://doi.org/10.3390/universe7100366
Chicago/Turabian StyleAlestas, George, Ioannis Antoniou, and Leandros Perivolaropoulos. 2021. "Hints for a Gravitational Transition in Tully–Fisher Data" Universe 7, no. 10: 366. https://doi.org/10.3390/universe7100366
APA StyleAlestas, G., Antoniou, I., & Perivolaropoulos, L. (2021). Hints for a Gravitational Transition in Tully–Fisher Data. Universe, 7(10), 366. https://doi.org/10.3390/universe7100366








