3.2. Trajectory Distortions
To illustrate the impact of the black hole’s spin on a test-body’s trajectory, we solve Equation (
23) for several cases with varying parameters
and
j. From the start, it may be noted that at great distances from the black hole, the relativistic impact on the trajectory can be captured via small corrections to the classical Lagrangian. These are scenarios with numerical values for the initial momentum
. At smaller
j, such as
(or
or
), the relativistic impact on the motion becomes significant. Furthermore, when
, the traveling body eventually becomes captured by the black hole. Conversely, when the body’s initial momentum
, the body manages to escape the zone of the black hole’s influence.
The shapes of the test-body’s trajectory within the zone of significant black hole influence (strong relativistic effects) may vary dramatically.
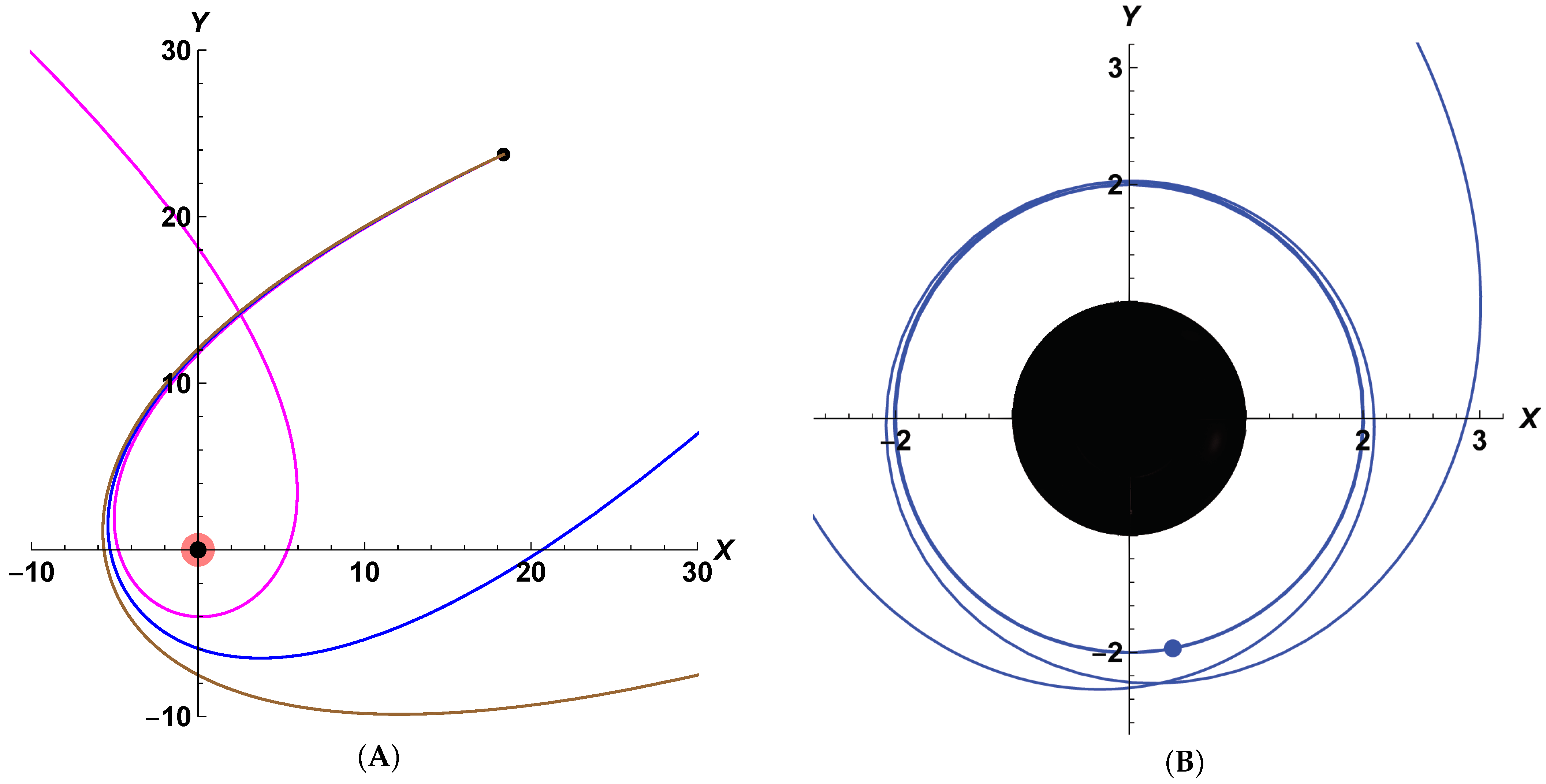
Figure 1A illustrates the variety and plots trajectories of a test-body with
(sufficient to escape in each case) for the scenarios when the black hole’s spin and the test-body’s momentum are co-aligned (
, magenta line), counter-aligned (
, brown line), and when the black hole does not spin at all (
, blue line). As revealed, depending on the black hole’s spin, the trajectory may twist significantly (as shown by the magenta line,
), or quasi-reverse (as shown by the blue line,
), or simply curve (as shown by the brown line,
). When the black hole’s spinning is co-aligned
with the body’s angular momentum, the movement of the body and the swirling of the time-space coincide. The essence of the effect may perhaps be grasped by visualizing a boat sailing with an ocean current or against the current—the boat’s trajectories relative to a distant observer would look quite different.
Particularly intriguing cases may occur when the initial angular momentum of the traveling body falls within a “narrow” range (not-too-fast but not-too-slow, defined by the system’s parameters; here ). For a non-spinning black hole (), the body may circle around the non-rotating black hole several times before departing towards infinity.
Figure 1B shows such trajectory’s details (recall that for a non-rotating black hole, the event-horizon coincides with the static limit). The Dark-Blue-Dot (in the lower-right quadrant of
Figure 1B) corresponds to the minimal distance (periastron) from the “center” of the black hole that is reached by the body. As the body passes through the periastron (Dark-Blue-Dot), its radial velocity turns to zero. Prior to passing through the periastron, the sign of the body’s radial velocity component is negative (the body is approaching); after the passing, the sign is positive (the body is moving away). If the energy diagram were drawn, the process would look as if the representative point was moving along the straight line (of constant energy), reaching the energy barrier (corresponding to Dark-Blue-Dot in
Figure 1B), reflecting from the barrier (passing trough the periastron), and moving in the opposite direction along the level of constant energy. (A similar discussion and underlying details can be found in [
17].) This explains the gradual spiraling of the trajectory closer towards the periastron (Dark-Blue-Dot) and the subsequent unwinding. Eventually, the body departs the black hole’s vicinity and generally the zone of influence.
3.3. Strong Shift
By comparing observational data (periastron shifts) for star trajectories near black holes with theoretical curves for a range of spin-values , it may be possible to estimate the actual black hole spin. Since relativistic effects are the strongest at periastron when the orbit of a star (test-body) is not quasi-circular but elongated (quasi-parabolic), observations of elongated orbits can be more revealing than data on quasi-circular orbits. Consequently, in this section, we demonstrate how to calculate the shift of the periastron for a parabolic trajectory (energy ) and provide the results from our numerical simulations for a sample of spin-values .
When a star begins its travel from infinity (where its radial inverse-coordinate
) and approaches a black hole along the incoming (upper) branch of the trajectory, the star’s angular coordinate
, for each
u, is derived (as a function of the radial coordinate
) from Equation (
23) and has the form
Here,
is the value of
u when solutions
and
merge (at the point
where
). Parameter
. Quantities
and
with
are the solutions of equation
Solution determines the periastron in which derivative .
Realization Domain: Not every combination of is realizable. For example, as mentioned earlier, when the test-body’s initial angular momentum is below , the body becomes captured by the black hole (its trajectory ends at the static limit). So those test-bodies, which can eventually complete their trajectories, without being captured, are described by the combinations within a limited “realization” domain. Such domain has two bounds: and .
The (initial) bound, , is obvious and reflects the fact that the test-body starts at the infinity with some initial angular momentum . (Because Lagrangian is invariant with respect to rotation, the test-body’s angular momentum is conserved, so momentum remains constant as the test-body approaches the black hole along the incoming branch of the parabolic trajectory with energy .)
The second (periastron) bound,
, is more complex.
Figure 2 plots several
u-curves composed of a solid part
and a dashed part
—merging at
—but it is the curves’ lower branches (
, solid lines) that serve as the second (periastron) bounds
. (The curves are plotted for the black hole spin-values
, from the left-most to the right-most: red
,
,
; black
; blue
,
).
For —which is the case when the test-body with initial momentum eventually escapes the black hole with spin —in the -space, the (corresponding to the test-body) state-point starts at the point and “moves” upward (along the vertical line ) until reaching the lower branch of one of the plotted u-curves (the one corresponding to the encountered black hole’s spin ). This point corresponds to the test-body’s trajectory’s periastron in the physical space. After the periastron, the test-body’s physical movement proceeds along the outbound branch of its physical trajectory, but in the -space, after “reflecting” at the periastron-representing state-point , the test-body-representing state-point follows the vertical line downward towards (now it is the exiting value at the infinity).
For the cases when the black hole captures the test-body and the body ends up falling onto the static limit (which happens when test-body’s initial angular momentum ), in the -space the test-body-representing state-point starts at the point and “moves” upward (along the vertical line ) until the horizontal line (the static limit, above which—within the ergozone—the metric-tensor component becomes negative).
Periastron Coordinates: The angular coordinate for periastron when
(or for the body when it falls onto the static limit when
) is defined by the integral
where, for simplicity, the Heaviside function
is used:
when
and
when
, with the half-maximum convention
. We remind readers that in the region
, quantity
is purely imaginary, and in the region
,
is purely real and positive. The integral Equation (
32) cannot be expressed in simple analytical functions. It can be either calculated numerically, or its asymptotics may be considered.
For large
j, Equation (
32) gives the following estimate
where only the leading terms are retained. The first term corresponds to classical Newtonian mechanics—the angular coordinate for the periastron is
. The second term gives the shift of the periastron due to the relativistic effect in the Schwarzschild metric. This term is always positive. The third term takes into account the black hole’s spin and can have any sign. At
, even for
, this correction term is small when compared to the previous one, since for the Kerr metrics
, always.
Figure 3 shows the angular coordinate for periastron
as a function of test-body’s momentum
j for three black hole spin-values:
(blue),
(black), and
(red).
As
Figure 3 reveals, for large values of initial angular momentum,
, the relativistic effects are indeed relatively small, placing the periastron slightly above
. However, the effect of the black hole’s spin
becomes rather significant for
. Notably, as shown in
Figure 4, the effect is strongest for
j near
. The logarithmic scale in the right panel of
Figure 4 reveals that
-function is not some power-function but is more complex. The left panel shows the case when the black hole’s spin is counter-aligned (
) with the test-body’s angular momentum
j. The right panel shows the case when the spin is co-aligned (
) with the momentum.
In the vicinity of
, integral
diverges. By expressing momentum
j as
, where
, and retaining only the leading terms, we find expression for
in the vicinity of
:
Here,
and
(which depend on
) are of order unity. For example, in the particular case of
, the values of the parameters are:
and
. For
, the value of the angular coordinate of the periastron turns out to be
.
The total number, N, of rotations of the compact star around the black hole—seen as if “captured onto a quasi-circular orbit” by a remote observer—is then estimated as . (Here of rotations occur before the body reaches the periastron, and of rotations occur after passing through the periastron.)
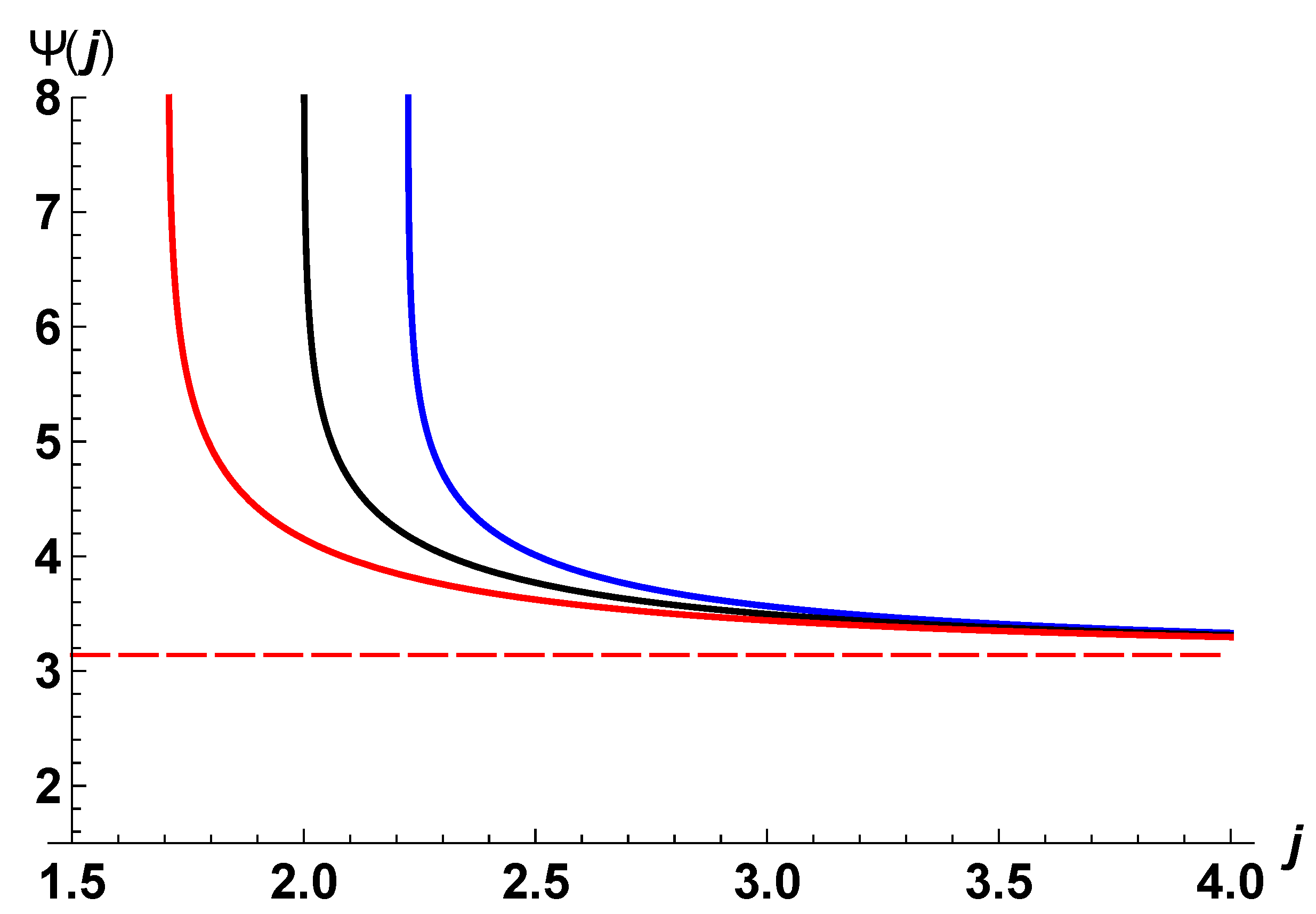
Finally,
Figure 5 compares the locations and shapes of
-curves when black hole spin is counter-aligned (
, red), absent (
, black), or co-aligned (
, blue) with the test-body momentum
j.
Figure 6 reveals the nuances of the differences in the shapes of
-curves when the test-body’s momentum-value happens to be in the vicinity of
(i.e., near
). For comparison, the Newtonian periastron
is plotted as the horizontal dashed line.