Abstract
Finding four-dimensional de Sitter spacetime solutions in string theory has been a vexing quest ever since the discovery of the accelerating expansion of the universe. Building on a recent analysis of bubble-nucleation in the decay of (false-vacuum) AdS backgrounds where the interfacing bubbles themselves exhibit a de Sitter geometry we show that this resonates strongly with a stringy cosmic brane construction that naturally provides for an exponential mass-hierarchy and the localization of both gravity and matter, in addition to an exponentially suppressed positive cosmological constant. Finally, we argue that these scenarios can be realized in terms of a generalization of a small resolution of a conifold singularity in the context of a (Lorentzian) Calabi–Yau 5-fold, where the isolated (Lorentzian) two complex dimensional Fano variety is a four-dimensional de Sitter spacetime.
1. Introduction
For almost a quarter of a century, a specter has been haunting string theory: the accelerated expansion of our universe implies an asymptotically and approximately de Sitter (dS) geometry with a small but positive cosmological constant [1,2]. Constructing solutions in string theory with these features has been argued to be notoriously hard if not impossible: see [3,4,5] for recent comprehensive reviews. However, recent work [6,7,8], as well as [9], turn out to correspond naturally with a stringy cosmic dS-brane toy-model [10,11,12,13,14,15], which we furthermore connect with a generalization of the proposal that allows for more general spacetime varying string vacua [16].
The main ideas are the following: (1) Both the AdS-decaying [6,7] and the so-called “axilaton” [10,12,13,14,15] scenarios are near a singularity; they are “resolutions/smoothings” of a singular/critical model, and so are inherently non-perturbative [8]. As such, a closer examination can (and does) find special configurations in which the various competing contributions do allow for a four-dimensional (sub-)spacetime of the desired dS geometry. (2) Just as in the AdS-decaying scenario, the axilaton models can be made dynamical by choosing their anisotropy, , differently on the two sides of the candidate for the observed universe, . (3) Calabi–Yau 5-folds, , provide an auxiliary Euclidean rendition of the total Lorentzian spacetime, , and a natural “home” for such phase-transition nucleating “bubble-worlds”: Just as in the AdS-decaying scenario, the “exceptional” (real codimension-six) sub-spacetimes naturally have positive curvature, while their complement and local neighborhood in is naturally hyperbolic.
The key effects of considering the theory near a singularity are discussed in Section 2, especially focusing on the conifold in Section 2.1, which leads us to review the AdS-decaying scenario in Section 2.2. In Section 3 we recall the salient features of the axilaton toy models and highlight the similarities in the overall spacetime geometry with the AdS-decaying solutions. This in turn lets us modify the former so as to afford a dynamical scenario akin to the latter. The global geometry of the ten-dimensional spacetime is reviewed in Section 4, where we present evidence that the most generic of spacetime geometries in string theory necessarily include exceptional four-dimensional sub-spacetimes of positive curvature, the simplest of which being . Finally, Section 5 summarizes our key points and conclusions, while Appendix A collects a few additional details about (spacetime) defects and their role in understanding dS solutions in string theory.
2. Nearly Singular Spacetimes
The early discovery that certain singular features in spacetime are innocuous to string dynamics [17,18] shows that the choice of available geometries is, in this respect, considerably more general than in conventional quantum field theory. A large class of such singular geometries affords topology change [19,20,21,22], in a milder sense [23,24], and so involve some form of a phase transition. This tends to harbor radical effects both in physics and in geometry: massless black holes [25], exoflops [23,26], D-branes [27], and orientifolds [28,29,30], and often involve strong coupling effects.
2.1. Warped Deformed Conifolds and Alike
Models that are even just near being singular then invariably involve multiple competing contributions to the effective (target-spacetime) action, some of which are often difficult to calculate. Nevertheless, suitable approximations have been carefully considered and well justified, as is the case of the warped deformations of conifold singularities [31,32,33]; see also [34,35]. Here, the complex structure deformation of the conifold singularity and the relative size of associated vanishing cycles, the -brane contributions and the metric warping all affect the target spacetime physics. A detailed examination of such a nearly singular warped direct product compactification scenario finds a fine-tuned regime within the parameter space in which the multiple competing contributions can be shown to induce a metastable dS metric in the non-compact spacetime factor [8]; see however also the review [36] and the references therein. Note that the vanishing cycles in the deformation-singularizing complex, compact Calabi–Yau 3-folds are real three-dimensional subspaces, matching in dimension the “probing” -branes. Thus, this example indicates that vacua with a stringy dS spacetime could require a highly specialized set of circumstances and qualities.
Mirror symmetry guarantees that the same type of phenomenon occurs near the conifold singularity on the Kähler (or symplectic) structure side, as is the case with very small relative sizes of so-called exceptional sets1 in a Calabi–Yau 3-fold compactification. As with the near singularization by complex structure deformation [8], one again expects a detailed balance of various contributing factors. While exact calculations on this, Kähler, side are much harder in general and are not amenable to explicit probing and direct computation, such mirror-symmetric configurations are qualitatively identical. In turn, however, Calabi–Yau 3-folds are known to generically have many such exceptional sets, real two- and four-dimensional subspaces, each one of which “resolves” a singularity by replacing it with a complex subvariety while preserving the complex structure outside the surgery locus [39,40,41]; by mirror symmetry, the (nearly) vanishing 3-cycles are then as abundant. This implies that the pool of such nearly singular models, on both mirror-symmetry sides, is populous albeit sub-generic, as the individual such models involve highly specialized arrangements.
Generally, the examples discussed so far are static background configurations, wherein the observable four-dimensional spacetime2, , and the extra dimensions () form a rigid direct product, as sketched at Figure 1a, where the geometry of and of the observable four-dimensional spacetime are independent of each other.
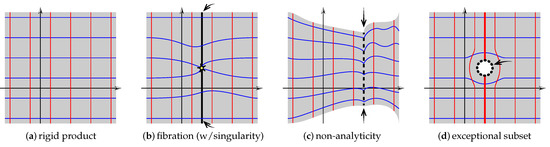
Figure 1.
Some possible geometries in target spacetime; these simplified illustrations hint at the variations in any of the relevant structures (complex, Kähler, symplectic, supersymmetry), and may be combined in various ways.
Allowing for to vary in some observable spatial directions was shown to necessarily include singularizations of that manifest as stringy cosmic strings (’branes) [42,43], as sketched in Figure 1b. Allowing furthermore for non-analytic variations of the geometry of some of the extra dimensions [44,45] warps the overall geometry and can allow for a simultaneous emergence of exponential mass-hierarchy, localization of gravity, matter, and an exponentially suppressed cosmological constant in [10,12,13,14]; see the sketch in Figure 1c. We will return to these constructions in Section 3.
2.2. De Sitter Bubble-Worlds
Consider now, in turn, the recent dynamical proposal with the spacetime geometry consisting of two copies of , glued together non-analytically across a 3-brane-world, [6,7]; see also [46,47,48] and especially ([49], Section 7); herein, we relabel coordinates so the shell is located at . The remaining five dimensions compactified on a suitable space of positive curvature, such as , complete a direct product ten-dimensional spacetime, as expected in string theory.
The hallmark novelty in the new “AdS-decaying” proposal [6,7], as compared with earlier literature, is that the key subspace, , emerges as a “bubble,” a domain wall-like interface between a metastable, false-vacuum and the nucleated, expanding true-vacuum . The discontinuity at in the total space must be sourced (via standard matching conditions) by a suitably chosen but otherwise unspecified matter distribution, which then also provides the interfacing shell, , with a constant tension. It is then further verified that neither bulk nor shell-localized matter invalidate the main result, that the “shellworld,” , is indeed a dS universe with the cosmological constant that can have phenomenologically acceptable values. As in [45], the graviton is shown to obey a Schrödinger-like equation, which guarantees the existence of a graviton mode duly localized to the shell, , although here this is not the mode trapped by the -function well [6,47]. Note that the so-obtained spacetime geometry is a combination of the sketches in Figure 1a,d: appears as a (non-factor) subspace within the first five-dimensional spacetime factor of .
Studied ever since the original proposal [50] (see [51] for a recent update), such vacuum decay phenomena have been estimated to be generic in string theory [52,53]3, implying then the same also for nucleation, a subset of which results in de Sitter bubble-worlds. These phenomena are again “near” phase transitions, for which no perturbative description can be expected to be complete. Notably, the analysis of Refs. [6,7] focuses on the dynamically enfolding aftermath of such a phase transition, and so again pertains to nearly singular configurations. Thus, both in the claimed ubiquity and in this inherently non-perturbative nature, this is reminiscent of the string theory realization [20,21] of “Reid’s phantasy” [41]. 4 In fact, as we will argue shortly, this can be made more specific in the context of spacetime varying string vacua generalizing the early work by one of the authors [16]. To see why this is the case, we will however next turn to a brief review of the axilaton toy model [13,14,15] in order to showcase the similarities with the -decay model [6,7].
3. A Discretuum of Toy Models
Generally accommodating the overall geometry types sketched in Figure 1a–c and aiming for a (de Sitter) candidate four-dimensional spacetime, the metric Ansatz has a direct sum format, , where and are appropriate line elements for the candidate observable spacetime, , and its co-factor, , while are “warp factors” that are most often allowed to vary over at least some directions in . The particular class of toy models [10,12,13,14] further specializes to
where ℓ sets the length-scale in , so the warp factors and the coordinates are dimensionless. The observable spacetime () is expected to have de Sitter geometry, and the warp factors are chosen to depend only on the log-radial coordinate, z; also, is the standard azimuthal angle in . The last summand, , could also be warped but is for now assumed to be independent of the other six coordinates; see, however, the below.
This class of toy models also neglects all other matter fields, but explicitly includes the “universal” axion–dilaton (“axilaton” ) field, , in string theory, which exhibit an -monodromy owing to modular invariance [56]. Setting separates variables in an evidently non-holomorphic (and so non-supersymmetric) way. There exist two 3-parameter classes of such solutions, which the -monodromy restricts to a discretuum. Notably, , and the -anisotropy, , appears in the Einstein–Friedan equation [57,58],
and sources the warped geometry (1) [13,14]:
with the harmonic functions
and the cosmological constant
where counts the source-branes5 [11]. In [13,14,15], the maximal, , was used for simplicity. Thus, the -anisotropy of the axilaton, , drives the cosmological constant (4d). Furthermore, the inequalities and are saturated only in the supersymmetric limit, where [13,14]. The value of the cosmological constant (4d) and its corresponding IR mass-scale were shown to be related via a see-saw formula to the typical Standard Model (Higgs) and the UV (Planck) scales, and to be in agreement with observations [13,14,15]. As analyzed in detail in [11,12,13], the z-dependence in (4c) induces a -like contribution to the Ricci tensor as well as the by now standard “volcano potential”-type (normalizable) localization of the gravitational field. The supersymmetric limit of the toy model renders the axilaton a constant and explicitly involves a stack of D7-branes and an orientifold plane with mutually cancelling RR charges [11]. These then “deform” into extended objects following the explicitly non-supersymmetric “deformation” of the axilaton system. A detailed description of such appropriately “deformed” extended objects remains an open question for now, but Ref. [14] shows that they must interpolate between well understood stringy models. Finally, the length-scale ℓ emerges in (2) via dimensional transmutation (akin to ), as this equation is the condition (the vanishing of the worldsheet QFT beta-function, to the lowest order) for the target-spacetime metric to not renormalize.
Notably, the metric (1)–(4) is continuous at with both sign-choices in (4a), where with merely “bounces” as does the flat-space line element in spherical coordinates at the origin. In stark contrast, assuming to be the Minkowski line element forces the solution with to exhibit a naked singularity at [10,11], beyond which the metric becomes complex. Thereby, the de Sitter metric (1) explicitly desingularizes the total spacetime in this class of toy models [13]. This is corroborated by verifying that the standard curvature invariants for (1)–(4) are all finite, whereas the Kretschmann (Riemann-squared) invariant diverges at in the Minkowski solution. Finally, (4c) implies that the cosmological constant effectively specifies the “distance” (in the parameter space) to the so-resolved singularity.
In this sense, this class of toy models also describes nearly singular spacetimes, much as those studied in Refs. [8,34,35,36]—except that the background configurations are here restricted to a discretuum by the -monodromy. Indeed, the axilaton, , varies over including values that oscillate about , even by a few orders of magnitude. For the whole model, this not only implies strong coupling, but is (owing to the -monodromy of ) also discontinuous along a branch-cut, for example, along . Across this branch-cut, the model non-perturbatively patches a stringy weak-coupling regime with a reciprocally strong-coupling regime—akin to “S-folds” [60]. Nevertheless, the effective observable string coupling, , remains perturbatively small in the sub-spacetime , preserving the impression of a weakly coupled effective field theory within this toy-model candidate for the observable universe [14,15].
For future reference, we note that the effective Planck mass-scale, , in is exponentially boosted [12,15],
as compared with the six-dimensional Planck mass-scale resulting after compactifying on . Here, is the “lower” incomplete Gamma function, and its “upper” complement, and . This in turn exponentially suppresses the cosmological constant, . As is by now standard [45], the graviton modes are governed by an effective potential that here depends on the source-counting parameter, , that also appears in (5) [12]. This potential also has a superposed -function well induced from the -dependence of the metric (4a), which guarantees the existence of a -localized graviton mode. A more detailed computation shows that the Newton potential is corrected by terms [13]. This is suppressed as compared to the naïve dimensional analysis estimate, , based on , and indicates that the effect depends on the (hyperbolic) curvature of near the mid-radius, . This non-analyticity also induces a -contribution in the Ricci tensor, which must be matched by matter localized to the exceptional spacetime factor by the same -function well in the effective potential. This populates the candidate observable spacetime with universally -localized modes of any matter added to this toy model.
With in (4a), the “transverse” annular region, , has so that is non-compact, as depicted in Figure 2 (left). In turn, with in (4a), we have , so that includes its two circular boundaries; see Figure 2 (left). In both of these solutions, the proper (log-radial) length of is infinite, although the surface area of is finite. The 2-point compactification/completion6 then allows us to regard as a 2-point puncturing of . Fibering the remaining factor, (e.g., K3), over shows that the unobservable space, in the axilaton models [13,14,15] is also obtainable as a 2-fiber puncturing of K3-fibrations over —the latter of which are well understood Calabi–Yau 3-folds, as they are used in static, Calabi–Yau compactifications to Minkowski spacetime [39]7.
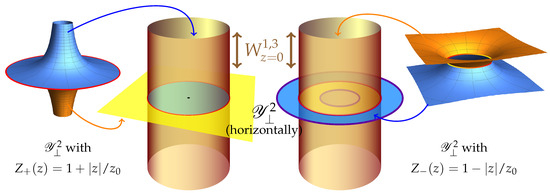
Figure 2.
A depiction of the fibration with (left) and with (right). Far left and far right: the proper distance plotted vertically in , indicating the radial dependence of the circumference—which is obscured in the two central depictions. Only the mid-radius fiber, , of the fibration is depicted as a vertical cylinder, ; it defines the “inside” and “outside’ part of the six-dimensional spacetime’; see (7), below.
The 2-fiber compactification/completion process8
may be understood as the right-hand side depicting a static, Minkowski/CY geometry being identified as the (double, supersymmetry-restoring) limit, , of the axilaton geometry on the left-hand side. Intermediate in this process is the “decompactification” of the Minkowski/CY geometry if is a non-compact, unbounded cylinder, or a cylinder with boundaries if . In this sense, the geometry given on the far left-hand side in (6) is the (supersymmetry-breaking, non-holomorphic) deformation of a punctured version of the geometry depicted on the far right-hand side. In turn, the configuration in the log-radial middle, , of the annulus serves as a “cylindrical” interface between the “inside” and “outside” regions; see Figure 2.
Although somewhat different in the technical details, the overall spacetime geometry in the axilaton toy model (1)–(5) [13,14,15] and in the -decay model [6,7] are remarkably similar: The Schrödinger-like potential governing the graviton exhibits a discontinuity at , which then properly localizes a graviton mode. Just as in the axilaton toy model, the -decay model also shows the metric within the so embedded to be of the de Sitter type, with the cosmological constant in the correct ballpark. The respective Ricci tensors also require a balancing source by matter modes, again localized to the same locus.
The two spacetime geometries, shown side-by-side, with the interfacing shown underscoring the joining (#) symbol:
The left-hand side scenario is rendered dynamical by choosing to be the false vacuum, with higher energy than the true-vacuum . This inequality provides the interfacing with tension and drives its spatial expansion. The left-hand side scenario (7) thus depicts a point-nucleation of the “true” within the “false” , with the four-dimensional boundary serving as the candidate observable spacetime, [6,7].
The right-hand side of (7) axilaton configuration has been presumed so far to be static and in/out-symmetric [13,14,15]—but this need not at all be the case. Since all physical features in this model depend on the anisotropy of the axilaton, , it suffices to choose . The two sides of the interfacing in (7) are
which are analogous to and , as depicted in Figure 2. Indeed, the log-radial z-dependence renders the proper distance between and infinite while keeping the surface area of finite, implying a hyperbolic geometry. This geometry is driven by the axilaton anisotropy, in , and differs from the well-known Ricci-flat geometry of the annular that one might have expected: the negative curvature of is forced by balancing the anisotropy-driven “pressure,” , in (2).
With different values of the axilaton anisotropy, the regions and harbor different “pressures,” which drives the expansion of one region into the other. By analogy then, the right-hand side configuration (7) depicts a cosmic string-sourced nucleation of an analogous phase transition with a -shaped “cylindrical” -dimensional interface. However, unlike in the AdS-decay model [6,7], the -monodromy of the axilaton models [13,14,15] restricts the anisotropy to discrete values. This allows only discrete variations, that is, tunneling from one configuration to another.
4. Calabi–Yau 5-Folds
Let us reconsider then the overall, total spacetime in string theory, relying only on the most general of restrictions while keeping the models of the foregoing discussion in the back of our mind. To this end, first generalize the geometry in the axilaton model by allowing for the K3 as in (6) to be fibered over the , and hence leading to a K3-fibered Calabi–Yau 3-fold in the limit. In addition, we consider an auxiliary, “Euclideanized” rendition, which affords relating algebro-geometric features of this depiction to the Lorentzian features of the original. This affords an old idea [16] a fresh look, and will turn out to improve this proposal.
String dynamics is generally understood to require the overall target spacetime, , to be Ricci-flat—as a starting point: Such spaces admit a metric the Ricci tensor of which is a total derivative. Stringy corrections to this metric proceed by the re-absorption of -corrections [61], and independently by addition of fluxes [62,63]. This provides an iterative framework for systematic adaptations for the original Ricci-flat metric. The original Ricci-flatness requirement follows from several related, but rather distinct vantage points:
- the inherent semi-infinite cohomology in string theory [64];
- the free loop space as the configuration space of (closed) strings [65,66,67,68,69,70,71,72,73];
- the worldsheet quantum field theory approach [74].
The orientability of closed strings [56] (including zero-modes [75,76,77]) implies that the second-listed analysis should be extended to the orientation-doubled loop-space and (Super)Diff. In lieu of this extension, we note that it will perforce include the results of the original loop-space approach. (Owing to the still very much developing nature of string theory, a technically precise meaning of this notion is still unclear, and the conceptual understanding itself may require some adjustments.) The above studies show that the free loop-space of must be Ricci-flat, which then determines the geometry of in turn [39]. Consider then a suitable Euclidean Wick-rotation of that is, at least in Type-II theories (owing to their supersymmetry) guaranteed to admit both a complex structure and a Kähler metric. This assigns to the ten-dimensional spacetime, , a corresponding auxiliary Calabi–Yau 5-fold, ; various dualities extend this argument throughout other types of string vacua.
Just as Calabi–Yau 3-folds generically contain numerous exceptional, isolated so-called “ curves” [41], Calabi–Yau 5-folds generically contain numerous exceptional, isolated Fano () compact complex surfaces,, i.e., real four-dimensional subspaces [16]. In the Lorentzian original, , (the preimage of) at least some of these isolated subspaces are soliton-like (rather than instanton-like), and so admit a metric of the -signature, perhaps singular at some (sub)locus. Owing to their positive scalar curvature9, the simplest of these will then admit a metric that is approximately de Sitter for most observers (see Appendix A), and which may serve as candidates for the observable spacetime. Recall that for all Einstein spacetimes, defines as the characteristic length scale, relating it to the curvature, and via also to the volume. Wick rotation changes the overall coefficient in this tensorial equation, and so preserves the relation. More precisely, it suffices for to admit a metric that equals the de Sitter metric within the past light-cone of a typical/current observer; see Appendix A for more detail. For such exceptional sets at least, parametrizes the relative size of such an exceptional, isolated real 4-manifold, —very much akin to the de Sitter desingularizing deformation (1)–(5).
Reid’s argument for 3-folds [41] generalizes straightforwardly to higher dimensions, so Calabi–Yau 5-folds are expected to abound in such exceptional real four-dimensional subspaces, making the pool of candidates abundant. Being the exceptional sets of small resolutions of conifold singularities the dynamical evolution of the Lorentzian of these four-dimensional subspaces may well enfold akin to the bubble-worlds discussed above (7). In the coarse classification discussed in Section 2 and referring to Figure 1, the scenario that is the preimage of the “Euclideanizing” Wick rotation assignment
is depicted in Figure 1d: the total spacetime, , is in no way assumed to factorize, nor even foliate10, and is an isolated, exceptional sub-spacetime. On general grounds, such non-factorizing spacetimes ought to be the generic case in string theory.
Now consider the auxiliary Calabi–Yau 5-fold, , a particular exceptional Fano surface in it, , and its non-compact complement, , as well as their respective Lorentzian counterparts: , and . Note that the Ricci curvature is not additive for such triples (nor is then the scalar curvature), but we have the Tian–Yau theorem [78,79]:
Here, the non-compact space on the right-hand side is known to admit a suitable Kähler metric/form, J, and a holomorphic volume-form, (which in turn implies the existence of a covariantly constant spinor, i.e., global supersymmetry), that satisfy the standard relationship asymptotically, near the locus where the compact Calabi–Yau n-fold was excised. It would then seem reasonable to expect that, analogously:
where Hyp denotes a “hyperbolic” complex -fold with negative Ricci curvature, again with analogous asymptotics near the locus where the compact Fano n-fold was excised. Both of these relations are well-nigh trivial and easily seen for :
- (a non-compact cylinder), which is well known to be Ricci-flat.
- is a 1-handled disc, and so a hyperbolic non-compact surface.
Furthermore, we will need the following specializing generalization
Locally, this result follows from the so-called adjunction theorem [39]: For example, and imply that the local neighborhood of is any one of the rank-2 bundles , with arbitrary . Depending on the choice of ℓ, the curvature of this normal bundle will be negative along some fibers but positive along others. However, we seek an isolated , which has no local holomorphic deformations, and which happens precisely when . In that exceptional case, the local neighborhood of that has a uniformly negative Ricci curvature. The claim (12) then aims to generalize this, albeit perhaps in an appropriate average sense, throughout the complement —and more generally, throughout ; we are not aware of a rigorous global result either way.
The so-generalized claim (12) then implies that the non-compact complex 5-fold admits a metric of negative Ricci curvature. (Again, locally, near an isolated , this is a consequence of the adjunction theorem.) With suitable boundary conditions to match the excised subspace , the Lorentzian counterpart, , should then also admit a metric with negative curvature—analogous to in the AdS-decaying scenario (7). However, these exceptional 4-manifolds, , have nothing “inside,” much as a circle inside does not carve it into two separate parts: The complement, is a single-component connected space since has real codimension 6. (This is unlike the real codimension-1 subspace in the AdS-decay scenario that does carve the total spacetime, , into two disconnected parts, an “outside” and an “inside.”) Having only the “outside,” , these exceptional sub-spacetimes are rather literally akin to “bubbles of nothing”; see [80] and also [81].
In the Euclidean (and holomorphic) rendition, the standard Kähler class, J, (every metric in that cohomology class) of any “bubble” (desingularizing exceptional set) is both positive over every complex submanifold of and has a positive square (“volume”): and are the standard conditions on the Kähler cone. In the simplest case, take the bubble to be . Then:
- The Kähler class of is positive over “all complex submanifolds,” all of which are equivalent to the at the North Pole “infinity” (This refers to the standard cell decomposition );
- There is therefore a Riemannian metric that differs from the above Kähler metric only in being null over the at the North pole;
- which is therefore a valid metric on , and fails in those positivity requirements only at the North pole, where it vanishes—and so is nowhere negative.
Together, these imply that has positive curvature, the simplest (most symmetric) of which is ; see also Appendix A.
Other Fano complex surface candidates for the bubble will contain more than one exceptional (complex) curve, each isomorphic to [39]. Their Lorentzian preimages, , will contain more than one corresponding exceptional real two-dimensional sub-spacetime, with a mutual intersection pattern characteristic to the Euclidean (and complex) . With a Lorentzian metric on , these sub-spacetimes can serve as specific loci of interest, such as space-like horizons at infinite past/future. A further exploration of such correlations between the Lorentzian metric structure of topologically nontrivial spacetimes and the (almost) complex structure of their auxiliary Euclidean renditions, but beyond our present scope.
As it is, (almost) Fano complex surfaces are , or a blow-up of at points. Their Euler numbers () are, in the given order: 4, or [39,82]. (The projective space, , itself may be regarded as a blowup of , by replacing a point in by the exceptional hyperplane .) By the Todd–Chern–Hirzebruch theorem for Fano surfaces, , so that , and all characteristic classes (and their integrals) are controlled by , i.e., the Euler number. As noted earlier, the defining property of these isolated Fano compact complex surfaces is that their 1st Chern class, represented by the Ricci tensor, is positive (), as is then also their scalar curvature. Exceptionally, the 9-point blowup is only almost Fano, so its Ricci tensor is non-negative but null in some directions. For completeness, we note that , so the signature of these (real) four-dimensional spaces is . For all (almost) Fano surfaces except , the above argument and standard properties of complex projective spaces combine to show [39,82] that they admit a metric that is nowhere negative, and merely becomes null at select exceptional locations, which in such a metric become “points”; the total space of these algebraic surfaces is then diffeomorphic to . In the “ruled (complex) surface,” , the meridians of either may be identified as “time,” which identifies the “Southern” and “Northern” instance of the other as the infinite past and future horizon, respectively. It seems plausible to expect a Lorentzian metric to exist wherein those exceptional loci are at infinite past/future, and whereby the positive curvature of of these surfaces (just as of ) should translate into a positive cosmological constant, for the most part of ; see Appendix A.
Even without computational details about the embedding , the fact that this is (a Lorentzian preimage of) a small resolution smoothing has strong consequences: Considering from “outside,” as a (metrically) isolated as may be, at least locally near its locus within , the whole spacetime must itself admit a Lorentzian metric with a co-laminar class of time coordinates. That is, any particular time-like geodesic, , will have infinitesimally near time-like geodesics, , such that . (This may well become ill-defined at certain special locations of , such as past/future horizons.) That is, the Lorentzian metric of must extend almost everywhere smoothly into the local neighborhood of and then itself. Thereby, the above-implied class of “time-sliced, static” snapshots and associated phase transition nucleation interpretation also extend to the ten-dimensional spacetime , at least in the local neighborhood of .
Finally, let us note that in this (putatively de Sitter) “exceptional sub-spacetime, ,” scenario is Ricci-flat, and so admits a standard, supersymmetry-preserving, spacetime metric. The putatively negative-curvature complement, , may well admit even multiple covariantly constant spinors away from but their restriction to will fail to be covariantly constant within. Now, in the Euclideanized complex rendition, an isolated is metrically null in the “bulk” Kähler metric; it needs an -localized “correction” to be positive everywhere on ; see [82] for a lower-dimensional explicit construction to this end. This isolation then implies that admits a metric in which is null, that is, a point, so that for a typical “bulk”- observer, supersymmetry is broken only at a point—a singularity of the supersymmetry structure11.
Thus, these metrically isolated, codimension-six sub-spacetimes, , are exceptional sets of local small resolution smoothings of the ostensibly most generic rendition of ten-dimensional string vacua; in these “measure-zero,” but generically abundant sub-spacetimes, supersymmetry is broken.
5. Summary, Outlook and Conclusions
In this paper, we have briefly reviewed some recent work on constructing concrete superstring models that do exhibit a sub-spacetime with a phenomenologically acceptable de Sitter geometry and cosmological constant [6,7,8]. Notably, these indicate two separate aspects that render such work more fruitful: (1) a careful analysis of multi-parameter and near-singular configurations, and (2) focusing on exceptional sub-spacetimes within larger-dimensional spacetimes with non-factoring geometry. These two ideas in fact naturally resonate closely with the discretuum of “axilaton” models [10,12,13,14,15] that may be viewed as a non-holomorphic and non-analytic deformation of the stringy cosmic string (’brane) scenario [42,43].
In particular, we have shown herein that this class of models exhibits both of these hallmark characteristics, and can also be adapted so as to model the dynamical scenario of [6,7]. In this variant, the model represents a stringy cosmic string-sourced nucleation in a phase transition, where the candidate observable world, , is in the interfacing boundary.
Inspired by these resonances, we have reexamined the global geometry of the ten-dimensional spacetime in string theory, , following [14,16]. This finds plenty of exceptional sub-spacetimes that map to exceptional sets, , of small resolution desingularizations of the auxiliary Euclidean, Calabi–Yau 5-fold re-rendering of the total spacetime, . Given their positive Ricci curvature, , the simplest of these have a de Sitter geometry and so can serve as candidates for the observed four-dimensional spacetime. Furthermore, the four-dimensional bubble-worlds, are metrically isolated, codimension-six sub-spacetimes, that have no “inside,” and their local neighborhood in has a negative Ricci curvature—on par with in (7) in the AdS-decaying scenario of Section 2.2.
It is striking to note that the above features pertain to the generic Ricci-flat ten-dimensional stringy spacetimes, each of which in turn contains a very large number of such sub-spacetimes. That is, no special requirement or restriction on the total ten-dimensional (super)stringy spacetime were needed for the above conclusions to hold, and only the general characteristics of (super)string spacetimes and their Euclideanized Calabi–Yau counterpart have been presumed.
Author Contributions
The coauthors have contributed equally to all aspects of this research article and share the responsibility equally. All authors have read and agreed to the published version of the manuscript.
Funding
The work of PB is supported in part by the Department of Energy grant DE-SC0020220. The work of DM is supported in part by Department of Energy (under DOE grant number DE-SC0020262) and the Julian Schwinger Foundation.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
We thank Giuseppe Dibitetto and Ivonne Zavala for their kind invitation to contribute to this special issue. PB would like to thank the CERN Theory Group for their hospitality over the past several years. TH is grateful to the Department of Mathematics, University of Maryland, College Park MD, and the Physics Department of the Faculty of Natural Sciences of the University of Novi Sad, Serbia, for the recurring hospitality and resources. DM is grateful to Perimeter Institute for hospitality and support.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. The Effect of Defects
As a toy example, a sphere is of course positively curved and evidently admits no global metric of non-positive curvature. Excising a point (e.g., the North pole) leaves a disc, which then admits all kinds of metrics, pretty much solely depending on (controlled by) the boundary conditions. For example, identifying all the points of the boundary with a single point maps back to the sphere, identifying the disc boundary with, e.g., the North Pole; see the left-hand side of Figure A1. In turn, dividing the boundary of the disk into eight segments, which are then identified in the interleaved fashion depicted in the middle of Figure A1 produces a genus-2 Riemann surface depicted on the right-hand side of Figure A1.
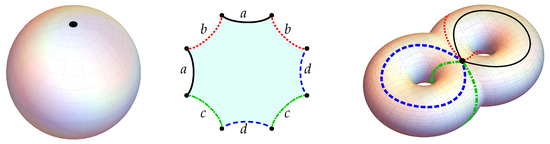
Figure A1.
A disc (middle, suggesting a hyperbolic metric), may be compactified to a sphere (left) by identifying the entire boundary with the “North pole.” Identifying the boundary segments in the indicated interleaved fashion produces the genus-2 Riemann surface (right, a basis of 1-cycles identified with the indicated boundary segments).
Within the differentiable category of smooth metrics, the metric on the three depicted objects need only differ in the infinitesimal neighborhood of the North pole of the sphere: Passing from the sphere (Figure A1, left) to the “double torus” (Figure A1, right) shows that the North Pole of the sphere () has effectively been “blown up”12 into the interleaving network of four cycles of the double torus, which span . That is to say, the entire topological (and curvature) difference between and can be concentrated into the “-neighborhood” of the North pole, replacing it by a 2-handled -disc:

In the Section 4 scenario where the candidate for our own Universe is a bubble-world, , within the Lorentzian preimage of the auxiliary Calabi–Yau 5-fold, , we are experiencing our bubble-world with time passing along a “meridian.” For example, in Figure A1 (left), our bubble-world cosmic time may well be aligned with the meridians, starting at the South pole (identified as the Big Bang) and advancing towards the North Pole (identified as The End). In that case, the topological “handles” confined within an -neighborhood of the North pole could not have been observed by any observer, throughout almost all of the history of such a bubble-world. The same then applies to any topological obstruction to a de Sitter metric. Therefore, it suffices that a candidate for our spacetime, , admit a Lorentzian metric that is indistinguishable from the de Sitter metric within our past light cone.
Furthermore, since in such a scenario the observed matter spectrum correlates with certain specific (co)homology groups valued both in intrinsic () and in extrinsic () structures pertaining to our bubble-world, , at least some of those may well pertain to topological (and (co)homological, etc.) features that are still outside of our past light cone, i.e., they could not have been observed yet. This reasoning implies it possible that, say, we have not observed a 4th generation of Standard Model particles yet, but may observe them sometime in the future, once the requisite topological “handle” in enters our past light cone. Since the requisite (co)homology elements are localized to those “handles,” they will then be the sources of such “new” matter. The “time-sliced, static” snapshots then appear to show a nucleation of a phase transition: with a 3-generation Standard Model vacuum all around, and a 4-generation vacuum nucleating and emanating from that particular “handle.”
Notes
| 1 | In a standard “blowup surgery,” these exceptional sets have long since been familiar in physics as gravitational instantons [37,38], while their higher codimension “small resolution” analogues show up as the so-called worldsheet instanton “-curves” in Calabi–Yau 3-folds [39]. |
| 2 | A candidate for the observable four-dimensional world with its geometry unspecified is denoted , while , and specify Minkowski, de Sitter and anti de Sitter geometries, respectively. |
| 3 | Refs. [52,53] in fact conjecture that all de Sitter vacua with small cosmological constant decay faster than their horizon size; the latter of these two notes the contradiction with the results of Ref. [54]. |
| 4 | There is also a natural connection to the more recent and rather vast cobordism generalization [55]. |
| 5 | The stringy cosmic string-like [59] limit includes a total of supersymmetric 7-branes. |
| 6 | To be precise: for in (4a), each of the two circular boundaries of shrinks to a point as , thus rendering compact. For in (4a), is non-compact and two points must be added to compactify . |
| 7 | We will return to this non-trivial K3-fibration in Section 4. |
| 8 | The product denotes that the warp-factors in the block-diagonal metric vary over . |
| 9 | Being Fano, , implies the scalar curvature invariant to be positive, . |
| 10 | For our present purposes, a foliation means that the total space looks locally at every point as a direct product of local portions of the two factors, X and Y. |
| 11 | Supersymmetry is in string theory largely correlated with complex structure, and as mentioned above, of course admits a complex structure, for which the excised point is an obstruction. |
| 12 | This may be pictured as a two-step process: (1) “open” the point into a circular boundary, then (2) identify segments of the boundary according to the template in Figure A1, middle. |
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Omega and Lambda from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Danielsson, U.H.; Van Riet, T. What if string theory has no de Sitter vacua? Int. J. Mod. Phys. 2018, D27, 1830007. [Google Scholar] [CrossRef]
- Cicoli, M.; De Alwis, S.; Maharana, A.; Muia, F.; Quevedo, F. De Sitter vs Quintessence in String Theory. Fortsch. Phys. 2018, 2018, 1800079. [Google Scholar] [CrossRef]
- Berglund, P.; Hübsch, T.; Minic, D. On de Sitter Spacetime and String Theory, to appear.
- Banerjee, S.; Danielsson, U.; Dibitetto, G.; Giri, S.; Schillo, M. Emergent de Sitter Cosmology from Decaying Anti–de Sitter Space. Phys. Rev. Lett. 2018, 121, 261301. [Google Scholar] [CrossRef]
- Banerjee, S.; Danielsson, U.; Dibitetto, G.; Giri, S.; Schillo, M. De Sitter Cosmology on an expanding bubble. J. High Energy Phys. 2019, 10, 164. [Google Scholar] [CrossRef]
- Bento, B.V.; Chakraborty, D.; Parameswaran, S.L.; Zavala, I. A New de Sitter Solution with a Weakly Warped Deformed Conifold. arXiv 2021, arXiv:2105.03370. [Google Scholar]
- Blåbäck, J.; Danielsson, U.; Dibitetto, G.; Giri, S. Constructing stable de Sitter in M-theory from higher curvature corrections. J. High Energy Phys. 2019, 2019, 1–24. [Google Scholar] [CrossRef]
- Berglund, P.; Hübsch, T.; Minic, D. Exponential Hierarchy From Spacetime Variable String Vacua. J. High Energy Phys. 2000, 9, 15. [Google Scholar] [CrossRef][Green Version]
- Berglund, P.; Hübsch, T.; Minic, D. Probing Naked Singularities in Non-supersymmetric String Vacua. J. High Energy Phys. 2001, 2, 10. [Google Scholar] [CrossRef][Green Version]
- Berglund, P.; Hübsch, T.; Minic, D. Localized Gravity and Large Hierarchy from String Theory? Phys. Lett. 2001, 512, 155–160. [Google Scholar] [CrossRef][Green Version]
- Berglund, P.; Hübsch, T.; Minic, D. De Sitter Spacetimes from Warped Compactifications of IIB String Theory. Phys. Lett. 2002, 534, 147–154. [Google Scholar] [CrossRef]
- Berglund, P.; Hübsch, T.; Minic, D. On Stringy de Sitter Spacetimes. J. High Energy Phys. 2019, 2019, 166. [Google Scholar] [CrossRef]
- Berglund, P.; Hübsch, T.; Minic, D. String Theory, the Dark Sector and the Hierarchy Problem. LHEP 2021, 2021, 186. [Google Scholar] [CrossRef]
- Hübsch, T. A Hitchhiker’s Guide to Superstring Jump Gates and Other Worlds. Nucl. Phys. Proc. Suppl. 1997, 52A, 347–351. [Google Scholar] [CrossRef]
- Dixon, L.J.; Harvey, J.A.; Vafa, C.; Witten, E. Strings on Orbifolds. Nucl. Phys. B 1985, 261, 678–686. [Google Scholar] [CrossRef]
- Dixon, L.J.; Harvey, J.A.; Vafa, C.; Witten, E. Strings on Orbifolds. 2. Nucl. Phys. B 1986, 274, 285–314. [Google Scholar] [CrossRef]
- Green, P.S.; Hübsch, T. Connecting Moduli Spaces of Calabi-Yau Threefolds. Commun. Math. Phys. 1988, 119, 431–441. [Google Scholar] [CrossRef]
- Green, P.S.; Hübsch, T. Possible Phase Transitions Among Calabi-Yau Compactifications. Phys. Rev. Lett. 1988, 61, 1163–1166. [Google Scholar] [CrossRef]
- Candelas, P.; Green, P.S.; Hübsch, T. Rolling Among Calabi-Yau Vacua. Nucl. Phys. B 1990, 330, 49–102. [Google Scholar] [CrossRef]
- Partouche, H.; Pioline, B. Rolling among G(2) vacua. J. High Energy Phys. 2001, 3, 5. [Google Scholar] [CrossRef]
- Aspinwall, P.S.; Greene, B.R.; Morrison, D.R. Calabi–Yau moduli space, mirror manifolds and space-time topology change in string theory. Nucl. Phys. B 1994, 416, 414–480. [Google Scholar] [CrossRef]
- Aspinwall, P.S.; Greene, B.R.; Morrison, D.R. Space-time topology change and stringy geometry. J. Math. Phys. 1994, 35, 5321–5337. [Google Scholar] [CrossRef]
- Strominger, A. Massless black holes and conifolds in string theory. Nucl. Phys. B 1995, 451, 96–108. [Google Scholar] [CrossRef]
- Hubsch, T.; Rahman, A. On the geometry and homology of certain simple stratified varieties. J. Geom. Phys. 2005, 53, 31–48. [Google Scholar] [CrossRef]
- Polchinski, J.; Chaudhuri, S.; Johnson, C.V. Notes on D-branes. arXiv 1996, arXiv:hep-th/9602052. [Google Scholar]
- Sagnotti, A. Open Strings and Their Symmetry Groups; NATO Advanced Summer Institute on Nonperturbative Quantum Field Theory (Cargese Summer Institute); Plenum Press: New York, NY, USA, 1987. [Google Scholar]
- Horava, P. Strings on World Sheet Orbifolds. Nucl. Phys. B 1989, 327, 461–484. [Google Scholar] [CrossRef]
- Bianchi, M.; Sagnotti, A. Twist symmetry and open string Wilson lines. Nucl. Phys. B 1991, 361, 519–538. [Google Scholar] [CrossRef]
- Klebanov, I.R.; Strassler, M.J. Supergravity and a confining gauge theory: Duality cascades and chi SB resolution of naked singularities. J. High Energy Phys. 2000, 8, 52. [Google Scholar] [CrossRef]
- DeWolfe, O.; Giddings, S.B. Scales and hierarchies in warped compactifications and brane worlds. Phys. Rev. D 2003, 67, 066008. [Google Scholar] [CrossRef]
- Douglas, M.R.; Shelton, J.; Torroba, G. Warping and supersymmetry breaking. arXiv 2007, arXiv:0704.4001. [Google Scholar]
- Douglas, M.R. Effective potential and warp factor dynamics. J. High Energy Phys. 2010, 3, 71. [Google Scholar] [CrossRef]
- Bena, I.; Graña, M.; Halmagyi, N. On the Existence of Meta-stable Vacua in Klebanov-Strassler. J. High Energy Phys. 2010, 9, 87. [Google Scholar] [CrossRef]
- Bena, I.; Graña, M. String cosmology and the landscape. Comptes Rendus Phys. 2017, 18, 200–206. [Google Scholar] [CrossRef]
- Eguchi, T.; Hanson, A.J. Selfdual Solutions to Euclidean Gravity. Ann. Phys. 1979, 120, 82. [Google Scholar] [CrossRef]
- Gibbons, G.W.; Pope, C.N. CP2 as a gravitational Instanton. Commun. Math. Phys. 1978, 61, 239–248. [Google Scholar] [CrossRef]
- Hübsch, T. Calabi-Yau Manifolds: A Bestiary for Physicists, 2nd ed.; World Scientific Publishing Co. Inc.: River Edge, NJ, USA, 1994. [Google Scholar]
- Hartshorne, R. Algebraic Geometry; Springer: New York, NY, USA, 1977. [Google Scholar]
- Reid, M. The moduli space of 3-folds with K=0 may nevertheless be irreducible. Math. Ann. 1987, 278, 329–334. [Google Scholar] [CrossRef]
- Greene, B.R.; Shapere, A.D.; Vafa, C.; Yau, S.T. Stringy Cosmic Strings and Noncompact Calabi–Yau Manifolds. Nucl. Phys. B 1990, 337, 1–36. [Google Scholar] [CrossRef]
- Green, P.S.; Hübsch, T. Spacetime Variable String Vacua. Int. J. Mod. Phys. A 1994, 9, 3203–3228. [Google Scholar] [CrossRef]
- Randall, L.; Sundrum, R. A Large mass hierarchy from a small extra dimension. Phys. Rev. Lett. 1999, 83, 3370–3373. [Google Scholar] [CrossRef]
- Randall, L.; Sundrum, R. An Alternative to compactification. Phys. Rev. Lett. 1999, 83, 4690–4693. [Google Scholar] [CrossRef]
- Hawking, S.W.; Hertog, T.; Reall, H.S. Brane new world. Phys. Rev. D 2000, 62, 043501. [Google Scholar] [CrossRef]
- Karch, A.; Randall, L. Locally localized gravity. J. High Energy Phys. 2001, 2001, 8. [Google Scholar] [CrossRef]
- Danielsson, U.H.; Panizo, D.; Tielemans, R.; Riet, T.V. A higher-dimensional view on quantum cosmology. arXiv 2021, arXiv:2105.03253. [Google Scholar]
- Basile, I.; Lanza, S. De Sitter in non-supersymmetric string theories: No-go theorems and brane-worlds. J. High Energy Phys. 2020, 10, 108. [Google Scholar] [CrossRef]
- Coleman, S.R.; De Luccia, F. Gravitational Effects on and of Vacuum Decay. Phys. Rev. D 1980, 21, 3305. [Google Scholar] [CrossRef]
- Banks, T.; Zhang, B. Comment on Coleman-DeLuccia Instantons. arXiv 2021, arXiv:2106.12696. [Google Scholar]
- Ooguri, H.; Vafa, C. Non-supersymmetric AdS and the Swampland. Adv. Theor. Math. Phys. 2017, 21, 1787–1801. [Google Scholar] [CrossRef]
- Freivogel, B.; Kleban, M. Vacua Morghulis. arXiv 2016, arXiv:1610.04564. [Google Scholar]
- Danielsson, U.H.; Dibitetto, G.; Vargas, S.C. Universal isolation in the AdS landscape. Phys. Rev. D 2016, 94, 126002. [Google Scholar] [CrossRef]
- McNamara, J.; Vafa, C. Cobordism Classes and the Swampland. arXiv 2019, arXiv:1909.10355. [Google Scholar]
- Polchinski, J. String Theory. Vol. 1: An Introduction to the Bosonic String; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Friedan, D.H. Nonlinear Models in 2+ϵ Dimensions. Phys. Rev. Lett. 1980, 45, 1057. [Google Scholar] [CrossRef]
- Friedan, D.H. Nonlinear Models in 2+ϵ Dimensions. Ann. Phys. 1985, 163, 318–419. [Google Scholar] [CrossRef]
- Shapere, A.D.; Wilczek, F. (Eds.) Geometric Phases in Physics; Advanced Series in Mathematical Physics, World Sci. Publishing: Singapore, 1989; Volume 5. [Google Scholar]
- Hull, C.; Israel, D.; Sarti, A. Non-geometric Calabi-Yau Backgrounds and K3 automorphisms. J. High Energy Phys. 2017, 11, 84. [Google Scholar] [CrossRef]
- Nemeschansky, D.; Sen, A. Conformal Invariance of Supersymmetric σ Models on Calabi-yau Manifolds. Phys. Lett. B 1986, 178, 365–369. [Google Scholar] [CrossRef]
- Douglas, M.R.; Kachru, S. Flux compactification. Rev. Mod. Phys. 2007, 79, 733–796. [Google Scholar] [CrossRef]
- Grana, M. Flux compactifications in string theory: A Comprehensive review. Phys. Rep. 2006, 423, 91–158. [Google Scholar] [CrossRef]
- Frenkel, I.B.; Garland, H.; Zuckerman, G.J. Semiinfinite Cohomology and String Theory. Proc. Nat. Acad. Sci. USA 1986, 83, 8442. [Google Scholar] [CrossRef]
- Bowick, M.J.; Yang, K.Q. String Equations of Motion from Vanishing Curvature. Int. J. Mod. Phys. 1991, A6, 1319–1334. [Google Scholar] [CrossRef]
- Bowick, M.J.; Lahiri, A. The Ricci Curvature of Diff S1/ SL(2,R). J. Math. Phys. 1988, 29, 1979. [Google Scholar] [CrossRef]
- Bowick, M.J.; Rajeev, S. The Complex Geometry of String Theory and Loop Space. In Johns Hopkins Workshop on Current Problems in Particle Theory; Duan, Y.S., Domókos, G., Kövesi-Domókos, S., Eds.; World Sci. Publishing: Singapore, 1987. [Google Scholar]
- Bowick, M.J.; Rajeev, S.G. Anomalies and Curvature in Complex Geometry. Nucl. Phys. B 1988, 296, 1007–1033. [Google Scholar] [CrossRef]
- Bowick, M.J.; Rajeev, S.G. The Holomorphic Geometry of Closed Bosonic String Theory and DiffS1/S1. Nucl. Phys. B 1987, 293, 348. [Google Scholar] [CrossRef]
- Bowick, M.J.; Rajeev, S.G. String Theory as the Kahler Geometry of Loop Space. Phys. Rev. Lett. 1987, 58, 535. [Google Scholar] [CrossRef]
- Alvarez-Gaume, L.; Gomez, C.; Reina, C. Loop groups, Grassmanians and string theory. Phys. Lett. B 1987, 190, 55. [Google Scholar] [CrossRef]
- Oh, P.; Ramond, P. Curvature of Superdiff S1/S1. Phys. Lett. B 1987, 195, 130–134. [Google Scholar] [CrossRef]
- Harari, D.; Hong, D.K.; Ramond, P.; Rodgers, V.G.J. The Superstring DiffS1/S1 and Holomorphic Geometry. Nucl. Phys. B 1987, 294, 556–572. [Google Scholar] [CrossRef]
- Pilch, K.; Warner, N.P. Holomorphic Structure of Superstring Vacua. Class. Quant. Grav. 1987, 4, 1183. [Google Scholar] [CrossRef]
- Freidel, L.; Leigh, R.G.; Minic, D. Metastring Theory and Modular Space-time. J. High Energy Phys. 2015, 2015, 1–76. [Google Scholar] [CrossRef]
- Freidel, L.; Leigh, R.G.; Minic, D. Intrinsic non-commutativity of closed string theory. J. High Energy Phys. 2017, 2017, 1–24. [Google Scholar] [CrossRef]
- Freidel, L.; Leigh, R.G.; Minic, D. Noncommutativity of closed string zero modes. Phys. Rev. D 2017, 96, 066003. [Google Scholar] [CrossRef]
- Tian, G.; Yau, S.T. Complete Kähler manifolds with zero Ricci curvature. I. J. Am. Math. Soc. 1990, 3, 579–609. [Google Scholar]
- Tian, G.; Yau, S.T. Complete Kähler manifolds with zero Ricci curvature. II. Invent. Math. 1991, 106, 27–60. [Google Scholar] [CrossRef]
- Witten, E. Instability of the Kaluza-Klein Vacuum. Nucl. Phys. B 1982, 195, 481–492. [Google Scholar] [CrossRef]
- Dibitetto, G.; Petri, N.; Schillo, M. Nothing really matters. J. High Energy Phys. 2020, 2020, 1–19. [Google Scholar] [CrossRef]
- Green, P.S.; Hübsch, T. Calabi-Yau Hypersurfaces in Products of Semi-Ample Surfaces. Commun. Math. Phys. 1988, 115, 231–246. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).